Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Математика для самых маленьких. Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим.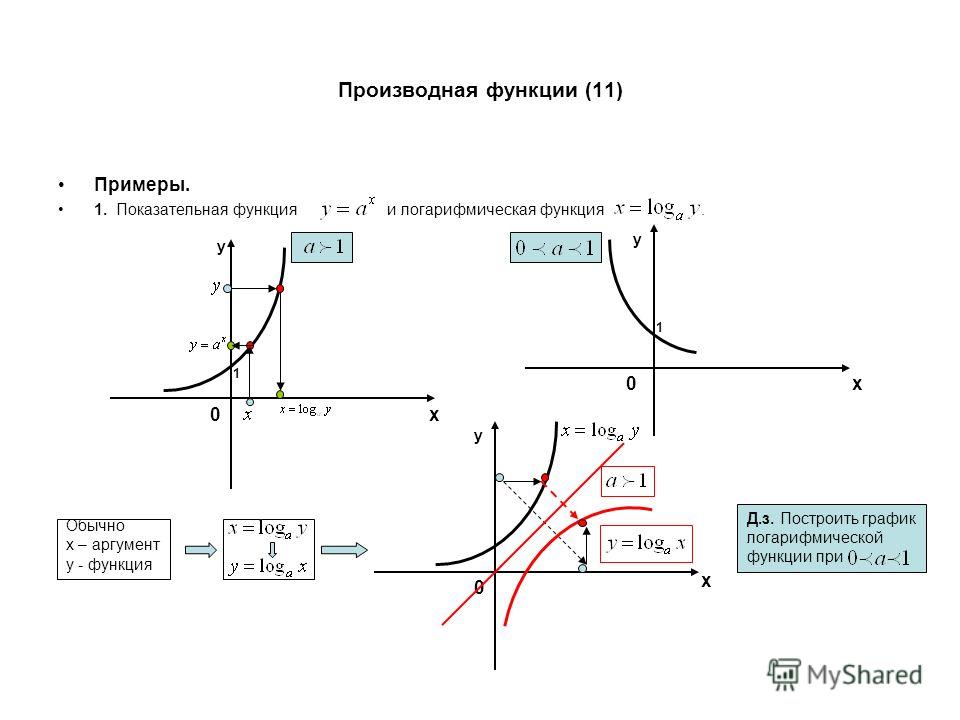 Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Геометрический смысл производной:
Правила дифференцирования:
Необходимое условие экстремума:
Табличные производные. Производная произведения. Производная частного. Производная сложной функции.Функция и производная: что это и чем они отличаются
Основной базой для всех учений, познающих мир, является математика. Точная наука использует формализованный язык и изучает порядок, структуру и отношения на выбранных абстрактных объектах. Не всем обучающимся нравится математика из-за её сложности и запутанности, а, скорее всего, из-за непонимания. Прочные изменения в отношении к математике потребуют увлеченности, сосредоточенности, последовательности, даже упрямства и, главное, практических решений. В изучении важно шаг за шагом разбираться изначально в простом и постепенно переходить к более сложному, не оставляя непонятного и непродуманного.
Существуют много различных разделов математики уже достаточно изученных и появившихся недавно. Далее рассказывается об азах математического анализа – основных начальных понятиях, определениях и правилах исследования простых функций одной переменной, производной и дифференцирования.
У студентов начальных курсов вузов появился афоризм: «Математика становится по-настоящему сложной, когда из неё пропадают цифры». И действительно, к пониманию некоторых определений и законов математической науки приближаются путем решения по правилам на конкретных примерах.
Основные определения
Начнем с терминологии – с простых общих смысловых значений первичных определений:
- Переменная – величина или символ, может принимать любое из ряда значений в
определенной области (вес или рост ребенка)
- Функция – назначение, работа, деятельность, определенное действие над переменной, обозначим f(x) (зависимость веса ребенка от его роста)
- Предел – лимит, граница, край (горизонт – граница обзора)
- Производная – образованная, вторичная, проистекшая от другого, обозначим f’(x) (скорость при движении)
- Дифференциал – разность, различие, разделение.
Функция это просто
Функция – это результат того, что она делает с переменной, что является итогом вычисления. Это взаимосвязь элементов, при которой изменение одного переменного обуславливает изменение в другом. Разделяют f(x) на простые и сложные.
Для отображения зависимостей используются следующие способы: алгебраический, графический, табличный, логический и даже программные.
Определяют числовые зависимости алгебраически с использованием символов переменных, равенств и неравенств (≤ и >), строится уравнение вида:
На рисунке ниже представлены простые графики 3-х различных соотношений. Видно, что в f(x) 3 получается наибольшее значение y при х конкретном, в f(x) 1 — наименьшее.
Функция
Различают следующие элементарные выражения: линейная (прямая), квадратичная (парабола), кубическая, гипербола, показательная, логарифмическая, тригонометрические (приведены в таблице ниже).
Для анализа каждого вида f(x) определяют присущие им свойства (перечислены ниже), для этого используют понятия производной и дифференциала.
Производная функции
Производная – оператор, который для исходной f(x) по законам дифференцирования ставит в соответствие другую функцию, она характеризует изменение первичной f(x) аргумента x в некоторой точке. Для её детального понимания следует разобраться с более сложными определениями предела зависимости и дифференцирования.
Предел – это определение динамическое. Выражение, что x стремится к n, понимают так – х обретает значения, которые близко приближаются к п и разнятся на мизерную величину.
Дифференциал – малое изменение какой-то величины. Приращение назовем дельтой.
Производной для f(x) в точке является предел деления дельты функции к дельте переменной в данной точке, если последняя стремится к 0.
Характеристика скорости изменения зависимости в данной точке, геометрически её можно показать, как значение tg угла наклона альфа касательной к функции.
Производная
Зависимость называется дифференцируемой, если определена f’(x). Нахождение производной называется дифференцированием. Правила вычисления f’(x) и соответствия f’(x) от элементарных f(x) приведены в таблице ниже
Производная функции также функция
Каждая зависимость имеет определенные свойства, зная и исследуя их можно анализировать характер состояния и изменения f(x).
Основные свойства:
- Данные промежутков определений и промежутков значений.
- Нулевые значения f(x)
- Функция возрастает или убывает в некоторых промежутках.
- Точки MAX и MIN функции, есть ли перегиб.
- Четная или нечетная f(x)
- Ограниченная и неограниченная функция.
- Есть ли асимптоты.
- Периодичность f(x).
Функции и производные
При установлении характеристик зависимости с помощью производной используют взаимосвязи свойств f’(x) со свойствами f(x) и наоборот. На графике функции легко определяются характеристики f’(x), и наоборот по графику f’(x) понимаются характеристики первичной f(x).
Фиксируя сущность каждой особенности функции, исследуют и устанавливают цепочку связей. Для определения асимптот в графиках используют понятие пределов.
Ниже приведены некоторые характеристики и зависимости f’(x) от f(x):
- При возрастании f(x) на промежутке, f’(x) положительна.
- В случае убывания f(x) на промежутке, f’(x) отрицательна.
- При наличии f(x) точки MAX, в ней f’(x)=0 может не определена, и tg угла касательной меняет знак с + на -.
- При наличии f(x) точки MIN, в ней f’(x)=0 может не определена, и tg угла касательной меняет знак с – на +.
- При перегибе в Е графика f(x) значение f’(x) не поменяло в точке знак, f’(x)=0.
Перегиб в точке Е графика функции
Для исследования f(x) составляют схему, где каждый шаг строится по определенному алгоритму вычислений и анализа взаимосвязей составляющих элементов.
Различия функции и производной
Правила сложения и вычитания f(x) одинаковы с правилами этих действий при дифференцировании.
Но правила нахождения f’(x) при действиях умножения и деления функций другие (как в таблице).
Функция первична, а производная – произведенная вторичная математическая операция, у них в большинстве случаев разные характеристики.
Точку перегиба непрерывной зависимости находят по её второй производной, должен меняться её знак в районе точки х0.
Есть такие типы функций не имеющих f’(x) в точке x0 (разрывные). В выражении ln(|x|-1) не определена в точке x0=1 производная.
Есть выражения «по модулю» аналогичные y=|x|, которые имеет излом в х0.
Для подобных зависимостей применяются лишь частично (на промежутках области определения) способы исследования их свойств с помощью производных и не всегда возможен переход от свойств f’(x) к свойствам первичной.
Нигде не обойтись без исключений из правил, и даже в математике. С целью разбора и закрепления изложенного материала обязательно следует порешать примеры, напрактиковаться, набраться опыта с пределами, дифференциалами и производными и смело переходить к интегралам.
НаукаКомментировать
Как определить значение производной по графику. Производная функции. Геометрический смысл производной. Вычисление точек максимума и минимума
В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x 0 ,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x 0 , и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x 1 ; y 1) и B (x 2 ; y 2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x 2 − x 1 и приращение функции Δy = y 2 − y 1 .
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается.
Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x 0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≥ f(x).
- Точка x 0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
- Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5.
Также отметим знаки:
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него.
А именно, точки x = −3,5 и x = 2. Получаем:
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется возрастающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется убывающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Т.е. большему значению аргумента соответствует меньшее значение функции.
Другими словами, чем больше значение аргумента, тем больше значение функции.Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке , достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
- Для того чтобы непрерывная функция f(x) убывала на отрезке , достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Задача.
На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l 2 = 5.
Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.
В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна . Мы не будем сейчас стремиться к математической строгости изложения.
Самое главное — понять смысл.
Запомним определение:
Производная — это скорость изменения функции.
На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?
Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.
Вот другой пример.
Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:
На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная , — разная. Что касается Матвея — у его дохода производная вообще отрицательна.
Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?
На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х.
Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.
Производная функции обозначается .
Покажем, как найти с помощью графика.
Нарисован график некоторой функции . Возьмем на нем точку с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной .
Производная функции в точке равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.
Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .
Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.
Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему.
Из треугольника :
Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике под номером .
Есть и другое важное соотношение. Вспомним, что прямая задается уравнением
Величина в этом уравнении называется угловым коэффициентом прямой . Она равна тангенсу угла наклона прямой к оси .
.
Мы получаем, что
Запомним эту формулу. Она выражает геометрический смысл производной.
Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
Другими словами, производная равна тангенсу угла наклона касательной.
Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.
Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.
В точке функция возрастает. Касательная к графику, проведенная в точке , образует острый угол с положительным направлением оси . Значит, в точке производная положительна.
В точке наша функция убывает. Касательная в этой точке образует тупой угол с положительным направлением оси . Поскольку тангенс тупого угла отрицателен, в точке производная отрицательна.
Вот что получается:
Если функция возрастает, ее производная положительна.
Если убывает, ее производная отрицательна.
А что же будет в точках максимума и минимума? Мы видим, что в точках (точка максимума) и (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.
Точка — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке с «плюса» на «минус».
В точке — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».
Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.
Если производная положительна, то функция возрастает.
Если производная отрицательная, то функция убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
Запишем эти выводы в виде таблицы:
| возрастает | точка максимума | убывает | точка минимума | возрастает | |
| + | 0 | — | 0 | + |
Сделаем два небольших уточнения. Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.
Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая :
В точке касательная к графику горизонтальна, и производная равна нулю.
Однако до точки функция возрастала — и после точки продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.
Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.
А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется
Сергей Никифоров
Если производная функции знакопостоянна на интервале, а сама функция непрерывна на его границах, то граничные точки присоединяются как к промежуткам возрастания, так и к промежуткам убывания, что полностью соответствует определению возрастающих и убывающих функций.
Фарит Ямаев 26.10.2016 18:50
Здравствуйте. Как же (на каком основании) можно утверждать, что в точке, где производная равна нулю, функция возрастает. Приведите доводы. Иначе, это просто чей-то каприз. По какой теореме? А также доказательство.
Спасибо.
Служба поддержки
Значение производной в точке не имеет прямого отношения к возрастанию функции на промежутке. Рассмотрите, например, функции — все они возрастают на отрезке
Владлен Писарев 02.11.2016 22:21
Если функция возрастает на интервале (а;b) и определена и непрерывна в точках а и b, то она возрастает на отрезке . Т.е. точка x=2 входит в данный промежуток.
Хотя, как правило возрастание и убывание рассматривается не на отрезке, а на интервале.
Но в самой точке x=2, функция имеет локальный минимум. И как объяснять детям, что когда они ищут точки возрастания (убывания), то точки локального экстремума не считаем, а в промежутки возрастания (убывания) — входят.
Учитывая, что первая часть ЕГЭ для «средней группы детского сада», то наверное такие нюансы- перебор.
Отдельно, большое спасибо за «Решу ЕГЭ» всем сотрудникам- отличное пособие.
Сергей Никифоров
Простое объяснение можно получить, если отталкиваться от определения возрастающей/убывающей функции.
Напомню, что звучит оно так: функция называется возрастающей/убывающей на промежутке, если большему аргументу функции соответствует большее/меньшее значение функции. Такое определение никак не использует понятие производной, поэтому вопросов о точках, где производная обращается в ноль возникнуть не может.
Ирина Ишмакова 20.11.2017 11:46
Добрый день. Здесь в комментариях я вижу убеждения, что границы включать нужно. Допустим, я с этим соглашусь. Но посмотрите, пожалуйста, ваше решение к задаче 7089. Там при указании промежутков возрастания границы не включаются. И это влияет на ответ. Т.е. решения заданий 6429 и 7089 противоречат друг другу. Проясните, пожалуйста, эту ситуацию.
Александр Иванов
В заданиях 6429 и 7089 совершенно разные вопросы.
В одном про промежутки возрастания, а в другом про промежутки с положительной производной.
Противоречия нет.
Экстремумы входят в промежутки возрастания и убывания, но точки, в которых производная равна нулю, не входят в промежутки, на которых производная положительна.
A Z 28.01.2019 19:09
Коллеги, есть понятие возрастания в точке
(см. Фихтенгольц например)
и ваше понимание возрастания в точке x=2 противочет классическому определению.
Возрастание и убывание это процесс и хотелось бы придерживаться этого принципа.
В любом интервале, который содержит точку x=2, функция не является возрастающей. Поэтому включение данный точки x=2 процесс особый.
Обычно, чтобы избежать путаницы о включении концов интервалов говорят отдельно.
Александр Иванов
Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.
В точке х=2 функция дифференцируема, а на интервале (2; 6) производная положительна, значит, на промежутке её значения строго положительны, значит функция на этом участке только возрастает, поэтому значение функции в левом конце x = −3 меньше, чем её значение в правом конце x = −2.
Ответ: φ 2 (−3) φ 2 (−2)
2) Пользуясь графиком первообразной Φ 2 (x ) (в нашем случае это синий график), определите какое из 2-ух значений функции больше φ 2 (−1) или φ 2 (4)?
По графику первообразной видно, что точка x = −1 находится на участке возрастания, следовательно значение соответсвующей производной положительно. Точка x = 4 находится на участке убывания и значение соответствующей производной отрицательно. Поскольку положительное значение больше отрицательного, делаем вывод — значение неизвестной функции, которая как раз и является производной, в точке 4 меньше, чем в точке −1.
Ответ: φ 2 (−1) > φ 2 (4)
Подобных вопросов по отсутствующему графику можно задать много, что обуславливает большое разноообразие задач с кратким ответом, построенных по такой же схеме. Попробуйте решить некоторые из них.
Задачи на определение характеристик производной по графику функции.
Рисунок 1.
Рисунок 2.
Задача 1
y = f (x ), определенной на интервале (−10,5;19). Определите количество целых точек, в которых производная функции положительна.
Производная функции положительна на тех участках, где функция возрастает. По рисунку видно, что это промежутки (−10,5;−7,6), (−1;8,2) и (15,7;19). Перечислим целые точки внутри этих интервалов: «−10″,»−9», «−8″,»0», «1»,»2″, «3»,»4″, «5»,»6″, «7»,»8″, «16»,»17″, «18». Всего 15 точек.
Ответ: 15
Замечания.
1. Когда в задачах о графиках функций требуют назвать «точки», как правило, имеют в виду только значения аргумента x , которые являются абсциссами соответствующих точек, расположенных на графике. Ординаты этих точек — значения функции, они являются зависимыми и могут быть легко вычислены при необходимости.
2. При перечислении точек мы не учитывали края интервалов, так как функция в этих точках не возрастает и не убывает, а «разворачивается».
Производная в таких точках не положительна и не отрицательна, она равна нулю, поэтому они называются стационарными точками. Кроме того, мы не рассматриваем здесь границы области определения, потому что в условии сказано, что это интервал.
Задача 2
На рисунке 1 изображен график функции y = f (x ), определенной на интервале (−10,5;19). Определите количество целых точек, в которых производная функции f » (x ) отрицательна.
Производная функции отрицательна на тех участках, где функция убывает. По рисунку видно, что это промежутки (−7,6;−1) и (8,2;15,7). Целые точки внутри этих интервалов: «−7″,»−6», «−5″,»−4», «−3″,»−2», «9»,»10″, «11»,»12″, «13»,»14″, «15». Всего 13 точек.
Ответ: 13
См. замечания к предыдущей задаче.
Для решения следующих задач нужно вспомнить еще одно определение.
Точки максимума и минимума функции объединяются общим названием — точки экстремума .
В этих точках производная функции либо равна нулю, либо не существует (необходимое условие экстремума ).
Однако необходимое условие — это признак, но не гарантия существования экстремума функции. Достаточным условием экстремума является смена знака производной: если производная в точке меняет знак с «+» на «−», то это точка максимума функции; если производная в точке меняет знак с «−» на «+» , то это точка минимума функции; если в точке производная функции равна нулю, либо не существует, но знак производной при переходе через эту точку не меняется на противоположный, то указанная точка не является точкой экстремума функции. Это может быть точка перегиба, точка разрыва или точка излома графика функции.
Задача 3
На рисунке 1 изображен график функции y = f (x ), определенной на интервале (−10,5;19). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
Вспомним, что уравнение прямой имеет вид y = kx + b , где k — коэффициент наклона этой прямой к оси Ox . В нашем случае k = 0, т.е. прямая y = 6 не наклонена, а параллельна оси Ox . Значит искомые касательные также должны быть параллельны оси Ox и также должны иметь коэффициент наклона 0. Таким свойством касательные обладают в точках экстремумов функций. Поэтому для ответа на вопрос нужно просто посчитать все точки экстремумов на графике. Здесь их 4 — две точки максимума и две точки минимума.
Ответ: 4
Задача 4
Функции y = f (x ), определенной на интервале (−11;23). Найдите сумму точек экстремума функции на отрезке .
На указанном отрезке мы видим 2 точки экстремума. Максимум функции достигается в точке x 1 = 4, минимум в точке x 2 = 8.
x 1 + x 2 = 4 + 8 = 12.
Ответ: 12
Задача 5
На рисунке 1 изображен график функции y = f (x ), определенной на интервале (−10,5;19). Найдите количество точек, в которых производная функции f » (x ) равна 0.
Производная функции равна нулю в точках экстремума, которых на графике видно 4:
2 точки максимума и 2 точки минимума.
Ответ: 4
Задачи на определение характеристик функции по графику её производной.
Рисунок 1.
Рисунок 2.
Задача 6
На рисунке 2 изображен график f » (x ) — производной функции f (x ), определенной на интервале (−11;23). В какой точке отрезка [−6;2] функция f (x ) принимает наибольшее значение.
На указанном отрезке производная нигде не была положительной, следовательно функция не возрастала. Она убывала или проходила через стационарные точки. Таким образом, наибольшего значения функция достигала на левой границе отрезка: x = −6.
Ответ: −6
Замечание: По графику производной видно, что на отрезке [−6;2] она равна нулю трижды: в точках x = −6, x = −2, x = 2. Но в точке x = −2 она не меняла знака, значит в этой точке не могло быть экстремума функции. Скорее всего там была точка перегиба графика исходной функции.
Задача 7
На рисунке 2 изображен график f » (x ) — производной функции f (x ), определенной на интервале (−11;23). В какой точке отрезка функция принимает наименьшее значение.
На отрезке производная строго положительна, следовательно функция на этом участке только возрастала. Таким образом, наименьшего значения функция достигала на левой границе отрезка: x = 3.
Ответ: 3
Задача 8
На рисунке 2 изображен график f » (x ) — производной функции f (x ), определенной на интервале (−11;23). Найдите количество точек максимума функции f (x ), принадлежащих отрезку [−5;10].
Согласно необходимому условию экстремума максимум функции может быть в точках, где её производная равна нулю. На заданном отрезке это точки: x = −2, x = 2, x = 6, x = 10. Но согласно достаточному условию он точно будет только в тех из них, где знак производной меняется с «+» на «−». На графике производной мы видим, что из перечисленных точек такой является только точка x = 6.
Ответ: 1
Задача 9
На рисунке 2 изображен график f » (x ) — производной функции f (x ), определенной на интервале (−11;23). Найдите количество точек экстремума функции f (x ), принадлежащих отрезку .
Экстремумы функции могут быть в тех точках, где её производная равна 0. На заданном отрезке графика производной мы видим 5 таких точек: x = 2, x = 6, x = 10, x = 14, x = 18. Но в точке x = 14 производная не поменяла знак, следовательно её надо исключить из рассмотрения. Таким образом, остаются 4 точки.
Ответ: 4
Задача 10
На рисунке 1 изображен график f » (x ) — производной функции f (x ), определенной на интервале (−10,5;19). Найдите промежутки возрастания функции f (x ). В ответе укажите длину наибольшего из них.
Промежутки возрастания функции совпадают с промежутками положительности производной. На графике мы видим их три — (−9;−7), (4;12), (18;19). Самый длинный из них второй. Его длина l = 12 − 4 = 8.
Ответ: 8
Задача 11
На рисунке 2 изображен график f » (x ) — производной функции f (x ), определенной на интервале (−11;23). Найдите количество точек, в которых касательная к графику функции f (x ) параллельна прямой y = −2x − 11
или совпадает с ней.
Угловой коэффициент (он же тангенс угла наклона) заданной прямой k = −2. Нас интересуют параллельные или совпадающие касательные, т.е. прямые с таким же наклоном. Исходя из геометрического смысла производной — угловой коэффициент касательной в рассматриваемой точке графика функции, пересчитываем точки, в которых производная равна −2. На рисунке 2 таких точек 9. Их удобно считать по пересечениям графика и линии координатной сетки, проходящей через значение −2 на оси Oy .
Ответ: 9
Как видите, по одному и тому же графику можно задать самые разнообразные вопросы о поведении функции и её производной. Также один тот же вопрос можно отнести к графикам разных функций. Будьте внимательны при решении этой задачи на экзамене, и она покажется Вам очень легкой. Другие виды задач этого задания — на геометрический смысл первообразной — будут рассмотрены в другом разделе.
Репетитор по математике — Производные — Теория
Репетитор по математике — Производные — Теория — Производная Здесь мы сначала вводим производную в точке. Затем мы смотрим на
производная как функция и показать некоторые
основные свойства. В конце смотрим
односторонние производные.
Мы естественным образом приходим к понятию производной, когда спрашиваем следующий вопрос: рассмотреть вопрос ( a , f ( a )) на график функции f . Можем ли мы провести касательную к этому графику в точке заданная точка?
Для начала рассмотрим хороший случай, функцию, которая выглядит гладкой. и существует в некоторой окрестности данной точки. Интуиция подсказывает, что там должна быть касательная.
Чтобы найти уравнение этой касательной, нам нужны две части данных. Нам дали одну точку, для второй части мы будем использовать наклон линия. Как мы его находим? Нам нужен какой-то подход, который позволил бы нам использовать расчеты (нам нужен точный ответ, поэтому построение графика и делать предположения недопустимо). Мы попробуем следующее.
Зафиксируем некоторое число х , близкое (но не равное) к , и рассмотрим
линия, проходящая через точки
( a , f ( a )) и
( x , f ( x )).
Мы можем легко вычислить наклон этой линии, используя очерченный треугольник, как
Убедите себя, что та же формула дает наклон, если x равно слева от а . Конечно, наклон, который мы получили, не совсем такой же, как наклон касательной. Однако, если x действительно действительно близко к a , тогда у нас действительно хорошее приближение. Более того, интуитивно, если мы переместим x «до конца» в a , то соответствующие наклоны должны в конечном итоге дать нам наклон касательной линия.
Но когда мы говорим о перемещении x в на , мы на самом деле говорим о предел. Теперь мы готов к определению.
Определение.
Пусть f — функция, определенная в некоторой окрестности точки и . Мы определяем производную от f at a по формулев предположении, что предел сходится.
Если она сходится, мы говорим, что функция дифференцируема в и .
Приведенное выше рассуждение можно выразить следующим образом:
Факт.
Пусть f — функция, определенная в некоторой окрестности точки и . Если он дифференцируем в точке a , то существует тангенс линии на графике f at a и ее наклон равен f ′′( a ).
Пример: Попробуем найти касательную к графику f ( x ) = в a = 1,
Чтобы увидеть, существует ли касательная, мы пытаемся вычислить производную в точке 1.
Предел сходится, поэтому производная равна 1, и, следовательно, мы также есть касательная к графику корня в точке 1. Он имеет наклон 1/2 и проходит через точку (1,1), поэтому его уравнение
( y — 1) = (1/2)⋅( x — 1),
который мы можем написать, например, так: 2 y = x + 1,
Производные — это гораздо больше, чем просто касательные линии, на самом деле все это
глава посвящена тому, что можно сделать с производными, поэтому мы
оставьте другие интересные примеры для следующих разделов. Здесь мы посмотрим
ближе к производной как понятию и задать несколько основных вопросов.
Во-первых, существует альтернативная формула для производной, более удобно в некоторых расчетах.
Эквивалентность двух определений очевидна, мы просто переименуем картинка выше; формально один предел может быть заменен другим с помощью замена x = a + ч .
Во-вторых, существование производной является более сильным понятием, чем понятие непрерывность:
Теорема.
Если функция в какой-то точке дифференцируема, то она должна быть также непрерывный там.
Однако обратное неверно, не всякая непрерывная функция дифференцируемый.
Пример: Рассмотрим функцию f ( x ) = | х | (абсолютное значение) при a = 0. Предел, который может дать производную, равен
Предела не существует, поэтому абсолютное значение не дифференцируемо
в 0. Когда мы смотрим на картинку, кажется, что это имеет смысл, так как нет
очевидный кандидат на касательную в начале координат.
В разделе о преемственность в Функции — Теория — Реальные функции мы заметили, что наличие функции непрерывный в одной конкретной точке не обязательно делает его «хорошим». То же самое верно и для дифференцируемости. В функция Дирихле в Функции — Теория — Элементарные функции есть странная функция, которая дифференцируема в 0, но она нигде не гладкая, даже не имеет любая непрерывная часть его графика. Чтобы действительно получить что-то хорошее из производной, мы должны смотреть на дифференцируемость на интервалах, которая следующая часть.
Производная как функция
Определение.
Рассмотрим функцию f и подмножество G ее области определения. Мы говорим, что f есть дифференцируемое на G , если оно дифференцируемый в каждой точке G .
Напомним, что для того, чтобы в какой-то момент иметь производную, нам нужно f для существуют в некоторой окрестности. Таким образом, мы обычно рассматриваем дифференцируемость на открытые наборы.
Рассмотрим функцию f , дифференцируемую на некотором открытом множестве G . Тогда для каждой точки a из G у нас есть производная ж ′′( а ), что является некоторым числом. Таким образом, мы фактически получаем предписание, которое присваивает номера всем точкам G , другими словами, получаем функцию.
Определение.
Пусть функция f дифференцируема в каждой точке некоторого открытого множества Г . Определим функцию , производную от f по G как функция f ′, заданная выражением и ↦ f ′( a ) для и из G .
Пример: Рассмотрим функцию f ( x ) = . Самый большой
открытое множество, на котором оно определено,
(0,∞). Так же, как
выше можно показать, что для a > 0,
Таким образом, мы получаем новую функцию на множестве (0,∞). Так как это принято использовать x для переменной, мы можем написать то, что мы только что нашли как
Таким образом, мы можем понимать процесс дифференциации как процедуру, которая изменяет функции на другие функции; эта процедура удовлетворяет некоторым удобным правила, которые будут рассмотрены в разделе Производная и операции. Они позволит нам найти производные алгебраически (то есть с помощью алгоритма который использует базовый словарный запас и некоторые правила грамматики), что намного проще чем оценка пределов. Мы обращаемся к этому разделу для получения дополнительной информации.
Мы отметили, что дифференцируемость в одной конкретной точке не обязательно должна
функция «хорошо». Однако теперь у нас есть дифференцируемость на множестве, т. е.
более мощное свойство. Напомним, что функция, являющаяся непрерывной на
интервал означает, что график должен быть здесь непрерывной кривой; Однако,
на нем все еще могут быть «углы» или острые изгибы. Но если эта функция
также дифференцируема на этом интервале, то ее график должен быть «гладким»,
без острых углов. Тем самым мы также предполагаем (снова), что существование
производной сильнее, чем простая непрерывность. Соответствующее местное
Теорему выше можно теперь переформулировать в глобальном масштабе.
Теорема.
Если функция дифференцируема на некотором открытом множестве, то она также должна быть непрерывный там.
Опять же, обратное неверно, не всякая непрерывная функция дифференцируемый.
Обратите внимание, что непрерывность не может быть расширена до конечных точек. Если у нас есть
функция, дифференцируемая на отрезке
( a , b ), то
мы ничего не можем утверждать о непрерывности (односторонней) на или б . Ведь заметим, что если мы изменим значение этой функции в точке a (или при b ), то это не влияет на его дифференцируемость
на ( а , б ), ср.
Теорема о среднем значении в
Теория — Теорема о среднем значении.
Прежде чем двигаться дальше, сделаем замечание относительно области определения производной функция. Так как для получения производной необходимо иметь исходную функцию, очевидно, домен f ′ должен быть подмножеством домена ф . Таким образом, понятие домена также зависит от настройки. За Например, функция 1/ x имеет набор всех действительных чисел, кроме 0 в качестве своего домена. Однако мы также увидим, что 1/ x является производной из ln( x ), который допускает только положительные числа. Поэтому область 1/ x в ситуации, когда мы используем его как [ln( x )]′ просто (0,∞).
В Функции — Теория — Реальные функции —
Преемственность мы
представил свойство промежуточной стоимости. Имеем следующий факт.
Теорема.
Если функция дифференцируема на некотором открытом интервале, то ее у дериватива есть IVP.
В этом разделе мы установили, что непрерывные функции имеют IVP на интервалах, теперь у нас есть другое семейство функций, которые также имеют его. Обратите внимание, что эти два типа не одинаковы. Хотя это может показаться странным, это может случиться что когда мы дифференцируем функцию, то ее производная существует, но она не является непрерывным, см., например, грех(1/ х ) в Функции — Теория — Элементарные функции.
Односторонние и неправильные производные
В примере с абсолютным значением выше мы увидели одну вещь, которая может пойти не так. с производной, а именно, когда предела вообще не существует. Что другие вещи, которые могут произойти? Интересен случай, когда предел есть, но это неправильно.Определение.
Пусть f — функция, определенная в некоторой окрестности точки и .существует и является неправильным.
В чем смысл такой производной? Геометрически касательная к график в этой точке вертикальный. Производная бесконечность означает, что функция растет, производная минус бесконечность означает, что функция идет вниз.
Пример: Рассмотрим функцию f ( x ) = x 1/3 (кубический корень) от до = 0. Производная равна
Итак, что бы ни случилось с пределом в производной, теперь мы знаем, что это такое.
означает. Что еще может пойти не так с производной? Самое первое предположение,
что f существует в некоторой окрестности a . Есть очень много
различные способы, которыми это предположение может пойти не так, слишком много, чтобы сделать
система его. Однако есть один случай, который настолько полезен, что заслуживает
собственное определение. А именно есть смысл попробовать «одностороннюю касательную»
на конечных точках доменов.
Например, выше мы исследовали производную от квадратный корень из (0,∞), но домен также включает 0. Если бы мы знали касательную в точке 0 справа, мы бы знали, как правильно построить график, то есть в каком направлении мы должно начинаться при переходе с 0.
Определение.
Пусть f — функция, определенная в некоторой правой окрестности точки и . Определим производную справа от ф в и пов предположении, что предел сходится.
Пусть f — функция, определенная в некоторой левой окрестности точки и . Определим производную слева от f при и по
в предположении, что предел сходится.
Пример: В примере с абсолютным значением выше мы фактически рассчитали, что f + (0) = 1 и f  ’ — (0) = −1. Это не должно быть на самом деле
удивительно, учитывая график абсолютного значения.
Односторонняя производная обладает теми же свойствами, что и обычная производная, все теоремы, использующие производную, также будут работать для односторонней производной, просто выводы должны быть приспособлены к односторонним ситуациям. Например:
Теорема.
Если функция в какой-то точке дифференцируема справа, то она также должно быть непрерывным справа.
Если функция в какой-то точке дифференцируема слева, то она также должен быть непрерывным слева.
Опять же, обратное неверно.
Как и следовало ожидать, можно восстановить понятие «двустороннего» из односторонние.
Теорема.
Функция f дифференцируема в некоторой точке a тогда и только тогда если он имеет как производную справа, так и производную слева в точке этой точке, и они равны. Тогда также f ′( a ) = f  ’ + ( a ).
Или же f ′( a ) = f  ’ — ( a ), что бы мы ни предпочли, они одинаковы в этой ситуации.
Обычно мы предпочитаем находить односторонние производные, используя пределы производных а не по определению, см. Производная и предел в теории — МВТ.
Мы также можем определить односторонние несобственные производные. Вместо того, чтобы давать формальное определение, которое теперь и так ясно, мы предпочитаем показать на примере.
Пример:
Это показывает, что для того, чтобы нарисовать график функции квадратного корня правильно, мы должны начать вверх с начала в 0.
Некоторые интерпретации производной,
обозначение Лейбница
Назад к теории — производная
производных рациональных функций | Brilliant Math & Science Wiki
Производную рациональной функции можно найти с помощью правила отношения:
92}}. h′(x)=(g(x))2g(x)⋅f′(x)−f(x)⋅g′(x).Мы начнем с основного определения производной, которая равна
.dh(x)dx=limΔx→0h(x+Δx)−h(x)Δx.\displaystyle \dfrac {dh(x)}{dx} =\lim _{\Delta x\rightarrow 0} }{ \frac { h(x+\Delta x)-h(x) }{ \Delta x } }. dxdh(x)=Δx→0limΔxh(x+Δx)−h(x).
Так как мы имеем f(x)g(x)=h(x) \frac{f(x)}{g(x)} = h(x) g(x)f(x)=h(x) , мы можем переписать его как
dh(x)dx=limΔx→0f(x+Δx)g(x+Δx)−f(x)g(x)Δx. \displaystyle \dfrac { dh(x)} }{dx} =\lim _{ \Delta x\rightarrow 0 }{ \dfrac { \frac { f(x+\Delta x)} }{g(x+\Delta x)} — \ frac { f (x) }{ g (x) } }{ \ Delta x } }. dxdh(x)=Δx→0limΔxg(x+Δx)f(x+Δx)−g(x)f(x).
Упрощая это, мы имеем
dh(x)dx=limΔx→0f(x+Δx)g(x)−f(x)g(x+Δx)Δxg(x)g(x+Δx)=limΔx→01g(x )g(x+Δx)limΔx→0f(x+Δx)g(x)−f(x)g(x+Δx)Δx=1(g(x))2limΔx→0f(x+Δx )g(x)−f(x)g(x+Δx)Δx.\begin{выровнено} \ гидроразрыв { dh (x) }{ dx } &=\lim _{ \Delta x\rightarrow 0 }{ \frac { f(x+\Delta x)g(x)-f(x)g(x+\Delta x)}{\Delta xg(x)g( х+\Дельта х) } } \\\\ &= \lim _{ \Delta x\rightarrow 0 }{ \frac { 1 }{g(x)g(x+\Delta x) } } \lim _{ \Delta x\rightarrow 0 }{ \frac { f( x+\Delta x)g(x)-f(x)g(x+\Delta x) }{ \Delta x } } \\\\ &=\frac { 1 }{\big(g(x)\big)^2} \lim _{ \Delta x\rightarrow 0 }{ \frac { f(x+\Delta x)g(x)-f( х)г(х+\Дельта х) }{\Дельта х } }.
Выполнение дифференцирования для рационального термина довольно сложно и запутанно, когда выражения очень сложны. В таких случаях можно принять числитель за одно выражение и знаменатель за одно выражение и найти их отдельные производные. Теперь напишите объединенную производную дроби, используя приведенную выше формулу, и подставьте ее напрямую, чтобы не было путаницы и уменьшились шансы сделать ошибку. Следующие несколько примеров иллюстрируют, как это сделать:
Если y=a−xa+x (x≠−a),y = \frac{a — x}{a + x}\ (x \neq -a),y=a+xa−x (x =−a), затем найдите dydx\frac{dy}{dx}dxdy.
Напишите u(x)=a−x ⟹ u′(x)=−1u(x) = a — x \ подразумевает u'(x) = -1u(x)=a−x⟹u′(x) =−1 и v(x)=a+x ⟹ v′(x)=1v(x) = a + x \ подразумевает v'(x) = 1v(x)=a+x⟹v′(x)= 1, так что y=u(x)v(x):y = \frac{u(x)}{v(x)}:y=v(x)u(x):
dydx=v(x)u′(x)−v′(x)u(x)(v(x))2=(a+x)(−1)−(a−x)(1)(a +x)2=−2aa2+2ax+x2.
Если y=ax+bcx+d (∣c∣+∣d∣≠0),y = \frac{ax + b}{cx + d}\ \big(|c| + |d| \neq 0\big ),y=cx+dax+b (∣c∣+∣d∣=0), затем найдите dydx\frac{dy}{dx}dxdy.
Напишите u(x)=ax+b ⟹ u′(x)=au(x) = ax + b \ подразумевает u'(x) = au(x)=ax+b⟹u′(x)=a и v(x)=cx+d ⟹ v′(x)=cv(x) = cx + d \ подразумевает v'(x) = cv(x)=cx+d⟹v′(x)=c, так что y=u(x)v(x):y = \frac{u(x)}{v(x)}:y=v(x)u(x): 92} .\ _\square \end{выровнено}dxdy=dxd(v(x)u(x))=(v(x))2v(x)u′(x)−v′(x )u(x)=(cx+d)2(cx+d)(a)−(c)(ax+b)=(cx+d)2ad−bc. □
Если y=1−xx1+xx (x>0),y = \frac{1 — x\sqrt{x}}{1 + x\sqrt{x}}\ (x > 0),y=1+xx 1−xx(x>0), затем найдите dydx\frac{dy}{dx}dxdy.
Напишите u(x)=1−xx ⟹ u′(x)=0−x−x2x=−3x2u(x) = 1 — x\sqrt{x} \ подразумевает u'(x) = 0 — \sqrt {x} — \frac{x}{2\sqrt{x}} = — \frac{3\sqrt{x}}{2}u(x)=1−xx⟹u′(x)=0− x−2xx=−23x и v(x)=1+xx ⟹ v′(x)=0+x+x2x=3×2.
Функционалы и функциональные производные — Мэтью Н. Бернштейн
Вариационное исчисление — это область математики, занимающаяся оптимизацией функций от функций, называемых функционалами. Эта тема не преподавалась мне в моем образовании в области информатики, но она лежит в основе ряда важных концепций и алгоритмов в науках о данных, таких как повышение градиента и вариационный вывод. В этом посте я дам объяснение функциональной производной и покажу, как она связана с градиентом обычной многомерной функции. 9n \rightarrow \mathbb{R}\] В этом сообщении блога мы обсуждаем вариационное исчисление , область математики, которая обобщает идеи многомерного исчисления, относящиеся к бесконечно малым изменениям традиционных числовых функций на функций функций , называемые функционалами . Функционалы довольно распространены в машинном обучении и статистическом выводе. Например, информационную энтропию можно рассматривать как функционал от вероятностных функций массы. Для данной дискретной случайной величины $X$ энтропию можно рассматривать как функцию, которая принимает в качестве входных данных функцию массы вероятности $X$, $p_X$, и выводит действительное число: , где $\mathcal{X}$ — поддержка $p_X$. Другим примером функционала является нижняя граница свидетельства (ELBO): функция, которая, как и энтропия, работает с вероятностными распределениями. ELBO — это основная величина, используемая в популярном алгоритме EM и вариационном выводе, используемом для выполнения статистического вывода с вероятностными моделями. В этом сообщении блога мы рассмотрим некоторые концепции традиционного исчисления, такие как частные производные, производные по направлениям и градиенты, чтобы представить определение функциональной производной , которая является просто обобщением градиента числовых функций для функционалы. В этом разделе мы представим несколько важных понятий многомерного исчисления: производные, частные производные, производные по направлению и градиенты. Прежде чем двигаться дальше, давайте быстро рассмотрим основное определение производной для одномерной функции $g$, которая отображает действительные числа в действительные числа. То есть Производная от $g$ на входе $x$, обозначаемая $\frac{dg(x)}{dx}$, описывает скорость изменения $g$ при $x$. Он строго определен как Геометрически $\frac{dg(x)}{dx}$ – это наклон линии, касательной к $g$ в точке $x$, как показано ниже: 92 \rightarrow \mathbb{R}$: Как видно выше, частная производная $\frac{f(\boldsymbol{x})}{\partial x_1}$ – это просто производная функции $f( x_1, x_2)$ при фиксации $x_1$. Мы можем видеть, что частная производная от $f(\boldsymbol{x})$ по $i$-му измерению векторного пространства может быть выражена как , где $\boldsymbol{e}_i$ — $i$-й стандартный базисный вектор, то есть вектор всех нулей, кроме единицы в $i$-я позиция. Геометрически мы можем рассматривать $i$-ю частную производную $f(\boldsymbol{x})$ как скорость изменения $f$ вдоль направления $i$-го стандартного базисного вектора векторного пространства . Размышляя в этом направлении, ничто не мешает нам обобщить эту идею на любой единичный вектор , а не только стандартные базисные векторы. Для некоторого единичного вектора $\boldsymbol{v}$ мы определяем производную по направлению от $f(\boldsymbol{x})$ вдоль направления $\boldsymbol{v}$ как Геометрически это просто скорость изменения $f$ вдоль направления, на которое указывает $\boldsymbol{v}$! Схематически это можно увидеть ниже: 9n \left( \frac{\partial f(\boldsymbol{x})}{\partial x_i} \right) v_i\] Доказательство этого уравнения см. Тогда мы можем представить производную по направлению как просто скалярное произведение между $\nabla f(\boldsymbol{x})$ и $\boldsymbol{v}$: Этот вектор $\nabla f(\boldsymbol {x})$ называется вектором градиента $f$ в точке $\boldsymbol{x}$. Как описано выше, вектор градиента ,$\nabla f(\boldsymbol{x})$ представляет собой вектор, построенный путем взятия частной производной от $f$ в точках $\boldsymbol{x}$ вдоль каждого базисный вектор. Получается, что вектор градиента указывает на направление наискорейшего подъема 9. Мы доказываем это свойство вектора градиента в теореме 2 Приложения к этому посту. Теперь попытаемся обобщить понятие градиентов на функционалы. Пусть $\mathcal{F}$ будет некоторым набором функций, и для простоты пусть каждая $f$ будет непрерывной функцией с действительным знаком. То есть для каждого $f \in \mathcal{F}$ имеем $f: \mathbb{R} \rightarrow \mathbb{R}$. Затем мы рассмотрим функционал $F$, который отображает каждое $f \in \mathcal{F}$ в число. то есть Теперь мы собираемся испортить изюминку определением функциональной производной: Определение 1 (Функциональная производная): Дано функция $f \in \mathcal{F}$, функциональная производная от $F$ в точке $f$, обозначаемая $\frac{\partial{F}}{\partial f}$, определяется как функция, для которой: \(\begin{align*}\int \frac{\partial F}{\partial f}(x) \eta(x) \ dx &= \lim_{h \rightarrow 0}\frac {F(f + h \eta) — F(f)}{h} \\ &= \frac{d F(f + h\eta)}{dh}\bigg\rvert_{h=0}\end{ выровнять*}\) , где $h$ — скаляр, а $\eta$ — произвольная функция из $\mathcal{F}$. Вау. Что здесь происходит? Как же это определяет функциональную производную? И почему функциональная производная $\frac{\partial{F}}{\partial f}$ скрыта внутри такого, казалось бы, сложного уравнения? Давайте разберемся. Во-первых, обратите внимание на сходство правой части уравнения определения 1 с определением направленного градиента: Действительно, уравнение в определении 1 описывает аналогию производной по направлению для функционалов! То есть он описывает скорость изменения $F$ при $f$ в направлении функции $\eta$! Как это работает? Когда мы уменьшаем $h$ до бесконечно малого числа, $f + h \eta$ становится сколь угодно близким к $f$. На иллюстрации ниже мы видим пример функции $f$ (красный) и еще одну функцию $\eta$ (синий). По мере уменьшения $h$ функция $f + h\eta$ (фиолетовая) становится более похожей на $f$: Таким образом, мы видим, что $h \eta$ — это «бесконечно малая» замена $f$, аналогичная бесконечно малой замене $\boldsymbol{x}$, которую мы описываем $h\boldsymbol{v} $ в определении производной по направлению. До сих пор мы только показали, что уравнение в определении 1 описывает нечто аналогичное производной по направлению для многомерных числовых функций. Мы показали это, сравнив правую часть уравнения в определении 1 с определением направленного градиента. Однако, как указано в определении 1, сама функциональная производная определяется как функция $\frac{\partial F}{\partial f}$ внутри интеграла в левой части уравнения. Что здесь происходит? Почему это функциональная производная? Теперь пришло время вспомнить о градиенте для традиционных многомерных функций. В частности, обратите внимание на сходство между альтернативной формулировкой производной по направлению, в которой используется градиент, и левой частью уравнения в определении 1: Обратите внимание, что эти уравнения имеют схожие формы. Вместо суммирования в определении производной по направлению мы имеем интеграл в уравнении для определения 1. Чтобы углубить это, вспомним, что мы можем представить производную по направлению как скалярное произведение между вектором градиента и $\boldsymbol{v}$: Чтобы прояснить эту связь, отметим, что скалярное произведение является скалярным произведением. Таким образом, мы можем записать это определение в более общем виде как Напомним также, что действительным скалярным произведением между непрерывными функциями $f$ и $g$ является Таким образом, мы видим что Иными словами, функциональный градиент функционала $F$ при функции $f$, обозначаемой $\frac{\partial F}{\partial f}$, представляет собой функцию, для которой задана любая произвольная функция $\eta$, скалярное произведение между $\frac{\partial F}{\partial f}$ и $\eta$ есть производная по направлению от $F$ в направлении $\eta$! В качестве игрушечного примера выведем функциональную производную от информационной энтропии. , где $\mathcal{X }$ — это поддержка $p_X$. Выведем его функциональную производную. Начнем с произвольной функции массы вероятности $\eta : \mathcal{X} \rightarrow [0,1]$. Тогда мы можем написать уравнение, определяющее функциональную производную: Упростим это уравнение: В частности, для заданного набора функций $\mathcal{F}$ функционал является отображением между $\mathcal{F}$ и действительными числами: Обзор производных и градиентов
Производные
То есть это наклон линии, касательной к функции $f(x_1, x_2)$ при фиксированном $x_1$. Производные по направлениям
в теореме 1 в приложении к этому посту. Теперь, если мы определим вектор всех частных производных $f(\boldsymbol{x})$ как Градиенты
0599 вдоль поверхности $f$ в точке $\boldsymbol{x}$. Схематически это можно показать ниже: Функциональные производные
Величина $h \eta$ называется вариацией величины $f$ (отсюда слово «вариационный» в названии «вариационного исчисления»). Более того, вместо суммирования по элементам вектора $\boldsymbol{v}$ мы «суммируем» (с помощью интеграла) каждое значение $\eta(x)$. Наконец, вместо каждой частной производной от $f$ теперь у нас есть каждое значение функции $\frac{\partial F}{\partial f}$ для каждого $x$. Эта функция $\frac{\partial F}{\partial f}(x)$ аналогична градиенту! Таким образом, это называется функциональной производной! Пример: функциональная производная от энтропии
Напомним, что в начале этого поста энтропию $H$ дискретной случайной величины $X$ можно рассматривать как функцию от функции массы вероятности $X$ $p_X$. Более конкретно, $H$ определяется как
Доказательство:
Пусть $\boldsymbol{x}$ и $\boldsymbol{v}$ фиксированы, и пусть $g(z) := f(\boldsymbol{x} + z\boldsymbol{v} )$. Тогда
\[\frac{dg(z)}{dz} = \lim_{h \rightarrow 0} \frac{g(z+h) — g(z)}{h}\]Оценка этой производной при $z = 0$, мы видим, что
\[\begin{align*} \frac{dg(z)}{dz}\bigg\rvert_{z=0} &= \frac{g(h) — g( 0)}{h} \\ &= \frac{g(\boldsymbol{x} + h\boldsymbol{v}) — f(\boldsymbol{x})}{h} \\ &= D _{\boldsymbol{ v}} f(\boldsymbol{x}) \end{align*}\] 9n$, производная по направлению $D_{\boldsymbol{v}} f(\boldsymbol{x})$ может быть вычислена путем скалярного произведения вектора градиента с $\boldsymbol{v}$: \[D_{ \boldsymbol{v}} f(\boldsymbol{x}) = \nabla f(\boldsymbol{x}) \cdot \boldsymbol{v}\]Скалярное произведение можно вычислить как
\[\nabla f(\ boldsymbol{x}) \cdot \boldsymbol{v} = ||\nabla f(\boldsymbol{x})|| ||\boldsymbol{v}|| \cos \theta\], где $\theta$ — угол между двумя векторами. Функция $\cos$ максимальна (и равна 1), когда $\theta = 0$, и, таким образом, производная по направлению максимальна, когда $\theta = 0$.