Как решать неравенства? Как решать дробные и квадратные неравенства?
Понятие математического неравенства возникло в глубокой древности. Это произошло тогда, когда у первобытного человека появилась потребность при счёте и действиях с различными предметами сравнивать их количество и величину. Начиная с античных времён неравенствами пользовались в своих рассуждениях Архимед, Евклид и другие прославленные деятели науки: математики, астрономы, конструкторы и философы.
Но они, как правило, применяли в своих работах словесную терминологию. Впервые современные знаки для обозначения понятий «больше» и «меньше» в том виде, каком их сегодня знает каждый школьник, придумали и применили на практике в Англии. Оказал такую услугу потомкам математик Томас Гарриот. А случилось это около четырёх столетий назад.
Известно множество видов неравенств. Среди них простые, содержащие одну, две и больше переменных, квадратные, дробные, сложные соотношения и даже представленные системой выражений. А понять, как решать неравенства, лучше всего на различных примерах.
А понять, как решать неравенства, лучше всего на различных примерах.
Не опоздать на поезд
Для начала представим себе, что житель сельской местности спешит на железнодорожную станцию, которая находится на расстоянии 20 км от его деревни. Чтобы не опоздать на поезд, отходящий в 11 часов, он должен вовремя выйти из дома. В котором часу это необходимо сделать, если скорость его движения составляет 5 км/ч? Решение этой практической задачи сводится к выполнению условий выражения: 5 (11 – Х) ≥ 20, где Х – время отправления.
Это понятно, ведь расстояние, которое необходимо преодолеть селянину до станции равно скорости движения, умноженной на количество часов в пути. Прийти раньше человек может, но вот опоздать ему никак нельзя. Зная, как решать неравенства, и применив свои умения на практике, в итоге получим Х ≤ 7, что и является ответом. Это значит, что селянину следует отправиться на железнодорожную станцию в семь утра или несколько ранее.
Числовые промежутки на координатной прямой
Теперь выясним, как отобразить описываемые соотношения на координатной прямой. Полученное выше неравенство не является строгим. Оно означает, что переменная может принимать значения меньше 7, а может быть равным этому числу. Приведём другие примеры. Для этого внимательно рассмотрим четыре рисунка, представленных ниже.
Полученное выше неравенство не является строгим. Оно означает, что переменная может принимать значения меньше 7, а может быть равным этому числу. Приведём другие примеры. Для этого внимательно рассмотрим четыре рисунка, представленных ниже.
На первом из них можно увидеть графическое изображение промежутка [-7; 7]. Он состоит из множества чисел, размещённых на координатной прямой и находящихся между -7 и 7, включая границы. При этом точки на графике изображаются в виде закрашенных кругов, а запись промежутка производится с использованием квадратных скобок.
Второй рисунок является графическим представлением строгого неравенства. В данной случае пограничные числа -7 и 7, показанные выколотыми (не закрашенными) точками, не включаются в указанное множество. А запись самого промежутка производится в круглых скобках следующим образом: (-7; 7).
То есть, выяснив, как решать неравенства такого типа, и получив подобный ответ, можно заключить, что он состоит из чисел, находящихся между рассматриваемыми границами, кроме -7 и 7. Следующие два случая необходимо оценивать аналогичным образом. На третьем рисунке даются изображения промежутков (-∞; -7] U [7; +∞), а на четвёртом — (-∞; -7) U (7; +∞).
Следующие два случая необходимо оценивать аналогичным образом. На третьем рисунке даются изображения промежутков (-∞; -7] U [7; +∞), а на четвёртом — (-∞; -7) U (7; +∞).
Два выражения в одном
Часто можно встретить следующую запись: 7 < 2Х – 3 < 12. Как решать двойные неравенства? Это значит, что на выражение налагаются сразу два условия. И каждое из них следует учитывать, чтобы получить правильный ответ для переменной Х. Приняв во внимание такое положение дел, получаем из соотношений 2Х – 3 > 7 и 2Х – 3 < 11 следующее:
5 < Х < 7. Окончательный ответ записывается таким образом: (5; 7). Это значит, что переменная принимает множество значений, заключённых в промежутке между числами 5 и 7, исключая границы.
Сходные свойства с уравнением
Уравнение представляет собой выражение, объединяемое знаком = , который означает, что обе части его (левая и правая) тождественны по величине. Поэтому часто подобные соотношения связывают с образом старинных весов, имеющих чаши, установленные и скрепляемые посредством рычага. Данное устройство всегда находится в равновесии, если оба конца наделены одинаковым весом. При этом положение не меняется, если левая и правая части дополняются или теряют грузы одинаковой массы.
Данное устройство всегда находится в равновесии, если оба конца наделены одинаковым весом. При этом положение не меняется, если левая и правая части дополняются или теряют грузы одинаковой массы.
В математическом уравнении к обеим частям равенства, чтобы оно не нарушилось, тоже можно прибавлять одно и то же число. При этом оно может быть положительным или отрицательным. Как решать неравенства в данном случае, и можно ли сделать с ними то же самое? Предыдущие примеры показали, что да.
Отличие от уравнения
Обе части выражения, соединённые знаками < или >, можно умножать и делить на любое положительное число. При этом истинность соотношения не нарушается. Но как решить неравенство с дробями отрицательными и целыми множителями, перед которыми стоит знак минус? Здесь дело обстоит совершенно иначе.
Разберём это на примере: -3Х < 12. Чтобы выделить переменную в левой части, приходится делить каждую из них на -3. При этом знак неравенства меняется на обратный.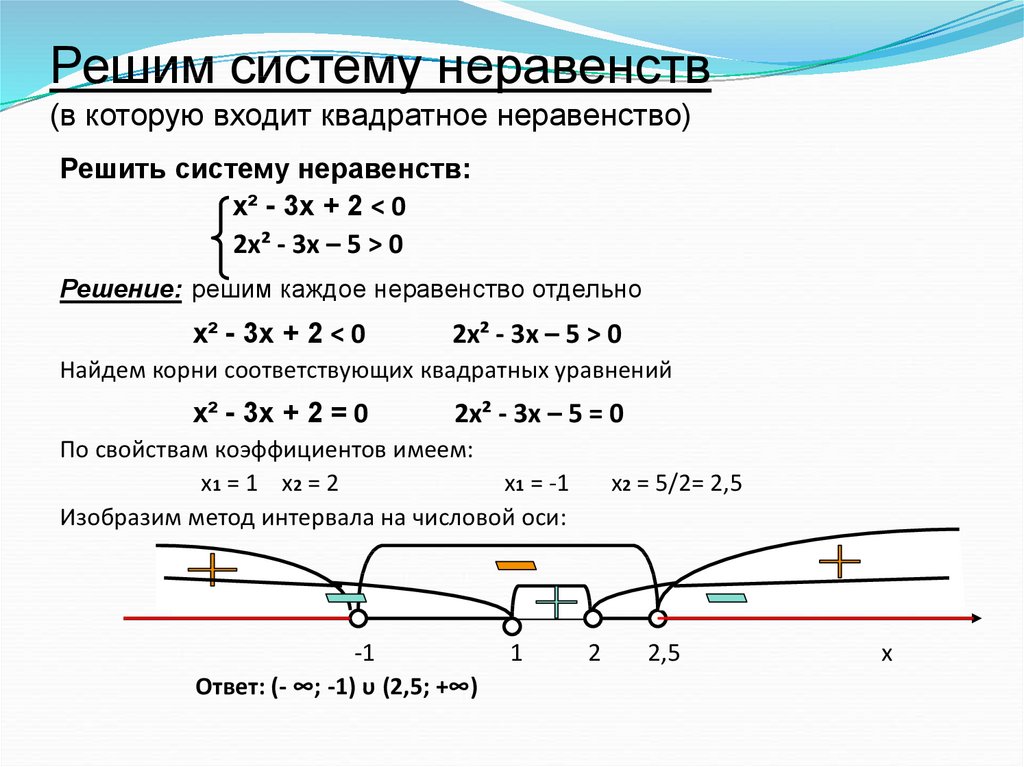 Получаем: Х > -4, что и является ответом поставленной задачи.
Получаем: Х > -4, что и является ответом поставленной задачи.
Метод интервалов
Неравенство называется квадратным в случае, если содержит переменную, возведённую во вторую степень. Примером подобного соотношения может служить следующее выражение: Х2 – 2Х + 3 > 0. Как решать квадратные неравенства? Самым удобным способом является метод интервалов. Для осуществления задуманного, следует разложить на множители левую часть соотношения. Получается: (Х – 3)(Х + 1). Потом рекомендуется найти нули функции и расположить полученные точки в правильном порядке на координатной прямой.
Далее нужно распределить знаки получившихся интервалов, подставив в выражение любое из чисел, принадлежащих данному промежутку. При этом в простых случаях обычно достаточно разобраться хотя бы с одним из них, а остальные — расставить по правилу чередования. В заключении остаётся только отобрать подходящие интервалы, чтобы получить окончательное решение.
Квадратные неравенства здесь подчиняются закону соответствия отрицательных областей минусам, а положительных — плюсам. То есть, если выражение больше нуля, то следует брать числовые промежутки, помеченные знаком + . А в обратном случае решением будут участки, отмеченные знаком — . Таким образом, решение нашего неравенства запишется так: (-∞; -1) U (3; +∞).
То есть, если выражение больше нуля, то следует брать числовые промежутки, помеченные знаком + . А в обратном случае решением будут участки, отмеченные знаком — . Таким образом, решение нашего неравенства запишется так: (-∞; -1) U (3; +∞).
Другие примеры применения метода интервалов
Описанный способ даёт ответ и на другой немаловажный вопрос: как решать дробные неравенства, если в данном случае вполне применим тот же метод интервалов? Рассмотрим подробнее, как это можно сделать, на примере соотношения, представленного ниже.
Здесь нулями функции являются точки -9 и 4. Для нахождения решения следует нанести их на координатную прямую и определить знаки промежутков, отобрав те из них, которые окажутся помеченными знаком плюс. При этом следует обратить внимание, что закрашенной будет только цифра 4.
Другая точка буде выколотой, так как -9 не входит в область значений, которые допустимы. Ведь при этом в знаменателе получается ноль, что в математике невозможно. Как решать дробные неравенства? В данном случае окончательным ответом станет объединение промежутков: (-∞; -9) U [4; +∞).
Параболы на графике
Выяснить всё о неравенствах часто помогают не только рисунки на координатной прямой, но и изображения в декартовой плоскости. Графиком квадратичной зависимости, как известно, является парабола. Даже схематичный рисунок такого типа способен практически полностью дать ответы на поставленные вопросы. Рассмотрим некоторые из типов парабол, дающих представления о решении квадратных неравенств.
Здесь прежде всего уясним для себя некоторые истины. Любое выражение такого типа приводится к виду: ах2 + вх + с = 0. При этом, если коэффициент а оказывается положительным, то параболу следует рисовать ветвями верх, в противоположно случае – вниз. А корни уравнения являются точками, где происходит пересечение графика функции с осью ОХ.
Толкования
Знать указанные выше утверждения очень важны для понимания квадратных неравенств и ответов на вопросы, связанные с ними. Начертив схему параболы на декартовой плоскости, для решения необходимо выяснить, в какой момент функция (то есть значения координат точек по оси ОУ) принимает показатели + и -. При этом, если в неравенстве стоит знак >, то решением его будет множество значений, принимаемых переменной Х при положительном У.
При этом, если в неравенстве стоит знак >, то решением его будет множество значений, принимаемых переменной Х при положительном У.
В случае знака < в ответе указываются показатели для Х при отрицательном У. Бывает так, что парабола и вовсе не пересекается с осью ОХ. Это происходит в случаях, когда Д < 0. Тогда, если график расположен в верхней полуплоскости, ответом для квадратного неравенства со знаком > окажется промежуток (-∞; +∞). А для < решением будет пустое множество. С нижней полуплоскостью дело обстоит с точностью да наоборот.
О пользе графических изображений
Изображения на декартовой плоскости существенно облегчают задачу для систем уравнений. Рисунки наглядно показывают решения, которые являются точками пересечения нанесённых линий. Остаётся только вычислить их координаты и записать ответ.
То же касается и неравенств. К примеру, решением соотношения у ≤ 6 – х (как понятно по рисунку) является сама прямая у = 6 — х, а также полуплоскость, размещённая ниже данной границы. Для точного ответа можно взять любую точку на графике (например (1; 3) и подставить её координаты в неравенство. Получаем: 3 ≤ 6 — 1, то есть верное соотношение. Значит, приведённые рассуждения были истинными.
Для точного ответа можно взять любую точку на графике (например (1; 3) и подставить её координаты в неравенство. Получаем: 3 ≤ 6 — 1, то есть верное соотношение. Значит, приведённые рассуждения были истинными.
Неравенство у ≥ х2 описывается областью на декартовой плоскости, расположенной в чаше параболы, включая границы её самой. А на пересечении указанных секторов можно найти решение соотношения, записанного в виде: х2 ≤ у ≤ 6 – х. Оно будет ограничиваться снизу линией параболы и отсекаться сверху прямой. Для уверенности снова сделаем проверку, подставив значения координат любой точки, пренадлежащей к этой области.
Возьмём (1; 4). Получаем: 1 ≤ 4 ≤ 6 — 1, то есть снова верное соотношение. Здесь опять есть смысл заметить, что неравенства обладают многими сходными чертами с уравнениями, хотя и наделены существенными отличиями.
Открытый урок по теме: «ДРОБНЫЕ РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА» | План-конспект урока по алгебре (9 класс) на тему:
ТЕМА УРОКА: ДРОБНЫЕ РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА
Цель урока: закрепить и углубить знания учащихся в процессе решения различных упражнений по заданной теме; содействовать развитию взаимовыручки и взаимопомощи, умению вести культурную дискуссию.
Задачи урока:
- закрепить умение решать рациональные неравенства методом интервалов; рассмотреть различного уровня сложности рациональные неравенства; проверить умение учащихся решать рациональные неравенства;
- создать условия для развития умений и навыков применять знания в новых ситуациях; для развития качеств мышления: гибкости, целенаправленности, рациональности, критичности с учетом индивидуальных особенностей.
ХОД УРОКА.
- Организация. Постановка задач.
- Актуализация опорных знаний. Устные упражнения. (Слайд 2-4)
1) Равносильны ли следующие неравенства?
а) и (нет)
б) и (да)
2) Определите метод решения уравнения:
а)
б)
в)
г)
д)
3) Определите ход решения неравенства:
а)
б) ﴾2х2+11х+6)﴾2х2+11х+13)
в)
г)
д)
- Повторить алгоритм решения рационального неравенства методом интервалов: (Слайд 5)
- В каждом множителе коэффициент при старшей степени переменной должен быть положительный, для этого надо вынести минус из всех множителей, в которых коэффициент при старшей степени отрицательный, и если перед выражением все же остался знак минус, то надо все неравенство умножить на (-1).

- Решить уравнение
Получим корни числителя и точки разрыва знаменателя .
- На числовой прямой отложим все полученные значения и проведем кривую знаков.
- Выпишем ответ для знака сравнения :
- Решение заданий. (Слайд 6, 7)
1. Решите неравенство .
Ответ:
2. Решите неравенство .
Ответ:
3. Найдите разность между целыми наибольшим и наименьшим решениями неравенства
.
Ответ: 4.
4. Решите неравенство .
Ответ:
5. Найдите произведение наибольшего целого отрицательного и наименьшего целого положительного решения неравенства
Ответ: -42.
6. Найдите наименьшее целое решение неравенства .
Ответ: 3.
7. Сколько простых чисел являются решениями неравенства ?
Ответ: 1.
- Персональные карточки для проверочных работ.

Карточка № 1.
1. Решить неравенство:
£ .
а) [-4; -2)È(0;5],
б) (–1, 0]È[1;7),
в) (-4; -3)È[5; 7],
г) нет решений.
2. Найти наибольшее целое х, удовлетворяющие неравенству:
— > 1.
а) хÎ(-¥; -3,5),
б) –3,
в) –4,
г) нет решений.
Карточка № 2.
1. Найти наибольшее целое х, удовлетворяющие неравенству:
— > -.
а)5,
б) –3,
в) 4,
г)нет решений.
2. Решить неравенство:
а) (-9; -5)È(0; 8),
б) (–8, -7)È(1;3),
в) (-¥; -7)È(1; 3),
г) нет решений.
Карточка № 3.
1. Решить неравенство:
—
а) (-¥; -3)È(0; 3,
б) (–3, 0)È(0; ¥),
в) (5; 7),
г) нет решений.
2. Найти целочисленные решения неравенств:
а) 0, 1, 2,
б) 4, 5,
в) 7,
г)нет решений.
Карточка № 4.
1. Решить неравенство:
а) (-¥; -3/25)È(0; ¥),
б) (–12, 0)È(7;9),
в) (-¥;)È ( ; 5),
г) нет решений.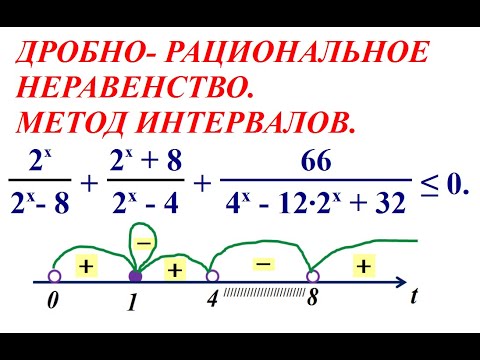
2. Найти сумму целых решений неравенства
а) 2,
б) 4,
в) 0,
г) 1,
д) 3.
- Подведение итогов.
В ходе урока учащиеся закрепили умение решать рациональные неравенства, рассмотрели решение рациональных неравенств различного уровня сложности. Учащиеся на практике показали умение применять метод интервалов при решении рациональных неравенств. Особое внимание следует уделить решению нестрогих рациональных неравенств.
- Домашнее задание
Решение полиномиальных и рациональных неравенств. Квадратное и кубическое неравенство
Мы будем использовать комбинацию алгебраических и графических методов для решения полиномиальных и рациональных неравенств.
Полиномиальные неравенства
Точно так же, как квадратное уравнение может быть записано в виде ax 2 + bx + c = 0, квадратное неравенство может быть записано в виде ax 2 + bx + c ? 0, где? равно , ≤ или ≥. Вот несколько примеров квадратных неравенств:
Вот несколько примеров квадратных неравенств: 3x 2 — 2x — 5 >0, (-1/2)x 2 + 4x -7 ≤ 0.
Квадратные неравенства являются одним из типов полиномиальных неравенств . Другие примеры полиномиальных неравенств:
-2x 4 + x 2 — 3 3 — 2x 20 > 5×0 + 7. знак равенства, формируется родственное уравнение
ПРИМЕР 1 Решите: x 3 — x > 0.
Решение Нас просят найти все значения x, для которых x 3 — x > 0. Чтобы найти эти значения, мы график f(x) = x 3 -x. Затем мы замечаем, что всякий раз, когда функция меняет знак, ее график проходит через x-перехват. Таким образом, чтобы решить x 3 — x > 0, мы сначала решим соответствующее уравнение x 3 — x = 0, чтобы найти все нули функции:
x 3 — x = 0
x(x 2 — 1) = 0
x(x + 1)(x — 1) = 0.
Нули равны -1, 0 и 1. Таким образом, x-пересечения графика равны (-1, 0), (0,0) и (1, 0), как показано на рисунке слева. Нули делят ось x на четыре интервала:
Для всех значений x в заданном интервале знак x 3 — x должен быть либо положительным, либо отрицательным. Чтобы определить, какой из них, мы выбираем тестовое значение для x из каждого интервала и находим f (x). Мы можем использовать набор функций TABLE в ASK.
режим для определения знака f(x) на каждом интервале. (См. таблицу слева.) Мы также можем определить знак f(x) в каждом интервале, просто взглянув на график функции.
| Интервал | Тестовое значение | Знак f(x) |
| (-∞ -1) | f(-2) = -6 | Отрицательный |
| (-1; 0) | f(-0,5) = 0,375 | Положительный |
| (0, 1) | f(0,5) = -0,375 | Отрицательный |
| (1, ∞) | f(2) = 6 | Положительный |
Поскольку мы решаем x 3 — x > 0, множество решений состоит только из двух из четырех интервалов, в которых знак f(x) положительный.
 Мы видим, что множество решений равно (- 1, 0) (1, ∞) или {x| — 1 1}.
Мы видим, что множество решений равно (- 1, 0) (1, ∞) или {x| — 1 1}. Чтобы решить полиномиальное неравенство:
1. Найдите эквивалентное неравенство с 0 на одной стороне.
2. Решите связанное полиномиальное уравнение.
3. Используйте решения, чтобы разделить ось X на интервалы. Затем выберите тестовое значение из каждого интервала и определите знак многочлена на интервале.
4. Определите интервалы, для которых выполняется неравенство, и запишите обозначение интервала или обозначение построителя множества для множества решений. Включите конечные точки интервалов в набор решений, если символ неравенства ≤ или ≥.
Пример 2 Решение: 3x 4 + 10x ≤ 11x 3 + 4.
Решение путем вычитания 11x 3 + 4, мы формируем эквивалент.
Алгебраическое решение
Чтобы решить связанное уравнение
3x 4 — 11x 3 + 10x — 4 = 0,
, нам нужно использовать теоремы из раздела 3. 4. Мы решили это уравнение в примере 5 в разделе 3.4. Решения:
4. Мы решили это уравнение в примере 5 в разделе 3.4. Решения:
-1, 2 — √2, 2/3 и 2 + √2,
или приблизительно
-1, 0,586, 0,667 и 3,414.
(-∞, -1), (-1, 2 — √2), (2 — √2, 2/3), (2/3, 2 + √2) и (2 + √2, ∞) .
Положим f(x) = 3x 4 — 11x 3 + 10x — 4 и, используя тестовые значения для f(x), определим знак f(x) в каждом интервале:
Значения функции отрицательны в интервалах (-1, 2 — √2) и (2/3, 2 + √2). Поскольку знак неравенства ≤, включаем концы интервалов в множество решений. Набор решений равен
[-1, 2 — √2] [2/3, 2 + √2], или {x|-1 ≤ x ≤ 2 — √2 или 2/3 ≤ x ≤ 2 + √2} .
Графическое решение
Построим график y = 3x 4 — 11x 3 + 10x — 4, используя смотровое окно, которое показывает кривизну графика.
Используя функцию ZERO, мы видим, что два нуля равны -1 и приблизительно равны 3,414 (2 + √2 ≈ 3,414).
Рассматриваемые интервалы: (-∞, -1), (-1, 0,586), (0,586, 0,667), (0,667, 3,414) и (3,414, ∞). Отмечаем на графике, где функция отрицательна. Затем, включая соответствующие конечные точки, мы находим, что набор решений приблизительно равен
[-1, 0,586] [0,667, 3,414] или {x|-1 ≤ x ≤ 0,586 или 0,667 ≤ x ≤ 3,414}.
Рациональные неравенства
Некоторые неравенства включают рациональные выражения и функции. Они называются рациональными неравенствами . Чтобы решить рациональные неравенства, нам нужно внести некоторые коррективы в предыдущий метод.
ПРИМЕР 3 Решите: $\frac{x-3}{x+4} \ge\frac{x+2}{x-5}$
Решение Сначала вычтем $\frac{x + 2 }{x — 5}$, чтобы найти эквивалентное неравенство с 0 на одной стороне:
Алгебраическое решение
Мы ищем все значения x, для которых родственная функция
$f(x) =\frac{x — 3}{x + 4} — \frac{x + 2}{x — 5}$
не определено или равно 0. Они называются критическими значениями .
Они называются критическими значениями .
Взгляд на знаменатели показывает, что не определено для x = -4 и x = 5. Затем мы решаем f(x) = 0:
$\frac{x — 3}{x + 4}-\frac{ x + 2}{x — 5}=0$
$(x+4)(x-5)[\frac{x-3}{x+4}-\frac{x+2}{x-5} ] = (x+4)(x-5)\cdot 0$
(x — 5)(x — 3) — (x + 4)(x + 2) = 0
(x 2 — 8x + 15) — (х 2 + 6х + 8) = 0
-14х + 7 = 0
х = 1/2.
Критические значения: -4, 1/2 и 5. Эти значения делят ось X на
четыре интервала:
(-∞, -4), (-4, 1/2), (1/2, 5), и (5, ∞).
Затем мы используем тестовое значение для определения знака f(x) в каждом интервале.
Значения функции положительны в интервалах (- ∞, -4) и (1/2, 5). Поскольку f(1/2) = 0, а символ неравенства ≥, мы знаем, что 1/2 должно быть в наборе решений. Обратите внимание, что поскольку ни -4, ни 5 не находятся в домене f, они не могут быть частью набора решений.
Набор решений равен (-∞ -4) [1/2, 5].

Графическое решение
Нарисуем график
$y=\frac{x-3}{x+4}-\frac{x+2}{x-5}$
в стандартном окне, которое показывает его кривизну.
Используя свойство ZERO, мы находим, что 0,5 — это ноль.
Затем мы ищем значения, для которых функция не определена. Рассматривая знаменатели x + 4 и x — 5, мы видим, что это не так.
определено для x = -4 и x = 5
Критические значения , где y либо не определено, либо равно 0, составляют -4, 0,5 и 5.
На графике показано, где y положительное, а где отрицательное. Обратите внимание, что -4 и 5 не могут быть в наборе решений, поскольку y не определено для этих значений. Однако мы включили 0,5, поскольку символ неравенства ≥ и f(0,5) = 0. Этот набор решений равен
Ниже приводится метод решения рациональных неравенств.
Чтобы решить рациональное неравенство:
1. Найдите эквивалентное неравенство с 0 на одной стороне.
2. Измените символ неравенства на знак равенства и решите соответствующее уравнение.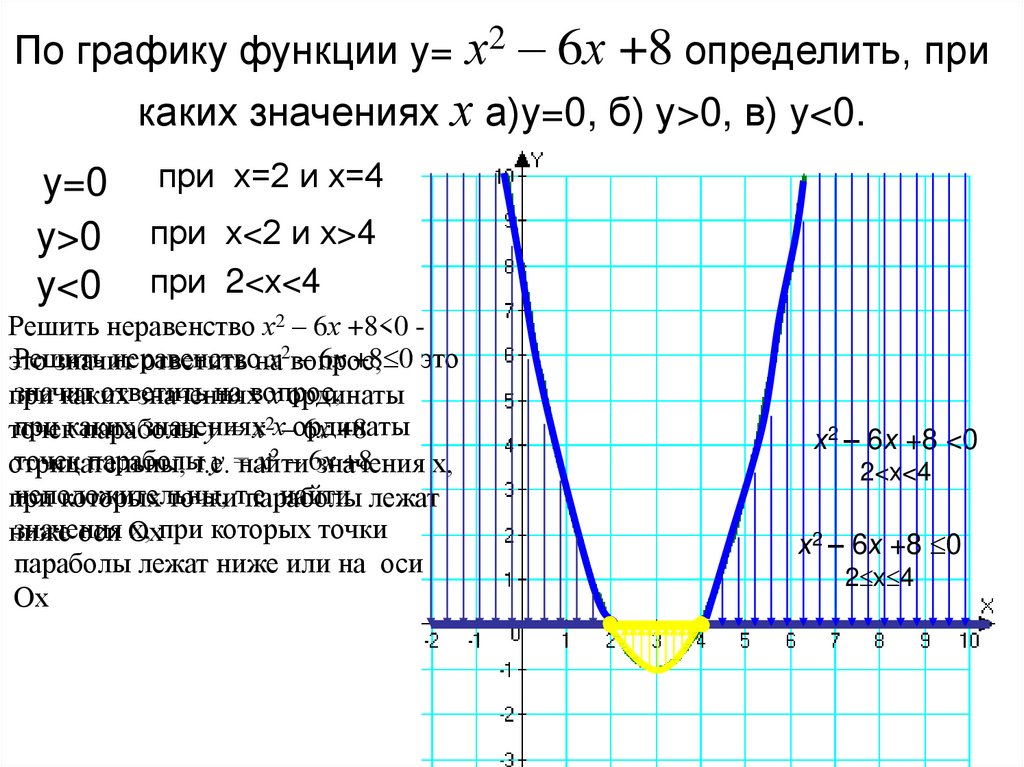 3. Найдите значения переменной, для которых соответствующая рациональная функция не определена.
4. Числа, найденные на шагах (2) и (3), называются критическими значениями. Используйте критические значения, чтобы разделить ось x на интервалы. Затем проверьте значение x из каждого интервала, чтобы определить знак функции в этом интервале.
5. Выберите интервалы, для которых выполняется неравенство, и запишите обозначение интервала или обозначение построителя набора для набора решений. Если символ неравенства ≤ или ≥, то решения шага (2) должны быть включены в набор решений. Значения x, найденные на шаге (3), никогда не включаются в набор решений.
3. Найдите значения переменной, для которых соответствующая рациональная функция не определена.
4. Числа, найденные на шагах (2) и (3), называются критическими значениями. Используйте критические значения, чтобы разделить ось x на интервалы. Затем проверьте значение x из каждого интервала, чтобы определить знак функции в этом интервале.
5. Выберите интервалы, для которых выполняется неравенство, и запишите обозначение интервала или обозначение построителя набора для набора решений. Если символ неравенства ≤ или ≥, то решения шага (2) должны быть включены в набор решений. Значения x, найденные на шаге (3), никогда не включаются в набор решений.
Эффективно использовать комбинацию алгебраических и графических методов для решения полиномиальных и рациональных неравенств. Алгебраические методы дают точные числа для критических значений, а графические методы позволяют легко увидеть, какие интервалы удовлетворяют неравенству.
6.6: Решение полиномиальных и рациональных неравенств
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 6273
- Анонимный
- LibreTexts
Цели обучения
- Решение полиномиальных неравенств.

- Решение рациональных неравенств.
Решение полиномиальных неравенств
A полиномиальное {2} (x − 4) \) дано в факторизованной форме, корни очевидны. Здесь корни: \(0, −3\) и \(4\). Из-за строгого неравенства постройте их, используя открытые точки на числовой прямой.
Рисунок \(\PageIndex{1}\)В этом случае критические числа разбивают числовую прямую на четыре области. Протестируйте значения в каждой области, чтобы определить, является ли f положительным или отрицательным. Здесь мы выбираем тестовые значения \(−5, −1, 2\) и \(6\). Помните, что нас интересует только знак \((+\) или \(-)\) результата. 9{2}(+)&=+\color{Cerulean} { Positive } \end{aligned}\)
После проверки значений мы можем заполнить диаграмму знаков.
Рисунок \(\PageIndex{2}\) Вопрос просит нас найти значения, где \(f (x) < 0\), или где функция отрицательна. Из таблицы знаков видно, что функция отрицательна для \(x\)-значений между \(0\) и \(4\).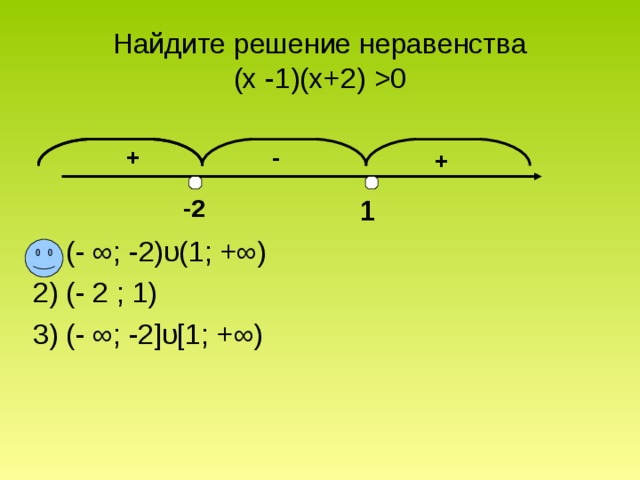
Этот набор решений можно выразить двумя способами:
\(\begin{aligned}\{x | 0<&x<4\} &\color{Cerulean} { Set \: обозначение } \\ (0,&4) &\color{Cerulean} { Интервал\: обозначение }\end{выравнивание}\)
В этом учебнике мы продолжим представлять наборы решений с использованием интервальной записи.
Ответ :
\((0,4)\)
Графические многочлены, такие как в предыдущем примере, выходят за рамки этого учебника. Однако график этой функции приведен ниже. Сравните график с соответствующей таблицей знаков.
Рисунок \(\PageIndex{4}\)Конечно, это может быть не тот случай, когда полином разложен на множители и не имеет нуля на одной стороне неравенства. Чтобы смоделировать функцию с помощью диаграммы знаков, все члены должны быть на одной стороне и равны нулю на другой. Общие шаги для решения полиномиального неравенства перечислены в следующем примере. 9{2}(+)(+)=+\end{aligned}\)
С помощью этой информации мы можем завершить таблицу знаков.
Шаг 4 : Используйте таблицу знаков, чтобы ответить на вопрос. Здесь решение состоит из всех значений, для которых \(f (x) > 0\). Заштрихуйте значения, дающие положительные результаты, а затем выразите этот набор в виде интервалов.
Рисунок \(\PageIndex{7}\)Ответ :
\(\left(-\infty,-\frac{3}{2}\right) \cup(3, \infty)\)
Пример \(\PageIndex{3}\) 9{2}-4\right) &=0 \\(x+1)(x+2)(x-2) &=0 \end{aligned}\)
Критические числа равны \(−2, − 1\) и \(2\). Из-за инклюзивного неравенства \((≤)\) мы нанесем их на график с помощью закрытых точек.
Рисунок \(\PageIndex{8}\)Используйте тестовые значения, \(-3\), \(-\frac{3}{2}\), \(0\) и \(3\) для составить схему знаков.
\(\begin{aligned} f(\color{OliveGreen}{-3}\color{black}{)}&=(\color{OliveGreen}{-3}\color{black}{+}1) (\color{OliveGreen}{-3}\color{black}{+}2)(\color{OliveGreen}{-3}\color{black}{-}2) &=(-)(-)(- )=- \\ f(\color{OliveGreen}{-\frac{3}{2}}\color{black}{)}&=(\color{OliveGreen}{-\frac{3}{2}} \color{black}{+}1)(\color{OliveGreen}{-\frac{3}{2}}\color{black}{+}2)(\color{OliveGreen}{-\frac{3} {2}}\color{black}{-}2) &=(-)(+)(-)=+\\ f(\color{OliveGreen}{0}\color{black}{)}&=( \color{OliveGreen}{0}\color{black}{+}1)(\color{OliveGreen}{0}\color{black}{+}2)(\color{OliveGreen}{0}\color{black }{-}2)&=(+)(+)(-)=- \\ f(\color{OliveGreen}{3}\color{black}{)}&=(\color{OliveGreen}{3} \color{black}{+}1)(\color{OliveGreen}{3}\color{black}{+}2)(\color{OliveGreen}{3}\color{black}{-}2)&= (+)(+)(+)=+\конец{выровнено}\) 9{2}>0\).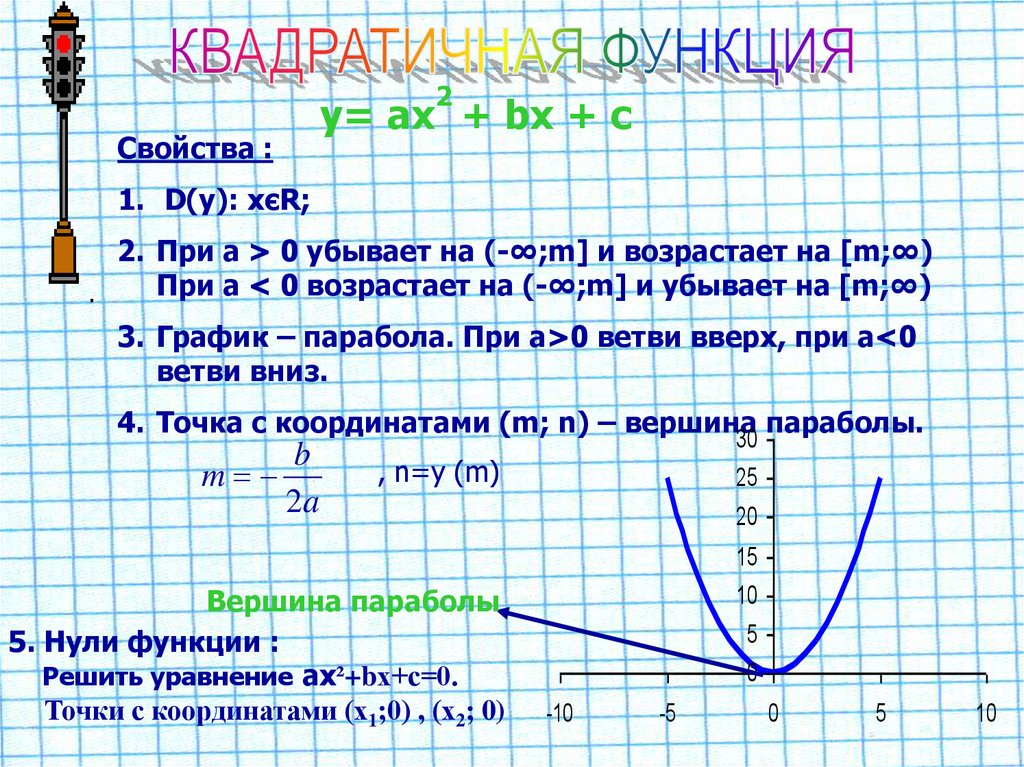
- Ответить
\((1,3)\)
www.youtube.com/v/EXpe_0LzbSY
Решение рациональных неравенств
A рациональное неравенство 19 — это математическое утверждение, которое связывает рациональное выражение как меньшее или большее другого. Поскольку рациональные функции имеют ограничения на область определения, мы должны соблюдать осторожность при решении рациональных неравенств. Кроме нулей, в множество критических чисел включим ограничения на область определения функции.
Пример \(\PageIndex{4}\)
Решить: \(\frac{(x-4)(x+2)}{(x-1)} \geq 0\)
Решение
Нули рациональной функции появляются, когда числитель равен нулю, а значения, дающие ноль в знаменателе, являются ограничениями. В этом случае
\(\begin{array}{c | c}{\text {Корни (числитель)}} & {\text{Ограничение(знаменатель)}} \\ {x-4=0 \text { или } x+2=0} & {x-1=0} \\ {\:\:\quad\quad\quad\: x=4 \quad\quad x=-2}& {x=1}\ конец{массив}\)
Следовательно, критическими числами являются \(−2, 1\) и \(4\). Из-за инклюзивного неравенства \((≥)\) используйте закрытую точку для корней \({−2, 4}\) и всегда используйте открытую точку для ограничений \({1}\). Ограничения никогда не включаются в набор решений.
Из-за инклюзивного неравенства \((≥)\) используйте закрытую точку для корней \({−2, 4}\) и всегда используйте открытую точку для ограничений \({1}\). Ограничения никогда не включаются в набор решений.
Используйте тестовые значения \(x = −4, 0, 2, 6\).
\(\begin{align} f(\color{OliveGreen}{-4}\color{black}{)} &=\frac{(\color{OliveGreen}{-4}\color{black}{- }4)(\color{OliveGreen}{-4}\color{black}{+}2)}{(\color{OliveGreen}{-4}\color{black}{-}1)}&=\frac {(-)(-)}{(-)}=-\\ f(\color{OliveGreen}{0}\color{black}{)} &=\frac{(\color{OliveGreen}{0}\ color{black}{-}4)(\color{OliveGreen}{0}\color{black}{+}2)}{(\color{OliveGreen}{0}\color{black}{-}1)} &=\frac{(-)(+)}{(-)}=+\\ f(\color{OliveGreen}{2}\color{black}{)} &=\frac{(\color{OliveGreen} {2}\color{black}{-}4)(\color{OliveGreen}{2}\color{black}{+}2)}{(\color{OliveGreen}{2}\color{black}{- }1)}&=\frac{(-)(+)}{(+)}=-\\ f(\color{OliveGreen}{6}\color{black}{)} &=\frac{(\ color{OliveGreen}{6}\color{black}{-}4)(\color{OliveGreen}{6}\color{black}{+}2)}{(\color{OliveGreen}{6}\color{ черный}{-}1)}&=\frac{(+)(+)}{(+)}=+\end{выровнено}\)
Затем заполните таблицу знаков.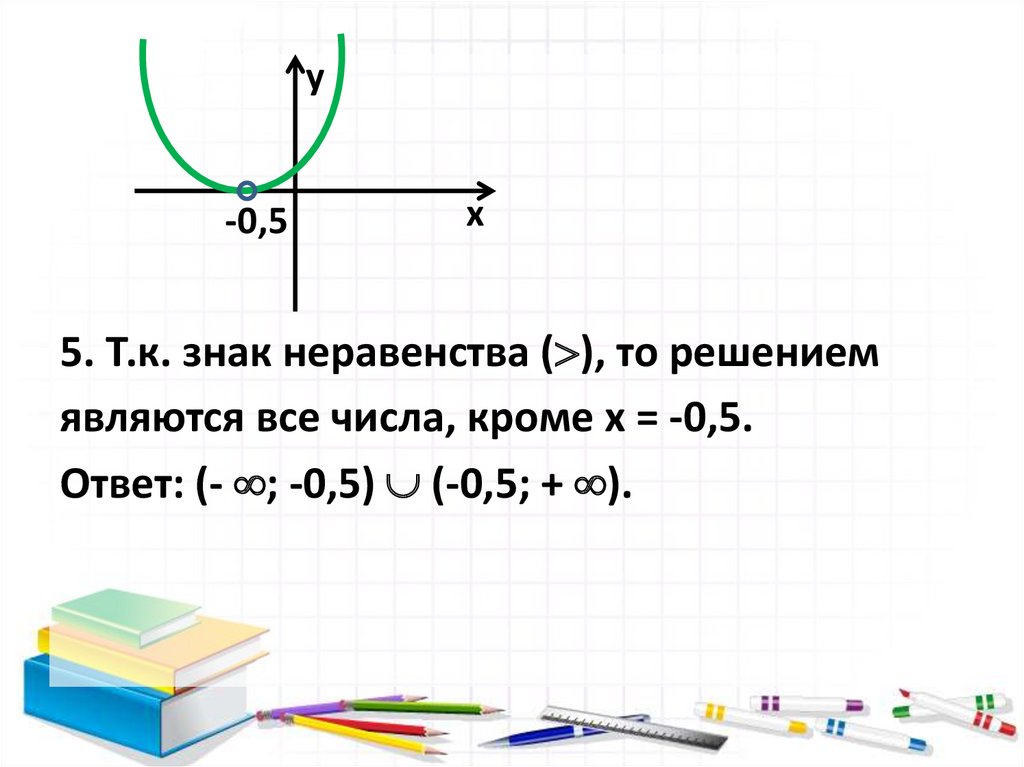
Задача состоит в том, чтобы найти значения, для которых \(f (x) ≥ 0\), другими словами, положительные или нулевые. Заштрихуйте соответствующие области и представьте набор решений в интервальной записи.
Рисунок \(\PageIndex{13}\)Ответ
\([-2,1) \cup[4, \infty)\)
Построение графика таких рациональных функций, как в предыдущем примере, невозможно охват этого учебника. Однако график этой функции приведен ниже. Сравните график с соответствующей таблицей знаков.
Рисунок \(\PageIndex{14}\) Обратите внимание, что ограничение \(x = 1\) соответствует вертикальной асимптоте, ограничивающей области, в которых функция изменяется с положительной на отрицательную. Хотя это ограничение не включено в набор решений, оно является критическим числом. Перед созданием диаграммы знаков мы должны убедиться, что неравенство имеет ноль с одной стороны. Общие шаги решения рационального неравенства показаны в следующем примере.
Пример \(\PageIndex{5}\):
Решить \(\frac{7}{x+3}<2\).
Решение
Шаг 1 : Начните с получения нуля в правой части.
\(\begin{aligned}\frac{7}{x+3}&<2 \\ \frac{7}{x+3}-2&<0\end{align}\)
Шаг 2 : Определите критические числа. Критические числа — это нули и ограничения. Начните с упрощения до одной алгебраической дроби.
\(\begin{aligned}\frac{7}{x+3}-\frac{2}{1}&<0 \\ \frac{7-2(x+3)}{x+3} &<0 \\ \frac{7-2 x-6}{x+3}&<0 \\ \frac{-2 x+1}{x+3}&<0\end{выровнено}\)
Затем найдите критические числа. Приравняйте числитель и знаменатель к нулю и решите.
\(\begin{array}{c|c} {\text{Корень}}&{\text{Ограничение}}\\ {-2x+1=0}\\{-2x=-1}&{ x+3=0}\\{x=\frac{1}{2}}&\quad\quad\:\:{x=-3} \end{array}\)
В этом случае строгое неравенство указывает, что мы должны использовать открытую точку для корня.
Рисунок \(\PageIndex{15}\) Шаг 3 : Создайте диаграмму знаков. Выберите тестовые значения \(−4, 0\) и \(1\).
Выберите тестовые значения \(−4, 0\) и \(1\).
\(\begin{aligned} f(\color{OliveGreen}{-4}\color{black}{)} &=\frac{-2(\color{OliveGreen}{-4}\color{black} {)}+1}{\color{OliveGreen}{-4}\color{black}{+}3}&=\frac{+}{-}=-\\ f(\color{OliveGreen}{0} \color{black}{)} &=\frac{-2(\color{OliveGreen}{0}\color{black}{)}+1}{\color{OliveGreen}{0}\color{black}{ +}3}&=\frac{+}{+}=+\\ f(\color{OliveGreen}{1}\color{black}{)} &=\frac{-2(\color{OliveGreen}{ 1}\color{black}{)}+1}{\color{OliveGreen}{1}\color{black}{+}3}&=\frac{-}{+}=-\end{aligned}\ )
И у нас есть
Рисунок \(\PageIndex{16}\)Шаг 4 : Используйте таблицу знаков, чтобы ответить на вопрос. В этом примере мы ищем значения, для которых функция отрицательна, \(f (x) < 0\). Заштрихуйте соответствующие значения, а затем представьте свой ответ, используя обозначение интервала.
Рисунок \(\PageIndex{17}\)Ответ :
\((-\infty,-3) \cup\left(\frac{1}{2}, \infty\right)\)
Пример \(\PageIndex{6}\):
Решение: \(\frac{1}{x^{2}-4} \leq \frac{1}{2-x}\). 9{2}-4}-\frac{1}{2-x} \leq 0} \\ {\frac{1}{(x+2)(x-2)}-\frac{1}{-( x-2)} \leq 0} \\ {\ frac {1} {(x + 2) (x-2)} + \ frac {1 \ color {Cerulean} {(x + 2)}} {\ color {черный}{(x-2)}\color{Cerulean}{(x+2)}}\color{black}{\leq} 0} \\ {\frac{1+x+2}{(x+ 2)(x-2)} \leq 0} \\ {\frac{x+3}{(x+2)(x-2)} \leq 0}\end{массив}\)
9{2}-4}-\frac{1}{2-x} \leq 0} \\ {\frac{1}{(x+2)(x-2)}-\frac{1}{-( x-2)} \leq 0} \\ {\ frac {1} {(x + 2) (x-2)} + \ frac {1 \ color {Cerulean} {(x + 2)}} {\ color {черный}{(x-2)}\color{Cerulean}{(x+2)}}\color{black}{\leq} 0} \\ {\frac{1+x+2}{(x+ 2)(x-2)} \leq 0} \\ {\frac{x+3}{(x+2)(x-2)} \leq 0}\end{массив}\)
Критические числа являются \(−3, −2\) и \(2\). Обратите внимание, что \(±2\) являются ограничениями, и поэтому мы будем использовать открытые точки при их построении на числовой прямой. Из-за инклюзивного неравенства мы будем использовать закрытую точку в корне \(−3\).
Рисунок \(\PageIndex{18}\)Выберите тестовые значения \(-4, -2\frac{1}{2} = -\frac{5}{2}, 0\) и \(3\ ).
\(\begin{align}f(\color{OliveGreen}{-4}\color{black}{)}&= \frac{\color{OliveGreen}{-4}\color{black}{+} 3}{(\color{OliveGreen}{-4}\color{black}{+}2)(\color{OliveGreen}{-4}\color{black}{-}2)}&=\frac{( -)}{(-)(-)}=- \\ f(\color{OliveGreen}{-\frac{5}{2}}\color{black}{)} &= \frac{\color{OliveGreen }{-\frac{5}{2}}\color{black}{+}3}{(\color{OliveGreen}{-\frac{5}{2}}\color{black}{+}2) (\color{OliveGreen}{-\frac{5}{2}}\color{black}{-}2)}&=\frac{(+)}{(-)(-)}=+\\ f (\ color{OliveGreen}{0}\color{black}{)}&=\frac{\color{OliveGreen}{0}\color{black}{+}3}{(\color{OliveGreen}{0} \color{black}{+}2)(\color{OliveGreen}{0}\color{black}{-}2)}&=\frac{(+)}{(+)(-)}=- \ \ f(\color{OliveGreen}{3}\color{black}{)}&=\frac{\color{OliveGreen}{3}\color{black}{+}3}{(\color{OliveGreen}{ 3}\color{black}{+}2)(\color{OliveGreen}{3}\color{black}{-}2)} &=\frac{(+)}{(+)(+)}= +\конец{выровнено}\) 9{2}+7 x-4} \geq \frac{x}{x+4}\).
- Ответить
\((-4,0] \cup\left(\frac{1}{2}, \infty\right)\)
www.youtube.com/v/3ljcHJqExBY
Ключевые выводы
- Когда полиномиальное неравенство имеет стандартную форму с нулем на одной стороне, корни полинома являются критическими числами. Создайте диаграмму знаков, которая моделирует функцию, а затем используйте ее, чтобы ответить на вопрос.
- Когда рациональное неравенство записывается в виде одной алгебраической дроби с нулем на одной стороне, критическими числами являются как корни, так и ограничения. Значения, дающие нуль в числителе, являются корнями, а значения, дающими нуль в знаменателе, являются ограничениями. Всегда используйте открытые точки для ограничений, независимо от заданного неравенства, потому что ограничения не являются частью предметной области. Создайте диаграмму знаков, которая моделирует функцию, а затем используйте ее, чтобы ответить на вопрос.
 9{2}>0\)
9{2}>0\) - Ответить
1. \((-1,0) \cup(3, \infty)\)
3. \((-\infty,-2)\)
5. \((-\infty,-3] \cup\left[-2, \frac{1}{2}\right]\)
7. \((-2,0)\)
9. \(\left(-\infty,-\frac{3}{4}\right] \cup[0, \infty)\)
11. \((-\infty,-5] \cup[5,5] \cup[10, \infty)\)
13. \(\left(-\frac{9}{4}, 0\right)\)
- Ответить
1. \([-6,0] \чашка[4, \infty)\)
3. \(\left(-\infty,-\frac{1}{2}\right) \cup(0,6)\)
5. \((-\infty,-5) \cup\left(\frac{4}{3}, \infty\right)\)
7. \((-\infty, 0)\)
9. \([-2,-1] \чашка[1,2]\)
11. \((-\infty,-2) \cup(2, \infty)\)
13. \((-\infty,-3] \cup\left[\frac{1}{3}, 3\right]\)
15. \((3, \infty)\)
- \(\frac{x}{x-3}>0\)
- \(\frac{x-5}{x}>0\)
- \(\ frac{(x-3)(x+1)}{x}<0\)
- \(\ frac{(x+5)(x+4)}{(x-2)}<0\)
- \(\frac{(2 x+1)(x+5)}{(x-3)(x-5)} \leq 0\)
- \(\frac{(3 x-1)(x+6)}{(x-1)(x+9)} \geq 0\)
- \(\frac{(x-8)(x+8)}{-2 x(x-2)} \geq 0\)
- \(\frac{(2 x+7)(x+4)}{x(x+5)} \leq 0\) 9{4}}<0\)
- Ответить
1. \((-\infty,-0) \cup(3, \infty)\)
3. \((-\infty,-1) \cup(0,3)\)
5. \(\left[-5,-\frac{1}{2}\right] \cup(3,5)\)
7. \([-8,0) \чашка(2,8]\)
9. \(\left(-\frac{3}{2}, \frac{3}{2}\right)\)
11. \((-\infty,-5) \cup[0,6)\)
13. \((-\infty, 5) \cup(5, \infty)\)
- \(\frac{1}{x+5}+\frac{5}{x-1}>0\)
- \(\frac{5}{x+4}-\frac{1}{x-4}<0\)
- \(\frac{1}{x+7}>1\)
- \(\ гидроразрыва{1}{x-1}<-5\)
- \(х \geq \frac{30}{x-1}\)
- \(х \leq \frac{1-2 x}{x-2}\)
- \(\frac{1}{x-1} \leq \frac{2}{x}\)
- \(\frac{3}{x+1}>-\frac{1}{x}\)
- \(\frac{4}{x-3} \leq \frac{1}{x+3}\)
- \(\frac{2 x-9}{x}+\frac{49{2}-7 x-4} \leq \frac{5}{1+2 x}\)
- Ответить
1.
 \((-\infty,-4) \cup(-1,12)\)
\((-\infty,-4) \cup(-1,12)\)3. \(\left[-6,-\frac{1}{2}\right) \cup[5, \infty)\)
5. \(\left(-3, \frac{1}{3}\right] \cup[1,3)\)
7. \((-\infty, 2) \cup(10, \infty)\)
9. \(\left(-2,-\frac{1}{4}\right] \cup\left[\frac{1}{2}, \frac{7}{2}\right)\)
11. \((-5,-4) \cup(1, \infty)\)
13. \((-7,-6)\)
15. \([-5,1) \чашка[6, \infty)\)
17. \((0,1) \чашка[2, \infty)\)
19. \((-\infty, 5] \cup(-3,3)\)
21. \([-4,-2) \чашка(0,6]\)
23. \((-\infty,-2) \cup(2,4)\)
25. \(\left(-3,-\frac{1}{2}\right) \cup\left(\frac{1}{2}, \infty\right)\)
- Всегда ли чередуется таблица знаков для любой заданной полиномиальной или рациональной функции? Объясните и проиллюстрируйте свой ответ несколькими примерами.
- Напишите свои действия по решению рационального неравенства и проиллюстрируйте их примером.

Упражнение \(\PageIndex{4}\) 9{2}+12 х+20<0\)
Упражнение \(\PageIndex{5}\)
Решить.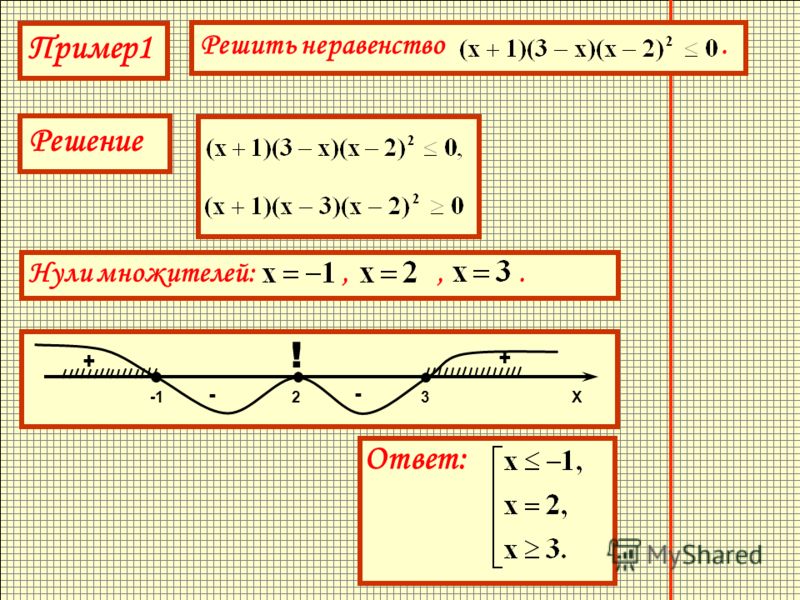
Упражнение \(\PageIndex{6}\) 9{2}+4 x-5} \geq 0\)
Упражнение \(\PageIndex{7}\)




 9{2}>0\)
9{2}>0\) \((-\infty,-4) \cup(-1,12)\)
\((-\infty,-4) \cup(-1,12)\)