Параллелограмм с равными диагоналями: Параллелограмм — признаки и свойства

Параллелограмм

• Определение параллелограмма
• Свойства параллелограмма
• Признаки параллелограмма
• Теоремы параллелограмма
• Углы параллелограмма
• Свойства диагоналей параллелограмма
• Как вычислить площадь параллелограмма?
• Как вписать параллелограмм в окружность?
• Как вписать окружность в параллелограмм?
• Как начертить параллелограмм?
• Трапеция — это параллелограмм?
• Средняя линия параллелограмма
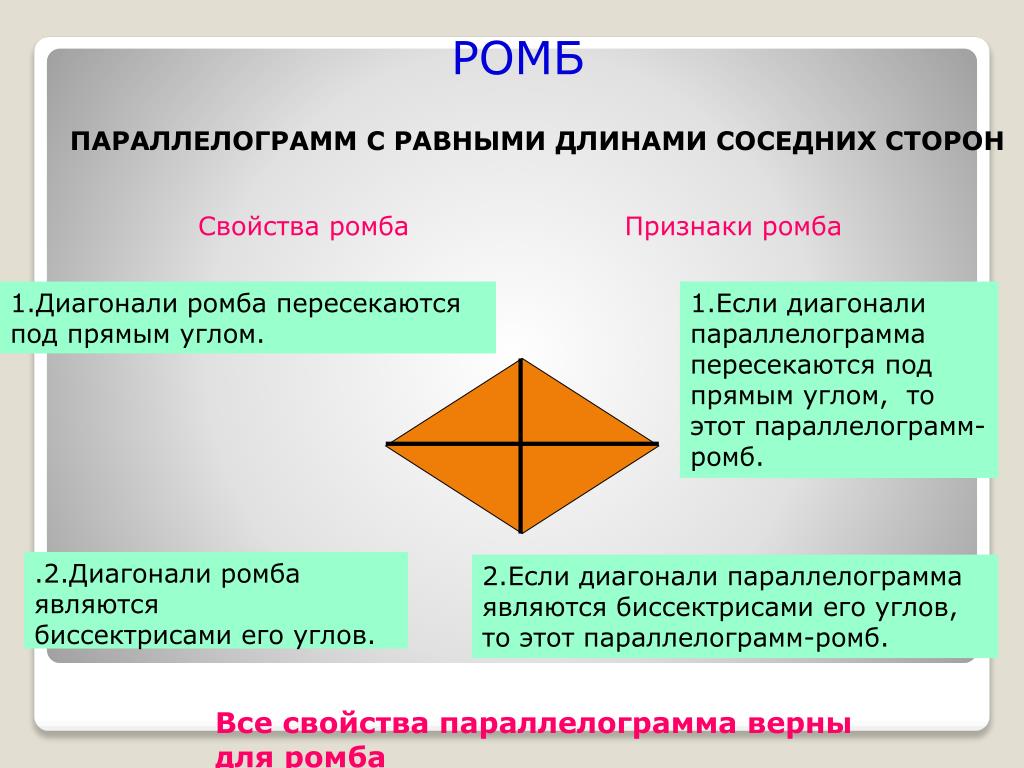
• Параллелограмм, у которого все стороны равны
• Ось симметрии параллелограмма

Определение параллелограмма

С этой фигурой знакомы все, освоившие курс школьной программы. Впервые с понятием «параллелограмм» встречаются в 8 классе на уроках геометрии.

Параллелограмм — геометрическая фигура, являющаяся разновидностью четырехугольника.

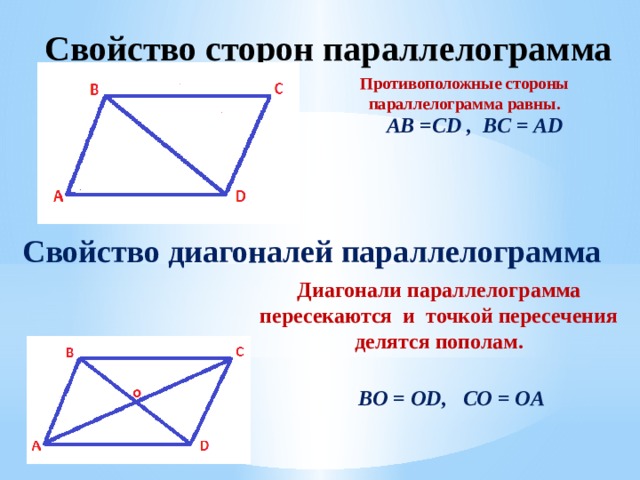
Противоположные стороны параллельны.

Стоит отметить, что всем известные фигуры, такие как квадрат, ромб, прямоугольник, являются параллелограммами. Исходя из этого, им можно дать следующие определения:

• Квадрат — параллелограмм с равными сторонами, пересекающимися под углом 90 градусов.
• Ромб — параллелограмм с равными между собой сторонами, не пересекающимися под углом 90 градусов.
• Прямоугольник — параллелограмм с неравными между собой сторонами, но пересекающимися под прямым углом.

Свойства параллелограмма

Для того чтобы определить параллелограмм, нужно обладать знанием о его свойствах. Рассмотрим их на примере четырехугольника MNPK.

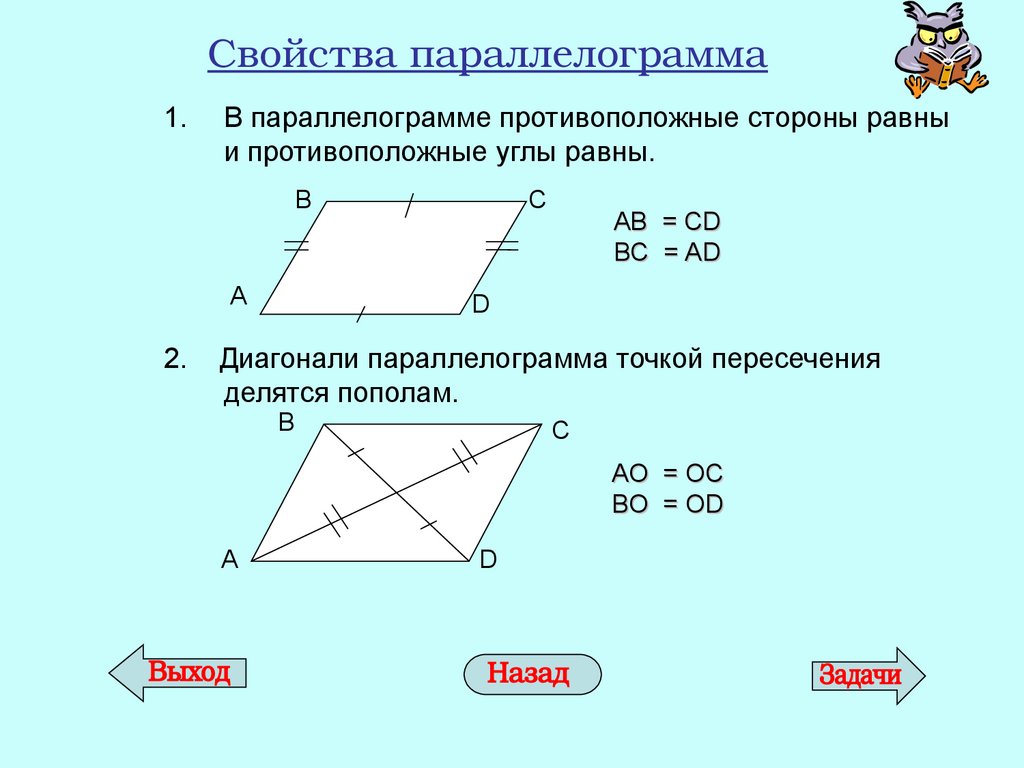
• Длина противоположных сторон фигуры одинакова.

MK=NP, MN=PK

• Противоположные стороны параллельны.

MK||NP, MN||PK

• Углы, являющиеся противоположными, равны.

∠NMK=∠NPK, ∠MNP=∠MKP

• Сумма всех четырех углов составляет 360 градусов.

∠NMK+∠NPK +∠MNP+∠MKP = 360°

• Сумма двух соседних углов равна 180 градусов.

∠NMK+∠MNP=∠NPK+∠MKP=∠MNP+∠NPK=∠MKP+∠NMK=180°

• Диагонали разделяют параллелограмм на два треугольника, равные между собой.
• При пересечении диагоналей образуется точка пересечения, представляющая собой центр симметрии.
• Диагонали пересекаются и точка их пересечения разделяет каждую диагональ пополам.
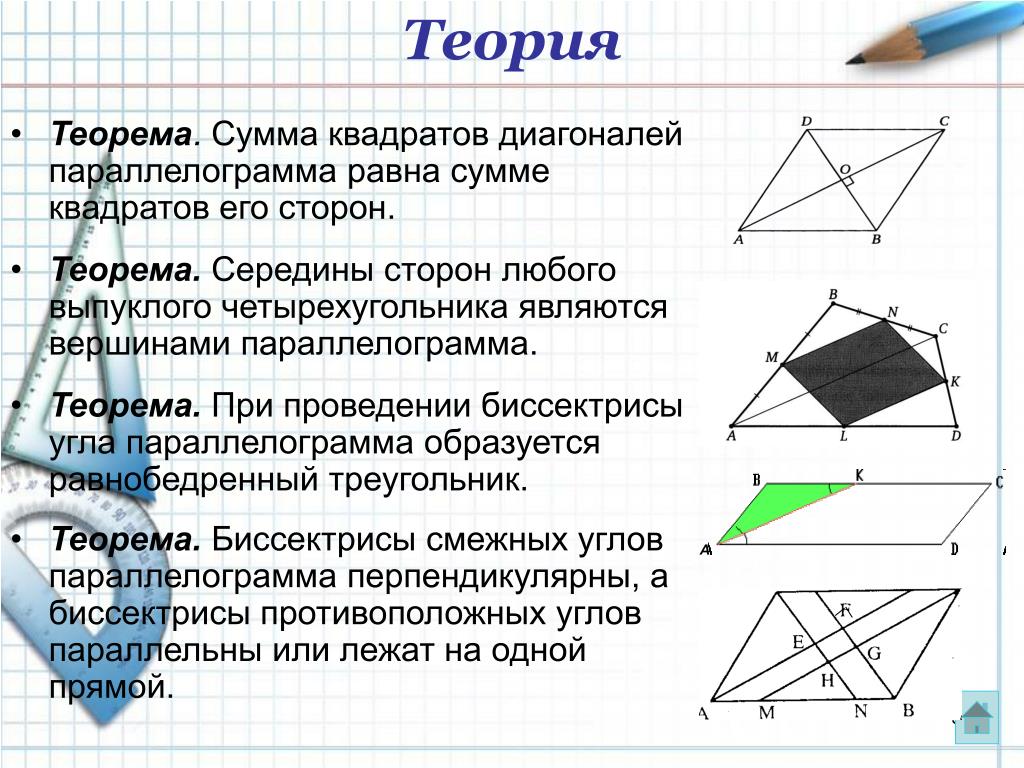
• Биссектриса, проведенная из любого угла, отделает от четырехугольника равнобедренный треугольник.

Признаки параллелограмма

Четырехугольник MNPK можно называть параллелограммом при выполнении минимум одного условия:

1. Противоположные стороны равны парами: MK=NP, MN=PK.
2. Противоположные углы равны парами: ∠NMK=∠NPK, ∠MNP=∠MKP.
3. Диагонали пересекаются, и точка их пересечения разделяет каждую диагональ пополам.
4. Противоположные стороны равны и параллельны между собой: MK=NP, MN|PK.
5. Сумма квадратов двух диагоналей равняется сумме квадратов четырех его сторон: MP²+NK²=MN²+NP²+PK²+MK².

Теоремы параллелограмма

Все существующие теоремы доказывают свойства параллелограмма и исходят из определения о том, что это четырехугольник с противоположно расположенными параллельными сторонами.

Основные теоремы доказывают, что:

• параллелограммом является выпуклый четырехугольник;
• противоположные стороны попарно равны;
• углы, являющиеся противоположными, попарно равны;
• точка пересечения диагоналей разделает их пополам.

Параллелограммом является выпуклый четырехугольник

Многоугольник признается выпуклым при условии отсутствия продления до прямой хотя бы одной из сторон, а все оставшиеся стороны будут располагаться по одну сторону от этой прямой.

Пусть дан параллелограмм MNPK, сторона MN противоположна PK, а MK противоположна NP. Следовательно, исходя из определения, следует вывод о том, что MN || PK, а MK || NP.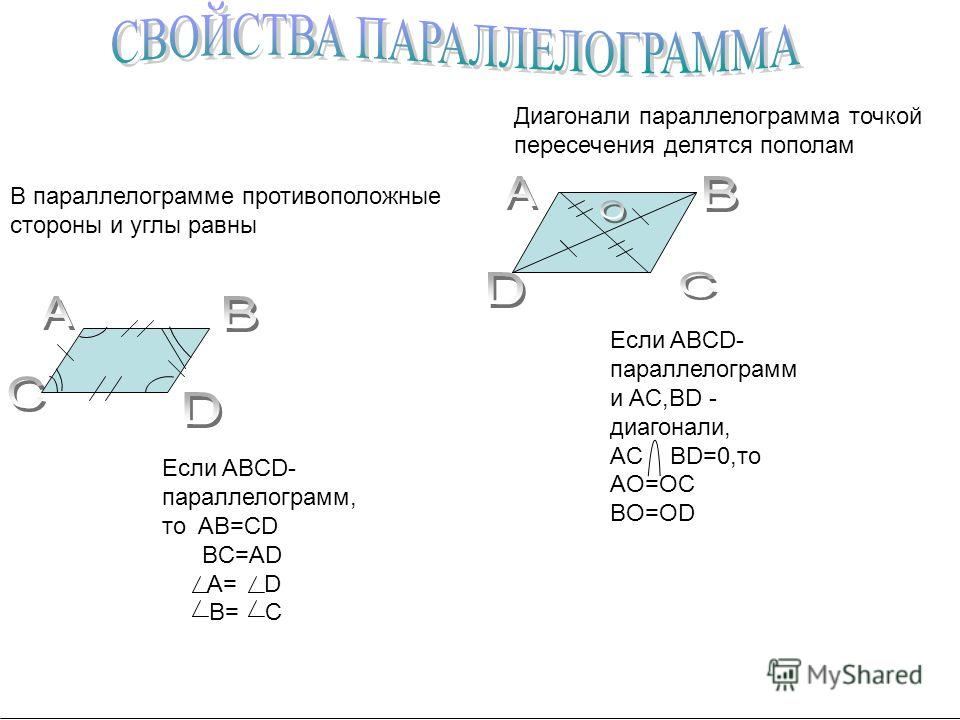

Параллельные отрезки общих точек соприкосновения не имеют. Следовательно, PK находится со стороной MN по одну сторону. Отрезок NP соединяет точку N отрезка MN с точкой P отрезка PK. Противоположный отрезок MK соединяет оставшиеся две точки отрезков, что дает право утверждать о нахождении отрезков NP и MK по одну сторону от прямой MN. Исходя из всего вышесказанного, можно сделать вывод о том, что три стороны PK, NP и MK располагаются по одну сторону от отрезка MN.

Аналогичный алгоритм доказательства предположения о нахождении трех других сторон по одну сторону относительно остальных.

Противоположные стороны и углы попарно равны

Имеется четырехугольник MNPK, у которого MK=NP, MN=PK, ∠NMK=∠NPK, ∠MNP=∠MKP.

Параллелограмм — это, как мы знаем, четырехугольник. Следовательно, имеет 2 диагонали. Зная о том, что это выпуклая фигура, делаем вывод о делении фигуры на два треугольника. В нашем случае образовались треугольники MNP и MKP.

У треугольников имеется общее — сторона MP.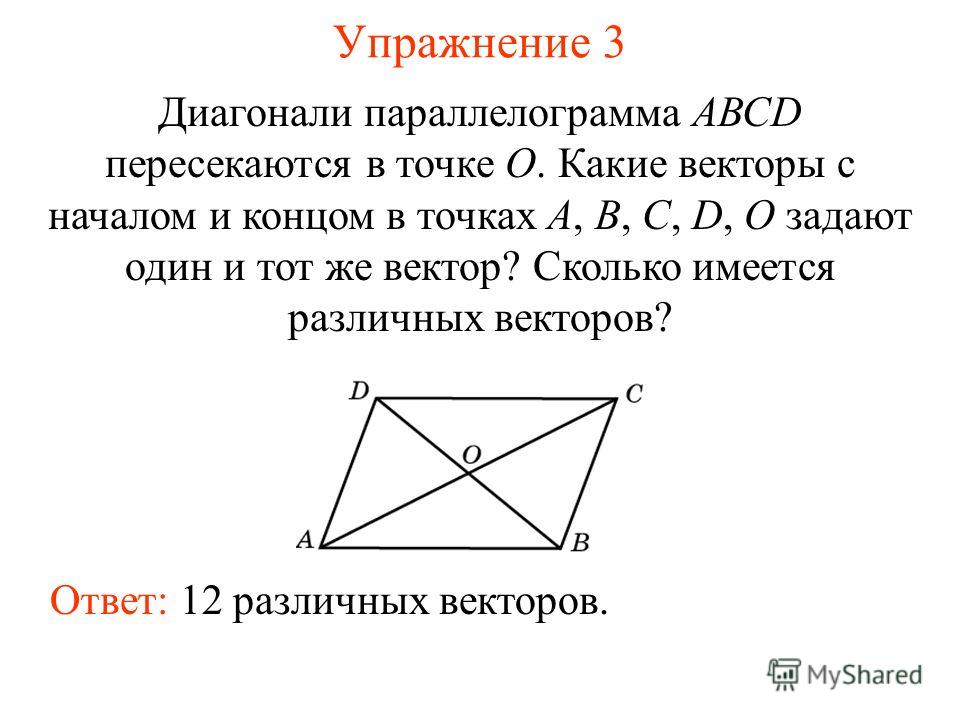 ∠NPM=∠PMK, а ∠NMP=∠MPK, так как накрест лежащие углы, пересекая параллельные прямые, равны.

Следовательно, ΔMNP=ΔMKP, так как одна общая сторона и два равных смежных угла. Отсюда NP=MK, MN=PK.

∠NMP=∠NMP+∠PMK

∠NPK=∠NPM+∠MPK

∠NPM=∠PMK и ∠NMP=∠MPK

Из равенств следует, что ∠NMK=∠NPK.

Таким образом, теорема о равенстве противоположных углов и сторон доказана.

Точка пересечения диагоналей разделяет их пополам

Зная, что параллелограмм представляет собой выпуклый четырёхугольник, можно сказать о наличии двух пересекающихся диагоналей.

Есть четырехугольник MNPK с диагоналями NK и PM, пересекающимися в точке O. Возьмем два полученных треугольника MNO и PKO.

Из свойства противоположно лежащих сторон параллелограмма следует равенство MN=PK. Угол MNO и угол OKP — накрест лежащие, следовательно, они равны. Аналогично, два других угла — NMO и OPK — являются равными. Делаем вывод о равенстве треугольников MNO и PKO по стороне и двум углам.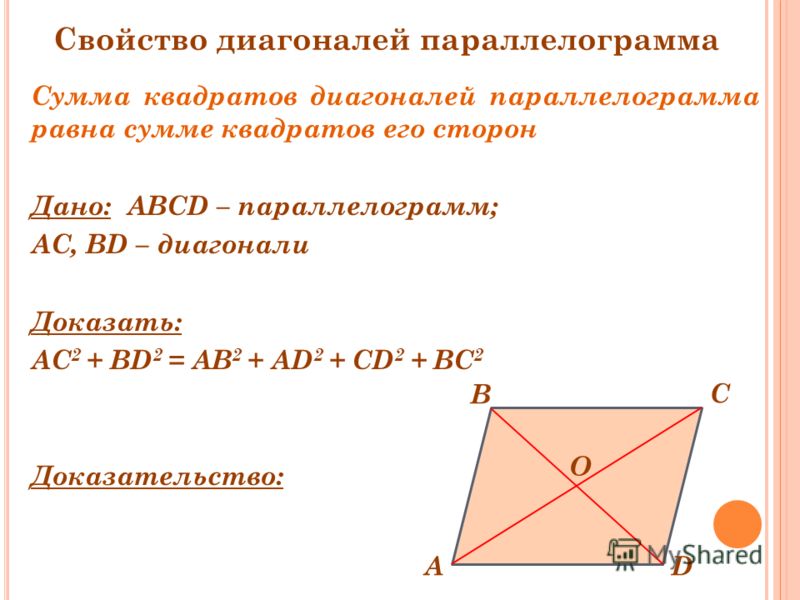

Из рисунка видно, что углы MON и KOP вертикальные, а значит, они равны.

Зная о равенстве образовавшихся треугольников, можно утверждать и о равенстве всех соответствующих элементов. Сторона MO равна стороне PO, как и сторона NO=OK. Каждая из пар вместе представляет собой диагональ параллелограмма.

Таким образом, теорема о делении диагоналей пополам доказана.

Углы параллелограмма

Для углов действует правило, согласно которому смежные углы в сумме дают 180 градусов, а два противоположных равны друг другу. Основываясь на этих утверждениях, значения остальных углов находятся по формуле:

∠α=180°-β

Свойства диагоналей параллелограмма

1. Точка пересечения диагоналей разделяет их пополам.
2. Любая диагональ разделяет фигуру на два треугольника, равные друг другу.
3. Сумма квадратов его диагоналей равняется сумме квадратов всех его сторон.
4. Площадь фигуры находится путем умножения длины диагоналей на синус угла, расположенного между ними, разделённый на 1/2.

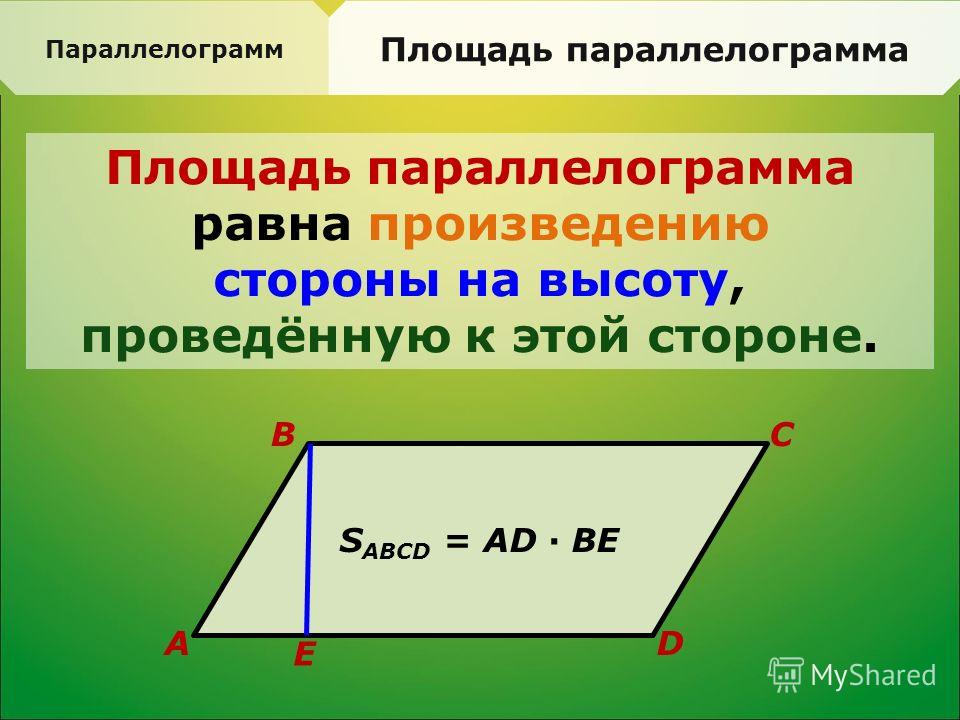
Как вычислить площадь параллелограмма?

Существует несколько вариантов нахождения площади:

1. По основанию и высоте: S=a*h.
2. Зная значение двух смежных сторон и угла между ними: S=a*b*sin(α)°.
3. По длине диагоналей и углу между ними: S=1/2*d₁*d₂*sin α.

Разберем подробнее последнюю формулу площади на примере. Дан параллелограмм с диагоналями АС и BD. Точка пересечения — О. Угол пересечения диагоналей в точке O = 60°. Отрезки AO=6 см и OD=5 см Площадь находится по формуле:

S=1/2*d₁*d₂*sin α

Зная свойство деления диагоналей точкой пересечения пополам, получаем:

AC=AO*2=12 см и DB=OD*2=10 см

Подставляем полученные значения в формулу:

S=1/2 * 12*10*1/2√3=51,962 см²

Как вписать параллелограмм в окружность?

Вписанный параллелограмм — это когда фигура находится внутри окружности.

Не каждый параллелограмм можно поместить внутрь окружности.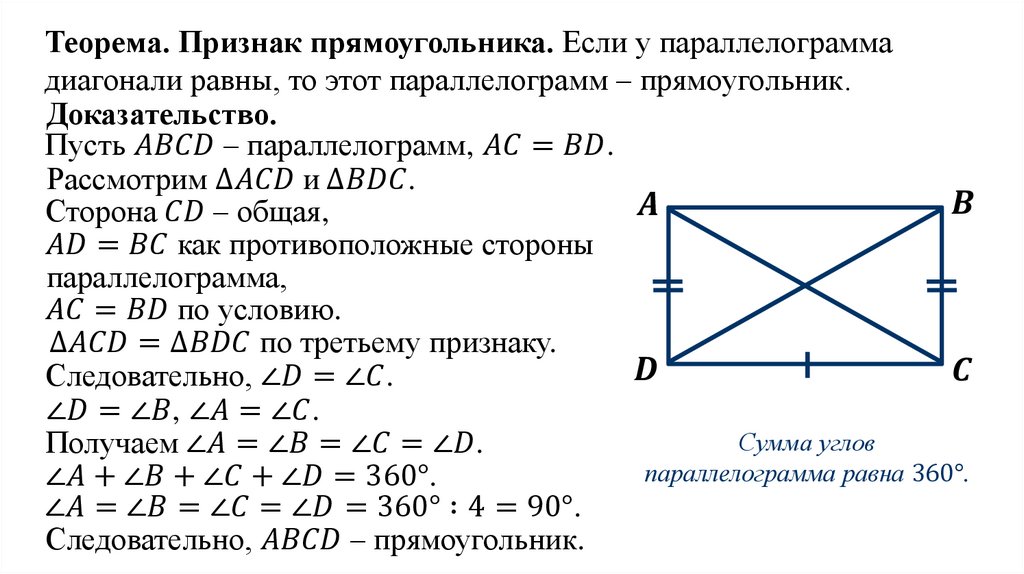 Эту манипуляцию можно проделать с той фигурой, у которой два противоположных угла в сумме составляют 180 градусов.

Из этого можно прийти к выводу, что у вписанного в окружность параллелограмма все четыре угла равны 90°. Параллелограмм бывает трех видов: квадрат, ромб, прямоугольник. Следовательно вписать в окружность можно прямоугольник, квадрат.

Алгоритм построения:

1. Начертить окружность.
2. Найти ее центр, обозначить буквой O.
3. Выбрать любую точку на окружности и назвать ее точкой A.
4. Если вписываем квадрат, то нужно построить два диаметра с углом между ними в 90 градусов. Точки пересечения диагоналей с окружностью соединить прямыми линиями.
5. Для прямоугольника нужно иметь значения угла между диагоналями или размеры сторон. Зная размеры сторон по теореме Пифагора, высчитываем угол между диагоналями. Проведя один диаметр, обозначить точки пересечения с окружностью. От точки O (центр окружности и середина диагонали) отмерить угол между диагоналями. Провести второй диаметр через центр и новую полученную точку. Соединить полученные точки прямыми.

Как вписать окружность в параллелограмм?

В окружность можно вписать параллелограмм при условии равнозначных сумм противолежащих сторон. Из трех вариантов параллелограмма сумма противоположных сторон одинакова только у ромба. Следовательно, если в параллелограмм вписана окружность, то этот параллелограмм является ромбом.

Алгоритм действий:

1. Начертить ромб можно, зная длину минимум одной стороны и одного угла.
2. Провести горизонтальную линию, равную длине стороны.
3. Транспортиром отмерить известный угол и провести луч.
4. На луче отмерить тот же самый размер стороны.
5. Оставшиеся две стороны нарисовать параллельно имеющимся.
6. Согласно свойству ромба и вписанной окружности, проводим две биссектрисы из смежных углов (они же диагонали в ромбе).
7. Пересечение биссектрис отметить точкой О.
8. Точка О будет центром окружности.
9. Вписанная окружность должна касаться всех сторон параллелограмма. Следовательно, стороны ромба будут касательными к окружности.
10. Касательные перпендикулярны радиусу, который проходит к точке касания. Таким образом, из центра окружности (точки О) надо опустить перпендикуляр к любой стороне ромба.
11. Иголку циркуля поставить в точку О, а ножку — на точку касания перпендикуляра со стороной ромба.
12. Начертить окружность.
13. Правильно начерченная фигура будет соприкасаться со всеми сторонами ромба.

Как начертить параллелограмм?

Рассмотрим схему построения каждого вида по отдельности.

Алгоритм построения квадрата

1. Узнать размер одной стороны. Этого достаточно, так как все стороны в квадрате равны.
2. Один из признаков квадрата — все углы равны 90 градусов.
3. Чертим прямую, равную длине одной стороны.
4. С каждой стороны проводим перпендикулярную линию.
5. На перпендикулярах отмечаем нужную длину и ставим точку.
6. Соединяем две точки, построенные на перпендикулярных прямых.

Построение ромба

1. Начертить ромб можно, зная длину минимум одной стороны и одного угла.
2. Провести горизонтальную линию, равную длине стороны.
3. Транспортиром отмерить известный угол и провести луч.
4. На луче отмерить тот же самый размер стороны.
5. Оставшиеся две стороны нарисовать параллельно имеющимся.

Как построить прямоугольник

1. Нужно знать значения длины и ширины.
2. Начертить прямую, равную длине.
3. Провести два перпендикуляра с обеих сторон отрезка.
4. Отметить на перпендикулярных линиях отрезок равный ширине прямоугольника.
5. Соединить полученные два отрезка.
6. При правильном построении полученная линия должны быть перпендикулярна длине (первой начерченной линии).

Трапеция — это параллелограмм?

Обе фигуры являются четырехугольниками с двумя противоположными сторонами, которые равны. Трапеция по определению имеет 2 непараллельные стороны. В параллелограмме все 4 стороны попарно параллельны.

Таким образом, трапеция не является параллелограммом.

Средняя линия параллелограмма

Под этим термином понимается отрезок, соединяющий середины противоположных сторон параллелограмма.

Средняя линия всегда равна параллельной ей стороне

Свойства средней линии в параллелограмме:

• точка пересечения диагоналей является точкой пересечения средних линий;
• точка пересечения делит средние линии пополам;
• точка пересечения выступает центром симметрии параллелограмма.

Параллелограмм, у которого все стороны равны

Все четыре стороны имеют равное значение в двух разновидностях фигуры — ромбе и квадрате.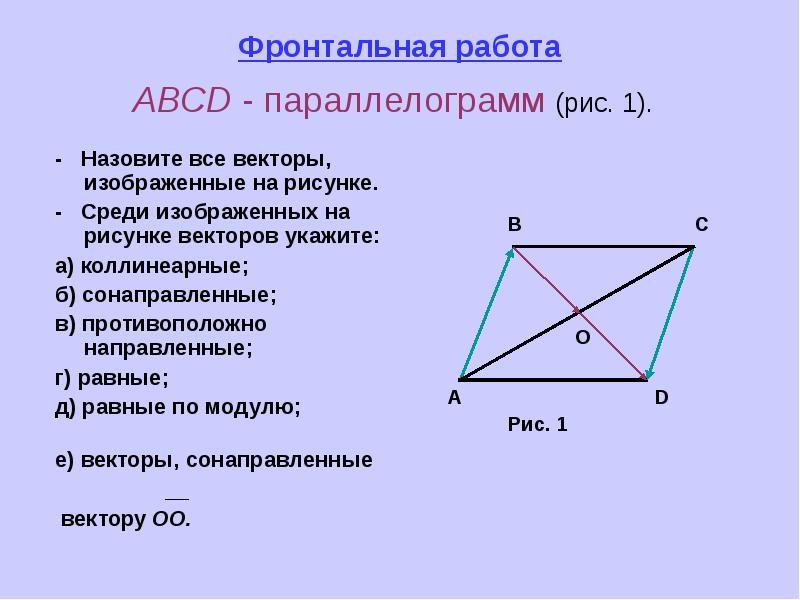

Ось симметрии параллелограмма

Под осью симметрии понимается прямая, разделяющая фигуру на две зеркально равные фигуры.

В прямоугольнике осью симметрии являются прямые, которые проходят через середину противоположной стороны.

В ромбе оси симметрии представляют собой его 2 диагонали.

Квадрат, объединяя в себе две предыдущие фигуры, имеет 4 оси симметрии: 2 диагонали и 2 средние линии.

Параллелограмм. Определение, свойства и признаки

Свойства параллелограмма

1. Противоположные стороны тождественны.

Доказательство

Первым делом проведем диагональ AC. Получаются два треугольника: ABC и ADC.

Так как ABCD — параллелограмм, то справедливо следующее:

AD || BC \Rightarrow \angle 1 = \angle 2 как лежащие накрест.

AB || CD \Rightarrow \angle3 = \angle 4 как лежащие накрест.

Следовательно, \triangle ABC = \triangle ADC (по второму признаку: \angle 1 = \angle 2, \angle 3 = \angle 4 и AC — общая).

И, значит, \triangle ABC = \triangle ADC, то AB = CD и AD = BC.

Доказано!

2. Противоположные углы тождественны.

Доказательство

Согласно доказательству свойства 1 мы знаем, что \angle 1 = \angle 2, \angle 3 = \angle 4. Таким образом сумма противоположных углов равна: \angle 1 + \angle 3 = \angle 2 + \angle 4. Учитывая, что \triangle ABC = \triangle ADC получаем \angle A = \angle C, \angle B = \angle D.

Доказано!

3. Диагонали разделены пополам точкой пересечения.

Доказательство

Проведем еще одну диагональ.

По свойству 1 мы знаем, что противоположные стороны тождественны: AB = CD. Еще раз отметим накрест лежащие равные углы.

Таким образом видно, что \triangle AOB = \triangle COD по второму признаку равенства треугольников (два угла и сторона между ними). То есть, BO = OD (напротив углов \angle 2 и \angle 1) и AO = OC (напротив углов \angle 3 и \angle 4 соответственно).

Доказано!

Признаки параллелограмма

Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.

Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?». То есть, как узнать, что заданная фигура это параллелограмм.

1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны.

AB = CD; AB || CD \Rightarrow ABCD — параллелограмм.

Доказательство

Рассмотрим подробнее. Почему AD || BC?

\triangle ABC = \triangle ADC по свойству 1: AB = CD, AC — общая и \angle 1 = \angle 2 как накрест лежащие при параллельных AB и CD и секущей AC.

Но если \triangle ABC = \triangle ADC, то \angle 3 = \angle 4 (лежат напротив AB и CD соответственно). И следовательно AD || BC (\angle 3 и \angle 4 — накрест лежащие тоже равны).

Первый признак верен.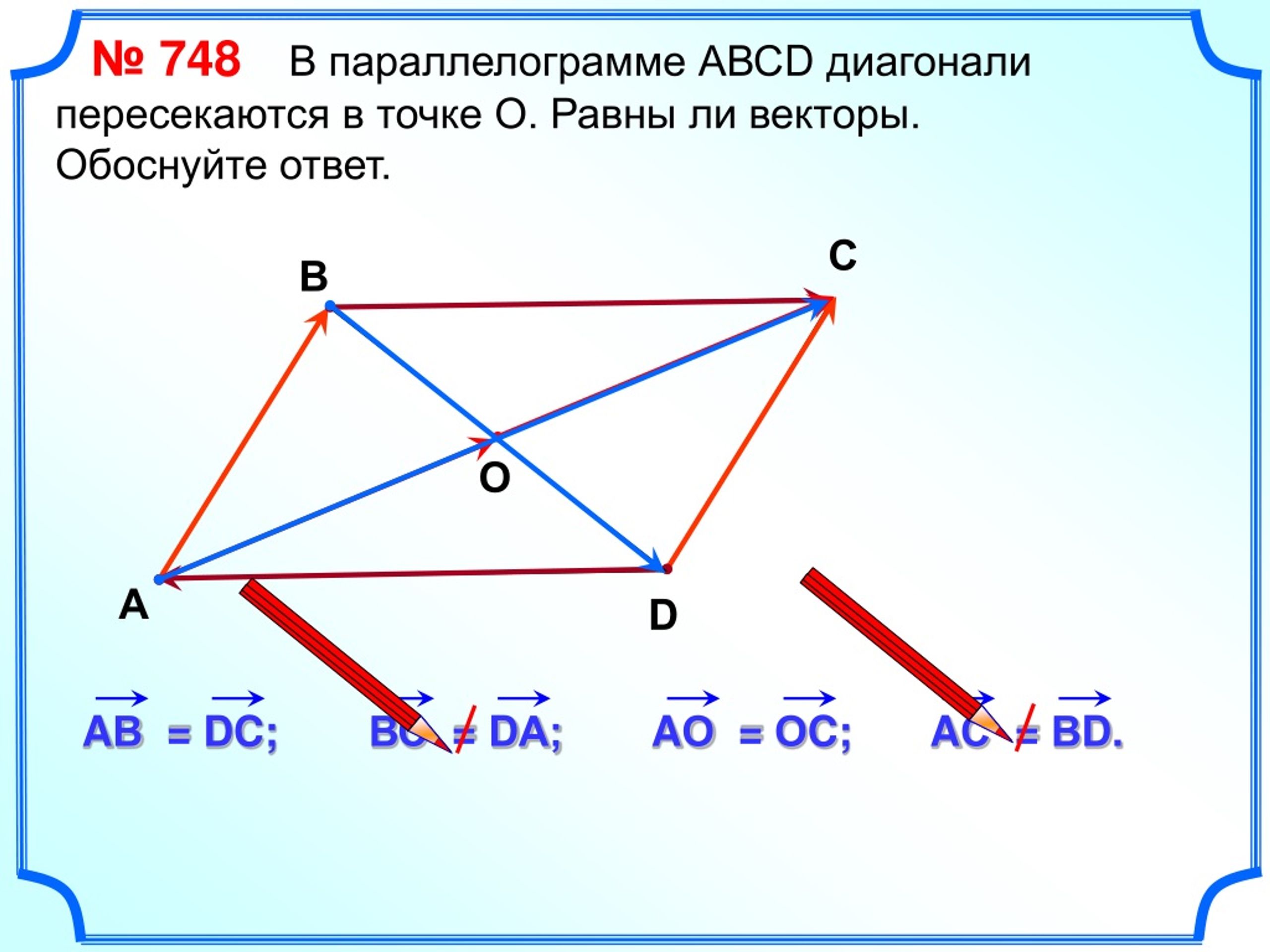 {\circ} говорит и о том, что AD || BC.

При этом \alpha и \beta — внутренние односторонние при секущей AD. И это значит AB || CD.

Третий признак верен.

4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам.

AO = OC; BO = OD \Rightarrow параллелограмм.

Доказательство

BO = OD; AO = OC, \angle 1 = \angle 2 как вертикальные \Rightarrow \triangle AOB = \triangle COD, \Rightarrow \angle 3 = \angle 4, и \Rightarrow AB || CD.

Аналогично BO = OD; AO = OC, \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8, и \Rightarrow AD || BC.

Четвертый признак верен.

геометрия — Является ли параллелограмм с равными сторонами обязательно ромбом? Обязательно ли прямоугольник с четырьмя прямыми углами (или равными диагоналями)?

Задавать вопрос

спросил 3 года, 1 месяц назад

Изменено 3 года, 1 месяц назад

Просмотрено 1к раз

$\begingroup$

Мы знаем, что ромб — это параллелограмм, у которого 1) равны стороны и 2) диагонали перпендикулярны друг другу.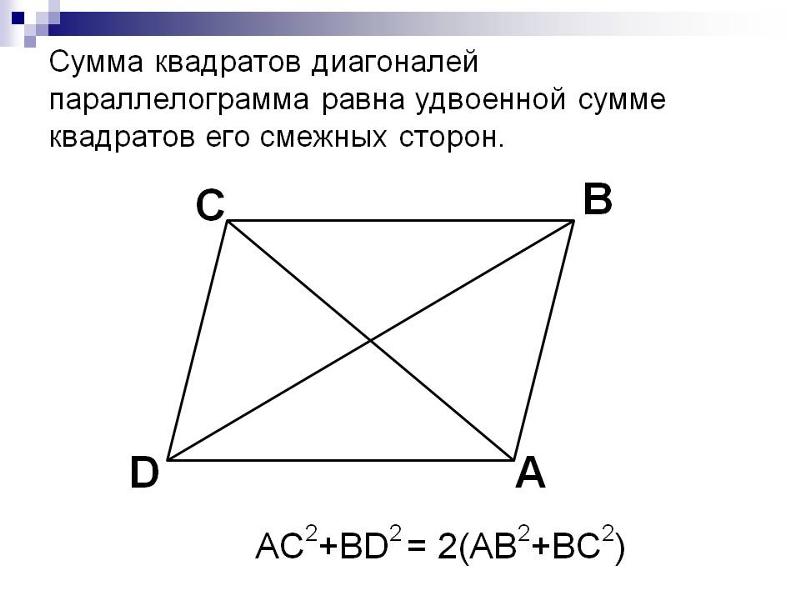 Если, например, нам говорят, что фигура является параллелограммом и что ее диагонали перпендикулярны, мы автоматически знаем, что это ромб, то есть мы знаем, что все его стороны равны.

Если нам говорят, что у параллелограмма все стороны равны, мы знаем, что это ромб?

С другой стороны, мы знаем, что прямоугольник — это параллелограмм, удовлетворяющий 1) всем углам равным 90° и 2) равные диагонали (т.е. равные диагонали).

Если нам говорят, что у параллелограмма 4 прямых угла, или, что то же самое, что у параллелограмма равны диагонали, можем ли мы сразу заключить, что это прямоугольник?

Подводя итог: четыре равные стороны в параллелограмме эквивалентны перпендикулярным диагоналям и, аналогично, четыре прямых угла в параллелограмме эквивалентны конгруэнтным диагоналям?

• геометрия
• прямоугольники
• четырехугольник

$\endgroup$

4

$\begingroup$

Вы должны быть ясны с определениями. Определение параллелограмма — это четырехугольник, противоположные стороны которого параллельны.Ромб определяется как четырехугольник с 4 равными сторонами.Теперь мы можем доказать, что в параллелограмме противоположные стороны имеют одинаковую длину. Теперь, если 2 смежные стороны параллелограмма равны, то он должен быть ромбом в соответствии с определением. Прямоугольник определяется как параллелограмм с одним из его углов прямым углом. А квадрат определяется как прямоугольник, смежные стороны которого equal.You может найти помощь в книге Евклидова геометрия первый курс-А Соломонович. И просьба указать свои сомнения в вопросе.

$\endgroup$

7

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Если диагонали параллелограмма равны, то докажите, что это прямоугольник…

Перейти к

• Четырехугольники — упражнение 8.1
• Четырехугольники — упражнение 8.2

• Система счисления
• Полиномы
• Координатная геометрия
• Линейные уравнения с двумя переменными
• Введение в геометрию Евклида
• Линии и углы
• Треугольники
• Четырехугольники
• Площади параллелограммов и треугольников
• Круги
• Конструкции
• Формула Герона
• Площади поверхности и объемы
• Статистика
• Вероятность

Главная > Решения НЦЭРТ Класс 9 Математика > Глава 8 — Четырехугольники > Четырехугольники — упражнение 8.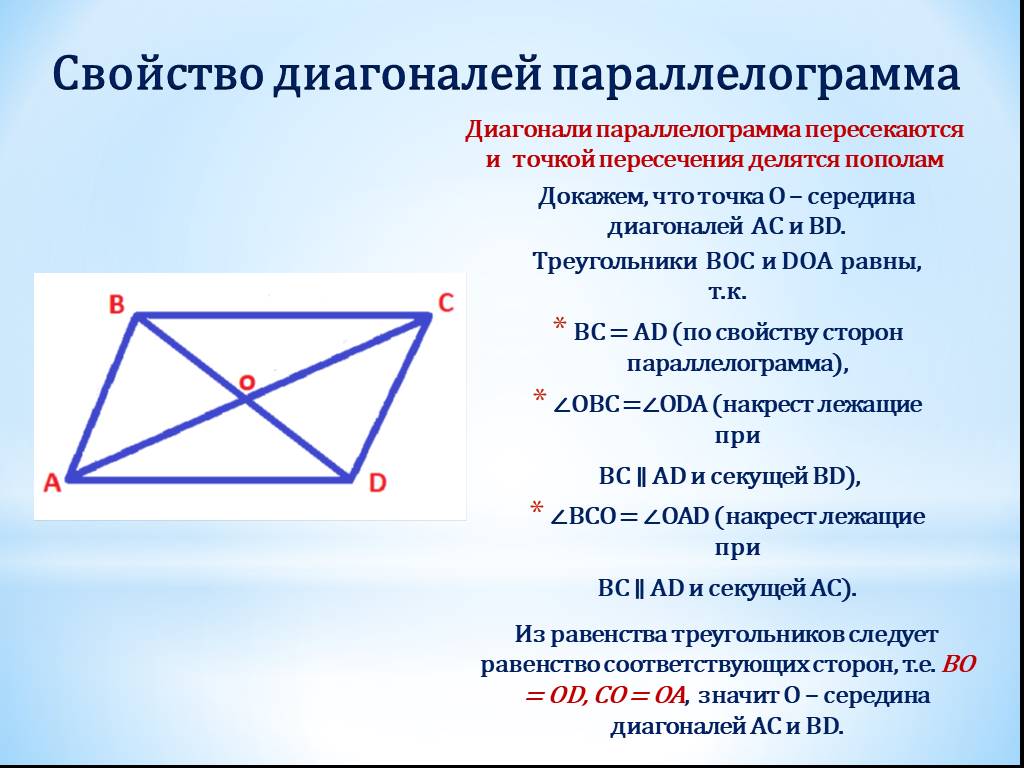 1 > Вопрос 2

Вопрос 2 Четырехугольники – Упражнение 8.1

Если диагонали параллелограмма равны, то докажите, что это прямоугольник.

Ответ:

Учитывая, что

AC = BD

Чтобы показать, что ABCD является прямоугольником, если диагонали параллелограмма равны

внутренние углы прямые.

Доказательство,

В ΔABC и ΔBAD,

BC = BA (Общий)

AC = AD (Противоположные стороны параллелограмма равны)

AC = BD (Дано)

Следовательно, ΔABC ≅ ΔBAD [Конгруэнтность SSS]

∠A = ∠B [Соответствующие части конгруэнтных треугольников] углы по одну сторону от секущей)

⇒ 2∠A = 180°

⇒ ∠A = 90° = ∠B

∴, ABCD — прямоугольник.

Отсюда Доказано.

Связанные вопросы

Углы четырехугольника относятся как 3 : 5 : 9: 13. Найдите все углы четырехугольника…

Докажите, что диагонали квадрата равны и делят друг друга пополам под прямым углом.

ABCD — прямоугольник, в котором диагональ AC делит пополам ∠A и ∠C. Покажите, что: (i) ABCD — квадрат (ii…

ABCD — параллелограмм, а AP и CQ — перпендикуляры из вершин A и C на диагонали BD (см.

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Четырехугольники — Упражнение 8.1

Четырехугольники — Упражнение 8.2

Главы

Система счисления

Многочлены

Координатная геометрия

Линейные уравнения в двух переменных

Введение в геометрию Euclids

Линии и углы

Треугольники

КВРЕДИЛИЧЕСКИЕ

СОЗДАНИЕ СОЗДАНИЕ

.