Прямоугольный треугольник косинус синус тангенс: синус, косинус, тангенс, котангенс угла

Синус, косинус и тангенс острого угла прямоугольного треугольника

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Синус, косинус и тангенс острого угла прямоугольного треугольника

Урок геометрии
в 8 классе

2. Устная работа

2. Составьте отношения
сходственных сторон подобных
треугольников ∆ABC и ∆KMN.
Устная работа
M
Решение :
AB AC BC
MK NK MN
B
2
N
3. Из пропорции составьте другие
верные пропорции.
1
AC BC
NK MN
K
6
MN BC
NK AC
C
3
∆ABC, ∆KMN –прямоугольные
∟С=∟N=90◦,∟A=∟K
1. Докажите, что ∆ABC~∆KMN
A
AC NK
BC MN
4. Проверьте верность составленных
пропорций при АС=3, ВС=6, NK=1,
MN=2
3 6
1 2
р
ве
но
2 6
1 3
р
ве
но
3 1
6 2
р
ве
но
5. Найдите гипотенузу каждого
треугольника.
AB 2 AC 2 BC 2
MK 2 MN 2 NK 2
AB 2 6 2 32 45
MK 2 2 2 12 5
AB 45 3 5
MK 5
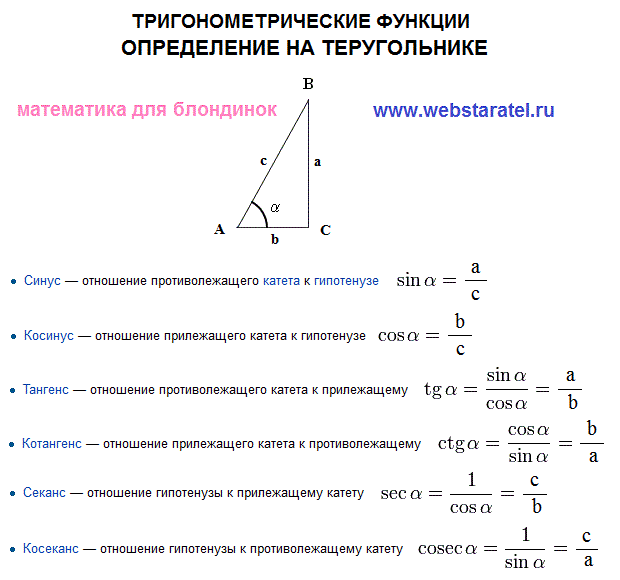
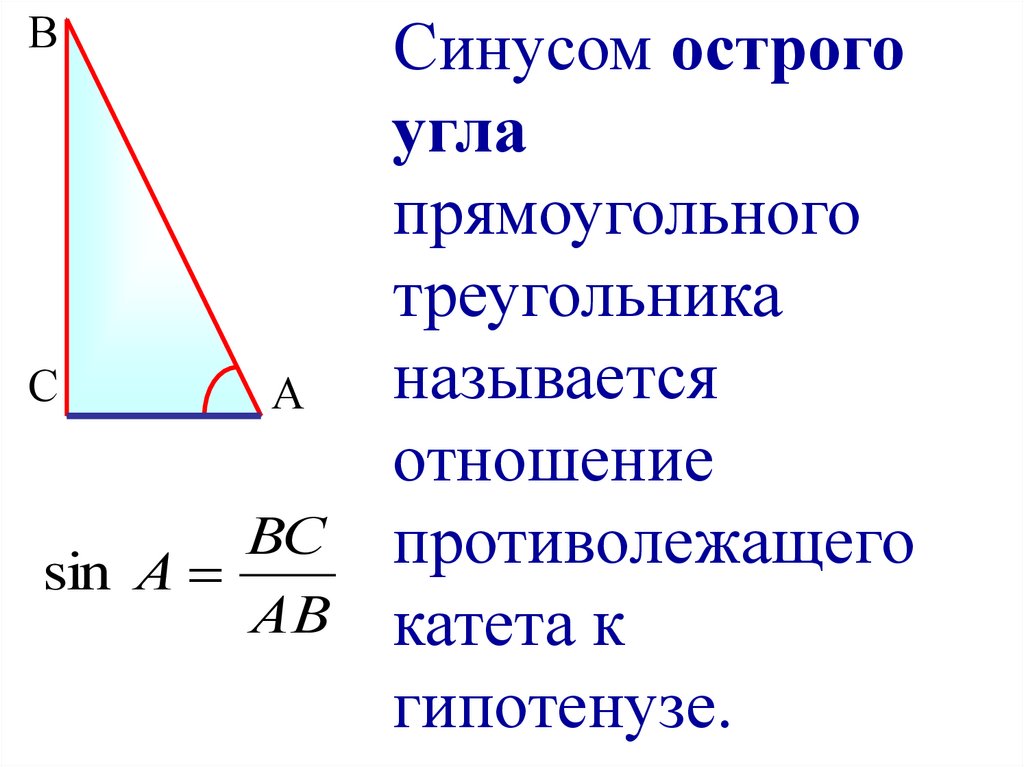
Рассмотрим прямоугольный треугольник АВС, где
∟С=90◦ и ∟А=α
В
Катет ВС является
противолежащим углу А.
Катет АС является
прилежащим к углу А.
АВ — гипотенуза
α
С
А
Работа с тренажером
Рассмотрим прямоугольный треугольник АВС, где ∟С=90◦ и ∟А=α
В
Синусом острого угла прямоугольного треугольника называется
отношение противолежащего катета к гипотенузе.
BC
BC
sin A
или sin
AB
AB
Косинусом острого угла прямоугольного треугольника
называется отношение прилежащего катета к гипотенузе.
cos A
AC
AC
или cos
AB
AB
Тангенсом острого угла прямоугольного
треугольника называется отношение
противолежащего катета к прилежащему.
α
С
А
tgA
BC
BC
или tg
AC
AC
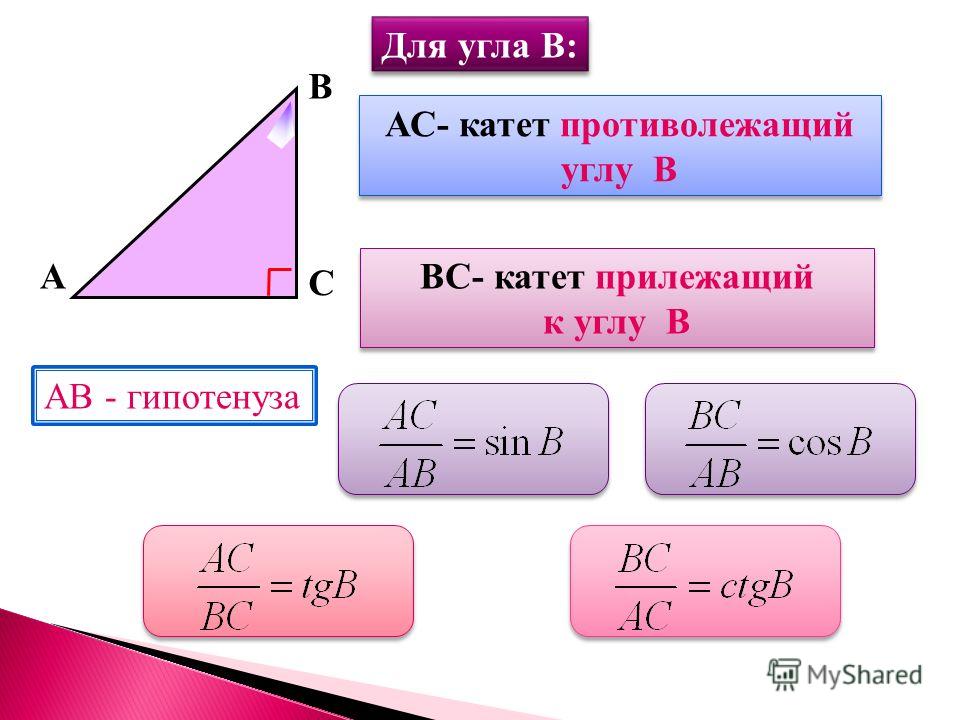
Исходя из определений, найдите синус, косинус и тангенс угла В.
В
Синусом острого угла прямоугольного треугольника называется
отношение противолежащего катета к гипотенузе.
AC
sin B
AB
Косинусом острого угла прямоугольного треугольника
называется отношение прилежащего катета к гипотенузе.
cos B
BC
AB
Тангенсом острого угла прямоугольного
треугольника называется отношение
противолежащего катета к прилежащему.
С
А
tgB
AC
BC
Найдите синус, косинус и тангенс углов А и В треугольника АВС с прямым
углом С, если ВС=8, АВ=17.
В
AC
AB 2 BC 2 289 64 225 15
sin А
cos A
8
17
tgA
BC 8
AB 17
AC 15
AB 17
BC 8
AC 15
sin B
AC 15
AB 17
cos B
BC 8
AB 17
tgB
С
15
А
AC 15
7
1
BC 8
8
Используя равенства
sin А
BC
AB
cos А
докажите, что
AC
AB
tgА
BC
AC
В
sin A
tgА
cos A
sin А cos A 1
2
2
При затруднении можно
использовать материал учебника.
А
С
sin A
tgА
cos A
sin А cos A 1
2
2
основное
тригономет рическое
тождество
Тригонометрия – математическая
дисциплина, изучающая зависимость
между сторонами и углами треугольника.
Слово «тригонометрия» составлено из
греческих слов: «тригонон» — треугольник
и «метрео» — измеряю, что означает
«измерение треугольников». Основная
задача тригонометрии состоит в решении
треугольников, т.е. в вычислении
неизвестных величин треугольника по
данным значениям других его величин.
Катет ВС является
противолежащим углу А.
В
Катет АС является
прилежащим к углу А.
АВ — гипотенуза
Синусом острого угла прямоугольного
треугольника называется отношение
противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного
треугольника называется отношение
прилежащего катета к гипотенузе.
С
А
Проверочная работа
Тангенсом острого угла
прямоугольного
треугольника называется
отношение
противолежащего катета к
прилежащему.
Творческое задание на выбор:
разработать чайнворд, кроссворд по данной
теме;
разработать мнемонические формулировки,
стихи и др.;
С тригонометрией сейчас
Знакомы даже звери.
Правила все говорят
Четко и уверенно.
И попросим мы зверят
Рассказать их для ребят.
Как мы косинус считаем,
Ты спроси медузу.
— Делим прилежащий катет
На гипотенузу.
Синус вычислить сумеет
Зверь любой из чащи:
На гипотенузу делит
Катет противолежащий.
Чтобы тангенс получить,
Нужно катеты делить.
Вы в числителе берете
Тот, что для угла напротив.
Тот, который прилежит,
В знаменателе пиши.

English     Русский Правила

«Синус, косинус и тангенс острого угла прямоугольного треугольника»

Урок по геометрии (8 класс) по теме: «Синус, косинус и тангенс острого угла прямоугольного треугольника»

Предмет:	Математика
Категория материала:	Конспекты
Автор:	Токарева Марина Алексеевна это Вы?

Урок разработан по теме: «Синус, косинус и тангенс острого угла прямоугольного треугольника» для класса базового уровня.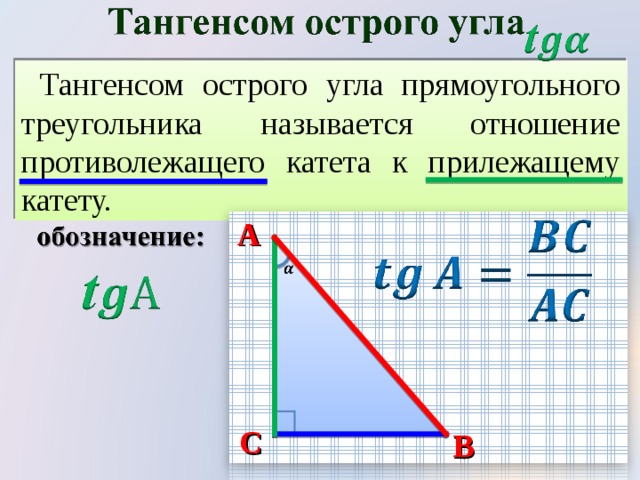 Предлагаемый материал для урока поможет учащимся отработать навыки решения заданий по указанной теме, которая используется в модуле «Геометрия» при сдаче ОГЭ. Кроме того, поможет систематизировать знания в процессе обучения. Упражнения на готовых чертежах дают возможность в течении минимума времени усвоить и повторить значительно больший объём материала и способствуют активизации мыслительной деятельности учащихся, являются эффективным средством усвоения и закрепления теоретического материала.

Муниципальное Бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №50

План урока

по геометрии

для учащихся 8 класса

по теме: ««Синус, косинус и тангенс острого угла

прямоугольного треугольника»

учителя математики М. А. Токаревой

Урок : «Геометрия» 8 класс

Тема: «Синус, косинус и тангенс острого угла

прямоугольного треугольника»

Эпиграф: «Где геометрический царствует лад, — там строгая царствует мысль.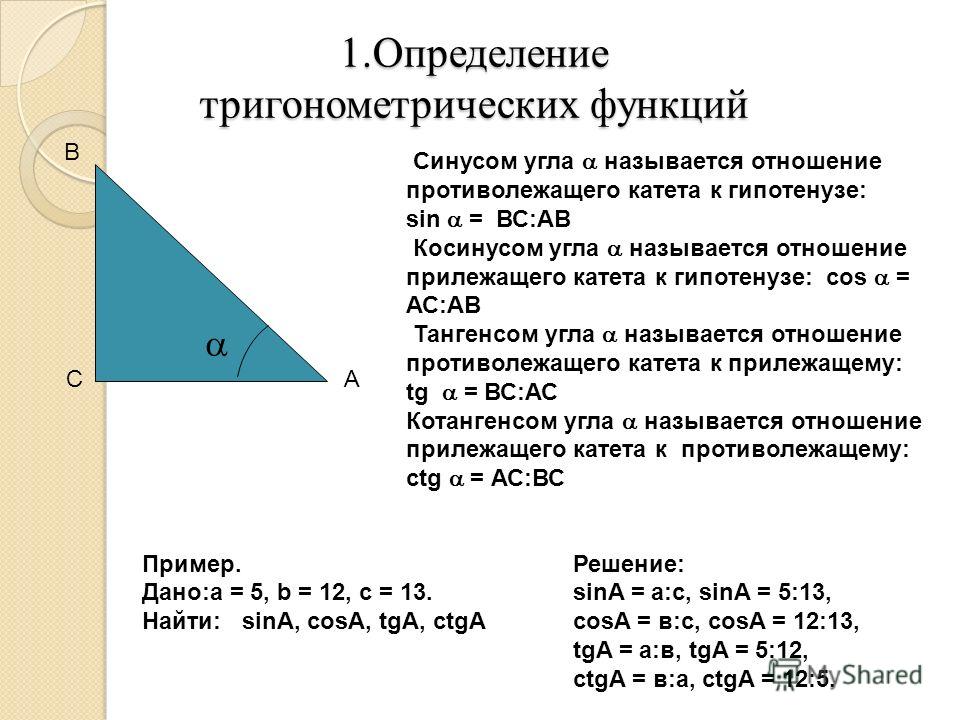 » (Э. Межелайтис)

Цели урока:

Дидактическая:

повторить понятия — синус, косинус, тангенс острого угла; научить применять полученные знания при решении прямоугольных треугольников;осуществить контроль и систематизацию знаний по данной темеРазвивающая:продолжить развитие алгоритмического мышления, памяти и мировоззрения учащихся, умения делать выводы и обобщать;продолжить развитие устной и письменной речи;продолжить становление и развитие личностных характеристикВоспитательная:сохранение физического и психического здоровья; воспитание нравственности и самостоятельности;воспитание на уроке воли и упорства для достижения конечных результатов, уважительного отношения друг к другу

Тип урока: урок закрепления знаний, их систематизации и формирования умений

Вид урока: обучение в сотрудничестве с элементами исследования

Методы проведения урока: словесный, наглядный, практический

Оборудование: тетради, опорные конспекты, ручки, раздаточный материал, мел, доска, чертежные инструменты

ХОД УРОКА

Организационный момент. Сообщение темы урока, постановка целейПриветствие.

Учитель: Как символ вечного союза,

Как вечный символ, знак простой,

Связала ты, гипотенуза,

Навеки катеты собой

На предыдущих уроках мы познакомились с вами с понятиями: синус, косинус, тангенс острого угла прямоугольного треугольника и основным тригонометрическим тождеством.

Тема нашего урока: Решение задач по теме «Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника».

Но прежде чем приступить к решению задач нам необходимо … Что?

Ученики: Нам необходимо повторить понятия тригонометрических функций, вспомнить основное тригонометрическое тождество, а также применять приобретённые знания при решении задач.

Актуализация опорных знаний. (Фронтальный опрос с элементами исследования)Проверка теоретических знаний:

Учитель:

На доске заготовлен прямоугольный треугольник

В

С А

Вопросы:

Какой треугольник называется прямоугольным?Как называются стороны у прямоугольного треугольника?Назовите катет, прилежащий к углу А?Назовите катет, прилежащий к углу В?Назовите катет, противолежащий углу А?Назовите катет, противолежащий углу В?Что называется синусом, косинусом, тангенсом острого угла прямоугольного треугольника?Запишите чему равен синус, косинус, тангенс угла А и угла В?Ученики: (формулируют определения).

Решение типовых задач по готовым чертежам. Самостоятельная работа1. Дан прямоугольный треугольник ЕКМ, катеты равны 3 см и 4 см. Вычислить синус, косинус и тангенс острых углов.

Е

К М

2. Гипотенуза АВ прямоугольного треугольника равна 10 см, а один из катетов равен 8 см.

Чему равны тангенсы его острых углов?

А

В С

Самостоятельная работа

I вариант

Дан прямоугольный треугольник АВС с прямым углом С.

II вариант

Дан прямоугольный треугольник NKP с прямым углом K.

С 12 В

Вычислить синус, косинус и тангенс острых углов.

Р

15 9

N K

Вычислить синус, косинус и тангенс острых углов.

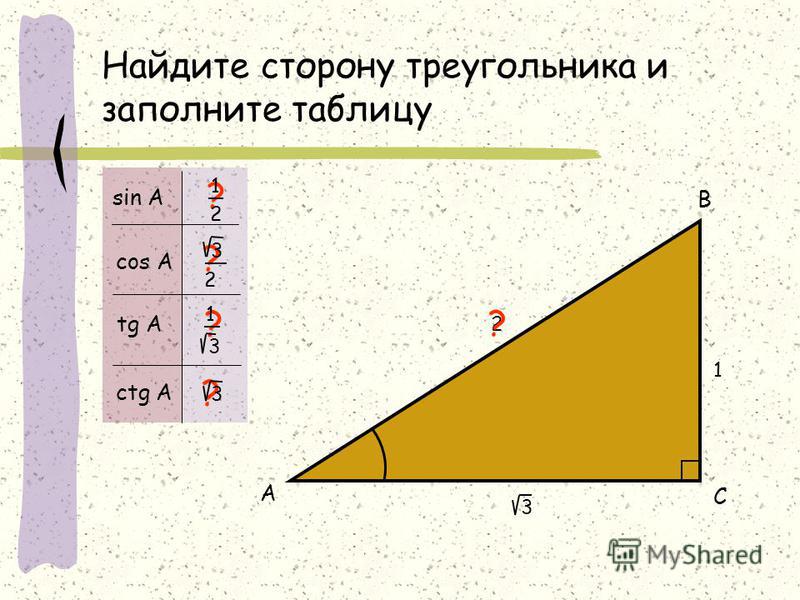
Значение синуса, косинуса и тангенса для углов 30°, 45° и 60°. Составление таблицы

Исследовательская работа – один учащийся работает у доски, выводим значения синуса, косинуса и тангенса для углов 30°, 45° и 60° (с помощью учителя) и заполняем таблицу значений для этих углов в опорных конспектах.

sin α

cos α

tg α

Подведение итогов: Выставление оценок.Домашнее задание: п.67, № 602

Тип материала:	Документ Microsoft Word (docx)
Размер:	174.33 Kb
Количество скачиваний:	253

Если Вы являетесь автором этой работы и хотите отредактировать, либо удалить ее с сайта — свяжитесь, пожалуйста, с нами.

7.2: Тригонометрия прямоугольного треугольника — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

50216

• OpenStax
• OpenStax

Цели обучения

• Использование прямоугольных треугольников для вычисления тригонометрических функций.
• Найдите значения функции для 30°(\(\dfrac{\pi}{6}\)), 45°(\(\dfrac{\pi}{4}\)) и 60°(\(\dfrac{ \pi}{3}\)).
• Использовать равные кофункции дополнительных углов.
• Используйте определения тригонометрических функций любого угла.
• Используйте тригонометрию прямоугольного треугольника для решения прикладных задач.

Эверест, расположенный на границе между Китаем и Непалом, является самой высокой горой в мире. Измерение его высоты — непростая задача, и на самом деле фактическое измерение было источником споров на протяжении сотен лет. Процесс измерения включает использование треугольников и раздел математики, известный как тригонометрия. В этом разделе мы определим новую группу функций, известную как тригонометрические функции, и выясним, как их можно использовать для измерения высоты, например высоты самых высоких гор.

Ранее мы определили синус и косинус угла через координаты точки на единичной окружности, пересекаемой конечной стороной угла:

\[ \begin{align*} \cos t &= x \\ \sin t &=y \end{align*} \]

В этом разделе мы увидим другой способ определения тригонометрических функций с использованием свойств прямоугольных треугольников .

Использование прямоугольных треугольников для вычисления тригонометрических функций

В предыдущих разделах мы использовали единичный круг для определения тригонометрические функции . В этом разделе мы расширим эти определения, чтобы их можно было применять к прямоугольным треугольникам. Значением функции синуса или косинуса \(t\) является ее значение в \(t\) радианах. Во-первых, нам нужно создать наш прямоугольный треугольник. На рисунке \(\PageIndex{1}\) показана точка на единичной окружности радиуса 1. Если мы опустим вертикальный отрезок из точки \((x,y)\) на ось x , мы получим прямоугольный треугольник, у которого вертикальная сторона имеет длину \(y\), а горизонтальная сторона имеет длину \(x\). Мы можем использовать этот прямоугольный треугольник, чтобы переопределить синус, косинус и другие тригонометрические функции как отношения сторон прямоугольного треугольника.

Рисунок \(\PageIndex{1}\)

Мы знаем

\[ \cos t= \frac{x}{1}=x \]

Аналогично, мы знаем

\[ \sin t= \frac {y}{1}=y \]

Эти отношения по-прежнему применяются к сторонам прямоугольного треугольника, когда не используется единичная окружность и когда треугольник не находится в стандартном положении и не отображается на графике с использованием \((x,y )\) координаты. Чтобы иметь возможность свободно использовать эти отношения, мы дадим сторонам более общие имена: вместо \(x\) мы будем называть сторону между данным углом и прямым углом примыкающая сторона к углу \(t\). (Adjacent означает «рядом с».) Вместо \(y\) мы будем называть сторону, наиболее удаленную от данного угла, противоположной стороной от угла \(t\). И вместо \(1\) мы будем называть сторону прямоугольного треугольника, противоположную прямому углу, гипотенузой . Эти стороны обозначены на рисунке \(\PageIndex{2}\).

Рисунок \(\PageIndex{2}\): отношение сторон прямоугольного треугольника к углу \(t\).

Понимание отношений прямоугольного треугольника

Дан прямоугольный треугольник с острым углом \(t\),

\[\begin{align} \sin (t) &= \dfrac{\text{противоположный}}{\text{гипотенуза}} \ label{sindef}\\ \cos (t) &= \dfrac{\text{смежный}}{\text{гипотенуза}} \label{cosdef}\\ \tan (t) &= \dfrac{\text{напротив }}{\text{adjacent}} \label{tandef}\end{align}\]

Обычная мнемоника для запоминания этих отношений — SohCahToa, образованная из первых букв « S ine is o pposite over ч ypotenuse, C osine это a djacent над h ypotenuse, T angent это o pposite над djacent. ”

как: Зная длины сторон прямоугольного треугольника и один из острых углов, найти синус, косинус и тангенс этого угла

1. Найти синус как отношение противолежащего катета к гипотенузе.
2. Найдите косинус как отношение прилежащего катета к гипотенузе.
3. Найдите тангенс отношения противолежащего катета к прилежащему.

Пример \(\PageIndex{1}\): вычисление тригонометрической функции прямоугольного треугольника

Учитывая треугольник, показанный на рисунке \(\PageIndex{3}\), найдите значение \(\cos α\) .

Рисунок \(\PageIndex{3}\)

Решение

Сторона, прилегающая к углу, равна 15, а гипотенуза треугольника равна 17, поэтому с помощью уравнения \ref{cosdef}:

\[\begin {align*} \cos (α) &= \dfrac{\text{adjacent}}{\text{гипотенуза}} \\[4pt] &= \dfrac{15}{17} \end{align*}\]

Упражнение \(\PageIndex{1}\)

Учитывая треугольник, показанный на рисунке \(\PageIndex{4}\), найдите значение \(\sin t\).

Рисунок \(\PageIndex{4}\)

Ответ

\(\frac{7}{25}\)

Взаимосвязь углов и их функции

При работе с прямоугольными треугольниками применяются одни и те же правила независимо от ориентации треугольника. На самом деле, мы можем вычислить шесть тригонометрических функций любого из двух острых углов треугольника на рисунке \(\PageIndex{5}\). Сторона, противолежащая одному острому углу, является стороной, примыкающей к другому острому углу, и наоборот.

Рисунок \(\PageIndex{5}\): Сторона, примыкающая к одному углу, противоположна другому.

Нас попросят найти все шесть тригонометрических функций для данного угла в треугольнике. Наша стратегия состоит в том, чтобы сначала найти синус, косинус и тангенс углов. Затем мы можем легко найти другие тригонометрические функции, потому что мы знаем, что обратная величина синуса является косекансом, обратная величина косинуса является секансом, а обратная величина тангенса является котангенсом.

как: Зная длины сторон прямоугольного треугольника, вычислить шесть тригонометрических функций одного из острых углов

1. При необходимости нарисуйте прямоугольный треугольник и обозначьте его угол.
2. Определите угол, прилежащую сторону, сторону, противоположную углу, и гипотенузу прямоугольного треугольника.
3. Найдите нужную функцию:
   • синус как отношение противолежащего катета к гипотенузе
   • косинус как отношение прилежащего катета к гипотенузе
   • тангенс как отношение противоположной стороны к прилежащей стороне
   • секанс как отношение гипотенузы к прилежащему катету
   • косеканс как отношение гипотенузы к противолежащему катету
   • котангенс как отношение прилежащей стороны к противолежащей стороне

Пример \(\PageIndex{2}\): оценка тригонометрических функций углов, не находящихся в стандартном положении

Используя треугольник, показанный на рисунке \(\PageIndex{6}\), оцените \( \sin α, \cos α , \tan α, \sec α, \csc α,\) и \( \cot α\).

Рисунок \(\PageIndex{6}\)

Решение

\[ \begin{align*} \sin α &= \dfrac{\text{напротив} α}{\text{гипотенуза}} = \dfrac {4}{5} \\ \cos α &= \dfrac{\text{рядом с}α}{\text{гипотенуза}}=\dfrac{3}{5} \\ \tan α &= \dfrac{ \text{напротив}α}{\text{рядом с}α}=\dfrac{4}{3} \\ \sec α &= \dfrac{\text{гипотенуза}}{\text{рядом с}α} = \dfrac{5}{3} \\ \csc α &= \dfrac{\text{гипотенуза}}{\text{напротив}α}=\dfrac{5}{4} \\ \cot α &= \ dfrac{\text{рядом с}α}{\text{напротив}α}=\dfrac{3}{4} \end{align*}\]

Упражнение \(\PageIndex{2}\)

Используя треугольник, показанный на рисунке \(\PageIndex{7}\), оцените \( \sin t, \cos t,\tan t, \sec t, \ csc t,\) и \(\cot t\).

Рисунок \(\PageIndex{7}\)

Ответ

\[\begin{align*} \sin t &= \frac{33}{65}, \cos t= \frac{56}{65},\tan t= \frac{33}{56}, \ \ \\ \sec t &= \frac{65}{56},\csc t= \frac{65}{33},\cot t= \frac{56}{33} \end{align*}\]

Нахождение тригонометрических функций специальных углов с использованием длин сторон

Мы уже обсуждали тригонометрические функции, связанные с специальными углами на единичной окружности.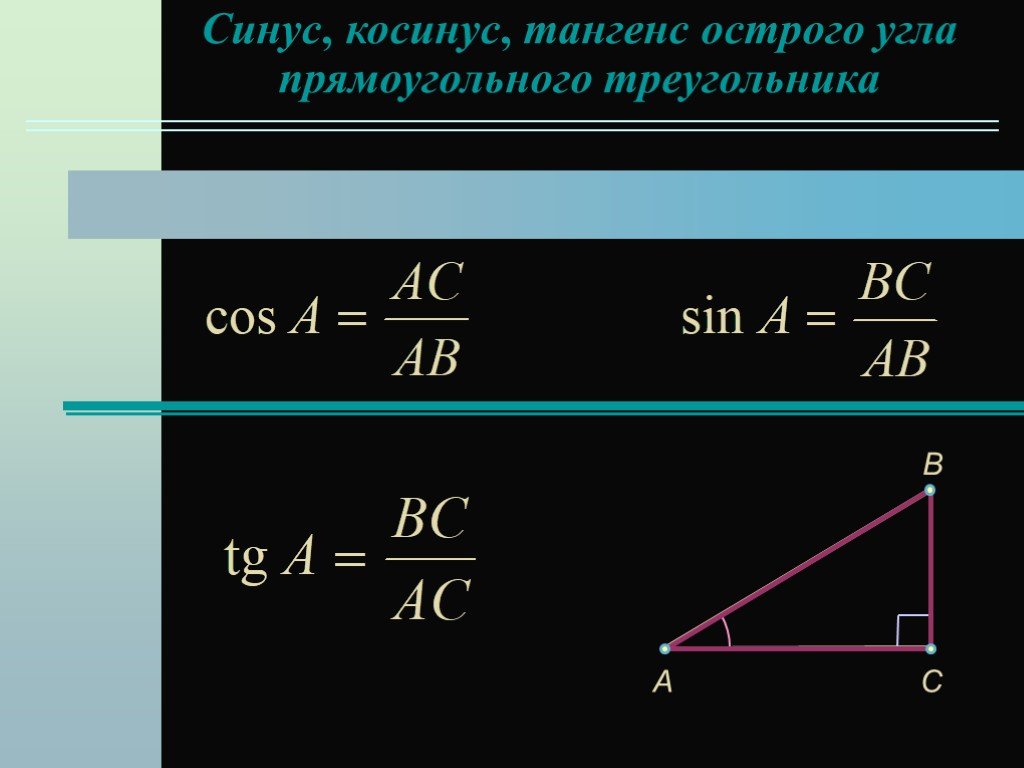 Теперь мы можем использовать эти отношения для оценки треугольников, содержащих эти особые углы. Мы делаем это потому, что когда мы оцениваем специальные углы в тригонометрических функциях, они имеют относительно удобные значения, значения, которые либо не содержат, либо содержат только один квадратный корень из отношения. Поэтому эти углы часто используются в математических и научных задачах. Мы будем использовать числа, кратные \(30°, 60°,\) и \(45°\), однако помните, что при работе с прямоугольными треугольниками мы ограничены углами между \(0° \text{ и } 90°\).

Предположим, у нас есть треугольник \(30°,60°,90°\), который также может быть описан как \(\frac{π}{6}, \frac{π}{3},\frac{ π}{2}\) треугольник. Стороны имеют длины в соотношении \(s,\sqrt{3}s,2s.\) Стороны треугольника \(45°,45°,90°\), который также может быть описан как \(\ frac{π}{4},\frac{π}{4},\frac{π}{2}\) треугольника, имеют длины в соотношении \(s,s,\sqrt{2}s.\) Эти отношения показаны на рисунке \(\PageIndex{8}\).

Рисунок \(\PageIndex{8}\): Длины сторон особых треугольников

Затем мы можем использовать отношения длин сторон для вычисления тригонометрических функций особых углов.

Даны тригонометрические функции специального угла, оцените их по длинам сторон.

1. Используйте длины сторон, показанные на рисунке \(\PageIndex{8}\), для специального угла, который вы хотите оценить.
2. Используйте соотношение длин сторон, соответствующее функции, которую вы хотите оценить.

Пример \(\PageIndex{3}\): вычисление тригонометрических функций специальных углов с использованием длин сторон

Найдите точное значение тригонометрических функций \(\frac{π}{3}\) с использованием длин сторон.

Решение

\[\begin{align*} \sin (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{hyp}}=\dfrac{\ sqrt{3}s}{2s}=\dfrac{\sqrt{3}}{2} \\ \cos (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text {hyp}} = \ dfrac {s} {2s} = \ dfrac {1} {2} \\ \ tan (\ dfrac {π} {3}) & = \ dfrac {\ text {opp}} {\ text {adj}} =\dfrac{\sqrt{3}s}{s}=\sqrt{3} \\ \sec (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{ \text{adj}} = \dfrac{2s}{s}=2 \\ \csc (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{opp}} = \dfrac{2s}{\sqrt{3}s}=\dfrac{2}{\sqrt{3}}=\dfrac{2\sqrt{3}}{3} \\ \cot (\dfrac{π} {3}) &= \dfrac{\text{adj}}{\text{opp}}=\dfrac{s}{\sqrt{3}s}=\dfrac{1}{\sqrt{3}}= \dfrac{\sqrt{3}}{3} \end{align*}\]

Упражнение \(\PageIndex{3}\)

Найдите точное значение тригонометрических функций \(\frac{π}{4}\), используя длины сторон.

Ответить

\( \ sin (\ frac {π} {4}) = \ frac {\ sqrt {2}} {2}, \ cos (\ frac {π} {4}) = \ frac {\ sqrt {2} {2}, \tan (\frac{π}{4})=1,\)

\( \sec (\frac{π}{4})=\sqrt{2}, \csc (\frac{π}{4})=\sqrt{2}, \cot (\frac{π}{ 4}) =1 \)

Использование равной кофункции дополнений

Если мы более внимательно посмотрим на соотношение между синусом и косинусом специальных углов относительно единичного круга, мы заметим закономерность. В прямоугольном треугольнике с углами \(\frac{π}{6}\) и \(\frac{π}{3}\) синус \(\frac{π}{3}\ ), а именно \(\frac{\sqrt{3}}{2}\), также является косинусом \(\frac{π}{6}\), а синус \(\frac{π}{ 6}\), а именно \(\frac{1}{2},\) также является косинусом \(\frac{π}{3}\) (рис. \(\PageIndex{9}\)).

\[\begin{align*} \sin \frac{π}{3} &= \cos \frac{π}{6}=\frac{\sqrt{3}s}{2s}=\frac{ \sqrt{3}}{2} \\ \sin \frac{π}{6} &= \cos \frac{π}{3}=\frac{s}{2s}=\frac{1}{2 } \end{выравнивание*}\]

Рисунок \(\PageIndex{9}\): синус \(\frac{π}{3}\) равен косинусу \(\frac{π}{6}\) и наоборот.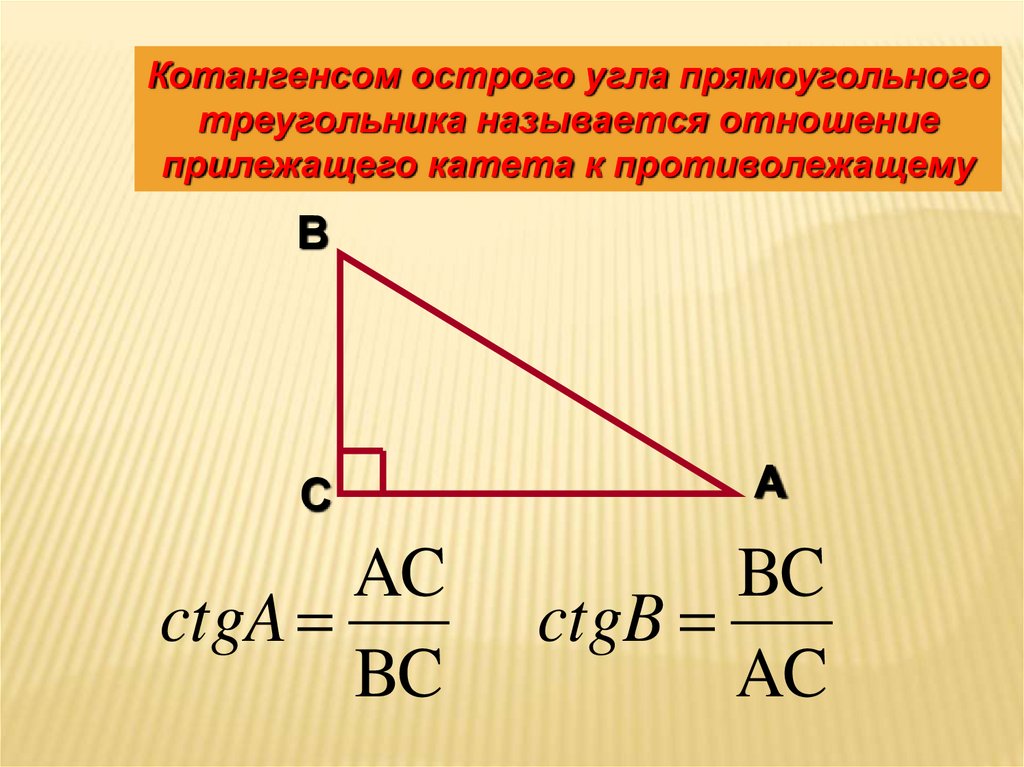

Этот результат не должен вызывать удивления, поскольку, как видно из рисунка \(\PageIndex{9}\), сторона, противоположная углу \(\frac{π}{3}\), также является стороной, примыкающей к \( \frac{π}{6}\), так что \(\sin (\frac{π}{3})\) и \(\cos (\frac{π}{6})\) имеют точно такое же отношение из тех же двух сторон, \(\sqrt{3} s\) и \(2s.\) Аналогично, \( \cos (\frac{π}{3})\) и \( \sin (\frac{ π}{6})\) также являются одним и тем же отношением, используя те же две стороны, \(s\) и \(2s\).

Взаимосвязь между синусом и косинусом фигур \(\frac{π}{6}\) и \(\frac{π}{3}\) также имеет место для двух острых углов любого прямоугольного треугольника, поскольку в каждом В этом случае отношение тех же двух сторон составит синус одного угла и косинус другого. Поскольку сумма трех углов треугольника равна π, а прямой угол равен \(\frac{π}{2}\), оставшиеся два угла также должны составлять \(\frac{π}{2}\) . Это означает, что прямоугольный треугольник может быть образован любыми двумя углами, которые складываются с \(\frac{π}{2}\) — другими словами, любыми двумя дополнительными углами.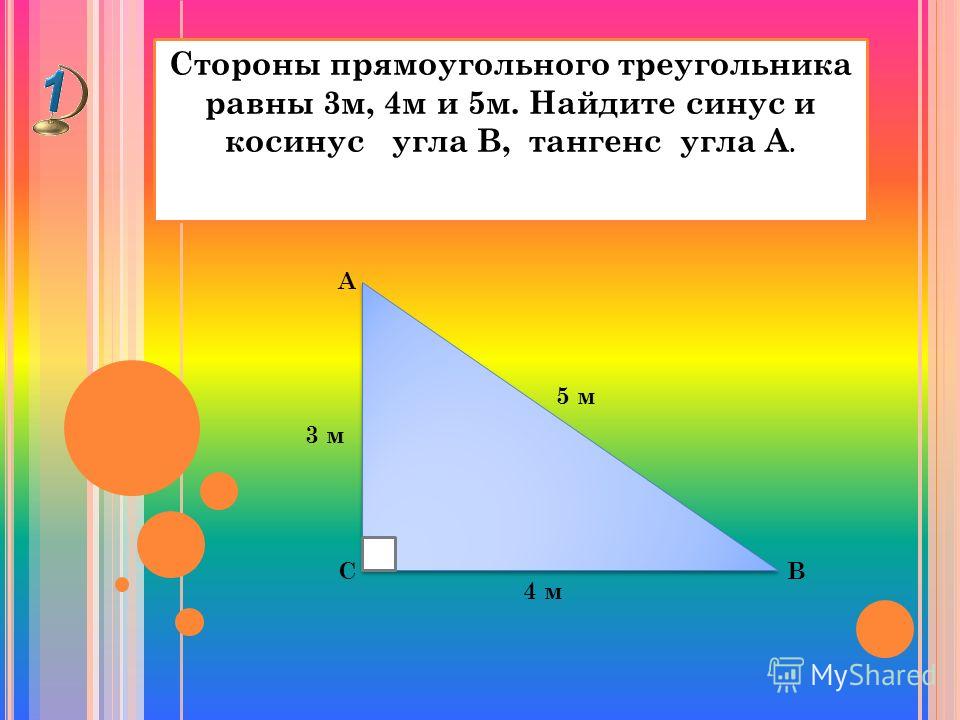 Таким образом, мы можем констатировать тождество кофункции : Если любые два угла дополняют друг друга, то синус одного равен косинусу другого, и наоборот. Это удостоверение показано на рисунке \(\PageIndex{10}\).

Рисунок \(\PageIndex{10}\): тождество кофункции синуса и косинуса дополнительных углов ) равен косинусу \(\frac{5π}{12}\), а синус \(\frac{5π}{12}\) равен косинусу \(\frac{π}{12}\ ). Мы также можем утверждать, что если для некоторого угла \(t, \cos t= \frac{5}{13},\), то \( \sin (\frac{π}{2}−t)=\frac {5}{13}\).

ИДЕНТИЧНОСТИ КОФУНКЦИЙ

тождества кофункций в радианах перечислены в таблице \(\PageIndex{1}\).

Таблица \(\PageIndex{1}\)

\( \cos t= \sin (\frac{π}{2}−t)\)	\( \sin t= \cos (\dfrac{π}{2}−t)\)
\( \tan t= \cot (\dfrac{π}{2}−t) \)	\( \cot t= \tan (\dfrac{π}{2}−t)\)
\( \sec t= \csc (\dfrac{π}{2}−t) \)	\( \csc t= \sec (\dfrac{π}{2}−t)\)

как: Зная синус и косинус угла, найти синус или косинус его дополнения.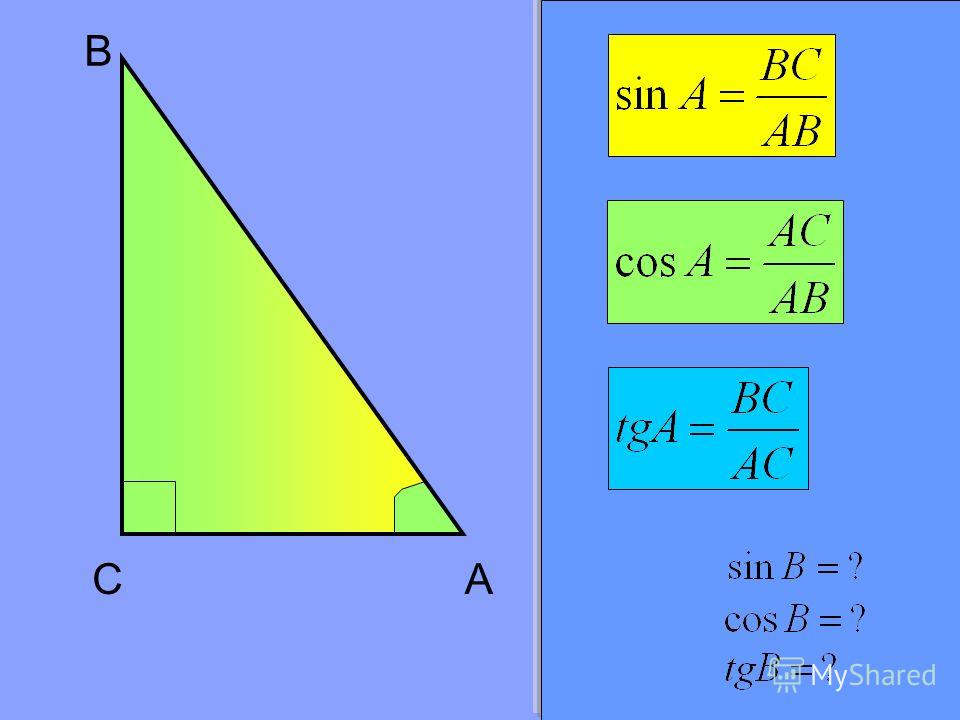

1. Чтобы найти синус дополнительного угла, найдите косинус исходного угла.
2. Чтобы найти косинус дополнительного угла, найдите синус исходного угла.

Пример \(\PageIndex{4}\): использование тождеств кофункций

Если \( \sin t = \frac{5}{12},\) найти \(( \cos \frac{π}{2} −t)\).

Решение

Согласно тождествам кофункций для синуса и косинуса,

\[ \sin t= \cos (\dfrac{π}{2}−t). \nonumber\]

Итак,

\[ \cos (\dfrac{π}{2}−t)= \dfrac{5}{12}. \nonumber\]

Упражнение \(\PageIndex{4}\)

Если \(\csc (\frac{π}{6})=2,\) найти \( \sec (\frac{π} {3}).\)

Решение

2

Использование тригонометрических функций

В предыдущих примерах мы вычисляли синус и косинус в треугольниках, для которых были известны все три стороны. Но настоящая сила тригонометрии прямоугольного треугольника проявляется, когда мы смотрим на треугольники, в которых мы знаем угол, но не знаем всех сторон.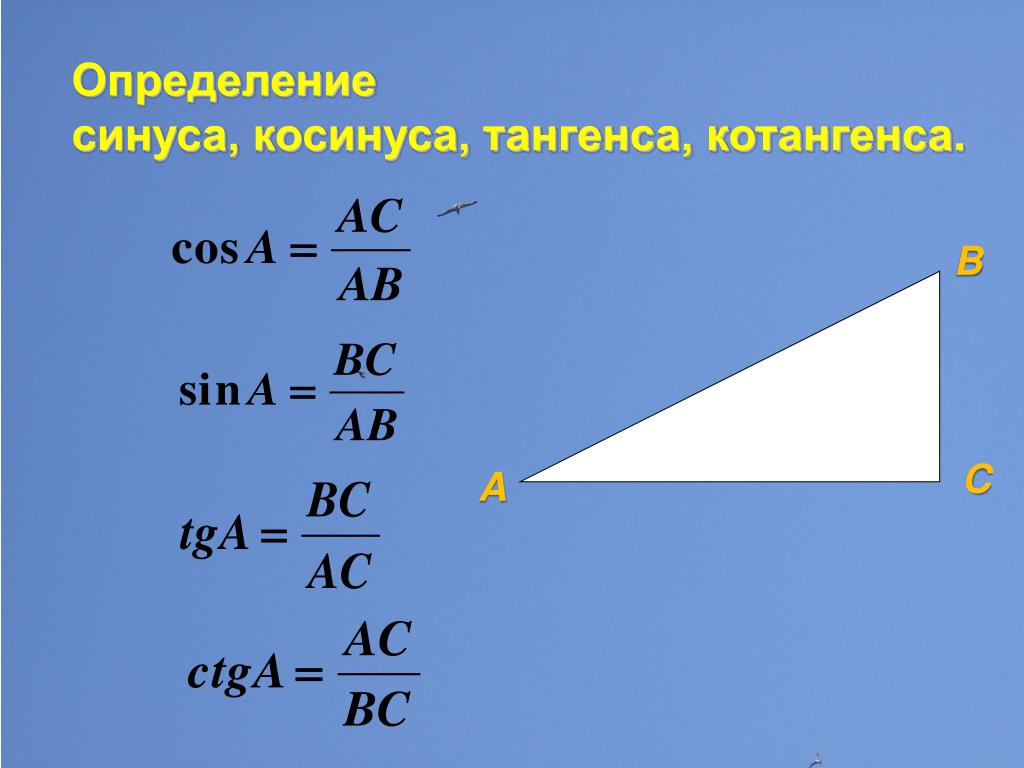

как: Имея прямоугольный треугольник, длину одной стороны и величину одного острого угла, найти остальные стороны знаменатель. Известная сторона, в свою очередь, будет знаменателем или числителем.

1. Напишите уравнение, в котором значение функции известного угла равно отношению соответствующих сторон.
2. Используя значение тригонометрической функции и известную длину стороны, найдите недостающую длину стороны.

Пример \(\PageIndex{5}\): нахождение недостающих длин сторон с помощью тригонометрических соотношений

Найдите неизвестные стороны треугольника на рисунке \(\PageIndex{11}\).

Рисунок \(\PageIndex{11}\)

Решение

Нам известны угол и противоположная сторона, поэтому мы можем использовать касательную, чтобы найти прилежащую сторону.

\[ \tan (30°)= \dfrac{7}{a} \nonumber\]

Перегруппируем, чтобы найти \(a\).

\[\begin{align} a &=\dfrac{7}{ \tan (30°)} \\ & =12.1 \end{align} \nonumber\]

Мы можем использовать синус, чтобы найти гипотенузу.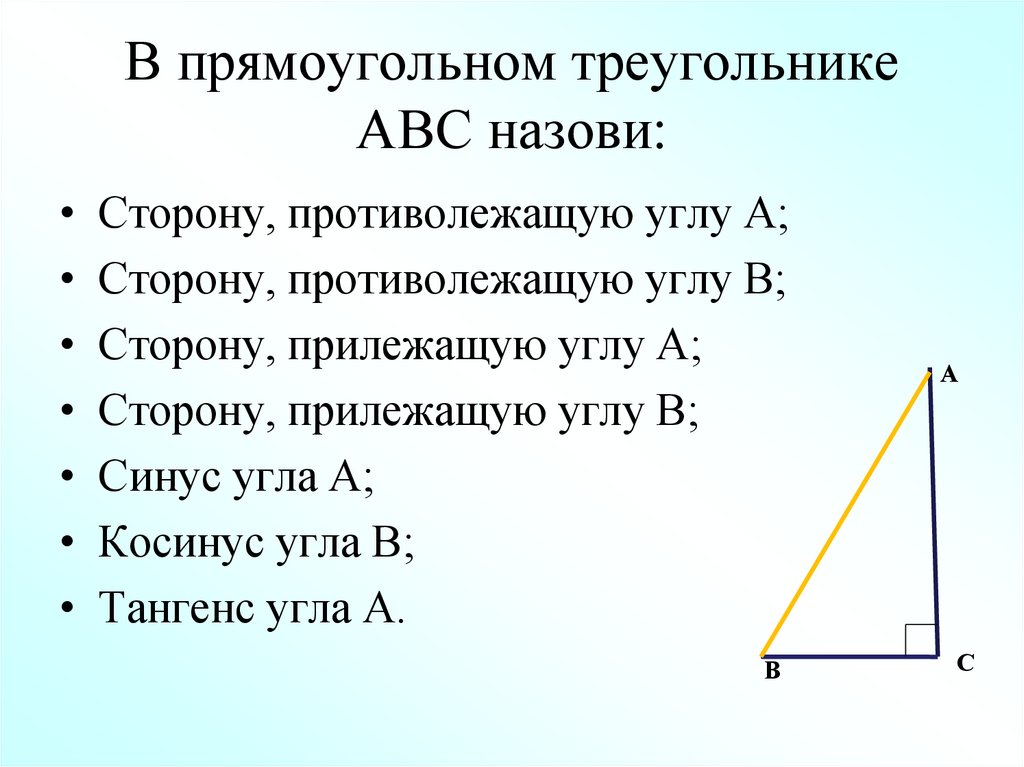

\[ \sin (30°)= \dfrac{7}{c} \nonumber\]

Снова переставляем, чтобы найти \(c\).

\[\begin{align*} c &= \dfrac{7}{\sin (30°)} =14 \end{align*}\]

Упражнение \(\PageIndex{5}\):

Прямоугольный треугольник имеет один угол \(\frac{π}{3}\) и гипотенузу 20. Найдите неизвестные стороны и угол треугольника.

Ответить

\(\mathrm{adjacent=10; напротив=10 \sqrt{3}; }\) недостающий угол равен \(\frac{π}{6}\)

Использование тригонометрии прямоугольного треугольника для решения прикладных задач

Тригонометрия прямоугольного треугольника имеет множество практических применений. Например, возможность вычислить длины сторон треугольника позволяет найти высоту высокого предмета, не взбираясь на его вершину и не протягивая рулетку по его высоте. Мы делаем это, измеряя расстояние от основания объекта до точки на земле на некотором расстоянии, откуда мы можем смотреть на вершину высокого объекта под углом. угол возвышения объекта над наблюдателем относительно наблюдателя — это угол между горизонталью и линией от объекта до глаза наблюдателя. Прямоугольный треугольник, создаваемый этим положением, имеет стороны, которые представляют собой неизвестную высоту, измеренное расстояние от основания и наклонную линию обзора от земли до вершины объекта. Зная измеренное расстояние до основания объекта и угол луча зрения, мы можем использовать тригонометрические функции для вычисления неизвестной высоты. Точно так же мы можем сформировать треугольник из вершины высокого объекта, глядя вниз. угол наклона объекта ниже наблюдателя относительно наблюдателя — это угол между горизонталью и линией, проведенной от объекта к глазу наблюдателя. См. рисунок \(\PageIndex{12}\).

Рисунок \(\PageIndex{12}\)

как: Имея высокий объект, косвенно измерьте его высоту

1. Сделайте набросок проблемной ситуации, чтобы отслеживать известную и неизвестную информацию.
2. Отметьте измеренное расстояние от основания объекта до точки, где хорошо виден верх объекта.
3. На другом конце измеренного расстояния посмотрите на верхнюю часть объекта. Измерьте угол, который линия взгляда образует с горизонтом.
4. Напишите уравнение, связывающее неизвестную высоту, измеренное расстояние и тангенс угла луча зрения.
5. Решите уравнение для неизвестной высоты.

Пример \(\PageIndex{6}\): Косвенное измерение расстояния

Чтобы найти высоту дерева, человек идет к точке в 30 футах от основания дерева. Она измеряет угол 57° 57° между линией обзора верхушки дерева и землей, как показано на рисунке \(\PageIndex{13}\). Найдите высоту дерева.

Рисунок \(\PageIndex{13}\)

Решение

Мы знаем, что угол возвышения равен \(57°\), а длина прилегающей стороны 30 футов. Противоположная сторона — неизвестная высота.

Тригонометрическая функция, связывающая сторону, противоположную углу, и сторону, примыкающую к углу, называется тангенсом.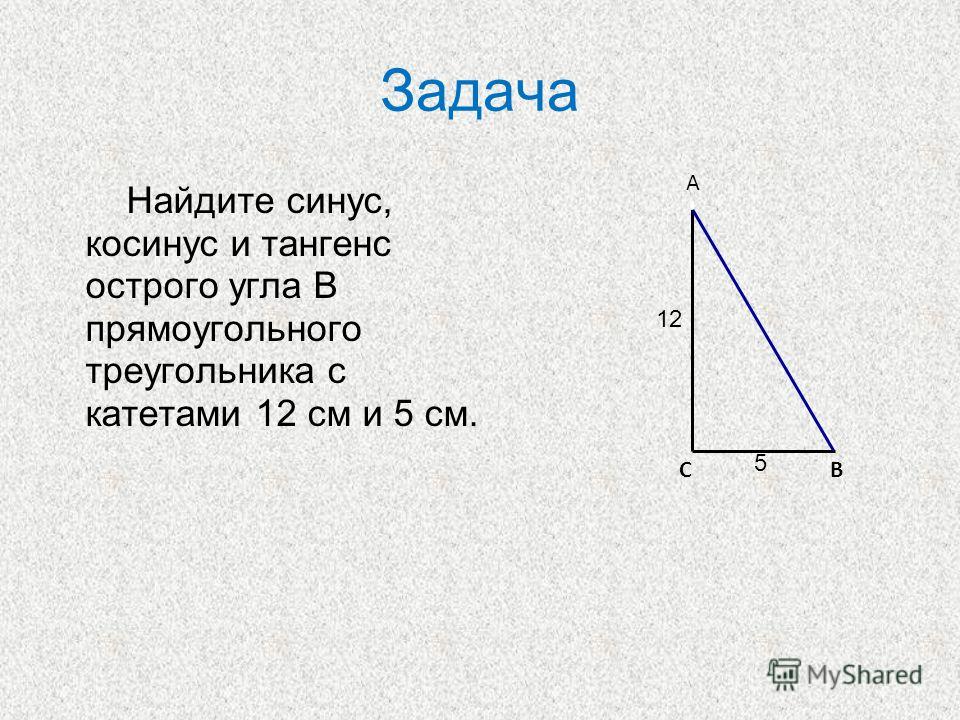 Таким образом, мы сформулируем нашу информацию в терминах тангенса \(57°\), пусть \(h\) будет неизвестной высотой.

\[\begin{array}{cl} \tan θ = \dfrac{\text{напротив}}{\text{смежный}} & \text{} \\ \tan (57°) = \dfrac{h }{30} & \text{Найти }h. \\ h=30 \tan (57°) & \text{Умножить.} \\ h≈46,2 & \text{Использовать калькулятор.} \end{массив} \]

Высота дерева примерно 46 футов.

Упражнение \(\PageIndex{6}\):

Какой длины потребуется лестница, чтобы добраться до подоконника на высоте 50 футов над землей, если лестница упирается в здание под углом \(\frac{5π}{12 }\) с землей? Округлить до ближайшего фута.

Ответить

Около 52 футов

СМИ:

Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики по тригонометрии прямоугольного треугольника.

• Поиск триггерных функций на калькуляторе
• Поиск триггерных функций с помощью прямоугольного треугольника
• Связь триггерных функций со сторонами прямоугольного треугольника
• Определение шести триггерных функций из треугольника
• Определить длину стороны прямоугольного треугольника

Посетите этот веб-сайт, чтобы получить дополнительные практические вопросы от Learningpod.

Ключевые уравнения

Тождества кофункций

\[\begin{align*} \cos t &= \sin ( \frac{π}{2}−t) \\ \sin t &= \cos (\frac{ π}{2}−t) \\ \tan t &= \cot (\frac{π}{2}−t) \\ \cot t &= \tan (\frac{π}{2}−t) \\ \sec t &= \csc (\frac{π}{2}-t) \\ \csc t &= \sec (\frac{π}{2}-t) \end{align*}\]

Ключевые понятия

• Тригонометрические функции можно определить как отношение длин сторон прямоугольного треугольника. См. Пример.
• Одинаковую длину сторон можно использовать для вычисления тригонометрических функций любого острого угла в прямоугольном треугольнике. См. Пример.
• Мы можем вычислить тригонометрические функции специальных углов, зная длины сторон треугольников, в которых они встречаются. См. Пример.
• Любые два дополнительных угла могут быть двумя острыми углами прямоугольного треугольника.
• Если два угла дополняют друг друга, тождества кофункций гласят, что синус одного равен косинусу другого и наоборот. См. Пример.
• Мы можем использовать тригонометрические функции угла, чтобы найти неизвестные длины сторон.
• Выберите тригонометрическую функцию, представляющую отношение неизвестной стороны к известной стороне. См. Пример.
• Тригонометрия прямоугольного треугольника позволяет измерять недоступные высоты и расстояния.
• Неизвестную высоту или расстояние можно найти, составив прямоугольный треугольник, в котором неизвестная высота или расстояние является одной из сторон, а другая сторона и угол известны. См. Пример.

Глоссарий

смежная сторона

в прямоугольном треугольнике, сторона между данным углом и прямым углом

угол наклона

угол между горизонталью и линией от объекта до глаза наблюдателя, при условии, что объект расположен ниже, чем наблюдатель

угол возвышения

угол между горизонталью и линией от объекта до глаза наблюдателя, при условии, что объект расположен выше наблюдателя

противоположная сторона

в прямоугольном треугольнике, сторона, наиболее удаленная от данного угла

гипотенуза

сторона прямоугольного треугольника, противоположная прямому углу

---

Эта страница под названием 7. 2: Тригонометрия прямоугольного треугольника распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх
• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать страницу TOC

   нет

   Включено

   да

2. Теги

   1. смежная сторона
   2. угол наклона
   3. угол места
   4. гипотенуза
   5. противоположная сторона
   6. источник@https://openstax. org/details/books/precalculus
   7. источник[1]-math-1515

тригонометрия — Синус, косинус, тангенс: определяются как отношения в прямоугольном треугольнике, но как понимать отрицательные значения для углов вне 0-90 градусов?

спросил 90$.

Я пытался рассуждать по закону косинуса, где очевидно, что вместо косинуса тупого угла используется отрицательный косинус добавочного (острого) угла, но это скорее повторение закона косинуса, чем причина отрицательное значение косинуса тупого угла.

Я пытался полагаться на единичный круг, чтобы представить $sine=\frac{vertical}{radius}$ при отслеживании звезды. Это привело к $cosine=\frac{horizontal}{radius}$. Хотя я не увлекаюсь астрономией. Затем я рассмотрел вертикальное измерение как положительное, если измерять от земли вверх, и отрицательное, если измерить от земли (когда звезда опускается за горизонт).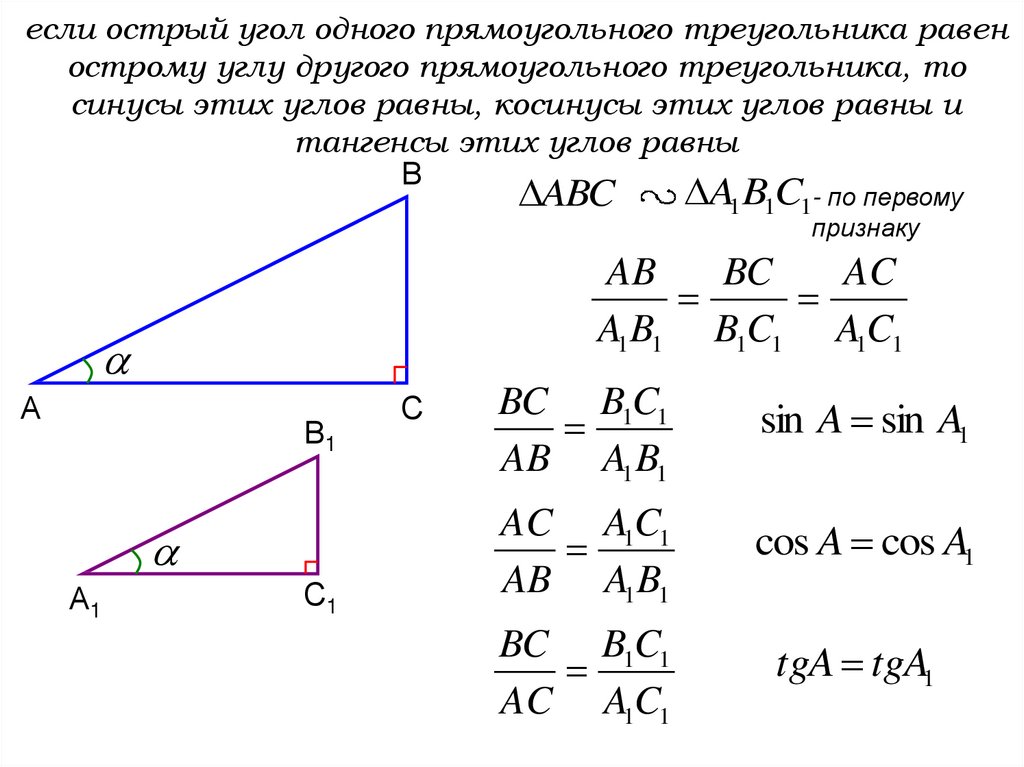 Что касается горизонтального измерения, я принял его отрицательным (как в «противоположном направлении») после того, как наблюдателю нужно было развернуться, чтобы продолжать отслеживать падающую звезду. Я сделал это, чтобы подогнать единичный круг. 90$

Есть ли более простое объяснение, почему тригонометрические функции иногда возвращают отрицательные значения?

• тригонометрия

$\endgroup$

4

$\begingroup$

В случае функции касательной $\tan(\theta)$ — это просто наклон конечной стороны $\theta$, когда угол находится в стандартном положении. Наклоны могут быть отрицательными, поэтому значения тангенса могут быть отрицательными. 92}$, который всегда положителен. Теперь мы можем определить: $\sin(\theta)=\frac{y}{r}, \cos(\theta)=\frac{x}{r}, \tan(\theta)=\frac{y} {х}$.

$\endgroup$

3

$\begingroup$

Именно так они и определены — wlog как прямоугольные декартовы координаты точек на единичной окружности, соответствующие углу.

No related posts.