Решение неполных квадратных уравнений.
Репетиторы ❯ Математика ❯ Решение неполных квадратных уравнений.
Автор: Валентина Галиневская
●
25.06.2015
●
Раздел: Математика
В данной статье мы рассмотрим решение неполных квадратных уравнений.
Но сначала повторим какие уравнения называются квадратными. Уравнение вида ах2 + bх + с = 0, где х – переменная, а коэффициенты а, b и с некоторые числа, причем а ≠ 0, называется квадратным. Как мы видим коэффициент при х2 не равен нулю, а следовательно коэффициенты при х или свободный член могут равняться нулю, в этом случае мы и получаем неполное квадратное уравнение.
Неполные квадратные уравнения бывают трех видов:
1) Если b = 0, с ≠ 0, то ах2 + с = 0;
2) Если b ≠ 0, с = 0, то ах2 + bх = 0;
3) Если b= 0, с = 0, то ах2 = 0.
- Давайте разберемся как решаются уравнения вида ах2 + с = 0.
Чтобы решить уравнение перенесем свободный член с в правую часть уравнения, получим
ах2 = ‒с. Так как а ≠ 0, то разделим обе части уравнения на а, тогда х2 = ‒с/а.
Если ‒с/а > 0 , то уравнение имеет два корня
x = ±√(–c/a).
Если же ‒c/a < 0, то это уравнение решений не имеет. Более наглядно решение данных уравнений представлено на схеме.
Давайте попробуем разобраться на примерах, как решать такие уравнения.
Пример 1. Решите уравнение 2х2 ‒ 32 = 0.
Решение
2х2 = 32
х2 = 32/2
х2 = 16
х = ± 4
Ответ: х1 = ‒ 4, х2 = 4.
Пример 2. Решите уравнение 2х2 + 8 = 0.
Решение
2х2 = ‒ 8
х2 = ‒ 8/2
х2 = ‒ 4
Ответ: уравнение решений не имеет.
- Разберемся как же решаются уравнения вида ах2 + bх = 0.
Чтобы решить уравнение ах2 + bх = 0, разложим его на множители, то есть вынесем за скобки х, получим х(ах+ b) = 0. Произведение равно нулю, если хотя бы один из множителей равен нулю. Тогда или х = 0, или ах+ b = 0. Решая уравнение ах
Закрепим наши знания на конкретном примере.
Пример 3. Решить уравнение 3х2 ‒ 12х = 0.
Решение
х(3х ‒ 12) = 0
х= 0 или 3х – 12 = 0
3х = 12
х = 12/3
х = 4
Ответ: х1 = 0, х2 = 4.
- Уравнения третьего вида ах2 = 0 решаются очень просто.
Если ах2 = 0, то х2 = 0. Уравнение имеет два равных корня х1 = 0, х2 = 0.
Для наглядности рассмотрим схему.
Убедимся при решении примера 4, что уравнения этого вида решаются очень просто.
Пример 4. Решить уравнение 7х2 = 0.
Решение
х2 = 0
х1,2 = 0
Ответ: х1, 2 = 0.
Не всегда сразу понятно какой вид неполного квадратного уравнения нам предстоит решить. Рассмотрим следующий пример.
Пример 5. Решить уравнение
Решение
Умножим обе части уравнения на общий знаменатель, то есть на 30
Сократим
5(5х2 + 9) – 6(4х2 – 9) = 90.
Раскроем скобки
25х2 + 45 – 24х2 + 54 = 90.
Приведем подобные
х2 + 99 = 90.
Перенесем 99 из левой части уравнения в правую, изменив знак на противоположный
х2 = – 9.
Ответ: корней нет.
Мы разобрали как решаются неполные квадратные уравнения. Надеюсь, теперь у вас не будет сложностей с подобными заданиями. Будьте внимательны при определении вида неполного квадратного уравнения, тогда у вас все получится.
Если у вас появились вопросы по данной теме, записывайтесь на мои уроки, мы вместе решим возникшие проблемы.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
Математика
Курсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Математика
Курсы по геометрии 8 класс
Французский язык
Курсы французского языка для начинающих
РЕШЕНИЕ КВАДРАТИЧНЫХ УРАВНЕНИЙ
РЕШЕНИЕ КВАДРАТИЧНЫХ УРАВНЕНИЙПримечание:
- Квадратное уравнение — это полиномиальное уравнение второй степени.

- U-образный график квадратичного уравнения называется параболой.
- Квадратное уравнение имеет два решения. Либо два различных реальных решения, одно двойное действительное решение или два мнимых решения.
- Существует несколько методов решения квадратного уравнения:
- Факторинг
- Завершение квадрата
- Квадратичная формула
- Графики
- Все методы начинаются с установки уравнения равным нулю.
Найдите x в следующем уравнении.
Пример 1:
Уравнение уже обнулено.
Метод 1: Факторинг
Способ 2: Заполнение квадрата
Разделите обе части уравнения на 2.
Добавьте к обеим частям уравнения.
Добавьте к обеим частям уравнения:
Фактор левой части и упрощение правой части:
Возьмите квадратный корень из обеих частей уравнения:
Добавьте к обеим частям уравнения:
Метод 3: квадратичная формула
Квадратичная формула
В уравнении a есть коэффициент
члена, b – коэффициент члена x , а c — константа.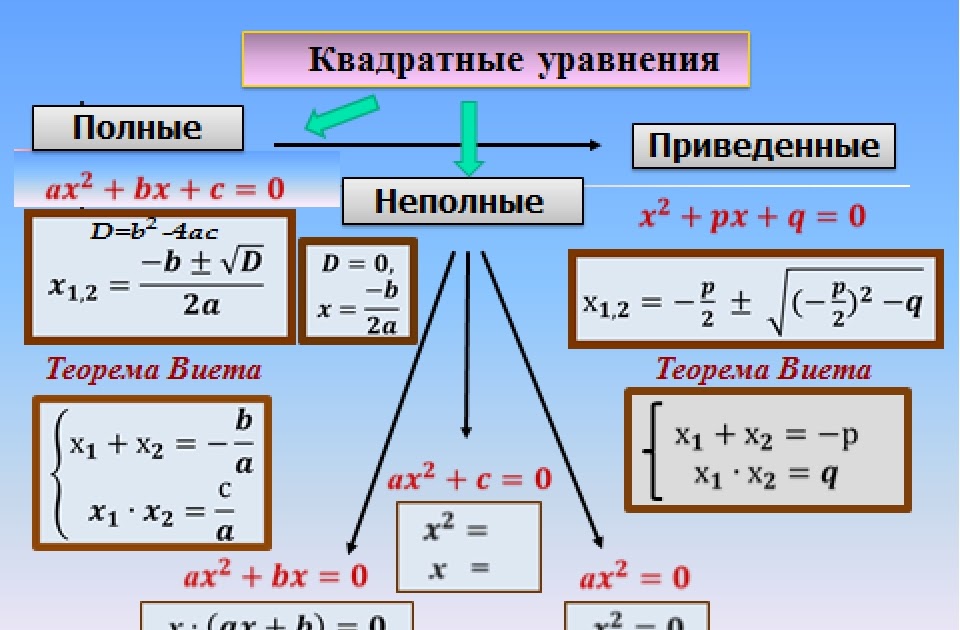 Замените 2 на на , -1 на b и -1 для c в квадратичной формуле и
упрощать.
Замените 2 на на , -1 на b и -1 для c в квадратичной формуле и
упрощать.
Метод 4: График
График y = левая часть уравнения или и графика y = правая часть уравнения или y =0. График y =0 не более того чем ось х. Итак, вы будете искать, где график пересекает ось x. Другой способ сказать это состоит в том, что x-перехваты являются решениями этого уравнения.
Вы можете видеть на графике, что есть два x-перехвата, один в 1 и один в .
Ответы 1 и Эти ответы могут или не могут быть решениями исходных уравнений. Вы должны убедиться, что эти ответы являются решениями.
Проверьте эти ответы в исходном уравнении.
Проверьте решение x =1, подставив 1 в исходное уравнение вместо x.
Если левая часть уравнения равна правой части
уравнение после замены, вы нашли правильный ответ.
- Левая сторона:
- Правая сторона:

Проверьте решение, подставив в
исходное уравнение для х. Если левая часть уравнения равна
правая часть уравнения после подстановки, вы нашли
правильный ответ.
- Левая сторона:
- Правая сторона:
Решения уравнения
1 и
Если вы хотите работать с другим примером, нажмите «Пример».
Если вы хотите проверить себя, решив некоторые задачи, подобные этой
например, нажмите Проблема
Если вы хотите вернуться к содержанию уравнения, нажмите
Содержание.
Домашняя страница S.O.S MATHematics
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.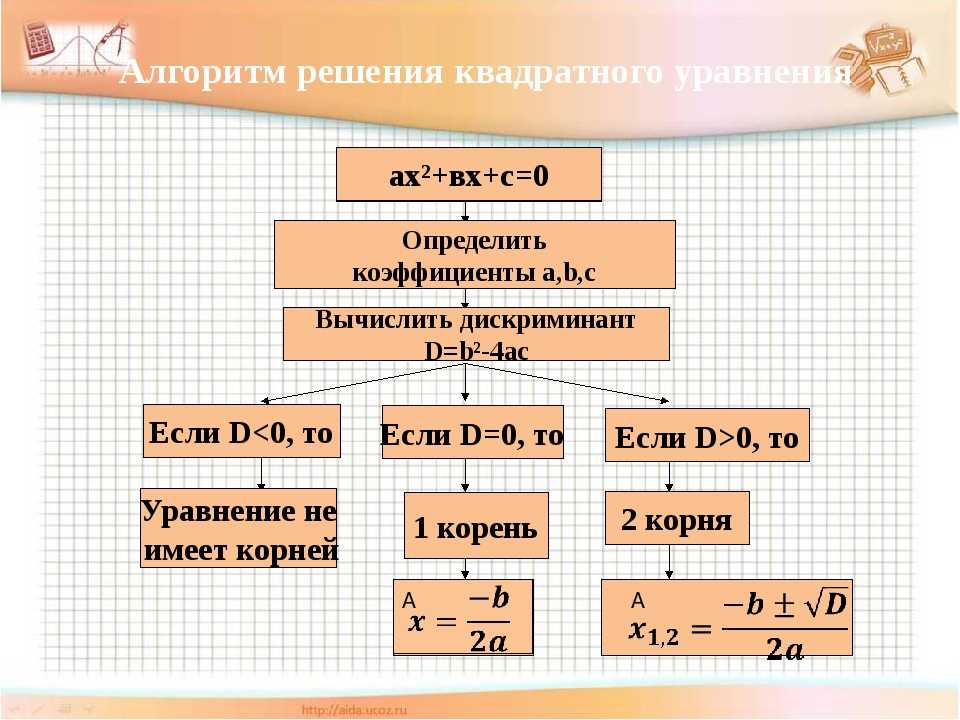
Свяжитесь с нами
Математика Медикс, ООО. — П.О. Box 12395 — Эль-Пасо, Техас 79913 — США
пользователей онлайн за последний час
Математический гений разработал чрезвычайно простой новый способ решения квадратных уравнений : ScienceAlert
Если вы изучали алгебру в старшей школе (или изучаете ее прямо сейчас), есть большая вероятность, что вы знакомы с квадратной формулой. Если нет, возможно, вы подавили его.
К этому моменту миллиарды из нас должны были выучить, запомнить и реализовать этот громоздкий алгоритм для решения квадратных уравнений, но, по словам математика По-Шен Ло из Университета Карнеги-Меллона, на самом деле существовал более простой и лучший способ. вдоль, хотя он оставался почти полностью скрытым в течение тысяч лет.
В новой исследовательской работе Ло прославляет квадратичную формулу как «выдающийся триумф ранних математиков», относящуюся к началу древневавилонского периода около 2000 г. до н.э., но также свободно признает некоторые из ее древних недостатков.
до н.э., но также свободно признает некоторые из ее древних недостатков.
«К сожалению, для миллиардов людей во всем мире квадратичная формула является также их первым (и, возможно, единственным) опытом работы с довольно сложной формулой, которую они должны запомнить», — пишет Лох.
Эта трудоемкая задача, которую выполняли студенты-математики с возрастом около четырех тысячелетий, не меньше, возможно, была не совсем необходимой, как это бывает. Конечно, всегда существовали альтернативы квадратичной формуле, такие как разложение на множители, завершение квадрата или даже разбиение миллиметровки.
Но квадратичная формула обычно считается наиболее полным и надежным методом решения квадратичных задач, даже если она немного непостижима. Вот как это выглядит:
Эту формулу можно использовать для решения квадратных уравнений стандартной формы, где x 2 + bx + c = 0.
В сентябре Лох провел мозговой штурм. математика, стоящая за квадратными уравнениями, когда он наткнулся на новый, упрощенный способ вывода той же формулы — альтернативный метод, который он описывает в своей статье как «эффективный в вычислительном отношении, естественный и легко запоминающийся алгоритм решения общих квадратных уравнений». .
«Я был ошеломлен, — говорит Ло об открытии. «Как это может быть, что я никогда не видел этого раньше, и я никогда не видел этого ни в одном учебнике?»
В новом методе Лох начинает со стандартного метода, пытаясь разложить квадратное число x² + bx + c на множители как (x − )(x − ), что сводится к поиску двух чисел, которые нужно поместить в пробелы с суммой −b и продукт c. Он использует метод усреднения, который концентрируется на сумме, в отличие от более распространенного метода, который фокусируется на произведении двух чисел, составляющих c, который требует догадок для решения задач.
«Сумма двух чисел равна 2, когда их среднее значение равно 1. » Объясняет Ло на своем сайте.
» Объясняет Ло на своем сайте.
«Итак, мы можем попытаться найти числа, которые равны 1 плюс некоторая сумма и 1 минус та же сумма. Все, что нам нужно сделать, это найти, существует ли u такой, что 1 + u и 1 — u работают как два числа, и u может быть 0».
Согласно Ло, допустимое значение u всегда можно определить с помощью альтернативного квадратичного метода Лоха интуитивно понятным способом, что позволяет решить любое квадратное уравнение.
В статье Ло он признает, что был бы «очень удивлен, если бы этот подход полностью ускользнул от человеческого открытия до сегодняшнего дня, учитывая 4000-летнюю историю этой темы», но говорит об альтернативной технике, которая сочетает в себе шаги, впервые примененные вавилонянами. , греческие и французские математики — «конечно, не широко преподаются и не известны (автору не удалось найти доказательств этого в английских источниках)».
Однако с тех пор, как в октябре Лох впервые поделился в Интернете предпечатной версией, описывающей простое доказательство, Ло говорит, что его внимание привлекла 1989 исследовательская статья, которая больше всего похожа на предыдущую работу, которую он нашел, что в какой-то мере оправдывает его неверие в то, что этот альтернативный метод не был идентифицирован до сих пор.
«Другая работа частично совпадала во всех расчетах, с очевидной логической разницей в предположении, что каждый квадратичный показатель может быть разложен на множители, и педагогической разницей в выборе знака», — объяснил Ло в ScienceAlert по электронной почте.
Остается только разгадать тайну того, почему этот метод не стал более широко известен до этого, поскольку он дает нам, по словам Лоха, «восхитительный альтернативный подход к решению квадратных уравнений, который практичен». для интеграции во все основные учебные программы».
(Конечно, не говоря уже о том, что это может просто означать, что никому больше не нужно запоминать квадратичную формулу.)
Мы до сих пор не знаем, как это ускользнуло от внимания на протяжении тысячелетий, но если инстинкты Ло верны, математика учебники могут оказаться на грани исторического переписывания, и мы не воспринимаем открытия, изменяющие учебники, легкомысленно.
«Я хотел как можно шире поделиться ею со всем миром, — говорит Ло, — потому что она может демистифицировать сложную часть математики, из-за которой многие люди считают, что математика, возможно, не для них».

