Производная 1 2 x: Производная от 1/2х чему равна?

Производная 1 порядка определение. Что такое производная?Определение и смысл производной функции

Производная — главнейшее понятие математического анализа. Она характеризует изменение функции аргумента x в некоторой точке. При этом и сама производная является функцией от аргумента x

Производной функции в точке называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю.

Наиболее употребительны следующие обозначения производной :

Пример 1. Пользуясь определением производной , найти производную функции

Решение. Из определения производной вытекает следующая схема её вычисления.

Дадим аргументу приращение (дельта) и найдём приращение функции:

Найдём отношение приращения функции к приращению аргумента:

Вычислим предел этого отношения при условии, что приращение аргумента стремится к нулю, то есть требуемую в условии задачи производную:

Физический смысл производной

К понятию производной

привело изучение Галилео Галилеем закона свободного падения тел, а в более широком смысле — задачи о мгновенной скорости неравномерного прямолинейного движения точки.

Пусть камешек поднят и затем из состояния покоя отпущен. Путь s , проходимый за время t , является функцией времени, то есть. s = s (t ). Если задан закон движения точки, то можно определить среднюю скорость за любой промежуток времени. Пусть в момент времени камешек находился в положении A , а в момент — в положении B . За промежуток времени (от t до ) точка прошла путь . Поэтому средняя скорость движения за этот промежуток времени, которую обзначим через , составляет

.

Однако движение свободно падающего тела явно неравномерное. Скорость v падения постоянно возрастает. И средней скорости уже недостаточно для характеристики быстроты движения на различных участках пути. Такая характеристика тем точнее, чем меньше промежуток времени . Поэтому вводится следующее понятие: мгновенной скоростью прямолинейного движения (или скоростью в данный момент времени

t ) называется предел средней скорости при :

(при условии, что этот предел существует и конечен).

Так выясняется, что мгновенная скорость есть предел отношения приращения функции s (t ) к приращению аргумента t при Это и есть производная, которая в общем виде записывается так:.

.

Решение обозначенной задачи представляет собой физический смысл производной . Итак, производной функции y=f (x ) в точке x называется предел (если он существует и конечен) приращения функции к приращению аргумента при условии, что последнее стремится к нулю.

Пример 2. Найти производную функции

Решение. Из определения производной вытекает следующая схема для её вычисления.

Шаг 1. Дадим аргументу приращение и найдём

Шаг 2. Найдём приращение функции:

Шаг 3. Найдём отношение приращения функции к приращению аргумента:

Шаг 4. Вычислим предел этого отношения при , то есть производную:

Геометрический смысл производной

Пусть функция определена на интервале и пусть точка М на графике функции соответствует значению аргумента , а точка Р – значению . Проведём через точки М и Р прямую и назовём её секущей . Обозначим через угол между секущей и осью . Очевидно, что этот угол зависит от .

Если существует

проходящую через точку , называют предельным положением секущей МР при (или при ).

Касательной к графику функции в точке М называется предельное положение секущей МР при , или, что то же при .

Из определения следует, что для существования касательной достаточно, чтобы существовал предел

,

причём предел равен углу наклона касательной к оси .

Теперь дадим точное определение касательной.

Касательной к графику функции в точке называется прямая, проходящая через точку и имеющая угловой коэффициент , т.е. прямая, уравнение которой

Из этого определения следует, что производная функции равна угловому коэффициенту касательной к графику этой функции в точке с абсциссой x . В этом состоит геометрический смысл производной.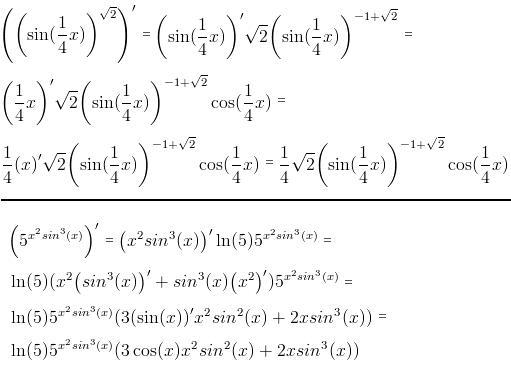

Вычисление производной часто встречается в заданиях ЕГЭ. Данная страница содержит список формул для нахождения производных.

Правила дифференцирования

1. (k⋅ f(x))′=k⋅ f ′(x).
2. (f(x)+g(x))′=f′(x)+g′(x).
3. (f(x)⋅ g(x))′=f′(x)⋅ g(x)+f(x)⋅ g′(x).
4. Производная сложной функции. Если y=F(u), а u=u(x), то функция y=f(x)=F(u(x)) называется сложной функцией от x. Равна y′(x)=Fu′⋅ ux′.
5. Производная неявной функции. Функция y=f(x) называется неявной функцией, заданной соотношением F(x,y)=0, если F(x,f(x))≡0.
6. Производная обратной функции. Если g(f(x))=x, то функция g(x) называется обратной функцией для функции y=f(x).
7. Производная параметрически заданной функции. Пусть x и y заданы как функции от переменной t: x=x(t), y=y(t). Говорят, что y=y(x) параметрически заданная функция на промежутке x∈ (a;b), если на этом промежутке уравнение x=x(t) можно выразить в виде t=t(x) и определить функцию y=y(t(x))=y(x).
8. Производная степенно-показательной функции. Находится путем логарифмирования по основанию натурального логарифма.

Советуем сохранить ссылку, так как эта таблица может понадобиться еще много раз.

Определение. Пусть функция \(y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \(x_0 \). Дадим аргументу приращение \(\Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции \(\Delta y \) (при переходе от точки \(x_0 \) к точке \(x_0 + \Delta x \)) и составим отношение \(\frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \(\Delta x \rightarrow 0 \), то указанный предел называют производной функции \(y=f(x) \) в точке \(x_0 \) и обозначают \(f»(x_0) \).

$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f»(x_0) $$

Для обозначения производной часто используют символ y». Отметим, что y» = f(x) — это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых существует указанный выше предел.

Эту функцию называют так: производная функции у = f(x) .

Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
\(k = f»(a) \)

Поскольку \(k = tg(a) \), то верно равенство \(f»(a) = tg(a) \) .

А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция \(y = f(x) \) имеет производную в конкретной точке \(x \):
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f»(x) $$
Это означает, что около точки х выполняется приближенное равенство \(\frac{\Delta y}{\Delta x} \approx f»(x) \), т.е. \(\Delta y \approx f»(x) \cdot \Delta x \). Содержательный смысл полученного приближенного равенства заключается в следующем: приращение функции «почти пропорционально» приращению аргумента, причем коэффициентом пропорциональности является значение производной в заданной точке х.

2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \). Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.

Сформулируем его.

Как найти производную функции у = f(x) ?

1. Зафиксировать значение \(x \), найти \(f(x) \)
2. Дать аргументу \(x \) приращение \(\Delta x \), перейти в новую точку \(x+ \Delta x \), найти \(f(x+ \Delta x) \)
3. Найти приращение функции: \(\Delta y = f(x + \Delta x) — f(x) \)
4. Составить отношение \(\frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.

Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием

функции у = f(x).

Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.

Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f»(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.

Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство \(\Delta y \approx f»(x) \cdot \Delta x \). Если в этом равенстве \(\Delta x \) устремить к нулю, то и \(\Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.

Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке .

Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.

Еще один пример. Функция \(y=\sqrt{x} \) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и \(f»(0) \)

Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?

Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.

Правила дифференцирования

Операция нахождения производной называется дифференцированием . При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. 2} $$

Пусть функция y = f(x) определена в промежутке X. Производной функции y = f(x) в точке х o называется предел

= .

Если этот предел конечный, то функция f(x) называется дифференцируемой в точке x o ; при этом она оказывается обязательно и непрерывной в этой точке.

Если же рассматриваемый предел равен  (или — ), то при условии, что функция в точке х o непрерывна, будем говорить, что функция f(x) имеет в точке х o бесконечную производную .

Производная обозначается символами

y , f (x o), , .

Нахождение производной называется дифференцированием функции. Геометрический смысл производной состоит в том,что производная есть угловой коэффициент касательной к кривой y=f(x) в данной точке х o ; физический смысл — в том, что производная от пути по времени есть мгновенная скорость движущейся точки при прямолинейном движении s = s(t) в момент t o .

Если с — постоянное число, и u = u(x), v = v(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

1) (с) » = 0, (cu) » = cu»;

2) (u+v)» = u»+v»;

3) (uv)» = u»v+v»u;

4) (u/v)» = (u»v-v»u)/v 2;

5) если y = f(u), u = (x), т.е. y = f((x)) — сложная функция, или суперпозиция , составленная из дифференцируемых функций  и f, то , или

6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), причем  0, то .

На основе определения производной и правил дифференцирования можно составить список табличных производных основных элементарных функций.

1. (u )» =  u  1 u» (  R ).

2. (a u)» = a u lna u».

3. (e u)» = e u u».

4. (log a u)» = u»/(u ln a).

5. (ln u)» = u»/u.

6. (sin u)» = cos u u».

7. (cos u)» = — sin u u».

8. (tg u)» = 1/ cos 2 u u».

9. (ctg u)» = — u» / sin 2 u.

10. (arcsin u)» = u» / .

11. (arccos u)» = — u» / .

12. (arctg u)» = u»/(1 + u 2).

13. (arcctg u)» = — u»/(1 + u 2).

Вычислим производную степенно-показательного выражения y=u v , (u>0), где u и v суть функции от х , имеющие в данной точке производные u» , v» .

Прологарифмировав равенство y=u v , получим ln y = v ln u.

Приравнивая производные по х от обеих частей полученного равенства с помощью правил 3, 5 и формулы для производной логарифмической функции, будем иметь:

y»/y = vu»/u +v» ln u, откуда y» = y (vu»/u +v» ln u).

(u v)»=u v (vu»/u+v» ln u), u > 0.

Например, если y = x sin x , то y» = x sin x (sin x/x + cos x ln x).

Если функция y = f(x) дифференцируема в точке x , т.е. имеет в этой точке конечную производную y» , то = y»+, где 0 при х 0; отсюда  y = y» х +  x.

Главная часть приращения функции, линейная относительно х, называется дифференциалом функции и обозначается dy: dy = y» х. Если положить в этой формуле y=x, то получим dx = x»х = 1х =х, поэтому dy=y»dx, т. е. символ для обозначения производной можно рассматривать как дробь.

Приращение функции  y есть приращение ординаты кривой, а дифференциал dy есть приращение ординаты касательной.

Пусть мы нашли для функции y=f(x) ее производную y = f (x). Производная от этой производной называется производной второго порядка функции f(x), или второй производной, и обозначается .

Аналогично определяются и обозначаются:

производная третьего порядка — ,

производная четвертого порядка —

и вообще производная n-го порядка — .

Пример 3 .15. Вычислить производную функции y=(3x 3 -2x+1)sin x.

Решение. По правилу 3, y»=(3x 3 -2x+1)»sin x + (3x 3 -2x+1)(sin x)» = = (9x 2 -2)sin x + (3x 3 -2x+1)cos x.

Пример 3.16 . Найти y», y = tg x + .

Решение. Используя правила дифференцирования суммы и частного, получим: y»=(tgx + )» = (tgx)» + ()» = + = .

Пример 3 .17. Найти производную сложной функции y= , u=x 4 +1.

Решение. По правилу дифференцирования сложной функции, получим: y» x =y » u u» x =()» u (x 4 +1)» x =(2u + . Так как u=x 4 +1,то (2 x 4 +2+ .

В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:

1. Значение производной в некоторой точке x 0 ,
2. Точки максимума или минимума (точки экстремума),
3. Интервалы возрастания и убывания функции (интервалы монотонности).

Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.

Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.

Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.

Вычисление значения производной. Метод двух точек

Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x 0 , и требуется найти значение производной в этой точке, применяется следующий алгоритм:

1. Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x 1 ; y 1) и B (x 2 ; y 2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
2. Зная координаты, легко вычислить приращение аргумента Δx = x 2 − x 1 и приращение функции Δy = y 2 − y 1 .
3. Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.

Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.

Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.

Найдем значение производной: D = Δy/Δx = 4/2 = 2.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .

Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.

Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .

Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.

Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.

Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.

Вычисление точек максимума и минимума

Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:

1. Точка x 0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≥ f(x).
2. Точка x 0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≤ f(x).

Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:

1. Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
2. Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
3. Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.

Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.

Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:

Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.

Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:

Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].

Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:

На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.

Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.

Нахождение интервалов возрастания и убывания функции

В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:

1. Функция f(x) называется возрастающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). Другими словами, чем больше значение аргумента, тем больше значение функции.
2. Функция f(x) называется убывающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Т.е. большему значению аргумента соответствует меньшее значение функции.

Сформулируем достаточные условия возрастания и убывания:

1. Для того чтобы непрерывная функция f(x) возрастала на отрезке , достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
2. Для того чтобы непрерывная функция f(x) убывала на отрезке , достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.

Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:

1. Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
2. Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
3. Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.

Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:

Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:

Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.

Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l 2 = 5.

ГК РФ Статья 1259. Объекты авторских прав \ КонсультантПлюс

Подготовлены редакции документа с изменениями, не вступившими в силу

ГК РФ Статья 1259. Объекты авторских прав

Перспективы и риски споров в суде общей юрисдикции. Ситуации, связанные со ст.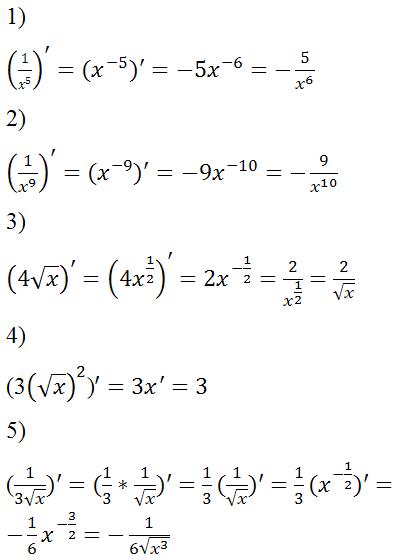 1259 ГК РФ

— Гражданин хочет подтвердить авторство произведения

— Правообладатель произведения хочет взыскать компенсацию за нарушение исключительного права на него

— Правообладатель хочет взыскать компенсацию за нарушение исключительного права на произведение при его использовании в интернете

1. Объектами авторских прав являются произведения науки, литературы и искусства независимо от достоинств и назначения произведения, а также от способа его выражения:

литературные произведения;

драматические и музыкально-драматические произведения, сценарные произведения;

хореографические произведения и пантомимы;

музыкальные произведения с текстом или без текста;

аудиовизуальные произведения;

произведения живописи, скульптуры, графики, дизайна, графические рассказы, комиксы и другие произведения изобразительного искусства;

произведения декоративно-прикладного и сценографического искусства;

произведения архитектуры, градостроительства и садово-паркового искусства, в том числе в виде проектов, чертежей, изображений и макетов;

фотографические произведения и произведения, полученные способами, аналогичными фотографии;

географические и другие карты, планы, эскизы и пластические произведения, относящиеся к географии и к другим наукам;

(в ред. Федеральных законов от 29.06.2015 N 205-ФЗ, от 30.12.2015 N 431-ФЗ)

(см. текст в предыдущей редакции)

другие произведения.

К объектам авторских прав также относятся программы для ЭВМ, которые охраняются как литературные произведения.

2. К объектам авторских прав относятся:

1) производные произведения, то есть произведения, представляющие собой переработку другого произведения;

2) составные произведения, то есть произведения, представляющие собой по подбору или расположению материалов результат творческого труда.

3. Авторские права распространяются как на обнародованные, так и на необнародованные произведения, выраженные в какой-либо объективной форме, в том числе в письменной, устной форме (в виде публичного произнесения, публичного исполнения и иной подобной форме), в форме изображения, в форме звуко- или видеозаписи, в объемно-пространственной форме.

4. Для возникновения, осуществления и защиты авторских прав не требуется регистрация произведения или соблюдение каких-либо иных формальностей.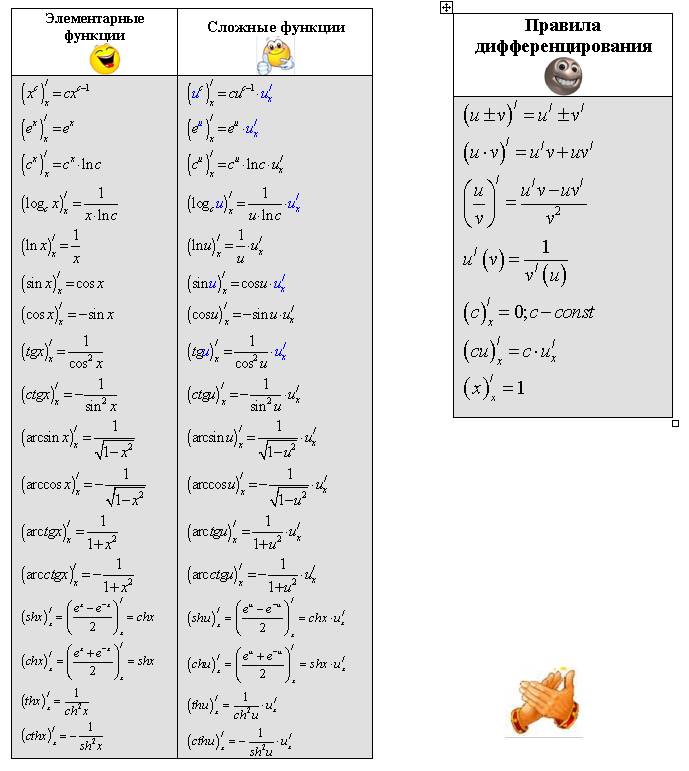

В отношении программ для ЭВМ и баз данных возможна регистрация, осуществляемая по желанию правообладателя в соответствии с правилами статьи 1262 настоящего Кодекса.

5. Авторские права не распространяются на идеи, концепции, принципы, методы, процессы, системы, способы, решения технических, организационных или иных задач, открытия, факты, языки программирования, геологическую информацию о недрах.

(в ред. Федерального закона от 29.06.2015 N 205-ФЗ)

(см. текст в предыдущей редакции)

6. Не являются объектами авторских прав:

1) официальные документы государственных органов и органов местного самоуправления муниципальных образований, в том числе законы, другие нормативные акты, судебные решения, иные материалы законодательного, административного и судебного характера, официальные документы международных организаций, а также их официальные переводы;

2) государственные символы и знаки (флаги, гербы, ордена, денежные знаки и тому подобное), а также символы и знаки муниципальных образований;

3) произведения народного творчества (фольклор), не имеющие конкретных авторов;

4) сообщения о событиях и фактах, имеющие исключительно информационный характер (сообщения о новостях дня, программы телепередач, расписания движения транспортных средств и тому подобное).

7. Авторские права распространяются на часть произведения, на его название, на персонаж произведения, если по своему характеру они могут быть признаны самостоятельным результатом творческого труда автора и отвечают требованиям, установленным пунктом 3 настоящей статьи.

практических задач по цепному правилу — Google Такой

AlleBilderVideosShoppingMapsNewsBücher

suchoptionen

Kettenregel (цепное правило)

Die Kettenregel ist eine der Grundregelnung. Mit ihr wird die Ableitung einer Verkettung von zwei Differentenzierbaren Funktionen berechnet. В лагранжевой нотации lautet die Kettenregel: {\ displaystyle [f] ‘= f’ \ cdot g’} Википедия

Исчисление I — Цепное правило (практические задачи) — Pauls Online Math Notes

tutorial.math.lamar.edu › задачи › calci › chainrule

16.11.2022 · Вот набор практических задач, которые сопровождают раздел «Цепное правило» главы «Производные» примечаний к «Исчислению Пола Докинза I . ..

Дифференцирование с использованием цепного правила — UC Davis Math

www.math.ucdavis.edu › ~kouba › chainruledirectory

ДИФФЕРЕНЦИИРОВАНИЕ С ИСПОЛЬЗОВАНИЕМ ЦЕПНОГО ПРАВИЛА. Следующие задачи требуют использования цепного правила. Цепное правило — это правило различения композиций … 92+2x-3}]=\,? dxd​[8×2+2x−3 ​]=?начальная дробь, d, деленная на, d, x, конечная дробь, …

[PDF] Исчисление — Практика цепных правил

www.npsd.k12. nj.us › cms › lib04 › Centricity › Домен › Исчисление -…

I d 2MvatdteI Nw5intkhZ oI5n1fFivnNiVtvev 4C3atlycRu2lWu7s1.2. Рабочий лист от Kuta Software LLC. -3-. Ответы на практику цепных правил.

Цепное правило: задачи и решения — Matheno.com

www.matheno.com › Learn › math › calculus-1 › ch…

Все это бесплатно и предназначено для того, чтобы помочь вам успешно пройти курс. Если вам просто нужно попрактиковаться в вычислении производных задач, у предыдущих студентов есть . ..

Степенное правило] · Экспоненты] · Триггерные функции] · Правило произведения и правило частного]

Практические задачи по цепному правилу — YouTube

www .youtube.com › смотреть

01.03.2018 · Практика цепных правил. 2,8K просмотров 5 лет назад Исчисление · Джеймс Хэмблин. Джеймс …
Дауэр: 11:03
Прислан: 01.03.2018

Примеры цепных правил — YouTube

www.youtube.com › смотреть

03.10.2007 · Примеры использования цепных правил Потренируйтесь прямо сейчас в Академии Хана: https://www . ..
Опубликовано: 9:25
Прислано: 03.10.2007

Ähnliche Fragen

Как вы решаете проблемы с цепными правилами?

Что является примером для цепного правила?

Цепное правило сложное?

Что такое цепное правило с 3 шагами?

Простое цепное правило: примеры и решения

mathsathome.com › дифференциация цепного правила

Примеры цепного правила с решениями ; f(𝑥) = sin(5𝑥), cos(5𝑥) × 5, f'(𝑥) = 5cos(5𝑥) ; f(𝑥) = cos(10𝑥), -sin(10𝑥) × 10, f'(𝑥) = -10sin(10𝑥) ; f(𝑥) = -3tan . ..

[PDF] Задачи: Практика цепных правил — MIT OpenCourseWare

ocw.mit.edu › курсы

Одним из применений цепного правила являются задачи, в которых вам дается функция х. 2 и y с входными данными в полярных координатах. Например, пусть w = (x + …

Практические задачи по цепным правилам — MST.edu

web.mst.edu › ~reflori › ChainRule › chain_rule

Практические задачи по цепным правилам. Правило цепочки относительно часто используется в динамике для получения производных по времени (или, по крайней мере, для введения производных по времени …

Ähnlichesuchanfragen

Упражнения по правилу цепочки с ответами

Практика по правилу цепочки, тип файла pdf

Правило цепочки для YouTube

Продукт упражнения по правилам

Деривативы тригонометрических функций Примеров и решений PDF

Проблемы с жесткой производной

Интегральные упражнения с решениями

Упражнения по расщеплению

.

)

Differenzierung trigonometrischer Funktionen ist der Mathematische Prozess, die Ableitung einer trigonometrischen Funktion oder ihre Änderungsrate in Bezug auf eine Variable zu finden. Википедия (английский)

Bilder

ALLE ANLEIGEN

ALLE ANZEIGEN

[PDF] Рабочий лист производных триг. Функция В. Упражнения 39-54, найдите производную тригонометрической функции.

[PDF] Дифференциация — Тригонометрические функции — Kuta Software

cdn.kutasoftware.com › Рабочие листы › Calc › 03 — Цепное правило с триггером

Рабочий лист от Kuta Software LLC. Программное обеспечение Kuta — Бесконечное исчисление … Дифференциация — Тригонометрические функции. Дифференцируйте каждую функцию по …

[PDF] Производные тригонометрических функций. Рабочие листы по математике 4 Kids

.ком. Найдите производные тригонометрических функций: = 4 sin. + 5 соед. = грех, потому что. = 2 сек + тангенс.

[PDF] Calculus 1 Tutor Worksheet 4 Производные тригонометрии . ..

s3.amazonaws.com › calculus-worksheets › Calculus+1+Tutor+-+Wor…

Calculus 1 Tutor — Worksheet 4 – Производные тригонометрических функций… Производная функции, умноженная на константу, есть константа.

Рабочий лист производных II — Superprof

www.superprof.co.uk › … › Расчет › производные

Bewertung 4,0

(2)

19.05.2022 · В этом ресурсе вы найдете 6 решенных упражнений на производные. … Продифференцируйте следующие тригонометрические функции:.

Исчисление I. Производные триггерных функций (практические задачи)

tutorial.math.lamar.edu › calci › difftrigfcns глава «Производные» заметок для Пола …

Рабочий лист для урока: Дифференциация тригонометрических функций — Нагва

www.nagwa.com › рабочие листы

В этом рабочем листе мы потренируемся находить производные тригонометрических функций и применять к ним правила дифференцирования.