Деление целых чисел. Делимое, делитель, частное.
Деление целых чисел отличается от деления натуральных чисел, только тем что у целых чисел нужно у частного посчитать знак. Как посчитать знак частного целых чисел? Рассмотрим подробно в теме.
Термины и понятия частного целых чисел.
Чтобы выполнить деление целых чисел нужно вспомнить термины и понятия. В делении есть: делимое, делитель и частное целых чисел.
Делимое – это то целое число, которое делят. Делитель – это целое число, на которое делят. Частное – это результат деления целых чисел.
Можно сказать “Деление целых чисел” или “Частное целых чисел” смысл этих фраз один и тот же, то есть нужно поделить одно целое число на другое и получить ответ.
Деление берет свое начало из умножения. Рассмотрим пример:
3∙4=12
У нас есть два множителя 3 и 4. Но допустим нам известно, что есть один множитель 3 и результат умножения множителей их произведение 12. Как найти второй множитель? На помощь приходит деление.
Как найти второй множитель? На помощь приходит деление.
12:3=4
Правило деления целых чисел.
Определение:
Частное двух целых чисел равно частному их модулей, со знаком плюс в результате, если числа одинаковых знаков, и со знаком минус, если они разных знаков.
Важно учитывать знак частного целых чисел. Кратко правила деления целых чисел:
Плюс на плюс дает плюс.
“+ : + = +”
Минус на минус дает плюс.
“– : – =+”
Минус на плюс дает минус.
“– : + = –”
Плюс на минус дает минус.
“+ : – = –”
А теперь рассмотрим подробно каждый пункт правила деления целых чисел.
Деление целых положительных чисел.
Вспомним, что целые положительные числа это тоже самое, что натуральные числа. Мы пользуемся теми же правила, что и при делении натуральных чисел. Знак частного от деления целых положительных чисел всегда плюс. Иными словами, при делении двух целых чисел “плюс на плюс дает плюс”.
Иными словами, при делении двух целых чисел “плюс на плюс дает плюс”.
Пример:
Выполните деление 306 на 3.
Решение:
Оба числа имеют знак “+”, поэтому ответ будет со знаком “+”.
306:3=102
Ответ: 102.
Пример:
Разделите делимое 220286 на делитель 589.
Решение:
Делимое 220286 и делитель 589 имеет знак плюс, поэтому частное тоже будет иметь знак плюс.
220286:589=374
Ответ: 374
Деление целых отрицательных чисел.
Правило деления двух отрицательных чисел.
Пусть у нас будут два отрицательных целых числа a и b. Нам нужно найти их модули и выполнить деление.
a:b=|a|:|b|
Результат деления или частное двух отрицательных целых чисел будет со знаком “+” или “минус на минус дает плюс”.
Рассмотрим пример:
Найдите частное -900:(-12).
Решение:
-900:(-12)=|-900|:|-12|=900:12=75
Ответ: -900:(-12)=75
Пример:
Выполните деление одного целого отрицательного числа -504 на второе отрицательное число -14.
Решение:
-504:(-14)=|-504|:|-14|=504:14=34
Записать выражение можно короче:
-504:(-14)=34
Деление целых чисел с разными знаками. Правило и примеры.
Правило:
При выполнении деления целых чисел с разными знаками, частное будет равно отрицательному числу.
Не важно положительное целое число делим на отрицательное целое число или отрицательное целое число делим на положительное целое число, результат деления всегда будет равен отрицательному числу.
Минус на плюс дает минус.
Плюс на минус дает минус.
Пример:
Найдите частное двух целых чисел с разными знаками -2436:42.
Решение:
-2436:42=-58
Пример:
Вычислите деление 4716:(-524).
Решение:
4716:(-524)=-9
Нуль деленный на целое число. Правило.
Правило:
При деление нуля на целое число ответ будет равен нулю.
Пример:
Выполните деление 0:558.
Решение:
0:558=0
Пример:
Разделите нуль на целое отрицательное число -4009.
Решение:
0:(-4009)=0
Правило:
На нуль делить нельзя.
Нельзя 0 разделить на 0.
Проверка частного деления целых чисел.
Как говорилось ранее деление и умножение тесно связаны. Поэтому чтобы проверить результат деления двух целых чисел, нужно выполнить умножение делителя и частного в результате должно получиться делимое.
Проверка результата деления краткая формула:
Делитель ∙ Частное = Делимое
Рассмотрим пример:
Выполните деление и сделайте проверку 1888:(-32).
Решение:
Обращаем внимание на знаки целых чисел. Число 1888 положительное и имеет знак “+”. Число (-32) отрицательное и имеет знак “–”. Поэтому при делении двух целых чисел с разными знаками ответ будет отрицательное число.
1888:(-32)=-59
А теперь выполним проверку найденного ответа:
1888 – делимое,
-32 – делитель,
-59 – частное,
Делитель умножаем на частное.
-32∙(-59)=1888
Вопросы по теме:
Что такое частное чисел?
Ответ: частное чисел – это результат деления деления двух чисел.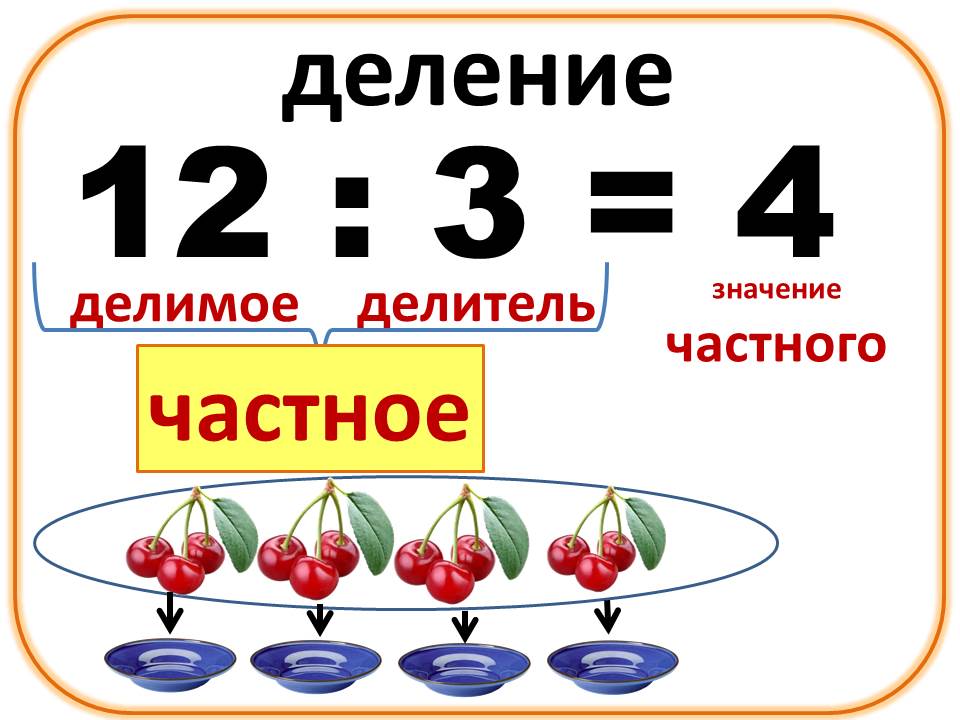
Как найти частное?
Ответ: нужно одно число поделить на другое, то есть делимое поделить на делитель и получим частное.
Чему равно частное от деления целых чисел?
Ответ: если целые числа делятся без остатка, то их частное равно целому числу. Иначе будет дробное число.
Что такое делимое и делитель?
Ответ: число которое делят называют делимым, а число на которое делят называют делителем.
Пример:
Найдите частное суммы и разности чисел 48 и 16.
Решение:
Находим сумму чисел 48 и 16.
48+16=64
Находим разность чисел 48 и 16.
48-16=32
Находим частное.
64:32=2
Ответ: 2.
Деление целых чисел. Делимое, делитель, частное. Что такое частное в математике
Частное, как результат деления Частное, как противопоставление общему Частное, как принадлежащее Частному лицу … Википедия
Результат деления … Большой Энциклопедический словарь
— [сн], частного, ср. (мат.). Число, полученное от деления одного числа на другое. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
(мат.). Число, полученное от деления одного числа на другое. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ЧАСТНОЕ, ого, ср. Результат, итог деления. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
Сущ., кол во синонимов: 1 термин (18) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Обвинение особый порядок производства в судебныхустановлениях дел о Ч. преступлениях; в более общем значении термин: Ч.обвинение обнимает собой все формы участия Ч. лиц в возбужденииуголовного преследования и в обличении обвиняемого на суде.… … Энциклопедия Брокгауза и Ефрона
частное — частное. Произносится [часное] … Словарь трудностей произношения и ударения в современном русском языке
частное — отношение коэффициент — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы отношениекоэффициент EN quotient … Справочник технического переводчика
ЧАСТНОЕ — результат операции деления; обозначается а:b, а/b или … Большая политехническая энциклопедия
Ого; ср.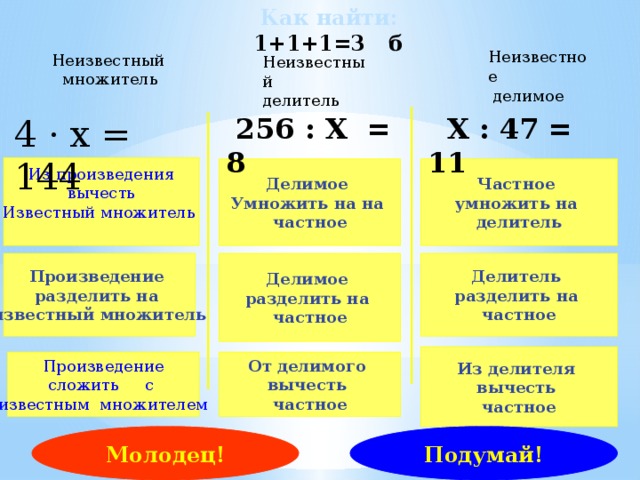 1. Матем. Результат деления одной величины на другую. Найти ч. В частном получилось слишком большое число. 2. То, что представляет собой отдельную часть, особенность чего л. От частного к общему. Уделить внимание частному. * * * частное… … Энциклопедический словарь
1. Матем. Результат деления одной величины на другую. Найти ч. В частном получилось слишком большое число. 2. То, что представляет собой отдельную часть, особенность чего л. От частного к общему. Уделить внимание частному. * * * частное… … Энциклопедический словарь
частное — вынести частное определение существование / создание … Глагольной сочетаемости непредметных имён
Книги
- Частное право Древнего Рима , В. В. Макеев, А. Г. Головко. Предлагаемое издание является учебным пособием по римскому частному праву. Новационность содержания и структуры не имеет на сегодняшний день аналога, так как охватывает буквально все стороны…
- Частное расследование , Фридрих Незнанский. Талантливый ученый и инженер А. Н. Грамов создает уникальный психотропный генератор, при помощи которого можно влиять на человека, где бы он ни находился. По сути им создано новейшее…
Только тем что у целых чисел нужно у частного посчитать знак. Как посчитать знак частного целых чисел? Рассмотрим подробно в теме.
Термины и понятия частного целых чисел.
Чтобы выполнить деление целых чисел нужно вспомнить термины и понятия. В делении есть: делимое, делитель и частное целых чисел.
Делимое – это то целое число, которое делят. Делитель
Можно сказать “Деление целых чисел” или “Частное целых чисел” смысл этих фраз один и тот же, то есть нужно поделить одно целое число на другое и получить ответ.
Деление берет свое начало из умножения. Рассмотрим пример:
У нас есть два множителя 3 и 4. Но допустим нам известно, что есть один множитель 3 и результат умножения множителей их произведение 12. Как найти второй множитель? На помощь приходит деление.
Правило деления целых чисел.
Определение:
Частное двух целых чисел равно частному их модулей, со знаком плюс в результате, если числа одинаковых знаков, и со знаком минус, если они разных знаков.
Важно учитывать знак частного целых чисел. Кратко правила деления целых чисел:
Плюс на плюс дает плюс.
“+ : + = +”
Минус на минус дает плюс.
“– : – =+”
Минус на плюс дает минус.
“– : + = –”
Плюс на минус дает минус.
“+ : – = –”
А теперь рассмотрим подробно каждый пункт правила деления целых чисел.
Деление целых положительных чисел.
Вспомним, что целые положительные числа это тоже самое, что натуральные числа. Мы пользуемся теми же правила, что и при делении натуральных чисел. Знак частного от деления целых положительных чисел всегда плюс . Иными словами, при делении двух целых чисел “плюс на плюс дает плюс ”.
Пример:
Выполните деление 306 на 3.
Решение:
Оба числа имеют знак “+”, поэтому ответ будет со знаком “+”.
306:3=102
Ответ: 102.
Пример:
Разделите делимое 220286 на делитель 589.
Решение:
Делимое 220286 и делитель 589 имеет знак плюс, поэтому частное тоже будет иметь знак плюс.
220286:589=374
Деление целых отрицательных чисел.
Правило деления двух отрицательных чисел.
Пусть у нас будут два отрицательных целых числа a и b. Нам нужно найти их модули и выполнить деление.
Результат деления или частное двух отрицательных целых чисел будет со знаком “+” или “минус на минус дает плюс”.
Рассмотрим пример:
Найдите частное -900:(-12).
Решение:
-900:(-12)=|-900|:|-12|=900:12=75
Ответ: -900:(-12)=75
Пример:
Выполните деление одного целого отрицательного числа -504 на второе отрицательное число -14.
Решение:
-504:(-14)=|-504|:|-14|=504:14=34
Записать выражение можно короче:
-504:(-14)=34
Деление целых чисел с разными знаками. Правило и примеры.
При выполнении деления целых чисел с разными знаками , частное будет равно отрицательному числу.
Не важно положительное целое число делим на отрицательное целое число или отрицательное целое число делим на положительное целое число, результат деления всегда будет равен отрицательному числу.
Минус на плюс дает минус.
Плюс на минус дает минус.
Пример:
Найдите частное двух целых чисел с разными знаками -2436:42.
Решение:
-2436:42=-58
Пример:
Вычислите деление 4716:(-524).
Решение:
4716:(-524)=-9
Нуль деленный на целое число. Правило.
При деление нуля на целое число ответ будет равен нулю.
Пример:
Выполните деление 0:558.
Решение:
0:558=0
Пример:
Разделите нуль на целое отрицательное число -4009.
Решение:
0:(-4009)=0
На нуль делить нельзя.
Нельзя 0 разделить на 0.
Проверка частного деления целых чисел.
Как говорилось ранее деление и умножение тесно связаны. Поэтому чтобы проверить результат деления двух целых чисел, нужно выполнить умножение делителя и частного в результате должно получиться делимое.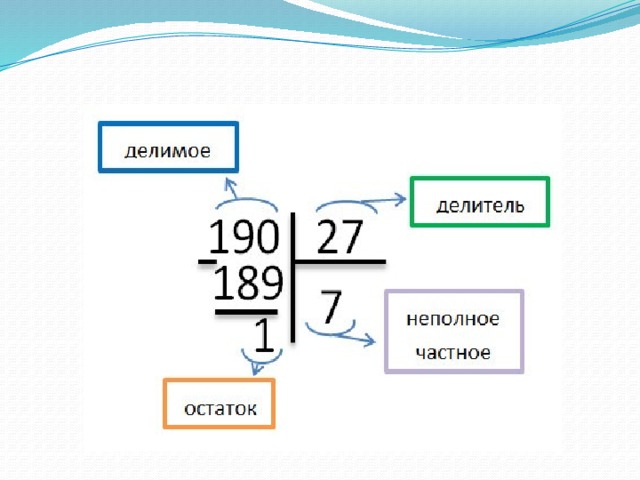
Проверка результата деления краткая формула:
Делитель ∙ Частное = Делимое
Рассмотрим пример:
Выполните деление и сделайте проверку 1888:(-32).
Решение:
Обращаем внимание на знаки целых чисел. Число 1888 положительное и имеет знак “+”. Число (-32) отрицательное и имеет знак “–”. Поэтому при делении двух целых чисел с разными знаками ответ будет отрицательное число.
1888:(-32)=-59
А теперь выполним проверку найденного ответа:
1888 – делимое,
-32 – делитель,
-59 – частное,
Делитель умножаем на частное.
-32∙(-59)=1888
Аноним
Давайте вспомним определение, что называется частным чисел.
Частное чисел — это результат деления одного числа на другое. Таким образом, частное чисел а и b будет число c, которое равно c = a: b. При этом число a будет делимым, а число — b делителем.
Иными словами, частное чисел — это математическая величина, которая получается в результате деления одного числа на другое.
Аноним
Частное чисел
1. Введем определение этого понятия. Частным чисел называется результат деления одного из чисел на другое. Частное чисел — это математическая величина.
2. Наглядное представление: a / b = c.
- а — делимое;
- b — делитель;
- c — частное.
3. Пример 1. 156 / 2. Если поделить число 156 на 2, то в результатом будет число 78. В этом случае число 78 представляет собой частное двух чисел, результат от деления числа 156 на 2. 156 — делимое, 2 — делитель. Число 156 больше, чем число 2, в 78 раз. Данные умозаключения можно проверить, достаточно лишь выполнить операцию, обратную делению. 78 * 2 = 156. Верно.
4. Усложненный пример. 153214 / 2. 153214 — делимое, 2 — делитель.
- Делим 15 на 2. Берем по 7. 7 * 2 = 14. Вычитаем из 15 полученное значение и получаем 1.
- Спускаем 3.
 13 делим на 2. Берем по 6. 6 * 2 = 12. Вычитаем из 13 полученное значение и получаем 1.
13 делим на 2. Берем по 6. 6 * 2 = 12. Вычитаем из 13 полученное значение и получаем 1. - Спускаем 2. 12 делим на 2. Берем по 6. 6 * 2 = 12. Вычитаем из 12 полученное значение и получаем 0.
- Спускаем единицу, прописываем ноль. Спускаем 4. 14 делим на 2. Берем по 7. 7 * 2 = 14. Вычитаем из 14 полученное значение и получаем 0.
Неполное частное
Пример пункта 3 довольно прост. Так число 2 содержится в числе 156 ровно 78 раз.
Приведем пример: 157 / 3. 157 — делимое, 3 — делитель. При делении мы получаем, что число 3 содержится в числе 157, 52 раза, но образуется еще и остаток, который равен единице. В данном случае число 52 будем называть неполным частным. Число 1 — это остаток от деления числа 157 на 3.
Большинство людей, окончивших среднюю общеобразовательную школу, имеют достаточно хорошее представление о том, что такое частное чисел в математике. Но тем не менее, давайте дадим определение этому термину.
Частное числа: значение
Частное чисел — это математическая величина, полученная при делении одного числа на другое. Частное показывает нам, во сколько раз одно число больше другого.
Частное показывает нам, во сколько раз одно число больше другого.
Если записать операцию деления в виде простой формулы
- a: b = c,
то в ней a — это «делимое», b — это «делитель», а c — это и есть «частное».
Рассмотрим также пример с конкретными цифрами. Если мы поделим число 39 на 3, то в ответе получим число 13. В данном случае 13 — это частное, результат деления числа 39 на 3. Другими словами можно сказать, что число 39 больше, чем число 3, в 13 раз.
А давайте задумаемся, так ли это на самом деле? Чтобы понять, ошиблись мы или нет, произведем проверку и выполним действие, обратное делению. Как вы, наверное, уже догадались, это умножение. Умножим число 13 на 3. В ответе получается 39. Мы не ошиблись.
Неполное частное
О приведенном выше математическом примере можно сказать, что число 3 содержится в числе 39 ровно 13 раз. Однако в большинстве реальных случаев такой красивый и простой ответ получить невозможно. Сколько раз, например, число 3 содержится в числе 40?
Данная математическая операция записывается следующим образом:
- 40: 3 = 13 (1).

Что означает эта запись? Число 3 содержится в числе 40 тоже 13 раз, но при этом еще образуется остаток, равный 1. В данном случае число 13 называется «неполным частным», а число 1 — «остатком от деления».
Частное — это что такое? Можно услышать о множестве вещей и процессов, которые используются с этим словом. Что же оно значит?
Общая информация
Частное — это значит, что что-то принадлежит одному человеку или же относительно небольшой группе людей. Причем они объединены на добровольной основе, а не в приказном порядке (как пример можно в последнем случае привести коммунальные предприятия). А это, в свою очередь, обозначает определённую специфику. Также, когда говорят про частное, это может означать отдельный, весьма редкий или вообще единичный случай чего-то. Кроме этого, так называется одноименный математический оператор.
Как видите, слово «частное» — это весьма широко используемый инструмент нашего языка. Чтобы лучше понять его использование, давайте рассмотрим его применение на практике. Для полноты обзора будет уделено внимание и общему примеру, и частному. Итак, приступим.
Для полноты обзора будет уделено внимание и общему примеру, и частному. Итак, приступим.
Общий пример
Сейчас нами будет рассмотрена частная собственность. Как уже ранее говорилось, так называется всё, что принадлежит отдельному человеку или небольшой группе людей, которые объединились на добровольном основании. В качестве иллюстрации можно привести такое понятие, как дача. Что это? Так называют землю и постройки, которые принадлежат определённому человеку или группе (семье). Это на которую посторонним входить без разрешения хозяев запрещено. В случае нарушения к ним могут быть применены силовые методы для задержания с последующей передачей правоохранительным органам.
Частная собственность — это одна из основ капитализма, поэтому она охраняется со всей строгостью. Нарушение этого принципа подрывает устои современного капитализма и ведёт к различным, как правило негативным, последствиям. Хотя у нас защищен любой тип собственности, нажитый законным путём, так уж повелось, что именно частная представляет наибольший интерес для подавляющего количества людей.
Частный пример
А сейчас давайте рассмотрим использование этого слова с немного иной точки зрения. Только теперь для нас интерес будут представлять не физические лица, а юридические. Мы рассмотрим частное предприятие. Это означает, что оно принадлежит определённому человеку или группе и было создано на добровольческих основаниях. Но при этом оно не претендует на определённые материальные ценности. Так, есть объекты коммунальной собственности, например — парки. Они находятся в ведении коммунальных служб городов, где расположены.
Частные предприятия могут претендовать на определённое количество земли, необходимое для ведения деятельности, но это подразумевает использование только определённых типов территории. Причем следует отметить статус, который имеет юридическое лицо. Если взять, к примеру, гипотетическое село, и там одновременно будет действовать и частное, и В обоих могут состоять все жители. Но тем не менее у них будут различные полномочия и возможности, от которых уже будет зависеть осуществляемая деятельность и конечные цели.
Формула остатка делителя делителя
Формула остатка частного делителя дивиденда показывает соотношение между делимым, делителем, частным и остатком, которое является одним из основных аспектов деления. Деление — это процесс, при котором число делится на равные части, оставляя после себя остаток, если число нельзя разделить дальше. Формула остатка делителя делителя является важным правилом при делении, давайте узнаем о нем больше, а также решим несколько примеров.
Что такое формула остатка делителя дивиденда?
Формула остатка частного делителя делителя состоит из 4 основных аспектов, используемых при делении, т. е. делимого, делителя, частного и остатка. Делимое – это число, которое делится на делитель. Делитель – это коэффициент, на который делится делимое. Результат, полученный в процессе деления, называется частным, а число, оставшееся после завершения деления, называется остатком. Формула остатка делителя делителя получается методом деления.
Формула остатка делителя делителя
Формула:
Дивиденд = делитель × частное + остаток
Это можно проверить делением, показанным выше: 9 = 2 × 4 + 1
Получение дивидендов Формула остатка от делителя
Формула остатка от делителя помогает проверить ответ, полученный методом деления. Обычно, когда мы делим одно число на другое число, это приводит к такому ответу, что;
a/b = c, где a – делимое, b – делитель и c – частное. Другими словами, это можно записать так:
Делимое/Делитель = Частное
Делимое = Делитель × Частное
Частное + остаток
Следовательно, формула остатка в частном делителя делителя такова: Дивиденд = делитель x частное + остаток
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
БЕСПЛАТНАЯ ПЕРЕМЕРНОЕ КЛАСС
Примеры с использованием коэффициента дивидендов Формула
Пример 1: Найдите остаток, когда дивиденд составляет 75, делитель составляет 5, а коэффициент — 15. Используйте кожурный кожур дивидендов.
Решение: Дано, делимое = 75, делитель = 5, частное = 15 и пусть остаток равен х
Отметив их в формуле:
Делимое = Делитель × Частное + Остаток
75 = 5 × 15 + х
75 = 75 + x
x = 75 — 75
x = 0
Таким образом, используя формулу, мы получили остаток, равный 0. Остаток = 0
Пример 2: Найдите дивиденды, когда остаток равен 1, делитель равен 3, а частное равно 31.
Решение: Дано, остаток = 1, делитель = 3, частное = 31 и пусть делимое равно x
Используя формулу делимого делителя остатка в частном:
Дивиденд = делитель × частное + остаток
Di виденд = 3 × 31 + 1
Дивиденд = 94
Следовательно, дивиденд равен 94
Пример 3: Разделите 120 на 5, используя метод деления, и проверьте это с помощью формулы делителя делителя.
Решение: Сначала разделим 120 на 5, используя простой метод деления:
120/5 = 24
Здесь 120 — делимое, 5 — делитель, 24 — частное, а 0 — остаток.
Проверим этот ответ, воспользовавшись формулой остатка в частном делимом:
Дивиденд = Делитель × Частное + Остаток мы видим, что LHS = RHS , значит, деление верное.
Часто задаваемые вопросы о формуле остатка делителя дивиденда
Что подразумевается под формулой остатка делителя дивиденда?
Остаток делителя делителя Формула состоит из 4 основных аспектов, которые используются в методе деления, т. е. делимого, делителя, частного и остатка. Формула остатка делителя делителя помогает проверить правильность выполнения процесса деления с помощью обычного метода деления. Это в основном обратный метод деления. Формула: Дивиденд = Делитель × Частное + Остаток
Что происходит, когда в формуле остатка делителя делителя используется ноль?
Если в формуле остатка частного делителя используется ноль, возможны три варианта:
- При делении нуля на число частное равно нулю
- Деление числа на ноль невозможно
- Если делимое полностью делится на делитель, то остаток равен 0.

Найдите значение x в 70 = 5 × x + 0, используя формулу остатка от делителя дивиденда.
Недостающее значение — это частное. Формула: Дивиденд = Делитель × Частное + Остаток
70 = 5 × x + 0
70 = 5x
x = 70/5
x = 14
Как мы можем применить Dividend Divisor Qu какая формула остатка?
Формула делителя делителя и частного остатка может быть применена, если мы знаем либо делимое, либо остаток, либо делитель. Формула может быть применена соответствующим образом. Для дивиденда используется следующая формула: Дивиденд = делитель × частное + остаток. Для делителя используется следующая формула: Дивиденд/Делитель = Частное + Остаток/Делитель.
Дивиденды – определение, формула и важные правила 3
•
Всего просмотров: 314,1k
•
Просмотров сегодня: 3,82 k
Делимое – это целое число или количество вещей, которые необходимо разделить на определенные равные части. Существует четыре основных операции над числами: сложение, вычитание, умножение и деление. Деление — это процесс деления числа на равные части, оставляющий после себя напоминание, если данное число нельзя разделить на части поровну. Таким образом, деление с остатком или евклидово деление содержит следующее:
Существует четыре основных операции над числами: сложение, вычитание, умножение и деление. Деление — это процесс деления числа на равные части, оставляющий после себя напоминание, если данное число нельзя разделить на части поровну. Таким образом, деление с остатком или евклидово деление содержит следующее:
Дивиденд — Дивиденд — это число, которое нужно разделить на делитель.
Делитель — Число, на которое нужно разделить делимое, называется делителем.
Частное — Результат деления называется частным.
Остаток — Число, оставшееся после деления, называется остатком.
В этой статье мы обсудим определение и формулу дивидендов. Мы также изучим методы нахождения дивидендов.
Деление без остатка:
Например, у вас есть 20 конфет, и вам нужно разделить их поровну между 4 детьми. Если разделить конфеты поровну, то каждая из них получит по 5 конфет. Рассмотрим в этом случае количество конфет (т. е. 20), которое должно быть разделено между детьми, называется делимым, а количество детей (т. е. 4), между которыми оно должно быть разделено, называется делителем. Помните, что делитель делит делимое или, другими словами, делимое делится на делитель. Результат равного распределения, то есть количество конфет у каждого члена, называется частным.
Дивиденд = 20
Делитель = 4
Частное = 5
Остаток = 0
Деление на остаток:
Рассмотрим тот же вышеупомянутый пример, но с модификацией. Предположим, что на этот раз конфеты нужно раздать трем участникам, то есть 20 конфет нужно раздать трем детям. Разделение показано ниже:
Здесь конфеты поровну распределены между 3 детьми так, что у каждого по 6 конфет, но осталось 2 конфеты, которые нельзя разделить на три целиком. Таким образом, остаток от этого деления называется остатком.
Таким образом, остаток от этого деления называется остатком.
Здесь
Дивиденд = 20
Делитель = 3
Частное = 6
Остаток = 2.
Формула дивиденда:
Если значение делитель, частное и остаток даны, то мы можем найти делимое, разделенное по следующей формуле дивидендов:
Дивиденд = Делитель x Частное + Остаток.
Это как раз обратный процесс деления. В приведенном выше примере мы сначала разделили делимое на делитель и вычли кратное вместе с делимым. То есть мы сначала разделили, а потом вычли. Таким образом, чтобы найти делимое, нам нужно сделать обратное, то есть сначала нужно умножить вместо деления, а затем сложить вместо вычитания.
Вот примеры делимых для лучшего понимания концепции:
Допустим, нам нужно разделить 11 на 2 равные целые части. Результат будет с остатком 1.
Здесь делимое = 11, делитель = 2, частное = 5 и остаток = 1.
Согласно формуле дивидендов,
Дивиденд = делитель x частное + остаток
9016 6 11 = (2 x 5) + 111 = 10 + 1
11 = 11
Левая сторона = Правая сторона.
Отсюда формула дивиденда
Дивиденд = (Делитель x Частное) + Остаток Дивиденд? Мы можем найти дивиденды, используя формулу дивидендов. Пример: При делении числа на 9 в частном получается 6, а в остатке остается 1. Найдите число. Решение: Пусть делимое будет x x = (9 x 6) + 1 = 54 + 1 = 55 Следовательно, значение делимого равно 55. Важные правила деления: Правило 1: Всякий раз, когда мы делим 0 на другое число, результат (частное) всегда равен нулю. |

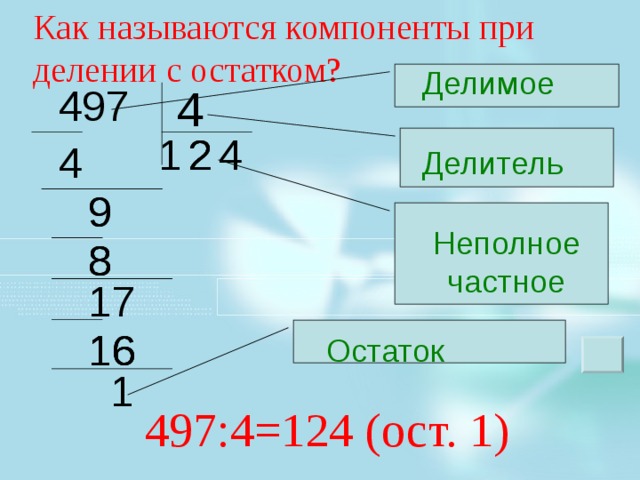 13 делим на 2. Берем по 6. 6 * 2 = 12. Вычитаем из 13 полученное значение и получаем 1.
13 делим на 2. Берем по 6. 6 * 2 = 12. Вычитаем из 13 полученное значение и получаем 1.

