Примеры деление и умножение дробей с разными знаменателями: Умножение и деление дробей, примеры, тесты

Умножение и деление обыкновенных дробей

Умножение обыкновенных дробей

Чтобы умножить дробь на дробь, нужно числитель первой дроби умножить на числитель второй – это будет числитель результата, а знаменатель первой дроби умножить на знаменатель второй – это будет знаменатель результата.

Пример 1. Вычислить произведение

3/7

*

5/11

.

3/7

*

5/11

=

3*5/7*11

=

15/77

.

Пример 2. Вычислить произведение

5/21

*

3/5

.

5/21

*

3/5

=

5*3/21*5

, сократим эту дробь на 3 и на 5, получим

5*3/21*5

=

1/7

.

Умножение смешанных дробей

Чтобы умножить смешанную дробь на смешанную, нужно обе дроби записать в виде неправильных дробей и перемножить их по правилу умножения дробей.

Пример 1. Вычислить произведение

1

1/2

* 3

2/3

.

1

1/2

* 3

2/3

=

3/2

*

11/3

=

33/6

=

11/2

= 5

1/2

.

Пример 2. Вычислить произведение

5

1/4

* 2

3/5

.

5

1/4

* 2

3/5

=

21/4

*

13/5

=

273/20

= 13

13/20

.

Деление обыкновенных дробей

Чтобы разделить одну дробь на другую, нужно числитель первой дроби умножить на знаменатель второй – это будет числитель результата, а знаменатель первой умножить на числитель второй – это будет знаменатель результата. Таким образом, деление дробей сводится к умножению.

Пример 1. Вычислить значение выражения

1/9

:

2/3

.

1/9

:

2/3

=

1*3/9*2

, сократим полученную дробь на 3:

1*3/9*2

=

1*1/3*2

=

1/6

.

Пример 2. Вычислить значение выражения

3

2/7

: 2

1/7

.

3

2/7

: 2

1/7

=

23/7

:

15/7

=

23*7/7*15

, сократим полученную дробь на 7:

23*7/7*15

=

23/15

= 1

8/15

.

Пример 3. Вычислить значение выражения

15 : 2

1/2

.

15 : 2

1/2

=

15/1

:

5/2

=

15*2/1*5

, сократим эту дробь на 5:

15*2/1*5

=

3*2/1*1

= 6

.

Пример 4. Вычислить значение выражения

7

2/9

: 13

.

7

2/9

: 13 =

65/9

:

13/1

=

65*1/9*13

, сократим эту дробь на 13:

65*1/9*13

=

5/9

.

Деление дробей с разными знаменателями – примеры и правила (5 класс, математика)

4.6

Средняя оценка: 4.6

Всего получено оценок: 284.

4.6

Средняя оценка: 4.6

Всего получено оценок: 284.

Дроби неприятны тем, что большое воздействие на действия с ними оказывают знаменатели. Часто ученики 5 класса приходят в ступор при виде дробей с разными знаменателями, начиная выполнять, лишние действия и терять время.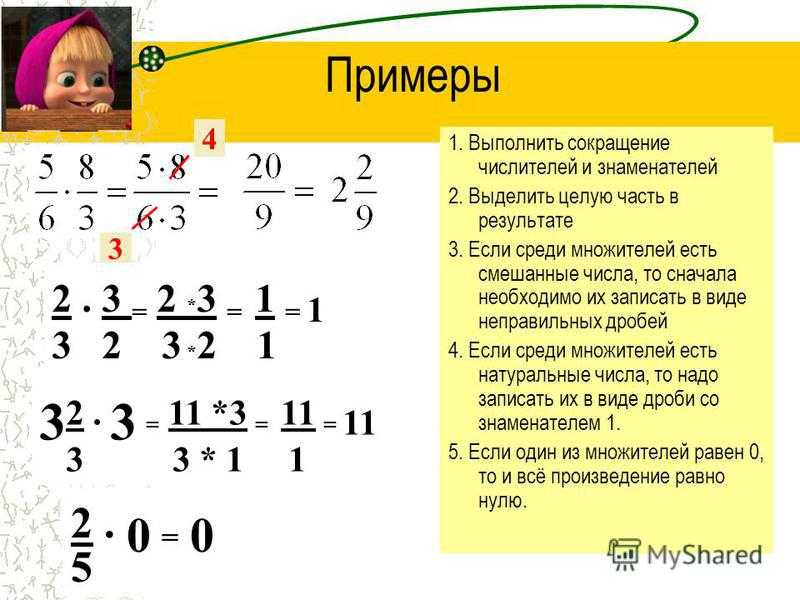 А ведь не для всех действий с дробями требуется наличие одинакового знаменателя, поговорим подробнее о данном вопросе.

Действия с дробями

Необходимость приведения к одному знаменателю зависит от выполняемых действий. Разобьем возможные действия на группы и разберемся с каждой из групп в отдельности.

Сложение и вычитание

Сложение и вычитание дробей основано на вынесении общего множителя. Рассмотрим на примере, как выглядит сложение дробей в подробности:

$${3\over{13}}+{5\over{13}}={1\over{13}}*(3+5)={8\over{13}}$$

Это значит, что сложение и вычитание дробей возможно только при условии наличия одинакового знаменателя. Если знаменатели у дробей разные, то необходимо привести дроби к общему знаменателю.

Если не привести дроби к одному знаменателю, то общий множитель просто не получится вынести, а принцип сложение осуществить не получится. Поэтому вычитание или сложение дробей с разными знаменателями невозможно. Это непреложное правило.

Умножение

Умножение дробей не требовательно к знаменателю.

Здесь используется совершенно иной принцип. Дело в том, что дробную черту можно заменить знаком деления. Тогда:

${3\over{5}}*{2\over{3}}=3:5*2:3=(3*2):(5*3)={6\over{15}}$ – для того, чтобы перемножить две дроби нужно умножить числитель на числитель, а знаменатель на знаменатель. Получившаяся дробь будет результатом умножения.

Деление

Деление использует те же принципы, что и умножение:

${3\over{5}}:{2\over{3}}=(3:5):(2:3)=3:5*3:2=9:10={9\over{10}}$ – для того, чтобы разделить одну дробь на другую необходимо перевернуть дробь-делитель. Для этого числитель меняется на знаменатель, а знаменатель на числитель. После этого делимое и перевернутый делитель необходимо перемножить. Результат умножение будет результатом деления изначальных чисел.

Одинаковый знаменатель ни для деления, ни для умножения дробей не требуется. Помните, что каждое действие в математике имеет свое основание.

Основанием для сложения и умножения является общий множитель. Значит нужно, чтобы этот общий множитель был. Поэтому требуется одинаковый знаменатель у двух дробей. Основание для деления и умножения – математический смысл дроби.

Этот принцип работает вне зависимости от значения знаменателя, поэтому деление дробей с разными знаменателями и деление дробей с одинаковым знаменателем не отличается. Последовательность действий при решении примеров деления дробей с разными знаменателями одна и та же.

Что мы узнали?

Мы поговорили о действиях с дробями. Выделили отдельные группы действий с дробями. Привели обоснование каждому из действий. Объяснили, когда необходимо наличие одинакового знаменателя, а когда нет. Отдельно рассмотрели деление дробей с разными знаменателями и сказали, что это действие возможно с любыми знаменателями дробей.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка статьи

4.6

Средняя оценка: 4. 6

Всего получено оценок: 284.

---

А какая ваша оценка?

Умножение дробей | Умножение дробей

Умножение дробей начинается с умножения заданных числителей, за которым следует умножение знаменателей. Затем полученная дробь еще больше упрощается и при необходимости сокращается до наименьших членов. Давайте узнаем больше об умножении дробей, как умножать дроби на целые числа, как умножать неправильные дроби, умножать смешанные дроби и правила умножения дробей в этой статье.

1.	Как умножать дроби?
2.	Правила умножения дробей
3.	Умножение дробей с одинаковым знаменателем
4.	Умножение дробей с разными знаменателями
5.	Умножение дробей на целые числа
6.	Умножение дробей со смешанными числами
7.	Как умножать неправильные дроби?
8.	Часто задаваемые вопросы об умножении дробей

Как умножать дроби?

Умножение дробей не похоже на сложение или вычитание дробей, где знаменатель должен быть одинаковым. Здесь можно легко перемножить любые две дроби с разными знаменателями. Единственное, что нужно иметь в виду, это то, что дроби не должны быть в смешанной форме, они должны быть либо правильными дробями, либо неправильными дробями. Давайте научимся умножать дроби, выполнив следующие шаги:

• Шаг 1: Умножьте числители.
• Шаг 2: Умножьте знаменатели.
• Шаг 3: Сократите полученную дробь до наименьшего значения.

Примечание: Другой способ умножения дробей состоит в том, чтобы упростить и сократить дроби между собой, а затем перемножить числители вместе и знаменатели вместе, чтобы получить конечный продукт.

Давайте разберем эти шаги на примере.

Пример: Умножьте следующие дроби: 1/3 × 3/5.

Решение: Начнем с умножения числителей: 1 × 3 = 3, затем умножим знаменатели: 3 × 5 = 15. Это можно записать как: (1 × 3)/(3 × 5) = 3 /15. Теперь уменьшите это значение до самой низкой формы. 3 — это наибольший общий делитель (НОД) 3 и 15, поэтому разделите и 3, и 15 на 3, чтобы упростить дробь. Следовательно, 1/3 × 3/5 = 1/5.

Метод 2: Теперь давайте воспользуемся другим методом умножения этих дробей, где мы можем упростить дроби между собой, а затем перемножить числители вместе, затем знаменатели вместе, чтобы получить конечный продукт. Здесь будет 1/3 × 3/5→ 1/1 × 1/5 = 1/5, и мы получим тот же ответ.

Правила умножения дробей

При умножении дробей необходимо помнить о следующих правилах:

• Правило 1: Первое правило состоит в преобразовании смешанных дробей в неправильные дроби, если таковые имеются. Затем умножьте числители данных дробей.
• Правило 2: Умножьте знаменатели отдельно.
• Правило 3: Упростите полученное значение до наименьшего члена.
• Правило 4: Еще один простой способ умножения дробей состоит в том, чтобы упростить и сократить дроби между собой, а затем перемножить числители вместе и знаменатели вместе, чтобы получить конечный продукт.

Эти правила можно применить к любым двум дробям, чтобы найти их произведение. Теперь давайте изучим отдельные случаи умножения дробей с разными типами дробей.

Умножение дробей с одинаковым знаменателем

Умножение дробей с одинаковым знаменателем не меняет правила умножения дробей. Дроби, имеющие одинаковые знаменатели, называются дробями. Хотя сложение и вычитание одинаковых дробей отличается от сложения и вычитания разнородных дробей, в случае умножения и деления метод остается тем же. Мы умножаем числители, затем знаменатели, а затем дробь сокращается до наименьших членов.

Пример: Умножить 1/3 × 5/3

Решение: Мы можем умножить эти дроби, используя следующие шаги.

• Шаг 1: Умножьте числители, 1 × 5 = 5.
• Шаг 2: Умножьте знаменатели, 3 × 3 = 9.
• Шаг 3: Произведение, которое мы получаем, равно 5/9. Это не может быть уменьшено дальше, поэтому ответ 5/9.

Умножение дробей с разными знаменателями

Умножение дробей с разными знаменателями точно такое же, как умножение одинаковых дробей. Давайте разберемся в этом на примере.

Пример: Умножьте 4/12 × 16/24.

Мы можем умножить эти дроби, используя следующие шаги:

• Шаг 1: Умножьте числители, 4 × 16 = 64.
• Шаг 2: Умножьте знаменатели, 12 × 24 = 288.
• Шаг 3: Произведение, которое мы получаем, равно 64/288. Это может быть уменьшено до 2/9. Таким образом, 2/9 является ответом.

Альтернативный метод

Те же дроби можно умножить другим методом, в котором мы упрощаем дроби между собой, а затем умножаем числители, затем знаменатели, чтобы получить конечный продукт.

Пример: Умножьте 4/12 × 16/24.

Умножим данные дроби, используя следующие шаги:

• Шаг 1: Упростим данные дроби между собой. Другими словами, эти дроби можно сократить до 1/3 × 2/3.
• Шаг 2: Умножим числители, 1 × 2 = 2.
• Шаг 3: Теперь умножим знаменатели, 3 × 3 = 9.
• Шаг 4: Следовательно, произведение, которое мы получаем, равно 2/9.

Умножение дробей на целые числа

Умножение дробей на целые числа — простая идея. Поскольку мы знаем, что умножение — это многократное сложение одного и того же числа, этот факт можно применить и к дробям.

Умножение дробей на целые числа Визуальная модель

Рассмотрим следующий пример: 4 × 2/3. Это означает, что 2/3 добавляется 4 раза. Представим этот пример с помощью визуальной модели. Четырежды две трети представлены как:

Шаги умножения дробей на целые числа

Чтобы умножать дроби с целыми числами, мы используем простое правило умножения числителей, затем умножения знаменателей, а затем сокращения их до наименьших членов. Однако в случае целых чисел мы запишем их в дробной форме, поставив «1» в знаменателе. Давайте разберемся в этом на примере.

Пример: Умножить: 5 × 3/4

Решение: Давайте используем следующие шаги, чтобы умножить данную дробь на целое число.

• Шаг 1: Здесь 5 — это целое число, которое можно записать как 5/1, а затем его можно умножить, как мы умножаем обычные дроби.
• Шаг 2: Это означает, что нам нужно умножить 5/1 × 3/4
• Шаг 3: Умножьте числители, 5 × 3 = 15
• Шаг 4: Умножьте знаменатели, 1 × 4 = 4
• Этап 5: Полученное произведение равно 15/4 и не может быть больше уменьшено.
• Шаг 6: Поскольку 15/4 — неправильная дробь, мы изменим ее на смешанную дробь, 15/4 = \(3\frac{3}{4}\)

Умножение смешанных дробей

Смешанные числа или смешанные дроби — это дроби, состоящие из целого числа и правильной дроби, например \(2\frac{3}{4}\), где 2 — целое число, а 3/4 — правильная дробь. Для умножения смешанных дробей нам нужно преобразовать смешанные дроби в неправильную дробь перед умножением. Например, если число равно \(2\frac{2}{3}\), нам нужно изменить его на 8/3. Давайте разберемся в этом с помощью примера.

Пример: Умножение \(2\frac{2}{3}\) и \(3\frac{1}{4}\)

Решение: Следующие шаги можно использовать для умножения дробей с смешанные числа.

• Шаг 1: Измените заданные смешанные дроби на неправильные, т. е. (8/3) × (13/4).
• Шаг 2: Умножьте числители неправильных дробей, а затем умножьте знаменатели. Это даст 104/12.
• Шаг 3: Теперь уменьшите полученную дробь до наименьшего значения, что сделает ее равной 26/3.
• Шаг 4: Далее, преобразуйте ответ обратно в смешанную дробь, которая будет \(8\frac{2}{3}\).

Как умножать неправильные дроби?

Теперь давайте разберемся с умножением неправильных дробей. Мы уже знаем, что неправильная дробь — это та, у которой числитель больше знаменателя. При умножении двух неправильных дробей часто получается неправильная дробь. Например, чтобы умножить 3/2 × 7/5, две неправильные дроби, нам нужно выполнить следующие шаги:

• Шаг 1: Умножьте числители и знаменатели. (3 × 7)/(2 × 5) = 21/10.
• Шаг 2: Дробь 21/10 не может быть сокращена до наименьшего значения.
• Шаг 3: Следовательно, ответ равен 21/10, что можно записать как \(2\frac{1}{10}\).

Советы и приемы умножения дробей

Вот несколько важных советов и приемов, которые помогут умножить дроби.

• Обычно учащиеся упрощают дробь после умножения. Однако, чтобы упростить расчеты, проверьте, не находятся ли две дроби, которые нужно умножить, в младших формах. Если нет, сначала упростите их, а затем умножьте. Например, 4/12 × 5/13 будет сложно умножить напрямую.
• Теперь, если мы сначала упростим дробь, мы получим 1/3 × 5/13 = 5/39
• Упрощение также можно выполнить для двух дробей. Если между числителем одной из дробей и знаменателем другой дроби есть общий множитель, можно их упростить и продолжить. Например, 5/28 × 7/9можно упростить до 5/4 × 1/9 перед умножением.

☛ Похожие темы

• Калькулятор умножения дробей
• Обратное число дробей
• Умножение десятичных дробей
• Умножение и деление целых чисел
• Сложение дробей
• Вычитание дробей
• Деление дробей

Cuemath — одна из ведущих мировых обучающих платформ по математике, которая предлагает онлайн-уроки по математике в режиме реального времени один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.

 

Умножение дробей Примеры

1. Пример 1: Найдите произведение дробей: 1/4 × 5/8

   Решение:

   Для умножения дробей с разными знаменателями, как указано в 1/4 × 5/8, мы начинаем с умножения числители: 1 × 5 = 5. После этого умножаем знаменатели: 4 × 8 = 32. Это можно записать так: (1 × 5)/(4 × 8) = 5/32. Теперь эту результирующую дробь нельзя упростить, поэтому ответ равен 5/32 9.0005

2. Пример 2: Изменяет ли правило умножения дробей умножение дробей на целые числа? Обоснуйте свой ответ и найдите произведение дробей: 4 × 6/5

   Решение:

   Нет, умножение дробей на целые числа не меняет правила умножения дробей. Нам просто нужно записать целое число в форме дроби. В этом случае 4 будет записано как 4/1, и тогда мы будем использовать тот же метод. Итак, мы будем умножать 4/1 × 6/5. При умножении числителей мы получаем 4 × 6 = 24. При умножении знаменателей мы получаем 1 × 5 = 5. Следовательно, результирующее произведение равно 24/5, которое нельзя уменьшить дальше. Поэтому мы изменим эту неправильную дробь 24/5 на смешанную дробь, чтобы представить ее как ответ, который равен 24/5 = \(4\frac{4}{5}\).

3. Пример 3: Найдите произведение дробей: 5/4 × 5/2 × 5/3

   Решение:

   Чтобы умножить три дроби, мы сначала умножим все три числителя, а затем все три знаменателя. Затем мы упростим окончательный ответ.

   ⇒ 5/4 × 5/2 × 5/3

   ⇒ (5 × 5 × 5)/(4 × 2 × 3)

   ⇒ 125/24

   Следовательно, 5/4 × 5/2 × 5/3 = 125/24 или \(5\frac{5}{24}\)

перейти к слайдуперейти к слайдуперейти к слайду

Готовы увидеть мир глазами математика?

Математика — это жизненный навык. Помогите своему ребенку усовершенствовать его с помощью реального приложения.

Записаться на бесплатный пробный урок

Практические вопросы по умножению дробей

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об умножении дробей

Как умножать дроби?

Умножение дробей означает нахождение произведения двух или более дробей. Метод, используемый для умножения дробей, отличается от сложения и вычитания дробей. Чтобы умножить любые две дроби, мы следуем шагам, указанным ниже. Давайте умножим 7/8 × 2/6, чтобы понять шаги.

• Умножьте числители. Итак, 7 × 2 = 14,
• Умножьте знаменатели. Это означает, что 8 × 6 = 48,
.
• Полученная дробь равна 14/48. Упростите полученную дробь до наименьших членов. Упрощение дроби 14/48 дает нам 7/24. Следовательно, ответ 7/24.
• Другой способ умножения этих дробей заключается в том, что мы можем упростить дроби между собой, а затем перемножить числители вместе, затем знаменатели вместе, чтобы получить конечный продукт. Здесь будет 7/8 × 2/6 → 7/8 × 1/3 = 7/24
.

Каковы правила умножения дробей?

Существует четыре простых правила умножения дробей.

• Сначала умножьте числители.
• Затем перемножьте знаменатели обеих дробей, чтобы получить результирующую дробь.
• Затем нам нужно упростить полученную дробь, чтобы получить окончательный ответ. Это можно понять на простом примере → 2/6 × 4/7 = (2 × 4)/(6 × 7) = 8/42 = 4/21.
• Другой способ умножения дробей заключается в том, что мы можем сократить дроби между собой, а затем перемножить числители вместе, затем знаменатели вместе, чтобы получить конечный продукт. Более простой способ можно сделать следующим образом: → 2/6 × 4/7 = 1/3 × 4/7 = (1 × 4)/(3 × 7) = 4/21.

Как умножать смешанные дроби?

Следующие шаги можно использовать для умножения смешанных дробей. Умножим 1/4 × \(3\frac{1}{2}\).

• Замените смешанную дробь на неправильную. Здесь \(3\frac{1}{2}\) станет 7/2. Итак, теперь нам нужно умножить 1/4 × 7/2.
• Умножьте числители, а затем знаменатели. Это означает, что (1 × 7)/(4 × 2) = 7/8.
• Убедитесь, что ответ указан в самом низком выражении. Поскольку 7/8 нельзя уменьшить дальше, ответом будет 7/8.

Как умножать дроби на целые числа?

Чтобы понять умножение дроби на целое число, мы можем взять простой числовой пример 2/7 × 3. Начните с перезаписи целого числа (3 в этом примере) в виде дроби 3/1. Теперь мы можем применить шаги, которые мы используем для умножения дробей. Это означает, что 2/7 × 3/1 = (2 × 3)/(7 × 1) = 6/7.

Как умножать дроби с одинаковым знаменателем?

Умножение дробей с одинаковыми знаменателями аналогично умножению других правильных дробей. Давайте разберемся в этом на примере. Умножим 4/5 × 3/5. Умножаем числители, то есть 4 × 3 = 12. Затем умножаем знаменатели, то есть 5 × 5 = 25. Это даст нам произведение как 12/25. Поскольку это нельзя уменьшить дальше, ответом будет 12/25.

Как умножать дроби с разными знаменателями?

Умножение дробей с разными знаменателями не меняет правила умножения дробей. Давайте разберемся в этом на примере. Умножьте 2/6 × 3/4. Мы можем умножить эти дроби, используя следующие шаги:

• Умножить числители, 2 × 3 = 6.
• Умножьте знаменатели, 6 × 4 = 24.
• Продукт, который мы получаем, 6/24. Это можно уменьшить до 1/4, следовательно, ответ 1/4.

Как умножить дробь на дробь?

Умножение между двумя дробями — простейшая форма арифметических операций между двумя дробями. Сначала умножаются числители обеих дробей, а затем умножаются знаменатели. Затем полученная дробь при необходимости упрощается до наименьших членов.

Чем умножение дробей отличается от сложения дробей?

Сложение дробей отличается от умножения дробей. При умножении сначала умножаются числители двух дробей, затем умножаются знаменатели, чтобы получить результирующую дробь. Однако в процессе сложения дробей нам сначала нужно сделать знаменатели обеих дробей равными, а затем сложить числители, чтобы получить результирующую дробь. Кроме сложения или вычитания дробей, мы не складываем и не вычитаем знаменатели отдельно.

Как умножать десятичные дроби?

Чтобы умножить дроби на десятичные, мы преобразуем десятичное число в дробь, а затем используем те же правила умножения дробей. Например, давайте умножим 5/7 × 0,6

• . Здесь мы преобразуем 0,6 в дробную форму, что даст 6/10.
• Теперь умножим 5/7 × 6/10 обычным способом.
• Умножим числители, 5 × 6 = 30.
• Умножим знаменатели, 7 × 10 = 70.
• Таким образом, результирующая дробь будет 30/70.
• Упростив полученную дробь, мы получим произведение как 3/7.

Как научить умножению дробей?

Умножению дробей можно научиться так же, как умножению целых чисел. Важным аспектом перед умножением дробей является преобразование смешанной дроби в неправильную дробь. После этого шага мы умножаем числители обеих дробей, а затем знаменатели обеих дробей, чтобы получить результирующую дробь. Для обучения умножению дробей можно использовать следующие способы:

• Максимально используйте визуальные модели для представления концепции. Учить учащихся понимать использование и процесс умножения дробей.
• Используйте рабочие листы для умножения дробей после обучения понятию.

Как умножить 3 дроби?

Чтобы умножить 3 дроби, мы используем те же правила умножения дробей. Например, давайте умножим 2/3 × 4/5 × 1/7. Умножим все числители, 2 × 4 × 1 = 8. Теперь умножим знаменатели, 3 × 5 × 7 = 105. Итак, произведение равно 8/105. Поскольку это нельзя уменьшить дальше, ответом будет 8/105.

Умножение и деление дробей: примеры и методы

Джон был приглашен на день рождения Эми, и она пригласила в общей сложности 7 друзей отпраздновать свой день рождения. Чтобы получить одинаковые кусочки торта, каждый из участников должен иметь \(\frac{1}{8}\) торта. Случайно Эми уронила свой кусок пирога, поэтому Джон решил отдать ей часть своего. Он разделил свой кусок пирога на 2 и отдал половину Эми.

Можем ли мы посчитать, какая часть торта досталась Эми в итоге? Ответ состоит в том, чтобы разделить дробь Джона на 2, то есть \(\dfrac{\dfrac{1}{8}}{2}=\dfrac{1}{16}\) торта.

В этой статье мы научимся выполнять операции умножения и деления с дробями.

Умножение и деление дробей шаг за шагом

Нас интересуют операции умножения и деления дробей. Прежде всего, давайте вспомним наши знания о дробях.

Дробь представляет часть целого . Он состоит из двух частей – числителя и знаменателя. Числитель пишется над чертой, а знаменатель — под чертой. Знаменатель не может быть равен нулю.

\(\dfrac{2}{3}, \dfrac{1}{2}, \dfrac{7}{8}, \cdots\) являются примерами дробей.

Мы знакомы с умножением и делением двух чисел. Теперь вопрос в том, как выполнять эти операции над дробями, а не над целыми числами.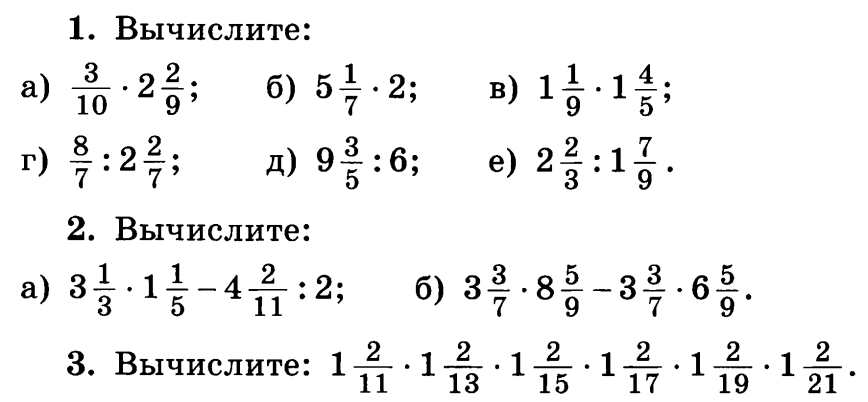

Предположим, вам даны две дроби, скажем, \(\dfrac{a}{b}\) и \(\dfrac{c}{d}\), мы хотим знать, что мы подразумеваем под \(\dfrac{ a}{b}\times \dfrac{c}{d}\) и \(\dfrac{\dfrac{a}{b}}{\dfrac{c}{d}}.\)

Умножение и деление правила дробей

Правила умножения дробей

Чтобы умножить две дроби \(\dfrac{a}{b}\) и \(\dfrac{c}{d}\), необходимо умножить числители вместе и знаменатели вместе. Таким образом. имеем

\[\dfrac{a}{b}\times \dfrac{c}{d}=\dfrac{a\times b}{c\times d}.\]

Мы, по сути, следуем следующие шаги, чтобы умножить дроби вместе.

Шаг 1. Перемножьте числители двух дробей вместе и знаменатели вместе.

Шаг 2. Разделите полученные числа, чтобы получить новую дробь.

На этом мы можем остановиться. Однако, если числитель и знаменатель новой дроби имеют общие делители, мы переходим к следующему шагу, чтобы получить простейшую форму дроби.

Шаг 3. Найдите общий делитель числителя и знаменателя новой дроби. Разделите числитель и знаменатель на этот общий множитель. Это дает простейшую форму дроби.

Перемножьте дроби \(\dfrac{3}{7}\) и \(\dfrac{5}{11}\).

Решение

Шаг 1. Перемножая числители дробей вместе, получаем \[3\times 5=15.\]

Перемножая знаменатели дробей вместе, получаем

\[7 \times 11=77.\]

Шаг 2. Деление полученных чисел дает новую дробь \(\dfrac{15}{77}.\)

Так как числитель и знаменатель новой дроби не имеют любые общие факторы, это самая простая форма.

Умножить \(\dfrac{2}{5}\) и \(\dfrac{7}{9}\).

Решение

Перемножая числители и знаменатели, получаем

\[\dfrac{2}{5}\times \dfrac{7}{9}=\dfrac{2\times 7}{5 \times 9}=\dfrac{14}{45}.\]

Умножить \(\dfrac{5}{8}\) и \(\dfrac{2}{3}.\)

Решение

Шаг 1. Умножая числители двух дробей, мы получаем

\(5 \times 2=10. \) Точно так же, делая то же самое со знаменателями, получаем \(8\times 3=24.\)

Шаг 2. Разделив полученные числа, мы получим новую дробь \(\dfrac{10}{24}.\)

Заметим, что числитель и знаменатель новой дроби имеют общий делитель 2.

Шаг 3. Мы получаем простейшую форму этой дроби путем деления общего делителя 2 из числителя 10 и знаменателя 24. Это дает нам \(10 \divsymbol 2=5\) и \(24\divsymbol 2=12\).

Таким образом, простейшая дробь равна \(\dfrac{5}{12}.\)

Правила деления дробей

Чтобы разделить две дроби, вы, по сути, инвертируете дробь, на которую делите, а затем умножаете ее на первую. Таким образом, деление двух дробей вида

\[\frac{a}{b}\divsymbol\frac{c}{d}=\frac{\frac{a}{b}}{\frac{c} {d}}\]

равносильно умножению дробей

\[\frac{a}{b}\times \frac{d}{c}.\]

Таким образом, мы имеем

\[ \frac{a}{b}\divsymbol\frac{c}{d} =\frac{a}{b}\times\frac{d}{c}.\]

Так как мы уже видели, как умножать две дроби, просто следуйте этим шагам.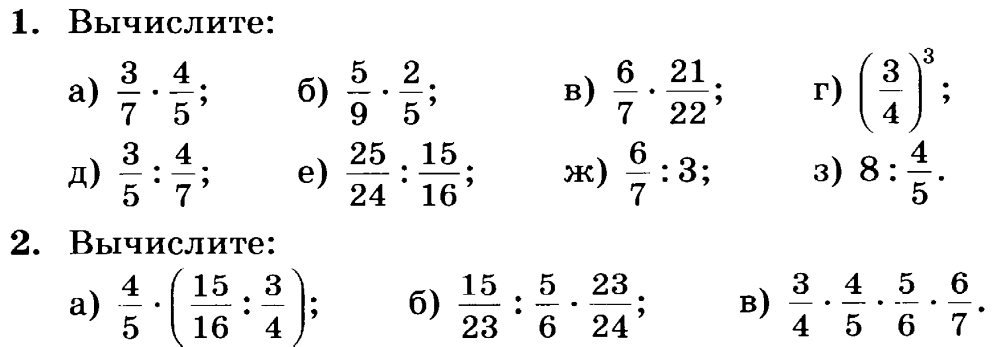

Таким образом, мы выполняем следующие шаги для выполнения деления на дроби,

Шаг 1. Инвертируем делитель дроби – числитель становится знаменателем, а знаменатель становится числителем.

Шаг 2. После инверсии перемножьте полученные дроби вместе, используя шаги, описанные для умножения дробей.

Разделим \(\dfrac{5}{8}\) на \(\dfrac{2}{3}.\)

Решение

Шаг 1. Обратив делитель, получим \(\ dfrac{3}{2}\).

Шаг 2. Теперь выполняем умножение полученных дробей,

\(\dfrac{5}{8}\) и \(\dfrac{3}{2}\), чтобы получить,

\ [\dfrac{5}{8}\times \dfrac{3}{2}=\dfrac{5\times 3}{8\times 2}=\dfrac{15}{16}.\]

числитель и знаменатель не имеют общих делителей, это простейшая форма.

Найдите \(\dfrac{2}{5}\divsymbol \dfrac{3}{8}\).

Решение

Здесь \(\dfrac{2}{5}\) — дробь делимого, а \(\dfrac{3}{8}\) — дробь делителя.

Шаг 1. Инвертируем делитель, получаем \(\dfrac{8}{3}.\)

Шаг 2. Теперь умножаем полученные дроби,

\[\frac{2}{ 5}\divsymbol\frac{3}{8}=\frac{2}{5}\times \frac{8}{3}=\frac{2\times 8}{3\times 5} =\frac{ 16}{15}.\]

Так как числитель и знаменатель не имеют общих множителей, это самая простая форма.

При умножении или делении дроби на целое число \(a\), \(a\) может быть записано как его эквивалентная форма \(\dfrac{a}{1}\), поэтому никаких изменений в процедуре не требуется .

Найдите \(\dfrac{\dfrac{2}{5}}{3}.\)

Решение

Здесь \(\dfrac{2}{5}\) — дробь делимого, а \( 3=\dfrac{3}{1}\) — делитель дроби.

Шаг 1. Переворачиваем делитель, получаем \(\dfrac{1}{3}\).

Шаг 2. Теперь умножьте дроби, чтобы получить

\[\dfrac{2}{5}\times \dfrac{1}{3}=\dfrac{2\times 1}{5\times 3}=\dfrac{2}{15}.\]

Так как числитель и знаменатель не имеют общих множителей, это самая простая форма.

Упростить \(\dfrac{4}{\dfrac{7}{9}}\).

Решение

Здесь \(4=\dfrac{4}{1}\) — дробь делимого, а \(\dfrac{7}{9}\) — дробь делителя.

Решение

Шаг 1. Переворачиваем делитель, получаем \(\dfrac{9}{7}\).

Шаг 2. Теперь перемножьте дроби, чтобы получить

\[\dfrac{4}{\dfrac{7}{9}}=\dfrac{4}{1}\times \dfrac{9} {7}=\dfrac{4\times 9}{1\times 7}=\dfrac{36}{7}.\]

Поскольку числитель и знаменатель не имеют общих множителей, это самая простая форма.

Чтобы упростить нашу работу, избегая гигантских умножений, мы можем «отменить» общие множители между числителями и знаменателями в начале, прежде чем мы перемножим члены вместе. Это изменит шаги для умножения дробей на следующие:

Шаг 1. Если какой-либо числитель и знаменатель имеют общий множитель, разделите соответствующий числитель и знаменатель на общий множитель, чтобы «уменьшить» общий множитель. Делайте это до тех пор, пока между числителями и знаменателями не останется общих множителей.

Шаг 2. Выполнить умножение полученных дробей.

В следующих примерах мы использовали вышеупомянутый метод.

Примеры умножения и деления дробей

До сих пор мы рассматривали примеры операций умножения и деления двух дробей. Вы можете умножать / делить несколько дробей вместе, используя те же правила, что описаны выше. Если есть цепочка из нескольких умножений и делений, вы должны сначала инвертировать члены делителя.

Упростить \(\dfrac{5}{9}\times\dfrac{18}{13}\times\dfrac{21}{20}\)

Решение

Здесь умножаются три дроби. Первый шаг состоит в том, чтобы умножить числители дробей вместе \(5\times 18\times 21\) и знаменатели вместе \(9\times 13\times 20.\)

Здесь мы видим, что мы получаем умножение огромных чисел. Чтобы избежать этого, мы собираемся сначала отменить общие факторы, где это возможно.

Шаг 1 . Числители 5,18,21, а знаменатели 9,13,20. Мы видим, что 9 и 18 имеют 9 в качестве общего делителя, а 5 и 20 имеют 5 в качестве делителя, таким образом, мы имеем

\[\frac{5}{9}\times\dfrac{18}{13}\times\dfrac{ 21}{20}=\dfrac{1}{1}\times\dfrac{2}{13}\times\dfrac{21}{4}.\]

Кроме того, мы можем упростить 2 и 4, разделив на 2, чтобы получить

\[\dfrac{5}{9}\times\dfrac{18}{13}\times\dfrac{21}{20}=\dfrac{1}{13} \times\dfrac{21}{2 }.\]

Шаг 2. И окончательный ответ:

\[\dfrac{5}{9}\times\dfrac{18}{13}\times\dfrac{21}{20}= \dfrac{21}{13\times 2}=\dfrac{21}{26}.\]

Упростить

\[\dfrac{14}{39}\times\dfrac{12}{35}\divsymbol \dfrac{8}{13}\times\dfrac{2}{9}\]

Решение

Шаг 1. Инвертируйте дробь делителя, чтобы получить

\[\dfrac{14}{39}\times\dfrac{12}{35}\divsymbol\dfrac{8}{13}\times\dfrac{2}{9}=\dfrac{14}{39} \times\dfrac{12}{35}\times\dfrac{13}{8}\times\dfrac{2}{9}\]

Шаг 2. Теперь попробуем привести члены к простейшему виду . Разделив 14 и 35 на 7, 13 и 39 на 13, 12 и 9 на 3, 2 и 8 на 2, получим

\[\dfrac{14}{39}\times\frac{12}{35}\ раз\dfrac{13}{8}\times\dfrac{2}{9}=\dfrac{2}{3}\times\dfrac{4}{5}\times\dfrac{1}{4}\times \dfrac{1}{3}\]

Шаг 3 . Отбросив 4, мы получим \[\dfrac{2}{3}\times\dfrac{4}{5}\times\dfrac{1}{4}\times\dfrac{1}{3}=\dfrac {2}{5}\times\dfrac{1}{5}\times \dfrac{1}{3}=\dfrac{2}{45}.\]

В следующем примере мы выполняем умножение и деление смешанных фракций.

Смешанная дробь представляет собой комбинацию целого числа и дроби. Чтобы умножить или разделить смешанные дроби, сначала преобразуйте их в неправильные дроби, а затем продолжите стандартный процесс.

Упрощение

\[4\dfrac{2}{7}\times 2\dfrac{1}{3}\div \dfrac{3}{5}.\]

Решение

Преобразование смешанных дробей в неправильные дроби , получаем

\[4\dfrac{2}{7}\times 2\dfrac{1}{3}\div \frac{3}{5} = \dfrac{30}{7}\times \ dfrac{7}{3} \div \dfrac{3}{5}. \]

Обратив делитель, получим

\[\dfrac{30}{7}\times\dfrac{7}{3 }\div\dfrac{3}{5}= \dfrac{30}{7} \times \dfrac{7}{3} \times \dfrac{5}{3}\]

Деление 30 и 3 на 3 , сократив 7 в числителе и знаменателе, получим

\[\dfrac{30}{7}\times\dfrac{7}{3}\times \dfrac{5}{3}= \dfrac{10}{1} \times \dfrac{1}{1 } \times \dfrac{5}{3}.\]

Умножение приведенных выше дробей дает

\[\dfrac{10}{1}\times\dfrac{5}{3}= \dfrac{50} {3} = 16\dfrac{2}{3}.\]

При необходимости ответ можно представить в виде смешанной или неправильной дроби.

Умножение и деление алгебраических дробей

Вы можете выполнять умножение и деление алгебраических дробей, содержащих переменную в числителе и/или знаменателе, следуя тем же шагам, которые мы использовали до сих пор. 92}. \]

Умножение и деление дробей – основные выводы

• Чтобы умножить дроби, нужно перемножить числители вместе и знаменатели вместе. Таким образом, умножение формы \( \dfrac{a}{b}\times \dfrac{c}{d}\) эквивалентно \(\dfrac{a\times c}{b\times d}.

  No related posts.