Линейная алгебра перестановки и подстановки: 05. Перестановки и подстановки

05. Перестановки и подстановки

Мы получили два эквивалентных определения определителя третьего порядка (формулы (4) и (5)). С помощью (4) определитель 3-го порядка вводится с помощью определителей второго порядка (разложение по столбцу). При этом легко проверяется, что все столбцы равноправны. Аналогично рекуррентным образом можно определить определитель n-го порядка (определитель квадратной матрицы n-го порядка), т. е.

=

= (7)

Но в этом случае уже не так просто, как для определителя третьего порядка, проверить, что разложения по остальным столбцам или строкам дают тот же самый результат. Поэтому чаще всего используют в качестве исходного другой подход к определению определителя n-го порядка. Но при этом используются в качестве вспомогательного материала перестановки и подстановки.

Пусть дан упорядоченный набор из N элементов. Элементы этого набора занумеруем числами 1, 2, 3, … , n. Очевидно, вместо того, чтобы говорить об элементах, можно говорить об их номерах.

Определение 5. Перестановкой Из N Чисел (или N символов) называется расположение этих чисел (или символов) в любом определённом порядке (без повторений).

Теорема 1. Число перестановок из N Символов равно n!

Доказательство. Составляя перестановку, в качестве первого её элемента можно выбрать точно n символов. Если первый элемент выбран, то в качестве второго элемента можно выбрать любой из оставшихся (n – 1) символов. Следовательно, первые два места можно заполнить n×(n – 1 ) способами. Если два места в перестановке уже заполнены, то на третье место можно поставить любой из оставшихся (n – 2) символов. Следовательно, первые три места можно заполнить n×(n – 1)×(n – 2 ) способами. Продолжая этот процесс, получим, что все n мест в перестановке можно заполнить n×(n – 1)×(n – 2)×…×3×2×1 = n! способами.

Говорят, что числа К и Р образуют в перестановке (…К…р…)

Инверсию, если К > Р, Но в перестановке К стоит раньше Р. Перестановка называется Чётной, если она содержит чётное число инверсий. Перестановка называется Нечётной, если она содержит нечётное число инверсий.

Пример. 1) Перестановка (9, 7, 1, 3, 4, 8, 5, 2, 6) чётная. В ней число 9 образует инверсии со всеми стоящими за ней числами, их 8. Число 7 образует новые инверсии со всеми стоящими за ней числами, кроме числа 8, их 6. Число 1 не образует ни одной новой инверсии. Числа 3 и 4 образуют по одной новой инверсии с числом 2. Число 8 образует ещё инверсии с 5, 2 и 6, их 3. Число 5 образует инверсию с числом 2. Итак, получается 8 + 6 + 1 + 1 + 3 + 1 = 20 инверсий.

2) Перестановка ( 2, 1, 3, 5, 4, 6, 9, 8, 7) нечётная. В ней инверсии образуют пары чисел 2 и 1, 5 и 4, 9 и 8, 9 и 7, 8 и 7. Получилось 5 инверсий.

Если в перестановке два символа поменять местами, а все остальные символы оставить на старых местах, то получим новую перестановку. Это преобразование перестановки называется

Транспозицией.

Теорема 2. Всякая транспозиция меняет чётность перестановки.

Доказательство. Пусть в перестановке символы К и Р меняются местами. При этом возможны два случая.

1) Символы К и Р В данной перестановке стоят рядом, т. е. (…К, Р …). После транспозиции получится перестановка (….Р, к …). Если К и Р Составляли инверсию в данной перестановке, то после инверсии они уже не будут составлять инверсию и наоборот. Число инверсий, которые К и Р Составляли в данной перестановке с остальными символами, не изменится. Следовательно, число инверсий изменится на 1, т. е. чётность перестановки изменится.

2) Символы К и Р В данной перестановке стоят не рядом, т. е. (….К,…,р…). После транспозиции получится перестановка (…Р,…,к…). Число инверсий, которые К и Р Составляли в данной перестановке с символами, стоящими перед К И после Р, не изменится. Если между К и Р Стоят M символов, то переставить К и Р можно следующим образом: переставить К последовательно с каждым из этих M Символов, затем переставить К и Р, затем в обратном порядке переставить Р с каждым из этих M символов. Получим 2m + 1 транспозиций соседних символов. По доказанному каждая из них меняет чётность перестановки. Итак, чётность перестановки изменилась.

Следствие. При n > 1 число чётных перестановок равно числе нечётных перестановок и равно 0,5×n!.

Определение 6. Подстановкой из N символов ( или Подстановкой N-ой степени) называется любое взаимнооднозначное отображение множества этих символов на себя.

Элементы данного множества будем обозначать 1, 2, …, n. Подстановка А может быть записана так: если число К переходит в число aК, то А = . Если в записи подстановки А Некоторые столбцы поменять местами, то получится то же самое отображение данного множества, т. е. та же подстановка. Например,

А = = .

Запись подстановки А = будем называть стандартной. Всякую подстановку можно записать в стандартном виде. Верхнюю и нижнюю строки подстановки можно рассматривать как перестановки. Подстановка А называется чётной, если её верхняя и нижняя строки есть перестановки одинаковой чётности, т. е. общее число инверсий в них – чётное. В противном случае

А Называется Нечётной. Так как перестановка столбцов равносильна транспозиции как в верхней так и в нижней строке, то при перестановке столбцов чётность подстановки не изменится, поэтому чётность подстановки можно вычислять по её стандартному виду и в этом случае она совпадает с чётностью нижней строки.

Подстановка Е = называется Тождественной Или Единичной.

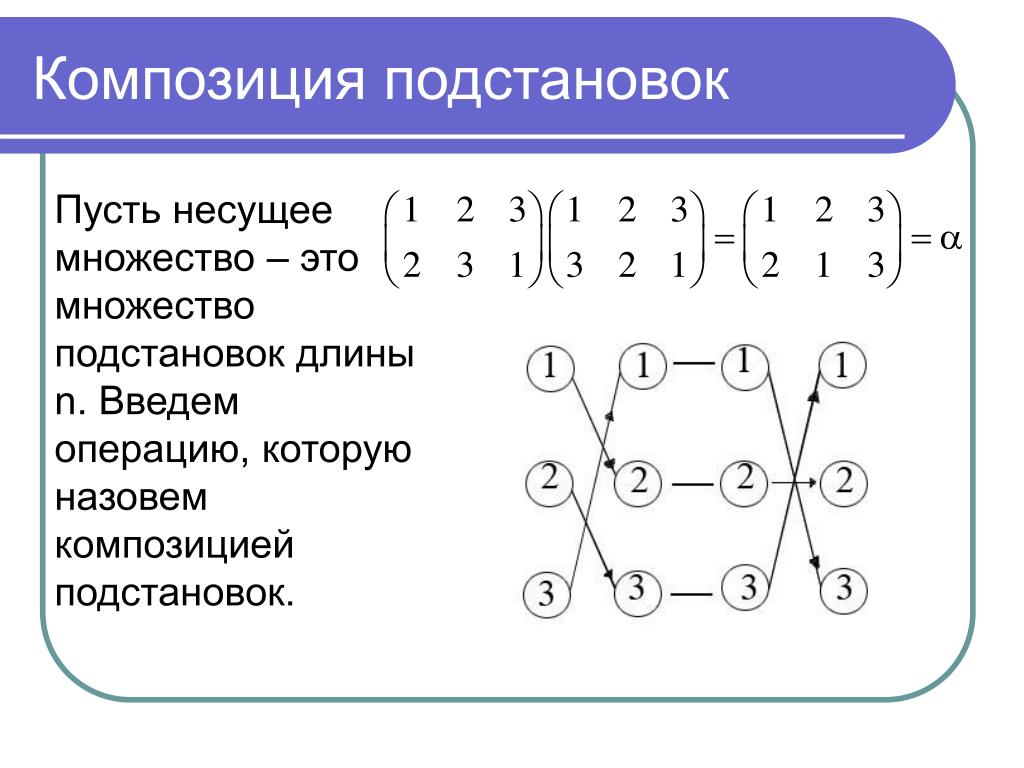
Произведением двух подстановок одного и того же порядка называется результат последовательного выполнения тех отображений, которые задают эти подстановки. Например, если А = , В = , то

А×В = . Действительно, первая подстановка переводит 1 в 5, вторая переводит 5 в 4, следовательно, окончательно 1 перейдёт в 4. Аналогично, , , следовательно, ; , , следовательно, ; , , следовательно, ; , , следовательно, ; , , следовательно, .

Аналогично получаем, что В×А = . Отсюда следует, что умножение подстановок не подчиняется коммутативному закону. Но можно проверить, что (А×В)×С = А×(В×С) для любых подстановок А, В, С Одного и того же порядка. Очевидно, А×Е = Е×А для любой подстановки А, Если А и Е Одного порядка. Для подстановок А = и В = очевидно А×В = В×А = Е. Следовательно, А-1 = В, т. е. каждая подстановка имеет обратную.

< Предыдущая		Следующая >

§ 4.

Перестановки и подстановки

Вычисление определителей 4-го и более высоких порядков не может быть представлено достаточно простой «геометрической схемой», как это сделано для определителей 2-го и 3-го порядков.

Для определения и изучения определителей n-го порядка используются понятия, относящиеся к конечным множествам некоторых элементов.

4.1. Перестановки.

Рассмотрим множество М целых чисел: 1, 2, … , n. Элементы множества М можно расположить разными способами.

Определение: всякое расположение чисел 1, 2, … , n в некотором порядке называется пе-рестановкой из n чисел. Общий вид записи перестановки из n элементов:

i₁ , i₂ , … , i_n , (42)

где каждое i_s есть одно из чисел 1, 2, … , n, причем ни одно из этих чисел не встречается дважды и не пропущено

.

В качестве i₁ можно выбрать любое из чисел 1, 2, … , n. Это дает n различных возможностей. Если i₁ уже выбрано, то в качестве i₂ можно выбрать лишь одно из оставшихся (n-1) чисел, т.е. различных способов выбрать числа (символы) i₁ и i₂ равно произведению n∙(n-1) и т.д. Число перестановок из n символов равно произведению:

Если в некоторой перестановке поменяем местами какие-либо два символа (не обязательно стоящие рядом), а все остальные оставим на месте, то получим новую перестановку. Такое преобразование перестановки называется транспозицией.

Теорема 1. Все перестановки из n символов можно расположить в таком порядке, что каждая следующая перестановка получается из предыдущей одной транспозицией, причем начинать можно с любой перестановки.

► При n=2 утверждение справедливо: 1, 2 → 2, 1;

2, 1 → 1, 2.

Рассмотрим все перестановки из n элементов, у которых на первом месте стоит символ i₁. Таких перестановок и их можно упорядочить в соответствии с требованиями теоремы для (n-1) символов. Пусть последняя из таких перестановок (с учетом того, что символ i₁ был все время неперемещаем) имеет вид:

i₁ , i₂ , … , i_n (43)

В перестановке (43), содержащей n символов, совершим транспозицию символа

i₁ с любым другим (например, с символом i₂) и вновь упорядочим все перестановки из (n-1) символов при фиксированном на первом месте i₂ и т.д. Так можно перебрать все перестановки из n символов. ◄

Следствие: от любой перестановки из n символов можно перейти к любой другой перестановке из тех же символов при помощи нескольких транспозицией.

Если в перестановке символ i₁ стоит раньше, чем символ i₂, но , то говорят, символы i₁ и i₂ составляют инверсию (нарушение порядка), иначе указанные символы составляют порядок. Перестановка называется четной, если ее символы составляют четное число инверсий, и нечетной – в противном случае.

Замечание: 1) всякая транспозиция меняет четность перестановки.

2) сумма порядков и инверсий постоянна и равна

☺ Пример 31. Определим четность перестановки 1, 2, … , n.

Решение: Заданная перестановка четная, т. к. в ней нет инверсий (нарушений порядка).

Ответ: Четная.

Пример 32. Определите четность перестановки 4 5 1 3 6 2.

Решение: Для подсчета числа инверсий воспользуемся таблицей 1, в которой указаны инверсии выделяемых элементов со всеми последующими (учет нарушений порядка).

	4	5	1	3	6	2
	╙		☼	☼		☼	=3
		╙	☼	☼		☼	=3
			╙				=0
				╙		☼	=1
					╙	☼	=1
	——————————————————
	Число инверсий :						=8

Ответ: Четная.

☻Решите примеры:

Пример 33. Укажите число инверсий в перестановке: 1, 9, 6, 3, 2, 5, 4, 7, 8.

Пример 34. В какой перестановке чисел 1, 2, 3, …, 99 число инверсий наибольшее и чему оно равно?

Пример 35. Сколько инверсий образует число 99, стоящее на 50 месте в перестановке 1, 2, …, 99.

Вопросы для самопроверки:

1. Перестановка – это матрица?

2. Что такое «транспозиция» двух элементов перестановки?

3. Что такое «инверсия» для двух выделенных элементов перестановки?

4. Что такое «порядок» для двух выделенных элементов перестановки?

5. Чему равна сумма числа инверсий и числа порядков в любой перестановке чисел 1, 2, … , 99.

4. 2. Подстановки.

Определение: Запишем одну перестановку под другой: . Эту запись

называют подстановкой, понимая под этим отображение (соответствие) множества символов, состоящего из первых n чисел: 1, 2, …, n, на себя: ; , , …,

Если учесть, что подстановка как отображение множества чисел 1, 2, … , n не меняется при транспозиции столбцов, выберем для нее простейшее выражение:

, (44)

где α_i – число, в которое переходит число i.

В выражении (44) подстановки порядка n различаются только перестановками в нижней строке записи, т.е. подстановку однозначно определяет перестановка, записан-ная в ее нижней строке. Это значит, что всего подстановок порядка n столько же, сколь-ко и перестановок, т.е. .

Определим понятие четности для подстановок:

А. Исходя из общего определения подстановки:

• подстановка четная, если четности верхней и нижней перестановок совпадают;

• подстановка нечетная, если четности верхней и нижней перестановок противоположны.

Б. Учитывая частную запись подстановки (44):

• подстановка четная, если ее определяет четная перестановок;

• подстановка нечетная, если ее определяет нечетная перестановка.

Кроме подсчета числа инверсий в перестановках для определения четности подстановок применяют также разложение их в циклы. Воспользуемся этим приемом (не обосновывая его, примем на веру), рассмотрев конкретный пример.

☺ Пример 36. Определим четность подстановки .

Решение: Для определения четности подстановки разложим ее в произведение циклов:

,

где скобки после знака “=” отражают циклы: (1→6→3→1), (2→5→2), (4→4), (7→7), (8→8), (9→9) отображения символов 1,2,…,9 по определению подстановки (в циклах учтены также символы «остающиеся на месте»). Имея разложение подстановки в циклы, определим число декремент: d = n – s, где n – порядок подстановки, s – число циклов в разложении подстановки. В рассматриваемом примере: d = 9 – 6 = 3 – нечетное число → подстановка нечетная.

Ответ: Четная.

Пример 37. Для определения четности подстановки разложим ее в произведение циклов:

,

где скобки после знака “=” отражают циклы: (1→5→1), (2→8→6→4→2),(3→9→7→3) отображения символов 1,2,…,9 по определению подстановки. Вычислим декремент для рассматриваемой подстановки: d = 9 – 3 = 6 – четное число → подстановка четная.

☻Решите примеры:

Пример 38. Укажите число инверсий в перестановке: 1, 9, 6, 3, 2, 5, 4, 7, 8.

Пример 39. В какой перестановке чисел 1, 2, 3, …, 99 число инверсий наибольшее и чему оно равно?

Пример 40. Сколько инверсий образует число 99, стоящее на 50 месте в перестановке 1, 2, …, 99.

Вопросы для самопроверки:

6. Подстановка – это матрица?

7. Что такое «транспозиция» столбцов подстановки?

8. Что такое «инверсия» в подстановке?

9. Что такое «порядок» в подстановке?

10. Чему равна сумма числа инверсий и числа порядков в любой подстановке чисел 1, 2, … , 99.

Линейная алгебра

— максимизируйте след матрицы, переставляя ее строки

Задавать вопрос

спросил 4 года 3 месяца назад

Изменено 4 года, 3 месяца назад

Просмотрено 1к раз

$\begingroup$

Я боролся с комбинаторной задачей, которая в итоге приводит к следующему:

Для заданной неотрицательной матрицы $n \times n$ найдите такую ​​перестановку строк, которая максимизирует след.

Я мог бы вычислить все перестановки $n!$ и найти ту, которая максимизирует след, но это неэффективно с вычислительной точки зрения. Каков наиболее эффективный способ добиться этого?

Если это поможет, то это то же самое, что найти $n$ элементов матрицы, два из которых не находятся в одной строке или столбце, так что сумма этих элементов максимальна.

• линейная алгебра
• матрицы
• алгоритмы
• линейное программирование
• дискретная оптимизация

$\endgroup$

10

$\begingroup$

Я рекомендую вам венгерский метод. Это алгоритм, который я не собираюсь описывать здесь, но он доступен во многих учебниках по комбинаторике, дискретной математике и теории графов, а также во многих местах в Интернете: в частности, Википедия поможет вам начать работу.

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Линейные комбинации

Марко Табога, доктор философии

Эта лекция посвящена линейным комбинациям векторы и матрицы. Линейный комбинации получаются умножением матриц на скаляры и добавлением их вместе. Поэтому, чтобы понять эту лекцию, нужно быть познакомиться с понятиями, введенными в лекциях по Сложение матриц и Умножение матрица скаляром.

Table of contents

1. Definition

2. Linear combinations of vectors

3. Solved exercises

   1. Exercise 1

   2. Exercise 2

   3. Exercise 3

Definition

Начнем с формального определения линейной комбинации.

Определение Позволять быть матрицы размерности . А матрица это линейная комбинация из тогда и только тогда, когда существуют скаляры , называется коэффициентами линейной комбинации, такой что

Другими словами, если вы берете набор матриц, вы умножаете каждую из них на скаляр, и вы складываете все полученные таким образом продукты, то вы получаете линейная комбинация.

Обратите внимание, что все матрицы, участвующие в линейной комбинации, должны иметь той же размерности (иначе сложение матриц было бы невозможно).

Пример Позволять а также быть матрицы, определенные как следует: пусть а также быть двумя скалярами. Затем матрикс линейная комбинация а также . Он вычисляется как следующим образом:

Линейные комбинации векторов

В большинстве случаев в линейной алгебре мы имеем дело с линейными комбинациями векторы-столбцы (или векторы-строки), то есть матрицы, имеющие только один столбец (или только одну строку).

Пример Позволять , а также быть векторы-столбцы, определенные как следует: пусть быть другим вектором-столбцом, определенным как есть линейная комбинация , а также ? Чтобы ответить на этот вопрос, заметим, что линейная комбинация , а также с коэффициентами , а также имеет следующее форма: Сейчас, представляет собой линейную комбинацию , а также тогда и только тогда, когда мы можем найти , а также такой, что который эквивалентен кНо мы знаем, что два вектора равны тогда и только тогда, когда их соответствующие элементы все равны между собой. Это означает, что приведенное выше уравнение удовлетворяется тогда и только тогда, когда следующие три уравнения одновременно удовлетворены: второе уравнение дает нам значение первого коэффициент:По подставив это значение в третье уравнение, получим получитьНаконец, подставив значение в первом уравнении мы получитьты можно легко проверить, что эти значения действительно представляют собой решение нашей проблема: Следовательно, ответ на наш вопрос утвердительный.

Решенные упражнения

Ниже вы можете найти несколько упражнений с поясненными решениями.

Упражнение 1

Определите два матрицы а также в качестве следует: пусть а также быть двумя скалярами. Вычислить линейный комбинация

Решение

Вычисляется как следующим образом:

Упражнение 2

Позволять а также быть векторы:Вычислить значение линейного комбинация

Решение

Это делается как следующим образом:

Упражнение 3

Позволять быть следующим матрица:Есть в нуль вектора линейная комбинация рядов ?

Решение

Обозначим строки по , а также . Линейная комбинация , а также с коэффициентами , а также можно написать как сейчас, в нулевой вектор представляет собой линейную комбинацию , а также тогда и только тогда, когда существуют коэффициенты , а также такой, что который то же самое какПотому что два вектора равны тогда и только тогда, когда все их соответствующие элементы равны относительно друг друга, это уравнение выполняется тогда и только тогда, когда следующая система двух уравнений доволен: это можно переписать как это означает, что какое бы значение мы ни выбрали для , система удовлетворена, если мы установили а также . Например, если мы выбираем , тогда нам нужно setПоэтому, одно решение Если мы выбираем другое значение, скажем , то у нас другой решение: В таким же образом можно получить бесконечно много решений, выбирая различные значения и изменение а также соответственно.