Линейная интерполяция онлайн калькулятор: Линейная интерполяция | Онлайн калькулятор

Содержание

Линейная интерполяция онлайн с решением и графиком

Подробности: Обновлено: 21.05.2018 11:30; Опубликовано: 31.03.2016 15:11

Калькулятор линейной интерполяции позволяет вычислить значение линейной функции промежуточной переменной, зная значения функции переменных меньше и больше искомого.

Если абсцисса (Х) искомой точки лежит за пределами отрезка интерполяции [X₁, X₂], то необходимо использовать калькулятор линейной экстраполяции.

Дано:

округление до 12345знаков после запятой

Решение:

Формула линейной интерполяции

расчет линейной интерполяции по двум точкам

Помощь на развитие проекта premierdevelopment.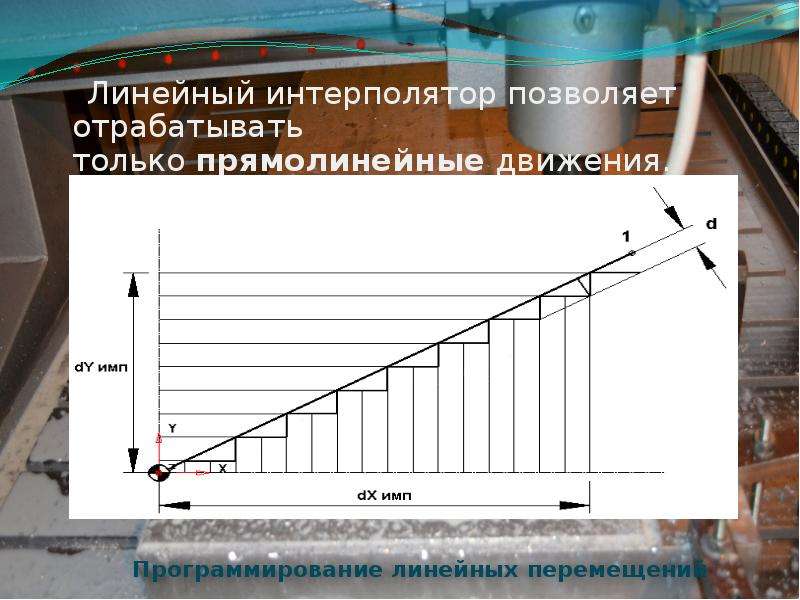 ru

Send mail и мы будем знать, что движемся в правильном направлении.

Спасибо, что не прошели мимо!

I. Порядок действий при расчете линейной интерполяции онлайн калькулятором:

Для проведения интерполяции требуется ввести значения координат 2 точек ([X₁, Y₁]; [X₂, Y₂]) и абсциссу (Х) той точки, значение которой необходимо вычислить.
Точка X₁ должна лежать левее точки X₂ (X₁ < X₂), а точка X должна лежать между точками X₁ и X₂ (X₁ < X < X₂).
В случае невыполнения одного из условий пункта 2, будет показано соответствующее предупреждение.
График справа позволяет визуализировать полученный линейной интерполяцией результат.

II. Для справки:

интерполяция: — способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
линейная интерполяция: — нахождение промежуточного значения функции по двум точкам (условно проведя прямую между ними).
квадратичная интерполяция: — нахождение промежуточного значения функции по трем точкам (интерполирующая функция многочлен второго порядка — парабола).
экстраполяция: — способ нахождения значений функции по уже известным нескольким ее значениям.

Калькулятор интерполяции — Найти точку интерполяции

Онлайн-калькулятор интерполяции помогает найти интерполированные значения для точек данных на линии или кривой. Калькулятор отображает интерполированную точку на линии и показывает пошаговое решение с использованием формулы линейной интерполяции.

Просто прочтите контекст, чтобы получить общее представление о том, как выполнять интерполяцию, ее формулу и некоторые стандартные термины, которые помогают понять интерполяцию.

Что такое линейная интерполяция в математике?

интерполяция калькулятор – это метод создания новых точек данных в уже известном дискретном наборе точек данных. В этой математической процедуре некоторые исходные точки данных могут быть интерполированы для создания простой и новой функции, которая будет близка к исходным данным. Эта интеграция нового значения называется интерполяцией. Другими словами, мы также можем сказать, что линейный интерполянт – это прямая линия, которая существует между двумя распознанными координатными точками (x0, y0) и (x1, y1). Вы можете легко найти значение интерполяции между двумя координатами на прямой с помощью калькулятор интерполяции.

Формула линейной интерполяции:

$$ y = y1 + ((x – x1) / (x2 – x1)) * (y2 – y1) $$

В этом уравнении интерполяции:

X = известное значение,
y = неизвестное значение,
x1 и y1 = координаты, которые ниже известного значения x
x2 и y2 = координаты выше значения x.

Кроме того, интерполяция онлайн калькулятор уклона помогает найти точки уклона или уклона A (x1, y1) и B (y1, y2) в декартовой координатной плоскости.

Пример1:

Если заданными точками данных являются (2, 4) и (6, 8), как вы рассчитаете значение y, когда x = 2.

На первом этапе мы извлечем координаты заданных точек данных.

$$ x1 = 2 $$

$$ y1 = 4 $$

$$ x2 = 6 $$

$$ y2 = 8 $$

На втором этапе мы возьмем следующие уравнения, чтобы получить значения m, а затем y

\ (m = y2 – y1 / x2 − x1 \) = уравнение 1
\ (y = y1 + m * (x – x1) \) = уравнение 2
Чтобы вычислить значение m, поместите значения в уравнение 1, \ (= m = 8−4 / 6−2 = 1 \)

Теперь у нас есть значение m, поэтому мы воспользуемся уравнением 2, чтобы найти значение y.
\ (у = 4 + 1 * (2–2) = 4 \)

Между тем, x находится в интервале \ ([x1, x2] \), поэтому мы выполнили расчет линейной интерполяции, чтобы найти значение y.

Однако интерполяция онлайн калькулятор поможет вам найти центр тяжести треугольника (ABC), N-точек и N-стороннего многоугольника для заданных координат. 2 \) в заданной строке, пока заданные данные

«$$ x1 = 4, y1 = 6, x2 = 8, x3 = 12, y3 = 14 $$».

Решение:

Поскольку у нас есть линейное интерполяционное уравнение:

$$ y_2 = (x_2 – x_1) x (y_3- y_1) / (x_3 – x_1) + y_1 $$

Пошаговое решение для нахождения y2 будет таким, как если бы вышеприведенное уравнение было следующим:

$$ y_2 = (x_3 − x_2) x (y_3 − y_1) / (x_3 − x_2) + y_3 $$

$$ y_2 = (12−8) x (14−6) / (12−8) + 14 $$

$$ y_2 = (4) x (8) / (4) + 14 $$

$$ y_2 = (32) / (4) + 14 $$

$$ y_2 = 8 + 14 $$

$$ y_2 = 22 $$

Как работает калькулятор интерполяции линейной?

Вот как работает онлайн-калькулятор для вычисления линейных интерполированных значений.

Вход:

Введите 5 различных точек данных, чтобы найти линейное интерполированное значение конкретной точки и выполнить интерполяцию.
Нажмите кнопку “Рассчитать”

Выход:

Онлайн-калькулятор интерполяции предоставит вам следующие результаты:

Новое интерполированное значение будет отображаться в той точке, где мы хотим провести интерполяцию.
Этот интерполятор нанесет точку интерполяции на линию.
Точки входных данных и формула линейной интерполяции
Это даст вам подробное пошаговое решение для вычисленного интерполированного значения.

Часто задаваемые вопросы (FAQ):

Какой метод можно использовать в любом вопросе интерполяции?

Обычно мы используем метод интерполяции калькулятор полиномов. Причины использования полиномов:

Их легко оценить
Дифференциация и интеграция просты.

Это называется полиномиальной интерполяцией.

Когда следует использовать интерполяцию?

Как мы уже знаем, с помощью интерполяции мы можем найти неизвестные точки, поэтому ее можно использовать всякий раз, когда нам нужно предсказать неизвестные значения для любых данных географических точек. Это полезно для прогнозирования осадков, полученных в результате концентраций химических веществ, оценки уровней шума и т. Д.

Какой метод интерполяции лучший?

Интерполяция с обратным взвешиванием по расстоянию (IDW) считается одним из лучших методов для достижения лучших результатов, чем любой другой метод интерполяции калькулятор.

Кригинг – это точная интерполяция?

Методика интерполяция калькулятор обычно связана с точной интерполяцией. Все предсказания Кригинга могут постепенно меняться в космосе. Они будут меняться после того, как попадут в место, где были собраны данные. В этот момент происходит «скачок» прогноза к наиболее точному значению, которое было измерено первым. Однако для быстрых и точных прогнозов можно использовать интерполятор.

интерполяция онлайн калькулятор момент:

Благодаря калькулятор интерполяции линейной для поиска неизвестной точки данных для заданных координат и построения точки на графиках. Кроме того, этот инструмент показывает формулу, которая используется для выполнения требований, с пошаговыми расчетами для облегчения конечных пользователей в кратчайшие сроки. Он обеспечивает бесплатную поддержку в учебных и образовательных целях. Поэтому давайте интерполяция калькулятор найти ответ, поместив известную точку данных в этот интерполятор!

Other Languages: Linear Interpolation Calculator, Kalkulator Interpolasi, Interpolacja Kalkulator, Interpolation Rechner, Interpolasyon Hesaplama, 補間計算, Calculadora De Interpolação, Calcul Interpolation Linéaire, Interpolar Calculadora, Calcolo Interpolazione Lineare, Lineární Interpolace Výpočet, حاسبة الاستيفاء, Interpolointi Laskin.

2 \) allow to estimate the value for $x = 3 $, here $f(x) = 9 $.

The Lagrange interpolation method allows a good approximation of polynomial functions.

There are others interpolation formulas (rather than Lagrange/Rechner) such as Neville interpolation also available online on dCode.

You can edit this Q&A (add new info, improve translation, etc.) » itemscope=»» itemtype=»http://schema.org/Question»>

What are the limits for Interpolating with Lagrange?

Since the complexity of the calculations increases with the number of points, the program is limited to 25 coordinates (with distinct x-values in the Q).

Ask a new question

Source code

dCode retains ownership of the source code of the script Lagrange Interpolating Polynomial online. Except explicit open source licence (indicated Creative Commons / free), any algorithm, applet, snippet, software (converter, solver, encryption / decryption, encoding / decoding, ciphering / deciphering, translator), or any function (convert, solve, decrypt, encrypt, decipher, cipher, decode, code, translate) written in any informatic langauge (PHP, Java, C#, Python, Javascript, Matlab, etc.

) which dCode owns rights will not be released for free. To download the online Lagrange Interpolating Polynomial script for offline use on PC, iPhone or Android, ask for price quote on

Интерполяция — метод нахождения промежуточных переменных функции по нескольким уже известным значениям. Впервые формулировка «интерполирование» была введена Джоном Валлисом в научном сочинении «Арифметика бесконечных».

Линейная интерполяция

Простейшим случаем интерполяции является «линейная», то есть нахождение величины по двум заданным точкам. Данный процесс вычисления можно рассмотреть как линейную функцию, тем самым делая расчёт более наглядным. Нанесение функции на систему координат называют аппроксимацией. Для этого на оси координат необходимо провести прямую через известные точки. Логично, что искомое значение, находящееся между первыми двумя точками, можно найти графически, зная абсциссу X. Если координата X искомой величины лежит за пределами известных значений (X 1 , X 2), то процесс вычисления называется экстраполяция.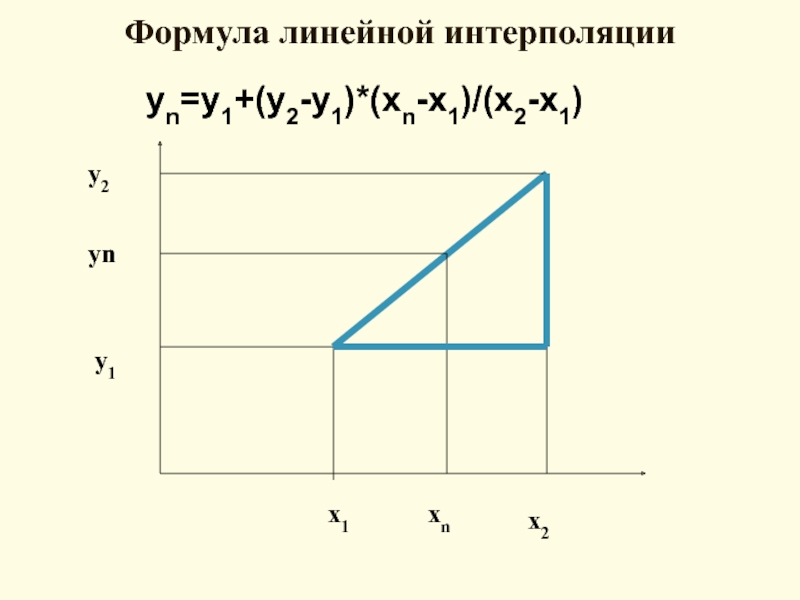

Калькулятор позволяет определить значение ординаты Y искомого значения, зная координаты X и Y двух других функций, а также её абсциссу. Для вычисления необходимо ввести значения заданных двух точек Х 1 , Y 1 и X 2 ,Y 2 , а также указать координату X искомой точки, а сервис автоматически определит метод расчёта и произведёт его.

Формула линейной интерполяции

Для вычисления используется следующая формула:

Пример расчёта

Дано: координаты двух точек А(3;1.5) и B(6;5).
Найти: ординату точки С с абсциссой 4.5.

После этого подставляем значения в указанную формулу:

Y = 5 + (1.5 — 5) / (3 — 6) · (4.5 — 6) = 5 + (-3.5) / (-3) · (-1.5) = 3.25.

Управляющая программа обработки детали представляет собой траекторию движения центра фрезы. Траектория движения состоит из отдельных, соединяющихся друг с другом участков, линейных или дуговых . Точки, которые задают траекторию, называются опорными . В действительности управляющая программа – это последовательный набор опорных точек.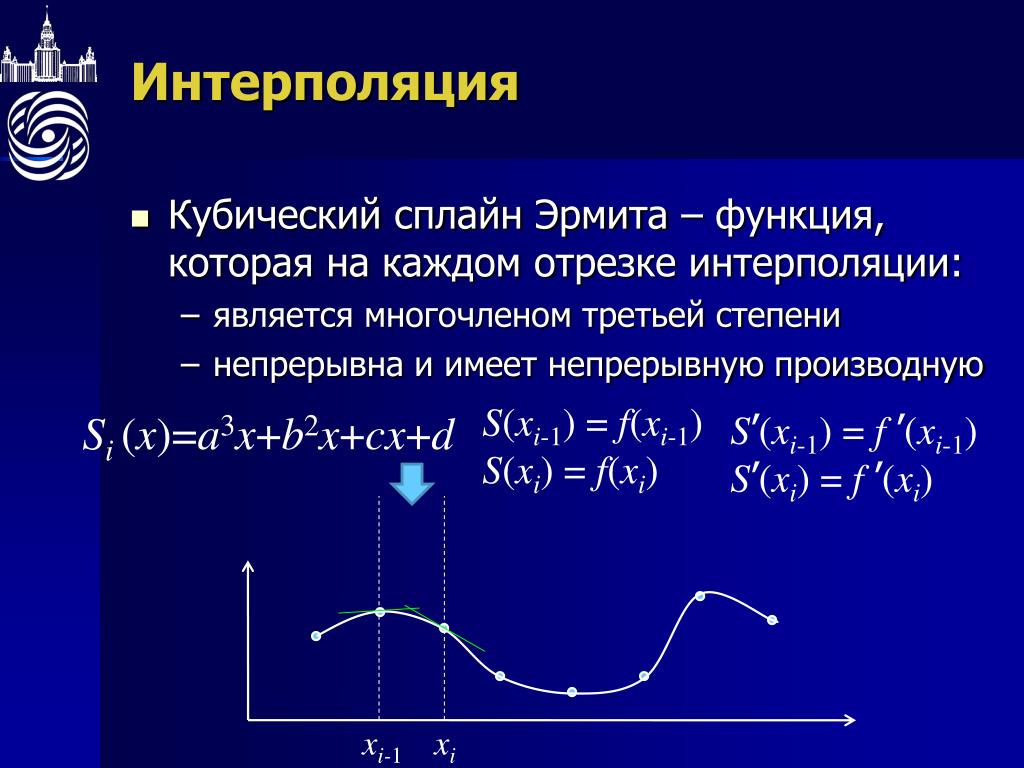

Опорные точки могут лежать в плоскости, для их задания используется две координаты (двух координатная обработка) или в пространстве (объемная трех координатная обработка).

На практике для перемещения инструмента системе ЧПУ не достаточно только опорных точек, необходимо более детальное ее представление. Для расчета промежуточных точек и выдачи команд движения по линейным осям используется специальное вычислительное устройство — интерполятор .

Интерполяторы делятся на линейные и круговые . Линейный интерполятор используется для отработки прямолинейного движения инструмента. На входе в интерполятор поступает информация о координатах опорных точек, на выходе для каждой координаты формируется последовательность импульсов необходимых для отработки заданной геометрии. Линейный интерполятор позволяет отрабатывать только прямолинейные движения. Однако обеспечить точное соответствие перемещения вдоль заданной прямой достаточно сложно. Итоговая траектория перемещения приближенно напоминает ломаную линию (рисунок ниже).

В процессе отработки прямой интерполятор попеременно управляет включением приводов то по оси X , то по оси Y (если прямая лежит в плоскости XY), посылая нужное количество импульсов на привода. На рисунке выше для отработки прямой на ось Y посылается один импульс, а на X — два импульса. Значение d определяет отклонение от заданной геометрии. Т.к. разрешающая способность позволяет задавать один импульс для перемещения на 0.001 мм, то итоговую ломаную кривую можно считать плавной .

Таким образом, линейный интерполятор рассчитывает необходимое количество импульсов по той или иной оси и выдает их на привода.

Программирование линейных перемещений

Чтобы использовать линейный интерполятор (осуществлять программирование линейных перемещений) используется подготовительная функция G01 и указываются координаты конечной точки перемещения с заданной скоростью.

G01 X n.n Yn.n Z n.n Fn.n, где

X, Y, Z – адреса линейных осей;

F – скорость перемещения;

Например, для программирования прямолинейного перемещения из точки A в точку B со скоростью 1000 мм/мин необходимо в УП сформировать следующий кадр.

— — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN linear interpolation …

линейная интерполяция — tiesinė interpoliacija statusas T sritis fizika atitikmenys: angl. linear interpolation vok. lineare Interpolation, f rus. линейная интерполяция, f pranc. interpolation linéaire, f … Fizikos terminų žodynas

ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ — способ приближенного вычисления значения функции f(x), основанный на замене функции f(х).линейной функцией параметры аи b к рой выбираются таким образом, чтобы значения L(х).совпадали со значениями f(x).в заданных точках х 1 и х 2: Этим условиям… … Математическая энциклопедия

интерполяция — Вычисление промежуточных значений между двумя известными точками.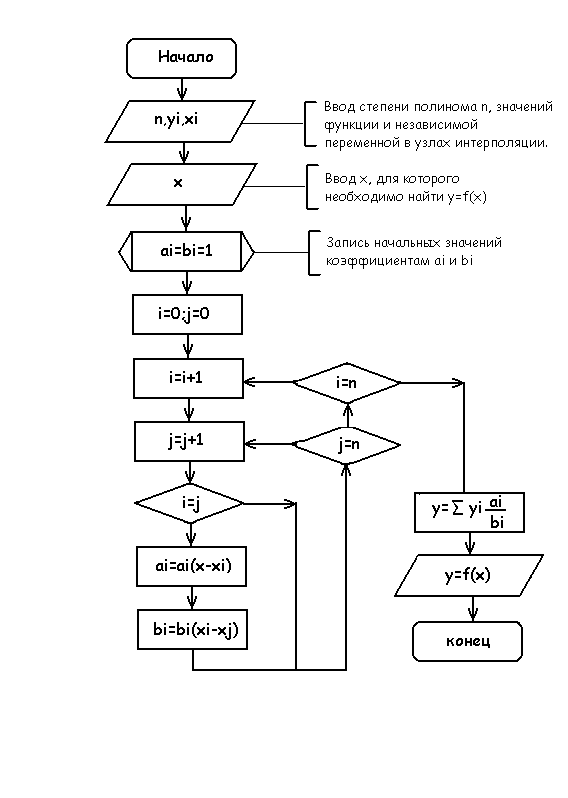 Например: linear линейная интерполяция exponential экспоненциальная интерполяция Процесс вывода цветного изображения, когда пикселы, относящиеся к области между двумя цветными… … Справочник технического переводчика

интерполяция — и, ж. interpolation f. &LT; лат. interpolatio изменение; переделка, искажение. 1. Вставка позднейшего происхождения в каком л. тексте, не принадлежащая оригиналу. БАС 1. В древних рукописях много интерполяций, внесенных переписчиками. Уш. 1934. 2 … Исторический словарь галлицизмов русского языка

Интерполяция — О функции, см.: Интерполянт. Интерполяция, интерполирование в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Многим из тех, кто сталкивается с научными и… … Википедия

Интерполяция (матем.)

Билинейная интерполяция — Билинейная интерполяция в вычислительной математике расширение линейной интерполяции для функций двух переменных. Ключевая идея заключается в том, чтобы провести обычную линейную интерполяцию сначала в одном направлении, затем в другом … Википедия

Интерполирование — О функции, см.: Интерполянт. Интерполяция в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Многим из тех, кто сталкивается с научными и инженерными расчётами часто … Википедия

Таблица поиска — (англ. lookup table) это структура данных, обычно массив или ассоциативный массив, используемая с целью заменить вычисления на операцию простого поиска. Увеличение скорости может быть значительным, так как получить данные из памяти… … Википедия

Это глава из книги Билла Джелена .

Задача: некоторые инженерные проблемы проектирования требуют использования таблиц для вычисления значений параметров. Поскольку таблицы являются дискретными, дизайнер использует линейную интерполяцию для получения промежуточного значения параметра. Таблица (рис. 1) включает высоту над землей (управляющий параметр) и скорость ветра (рассчитываемый параметр). Например, если надо найти скорость ветра, соответствующую высоте 47 метров, то следует применить формулу: 130 + (180 – 130) * 7 / (50 – 40) = 165 м/сек.

Скачать заметку в формате или , примеры в формате

Как быть, если существует два управляющих параметра? Можно ли выполнить вычисления с помощью одной формулы? В таблице (рис. 2) показаны значения давления ветра для различных высот и величин пролета конструкций. Требуется вычислить давление ветра на высоте 25 метров и величине пролета 300 метров.

Решение: проблему решаем путем расширения метода, используемого для случая с одним управляющим параметром. Выполните следующие действия.

Начните с таблицы, изображенной на рис. 2. Добавьте исходные ячейки для высоты и пролета в J1 и J2 соответственно (рис. 3).

Рис. 3. Формулы в ячейках J3:J17 объясняют работу мегаформулы

Для удобства использования формул определите имена (рис.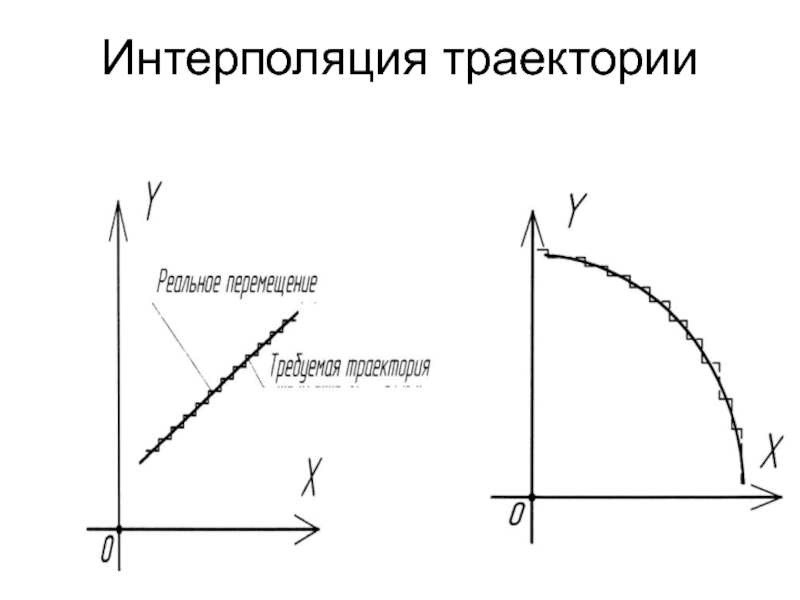 4).

Проследите за работой формулы последовательно переходя от ячейки J3 к ячейке J17.

Путем обратной последовательной подстановки соберите мегаформулу. Скопируйте текст формулы из ячейки J17 в J19. Замените в формуле ссылку на J15 на значение в ячейке J15: J7+(J8-J7)*J11/J13. И так далее. Получится формула, состоящая из 984 символов, которую невозможно воспринять в таком виде. Вы можете посмотреть на нее в приложенном Excel-файле. Не уверен, что такого рода мегаформулы полезны в использовании.

Резюме: линейная интерполяция используется для получения промежуточного значения параметра, если табличные значения заданы только для границ диапазонов; предложен метод расчета по двум управляющим параметрам.

двойная интерполяция онлайн калькулятор

Вы искали двойная интерполяция онлайн калькулятор? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и интерполятор онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «двойная интерполяция онлайн калькулятор».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как двойная интерполяция онлайн калькулятор,интерполятор онлайн,интерполяция онлайн двойная онлайн,интерполяция онлайн калькулятор двойная,калькулятор интерполяции онлайн,квадратичная интерполяция онлайн,линейная экстраполяция онлайн,метод интерполяции онлайн,метод интерполяции онлайн калькулятор,метод экстраполяции онлайн калькулятор,онлайн интерполятор,онлайн интерполяция калькулятор,онлайн калькулятор интерполяции,экстраполяция калькулятор онлайн,экстраполяция онлайн калькулятор,экстраполяция онлайн расчет,экстраполяция расчет онлайн. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и двойная интерполяция онлайн калькулятор. Просто введите задачу в окошко и нажмите «решить» здесь (например, интерполяция онлайн двойная онлайн).

Где можно решить любую задачу по математике, а так же двойная интерполяция онлайн калькулятор Онлайн?

Решить задачу двойная интерполяция онлайн калькулятор вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Интерполяционный многочлен Лагранжа (полином Лагранжа)

Этот калькулятор может пригодиться при решении задач на интерполяцию полиномом Лагранжа. В таких задачах обычно требуется интерполировать значение неизвестной функции, соответствующее некоторому значению x, использую формулу интерполяционного многочлена Лагранжа, полученную из известного набора точек со значениями неизвестной функции (x, f(x)).

Калькулятор ниже обладает следующими функциями:

Он находит формулу полинома Лагранжа для заданного набора точек.
Он отображает пошаговый вывод формулы.
Он вычисляет значения интерполяционного многочлена Лагранжа для заданных точек (интерполирует функцию полиномом Лагранжа в заданных точках интерполяции)
Он отображает набор точек, значения в точках интерполяции, полином Лагранжа и все базисные полиномы на графике.

Как пользоваться

Сначала вводите набор точек — одна точка на строку в форме x f(x), значения разделены пробелом. Если вы хотите получить интерполяцию, вводите значения точек интерполяции в следующее поле в виде значений x, разделенных пробелом.

По умолчанию, калькулятор отображает формулу многочлена и его значения в точках интерполяции. Если нужно пошаговое решение, включите опцию «Показать пошаговое решение». Также можно отключить отображение базисных полиномов.

Теория и формулы, как обычно, описаны под калькулятором.

Интерполяционный многочлен Лагранжа (полином Лагранжа)

0 -1 1 1 4 1

Набор точек, одна точка на строку, значения разделяются пробелом

Точность вычисления

Знаков после запятой: 2

Полином Лагранжа

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Загрузить close

Показать решение по шагам

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Загрузить close

Показать базисные полиномы

Полином Лагранжа

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Загрузить close

content_copy Ссылка save Сохранить extension Виджет

Интерполяционный многочлен Лагранжа

Предположим, что у нас есть набор значений, соответствующих неизвестной функции, при этом все x различны:

Сконструируем следующий многочлен (называемые многочленом Лагранжа):

где — базисный полином Лагранда

Если посмотреть на формулу базисного полинома для любого j, то видно что для всех точек i не равных j, значение этого полинома обращается в ноль, а в самой точке j значение этого полинома j равно единице. Таким образом,

что означает, что полином Лагранжа точно интерполирует значение функции в заданных точках.

Стоит заметить, что формула интерполяционного многочлена Лагранжа подвержена воздействию так называемого феномена Рунге. Феномен Рунге связан к увеличением колебаний полинома на краях интервала при использовании полиномов высоких степеней на равноудаленных друг от друга точках. Таким образом, наличие большого количества точек далеко не всегда приводит к улучшению точности интерполяции.

Однако также стоит заметить, что в отличие от некоторых других формул интерполяции, формула Лагранжа не требует того, чтобы точки в наборе были равноудалены друг от друга. Это используется в некоторых способах борьбы с феноменом Рунге, например, при использовании в качестве точек интерполяции узлов Чебышева.

Калькулятор Интерполяции

Калькулятор онлайн вычисляет линейную экстраполяцию по двум точкам, выводит формулу с подробным решением и графиком

Формула линейной экстраполяции

расчет линейной экстраполяции по двум точкам

Помощь на развитие проекта premierdevelopment.ru

Send mail и мы будем знать, что движемся в правильном направлении.

Спасибо, что не прошели мимо!

I. Порядок действий при расчете линейной экстраполяции онлайн калькулятором:

Для проведения экстраполяции требуется ввести значения координат 2 точек ([X1, Y1]; [X2, Y2]) и абсциссу (Х) той точки, значение которой необходимо вычислить.
График справа позволяет визуализировать полученный линейной экстраполяцией результат.

II. Для справки:

интерполяция — способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.линейная интерполяция — нахождение промежуточного значения функции по двум точкам (условно проведя прямую между ними).квадратичная интерполяция — нахождение промежуточного значения функции по трем точкам (интерполирующая функция многочлен второго порядка – парабола).экстраполяция — способ нахождения значений функции по уже известным нескольким ее значениям.

ФорумСпециалистыО нас

Ссылка для цитирования в списке литературы:

CAE-CUBE: [Электронный ресурс]. URL: https://premierdevelopment.ru/ (дата обращения )

e-mail: Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра.

Линейная интерполяция

Простейшим случаем интерполяции является “линейная”, то есть нахождение величины по двум заданным точкам. Данный процесс вычисления можно рассмотреть как линейную функцию, тем самым делая расчёт более наглядным. Нанесение функции на систему координат называют аппроксимацией. Для этого на оси координат необходимо провести прямую через известные точки. Логично, что искомое значение, находящееся между первыми двумя точками, можно найти графически, зная абсциссу X. Если координата X искомой величины лежит за пределами известных значений (X1, X2), то процесс вычисления называется экстраполяция.

Калькулятор позволяет определить значение ординаты Y искомого значения, зная координаты X и Y двух других функций, а также её абсциссу. Для вычисления необходимо ввести значения заданных двух точек Х1, Y1 и X2,Y2, а также указать координату X искомой точки, а сервис автоматически определит метод расчёта и произведёт его.

Информация

Такие науки, как статистика и математика, используют в своей методологии инструмент «Интерполяция». Он используется инженерии и архитектурном проектировании.

Интерполяция применима в следующих случаях:

Явление было изучено со всесторонне, а не одним путем определенного исчисления.
Применение данного инструмента возможно только в случаях, когда допускается изменение погрешности, между проверенными точками, которое также подчиняется конкретному закону.
Применение может быть оправдано не во всех случаях, так как при эмпирических функциях может возникнуть ряд других нюансов.

Так или иначе, применяя метод линейной интерполяции, допущение ошибок при расчетах недопустимо. Для того, чтобы обезопасить специалистов от возникновения ошибок по причине допущения просчета, мы разработали калькулятор линейной интерполяции онлайн. Благодаря этому инструменту теперь есть возможность избежать допущения каких-либо ошибок, поскольку калькулятор имеет предельную точность в расчетах.

Линейная интерполяция онлайн:

Обезопасить себя от допущения ошибок, которые в случаях со строительством жилых зданий могут приводить к ужасным последствиям.
Избавить себя от необходимости самостоятельного расчета формулы и просто ввести необходимые значения в соответствующие поля и получить готовый ответ.
Метод линейной интерполяции покажется очень простым, благодаря интерфейсу нашего калькулятора.

Наш калькулятор, осуществляя расчет методом линейной интерполяции, использует следующую формулу:

Y = y1+(x-x1)/(x2-x1)*(y2-y1),

где y – показатель линейной интерполяции,

y1, y2, x, x1, x2 – известные значения, которые необходимо вставить в поля калькулятора.

Таким образом, используя наш онлайн калькулятор, Вы получите точный ответ, легко разберетесь в функционале калькулятора, благодаря простому интерфейсу, и никогда не допустите ошибки по причине человеческого фактора.

Использование экстраполяции

В отличие от интерполяции, задачей которой является нахождения значения функции между двумя известными аргументами, экстраполяция подразумевает поиск решения за пределами известной области. Именно поэтому данный метод столь востребован для прогнозирования.

В Экселе можно применять экстраполяцию, как для табличных значений, так и для графиков.

Способ 1: экстраполяция для табличных данных

Прежде всего, применим метод экстраполяции к содержимому табличного диапазона. Для примера возьмем таблицу, в которой имеется ряд аргументов (X) от 5 до 50 и ряд соответствующих им значений функции (f(x)). Нам нужно найти значение функции для аргумента 55, который находится за пределом указанного массива данных. Для этих целей используем функцию ПРЕДСКАЗ.

Выделяем ячейку, в которой будет отображаться результат проведенных вычислений. Кликаем по значку «Вставить функцию», который размещен у строки формул.

Запускается окно Мастера функций. Выполняем переход в категорию «Статистические» или «Полный алфавитный перечень». В открывшемся списке производим поиск наименования «ПРЕДСКАЗ». Найдя его, выделяем, а затем щелкаем по кнопке «OK» в нижней части окна.

Мы перемещаемся к окну аргументов вышеуказанной функции. Она имеет всего три аргумента и соответствующее количество полей для их внесения.

В поле «X» следует указать значение аргумента, функцию от которого нам следует вычислить. Можно просто вбить с клавиатуры нужное число, а можно указать координаты ячейки, если аргумент записан на листе. Второй вариант даже предпочтительнее. Если мы произведем внесение именно таким способом, то для того, чтобы просмотреть значение функции для другого аргумента нам не придется менять формулу, а достаточно будет изменить вводную в соответствующей ячейке. Для того, чтобы указать координаты этой ячейки, если был выбран все-таки второй вариант, достаточно установить курсор в соответствующее поле и выделить эту ячейку. Её адрес тут же отобразится в окне аргументов.

В поле «Известные значения y» следует указать весь имеющийся у нас диапазон значений функции. Он отображается в колонке «f(x)». Следовательно, устанавливаем курсор в соответствующее поле и выделяем всю эту колонку без её наименования.

В поле «Известные значения x» следует указать все значения аргумента, которым соответствуют внесенные нами выше значения функции. Эти данные находятся в столбце «x». Точно так же, как и в предыдущий раз выделяем нужную нам колонку, предварительно установив курсор в поле окна аргументов.

После того, как все данные внесены, жмем на кнопку «OK».

После этих действий результат вычисления путем экстраполяции будет выведен в ячейку, которая была выделена в первом пункте данной инструкции перед запуском Мастера функций. В данном случае значение функции для аргумента 55 равно 338.

Если все-таки был выбран вариант с добавлением ссылки на ячейку, в которой содержится искомый аргумент, то мы легко сможем его поменять и просмотреть значение функции для любого другого числа. Например, искомое значение для аргумента 85 буде равно 518.

Урок: Мастер функций в Excel

Способ 2: экстраполяция для графика

Выполнить процедуру экстраполяции для графика можно путем построения линии тренда.

Прежде всего, строим сам график. Для этого курсором при зажатой левой кнопке мыши выделяем всю область таблицы, включая аргументы и соответствующие значения функции. Затем, переместившись во вкладку «Вставка», кликаем по кнопке «График». Этот значок расположен в блоке «Диаграммы» на ленте инструментов. Появляется перечень доступных вариантов графиков. Выбираем наиболее подходящий из них на свое усмотрение.

После того, как график построен, удаляем из него дополнительную линию аргумента, выделив её и нажав на кнопку Delete на клавиатуре компьютера.

Далее нам нужно поменять деления горизонтальной шкалы, так как в ней отображаются не значения аргументов, как нам того нужно. Для этого, кликаем правой кнопкой мыши по диаграмме и в появившемся списке останавливаемся на значении «Выбрать данные».

В запустившемся окне выбора источника данных кликаем по кнопке «Изменить» в блоке редактирования подписи горизонтальной оси.

Открывается окно установки подписи оси. Ставим курсор в поле данного окна, а затем выделяем все данные столбца «X» без его наименования. Затем жмем на кнопку «OK».

После возврата к окну выбора источника данных повторяем ту же процедуру, то есть, жмем на кнопку «OK».

Теперь наш график подготовлен и можно, непосредственно, приступать к построению линии тренда. Кликаем по графику, после чего на ленте активируется дополнительный набор вкладок – «Работа с диаграммами». Перемещаемся во вкладку «Макет» и жмем на кнопку «Линия тренда» в блоке «Анализ». Кликаем по пункту «Линейное приближение» или «Экспоненциальное приближение».

Линия тренда добавлена, но она полностью находится под линией самого графика, так как мы не указали значение аргумента, к которому она должна стремиться. Чтобы это сделать опять последовательно кликаем по кнопке «Линия тренда», но теперь выбираем пункт «Дополнительные параметры линии тренда».

Запускается окно формата линии тренда. В разделе «Параметры линии тренда» есть блок настроек «Прогноз». Как и в предыдущем способе, давайте для экстраполяции возьмем аргумент 55. Как видим, пока что график имеет длину до аргумента 50 включительно. Получается, нам нужно будет его продлить ещё на 5 единиц. На горизонтальной оси видно, что 5 единиц равно одному делению. Значит это один период. В поле «Вперед на» вписываем значение «1». Жмем на кнопку «Закрыть» в нижнем правом углу окна.

Как видим, график был продлен на указанную длину с помощью линии тренда.

Урок: Как построить линию тренда в Excel

Итак, мы рассмотрели простейшие примеры экстраполяции для таблиц и для графиков. В первом случае используется функция ПРЕДСКАЗ, а во втором – линия тренда. Но на основе этих примеров можно решать и гораздо более сложные задачи прогнозирования.

Мы рады, что смогли помочь Вам в решении проблемы. Опишите, что у вас не получилось.

Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

ДА НЕТ

Поделиться статьей в социальных сетях:

Еще статьи по данной теме:

Линейная регрессия

Уравнение регрессии:

Коэффициент a:

Коэффициент b:

Коэффициент линейной парной корреляции:

Коэффициент детерминации:

Средняя ошибка аппроксимации:

Что такое линейная интерполяция в математике?

Формула линейной интерполяции:

$$ y = y1 + ((x – x1) / (x2 – x1)) * (y2 – y1) $$

В этом уравнении интерполяции:

X = известное значение,
y = неизвестное значение,
x1 и y1 = координаты, которые ниже известного значения x
x2 и y2 = координаты выше значения x.

Пример1:

Если заданными точками данных являются (2, 4) и (6, 8), как вы рассчитаете значение y, когда x = 2.

На первом этапе мы извлечем координаты заданных точек данных.

$$ x1 = 2 $$

$$ y1 = 4 $$

$$ x2 = 6 $$

$$ y2 = 8 $$

На втором этапе мы возьмем следующие уравнения, чтобы получить значения m, а затем y

(m = y2 – y1 / x2 − x1 ) = уравнение 1
(y = y1 + m * (x – x1) ) = уравнение 2
Чтобы вычислить значение m, поместите значения в уравнение 1, (= m = 8−4 / 6−2 = 1 )

Теперь у нас есть значение m, поэтому мы воспользуемся уравнением 2, чтобы найти значение y. 2 ) в заданной строке, пока заданные данные

«$$ x1 = 4, y1 = 6, x2 = 8, x3 = 12, y3 = 14 $$».

Решение:

Поскольку у нас есть линейное интерполяционное уравнение:

$$ y_2 = (x_2 – x_1) x (y_3- y_1) / (x_3 – x_1) + y_1 $$

Пошаговое решение для нахождения y2 будет таким, как если бы вышеприведенное уравнение было следующим:

$$ y_2 = (x_3 − x_2) x (y_3 − y_1) / (x_3 − x_2) + y_3 $$

$$ y_2 = (12−8) x (14−6) / (12−8) + 14 $$

$$ y_2 = (4) x (8) / (4) + 14 $$

$$ y_2 = (32) / (4) + 14 $$

$$ y_2 = 8 + 14 $$

$$ y_2 = 22 $$

Формула линейной интерполяции

Для вычисления используется следующая формула:

Часто задаваемые вопросы (FAQ):

Какой метод можно использовать в любом вопросе интерполяции?

Обычно мы используем метод интерполяции калькулятор полиномов. Причины использования полиномов:

Их легко оценить
Дифференциация и интеграция просты.

Это называется полиномиальной интерполяцией.

Когда следует использовать интерполяцию?

Какой метод интерполяции лучший?

Кригинг – это точная интерполяция?

Пример расчёта

Дано: координаты двух точек А(3;1.5) и B(6;5).
Найти: ординату точки С с абсциссой 4.5.

Для удобства рекомендуется построить график: нанести точки на систему координат и провести прямую.

После этого подставляем значения в указанную формулу:

Y = 5 + (1.5 – 5) / (3 – 6) · (4.5 – 6) = 5 + (-3.5) / (-3) · (-1.5) = 3.25.

интерполяция онлайн калькулятор момент:

Линейная интерполяция

Линейная интерполяция — интерполяция алгебраическим двучленом P 1 = ax + b функции f, заданной в двух точках x 0 и x 1 отрезка. В случае, если заданы значения в нескольких точках, функция заменяется кусочно-линейной функцией.

1. Геометрическая интерпретация
Геометрически это означает замену графика функции f {\displaystyle f} прямой, проходящей через точки x 0, f x 0) {\displaystyle x_{0},fx_{0})} и x 1, f x 1) {\displaystyle x_{1},fx_{1})}.
Уравнение такой прямой имеет вид:
y − f x 0 f x 1 − f x 0 = x − x 0 x 1 − x 0 {\displaystyle {\frac {y-fx_{0}}{fx_{1}-fx_{0}}}={\frac {x-x_{0}}{x_{1}-x_{0}}}}
отсюда для x ∈ }|fx|,\quad h=x_{1}-x_{0}.{-1}{\begin{pmatrix}x\\y\\z\\1\\\end{pmatrix}}}

3. Применение
Линейная интерполяция применяется для уплотнения таблиц.
Формула линейной интерполяции является частным случаем интерполяционной формулы Лагранжа и интерполяционной формулы Ньютона.

Термин интерполяция впервые употребил Джон Валлис в своём трактате Арифметика бесконечных 1656 В функциональном анализе интерполяция линейных операторов
Билинейная интерполяция — в вычислительной математике — обобщение линейной интерполяции одной переменной для функций двух переменных. Обобщение основано
Интерполяция линейных операторов — направление функционального анализа. рассматривающее банаховы пространства как элементы некоторой категории. Общая
основой для множества других работ. Способы интерполяции Интерполяция методом ближайшего соседа. Линейная интерполяция Интерполяционная формула Ньютона Метод
общественном достоянии англ. Интерполяция методом ближайшего соседа Линейная интерполяция Билинейная интерполяция Бикубическая интерполяция Кубический сплайн
Бикубическая интерполяция — в вычислительной математике расширение кубической интерполяции на случай функции двух переменных, значения которой заданы
О способе нахождения промежуточных значений см. Интерполяция Интерполянт или интерполирующая функция — в вычислительной математике это функция, которая
ячейке. Для улучшения качества получаемой изолинии применяется линейная интерполяция В таком случае конец сегмента изолинии на ребре квадрата делит
диапазона, чтобы аппроксимация больше походила на реальную кривую см. также Интерполяция Пример таблицы синусов на языке программирования C 8 — битная таблица
апроксимированное эмпирическое правило, которое гласит, что существует линейная зависимость при постоянной температуре между свойствами кристаллической
концентраций, превышающих ПДК. Оценочный бал рассчитывается как результат линейной интерполяции по следующим диапазонам: Среднее значение кратности превышения ПДК
имеющимся. Идеальная интерполяция позволяет точно восстановить значения сигнала в промежуточных отсчётах. Стандартный алгоритм интерполяции сигнала с целым

символы или, например, от 1 до 26 только латинский алфавит и т. д. Интерполяция может производиться на основе функции, аппроксимирующей распределение
ISBN 978 — 5 — 8459 — 1524 — 5, ДИАЛЕКТИКА 2009 Крейн С. Г., Петунин Ю. И., Семенов Е. М. Интерполяция линейных операторов — М.: Наука, 1978 — 400 с.
соросовский профессор. Крейн С. Г., Петунин Ю. И., Семёнов Е. М. Интерполяция линейных операторов — М.: Наука, 1978 — 400 с. Воспоминания Татьяны Крейн:
Монте — Карло Алгоритм имитации отжига Обыкновенные дифференциальные уравнения Интерполяция Численное дифференцирование Разложение по полиномам Чебышёва Суммирование
Интерактивное введение в сплайны Интерактивный расчет сплайна с помощью Mathcad Maple Application Server неактивна Сплайновая интерполяция неактивна
3D графики, анимация Линейная алгебра, разреженные матрицы sparse matrices Полиномиальные и рациональные функции Интерполяция аппроксимация Симуляция:
предположениях кригинг дает наилучшее линейное несмещенное предсказание промежуточных значений. Методы интерполяции основанные на других критериях, таких
И. Мальцева 2009 — за серию научных работ Неявная определимость и интерполяция в неклассических логиках премия Правительства РФ в области образования
с. 19. Крейн, 1978, с. 9. Крейн, 1978, с. 28. Крейн С. Г., Петунин Ю. И., Семенов Е. М. Интерполяция линейных операторов — М.: Наука, 1978 — 400 с.
аппроксимировала функцию 1 z параболической интерполяцией и такая интерполяция по качеству превосходила кусочно — линейную использовавшуюся в решениях конкурентов

методах функция представлена линейной комбинацией элементов. При этом дискретная функция также может рассматриваться как линейная комбинация полиномов. Прямые
усиления эффекта антиалиасинга: Интерполяция методом ближайшего соседа Билинейная интерполяция Бикубическая интерполяция Реконструкционные фильтры также
телеэкрану сверху вниз. Для разрешения конфликта систем применяется интерполяция кадровой частоты. При этом происходит преобразование, называемое профессионалами
первый программный код, доказывающий, что линейная масштабируемость от числа неизвестных в системе линейных уравнений может быть достигнута без привлечения
за прошлые дни, скорректированные с учётом изменения рынка или линейная интерполяция ставок по заключённым сделкам на другие сроки уровень 3 — экспертная
куба, на котором она лежала изначально. Позиция вычисляется путём линейной интерполяции значений скалярного поля в концах ребра. Заранее вычисленный массив
collections. Геометрия является линейной в том смысле, что границы неявно определяются путем линейной интерполяции между вершинами. Геометрия вложена
interpolate Инструменты для интерполяции io Ввод — вывод данных. lib Работа со сторонними библиотеками. linalg Линейная алгебра. misc Разное. optimize

Линейная интерполяция: линейная интерполяция формула, линейная интерполяция пример решения, линейная интерполяция в excel, линейная интерполяция с++, линейная интерполяция для чайников, нелинейная интерполяция, линейная интерполяция формула пример, линейная интерполяция чпу

Линейная интерполяция для чайников.

Н.В. Байдакова. Линейная интерполяция на тетраэдре С. 80 84. Текст научной работы на тему Оптимальная линейная интерполяция с условием на алгоритм. а 0 а min 1.1, 0 т при т 1 должно быть b0. Линейная интерполяция с. Линейная интерполяция онлайн калькулятор. Линейная интерполяция. В данном разделе мы рассмотрим самый простой метод нахождения линейной интерполяции таблично заданной функции. Линейная интерполяция чпу. Interp NumPy PyProg.x.y.y, dt увеличиваю y. Интерполяция function linearInterpolation x0,x1,y0,y1,x return x.

Линейная интерполяция формула.

ЧПУ. Линейная интерполяция. Где y – показатель линейной интерполяции. y1, y2, x, x1, x2 – известные значения, которые необходимо вставить в поля калькулятора. Таким образом,. Линейная интерполяция в excel. Фасад.РУ Линейная интерполяция. Воспользуйтесь нашим удобным онлайн расчетом линейной интерполяции. Так же имеются другие виды расчетов интерполяции.

Интерполяция и функции предсказания Руководство.

Интерполяция линейная логарифмическая шкала С. Программирование, C, Алгоритмы. Понадобилось мне как то сделать. ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ Математический справочник. ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ. ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ приближенное вычисление значений функции для внутренних точек отрезка по. Линейная интерполяция ru. Линейная интерполяция дает ошибку при определенных входных значениях между 70% и 80%. У меня есть очень специфическая проблема excel. Линейная интерполяция Аппаратная платформа Arduino. Билинейная интерполяция. Билинейной интерполяцией называют расширение линейной.

Линейная интерполяция – G01 Планета CAM.

Линейная интерполяция на евклидовом шаре в Rⁿ. совокупность многочленов от n переменных степени ≤1, то есть линейных функций на Rn. Линейная интерполяция дает ошибку при определенных. Синонимы к словосочетанию ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ: линейная функция, линейное преобразование, полная линейная группа, линейная. МЕТОДЫ ИНТЕРПОЛЯЦИИ И АППРОКСИМАЦИИ. Глава 6. Обработка экспериментальных данных. 6.1 Линейная интерполяция. Встроенные функции MathCAD позволяют при интерполяции проводить. Линейная интерполяция. Линейная интерполяция. Самый простой вид интерполяции линейная, которая представляет искомую зависимость y x в виде ломаной линии.

Определение промежуточного значения методом линейной.

Приведенная ниже формула Microsoft Excel выполняет линейную Чтобы создать пример линейной формулы интерполяции,. Линейная интерполяция Пусть есть неизвестная функция. Линейная интерполяция продолжение листинга 13.1. Для построения линейной интерполяции служит встроенная функция linterp листинг 13.1. 3. Интерполяция Численные методы. В простейших случаях эта задача может быть решена путем линейной интерполяции. Линейная интерполяция опирается на предположение, что в.

ЛИНЕЙНО ИНТЕРПОЛИРОВАННОЕ ВЕКТОРНОЕ ПОЛЕ И.

Линейная и квадратичная интерполяция. Постановка задачи аппроксимации функций. Постановка задачи: требуется приближенно заменить. Линейная интерполяция Gravbiz настольные гравировальные. Пусть координаты первой точки линейной функции Х0, Y0, второй Х1, Y1. Прямая между этими точками представляет собой линейную интерполяцию. Интерполяция Loginom. Н.В. Байдакова. Линейная интерполяция на тетраэдре С. 80 84. Опубликовано пт, 30 11 2018 пользователем sez. Том 24, номер 4, 2018.

Линейная интерполяция m.

В этом случае на помощь приходит метод линейной интерполяции, который помогает найти промежуточные значения. Он достаточно. Линейная интерполяция онлайн с решением и графиком. Доброго времени суток! Нужно выполнить линейную интерполяцию экстраполяцию данных. Для решения сей задачи, в связи с. 3.2 Линейная интерполяция:. 2.8. Рис. 2.8. Линейная и сплайновая интерполяция. Формула линейной интерполяции. Графически это означает простое соединение. Линейная интерполяция Языки программирования Life Prog. Сервис интерполяции и экстраполяции онлайн линейная интерполяция экстраполяция поможет вам вычислить значение линейной функции, имея в.

Линейная интерполяция на евклидовом шаре в Rⁿ Невский.

Линейная интерполяция, формально примененная к паре величин Рост – Вес, показана на рис. 2. Были взяты данные двух студентов маленький. Синонимы к словосочетанию ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ. Онлайн калькулятор показывает значение, полученное линейной интерполяцией и формулы, по которым проводилось вычисление. Формулы удобно. Интерполяция функций двух переменных, проблема выбора узлов. ИП Кто? Что? линейная интерполяция, линейные интерполяции. РП Кого? Чего? линейной интерполяции, линейных интерполяций. ДП Кому? Чему. Линейная интерполяция величины по нескольким параметрам. §5. Программирование ЧПУ. Линейная интерполяция. 30.12.2012. Управляющая программа обработки детали представляет собой траекторию. Лекция Интерполяция функций НОУ ИНТУИТ. Эти величины, в свою очередь, находятся путём линейной интерполяции по таблицам СП 23 102 2003 Естественное освещение. Линейная интерполяция Онлайн калькулятор. Линейная интерполяция используется для получения промежуточного значения параметра предложен метод расчета по двум.

Линейная интерполяция функции.

Линейная интерполяция. Самый простой вид интерполяции – кусочно постоянная. Ее смысл состоит в том, что на каждом промежутке между. Линейная интерполяция Центр дистанционного обучения. При линейной интерполяции Mathcad соединяет существующие точки данных прямыми линиями. Это выполняется функцией linterp, описанной ниже. ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ это Что такое ЛИНЕЙНАЯ. В математике линейная интерполяция метод установки кривой, используя линейные полиномиалы. Линейная интерполяция между двумя известными. Метод вычисления значения шага интерполяции в Excel. Рассматривается задача алгебраической интерполяции. Простейший способ интерполяции кусочно линейная, требующая.

Линейная интерполяция склонение и спряжение Промт.

Наиболее простым методом является линейная интерполяция, когда предполагается, что промежуточные точки лежат на прямых, соединяющих ее. Линейная и билинейная интерполяция. Код G01 предназначен для выполнения линейной интерполяции, или, говоря простым языком, для перемещения инструмента по прямой линии с. Интерполяция, экстраполяция и сглаживание. Кусочно линейная интерполяция. При решении ряда задач требуется восстановить функцию y f x для произвольного значения x на отрезке, если. 13.1.1. Линейная интерполяция MathCAD 12 руководство. Линейная интерполяция. После заполнения всех значений результат вычисляется автоматически. Плоская задача 2D.

Линейная интерполяция для рассчета траектории движения.

В статье рассматривается линейная интерполяция двумерного векторного поля, которая получается по трем значениям в вершинах единичного. Н. В. Байдакова, Линейная интерполяция на тетраэдре, Тр. Линейной интерполяции, поэтому продолжим вычисления далее. Также заметим, что исходные данные избыточны, т.к. достаточно было указать только.

Линейная интерполяция Тепломассообмен.

Линейная интерполяция Matlab. Не будем вдаваться в математические определения и термины, перейдём сразу к сути: Алгоритм. Постановка задачи. Кусочно линейная интерполяция. Считаем методом интерполяции. y y1 x x1 x2 x1 y2 y1. y 130 133.

линейная интерполяция пример решения, линейная интерполяция формула пример

Дата публикации:

05-16-2020

Дата последнего обновления:

05-16-2020

Калькулятор и формула линейной интерполяции — [100% бесплатно]

Используйте этот калькулятор линейной интерполяции для поиска точек на заданной линии. Вы можете определить значение либо с помощью формы пересечения уклона, либо с помощью двух координат. В этой статье вы узнаете, как пользоваться калькулятором, и прочую информацию о линейной интерполяции. Читайте дальше, чтобы узнать больше.

Как пользоваться калькулятором линейной интерполяции?

Этот очень простой калькулятор интерполяции служит удобным инструментом, когда вам нужно найти нужные значения.Вместо того, чтобы решать вручную с использованием формулы линейной интерполяции, этот калькулятор намного проще и мгновенно предоставляет вам результаты. Вот шаги, которые необходимо выполнить для этого онлайн-инструмента:

Сначала введите значения x1 и y1 .
Затем введите значения x2 и y2 .
Наконец, введите значения x3 и y3 .
После ввода всех требуемых значений калькулятор линейной интерполяции автоматически генерирует для вас значения m и b с учетом формы пересечения наклона формулы:

y = mx + b.

Под этими значениями вы также можете увидеть всю формулу с уже подставленными в нее значениями. Это дает вам хорошую справочную информацию о том, как записать формулу вместе с необходимыми значениями.

Что такое метод интерполяции?

Метод интерполяции относится к статистическому методу, с помощью которого вы используете связанные известные значения для получения оценки неизвестной потенциальной доходности или цены данной ценной бумаги. Вы можете достичь этого метода, используя другие известные значения, связанные с ним, которые идут последовательно с неизвестными значениями.

По сути, интерполяция — это простое математическое понятие. Если вы заметили тенденцию в наборе точек данных, которая в целом согласована, вы можете дать разумную оценку ценности набора данных даже в тех точках, которые вы еще не рассчитали. Конечно, это в лучшем случае лишь оценка. Проблема с интерполяторами в том, что вы никогда не можете полностью доверять их оценкам.

Есть разные виды интерполяции, с которыми вы можете работать.К ним относятся полиномиальная интерполяция, кусочно-постоянная интерполяция и линейная интерполяция. Среди всех этих методов наиболее распространенным и простым является линейная интерполяция. Для этого метода вы можете использовать уравнение линейной интерполяции или калькулятор линейной интерполяции, что намного удобнее.

Это очень полезно, когда вы пытаетесь оценить стоимость процентной ставки или ценной бумаги для определенной точки, по которой нет доступных данных.Не путайте интерполяцию с экстраполяцией. Последнее относится к методу, с помощью которого вы можете получить оценку для точки данных за пределами известного диапазона данных.

Часто графики, которые представляют историю акций, широко интерполируются. Они используют линейную регрессию для создания кривых, которые приблизительно соответствуют колебаниям цены ценной бумаги. Даже если диаграмма, которая измеряет акции в течение года, включает точки данных за каждый день, невозможно с полной уверенностью сказать, где бы стоимость акций была оценена в данный момент времени.

Хотя это определение сначала может сбивать с толку, на самом деле концепция интерполяции относительно проста. Человеческие цивилизации веками использовали интерполяцию, особенно ранними месопотамскими астрономами, а также астрономами из Малой Азии, когда они пытались заполнить пробелы.

Хотя несколько факторов влияют на движения планетных тел, они все же лучше подходят для неточной интерполяции по сравнению с колебаниями запасов, которые очень непредсказуемы.Тем не менее, с учетом огромного количества данных, используемых для анализа ценных бумаг, довольно сложно избежать интерполяции с точки зрения движения цен.

Что такое формула линейной интерполяции?

Хотя использовать этот калькулятор линейной интерполяции проще, вы все равно можете выполнить вычисления вручную, используя уравнение линейной интерполяции. Для этого представьте, что вам нужно измерить зависимость между тем, сколько муки вам нужно и сколько печенья вы хотите испечь.

В первый раз, когда вы испекли партию печенья, вы использовали 200 граммов муки и в итоге получили 15 печений. Во второй раз, когда вы испекли партию печенья, вы использовали 300 граммов муки и в итоге получили 20 печений. Теперь вы хотите знать, сколько печенья вы получите, если использовать 250 граммов муки.

Предположим, что эта ситуация имеет линейную зависимость, поэтому вы можете найти решение для линейной интерполяции. Если вам нужно найти значение, выходящее за пределы уже протестированного вами диапазона, это относится к экстраполяции. Но если вы хотите найти решение для линейной интерполяции, используйте формулу линейной интерполяции:

y = (x — x₁) * (y₂ — y₁) / (x₂ — x₁) + y₁

где:
(x₁, y₁) относятся к координатам 1-й известной точки данных
(x₂, y₂) относятся к координатам 2-й первой известной точки данных
(x, y) относятся к координаты точки, которую вы решаете для

Эта формула в точности совпадает с формулой экстраполяции.Помните, что экстраполяция часто дает результат, не подтвержденный никакими экспериментальными данными. Вот почему рекомендуется использовать интерполяцию.

Что такое квадратичная интерполяция?

Мы можем лучше всего определить квадратичную интерполяцию с помощью формулы. Если бы у вас была таблица значений

yi = f (xi), 0≤i≤2n

На каждом из интервалов [x2j, x2j + 2], 0≤j≤n − 1 , вы должны использовать квадратичный интерполирующий полином на интервале для интерполяции данных.

Как сделать линейную интерполяцию в Excel?

Интерполяция — это метод, который можно использовать для определения фактора будущей или текущей стоимости, когда точное значение не отображается в таблице значений. Интерполяция предполагает, что любое изменение между двумя заданными значениями линейно с незначительной погрешностью.

Помимо использования калькулятора интерполяции, вы также можете выполнить линейную интерполяцию в Excel. Для этого вам необходимо ввести специальную формулу, которая выполняет метод линейной интерполяции, вычисляя значение шага интерполяции. Используемая формула Excel:

= (конец-начало) / (СТРОКА (конец) -СТРОКА (начало))

где:
конец относится к адресу большего ячейка номера
начало относится к адресу ячейки меньшего числа

Калькулятор интерполяции — Calculator Academy

Введите две точки вдоль линии (X1, Y1) (X2, Y2), а также конечную координату X (X3) для интерполяции конечной позиции Y этой точки.Линейная интерполяция использует известные координаты и наклон для вычисления неизвестной точки.

Формула интерполяции

Следующая формула используется для вычисления линейной интерполяции.

y3 = y1 + (X3-X1) * {(y2-y1) / (x2-x1)}

Где Y3 — отсутствующее значение интерполяции
X3, X2, X1 — точки координат
Y2, Y1 — известные точки координат

Определение линейной интерполяции

Интерполяция определяется как экстраполяция данных с использованием прошлых данных.Например, в отношении акций вы можете сказать, что цена выросла на 10% за последний год, поэтому вы собираетесь экстраполировать, что акции вырастут на 10% и в следующем году. На самом деле это может быть неправдой, но это пример использования прошлых данных для интерполяции.

Линейная интерполяция конкретно относится к экстраполяции данных по линейной линии. Например, предположим, что у вас есть 2 точки (X1, Y1) (X2, Y2). Эти две точки представляют собой линию. Теперь предположим, что вы хотите продлить эту линию до новой точки, скажем, X3.Вы можете вычислить значение Y3, умножив наклон этой линии на X3, или, другими словами, Y3 = slope * X3, где наклон равен (X2-X1) / (Y2-Y1). Это пример линейной интерполяции.

Как видите, вы можете интерполировать точку данных Y3 или X3, изменив уравнение. Если у вас есть наклон линии и две точки вдоль этой линии, вы можете определить конечный пункт назначения любой точки по координате X или Y.

Как выполнить линейную интерполяцию?

Выполнить линейную интерполяцию так же просто, как использовать приведенное выше уравнение.Сначала найдите известные точки координат, затем вставьте значения в калькулятор или в формулу.

FAQ

Что такое интерполяция?

Интерполяция определяется как экстраполяция данных с использованием прошлых данных.

Формула линейной интерполяции — Образование

Формула интерполяции: Метод поиска новых значений для любой функции с использованием набора значений выполняется путем интерполяции. Неизвестное значение точки находится по этой формуле.Если речь идет о формуле линейной интерполяции, то ее следует использовать для нахождения нового значения из двух заданных точек. По сравнению с формулой интерполяции Лагранжа, должен быть доступен набор чисел «n», и для нахождения нового значения следует использовать метод Лагранжа.

Интерполяция — это процесс нахождения значения между двумя точками на линии или кривой. Чтобы помочь нам запомнить, что это означает, мы должны думать о первой части слова «интер» как о значении «ввод», которое напоминает нам о том, чтобы заглянуть «внутрь» данных, которые у нас изначально были.Этот инструмент, интерполяция, полезен не только в статистике, но также полезен в науке, бизнесе или в любое время, когда необходимо предсказать значения, которые попадают в две существующие точки данных.

Формула линейной интерполяции

Если две известные точки заданы координатами {\ displaystyle (x_ {0}, y_ {0})} и {\ displaystyle (x_ {1}, y_ {1})}, линейный интерполянт является прямая линия между этими точками. Для значения x в интервале {\ displaystyle (x_ {0}, x_ {1})} значение y вдоль прямой линии определяется из уравнения наклонов

{\ displaystyle {\ frac {y-y_ {0}} {x-x_ {0}}} = {\ frac {y_ {1} -y_ {0}} {x_ {1} -x_ {0}) }},}

, который геометрически может быть получен из рисунка справа.Это частный случай полиномиальной интерполяции с n = 1.

Решение этого уравнения относительно y , которое является неизвестным значением при x , дает

{\ displaystyle y = y_ {0} + (x-x_ {0}) {\ frac {y_ {1} -y_ {0}} {x_ {1} -x_ {0}}} = {\ frac {y_ {0} (x_ {1} -x) + y_ {1} (x-x_ {0})} {x_ {1} -x_ {0}}},}

, который представляет собой формулу линейной интерполяции в интервале {\ displaystyle (x_ {0}, x_ {1})}. За пределами этого интервала формула идентична линейной экстраполяции.

Эту формулу также можно понимать как средневзвешенное значение. Веса обратно пропорциональны расстоянию от конечных точек до неизвестной точки; более близкая точка имеет большее влияние, чем более удаленная. Таким образом, веса равны {\ textstyle {\ frac {x-x_ {0}} {x_ {1} -x_ {0}}}} и {\ textstyle {\ frac {x_ {1} -x} {x_ { 1} -x_ {0}}}}, которые представляют собой нормализованные расстояния между неизвестной точкой и каждой из конечных точек. Потому что эти суммы равны 1

{\ displaystyle y = y_ {0} \ left (1 — {\ frac {x-x_ {0}} {x_ {1} -x_ {0}}} \ right) + y_ {1} \ left ( 1 — {\ frac {x_ {1} -x} {x_ {1} -x_ {0}}} \ right) = y_ {0} \ left (1 — {\ frac {x-x_ {0}} { x_ {1} -x_ {0}}} \ right) + y_ {1} \ left ({\ frac {x-x_ {0}} {x_ {1} -x_ {0}}} \ right),}

Калькулятор формул интерполяции

Решенные примеры

Вопрос 1: Используя формулу интерполяции, найти значение y при x = 8 для некоторого набора значений (2, 6), (5, 9)?
Решение:

Известные значения: x0 = 8, x1 = 2, x2 = 5, y1 = 6, y2 = 9y = y1 + (x − x1) (x2 − x1) × (y2 − y1)

у = 6 + ((8−2) (5−2) × (9−6)

у = 6 + 6

г = 12

Что такое метод линейной интерполяции?

Линейная интерполяция — это простейший метод получения значений в положениях между точками данных.Точки просто соединяются отрезками прямых линий.

Как найти интерполяцию между двумя числами?

Знать формулу для процесса линейной интерполяции . Формула : y = y1 + ((x — x1) / (x2 — x1)) * (y2 — y1), где x — известное значение, y — неизвестное значение, x1 и y1 — координаты, которые ниже известного значения x, а x2 и y2 — координаты выше значения x.

Что такое метод интерполяции?

В математической области численного анализа интерполяция — это метод построения новых точек данных в диапазоне дискретного набора известных точек данных.… Несколько точек данных из исходной функции можно интерполировать , чтобы получить более простую функцию, которая все еще довольно близка к исходной.

Формула интерполяции Excel

Вот пример, иллюстрирующий концепцию интерполяции. Садовник посадил помидор, и она измеряла и отслеживала его рост через день. Этот садовник — любопытный человек, и она хотела бы оценить, насколько высоким было ее растение на четвертый день.

Читайте также: Средняя и мгновенная скорость изменения

Ее таблица наблюдений выглядела так:

Исходя из диаграммы, нетрудно определить, что на четвертый день растение было примерно 6 мм в высоту. Это потому, что это дисциплинированное растение томата росло линейно; была линейная зависимость между количеством измеренных дней и ростом растения. Линейный образец означает, что точки образуют прямую линию.Мы могли даже оценить, нанеся данные на график.

Но что, если растение росло не по удобной линейной схеме? Что, если бы его рост выглядел примерно так?

Что бы сделал садовник, чтобы сделать оценку на основе приведенной выше кривой? Что ж, вот здесь и пригодится формула интерполяции.

Формула интерполяции Thermo

Линейная интерполяция использовалась с древних времен для заполнения пробелов в таблицах.Предположим, у вас есть таблица, в которой перечислено население какой-либо страны в 1970, 1980, 1990 и 2000 годах, и вы хотите оценить численность населения в 1994 году. Линейная интерполяция — простой способ сделать это. Считалось, что метод использования линейной интерполяции для составления таблиц использовался вавилонскими астрономами и математиками в Месопотамии Селевкидов (последние три века до нашей эры), а также греческим астрономом и математиком Гиппархом (2 век до нашей эры). Описание линейной интерполяции можно найти в Альмагесте (2 век нашей эры) Птолемея.

Основная операция линейной интерполяции между двумя значениями обычно используется в компьютерной графике. На жаргоне этой области его иногда называют lerp . Термин может использоваться как глагол или существительное для операции. например «Алгоритм Брезенхема постепенно перемещается между двумя конечными точками линии».

Операции Lerp встроены в аппаратное обеспечение всех современных процессоров компьютерной графики. Их часто используют в качестве строительных блоков для более сложных операций: например, билинейную интерполяцию можно выполнить за три лерпа.Поскольку эта операция стоит недорого, это также хороший способ реализовать точные таблицы поиска с быстрым поиском плавных функций без слишком большого количества записей в таблице.

Читайте также: Что такое буквенно-цифровые символы?

Формула интерполяции

Допустим, у нас есть две известные точки x1, y1x1, y1 и x2, y2x2, y2.

Теперь мы хотим оценить, какое значение yy мы получили бы для некоторого значения xx, которое находится между x1x1 и x2x2. Назовите это значение yy оценкой — интерполированное значение .

На ум приходят два простых метода выбора yy. Во-первых, нужно посмотреть, ближе ли xx к x1x1 или к x2x2. Если xx ближе к x1x1, тогда мы используем y1y1 в качестве оценки, в противном случае мы используем y2y2. Это называется интерполяцией ближайшего соседа .

Второй — провести прямую линию между x1, y1x1, y1 и x2, y2x2, y2. Мы смотрим, чтобы увидеть значение yy в строке для нашего выбранного xx. Это линейная интерполяция .

Можно показать, что формула линии между x1, y1x1, y1 и x2, y2x2, y2:

y = y1 + (x − x1) y2 − y1x2 − x1y = y1 + (x − x1) y2 − y1x2 − x1

Формула двойной интерполяции

Чтобы выполнить линейную интерполяцию в Excel, мы будем использовать приведенное ниже уравнение, где x — независимая переменная, а y — значение, которое мы хотим найти:

Линейная интерполяция в Excel — Dagra Data Digitizer

Как работает реализация Excel

Простую реализацию легче всего понять, проанализировав извне и работая внутри.Вот полное уравнение:
= ПРОГНОЗ ( NewX , OFFSET ( KnownY , MATCH ( NewX , KnownX , 1) -1,0,2), OFFSET ( KnownX , MATCH ( NewX) , ИзвестноX , 1) -1,0,2))
Вкратце уравнение состоит из 3 частей:

функция ПРОГНОЗ для вычисления линейной интерполяции,
два вызова функции ПОИСКПОЗ, чтобы найти ближайшее табличное значение x, но меньше нового значения x, и
два вызова функции OFFSET для ссылки на табулированные значения x и значения y чуть выше и чуть ниже нового значения x.

Более подробно, функция ПРОГНОЗ выполняет фактическую интерполяцию, используя уравнение линейной интерполяции, показанное выше. Его синтаксис: ПРОГНОЗ ( NewX , known_y_pair , known_x_pair ).

Первый параметр NewX — это просто значение для интерполяции. Следующие два параметра, известная_y_ пара и известная_x_ пара , являются значениями по обе стороны от NewX . То есть {x1, x2} и {y1, y2} на диаграмме выше.

Функция ПОИСКПОЗ используется для нахождения табличного значения x чуть ниже NewX . Его синтаксис: MATCH ( lookup_value , lookup_table , match_type ). ПОИСКПОЗ возвращает относительное положение элемента в отсортированном массиве. Итак, lookup_value — это значение для интерполяции, lookup_table — это массив значений KnownX , а match_type — 1, чтобы найти наибольшее значение в массиве, которое меньше или равно NewX .

Функция ПОИСКПОЗ возвращает индекс, но для функции ПРОГНОЗ требуется два диапазона ячеек: один для пары известных_х_х_ и один для пары_известных_г_ . Таким образом, функция СМЕЩЕНИЕ используется дважды для создания этих диапазонов. Его синтаксис: OFFSET ( ссылка , row_offset , column_offset , row_count , column_count ). Он берет начальную точку, ссылку , и создает ссылку на ячейку с заданным смещением и размером.Чтобы получить диапазон known_y_pair , ссылка устанавливается в таблицу значений KnownY ; для диапазона known_x_pair ссылка установлена на массив значений KnownX . Если табличные значения расположены вертикально, row_offset является результатом функции MATCH меньше 1, а row_count равно 2; column_offset равен 0, а column_count равен 1. Это дает нам ссылку на массив ячеек на 2 ячейки в высоту и 1 ячейку в ширину.Если табличные значения расположены горизонтально, строка и столбец переключаются в функции СМЕЩЕНИЕ.

Программа Python для линейной интерполяции

Чтобы интерполировать значение зависимой переменной y в некоторой точке независимой переменной x с использованием Linear Interpolation , мы берем две точки, т.е. если нам нужно интерполировать y, соответствующий x, который находится между x ₀ и x ₁, затем мы берем две точки [x ₀, y ₀] и [x ₁, y ₁] и строим Linear Interpolants , который представляет собой прямую линию между этими точками i.е.

y - y ₀ = ((y ₁ - y ₀) / (x ₁ - x ₀)) * (x - x ₀)

И если необходимо получить значение y, то, используя приведенное выше уравнение, мы вычисляем yp при x = xp как:

yp = y ₀ + ((y ₁ - y ₀) / (x ₁ - x ₀)) * (xp - x ₀)

Точно так же, если нам нужно интерполировать y, соответствующий x, который находится между x ₁ и x ₂, тогда мы берем две точки [x ₁, y ₁] и [x ₂, y ₂] и строит Linear Interpolants , который представляет собой прямую линию между этими точками i.е.

y - y ₁ = ((y ₂ - y ₁) / (x ₂ - x ₁)) * (x - x ₁)

И если необходимо получить значение y, то, используя приведенное выше уравнение, мы вычисляем yp при x = xp как:

yp = y ₁ + ((y ₂ - y ₁) / (x ₂ - x ₁)) * (xp - x ₁)

Эта программа на Python реализует алгоритм линейной интерполяции , как обсуждалось выше, для интерполяции промежуточного значения.

Исходный код Python: линейная интерполяция

 
# Линейная интерполяция в Python

# Раздел ввода
# Чтение первой точки
print ('Введите первую точку:')
x0 = float (ввод ('x0 ='))
y0 = float (вход ('y0 ='))

# Чтение второй точки
print ('Введите вторую точку:')
x1 = float (ввод ('x1 ='))
y1 = float (ввод ('y1 ='))

# Чтение точки расчета
xp = float (input ('Введите точку вычисления xp:'))

# Расчет интерполированного значения
yp = y0 + ((y1-y0) / (x1-x0)) * (xp - x0)

# Отображение результата
print ('Интерполированное значение в% 0.4f составляет% 0,4f '% (xp, yp))

Вывод: линейная интерполяция Python

Предположим, у нас есть проблема интерполяции, сформулированная следующим образом: «По некоторым наблюдениям установлено, что давление, зарегистрированное при температуре 35 ° C, составляет 5,6 кПа, а при 40 ° C — 7,4 кПа. Позже требуется, чтобы используйте давление при 37 ° C, которого нет в таблице наблюдений. Таким образом, значение давления при 37 ° C необходимо интерполировать, и его можно рассчитать с помощью вышеуказанной программы как: «

Введите первую точку:
х0 = 35
y0 = 5,6
Введите вторую точку:
х1 = 40
у1 = 7.4
Введите расчетную точку xp: 37
Интерполированное значение при 37,0000 составляет 6,3200.

Интерполяция с помощью Excel — Excel вне сетки

Интерполяция — это процесс оценки точек данных в существующем наборе данных. Поскольку это блог об Excel, очевидно, что мы хотим ответить на следующий вопрос: можем ли мы выполнять интерполяцию с помощью Excel. Это частый вопрос. Фактически, это был следующий вопрос от читателя, который первым заставил меня изучить эту тему:

«У меня есть вопрос Excel — есть ли способ интерполировать значение из таблицы? У меня есть X и Y, которых нет в таблице, но есть коррелированные данные, поэтому я хочу вычислить интерполированное значение ».

В качестве простого примера: если пройти 1 милю в понедельник за 15 минут, а во вторник — за 1 час, мы могли бы разумно оценить, что пройти 2 мили потребуется 30 минут.

Не следует путать с экстраполяцией, которая оценивает значения вне набора данных. Оценка того, что пройти 8 миль займет 2 часа, будет экстраполяцией, поскольку оценка выходит за рамки известных значений.

Excel — отличный инструмент для интерполяции, так как в конечном итоге это большой визуальный калькулятор.

Загрузите файл с примером

Я рекомендую вам загрузить файл с примером для этого поста. Тогда вы сможете работать с примерами и увидеть решение в действии, а файл будет полезен для дальнейшего использования.

Загрузите файл: 0020 Interpolate with Excel.xlsx

Посмотрите видео

Посмотрите видео на YouTube.

Варианты интерполяции в Excel

С точки зрения ответа на вопрос, есть несколько сценариев, которые могут привести к различным решениям.

Во-первых, мы могли использовать простую математику. Это сработало бы, если бы результаты были абсолютно линейными (т.е. значения X и Y перемещались синхронно друг с другом). Но в противном случае мы могли бы получить немного искаженный результат.

В качестве альтернативы мы могли бы использовать функцию ПРОГНОЗ в Excel (или ПРОГНОЗ.ЛИНЕЙНЫЙ в Excel 2016 и последующих версиях). Судя по названию, функция ПРОГНОЗ выглядит странным выбором. Казалось бы, это функция специально для экстраполяции; однако это также один из лучших вариантов линейной интерполяции в Excel.FORECAST использует все значения в наборе данных для оценки результата; поэтому он отлично подходит для линейных отношений, даже если они не полностью коррелированы.

Тогда еще одна мысль, а что, если отношения X и Y вообще не линейны? Как мы могли интерполировать значение, когда данные экспоненциальны?

Давайте рассмотрим все эти сценарии.

Интерполяция с использованием простой математики

Простая математика хорошо работает, когда есть только две пары чисел или когда отношения между X и Y совершенно линейны.

Вот базовый пример (см. Вкладку Пример 1 в вспомогательном файле загрузки):

Формула в ячейке E4:

 = B2 + (E2-A2) * (B3-B2) / (A3-A2)

Кому-то это может показаться немного сложным, поэтому вот краткий обзор формулы.

 = B2 + (E2-A2) *  (B3-B2) / (A3-A2)

В последнем разделе (выделенном зеленым цветом выше) вычисляется, насколько изменяется значение Y при изменении значения X на 1. В В нашем примере Y сдвигается на 1.67 для каждого 1 из X.

 = B2 +  (E2-A2) *  (B3-B2) / (A3-A2)

Второй раздел (выделенный зеленым цветом выше) вычисляет, как далеко интерполированный X отстоит от сначала X, затем умножается на вычисленное выше значение. В нашем примере результат рассчитывается как 17,5 (ячейка E2) минус 10 (ячейка A2), результат затем умножается на 1,67. Все это равно 12,5.

 =  B2 +  (E2-A2) * (B3-B2) / (A3-A2)

Наконец, мы переходим к первой части формулы (выделенной зеленым цветом выше), которая складывает первое значение Y.В нашем примере это дает окончательный результат 77,5 (65 + 12,5). Для тех, кто помнит математику в средней школе, формула будет следующей:

Вот результат, наложенный на диаграмму.

Даже если вы не помните линейную интерполяцию в школе, хорошая новость заключается в том, что Excel предоставил нам более простой вариант — функцию ПРОГНОЗ.

Formula Magic с динамическими массивами

Из всех функций, доступных в Excel, динамические массивы обеспечивают максимальную мощность при минимальных затратах времени.Однако большинство пользователей Excel даже не знают, что они собой представляют.

Вы когда-нибудь сталкивались с подобными сценариями работы с электронными таблицами?

Как я могу использовать ВПР для возврата всех совпадающих элементов , а не только первого?
Как отсортировать информацию по формуле , чтобы не нажимать кнопку сортировки постоянно?
Как я могу быстро создать уникальные списки элементов для использования с моим вычислением СУММЕСЛИМН?
Как я могу остановить копирование формул каждый раз, когда мои исходные данные меняются.
Как я могу создать отчет в виде сводной таблицы , но с использованием формул , чтобы мне больше не приходилось нажимать кнопку «Обновить».

Что ж, я здесь, чтобы сообщить вам хорошие новости. с динамическими массивами все это может быть легко достигнуто 🙂

Интерполяция с помощью функции ПРОГНОЗ

В версии Excel 2016 было добавлено множество новых статистических функций. Чтобы освободить место для этих новых функций, ПРОГНОЗ был заменен на ПРОГНОЗ.Линейная функция. Хотя ПРОГНОЗ остается на данный момент с целью обратной совместимости с Excel 2013 и ранее.

Поскольку FORECAST и FORECAST.LINEAR фактически одно и то же, мы будем использовать эти термины как синонимы.

Интерполяция при идеальной линейности

Теперь давайте воспользуемся ПРОГНОЗОМ для интерполяции результата.

Используя те же числа из приведенного выше примера, формула в ячейке E6:

 = ПРОГНОЗ (E2, B2: B3, A2: A3)

Функция ПРОГНОЗ имеет следующий синтаксис:

 = ПРОГНОЗ (x, известные_y, известные_x)

Три аргумента в функции:

x — точка данных, для которой мы хотим спрогнозировать значение
known_y’s — диапазон ячеек или массив значений содержащие известные значения Y
известные_x — диапазон ячеек или массив значений, содержащий известные значения X

При использовании функции ПРОГНОЗ результат ячейки E6 также равен 77.5 (как и в математическом подходе).

Для полноты картины файл примера также содержит использование функции FORECAST.LINEAR. Как и следовало ожидать, результат идентичен устаревшей функции ПРОГНОЗ.

Интерполяция, когда приблизительно линейна

Но … что, если наши данные не совсем линейны? Посмотрите на диаграмму ниже, данные явно имеют линейную зависимость, но она не идеальна. Посмотрите на вкладку Пример 2 во вспомогательном файле.

В этих обстоятельствах функция ПРОГНОЗ даже более полезна, поскольку она не просто интерполирует между первым и последним значениями.Вот данные, использованные в диаграмме.

Функция ПРОГНОЗ в ячейке E4 интерполирует значение Y на основе значения X, равного 17,5.

 = ПРОГНОЗ (E2, B2: B11, A2: A11)

В этом сценарии ПРОГНОЗ оценивает значение на основе всех доступных точек данных, а не только начала и конца. Результат функции ПРОГНОЗ в ячейке E4 равен 77,3 (округлено до 1 десятичного знака), что в большинстве случаев будет более точным, чем простая линейная интерполяция, применяемая в математическом подходе.

Помните, что для оценки значений используется интерполяция. 77.3 может быть неточным результатом, но это разумная оценка, основанная на имеющейся у нас информации.

И снова FORECAST.LINEAR вычисляет тот же результат.

Интерполяция, когда данные не линейны

Но вот более сложный вопрос: что, если данные вообще не линейны? Тогда что?

Посмотрите на вкладку Example 3 во вспомогательном файле. Вот наш новый сценарий графика:

Если бы мы использовали простой линейный подход, это дало бы нам значение 77.5, который, как вы можете видеть ниже, довольно далеко от кривой. Использование функции ПРОГНОЗ даст результат 70,8, что лучше, но также далеко от кривой.

Есть еще два варианта для получения более точной оценки (1) интерполяция экспоненциальных данных с помощью функции РОСТА (2) вычисление внутренней линейной интерполяции

Интерполировать экспоненциальные данные

Функция РОСТА аналогична ПРОГНОЗУ, но может применяться к данным с экспоненциальным ростом.

Результат функции РОСТ в ячейке E10 равен 70,4. Опять же, это ближе к черте, но все же немного дальше.

Формула в ячейке E10:

 = РОСТ (B2: B11, A2: A11, E2)

Функция РОСТ имеет следующий синтаксис:

 = РОСТ (известные_y, [известные_x], [новые_x] , [const])

Четыре аргумента в функции РОСТ (только имейте в виду, что аргументы не в том же порядке, что и функция ПРОГНОЗ).

known_y’s — диапазон ячеек или массив значений, содержащих известные значения Y
[известные_x] — диапазон ячеек или массив значений, содержащий известные значения X
[new_x’s] — точка данных, для которой мы хотим спрогнозировать значение
[Const] — мера истина / ложь, указывающая, как должна вычисляться формула. В нашем сценарии мы можем оставить этот последний аргумент.

Квадратные скобки указывают, какие аргументы являются необязательными для функции для вычисления результата.Нам нужны известные_y , известные_x, и новые_x , но мы проигнорировали аргумент const .

Хотя результат 70,4 является более близким приближением, мы не должны слепо использовать функцию РОСТ. Проверьте свои интерполяции, чтобы убедиться, что они разумны.

Внутренняя линейная интерполяция

Разумным вариантом может быть найти результат выше и ниже нового значения X, а затем применить линейную интерполяцию между этими двумя точками.Это было бы довольно близко.

В нашем примере значения по обе стороны от X, равного 17,5:

X: 16 и 18
Y: 66,3 и 68

Используя эти значения, теперь мы можем выполнить стандартную линейную интерполяцию. .

Быстрый одноразовый метод

Если бы это было разовое действие, мы могли бы сделать это быстро, включив в формулу только основные ячейки.

 = ПРОГНОЗ (E2, B6: B7, A6: A7)

Однако, как только мы изменим интерполированное значение, ПРОГНОЗ может вычислить неточный результат.Итак, давайте перейдем к рассмотрению гибкого метода.

Гибкий подход

Чтобы создать гибкий подход, мы будем использовать вместе функции ИНДЕКС, ПОИСКПОЗ и ПРОГНОЗ. Это может показаться сложным, но не волнуйтесь, мы рассмотрим это медленно. В конечном итоге мы пытаемся достичь того же результата, что и описанный выше одноразовый метод, но автоматически корректируем диапазоны в зависимости от интерполируемого значения.

ПРИМЕЧАНИЕ. Для работы этого метода требуется, чтобы диапазон известных X был указан в порядке возрастания.

Функция ПОИСКПОЗ

Во-первых, мы используем функцию ПОИСКПОЗ, чтобы получить позицию значения ниже 17,5.

 = ПОИСКПОЗ (E2, A2: A11,1)

Эта формула говорит, что найдите значение в ячейке E2 из диапазона ячеек A2-A11. 1 в конце формулы сообщает функции ПОИСКПОЗ, что мы хотим использовать приблизительное совпадение (т. Е. Ближайшее значение ниже искомого значения). 16 — ближайшее значение ниже 17,5. Поскольку 16 — это 5-й элемент в ячейках A2-A11, ПОИСКПОЗ возвращает значение 5.

ИНДЕКС функция

Определив на предыдущем этапе, что пятая позиция содержит значение ниже, мы можем использовать функцию ИНДЕКС, чтобы определить ссылку на ячейку для этого значения.

 ИНДЕКС (A2: A11, MATCH (E2, A2: A11,1))

Это вернет ссылку на ячейку A6.

Чтобы найти указанное выше значение, мы можем использовать ту же функцию, но добавить 1 к функции ПОИСКПОЗ.

 ИНДЕКС (A2: A11, ПОИСКПОЗ (E2, A2: A11,1)  +1 )

Приведенная выше формула вернет ссылку на ячейку A7.

Динамический диапазон

Теперь все становится интереснее. Мы можем объединить эти функции с двоеточием (:) в середине, чтобы создать диапазон для двух значений X.

  ИНДЕКС (A2: A11, ПОИСКПОЗ (E2, A2: A11,1)): ИНДЕКС (A2: A11, ПОИСКПОЗ (E2, A2: A11,1) +1)

Первая функция ИНДЕКС возвращает ссылку в ячейку A6 (результат выделенного зеленым цветом раздела). Вторая функция ИНДЕКС возвращает ссылку на ячейку A7 (результат выделенного фиолетовым цветом раздела).Они разделены двоеточием (:) (выделены красным), чтобы создать диапазон — A6: A7

Мы можем сделать то же самое, чтобы создать диапазон для двух значений Y. Единственная разница в том, что функции ИНДЕКС будут смотреть на ячейки B2-B11.

 ИНДЕКС (B2: B11, ПОИСКПОЗ (E2, A2: A11,1)): ИНДЕКС (B2: B11, ПОИСКПОЗ (E2, A2: A11,1) +1)

Используя ячейки B2-B11 в ИНДЕКСЕ функция, она вычислит диапазон B6: B7.

ИНДЕКС СООТВЕТСТВИЕ И ПРОГНОЗ

Теперь у нас есть два диапазона; значения X A6: A7 и значения Y B6: B7.Давайте объединим все это в функции ПРОГНОЗ.

 = ПРОГНОЗ (E2,
ИНДЕКС (B2: B11; ПОИСКПОЗ (E2; A2: A11,1)): ИНДЕКС (B2: B11; ПОИСКПОЗ (E2; A2: A11,1) +1),
ИНДЕКС (A2: A11, MATCH (E2, A2: A11,1)): INDEX (A2: A11, MATCH (E2, A2: A11,1) +1))

Это довольно большая формула, верно. Но, надеюсь, мне удалось объяснить это так, что это не слишком страшно.

Результат внутренней линейной интерполяции с использованием функции ПРОГНОЗ составляет 67,6 (с точностью до 1 десятичного знака, показан в ячейке E14). Взгляните на график еще раз; вы увидите, что 67.6 — разумная оценка, основанная на имеющихся данных.

ПРЕДУПРЕЖДЕНИЕ. В конечном счете, это все еще вычисление линейной интерполяции, основанное на двух значениях по обе стороны от значения X. Расстояние между значениями выше и ниже будет иметь прямое влияние на точность интерполяции.

Заключение

Первоначально то, что казалось простым вопросом, привело нас к множеству потенциальных решений для трех различных сценариев. Ключевым моментом является то, что вам необходимо знать свои данные, чтобы выбрать метод, обеспечивающий наиболее точные результаты.

В процессе мы рассмотрели функции FORECAST и FORECAST.LINEAR и убедились, что они полезны как для интерполяции, так и для экстраполяции.

Кроме того, в этом посте мы использовали ИНДЕКС и ПОИСКПОЗ для создания динамических диапазонов, что является очень мощным методом для сложных формул в Excel.

Если вам нужна дополнительная информация о методах прогнозирования в Excel, загляните в Engineer Excel (https://engineerexcel.com/blog). Хотя вы, возможно, не работаете в инженерном контексте, методы применимы во многих других обстоятельствах.

Получите нашу БЕСПЛАТНУЮ электронную книгу на VBA с 30 наиболее полезными макросами Excel VBA.
Автоматизируйте Excel, чтобы сэкономить время и перестать выполнять ту работу, которую могла бы выполнять обученная обезьяна.

Вводя свой адрес электронной почты, вы соглашаетесь получать электронные письма от Excel Off The Grid. Мы будем уважать вашу конфиденциальность, и вы можете отказаться от подписки в любое время.

Не забудьте:

Если вы нашли этот пост полезным или у вас есть лучший подход, оставьте комментарий ниже.

Вам нужна помощь в адаптации этого к вашим потребностям?

Я полагаю, что примеры в этом посте не совсем соответствуют вашей ситуации. Все мы используем Excel по-разному, поэтому невозможно написать сообщение, которое удовлетворит потребности всех. Потратив время на то, чтобы понять методы и принципы, описанные в этом посте (и в других местах на этом сайте), вы сможете адаптировать их к своим потребностям.

Но, если вы все еще боретесь, вам следует:

Прочитать другие блоги или посмотреть видео на YouTube на ту же тему.Вы получите гораздо больше пользы, открыв свои собственные решения.
Спросите «Excel Ninja» в своем офисе. Удивительно то, что знают другие люди.
Задайте вопрос на форуме, например в Mr Excel, или в сообществе ответов Microsoft. Помните, что люди на этих форумах обычно проводят свое время бесплатно. Так что постарайтесь сформулировать свой вопрос, сделайте его ясным и кратким. Составьте список всего, что вы пробовали, и предоставьте снимки экрана, фрагменты кода и примеры рабочих книг.
Воспользуйтесь Excel Rescue, моим партнером-консультантом.Они помогают, предлагая решения небольших проблем с Excel.

Что дальше?
Не уходите, есть еще много чего узнать об Excel Off The Grid. Ознакомьтесь с последними сообщениями:

LinearSplineInterpolate — LinearSplineInterpolate — LinearSplineInterpolate — LinearSplineInterpolate

1	Конвертер	Преобразует число из одной системы измерения в другую.
2	SG2API	SG2API — Преобразует удельную плотность масла в плотность API
3	API2SG	API2SG — Преобразует плотность в градусах API в удельный вес нефти (вода = 1.0)
4	Данные	Производная для выборок данных в точке t со сглаживанием.
5	ExpIntegralEi	ExpIntegralEi — экспоненциальная интегральная функция — Ei (x)
6	Проксимальный	ProximalInterpolate — Алгоритм проксимальной (ближайшего соседа) интерполяции.Интерполировать в точке t.
7	CubicSplineInterpolate	Естественный кубический сплайн с непрерывной второй производной внутри и нулевой второй производной в конечных точках.Интерполировать в точке t.
8	CubicSpline	Естественный кубический сплайн с непрерывной второй производной внутри и нулевой второй производной в конечных точках.Дифференцируйте в точке t.
9	CubicSplineИнтегрировать	Естественный кубический сплайн с непрерывной второй производной внутри и нулевой второй производной в конечных точках.Интегрируйте до точки t.
10	CubicSplineIntegrateT1T2	Естественный кубический сплайн с непрерывной второй производной внутри и нулевой второй производной в конечных точках.Проинтегрируем от точки t1 до точки t2.
11	КубическиеСплайныПересечение	x значение точки пересечения двух кубических шлицев.
12	LinearSplineInterpolate	LinearSplineInterpolate — LinearSplineInterpolate — LinearSplineInterpolate — LinearSplineInterpolate — LinearSplineInterpolate — Алгоритм интерполяции линейного сплайна.Интерполировать в точке t.
13	Линейный	Алгоритм интерполяции линейным сплайном. Дифференцируйте в точке t.
14	Линейный	LinearSplineIntegrate — алгоритм интерполяции линейного сплайна.Интегрируйте до точки t.
15	LinearSplineIntegrateT1T2	Алгоритм интерполяции линейным сплайном. No related posts. Навигация по записям Предыдущая статьяПримеры решения тригонометрических уравнений примеры с ответами – Тригонометрические уравнения. Подготовка к ЕГЭ по математике. Следующая статьяКарточки таблица умножения на 9 и 8 – Материал (2 класс) на тему: Карточки для проверки таблицы умножения и деления на 2,3,4,5,6,7,8,9. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Найти: Рубрики Геометрия Математика Физика Химия Школьная жизнь Разное © 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа» Карта сайта