Линейные неравенства калькулятор: Решение неравенств с модулем онлайн · Как пользоваться Контрольная Работа РУ

Инженерный калькулятор Casio FX-991CEX, цена 1659 грн — Prom.ua (ID#1240984308)

К сожалению, товар недоступен. Купить калькуляторы вы можете у других продавцов.

Характеристики и описание

• Основные

  • Производитель

    Casio

  • Вид

    Карманный

  • Гарантийный срок

    24 мес

Интегралы, Операции над дробями, Гиперболические функции, Функции распределения, Преобразование систем счисления, Преобразование систем координат, Преобразование координат, Квадраты чисел, кубы и степени с любым показателем, Обратное число, Комплексные числа, Десяточные логарифмы, Натуральные логарифмы, Логарифмы какой основы, Матрицы, Минимальная/максимальная квадратическая функция, Линейные неравенства, Корни, Проценты, Решение уравнений, Тригонометрические, Абсолютное значение, Отображение результатов в формате иррациональных чисел

Производитель:	Casio
Тип:	Инженерный калькулятор
Разрядность, бит:	нет данных
Питание:	ААА+солнечная батарея
Звук клавиатуры:	нет
Подсветка экрана:	нет данных
Удаление последнего введенного символа:	есть
Габариты, мм:	77 х 165,5 х 11,1
Масса, г:	90
Дополнительно:	Более 600 функций, поддержка QR-кода

 

 

Код: 162005

Недоступен

1 659  грн

Популярные производители в категории Калькуляторы

Citizen

Brilliant

Keenly

Assistant

Optima

Daymon

Nobrand

Color-it

У нас покупают

Комплектующие для систем видеонаблюдения

Офисные и компьютерные кресла

Тепловое оборудование horeca&fast-food

Профессиональные кофемашины

Блоки питания

Источники бесперебойного питания (ибп)

Профессиональные тренажеры

Экспресс-тесты

Сетевые накопители

Оборудование и материалы для салонов красоты

Шредеры

Оборудование для автомоек

Аппараты высокого давления

Камеры видеонаблюдения

Оборудование для мероприятий и клубов

Упаковочное оборудование

Кассовое/прикассовое оборудование

Принтеры этикеток, штрихкодов, чеков

Точки доступа

Лабораторное оборудование

ТОП теги

Калькуляторы

Брилиантс

Настольные калькуляторы brilliant

Инженерные калькуляторы casio

Инженерные калькуляторы brilliant

Магнитный кабель синхронизации

Калькулятор eates dc-990

Насколько вам
удобно на проме?

линейные, квадратные и дробные.

Выражения через гиперболические функции

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .

Дискриминант

Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D
2. Если D = 0, есть ровно один корень;
3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x 2 − 8x + 12 = 0;
2. 5x 2 + 3x + 7 = 0;
3. x 2 − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

1. x 2 − 2x − 3 = 0;
2. 15 − 2x − x 2 = 0;
3. x 2 + 12x + 36 = 0.

Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x 2 + 9x = 0;
2. x 2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c /a )

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x 2 − 7x = 0;
2. 5x 2 + 30 = 0;
3. 4x 2 − 9 = 0.

x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.

5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.

Рассмотрим функцию y=k/y. Графиком этой функции является линия, называемая в математике гиперболой. Общий вид гиперболы, представлен на рисунке ниже. (На графике представлена функция y равно k разделить на x, у которой k равно единице.)

Видно, что график состоит из двух частей. Эти части называют ветвями гиперболы. Стоит отметить также, что каждая ветвь гиперболы подходит в одном из направлений все ближе и ближе к осям координат. Оси координат в таком случае называют асимптотами.

Вообще любые прямые линии, к которым бесконечно приближается график функции, но не достигает их, называются асимптотами. У гиперболы, как и у параболы, есть оси симметрии. Для гиперболы, представленной на рисунке выше, это прямая y=x.

Теперь разберемся с двумя общими случаями гипербол. Графиком функции y = k/x, при k ≠0, будет являться гипербола, ветви которой расположены либо в первом и третьем координатных углах, при k>0, либо во втором и четвертом координатных углах, при k

Основные свойства функции y = k/x, при k>0

График функции y = k/x, при k>0

5. y>0 при x>0; y6. Функция убывает как на промежутке (-∞;0), так и на промежутке (0;+∞).

10. Область значений функции два открытых промежутка (-∞;0) и (0;+∞).

Основные свойства функции y = k/x, при k

График функции y = k/x, при k

1. Точка (0;0) центр симметрии гиперболы.

2. Оси координат — асимптоты гиперболы.

4. Область определения функции все х, кроме х=0.

5. y>0 при x0.

6. Функция возрастает как на промежутке (-∞;0), так и на промежутке (0;+∞).

7. Функция не ограничена ни снизу, ни сверху.

8. У функции нет ни наибольшего, ни наименьшего значений.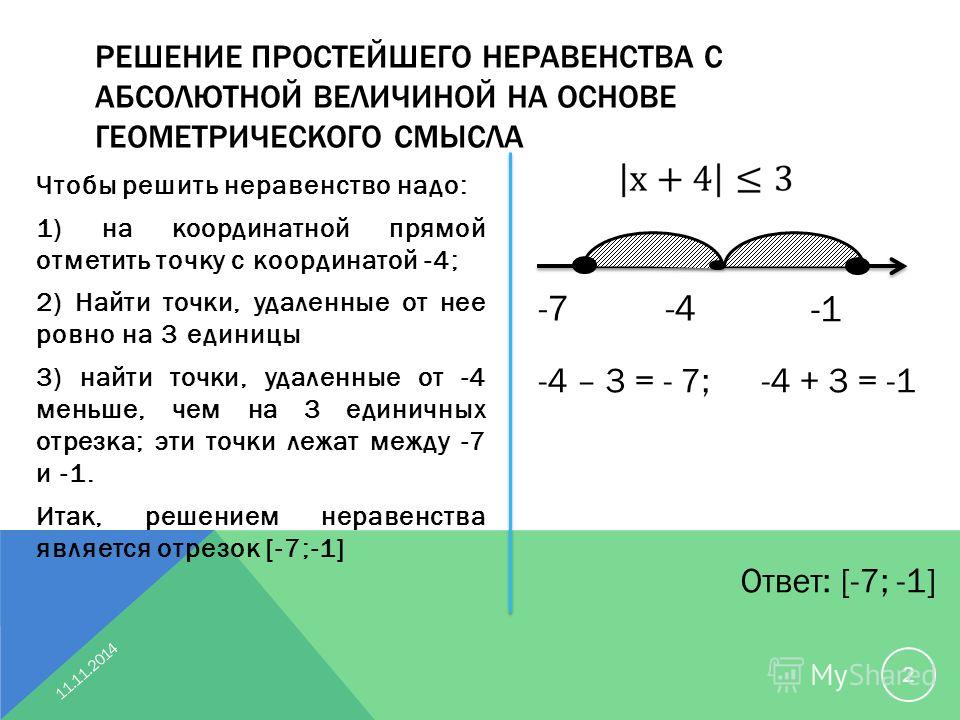

9. Функция непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.

На канал на youtube нашего сайта сайт, чтобы быть в курсе всех новых видео уроков.

Для начала вспомним основные формулы степеней и их свойства.

Произведение числа a само на себя происходит n раз, это выражение мы можем записать как a a … a=a n

1. a 0 = 1 (a ≠ 0)

3. a n a m = a n + m

4. (a n) m = a nm

5. a n b n = (ab) n

7. a n /a m = a n — m

Степенные или показательные уравнения – это уравнения в которых переменные находятся в степенях (или показателях), а основанием является число.

Примеры показательных уравнений:

В данном примере число 6 является основанием оно всегда стоит внизу, а переменная x степенью или показателем.

Приведем еще примеры показательных уравнений.
2 x *5=10
16 x — 4 x — 6=0

Теперь разберем как решаются показательные уравнения?

Возьмем простое уравнение:

2 х = 2 3

Такой пример можно решить даже в уме. Видно, что x=3. Ведь чтобы левая и правая часть были равны нужно вместо x поставить число 3.
А теперь посмотрим как нужно это решение оформить:

2 х = 2 3
х = 3

Для того, чтобы решить такое уравнение, мы убрали одинаковые основания (то есть двойки) и записали то что осталось, это степени. Получили искомый ответ.

Теперь подведем итоги нашего решения.

Алгоритм решения показательного уравнения:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем степени и решаем полученное новое уравнение.

Теперь прорешаем несколько примеров:

Начнем с простого.

Основания в левой и правой части равны числу 2, значит мы можем основание отбросить и приравнять их степени.

x+2=4 Получилось простейшее уравнение.
x=4 — 2
x=2
Ответ: x=2

В следующем примере видно, что основания разные это 3 и 9.

3 3х — 9 х+8 = 0

Для начала переносим девятку в правую сторону, получаем:

Теперь нужно сделать одинаковые основания. Мы знаем что 9=3 2 . Воспользуемся формулой степеней (a n) m = a nm .

3 3х = (3 2) х+8

Получим 9 х+8 =(3 2) х+8 =3 2х+16

3 3х = 3 2х+16 теперь видно что в левой и правой стороне основания одинаковые и равные тройке, значит мы их можем отбросить и приравнять степени.

3x=2x+16 получили простейшее уравнение
3x — 2x=16
x=16
Ответ: x=16.

Смотрим следующий пример:

2 2х+4 — 10 4 х = 2 4

В первую очередь смотрим на основания, основания разные два и четыре. А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (a n) m = a nm .

4 х = (2 2) х = 2 2х

И еще используем одну формулу a n a m = a n + m:

2 2х+4 = 2 2х 2 4

Добавляем в уравнение:

2 2х 2 4 — 10 2 2х = 24

Мы привели пример к одинаковым основаниям. Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 2 2х,вот и ответ — 2 2х мы можем вынести за скобки:

2 2х (2 4 — 10) = 24

Посчитаем выражение в скобках:

2 4 — 10 = 16 — 10 = 6

Все уравнение делим на 6:

Представим 4=2 2:

2 2х = 2 2 основания одинаковые, отбрасываем их и приравниваем степени.
2х = 2 получилось простейшее уравнение. Делим его на 2 получаем
х = 1
Ответ: х = 1.

Решим уравнение:

9 х – 12*3 х +27= 0

Преобразуем:
9 х = (3 2) х = 3 2х

Получаем уравнение:
3 2х — 12 3 х +27 = 0

Основания у нас одинаковы равны трем.В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить методом замены . Число с наименьшей степенью заменяем:

Тогда 3 2х = (3 х) 2 = t 2

Заменяем в уравнении все степени с иксами на t:

t 2 — 12t+27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D=144-108=36
t 1 = 9
t 2 = 3

Возвращаемся к переменной x .

Берем t 1:
t 1 = 9 = 3 х

Стало быть,

3 х = 9
3 х = 3 2
х 1 = 2

Один корень нашли. Ищем второй, из t 2:
t 2 = 3 = 3 х
3 х = 3 1
х 2 = 1
Ответ: х 1 = 2; х 2 = 1.

На сайте Вы можете в разделе ПОМОГИТЕ РЕШИТЬ задавать интересующие вопросы мы Вам обязательно ответим.

Вступайте в группу

y(x) = e x , производная которой равна самой функции.

Экспоненту обозначают так , или .

Число e

Основанием степени экспоненты является число e . Это иррациональное число. Оно примерно равно
е ≈ 2,718281828459045…

Число e определяется через предел последовательности. Это, так называемый, второй замечательный предел :
.

Также число e можно представить в виде ряда:
.

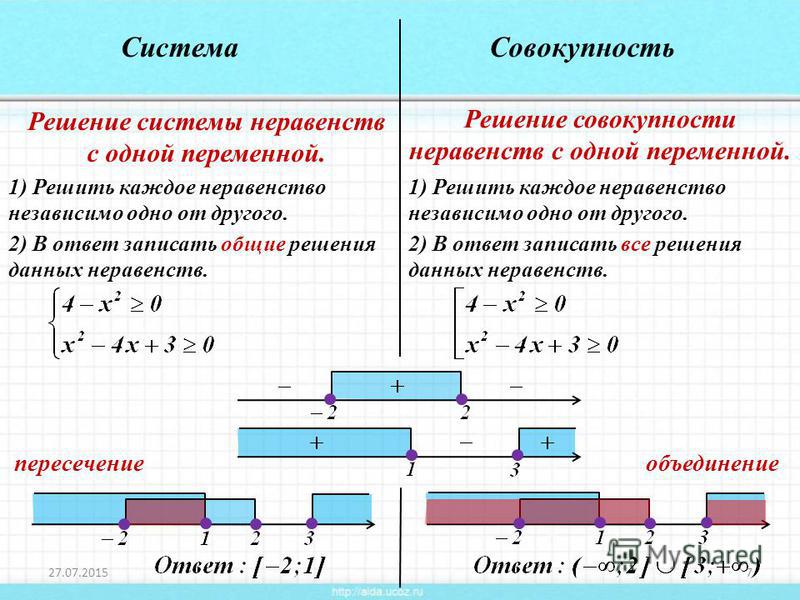
График экспоненты

График экспоненты, y = e x .

На графике представлена экспонента, е в степени х .
y(x) = е х
На графике видно, что экспонента монотонно возрастает.

Формулы

Основные формулы такие же, как и для показательной функции с основанием степени е .

;
;
;

Выражение показательной функции с произвольным основанием степени a через экспоненту:
.

Частные значения

Пусть y(x) = e x . Тогда
.

Свойства экспоненты

Экспонента обладает свойствами показательной функции с основанием степени е > 1 .

Область определения, множество значений

Экспонента y(x) = e x определена для всех x .
Ее область определения:
— ∞ Ее множество значений:
0

Экстремумы, возрастание, убывание

Экспонента является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.

Обратная функция

Обратной для экспоненты является натуральный логарифм .
;
.

Производная экспоненты

Производная е в степени х равна е в степени х :
.
Производная n-го порядка:
.
Вывод формул > > >

Интеграл

Комплексные числа

Действия с комплексными числами осуществляются при помощи формулы Эйлера :
,
где есть мнимая единица:
.

Выражения через гиперболические функции

; ;
.

Выражения через тригонометрические функции

; ;
;
.

Разложение в степенной ряд

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Combined inequality solver

 

• Expression
• Equation
• Inequality
• Contact us

• Simplify
• Factor
• Expand
• GCF
• LCM

• Solve
• Graph
• System

• Решение
• График
• Система

• Математический решатель на вашем сайте

комбинированный решатель неравенства
Похожие темы:
алгебра решатель скачать за деньги | расширяющие алгебраические выражения | mcdougal littell алгебра 1 ответ | как решать одновременные нелинейные дифференциальные уравнения | калькулятор линейных уравнений | листы с вопросами по математике | калькулятор эллипса

Автор	Сообщение
тджхон Зарегистрирован: 10. 08.2001 Откуда: На поу-стике вон там.	Размещено: вторник, 21 августа, 08:47. комбинированный решатель неравенства — моя самая большая проблема. Может ли кто-нибудь помочь мне понять это? Я новичок в этом. Какую книгу или другой источник вы предлагаете для начала этого предмета?
Наверх
Вофий Тимидов Дата регистрации: 06. 07.2001 Откуда: Болгария	Размещено: Среда, 22 августа, 16:20 Вам действительно не стоило тратить деньги на репетитора по математике. Если бы вы разместили это сообщение до того, как наняли одного из них, вы могли бы сэкономить кучу денег! В любом случае, что сделано, то сделано. Теперь, чтобы убедиться, что вы хорошо сдаете экзамены, я бы рекомендовал попробовать Algebrator. Это очень простое в использовании программное обеспечение. Он может решить действительно сложные проблемы за вас, и что еще круче, так это то, что он даже может объяснить, как он это сделал! В какой-то момент даже у меня возникли трудности с пониманием х-перехвата, трехчлена идеального квадрата и радикальных уравнений. Но благодаря Algebrator теперь все хорошо.
Наверх
Эш Дата регистрации: 08.07.2001 От:	Размещено: Пятница, 24 августа, 08:39 Я всегда использую Алгебратор, чтобы помочь мне с моими домашними заданиями по математике. Я пробовал несколько других программ, но пока это лучшее, что я видел. Я предполагаю, что именно несложный способ объяснения решения проблем делает весь процесс таким легким. Это действительно очень хорошая программа, и я могу за нее поручиться.
Наверх
daujk_vv7 Зарегистрирован: 06.07.2001 От кого: Не знаю, потерял.	Размещено: Воскресенье, 26 августа, 10:32 Помню, у меня были трудности с корнями, сложением дробей и геометрией. Algebrator — действительно отличная программа для алгебры. Я использовал его на нескольких математических занятиях — алгебре 2, алгебре 2 и алгебре 1. Я просто вводил задачу из рабочей тетради, и, нажимая «Решить», появлялось пошаговое решение. Программа настоятельно рекомендуется.
Наверх

Графический калькулятор по MathLab: Руководство пользователя

Поиск

ВВЕДЕНИЕ
Pro Features против бесплатной версии
Часто задаваемые вопросы, FAQS

1.1 Navigation
1.2 Element , Кнопки Clear и UNDO
1.5 Рабочая область
1.6 Редактирование выражений/уравнений
1.7 Использование последнего ответа
1,8 Запись Комментарии
1.9 Очистка, Комиссия Копии и Вставки
1.10 РАСПРАВЛЕНИЯ РЕЗНИКИ

2. 1 Общие
2.2 Калькулятор
2.3. График

3.1 Константы
3.2. Результаты расчетов/графики в библиотеку

4.1 2D-графики
4.2 3D-графики
4.3 Увеличение области графика
4.4 Изменение фона на белый
4.5 Скрыть клавиатуру
4.6 Градусная или радианная шкала
4.7 Фиксированная шкала
4.8 Шкала по оси R
4.9 Логарифмическая шкала
4.10 Отслеживание значений и наклонов графиков
4.11 Специальные точки: корни и критические точки
4.12 Пересечения графиков
Пересечения
4.15 Полноэкранный режим

5.1 Совместное использование функций
5.2 2D-таблица
5.3 3D-таблица
5.4 Функции редактирования
5.5 Прокрутка результатов
5.6 Результаты Точность
5.7 Управление масштабированием 90800047 5.9 Таблица тригонометрических функций в градусах

6.1 Десятиц
6.2 Фракции
6,3 Пресцены
6,4 Научная нотация
6,5 Инженерная нотация
6,6 Закругление
6. 7 Интехновые и фракционные части
6.8 Заказ Операции
6,97 6.7. Делитель
6.11 Модуль
6.12 Двоичные, восьмеричные, десятичные, шестнадцатеричные числа
6.13 Комплексные числа
6.14 Полярная форма комплексных чисел
6.15 Полярно-прямоугольные координаты

7.1 Arithmetic Operations
7.2 Exponents
7.3 Absolute Values ​​
7.4 Variables
7.5 Evaluating Expressions
7.6 Polynomials
7.7 Roots
7.8 Logarithms

8.1 Linear Equation
8.2 Absolute Value Equation
8.3 Quadratic Equation
8.4 Cubic Equation
8.5 Polynomial Уравнение
8.6 Рациональное уравнение
8.7 Радикальное уравнение
8.8 Показательное уравнение
8.9 Логарифмическое уравнение

9.1 Символы неравенства
9.2 Linear Inequality
9.3 Absolute Value Inequality
9.4 Quadratic Inequality
9.5 Polynomial Inequality
9.6 Rational Inequality
9.7 Compound Inequalities
9. 8 Inequalities with Constants

10.1 Linear Equations
10.2 Systems of Linear Equations
10.3 Graphing Inequalities
10.4 Multiple Graphing неравенств
10.5 Графики систем неравенств
10.6 Решение неявных уравнений

11.1 Построение точек
11.2 Как построить график функций?
11,3 Установка прикладного домена
11,4 Линейная функция
11,5 Функция абсолютного значения
11,6 квадратичная функция
11,7 Полиномиальная функция
11,8 Рациональная функция
11,9 Радикальная функция
11.10 Логариритмическая функция
11.11 Эксп. Функция
11.10 1100 FINDIN Функция -wise

12.1 Операции с матрицами
12.2 Редактирование записей матрицы
12.3 Переменные матрицы
12.4 Матричные и векторные формы
12.5 Преобразование матрицы переменных в систему линейных уравнений
12.6 Решение систем линейных уравнений с использованием матричных уравнений

13.1 Градусы и радианы
13. 2 Тригонометрические функции и ее кратные
13.6 График тригонометрической функции
13.7 График гиперболической функции
13.8 График обратной функции

14.1 Конические сечения
14,2 Параметрические уравнения
14,3 Полярные графики
14,4 3D График

15,1 Правый предел
15,2 Левый предел
15,3 Предел функции
15,4 Предел полинома
15,5 Предел предела реля
15.6 15.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6.6 15.6. a Радикальная функция
15.7 Предел функции абсолютного значения
15.8 Предел тригонометрической функции
15.9 Предел экспоненциальной и логарифмической функций
15.10 Предел кусочной функции
15.11 Пределы на бесконечности
15.12 Неопределенные формы
15.13 Предел гиперболической функции

16.1 Ключ первого производного
16.2 Второй производной ключ
16,3 Третий и более высокий производный ключи
16,4 Правила дифференцировки
16,5 Производители. Тригонометрические, логарифмические и экспоненциальные функции
16.8 Дополнительные сведения о производных

17.1 Приращения
17.2 Производная функции df (или dy)
17,3 Производная функция DF (f не в терминах x)
17,4 Частичные производные
17,5 Частичные производные более высокого порядка
17,6 Общая производные

18,1 Неопределенные интегралы
18,2 Определенные интегралы

19.1 Суммирование Новация
19.2. и максимум
19,4 Факториал, nCr и nPr
19,5 Показатели центральной тенденции
19,6 Показатели изменчивости
19,7 Показатели положения
19,8 Двумерный анализ данных

20,1 Гамма -функция
20.2 Логарифмическая гамма -функция
20,3 Функция Digamma

21,1 Арифметика
21,2 Алгебра
21,3 Тригонометрия
21,4 Статистика
21,5 Calculus
900337

9141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414147.