Письменный. 2 курс Сборник задач по высшей математике.
Письменный Д.Т. Лунгу К.Н.
На сайте Класс.Москва вы можете прочитать гдз, решебник и ответы для — Письменный. 2 курс Сборник задач по высшей математике., часть №1 бесплатно.
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580 581 582 583 584 585 586 587 588 589 590 591 592 ♥♥♥♥
← ТудаСюда →
Поиск материала «Сборник задач по высшей математике, 2 курс, Лунгу К.
 Н., Норин В.П., 2007» для чтения, скачивания и покупки
Н., Норин В.П., 2007» для чтения, скачивания и покупкиНиже показаны результаты поиска поисковой системы Яндекс. В результатах могут быть показаны как эта книга, так и похожие на нее по названию или автору.
Search results:
- Сборник задач по высшей математике. 2 курс — Лунгу…
Книга является второй частью вышедшего ранее и выдержавшего несколько изданий «Сборника задач по высшей математике».
Сборник содержит три с лишним тысячи задач по высшей математике, охватывая материал, обычно изучаемый во II—IV семестрах технических вузов.
11klasov.net
- Книга Сборник задач по высшей математике. 2 курс (Лунгу…)
2 курс» — читать интересную книгу автора (Лунгу К.
Н., Норин В.П., Письменный Д.Т.
bookree.org
-
Купить эту книгу
- Канцтовары
Канцтовары: бумага, ручки, карандаши, тетради. Ранцы, рюкзаки, сумки. И многое другое.
my-shop.ru
- Сборник задач по высшей математике. 2 курс — Лунгу…
Школьные учебники / Презентации по предметам » Математика » Сборник задач по высшей математике. 2 курс — Лунгу К.Н., Норин В.П. и др.
Сборник содержит три с лишним тысячи задач по высшей математике, охватывая материал, обычно изучаемый во II—IV семестрах технических вузов.
psschool.ru
- Сборник задач по
 2 курс
2 курсКнига является второй частью вышедшего ранее и выдержавшего несколько изданий «Сборника задач по высшей математике».
Этому способствуют необходимые теоретические пояснения ко всем разделам сборника, детально разобранные типовые задачи, изрядное количество разнообразных заданий различных уровней сложности для самостоятельного решения, а также наличие контрольных работ, устных задач и «качественных» вопросов.
lib.agu.site
- Сборник задач по высшей математике. 2 курс | Лунгу…
Книга является второй частью вышедшего ранее и выдержавшего несколько изданий «Сборника задач по высшей математике».
Этому способствуют необходимые теоретические пояснения ко всем разделам сборника, детально разобранные типовые задачи, изрядное количество разнообразных заданий различных уровней сложности для самостоятельного решения, а также наличие контрольных работ, устных задач и «качественных» вопросов.

libcats.org
- Лунгу К.Н., Норин В.П., Письменный Д.Т. и др. Сборник задач по…
Книга содержит упражнения по курсу «Высшая математика» для студентов I и II курсов естественных факультетов государственных университетов, где на преподавание математики отводится до 200 учебных часов. Некоторые задачи, включенные в сборник заимствованы из различных распространенных сборников задач по высшей математике, в частности, из «Сборнике задач и упражнений по математическому анализу» Б. П. Демидовича и «Сборника задач по высшей математике…
www.studmed.ru
- Лунгу К.Н., Норин В.П., Письменный Д.Т., Шевченко…
Книга содержит упражнения по курсу «Высшая математика» для студентов I и II курсов естественных факультетов государственных университетов, где на преподавание математики отводится до 200 учебных часов.
 Некоторые задачи, включенные в сборник заимствованы из различных распространенных сборников задач по высшей математике, в частности, из «Сборнике задач и упражнений по математическому анализу» Б. П. Демидовича и «Сборника задач по высшей математике…
Некоторые задачи, включенные в сборник заимствованы из различных распространенных сборников задач по высшей математике, в частности, из «Сборнике задач и упражнений по математическому анализу» Б. П. Демидовича и «Сборника задач по высшей математике…www.studmed.ru
- Письменный. 2 курс читать онлайн сборник задач по высшей …
Название: Сборник задач по высшей математике. Язык: только русский. Автор: Письменный Д. Т. Лунгу К. Н. Размер: 48 Страниц: 489 Год: 2007 Письменный. 2 ку.
Д. Т. Письменный, К. Н. Лунгу «Сборник задач по высшей математике с контрольными работами» 2 курс. Сборник подойдет для самостоятельной подготовки студентов к экзаменам. Перед каждым разделом сборника представлен теоретический материал и подробное решение типовых задач.
gdz-online.ws
- MATEMATIKA 2 ( Сборник задач по высшей математике часть.
 ..
..MATEMATIKA 2 ( Сборник задач по высшей математике часть 2 К.Н Лунг ,В .П. Норин , Д.Т…
archive.org
- Лунгу
Книга содержит упражнения по курсу «Высшая математика» для студентов I и II курсов естественных факультетов государственных университетов, где на преподавание математики отводится до 200 учебных часов. Некоторые задачи, включенные в сборник заимствованы из различных распространенных сборников задач по высшей математике, в частности, из «Сборнике задач и упражнений по математическому анализу» Б. П. Демидовича и «Сборника задач по высшей математике…
www.studmed.ru
- Сборник задач по высшей математике. 2 курс.
 Лунгу…
Лунгу…Сборник содержит три с лишним тысячи задач по высшей математике, охватывая материал, обычно изучаемый во II—IV семестрах технических вузов.
Этому способствуют необходимые теоретические пояснения ко всем разделам сборника, детально разобранные типовые задачи, большое количество разнообразных заданий различных уровней сложности для самостоятельного решения, а также наличие контрольных работ, устных задач и «качественных» вопросов.
alleng.net
- Сборник задач по высшей алгебре
Этот задачник предназначен для студентов физико-математического факультета педагогических институтов и содержит задачи, посвященные теории определителей, общей теории систем линейных уравнений с несколькими неизвестными, теории матриц, группам, кольцам и полям, комплексным числам, многочленам от одного неизвестного, алгебраическим расширениям и решениям алгебраических уравнений в квадратных радикалах, теории симметрических многочленов и теории исключения.

lib.agu.site
- Сборник задач по высшей математике. 2 курс. Лунгу… — alleng.me
Сборник содержит три с лишним тысячи задач по высшей математике, охватывая материал, обычно изучаемый во II—IV семестрах технических вузов.
Этому способствуют необходимые теоретические пояснения ко всем разделам сборника, детально разобранные типовые задачи, большое количество разнообразных заданий различных уровней сложности для самостоятельного решения, а также наличие контрольных работ, устных задач и «качественных» вопросов.
uchebniki.alleng.me
- Сборник задач по высшей математике. 2 курс. Лунгу… — alleng.me
Сборник содержит три с лишним тысячи задач по высшей математике, охватывая материал, обычно изучаемый во II—IV семестрах технических вузов.

Этому способствуют необходимые теоретические пояснения ко всем разделам сборника, детально разобранные типовые задачи, большое количество разнообразных заданий различных уровней сложности для самостоятельного решения, а также наличие контрольных работ, устных задач и «качественных» вопросов.
alleng.alleng.me
- Сборник задач по высшей математике
Предлагаемый вашему вниманию сборник задач охватывает традиционный курс высшей математики в объеме первого курса технического вуза. Книга подготовлена преподавателями нескольких московских вузов, имеющими многолетний опыт лекционной и семинарской работы со студентами. Опираясь на этот опыт, а также учитывая достоинства и недостатки существующих пособий, авторы попытались создать в каком-то смысле универсальный задачник, пригодный как для самообразования, так и для активной работы с преподавателем на практических занятиях.

studfile.net
- Сборник задач по высшей математике. 2 курс | Лунгу…
2 курс. Лунгу К. Н., Письменный Д. Т., Федин С. Н., Шевченко Ю. А. Скачать книгу бесплатно (djvu, 4.10 Mb). Читать «Сборник задач по высшей математике. 2 курс ».
libcats.org
- Лунгу К.Н., Норин В.П. и др. Сборник задач по высшей…
Автор: Лунгу К.Н., Норин В.П. и др. Название: Сборник задач по высшей математике. 2 курс Формат: PDF Размер: 5,95 Мб Язык: Русский.
Книга является второй частью вышедшего ранее и выдержавшего несколько изданий «Сборника задач по высшей математике». Сборник содержит три с лишним тысячи задач по высшей математике, охватывая материал, обычно изучаемый во II—IV семестрах технических вузов.

www.psyoffice.ru
- Сборник задач по высшей математике. 2 курс — Лунгу…
2 курс — Лунгу К.Н., Норин В.П. и др. Книга является второй частью вышедшего ранее и выдержавшего несколько изданий «Сборника задач по высшей математике».
cdnpdf.com
- Сборник задач по высшей математике 2 курс Лунгу К.Н., Норин…
Помочь с изучением дисциплины может решебник к сборнику задач К.Н. Лунгу в двух частях. В нем содержатся полные, качественные решения разных заданий. В решебнике также есть подробные пояснения к задачам. Конечно, ответы можно найти на некоторых сайтах, но разобрать почерк авторов нереально. Да и информация там не всегда проверенная.
 На других ресурсах часто предлагается помощь от людей, которые хорошо разбираются в математике. Но стоят их услуги немало, особенно если задание должно быть выполнено в кратчайшие сроки.
На других ресурсах часто предлагается помощь от людей, которые хорошо разбираются в математике. Но стоят их услуги немало, особенно если задание должно быть выполнено в кратчайшие сроки.gdzlungu.ru
- Сборник задач по высшей математике. 2 курс — Лунгу…
К.Н. Лунгу, В.П. Норин, Д.Т. Письменный, Ю.А.Шевченко Под редакцией С. Н. Федина СБОРНИК ЗАДАЧ_ ПО ВЫСШЕЙ МАТЕМАТИКЕ С контрольными работами Ряды и интегралы_ Векторный и комплексный анализ Дифференциальные уравнения Теория вероятностей 2 Операционное исчисление курс 6-е издание МОСКВА АЙРИС ПРЕСС 2007. УДК 517(075.8) ББК 22.1я73-4 С23 Авторы: Лунгу Константин Никитович Норин Владимир Павлович Письменный Дмитрий Трофимович Шевченко Юрий Алексеевич Куланин Евгений…
djvu.online
- Сборник задач по высшей математике Лунгу 1 курс
Описание: Учебное пособие по математике для студентов и преподавателей высших учебных заведений.
 Сборник содержит более 3,5 тысяч задач разной степени сложности. К каждому параграфу имеется несколько типовых задач с подробным решением, которые можно использовать для примера при решении своего индивидуального задания.
Сборник содержит более 3,5 тысяч задач разной степени сложности. К каждому параграфу имеется несколько типовых задач с подробным решением, которые можно использовать для примера при решении своего индивидуального задания.Сборник задач Лунгу 1 курс онлайн. Вы можете ознакомиться с учебным пособием в онлайн режиме. Плагин может не подерживаться мобильными устройствами.
gdzlungu.ru
- Лунгу К.Н., Норин В.П., Письменный Д.Т. и др. Сборник задач по…
М.: Айрис-пресс, 2007. — 592 с. 6-е изданиеКнига является второй частью вышедшего ранее и выдержавшего несколько изданий «Сборника задач по высшей математике». Сборник содержит три с лишним тысячи задач по высшей математике, охватывая материал, обычно изучаемый во II-IV семестрах технических вузов.
nashaucheba.ru
- Сборник задач по высшей математике.
 1 курс — Лунгу…
1 курс — Лунгу…Сборник содержит свыше трех с половиной тысяч задач по высшей математике. Ко всем разделам книги даны необходимые теоретические пояснения. Детально разобраны типовые задачи, приведено изрядное количество разнообразных заданий различных уровней сложности для самостоятельного решения. Рубрика: Математика / Студентам Математика Студентам Математика. Автор: Лунгу К.Н., Письменный Д.Т. и др. Год: 2008. Язык учебника: Русский.
11klasov.net
- Сборник задач по высшей математике. 2 курс | Лунгу…
Книга является второй частью вышедшего ранее и выдержавшего несколько изданий «Сборника задач по высшей математике».
Этому способствуют необходимые теоретические пояснения ко всем разделам сборника, детально разобранные типовые задачи, изрядное количество разнообразных заданий различных уровней сложности для самостоятельного решения, а также наличие контрольных работ, устных задач и «качественных» вопросов.

b-ok.cc
- Математика. Полезные материалы. Перейти в раздел: https…
Элементарная математика с точки зрения высшей. Том 1 (1987).djvu.
Сборник задач по высшей математике. 1 курс_Лунгу К.Н., Письменный Д.Т. и др_2008 -576с.pdf.
vk.com
- Сборник задач по высшей математике 2 курс (К.Н. Лунгу…)
Сборник содержит три с лишним тысячи задач по высшей математике, охватывая материал, обычно изучаемый во II-IV семестрах технических вузов.
Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом другом регионе России, вы можете оформить заказ на книгу К.Н. Лунгу, В.П. Норин, Д.Т. Письменный, Ю.А. Шевченко, Е.Д. Куланин «Сборник задач по высшей математике 2 курс» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка почтой.

www.chitai-gorod.ru
- Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник…
Книга содержит упражнения по курсу «Высшая математика» для студентов I и II курсов естественных факультетов государственных университетов, где на преподавание математики отводится до 200 учебных часов. Некоторые задачи, включенные в сборник заимствованы из различных распространенных сборников задач по высшей математике, в частности, из «Сборнике задач и упражнений по математическому анализу» Б. П. Демидовича и «Сборника задач по высшей математике…
www.studmed.ru
- Сборник задач по высшей математике. 2 курс | Лунгу К.Н., и др.
Лунгу К.Н., и др. Скачать книгу бесплатно (djvu, 6.50 Mb). Читать «Сборник задач по высшей математике. 2 курс».

libcats.org
- Лунгу К.Н., Макаров Е.В. Высшая математика. Руководство…
Книга содержит упражнения по курсу «Высшая математика» для студентов I и II курсов естественных факультетов государственных университетов, где на преподавание математики отводится до 200 учебных часов. Некоторые задачи, включенные в сборник заимствованы из различных распространенных сборников задач по высшей математике, в частности, из «Сборнике задач и упражнений по математическому анализу» Б. П. Демидовича и «Сборника задач по высшей математике…
www.studmed.ru
- Сборник задач по высшей математике. 2 курс | Лунгу…
Книга является второй частью вышедшего ранее и выдержавшего несколько изданий «Сборника задач по высшей математике».
Этому способствуют необходимые теоретические пояснения ко всем разделам сборника, детально разобранные типовые задачи, изрядное количество разнообразных заданий различных уровней сложности для самостоятельного решения, а также наличие контрольных работ, устных задач и «качественных» вопросов.
 Книга будет полезна студентам младших курсов и преподавателям вузов для проведения…
Книга будет полезна студентам младших курсов и преподавателям вузов для проведения…libcats.org
- Письменный Д.Т., Лунгу К.Н., Федин С.Н., Шевченко Ю.А. Сборник…
Книга содержит упражнения по курсу «Высшая математика» для студентов I и II курсов естественных факультетов государственных университетов, где на преподавание математики отводится до 200 учебных часов. Некоторые задачи, включенные в сборник заимствованы из различных распространенных сборников задач по высшей математике, в частности, из «Сборнике задач и упражнений по математическому анализу» Б. П. Демидовича и «Сборника задач по высшей математике…
www.studmed.ru
- Сборник задач по высшей математике. 2 курс — Лунгу…
Previous Page. 1/598. Next Page. Toggle Outline/Bookmark.
 Toggle Thumbnails. Zoom In. Zoom Out.
Toggle Thumbnails. Zoom In. Zoom Out.cdnpdf.com
На данной странице Вы можете найти лучшие результаты поиска для чтения, скачивания и покупки на интернет сайтах материалов, документов, бумажных и электронных книг и файлов похожих на материал «Сборник задач по высшей математике, 2 курс, Лунгу К.Н., Норин В.П., 2007»
Для формирования результатов поиска документов использован сервис Яндекс.XML.
Нашлось 711 тыс. ответов. Показаны первые 32 результата(ов).
Дата генерации страницы:
Конспект лекций — Введение в высшую математику — MTH 311 Введение в высшую математику Д-р Адам С. Сикора
MTH 311
Введение
по
Высшая математика
Д-р Адам С. Сикора заметки по 1 д-ру Адаму С. Сикоре 900 на основе 1 900 . Майкл Коуэн и др.
Версия от 2 декабря 2016 г. ©c Адам Сикора, Департамент математики
математики, Университет в Буффало.
Предисловие для учителя А. Сикора
После введения в логику, множества и функции эти примечания следуют за традиционное развитие чисел, начиная с аксиом Пеано для натуральные числа, а затем последовательные определения целых, рациональных, действительных, и комплексные числа. Студенты изучают различные темы на протяжении способ: Числа Фибоначчи и другие рекурсивные последовательности, ре- отношения, Маленькая теорема Ферма, Великая теорема Ферма, Двойное простое число и гипотезы Гольдбаха. Кроме того, существует еще ряд представлены расширенные темы, такие как парадокс Рассела, гипотеза Кантора и его независимость от аксиом Пеано, количественных чисел. Наконец, вводятся некоторые элементарные понятия алгебры: кольца (включая Z[
√
d], кольца функций, кольца матриц) и поля, в- включая примеры Q, Q, R, Cas. Значительное количество доказательств и примеры включены в эти примечания.
Из предисловия для студента М. Коуэна
Обратите внимание на точность. Математика — это точный язык.
Имеет значение, что означает прообраз f− 1 (Y) множества; студенты будут
не сможет решить ни одну из задач, связанных с прообразом
установить, если они не знают, что такое прообраз.
Чтобы получить максимальную отдачу от этого курса, вам необходимо выполнить как минимум
следующие 2 задания:
Математика — это точный язык.
Имеет значение, что означает прообраз f− 1 (Y) множества; студенты будут
не сможет решить ни одну из задач, связанных с прообразом
установить, если они не знают, что такое прообраз.
Чтобы получить максимальную отдачу от этого курса, вам необходимо выполнить как минимум
следующие 2 задания:
(1) ВНИМАТЕЛЬНО ИЗУЧИТЕ ОПРЕДЕЛЕНИЯ — Запомните каждое определение. — Пройдитесь по каждому определению, приводя примеры и не примеры, пока вы не поймете идею определения. — Просмотрите каждое определение, его значение, его примеры и его не-примеры, пока вы не сможете перечислить всю эту информацию в твой сон.
(2) УЗНАЙТЕ ПРЕДЛОЖЕНИЯ И ИДЕИ
ИХ ТЩАТЕЛЬНО
— Запомните формулировку каждого предложения (теоремы, леммы,
следствие).
— Повторяйте каждое предложение, пока не поймете центральное
идея позади него.
— Изучите поток доказательства: что приходит первым, что приходит
последний. — Запомните основные идеи доказательств. Не надо
запомнить доказательства.
— Запомните основные идеи доказательств. Не надо
запомнить доказательства.
Содержание
- Предисловие для учителя А. Сикора
- Из предисловия для студента М. Коуэна
- Базовая логика
- Наборы
- Квантификаторы
- Функции
- Обратные функции
- Натуральные числа
- Целые числа
- Подробнее Индукция
- Делимость, сравнения, интегральные частные
- Другие свойства чисел
- Бинарные отношения
- Рациональные числа
- Кольца и поля
- Порядок, наименьшие верхние границы, действительные числа
- Комплексные номера
- Эквивалентность наборов
- Кардинальные числа
- Приложение: Построение действительных чисел
1.
 Базовая логика
Базовая логикаОпределение 1 (оператор). эматические доказательства», Ч. 2 или «Как доказать это» гл. 1-2,1.
правда или ложь (но не то и другое одновременно).
Например, «Куры — это птицы» — это утверждение. Однако «у большинства коров четыре ноги» — это не утверждение, поскольку слово «большинство» не имеет точного значения.
Определение 1 (Отрицание). Если P является высказыванием, то отрицание Pis¬P, читать «неP». Отрицание P считается истинным, если P ложно и ложно, если P истинно.
П ¬П Т Ф F T
Определение 1(Конъюнкция).ЕслиPandQявляются операторами, то их конъюнкция P∧Q, читаемая как «PandQ», истинна, если оба P и Q истинны; в противном случае их соединение ложно.
П Q П∧Q Т Т Т Т Ф Ф Ф Т Ф Ф Ф Ф Обратите внимание на сходство между символом «∧» и буквой «А» для «а также».
Определение 1(Дизъюнкция).IfPandQare операторы, то их
дизъюнкция P∨Q, читаемая как «PorQ», истинна, если либо PorQ, либо оба
истинный; в противном случае их дизъюнкция ложна.
П Q П∨Q Т Т Т Т Ф Т Ф Т Т F F F
Обратите внимание, что ∨ означает включающее «или», например. «1 + 1 = 2» ∨ «2 × 2 = 4» правда. В обычном (нематематическом) использовании также встречается эксклюзивное «или»: «Хочешь колу или пепси?»
Определение 1 (формальное следствие). Если операторы PandQare, то импликация P ⇒ Q, читается как «если P, то Q», является утверждением, что если P истинно, тогда Q истинно. P называется посылкой, а Q называется отрицанием
, ∧, ∨, а «=» используется в компьютерном языке C. катионы не реализуются в C.) Следовательно, P ∨ Q ∧ ¬P ⇒ Q означает (P∨(Q∧(¬P)))⇒Q. Однако, чтобы избежать двусмысленности, вы можете использовать круглые скобки. Утверждение, верное для всех возможных значений его компонентов называется тавтологией. Например, P∨¬P — это тавтология.
Теорема 1 (Законы Де Моргана).
- ¬(P∨Q) ⇐⇒ ¬P∧¬Q
- ¬(P∧Q) ⇐⇒ ¬P∨¬Q
В порядке старшинства правые части выше означают (¬P) ∧ (¬Q)
и (¬P)∨(¬Q) соответственно.
Определение 1.9, противоположное импликации P ⇒ Q импликация¬Q⇒¬P.
Теорема 1 (импликация и ее контрапозиция эквивалентны).
(P⇒Q)⇔(¬Q⇒¬P).
Доказательство построения таблицы истинности.
Из приведенной выше теоремы следует, что для доказательства P⇒Q достаточно показать его противоположность, ¬Q ⇒ ¬P.
ЗАДАЧИ 1.
Задача 1.1 каждое из следующих утверждений, findPandQso что утверждение эквивалентно импликации P⇒Q:
(1) Я счастлив, если слушаю музыку. (2) Я счастлив, только если слушаю музыку. (3) Для службы в США необходимо быть не моложе 30 лет. Сенат. (4) Рождение в США является достаточным условием для того, чтобы быть гражданином США.
Задача 1.2 о том, что (P⇒Q) ⇐⇒ (¬P∨Q) является тавтологией.
2. Наборы
«Математические доказательства». Согласно Википедии, «Набор — это набор отдельных объектов, Ч. 1 и гл. 4-6, «Как Докажи это», гл. 1-4.
рассматривается как самостоятельный объект».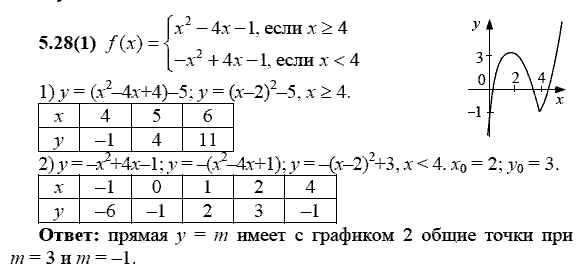
Примеры:
- ∅– «пустое множество» (множество без элементов)
- {яблоко, лошадь, 2}
Мы используем греческую букву epsilon,∈, чтобы написать, что определенный объект элемент множества, т.е. 2∈{яблоко, лошадь, 2}.
Определение 2 (Подмножество). Пусть А и В — множества. Мы говорим, что А есть содержащееся в B или A, является подмножеством B, записанным как A ⊂ B или A ⊆ B, если всякий раз, когда x∈A, тоx∈B. В качестве альтернативы мы иногда говорим что B содержит A, написанное B⊃A или B⊇A.
Примечание. Обозначение A⊆B (в соответствии с записью x≤y) иногда
используется, чтобы подчеркнуть возможность того, что A совпадает с B. Однако,
⊂ и ⊆ всегда означают одно и то же. Мы говорим, что A является собственным подмножеством
BifA⊆BbutA 6 =B. Мы можем обозначить его через A(B.
Примечание:∅⊂Aдля всех наборовA.
Если A — множество, то мы часто определяем его подмножества, записывая {x∈A:x
удовлетворяет некоторому условию}, т.е. {x∈Z : 3|x 2 +x} — множество всех
целые числа x такие, что x 2 +xi делится на 3.
Определение 2 (равенство множеств). Мы говорим, что AequalsB, записанное A=B, если A⊂BandA⊃B.
Отсюда {яблоко, лошадь, 2}={лошадь, 2, яблоко}={лошадь, 2, яблоко, лошадь}. Наборы могут быть элементами других наборов, например = {{ 3 , 5 , 7 }, 1 } — это набор из двух элементы, одним из которых является множество. Если В = {1, 3, 5, 7}, то А 6 = В, так как B имеет 4 элемента. Кроме того, A 6 = {{ 1 , 3 , 5 }, 7 }, так как 7 не является элемент А. Число элементов множества A называется его мощностью и равно обозначается |A|. Например, |{ 3 ,{ 3 }}|= 2,|R|=∞.
Парадокс Рассела. Приведенное выше интуитивное понятие множеств было принято за предоставляется до 1901, когда британский философ Бертран Рассел нашел смертельный недостаток в нем. Прежде чем мы объясним это, обратите внимание, что согласно определение из Википедии, совокупность всех наборов сама по себе является набором. Этот set содержит себя как собственный элемент! Кто-то мог бы согласиться,
Определение 2 (объединение и пересечение). Объединение A ∪ B двух множеств
A и B определяются как A∪B={x: x∈Aorx∈B}. Обратите внимание, что «или»
в математике означает «и/или». Пересечение A ∩ B определяется равенством
А∩B={x: x∈Aandx∈B}.
Объединение A ∪ B двух множеств
A и B определяются как A∪B={x: x∈Aorx∈B}. Обратите внимание, что «или»
в математике означает «и/или». Пересечение A ∩ B определяется равенством
А∩B={x: x∈Aandx∈B}.
Иногда могут пригодиться бесконечные союзы. Например, совокупность всех действительные числа x такие, что sin(x) > 0 можно записать как {x ∈ R : грех(х) > 0 }или, точнее, как
⋃
k∈Z(2πk, 2 πk+π), что означает объединение интервалов (2πk, 2 πk+π) для всех возможных целых значений k. Здесь и далее в примечаниях символы R и Z обозначают множество всех действительных чисел и всех целых чисел (целых чисел), в отличие от букв R, Z, которыми можно обозначать разные вещи.
Определение 2(Непересекающиеся).МножестваAandB являются непересекающимися, если A∩B=∅.
Определение 2 (множество мощностей). Множество мощностей множества A, обозначенное как 2 A, есть
множество всех подмножеств множества A. То есть 2 A={X: X⊂A}.
Пример 2.7 подмножество BofA={ 1 , 2 , 3 } определяется
последовательность ответов ДА и/или НЕТ, отвечающих на следующие три вопроса:
1 принадлежит B? 2 принадлежит B? 3 принадлежит B?
Например, Y, N, Y соответствует B = {1, 3} ⊂A и N, N, N
соответствует ∅⊂A. Поскольку существует 2 × 2 × 2 = 8 возможных последовательностей
вот так, | 2 A|= 8.
Поскольку существует 2 × 2 × 2 = 8 возможных последовательностей
вот так, | 2 A|= 8.
В более общем случае можно доказать, что| 2 A|= 2|A|. Этот факт мотивирует термин «энергетическое множество» и обозначения для него.
Предложение 2. [Основные свойства множеств] Если A, B, Care множества, то
(1)∅∩А=∅;∅∪А=А (2)А∩В⊂А (3)А⊂А∪В (4)А∪В=В∪А;А∩В=В∩А (5)А∪(В∪С) = (А∪В)∪С (6)А∪А=А∩А=А (7) Если A⊂B, то A∪C⊂B∪C и A∩C⊂B∩C («Предложения» — это «маленькие» теоремы. Подробнее прокомментируем их позже.)
Доказательства очень просты. Докажем (2) например: Пусть x∈A∩B∈Aиx∈B. Отсюда, в частности, x∈A Другими словами, каждый элемент A ∩ B принадлежит A.
Предложение 2. [Правила дистрибутивности] Если A, B, Care множества, то
(1)A∩(B∪C) = (A∩B)∪(A∩C)
(2)A∪(B ∩C) = (A∪B)∩(A∪C)
Доказательство (1): чтобы доказать, что два множества, X и Y совпадают (т.е. равны),
обычно нужно показать отдельно, что X ⊂ Y и Y ⊂ X.
Доказательство A∩(B∪C)⊂(A∩B)∪(A∩C): Пусть x∈A∩(B∪C). затем
x∈Aи, кроме того,x∈Borx∈C. Следовательно, x∈A∩Bin
первом случае и x∈A∩C в другом. Следовательно, x∈A∩B∪A∩C
для всех такихx.
Доказательство A ∩ (B ∪ C) ⊃ (A ∩ B) ∪ (A ∩ C): в классе или hw.
затем
x∈Aи, кроме того,x∈Borx∈C. Следовательно, x∈A∩Bin
первом случае и x∈A∩C в другом. Следовательно, x∈A∩B∪A∩C
для всех такихx.
Доказательство A ∩ (B ∪ C) ⊃ (A ∩ B) ∪ (A ∩ C): в классе или hw.
Доказательство (2): в классе или HW.
Замечание 2.10 не может доказать Предложения 2.8 и 2 «опытным путем». ple», потому что утверждение состоит в том, что утверждения верны для всех множеств A, B, C. Например, проверка
А∩(В∪С) = (А∩В)∪(А∩С)
для A={a, b, c}, B={d, e}, C={a, d}
не является доказательством предложения 2(1).
Определение 2 (Дополнение). Если X и A являются множествами, дополнение, ofAinX, обозначаемый X−A, определяется какX−A={x∈X: x /∈A}
X−A альтернативно записывается как X\A.
Предложение 2 (законы де Моргана). Если множества A, BandX являются множествами, то
(1)X−(A∪B) = (X−A)∩(X−B)
(2)Х-(А∩В) = (Х-А)∪(Х-В)
Доказательства этих свойств можно визуализировать с помощью диагонали Венна.
грамм.
Не существует четко установленного всеобъемлющего порядка старшинства в
теория множеств. Однако ∩, ∪ и = соответствуют ∧, ∨ и ⇔. Следовательно,
эти операции теории множеств следует интерпретировать в порядке написания
выше. Например, первое дистрибутивное правило выше может быть записано как
А∩(В∪С) = А∩В∪А∩С.
Согласно этой аналогии между теорией множеств и логикой,
тяга должна предшествовать ∩, но это правило не всегда соблюдается. К
избегайте двусмысленностей, вместо этого используйте круглые скобки.
См. «Математика
Доказательства» 1 и
«Как доказать
4. Они терпят неудачу
однако определить
«заказные пары»
и просто берет
их интуитивно
как должное.
Однако ∩, ∪ и = соответствуют ∧, ∨ и ⇔. Следовательно,
эти операции теории множеств следует интерпретировать в порядке написания
выше. Например, первое дистрибутивное правило выше может быть записано как
А∩(В∪С) = А∩В∪А∩С.
Согласно этой аналогии между теорией множеств и логикой,
тяга должна предшествовать ∩, но это правило не всегда соблюдается. К
избегайте двусмысленностей, вместо этого используйте круглые скобки.
См. «Математика
Доказательства» 1 и
«Как доказать
4. Они терпят неудачу
однако определить
«заказные пары»
и просто берет
их интуитивно
как должное.
Пары и декартовы произведения. Как упоминалось в примечании 2, все математические понятия могут быть определены в терминах теории множеств. Позволь нам примите первый вызов, а затем определите пару (a, b), подобную той, что использовалась для обозначения координат точки на плоскости. Заметим, что (а, б) 6 = {а, б} так как (а, b) 6 = (b, а) для а 6 = b.
Типы математических выражений.
Важные математические утверждения называются теоремами. (Они
часто имеют свои названия, например, основная теорема исчисления,
говоря, что производная F(x) =
(Они
часто имеют свои названия, например, основная теорема исчисления,
говоря, что производная F(x) =
∫х a f(x)dx есть f(x).). Меньше высказывания называются «предложениями». Еще меньшие – это «леммы»
- это вспомогательные утверждения, необходимые для доказательства теоремы и предложения. Математические утверждения обычно имеют вид «Если А, то В» или «Пусть предположим A. Затем B» или что-то подобное. «А» называется предположением или помещение. «В» — гипотеза.
«Как это доказать»
О доказательствах. Ч. 3
Доказательство — это дедуктивный аргумент «утверждения» или «утверждения». Это часто
включает в себя несколько шагов, начиная с того, что дано («предположения») и
затем каждый шаг, вытекающий из предыдущих.
Доказательства похожи на головоломки. Они как найти свой путь
лабиринт. Пошаговых алгоритмов решения этих задач нет.
(в отличие от большинства задач исчисления). То же самое относится и к написанию доказательств.
Это часто требует от вас нескольких попыток, каждая из которых улучшает предыдущую. один, чтобы добиться правильного и полного доказательства. Когда вы тренируетесь писать
пруфы, они станут для вас легче!
один, чтобы добиться правильного и полного доказательства. Когда вы тренируетесь писать
пруфы, они станут для вас легче!
«Математические доказательства»
Написание доказательств. 1 доказать утверждение «iff», как правило, нужно для гл. 0.
отдельно доказать импликации «⇒» и «⇐». Пожалуйста, четко отметьте
эти две части доказательства «Доказательство⇒: …» и «Доказательство⇐: …»
Исключением из этого правила являются простые утверждения типа «x 3 = −8 тогда и только тогда, когда
х 5 =- 32 ».
2. Как отмечалось ранее, утверждение, относящееся ко всем множествам (явно или
неявно) не может быть доказано «на примере».
3. Доказательство того, что два множества равны, A=B, обычно требует демонстрации
что утверждения A ⊂ B и B ⊂ A иногда можно доказать
последовательностями «iff». Например, для любых множеств A, B, C
А∩(В-С) = (А∩В)-С.
Доказательство:x∈A∩(B−C) тогда и только тогда, когдаx∈A∧x∈B−Ciffx∈A∧x∈B∧x6∈C
тогда и только тогда, когда x∈(A∩B)−C.
4. За исключением кратких доказательств, как указано выше, если символ, sayx, не де-
оштрафован, не начинайте предложение с x= 2 или x∈A
грамматика:
(a) «Пусть x∈A», «Возьмем любойx∈A», «Рассмотрим любойx∈A»
(b) Для каждого x∈A происходит то и это. (Утверждения в (а)
и в (b) имеют то же значение.)
(Утверждения в (а)
и в (b) имеют то же значение.)
(c) Существует x∈A такое, что происходит то и это. 5. Заканчивайте каждое предложение точкой!!! Восклицательные знаки принимаются тоже умеет! Трудно понять вашу логику, если читатель не знать, где заканчиваются предложения. 6. Используйте запятые там, где это необходимо. Например, после «например», «следовательно», «следовательно». 7 соответствующих символов и обозначений. Не путайте {,[(. 8. Доказывая утверждение в этих заметках, вы можете ссылаться на состояние- предшествует ему, но не следует за ним. Следовательно, вы не можете доказать утверждение в разделе 3, ссылаясь на утверждение в разделе 4. Аналогично, в Чтобы доказать Предложение 2 (2), вы можете ссылаться на часть (1), но а не наоборот, поскольку это привело бы к круговым рассуждениям.
Если вы проигнорируете эти правила, возможно, вам придется переделать hw!
Пожалуйста, ознакомьтесь с дальнейшим обсуждением написания математики в «Mathe-
математические доказательства», Глава 0. Большинство утверждений можно доказать различными способами. Нет «стан-
dard» доказательство для них или блок-схема, сопоставляющая доказательство с состоянием-
мент. Это значительно усложняет доказательство утверждений, чем решение вычислений.
кулусные проблемы. Например, математические программы, такие как Mathemat-
ica, Maple или Sage могут вычислять интегралы, производные, площади и могут
решать уравнения. Но они не могут доказать теоремы! Вам часто будут нужны
разработать свои собственные доказательства в этом курсе (на основе примеров в классе).
Именно поэтому этот курс сложнее, чем другие математические курсы.
Любое логически правильное и полное доказательство является удовлетворительным, хотя
более простые и короткие доказательства предпочтительнее длинных и сложных
Пожалуйста, прочтите главы о доказательствах в дополнительных учебниках.
Теория множеств очень удобна для отработки доказательств. Например, кон-
сторона:
Большинство утверждений можно доказать различными способами. Нет «стан-
dard» доказательство для них или блок-схема, сопоставляющая доказательство с состоянием-
мент. Это значительно усложняет доказательство утверждений, чем решение вычислений.
кулусные проблемы. Например, математические программы, такие как Mathemat-
ica, Maple или Sage могут вычислять интегралы, производные, площади и могут
решать уравнения. Но они не могут доказать теоремы! Вам часто будут нужны
разработать свои собственные доказательства в этом курсе (на основе примеров в классе).
Именно поэтому этот курс сложнее, чем другие математические курсы.
Любое логически правильное и полное доказательство является удовлетворительным, хотя
более простые и короткие доказательства предпочтительнее длинных и сложных
Пожалуйста, прочтите главы о доказательствах в дополнительных учебниках.
Теория множеств очень удобна для отработки доказательств. Например, кон-
сторона:
Задача 2.16∩C⊂Banda∈C, что a6∈A−B.
Доказательство от противного Предположим, что a∈A−B∈Aanda6∈B. По предположению,a∈C и, следовательно,a∈A∩C, по предположению,
a∈B– противоречие.
По предположению,a∈C и, следовательно,a∈A∩C, по предположению,
a∈B– противоречие.
Математические обозначения в доказательствах.
Помимо математических символов, описанных выше, Количество дополнительных символов, используемых в математических доказательствах:
- Конец доказательства обычно обозначается буквами «QED» для Латинская фраза «quod Erat Demostrandum» или, чаще, .
Задача 2.12={a, b}, определить A×P(A), где P(A) есть силовой набор А.
Задание 2.13 комплектов. Докажите, что A×∅=∅×B=∅.
Задача 2.14, B, C — непустые множества, причем B ⊂ C. Докажите что А×В⊂А×С.
Задача 2.15, Б, С — непустые множества. Докажи это (i)А×(В∪С) = (А×В)∪(А×С) (ii)А×(В∩С) = (А×В)∩(А×С).
Задача 2.16 непустые множества. Докажите, что A×B= B×A тогда и только тогда, когда A=B. Где вы используете это A и B непустой?
3. Кванторы
Определение 3.1 предложения, истинностное значение которого зависит от значений «Как доказать
это» гл. 2 и
«Математический
Доказательства», гл.
2.
2 и
«Математический
Доказательства», гл.
2.
некоторой переменной является открытым предложением.
Мы пишем P(x), P(x, y) и т.д. для открытых предложений в зависимости от переменныеxorxandy и т. д.
Определение 3 (Квантор существования). обозначается символом ∃, читается как «существует».
Определение 3 (Универсальный квантор). отмечен символом ∀, читается «для всех» или «для каждого».
Пример 3.4={a, b}тогда∀x∈XP(x) =P(a)∧P(b)и ∃x∈XP(x) =P(a)∨P(b).
Например, наличие
√
2 можно записать как
∃x∈R, так что x 2 = 2,
или, более компактно, как
∃x∈Rx 2 = 2. Обратите внимание, что вы ставите часть предложения перед словами «такие, что» в нижнем индексе после ∃. Кроме того, квантификатор∃! используется для подтверждения существования уникального элемент с определенным свойством. Например,
∃!x∈(0,∞)x 2 = 2
выполняется, а
∃!x∈Rx 2 = 2
— нет (поскольку 2 = 2 для двух вещественных чисел:
√ 9002
2 и-
√
2).

Тот факт, что
√
2 иррационально, можно записать как (Набор рациональных чисел традиционно обозначается буквой Q, от слова «частное».)
Теорема 3.5(x) и Q(x) — открытые предложения. Тогда
(1)¬(∀x∈XP(x))⇔(∃x∈X¬P(x)) (2)¬(∃x∈XP(x))⇔(∀x∈X¬P(x))
ЗАДАЧИ 3.
Задача 3.(a) Запишите отрицание утверждения «Существует кошка с 9жизни» на стандартном английском языке. (Вы не можете начать с «Это неправда, что…») б) Напишите отрицание утверждения «У всех кошек 9 жизней». (Ты нельзя начинать с «Это неправда, что…» или «Не все кошки…»).
Задача 3.
(1) Пусть P будет утверждением «x 2 +2 = 11 для всех действительных чисел x таких
что x 3 + 32 = 5». ИСП правда? Почему или почему нет?
(2) Пусть Q будет утверждением «x 3 +32 = 5 для всех действительных чисел x таких
что x 2 + 2 = 11». Qправда? Почему или почему нет?
(3) Пусть R будет утверждением «x 3 +32 = 5 для всех действительных чисел x таких
что x 2 + 32 = 0». Правда? Почему или почему нет?
Правда? Почему или почему нет?
Задача 3. Как вы помните из исчисления, каждая кубическая многочлен с действительными коэффициентами имеет действительный корень. Выразите это утверждение используя∀,∃квантификаторы и другие математические символы, но без использования каких-либо слова. (Кстати, обратите внимание, что не всякий квадратичный многочлен имеет действительный корень.)
Задача 3.4 следующие утверждения верны для любого множества X и утверждения P(x) и Q(x)? (а)(∀x∈XP(x)⇒Q(x))⇒(∃x∈XP(x)⇒Q(x)). (б)((∃x∈XP(x))∧(∀x∈XP(x)⇒Q(x)))⇒∃x∈XQ(x). Обосновать ответ.
Задача 3. Докажите или опровергните следующее утверждение: Для каждого множества A, B, C, A∩(B∪C) = A∩B∩C.
Задача 3.6 верно, что если A ∩ B ∩ C = ∅, то одно из множеств A ∩ B, B ∩ C или C ∩ A тоже пусты?
4. Функции
«Математические доказательства». Неформально говоря, функция f из множества X в множество Y является Ч. 9, «Как Докажи это», гл. 5-2,5.
присвоение, при котором каждому элементу X назначается элемент Y. Мы пишем f:X→Y,f(x)=y.
Мы упоминали ранее, что все математические понятия могут быть определены
строго на основе теории множеств. Можем ли мы определить функции как множества
тогда? Да! Для этого воспользуемся тем, что каждая функция определена
по его графу, который является подмножеством X × Y.
Определение 4.1. Функция — это тройка (X, Y, f), где X, Y — множества
и f является подмножеством X×Y со следующими свойствами:
Мы пишем f:X→Y,f(x)=y.
Мы упоминали ранее, что все математические понятия могут быть определены
строго на основе теории множеств. Можем ли мы определить функции как множества
тогда? Да! Для этого воспользуемся тем, что каждая функция определена
по его графу, который является подмножеством X × Y.
Определение 4.1. Функция — это тройка (X, Y, f), где X, Y — множества
и f является подмножеством X×Y со следующими свойствами:
(1) Если x∈X, то существует y∈Y такое, что (x, y)∈f.
(2) Если (x, y)∈f и (x,z)∈f, тоny=z.
Обратите внимание, что использование квантора∃! введенный в разделе 2, мы можем объединить
эти условия в одно: ∀x∈X∃!y∈Y(x, y)∈f.
Мы называем X доменом функции, а Y — кодовым доменом. Чем больше
традиционная запись функции (X, Y, f) есть f:X→Y. (С этого момента
далее мы будем использовать это обозначение.) Мы пишем f(x) =yif (x, y)∈f
что (1) означает, что для каждого x∈X существует f(x). Условие (2) означает
thatf(x) имеет уникальное значение. («уникальный» = «только один»). Другими словами
(2) — тест вертикальной линии.
Функции также часто называют картами.
Другими словами
(2) — тест вертикальной линии.
Функции также часто называют картами.
Определение 4 (Композиция). Если: X→Y и g:Y→Z, то Композиция g с f — это функция g◦f из X в Z, определяемая формулой (g◦f)(x) =g(f(x)).
Пример 4.3 f, g :R → R, f(x) =x 2 и g(x) = x+ 1, тогда g◦f=… и f◦g=…. Определение 4(Изображение). Пусть f:X→Y — функция, а A — функция. подмножество X. Тогда образ Aunderf, обозначаемый f(A), определяется byf(A) = {f(a) : a ∈A}. Альтернативно, f(A) = {y∈Y : y= f(a)для некоторого a∈A}.
Imageoff isf(X), т.е. это образ X underf, часто называется диапазоном. То есть изображение выключено, а.к диапазон выключен {f(x) : x∈X}.
Определение 4 (обратное изображение). Пусть f:X → Y — функция и пусть B будет подмножеством Y. Тогда прообраз B относительно f или прообраз Бундерf, обозначаемый f− 1 (B), есть f− 1 (B) = {x∈X: f(x)∈ Б}.
Описание курсов по математике — школа White Oak
Описание курсов математикиdoug2017-05-30T23:54:27+00:00
Курсы математики для средней школы (2 семестра: 1 кредит)
Курсы математики для подготовки к колледжу (CP) в White Oak перечислены ниже. Навыки, изучаемые на каждом уровне, соответствуют основам учебной программы MA, а также соответствуют общей базовой учебной программе.
Навыки, изучаемые на каждом уровне, соответствуют основам учебной программы MA, а также соответствуют общей базовой учебной программе.
Основы алгебры I
На этом курсе подготовки к колледжу учащиеся закладывают основы высшей математики в качестве подготовки к MCAS. Учащиеся сосредотачиваются на расширении своего понимания системы действительных чисел; интерпретация и запись алгебраических выражений; выполнение операций над полиномами; понимание, создание, графическое представление и решение уравнений и неравенств; интерпретация, построение, сравнение и анализ вводных функций; интерпретация, обобщение и представление данных и линейных моделей. Акцент на языковые навыки является основой для изучения содержания, и учащиеся работают над развитием навыков в области идентификации чисел, числовой последовательности, вычислений, математического языка и стратегий организации и самостоятельной работы.
Основы геометрии
В этом курсе CP учащиеся закладывают основу для высшей математики и готовятся к сдаче MCAS. Учащиеся изучают преобразования на плоскости, строят геометрические построения, используют единицы измерения и различные формулы для определения размеров, изучают конгруэнтность, подобие, прямоугольные треугольники и окружности. Они также сосредоточены на выражении геометрических свойств с помощью уравнений, решении задач с помощью уравнений и моделировании геометрических понятий. Акцент на языковые навыки является основой для изучения содержания, и учащиеся работают над развитием навыков в области идентификации чисел, числовой последовательности, вычислений, математического языка и стратегий организации и самостоятельной работы.
Учащиеся изучают преобразования на плоскости, строят геометрические построения, используют единицы измерения и различные формулы для определения размеров, изучают конгруэнтность, подобие, прямоугольные треугольники и окружности. Они также сосредоточены на выражении геометрических свойств с помощью уравнений, решении задач с помощью уравнений и моделировании геометрических понятий. Акцент на языковые навыки является основой для изучения содержания, и учащиеся работают над развитием навыков в области идентификации чисел, числовой последовательности, вычислений, математического языка и стратегий организации и самостоятельной работы.
Essentials of Algebra II
В этом курсе CP акцент будет сделан на отработке и расширении алгебраических тем, изучаемых в Algebra I, чтобы позволить учащимся использовать математику в качестве языка моделирования для решения реальных задач. Студенты будут выполнять арифметические операции с полиномами, интерпретировать структуру рациональных выражений и записывать выражения в эквивалентных формах для решения задач. Учащиеся также сосредоточатся на графическом представлении и решении уравнений и неравенств, а также на интерпретации, анализе и построении функций, которые моделируют отношения между двумя величинами. Они будут работать над построением и сравнением линейных, квадратичных и экспоненциальных моделей и решать проблемы. Тригонометрические функции и исследования по статистике и вероятности будут представлены и изучены, когда позволит время. Акцент на языковых навыках обеспечивает основу для изучения содержания, и с этой целью учащиеся сосредоточатся на развитии навыков в области идентификации чисел, числовой последовательности, вычислений, математического языка и стратегий организации и самостоятельной работы.
Учащиеся также сосредоточатся на графическом представлении и решении уравнений и неравенств, а также на интерпретации, анализе и построении функций, которые моделируют отношения между двумя величинами. Они будут работать над построением и сравнением линейных, квадратичных и экспоненциальных моделей и решать проблемы. Тригонометрические функции и исследования по статистике и вероятности будут представлены и изучены, когда позволит время. Акцент на языковых навыках обеспечивает основу для изучения содержания, и с этой целью учащиеся сосредоточатся на развитии навыков в области идентификации чисел, числовой последовательности, вычислений, математического языка и стратегий организации и самостоятельной работы.
Интегрированная математика для подготовки к колледжу
Интегрированная математика, которую обычно изучают в старших классах, представляет собой синтез алгебраических и геометрических понятий и их приложений в реальной жизни. Получив оценки на уровне колледжа, учащиеся определят области личных проблем и сосредоточатся на управляемом последовательном обзоре целевых математических тем по арифметике, алгебре, функциям, геометрии, статистике и вероятности. Они будут более глубоко изучать ранее затронутые математические темы, расширяя свои исследования и работая над укреплением и расширением своего критического мышления и навыков решения проблем. Акцент на языковых навыках обеспечивает основу для изучения содержания, и с этой целью учащиеся сосредоточатся на развитии навыков в области идентификации чисел, числовой последовательности, вычислений, математического языка и стратегий организации и самостоятельной работы.
Они будут более глубоко изучать ранее затронутые математические темы, расширяя свои исследования и работая над укреплением и расширением своего критического мышления и навыков решения проблем. Акцент на языковых навыках обеспечивает основу для изучения содержания, и с этой целью учащиеся сосредоточатся на развитии навыков в области идентификации чисел, числовой последовательности, вычислений, математического языка и стратегий организации и самостоятельной работы.
4–8 классы Курсы общей математики
Предварительная алгебра
Учащиеся сосредотачиваются на «больших идеях» алгебры и преодолении разрыва между арифметикой и алгеброй. Они будут исследовать отношения и пропорциональные отношения, проверять и совершенствовать свои способности к вычислениям с рациональными числами и сосредоточатся на решении реальных и математических задач, используя числовые и алгебраические выражения и уравнения. Они будут работать с целыми числами и показателями, анализировать и решать линейные уравнения, а также определять и оценивать функции. Если позволит время, они также сосредоточатся на понимании и решении задач с использованием геометрических понятий: конгруэнтность и подобие, теорема Пифагора и объем цилиндров, конусов и сфер. Учащиеся рисуют, строят и описывают геометрические фигуры. Кроме того, будут рассмотрены исследования в области статистики и вероятности. Акцент на языковых навыках обеспечивает основу для изучения содержания, и с этой целью учащиеся сосредоточатся на развитии навыков в области идентификации чисел, числовой последовательности, вычислений, математического языка и стратегий организации и самостоятельной работы.
Если позволит время, они также сосредоточатся на понимании и решении задач с использованием геометрических понятий: конгруэнтность и подобие, теорема Пифагора и объем цилиндров, конусов и сфер. Учащиеся рисуют, строят и описывают геометрические фигуры. Кроме того, будут рассмотрены исследования в области статистики и вероятности. Акцент на языковых навыках обеспечивает основу для изучения содержания, и с этой целью учащиеся сосредоточатся на развитии навыков в области идентификации чисел, числовой последовательности, вычислений, математического языка и стратегий организации и самостоятельной работы.
Базовая математика
Учащиеся сосредоточатся на выполнении четырех операций с целыми числами, познакомятся с факторами и множителями, а также найдут и определят закономерности. Ключевыми областями внимания будут основные области десятичного разряда и операции с многозначными числами, а также понимание и операции с дробями, десятичными знаками и процентами. Студенты также будут работать над решением задач, связанных с измерением и преобразованием измерений.


 2 курс
2 курс
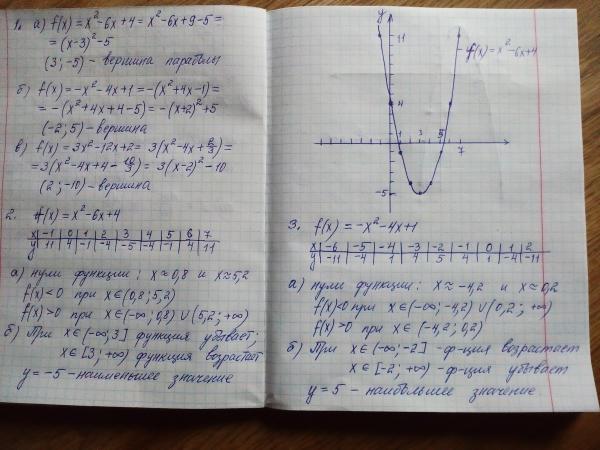 Некоторые задачи, включенные в сборник заимствованы из различных распространенных сборников задач по высшей математике, в частности, из «Сборнике задач и упражнений по математическому анализу» Б. П. Демидовича и «Сборника задач по высшей математике…
Некоторые задачи, включенные в сборник заимствованы из различных распространенных сборников задач по высшей математике, в частности, из «Сборнике задач и упражнений по математическому анализу» Б. П. Демидовича и «Сборника задач по высшей математике… ..
.. Лунгу…
Лунгу…



 На других ресурсах часто предлагается помощь от людей, которые хорошо разбираются в математике. Но стоят их услуги немало, особенно если задание должно быть выполнено в кратчайшие сроки.
На других ресурсах часто предлагается помощь от людей, которые хорошо разбираются в математике. Но стоят их услуги немало, особенно если задание должно быть выполнено в кратчайшие сроки. Сборник содержит более 3,5 тысяч задач разной степени сложности. К каждому параграфу имеется несколько типовых задач с подробным решением, которые можно использовать для примера при решении своего индивидуального задания.
Сборник содержит более 3,5 тысяч задач разной степени сложности. К каждому параграфу имеется несколько типовых задач с подробным решением, которые можно использовать для примера при решении своего индивидуального задания. 1 курс — Лунгу…
1 курс — Лунгу…

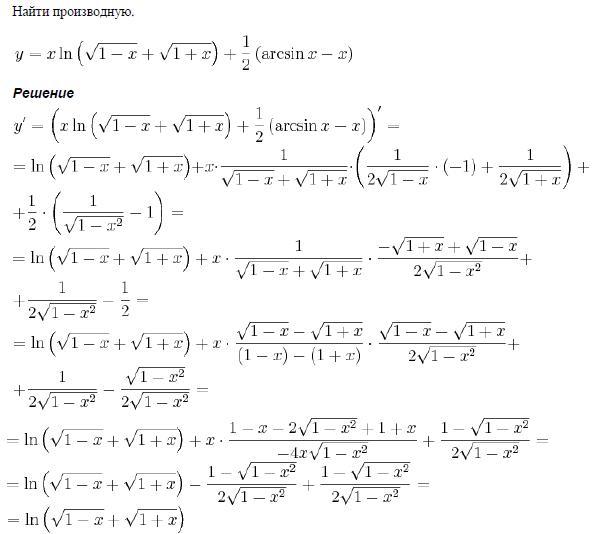
 Книга будет полезна студентам младших курсов и преподавателям вузов для проведения…
Книга будет полезна студентам младших курсов и преподавателям вузов для проведения… Toggle Thumbnails. Zoom In. Zoom Out.
Toggle Thumbnails. Zoom In. Zoom Out.