Дуга знак в геометрии: Дуга (геометрия) | это… Что такое Дуга (геометрия)?

Содержание

mathtype

Equation Editor Tips & Tricks

Советы и Уловки Редактора Equation

files/mathtypeg.GIF»>

Placing an arc over

more than one

character

Размещение дуги над

более чем одним

символом

One limitation of Equation Editor that many people run into is that its arc embellishment (or accent) will only cover a single character.

Многие сталкиваются с одним из ограничений Редактора Equation: знак «дуга» располагается только над одним единственным символом.

This makes it hard to describe arcs for grade-school geometry.

Поэтому сложно описывать дуги в геометрии для средней школы.

For example:

Например:

With a little resizing and nudging, though, you can get a reasonable approximation.

При небольшом изменении размеров и «подталкивании» Вы всё же можете получить разумное приближение.

Here are the steps:

Вот предлагаемые шаги:

Insert the «small-over-large» template (it’s on the 3rd template palette from the left).

Введите шаблон «маленький-над-большим» (он находится на 3-ей палитре шаблонов слева).

Type the material to go under the arc into the lower slot. In this case, «ABC».

Напечатайте материал, который собираетесь расположить под дугой, в нижнем слоте.

В нашем случае — «АВС».

Click into the smaller slot to place the insertion point there.

Щелкните по меньшему слоту, чтобы курсор разместился именно там.

Use the Other command on the Style menu to select the MT Extra font.

Используйте команду Иной из меню Стиль, чтобы выбрать шрифт MT Extra.

Type a «)». This will insert the arc.

Напечатайте «)». Дуга будет вставлена.

Select the arc.

Выделите дугу.

Use the Other command on the Size menu to increase the size of the arc until it covers the characters.

You may not be able to cover them completely before the arc starts to look ugly but do the best you can. If the characters under the arc are 12 points, you may need to make the arc around 40 points in size.

Используйте команду Другой меню Размер, чтобы увеличить размер дуги, пока она не охватит все буквы. Возможно, Вам не захочется полностью охватить все буквы (дуга станет уродливой).

Остановитесь на подходящем варианте. Если буквы под дугой — из 12 точек, то дугу пришлось бы делать длиною в 40 точек.

Use nudging to adjust the arc’s placement over the characters. Type the arrow keys while holding the Ctrl key down (on the Macintosh use the Command key) to move the arc in the desired direction.

Используйте подталкивание, чтобы отрегулировать размещение дуги над буквами.

Нажимайте клавиши со стрелками при нажатой клавише Ctrl (на Макинтоше используйте клавишу Команда), чтобы переместить дугу в желательном направлении.

Here’s the final result:

Вот — результат:

This tip is unnecessary if you own MathType as it includes templates for placing arcs over many characters.

Этот совет не нужен, если Вы имеете MathType, поскольку он содержит шаблоны для размещения дуг над многими символами сразу.

Click here to find out more about MathType.

Щёлкните здесь, чтобы узнать больше о MathType.

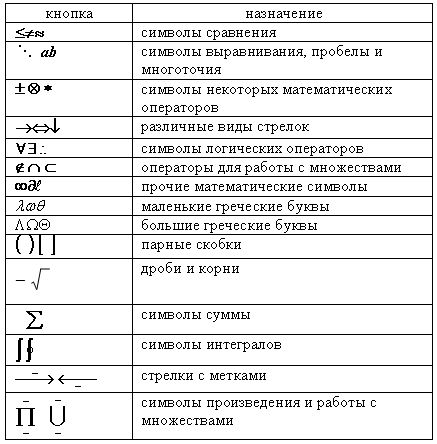
Понятие кривизны в геометрии

Рассмотрим два понятия кривизны, которые используются в геометрии и необходимы для описания нашего пространства-времени в Общей теории относительности:

Внешняя кривизна, для кривой или поверхности S, которая находится в некотором пространстве E большей размерности — это мера того, насколько S отличается от прямой линии в E.
Внутренняя кривизна определяет насколько геометрические свойства фигуры внутри заданного пространства отличаются от «плоской геометрии»( которая содержит афинную геометрию), в независимости от любого другого пространства, содержащего рассматриваемую фигуру.

Внешняя кривизна

Если двигаться вдоль кривой, ее направление(вектор касательной) может изменяться. Угол отклонения этого направления для дуги гладкой кривой S возле заданной точки P, обычно пропорциональный ее длине, точно( в случае дуги окружности) или приближенно( приближение тем лучше, чем меньше дуга). Внешняя кривизна S в точке P определяется как соотношение отклонения( коэффициент пропорции):

Предел(для малых дуг S, содержащих P), от (Угла отклонения (в радианах) / Длина дуги).

Кривизна окружности в эвклидовой плоскости есть величина обратная к радиусу этой окружности.

На сфере «прямые линии»( кривые с нулевой кривизной ) это «большие окружности» с центром в центре сфере. На Земном шаре, который приближенно является сферой, экватор и меридианы — прямые, но параллели( окружности широты) являются кривыми.
Можно интуитивно понимать кривизну кривой на плоскости, рассматривая случай дороги на горизонтальной поверхности, по которой едет автомобиль: кривизна дороги возле каждой точки «измеряется» направлением колес, которое необходимо чтобы ехать по дороге и также как ощущение бокового давления при движении на постоянной скорости.

Для подпространства S пространства E, внешняя кривизна S в E является мерой того, насколько кривая «прямая внутри S» изогнута внутри E. Когда S имеет размерность > 1, это искривление, как правило, не едиственное, а это многомерный объект, поскольку это дает направление, перпендикулярное (касательной подпространстве) S в (квадратичной) функции выбранного направления кривой внутри S (точнее, если n = dim S и m = dim E, то внешняя кривизна имеет n(n+1)(m−n)/2 координат). Но эту кривизну можно рассматривать как одну величину, если она состоит из одинаковых значений во всех направлениях.

Гауссова (внутренняя) кривизна

Гауссова кривизна — это внутренняя кривизна для частичного случая поверхности(2-мерного пространства), когда она является скалярным полем.

Гауссову кривизну можно понимать как «плотность углов» описанную далее.

Для любой поверхности(2-мерного пространства, только приблизительно эвклидового в малых масштаба), сумма углов в радианах любого треугольника, может отличаться от π. Например, на Земле, треугольник состоящий из экватора и двух меридианов имеет два прямых угла, а третий угол( с вершиной в полюсе) может иметь любое значение.
Более того, параллельный перенос вдоль любой замкнутой кривой индуцирует поворот на угол α, который в случае треугольника совпадает с разницей углов:

α = (∑ angles) − π.

В случае (2-мерной) сферы радиуса r в 3-мерном эвклидовом пространстве, этот угол α пропорционален площади A области окруженной кривой, согласно формуле

α = r^-2A

Гауссова кривизна этой сферы имеет коэффициент пропорциональности R = r^-2, который равен квадрату внешней кривизны(r^-1).

Сферы являются особенным случаем кривых поверхностей, поскольку имеют постоянную Гауссову кривизну. В более общем случае, Гауссова кривизна поверхности является( неконстантным) полем и угол поворота α индуцированный параллельным переносом вдоль замкнутой кривой, есть интегралом этого поля по поверхности которую замыкает кривая.

Риманова кривизна

Риманова кривизна является общим случаем внутренней кривизны для пространства произвольной размерности( выше 2).

Это поле, которое нескалярное, но многомерное( то есть описывается несколькими компонентами в заданной системе координат). Для 3-мерного пространства, Риманова кривизна вокруг каждой точки имеет размерность 6. Для 4-мерного пространства( такого как наше пространство-время) она имеет размерность 20.

Есть разные способы описания этого поля. Стандартный, «математический» способ, основывается на свойствах оператора ковариантной производной, который описывает изменения любого векторного поля по соседству с каждой точкой.

В общем случае, метафорическое описание поля как чего-то измеряемого в каждой точке; изменения поля любого типа объектов(векторов или чего-то еще) описывается линейным оператором действующим из пространства «векторов скорости» измеряемых прибором в данной точке со значением( в векторном пространстве где поле принимает значения) скорости изменения измеряемых значений поля.

Ковариантная производная векторного поля в каждой точке есть «наиболее точная» картина изменения поля вокруг этой точки, в том смысле, что она соответствует частичным производным этого поля, если выбрать систему координат, которая «наименее искажена» возле этой точки.

Свойства ковариантной производной отличаются от подобных свойств частичных производных в любой фиксированной системе координат. Потому, что (если кривизна ненулевая) координатная система не может быть «наименее искаженной» во всей окрестности точки, таким образом в окрестности не возможно выбрать фиксированную систему координат, в которой ковариантная производная прямо задается частичными производными. Другими словами, изменения измеряемые частичными производными те которые получаются из афинной структуры пространства заданного в выбранной системе координат, однако афинная структура соответствует плоской геометрии, с отсутствием кривизны, что не является объектом нашего изучения.

Теперь мы дадим интуитивное описание кривизны с помощью расширения на высшие размерности выше указанной идеи о параллельном переносе вдоль кривой.

Для каждой маленькой петли возле точки представим, что это замкнутая петля, которую мы разрежем в точке и переместим в плоское геометрическое пространство. Оба окончания в начале совпадавшие теперь отличаются.
Чтобы они совпадали снова можно вырезать петлю в другой точке, таким образом получив две части, а после этого переместить одну часть по отношению к другой.
Это перемещение, которое должно быть применено к одной части по отношению к другой так, чтобы концы совпали( но концы от нового разреза отличались), являетс поворотом( в общем случае, малым эвклидовым движением, которое более поворачивает чем переносит в том смысле, что в случае поворота его центр находится в или возле рассматриваемой области).

В первом приближении(для малых петель), этот поворот(его координаты: направление, малый угол…), не зависит от точки в которой мы разрезали петлю.

Теперь в качестве петель можем взять маленькие параллелограммы. Результатом параллельного переноса на любой петле может быть получена из этих малых параллелограммов взяв поверхностьограниченную этой петлей и разделив эту поверхность на большое количество малых параллелограммов( или треугольников, которые являются половиной параллелограмма): общий поворот при параллельном переносе вокруг петли получается суммированием( интегрированием ) всех малых поворотов полученными параллельным переносом вдоль каждого параллелограмма.

Операция, которая каждой паре (малых) векторов сопоставляет (малый) поворот полученный при параллельном переносе вдоль малого параллелограмма, чье направление задано этими векторами, является билинейной, антисимметричной функцией этих векторов.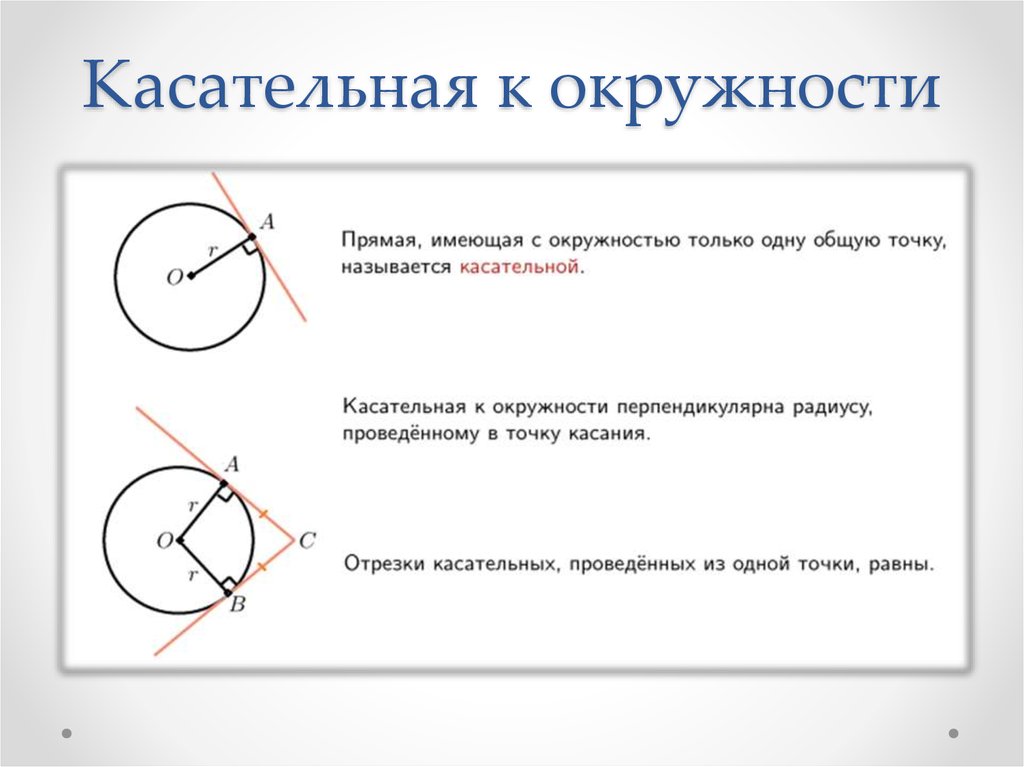

Малые повороты( значения этой функции) могут быть определены как билинейные антисимметричные формы, описанные антисимметричными матрицами.

Чтобы описать Риманову кривизну через координаты, возьмем приблизительную «Декартову систему координат» малой окрестности( в случае космологии, это значит «малая» по сравнению с размерами вселенной, но большая по сравнению с галактикой ;-). По сути мы будет использовать эти названия координат как метки попарно ортогональных осей в этой окрестности. Тогда каждая пара осей определяет малый параллелограмм в этой окрестности.

Пространство билинейных антисимметричных форм n-мерного пространства имеет размерность n(n-1)/2, что соответствует количеству пар осей координат.
При n=4, как в пространстве-времени с координатами (x,y,z,t), имеем 6 пар : (x,y), (x,z), (y,z), (x,t), (y,t), (z,t).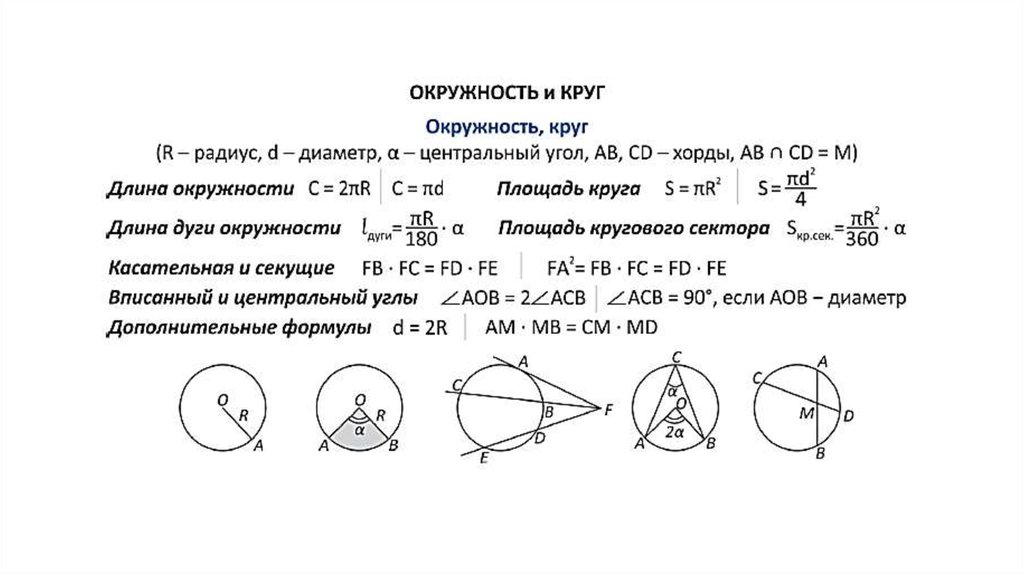

Собрав вместе выше изложенное имеем, что кривизна может быть описана как тензор с 4 индексами, полученным из двух антисимметричных пар. В координатах, каждая компонента Римановой кривизны должна быть помечена двумя парами координат:

одна пара координат помечает направление малой поверхности (параллелограмм), вокруг которой был сделан параллельный перенос,
другая пара помечает компоненту малого поворота, полученного при этом переносе.

Риманова кривизна является антисимметричной по отношению изменения обоих направлений в каждой паре, но она симметричная по отношению к изменению обеих пар.

Таким образом Риманова кривизна вокруг каждой точки 4-мерного пространства, в приблизительной декартовой системе координат вокруг этой точки, описывается симметричной матрицей 6×6, где каждая строчка и каждый столбик соответствуют паре координат.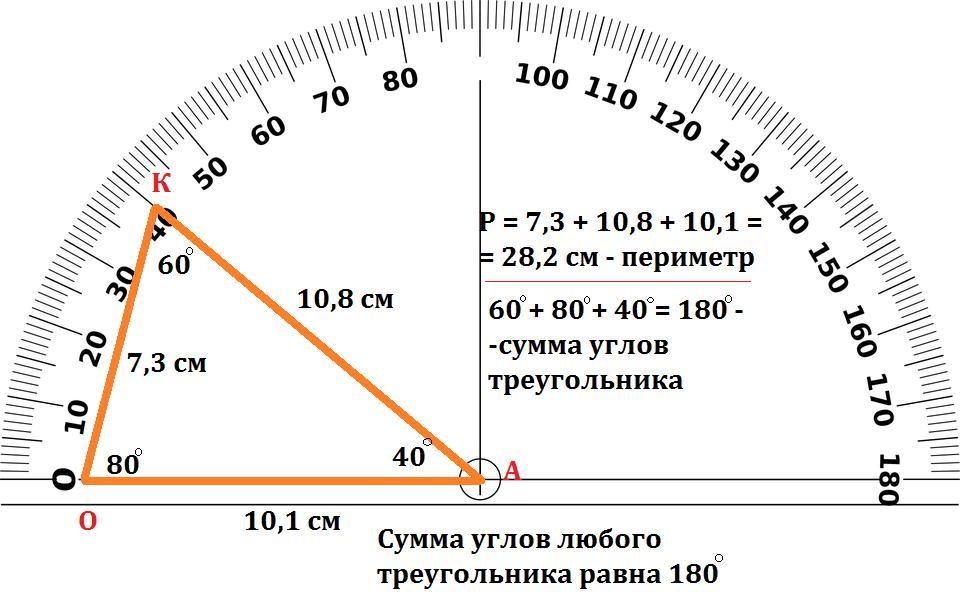

Особым случаем кривых геометрических пространств есть пространство с постоянной кривизной, которое эквивалентно определяется как

Обобщение сферической геометрии на любую размерность и любой знак кривизны
Если предположить, что любая внешне плоская малая поверхность внутри нее имеет ту же Гауссову кривизну.
Если многообразие является Римановым (т.е. чистое пространство, а не пространства-времени: каждое касательное пространство является евклидовым): матрица Римановой кривизны в локальной приблизительной декартовой системе координат каждой малой области, есть единичной матрицей умноженной на коэфициент.

Теперь можно перейти к объяснению расширения Вселенной в Общей теории относительности.

Почему размерность 20, а не 21?

Пространство симметричных матриц размера 6×6 имеет размерность 6×7/2=21.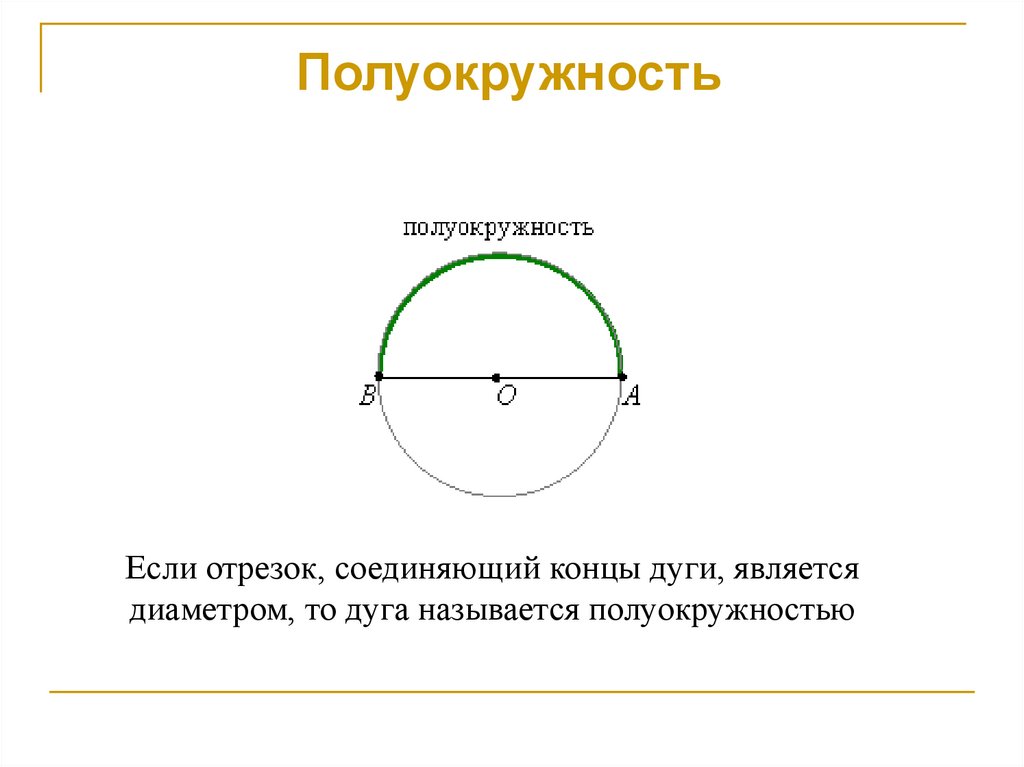

Но тензор Римановой кривизны не может принимать в данной ситуации любое значение, так как он имеет одно соотношение, которое сокращает размерность с 21 до 20.
Это отношение называется «полной антисимметричной» частью этого тензора, и определяется как сума компонент обозначенных ((x,y),(z,t)), ((y,z),(x,t)) и ((z,x),(y,t)).

Причину этого, вместе с симметрией при смене обеих пар, можно объяснить способом того, как считается кривизна исходя из метрической структуры пространства.

Метрическая структура это поле, которое в каждой точке задает локальную геометрическую структуру( локально эвклидовую или структуру Минковского, в добавок к простой локальной афинной структуре, которая задана гладкостью пространства). Значения этого поля в каждой точке есть симметричной билинейной формой с касательными векторами в этой точке( интуитивно, векторы скорости для частиц которые проходят), которые определяют локальное произведение между ними.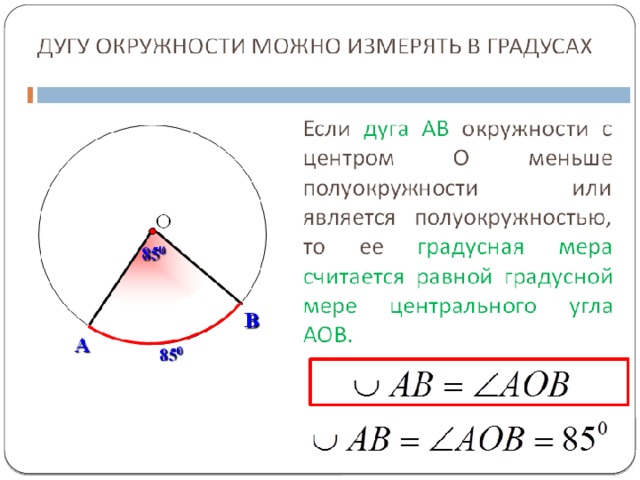

В заданной системе координат (или что эквивалентно, в карте рассматриваемого пространства в плоском пространстве — можно сделать соответствие в первом приближение вокруг точки, таким образом первые производные в метрике в этой точке… по причине достаточно технической чтобы объяснять), кривизна вычисляется из вторых производных метрики.
Симметрия метрики, вместе с симметрией вторых производных в системе координат, естественно изменяет результат таких выражений, которые просто «невозможно произвести любую асимметричность» по причине симметричных вхождений. Детали этого аргумента требуют понимания тензорного исчисления.

Back : Set theory and foundations of mathematics

Что такое дуга в математике? Определение, угол, длина, окружность, примеры

Что такое дуга в математике?

В математике дуга определяется как часть границы окружности или кривой. Его также можно назвать открытой кривой.

Граница круга — это периметр или расстояние вокруг круга, также известное как длина окружности. Итак, дуга — это расстояние между любыми двумя точками, проведенными по его окружности.

Поясним это на примере:

На этом рисунке расстояние между точками A и B представляет собой дугу, проведенную по окружности окружности. Вы можете назвать это дугой AB. Дуга обозначается символом «⌢». Итак, дугу AB можно записать в виде $\widehat{AB}$. Вы также можете записать его как $\widehat{BA}$. Порядок точек не имеет значения.

Как сделать дугу

Чтобы сделать дугу, вам понадобится либо хорда, либо центральный угол.

Хорда — это отрезок, соединяющий любые две точки окружности.

Центральный угол — это угол между любыми двумя радиусами окружности. Например, центральный угол на диаграмме между радиусами QA и QB, как показано ниже, равен 60°.

Типы дуг

Вы, должно быть, заметили, что дуга делит окружность на две части.

У одного расстояние между двумя конечными точками меньше (малая дуга), а у другого расстояние больше (большая дуга).

Если не указано иное, дуга всегда будет считаться второстепенной дугой. Чтобы указать большую дугу, вы можете взять третью точку на дуге окружности и использовать три буквы в имени.

На приведенной выше диаграмме $\widehat{AB}$ — это малая дуга, а $\widehat{ADB}$ — большая дуга.

Дуга полукруга

Полуокружность — это дуга, концы которой совпадают с диаметром окружности.

Как найти длину дуги?

Вы можете рассчитать длину дуги, используя приведенную ниже формулу.

Длина дуги окружности = $\frac{y}{360}$ ✕ $2 π r$

Где r = радиус окружности

y = угол (в градусах), образуемый дугой в центре круга

360 = угол одного полного оборота.

Значение $π$ (пи) = 3,14

Решенные примеры

Пример 1: Вычислить длину дуги, образующей угол 60 градусов в центре круга радиусом 5 см.

Решение : Мы знаем, что формула длины дуги $\frac{y}{360} ✕ $2 π r$

например, мы получаем

Длина дуги = $\frac{60}{360}$ ✕ 2 ✕ 3,14 ✕ 5 = 5,23 см

Пример 2. Вычислите длину дуги, образующей угол 40 градусов в центре окружности с радиус 6 см.

Решение: Мы знаем, что формула длины дуги $\frac{y}{360}$ ✕ $2 π r$

В этом примере

y = 40 и r = 6

Подставляя эти значения в Например, мы получаем

Длина дуги = $\frac{40}{360}$ ✕ 2 ✕ 3,14 ✕ 6 = 4,186 см

Пример 3: Определите большую дугу в этом круге.

Мы знаем, что большая дуга — это большое расстояние между двумя конечными точками. Итак, здесь $\widehat{ADC}$ — это большая дуга, а $\widehat{ABC}$ — меньшая дуга.

Практические задачи

Вычислите длину дуги, образующей угол 120 градусов в центре круга радиусом 10 см.

20,93 см

10,93 см

14,56 см

30,46 см

Правильный ответ: 20,93 см
Длина дуги = $\frac{y}{360}$ ✕ $2 π r$
Подставляя y = 120 и r = 10 см, получаем
Длина дуги = $\frac{40} {360}$ ✕ 2 ✕ 3,14 ✕ 10 = 20,93 см

Определите малую дугу на рисунке ниже.

$\widehat{AB}$

$\widehat{BD}$

$\widehat{DA}$

$\widehat{ADB}$

Правильный ответ: $\widehat{AB}$
$\widehat{AB}$ — малая дуга на этой диаграмме.

На окружности проведена дуга, покрывающая четверть окружности. Какова будет величина центрального угла в этом случае?

90°

60°

45°

30°

Правильный ответ: 90°
Для дуги, охватывающей четверть окружности, радиусы, проведенные из ее концов, будут перпендикулярны друг другу.

Какой из этих центральных углов образует наибольшую дугу?

81°

76°

45°

99°

Правильный ответ: 99°
Центральный угол образован соединением концов дуги с центром окружности. Следовательно, чем больше центральный угол, тем больше будет длина образуемой дуги.

Часто задаваемые вопросы

Что такое дуга полукруга?

Полуокружность — это дуга, концы которой лежат на диаметре окружности.

Здесь и $\widehat{AB}$, и $\widehat{ACB}$ являются полуокружностями.

Что такое центральный угол дуги?

Центральный угол — это угол, на который опирается дуга в центре.

Может ли дуга быть прямой линией?

Нет. Дуга всегда является открытой кривой.

Arc — определение математического слова

Arc — определение математического слова — Math Open Reference

Открытый справочник по математике

Дом Контакт О Тематический указатель

Определение: Часть окружности круга

Попробуйте это Перетащите одну из оранжевых точек, определяющих конечные точки синей дуги. Дуга соответственно изменится.

Дуга – это часть окружности окружности. На рисунке выше дуга — это синяя часть круга. Строго говоря, дуга может быть частью какой-либо другой изогнутой формы, например эллипса, но почти всегда она относится к кругу. Чтобы избежать всех возможных ошибок, ее иногда называют дугой окружности.

Прямая линия, проведенная между конечными точками дуги, будет хорда окружности.

Если длина дуги составляет ровно половину окружности, она называется полуокружной дугой. См. определение полукруга.

Именование и идентификация

Дуги называются по их конечным точкам. Синяя дуга выше будет называться «дугой AB». или «дуга ВА», т.е. порядок конечных точек не имеет значения. В сокращении это можно записать как буквы AB с изогнутой линией над ними
Пример: который читается как «дуга AB».

Обратите внимание, что это имя может быть неоднозначным. Например, это может означать большая дуга АВ, где вы идете длинный путь вокруг нижней части круга. Если не указано иное, это всегда означает малая дуга — самая короткая из двух.

Если вы хотите указать большую дугу, добавьте дополнительную точку и используйте три буквы в названии. Например, на диаграмме выше главная дуга обозначена как это длинная дуга от А до В, огибающая дно через К.

Есть две меры дуги

Длина дуги
Угол дуги

Длина дуги

Длина дуги — это расстояние вдоль изогнутой линии, образующей дугу. Он будет измеряться в единицах измерения расстояния, например, в метрах. Чтобы указать эту меру, дуге предшествует строчная буква L (для «длины»). Для аксклена будет читаться как «длина дуги АВ 6 дюймов». Дополнительную информацию см. на странице «Длина дуги».

Измеритель угла

Мерой угла является угол, образованный дугой в центре окружности. На это указывает маленькая буква М перед именем. Например читается как «дуга AB имеет меру 35 градусов». Дополнительные сведения см. в разделе Измерение угла дуги.

Атрибуты

Длина дуги	Длина изогнутой линии дуги. Дополнительную информацию см. на странице «Длина дуги».
Радиус		Радиус окружности, частью которой является дуга. См. Радиус дуги способы расчета радиуса дуги, когда известны другие свойства дуги.
Центральный угол		Угол, образуемый дугой с центром окружности, частью которой она является. Этот угол всегда вдвое больше окружного угла (см. ниже). См. определение центрального угла для получения дополнительной информации.
Вписанный угол		Угол, образуемый дугой с любой точкой на окружность круга, частью которого он является. Этот угол всегда равен половине центрального угла (см. выше). Подробнее см. Вписанный угол дуги.

Другие темы кружка

Общий

Определение круга
Радиус окружности
Диаметр круга
Длина окружности
Части круга (схема)
Определение полукруга
Касательная
Секанс
Аккорд
Теорема о пересекающихся хордах
Теорема о пересекающихся секущих длинах
Теорема о пересекающихся секущих углах
Площадь круга
Концентрические окружности
Кольцо
Площадь кольца
Сектор круга
Площадь сектора круга
Сегмент круга
Площадь сегмента окружности (данный центральный угол)
Площадь сегмента круга (данная высота сегмента)

Уравнения окружности

Основное уравнение окружности (центр в начале координат)
Общее уравнение окружности (центр в любом месте)
Параметрическое уравнение окружности

Уголки по окружности

Угол вписанный
Центральный уголок
Теорема о центральном угле

Дуги

Дуга
Длина дуги
Измеритель угла дуги
Смежные дуги
Большая/малая дуги
Перехваченная дуга
Сектор круга
Радиус дуги или сегмента при заданной высоте/ширине
Стрелец — высота дуги или сегмента