Функция нескольких переменных. Общие свойства. Непрерывность функции. Линии уровня, поверхности уровня. (Семинар 21)
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Функция нескольких переменных. Общие свойства. Непрерывность функции. Линии уровня, поверхности уровня.
Семинар 21Определение 1
Если каждой паре (x,y) значений двух независимых друг от друга переменных
величин x,y из некоторой области их изменения D соответствует
определенное значение величины z, то z есть функция двух независимых
переменных x,y, определенных в области D.

Обозначение: z=f(x,y), z=F(x,y), и так далее.
Определение 2
Совокупность пар (x,y) значений x,y, при которых определена функция
z=f(x,y), называется областью определения или областью существования этой
функции.
Пусть дана функция z=f(x,y), определенная в некоторой области G плоскости
OXY. Рассмотрим некоторую определенную точку
, лежащую в
области G или на ее границе.
Определение 3
Число А называется пределом функции f(x,y) при стремлении точки M(x,y) к
точке
, если для каждого числа
найдется такое число r>0, что
для всех точек M(x,y), для которых выполняется неравенство
имеет
место неравенство
Определение 4
Пусть точка
принадлежит области определения функции f(x,y).
Функция z=f(x,y) называется непрерывной в точке
, если имеет место
равенство
(1)
Причем точка M(x,y) стремится к точке
произвольным образом,
оставаясь в области определения функции.

Функция, непрерывная в каждой точке некоторой области, называется
непрерывной в этой области.
Если в некоторой точке
не выполняется условие (1), то точка
называется точкой разрыва функции z=f(x,y). Условие (1) может не
выполняться, например, в следующих случаях:
1) z=f(x,y) определена во всех точках некоторой окрестности точки
,
за исключением самой точки
.
2) z=f(x,y) определена во всех точках окрестности точки
, но не
существует
3) z=f(x,y) определена во всех точках окрестности точки
и
существует
, но
Определение 5
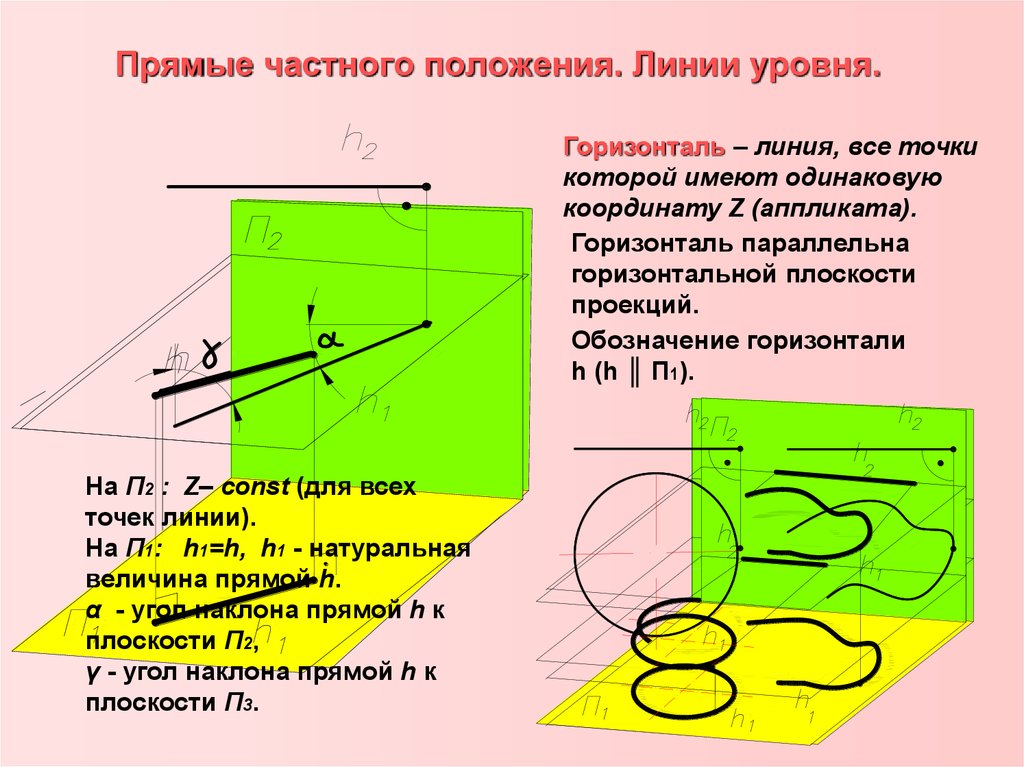
Линией уровня функции z=f(x,y) называется линия z=f(x,y)=с на плоскости
OXY, в точках которой функция сохраняет постоянное значение z=c.
Определение 6
Поверхностью уровня функции u=f(x,y,z) называется поверхность u=f(x,y,z)=с
плоскости, в точках которой функция сохраняет постоянное значение u=c.
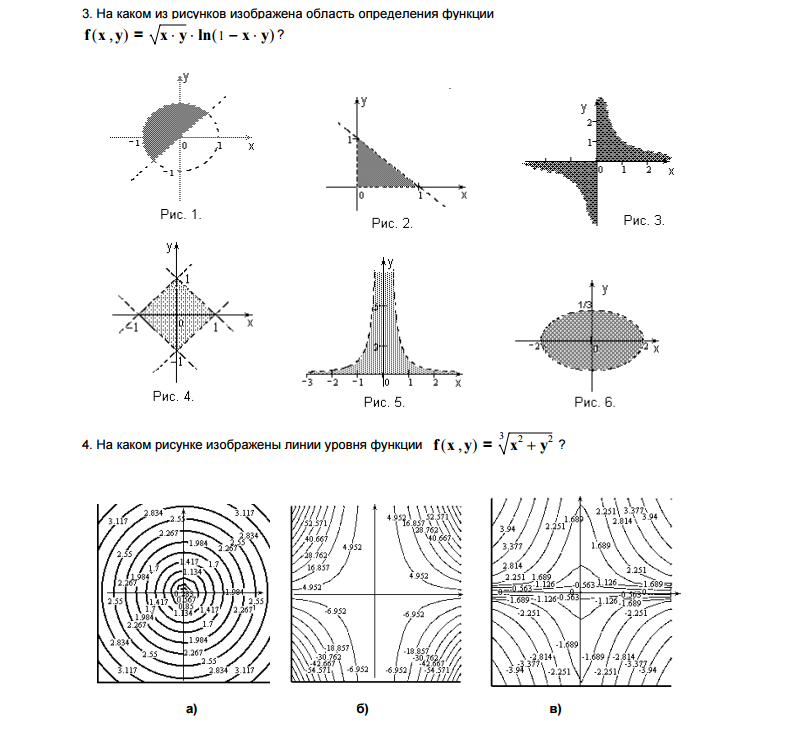
1. Найти область определения функции
.
Решение.
Функция принимает действительные значения при условии
или
, т.
 е. областью определения данной функции является круг радиуса
е. областью определения данной функции является круг радиусаа с центром в начале координат, включая граничную окружность.
2. Найти область определения функции
.
Решение.
Функция определена, если
Областью определения
функции является плоскости, заключенная между двумя параболами
, за исключением точки О(0,0).
3. Найти область определения функции
.
Решение.
Данная функция зависит от трех переменных и принимает действительные
значения при
, т. е. область определения –
часть пространства, заключенная внутри полостей двуполостного
гиперболоида.
4. Найти линии уровня функции
Решение.
Уравнение семейства линий уровня имеет вид
.
Придавая С различные действительные значения, получим концентрические
окружности с центром в начале координат.
5. Найти поверхности уровня функции
Решение.
Уравнение семейства поверхностей имеет вид
.
Если С=0, то получаем
— конус.
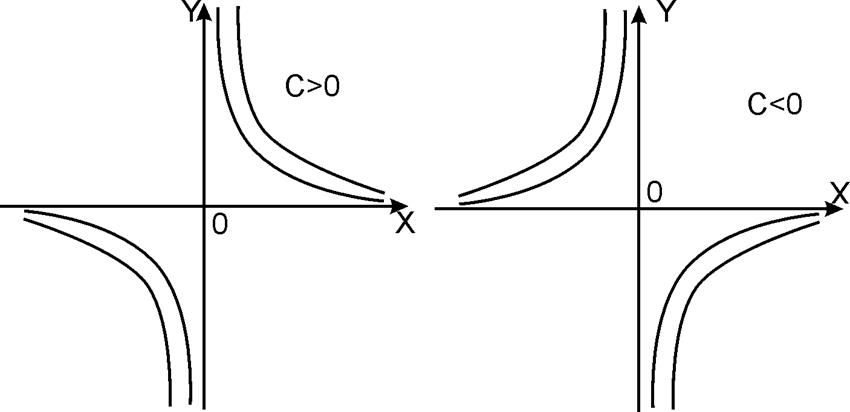
Если С>0, то получаем
— семейство однополостных
гиперболоидов;
Если С<0, то получаем
— семейство двуполостных гиперболоидов;
Примеры для самостоятельного решения
1.
 Найти области определения функции
Найти области определения функции2. Найти линии уровня функций:
3. Найти поверхности уровня функций:
English Русский Правила
Линия уровня — Энциклопедия по экономике
Множество допустимых значений вектора на рис. 1.8. На этом рисунке также изображены линии уровня критерия U( x). [c.51]Здесь p — параметр, не меньший размерности пространства критериев г, BI,. .., ег — положительные малые параметры. Чтобы представить себе смысл функции полезности (3.12), рассмотрим ее линии уровня (кривые безразличия) в пространстве критериев / при заданном значении / (рис. 6.6). [c.303]
Теперь рассмотрим случай р > г. Изучим структуру линий уровня функции (3.12) в том случае, когда не выполняется условие / /. Пусть min(/j — fj) достигается при / = /о. Так как ус-
[c.304]
Пусть min(/j — fj) достигается при / = /о. Так как ус-
[c.304]
Линии уровня дйя этого случая приведены на рис. 6.6, в. В промежуточном случае, как можно проверить, линии уровня имеют вид, изображенный на рис. 6.6, б. [c.304]
Однако экономически содержательная интерпретация может быть наиболее убедительно продемонстрирована на плоскости ( 1(0, 0, поверхности безразличия в виде кривых функции полезности. Более подробное изображение этой плоскости представлено на рис. 11.4, который помогает прояснить логику геометрического способа построения кривых безразличия. [c.234]
Если провести на рис. 2.2 и 2.3 горизонтальную прямую, соответствующую достигнутому на молотовых линиях уровню приведенных затрат для коленчатого вала 10,9 р./шт. и для балки 10,4 р./шт., то экономически оправданными будут только те значения q и г 3, которые лежат ниже достигнутого уровня. [c.55]
Не только доходности достигли ключевой целевой области, но также и несколько циклов, наблюдаемых за эти годы проектировали, что облигации провели достаточно времени, падая в цене (повышаясь в доходности). С тестированием трендовой линией уровня 1981, это было хорошее место для изменения тренда. Когда доходность, коротко проколола эту восемнадцати-с-лишним-летнюю трендовую линию и не смогла пойти выше, прозвенел звонок (для агрессивных трейдеров) с сигналом покупать облигации. (Одна из стратегий, используемых агрессивными трейдерами заключается в противоположной торговле, когда рынок оказывается не в состоянии производить «ожидаемое» поведение. Прорыв восемнадцатилетней трендовой линии должен был привести к большой распродаже. Когда это не произошло, были сделаны покупки.)
[c.200]
С тестированием трендовой линией уровня 1981, это было хорошее место для изменения тренда. Когда доходность, коротко проколола эту восемнадцати-с-лишним-летнюю трендовую линию и не смогла пойти выше, прозвенел звонок (для агрессивных трейдеров) с сигналом покупать облигации. (Одна из стратегий, используемых агрессивными трейдерами заключается в противоположной торговле, когда рынок оказывается не в состоянии производить «ожидаемое» поведение. Прорыв восемнадцатилетней трендовой линии должен был привести к большой распродаже. Когда это не произошло, были сделаны покупки.)
[c.200]
Нижние две линии Фибоначчи, построенные на медвежьем тренде, явились неплохими уровнями сопротивления для будущего рынка, а верхняя линия — уровнем поддержки после быстрого ее пробития. [c.134]
На рисунке 11 приведены линии уровня целевой функции цен- [c.71]
| Рис. 12. Линии уровня суммарного действия в зависимости |
 Но требуется найти наиболее выгодное их сочетание. Пунктирные линии, как и в предыдущем примере, — линии уровня. Здесь они соединяют планы, при которых себестоимость смесей
[c.172]
Но требуется найти наиболее выгодное их сочетание. Пунктирные линии, как и в предыдущем примере, — линии уровня. Здесь они соединяют планы, при которых себестоимость смесей
[c.172]Различные виды функций й(/о,/, А) в разной степени отвечают этим требованиям. Чтобы выбрать способ расширения и обосновать существование Л, важно разобраться в том, как изменяется максимальное значение функции /о при переходе от одной линии уровня функции / к другой. [c.338]
| Рис. 9.6. Линии уровня ограничения и множество допустимых значений переменных |
| Рис. 9.7. Линии уровня целевой функции, функции / (о) и функции достижимости (б) для задачи, изображенной на рис. 9.4 |
| Рис. 9.8. Случай совпадения условного и безусловного максимумов (а) — линии уровня целевой функции и ограничения (б) — характер функции достижимости |
 1.2 это направление показано стрелкой. Чтобы найти оптимальное решение, следует перемещать прямую, характеризующую прибыль (линию уровня целевой функции) в направлении вектора-
[c.442]
1.2 это направление показано стрелкой. Чтобы найти оптимальное решение, следует перемещать прямую, характеризующую прибыль (линию уровня целевой функции) в направлении вектора-
[c.442]Представление о функции может дать и метод линий уровня. Геометрическое место точек плоскости, в которых функция z — /(ж, у) принимает постоянное значение, называется линией уровня. Это линия пересечения поверхности z — /(ж, у) плоскостью z = С и ортогонально спроектированная на плоскость Оху. Сделав несколько таких сечений плоскостями z = С, [c.280]
Сечения плоскостями z = 1, Линии уровня окружности z — 2, z — 3 радиуса 1, /2, /3 [c.281]
| Рис. 14.2. Линии уровня функции z = х1 + у1 |
Линии уровня функции z = х2 + у2 — концентрические окружности [c.345]
Параллельный способ строения учетных регистров предусматривает размещение записей в процессе их регистрации по дебету и кредиту на одной линии (уровне), хотя сам регистр по строению может быть представлен в форме односторонней таблицы, двусторонней или мнографной (штафельной). Применение соответствующей формы регистрации связано прежде всего с содержанием хозяйственной операции.
[c.327]
Применение соответствующей формы регистрации связано прежде всего с содержанием хозяйственной операции.
[c.327]
| Рис. 38. Двумерные (линии уровня) и трехмерные графики распределения ценовых приращений в интервале 200 торговых дней, с центром 19 октября 1987 (соответствует О абсциссы). Масштаб плотности вероятности (ось Z) поверхностного участка логарифмический, что обеспечивает для прямого затухания экспоненциальное распределение. График изоквант (линий, на которых логарифм функции плотности вероятности принимает одинаковое значение) на верхней грани куба кодируется яркостью. Самая яркая область контурного участка соответствует наиболее вероятному значению. Символ R означает return (исход или приращение). Источник [267]. |
 3. Здесь же мы рассмотрим их более подробно. Сторонники теханализа считают, что существующая тенденция должна проявлять себя внутри линий тренда. Эти линии, таким образом, служат чем-то вроде рельсов, по которым катится локомотив рынка. Если, скажем, происходит пробой линии, то это важный сигнал к смене тенденции. Например, если пробивается линия поддержки на восходящем тренде, то это веский аргумент в пользу того, что восходящий тренд сменится либо горизонтальной, либо нисходящей тенденцией (см. рис. 51) [116] [c.137]
3. Здесь же мы рассмотрим их более подробно. Сторонники теханализа считают, что существующая тенденция должна проявлять себя внутри линий тренда. Эти линии, таким образом, служат чем-то вроде рельсов, по которым катится локомотив рынка. Если, скажем, происходит пробой линии, то это важный сигнал к смене тенденции. Например, если пробивается линия поддержки на восходящем тренде, то это веский аргумент в пользу того, что восходящий тренд сменится либо горизонтальной, либо нисходящей тенденцией (см. рис. 51) [116] [c.137]Линия l(q) уровня q —f(L,K) производственной функции Q = f(L,K) называется изоквантой. Иными словами, линия уровня q — это множество точек, в которых объем производства постоянен и равен q. Различные наборы (v v и (wj, w затрачиваемых (используемых) ресурсов, принадлежащие одной и той же изо-кванте l(q), дают один и тот же объем выпуска q. Как и в случае с кривыми безразличия, углу наклона изокванты соответствует предельная норма технической замены одного ресурса другим. [c.175]
[c.175]
БАЗИСНОЕ РЕШЕНИЕ (опорный план) [basi solution] — термин линейного программирования, одно из допустимых решений, находящихся в вершинах области допустимых решений, либо (если линия уровня параллельна одному из отрезков границы области) Б.р. — весь этот отрезок (см. рис. Л.2 к ст. «Линейное программирование»). Оно является решением системы линейных ограничений, которое нельзя представить в виде линейной комбинации никаких других решений. [c.26]
КРИВЫЕ БЕЗРАЗЛИЧИЯ [indifferen e urves] — геометрическое место точек пространства товаров, характеризующихся состоянием безразличия с точки зрения равной полезности для потребителя. Она является линией уровня для функции полезности этого потребителя. С другой стороны, это графическая иллюстрация взаимозаменяемости товаров. Применение К.б. — метод теоретического анализа спроса и потребления (а также некоторых других экономических явлений). [c.162]
Остается найти ту из них, которая даст наибольшую прибыль, т.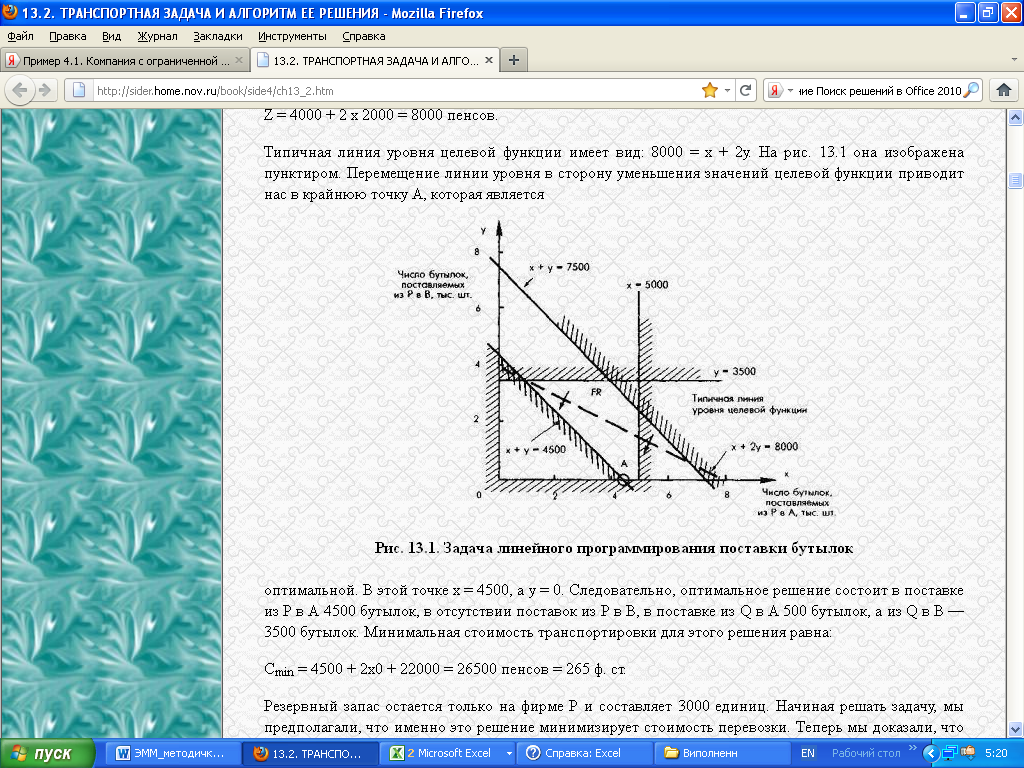 е. максимум целевой функции. Выбрав произвольно прямую с1х1 + с2х2 = П с произвольной константой П и обозначив ее ММ, находим на чертеже все точки (варианты планов), где прибыль одинакова при любом сочетании х, и х2 (см. Линия уровня). Перемещая эту линию параллельно ее исходному положению, найдем точку, которая в наибольшей мере удалена от начала координат, однако не вышла за пределы области допустимых значений. (Перемещая линию уровня еще дальше, уже выходим из нее и, следовательно, нарушаем ограничения задачи.) Точка М0 и будет искомым оптимальным планом. Она находится в одной из вершин многоугольника. Мо-
[c.171]
е. максимум целевой функции. Выбрав произвольно прямую с1х1 + с2х2 = П с произвольной константой П и обозначив ее ММ, находим на чертеже все точки (варианты планов), где прибыль одинакова при любом сочетании х, и х2 (см. Линия уровня). Перемещая эту линию параллельно ее исходному положению, найдем точку, которая в наибольшей мере удалена от начала координат, однако не вышла за пределы области допустимых значений. (Перемещая линию уровня еще дальше, уже выходим из нее и, следовательно, нарушаем ограничения задачи.) Точка М0 и будет искомым оптимальным планом. Она находится в одной из вершин многоугольника. Мо-
[c.171]
ЛИНИЯ УРОВНЯ [ ontour line] (или линия равного уровня) — геометрическое место точек пространства аргументов, для которых значения исследуемой функции одинаковы. Это определение можно записать так [c.174]
Поясним причины недифференцируемости функции достижимости в случае вырожденного решения. Причина заключается в том, что вырожденному решению соответствует изолированная точка а на плоскости х. На рис. 9.7, а показано расположение линий уровня, соответствующих задаче, изображенной на рис. 9.4. При замене равенства /1 = 0 на /1 = С поверхность Д перестанет касаться с плоскостью, соответствующей значению С . Если точка касания а при сколь угодно малом изменении С исчезнет, то произойдет скачок функции достижимости в сторону ее уменьшения (рис. 9.7, б).
[c.340]
На рис. 9.7, а показано расположение линий уровня, соответствующих задаче, изображенной на рис. 9.4. При замене равенства /1 = 0 на /1 = С поверхность Д перестанет касаться с плоскостью, соответствующей значению С . Если точка касания а при сколь угодно малом изменении С исчезнет, то произойдет скачок функции достижимости в сторону ее уменьшения (рис. 9.7, б).
[c.340]
Градиент совпадает с нормалью к линии уровня /(ж, у) = = onst в точке MQ. [c.294]
Переход к производственным функциям с семейством монотонных линий уровня f (k, I) — onst, имеющих горизонтальные и вертикальные асимптоты и конечные пределы вида lim / (k, 10) = F (/0) и lim f (k0t. [c.46]
I) = G (k0), не позволяет отразить в производственной функции внешние связи и связи между факторами и показателями их эффективности. Представляется, что производственные функции у = f (k, I) с линиями уровня f (k, I) = onst, задаваемыми немонотонными кривыми k — k (I), дают возможность более полного учета связей между факторами и внешних связей.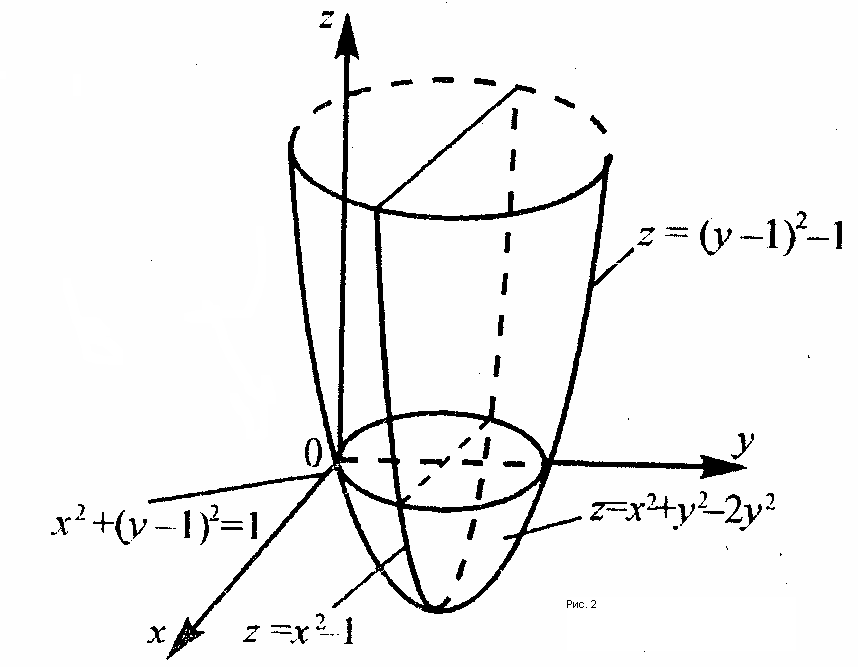 [c.46]
[c.46]
Заметим также, что при использовании производственных функций с монотонными линиями уровня у = onst оценка параметров на основе имеющейся статистики неизбежно приводит к экстраполяции свойств производственной функции, присущих ограниченной области изменения ее аргументов, на более широкую область. Между тем для анализа и прогноза темпов экономического развития при качественно новых соотношениях для его факторов выход в эту, не просканированную практически область может стать принципиально необходимым. В таком случае от производственной функции придется требовать правильного отражения соче- [c.46]
Civil 3D Grading — когда характерные линии пересекаются — Cadapult Software
Использование характерных линий для профилирования в Civil 3D было областью программы, которая продолжала развиваться с каждым выпуском. Характерные линии в Civil 3D изначально были основаны на концепциях и инструментах, которые многие из нас использовали в Land Desktop, оценивая их с помощью 3D-полилиний, а затем добавляя функциональные возможности, которые мы могли только желать в LDT.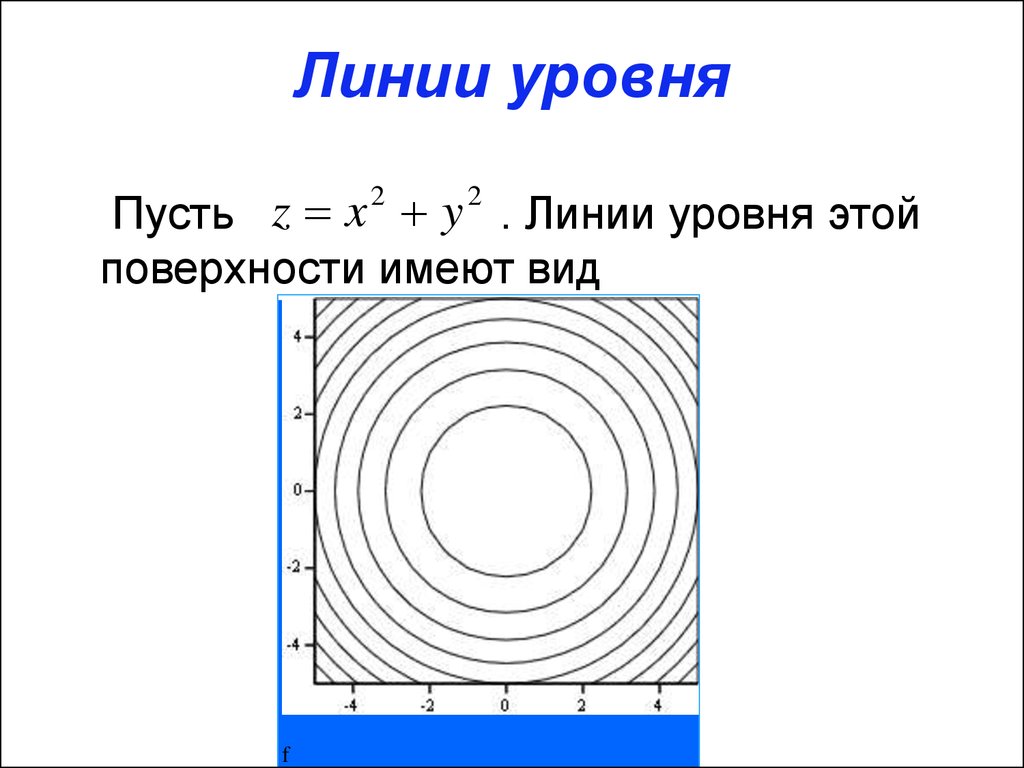
Одним из сценариев, которого пользователи всегда старались избегать при профилировании с помощью 3D-полилиний, было создание пересекающихся 3D-полилиний, которые, в свою очередь, создавали пересекающиеся структурные линии. Если вы были осторожны и обязательно соединили эти 3D-полилинии вместе в точке их пересечения, чтобы линии пересекались на одной и той же высоте, тогда все в порядке. Однако это был сценарий, который был общей проблемой для многих пользователей.
С помощью характерных линий в Civil 3D теперь можно безопасно создавать пересекающиеся характерные линии, и вы даже можете сделать это намеренно, как только научитесь управлять ими. Сначала вам нужно знать, что характерные линии включены в сайты в Civil 3D. Это означает, что Характерные линии будут взаимодействовать с другими Характерными линиями, включенными в тот же Сайт. (Если вы не хотите, чтобы они взаимодействовали друг с другом, поместите их на разные сайты.) Таким образом, если вы создадите две характерные линии, которые пересекаются друг с другом, в месте пересечения будет создана точка разделения.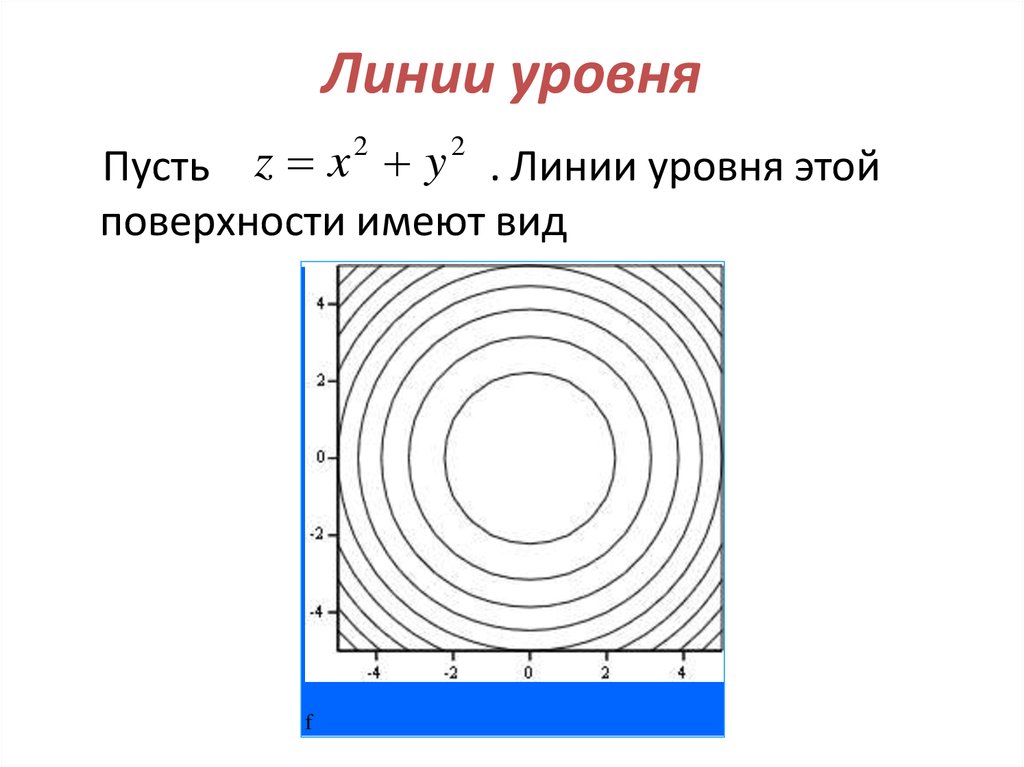 Эта точка разделения гарантирует, что характерные линии пересекаются на одной и той же высоте.
Эта точка разделения гарантирует, что характерные линии пересекаются на одной и той же высоте.
Теперь, когда вы знаете, что точка разделения создана, вам, вероятно, интересно, на какой отметке она создается и к какой характерной линии она добавляется. Чтобы ответить на оба этих вопроса, Autodesk использует так называемое правило «последний побеждает». По сути, та функция, которая была создана последней, имеет приоритет. Характерная линия, созданная первой и пересекаемая новой характерной линией, имеет точку разделения, добавленную к ней на отметке, на которой она пересекает новую характерную линию. Это изменяет наклоны сегментов исходной характерной линии, которые соединяются с новой точкой разделения.
Для управления приоритетом пересечения характерных линий и отмены правила «Выигрывает последний» начните с назначения различных стилей пересекающимся характерным линиям. Затем перейдите в навигатор, разверните сайт, щелкните правой кнопкой мыши коллекцию Feature Line и выберите «Свойства».
Выберите вкладку «Параметры» в диалоговом окне «Свойства площадки характерной линии». Здесь вы можете настроить порядок приоритета характерных линий для разрешения точки разделения в соответствии с их стилем.
Наконец, лучший способ понять пересечение характерных линий — это попробовать. Вы можете использовать очень простой пример. Начните новый чертеж в Civil 3D, используя свой шаблон. Затем нарисуйте две характерные линии с помощью команды Grading >> Draw Feature Line. Нарисуйте первую линию вертикально с отметкой 0, а вторую линию горизонтально с отметкой 10, чтобы они пересекались. Теперь изучите характерную линию с помощью команды Grading >> Edit Feature Line Elevations >> Elevation Editor.
Вы увидите точку разделения, показанную на вертикальной линии, как показано выше, но не на горизонтальной линии. Это потому, что вертикальная линия была нарисована первой. Вы также можете попробовать назначить разные стили для двух характерных линий и изменить порядок стилей в настройках разрешения точки разделения, чтобы увидеть изменения после изменения приоритета характерных линий.
Применение метаданных уровня объектов (топографическая продукция) — ArcGIS Pro
К началу
В этом разделе
- Сводка
- Использование
- Параметры
- Среды
- Информация о лицензировании
Сводка
Применяет значения из записи метаданных в таблице FeatureLevelMetadata к выбранным объектам с соответствующими полями атрибутов.
Usage
Значение параметра Metadata Favorite является записью в таблице FeatureLevelMetadata. Инструмент применит связанные значения записи к соответствующим атрибутам для указанных объектов в параметре Входные объекты.
Таблица FeatureLevelMetadata включена в файлы данных продуктов ArcGIS Defense Mapping и ArcGIS Production Mapping.
Типы полей в таблице FeatureLevelMetadata должны совпадать с типами полей в обновляемых векторных слоях.
 В противном случае инструмент завершит работу с сообщением об ошибке, указывающим, что перед обработкой типы полей должны совпадать.
В противном случае инструмент завершит работу с сообщением об ошибке, указывающим, что перед обработкой типы полей должны совпадать.
Параметры
| Этикетка | Пояснение | Тип данных |
Входные характеристики | Входные данные, к которым будет применяться значение параметра «Избранное метаданных». | Слой признаков |
Таблица входных метаданных | Путь к таблице метаданных содержащие записи, которые будут использоваться для заполнения атрибутов. | Представление таблицы |
Избранное метаданных | Запись, которая будет использоваться для заполнения атрибутов. | Строка |
Производный вывод
| Метка | Объяснение | Тип данных | Обновления 909071 |
Слой входных объектов с обновленными атрибутами. | Слой объектов; Класс объектов |
arcpy.topographic.ApplyFeatureLevelMetadata(in_features, in_metadata_table, metadata_favorite)
| Имя | Объяснение | Тип данных |
in_features [in_features,…] 3 2 Входные данные, к которым будет применено значение параметра metadata_favorite. | Feature Layer | |
in_metadata_table | Путь к таблице метаданных
содержащие записи, которые будут использоваться для заполнения атрибутов. | Table View |
metadata_favorite | Запись, которая будет использоваться для заполнения атрибутов. Доступные параметры зависят от записей, доступных в таблице метаданных. | Строка |
Производный вывод
| Имя | Объяснение | Тип данных | 1
Слой in_features с обновленными атрибутами. | Слой объектов; Feature Class |
Пример кода
Пример ApplyFeatureLevelMetadata (автономный скрипт)В следующем примере кода показано, как использовать функцию ApplyFeatureLevelMetadata в Python.
# Имя: ApplyFeatureLevelMetadata_sample.py # Описание: используйте инструмент «Применить метаданные уровня функций», чтобы применить значения из # запись метаданных в таблице метаданных уровня функций для выбранных функций # которые имеют соответствующие поля атрибутов # Импорт системных модулей импортировать аркпи # Проверьте расширения arcpy.

 В противном случае инструмент завершит работу с сообщением об ошибке, указывающим, что перед обработкой типы полей должны совпадать.
В противном случае инструмент завершит работу с сообщением об ошибке, указывающим, что перед обработкой типы полей должны совпадать.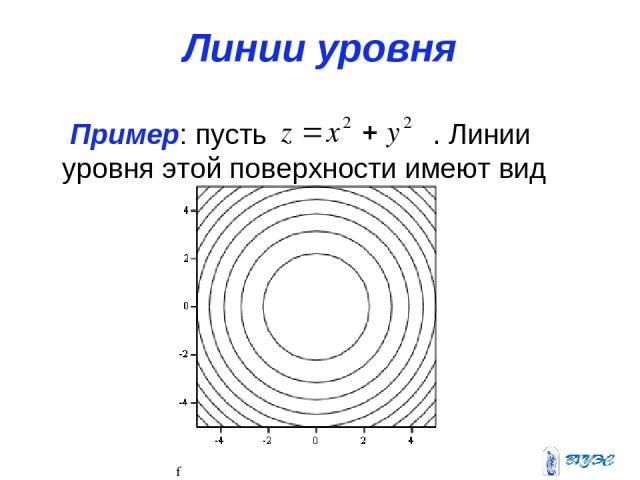 Доступные параметры зависят от записей, доступных в таблице метаданных.
Доступные параметры зависят от записей, доступных в таблице метаданных.