Решение математических уравнений с помощью помощника по преобразованию в математические выражения в OneNote
OneNote
Создание заметок
Создание заметок
Решение математических уравнений с помощью помощника по преобразованию в математические выражения в OneNote
OneNote для Интернета OneNote для Windows 10 Помощник по преобразованию в математические выражения Еще…Меньше
Напишите или введите любую математическую задачу, и помощник по преобразованию в математические выражения в OneNote решит ее для вас: поможет быстро найти решение или покажет пошаговые инструкции, которые помогут вам найти решение самостоятельно. После решения уравнения можно пользоваться различными возможностями изучения математики в помощнике по преобразованию в математические выражения.
Примечание: Эта функция доступна только в том случае, если у вас есть подписка на Microsoft 365.
Если вы являетесь подписчиком Microsoft 365, убедитесь, что у вас установлена последняя версия Office.
Шаг 1. Введите уравнение.
На вкладке Рисование напишите или введите уравнение. Используйте средство Lasso Select для рисования круга вокруг уравнения. Затем выберите «Математические вычисления». Откроется панель помощника по преобразованию в математические выражения.
Дополнительные сведения: создание уравнения с помощью рукописного ввода или текста.
Шаг 2. Решите уравнение.
Чтобы решить текущее уравнение, выполните одно из следующих действий:
Щелкните или нажмите поле Выберите действие, затем выберите нужное действие помощника по преобразованию в математические выражения.
Дополнительные сведения: проверьте вкладку «Поддерживаемые уравнения » и типы проблем, поддерживаемые Помощником по математическим вычислениям
Просмотрите решение, которое OneNote выводит под выбранным действием. В приведенном ниже примере решение отображается для выбранного варианта Решение для x.
-
Чтобы узнать, как OneNote решил задачу, можно щелкнуть или нажать Показать действия, а затем выбрать интересующие вас сведения. Варианты, которые доступны в этом раскрывающемся меню, зависят от выбранного уравнения.
-
Чтобы прослушать шаги по решению вслух, Иммерсивное средство чтения запустить его из OneNote.
-
Создайте учебный тест, чтобы научиться решать уравнения такого типа.
Предупреждение: Тест создания практики в настоящее время недоступен, так как мы работаем над оптимизацией работы. Возможность создавать тесты для практики будет возвращена позже в этом году.
Совет: Этапы решения можно перетащить в любое место на странице.
Дополнительные сведения
Создание математических формул с помощью рукописного ввода или текста в OneNote с использованием помощника по преобразованию в математические выражения
Типы задач, поддерживаемые помощником по преобразованию в математические выражения
Построение графиков математических функций в OneNote с использованием помощника по преобразованию в математические выражения
Создание учебного теста в OneNote с использованием помощника по преобразованию в математические выражения
Типы проблем, поддерживаемые помощником по математическим вычислениям
При использовании помощника по математике в OneNote вы заметите, что раскрывающийся список «Выбрать действие» под уравнением изменяется в зависимости от выбранного уравнения.
Примечание: Эта функция доступна только в том случае, если у вас есть подписка на Microsoft 365. Если вы являетесь подписчиком Microsoft 365, убедитесь, что у вас установлена последняя версия Office.
|
Массивы |
Для списка реальных чисел поддерживаются все приведенные ниже значения.
 org/ListItem»>
Среднее  org/ListItem»>
Наименее распространенное кратное |
Выражения |
Для любого выражения доступны следующие действия:
 org/ListItem»>
Фактор (если применимо) |
|
|
Для уравнений и неравенства доступны следующие действия:
 org/ListItem»>
Решение для {переменной} |
|
Системы |
Важно иметь одинаковое количество уравнений и переменных, чтобы обеспечить доступность правильных функций.
|
|
Производные и целочисленные объекты |
Производные могут быть записаны либо с помощью d/dx перед функцией, либо с помощью простого знака. Действия, доступные для производных и целочисленных элементов: |
|
Матриц |
Матрицы могут быть написаны квадратными или круглыми скобками. Для матриц поддерживаются следующие действия:
 org/ListItem»>
Вычисление трассировки Матричные уравнения в настоящее время не поддерживаются. |
|
График в полярных координатах |
Для графирования функции в полярных координатах r должен быть выражен как функция theta.
|
|
Сложный режим |
Примечание. Выберите параметры для переключения между реальными числами и сложными числами. Для сложных выражений и чисел, содержащих мнимую единицу i, доступны следующие действия. |
Системы могут быть написаны двумя разными способами: 
Дополнительные сведения
Создание математического теста в Microsoft Forms
Создание математического теста для практики в OneNote с использованием помощника по преобразованию в математические выражения
Решение математических уравнений с помощью помощника по преобразованию в математические выражения в OneNote
Что такое уравнение? Как решать уравнения?
Уравнение — одно из краеугольных понятий всей математики.
Как школьной, так и высшей. Имеет смысл разобраться, правда? Тем более, что это очень простое понятие. Ниже сами убедитесь. 🙂 Так что же такое уравнение?
То, что это слово однокоренное со словами «равный», «равенство», возражений, думаю, ни у кого не вызывает.
Уравнение — это два математических выражения, соединённых между собой знаком «=» (равно).
Но… не каких попало. А таких, в которых (хотя бы в одном) содержится неизвестная величина. Или, по-другому, переменная величина. Или, сокращённо, просто «переменная». Которая обычно обозначается буквой «х».
Переменных может быть одна, может быть несколько. В школьной математике чаще всего рассматриваются уравнения с одной переменной. И мы тоже пока что будем рассматривать уравнения с одной переменной. С двумя переменными или более — в специальных уроках.
Что значит решить уравнение?
Идём дальше.
Переменная, входящая в уравнение, может принимать любые допустимые математикой значения. На то она и переменная. 🙂 При каких-то значениях переменной получается верное числовое равенство, а при каких-то — нет.
Так вот:
Решить уравнение означает найти ВСЕ такие значения переменной, при подстановке которых в исходное уравнение получается верное равенство. Или, более научно, верное тождество. Или доказать, что таких значений переменной не существует.
Что такое верное равенство? Это равенство, не вызывающее сомнений даже у человека, абсолютно не отягощённого глубокими математическими познаниями. Например, 5=5, 0=0, -10=-10. И так далее. 🙂
Значения переменной, при подстановке которых достигается это самое верное равенство, называются очень красиво и научно — корни уравнения.
Корень может быть один, может быть несколько.
А может быть и бесконечно много корней — целый интервал или даже вообще вся числовая прямая от –∞ до +∞. Да, такое тоже бывает! Всё от конкретного уравнения зависит.)
А бывает и такое, что нельзя найти такие иксы, которые давали бы нам верное равенство. Принципиально нельзя. По определённым причинам. Нету таких иксов…
В таких случаях обычно говорят, что уравнение не имеет корней.
Для чего нужны уравнения?
Вопрос смешной. Для жизни! В школе, как правило, уравнения нужны для решения текстовых задач. Это, напоминаю, задачи на движение, на работу, на проценты и многие другие.
А во взрослой жизни без уравнений невозможны было бы ответить даже на самые обычные, но жизненно важные вопросы повседневности: какая будет погода завтра, выдержит ли заданную нагрузку здание. Или лифт. Или самолёт. Куда попадёт ракета… И не было бы сейчас среди нас ни синоптиков, ни инженеров, ни бухгалтеров, ни экономистов, ни программистов… За ненадобностью.
Внушает?)
Почему это так? А потому, что уравнениями описываются почти все известные человеку природные явления и процессы. Изменение давления и температуры воздуха с высотой, закон всемирного тяготения, размножение бактерий, радиоактивный распад, химические реакции, электричество, спрос и предложение — в основе всего этого лежат математические уравнения! Простые, сложные — всякие. Какое явление или ситуация, такое и уравнение.)
Итак, запоминаем:
Уравнения — очень мощный и универсальный инструмент для решения самых разных прикладных задач.
А какие бывают уравнения?
Уравнений в математике несметное количество. Самых разных видов. Но всё многообразие уравнений можно условно разделить всего на 4 категории:
1. Линейные,
2. Квадратные,
3. Дробные (или дробно-рациональные),
4. Прочие.
Разные категории уравнений требуют и разного подхода к их решению: линейные уравнения решаются одним способом, квадратные — другим, дробные — третьим, тригонометрические, логарифмические, показательные и прочие — тоже решаются своими методами.
Прочих уравнений, разумеется, больше всего, да…) Это и иррациональные, и тригонометрические, и показательные, и логарифмические, и многие другие уравнения. И даже дифференциальные уравнения (для студентов), где роль неизвестного играет не число, а функция. Или даже семейство функций. 🙂
В соответствующих уроках мы подробно разберём все эти типы уравнений. А здесь у нас — базовые приёмы и правила.
Называются эти правила — тождественные (или — равносильные) преобразования уравнений. Их всего два. И нигде их не обойти. Так что знакомимся!
Как решать уравнения? Тождественные (равносильные) преобразования уравнений.
Решение любого уравнения заключается в поэтапном преобразовании входящих в него выражений. Но преобразований не абы каких, а таких, чтобы от шага к шагу суть всего уравнения не менялась. Несмотря на то, что после каждого преобразования уравнение будет видоизменяться и, в конечном счёте, станет совсем не похоже на исходное.
Такие преобразования в математике называются равносильными или тождественными. Их довольно много, но среди всего многообразия тождественных преобразований уравнений выделяется два базовых. О них и пойдёт речь в этом уроке. Да-да, всего два! Но — крайне важных! И каждое из них заслуживает отдельного внимания.
Применение этих двух тождественных преобразований в том или ином порядке гарантирует успех в решении 99% уравнений математики. Заманчиво, правда?
Итак, вперёд!
Первое тождественное преобразование:
К обеим частям уравнения можно прибавить (или отнять) любое (но одинаковое!) число или выражение (в том числе и с переменной). Суть уравнения от этого не изменится.
Это преобразование вы применяете всюду, наивно думая, что переносите какие-то члены из одной части уравнения в другую, меняя знаки. 🙂
Например, такое крутое уравнение:
Тут и думать нечего, перебрасываем тройку вправо, меняя минус на плюс:
А что же происходит в действительности? А на самом деле вы… прибавляете к обеим частям уравнения тройку!
Вот что у вас происходит:
И результат получается тем же самым:
Вот и всё.
Слева остаётся чистый икс (чего мы, собственно, и добиваемся), а справа — что уж получится. Но самое главное то, что от прибавления тройки к обеим частям суть всего уравнения не изменилась!
Дело в том, что привычный нам перенос слагаемых из одной части в другую со сменой знака — это просто сокращённый вариант первого тождественного преобразования.
И зачем нам так глубоко копать? В уравнениях — незачем. Переносите себе спокойно и не парьтесь. Только знаки менять не забывайте.) А вот в неравенствах привычка к переносу может и слегка обескуражить, да…
Это было первое тождественное преобразование. Переходим ко второму.
Второе тождественное преобразование:
Обе части уравнения можно умножить (разделить) на одно и то же отличное от нуля число или выражение.
Это тождественное преобразование мы вы постоянно применяете, когда решаете что-нибудь совсем уж жуткое типа:
Тут каждому ясно, что х=3.
А вот как вы получили этот ответ? Подобрали? Угадали?
Чтобы не подбирать и не гадать (мы с вами математики, а не гадалки), нужно понять, что вы просто поделили обе части уравнения на четвёрку. Которая нам и мешает.
Вот так:
Эта палка с делением означает, что на четвёрку делятся обе части нашего уравнения. Через дроби эта процедура выглядит так:
Слева четвёрки благополучно сокращаются, остаётся икс в гордом одиночестве. А справа при делении 12 на 4 получается, понятное дело, тройка. 🙂
И все дела.)
Звучит невероятно, но эти два (всего два!) простых преобразования лежат в основе решения всех уравнений математики! Да-да, именно всех, я нисколько не преувеличиваю! От линейных и квадратных в школе до дифференциальных в ВУЗе.)
Ну что, посмотрим на тождественные преобразования уравнений в действии?
Применение тождественных преобразований к решению уравнений.
Начнём с первого тождественного преобразования. Переноса вправо-влево.
Пример для новичков:
1 — х = 3 — 2х
Дело нехитрое. Это линейное уравнение. Работаем прямо по заклинанию: «С иксами влево, без иксов — вправо».
Эта мантра — универсальная инструкция по применению первого тождественного преобразования. Вот и смотрим на уравнение. Какое слагаемое с иксом у нас справа? Что? 2х? Не-а!) Справа у нас -2х (минус два икс)! Поэтому при переносе в левую часть минус поменяется на плюс:
1 — х +2х = 3
Полдела сделано, иксы собрали слева. Осталось все числа собрать справа. Слева в уравнении стоит единичка. Опять вопрос — с каким знаком? Ответ «с никаким» не катит.) Слева перед единицей и вправду ничего не написано. А это значит, что перед ней стоит знак «плюс».
Так уж в математике повелось: ничего не написано — значит, плюс.)
И поэтому вправо единичка перенесётся уже с минусом:
-х + 2х = 3 — 1
Вот почти и всё. Слева приводим подобные, а справа — считаем. И получаем:
х = 2
Это было совсем примитивное уравнение.
Теперь пример покруче, для старшеклассников:
Решить уравнение:
Уравнение логарифмическое. Ну и что? Какая разница? Всё равно первым шагом делаем базовое тождественное преобразование («С иксами влево ….»). Для этого слагаемое с иксом (то есть, —log3x) переносим влево. Со сменой знака:
А числовое выражение (log34) переносим вправо. Также со сменой знака, разумеется:
Вот и всё.
Справа получилась чистая формула. Кто дружит с логарифмами, тот в уме дорешает уравнение и получит:
х=3
Что? Хотите синусы? Пожалуйста, вот вам синусы:
И снова всё то же самое! Выполняем первое тождественное преобразование — переносим sin x влево (с минусом), а -0,25 переносим вправо (с плюсом):
Получили простейшее тригонометрическое уравнение с синусом, решить которое (для знающих) также не составляет никакого труда.
Видите, насколько универсально первое равносильное преобразование! Встречается везде и всюду и не обойти его никак… Именно поэтому так важно уметь его делать на автомате и без ошибок.
Собственно, ошибиться здесь можно лишь в одном — забыть сменить знак при переносе. Что и происходит сплошь и рядом. Внимательность никто не отменял, да…)
Ну что, продолжаем наши игры? Развлекаемся теперь со вторым преобразованием!)
Решить уравнение:
7х=28
Крутяк, прямо скажем.
) Ладно, это эмоции…
Смотрим и соображаем: что нам мешает в этом уравнении? Что-что… Да семёрка мешает! Хорошо бы от неё избавиться. Да так, чтобы исходное уравнение не испортить.)
Но как? Перенести вправо? Ээээ… Стоп! Нельзя.) Семёрка с иксом умножением связана. Коэффициент, видите ли.) Нельзя её оторвать от икса и вправо перенести. Вот всё выражение 7х целиком — пожалуйста (вопрос — зачем?). А семёрку отдельно — никак нет.
Самое время про умножение/деление вспомнить! Нам ведь в ответе чистый икс нужен, не так ли? А семёрка — мешает. Вот и делим левую часть на семь. «Очищаем» икс от коэффициента. Так нам надо. Но тогда и правую часть тоже надо поделить на семь: этого уже математика требует. Что уж там получится, то и получится. Но пример хороший. Я старался.) 28 на 7 замечательно делится. Получится 4.
Ответ: х=4
Или такое уравнение:
Что здесь нам мешает? Дробь 1/6, не так ли? Вот давайте и избавимся от неё.
Безопасно для уравнения.) Как? Ну, можно поступить аналогично — поделить обе части на эту самую 1/6. Но в уме это не очень удобно. Кое-кто и запутается…
Но мы же не только делить, мы ещё и умножать умеем!) Вспоминаем из младших классов, после какого действия у нас пропадает дробь? Правильно! Дробь у нас пропадает при умножении на число, равное (или кратное) её знаменателю. Вот и умножим обе части нашего уравнения на 6. Слева всё равно чистый икс получится, а умножение правой части на 6 — не самая трудная работа.)
Вот и всё.) Умножение обеих частей уравнения на нужное число позволяет сразу избавляться от дробей, минуя промежуточные выкладки, в которых, между прочим, запросто можно и ошибок наляпать. Короче дорога — меньше ошибок!
Теперь снова на машину времени и — в старшие классы:
Решить уравнение:
Чтобы добраться до икса и тем самым решить это крутое тригонометрическое уравнение, нам надо сначала получить слева чистый косинус, безо всяких коэффициентов.
А двойка мешает. 🙂 Вот и делим на 2 всю левую часть:
Но тогда и правую часть тоже придётся разделить на двойку: это уже МАТЕМАТИКЕ надо. Делим:
Получили справа табличное значение косинуса. И теперь уравнение решается за милую душу.)
Вот и вся премудрость. Как видите, тождественные преобразования уравнений — штука полезная. И при этом не самая сложная. Перенос да умножение/деление. Однако далеко не у всех они получаются с первого раза и без ошибок, ох не у всех… Основные проблемы здесь две.
Проблема первая (для малоопытных):
Иногда ученик думает, что упрощение уравнений делается по одному, раз и навсегда установленному правилу. И никак не может уловить и понять это правило: в каких-то примерах начинают с домножения (или деления), в каких-то — с переноса. Где-то три раза переносят и ни разу не домножают…
Например, такое линейное уравнение:
10х + 5 = 5х — 20
С чего начинать? Можно начать с переноса:
10х — 5х = -20 — 5
А можно сначала поделить обе части на пятёрку, а затем уж переносить.
Тогда сразу числа попроще станут:
Как видим, и так и сяк решать можно. И это — в примитивном примере! Вот и возникает у неопытных учеников вопрос: «Как правильно?»
По-всякому правильно! Кому как удобнее. 🙂 Универсального рецепта здесь нет и быть не может. Математика предлагает вам на выбор два вида преобразований уравнений. А порядок этих самых преобразований зависит исключительно от исходного уравнения, а также от личных предпочтений и привычек решающего.
Проблема вторая (для всех…ну… почти):
Ошибки в вычислениях. В преобразованиях постоянно приходится перемножать скобки. Заключать выражения в скобки и раскрывать скобки. Умножать и делить дроби. Работать со степенями… Короче, в наличии весь набор элементарных действий математики. Со всеми вытекающими…
Обе эти проблемы устраняются только одним способом — практикой. Исчезают сомнения и ошибки.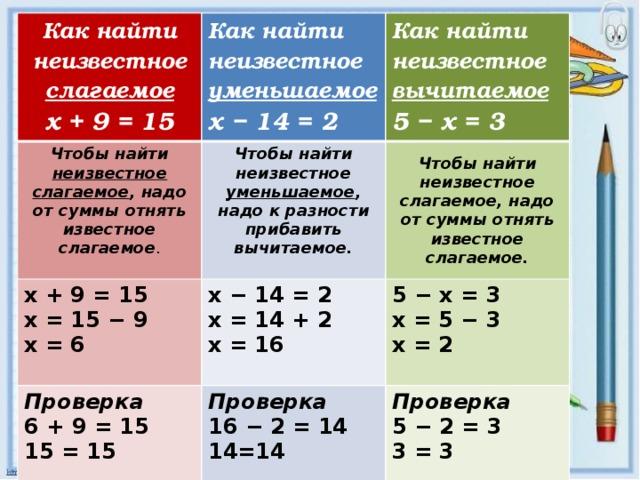
Примеры становятся проще, задания — легче. И в итоге не математика командует вами, а вы — математикой. 🙂
Решение простых уравнений
Решая простое уравнение, думайте об уравнении как о балансе, где знак равенства (=) является точкой опоры или центром. Таким образом, если вы делаете что-то с одной частью уравнения, вы должны сделать то же самое с другой стороной. Выполняя одно и то же действие с обеими сторонами уравнения (скажем, прибавляя по 3 к каждой стороне), уравнение остается сбалансированным.Решение уравнения – это процесс получения искомого или решения по одну сторону знака равенства, а всего остального по другую. Вы действительно сортируете информацию. Если вы решаете для x , вы должны получить x с одной стороны.
Уравнения сложения и вычитания
Некоторые уравнения включают только сложение и/или вычитание.
Пример 1
Найдите x .
x + 8 = 12
Чтобы решить уравнение x + 8 = 12, вы должны получить x отдельно с одной стороны.
Следовательно, вычтите 8 с обеих сторон.
Чтобы проверить свой ответ, просто подставьте его в уравнение:
Пример 2
Найдите y .
г – 9 = 25
Чтобы решить это уравнение, вы должны получить y отдельно с одной стороны. Поэтому прибавьте 9 к обеим сторонам.
Для проверки просто замените y на 34:
Пример 3
Найдите x .
x + 15 = 6
Чтобы решить, вычтите 15 с обеих сторон.
Для проверки просто замените x на –9 :
.
Обратите внимание, что в каждом случае выше используются противоположные операции ; то есть, если в уравнении есть сложение, вы вычитаете из каждой стороны.
Уравнения умножения и деления
Некоторые уравнения включают только умножение или деление. Обычно это происходит, когда переменная уже находится в одной части уравнения, но имеется более одной переменной, например 2 x или часть переменной, например
или
Таким же образом, как при сложении или вычитании, вы можете умножать или делить обе части уравнения на одно и то же число , если оно не равно нулю , и уравнение не изменится.
Пример 4
Найдите x .
3 x = 9
Разделите каждую часть уравнения на 3.
Для проверки замените x на 3:
Пример 5
Найдите y .
Чтобы решить, умножьте каждую сторону на 5.
Для проверки замените y на 35:
Пример 6
Найдите x .
Чтобы решить, умножьте каждую сторону на .
Или без отмены
Обратите внимание, что слева вы обычно не пишете, потому что это всегда отменяется до 1 x или x .
Комбинации операций
Иногда для решения уравнения приходится использовать более одного шага. В большинстве случаев сначала выполните шаг сложения или вычитания. Затем, после того как вы отсортировали переменные с одной стороны, а числа с другой, умножьте или разделите, чтобы получить только одну из переменных (то есть переменную без номера или 1 перед ней: x , а не 2 x ).
Пример 7
Решите для х .
2 x + 4 = 10
Вычтите 4 с обеих сторон, чтобы получить 2 x отдельно с одной стороны.
Затем разделите обе части на 2, чтобы получить x .
Для проверки подставьте свой ответ в исходное уравнение:
Пример 8
Найдите x .
5x – 11 = 29
Добавьте 11 с обеих сторон.
Разделите каждую сторону на 5.
Для проверки замените x на 8:
Пример 9
Найдите x .
Вычтите 6 с каждой стороны.
Умножить каждую сторону на .
Для проверки замените x на 9:
Пример 10
Найдите y .
Добавьте 8 с обеих сторон.
Умножить каждую сторону на .
Для проверки замените y на -25:
Пример 11
Найдите x .
3 x + 2 = x + 4
Вычесть 2 с обеих сторон (то же самое, что добавить -2).
Вычтите x с обеих сторон.
Обратите внимание, что 3 x – x равно 3 x – 1 x .
Разделите обе части на 2.
Для проверки замените x на 1:
Пример 12
Найдите y .
5 у + 3 = 2 у + 9
Вычесть 3 с обеих сторон.
Вычтите 2 y с обеих сторон.
Разделите обе части на 3.
Для проверки замените y на 2:
Иногда вам нужно упростить каждую сторону (объединить одинаковые термины) перед тем, как начать процесс сортировки.
Пример 13
Найти x .
3 x + 4 + 2 = 12 + 3
Во-первых, упростите каждую сторону.
Вычесть 6 с обеих сторон.
Разделите обе части на 3.
Для проверки замените x на 3:
Пример 14
Найдите x .
4 x + 2 x + 4 = 5 x + 3 + 11
Упростите каждую сторону.
6 x + 4 = 5 x + 14
Вычесть 4 с обеих сторон.
Вычтите 5 x с обеих сторон.
Для проверки замените x на 10:
Лучшие приложения и сервисы для решения математических уравнений на 2022 год
Учиться тяжело всем. Это долгий и утомительный процесс, и мы уверены, что вы бы предпочли заняться чем-нибудь другим.
Математика — отличный пример того, насколько сложной может быть учеба. У многих то, чему они научились в школе, не приходит в голову к тому времени, когда они возвращаются домой и начинают делать домашнее задание. И учителя хотят, чтобы вы показывали свою работу, что кажется глупым в эпоху цифровых технологий.
Хотя математика является важным навыком, многие сложности можно решить с помощью математических приложений. Хорошее приложение для решения математических задач поможет вам быстро найти правильные решения, а многие даже показывают шаги, которые потребовались для этого. Лучшие приложения полезны для широкого круга математических дисциплин, таких как алгебра, геометрия, тригонометрия, статистика и т. д.
Мы покажем вам, как решить любую математическую задачу с помощью некоторых невероятных пошаговых приложений для решения математических задач для вашего Mac, независимо от того, какой уровень математики вы изучаете в школе.
Как решить мою математическую задачу?
Прокладывая свой путь в сфере образования, вы узнаете все тонкости математики, что поможет решать уравнения вручную и понимать, как решать математические задачи. Как только вы поймете, как работает математика, знание того, как решать уравнения на бумаге, скорее всего, будет пустой тратой времени.
Это особенно верно, когда вы приступаете к продвинутой курсовой математике. В большинстве случаев утомительное написание задач от руки не нужно, нежелательно для инструкторов и требует много времени.
Вот несколько популярных вариантов решения математических уравнений:
- Продолжайте решать математические задачи шаг за шагом на бумаге . Если вы хотите положить карандаш на бумагу, будьте нашим гостем — но есть более простые способы!
- Посетите сайт бесплатного калькулятора алгебры . Есть много сайтов, которые позволяют вам вводить математические уравнения, чтобы увидеть решение. Большинство из них бесплатны для использования и могут предлагать пошаговые решения, но вы зависите от подключения к Интернету. Также неясно, используются ли ваши данные для чего-то еще, или сайт загружает вредоносное ПО на ваш компьютер без вашего ведома. За использование веб-сайта также может взиматься высокая плата за подписку.
- Использовать Excel . Вы можете использовать Microsoft Excel для некоторых математических вычислений, но для этого требуется много настроек, а интерфейс сильно отличается от других математических приложений и служб. Excel не предназначен для чистой математики, и это видно. Вы также не сможете экспортировать свои расчеты в формате, пригодном для исследовательских работ.
- Возьмите хороший калькулятор . Ни для кого не секрет, что многие студенты предпочитают решать математические уравнения с помощью калькулятора. Начиная с алгебры, почти у каждого ученика в сумке есть калькулятор. Это хорошие машины, ручные машины для математики, но есть способ получше.
- Загрузите собственное приложение . Хорошее родное математическое приложение для вашего Mac может быть любым и всем, что вам нужно. Это может быть калькулятор, инструмент для рисования и надежное средство решения математических задач с подробно изложенными шагами. Лучше всего то, что вам не нужно подключение к сети для использования собственных приложений!
Вы можете использовать Microsoft Excel для некоторых математических вычислений, но для этого требуется много настроек, а интерфейс сильно отличается от других математических приложений и служб. Excel не предназначен для чистой математики, и это видно. Вы также не сможете экспортировать свои расчеты в формате, пригодном для исследовательских работ.Лучшие математические приложения для решения уравнений для Mac
В математике уравнения определяются строго знаком равенства: =.
Когда вы видите знак равенства, у вас есть уравнение. Но это еще не все, что есть в уравнении, особенно в алгебраической математике и не только.
На снимке экрана выше первые пять (5) — это «коэффициент», а «x» называется «переменной». Знаки вычитания и плюса (-, +) определяются как «операторы», а последние пять (5) являются константой. Решение, ноль (0), также является константой. Все, что находится слева от знака равенства, называется «выражением».
Каждая сторона оператора определяется как «термин». В приведенном выше уравнении 5x, 8x, 5 и 0 являются членами. После введения оператора терм считается закрытым. Чтобы быть правильным, все в левой части уравнения должно быть равно решению в правой части знака равенства. Такие приложения, как MathKey, быстро решают такие задачи.
Математические уравнения сложны, и это одно из самых распространенных препятствий, которое приходится преодолевать каждому ученику. Как и MathKey, существует множество отличных приложений, которые могут помочь учащимся решать математические уравнения и создавать потрясающие отчеты для занятий.
Вы можете спросить: «Какое приложение подходит для решения моей математической задачи?» Как и математические задачи, приложения бывают самые разнообразные. Лучше сначала подумать о своих потребностях. Здесь мы обсудим приложения для решения математических задач и алгебраические калькуляторы, оба из которых полезны в зависимости от уровня математики, который вы изучаете, и ваших потребностей в ваших классах.
Лучшее средство решения математических уравнений
Опытные студенты-математики могут воспользоваться преимуществами MathKey и его невероятного движка LaTex. Другие на этом уровне и чуть ниже могут вместо этого использовать PocketCAS, который имеет некоторые мощные функции для студентов-математиков уровня колледжа.
PocketCAS позиционирует себя как «калькулятор TI-89, встроенный в вашу macOS», и это справедливая оценка. Он может строить графики в 2D или 3D, имеет встроенный редактор визуальных матриц, а также встроенные константы и символы, которые помогут вам вводить точные расчеты, которые вам нужны.
Если вы предпочитаете использовать свой iPhone или iPad, PocketCAS синхронизируется со своими приложениями для iOS и iPadOS через iCloud, чтобы вся ваша работа была в одном месте.
Первый пример, который мы предоставили, был алгебраическим, но как насчет более сложной математики, такой как тригонометрия? PocketCAS идеален. Его богатая библиотека символов поможет вам ввести любое уравнение, а также принимает ввод с клавиатуры. Когда вы вводите уравнения, PocketCAS идентифицирует компоненты этой переменной и меняет их цвет. В приведенном ниже примере «загар» стал фиолетовым, когда он был введен в PocketCAS:
Поскольку PocketCAS принимает ввод с клавиатуры, используйте встроенное сочетание клавиш (опция + 0) для символов градусов как принятых. приложение также может отображать графики, создавать 2D- или 3D-графики и составлять сценарии для ваших уравнений с помощью C-подобного механизма поддержки сценариев. Еще одна интересная особенность PocketCAS заключается в том, что когда вы делаете ошибку, просто дважды щелкнув решение в приложении, вы вернетесь в поле ввода уравнения, где вы сможете внести изменения.
Еще одно замечательное приложение для Mac, iPhone и iPad — Euclid. Он следует за более знакомым расположением функций, цифр и операторов в главном окне с решением вверху. Из всех приложений-калькуляторов, доступных для Mac, это самое похожее на калькулятор!
Евклид также невероятно силен. Одной из ключевых особенностей является то, что Euclid позволяет вам использовать ваши любимые формулы Excel, удобный инструмент, если вы использовали Excel для расчетов. Это также редактор LaTex, с легкостью вычисляющий даже самые трудоемкие уравнения.
Euclid также удобен для преобразования и утверждает, что может «преобразовать что угодно». Измерения, валюты, электричество — вы называете это, Евклид, вероятно, может преобразовать это. Одни только эти функции делают его отличным приложением для всех.
Лучший алгебраический калькулятор с шагами
Если вам нужно отличное приложение для алгебры для Mac, есть много отличных вариантов на выбор. Одним из наиболее популярных приложений является Numi, бесплатный калькулятор для вашего Mac, который использует ввод на естественном языке для решения уравнений.
Поскольку Numi использует естественный язык, он также позволяет вам определять свои собственные переменные. В приведенном ниже примере мы определили стоимость за единицу товара, а также скидку на заказ. Простое изменение суммы изменило окончательную стоимость; это отличный инструмент, если у вас есть определенная сумма, которую нужно потратить, и вам нужно точно знать, сколько товаров нужно заказать.
Вот как это делается:
- Откройте Numi на вашем Mac
- Введите имя переменной, а затем знак равенства
- Присвойте переменной значение
- Используйте предложение на естественном языке с именами ваших переменных, чтобы получить решение. Numi не требует изучения специальной языковой модели; просто напечатайте в обычном режиме и позвольте ему сделать все остальное
Когда вам нужно выйти за рамки обычного языка и простого преобразования, PocketCAS, вероятно, станет шагом вперед по сравнению с Numi.
Лучший блокнот-калькулятор
Калькуляторы предназначены для компьютеров, но калькулятор Soulver снова делает их людьми.
Вы можете вводить математические вычисления, функции, даты и преобразования единиц измерения, которые легко читать и форматировать, и приложение даст вам результаты, которые вы можете использовать.Это особенно полезно, если вы много работаете с различными комбинациями единиц измерения или часто используете одни и те же расчеты, но подставляете разные числа.
Заключение
Студенты-математики во всем мире могут извлечь пользу из упомянутых здесь замечательных приложений. Независимо от вашего уровня образования или потребностей, эти приложения помогут вам получить нужные результаты.
Все четыре приложения — Numi, Euclid, PocketCAS и Soulver — доступны бесплатно в рамках семидневной пробной версии Setapp, самого полного в мире набора приложений для повышения производительности для вашего Mac. Наряду с этими четырьмя замечательными приложениями у вас также будет полный доступ ко всей библиотеке Setapp, включающей почти 200 других родных приложений для Mac.
Вы можете вводить математические вычисления, функции, даты и преобразования единиц измерения, которые легко читать и форматировать, и приложение даст вам результаты, которые вы можете использовать.