Уравнения с параметром
Справочный материал
Уравнение вида f(x; a) = 0 называется уравнением с переменной х и параметром а.
Решить уравнение с параметром а – это значит, для каждого значения а найти значения х, удовлетворяющие этому уравнению.
Пример 1. ах = 0
- Если а = 0, то 0х = 0
х – любое действительное число - Если а 0, то х =
х = 0
Пример 2. ах = а
- Если а = 0, то 0х = 0
х – любое действительное число - Если а 0, то х =
х = 1

х + 2 = ах
х – ах = -2
х(1 – а) = -2
Если 1 – а = 0, т.е. а = 1, то х0 = -2 корней нет
Если 1 – а 0, т.е. а 1, то х =
Пример 4.
(а2 – 1) х = 2а2 + а – 3
(а – 1)(а + 1)х = 2(а – 1)(а – 1,5)
(а – 1)(а + 1)х = (1а – 3)(а – 1)
Если а = 1, то 0х = 0
х – любое действительное число
Если а = -1, то 0х = -2
Корней нет
Если а 1, а -1, то х = (единственное решение).
Это значит, что каждому допустимому значению а
соответствует единственное значение х.
Например:
если а = 5, то х = = ;
если а = 0, то х = 3 и т. д.
Дидактический материал
1. ах = х + 3
2. 4 + ах = 3х – 1
3. а = +
4. + 3(х+1)
5. = –
6. =
Ответы:
- При а 1 х =;
при а = 1 корней нет.
- При а 3 х = ;
при а = 3 корней нет.
- При а 1, а -1, а 0 х = ;
при а = 1 х – любое действительное число, кроме х = 1
при а = -1, а = 0 решений нет.
- При а 2, а 0 х = ;
при а = 0, а = 2 решений нет.
- При а -3, а -2, а 0, 5 х =
при а = -3, а = 0, 5, а = -2 решений нет
- При а + с 0, с 0 х = ;
при а = —с, с = 0 решений нет.
Квадратные уравнения с параметром
Пример 1. Решить уравнение
(а – 1)х2 = 2(2а + 1) х + 4а + 3 = 0
При а = 1 6х + 7 = 0
х = –
В случае а 1 выделим
те значения параметра, при которых Д
обращается в нуль.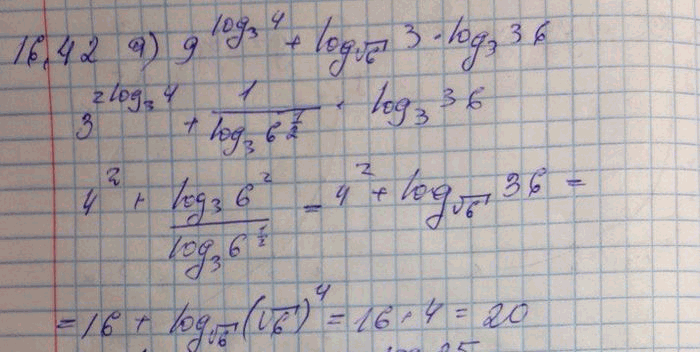
Д = (2(2а + 1))2 – 4(а – 1)(4а + 30 = 16а2 + 16а + 4 – 4(4а2 + 3а – 4а – 3) = 16а2 + 16а + 4 – 16а2 + 4а + 12 = 20а + 16
20а + 16 = 0
20а = -16
a =
a =
Если а < -4/5, то Д < 0, уравнение имеет действительный корень.
Если а > -4/5 и а 1, то Д > 0,
х =
Если а = 4/5, то Д
х = – = –
Пример 2. При каких значениях параметра а уравнение
х2 + 2(а + 1)х + 9а – 5 = 0 имеет 2 различных отрицательных корня?
Д = 4(а + 1)2 – 4(9а – 5) = 4а2 – 28а + 24 = 4(а – 1)(а – 6)
4(а – 1)(а – 6) > 0
по т. Виета: х1 + х2 = -2(а + 1)
Виета: х1 + х2 = -2(а + 1)
х1х2 = 9а – 5
По условию х1 < 0, х2 < 0 то –2(а + 1) < 0 и 9а – 5 > 0
| В итоге | 4(а – 1)( а – 6) > 0 — 2(а + 1) < 0 9а – 5 > 0 |
а < 1: а > 6 а > — 1 а > 5/9 |
(Рис. 1) < a < 1, либо a > 6 |
Пример 3. Найдите значения а, при которых данное уравнение имеет решение.
х2 – 2(а – 1)х + 2а + 1 = 0
Д = 4(а – 1)2 – 4(2а + 10 = 4а2 – 8а + 4 – 8а – 4 = 4а2 – 16а
4а2 – 16 0
4а(а – 4) 0
а(а – 4)) 0
а(а – 4) = 0
а = 0 или а – 4 = 0
а = 4
(Рис.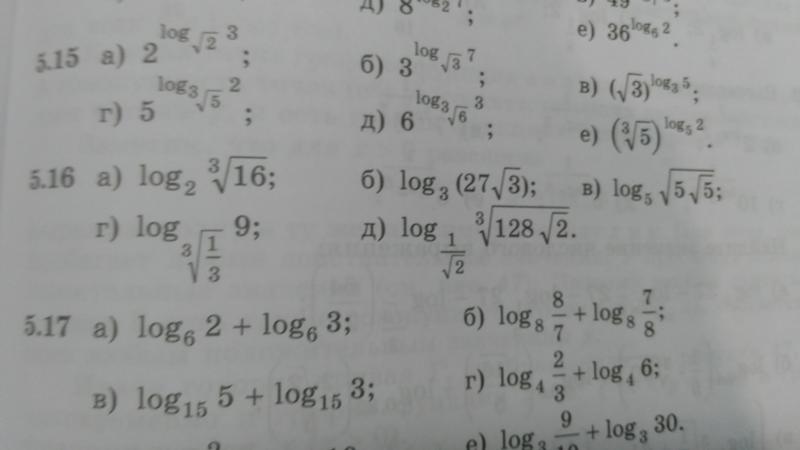 2)
2)
Ответ: а 0 и а 4
Дидактический материал
1. При каком значении а уравнение ах2 – (а + 1) х + 2а – 1 = 0 имеет один корень?
2. При каком значении а уравнение (а + 2) х2 + 2(а + 2)х + 2 = 0 имеет один корень?
3. При каких значениях а уравнение (а2 – 6а + 8) х2 + (а2 – 4) х + (10 – 3а – а2) = 0 имеет более двух корней?
4. При каких значениях а уравнение 2х2 + х – а = 0 имеет хотя бы один общий корень с уравнением 2х
2 – 7х + 6 = 0?5. При каких значениях а уравнения х2 +ах + 1 = 0 и х2 + х + а = 0 имеют хотя бы один общий корень?
Ответы:
1.
При а = — 1/7, а = 0, а = 1
2. При а = 0
3. При а = 2
4. При а = 10
5. При а = — 2
Показательные уравнения с параметром
Пример 1.Найти все значения а, при которых уравнение
9х – (а + 2)*3х-1/х +2а*3-2/х = 0 (1) имеет ровно два корня.
Решение. Умножив обе части уравнения (1) на 32/х, получим равносильное уравнение
32(х+1/х) – (а + 2)*3х+1/х + 2а = 0 (2)
Пусть 3х+1/х = у, тогда уравнение (2) примет вид у2 – (а + 2)у + 2а = 0, или
(у – 2)(у – а) = 0, откуда у1 =2, у2 = а.
Если у = 2, т.е. 3х+1/х = 2 то х + 1/х =
log32 , или х2 – хlog32 + 1 = 0.
Это уравнение не имеет действительных корней, так как его Д = log232 – 4 < 0.
Если у = а, т.е. 3х+1/х = а то х + 1/х = log3а, или х2 – хlog3а + 1 = 0. (3)
Уравнение (3) имеет ровно два корня тогда и только тогда, когда
Д = log232 – 4 > 0, или |log3а| > 2.
Если log3а > 2, то а > 9, а если log3а < -2, то 0 < а < 1/9.
Ответ: 0 < а < 1/9, а > 9.
Пример 2. При каких значениях а уравнение 22х – (а – 3) 2х – 3а = 0 имеет решения?
Для того чтобы заданное уравнение имело
решения, необходимо и достаточно, чтобы
уравнение t2 – (a – 3) t – 3a = 0
имело хотя бы один положительный корень.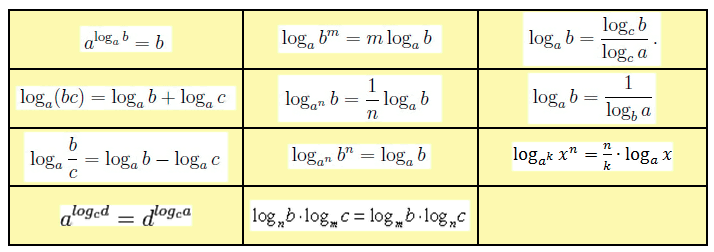 Найдем
корни по теореме Виета: х1 = -3, х2
= а = >
Найдем
корни по теореме Виета: х1 = -3, х2
= а = >
а – положительное число.
Дидактический материал
1. Найти все значения а, при которых уравнение
25х – (2а + 5)*5х-1/х + 10а * 5-2/х = 0 имеет ровно 2 решения.
2. При каких значениях а уравнение
2(а-1)х?+2(а+3)х+а = 1/4 имеет единственный корень?
3. При каких значениях параметра а уравнение
4х — (5а-3)2х +4а2 – 3а = 0 имеет единственное решение?
Ответ:
- 0 < а < 1/50, а > 25/2
- при а = 1, а = -2,2
- 0 < а 3/4 и а = 1
Логарифмические уравнения с
параметром
Пример 1.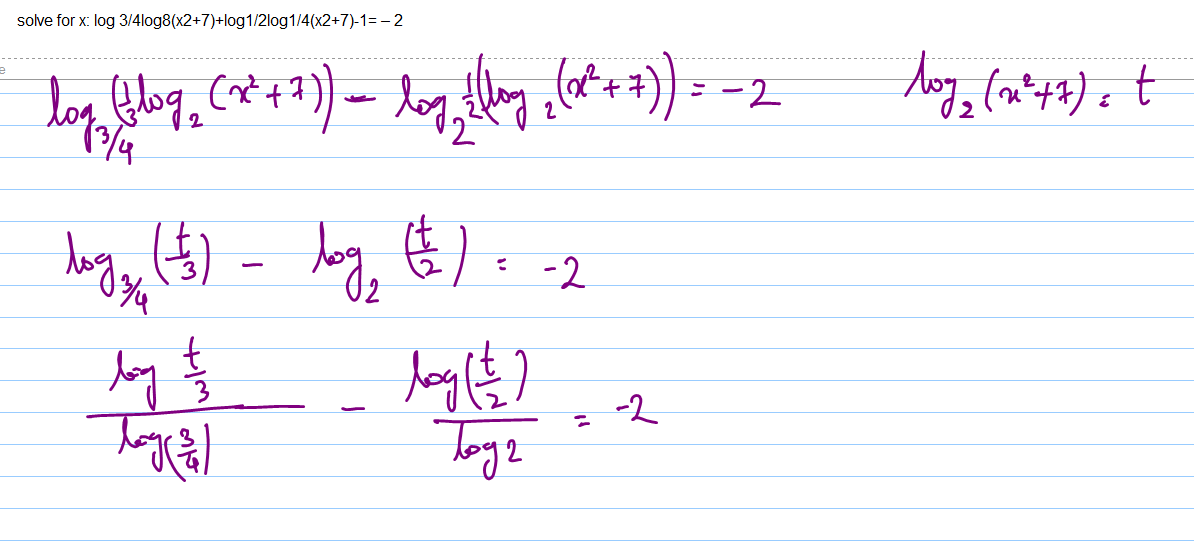 Найти все значения а,
при которых уравнение
Найти все значения а,
при которых уравнение
log4x(1 + ах) = 1/2 (1)
имеет единственное решение.
Решение. Уравнение (1) равносильно уравнению
1 + ах = 2х при х > 0, х 1/4 (3)
х = у
ау2 –у + 1 = 0 (4)
| Если а = 0, то – | 2у + 1 = 0 2у = 1 у = 1/2 х = 1/2 х = 1/4 |
Не выполняется (2) условие из (3).
Пусть а 0, то ау2 – 2у + 1 = 0 имеет действительные корни тогда и только тогда, когда Д = 4 – 4а 0, т.е. при а 1.
Если Д = 0 (а = 1), то (4) имеет единственный
положительный корень х = 1, удовлетворяющий
условиям (3).
Пусть Д > 0 (а < 1), тогда уравнение (4) имеет два различных корня. Так как у = х 0, то в случае Д > 0 уравнение (4) имеет действительные корни разных знаков. Это условие выполняется тогда и только тогда, когда Д > 0 и 1/а < 0, т.е. при а < 0.
Пример 2. Найти все значения а, при которых уравнение
log5(x = 2-a ) – log1/5(a-1-x) = log259 имеет решение.
Решение. log5(x + 2-a) –log5(f – 1 – x) = log53
(1) х + 2 – а = 3(а – 1 – х), если
(2) а – 1 > х
Выражая х из (1) и подставляя в (2), получаем неравенство
2 – а > 1 – а (3)
Чтобы решить неравенство (3), построим графики
функций у = 2 – а и
у = 1 – а.
Рис. 3
Решения неравенства (3) образуют промежуток (а0; 2), где а0 < 0 и а0 – корень уравнения 2 – а = 1 – а.
Тогда 2 – а = (1– а)2
а2 – а – 1 = 0
а0 =
Ответ: < a 2
Дидактический материал
- Найдите, при каких значениях а уравнение log 3 (9x + 9a3)= x имеет ровно два корня.
- Найдите, при каких значениях а уравнение log 2 (4x – a) = x имеет единственный корень.
- При каких значениях а уравнение х – log 3 (2а
– 9х) = 0 не имеет корней.

Ответы:
- при а < 1/3 36
- при а = -1/4
- при а < -1/8
Литература
Гусев В.А., Мордкович А.Г. Математика.
Справочные материалы. – М.: Просвещение, 1990.
 – М.: Просвещение,
2001.
– М.: Просвещение,
2001.Логарифмические уравнения
Репетиторы ❯ Математика ❯ Логарифмические уравнения
Автор: Валентин В., онлайн репетитор по математике
●
29.10.2011
●
Раздел: Математика
Для начала обратимся к задаче.
Задача.
Решить уравнение log2 (х + 1) + log2 (х + 3) = 3 (1).
Решение.
Предположим, что х – такое число, при котором равенство (1) является верным, т.е х – корень уравнения (1). Тогда, опираясь на свойство логарифма, получаем верное равенство log2 (х + 1)(х + 3) = 3 (2). По определению логарифма из этого равенства получаем:
(х + 1)(х + 3) = 8, откуда х2 + 4х + 3 = 8,
т.е. х2 + 4х – 5 = 0.
Последнее равенство верно, если х1 = 1 или х2 = -5.
Итак, результатом предположения, что число х – корень уравнения (1), стало доказательство того, что х может быть равным или 1 или -5.
Проверим, являются ли полученные числа корнями уравнения (1). Подставляем х = 1 в левую часть данного уравнения и получаем
log2 (1 + 1) + log2 (1 + 3) = log2 2 + log2 4 = 1 + 2 = 3,
т.е. х = 1 – корень уравнения (1).
При х = -5 числа х + 1 и х + 3 отрицательны, и поэтому левая часть уравнения (1) смысла не имеет, то есть х = -5 не является корнем рассматриваемого уравнения.
Ответ. х = 1.
Заметим, что х = -5 является корнем уравнения (2), т.к. log2 (-5 + 1)(-5 + 3) = log2 8 = log2 23 = 3.
Получается, что число х = 1 является корнем и уравнения (1), и уравнения (2), а число х = -5 не является корнем уравнения (1), но при этом является корнем уравнения (2). Таким образом, при получении из уравнения (1) уравнения (2) корень х = 1 сохранился, но и появился посторонний корень х = -5. В таком случае уравнение (2) получило название следствия уравнения (1).
!!! Следствием первого уравнения называется второе уравнение, если все корни первого уравнения являются корнями второго уравнения.
Отметим, что в уравнении, которое является следствием данного, появление посторонних корней не рассматривается как обязательное явление; важно лишь не потерять корни исходного уравнения.
В большинстве случаев, как и в рассмотренной задаче, уравнение решается постепенным «передвижением» к более простым уравнениям – следствиям исходного уравнения. В таких случаях после нахождения корней необходима их проверка.
В таких случаях после нахождения корней необходима их проверка.
Рассмотрим задачу.
Задача.
Решить уравнение log2 (1 – х) = 3 – log2 (3 – х).
Решение.
1) Перенесем логарифм из правой части в левую: log2 (1 – х) + log2 (3 – х) = 3, откуда
log2 (1 – х)(3 – х) = 3 → (1 – х)(3 – х) = 8.
2) Решим полученное уравнение. Получим х1 = 5, х2 = -1.
3) Проведем проверку корней уравнения. Число х1 = 5 не является корнем исходного уравнения, так как при
х = 5 теряют смысл левая и правая части уравнения. Число х2 = -1 является корнем исходного уравнения.
Ответ. х = -1.
Равносильными называются уравнения, имеющие одно и то же множество корней. В частности, если два уравнения корней не имеют, они также являются равносильными.
Отметим, что любое из двух равносильных уравнений является следствием другого.
Напомним, что уравнение приводит нас к уравнениям, равносильным ему, в результате следующих преобразований:
1) можно переносить из одной части в другую любой член уравнения, помня при этом, что знак этого компонента необходимо заменить на противоположный;
2) можно умножить или разделить на одно и то же число обе части уравнения при условии, что это число не равно нулю.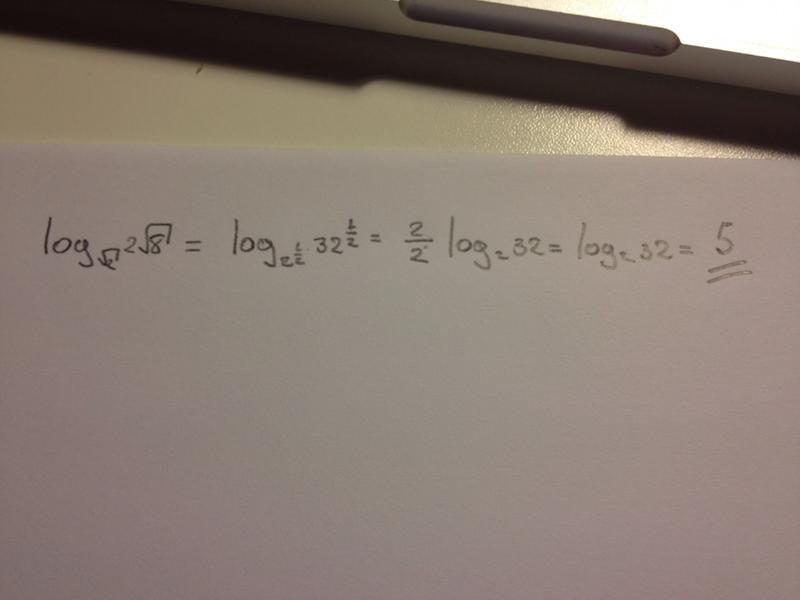
Однако не при любом преобразовании уравнение меняется на равносильное. Например, если мы возведем в квадрат обе части уравнения √х = х – 2, то получим уравнение х = (х – 2)2, которое является следствием первого, но в то же время не равносильно ему. Поэтому после решения второго уравнения обязательно необходимо проверить, являются ли его корни корнями исходного уравнения.
!!! Следует помнить, что при делении обеих частей уравнения на выражение, которое содержит неизвестное, может произойти потеря корней. Следовательно, уравнение, в обеих частях которого есть общий множитель, решают путем переноса всех членов в одну часть и разложения на множители.
При решении уравнений важно не потерять корни, а вот посторонние корни можно установить посредством проверки. Поэтому необходимо следить за тем, чтобы при преобразовании уравнения каждое последующее уравнение было следствием предыдущего.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
Математика
Курсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Математика
Курсы по геометрии 8 класс
Французский язык
Курсы французского языка для начинающих
3-8log((sqrt(2)+1))(sqrt(2)-1)=
- Курс
- NCERT
- Класс 12
- Класс 11
- Класс 1 0
- Класс 9
- Класс 8
- Класс 7
- Класс 6
- IIT JEE
- NCERT
- Экзамен
- JEE MAINS 90 907 JEE ADVANCED
- X BOARDS
- XII BOARDS
- NEET
- Neet Предыдущий год (по годам)
- Физика Предыдущий год
- Химия Предыдущий год
- Биология Предыдущий год
- Нет Все образцы работ
- Образцы работ Биология
- Образцы работ Физика
- Образцы работ Химия 909 12
- Скачать PDF-файлы
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8
- Класс 7
- Класс 6
- Экзаменационный уголок
- Онлайн-класс
- Викторина
- Задать вопрос в Whatsapp
- Поиск Doubtnut
- Английский словарь
- Toppers Talk
- Блог
- О нас Us
- Карьера
- Скачать
- Получить приложение
Вопрос
Обновлено: 07.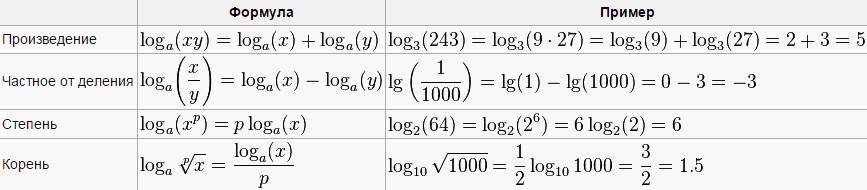


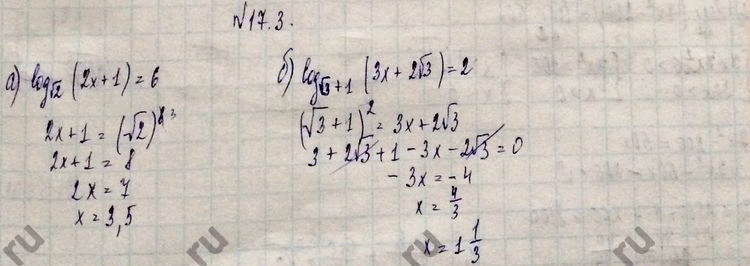 При а = — 1/7, а = 0, а = 1
При а = — 1/7, а = 0, а = 1