Длина окружности формула по диаметру: Длина окружности. Площадь круга — урок. Математика, 6 класс.

Длина окружности — формула, как ее найти

Обновлено 22 июля 2021 Просмотров: 51 423 Автор: Дмитрий Петров

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня у нас очередная математическая тема. Ее проходят в 6-м классе. Называется она – ДЛИНА ОКРУЖНОСТИ.

Эта важная величина для решения многих задачек. В том числе и во время Единого госэкзамена.

Так что наша статья будет крайне полезна школьникам-выпускникам. А для всех остальных это хороший повод освежить свои знания.

Что такое окружность

Но для начала напомним, что называют окружностью.

Окружность – это кривая замкнутая линия, которая состоит из множества точек. И эти точки находятся на одном расстоянии от центра окружности.

Определение несколько «тяжеловатое», но это официальная формулировка, которая также приводится в школьных учебниках. Графически все выглядит гораздо проще.

Вот пример окружности, у которой все точки на кривой «С» равноудалены от центра «О».

Кстати, расстояние от центра до границы окружности называется радиус и обозначается он буквой «R».

А отрезок, который соединяет две точки на окружности и проходит через ее центр – это диаметр «D». И, как всем известно, диаметр – это два сложенных радиуса (D = 2R).

Интересный факт! Точка тоже является в некотором роде окружностью. В математике ее называют «окружностью нулевого радиуса».

А чтобы начертить правильную окружность, нужно воспользоваться специальным прибором – циркулем. Им же можно нарисовать и окружность нужного радиуса.

Длина окружности через диаметр

Зачем мы так подробно рассказали о самой окружности, ее радиусе и диаметре? Все просто – без них не обойтись при расчете длины окружности.

Эту зависимость заметили еще в Древнем Египте. Тогдашние математики были весьма продвинуты в различных инженерных расчетах. Достаточно вспомнить, насколько надежно построены пирамиды. Им более 5 тысяч лет, а кажется, что простоят еще столько же и даже больше.

Так вот, египтяне определили, что соотношение длины окружности и ее диаметра – величина постоянная.

Другими словами, если взять совершенно разные по размерам окружности, а потом поделить их длины на их же диаметры, то получится одно и то же число.

У египтян это было число 3. Но впоследствии было получено более точное значение, которое равно 22/7 или 3 целых и 1/7.

Так появилась математическая постоянная «ПИ». Сейчас это один из столпов науки, с помощью которого решаются многие задачи.

Кстати, само название «пи» происходит от греческого слова «περιφέρεια», что как раз переводится как окружность. А «περίμετρος» — это диаметр.

Этими обозначениями и воспользовался математик Леонард Эйлер, когда в 1737 году представил научному сообществу число «пи», обозначив его изначально буквой выше упомянутых слов.

И сейчас уже каждый школьник знает, что число «пи» равно 3,14. Это значение взято за базовое, хотя на самом деле в нем бесконечное количество знаков после запятой.

Формула длины окружности

Ну а теперь главный вывод из этого исторического экскурса. Согласно вычислениям еще древнеегипетских ученых, формула длины окружности выглядит так:

Но чаще всего эту формулу принято писать без знаков умножения:

Формула эта единственная. И других возможностей рассчитать длину окружности — нет. Хотя ее можно представить, как диаметр умноженный на ПИ, но это уже банальность.

Вот и все, что мы хотели рассказать по этой теме, а более подробно смотрите в приведенном видеоролике:

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

• Математика

Длина окружности. Онлайн калькулятор.

1. Длина окружности по радиусу
2. Длина окружности по диаметру
3. Длина окружности по площади
4. Длина окружности по стороне вписанного квадрата
5. Длина окружности по стороне описанного квадрата
6. Длина окружности по стороне вписанного правильного треугольника
7. Длина окружности по стороне описанного правильного треугольника
8. Длина окружности по стороне вписанного правильного многоугольника
9. Длина окружности по стороне описанного правильного многоугольника

Длина окружности по радиусу

Введите радиус

Формула длины окружности по радиусу

P=2πR

Где R — радиус окружности, π=3. 1415926536

Длина окружности по диаметру

Введите диаметр

Формула длины окружности по диаметру

P=πd

Где d — диаметр окружности, π=3.1415926536

Длина окружности по площади

Введите площадь

Формула длины окружности по площади

Из формулы площади окружности выразим радиус R

Подставим радиус R в формулу длины окружности через радиус

Где S — площадь окружности, π=3.1415926536

Длина окружности по стороне вписанного квадрата

Введите сторону a

Формула длины окружности по стороне вписанного квадрата

По теореме пифагора

Подставим диаметр d в формулу длины окружности через диаметр

Где a — сторона квадрата, π=3.1415926536

Длина окружности по стороне описанного квадрата

Введите сторону a

Формула длины окружности по стороне описанного квадрата

Т.к. диаметр равен стороне описанного около окружности квадрата

P=πd=πa

Где a — сторона описанного около окружности квадрата, π=3. 1415926536

Длина окружности по стороне вписанного правильного треугольника

Введите сторону a

Формула длины окружности по стороне вписанного в неё правильного треугольника

Т.к. в равностороннем треугольнике медианы равны и в точке пересечения делятся в отношении 2:1. А точка пересечения будет центром окружности.

Из этого следует что нам нужно найти радиус окружности, а он будет равен 2/3 от медианы(высоты) BD.

По теореме Пифагора найдём BD.

Подставим полученный радиус в формулу окружности по радиусу

Где a — сторона правильного треугольника, π=3.1415926536

Длина окружности по стороне описанного правильного треугольника

Введите сторону a

Формула длины окружности по стороне описанного правильного треугольника

Т.к. в равностороннем треугольнике медианы равны и в точке пересечения делятся в отношении 2:1. А точка пересечения будет центром окружности.

Из этого следует что нам нужно найти радиус окружности, а он будет равен 1/3 от медианы(высоты) BD т. е. OD.

По теореме Пифагора найдём BD.

Подставим полученный радиус в формулу окружности по радиусу

Где a — сторона правильного треугольника, π=3.1415926536

Длина окружности по стороне вписанного правильного многоугольника

Введите сторону многоугольника

Введите количество вершин многоугольника

Формула длины окружности по стороне вписанного правильного многоугольника

Проведём из центра окружности к двум ближайшим вершинам A и C отрезки. Т.к. они одинаковые обозначим их за x. Т.к. вершины лежат на окружности то длина этих отрезков и будет радиусом окружности.

В итоге у нас получится равнобедренный треугольник ACO с двумя равными сторонами AO и CO.

Проведём высоту OB

Угол y будет равен 360/2n=180/n, где n-количество вершин многоугольника.

y=180/n

AB=a/2

Из прямоугольного треугольника ABO следует

Выразим x

Т.к. x=R

Где a — сторона правильного многоугольника, π=3.1415926536, n — количество вершин многоугольника

Длина окружности по стороне описанного правильного многоугольника

Введите сторону многоугольника

Введите количество вершин многоугольника

Формула длины окружности по стороне описанного правильного многоугольника

Проведём из центра окружности к двум ближайшим вершинам A и C отрезки. Получится равнобедренный треугольник ACO. С вершины O треугольника проведём высоту. Которая разделит сторону AC пополам в точке B.

Угол y будет равен 360/2n=180/n, где n-количество вершин многоугольника.

y=180/n

AB=a/2

Из прямоугольного треугольника ABO следует

Выразим x

Т.к. x=R

Где a — сторона правильного многоугольника, π=3.1415926536, n — количество вершин многоугольника

Видео-вопрос: определение диаметра круга по длине его окружности

Стенограмма видео

Используя три целых четыре десятых, чтобы аппроксимировать 𝜋, каков диаметр круга с окружностью сто двадцать пять целых шесть сантиметров.

Итак, вот небольшой набросок того, что мы знаем. Окружность составляет сто двадцать пять целых шесть десятых сантиметра, и мы пытаемся найти диаметр этой окружности. Теперь у нас есть две формулы, которые говорят нам о длине окружности. Во-первых, длина окружности равна 𝜋, умноженному на диаметр круга, а во-вторых, она равна удвоенному 𝜋, умноженному на радиус круга. Теперь помните, что диаметр — это расстояние от одной части окружности до противоположной части окружности по прямой линии через центр окружности. А радиус — это расстояние от центра круга до окружности круга, так что это половина диаметра.

Теперь мы знаем длину окружности и ищем диаметр. Итак, похоже, что первая формула будет для нас наиболее полезной. Тогда ладно. Давайте подставим полученную информацию и посмотрим, сможем ли мы изменить это уравнение, чтобы найти диаметр. Нам говорят, что длина окружности составляет сто двадцать пять целых шесть десятых сантиметра. Нам говорят использовать три целых четыре десятых в качестве приблизительного значения для 𝜋. И мы хотим знать, каков диаметр.

Так что давайте просто назовем это d. Таким образом, сто двадцать пять целых шесть десятых равняется трем целых четырем d. Теперь я просто хочу знать, что такое one times d. Итак, если я разделю правую часть этого уравнения на три целых четыре десятых, а затем разделю верхнюю часть и разделю нижнюю часть на три целых четыре десятых, эти вещи исчезнут. Но теперь я разбалансировал свое уравнение, поэтому мне нужно сделать то же самое с другой стороной. Три целых четыре десятых идут в знаменателе. Таким образом, d равно ста двадцати пяти целых шести десятых на три целых четыре десятых. А единицы — сантиметры. Но давайте посмотрим правде в глаза. Мы не собираемся писать это как наш ответ. Осталось немного посчитать. И у нас есть дробь, в которой есть десятичные дроби, так что это не очень хорошо.

Итак, давайте посмотрим, сможем ли мы вообще упростить эту дробь. Ну, что я собираюсь сделать, так это умножить низ на сотню и умножить верх на сотню, чтобы я мог избавиться от всех этих десятичных знаков. Поэтому я умножаю верх и низ на одно и то же число, чтобы они сокращались. Так что я не меняю размер этого числа, я просто меняю его на эквивалентную дробь. Таким образом, умножение числителя на сто дает мне двенадцать тысяч пятьсот шестьдесят. А умножив знаменатель на сто, я получаю триста четырнадцать. Теперь, если вы хорошо разбираетесь в таблице умножения на триста четырнадцать, вы будете знать, что триста четырнадцать умножить на сорок равно двенадцати тысячам пятистам шестидесяти. И вы сразу сможете добраться до правильного ответа. Но давайте предположим, что вы не так уж хороши. И давайте для начала сделаем более простую отмену с немного меньшими числами. Делим верх и низ на два. А половина от двенадцати тысяч пятисот шестидесяти составляет шесть тысяч двести восемьдесят. А половина от трехсот четырнадцати будет сто пятьдесят семь.

Когда мы этим занимались, я заметил, что триста четырнадцать умножить на два равно шестистам двадцати восьми, так что, похоже, это отменяется. Давайте перепишем шесть тысяч двести восемьдесят как триста четырнадцать раз с чем-то. Итак, триста четырнадцать умножить на два — это шестьсот двадцать восемь. Но я ищу шесть тысяч двести восемьдесят, поэтому мне нужно умножить на двадцать, чтобы получить шесть тысяч двести восемьдесят. Теперь мы знаем, что только что разделили триста четырнадцать на два и получили сто пятьдесят семь. Таким образом, мы можем переписать триста четырнадцать как сто пятьдесят семь раз два, что дает нашу дробь сто пятьдесят семь раз два раза по двадцать больше ста пятидесяти семи. Теперь, если я разделю верх на сто пятьдесят семь, а низ на сто пятьдесят семь, они оба сократятся. Итак, мой ответ: два раза по двадцать, то есть сорок.

И не забывая, что наши единицы измерения были в сантиметрах, ответ таков, что диаметр равен сорока сантиметрам.

Расчет соотношения диаметра и длины окружности

Все математические ресурсы GMAT

22 Диагностические тесты 693 практических теста Вопрос дня Карточки Learn by Concept

Помощь по математике GMAT » Проблемные вопросы » Геометрия » Круги » Диаметр » Расчет соотношения диаметра и длины окружности

Каково отношение длины окружности к диаметру любого круга?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы вычислить отношение длины окружности к диаметру, нам нужно уравнение, включающее обе переменные. Формула длины окружности выглядит следующим образом:

Нам нужно выразить радиус через диаметр. Радиус круга равен половине его диаметра, поэтому формулу можно переписать так:

Если мы разделим обе стороны на диаметр, то в левой части будет отношение длины окружности к диаметру: равно , что на самом деле является определением этой очень важной математической константы.

Сообщить об ошибке

Каково отношение диаметра любой окружности к длине окружности?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти соотношение между диаметром и длиной окружности, нам нужно использовать формулу для длины окружности:

Мы видим, что эта формула выражена в терминах радиуса, поэтому нам нужно выразить это так, что длина окружности выражается через диаметр.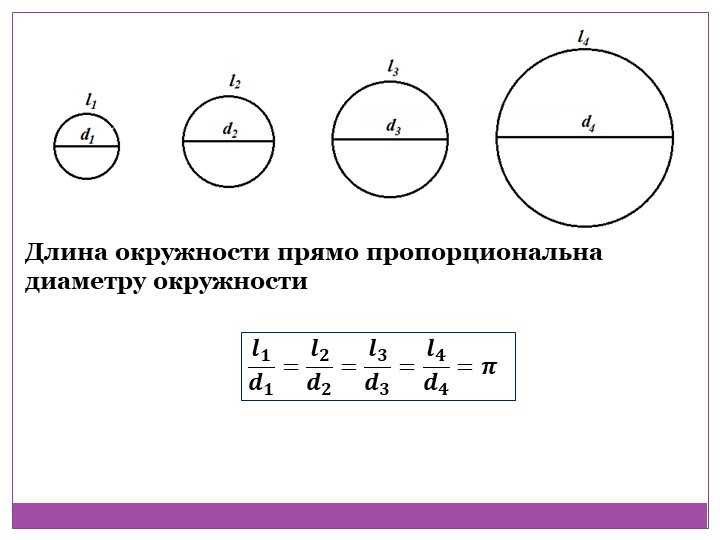 Используя знание того, что радиус равен половине диаметра:

Теперь, когда у нас есть простая формула, включающая длину окружности и диаметр, мы можем видеть, что у нас будет отношение диаметра к длине окружности, если мы разделим обе стороны на длину окружности. . Затем мы делим обе стороны на  , чтобы выделить отношение диаметра к длине окружности, и находим наше решение:

Сообщить об ошибке

Окружность с центром вписана в квадрат. Каково отношение диаметра к длине окружности, если площадь квадрата равна ?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы вычислить отношение диаметра к длине окружности квадрата, мы должны сначала получить диаметр, который равен длине стороны квадрата. Для этого нам просто нужно взять квадратный корень из площади квадрата, который равен 4.

Также мы должны помнить, что длина окружности определяется как , где  – длина радиуса.

Теперь заметим, что эту формулу тоже можно записать .

Соотношение, которое мы ищем, . Поэтому это соотношение будет всегда  и это наш окончательный ответ.

Сообщить об ошибке

Равносторонний треугольник  вписан в окружность. Периметр треугольника равен . Каков радиус окружности?

Возможные ответы:

Правильный ответ:

Объяснение:

Периметр окружности позволяет найти сторону равностороннего треугольника ABC; или 2.

Отсюда мы также можем найти длину высоты равностороннего треугольника ABC по формуле , которая оказывается .

Поскольку в равностороннем треугольнике центр тяжести находится в  от любой вершины, радиус окружности равен .

Сообщить об ошибке

Длина окружности   и радиус  . Каково отношение длины окружности к ее диаметру?

Возможные ответы:

Правильный ответ:

Объяснение:

Для данного круга окружности  и радиуса , .

Поскольку радиус круга равен половине диаметра круга, мы можем определить  как

 .

Следовательно, отношение длины окружности к диаметру этого и всех других кругов равно .

Сообщить об ошибке

Длина окружности   и радиус  . Каково отношение длины окружности к ее диаметру?

Возможные ответы:

Правильный ответ:

Объяснение:

Для данного круга окружности  и радиуса , .

Поскольку радиус круга равен половине диаметра круга, мы можем определить его как

.