Логарифм 5 по основанию 625: Вычислите log числа 625 по основанию 5+log числа (0,5)степени 6 по основанию 2

Понятие логарифма — Математика для всех

Что такое логарифм

Логарифм это математическая функция. В простейшей форме логарифм отвечает на вопрос:

Сколько раз нужно умножить число на само себя, чтобы получить другое число

Логарифм обозначается символом «log»

Пример:

Сколько раз нужно число 2 умножить друг на друга, чтобы получить 8 ?

Ответ: 2 · 2 · 2 = 8, нам пришлось число 2 умножить 3 раза, чтобы получить 8.

Таким образом, логарифм равен 3.

Записывается это следующим образом: log ₂ (8) = 3 .

Итак, это одно и тоже:

Число, которое мы умножаем, называется основание, поэтому говорят так:

логарифм 8 по основанию 2 равен 3

Обратите внимание, что мы имеем дело с тремя числами:

• основание — число, которое мы умножаем (в предыдущем примере это 2)
• число, показывающее сколько раз мы умножаем основание ( 3 раза — этому и равен логарифм)
• число, которое мы хотим получить ( число 8 )

Примеры логарифмов

Пример: чему равен логарифм log ₅ (625) … ?

Мы спрашиваем, сколько раз нужно умножить 5 на само себя, чтобы получить 625?

5 · 5 · 5 · 5 = 625, таким образом, нужно умножить 4 раза.

Ответ: log ₅ (625) = 4

Пример: чему равен логарифм log ₂ (64) … ?

Мы спрашиваем, сколько раз нужно умножить 2 на само себя, чтобы получить 64?

2 · 2 · 2 · 2 · 2 · 2 = 64, таким образом, нужно умножить 6 раз.

Ответ: log ₂ (64) = 6

Степени

Давайте вспомним, что такое степень:

Показатель говорит, сколько раз нужно умножить основание

В этом примере число 2 нужно умножить 3 раза, чтобы получить 8

Логарифмы и степени связаны между собой. Посмотрим как …

Логарифм говорит нам, какой нужен показатель степени

В этом примере основание равно 2, а показатель степени 3:

Логарифм отвечает на вопрос:

Какой нужен показатель степени

(чтобы одно число стало другим) ?

Еще примеры

Пример: вычислите log ₁₀ (100) … ?

10 ² = 100

Поэтому, нужно возвести 10 во вторую степень, чтобы получить 100

Ответ: log ₁₀ (100) = 2

Пример: вычислите log ₃ (81) … ?

3 ⁴ = 81

Поэтому, нужно возвести 3 в четвертую степень, чтобы получить 81

Ответ: log ₃ (81) = 4

Десятичные логарифмы: основание 10

Иногда логарифм пишется без основания, например:

lg (100)

Это означает, что основание такого логарифма равен 10

Сколько раз нам нужно перемножить 10 , чтобы получить желаемое число.

Пример:

lg (1000) = log ₁₀ (1000) = 3

Натуральные логарифмы

Другое основание, которое часто используется, это число е,  которое составляет примерно 2,71828.

Обозначается такой логарифм «ln»

Этот логарифм означает:

Сколько раз нам нужно использовать «e» в умножении, чтобы получить желаемое число.

Пример :

ln (7,389) = log _e ( 7.389 ) ≈ 2

Потому что : 2.71828 ² ≈ 7,389

Слово «логарифм»

«Логарифм» — это слово, составленное шотландским математиком Джоном Непером (1550-1617), из греческих слов «логос», означающего «отношение», и  «арифмос», означающего «число», … которое вместе составляет «отношение-число»!

как решать, правила с подробным решением, простейшие примеры

Определение логарифмического неравенства

В процессе решения заданий в виде логарифмических неравенств пригодится знание теории: свойства монотонности и ключевых формул.  

Определение 1

Логарифмом положительного числа b по основанию a называют показатель степени, в которую необходимо возвести a, чтобы получить b:

logab=c⇔ac=b.

Здесь b > 0, a > 0, a отлично от единицы.

Главным логарифмическим тождеством является:

alogab=b,

logaac=c.

В процессе решения задач будут полезны такие формулы для логарифмов:

1. Логарифм произведения равен сумме логарифмов: loga(bc)=logab+logac.
2. Логарифм частного равен разности логарифмов: logabc=logab-logac.
3. Формула для вычисления логарифма степени: logabm=mlogab.

Переход к другому основанию реализован по формуле:

logab=logcblogca

logab=1logba.

Определение 2

Простейшее логарифмическое неравенство — это соотношение, которое записано в виде:

loga fx > logagx,

при fxиgx некоторых выражениях, которые зависят от x. Например, fx=1+2x+x2, gx=3x-1.

Заметим, что знак «>» — больше — допускается заменять другими знаками: ≥,≤,<.

1. loga fx >loga gx => fx>gx при a>1
2. loga fx >loga gx => fx<gx при 0<a<1

Виды логарифмических неравенств

Логарифмические неравенства могут быть записаны в следующем виде:

1. Простейшие, как log2x>-1.
2. Неравенства, которые могут быть сведены к простейшим: как log12(x+1)≤log12(2x+3).
3. Неравенства, в которых использованы логарифмические свойства: как log2(x+1)+log2(x-1)≤2.
4. Неравенства, решаемые с помощью замены: такие, как log22x-log2x-2≤0.
5. Выражения с основанием, где присутствует переменная: например, logx2≤1.

Нахождение области допустимых значений логарифмического неравенства

Корректность решения логарифмических неравенств зависит от правильности определения области допустимых значений. Разберем наглядный пример:

log 22x+4 > log 23

Заметим, что в стандартной формуле логарифма роль b играет в данном случае выражение 2x+4. Тогда по определению:

2x+4>0

Если обратиться к определению логарифмического неравенства, то можно убедиться в том, что записанное выражение должно быть больше нуля.   В результате х >-2.

После определения ОДЗ можно приступить к решению неравенства:

log22x+4>log23

В первую очередь следует избавиться от log2 в обеих частях выражения. Тогда:

2x+4>3

Таким образом:

2x>-1

x>-12

Далее требуется доказать, что решение, которое получилось, соответствует определенной ранее области допустимых значений:

Изобразим числовую прямую, на которой определим полученные точки:

-2 и -12).

 

В итоге окончательное решение неравенства является участком с двумя проходящими дугами:

x∈-0.5;+∞

Разберем несколько иной пример:

log0.22x+4>log0.23

По сравнению с предыдущей задачей здесь изменено основание с 2 на 0,2. На принцип решения задачи это сильно не повлияет. Область допустимых значений остается прежней:

x>-2

Таким образом:

2x+4<3

x<-12

В результате начальное неравенство является равносильным системе:

x>-2x<-12

Решим эту систему:

x∈-2;-12.

Правило 1

Когда основание логарифма в неравенстве больше по сравнению с единицей, знак неравенства остается без изменений и в случае fx, и в случае gx. Когда основание логарифма больше нуля и меньше единицы, знак между fx и gx следует изменить на противоположный:

logafx>logagx⇒fx>gx при a>1logafx>logagx⇒fx<gx при 0<a<1

Руководствуясь записанным правилом, можно рассмотреть еще одно логарифмическое неравенство:

log0.2×2+6x+8>log0.25x+10.

Определим ОДЗ:

x2+6x+8>0.

Такое неравенство решается с помощью метода интервалов. Вычислим корни уравнения:

x2+6x+8=0

Получим:

x1=-4, x2=-2.

Перенесем значения на числовую ось. Для определения знаков можно использовать подстановку нуля в начальное выражение. При этом получится число 8, которое является положительным. В результате первый интервал имеет знак плюс:

В данном случае нам интересен промежуток с положительным знаком. Для первого выражения областью допустимых значений является следующее множество:

.

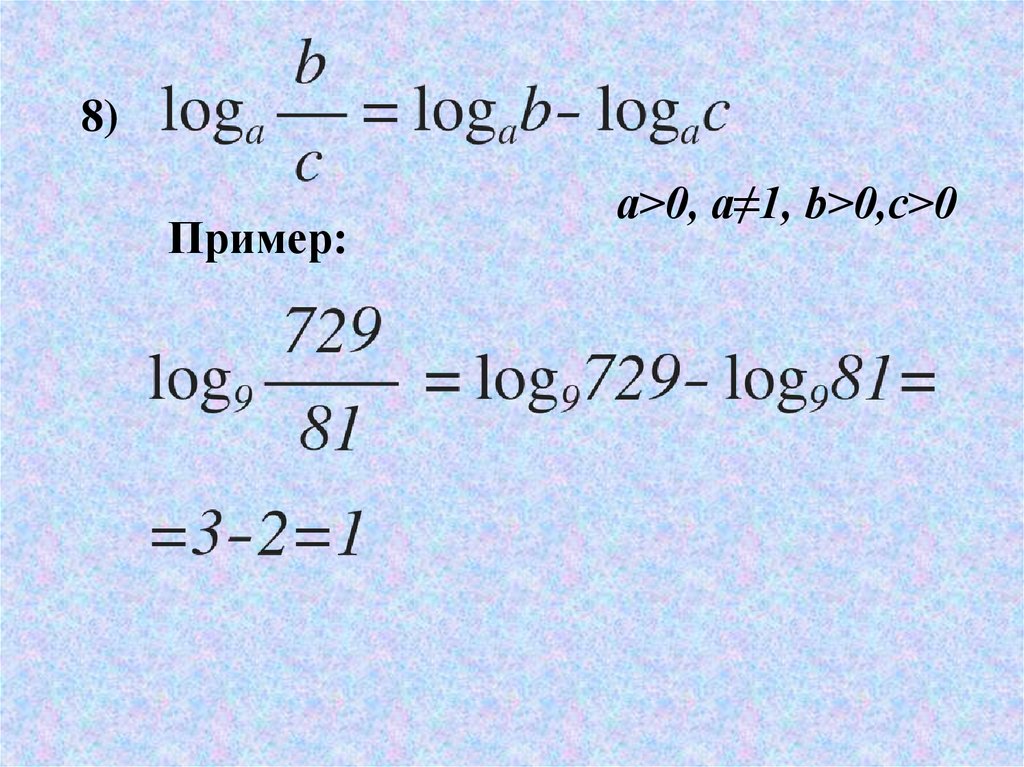
Вторым ОДЗ является:

5x+10>0

Тогда:

x>-2.

На координатной прямой необходимо совместить оба ОДЗ:

 

Участок, на котором совпадают все ОДЗ, соответствует окончательной области допустимых значений:

-2;+∞.

Решим неравенство:

log0.2×2+6x+8>log0.25x+10

Заметим, что основание 0.2<1. В таком случае, следует изменить знак неравенства:

x2+6x+8<5x+10

Выражение можно упростить:

x2+x-2<0

С помощью уже знакомого метода интервалов, найдем решения:

x∈-2;1.

Итоговое решение соответствует участку, на котором ОДЗ пересекается с полученным множеством:

 

В соответствии с полученной областью можно записать ответ:

x∈-2;1.

Методы решения логарифмических неравенств

Простейшие логарифмические неравенства, которые записаны в виде:

logafx>logagx

решают по алгоритму:

1. Поиск ОДЗ: . Запись в виде системы означает одновременное выполнение условий.
2. Исследование основания. При a>1 следует решить неравенство fx>gx. При 0<a<1 необходимо решить неравенство fx<gx.
3. Полученное решение требуется совместить с определенным ранее ОДЗ.

Другие виды логарифмических неравенств также можно решать с помощью описанной последовательности действий.  

В том случае, когда основание не является однозначным, а переменным, следует рассмотреть два варианта:

• основание больше, чем единица;
• основание заключено в промежуток между нулем и единицей.

Когда логарифмическое неравенство не записано в виде простейшего, его решение сводится к приведению к простейшему виду.  

Рассмотрим применение алгоритма на примере. Допустим, требуется решить неравенство:

log0.3x+4>log0.3×2+2x-2

В первую очередь следует определить область допустимых значений:

Заметим, что в первом неравенстве:

x>-4

Второе неравенство целесообразно решить с помощью метода интервалов. В результате получаются следующие корни:

x1=3-1

x2=-1-3

В таком случае, множество решений x2+2x-2>0 определено, как:

Заметим, что -4<-1-3. Результирующее ОДЗ:

Приступим к решению неравенства:

x+4<x2+2x-2

Данное неравенство является равносильным следующему:

0<x2+x-6

С помощью метода интервалов получим:

Исходя из того, что -3<-1-3, 2>3-1:

Правило 2

Решение логарифмического неравенства, которое записано в виде logafx<logagx, сводится к решению таких систем:

Неравенство logafx>logagx в каждом из рассмотренных вариантов сводится к какой-то из этих систем:

Упростить решение логарифмических неравенств можно путем перехода к постоянному основанию. Разберем данный метод на примере:

log|x|-2|x-3|≤0.

Определим ОДЗ:

Источник: ege-study.ru

Руководствуясь формулой logab=logcblogca, выполним переход к основанию 10:

lg|x-3|lg(|x|-2)≤0.

С помощью обобщенного метода интервалов можно представить в виде функции левую часть выражения:

g(x)=lg|x-3|lg(|x|-2).

Заметим, что данная функция изменяет знак при переходе точек с нулевыми значениями или при отсутствии значений. Выражение lg |x − 3| примет нулевое значение при |x − 3| = 1.

В таком случае: x = 4, либо x = 2. Выражение lg (|x| − 2) примет нулевое значение при |x| = 3. Такими точками являются 3 и −3. Учитывая область допустимых значений для начального неравенства, изобразим числовую прямую с определенными точками:

Источник: ege-study.ru

Определим знаки, которые принимает функция g(x) для каждого интервала и запишем ответ.

Ответ: x∈-3;-2∪(3;4].

Следующий пример заключается в решении логарифмического неравенства через систему:

log3x2+7x+10+log13x+59+1≥log33x2+16x+20

Записанное выражение является равносильным системе:

x2+7x+10>0x+5>03×2+16x+20>0log3x2+7x+10-log3x+59+log33≥log33x2+16x+20

⇔(x+5)(x+2)>0x+5>0(x+2)(x+103)>0log3(x+5)(x+2)·9·3(x+5)>log33(x+2)(x+103)

x>-29·(x+2)≥(x+2)(x+103)

x>-2x+103≤9<=>x>-2x≤173

 x2+7x+10=0\hfill D=0; x1,2 =-7±32; x1=-5x; x2=-2; 3×2+16x+20=0 D=162-12·20= =16·(16-3·5)=16; x1,2=-16±46; x1=-2; x2=-103

Ответ: x∈-2;173.

Простейшие примеры

Задача 1

Решить неравенство:

log0.3-x+2≤log0.32x-2

Решение

Определим ОДЗ:

Таким образом:

x∈1;2

Решим неравенство:

log0.3-x+2≤log0.32x-2

Так как 0.3<1, нужно изменить знак:

-x-2≥2x-2

-3x≥0

x≤0

Данное решение не соответствует ОДЗ. Неравенство не имеет решений.

Ответ: решения отсутствуют.

Задача 2

Найти решения неравенства:

 4logx4+3log4x4+4log16x4≤0

Решение

Заметим, что основание логарифма должно быть больше нуля и отлично от единицы:

x>0;4x≠1;x≠1;16x≠1.

Преобразуем систему, чтобы записать ее в упрощенном варианте:

Получилось определить ОДЗ неравенства. Заметим наличие переменной в основании логарифма. Тогда следует перейти к постоянному основанию 4:

4log4x+3log44x+4log4(16x)≤0;

4log4x+31-log4x+42+log4x≤0

Выполним замену log4x=t:

4t+31-t+42+t≤0

Упростим выражение и вычислим его решения способом интервалов:

(t-2)(t+45)t(1-t)(2+t)≥0.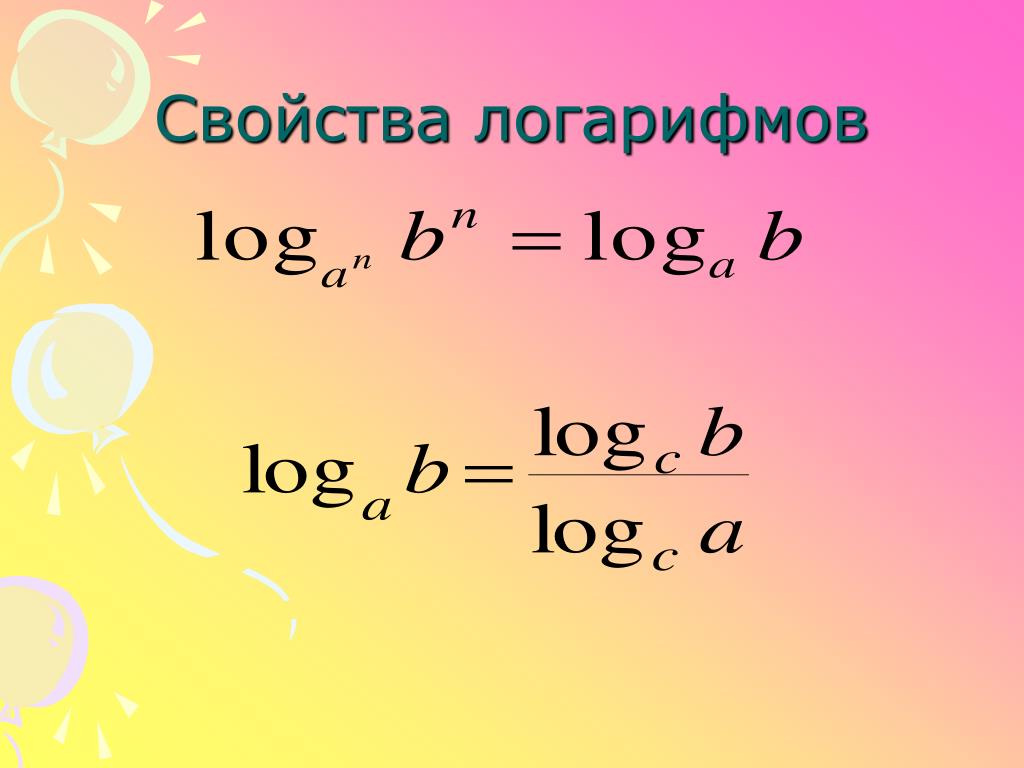

В результате:

t∈-∞;-2∪-45;0∪(1;2].

Источник: ege-study.ru

Обратимся к переменной х:

Источник: ege-study.ru

С учетом условия x > 0, согласно определенной ОДЗ, запишем ответ.

Ответ: x∈0;116∪4-45;1∪(4;16]

Задача 3

Решить неравенство, используя метод интервалов:

log132-3xx≥-1

Решение

Определим ОДЗ:

2-3xx>0

Перепишем выражение слева в виде логарифма с основанием 3:

log3x2-3x≥-1.

Выражение справа также можно переписать в виде логарифма с основанием 3. Тогда получим алгебраическое неравенство:

log3x2-3x≥log313

x2-3x≥13

Заметим, что условие по соответствию ОДЗ будет выполнено автоматически, что делает решение проще:

x2-3x-13≥0

3x-12-3x≥0

Воспользуемся методом интервалов и запишем ответ.

Источник: ege-study.ru

Ответ: x∈13;23.

Задача 4

Найти решения неравенства:

log25-x2-35-x2+9-1+log25-x2-35-x2+9-1>log254-x2-22.

Решение

Обратим внимание на повтор выражения:

5-x2

Выполним замену:

5-x2=t

Исходя из того что показательная функция может иметь лишь положительные значения, запишем:

t > 0

В результате:

5-x2+9=59·t

54-x2=54·t=625t

Преобразуем неравенство:

log2t-359·t-1+log2t-359·t-1>log2625t-22

Определим ОДЗ:

t > 0

(t − 3) (59 · t − 1) > 0

При выполнении записанного условия значение частного t-359·t-1 также является положительным. Выражение справа, расположенное под логарифмом, (625t-2)2 имеет знак плюс. Тогда:

(625t-2)2≠0

t≠2625

Определим ОДЗ:

С помощью метода интервалов найдем решения:

Источник: ege-study.ru

В результате:

t∈0;159∪3;+∞.

Решим неравенство путем представления суммы логарифмов в виде логарифма произведения:

Источник: ege-study.ru

Избавимся от логарифмов, а знак неравенства оставим без изменений:

(t-3)2>(625t-2)2

Перенесем имеющиеся выражения влево. Воспользуемся формулой разности квадратов:

 (t-3)2-(625t-2)2>0

(t-3-625t+2)(t-3+625t-2)>0

(-624t-1)(626t-5)>0

Источник: ege-study.ru

Вспомним ОДЗ неравенства:

t∈0;159∪3;+∞

Определим, где пересекаются полученные промежутки:

Источник: ege-study.ru

В результате:

t<159

Зная, что:

t=5-x2

Получим:

5-x2<5-9;-x2<-9;x2>9;(x-3)(x+3)>0

Источник: ege-study.ru

Ответ: x∈(-∞;-3)∪(3;+∞).

Задача 5

Требуется решить неравенство:

logx+2(36+16x-x2)-116logx+22(x-18)2≥2.

Решение

Определим ОДЗ:

x+2>0x+2≠136+16x-x2>0x≠18        ⇔     x>-2x≠-1x∈(-2;18)

x∈(-2;-1)∪(1;18)

Заметим, что:

36+16x-x2=-(x+2)(x-18).

Начальное неравенство можно переписать в кратком виде, то есть упростить:

logx+2((18-x)(x+2))-116logx+22(x-18)2≥2

1+logx+2(18-x)-116logx+22(x-18)2≥2

При условии, что:

(x-18)2=(18-x)2

В таком случае:

1+logx+2(18-x)-116logx+22(18-x)2≥2

Обратим внимание на запись:

loga2b

Данное выражение означает, что в первую очередь следует определить логарифм, а далее можно приступать к возведению выражения, которое получилось, в квадрат.

logx+22(18-x)2=(logx+2(18-x)2)2=(2logx+2(18-x))2=4logx+22(18-x).

Выполним замену:

logx+2(18-x)=t

t-14t2≥1

t2-4t+4≤0

(t-2)2≤0

Выражение слева не может быть меньше нуля. По этой причине:

t = 2

В результате:

logx+2(18-x)=2;   logx+2(18-x)=logx+2(x+2)2;   18-x=x2+4x+4;   x2+5x-14=0;

x1=-7 является посторонним корнем, так как не соответствует ОДЗ

x2=2

Ответ: 2

х = N\). Как правило, большие астрономические и научные расчеты выражаются в экспоненциальной форме, и здесь мы можем использовать логарифмическую форму преобразования в экспоненциальную.

Логарифмы иногда преобразуются с помощью антилогарифмических таблиц в нормальную форму, а не в экспоненциальную форму. Давайте узнаем больше о логарифмическом преобразовании в экспоненциальную форму и их формулах с помощью примеров и часто задаваемых вопросов.

1.	Что такое преобразование в экспоненциальную форму?
2.	Запись в экспоненциальную форму — формулы
3.	Примеры записи в экспоненциальную форму
4.	Практические вопросы
5.	Часто задаваемые вопросы о входе в экспоненциальную форму

Что такое преобразование в экспоненциальную форму?

Логарифмическая экспоненциальная форма — это распространенная форма преобразования одной формы математического выражения в другую форму. Обе эти формы помогают легко вычислять огромные числовые значения. Довольно часто при вычислении огромных астрономических вычислений экспоненциальная форма представляется в логарифмической форме, а затем логарифмическая форма преобразуется обратно в экспоненциальную форму. Логарифм числа N в основании a равно x , что при преобразовании в экспоненциальную форму можно принять как a в степени x равно N .

Приведенная выше формула дает общее представление и перевод логарифма в экспоненциальную форму. Как правило, экспоненциальная форма преобразуется в логарифмическую форму, которая иногда преобразуется с использованием антилогарифмов, а не обратно в экспоненциальную форму. Логарифмическое от и антилогарифмическое от требуют использования логарифмических таблиц для расчета.

Запись в экспоненциальную форму — формулы

Запись в экспоненциальную форму требует определенных формул логарифмов и показателей степени. Логарифмы помогают легко преобразовать умножение и деление чисел в сложение и вычитание. А экспоненты помогают работать с числами с разным основанием и разной степенью. Давайте посмотрим на некоторые важные формулы журналов и экспонент.

Формулы логарифмов

Логарифмические свойства полезны при работе со сложными логарифмическими выражениями. Все общие арифметические операции с числами преобразуются в другой набор операций с логарифмами. Произведение двух чисел, взятое внутри логарифмических функций, равно сумме логарифмических значений двух функций. Точно так же операция деления преобразуется в разность логарифмов двух чисел. Давайте посмотрим на следующие важные формулы логарифмов.

• логаб = лога + логб
• loga/b = loga — logb
• \(log_b a = \frac{loga}{logb}\)
• логи ^х = х логарифм
• \(log_1 а \) = 0
• \(log_a\) = 1
• д/дх. Логх = 1/х

Экспоненциальные формулы

Экспоненциальная форма полезна для объединения и записи большого выражения произведения одного и того же числа с помощью простой формулы. Экспоненты помогают легко представлять большие алгебраические выражения. Экспоненциальные формы иногда преобразуются в логарифмическую форму для облегчения вычислений. Давайте посмотрим на приведенные ниже формулы экспоненциальной формы.

• a ^p = a × a × a × a × a × a × ….. p раз
• а ^р . а ^q = а ^{p + q}
• a ^p /a ^q = a ^{p — q}
• (a ^p ) ^q = a ^pq
• а ^р .б ^р = (аб) ^р
• а ⁰ = 1
• ¹ =
• а ^-1 = 1/а

☛ Связанные темы

• Экспоненциальная форма
• Производная показательной функции
• Логарифмические функции
• Логарифмическое дифференцирование
• Дифференцирование e в степени x

 

Примеры преобразования журнала в экспоненциальную форму

1. Пример 1: Учитывая, что \(log_5625 = 4\). Преобразуйте этот журнал в экспоненциальную форму.

   Решение:

   Учитывая, что \(log_5625 = 4\).

   Логарифмическая форма \(log_aN=x\). При преобразовании в экспоненциальную форму N = a ^x .

   Следовательно, логарифмическая форма \(log_5625 = 4\), записанная в экспоненциальной форме, равна 625 = 5 ⁴ .

   Следовательно, экспоненциальная форма данного логарифмического выражения равна 625 = 5 ⁴ .

2. Пример 2: Найдите значение Log 72, учитывая, что log 2 = 0,301, а log 3 = 0,477.

   Решение:

   Дано, что log 2 = 0,301, а log 3 = 0,477

   Нам нужно найти значение log 72.

   Log72 = Log(8 × 9)

   Log 72 = Log 72 (2 ³ x 3 ² )

   log 72 = 3log 2 + 2log3

   log 72 = 3 (0,301) + 2 (0,477)

   log72 = 0,903 + 0,954

   log72 = 1,857

   + 0,954

   = 1,857

   . Это могло также могут быть вычислены путем преобразования логарифмической формы в экспоненциальную форму.

   Следовательно, значение log72 равно 1,857.

перейти к слайдуперейти к слайду

Хотите создать прочную основу для изучения математики?

Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.

Забронировать бесплатный пробный урок

Практические вопросы по журналу в экспоненциальной форме

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о входе в экспоненциальную форму

Что такое преобразование в экспоненциальную форму? 9x = N\), если записать в логарифмической форме, равно \(log_aN = x\).

Рабочие листы по математике и визуальная программа

ln( 625 )%3f| Калькулятор натурального (ln) логарифма

Введите положительное число (x) для расчета ln(x): пер(  ) = ?

Результат: Натуральный логарифм 625 равен 6,4377516497364 или ln(625) = 6,4377516497364.

Примечания: i) e и pi являются допустимыми значениями. ii) 1,2 x 10 3 следует вводить как 1,2e3 и iii) 1,2 x 10 -3 как 1.2e-3

Вот ответ на такие вопросы, как: ln( 625 )%3f или Как найти натуральный логарифм 625?

Воспользуйтесь нашим калькулятором e log, чтобы найти натуральный логарифм любого положительного действительного числа.

Что такое натуральный логарифм?

Натуральный логарифм представляет собой логарифм по основанию числа e и является обратной функцией экспоненциальной функции. Натуральный логарифм является частным случаем логарифмов и обычно используется при решении задач времени, роста/убывания.

Число «е» — иррациональная константа, приблизительно равная 2,718281828459. Натуральный логарифм x обычно записывается как ln(x) или log _e x.

Натуральный логарифм x — это степень, в которую нужно возвести e, чтобы оно равнялось x. Например, ln(10) равно 2,30258509…, потому что e ^{2,30258509…} = 10.

Основные правила натурального логарифма

Название правила	Правило	Пример
Правило продукта	ln( x ∙ y ) = ln( x ) + ln( y )	пер(5 ∙ 3) = пер(5) + пер(3)
Правило частных	ln( x/y ) = ln( x ) — ln( y )	пер(5 / 3) = пер(5) — пер(3)
Силовое правило	ln( x y ) = y ∙ ln( x )	пер(3 5 ) = 5 ∙ пер(3)
Взаимный	ln(1/x) = −ln(x)
ln отрицательного числа	ln( x ) не определено, когда x ≤ 0
лн е	ln(e) = 1
нулевой	ln(0) не определено
шт.	ln(1) = 0
л бесконечности	lim ln( x ) = ∞ , когда x →∞
Пер. производная	[ln( х )]’ = 1 / х
Интеграл	∫ ln( x ) dx = x ∙ (ln( x ) — 1) + C

Таблица натуральных логарифмов (

<= 1,0)9

n	log e n	n	log e n	n	log e n	n	log е н
0.01	-4.60517	0.26	-1.34707	0.51	-0.67334	0.76	-0.27443
0.02	-3.		0. 27	-1.30933	0.52	-0.65392	0.77	-0.26136
0,03	-3,50655	0,28	-1,27296	0,53	-0,63488	0,78	-0,24846
0.04	-3.21887	0.29	-1.23788	0.54	-0.61618	0.79	-0.23572
0.05	-2.99573	0.30	-1.20397	0.55	-0.59783	0.80	-0.22314
0,06	-2,81341	0,31	-1,17118	0,56	-0,57982	0,81	-0,21072
0,07	-2,65926	0,32	-1,13943	0,57	-0,56212	0,82	-0,19845	0,82	-0,19845	0,82	-0,19845	0,82	-0,19845	0,82	-0,19845	0,82	-0,
0,08	-2,52573	0,33	-1,10866	0,58	-0,54472	0,83	-0,18633	0,83	-0,18633	0,83	-0,18633	0,83	-0,18633	0,83	-0,18633	0,83	-0,18633	.
0,09	-2,40794	0,34	-1,07881	0,59	-0,52763	0,84	-0,17435
0,10	-2,30258	0,35	-1,04982	0,60	-0,51082	0,85	-0,16252	0,85	-0,16252	0,85	-0,16252	0,85	-0,
0.11	-2.20727	0.36	-1.02165	0.61	-0.49430	0.86	-0.15082
0,12	-2,12026	0,37	-0,99425	0,62	-0,47803	0,87	-0,13926
0.13	-2.04022	0.38	-0.96758	0.63	-0.46203	0.88	-0.12783
0.14	-1.96611	0.39	-0.94161	0.64	-0. 44629	0.89	-0.11653
0,15	-1,89712	0,40	-0,91629	0,65	-0,43078	0,90	-0,10536
0.16	-1.83258	0.41	-0.89160	0.66	-0.41551	0.91	-0.09431
0.17	-1.77196	0.42	-0.86750	0.67	-0.40047	0.92	-0.08338
0,18	-1,71480	0,43	-0,81419	0,68	-0,38566	0,93	-0,07 21
0.19	-1.66073	0.44	-0.82098	0.69	-0.37106	0.94	-0.06187
0,20	-1,60944	0,45	-0,79851	0,70	-0,35667	0,95	-0,05129	0,95	-0,05119	0,95	-0,0519	0,95	-0,0519	0,95	-0,0519	0,95	-0,0519	0,95	-0519
0,21	-1,56065	0,46	-0,77653	0,71	-0,34249	0,96	-0,04082	0,96	-0,04082
0,22	-1,51412	0,47	-0,75502	0,72	-0,32850	0,97	-0. 03
0,23	-1,46968	0,48	-0,73397	0,73	-0,31471	0,98	-0,02020	0,98	-0,02020201471	0,98	-0,02020971	0,98	-0,0202014710012
0.24	-1.42711	0.49	-0.71335	0.74	-0.30110	0.99	-0.01005
0,25	-1,38629	0,50	-0,69214	0,75	-0,28768	1,00	-0,00000	1,00	-0,00000

Таблица натуральных логарифмов (>= 1,0)

00120012

n	бревно e 9д
1,0	0,00000	3.0	1,09861	5,0	1,60944	25,0	3.21887
1,1	0,09531	3.1	1. 13140	6,0	1,79176	26,0	3.25809
1,2	0,18232	3,2	1.16315	7,0	1,94591	27,0	3.29583
1,3	0,26236	3,3	1.19392	8,0	2,07944	28,0	3,33220
1,4	0,33647	3,4	1.22377	9,0	2,19722	29,0	3,36729
1,5	0,40546	3,5	1.25276	10,0	2,30258	30,0	3.40119
1,6	0,47000	3.6	1.28093	11,0	2.39789	40,0	3.68888
1,7	0,53063	3.7	1.30833	12,0	2.48491	50,0	3,
1,8	0,587779	3,8	1. 33500	13,0	2,56495	60,0	4,09434
1,9	0,64185	3.9	1,36097	14,0	2,63905	70,0	4.24849
2,0	0,69314	4,0	1,38629	15,0	2,70805	80,0	4,38202
2.1	0,74193	4.1	1.41099	16.0	2,77259	90,0	4.49981
2,2	0,78845	4,2	1,43508	17,0	2,83321	100,0	4.60517
2,3	0,83291	4,3	1,45861	18,0	2,89037	200,0	5,29832
2,4	0,87547	4,4	1,48160	19,0	2,94444	300,0	5,70378
2,5	0,91629	4,5	1. 50408	20,0	2,99573	400,0	5,9146
2,6	0,95551	4,6	1,52605	21,0	3.04452	500,0	6.21461	500,0	6.21461
2,7	0,99325	4,7	1,54756	22,0	3,09104	600,0	6,39693
2,8	1.02962	4.8	1.56861	23,0	3.13549	700.0	6,55108
2.9	1.06471	4.9	1,58923	24.0	3.17805	800.0	6.68461	800,0	6.68461

Натуральный (ln) Log Calculator

Ссылка на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.