Формула разности синусов: Формулы синуса и косинуса суммы и разности аргументов — урок. Алгебра, 10 класс.

вывод формул, примеры Сумма синусов и тангенсов с разными аргументами

Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α — β 2 . Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.

Yandex.RTB R-A-339285-1

Формулы суммы и разности синусов и косинусов

Запишем, как выглядят формулы суммы и разности для синусов и для косинусов

Формулы суммы и разности для синусов

sin α + sin β = 2 sin α + β 2 cos α — β 2 sin α — sin β = 2 sin α — β 2 cos α + β 2

Формулы суммы и разности для косинусов

cos α + cos β = 2 cos α + β 2 cos α — β 2 cos α — cos β = — 2 sin α + β 2 cos α — β 2 , cos α — cos β = 2 sin α + β 2 · β — α 2

Данные формулы справедливы для любых углов α и β . Углы α + β 2 и α — β 2 называются соответственно полусуммой и полуразностью углов альфа и бета.

Дадим формулировку для каждой формулы.

Определения формул сумм и разности синусов и косинусов

Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.

Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.

Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.

Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.

Вывод формул суммы и разности синусов и косинусов

Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже

sin (α + β) = sin α · cos β + cos α · sin β sin (α — β) = sin α · cos β — cos α · sin β cos (α + β) = cos α · cos β — sin α · sin β cos (α — β) = cos α · cos β + sin α · sin β

Также представим сами углы в виде суммы полусумм и полуразностей.

α = α + β 2 + α — β 2 = α 2 + β 2 + α 2 — β 2 β = α + β 2 — α — β 2 = α 2 + β 2 — α 2 + β 2

Переходим непосредственно к выводу формул суммы и разности для sin и cos.

Вывод формулы суммы синусов

В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим

sin α + sin β = sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2

Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см. формулы выше)

sin α + β 2 + α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу

sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α + β 2 cos α — β 2

Действия по выводу остальных формул аналогичны.

Вывод формулы разности синусов

sin α — sin β = sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 — sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α — β 2 cos α + β 2

Вывод формулы суммы косинусов

cos α + cos β = cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 + cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = 2 cos α + β 2 cos α — β 2

Вывод формулы разности косинусов

cos α — cos β = cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 — cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = — 2 sin α + β 2 sin α — β 2

Примеры решения практических задач

Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов. Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.

Пример 1. Проверка формулы суммы синусов двух углов

α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 — π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2

Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.

Пример 2. Применение формулы разности синусов

α = 165 ° , β = 75 ° sin α — sin β = sin 165 ° — sin 75 ° sin 165 — sin 75 = 2 · sin 165 ° — sin 75 ° 2 cos 165 ° + sin 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · — 1 2 = 2 2

С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Данный электронный ресурс является отличным материалом для проведения интерактивного обучения в современных школах. Он составлен грамотно, обладает четкой структурой и соответствует школьному плану. Благодаря подробным объяснениям, тема, которая представлена в видеоуроке станет понятна как можно большему количеству учеников в классе. Учителя должны помнить, что не все ученики имеют одинаковую степень восприятия, быстроты понимания, базу. Справиться с трудностями и догнать своих сверстников, исправить успеваемость, помогут подобные материалы. С помощью них в домашней спокойной обстановке, самостоятельно либо вместе с репетитором, ученик может разобраться в той или иной теме, изучить теорию и просмотреть примеры практического применения той или иной формулы и т.

д.

Данный видеоурок посвящен теме «Синус и косинус разности аргументов». Подразумевается, что ученики уже изучили основы тригонометрии, ознакомлены с основными функциями и их свойствами, формулами привидения и таблицами тригонометрических значений.

Также, до того, как перейти к изучению данной темы, необходимо иметь понятие о синусе и косинусе суммы аргументов, знать две основные формулы и уметь ими пользоваться.

Вначале видеоурока диктор напоминает школьникам эти две формулы. Далее демонстрируется первая формула — синус разности аргументов. Помимо того, как выводится сама формула, показывается каким образом она получается от другой. Таким образом, школьнику не придется зазубривать новую формулу без понимания, что является частой ошибкой. Это очень важно для учеников в этом классе. Нужно всегда помнить, что перед знаком минуса всего можно добавить знак +, а минуса на знак плюс в итоге превратится в минус. С помощью такого нехитрого шага, можно воспользоваться формулой синуса суммы и получить формулу синуса разности аргументов.

Аналогичным образом выводится формула косинуса разности из формулы косинуса суммы аргументов.

Диктор пошагово все объясняет, а в результате выводится общая формула косинуса суммы и разности аргументов и синуса, аналогично.

Первый пример из практической части данного видеоурока предлагает найти косинус Пи/12. Предлагается представить данное значение в виде некоторой разности, при котором уменьшаемое и вычитаемое будут являться табличными значениями. Далее применятся формула косинуса разности аргументов. Заменив выражение, можно подставить полученные значения и получить ответ. Диктор зачитывает ответ, который выводится в конце примера.

Второй пример представляет собой уравнение. И в правой, и в левой сторонах мы видим косинусы разностей аргументов. Диктор напоминает формулы приведений, которые используются для замены и упрощения этих выражения. Эти формулы записываются с правой стороны, чтобы школьники могли понять, откуда появляются те или иные изменения.

Еще один пример, третий, представляет собой некоторую дробь, где и в числителе и в знаменателе имеем тригонометрические выражения, а именно, разности произведений.

Здесь также при решении используются формулы приведений. Таким образом, школьники могут убедиться, что пропустив одну тему в тригонометрии, понять остальные будет все сложнее.

И, наконец, четвертый пример. Это также уравнение, при решении которых необходимо использовать новые изученные и старые формулы.

Примеры, которые приводятся в видеоуроке, можно рассмотреть более подробно и попробовать решить самостоятельно. Их можно задать в качестве домашнего задания школьникам.

ТЕКСТОВАЯ РАСШИФРОВКА:

Тема занятия «Синус и косинус разности аргументов».

На предыдущем курсе мы познакомились с двумя тригонометрическими формулами синус и косинус суммы аргументов.

sin(x + y) = sin x cos y + cos x sin y,

cos (x + y) = cos x cos y — sin x sin y.

синус суммы двух углов равен сумме между произведением синуса первого угла и косинусом второго угла и произведением косинуса первого угла и синуса второго угла;

косинус суммы двух углов равен разности между произведением косинусов этих углов и произведением суммы этих углов.

При помощи этих формул выведем формулы Синус и косинус разности аргументов.

Синус разности аргументов sin(x- y)

Две формулы (синус суммы и синус разности) можно записать в виде:

sin(x y) = sin x cos y cos x sin y.

Аналогично выведем формулу косинуса разности:

Косинус разности аргументов перепишем в виде суммы и применим уже известную формулу косинуса суммы: cos (x + y) = cosxcosy — sinxsiny.

только для аргументов х и -y. Подставив данные аргументы в формулу, получим cosxcos(- y) — sinxsin(- y).

sin(- y)= — siny). и получим окончательное выражение cosxcosy + sinxsiny.

cos (x — y) = cos (x +(- y)) =cos xcos(- y) — sin x sin(- y)= cosx cos y + sin xsin y.

Значит, cos (x — y) = cosxcos y + sin xsin y.

косинус разности двух углов равен сумме между произведением косинусов этих углов и произведением синусов этих углов.

Объединяя две формулы (косинус суммы и косинус разности) в одну, запишем

cos (x y) = cosxcos y sin xsin y.

Запомним, что формулы на практике можно применять как слева направо, так и наоборот.

Рассмотрим примеры.

ПРИМЕР 1. Вычислить cos (косинус пи, деленное на двенадцать).

Решение. Запишем пи, деленное на двенадцать, как разность пи на три и пи, деленное на четыре: = — .

Подставим значения в формулу косинуса разности: cos (x — y) = cosxcosy + sinxsiny, таким образом cos = cos (-) = cos cos + sin sin

Нам известно, что cos = , cos = sin= , sin = . Показать таблицу значений.

Заменим значение синуса и косинуса числовыми значениями и получим ∙ + ∙ при умножении дробь на дробь числители и знаменатели перемножаем, получаем

cos = cos (-) = cos cos + sin sin = ∙ + ∙ = = =.

Ответ: cos =.

ПРИМЕР 2. Решить уравнение cos(2π — 5х) = cos(- 5х) (косинус два пи минус пять икс равно косинусу от пи на два минус пять икс).

Решение. К левой и правой частям уравнения применим формулы приведения cos(2π — cos (косинус два пи минус альфа равен косинусу альфа) и cos(- = sin (косинус пи на два минус альфа равно синусу альфа), получим cos 5х = sin 5х, приведем его к виду однородного уравнения первой степени и получим cos 5х — sin 5х = 0. Это однородное уравнение первой степени. Разделим почленно обе части уравнения на cos 5х. Имеем:

cos 5х: cos 5х — sin 5х: cos 5х = 0, т.к. cos 5х: cos 5х =1, а sin 5х: cos 5х= tg 5x, то получим:

Так как мы уже знаем, что уравнение tgt = а имеет решение t = arctgа + πn, а так как у нас t=5х, а =1, то получим

5x = arctg 1 + πn,

а значение arctg 1, тогда tg 1= Показать таблицу

подставим значение в уравнение и решим его:

Ответ: х = + .

ПРИМЕР 3. Найти значение дроби. (в числителе разность произведения косинусов семидесяти пяти градусов и шестидесяти пяти градусов и произведения синусов семидесяти пяти градусов и шестидесяти пяти градусов, а в знаменателе разность произведения синуса восьмидесяти пяти градусов и косинуса тридцати пяти градусов и произведения косинуса восьмидесяти пяти градусов и синуса тридцати пяти градусов).

Решение. В числителе данной дроби разность можно «свернуть» в косинус суммы аргументов 75° и 65°, а в знаменателе — разность «свернем» в синус разности аргументов 85° и 35°. Получим

Ответ: — 1.

ПРИМЕР 4. Решить уравнение: cos(-х) + sin(-х) = 1(косинус разности пи на четыре и икс плюс синус разности пи на четыре и икс равно одному).

Решение. Применим формулы косинус разности и синус разности.

Показать общую формулу косинуса разности

Тогда cos (-х) = cos cos х + sinsinх

Показать общую формулу синуса разности

а sin (-х)= sin cosх — cos sinх

Подставим данные выражения в уравнение cos(-х) + sin(-х) = 1 и получим:

cos cos х + sinsin х + sin cos х — cos sin х = 1,

Так как cos= и sin= Показать таблицу значение синуса и косинуса

Получим ∙ cos х + ∙ sinх + ∙ cos х — ∙ sinх = 1,

второе и четвертое слагаемые противоположны, поэтому взаимно уничтожаются, остается:

∙ cos + ∙ cos = 1,

Решим данное уравнение и получим, что

2∙ ∙ cos x= 1,

Так ка мы уже знаем, что уравнение cos = а имеет решение t = arcos a + 2π k , а так как у нас t=x, а =, то получим

х = arccos + 2πn,

а так как значение arccos, тогда cos =

Сумма и разность синусов.

Сумма и разность косинусов

Урок 31. Алгебра 10 класс ФГОС

В этом видеоуроке мы рассмотрим формулы суммы и разности синусов и формулы суммы и разности косинусов. Познакомимся с формулами преобразования произведения в сумму или разность.

Конспект урока «Сумма и разность синусов. Сумма и разность косинусов»

Вспомним формулы сложения для синуса: , ; косинуса: , . Эти формулы мы будем использовать при доказательстве формул суммы и разности синусов и формул суммы и разности косинусов.

Итак, докажем, что .

Обозначим , . Тогда , а . Таким образом, можем записать,  [, ]

 [вернёмся к замене] . Формула  доказана.

Читается эта формула так: сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус их полуразности.

. Эта формула получается из формулы  заменой  на : . Выполним преобразования и получим: .

Читается эта формула так: разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус их полусуммы.

Теперь докажем формулу суммы косинусов: .

Обозначим , . Тогда , а .

Поэтому  [, ]  [вернёмся к замене] . Таким образом, формула  доказана. Читается формула так: сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы этих углов на косинус их полуразности.

И нам осталось рассмотреть формулу разности косинусов.

Она получается из формулы  заменой  на ? Нет. Формула разности косинусов доказывается так же, как формулы  и .

Докажем, что .

Обозначим , . Тогда , а .

Поэтому  [, ]

 

.

Вернёмся к замене и получим: .

Читается формула следующим образом: разность косинусов двух углов равна взятому со знаком «минус» удвоенному произведению синуса полусуммы этих углов на синус их полуразности.

Таким образом, мы с вами познакомились с формулами суммы и разности синусов и формулами суммы и разности косинусов.

Давайте вычислим . Для этого воспользуемся формулой . Имеем:

 

.

И преобразуем в произведение выражение:

.  [запишем  как ]  []

 [воспользуемся формулой ]

 

.

А сейчас рассмотрим следующие три формулы: , , . Это формулы преобразования произведений в сумму или разность.

Давайте с вами докажем, например, формулу . Для этого преобразуем правую часть равенства к левой:  [к выражению в скобках применим формулу  и формулу ]

 

.

Итак, мы привели правую часть равенства к левой, следовательно, доказали, что произведение синуса угла альфа и синуса угла бета равно полуразности косинуса разности этих углов и косинуса их суммы. Формулы  и  доказываются так же, как и формула .

А теперь закрепим новые знания на практике.

Задание первое. Представьте в виде произведения следующие выражения: а) ; б) ; в) ; г) .

Решение.

 

Второе задание. Представьте в виде суммы или разности выражения: а) ; б) ; в) .

Решение.

И выполним ещё одно задание, в котором надо найти значения следующих выражений: а) ; б) .

Решение.

Предыдущий урок 30 Формулы приведения

Следующий урок 32 Уравнение cosx=a

Получите полный комплект видеоуроков, тестов и презентаций Алгебра 10 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Мэтуэй | Популярные задачи

92

1	Найти точное значение	грех(30)
2	Найти точное значение	грех(45)
3	Найти точное значение	грех(30 градусов)
4	Найти точное значение	грех(60 градусов)
5	Найти точное значение	загар (30 градусов)
6	Найти точное значение	угловой синус(-1)
7	Найти точное значение	грех(пи/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	грех(45 градусов)
10	Найти точное значение	грех(пи/3)
11	Найти точное значение	арктан(-1)
12	Найти точное значение	cos(45 градусов)
13	Найти точное значение	cos(30 градусов)
14	Найти точное значение	желтовато-коричневый(60)
15	Найти точное значение	csc(45 градусов)
16	Найти точное значение	загар (60 градусов)
17	Найти точное значение	сек(30 градусов)
18	Найти точное значение	cos(60 градусов)
19	Найти точное значение	cos(150)
20	Найти точное значение	грех(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	загар (45 градусов)
23	Найти точное значение	arctan(- квадратный корень из 3)
24	Найти точное значение	csc(60 градусов)
25	Найти точное значение	сек(45 градусов)
26	Найти точное значение	csc(30 градусов)
27	Найти точное значение	грех(0)
28	Найти точное значение	грех(120)
29	Найти точное значение	соз(90)
30	Преобразовать из радианов в градусы	пи/3
31	Найти точное значение	желтовато-коричневый(30)
32
35	Преобразовать из радианов в градусы	пи/6
36	Найти точное значение	детская кроватка(30 градусов)
37	Найти точное значение	арккос(-1)
38	Найти точное значение	арктан(0)
39	Найти точное значение	детская кроватка(60 градусов)
40	Преобразование градусов в радианы	30
41	Преобразовать из радианов в градусы	(2 шт. )/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	тан(пи/2)
45	Найти точное значение	грех(300)
46	Найти точное значение	соз(30)
47	Найти точное значение	соз(60)
48	Найти точное значение	соз(0)
49	Найти точное значение	соз(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	сек(60 градусов)
53	Найти точное значение	грех(300 градусов)
54	Преобразование градусов в радианы	135
55	Преобразование градусов в радианы	150
56	Преобразовать из радианов в градусы	(5 дюймов)/6
57	Преобразовать из радианов в градусы	(5 дюймов)/3
58	Преобразование градусов в радианы	89 градусов
59	Преобразование градусов в радианы	60
60	Найти точное значение	грех(135 градусов)
61	Найти точное значение	грех(150)
62	Найти точное значение	грех(240 градусов)
63	Найти точное значение	детская кроватка(45 градусов)
64	Преобразовать из радианов в градусы	(5 дюймов)/4
65	Найти точное значение	грех(225)
66	Найти точное значение	грех(240)
67	Найти точное значение	cos(150 градусов)
68	Найти точное значение	желтовато-коричневый(45)
69	Оценить	грех(30 градусов)
70	Найти точное значение	сек(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	КСК(30)
73	Найти точное значение	arcsin(( квадратный корень из 2)/2)
74	Найти точное значение	загар((5pi)/3)
75	Найти точное значение	желтовато-коричневый(0)
76	Оценить	грех(60 градусов)
77	Найти точное значение	arctan(-( квадратный корень из 3)/3)
78	Преобразовать из радианов в градусы	(3 пи)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	угловой синус(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	КСК(45)
83	Упростить	арктан(квадратный корень из 3)
84	Найти точное значение	грех(135)
85	Найти точное значение	грех(105)
86	Найти точное значение	грех(150 градусов)
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	загар((2pi)/3)
89	Преобразовать из радианов в градусы	пи/4
90	Найти точное значение	грех(пи/2)
91	Найти точное значение	сек(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	угловой синус(0)
95	Найти точное значение	грех(120 градусов)
96	Найти точное значение	желтовато-коричневый ((7pi)/6)
97	Найти точное значение	соз(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень из 2)/2)
100	Преобразование градусов в радианы	88 градусов

Калькулятор суммы и разности тождеств

Тригонометрические функции могут быть очень сложными и требуют много времени для понимания и решения. В общем, у нас есть шесть основных тригонометрических тождеств и для каждого из них и формулы суммы, и формулы разности. Таким образом, всего у нас есть 12 сложных формул, которые нужно запомнить в тригонометрии.

К счастью, это было исправлено введением нашего Калькулятора сумм и разностей тождеств , который мгновенно помогает нам в решении сумм и разностей тождеств . Если вы хотите проверить это и узнать, что такое личность и как использовать калькулятор, не стесняйтесь просмотреть текст ниже.

Для получения дополнительных продуктов, связанных с тригонометрией и математикой, мы подготовили для вас список рекомендуемых ниже:

• Тригонометрический калькулятор
• Калькулятор тригонометрических функций
• Калькулятор закона синусов
• Калькулятор тригонометрического закона косинусов

8 Функции

Несомненно, тригонометрия — обширная тема, и чтобы понять тригонометрические функции, нам следует сначала вернуться в Древнюю Грецию, где все началось.

В то время древние математики интересовались геометрией, и они хотели глубоко изучить треугольник. Их увлечение треугольником привело их к открытию знаменитой теоремы Пифагора. Это открытие имело решающее значение и для тригонометрических функций.

Мир геометрии довольно хаотичен, и есть правила, которым мы должны следовать. Тригонометрия строится на том же наблюдении.

Триггерные функции описывают отношения между сторонами прямоугольного треугольника. На картинке ниже перечислены формулы всех шести тригонометрических функций. Мы рассмотрим более подробную информацию в следующих разделах.

Тригонометрия прямоугольного треугольника

Область и диапазон тригонометрических функций

Значение θ (тета) представляет собой область определения тригонометрических функций, а результирующее значение представляет диапазон тригонометрической функции. Значения домена показаны в градусах или радианах, а домен тригонометрической функции представляет собой действительное число, но в некоторых случаях результаты могут быть бесконечными значениями. Однако триггерная функция по определению является периодической функцией.

Функции TRIG	Домен	Диапазон
SIN θ	(-∞, +∞)	[-1, +1]
COS θ	(-, +∞)	[ -1, +1]
Tan θ	R – (2n + 1)π/2	(-∞, +∞)
Cot θ	R – 0n +∞)
Сек θ	R – (2n + 1)π/2	(-∞, -1] U [+1, +∞)
Coсек θ	R – nπ	(-∞, -1] U [+1, +∞)

Область определения и область значений тригонометрических функций

Примечание: Мы никогда не делаем вычисления вручную, потому что это непростая задача . В большинстве случаев мы используем внешние инструменты, такие как калькуляторы, которые мы создали индивидуально для каждой триггерной функции. Не стесняйтесь смотреть на список ниже, если вам нужно использовать их для расчетов:

• Калькулятор синуса
• Калькулятор косинуса
• Калькулятор тангенса
• Калькулятор котангенса
• Калькулятор секанса
• Калькулятор косеканса

Тождества суммы и разности

Тригонометрическое тождество веками применялось в реальном мире, в том числе для расчета больших расстояний.

В основном мы используем тождества суммы и разности функций синуса, косинуса и тангенса, но у нас есть еще несколько тригонометрических тождеств. Их приложения различны, включая определение расстояния от Земли до Солнца или измерение высоты горы.

Мы используем тождества суммы и разности для решения различных математических задач и доказательства тригонометрических формул и тождеств. Всего у нас есть шесть основных формул суммы и разности для тригонометрических функций:

 {sin(A + B) = sinA cosB + cosA sinB} 

 {sin(A - B) = sinA cosB - cosA sinB} 

 {cos(A + B) = cosA cosB - sinA sinB} 

 {cos(A - B) = cosA cosB + sinA sinB} 

 tan(A + B) = \frac{(tanA + tanB)}{( 1 - tanA \times tanB)} 

 tan(A - B) = \frac{(tanA - tanB)}{(1 + tanA \times tanB)} 

Формулы сложения синусов и сложения косинусов

Формулы суммы и разности вычисляют значения тригонометрических функций, представляя их в терминах примерно равных функций, но с разными аргументами. По сути, мы берем начальный угол и разлагаем его на сумму или разность двух других углов. В результате мы находим начальное значение, используя новые вместо применения формулы суммы или разности.

Давайте начнем и рассмотрим две наиболее часто используемые тригонометрические формулы:

Формула сложения Sin:

sin(α + β) = sin(α)cos(β) + cos(α)sin(β)

Формула сложения Cos:

cos(α + β) = cos(α)cos(β) — sin(α)sin(β)

В случае, когда угол α и угол β равны (α = β), формулы сложения cos и sin выглядят так:

sin (α + α) = sin(α)cos(α) + cos(α)sin(α)
cos(α + α) = cos(α)cos(α) — sin(α)sin(α)

Или проще:

sin(2α) = 2sin(α)cos(α)
cos(2α) = cos²(α) — sin²(α)

Но как насчет их разности тождеств? Что ж, поскольку мы уже знаем, что сложение и вычитание — две почти одинаковые операции, только с перевернутыми знаками, мы можем легко сделать тождествами разность sin и cos, используя приведенные выше формулы:

Формула разности синусов:

sin(α — β) = sin(α)cos(β) — cos(α)sin(β)

Формула разности cos:

cos(α — β) = cos(α)cos(β) + sin(α )sin(β)

Другие тригонометрические тождества суммы и разности

Ранее мы упоминали, что помимо основных формул синусов и косинусов, у нас также есть более сложные тригонометрические тождества, такие как:

• тангенс
• котангенс
• секанс и

Мы можем быстро и легко решить формулы синуса и косинуса, но это становится сложным и запутанным, когда нам нужно решить тождества суммы тангенса и котангенса и тригонометра разности. Конечно, одной из причин, по которой они могут стать сложными, является тот факт, что нам нужно решать дроби. Как насчет формул секанса и косеканса? Ну, это еще хуже и грязнее.

Вот список формул сложения и разности для тангенса, котангенса, секанса и косеканса:

 tan(x−y) = \frac{tan(x) – tan(y)}{1+tan(x) \times tan(y)} 

 tan(x+y) = \frac{tan(x) + tan(y)}{1-tan(x) \times tan(y)} 

 cot(x+y) ) = \frac{tan(x) + tan(y)}{1−tan(x) \times tan(y)} 

 cot(xy) = \frac{tan(x) - tan(y)}{ 1+tan(x) \times tan(y)} 

 sec(x+y) = \frac{tan(x) + tan(y)}{1-tan(x) \times tan(y)} 

 сек(x-y) = \frac{tan(x) - tan(y)}{1+tan(x) \times tan(y)} 

 csc(x+y) = \frac{tan(x) + tan(y)}{1-tan(x) \times tan(y)} 

 csc(x-y) = \frac{tan(x) - tan(y)}{1+tan(x) \times tan(y)} 

Калькулятор суммы и разности тождеств – Как пользоваться?

Думаю, теории было достаточно. Теперь пришло время показать вам, как вы можете быстро решить тождества сложения и различия для любого из 6 доступных вариантов, которые вы можете выбрать.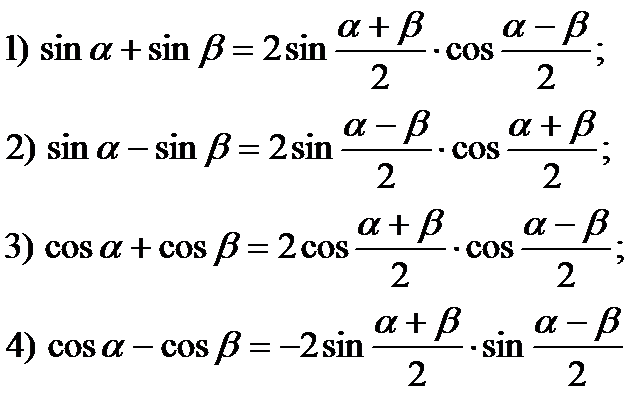 Самое главное, что вам не нужно ничего рассчитывать самостоятельно. Вместо этого используйте наш Калькулятор суммы и разности идентичностей и мгновенно получите результат.

Шаги:

1. Выберите один из шести вариантов из выпадающего списка (синус, косинус, тангенс, котангенс, секанс или косеканс)
2. Введите угол α и угол β в градусах или радианах
3. Стрела, Вы получили результаты!

Калькулятор сумм и разностей тождеств — Пример

Поскольку мы объяснили, как работает наш калькулятор, давайте теперь применим его на практике и посмотрим, как он работает в реальном сценарии.

Сценарий:  Предположим, что мы хотим решить тождества косинуса и тангенса для угла α = 65° и угла β = 20°.

Шаг №1:

1. Выберите функцию косинуса из списка
2. Введите угол α и угол β в соответствующие поля
3. Посмотрите результат 

cos(65° + 20°) = cos(65°) \times cos(20°) — sin(65°) \times sin(20°) = 0,423 \times 0,94 — 0,906 \times 0,342 = 0,087

cos(65° — 20°) = cos(65°) \times cos(20°) + sin(65°) \times sin(20°) = 0,423 \times 0,94 + 0,906 х 0,342 = √2/2 = 0,707

Шаг 2:

1. Выберите функцию касательной из списка
2. Введите углы в соответствующие поля углов tan(65° + 20°) = tan(65°) + tan(20°) \div (1 — tan(65°) \times tan(20°) = (2,145 + 0,364) \div (1 — 2,145 \ умножить на 0,364) = 11,43

   tan(65° — 20°) = (tan(65°) — tan(20°)) \div (1 + tan(65°) \times tan(20°)) = (2,145 — 0,364) \div (1 + 2,145 х 0,364) = 1

   Часто задаваемые вопросы

   Что такое тригонометрические тождества?

   Тригонометрические функции описывают отношения между сторонами прямоугольного треугольника.

   No related posts.