вычисления логарифмов — Колпаков Александр Николаевич
Комплект простейших заданий уровня А на вычисление логарифмов, который репетитор по математике регулярно использует на своих занятиях с большинством учеников. Материал предназначен для учащихся 10-11 классов и преподавателей в помощь при подготовке к ЕГЭ, а также для текущей школьной работы, направленной на отработку вычислительных навыков.
Вычислите:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
Напутствие репетитора по математике:
Вычисляя логарифмы, применяйте следующие формулы:
и
Для решения каждого задания представьте основание логарифма и число под его знаком в виде степени с одним и тем же основанием и вынесите полученные показатели из-под логарифма в его коэффициент. Логарифм с оставшимися равными числами будет равен единице.
Надо сказать, что в 80% задачниках по математике (школьных учебниках и пособиях по подготовке к ЕГЭ) крайне мало вычислительных упражнений на логарифмы, связанных со свойствами степеней. Если репетитор по математике использует стандартные пособия, то в его распоряжении оказывается обычно не более 5 — 6 примеров на логарифмы по каждому алгоритму их вычисления. Я уже давно не пользуюсь никакими задачниками и предлагаю ученикам свои материалы. В заданиях перемешиваю различные виды чисел: десятичные, обыкновенные, корни, дроби, степени с отрицательными показателями.
Вычислите логарифмы с использованием следующих формул:
и
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
Задачи на основное логарифмическое тождество:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
Задачи на формулу перехода к новому основанию
1)
2)
3)
4)
5)
6)
7)
8)
9)
Комментарий репетитора по математике относительно состава задач.
Задания на логарифмы составлены по классическим законам методики и дидактики и имеют достаточное количеством однотипных упражнений. На первый взгляд может показаться, что все номера, взятые из одного раздела, как две капли воды похожи друг на друга. Отличие наблюдается только в числах. Но любой опытный репетитор по математике Вам скажет, что достаточно в одном из таких однотипных примеров поменять какое-нибудь целое число, например, на иррациональное или на дробное и перед ученик мгновенно растеряется. Поэтому я постарался обыграть все возможные числовые ситуации разнообразить номера десятичными и обыкновенными дробями, корнями разных степеней, комбинациями действий и коэффициентов, окружающих логарифмы.
В реальности я подаю задания ученику на отдельном листочке А4 с максимально плотным расположением примеров. Все на одном листе! Один из таких планов с представлен ниже:
Ученикам:
Задания можно использовать для самостоятельной подготовки к ЕГЭ по математике с целью научиться решать простейшие задачи на логарифмы из части В.
Регулярно повторяйте с репетитором формулы, ибо без их уверенного запоминания Вам будет нелегко соориентироваться в вычислениях, в которых применяются сразу две или даже три формулы сразу.
Преподавателям:
Напишите свое мнение о качестве материалов. Понравилась ли Вам подборка упражнений? Насколько велика потребность в таких задачах у репетитора по математике? Помогли ли мои упражнения в практической работе? Пишите, комментируйте! Присылайте интересные логарифмические задания на вычисления, которые встретились Вам в тот или иной период подготовки к ЕГЭ.
Колпаков А.Н. Репетитор по математике — автор комплекта.
51. Логарифмические уравнения
Логарифмическим уравнением называется уравнение, в котором неизвестная величина содержится под знаком логарифма или в его основании.
При решении логарифмических уравнений обязательно учитывается ОДЗ логарифма. Если ОДЗ найти сложно, то можно только выписать условия, а затем проверить полученные корни подстановкой в ОДЗ (можно проверять подстановкой в уравнение, не выписывая ОДЗ).
Типы уравнений и способы их решения
Всюду далее F(X), G(X), H(X) – некоторые выражения с переменной (число).
I тип: уравнение вида
(6.8)
Где C Î R.
ОДЗ:
На указанной ОДЗ уравнение (6.8) решают по определению логарифма:
II тип: уравнение вида
(6.9)
ОДЗ:
На основании равенства логарифмов, уравнение (6.9) сводится к равносильному ему (на указанной ОДЗ) уравнению:
(6.10)
ОДЗ:
Данное уравнение на ОДЗ равносильно совокупности уравнений:
III тип: уравнения, решаемые заменой переменной
(6.11)
Где F – некоторое выражение относительно
Необходимо определить ОДЗ уравнения, учитывая все условия существования логарифма и выражения F.
Далее заменяют и решают уравнение
Если – корни последнего уравнения, то, после возвращения к старой переменной, необходимо решить совокупность
Полученные корни проверяют по ОДЗ.
З а м е ч а н и е. Если вместо какого-либо выражения F(X), G(X), H(X) уравнения (6.8)–(6.11) содержат число, то соответствующее условие не записывают в ОДЗ.
Пример 1. Решить уравнение
Решение. Находим ОДЗ:
Решение системы:
Преобразуем уравнение к виду
Получили уравнение I типа, которое решается по определению логарифма:
Откуда
Из полученных значений корень Х = 4 не подходит по ОДЗ.
Получаем ответ: Х = 6.
Пример 2. Решить уравнение
Решение. Записываем условия, определяющие ОДЗ:
Заданное уравнение относится к I типу. Получаем:
Снова используем определение логарифма:
т. е. откуда
Полученные корни проверяем подстановкой в условия, определяющие ОДЗ уравнения. Убеждаемся, что корень подходит, а корень не подходит по ОДЗ.
Получаем ответ:
Пример 3.
Решить уравнение
Решение. Записываем условия, определяющие ОДЗ:
Данное уравнение относится ко II типу, т. е. решается по свойству равенства логарифмов. Получаем:
т. е.
Раскладываем левую часть на множители:
откуда получаем
Подставляем найденные значения в ОДЗ, находим, что уравнение имеет только один корень Х = 3.
В ответе имеем: Х = 3.
Пример 4. Решить уравнение
Решение. Находим ОДЗ:
т. е.
Данное уравнение относится ко II типу. Решаем совокупность:
По ОДЗ подходит только корень Х = 2, так как
Получаем ответ: Х = 2.
Пример 5. Решить уравнение
Решение. ОДЗ: Преобразуем уравнение:
Имеем квадратное уравнение относительно (уравнение III типа). Заменяем
Решая полученное квадратное уравнение, находим корни Возвращаемся к переменной X:
Оба корня подходят по ОДЗ, получаем ответ:
Пример 6.
Решить уравнение
Решение. Запишем условия ОДЗ:
Воспользуемся тем, что
Тогда
Решаем полученное уравнение как уравнение I типа:
Среди целых делителей свободного члена находим корень Х = –2. Он подходит по ОДЗ.
Пришли к ответу: Х = –2.
Пример 7. Решить уравнение
Решение. ОДЗ: т. е.
Воспользуемся свойствами модуля: если и Тогда уравнение перепишется в виде
Заменяем и приходим к квадратному уравнению
Корнями которого являются числа
Возвращаемся к старой переменной:
Раскрываем модуль, используя ОДЗ:
Получаем ответ:
Пример 8. Решить уравнение
Решение. ОДЗ: т. е. Х Î R.
Рассмотрим левую часть уравнения:
Преобразуем правую часть. Получим:
Используя функциональный метод решения, заключаем, что решением исходного уравнения является решение системы
т.
е. Х = –2.
Получаем ответ: Х = –2.
Пример 9. Найти сумму корней уравнения
Решение. Для данного уравнения характерно следующее: если Х – корень уравнения, то и (–Х) тоже корень уравнения. Поэтому если уравнение имеет корни, то их сумма будет равна нулю. Подстановкой находим корни
Получаем ответ: 0.
| < Предыдущая | Следующая > |
|---|
Решения вышеуказанных проблем
Подробнее о Логарифм и экспоненциальные вопросы с ответами и решениями — 11 класс сообщите об этом объявлении |
Экспресс-журнал 4 (10) в плане б. 
а = 1 
4 — 2 пер. 4 = х пер. 3 + 4 пер. 3 Логарифм — Aptitude Вопросы и ответы
Почему я должен научиться решать вопросы и ответы Aptitude в разделе «Логарифм»?
Учитесь и практикуйтесь в решении раздела вопросов и ответов Aptitude в разделе «Логарифм», чтобы улучшить свои навыки, чтобы вы могли пройти собеседования, конкурсные экзамены и различные вступительные тесты (CAT, GATE, GRE, MAT, банковские экзамены, железнодорожные экзамены и т.
д. ) с полной уверенностью.
Где я могу получить раздел вопросов и ответов Aptitude по теме «Логарифм»?
IndiaBIX предоставляет вам множество вопросов и ответов Aptitude, основанных на «логарифме», а также полностью решенные примеры и подробные объяснения, которые будут легко понять.
Где я могу получить раздел о способностях в вопросах и ответах типа MCQ «Логарифм» для собеседования (объективный тип, множественный выбор)?
Здесь вы можете найти вопросы и ответы Aptitude с несколькими вариантами ответов, основанные на «логарифме», для собеседований при приеме на работу и конкурсных экзаменов. Также даны вопросы объективного типа и типа «истина или ложь».
Как загрузить раздел вопросов и ответов Aptitude по теме «Логарифм» в формате PDF?
Вы можете загрузить раздел вопросов и ответов теста Aptitude на тему «Логарифм» в виде файлов PDF или электронных книг.
Как решить задачи викторины на определение способностей на основе «логарифма»?
Вы можете легко решать задачи викторины на определение способностей, основанные на «логарифме», выполняя приведенные упражнения, включая короткие пути и приемы.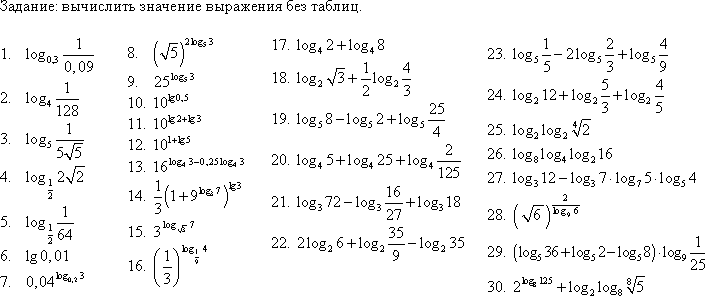
Упражнение: Логарифм. Общие вопросы
1.
Какое из следующих утверждений неверно?
log 10 10 = 1
log (2 + 3) = log (2 x 3)
log 10 1 = 0
log (1 + 2 + 3) = log 1 + log 2 + log 3
Ответ: Вариант
Объяснение:
(a) Поскольку log a a = 1, поэтому log 10 10 = 1. log 5 и log (2 x 3) = log 6 = log 2 + log 3
log (2 + 3) log (2 x 3)
(c) Поскольку log a 1 = 0, поэтому log 10 1 = 0.
(d) log (1 + 2 + 3) = log 6 = log (1 x 2 x 3) = log 1 + log 2 + log 3.
Итак, (b) неверно.
2.
Если log 2 = 0,3010 и log 3 = 0,4771, значение log 5 512 равно:
Ответ: Опция
Объяснение:
| бревно 5 512 |
| |||
| ||||
| ||||
| ||||
| ||||
| ||||
| = 3,876 |
3.
| бревно 8 | равно: |
| журнал 8 |
Ответ: Опция
Объяснение:
| журнал 8 | = | журнал (8) 1/2 | = | журнал 8 | = | 1 | . |
| журнал 8 | журнал 8 | журнал 8 | 2 |
4.
Если log 27 = 1,431, то значение Log 9 IS:
Ответ: Опция
Объяснение:
Log 27 = 1.431
(3 9037 3 3 6) = 1,431
6 (3 3 6) = 1,431
6 (3 3
).
3 log 3 = 1,431
log 3 = 0,477
log 9 = log(3 2 ) = 2 log 3 = (2 x 0,477) = 0,954.
5.
| Если журнал | и | + | журнал | б | = логарифм ( a + b ), тогда: |
| б | и |
а + б = 1
а — B = 1
A 2 — B 2 = 1
ОТВЕТ: Опция
. 44463666666669666966666666695666666666666695666.
и + журнал б = журнал ( a + b ) б и журнал ( a + б ) = логарифм и х б = журнал 1. 