«Логарифмы. Вычисление значений показательных и логарифмических выражений»
Конспект урока
Тема Логарифмы. Вычисление значений показательных и логарифмических выражений
Курс 1 группа _________ Дата__________
Цели и задачи урока:
рассмотреть понятие логарифма числа и свойства логарифмов;дать понятие десятичного и натурального логарифма;
развивать мышление учащихся при выполнении упражнений;
продолжить формировать умение правильно воспринимать и активно запоминать новую информацию;
Тип урока: усвоение новых знаний.
Методическое обеспечение: проектор, презентация к уроку, учебники, индивидуальные карточки.
Ход урока
1. Организационный момент
Приветствие учащихся, определение отсутствующих. Сообщается тема и цель урока.
2. Повторение ранее изученного материала
Экспресс-опрос
а) Что такое степень; что такое основание степени; что такое показатель степени.
б) Работа над основными свойствами степеней. Рассмотреть связь между показателями степеней в равенствах
в) Решить устно примеры:
3. Изучение нового материала
План
1. Логарифм числа. Основные свойства логарифмов.
2. Основное логарифмическое тождество.
2. Формула перехода одного основания логарифмов к другому.
3. Десятичный логарифм.
4. Натуральный логарифм.
Преподаватель излагает новый учебный материал
Логарифм числа
Понятие логарифма числа связано с решением показательных уравнений.
Остановимся на решении двух показательных уравнений. Решение уравнения не вызывает труда. Так как то данное уравнение примет вид Поэтому уравнение имеет единственное решение
А теперь попробуем решить уравнение По теореме о корне это уравнение также имеет единственное решение. Однако, в отличие от предыдущего уравнения, это уравнение является иррациональным числом. Докажем, что корень данного уравнения является числом рациональным, т.
е. Тогда выполняется равенство или Но в любой натуральной степени будет числом четным, а в любой натуральной степени – число нечетное. Получаем противоречие, которое и доказывает, что корень уравнения – число иррациональное. Обдумывая, ситуацию с показательным уравнением математики ввели в рассмотрение новый символ – логарифм. С помощью этого символа корень уравнения записали так: (читается : логарифм числа по основанию
Остановимся теперь на понятии логарифма числа. Очень часто приходится решать задачу: известно, что необходимо найти показатель степени т.е. решить задачу, обратную возведению числа в степень. При нахождении этого показателя степени и возникает понятие логарифма числа по основанию
дается определение логарифма
Введение основного логарифмического тождества
Обратите внимание на то, что является корнем уравнения , а поэтому =8
Таким образом и получается основное логарифмическое тождество
Это равенство является краткой символической записью определения логарифмов.
Решить примеры согласно тождеству: ;
=5; .
Подчеркнем, что и одна и таже математическая модель
Основные свойства логарифмов
Эти свойства вытекают из определения логарифма и свойств показательной функции.
При любом a 0 (a 1) и любых положительных x и y выполнены равенства:
для любого действительного p.
Десятичные и натуральные логарифмы
На практике рассматриваются логарифмы по различным основаниям, в частности по основанию 10.
Логарифмом положительного числа по основанию 10 называют десятичным логарифмом числа в и обозначается, т.е. вместо пишут .
Например,
Натуральным логарифмом (обозначается In) называется логарифм по основанию e
Примеры вычисления десятичных логарифмов
Формулы перехода от одного основания логарифм к другому
На практике рассматривается логарифм по различным основаниям. Отсюда возникает необходимость формулы перехода от одного основания к логарифму по другому основанию.
Решить пример типа: Упростить выражения:
a)
б)
в)
Ответ. a) ; б); в)
4. Закрепление изученного материала
1) 2) 3) 4)
5. Подведение итогов
1. Выставление оценок на уроке
2. Домашнее задание: прочитать лекцию, решить №204-206, 207
6. Рефлексия
Какая тема была изучена на уроке?
Достигнута ли цель урока?
Что вам сегодня больше всего запомнилось на уроке, что понравилось?
Домашнее задание по теме «Логарифм числа. Вычисление логарифмов»
Домашнее задание по теме «Логарифм числа. Вычисление логарифмов»| 12+ Свидетельство СМИ ЭЛ № ФС 77 — 70917 Лицензия на образовательную деятельность №0001058 | Пользовательское соглашение Контактная и правовая информация |
Педагогическое сообщество | Бесплатные всероссийские конкурсы | Бесплатные сертификаты | Нужна помощь? Инструкции для новых участников | Бесплатная онлайн-школа для 1-4 классов |
РФВсё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости
Библиотека
▪Методические разработки
▪Фрагменты уроков
Материал опубликовала
25
#10 класс #11 класс #Алгебра #Математика #Методические разработки #Учитель-предметник #Школьное образование #Фрагмент урока
Победитель конкурса Всероссийский конкурс педагогического мастерства на лучшую разработку «Нестандартное домашнее задание» |
Пояснительная записка
Предмет | Математика |
Аудитория | 1 курс СПО, 10-11 класс |
Тема | «Логарифм числа» |
| Цель и задачи | Цель: совершенствование навыков вычисления логарифмов. Задачи:
|
Проверяемые элементы содержания | Логарифм числа; основное логарифмическое тождество; понятие десятичного и натурального логарифма; свойства логарифмов. |
Степень сложности | Основное задание – средняя; дополнительное задание – высокая. |
Тип задания | Индивидуальное |
Рекомендуемое количество времени | Основное задание – 15-30 минут в зависимости от степени подготовленности учащихся. Дополнительное задание выполняется по желанию, на выполнение дается несколько дней. |
Вид задания | Головоломка |
Способ проверки и критерии оценки задания. | Основное задание – проверка учителем, самопроверка, взаимопроверка. Дополнительное задание – проверка учителем; выставка работ; конкурс на лучшую числовую головоломку по теме «Логарифм числа». Критерии оценки выполненных работ:
|
| Использованный источник | Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10-11 класс. Алимов Ш.А., Колягин Ю.М., Ткачева М.В. и другие. — М: Просвещение, 2022. |
Задание для учащихся:
Основное:
Разгадать головоломку «Цепочка логарифмов».
Результат представить в виде последовательности верных ответов. Например, 2 – 4 – 6 – 8 – и т.д.
Дополнительное:
Разработать собственную числовую головоломку по теме «Логарифм числа» любого вида (числовой кроссворд, числовой ребус, числовой лабиринт и т.д.). Головоломка должна содержать примеры на вычисление логарифмов и правильные ответы.
Файл для распечатки:
Головоломка
PDF / 537.56 Кб
(В файле два варианта головоломки на выбор преподавателя: первый на 16 примеров, второй на 9 примеров.)
Ответ на головоломку:
В данной цепочке в каждом логарифме вместо квадратика подставляется результат вычисления предыдущего логарифма.
Правильная цепочка ответов:
½ — 2 – 2 – 2 – 1/8 – 1 – 49 – 4 – 10 – ½ — 4 –(- ¼) – 2 – 2 – (-1) — 0
Примеры выполненных работ:
Опубликовано в группе «ГОЛОВОЛОМКИ образовательные»
Панов Егор Игоревич, 22.12.22 в 05:23 2ОтветитьПожаловаться
Поздравляю с победой в конкурсе. Желаю дальнейших творческих успехов!
Латышева Надежда Леонидовна, 22.12.22 в 09:47 0ОтветитьПожаловатьсяСпасибо большое, Егор Игоревич!
Чтобы написать комментарий необходимо авторизоваться.
Закрыть
Алгоритм— Как компьютеры вычисляют логарифм?
спросил
Изменено 1 год, 11 месяцев назад
Просмотрено 867 раз
Я хотел знать, как компьютеры считают логарифмы?
Я не имею в виду связанные функции.
Например, Python использует math.log() функция. Но я хочу знать, что именно делает эта функция? И можно ли его смоделировать еще раз и более точно?
Есть ли формула для этого? Или алгоритм? (Я не думаю, что у компьютера есть таблица журнала!)
Спасибо
- алгоритм
- информатика
- логарифм
3
Библиотека GNU C, например, использует вызов ассемблерной инструкции fyl2x(), что означает, что логарифмы вычисляются непосредственно аппаратно. Следовательно, следует спросить: какой алгоритм используется для вычисления логарифмов компьютерами? Зависит от процессора. Для Intel IA64 они используют серию Taylor в сочетании с таблицей.
Дополнительную информацию можно найти здесь: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.24.5177
и здесь: http://www.computer.org/csdl/proceedings /arith/1999/0116/00/01160004.pdf
Это очень открытый, широкий и «зависящий».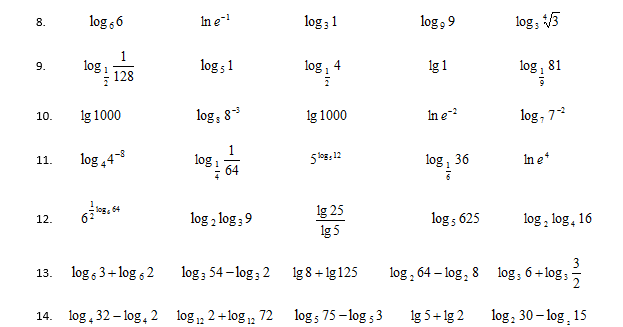
Для каждого языка программирования, каждой основной библиотеки, каждой отдельной системы и т. д. могут существовать разные алгоритмы/механизмы и инструкции машинного кода для выполнения математических (и любых других типов) вычислений.
Кроме того, даже если бы все языки программирования в этом мире использовали один и тот же алгоритм «X», это все равно не означает, что Компьютер вычисляет логарифм способом X , потому что компьютер все равно будет (скорее всего) выполнять свою работу на машинном уровне по-разному, в разных обстоятельствах, не принимая во внимание тот факт, что алгоритмы одинаковы (что очень маловероятно).
Имейте в виду, что компьютерные архитектуры различаются, операционные системы различаются, а инструкции на ассемблере могут сильно отличаться от ЦП к ЦП.
Я действительно думаю, что вам следует задавать более конкретные и конкретные вопросы на этом сайте.
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
логарифмов: ранняя история знакомой функции — Джон Нейпир знакомит с логарифмами
‹ Логарифмы: ранняя история знакомой функции — До логарифмов: вычислительные требования конца шестнадцатого века
вверх
Логарифмы: ранняя история знакомой функции — Йоост Бюрги знакомит с логарифмами неудивительно, что многие математики остро осознавали проблемы вычислений и стремились избавить практиков от вычислительного бремени.
Рис. 1. Джон Нейпир (1550-1617)
(из архива истории математики MacTutor)
Нейпир впервые опубликовал свою работу по логарифмам в 1614 году под названием Mirifici logarithmorum canonis descriptio, , что буквально переводится как Описание чудесной таблицы логарифмов.
В самом деле, само название, выбранное Нейпиром, свидетельствует о его высоких амбициях в отношении этой техники — предоставления таблиц, основанных на отношении, которое было бы не чем иным, как «чудодейственным» для практиков. Помимо краткого обзора математических деталей, Нейпир дал своей концепции техническое выражение. Он придумал термин из двух древнегреческих терминов логос, — пропорция, — арифмос, — число; соединяя их, получается слово «логарифм». Нейпир использовал это слово, а также обозначения «естественные» и «искусственные» для чисел и их логарифмов соответственно в своем тексте.
Несмотря на очевидную связь с существующими методами протезирования и секвенциями, Нэпир обосновал свою концепцию логарифма в кинематической структуре. Мотивация этого подхода до сих пор не совсем понятна историками математики. Нейпир представил две частицы, движущиеся по двум параллельным линиям. Первая линия имела бесконечную длину, а вторая — фиксированную длину (см.
рис. 2 и 3). Нейпир представил, что две частицы стартуют из одного и того же (горизонтального) положения в одно и то же время с одинаковой скоростью. Первую частицу он привел в равномерное движение по линии бесконечной длины так, чтобы она прошла равные расстояния за равные времена. Вторую частицу он привел в движение на конечном отрезке так, чтобы ее скорость была пропорциональна расстоянию, оставшемуся от частицы до фиксированной конечной точки отрезка.
Рисунок 2. Две параллельные линии Нейпира с движущимися частицами
(Изображение предоставлено Landmarks of Science Series, NewsBank-Readex) линия была синусом, а пройденное расстояние по первой (бесконечной) линии было логарифмом синуса. Это привело к тому, что по мере уменьшения синусов логарифмы Непера увеличивались. При этом синусы уменьшались в геометрической пропорции, а логарифмы возрастали в арифметической пропорции. Мы можем резюмировать объяснение Нэпьера следующим образом ( Описание I, 1 (стр.
4); см. рисунок 3): \[AC = \log_{nap}(\gamma\omega)\;\;{\rm где}\;\;\gamma\omega = {\rm Sin}\,\theta_{1} \]
\[AD = \log_{nap}(\delta\omega)\;\;{\rm где}\;\;\delta\omega = {\rm Sin}\,\theta_{2}\ ]
\[AE = \log_{nap}(\epsilon\omega)\;\;{\rm где}\;\;\epsilon\omega = {\rm Sin}\,\theta_{3}\]
и так далее, так что в более общем виде: \[x={\rm Sin}\,(\theta)\]
\[y={\log_{nap}}(x)\] где \( \log_{nap}\) использовался для того, чтобы отличить конкретное понимание Нейпиром концепции логарифма от современного.
Рисунок 3. Соотношение между двумя линиями и логарифмами и синусоидами
Napier сгенерировал числовые записи для таблицы, воплощающей это отношение. Он упорядочил свою таблицу, делая приращения дуги \(\тета\) минуту за минутой, затем перечисляя синус каждой дуги минуты, а затем соответствующий логарифм. Однако с точки зрения того, как он на самом деле вычислял эти записи, он фактически работал бы противоположным образом, сначала генерируя логарифмы, а затем выбирая те, которые соответствуют синусу дуги, которые соответственно формировали аргумент.
7}.\] 9{\circ}\) в угловых минутах и по симметрии предоставил значения для всего первого квадранта. Отрывок на рисунке 4 дает первую половину первой степени и, по симметрии, справа последнюю половину восемьдесят девятой степени.
Чтобы заполнить таблицы, Нейпир вычислил почти десять миллионов записей, из которых выбрал соответствующие значения. Сам Нейпир подсчитал, что вычисление такого количества записей заняло у него двадцать лет, что означает начало его усилий еще в 159 г.4.
Рисунок 4. Первая страница таблиц Нейпира
(Изображение предоставлено Landmarks of Science Series, NewsBank-Readex)
Нейпир часто демонстрировал преимущества своего метода. Например, он решал задачу, связанную с вычислением средних пропорций, иногда называемых средним геометрическим. Он рассмотрел обычный способ, которым это должно быть вычислено, и указал, что его метод с использованием логарифмов не только находит ответ «раньше» (то есть быстрее!), но также использует только одно сложение и одно деление на два! Он заявил:
.
Пусть даны крайние значения 1000000 и 500000 и ищется среднее пропорциональное: это обычно находится путем умножения данных крайних значений одно на другое и извлечения квадратного корня из произведения. Но мы находим это раньше таким образом; Мы складываем логарифм экстремумов 0 и 693147, сумма которых равна 693147, которую мы делим на 2, а частное 346573 будет логарифмом. среднего пропорционального желаемого. По которому среднее пропорциональное 707107, а его дуга 45 градусов находятся по-прежнему…. находят сложением одного и делением на два. (Книга I, 5 (стр. 25), в переводе Эдварда Райта)
Пусть даны крайние значения 1000000 и 500000 и ищется среднее пропорциональное: это обычно находится путем умножения данных крайних значений одно на другое и извлечения квадратного корня из произведения. Но мы находим это раньше таким образом; Мы складываем логарифм экстремумов 0 и 693147, сумма которых равна 693147, которую мы делим на 2, а частное 346573 будет логарифмом. среднего пропорционального желаемого. По которому среднее пропорциональное 707107, а его дуга 45 градусов находятся по-прежнему…. находят сложением одного и делением на два. (Книга I, 5 (стр. 25), в переводе Эдварда Райта)Чтобы найти среднее пропорциональное традиционными методами, Нейпир заметил, что нужно вычислить произведение, а затем извлечь квадратный корень; то есть: \[\sqrt{1 000 000 \times 500 000} = \sqrt{500 000 000 000} \приблизительно 707106,78\] Этот метод включает умножение двух больших чисел и длительное извлечение квадратного корня. В качестве альтернативы Нейпир предложил (с вычислениями до 6 значащих цифр):0005
\[693147 \div 2 = 346573\;\;\;{\rm to}\;\;6\;\;{\rm значащее}\;\;{\rm цифры}\]
\[ \Rightarrow {\rm означает}\;\;{\rm пропорционально} = 707107,\;\;\;{\rm as}\;\;{\rm требуется,}\], что, по его справедливому мнению, было намного проще для вычислить.