Любое число в степени 0 равно чему: Степень с показателем 0 — урок. Алгебра, 7 класс.

0. Если брать действительные числа, то предел, как ни странно, будет 1. График такой штуки будет выглядеть как некого рода «крыша», исходящая из нули, и подойти к началу координат можно с двух сторон (справа и слева для простоты) Однако если рассматривать комплексные числа, то введя третью ось, мы сможем подойти с любой стороны, что… Читать далее

Комментировать ответ…Комментировать…

Сергей Шамов

4,8 K

Пользователь TheQuestion  · 23 янв 2018

Возведение в степень — это просто сокращённая форма записи некоторого числа одинаковых умножений. А по отношению к операции умножения единица является так называемым нейтральным элементом… т.е. умножение на единицу не меняет результат. (Точно так же, как и ноль по отношению к операции сложения.)  Смысл правила «любое число в нулевой степени равно единице» состоит в… Читать далее

Nataly Kap

29 июля 2021

любое число в степени 0 равно 1, приводят этому доказательство, что 2^0=2^(3-3)=2^3/2^3=1, то почему так же нет. n и докажите… Читать дальше

Комментировать ответ…Комментировать…

Arsenii O

Математика

500

МГУ, НМУ  · 20 янв 2018

Отвечу на вопрос с позиции математического формализма (не ориентируясь на прикладную значимость, к коей отсылали в ранних ответах).  Шаг первый. У нас есть некоторая аксиоматика теории множеств (в общем, как мне видится, здесь любая подойдёт) и определение алгебраического поля. Задаём на поле порядок и из множества пересечений всех его индуктивных подмножеств строим… Читать далее

Никита К.

21 января 2018

Ноль не натуральное число

Комментировать ответ…Комментировать…

Вы знаете ответ на этот вопрос?

Поделитесь своим опытом и знаниями

Войти и ответить на вопрос

Деление на ноль — пример, решенный пример и часто задаваемые вопросы

Деление — это метод деления группы вещей на равные части. Это одна из четырех основных арифметических операций, которые дают справедливый результат обмена. Основная цель деления состоит в том, чтобы увидеть, сколько равных групп или сколько в каждой группе справедливо делится. Можно также сказать, что деление — это операция, обратная умножению.

Пример:

При делении, если 12 разделить на 3 равные группы, то в каждой группе будет по 4. В математическом смысле это можно записать как 12/3=4,9.0003

Некоторые факты о делении:

• При делении число, которое делится, называется делимым. Число, на которое оно делится, называется делителем. Число, полученное при делении, называется частным, а оставшееся число называется остатком.

• Например, если мы разделим 17 на 2, мы получим 8. Здесь 17 — делимое, 2 — делитель, 8 — частное, а 1 — остаток.

• Произведение частного и делителя, прибавленного к остатку, всегда равно делимому. Это можно записать как (делитель × частное) + остаток = дивиденд или (d × Q) + R = D

• Например, если мы разделим 23 на 2, мы получим 11. Здесь 23 — делимое, 2 — делитель, 11 — частное, а 1 — остаток. Если мы будем следовать приведенному выше правилу, то, решив (2 x 11) + 1, мы получим 23, что является делимым. Следовательно, указанное выше свойство имеет место.

• Когда мы делим что-то на 1, результатом всегда будет одно и то же число. Это означает, что если делитель равен 1, то частное будет равно делимому.

Например: 10 ÷ 1= 1

• При делении остаток всегда меньше делителя.

• Деление на ноль считается неопределенным. (Обсудим это подробнее)

• Если делимое и делитель совпадают при делении, то результатом всегда будет 1.   

Например: 5 ÷ 5 = 1. 

Ноль:

Ноль — это целое число, непосредственно предшествующее 1. Это четное число, которое не является ни положительным, ни отрицательным. Хотя ноль считается целым числом, это не счетное число. Значение нулевого числа ничто.

Разделение нуля на число:

Разделив 0 на любое число, мы получим ноль. Ноль никогда не изменится, если вы умножите или разделите на него любое число.

⇒ 0/x = 0

Например, у человека нет ирисок, которые нужно разделить между 7 (скажем) детьми. Это означает, что нечего делить или распределять между 7 детьми. Если ничем не делиться, то ириски никто не получит. Следовательно, 0, деленный на любое число, дает 0 как частное.

Следовательно, 0/1 = 0

Число, деленное на ноль:

Никогда не делите любое число на ноль. Нас всех этому учили в школе, и это хороший совет. Делить на ноль редко имеет смысл. Деление на ноль не имеет смысла, потому что в арифметике деление на ноль также может интерпретироваться как умножение на ноль. Предположим, мы получили уравнение 5/0=X. Это также интерпретирует то же уравнение как 0*X=5. Здесь нет числа, которое могло бы вместить X, чтобы уравнение работало.

 

Со ссылкой на приведенный выше пример, если мы рассмотрим 0 на 0 до X, т. е. 0/0=X, это также можно переписать как 0*X=0, и проблема в том, что работает любое число. X может быть любым, так что это уравнение совершенно бесполезно. Следовательно, если мы разделим на ноль, это считается «неопределенным».

Например, если у нас есть 20 бананов и мы хотим раздать их поровну на 4 человек, то по определению деления каждый ученик получит 20/4 бананов, т.е. по 5 бананов. Если использовать ту же логику, x/0 означает распределение x бананов поровну между 0 людьми. Это совершенно бессмысленно; не существует рационального способа распределения группы предметов среди 0 человек, поэтому мы можем сказать, что это не определено.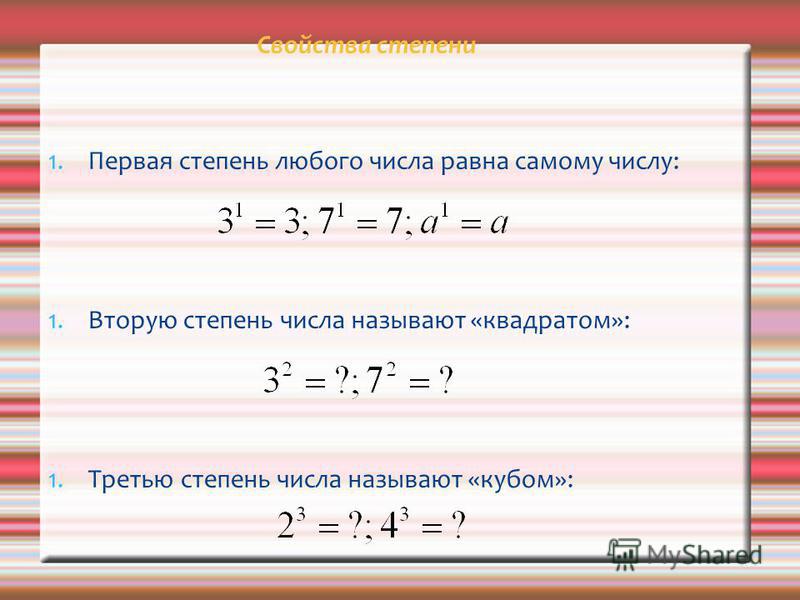

Что не определено?

Иногда, когда вы видите «неопределенное» на уроке математики, это кажется очень странным. Математики никогда не определяли, что значит делить на ноль. Какова ценность этого? Они не сделали этого, потому что не смогли найти хороший ответ. Нет хорошего ответа, нет хорошего определения. И из-за этого любое ненулевое число, деленное на ноль, остается «неопределенным».

Решено Пример: 

Если у вас дома 5 яблок и 5 друзей, сколько яблок получит каждый друг в справедливой доле? Каждый получит по яблоку, верно?

Если у вас такое же количество яблок и нет друзей в вашем доме, вы делите яблоки между людьми? Как мы можем понять это? Это не имеет смысла, и это то, что называется undefined.

Знаете ли вы?

• Понятие числа ноль появилось в 7 веке, намного позже изобретения других натуральных чисел. Брахмагупта был математиком и астрономом, который нашел концепцию нуля. Он также дал правила сложения и вычитания с нулем.

• Ноль является действительным числом, целым, рациональным, а также целым числом.

• Ноль всегда нейтрален, а это означает, что нет такой вещи, как -0 или +0.

• Ноль не является ни простым, ни составным числом.

• Если к любому числу прибавить или вычесть ноль, то число останется прежним. Но если ноль умножить на любое число, то произведение равно нулю.

• Степень любого числа, увеличенного на ноль, всегда равна единице.

Заключение

Высококвалифицированные специалисты в предметной области тщательно подбирают учебный материал с учетом потребностей учащегося. Статьи, решения и примеры вопросов — отличный способ концептуального обучения. Поскольку известно, что математика требует практики, ожидается, что учащиеся будут обращаться к предоставленному материалу, что важно для лучшего обучения. Понимание этого ключевого требования и работа над учебным планом с учетом этого является важным аспектом успеха. Вы можете легко скачать бесплатные PDF-файлы и учиться конструктивно.

Часто задаваемые вопросы: Почему 0,3 — 0,2 — 0,1 не равно нулю? — Ответы MATLAB

367 просмотров (последние 30 дней)

Ответил: Уолтер Роберсон 29 июня 2022 г.

Принято Ответ: Январь

Почему

0,3 — 0,2 — 0,1 == 0

или

v = 0:0,1:1;

любой (v == 0,3)

(или аналогичные числа) ответ неверный?

Ответ принят

Отредактировано: Январь 26 декабря 2012 г.

0,3 — 0-2 — 0,1 возвращает -2,7756e-17.

Как часто упоминается в новостных группах, некоторые числа с плавающей запятой не могут быть точно представлены в двоичной форме. Вот почему вы видите очень маленький, но не нулевой результат. См. ЭПС.

Разница в том, что 0:0.1:0.4 увеличивается на число, очень близкое, но не совсем 0,1 по причинам, упомянутым ниже. Таким образом, через несколько шагов он будет отключен, тогда как [0 0,1 0,2 0,3 0,4] приводит числа к их правильному значению, настолько точно, насколько они могут быть представлены в любом случае.

а = [0 0,1 0,2 0,3 0,4];

б = 0:.1:.4;

as = sprintf(‘%20.18f\n’,a)

>> as =

0.000000000000000000 % ==

0.100000000000000010 % ==

0.200000000000000010 % ==

0.299999999999999990 % ~= bs !

0,400000000000000020 % ==

BS = Sprintf (‘ % 20,18F \ N’, B)

>> BS =

0,000000000000000000 % ==

0,100000000000010 % = 818 0,200301100100000000000000000000000000010000001000010000001000000100000010000001000000100001000010010001000010010010 гг.0003

0.300000000000000040 % ~= as !

0,400000000000000020 % ==

и:

шестнадцатеричный формат;

hd = [a. ‘,b.’]

>> hd =

0000000000000000 0000000000000000 % ==

3fb999999999999a 3fb999999999999a % ==

3fc999999999999a 3fc999999999999a % ==

3fd3333333333333 3fd3333333333334 % ~= !

3fd999999999999a 3fd999999999999a % ==

Если вы пытаетесь сравнить два числа с плавающей запятой, будьте очень осторожны при использовании == для этого. Альтернативный метод сравнения состоит в том, чтобы проверить, являются ли два сравниваемых числа «достаточно близкими» (что выражается допуском) друг к другу:

% вместо a == b

% используйте:

areEssentiallyEqual = abs(a-b) < tol

% для некоторого небольшого значения tol относительно a и b

% возможно определяется с помощью eps(a) и/ или eps(b)

Вы можете увидеть такое же поведение вне MATLAB. Используя карандаш и бумагу (или классную доску, или белую доску, и т. д.), вычислите x = 1/3 с любым числом знаков после запятой. Однако количество десятичных разрядов должно быть конечным.

Теперь вычислите y = 3*x. В точной арифметике у будет ровно 1; однако, поскольку x не равно одной трети, а является округленным приближением к одной трети, y не будет точно равно 1,9.0003

Читаемое введение в арифметику с плавающей запятой можно найти в статье Cleve’s Corner 1996 года: Floating Points (PDF) http://www.mathworks.com/company/newsletters/news_notes/pdf/Fall96Cleve.pdf

и подробную информацию об арифметике с плавающей запятой см. в следующем документе: Что должен знать каждый компьютерный ученый об арифметике с плавающей запятой http://docs.sun.com/source/806-3568/ncg_goldberg.html

Другим ресурсом является Техническое примечание 1108. http://www.mathworks.com/support/tech-notes/1100/1108.html в разделе поддержки веб-сайта The MathWorks.

Этот ответ скопирован и слегка изменен с сайта matlab.wikia.com/wiki/FAQ: Why_is_0.3-0.2-0.1_not_equal_to_zero

Больше ответов (2)

Под редакцией: Джон Д’Эррико 30 августа 2021 г.

Вошел:

Позвольте мне добавить свой взгляд на проблему.

Предположим, мы попытаемся представить эти числа в двоичной форме? То есть представить 1/10 = 0,1 в десятичном виде, а в виде двоичного числа? Мы должны сделать это, потому что все числа с плавающей запятой хранятся в двоичной форме. Даже если бы использовалось десятичное хранение, у нас все равно были бы проблемы. Например, 2/3 — 1/3 == 1/3? Конечно, это должно быть верно в десятичной арифметике?

Предположим, мы работали с точностью до 10 знаков в десятичной арифметической форме хранения. Как будет выглядеть 1/3?

X = 0,3333333333

Y = 0,6666666667

Я округлил оба значения до их ближайшего приближения, которое я могу найти в десятичной форме, только с 10 цифрами после точки. Теперь Y-X будет:

Y — X = 0,6666666667 — 0,3333333333 = 0,3333333334

И это не то же самое значение, что и X. Но вы говорите, что вместо этого я должен был использовать Y = 0,6666666666, округляя в меньшую сторону. Тогда у нас будет Y-X=X.

Но тогда мы также должны иметь X + Y = 3/3 = 1. И если бы мы округли Y в меньшую сторону, чтобы последний результат работал, то мы бы увидели:

X = Y = 0,3333333333 + 0,6666666666 = 0,9999999999

Таким образом, всегда будет какое-то противоречие, пока мы вынуждены использовать конечное десятичное хранилище для чисел, которые не имеют конечного представления в этой базе.

То же самое относится к любой бинарной форме хранения. Вот как двойные и одиночные числа хранятся в MATLAB. Двойник использует 52 двоичных бита для хранения числа. MATLAB подходит настолько близко, насколько это возможно, но только 52 бита представляют мантисса. 9[-4 -5 -8 -9 -12 -13 -16 -17 -20 -21 -24 -25 -28 -29 -32 -33 -36 -37 -40 -41 -44 -45 -48 -49 — 52 -53 -55])

ок =

0,1

Что выглядит как 0,1, отображаемое в MATLAB, но так ли это? ТОЧНО 0,1?

sprintf(‘%0.55f’,approx)

ans = ‘0.1000000000000000055511151231257827021181583404541015625’

sprintf(‘%0. 55f’,1/10)

ans = ‘0.1000000000000000055511151231257827021181583404541015625’

As you can see, both values ​​are теперь видно, что то же самое. Но ни то, ни другое не равно 0,1, только самое близкое приближение, которое MATLAB смог найти для этого числа.

Точно так же мы могли бы попытаться аппроксимировать 0,2 и 0,3 в виде двоичных чисел, но опять же, мы потерпим неудачу, если будем вынуждены использовать для аппроксимации конечное число двоичных битов. И, как мы уже видели в примерах с десятичными числами, мы всегда будем иногда терпеть неудачу. Иногда все работает. Например, попробуйте эти два примера:

0,2 — 0,1 == 0,1

ans = логическое

1

0,3 — 0,2 == 0,1

инс = логический

0

Итак, кажется, что одно из этих тривиальных математических тождеств работает, а другое нет. Опять же, проблема в том, что MATLAB может использовать только конечное число битов для представления любого числа. И когда эти числа не могут быть точно представлены в конечном числе битов, мы ИНОГДА будем видеть противоречие тому, что, как мы ожидаем, должно быть правдой. -1 + 90 нет степени 2, которая точно делится на 10.

И, следовательно, не существует возможного конечного позиционного представления по основанию 2 числа 1/10 (или 1/100, или 1/1000). И поэтому, пока вы используете конечное двоичное представление, 0,001 (основание 10) никогда не может точно равняться 1/1000. Поэтому, когда вы умножаете 0,001, представленное в двоичном виде с конечными позициями, на 350, вы никогда не получите ровно 350/1000.

Тогда возникает вопрос, является ли значение, которое вы получаете для 350 * 0,001, тем же приближением, что и для записи 0,350 . И ответ на это оказывается НЕТ. И если бы это было то же самое, это было бы случайно, и были бы разные числа, которые не сработали.

При любой конкретной системе округления, даже при любом фиксированном количестве дополнительных «защитных» цифр для умножения, вы можете показать, что, пока вы используете конечную позиционную целочисленную систему счисления, будут такие случаи, когда округление представления не будут равны после умножения.

Я подчеркиваю, что это не ошибка MATLAB: это проблема, присущая каждой конечной позиционной целочисленной системе счисления.

Вы могли бы уменьшить проблемы, если бы немедленно переключили все на рациональные числа неопределенной точности и выполняли вычисления как рациональные числа, но (A) это потребовало бы растущих объемов памяти по мере выполнения вычислений; и (B) это все равно не решит проблемы полностью. (Например, если пользователь написал 0,3333333333, то он «намеревался» написать рациональную 1/3 или «намеревался» написать рациональное число 33333333333/10000000000?)

MATLAB выбрал конечное двоичное представление, потому что именно его использует аппаратное обеспечение вашего компьютера.

Произошла ошибка

Не удалось выполнить действие из-за изменений, внесенных на страницу. Перезагрузите страницу, чтобы увидеть ее обновленное состояние.

Выберите веб-сайт

Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и увидеть местные события и предложения.