Функции МАКС и МИН в Excel по условию
Подсчет максимального и минимального значения выполняется известными функциями МАКС и МИН. Бывает, что вычисления нужно произвести по группам или в зависимости от условия, как в СУММЕСЛИ.
Долгое время в Excel не было аналога СУММЕСЛИ или СРЗНАЧЕСЛИ для расчета максимального и минимального значения, поэтому использовали формулу массивов.
Пусть имеются данные
Нужно подсчитать максимальное значение в указанной группе. Название группы (критерий) введем в отдельную ячейку (D2). Пусть для начала это будет группа Б. Рядом введем следующую формулу:
=МАКС(ЕСЛИ(A2:A13=D2;B2:B13))
Это формула массивов, поэтому ввести ее нужно комбинацией Ctrl + Shift + Enter.
Теперь, меняя название группы, можно без всяких фильтров и сводных таблиц видеть максимальное значение внутри этой группы.
Как это работает? Очень просто. Первым делом нужно указать диапазон, который будет использоваться в качестве аргумента функции МАКС, то есть только те ячейки, которые соответствуют указанной группе.
ЕСЛИ(A2:A13=D2;B2:B13)
Указанное выражение отбирает только те значения, для которых название группы совпадает с условием в ячейке D2. Вот, как это видит Excel
На следующем этапе укажем функцию МАКС, аргументом которой выступает полученный выше массив. Excel воспринимает примерно так.
Видно, что максимальное значение внутри массива равно 31. Его и мы и увидим в ячейке с формулой. Нужно только не забыть итоговую функцию ввести комбинацией клавиш Ctrl + Shift + Enter, иначе ничего не получится. В строке формул формула массива отображается внутри фигурных скобок. Добавляются сами, специально дорисовывать не нужно.
Если функцию МАКС заменить на МИН, то по указанному условию (названию группы) будет выдаваться минимальное значение.
В MS Excel добавили новые статистические функции — МАКСЕСЛИ и МИНЕСЛИ. Обе функции имеют возможность учитывать несколько условий и некоторое время в их названиях в конце были буквы -МН. Потом убрали, хотя в скриншотах ниже используется вариант названий с -МН.
Есть ряд значений, каждое из которых входит в некоторую группу. Нужно рассчитать максимальное значение по группе А. Используем формулу МАКСЕСЛИ.
Все очень просто. Как и у СУММЕСЛИМН вначале указываем диапазон, где находится искомое максимальное значение (колонка В), затем диапазон с критериями (колонка А) и далее сам критерий (в ячейке D2). Можно указать сразу несколько условий. Таким же способом легко рассчитать минимальное значение по условию.
Максимумы и минимумы — определение, типы, графики, примеры
Максимумы и минимумы известны как экстремумы функции. Максимумы и минимумы — это максимальное или минимальное значение функции в заданном наборе диапазонов. Для функции во всем диапазоне максимальное значение функции известно как абсолютный максимум, а минимальное значение известно как абсолютный минимум.
Существуют другие максимумы и минимумы функции, которые не являются абсолютными максимумами и минимумами функции и известны как локальные максимумы и локальные минимумы. Давайте узнаем больше о локальных максимумах и минимумах, абсолютных максимумах и минимумах, а также о том, как найти максимумы и минимумы функции.
| 1. | Максимумы и минимумы функции |
| 2. | Локальные максимумы и минимумы |
| 3. | Абсолютные максимумы и минимумы |
4. | Как найти максимумы и минимумы функции? |
| 5. | Часто задаваемые вопросы о Maxima и Minima |
Что такое максимумы и минимумы функции?
Максимумы и минимумы — это пики и впадины на кривой функции. У функции может быть любое количество максимумов и минимумов. В исчислении мы можем найти максимальное и минимальное значение любой функции, даже не глядя на график функции. Максимум будет самой высокой точкой на кривой в заданном диапазоне, а минимум будет самой низкой точкой на кривой.
Комбинация максимумов и минимумов является экстремумом. На изображении, приведенном ниже, мы можем видеть различные пики и впадины на графике. При x = a и при x = 0 мы получаем максимальные значения функции, а при x = b и x = c получаем минимальные значения функции. Все пики являются максимумами, а впадины — минимумами.
В функции существует два типа максимумов и минимумов:
- Локальные максимумы и минимумы
- Абсолютные или глобальные максимумы и минимумы
Давайте узнаем о них подробнее.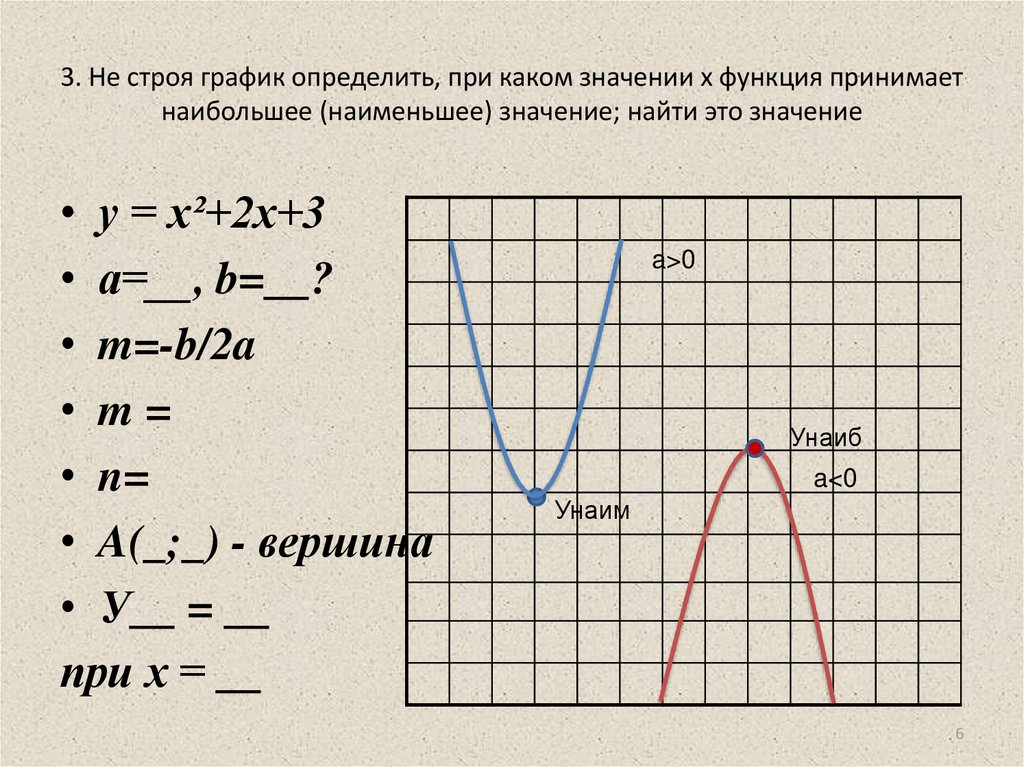
Локальные максимумы и минимумы
Локальные максимумы и минимумы – это максимумы и минимумы функции, возникающие в определенном интервале. Локальные максимумы будут значением функции в точке определенного интервала, для которого значения функции вблизи этой точки всегда меньше, чем значение функции в этой точке. Принимая во внимание, что локальные минимумы будут значением функции в точке, где значения функции вблизи этой точки больше, чем значение функции в этой точке.
Локальные максимумы: Точка x = b является точкой локального максимума для f(x), если в окрестности точки b, т.е. в (b−𝛿, b+𝛿), где 𝛿 можно сделать произвольно малым, f( x) < f(b) для всех x ∈ (b−𝛿, b+𝛿)∖{b}. Это просто означает, что если мы рассмотрим небольшую область (интервал) вокруг x = b, f(b) должно быть максимальным в этом интервале.
Локальные минимумы: Точка x = a является точкой локального минимума для f(x), если в окрестности a , т.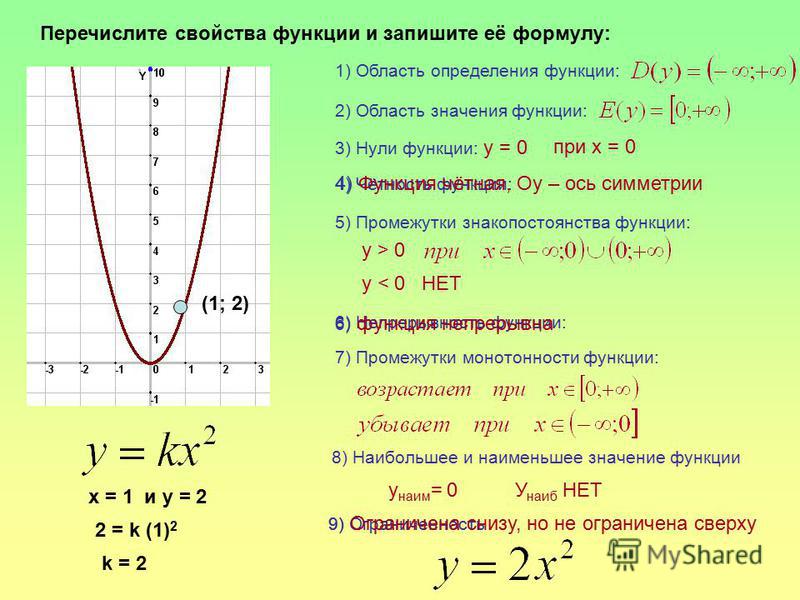
е. в (a−𝛿,a+𝛿), (где 𝛿 может иметь сколь угодно малое значений), f(x) > f(a) для всех x ∈ (a−𝛿,a+𝛿)∖{a}. Это означает, что если мы рассмотрим небольшой интервал вокруг x = a, f(a) должен быть минимумом в этом интервале.
На приведенном ниже изображении видно, что x = b и x = d — локальные максимумы, а x = a и x = c — локальные минимумы.
Абсолютные максимумы и минимумы
Высшая точка функции во всей области известна как абсолютный максимум функции, тогда как самая низкая точка функции во всей области функции известна как абсолютный минимум функции. Может быть только один абсолютный максимум функции и один абсолютный минимум функции во всей области. Абсолютные максимумы и минимумы функции также можно назвать глобальными максимумами и глобальными минимумами функции.
- Абсолютные максимумы: Точка x = a является точкой глобального максимума для f(x), если f(x) ≤ f(a) для всех x∈D (область определения f(x)).
- Абсолютный минимум: точка x = a является точкой глобального минимума для f(x), если f(x) ≥ f(a) для всех x∈D (область определения f(x)).
На приведенном ниже изображении точка x = a является абсолютным максимумом функции, а точка x = b — абсолютным минимумом функции.
Как найти максимумы и минимумы функции?
Максимумы и минимумы функции можно вычислить с помощью теста производной первого порядка и теста производной второго порядка. Производные тесты — это самый быстрый способ найти максимумы и минимумы функции. Давайте обсудим их один за другим.
Критерий производной первого порядка для максимума и минимума
Первая производная функции дает наклон функции. Вблизи точки максимума наклон кривой увеличивается по мере приближения к точке максимума, затем становится равным 0 в точке максимума, а затем уменьшается по мере удаления от точки максимума. Точно так же вблизи точки минимума наклон функции уменьшается по мере продвижения к точке минимума, затем становится равным 0 в точке минимума, а затем увеличивается по мере удаления от точки минимума. Мы используем эту информацию, чтобы узнать, является ли точка максимумом или минимумом.
Допустим, у нас есть функция f, непрерывная в критической точке, определенная в открытом интервале I, и f’(c) = 0 (наклон равен 0 в точке c). Затем мы проверяем значение f'(x) в точке слева от кривой и справа от кривой и проверяем природу f'(x), тогда мы можем сказать, что данная точка будет:
- Локальные максимумы: . Если f'(x) меняет знак с положительного на отрицательный по мере увеличения x через точку c, то f(c) дает максимальное значение функции в этом диапазоне.
- Локальные минимумы: Если f’(x) меняет знак с отрицательного на положительный по мере увеличения x через точку c, то f(c) дает минимальное значение функции в этом диапазоне.
- Точка перегиба: Если знак f'(x) не меняется при увеличении x через c, а точка c не является ни максимумом, ни минимумом функции, то точка c называется точкой перегиба .
Критерий производных второго порядка для максимумов и минимумов
В тесте производной второго порядка для максимумов и минимумов находим первую производную функции и, если она дает значение наклона, равное 0 в критической точке x = c (f'(c) = 0), то находим вторую производную функции.
Если вторая производная функции существует в заданном диапазоне, то заданная точка будет:
- Локальные максимумы: Если f»(c) < 0
- Локальные минимумы: Если f»(c) > 0
- Тест не пройден: Если f»(c) = 0
Важные примечания о максимумах и минимумах:
- Максимумы и минимумы — это пики и впадины на кривой функции.
- Во всей области может быть только один абсолютный максимум функции и один абсолютный минимум функции.
- Функция f называется монотонной функцией на интервале I, если f либо возрастает по I, либо убывает по I.
Связанные темы по максимумам и минимумам:
- Домен и диапазон функции
- Абсолютное значение
Часто задаваемые вопросы о Maxima и Minima
Что такое максимумы и минимумы функции?
Максимумы и минимумы функции — это точки, в которых значение функции максимально или минимально в пределах дельта-окрестности точки.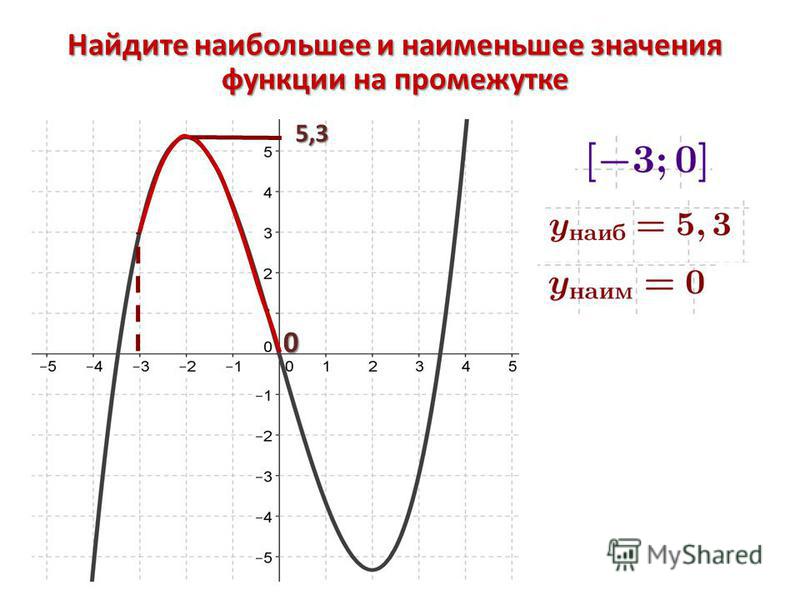
Что такое локальные максимумы и минимумы?
Локальные максимумы и минимумы — это максимумы и минимумы функции, возникающие в определенном интервале. Локальными максимумами будут точки в определенном интервале, для которых значения функции вблизи этой точки всегда меньше, чем значение функции в этой точке. Принимая во внимание, что локальные минимумы будут точками, в которых значения функции вблизи этой точки больше, чем значение функции в этой точке.
Что такое абсолютные максимумы и минимумы?
Высшая точка функции во всей области известна как абсолютный максимум функции, тогда как самая низкая точка функции во всей области функции известна как абсолютный минимум функции. Может быть только один абсолютный максимум функции и один абсолютный минимум функции по всей области.
Как найти локальные максимумы и минимумы на графике?
Максимумы и минимумы — это пики и впадины на кривой функции. У функции может быть любое количество максимумов и минимумов.
На графике функции, если мы хотим найти локальные максимумы и минимумы, мы просто ищем пики и впадины на графике. Все пики будут нашими локальными максимумами, а долины будут локальными минимумами.
Как найти максимумы и минимумы алгебраически?
Максимумы и минимумы функции можно вычислить с помощью теста производной первого порядка и теста производной второго порядка. Производные тесты — это самый быстрый способ найти максимумы и минимумы функции.
Что такое первый производный тест для максимумов и минимумов функции?
Первая производная функции дает наклон функции. Согласно критерию первой производной, вблизи точки максимума наклон кривой увеличивается по мере продвижения к точке максимума, затем становится равным 0 в точке максимума, а затем уменьшается по мере удаления от точки максимума. Точно так же вблизи точки минимума наклон функции уменьшается по мере продвижения к точке минимума, затем становится равным 0 в точке минимума, а затем увеличивается по мере удаления от точки минимума.
Мы используем эту информацию, чтобы узнать, является ли точка максимумом или минимумом.
Что такое критерий производных второго порядка для максимума и минимума функции?
В тесте производной второго порядка сначала находим первую производную функции, и если она дает значение наклона, равное 0 (f'(c) = 0), то находим вторую производную функции . Если вторая производная функции существует в заданном диапазоне, то заданная точка будет:
- Локальные максимумы: Если f”(c) < 0
- Локальные минимумы: Если f”(c) > 0
- Тест не пройден: Если f”(c) = 0
Может ли быть 2 абсолютных максимума в максимуме и минимуме?
Высшая точка функции во всей области называется абсолютным максимумом функции, а самая нижняя точка функции во всей области функции известна как абсолютный минимум функции. Может быть только один абсолютный максимум функции и один абсолютный минимум функции во всей области.
максимумы минимумы — Может ли функция иметь одинаковое максимальное и минимальное значение?
$\begingroup$
Когда я услышал, что максимальное значение может быть меньше минимального, меня поразило, могут ли они оба быть равными. Я хочу узнать, правда ли это.
- максимум-минимум
$\endgroup$
2
$\begingroup$
(A) $\bf 1$ Переменная функция:
Возможно, что ( минимума $\leq$ максимума ) ИЛИ ( минимума $>$ максимума ), хотя это будет различных точки на кривой.
Графически мы можем видеть, что здесь:
На приведенном выше графике, как вы можете видеть, у нас есть минимумы в точке $A$, и для каждой из $3$ различных фиолетовых кривых у нас есть точка $B$, где $\bf \text{Maxima}>\text{or}=\text{or}<\text{Minima}$ (соответственно сверху вниз).