Виды углов. Прямой угол. 2-й класс
Тип урока: объяснение нового материала.
Место урока в структуре по теме: данная тема изучается в разделе “Табличное сложение однозначных чисел с переходом через десяток”.
Цель урока: Познакомить учащихся с понятием “прямой угол” и научить применять полученные знания на практике.
Задачи урока:
1. Образовательные:
- Познакомить учащихся с понятием “прямой угол”;
- Сформировать практические навыки определения прямого угла при помощи треугольника и без него;
- Продолжить работу по совершенствованию навыка устного счёта в пределах 100;
2. Развивающие:
- Развитие логического мышления, внимания, памяти, пространственного воображения;
- Развитие творческих умений и навыков по теме для успешного выполнения заданий;
- Развитие культуры речи и эмоций учащихся.

3. Воспитательные:
- В целях решения задач нравственного воспитания содействовать воспитанию гуманности и коллективизма, наблюдательности и любознательности, развитию познавательной активности, формированию навыков самостоятельной работы;
- В целях решения задач эстетического воспитания содействовать развитию у учащихся чувства прекрасного.
ХОД УРОКА
I. Организационный момент.
Ну-ка проверь, дружок,
Ты готов начать урок?
Все ль на месте
Все ль в порядке,
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать
Только лишь оценку “5”.
— Ребята, сегодня мы опять отправимся в
путешествие по королевству Геометрия.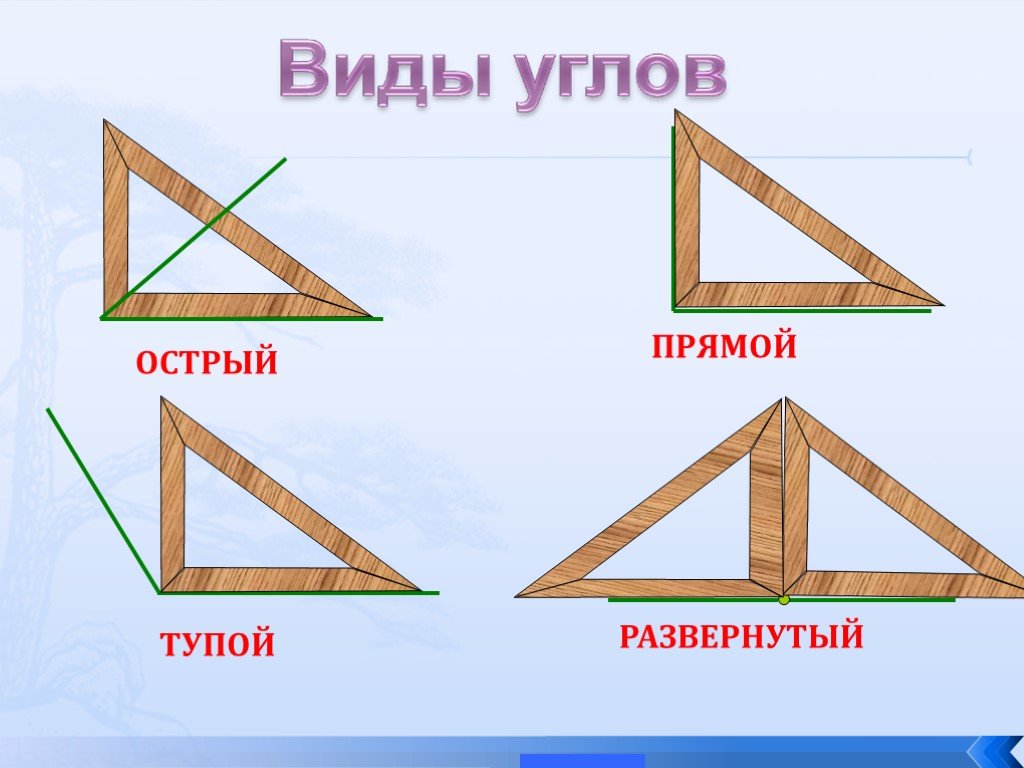
3. Устный счёт.
2 слайд
– У ворот нас встречают король Точка и его дочь – принцесса Прямая. Прежде чем король и принцесса познакомят нас с жителями своего королевства, они хотят вас испытать.
II. Устный счет.
(Слайд 3)
1) Игра “Гусеница-растеряша”.
— Гусеница растеряла числа, посмотрите на оставшиеся, разгадайте по какому правилу можно продолжить ряд чисел. (Дети называют правило: это чётные числа; каждое последующее число на 2 больше предыдущего).
— Какие же числа растеряла гусеница? (2,4,6,8,10,12,14,16)
(Слайд 4)
2) Игра “Математический баскетбол”.
Баскетбол — командная спортивная игра, цель которой забросить руками мяч в подвешенную корзину.
— Любой из вас забьёт гол, если правильно решит пример. (Дети по цепочке решают примеры). 30 + 7 25 + 5 32 – 12 66 + 4 80 – 7 28 – 10 45 – 45 53 + 7 59 – 9 90 + 9
Слайд 5
Задание на логику
— Сколько пятачков у 15 поросят? (15)
— Когда гусь стоит на двух ногах, то весит 4 кг.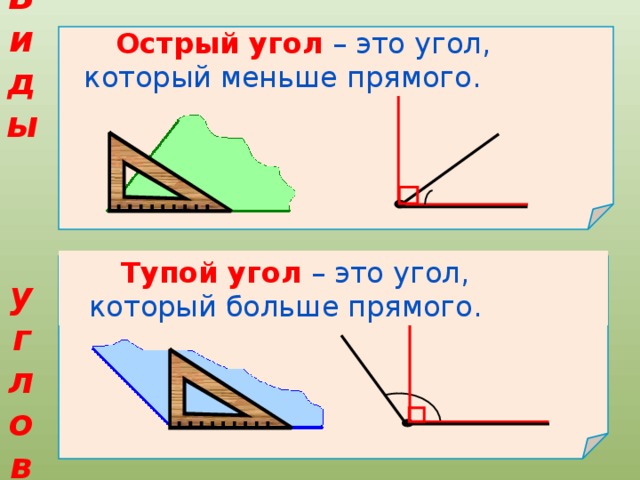 Сколько будет весить гусь, когда встанет на одну
ногу?
Сколько будет весить гусь, когда встанет на одну
ногу?
6 слайд
– Вы прошли все испытания. Король и принцесса очень довольны вами и готовы познакомить вас с жителями королевства “Геометрия”!
(По щелчку створки ворот открываются.)
(Слайд 7)
— Ребята, перед вами жители королевства “Геометрия”.
— Посмотрите на фигуры в каждой рамке. Какая из них лишняя? Почему?
(Учащиеся называют лишние фигуры, обосновывают свой выбор).
— Разделите все оставшиеся фигуры на две группы. Как это можно сделать? (Оставшиеся фигуры можно разделить на две группы: линии и многоугольники.)
— Назовите виды линий и многоугольников, известные вам. (Линии: прямая, ломаная, кривая. Многоугольники: квадрат, трапеция, прямоугольник, четырёхугольник, пятиугольник, шестиугольник, многоугольник).
IV. Работа над новым материалом.
(Слайд 8)
1) — Тему урока вам подскажет кроссворд. Кроссворд “Геометрический”.
Кроссворд “Геометрический”.
1) Часть прямой, у которой есть начало, но нет конца. (Луч).
2) Геометрическая фигура, не имеющая углов. (Круг).
3) Самая маленькая геометрическая фигура. (Точка).
4) Геометрическая фигура, имеющая форму вытянутого круга. (Овал).
— Тема нашего урока спряталась по вертикали. Найдите её. (Угол). (щелчок вылетают геометрические фигуры).
— Сформулируйте пожалуйста тему нашего урока.
— Ребята, а зачем мы будем изучать углы?
— Как Вы думаете, вам эти знания пригодятся?
(Ответы детей)
— Углы окружают нас и в повседневной жизни. Приведите свои примеры, где можно найти углы вокруг нас.
— Ребята, а может, кто-то знает, что такое угол? (выслушиваются мнения детей)
Правильность нашей формулировки, мы проверим чуть позже.
— Люди, каких профессий чаще всего встречаются с
углами? (конструктор, инженер, дизайнер,
строитель, архитектор, моряк, астроном,
архитектор, портной и т. д.)
д.)
Слайд 9.
Посмотрите на рисунки: уголок соединительный для труб и уголок канцелярский для бумаг; угольник плотника и угольник чертёжный; угловой стол и угловой диван.
— Ребята, а сейчас Король и Принцесса предлагают немного поиграть.
Слайд 10.
Игра “Им угол имя подарил”.
— Угол важная фигура. Многим фигурам он помог дать имя. Назовите фигуры.
— Что общего в названиях фигур? (что они имеют угольник – общая часть)
— Почему первая часть слов везде разная? (потому что углов разное количество)
Физминутка 11-16 слайды
Открываем тетради, записываем 18 января, классная работа. (слайд 17)
Слайд 18.
— Ребята, а теперь от красных полей отступите одну клеточку и поставьте точку О. От этой точки проведите два луча.
На доске заранее нарисовать точку О (4-5). Вызвать
4-5 детей, чтобы они провели лучи на доске.
— Что за фигуры у нас получилась? (угол)
— Посмотрите, какие разные эти углы.
— Ребята, а теперь соберите правило из слов.
Работа в парах.
(Вывод: угол — это геометрическая фигура, образованная двумя разными лучами
с общим началом).
— Ребята, а теперь посмотрите на фигуру, которую нарисовала я.
— Это угол, или нет.
(Дети говорят – нет, еще раз возвращаемся к правилу, после этого делаем вывод о том, что это тоже угол – развернутый)
Слайд 19. (вывод по углу)
Плакат на доске
Точка О – вершина угла. Угол можно назвать одной буквой, записанной около его вершины. Угол О. Но может быть несколько углов, имеющих одну вершину. Как быть тогда? (На листе чертеж таких углов)
Ответы детей.
— В таких случаях если называть разные углы
одной буквой, то будет непонятно, о каком угле
идёт речь.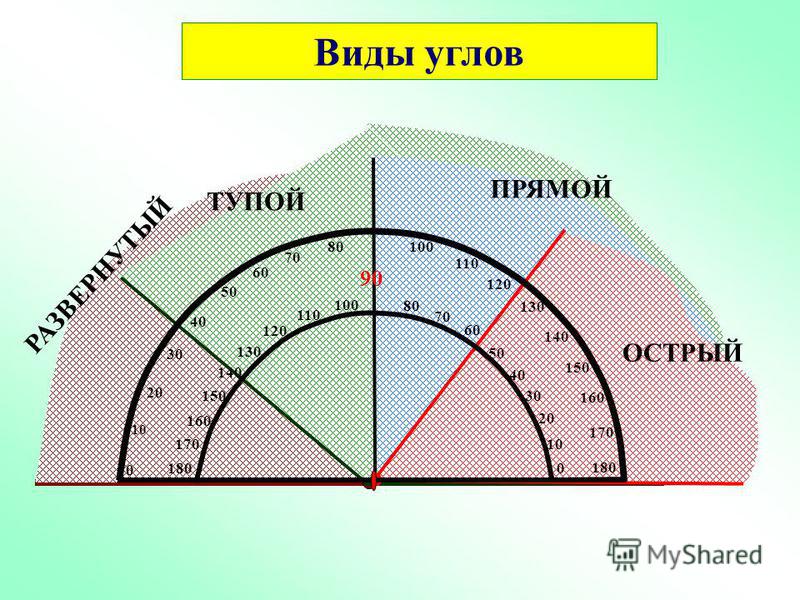
Плакат на доске
Слайд 20.
— Ребята, у вас на столах лежат разные виды углов. Найдите пожалуйста одинаковые виды углов.
— Как будете искать? (Ответы детей)
Один человек на моих моделях ищет одинаковые углы.
— Ребята, смотрите, номера 6 и 7 совпали полностью, а 1 и 5 — нет. № 5 больше.
— Какой можно сделать вывод? После ответа детей появляется слайд.
ВЫВОД: слайд 21
- Равные углы при наложении совпадают
- Если один угол наложить на другой и они совпадут, то эти углы равны
Слайд 22.
Изготовление модели прямого угла.
Слайд 23
Не всегда удобно определять прямой угол на глаз. Для этого используют линейку-угольник.
— Каким цветом выделен угол больше прямого? (Голубым).
— Меньше прямого? (Зелёным).
— Какой же угол из трёх предложенных прямой?
— Почему вы так решили? (Вершина и стороны угла совпали с прямым углом на линейке-угольнике).
— Как же определить вид угла?
ВЫВОД:
- Чтобы определить вид угла, надо совместить его вершину и сторону соответственно с вершиной и стороной прямого угла на угольнике.
Слайд 24
— Каждый из углов имеет своё название. Острый угол – это угол, который меньше прямого. Тупой угол – это угол, который больше прямого.
(На доске появляются таблички с названием углов)
— Какой угол мы будем считать главным?
Мама мой взяла листок,
И загнула уголок,
Угол вот такой у взрослых
Называется ПРЯМЫМ.
Если угол уже — ОСТРЫМ,
Если шире, то — ТУПЫМ.
Слайд 25.
— Ребята, а всегда возможно наложить углы?
— Нет. (Если начерчены в тетради…)
— Для этого существует транспортир, с помощью которого измеряют углы. Углы измеряют в градусах. Посмотрите на виды транспортиров.
Слайд 26.
Очень часто углы мы можем наблюдать на часах. Углы образуют часовые стрелки.
Работа по учебнику.
Задание: Используя модель прямого угла, найди прямые углы и выпиши их номера. (Дети выполняют задание самостоятельно, затем один ученик называет свой вариант ответа, все проверяют работу).
— С помощью угольника удобно не только определять прямые углы, но главное – строить их. Построим прямой угол, каждый сам назовёт его одной или тремя буквами.
Слайд 27-29 (Учитель на доске, а дети в тетрадях
строят прямой угол. Выполняется взаимопроверка в
парах).
Выполняется взаимопроверка в
парах).
Я ОСТРЫЙ — начертить хочу,
Сейчас возьму и начерчу.
Веду из точки две прямых,
Как будто два луча,
И видим ОСТРЫЙ УГОЛ мы,
как остриё меча.А для УГЛА ТУПОГО
Всё повторяем снова:
Из точки две прямых ведём,
Но их пошире разведём.
На чертёж мой посмотри,
Он, как ножницы внутри,
Если их за два кольца
Мы раздвинем до конца.
Практическая работа по закреплению изученного.
На партах у вас проволока. Сделайте из нее прямой угол и проверьте с помощью угольника, затем сделайте острый и тупой.
7. Итог урока.
— Расскажите мне по схеме о том, что вам дал сегодняшний урок математики?
8. Домашнее задание.
определение угла, измерение углов, обозначения и примеры.
 Прямой угол Что такое прямой угол 3
Прямой угол Что такое прямой угол 3При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.
Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.
Теорема Пифагора
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы . В виде формулы записывается это так:
a²+b²=c²
Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза.
Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную.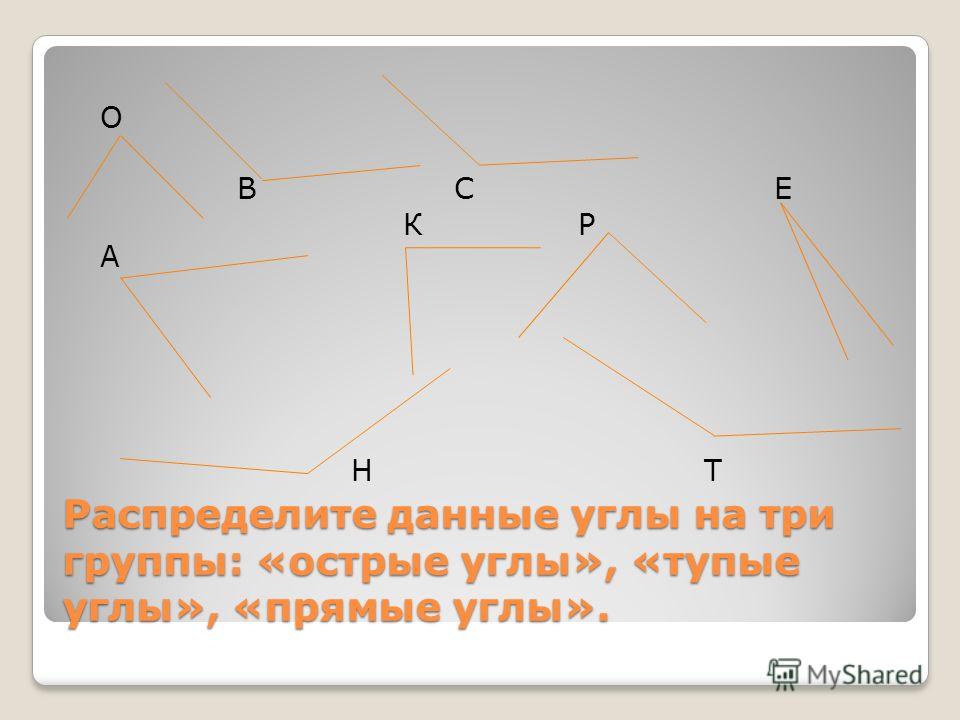 А следовательно можем
размечать прямые углы, а также проверять их.
А следовательно можем
размечать прямые углы, а также проверять их.
Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!
А теперь применим теорему на практике.
Проверка прямого угла
Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.
Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих
стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно
больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250
см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат
(умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 —
это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра
должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали —
проверяемый угол развернут и имеет отклонение от 90°.
Например, мы отметили 2,5 метра (или 250
см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат
(умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 —
это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра
должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали —
проверяемый угол развернут и имеет отклонение от 90°.
Калькулятор расчета диагонали прямого угла
Внимание! Для работы калькулятора необходимо включить поддержку JavaScript в вашем браузере!
Длина a
Длина b
Диагональ c
Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же,
не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом.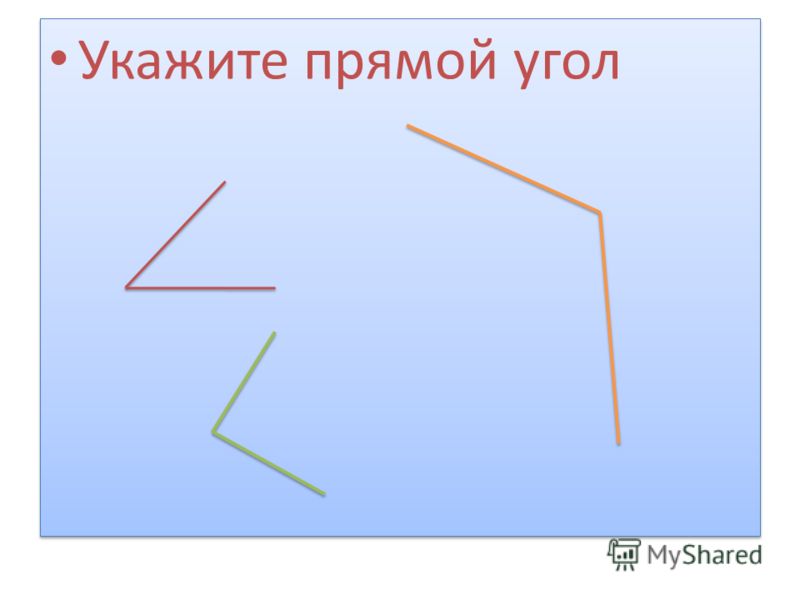 Нужно
лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у
прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого
метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны
быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать
о первоначальном способе совсем — в некоторых случаях он очень актуален.
Нужно
лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у
прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого
метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны
быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать
о первоначальном способе совсем — в некоторых случаях он очень актуален.
Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.
Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены
на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.
Как разметить прямой угол рулеткой
Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!
Как разметить острый угол
Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных
фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные
или натянутые шнурами — дело это непростое.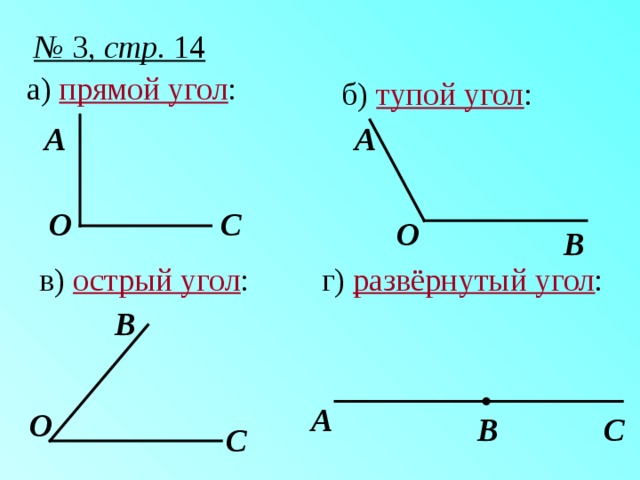 Поэтому я предлагаю использовать упрощенный метод. Сначала размечается
прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить
45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим
два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм
вам понятен.
Поэтому я предлагаю использовать упрощенный метод. Сначала размечается
прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить
45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим
два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм
вам понятен.
Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.
Посмотрите на картинку. (Рис. 1)
Рис. 1. Иллюстрация к примеру
Из каких знакомых вам геометрических фигур она состоит?
Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников. Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис.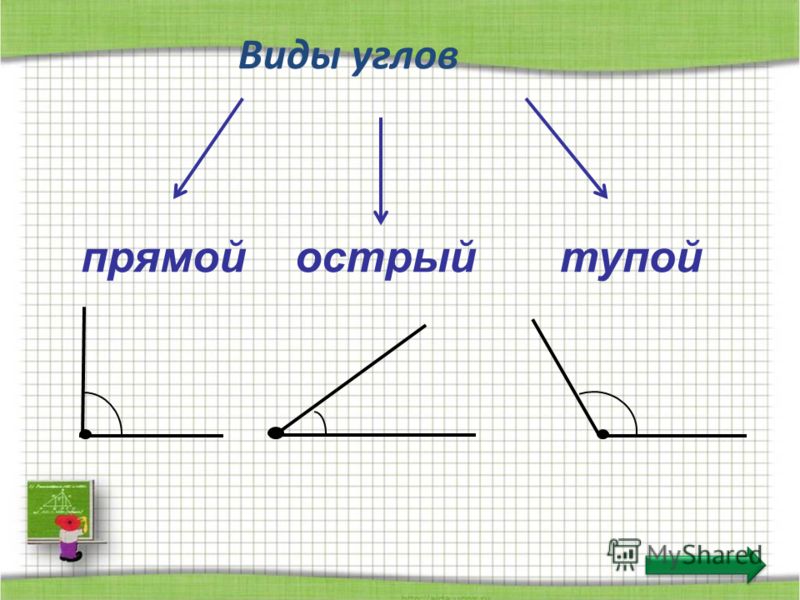 2).
2).
Рис. 2. Определение угла
Сегодня мы будем учиться чертить прямой угол.
В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3)
Рис. 3. Угольник
В самом угольнике уже есть прямой угол. (Рис. 4)
Рис. 4. Прямой угол
Он и поможет нам изобразить эту геометрическую фигуру.
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).
1.
2.
3.
4.
Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник.
Рис. 5. Иллюстрация к примеру
Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).
Рис. 6. Иллюстрация к примеру
Мы видим, что прямой угол совпал с углом ВОМ. Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Рис.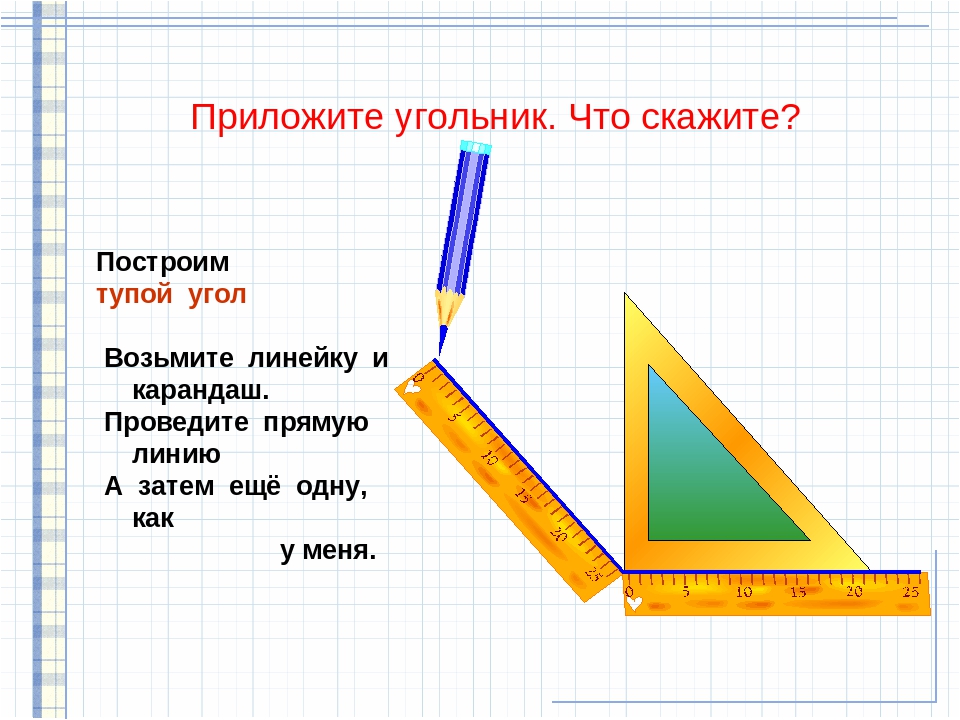 7. Иллюстрация к примеру
7. Иллюстрация к примеру
Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)
Рис. 8. Иллюстрация к примеру
Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.
На этом уроке мы учились строить прямой угол с помощью угольника.
Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол.
Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником.
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение 1
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения .
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2
Дана прямая a на плоскости. На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O .
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв.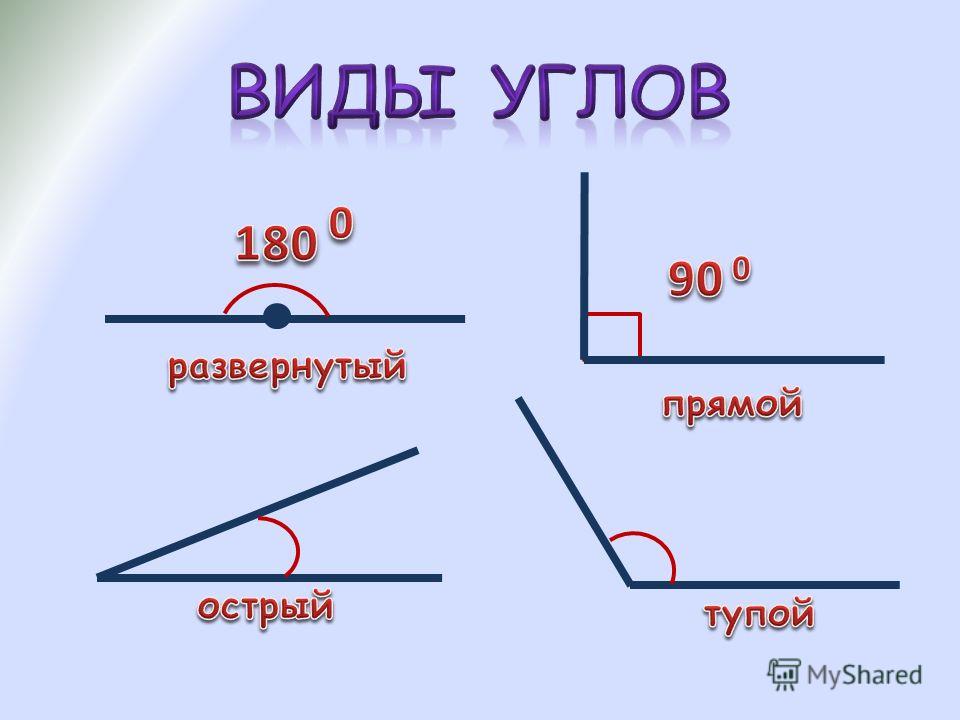 Рассмотрим подробнее на чертеже.
Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым .
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O .
Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла , другая – внешняя область угла . Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5
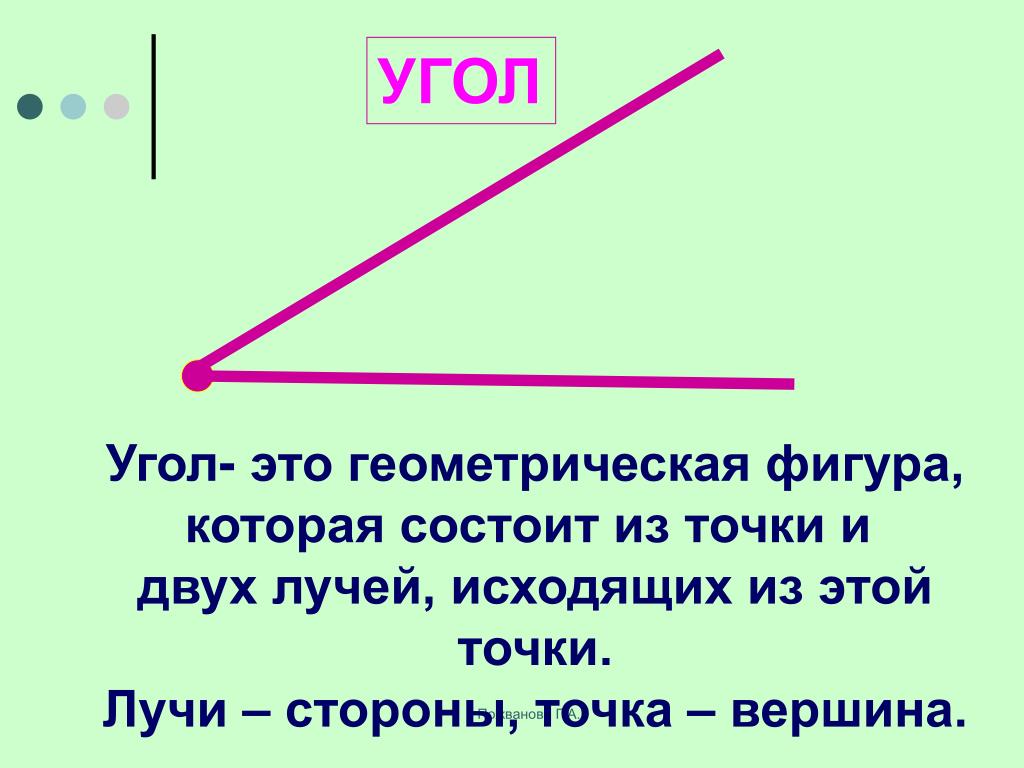
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.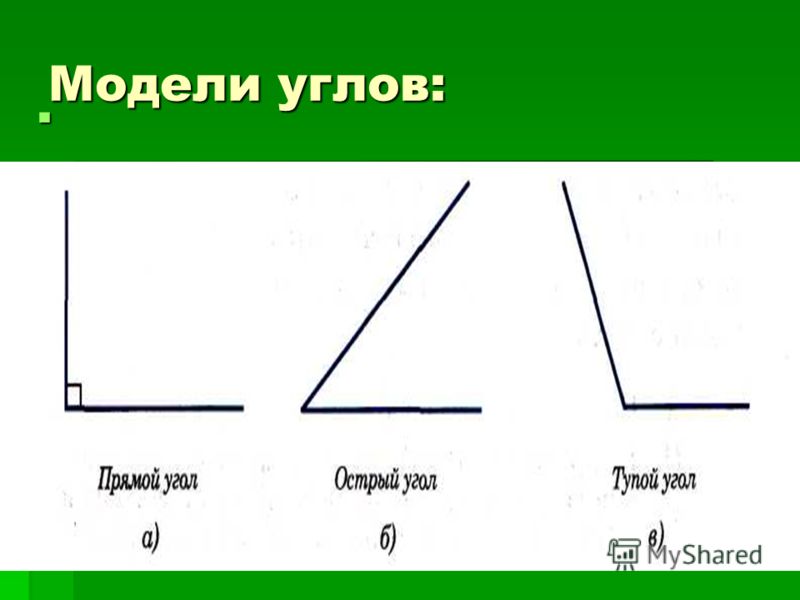
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение 6
Два угла называют смежными , если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Определение 7
Два угла называют вертикальными , если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Ниже показано на рисунке.
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные .
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус .
Определение 8
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.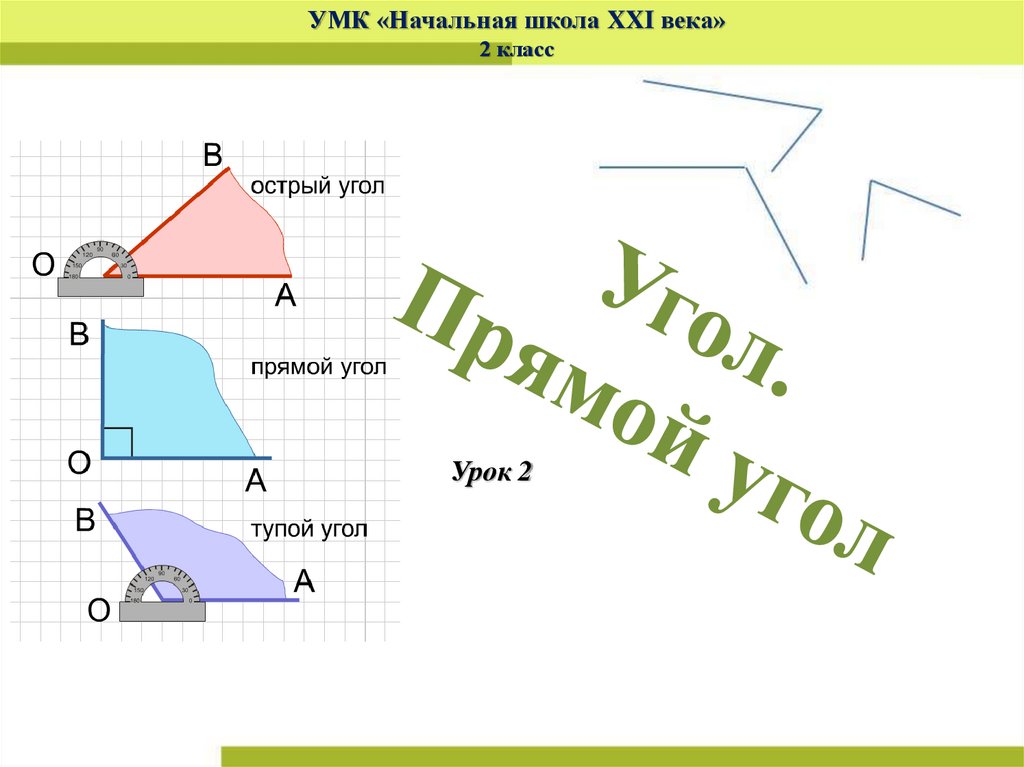
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты.
Определение 9
Минутой называют одну шестидесятую часть градуса.
Определение 10
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают « » », а секунды « «» ». Имеет место обозначение:
1 ° = 60 » = 3600 «» , 1 » = (1 60) ° , 1 » = 60 «» , 1 «» = (1 60) » = (1 3600) ° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 » 59 «» .
Определение 11
Приведем пример обозначения градусной меры угла равного 17 ° 3 » 59 «» . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 .
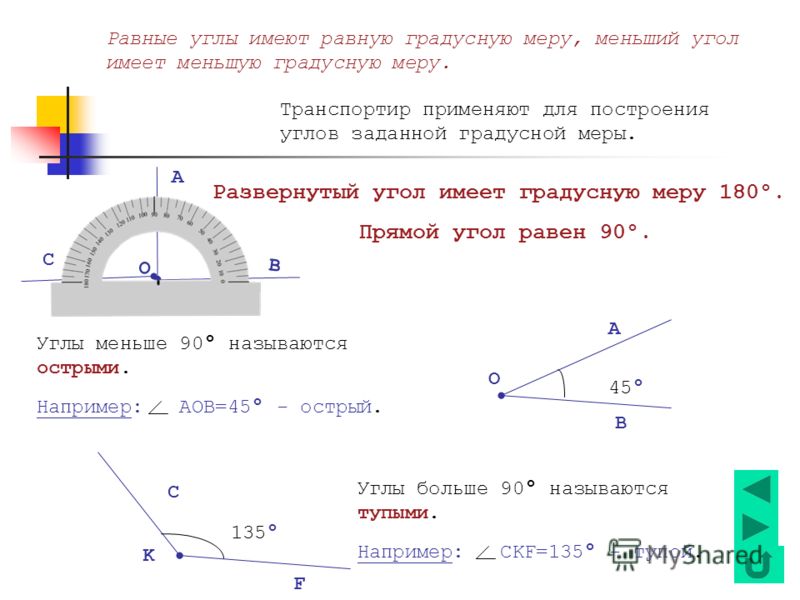
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам».
В геометрии используется мера угла из интервала (0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0 , 90) , а тупой – (90 , 180) . Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны . Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С, С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными. Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом . Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой, с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В. По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А.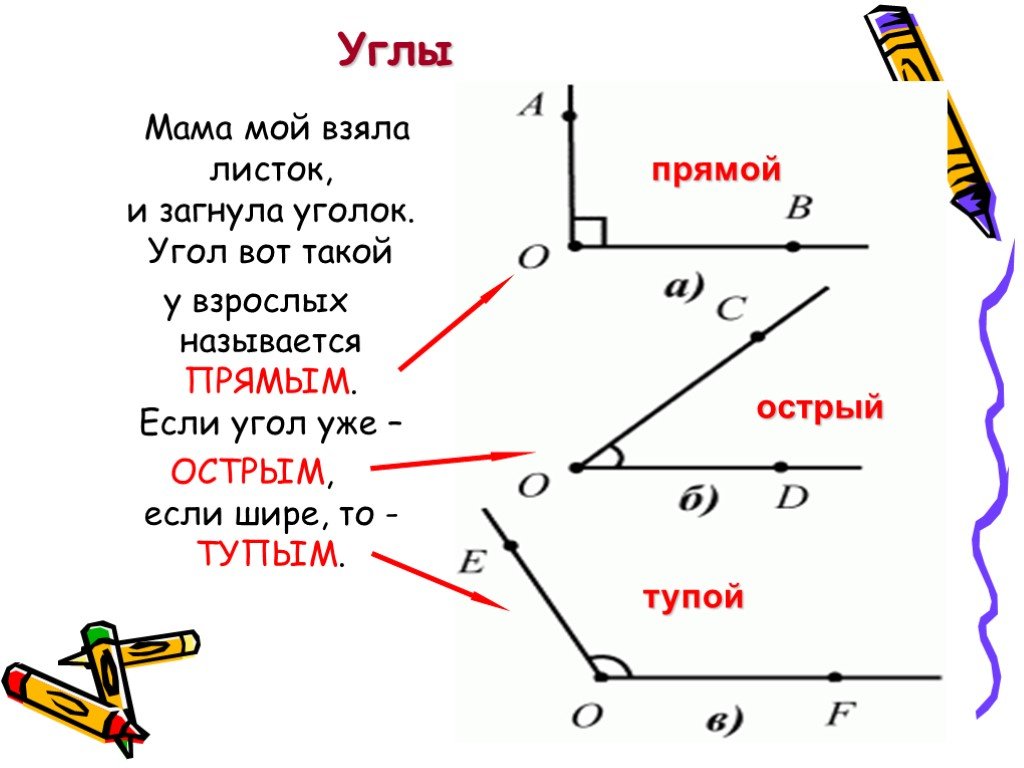
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного.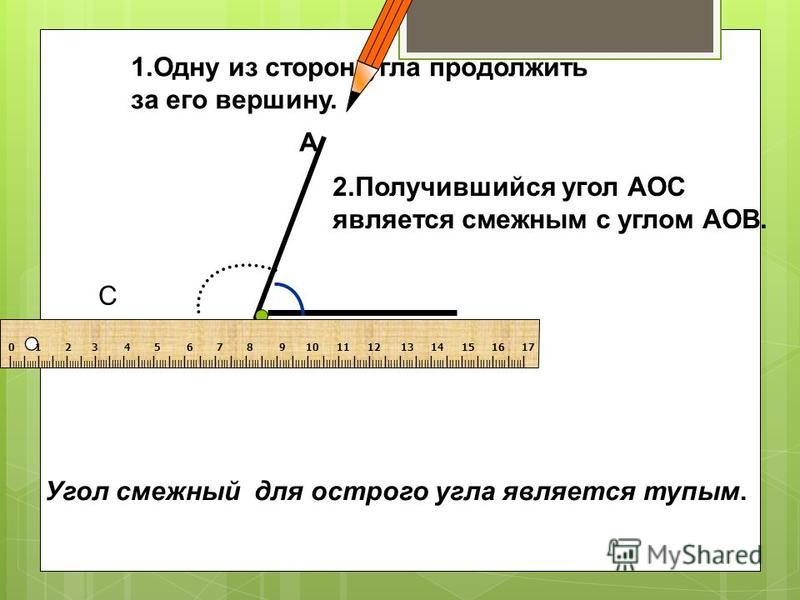 На чертеже изображено правильное обозначение острых, равных и неравных углов.
На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
ПРЯМОЙ, ая, ое; прям, пряма, прямо, прямШы и прямы. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
прямой угол — — Тематики нефтегазовая промышленность EN right angle …
Угол, равный своему смежному. * * * ПРЯМОЙ УГОЛ ПРЯМОЙ УГОЛ, угол, равный своему смежному … Энциклопедический словарь
Угол, равный своему смежному; в градусном измерении равен 90° … Естествознание. Энциклопедический словарь
Энциклопедический словарь
См. Угол … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
1) угол, равный своему смежному. 2) Внесистемная ед. плоского угла. Обозначение L. 1 L = 90° = ПИ/2 рад 1,570 796 рад (см. Радиан) … Большой энциклопедический политехнический словарь
Прямая, прямое; прям, пряма, прямо. 1. Ровно вытянутый в каком–н. направлении, не кривой, без изгибов. Прямая линия. «Прямая дорога обрывалась и уж шла вниз.» Чехов. Прямой нос. Прямая фигура. 2. Беспересадочный (ж.–д. и разг.). Прямой маршрут.… … Толковый словарь Ушакова
ПРЯМОЙ, ая, ое; прям, пряма, прямо, прямы и прямы. 1. Ровно идущий в каком н. направлении, без изгибов. Прямая линия (линия, образом к рой может служить бесконечная туго натянутая нить). Провести прямую (т. е. прямую линию; сущ.). Дорога идёт… … Толковый словарь Ожегова
угол основного профиля витка — (αb) Угол между основным профилем витка эвольвентного червяка и прямой, составляющей с осью червяка прямой угол скрещивания. Примечание Угол прямолинейного основного профиля витка эвольвентного червяка αb равен основному углу подъема… … Справочник технического переводчика
Примечание Угол прямолинейного основного профиля витка эвольвентного червяка αb равен основному углу подъема… … Справочник технического переводчика
Книги
- Таблицы для численного решения граничных задач теории гармонических функций , Канторович Л. В., Крылов В. И., Чернин К. Е.. Граничные задачи для гармонических функций часто возникают при математическом анализе многих важных вопросов физики и техники (задачи расчета электрического и теплового поля, задачи…
- Математика. 2 класс. Учебник. В 2-х частях. Часть 2 , Моро М.И.. Учебник «Математика» входит в образовательную систему» Школа России» . Материал учебника позволяет реализовать системно-деятельностный подход, организовать дифференцированное обучение и…
Что такое прямой угол? — Turito
Прямой угол — это угол в геометрии, равный 90˚. Мы не можем представить свою жизнь без прямых углов. Везде присутствует прямой угол. Верхняя часть стола и ножки соединяются вместе под прямым углом. Пол вашего дома образует прямые углы со всеми примыкающими к нему стенами. При правильном расположении стопка книг образует прямые углы, и этот список никогда не заканчивается. Поэтому в этой статье мы изучим основные понятия прямых углов и как сделать прямые углы и прямоугольные треугольники. Но сначала
При правильном расположении стопка книг образует прямые углы, и этот список никогда не заканчивается. Поэтому в этой статье мы изучим основные понятия прямых углов и как сделать прямые углы и прямоугольные треугольники. Но сначала
Вы все знаете, что такое угол? Если два луча, идущие с разных сторон, пересекаются в одной точке, они образуют угол. Точка пересечения называется вершиной. В зависимости от ориентации лучей можно получить три основных типа углов, которые перечислены ниже:
Острый угол: Угол, образованный двумя лучами меньше 90˚, называется острым углом. Острый угол колеблется от 0˚ до 90˚ (исключая 90˚).
Тупой угол: Угол между двумя лучами, значение которого больше 90° называется тупым углом. Диапазон тупых углов от 90˚ до 180˚ (исключая 90˚)
Прямой угол: Когда лучи образуют угол, равный 90˚, он называется прямым углом.
Примечание: Углы измеряются в градусах с символом «˚» или в радианах с сокращением «рад».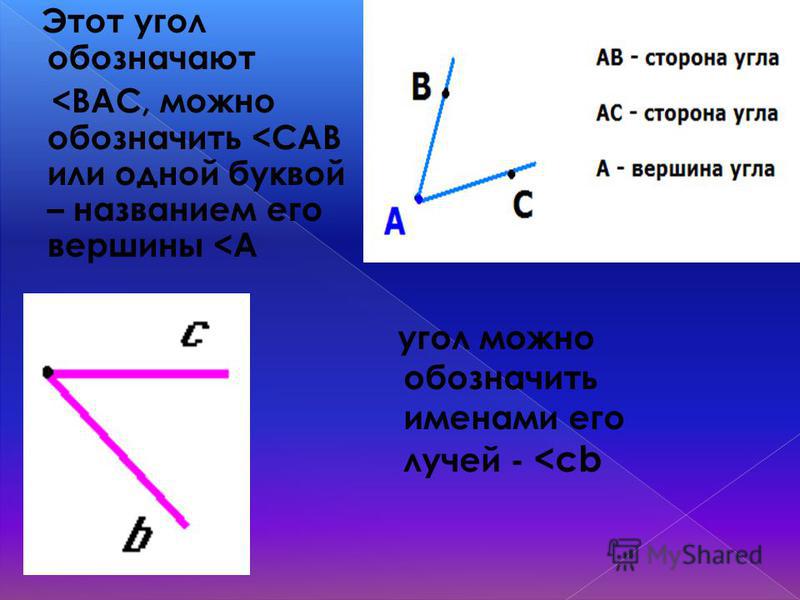 В радианах мера прямого угла равна π/2. Это связано с тем, что в радианной метрической системе значение π = 180˚. Следовательно, 180˚/2 или π/2 = 90˚.
В радианах мера прямого угла равна π/2. Это связано с тем, что в радианной метрической системе значение π = 180˚. Следовательно, 180˚/2 или π/2 = 90˚.
Теперь, когда мы рассмотрели все основы, давайте углубимся в теории и концепции прямых углов.
Где находятся прямые углы?
Мы уже обсудили несколько практических сценариев поиска правильных углов. Но это не так! В этом разделе мы узнаем обо всех местах, где можно найти прямые углы. Ниже приведен список, состоящий из всех математических аспектов прямых углов:
- В прямоугольном треугольнике один из углов равен 90˚.
- Все четыре стороны прямоугольника и квадрата образуют прямые углы друг с другом, или мы можем сказать, что все четыре угла внутри прямоугольника и квадрата равны 90˚.
- Диагонали квадрата и ромба пересекаются под прямым углом.
- Углы вашей комнаты, где вы спите или занимаетесь, находятся под прямым углом.
- У куба и прямоугольного параллелепипеда все углы равны 90˚.
 Например, кубик Рубика.
Например, кубик Рубика.
Как сделать прямой угол?
Самый простой способ сделать прямой угол — провести две прямые линии. Сделайте одну линию горизонтальной, а другую вертикальной. Сделайте так, чтобы они пересекались друг с другом. Угол, образованный между двумя линиями, будет прямым углом. Следите за тем, чтобы линии были прямыми по вертикали и горизонтали. Для этой цели можно использовать шкалу. Но этот метод не всегда точен. Много раз ваша рука может соскальзывать, что приводит к искажению линии. Давайте узнаем два способа всегда делать идеальный прямой угол.
Метод 1: Использование транспортира
Шаг 1: Возьмите линейку и начертите в блокноте прямую горизонтальную линию.
Шаг 2: Теперь возьмите транспортир и поместите его над горизонтальной линией. Делать это нужно таким образом, чтобы последняя самая нижняя линия транспортира и сделанная вами горизонталь совпадали.
Шаг 3: Посмотрите на свой транспортир и поставьте точку чуть выше точки, написанной как 90. Это 90° от горизонтальной линии.
Это 90° от горизонтальной линии.
Шаг 4: Снова возьмите весы и проведите прямую линию с помощью транспортира к горизонтальной линии от отмеченной точки.
Шаг 5: Вы сделали идеальный прямой угол.
Примечание: Всегда очищайте линейки и транспортиры перед работой с ними. Они могут содержать графит или чернила от последней задачи, для которой они использовались, и испортить вашу работу.
Способ 2: Использование компаса
Шаг 1: Начертите в блокноте горизонтальную линию, скажем, АВ.
Шаг 2: Возьмите свой компас. Поместите в него карандаш и выровняйте кончик карандаша с кончиком циркуля. Теперь возьмем на ней угол любой меры.
Шаг 3: Поместите кончик циркуля в точку «А» и переместите карандаш, описывая дугу на линии.
Шаг 4: Отметьте точку, где дуга касается линии «AB», как «C».
Шаг 5: Теперь поместите наконечник в точку «С» и сделайте еще одну дугу на первой дуге. Поставьте точку «D».
Поставьте точку «D».
Шаг 6: Теперь поместите наконечник в точку «D» и нарисуйте еще одну дугу на первой. Поставьте точку «Е». Также нарисуйте еще одну дугу, используя эту точку чуть выше горизонтальной линии.
Шаг 7: Поместите наконечник в точку E и вырежьте дугу, которую вы сделали над горизонтальной линией. Назовите перекресток как F.
Шаг 8: Нарисуйте прямую линию, идущую из точки F в точку A.
Шаг 9: Вы успешно нарисовали прямой угол.
Теперь вы хорошо разбираетесь в том, как нарисовать идеальный прямой угол. Вы также можете попробовать квадраты и установить квадраты, чтобы получить безупречные прямые углы. Они похожи на весы, но имеют форму прямоугольного треугольника. В следующем разделе мы узнаем больше о прямоугольном треугольнике и о том, как найти угол прямоугольного треугольника.
Прямоугольный треугольник
Когда значение одного из углов внутри треугольника точно равно 90 градусов, его называют прямоугольным треугольником, так как все мы знаем, что треугольник имеет внутри три угла. В прямоугольном треугольнике остальные два угла всегда острые. Сумма двух острых углов всегда должна быть 90˚. Это можно доказать из приведенного ниже примера:
В прямоугольном треугольнике остальные два угла всегда острые. Сумма двух острых углов всегда должна быть 90˚. Это можно доказать из приведенного ниже примера:
Пусть треугольник ABC является прямоугольным треугольником с прямым углом в точке A. Мы знаем, что свойство суммы углов треугольника гласит, что сумма всех трех углов внутри треугольника равна 180°. ˚.
Следовательно, А + В + С = 180˚.
90º + b + c = 180 °
b + c = 180 ° 90 °
b + c = 90 °
Также на основе таких параметров, как боковые и углы, правозаулитые треугольники равен двум типам :
Равнобедренный прямоугольный треугольник: Равнобедренный прямоугольный треугольник сочетает в себе свойства равнобедренного треугольника и прямоугольного треугольника. Это треугольник, у которого две стороны равны, а угол между этими прямыми точно равен 9.0 градусов.
Прямоугольный разносторонний треугольник: Прямоугольный разносторонний треугольник сочетает в себе свойства прямоугольного треугольника и разностороннего треугольника. Все стороны неравны, а один из углов в таких треугольниках равен 90 градусов.
Все стороны неравны, а один из углов в таких треугольниках равен 90 градусов.
Давайте теперь узнаем больше терминов, связанных с прямоугольным треугольником:
Перпендикуляр : Высота прямоугольного треугольника известна как перпендикуляр.
Основание: Сторона, на которой построен прямоугольный треугольник, является основанием.
Гипотенуза: Самая длинная сторона прямоугольного треугольника называется гипотенузой.
Перпендикуляр и основание треугольника всегда образуют друг с другом углы 90˚. Ни гипотенуза и основание, ни гипотенуза и перпендикуляр не образуют прямого угла. Они будут образовывать только острые углы.
Прямоугольный треугольник настолько особенный, что греческий математик Пифагор изобрел формулу для этого треугольника. Правило Пифагора гласит, что в любом прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов перпендикуляра и основания.
Формула: (Гипотенуза) 2 = (Перпендикуляр) 2 + (Основание) 2 .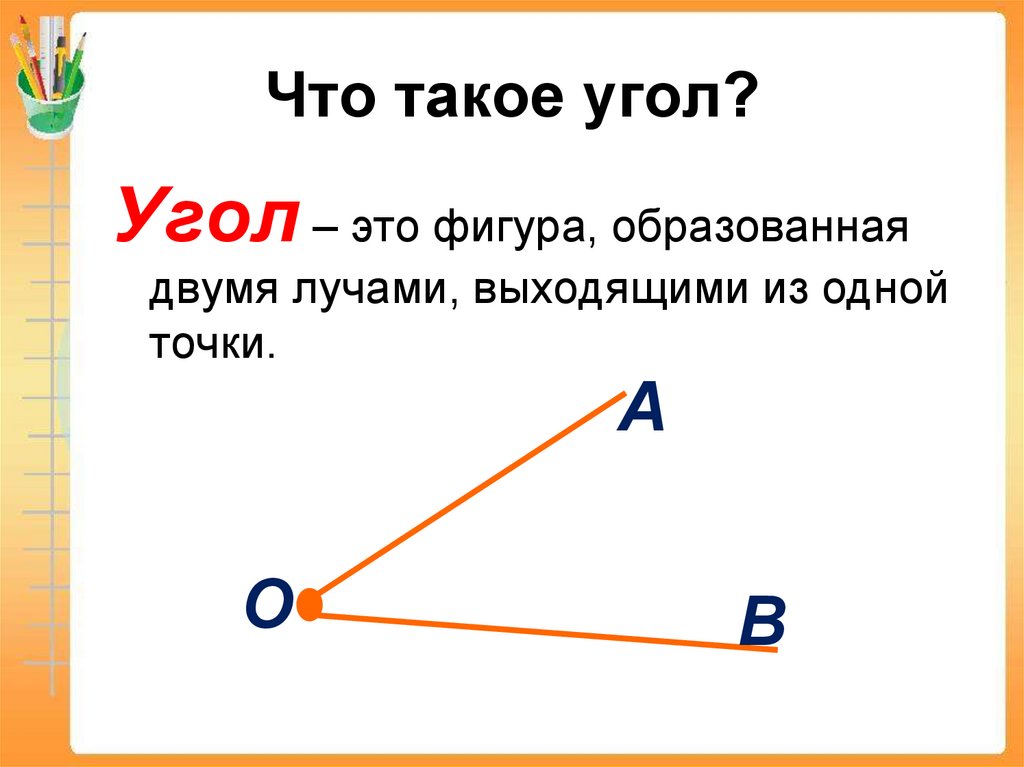
Ниже приведены некоторые примеры прямоугольного треугольника из реальной жизни:
- Горка для детей в парке является примером прямоугольного треугольника.
- Самый лучший и самый популярный пример прямоугольного треугольника — это тригонометрия. Важным результатом является то, что целая отрасль математики основана на тригонометрии. Тригонометрия также является самой опасной математической темой в школах.
Важные моменты, о которых следует помнить:
- Когда две линии встречаются под прямым углом, эти две линии перпендикулярны друг другу.
- Прямой угол равен 90 градусов, образованным основанием и гипотенузой.
- Прямые углы в основном используются на строительных площадках для обеспечения необходимой поддержки углов.
- Они используются для поддержки длиннопролетных мостов и водопропускных труб.
- Прямые углы весьма сильны в практической жизни. Угол не ломается при тяжелых условиях эксплуатации.
 Это потому, что он получает поддержку с двух сторон.
Это потому, что он получает поддержку с двух сторон.
Часто задаваемые вопросы
- Что означает «прямой угол»?
Ответ) Прямой угол — это угол в геометрии, равный 90˚
- Сколько прямых углов в треугольнике?
Ответ) Поскольку треугольник имеет только три угла, он может содержать только один прямой угол. В треугольнике может быть только один прямой угол.
- Как лучше всего измерить прямой угол?
Ответ) Прямой угол лучше всего измерять с помощью транспортира, угольника или пробного угольника.
- Как сделать прямой угол?
Ответ) Самый простой способ сделать прямой угол — провести две прямые линии. Сделайте одну линию горизонтальной, а другую вертикальной. Сделайте так, чтобы они пересекались друг с другом. Угол, образованный между двумя линиями, будет прямым углом.
Что такое прямоугольный треугольник? (Определение, типы и свойства)
Автор:
Malcolm McKinsey
Факт проверено
Пол Маццола
Определение прямоугольного треугольника
Все треугольники имеют внутренние углы, добавленные к 180° . Когда один из этих внутренних углов имеет размеры 90° , это прямой угол , а треугольник прямоугольный . В прямоугольных треугольниках внутренний угол 90° обозначается квадратиком □ в вершине.
Прямоугольный треугольник по сравнению с непрямоугольным треугольникомТермин «правильный» треугольник может ввести вас в заблуждение, полагая, что существуют «левые» или «неправильные» треугольники; они не. «Правильно» относится к латинскому слову rectus , что означает «прямой».
Гипотенуза и стороны прямоугольного треугольника
Мы уже знаем, что квадратная вершина прямоугольного треугольника является прямым углом. Напротив него находится гипотенуза треугольника , самая длинная из трех сторон, обычно обозначаемая как c .
Два других угла прямоугольного треугольника в сумме составляют 90° ; они дополняют друг друга. Стороны , противоположные дополнительным углам , являются сторонами треугольника и обычно обозначаются a и b .
Свойства прямоугольных треугольников
Прямоугольный треугольник должен иметь один внутренний угол, точно равный 90° . Он может быть разносторонним или равнобедренным, но никогда не равносторонним.
Постройте прямоугольный треугольник
Используйте две сырые нити спагетти, чтобы сделать свой собственный прямоугольный треугольник. Оставьте одного в покое; разломите другую прядь на две неравные длины.
Поместите две короткие нити a и b , так что они встречаются в двух конечных точках и образуют угол 90° . Если уложить третью нить c вниз, чтобы пересечь две конечные точки аа и bb, получится прямоугольный треугольник.
Вы можете построить более точный прямоугольный треугольник, используя миллиметровую бумагу и линейку. Нарисуйте отрезок (любой желаемой длины) вдоль напечатанных линий миллиметровки. Следуйте линиям, чтобы сделать второй отрезок любой желаемой длины точно 90 231 90° 90 232 к первому отрезку.
Если соединить две конечные точки этих отрезков, получится прямоугольный треугольник.
Геометрия использует символы в качестве сокращений. Здесь важны знать:
∼ математик Пифагор получил признание, но другие цивилизации знали об этой теореме. Пифагорейская теорема описывает взаимосвязь между длиной ног A и B любого правого треугольника до длины гипотена, C :
. 9023. 46:. ,,,,,,,,,, , , , , , , . a и b , равны квадрату гипотенузы, c илидо того, как он стал президентом этой теоремы.
 ). Одно доказательство легко сделать с помощью миллиметровой бумаги, линейки, карандаша и ножниц.
). Одно доказательство легко сделать с помощью миллиметровой бумаги, линейки, карандаша и ножниц.Конструкция △ABC с опорами, a и b , слева и снизу и гипотенузой, c
2 90 справа вверху. Катет a противен ∠A , катет bb против ∠B , а гипотенуза cc против прямого угла C .Пусть длина a=3 , b=4 , а гипотенуза c=5 .
Постройте квадрат, используя катет аа в качестве правой стороны квадрата. будет 9{2}с2.
Пример доказательства теоремы ПифагораУзнайте, как использовать теорему Пифагора для вычисления длины одной стороны прямоугольного треугольника.
Теорема о высоте прямоугольного треугольника
Теорема о высоте прямоугольного треугольника говорит нам, что высота прямоугольного треугольника, проведенная к гипотенузе c , образует два подобных прямоугольных треугольника, которые также подобны исходному прямоугольному треугольнику.

Построить △ABC так, чтобы гипотенуза c является горизонтальным и противоположным прямым углом C , что означает, что катеты аа и bb пересекаются выше c и образуют прямой угол C . Это помещает ∠A в нижний левый угол, а ∠B в нижний правый.
Построить высоту (или высоту) h от внутреннего прямого угла C до гипотенузы c (так что он перпендикулярен c 0246).
Эта высота h создает два меньших треугольника внутри нашего исходного треугольника. Высота делила ∠C , а также образовывала два прямых угла в местах пересечения гипотенузы c .
Назовите точку, где высота h касается гипотенузы, c , точка D . Теперь у вас есть два треугольника: △ACD и △BCD . Каждый из этих треугольников подобен другому треугольнику, и оба подобны исходному треугольнику.




 Например, кубик Рубика.
Например, кубик Рубика.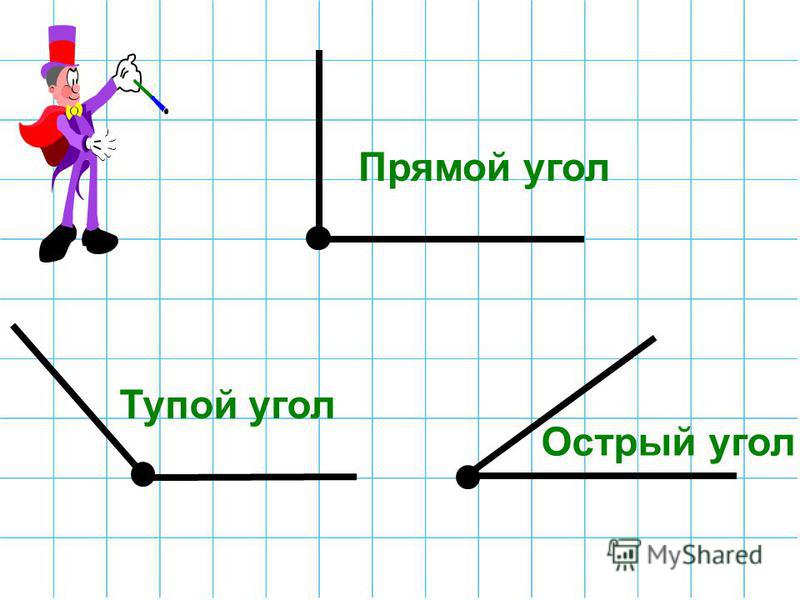 Это потому, что он получает поддержку с двух сторон.
Это потому, что он получает поддержку с двух сторон.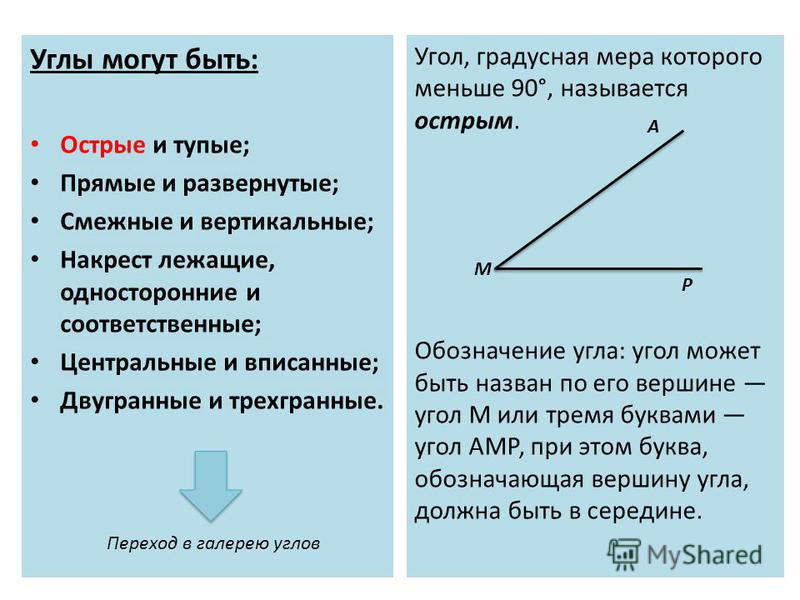 ). Одно доказательство легко сделать с помощью миллиметровой бумаги, линейки, карандаша и ножниц.
). Одно доказательство легко сделать с помощью миллиметровой бумаги, линейки, карандаша и ножниц.