Математическая сложная формула: Сложные математические формулы в программировании

24 знаков после запятой!

Подробно об этой формуле в этом выпуске Numberphile:

https://youtube.com/watch?v=xgBGibfLD-U%3Fwmode%3Dopaque

Андрей Бахматов

29 августа 2021

О, сколько нам открытий чудных готовит второй замечательный предел!

Комментировать ответ…Комментировать…

N & O

Физика

1,6 K

Астрономия физика космология квантовая механика   · 7 мая 2021

Конечно же основное тригонометрическое тождество:

sin²α + cos²α = 1

Вместе с тригонометрическим кругом он заменяет десятки таблиц и формул, которых вдруг вы забыли.

Комментировать ответ…Комментировать…

Валентина Касумова

1

Валентина Касумова, юрист, инженер, профессиональная переподготовка учитель.

..  · 18 июн 2020

Ребята, давайте я вам загадаю загадку. Возьмите лист бумаги, в верхнем углу листа поставьте точку, сверните лист в трубочку, совместив верхний край с нижним, проткните иглой точку, а теперь вопрос: Какой физический процесс вам напоминает данный опыт? Про формулу напишу позднее.

Комментировать ответ…Комментировать…

Александр Чигишев

38

Инжинирую по-немногу, в курсе за БЖУ и присед  · 21 сент 2017

Выдвигаю в кандидаты обобщение варианта, предложенного Elias Chashchin: формулу Стокса В этих нескольких закорючках столько информации и труда, что посчитать тяжело. Сильное утверждение, как говорится. P.S. Прошу прощения за количество шакалов (качество картинки). Читать далее

Комментировать ответ…Комментировать…

Рубен Вартанян

19

Студент Московского Технологического Университета (бывш. 2 = -1

Мнимая единица, господа и дамы, единственное число, квадрат (да и любая четная степень) которого меньше нуля. 

*далее идет текст для символов, не читать*

Пипидастер Увечкин

27 февраля 2018

Корень из любого отрицательно числа дает в квадрате отрицательное число.

Комментировать ответ…Комментировать…

Виктор Воеводов

916

Увлекаюсь математическими проблемами.  · 21 нояб 2021

Та, которая ещё не открыта. Или та, которую откроете именно вы. А пока это всем известная формула Эйлера, о которой уже указывалось в самом популярном ответе.

Комментировать ответ…Комментировать…

Серёжа Мутыгуллин

432

Видеомонтажёр, фотограф  · 20 сент 2017

Мне кажется, что самая красивая формула — это a/b = (a+b)/a — формула золотого сечения. Самая популярная её визуализация — это золотая спираль, к которой в свою очередь максимально близка спираль, строящаяся еще на одном красивом математическом явлении — ряде чисел Фибоначчи (ставшая в последнее время достаточно популярной). Читать далее

Комментировать ответ…Комментировать…

Олег Валиулин

1,6 K

Студент-лингвист, меломан, футбольный болельщик  · 1 авг 2017

Мне безумно доставляет бином Ньютона и отсылающий к нему треугольник Паскаля (что не совсем формула, но это абсолютно гениально). 

В треугольнике есть просто шикарные плюшки. Про это Numberpbile тоже делали видео)

Олег Валиулин

1 августа 2017

https://youtube.com/watch?v=0iMtlus-afo%3Fwmode%3Dopaque

Комментировать ответ…Комментировать…

Elias

10,5 K

Миллениал (inst: @p3wx2)  · 16 мар 2017

Формула Гаусса-Остроградского — формула, которая выражает поток непрерывно-дифференцируемого векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью. Вроде «очень сложно, до свидания», но на самом деле всё достаточно банально и ёмко записано, а в переходе интегралов какая-то грация: Периодические точки… Читать далее

Комментировать ответ…Комментировать…

Величайшая формула математики | Математика, которая мне нравится

Без дальнейших церемоний, вот она:

   

Ее обычно называют тождеством Эйлера в честь великого швейцарского математика Леонарда Эйлера (1707 — 1783). Ее можно увидеть на футболках и кофейных кружках, и несколько опросов среди математиков и физиков удостоили ее такого названия, как “величайшее уравнение” (Crease, Robert P., “The greatest equations ever”).

Ощущение красоты и элегантности тождества происходит из того, что оно сочетает в простой форме пять самых важных чисел математических констант: — основание натурального логарифма, — квадратный корень из и . Глядя на него внимательно, большинство людей задумываются о показателе: что значит возвести число в мнимую степень? Терпение, терпение, мы до этого доберемся.

Чтобы объяснить, откуда возникает эта формула, мы должны сначала получить более общую формулу, найденную Эйлером, а затем показать, что наше равенство является всего лишь частным случаем этой формулы. Общая формула удивительна сама по себе и имеет множество замечательных приложений в математике, физике и технике.

Первый шаг в нашем путешествии — понять, что большинство функций в математике может быть представлено в виде бесконечной суммы по степеням аргумента. Это пример:

   

Здесь измеряется в радианах, а не в градусах. Мы можем получить хорошее приближение для конкретного значения , используя только несколько первых членов ряда. Это пример ряда Тейлора, и довольно легко вывести эту формулу, используя математический анализ. Здесь я не предполагаю знание математического анализа, поэтому прошу читателя принять ее на веру.

Соответствующая формула для косинуса:

   

Наконец,

   

Число — константа, равная , и Эйлер был первым, кто признал его фундаментальное значение в математике и вывел последнюю формулу (две предыдущие были найдены Исааком Ньютоном).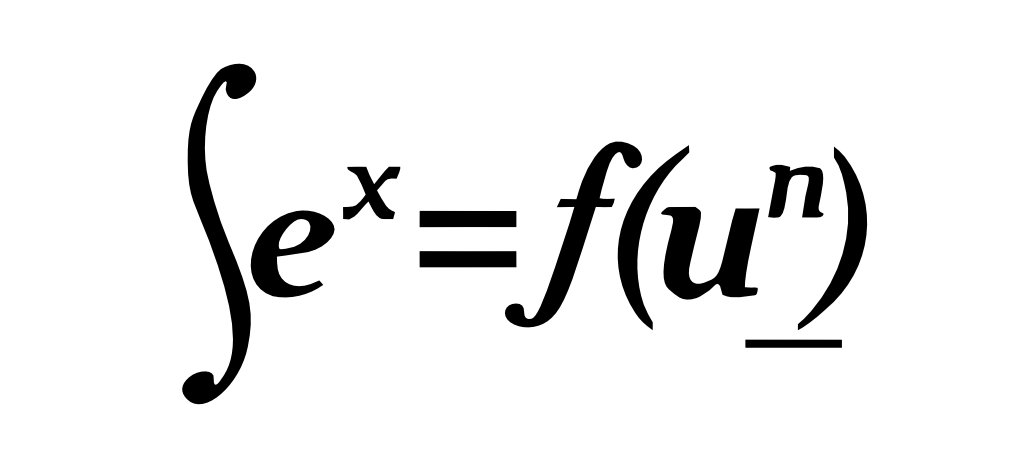

О числе написаны книги (например, Maor, E. (1994). e, the story of a number. Princeton University Press), можно также прочитать о нем здесь.

Примерно в 1740 году Эйлер посмотрел на эти три формулы, расположенные приблизительно так, как мы их здесь видим. Сразу видно, что каждое слагаемое в третьей формуле также появляется в любой предыдущей. Тем не менее, половина членов в первых равенствах являются отрицательными, в то время как каждый член в последнем положителен. Большинство людей так бы это и оставили, но Эйлер увидел во всем этом закономерность. Он первый сложил первые две формулы:

   

Обратите внимание на последовательность знаков в этом ряду: , она повторяется группами по 4. Эйлер заметил, что эта же последовательность знаков получается, когда мы возводим мнимую единицу в целые степени:

   

Это означало, что можно заменить в последней формуле на и получить:

   

Теперь знаки соответствуют знакам в предыдущей формуле, и новый ряд совпадает с предыдущим, за исключением того, что члены разложения умножаются на . То есть получаем в точности

   

Это удивительный и таинственный результат, он свидетельствует о существовании тесной связи между числом и синусами и косинусами в тригонометрии, хотя было известно только из задач, не связанных с геометрией или треугольниками. Кроме ее элегантности и странности, однако, было бы трудно переоценить важность этой формулы в математике, которая увеличивалась с момента ее открытия. Она появляется везде, и не так давно вышла книга примерно в 400 страниц (Nahin P. Dr. Euler’s Fabulous Formula, 2006), посвященная описанию некоторых приложений этой формулы.

Обратите внимание, что старый вопрос о мнимых показателях в настоящее время решен: для возведения в мнимую степень просто поставьте мнимое число в формулу Эйлера. Если основание – число, отличное от , требуется только ее незначительная модификация.

Теперь вернемся к волшебному равенству. Мы можем подставить в него любое вещественное число , и в результате получим некоторое комплексное число. Один возможный выбор для — это . Вспомним из тригонометрии, что радиан — это 180 градусов. Косинус 180 градусов равен , а синус равен .

Поэтому

   

, или

   

Все это дает понятие о мощи и творческих способностях Леонарда Эйлера, и о том, почему его иногда называют выдающимся умом восемнадцатого века. Я буду еще писать о нем и некоторых его результатах в серии Euler’s Greatest Hits.

Перевод статьи Larry Phillips, The Greatest Formula in Mathematics, http://brightstartutors.com/blog/2010/01/29/the-greatest-formula-in-mathematics.

Дробные комплексные преобразования для дробных дифференциальных уравнений | Достижения в непрерывных и дискретных моделях

• Исследования
• Открытый доступ
• Опубликовано: 06 ноября 2012 г.

• Рабха В. Ибрагим ¹  

Успехи в разностных уравнениях том 2012 , Номер статьи: 192 (2012) Процитировать эту статью

• 23 тыс. обращений

• 40 цитирований

• Сведения о показателях

Abstract

Дробное комплексное преобразование используется для аналитического преобразования дробных дифференциальных уравнений в смысле дробного оператора Шриваставы-Овы и его обобщения в единичном круге. Проиллюстрированы примеры, поясняющие процедуру решения, включая пространственно-временное дробное дифференциальное уравнение в комплексной области, сингулярные задачи и задачи Коши. Здесь мы рассматриваем аналитические решения в комплексной области.

МСК: 30C45.

1 Введение

Теория дробного исчисления была применена в теории аналитических функций. Классические понятия дробно-дифференциального оператора и дробно-интегрального оператора и их обобщения были плодотворно использованы при нахождении, например, свойств характеризации, оценок коэффициентов [1], неравенств искажения [2] и свойств свертки для разностных подклассов аналитических функций .

Дробные дифференциальные уравнения рассматриваются как альтернативные модели нелинейных дифференциальных уравнений. Разновидности их играют важную роль и служат инструментами не только в математике, но и в физике, динамических системах, системах управления и технике для создания математического моделирования многих физических явлений. Кроме того, они используются в социальных науках, таких как пищевые добавки, климат и экономика. Дробные дифференциальные уравнения относительно дробных операторов Римана-Лиувилля или производной Капуто рекомендуются многими авторами (см. [3–10]).

В последнее время сложное моделирование явлений в природе и обществе стало предметом нескольких исследований, основанных на методах, первоначально разработанных в физическом контексте. Эти системы являются следствием способности людей разрабатывать стратегии. Они встречаются в кинетической теории [11], сложных динамических системах [12], хаотических сложных системах и гиперхаотических сложных системах [13], а также сложной лоренцоподобной системе, которая была обнаружена в лазерной физике при анализе бароклинной неустойчивости геофизических течений в в атмосфере (или в океане) [14, 15]. Сэйнти [16] рассмотрел комплексное уравнение теплопроводности, используя комплексный броунов. Модель сложных дробных уравнений введена Джумари [17–20] с использованием различных типов дробных производных. Балеану и др. [21–23] наложил несколько приложений дробного исчисления, включая сложное моделирование. Автор изучал различные типы дробных дифференциальных уравнений в комплексной области, такие как уравнение Коши, уравнение диффузии и телеграфные уравнения [24–28].

Преобразование — важный метод решения математических задач. В открытой литературе появилось много полезных преобразований для решения различных задач, таких как преобразование волн, преобразование Лапласа, преобразование Фурье, преобразование Бюклунда, интегральное преобразование, локальное дробно-интегральное преобразование и дробно-комплексное преобразование (см. [29])., 30]).

В этой статье мы введем два обобщения волнового преобразования в комплексной области. Эти обобщения зависят от операторов дробного дифференциала для комплексных переменных. Эти преобразования преобразуют дробные дифференциальные уравнения в комплексной области в обыкновенные дифференциальные уравнения для получения аналитических или точных решений. Примеры проиллюстрированы.

В [31] Сривастава и Ова дали определения дробных операторов (производных и интегральных) в комплексе z -самолет ℂ следующим образом.

Определение 1.1 Дробная производная порядка α определяется для функции f(z) формулой

)αdζ;0≤α<1,

где функция f(z) аналитична в односвязной области комплексной z -плоскости ℂ, содержащей начало координат, и кратность (z−ζ)−α удаляется требованием, чтобы log(z−ζ) был вещественным, когда (z−ζ)>0.

Определение 1.2 Дробный интеграл 9-го порядка0053 α определяется для функции f(z) формулой

Izaf(z):=1Γ(α)∫0zf(ζ)(z−ζ)α−1dζ;α>0,

, где функция f(z) аналитична в односвязной области комплексной z -плоскости (C), содержащей начало координат, а кратность (z−ζ)α−1 устраняется требованием, чтобы log(z−ζ) быть действительным, когда (z−ζ)>0.

Замечание 1.1 Из определений 1.1 и 1.2 имеем

Dzαzβ=Γ(β+1)Γ(β−α+1)zβ−α,β>−1;0≤α<1

Izαzβ=Γ(β+1)Γ(β+α+1)zβ+α,β>−1;α>0.

В [32] автор вывел формулу для обобщенного дробного интеграла. Рассмотрим для натуральных n∈N={1,2,…} и вещественных µ n -кратный интеграл вида

)dζn,

(1)

что дает

n−1)!∫0z(zµ+1−ζµ+1)n−1ζµf(ζ)dζ,

откуда следует дробный оператор типа

Izα,µf(z)=(µ+1)1−αΓ(α)∫0z(zµ+1−ζµ+1)α−1ζµf(ζ)dζ,

(2)

, где a и µ≠−1 — действительные числа, а функция f(z) аналитична в односвязной области комплексной z -плоскости ℂ, содержащей начало координат, и кратность (zµ+1−ζµ+1)− α удаляется, требуя, чтобы log(zµ+1−ζµ+1) был вещественным, когда (zµ+1−ζµ+1)>0.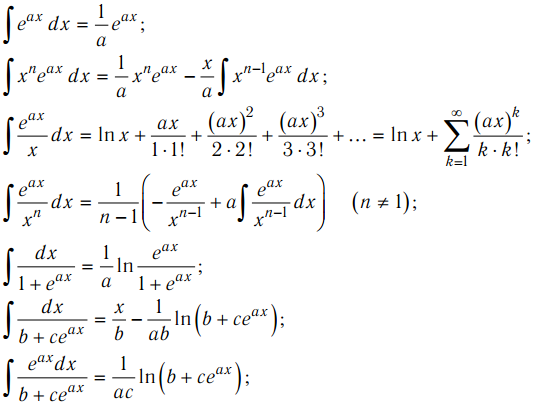 Когда µ=0, мы получаем стандартный дробный интеграл Шриваставы-Овы, который применяется для определения дробных производных Шриваставы-Овы. Из расчета следует [32]

Izα,μzν=zα(μ+1)+ν(μ+1)αΓ(ν+μ+1μ+1)Γ(α+ν+μ+1μ+1).

(3)

При µ=0 получаем Izazν=Γ(ν+1)Γ(α+ν+1)zα+ν (см. замечание 1.1).

В соответствии с обобщенными дробными интегралами (2) мы наложили обобщенный дифференциальный оператор.

Определение 1.3 Обобщенная дробная производная порядка α определяется для функции f(z) формулой

Dzα,µf(z):=(µ+1)αΓ(1−α)ddz∫ 0zζµf(ζ)(zµ+1−ζµ+1)αdζ;0≤α<1,

(4)

, где функция f(z) является аналитической в ​​односвязной области комплексной z -плоскости ℂ, содержащей начало координат, а кратность (zµ+1−ζµ+1)−α удалена требованием log (zµ+1−ζµ+1) вещественным, когда (zµ+1−ζµ+1)>0. Расчет дает

Dzα,μzν=(μ+1)α−1Γ(νμ+1+1)Γ(νμ+1+1−α)z(1−α)(μ+1)+ν−1.

(5)

При µ=0 получаем Dzαzν=Γ(ν+1)Γ(ν+1−α)zν−α (см. замечание 1.1).

Для аналитических функций вида

f(z)=∑n=1∞anzn,z∈U,

(6)

имеем следующее свойство:

Dzα,µIzα,µf(z)=Izα,µDzα,µf(z)=f(z),z∈U.

2 Дробное комплексное преобразование

В последнее время появился один из наиболее важных и полезных методов дробного исчисления, называемый дробным комплексным преобразованием [33–36]. Дробное комплексное преобразование предназначено для преобразования дробных дифференциальных уравнений в обыкновенные дифференциальные уравнения, что дает чрезвычайно простую процедуру решения. В этом разделе мы проиллюстрируем некоторое дробное комплексное преобразование, используя свойства дробного оператора Шриваставы-Овы и его обобщение. Аналогично волновому преобразованию

η=az+bw+cu+⋯,

(7)

где a , b и c константы, дробно-комплексное преобразование равно

η=azγ+

(8)

для дробных дифференциальных уравнений в смысле дробных операторов Шриваставы-Овы. В то время как дробное комплексное преобразование формы

η=Azα(µ+1)+Bwβ(µ+1)+Cuγ(µ+1)+⋯

(9)

применяется к дробным дифференциальным уравнениям в смысле обобщенных операторов (2) и (4). Очевидно, что при µ=0, (9) сводится к (8). Кроме того, в вещественном случае из (9) следует дробно-комплексное преобразование, определенное в [34]. Накладываем дробное комплексное преобразование

Dzαf(z)=∂f∂ZDzαZ,Z:=zα

(10)

, если обозначить Dzαf(z):=∂αf∂zα, получается

∂αf∂ zα=∂f∂Z∂αZ∂zα:=∂f∂Zθα,

(11)

, где θα — индекс фрактала, обычно определяемый через гамма-функции. Аналогично можно получить

Dzα,µf(z)=∂f∂ZDzα,µZ,Z:=zα(µ+1)

(12)

, если положить Dzα,µf(z):=∂α(µ+1)f∂zα(µ+1), откуда следует

∂α(µ+1)f∂zα(µ+1)=∂ f∂Z∂α(µ+1)Z∂zα(µ+1):=∂f∂ZΘα,µ.

(13)

Пример 2.1 Пусть Z=zα и f=Zn, n≠0, тогда с учетом замечания 1.1 получаем

∂αf∂zα=∂f∂Z∂αZ∂zα=Γ( 1+nα)znα−αΓ(1+nα−α):=∂f∂Zθα=nθαznα−α.

Отсюда можно получить, что

θα=Γ(1+nα)nΓ(1+nα−α).

Пример 2.2 Пусть Z=zα(µ+1) и f=Znµ+1, n≠0, тогда в силу (5) имеем

∂α(µ+1)f∂zα(µ+1)=∂f∂Z∂α(µ+1)Zn∂zα(µ+1)=(µ+1)α−1Γ(nαµ+1+ 1)Γ(nαµ+1+1−α)z(1−α)(µ+1)+nα−1:=∂f∂ZΘα,µ=nΘα,µµ+1z(1−α)(µ+1 )+nα−1.

Таким образом, имеем

Θα,µ=(µ+1)αΓ(nαµ+1+1)nΓ(nαµ+1+1−α).

3 Приложения

Пример 3.1 Рассмотрим следующее уравнение: ,1]u(0,z)=0,в окрестности z=0,

(14)

, где u(t,z) — неизвестная функция ρ∈(0,1) и β∈(0 ,1].

Мы предлагаем показать, что (14) имеет единственное аналитическое решение, используя теорему Банаха о неподвижной точке. Приняв

u(t,z)=µ(z)t+v(t,z)(v(t,z)=O(t2))

в качестве формального решения, где µ(z)=O (zβ), расчеты дают

Dzβu(t,z)=Dzβ(µ(z)t+v(t,z))=tDzβµ(z)+vβ(t,z).

Следовательно, µ(z) удовлетворяет

ρµ(z)+Dzβµ(z)=0,

, что эквивалентно

Dzβµ(z)=g(z,µ(z)),

(15)

где

g(z,µ(z))=−ρµ(z).

Теперь g(z,µ(z)) является сжимающим отображением, если ρ∈(0,1); следовательно, ввиду теоремы Банаха о неподвижной точке уравнение (15) имеет единственное аналитическое решение в единичном круге и, следовательно, задача (14).

Для вычисления индекса фрактала уравнения

Dzβµ(z)+ρµ(z)=0,µ(0)=1,

(16)

примем преобразование Z=zβ и решение может быть выражается в ряду в виде

µ(Z)=∑m=0∞µmZm,

(17)

где µm – константы. Подставляя (17) в уравнение (16) дает

∂∂Z∑m=0∞θβmμmZm+ρ∑m=0∞μmZm=0.

(18)

Поскольку

θβm=Γ(1+mβ)mΓ(1+mβ−β),

, то вычисление накладывает соотношение

Γ(1+mβ)Γ(1+mβ−β )µm+ρµm−1=0

с µ(0)=1, и, следовательно, получаем

µm=(−ρ)mΓ(1+mβ).

Таким образом, имеем следующее решение:

µ(Z)=∑m=0∞(−ρ)mΓ(1+mβ)Zm

, что эквивалентно

μ(z)=∑m=0∞(−ρ)mΓ(1+mβ)zmβ=Eβ(−ρzβ),

, где Eβ — функция Миттаг-Леффлера. Последнее утверждение является точным решением задачи (16), а следовательно, и (14).

Пример 3.2 Рассмотрим следующее уравнение: =zβt,t∈J=[0,1],u(0,z)=0,в окрестности z=0,

(19)

, где u(t,z) — неизвестная функция, а β ∈(0,1]. Аналогично примеру 3.1 положим

u(t,z)=µ(z)t+v(t,z)(v(t,z)=O(t2))

как формальное решение, где µ(z)=O(zβ ) и

|µ′(z)−ν′(z)|<λ|µ(z)−ν(z)|,λ<18.

Из оценок следует

и

Dzβu(t,z)=Dzβ(µ(z)t+v(t,z))=tDzβµ(z)+vβ(t,z).

Следовательно, µ(z) удовлетворяет

µ(z)2+4zµ′(z)+Dzβµ(z)−zβ=0,

, что эквивалентно

Dzβµ(z)=G(z,µ (z),zµ′(z)),

(20)

, где

G(z,µ(z),zµ′(z))=zβ−1/2µ(z)−4zµ′(z ).

Теперь, чтобы показать, что G(z,µ(z),zµ′(z)) является сжимающим отображением,

Таким образом, с учетом банаховой теоремы о неподвижной точке уравнение (20) имеет единственное аналитическое решение в единичном круге и, следовательно, задача (19).

Для вычисления индекса фрактала уравнения преобразовать Z=zβ, и решение можно представить в виде (17). Подставляя (17) в уравнение (21) имеем

∂∂Z∑m=0∞θβmμmZm+12∑m=0∞µmZm+4∑m=1∞mμmZm−Z=0,

(22)

где

θβm=Γ(1+mβ)mΓ(1+mβ−β).

Следовательно, вычисление накладывает соотношение

(Γ(1+mβ)Γ(1+mβ−β)+4m)µm+12µm−1=0

с µ(0)=1, и, следовательно, получаем

мкм:=(Bm)mΓ(1+mβ),

, где Bm в терминах гамма-функции. Если мы допустим B:=maxm{Bm}, то решение приближается к

µ(Z)≃∑m=0∞(B)mΓ(1+mβ)Zm,

, что эквивалентно

µ(z )=∑m=0∞(B)mΓ(1+mβ)zmβ=Eβ(Bzβ).

Последнее утверждение является точным решением задачи (21) и, следовательно, (19).

Далее рассмотрим задачу Коши, используя обобщенный оператор дробного дифференциала (4). Покажем, что решение такой задачи можно определить с помощью функции Фокса-Райта [37]:

, где Aj>0 для всех j=1,…,p, Bj>0 для всех j=1, …,q и 1+∑j=1qBj−∑j=1pAj≥0 для подходящих значений |w|<1 и ai, bj являются комплексными параметрами.

Пример 3.3 Рассмотрим задачу Коши в терминах дифференциального оператора (4)

Dzα,µu(z)=F(z,u(z)),

(23)

где F(z,u(z)) аналитична в и и u(z) аналитична в единичном круге. Таким образом, F можно выразить как

F(z,u)=ϕu(z).

Пусть Z=zα(µ+1). Тогда решение можно сформулировать следующим образом:

u(Z)=∑m=0∞umZm,

(24)

где um — константы. Подставляя (24) в уравнение (23) подразумевает

∂∂Z∑m=0∞Θα,μ,mumZm−ϕ∑m=0∞umZm=0.

(25)

Поскольку

Θα,µ,m=(µ+1)αΓ(mαµ+1+1)mΓ(nαµ+1+1−α),

, то вычисление дает соотношение

(μ+1)αΓ(mαμ+1+1)Γ(mαμ+1+1−α)um−ϕum−1=0;

следовательно, получаем

um=[ϕ(µ+1)α]mΓ((m−1)αµ+1+1−α)Γ(mαµ+1+1−α)Γ((m−1 )αµ+1+1)Γ(mαµ+1+1).

Таким образом, имеем следующее решение:

u(Z)=∑m=0∞[ϕ(µ+1)α]mΓ((m−1)αµ+1+1−α)Γ(mαµ+ 1+1−α)Γ((m−1)αµ+1+1)Γ(mαµ+1+1)Zm

, что эквивалентно

u(Z)=∑m=0∞[ϕ(µ+1)α]mΓ(m+1)Γ((m−1)αµ+1+1−α)Γ( mαµ+1+1−α)Γ((m−1)αµ+1+1)Γ(mαµ+1+1)Zmm!.

Поскольку ϕ — произвольная константа, мы предполагаем, что

ϕ:=(µ+1)α.

Таким образом, для подходящего α мы представляем

или

, где |z|<1.

4 Заключение

В статье предлагается обобщенное дробно-комплексное преобразование для нахождения точных решений дробно-дифференциальных уравнений в единичном круге. Мы преобразовали некоторые классы дробных дифференциальных уравнений в смысле дробного оператора Шриваставы-Овы и его обобщения в обыкновенные дифференциальные уравнения. Следовательно, накладываются точные решения. Процедура решения проста и может найти широкое применение в обработке изображений и обработке сигналов с использованием маски дробного фильтра. Примеры 3.1 и 3.2 показали преобразование дифференциальных уравнений дробного времени в пространстве в нормальный случай. Точные решения вводятся в выражение функции Миттаг-Леффлера. В то время как пример 3.3, задача Коши дробного порядка в единичном круге, предлагает точное решение в терминах функции Фокса-Райта.

Ссылки

1. Дарус М., Ибрагим Р.В.: Оценки радиуса подкласса однолистных функций. Матем. Весник 2011, 63: 55–58.

   MathSciNet МАТЕМАТИКА Google ученый

2. Шривастава Х.М., Линг Ю., Бао Г.: Некоторые неравенства искажения, связанные с дробными производными аналитических и однолистных функций. ДЖИПАМ. Дж. Неравный. Чистое приложение Мат. 2001, 2: 1–6.

   MathSciNet МАТЕМАТИКА Google ученый

3. Миллер К.С., Росс Б.: Введение в дробное исчисление и дробные дифференциальные уравнения . Уайли, Нью-Йорк; 1993.

   МАТЕМАТИКА Google ученый

4. Подлубный I Математика в науке и технике 198. В Дифференциальные уравнения дробного порядка . Академическая пресса, Сан-Диего; 1999.

   Google ученый

5. Хильфер Р: Применение дробного исчисления в физике . Мировое научное издательство, River Edge; 2000.

   Книга МАТЕМАТИКА Google ученый

6. Вест Б.Дж., Болонья М., Григолини П. Институт нелинейных наук. В Физика фрактальных операторов . Спрингер, Нью-Йорк; 2003.

   Глава Google ученый

7. Килбас А.А., Сривастава Х.М., Трухильо Дж.Дж. Математические исследования Северной Голландии 204. В Теория и приложения дробных дифференциальных уравнений . Эльзевир, Амстердам; 2006.

   Google ученый

8. Сабатье Дж., Агравал О.П., Мачадо Дж.А.: Прогресс в области дробного исчисления: теоретические разработки и приложения в физике и технике . Спрингер, Дордрехт; 2007.

   Книга МАТЕМАТИКА Google ученый

9. Baleanu D, Guvenc B, Tenreiro JA: Новые тенденции в нанотехнологиях и приложениях дробного исчисления . Спрингер, Нью-Йорк; 2010.

   Книга МАТЕМАТИКА Google ученый

10. Лакшмикантам В., Лила С., Васундхара Дж.: Теория дробных динамических систем . Кембриджское академическое издательство, Кембридж; 2009.

    МАТЕМАТИКА Google ученый

11. Бьянка К. О наборе нелинейности в моделях термостатируемых активных частиц для сложных систем. Нелинейный анализ. Реальное применение. 2012, 13: 2593–2608. 10.1016/j.nonrwa.2012.03.005

    Статья MathSciNet МАТЕМАТИКА Google ученый

12. Махмуд Г., Махмуд Э.: Модифицированная проективная лаг-синхронизация двух неидентичных гиперхаотических сложных нелинейных систем. Междунар. Дж. Бифурк. Хаос 2011, 2(8):2369–2379.

    Артикул МАТЕМАТИКА Google ученый

13. «>

    Махмуд Г., Махмуд Э., Ахмед М.: О гиперхаотической сложной системе Лю. Нелинейная динам. 2009, 58: 725–738. 10.1007/s11071-009-9513-0

    Артикул MathSciNet МАТЕМАТИКА Google ученый

14. Фаулер А.С., Гиббон ​​Дж.Д., МакГиннесс М.Дж.: Комплексные уравнения Лоренца. Физика Д 1982, 4: 139–163. 10.1016/0167-2789(82)

    -4

    Артикул MathSciNet МАТЕМАТИКА Google ученый

15. Раут А., Ганнибал Л., Абрахам Н.Б.: Свойства глобальной устойчивости сложной модели Лоренца. Physica D 1996, 99: 45–58. 10.1016/S0167-2789(96)00129-7

    Артикул MathSciNet МАТЕМАТИКА Google ученый

16. Сэйнти П. Сокращение комплекснозначного дробного броуниана порядка п . Дж. Матем. физ. 1992, 33(9):3128–3149. 10.1063/1.529976

    Артикул MathSciNet МАТЕМАТИКА Google ученый

17. Джумари Г. Дробное броуновское движение со сложной дисперсией посредством случайного блуждания в комплексной плоскости и приложения. Солитоны Хаоса Фракталы 2000, 11: 1097–1111. 10.1016/S0960-0779(99)00015-6

    Артикул MathSciNet МАТЕМАТИКА Google ученый

18. Джумари Г.: Уравнение Шредингера для квантового фрактального пространства-времени порядка n через комплекснозначное дробное броуновское движение. Междунар. Дж. Мод. физ. А 2001, 16: 5061–5084. 10.1142/S0217751X01005468

    Артикул MathSciNet МАТЕМАТИКА Google ученый

19. Джумари Г. Дробные броуновские движения через случайное блуждание в комплексной плоскости и через дробную производную. Сравнение и дальнейшие результаты. Солитоны Хаоса Фракталы 2004, 22: 907–925. 10.1016/j.chaos.2004.03.020

    Статья MathSciNet МАТЕМАТИКА Google ученый

20. Джумари Г.: Дробление комплекснозначного броуновского движения порядка n с использованием производной Римана-Лиувилля. Приложения к математическим финансам и стохастической механике. Солитоны Хаоса Фракталы 2006, 28: 1285–1305. 10.1016/j.chaos.2005.08.083

    Статья MathSciNet МАТЕМАТИКА Google ученый

21. Балеану Д., Дитхельм К., Скалас Э., Трухильо Дж. Дж.: Модели дробного исчисления и численные методы (серия по сложности, нелинейности и хаосу) . Всемирный научный, Сингапур; 2012.

    МАТЕМАТИКА Google ученый

22. Балеану Д., Трухильо Дж. Дж.: О точных решениях класса дробных уравнений Эйлера-Лагранжа. Нелинейная динам. 2008, 52: 331–335. 10.1007/s11071-007-9281-7

    Артикул MathSciNet МАТЕМАТИКА Google ученый

23. Magin R, Feng X, Baleanu D: Решение уравнения Блоха дробного порядка. Концепты Magn. Резон., ч. А 2009, 34А: 16–23. 10.1002/cmr.a.20129

    Артикул Google ученый

24. Ибрагим Р.В., Дарус М.: Субординация и суперординация одновалентных решений дифференциальных уравнений дробного порядка. Дж. Матем. Анальный. заявл. 2008, 345: 871–879. 10.1016/j.jmaa.2008.05.017

    Статья MathSciNet МАТЕМАТИКА Google ученый

25. Ибрагим РВ: О решениях задач дробной диффузии. Электрон. Дж. Дифференц. Экв. 2010, 147: 1–11.

    MathSciNet Google ученый

26. «>

    Ибрагим Р.В.: Существование и единственность голоморфных решений дробной задачи Коши. Дж. Матем. Анальный. заявл. 2011, 380: 232–240. 10.1016/j.jmaa.2011.03.001

    Артикул MathSciNet МАТЕМАТИКА Google ученый

27. Ибрагим Р.В.: Устойчивость по Уламу для дробного дифференциального уравнения в комплексной области. Абстр. заявл. Анальный. 2012., 2012: ID статьи 649517. doi:10.1155/2012/649517

    Google ученый

28. Ибрагим Р.В.: О голоморфном решении дробных телеграфных уравнений пространства и времени в комплексной области. J. Функц. Пространства Appl. 2012., 2012: ID статьи 703681. doi:10.1155/2012/703681

    Google ученый

29. Гордоа П.Р., Пикеринг А., Чжу З.Н. Преобразования Бюклунда для второго матричного уравнения Пенлева. Физ. лат. А 2010, 374(34):3422–3424. 10.1016/ж.физлета.2010.06.034

    Статья MathSciNet МАТЕМАТИКА Google ученый

30. Моллик Р., Батиха Б.: Приближенные аналитические решения дробных уравнений Захарова-Кузнецова методом дробно-комплексного преобразования. Междунар. Дж. Инж. Технол. 2012, 1(1):1–13.

    Артикул Google ученый

31. Шривастава Х.М., Ова С.: Одновалентные функции, дробное исчисление и их приложения . Уайли, Нью-Йорк; 1989.

    МАТЕМАТИКА Google ученый

32. Ибрагим РВ: Об обобщенных дробных операторах Шриваставы-Овы в единичном круге. Доп. Отличаться. Экв. 2011, 55: 1–10.

    MathSciNet МАТЕМАТИКА Google ученый

33. «>

    Li ZB, He JH: Дробное комплексное преобразование для дробных дифференциальных уравнений. Матем. вычисл. заявл. 2010, 15: 970–973.

    MathSciNet МАТЕМАТИКА Google ученый

34. Li ZB: расширенное дробно-комплексное преобразование. Междунар. J. Нелинейные науки. Число. Симул. 2010, 11: 0335–0337.

    Google ученый

35. Li ZB, He JH: Применение дробного комплексного преобразования к дробным дифференциальным уравнениям. Нелинейная наука. лат. А 2011, 2: 121–126.

    Google ученый

36. He JH, Elagan SK, Li ZB: Геометрическое объяснение дробного комплексного преобразования и правила цепочки производных для дробного исчисления. Физ. лат. А 2012, 376: 257–259. 10.1016/ж.физлета.2011.11.030

    Статья MathSciNet МАТЕМАТИКА Google ученый

37. «>

    Шривастава Х.М., Карлссон Т.П.: Множественный гипергеометрический ряд Гаусса . Уайли, Нью-Йорк; 1985.

    МАТЕМАТИКА Google ученый

Скачать ссылки

Благодарности

Автор благодарен рецензентам за полезные предложения по улучшению этой статьи.

Информация об авторе

Авторы и организации

1. Институт математических наук, Малайский университет, Куала-Лумпур, 50603, Малайзия

   Рабха В. Ибрагим

Авторы

1. Рабха В. Ибрагим

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

Автор, ответственный за переписку

Рабха В. Ибрагим.

Дополнительная информация

Конкурирующие интересы

Автор заявляет об отсутствии конкурирующих интересов.

Права и разрешения

Открытый доступ Эта статья распространяется в соответствии с условиями международной лицензии Creative Commons Attribution 2. 0 (https://creativecommons.org/licenses/by/2.0), которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе, при условии, что оригинальная работа правильно процитирована.

Перепечатка и разрешения

Об этой статье

17 уравнений, изменивших мир

17 уравнений, изменивших мир Значок поискаУвеличительное стекло. Это означает: «Нажмите, чтобы выполнить поиск». Логотип InsiderСлово «Инсайдер».

Рынки США Загрузка… ЧАС М С В новостях

Значок шевронаОн указывает на расширяемый раздел или меню, а иногда и на предыдущие/следующие параметры навигации.ДОМАШНЯЯ СТРАНИЦА

Рынки

Значок «Сохранить статью» Значок «Закладка» Значок «Поделиться» Изогнутая стрелка, указывающая вправо.

Скачать приложение

Ранее в этом году математик Ян Стюарт выпустил прекрасную и глубоко проработанную книгу под названием «В погоне за неизвестным: 17 уравнений, которые изменили мир», в которой рассматриваются самые важные уравнения всех времен и излагаются они с точки зрения человека. , а не технический контекст.

Мы спросили профессора Стюарта, почему он решил написать эту книгу:

«Уравнения определенно МОГУТ быть скучными, и они МОГУТ казаться сложными, но это потому, что они часто представлены скучно и сложно. У меня есть преимущество перед школой. Учителя математики: Я не пытаюсь показать вам, как самостоятельно складывать суммы. Вы можете оценить красоту и важность уравнений, не зная, как их решать….. Намерение состоит в том, чтобы найти их в их культурном и человеческом контексте. , и приподнимите завесу над их скрытым влиянием на историю. Уравнения являются жизненно важной частью нашей культуры. Истории, стоящие за ними — люди, которые открыли/изобрели их, и периоды, в которые они жили — завораживают».

Это должно быть особенно актуально для всех, кто пострадал от финансового кризиса.

Нажмите здесь, чтобы увидеть 17 уравнений >

Блэка Шоулза, производное уравнение ценообразования и номер 17 в этом списке помогли его вызвать.

Из переписки с профессором Стюартом по электронной почте:

«С математической точки зрения это довольно простое уравнение. Проблемы вызвала сложность системы, которую математика должна была смоделировать… На самом деле вам не нужно быть ученым-ракетчиком, чтобы понять, что давать взаймы сотни миллиардов долларов людям, у которых нет перспективы когда-либо их вернуть, — плохая идея…»

Люди слишком серьезно относились к теоретическому уравнению, преувеличивали его предположения, использовали его для оправдания неправильных решений и строили на нем карточный домик на триллион долларов. Это сделало кризис неизбежным:

«Я думаю, что кризис стал неизбежным, когда финансовые инструменты, торгуемые в гигантских количествах, стали настолько сложными, что никто не мог понять ни их стоимость, ни связанные с ними риски. Когда рынки торгуют реальными товарами за реальные деньги, излишества могут расти только до пределов того, что есть на самом деле. Когда они торгуют виртуальными товарами (деривативами) за виртуальные деньги (кредитное плечо), реальных ограничений нет, поэтому рынки могут ускакать в Страну облачных кукушек».

Вы можете купить полную книгу здесь.

Теорема Пифагора

Что это значит:  Квадрат гипотенузы треугольника равен сумме квадратов катетов.  

История:  Хотя приписывается Пифагору, нет уверенности, что он был первым человеком, доказавшим это. Первое ясное доказательство было получено от Евклида, и, возможно, эта концепция была известна вавилонянам за 1000 лет до Питорага.

Важность:  Уравнение лежит в основе большей части геометрии, связывает ее с алгеброй и является основой тригонометрии. Без него точная съемка, картографирование и навигация были бы невозможны.

Современное использование:  Триангуляция по сей день используется для точного определения относительного местоположения для GPS-навигации.

Источник: В погоне за неизвестным: 17 уравнений, которые изменили мир

Логарифм и его тождества

Что это значит:  Вы можете умножать числа, складывая связанные числа.

История:  Первоначальная концепция была открыта шотландским лэрдом Джоном Нейпиром из Мерчистона в попытке сделать умножение больших чисел, которое тогда было невероятно утомительным и трудоемким, проще и быстрее. Позже он был усовершенствован Генри Бриггсом, чтобы упростить расчет справочных таблиц и сделать их более полезными.

Важность: Логарифмы были революционными, делая расчеты быстрее и точнее для инженеров и астрономов. Это стало менее важным с появлением компьютеров, но они по-прежнему важны для ученых.

Современное использование:  Логарифмы до сих пор определяют наше понимание радиоактивного распада.

Источник: В погоне за неизвестным: 17 уравнений, которые изменили мир    

Основная теорема исчисления

Что это значит?:  Позволяет рассчитать мгновенную скорость изменения.

История: Исчисление в том виде, в каком мы его знаем в настоящее время, было описано приблизительно в конце 17 века Исааком Ньютоном и Готфридом Лейбницем. Были длительные дебаты о плагиате и приоритете, которые, возможно, никогда не будут решены. Сегодня мы используем скачки логики и части обозначений обоих мужчин.

Важность:  По словам Стюарта,   «Он создал современный мир больше, чем любой другой математический метод». Исчисление необходимо для нашего понимания того, как измерять твердые тела, кривые и площади. Это основа многих законов природы и источник дифференциальных уравнений.

Современное использование: Любая математическая задача, требующая оптимального решения. Необходим для медицины, экономики и компьютерных наук.

Источник: В погоне за неизвестным: 17 уравнений, которые изменили мир

Закон всемирного тяготения Ньютона

Что это значит?:  Вычисляет силу притяжения между двумя объектами.

История:  Исаак Ньютон вывел свои законы с помощью более ранних работ Иоганна Кеплера. Он также использовал и, возможно, заимствовал работы Роберта Гука.

Важность:  Использованные методы исчисления для описания того, как устроен мир. Хотя позже она была вытеснена теорией относительности Эйнштейна, она по-прежнему важна для практического описания того, как объекты взаимодействуют друг с другом. Мы используем его по сей день для проектирования орбит для спутников и зондов.

Значение:  Когда мы запускаем космические миссии, уравнение используется для нахождения оптимальных гравитационных «труб» или путей, чтобы они были максимально энергоэффективными. Также делает возможным спутниковое телевидение.

Источник: В погоне за неизвестным: 17 уравнений, изменивших мир

Происхождение комплексных чисел

Что это значит?:  Квадрат мнимого числа отрицателен.   

История:  Мнимые числа были первоначально постулированы знаменитым игроком и математиком Джироламо Кардано, а затем расширены Рафаэлем Бомбелли и Джоном Уоллисом. Они все еще существовали как своеобразная, но существенная проблема в математике, пока Уильям Гамильтон не дал это определение.

Важность:  По словам Стюарта   «… без них невозможно было бы изобрести большинство современных технологий, от электрического освещения до цифровых камер». Мнимые числа позволяют проводить комплексный анализ, что позволяет инженерам решать практические задачи, работая на плоскости.

Современное использование: Широко используется в электротехнике и сложной математической теории.

Источник: В погоне за неизвестным: 17 уравнений, изменивших мир

Формула Эйлера для многогранников

Что это значит?:  Описывает форму или структуру пространства независимо от выравнивания.

История:  Отношение было впервые описано Декартом, затем уточнено, доказано и опубликовано Леонардом Эйлером в 1750 году. Необходимый инструмент для инженеров и биологов.

Современное использование: Топология используется для понимания поведения и функций ДНК.

Источник: В погоне за неизвестным: 17 уравнений, которые изменили мир

Нормальное распределение

Что это значит?:  Определяет стандартное нормальное распределение, колоколообразную кривую, на которой вероятность наблюдения точки максимальна вблизи среднего значения и быстро снижается по мере удаления.   

История:  Первоначальная работа была написана Блезом Паскалем, но распространение стало возможным благодаря Бернулли. Колоколообразная кривая в том виде, в каком мы ее знаем сейчас, принадлежит бельгийскому математику Адольфу Кетле.

Важность:  Уравнение является основой современной статистики. Без него наука и социальные науки не существовали бы в их нынешнем виде.

Современное использование:  Используется для определения того, достаточно ли эффективны лекарства в отношении отрицательных побочных эффектов в клинических испытаниях.

Источник: В погоне за неизвестным: 17 уравнений, которые изменили мир

Волновое уравнение

Что это значит?:  Дифференциальное уравнение, описывающее поведение волн, первоначально поведение колеблющейся струны скрипки.

История:  Математики Даниэль Бурнулли и Жан Д’Аламбер были первыми, кто описал эту зависимость в 18 веке, хотя и несколько по-разному.

Важность:  Поведение волн обобщает то, как работает звук, как происходят землетрясения и поведение океана.

Современное использование:  Нефтяные компании взрывают взрывчатку, а затем считывают данные с исходящих звуковых волн, чтобы предсказать геологические формации.

Источник: В погоне за неизвестным: 17 уравнений, которые изменили мир

Преобразование Фурье

Что это значит?:  Описывает закономерности во времени как функцию частоты.

История:  Жозеф Фурье открыл уравнение, являющееся продолжением его знаменитого уравнения теплового потока и ранее описанного волнового уравнения.

Важность:  Уравнение позволяет разбивать, очищать и анализировать сложные закономерности. Это важно во многих типах анализа сигналов.

Современное использование:  Используется для сжатия информации для формата изображения JPEG и изучения структуры молекул.

Источник: В погоне за неизвестным: 17 уравнений, изменивших мир

Уравнения Навье-Стокса

Что это значит?: 908:30 Слева — ускорение небольшого количества жидкости, справа — силы, действующие на него.  

История:  Леонард Эйлер предпринял первую попытку моделирования движения жидкости, французский инженер Клод-Луи Навье и ирландский математик Джордж Стоукс сделали скачок к модели, используемой до сих пор

Важность:  Когда компьютеры стали достаточно мощными решение этого уравнения открыло сложную и очень полезную область физики. Это особенно полезно для улучшения аэродинамики автомобилей.

Современное использование:  Помимо прочего, позволил разработать современные пассажирские самолеты.

Источник: В погоне за неизвестным: 17 уравнений, изменивших мир

Уравнения Максвелла

Что это значит?:   Отображает взаимосвязь между электрическими и магнитными полями.

История:  Майкл Фарадей провел новаторскую работу по изучению связи между электричеством и магнетизмом, Джеймс Клерк Максвелл перевел ее в уравнения, коренным образом изменив физику.

Важность:  Помогал предсказывать и понимать электромагнитные волны, помогая создавать многие технологии, которые мы используем сегодня.

Современное использование: 908:30 Радар, телевидение и современные средства связи.

Источник: В погоне за неизвестным: 17 уравнений, которые изменили мир

Второй закон термодинамики

Что это значит?:  Энергия и тепло со временем рассеиваются.   

История: Сади Карно первым предположил, что в природе нет обратимых процессов. Математик Людвиг Больцман расширил закон, а Уильям Томсон официально сформулировал его.

Важность:  Необходим для нашего понимания энергии и Вселенной через концепцию энтропии. Это помогает нам осознать ограничения на извлечение работы из тепла и помогло создать более совершенный паровой двигатель.

Современное использование:  Помог доказать, что материя состоит из атомов, что было несколько полезно.  

Источник: В погоне за неизвестным: 17 уравнений, которые изменили мир

Теория относительности Эйнштейна

Что это значит?:  Энергия равна массе, умноженной на квадрат скорости света.

История:  Менее известным (среди нефизиков) происхождением уравнения Эйнштейна был эксперимент Альберта Майкельсона и Эдварда Морли, который доказал, что свет не движется ньютоновским образом по сравнению с изменяющейся системой отсчета. Эйнштейн развил это понимание в своих знаменитых работах по специальной теории относительности (1905 г.) и общей теории относительности (1915 г.).

Важность: 908:30 Вероятно, самое известное уравнение в истории. Полностью изменился наш взгляд на материю и реальность.

Современное использование:  Помогли привести к созданию ядерного оружия, и если бы GPS не учитывал это, ваши направления отклонялись бы на тысячи ярдов.

Источник: В погоне за неизвестным: 17 уравнений, которые изменили мир

Уравнение Шредингера

Что это значит?:  Модели имеют значение как волна, а не как частица.

История:  Луи-Виктор де Бройль указал на двойственную природу материи в 1924 году. Уравнение, которое вы видите, было выведено Эрвином Шредингером в 1927 году на основе работ таких физиков, как Вернер Гейзенберг.

Важность:  Революционное представление физики в малых масштабах. Понимание того, что частицы на этом уровне существуют в диапазоне возможных состояний, было революционным.

Современное использование:  Необходим для использования полупроводников и транзисторов и, следовательно, большинства современных компьютерных технологий.

Источник: В погоне за неизвестным: 17 уравнений, которые изменили мир

Логистическая модель роста населения

Что это значит?:  Оценивает изменение популяции существ от поколения к поколению с ограниченными ресурсами.

История:  Роберт Мэй был первым, кто указал, что эта модель роста населения может привести к хаосу в 1975 году. Важная работа математиков Владимира Арнольда и Стивена Смейла помогла понять, что хаос является следствием дифференциальных уравнений.

Важность:  Помогал в разработке теории хаоса, которая полностью изменила наше понимание того, как работают природные системы.

Современное использование: Используется для моделирования землетрясений и прогнозирования погоды.

Источник: В погоне за неизвестным: 17 уравнений, изменивших мир

Модель Блэка-Шоулза

Что это значит?:  Оценивает производный инструмент, исходя из предположения, что он безрисков и что при правильной оценке нет возможности арбитража.

История: Разработано Фишером Блэком и Майроном Скоулзом, затем расширено Робертом Мертоном. Последние два получили Нобелевскую премию по экономике 1997 года за это открытие.

Важность:  Помогла создать рынок деривативов на несколько триллионов долларов. Утверждается, что неправильное использование формулы (и ее потомков) способствовало финансовому кризису. В частности, уравнение поддерживает несколько допущений, которые не выполняются на реальных финансовых рынках.

Современное использование:  Варианты все еще используются для оценки большинства деривативов, даже после финансового кризиса, 

Источник: В погоне за неизвестным: 17 уравнений, которые изменили мир

 

9004 !

Пи

Читать далее

LoadingЧто-то загружается.

No related posts.