| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
Что общего у 5 и 8? – Обзоры Вики
Поскольку, 1 является единственным общим множителем между 5 и 8.
Итак, каков наименьший общий знаменатель чисел 5 и 5? LCM 5 и 5 5.
Чему равен знаменатель числа 8? Ответ: Наименьший общий знаменатель чисел 8 и 9 равен 72.
Давайте посмотрим на решение. Объяснение: Наименьший общий знаменатель — это наименьшее общее кратное знаменателей набора дробей или заданных целых чисел. LCM 8 и 9 = 8 × 9 = 72.
Дополнительно Как мне найти общий знаменатель? Чтобы найти общий знаменатель, нам нужно найти наименьшее общее кратное (НОК) знаменателей. Тогда мы можем использовать LCM в качестве нашего общего знаменателя. Фактически, мы называем это «наименьшим общим знаменателем», потому что это наименьший общий знаменатель, который мы можем использовать.
Что такое LCD в математике? существительное Математика. наименьшее число, являющееся общим знаменателем данного набора дробей. Также называемый наименьший общий знаменатель.
Какой знаменатель равен 5?
Знаменатель равен 5. Знаменатель равен 10.
Другой способ записать 5/10 — это 1/2, 10/20 или 30/60. Есть бесконечные возможности записать соотношение 1:2.
Что такое числитель знаменатель? Во-первых, дробь состоит из двух целых чисел — одного сверху и одного снизу. Верхний называется числителем, нижний называется знаменателем, и эти два числа разделены линией.
Что такое числитель и знаменатель? Чай знаменатель = количество равных частей, составляющих одно целое. Числитель – это количество частей, которые вы считаете.
Как поменять знаменатели на одинаковые?
Чтобы сделать знаменатели одинаковыми, мы можем: Умножьте верхнюю и нижнюю часть каждой дроби на знаменатель другой.. Мы упростили дробь 2032 до 1016, а затем до 58, разделив верхнюю и нижнюю части на 2 каждый раз, и это настолько просто, насколько это возможно!
Также Что такое числитель знаменателя? Во-первых, дробь состоит из двух целых чисел — одного сверху и одного снизу. Верхний называется числителем, нижний называется знаменателем, и эти два числа разделены линией.
Какой пример знаменателя?
Знаменатель расположен в нижней части дробной черты дроби. Например, в дроби 3/4 в знаменателе стоит 4.
Какой ЖК у 5 и 7? LCM 5 и 7 35.
LCD и LCM — это одно и то же?
Для ЖК-дисплея и LCM требуется один и тот же математический процесс: поиск общего кратного двух (или более) чисел. Единственная разница между LCD и LCM состоит в том, что ЖК-дисплей — это НОК в знаменателе дроби. Итак, можно сказать, что наименьшие общие знаменатели — это частный случай наименьших общих кратных.
Какой ЖК у 6 и 8?
НОК 6 и 8 — это 24. Чтобы найти наименьшее общее кратное (НОК) 6 и 8, нам нужно найти кратные 6 и 8 (кратные 6 = 6, 12, 18, 24; кратные 8 = 8, 16, 24, 32) и выберите наименьшее кратное, которое точно делится на 6 и 8, т. е. на 24.
Что такое пример знаменателя? знаменатель находится внизу дробной черты дроби. Например, в дроби 3/4 в знаменателе стоит 4.
Что такое рационализация знаменателя? Рационализация знаменателя означает процесс перемещения корня, например, кубический или квадратный корень из нижней части дроби (знаменатель) в верхнюю часть дроби (числитель).
Таким образом, мы приводим дробь к простейшей форме, благодаря чему знаменатель становится рациональным. Иррациональный знаменатель.
Как решить дроби?
В чем разница между числителем и знаменателем? Числитель представляет собой общее количество учитываемых частей. Принимая во внимание, что знаменатель представляет собой общее количество равных частей в доля. Наибольшее число в дроби всегда считается числителем. Нижнее число в дроби считается знаменателем.
Почему он называется числителем и знаменателем?
По математике верхнее число дроби называется числителем. … Знаменатель показывает, на сколько равных частей разделена пицца, а числитель показывает, сколько таких частей у вас есть. На латыни числитель означает «счетчик или нумератор».
Что означает Номинация? 18 июня 2018 г. Номинант лицо, подающее заявку на рассмотрение.
Номинантом является организация, которая была представлена для рассмотрения на получение награды.
Что такое дробная математика?
дробь, В арифметике, число, выраженное как частное, в котором числитель делится на знаменатель. В простой дроби оба являются целыми числами. У сложной дроби в числителе или знаменателе есть дробь. В правильной дроби числитель меньше знаменателя.
Как умножать дроби?
Есть 3 простых шага для умножения дробей
- Умножьте верхние числа (числители).
- Умножьте нижние числа (знаменатели).
- При необходимости упростите дробь.
Зачем нужны общие знаменатели? Для того, чтобы сложить или вычесть одну дробь из другой, они должны иметь общий знаменатель, или одинаковый знаменатель. Это потому что это невозможно сложить две дроби, имеющие разное количество частей.
ЖК-калькулятор — вычислить наименьший общий знаменатель
Пусть этот бесплатный ЖК-калькулятор найдет наименьший общий знаменатель для каждой комбинации дробей. Наиболее важной целью этого калькулятора с наименьшим общим знаменателем является облегчение выполнения арифметических операций с дробями на ЖК-дисплее.
Достаточно! Рассмотрим вкратце понятие наименьшего общего знаменателя.
Что такое наименьший общий знаменатель?
«Наименьшее число, которое можно считать общим знаменателем для пары или более дробей, называется LCD».
По сути, общий знаменатель на самом деле является кратным знаменателя каждой дроби в наборе. Бесплатный ЖК-калькулятор ищет это общее число и отображает его на экране за считанные секунды.
Как найти ЖК-дисплей целых чисел, дробей или смешанных чисел?
Наименьший знаменатель — это второе имя, используемое для наименьшего общего кратного, которое можно найти с помощью различных методов.
Кроме того, мы обсудим сводку всех методов через пару шагов ниже:
- Прежде всего, вам нужно преобразовать все целые числа и смешанные числа в неправильные дроби
- После этого определите наименьший общий знаменатель всех дробей
- В конце запишите все полученные дроби, используя LCD в качестве знаменателя all
Бесплатный ЖК-калькулятор также следует всем вышеупомянутым условиям, чтобы найти общий знаменатель.
ЖК-таблица:
Здесь у нас есть таблица, которая показывает наименьшие общие знаменатели для различных комбинаций дробей:
Дроби | ЖК-дисплей |
| 1/2, 1/4 | 4 |
1/2, 1/3 | 6 |
| 2/3, 5/9 | 9 |
2/3, 4/9, 5/6 | 18 |
| 2/3, 3/4, 4/5 | 60 |
2/3, 4/5 | 15 |
| 2/3, 1 | 3 |
2/3, 3/5, 4/7 | 105 |
| 2/3, 2 | 3 |
2/3, 6/7 | 21 |
| 3/4, 6/7, 9/8 | 56 |
3/2, 5/4 | 4 |
3/4, 1/2 | 4 |
3/4, 5/6 | 12 |
| 3/6, 2/12 | 12 |
4/5, 2/3, 5/7 | 105 |
| 4/5, 5/6, 7/15 | 30 |
4/3, 8/9, 3/5 | 45 |
| 5/6, 15/8 | 24 |
5/2, 8/9, 11/14 | 126 |
| 5/9, 4/15, 1/45 | 45 |
6/5, 8/25 | 25 |
| 6/8, 4/32 | 32 |
8/9, 10/27, 16/81 | 81 |
| 8/51, 19/85 | 255 |
9/2, 3, 9/4 | 4 |
| 9/14, 3/7 | 14 |
Вы можете выбрать любой набор дробей из приведенной выше таблицы и проверить результаты с помощью нашего бесплатного ЖК-калькулятора.
Как численно найти наименьший общий знаменатель?
Что вы думаете о том, чтобы решить пару примеров, чтобы вспомнить вашу концепцию? Давай сделаем это вместе!
Пример #01:
Как найти ЖКИ для следующего набора дробей:
3, 1 2/3, 4/5, 5/8
Решение:
Здесь имеем
3 = 3/1
1 2/3 = 5/3
Теперь возьмем все знаменатели и найдем их ЖК следующим образом:
1, 3, 5, 8
LCD = 120
эквивалентные фракции с LCD:
3 = 3 * 120/120 = 360/120
1 2/3 = 1 2/1/2/2/260/120
1 2/3 = 1 2/1/ 3 * 40/40 = 200/1204/5 = 4/5 *24/24 = 96/120
5/8 = 5/8 * 15/15 = 75/120
3
3 Итак, мы имеем: Эквивалентные дроби = 360/120, 200/120, 96/120, 75/120
Вы также можете запустить этот бесплатный калькулятор наименьшего общего знаменателя, чтобы проверить подлинность результатов.
Пример #02:
Вам дана следующая комбинация дробей:
3/5, 6/3, 6/2, 3/9, 4
Как найти наименьший общий знаменатель для этого ЖК-дисплея сочетание дробей.
Решение:
Здесь:
4 = 4/1
Здесь мы имеем знаменатели следующим образом:
5, 3, 2,
Фракция Общая деноминатор = 90
Эквивалентные дроби с ЖК-дисплеем:
3/5 = 3/5 * 18/18 = 54/90
6/3 = 6/3 * 30/30 = 180/90
6/2 = 6/2 * 45 /45 = 270/90
3/9 = 3/9 * 10/10 = 30/90
4 = 4/1 * 90/90 = 360/90
Итак, имеем:
Эквивалентные дроби = 54/90, 180/90, 270/90, 30/90, 360/90
Как работает ЖК-калькулятор?
Этот калькулятор наименьшего общего знаменателя учитывает целые числа, дроби или смешанные числа для определения наименьшего общего положительного целого числа. Давайте посмотрим на его работу!
Ввод:
- Запишите числа, смешанные числа или дроби в специальном поле
- Убедитесь, что вы разделяете все числа или дроби запятыми
- После того, как вы закончите, нажмите кнопку расчета
Вывод:
Бесплатный определитель общего знаменателя находит:
- Наименьший общий знаменатель предоставленного набора дробей
- Эквивалентные дроби с одинаковым ЖК-дисплеем
Часто задаваемые вопросы:
Какой наименьший общий знаменатель у чисел 3/8, 9/2 и 8/5?
Наименьший общий знаменатель для данных дробей равен 40, что вы также можете перепроверить с помощью ЖК-калькулятора.
Какой общий знаменатель у приведенных ниже дробей:
-2/7, 9/9, -4 7/3 ДЦП для данной комбинации дробей равен 63.
Есть ли разница между НЦМ и ДЦП ?
Да, конечно! Вы можете рассматривать LCD как частный случай LCM. LCD — это LCM, но это верно для знаменателей дробей.
Что вы подразумеваете под общим числителем?
Частное число, которое на самом деле кратно всем числителям дробей, входящих в набор, называется их общим числителем.
Как бы вы сравнили дроби с разными знаменателями?
Если у нас есть дроби с разными знаменателями, то единственный способ их сравнить — вычислить их ЖКД. Более того, самый быстрый способ сравнить их — использовать онлайн-калькулятор наименьшего общего знаменателя.
Какой общий знаменатель у дробей 9/7 и 2/7?
Так как это дроби с общими знаменателями, то их ЛП тоже будет 7.
Как распознать меньшую или большую дробь с одинаковыми числителями?
Предположим, что у вас есть пара дробей с одинаковыми числителями, всегда помните, что дробь с большим знаменателем считается меньшей. С другой стороны, больше та дробь, у которой знаменатель меньше.
Какие дроби имеют разные знаменатели?
Дроби, имеющие разные знаменатели, называются неодинаковыми.
Какая самая маленькая положительная дробь в мире?
10/60 — самая маленькая дробь в мире. Это связано с тем, что 10/60 = 1/6 = 0,16666…
Вывод:
Основное внимание при определении LCD уделяется упрощению сложения, вычитания, умножения и деления дробей. Вот почему наш лучший ЖК-калькулятор — это самый быстрый и надежный способ найти наименьший общий знаменатель набора дробей. Это поможет вам решить проблемы дроби более достоверно.
Ссылки:
Из источника Википедии: Описание, Роль в арифметике и алгебре, Практическое использование
Из источника Академии Хана: Наименьшее общее кратное, повторяющиеся множители , Метод простых множителей
Наименьший (наименьший) общий знаменатель – определение, примеры и диаграммы
Определение
Наименьший или наименьший общий знаменатель (НОД) – это наименьший из всех общих знаменателей данных дробей.
В дробях ${\dfrac{3}{7}}$, ${\dfrac{5}{7}}$ и ${\dfrac{6}{7}}$ общий знаменатель равен 7.
Почему нам нужно найти общий знаменатель?
Нам нужно найти общий знаменатель, потому что мы не можем складывать или вычитать дроби с разными знаменателями.
В поисках общего знаменателя Но 24 кусочков слишком много. Можем ли мы иметь управляемое количество срезов?
Нахождение наименьшего общего знаменателя Да, можем. Вот где мы вычисляем ЖК-дисплей .
Как найти наименьший общий знаменатель
Чтобы найти НКО, мы вычисляем наименьшее общее кратное (НОК) знаменателей дробей с разными знаменателями (в отличие от дробей).
Рассматривая приведенный выше пример пиццы, мы увидим, как мы находим ЖК-дисплей.
Наименьший общий знаменатель Нахождение ЖК с наибольшим общим делителем
Теперь давайте вычислим наименьший общий знаменатель чисел 6, 8 и 15.
Мы найдем НОК трех чисел: 6, 8 и 15.
Это 120.
Например, при сложении ${\dfrac{4}{9}}$ и ${\dfrac{5}{12}}$ нам нужно найти наибольший общий делитель (НОД) 9 и 12, то есть 3.
Мы можем сделать это двумя способами:
- Либо умножить знаменатели и разделить на GCF, т. е. 9 × 12 = 108, 108 ÷ 3 = 36
- Или, делим один из знаменателей на GCF, а затем умножаем результат на другой знаменатель, т. е. 9 ÷ 3 = 3, 3 × 12 = 36.
Следовательно, LCD = 36
Теперь переименуем дроби. Вот как мы это делаем:
- Делим LCD на один знаменатель. т. е. 36 ÷ 9 = 4,
- После шага 1, 36 ÷ 12 = 3,
- Добавление переименованных дробей:
- ${\dfrac{4}{9}\times \dfrac{4}{4}+ \dfrac{5}{12}\times \dfrac{3}{3}}$
${=\dfrac{16}{36}+\dfrac{15}{36}}$
${= \dfrac{16+15}{36}}$
${=\dfrac{31}{36}}$
${\следовательно \dfrac{4}{9}+\dfrac{5}{12} =\dfrac{31}{36}}$
Когда знаменатели уравняли, нам было легко сложить две разные дроби.
Теперь давайте вычтем 2 указанные выше дроби:
${\dfrac{4}{9}-\dfrac{5}{12}}$
${\dfrac{4}{9}\times \dfrac{ 4}{4}-\dfrac{5}{12}\times \dfrac{3}{3}}$
${=\dfrac{16}{36}-\dfrac{15}{36}}$
${=\dfrac{16-15}{36}}$
${=\dfrac{1}{36}}$
${\следовательно \dfrac{4}{9}-\dfrac{5}{ 12}=\dfrac{1}{36}}$
Решенные примеры
Найдите наименьший общий знаменатель чисел 12, 15 и 18.
Вам дана следующая комбинация дробей:
Здесь:
Давайте посмотрим на его работу!
LCD — это LCM, но это верно для знаменателей дробей.
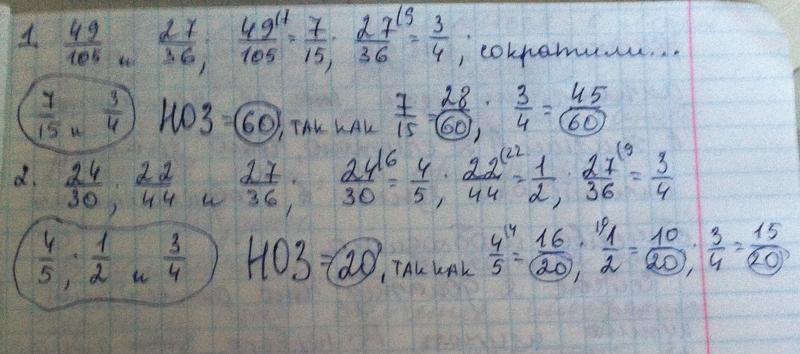
${\dfrac{4}{9}\times \dfrac{ 4}{4}-\dfrac{5}{12}\times \dfrac{3}{3}}$
${=\dfrac{16}{36}-\dfrac{15}{36}}$
${=\dfrac{1}{36}}$
${\следовательно \dfrac{4}{9}-\dfrac{5}{ 12}=\dfrac{1}{36}}$
Найдите наименьший общий знаменатель чисел 12, 15 и 18.