Математика сравнение: Сравнение, в математике | это… Что такое Сравнение, в математике?

Урок 4. сравнение натуральных чисел — Математика — 5 класс

Математика

5 класс

Урок № 4

Сравнение натуральных чисел

Перечень вопросов, рассматриваемых в теме:

— сравнение натуральных чисел;

— упорядочивание натуральных чисел;

— знаки сравнения чисел.

Тезаурус

Числа можно сравнивать при помощи натурального ряда.

Натуральный ряд – последовательность всех натуральных чисел, расположенных в порядке возрастания.

Число, которое больше нуля, называют положительным.

Обязательная литература

1. Никольский С. М. Математика: 5 класс. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 2017. – 272 с.
2. Потапов М. К. Математика. Книга для учителя. 5-6 классы. // М. К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.

Дополнительная литература

1. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с.
2. Потапов М. К. Математика: дидактические материалы. 6 класс. // М. К. Потапов, А. В. Шевкин – М.: Просвещение, 2010.- 118 с.
3. Чесноков А. С. Дидактические материалы по математике 5 класс. // А. С. Чесноков, К. И. Нешков. – М.: Академкнига, 2014.- 124 с.

Теоретический материал для самостоятельного изучения

Числа можно сравнивать при помощи натурального ряда.

Вспомним, что называют натуральным рядом.

Натуральные числа 1, 2, 3, 4 и так далее, записанные в порядке возрастания и без пропусков, образуют натуральный ряд, или ряд натуральных чисел.

Из двух натуральных чисел больше то, которое в ряду натуральных чисел стоит правее (дальше от начала).

Рассмотри пример. Сравним числа:

1) 7 и 4,

7 > 4, так как в ряду натуральных чисел 7 стоит правее, чем 4.

2) 6 и 2;

6 > 2, так как в ряду натуральных чисел 6 стоит правее, чем 2.

Натуральные числа можно сравнивать по их десятичной записи.

Из двух натуральных чисел больше то, у которого разрядов больше.

Например, сравним числа 2002 и 898.

2002 > 898, так как число 2002 содержит разрядов больше, чем число 898.

Из двух натуральных чисел с одинаковым числом разрядов больше то, у которого больше первая (если читать слева направо) из неодинаковых цифр.

Например, сравним числа 3821 и 3819.

3821 > 3819, потому что у них одинаковое число разрядов, цифры четвёртых и третьих разрядов одинаковые, а цифры второго разряда у них разные: у первого числа больше, чем у второго.

Два натуральных числа равны, если у них одинаковое число разрядов и цифры одинаковых разрядов равны.

Сравним числа: 47 834 567 362 и 47 834 567 362.

47 834 567 362 = 47 834 567 362, так как у них одинаковое число разрядов и цифры одинаковых разрядов равны.

Числа иногда удобно обозначать буквами латинского алфавита.

Если число а больше числа b, то пишут а > b и говорят: «а больше b», или пишут b < а и говорят: «b меньше а».

Если а, b, с – натуральные числа и число b в ряду натуральных чисел находится правее числа а, а число с находится правее числа b, то из этого следует, что число с находится правее числа а, то есть из а < b и b < с следует, что а < с.

В таких случаях пишут а < b < с (двойное неравенство) и говорят: «b больше а, но меньше с».

Если числа а и b равны, то пишут а = b.

Вообще, равенство а = b означает, что а = b одно и то же число.

Каждое натуральное число а больше нуля; это записывают так: а > 0.

Число, которое больше нуля, называют положительным.

Поэтому натуральные числа называют ещё целыми положительными числами. Число нуль также целое, но не положительное.

Натуральные числа и число нуль называют ещё целыми неотрицательными числами, так как, кроме неотрицательных чисел, есть ещё и отрицательные числа. Они будут изучаться в дальнейшем.

Если к ряду натуральных чисел приписать слева число 0, то получится ряд неотрицательных целых чисел: 0, 1, 2, 3, 4…

Разбор решения заданий тренировочного модуля

№ 1. На числовом луче подпишите натуральные числа, которые удовлетворяют неравенству b < 5.

Решение: так как нам задано неравенство b < 5, то нам подойдут все натуральные числа, которые находятся левее числа 5, а это 1, 2, 3, 4. Запишем их на числовой прямой:

№ 2. Расставьте числа по возрастанию: 8, 87, 9, 231, 14, 17.

Решение: расставить числа по возрастанию – это значит записать, начиная с самого маленького числа. В данном случае у нас самое маленькое число – 8, после него будет 9, затем 14, и так далее, до самого большого – 231.

Ответ: 8, 9, 14, 17, 87, 231.

Как правильно сравнивать дроби?

Сравнение дробей с одинаковыми знаменателями

Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби. 

Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:

Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.

А теперь на примерах.

Пример 1. Сравните дроби:

• Мы видим, что знаменатели дробей — равны. Значит сравниваем числители:
  8 < 12
  12 > 8
• Это значит, что < Изи!

Пример 2. Сравните дроби:

• Как и в прошлом примере, знаменатели дробей — равны. Сравниваем числители:
  9  > 10
  1 < 10
• Это значит, что >

Пример 3. Сравните дроби:

• Знаменатели дробей снова равны. Сравниваем числители:
  3  > 1
  1 < 3
• Это значит, что >

Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший числитель. 

Давайте разберем наглядный пример сравнения дробей. Еще больше наглядных примеров — на курсах по математике в онлайн-школе Skysmart!

Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.
 

• Запишем в виде дробей: и
• А теперь сравним полученные дроби: знаменатели — равны, сравниваем числители:
  6  > 5
  5 < 6.
• Это значит, что >

Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей.

Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Сравнение дробей с одинаковыми числителями

Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями. 

Запомните правило:

Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.

А теперь наши любимые примеры. Погнали!

Пример 1. Сравните дроби:

• У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
  9  > 7
  7 < 9
• Значит, дробь с меньшим знаменателем — больше:
  

Пример 2. Сравните дроби:

• У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
  10  < 11
  11 > 10
• Значит дробь с меньшим знаменателем — больше:
  

Пример 3. Сравните дроби:

• У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
  6  > 3
  3 < 6
• Значит, дробь с меньшим знаменателем — больше.
  

Для наглядности представим ситуацию, в которой вам предстоит разделить торт между тремя друзьями. Это значит, что 6 кусков торта равномерно распределяются по 3 людям: каждому достается 6:3 = 2 по 2 кусочка. 

А теперь представим более приятную ситуацию: кусков торта по-прежнему 6, а друзей уже только 2. Тогда каждому достанется по 3 вкуснейших кусочка:

Как видите, сравнение дробей может вам пригодиться в самых неожиданных ситуациях. Теперь, когда снова придется хорошенько задуматься о соотношении кусков торта и приглашенных гостях, изученная тема поможет вам принять верное решение😉.

 

Сравнение дробей с разными числителями и разными знаменателями

Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.

Запоминаем

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю, а затем сравнить числители.

Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.

• Нужно подобрать число, которое будет делиться на 7 и на 2, например, 14. Проверим:
  14:7 = 2
  14 : 2 = 7
• Первую дробь умножаем на дополнительный множитель 2:
  
• Вторую дробь умножаем на дополнительный множитель 7:
  
• Дроби приведены к общему знаменателю:
  

Давайте потренируемся в сравнении дробей. 

Пример 1. Сравните дроби:

• Приведем дроби к общему знаменателю. 30 делится на 15 и на 2.
  30 : 15 = 2
  30 : 2 = 15
• Первую дробь умножаем на дополнительный множитель 2:
  
• Вторую дробь умножаем на дополнительный множитель 15:
  
• Дроби приведены к общему знаменателю:
  
• Если две дроби имеют одинаковые знаменатели, то, согласно правилу, больше та дробь, чей числитель больше:
  

При сравнении неправильных дробей с правильными помните, что неправильная дробь всегда больше правильной.

Пример 2: Сравните дроби:

• 6/5 — неправильная дробь. 
• Выделим целую часть:
• Значит, что

Учёба без слёз (бесплатный гайд для родителей)

Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.

Вычитание смешанных чисел

Вычитание проходит гладко, когда уменьшаемое больше вычитаемого. 

• 12 — 7 = 6
  12 — уменьшаемое
  7 — вычитаемое
  5 — разность

В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы». 

При вычитании дробей действует тот же самый принцип: вычитаемое должно быть меньше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.

 

Пример 1. Вычислите:

Вычитаемая дробь меньше уменьшаемой

• Выполняем вычитание:

Пример 2.Найдите разность:

• Смешанные дроби превращаем в неправильные:
  
• Чтобы найти разность дробей с разными числителями и знаменателями, нужно привести их к общему знаменателю:
  
• Наименьшее общее кратное — 40
  40 : 8 = 5
  40 : 5 = 8
• Умножаем первую дробь на дополнительный множитель 5:
  
• Умножаем вторую дробь на дополнительный множитель 8:
  
• Дроби приведены к общему знаменателю:
  
  

Примеры для самопроверки

Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.

Пример 1. Сравните дроби:

Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что

Пример 2. Сравните дроби:

Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что

Пример 3. Сравните дроби:

Как решаем:

Ответ:.

• По правилу сравнения дробей с разными числителями и знаменателями, сначала нужно привести дроби к общему знаменателю:
  
• Наименьшее общее кратное — 15:
  15 : 15 = 1
  15 : 5 = 3
• Умножаем первую дробь на дополнительный множитель 1:
  
• Умножаем вторую дробь на дополнительный множитель 3:
  
• Дроби приведены к общему знаменателю:
  
• Сравниваем числители получившихся дробей: 3 < 6
  

Пример 4.

Найдите разность:

Как решаем:

• Смешанные дроби превращаем в неправильные:
  
• Чтобы найти разность дробей с разными числителями и знаменателями, нужно привести их к общему знаменателю.
  
• Наименьшее общее кратное — 42:
  42 : 7 = 6
  42 : 6 = 7
• Умножаем первую дробь на дополнительный множитель 6:
  
• Умножаем вторую дробь на дополнительный множитель 7:
  
• Дроби приведены к общему знаменателю.
  
• Теперь можно вычитать:
  

Ответ:

Математика Сравнение трехзначных чисел

Материалы к уроку

Конспект урока

38. Сравнение трехзначных чисел

Организационный этап   Добрый доктор Айболит! Он под деревом сидит. Приходи к нему лечиться И корова, и волчица, И жучок, и червячок, И медведица! Всех излечит, исцелит Добрый доктор Айболит!

Минутка чистописания   Сегодня мы поможем Айболиту лечить зверей. Сколько зверей пришло к доктору? Верно. 5 зверей. Пропишем это число в первой строчке. Используя данную цифру 3 раза, назовите трехзначное число. Число 555. Пропишем это число во второй строчке Назовите разрядные единицы числа 555. 5 сотен, 5 десятков, 5 единиц. Молодцы, вы справились с заданием.

Этап подготовки учащихся к активному сознательному усвоению знаний   Устный счёт   Вдруг откуда-то шакал На кобыле прискакал: «Вот вам телеграмма От Гиппопотама!» Чтобы прочитать телеграмму, нужно решить примеры. Запишите только ответы. 264 – 60 – 4 900 + 99 + 1 600 – 1 – 500 400 + 10 + 3 709 + 70 + 1 290 – 90 – 200 Проверьте себя. 200   1000   99   413   780   0   Можно прочитать телеграмму? «Приезжайте, доктор, В ……. скорей И спасите, доктор, Наших малышей!» Не хватает одного слова. Расставьте числа в порядке убывания. Какое слово получилось? Правильно. Получилось слово Африка, теперь мы можем прочитать телеграмму. «Приезжайте, доктор, В Африку скорей. И спасите, доктор, Наших малышей!» И сейчас же к нему из-за ёлки Выбегают мохнатые волки: «Садись, Айболит, верхом, Мы живо тебя довезем». Добираться будем на волках и разными путями. Давайте посмотрим, какой ряд доберётся до места быстрее. 7 · 6 + 100 – 2 – 40 5 · 9 + 200 – 100 – 45     6 · 8 + 300 – 8 – 140 Проверьте себя. 7 · 6 + 100 – 2 – 40 = 100 5 · 9 + 200 – 100 – 45 = 100  6 · 8 + 300 – 8 – 240 = 100   Молодцы!  Вы все успели вовремя добраться до места.

Работа над новым материалом   Кто помнит. Чем заболели зверята в Африке? И корь, и дифтерит у них, И оспа, и бронхит у них, И голова болит у них, И горлышко болит. Нужно помочь зверятам и приготовить лекарство. Устно сравните числа, тогда у нас появятся лекарства. 56 и 68……… 56 40 и 100……. 40 567 и 756……. 567  Какие числа нам было сравнить труднее? Верно, 567 и 756. Как вы думаете, почему? Такие числа ранее мы не сравнивали. Сегодня на уроке мы будем учиться сравнивать трехзначные числа. Чтобы правильно сравнивать трехзначные числа, нужно вывести алгоритм сравнения трёхзначных чисел: Начинаем сравнивать с наивысшего разряда, с сотен. Определим, в каком числе больше сотен. Если их количество равно, переходим к следующему разряду. Сравним количество десятков, если их количество равно, переходим к единицам. Сравниваем единицы. Сравните 557 и 776 Сравниваем сотни. 5 сотен меньше 7 сотен, значит 557 меньше 756 Сравните 567 и 542   Количество сотен одинаковое, сравниваем десятки, 6 десятков больше 4 десятков, значит 567 больше 542   Сравните 565 и 563 Сравниваем сотни. Сотен в обоих числах одинаково. Сравниваем десятки. Количество десятков в обоих числах одинаково. Сравниваем единицы: 5 ед. больше 3 ед. Значит 565 больше 563

Закрепление материала   Давайте повторим алгоритм сравнения трехзначных чисел. Начинаем сравнивать с наивысшего разряда, с сотен. Определим, в каком числе больше сотен. Если их количество равно, переходим к следующему разряду. Сравним количество десятков, если их количество равно, переходим к единицам. Сравниваем единицы.   Используя алгоритм сравнения чисел, сравните. 870 и 780 678 и 648 850 и 852 202 и 220 315 и 305 677 и 767 Проверьте себя. 870>780 678>648 850 202 315>305 677 Молодцы, вы правильно сравнили числа. Теперь мы сможем изготовить лекарство для бедных и больных зверят.

И бежит Айболит к бегемотикам, И хлопает их по животикам, И к полосатым Бежит он тигрятам, И к бедным горбатым Больным верблюжатам. Вы готовы изготовить лекарство для зверят?   Решите задачу. Для лечения больных зверей необходимо приготовить 15 кг лекарств и в 5 раз больше витаминов. На сколько больше потребуется витаминов, чем лекарств. Решите задачу. Давайте проверим. 1)15 · 5 = 75 (кг) — витаминов необходимо приготовить 2) 75 — 15 = 60 (кг) — больше. Ответ: на 60 кг больше потребуется витаминов, чем лекарств.

Молодцы! Вы помогли изготовить лекарства и витамины для зверят. Десять ночей Айболит Не ест и не пьет, и не спит, Десять ночей подряд Он лечит несчастных зверят, И ставит, и ставит им градусники. Давайте поможем теперь вылечить зверят. Решите уравнения. Х+40=120 Х-40=120 Х·40=120 Х:4=120 Проверим, кто из вас помог доктору Айболиту. Х+40=120 Х=120-40 Х=80 Проверка. 80+40=120 120=120   Х-40=120 Х=120+40 Х=160 Проверка. 160-40=120 120=120   Х·40=120 Х=120:40 Х=3 Проверка. 3·40=120 120=120   Х:4=120 Х=120·4 Х=480 Проверка. 480:4=120 120=120   Вот и вылечил Айболит, Лимпопо! Вот и вылечил больных, Лимпопо! И пошли они смеяться, Лимпопо! И плясать, и баловаться, Лимпопо!

Этап подведения итогов   Нам пора заканчивать урок. Давайте повторим алгоритм сравнения трехзначных чисел. Начинаем сравнивать с наивысшего разряда, с сотен. Определим, в каком числе больше сотен. Если их количество равно, переходим к следующему разряду. Сравним количество десятков, если их количество равно, переходим к единицам. Сравниваем единицы.

Рефлексия   Ребята, если вам всё понятно, нарисуйте звёздочку красного цвета, если понятно, но не совсем, то звёздочка синего цвета, а если не понятно ничего – ваша звёздочка – жёлтая.

 

                                     

 

 

 

 

Остались вопросы по теме? Наши репетиторы готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитора

Сравнение A Level и ЕГЭ

Сравнение A Level и ЕГЭ по математике.

Форматы, полезность, сложность, признание

В этой статье Вы найдете сравнение программ, стилей задач, формата нашего «профильный ЕГЭ по математике» и выпускного экзамена по математике в программе A Level (обычный «A Level Mathematics», не «Further Mathematics»).

Под егэ по математике в моем разборе имеется ввиду только профильный уровень, так как базовое егэ – фактически второй огэ, который просто не сравним с современным экзаменом за старшую школу.

Содержание:

• формат экзамена
• сравнение задач
• признание экзаменов
• выводы
• лирическое

Форматы экзаменов

Старшекласник должен изучить следующие модули математики:

• Pure Mathematics
• Staticstics
• Mechanics

В отличии от программы ЕГЭ, математика в A Level разбита на модули. В зависимости от школы, необходимо сдать 3 – 6 экзаменов. Какие именно экзамены выбрать? Зависит от вступительных пожаланий будущего Университета. К такому количеству экзаменов реально подготовиться, так как старшеклассники изучают всего 4 школьные дисциплины.

Три главных различия в форматах проведения:

• Экзамены A Level (не только по математики) проводятся 2 раза в году: ноябрь и Май. Иногда еще есть январская сессия (для Edexcel exam boad).
• Пересдавать можно любые оценки. Даже если Вы сдали на A, а лучший Универ требует результата A*, и у Вас еще есть время, то можно пересдать A на A*. Увы, в ЕГЭ можно пересдать только двойку в текущем году.
• Необходимо использовать калькулятор. Встречаются задачи, где надо считать синусы/косинусы от неудобных углов, оценивать свойства статистических распределений, дисперсии, сочетания (в комбинаторике).

Темы в A Level, которых нет в ЕГЭ

• Численные методы
• Распределения непрерывных и дискретных случайных величин
• Приложение производных (в экономике и физике)
• Функции двух переменных
• Интегрирование по частям
• Бином Ньютона
• Комбинаторика
• Статистика (корреляция, построение гипотез)
• Числовые ряды и дифференциальные уравнения
• Теория графов*
• Основы теории групп*
• Модулярная арифметика*
• Комплексные числа*

* данные темы изучаются только в Further Mathematics

Олимпиадные темы

В A level узкоспециальные (и некоторые олимпиадные) темы выделяются в отдельный раздел Further mathematics, а не смешиваются с общим экзаменом. Further mathematics — это раздел для 1) выпускников, кто любит математику и станет математиком; 2) для тех, кому математика потребуется в качестве основного инструмента.

Итак, сравним некоторые задачи. Это аналоги нашего ЕГЭ с первым (самым простым экзаменом по метаматике (Unit 1, Paper1, PM1 — может называться по-разному).

Задачи по геометрии:

на сектора в окружностях:

логарифмы нужны везде!

Интегралы у нас довольно простые. На A Level они есть в каждом экзамене!

Задачи на моделирование тоже есть везде.

И прогресии.

Внимание! Несмотря на угрожающую (с виду) формулировку задач, их решение доступно для освоения. Никаких сверхъестественных способностей не требуется. Помимо математики, Вы должны изучить в старших классах всего лишь еще 3 дисциплины, а не 10, как у нас. Не волнуйтесь! 🙂

Теперь посмотрим вторые экзамены.

A Level, CIE Paper 2 June 2016

A Level, CIE Paper 2 June 2016

Некоторые задачи с третьего экзамена. Вот, например, дифференциальные уравнения. Как у нас, на 2 (ну иногда на 1 курсе)

OCR Pure Mathematics and Mechanics, June 2018 Статистика:

A Level Mathematics, Pure Mathematics and Statistics, June 2018 Механика:

А есть ли в нашем ЕГЭ задачи, недоступные выпускнику английской школы?

Да, такие задачи есть. Например, задачи 15, 16, 18, 19:

Они стоят несколько в стороне от современных приложений математики. Они, фактически, для будущих математиков. Да, аналоги таких задачек в качестве подзадачи могут понадобиться и астрофизику и конструктору. А могут и не понадобиться. Но, когда его «препрет» научная необходимость, он сможет изучить эти темы за пару часов.

Признание результатов экзаменов A Level и ЕГЭ

Английская система школьного образования уважаема во всем мире. Диплом выпускника A Level высоко ценится в европейских и американских Университетах (правда, в Америке некоторые Универы просят сдать AP или SAT). Результаты экзамена по математике засчитывают все топовые европейские Университеты. Наш eгэ признается за рубежом только в республике Бeларусь.

Также есть возможность конвертировать наш аттестат (за 11 класс) в сертификат IGCSE. С этим документов можно поступать в профессиональный учебные заведения Англии (например, летная школа, музыкальное училище, технические училища).

А что делать тем, у кого есть результаты ЕГЭ (почти 100 баллов), но хотят учиться в Англии? Сдавать вступительные экзамены.

Выводы

Основное отличие – это модульность. Ученик старших классов A Level школы выбирает те разделы математики, которые нужны ему для дальнейшей учебы. Следствием этого является то, что в Университет он уже приходит прекрасно подготовленным и быстрее сможет освоить современные разделы знаний. Наши же студенты начинают изучать высшую математику только с первого курса и с нуля.

Сможет ли наше математическое образование стать таким же современным в ближайшее время?

Нет, так как необходимо в короткие сроки:

• Объяснить учителям новые темы, которые они, скорее всего, даже не изучали в педвузах или изучали один семестр. Это темы по механике, статистике и дискретной математике.
• Для школьных учителей должны быть созданы условия и появиться мотивация изучить и понять эти сложные разделы.
• Миллиардные затраты: аренда помещений для лекций и семинаров, оплата труда преподавателей, которые будут проводить повышение квалификации, проверка знаний, оплата дополнительных часов тех же учителей.
• Для создания задач к современному экзамену надо привлечь большое количество профессионалов. Многие задачи в ЕГЭ довольно просты и генерируются на компьютерах (кроме задач из 2 части). Также нужно подготовить экспертов, которые проверяют и оценивают работы.

Лирическое

Вопрос: Но ведь несмотря на это, почему же российские математики считаются лучшими в мире?

Считаются одними из лучших в мире. Лучшие наши математики лучше лучших западных (хотя многие из наших сверхматематиков работают на Западе).

Но средний западный старшеклассник и студент Университета знает математику лучше среднего нашего. Хотя бы потому, что программа у него была шире. И выпускник западного Универа обычно более компетентен в инженерных и экономических специальностях.

К сожалению, наши сборные по математике в последнее десятилетие редко поднимались на пьедестал международной олимпиады:

(источники: ru.wikipedia.org/wiki/Международная математическая олимпиада или www.imo-official.org/)

Это, видимо, о чем-то говорит.

Сравнение (I)GSCE и ЕГЭ

A Level Further Mathematics

A Level школы России

Предметы, изучаемые в A Level

6 класс. Математика. Сравнение чисел — Сравнение чисел

Комментарии преподавателя

По­ло­жи­тель­ные числа мы ис­поль­зу­ем для обо­зна­че­ния раз­ных ко­ли­честв – целых и дроб­ных. На­при­мер, три яб­ло­ка, пол­то­ра литра мо­ло­ка.

От­ри­ца­тель­ных ко­ли­честв не су­ще­ству­ет. От­ри­ца­тель­ные числа – это ин­стру­мент для упро­ще­ния рас­че­тов.

На­при­мер, таких:

Ключ имеет одну функ­цию – от­кры­вать или за­кры­вать замок. Если нет замка, то ключ прак­ти­че­ски бес­по­ле­зен, ему труд­но найти при­ме­не­ние.

Так и от­ри­ца­тель­ные числа – без са­мо­го «замка», без раз­лич­ных ма­те­ма­ти­че­ских рас­че­тов они ис­поль­зу­ют­ся не очень много.

Тем не менее есть и пря­мое при­ме­не­ние от­ри­ца­тель­ным чис­лам. Вы мо­же­те прой­ти по ссыл­ке, где мы об­суж­да­ем ис­поль­зо­ва­ние от­ри­ца­тель­ных чисел в окру­жа­ю­щем мире.

Как мы по­ни­ма­ли, что одно по­ло­жи­тель­ное число боль­ше дру­го­го?

Из 8 яблок можно взять 5 яблок. 5 – это часть вось­ми. По­это­му мы с вами и знаем, что 5 мень­ше 8.

Но про числа -8 и -5 нель­зя ска­зать, что одно – часть дру­го­го. От­ри­ца­тель­но­го ко­ли­че­ства не су­ще­ству­ет.

Но что же такое тогда от­ри­ца­тель­ное число?

От­ри­ца­тель­ное число – это и число, и знак вы­чи­та­ния.

Что зна­чит к 10 до­ба­вить -8?

Это зна­чит вы­честь 8.

А до­ба­вить -5 – озна­ча­ет вы­честь 5.

Мы к од­но­му и тому же числу 10 до­ба­ви­ли два раз­ных от­ри­ца­тель­ных. Во вто­ром слу­чае ре­зуль­тат был боль­ше. Есте­ствен­но счи­тать, что вто­рое от­ри­ца­тель­ное число было боль­ше.

То есть чем боль­шее число мы вы­чи­та­ем, тем мень­ше будет ре­зуль­тат. Это оче­вид­но, но если это за­пи­сать на языке от­ри­ца­тель­ных чисел, то мы и по­лу­чим пра­ви­ла их срав­не­ния.

Сфор­му­ли­ру­ем те­перь пра­ви­ла, как срав­ни­вать от­ри­ца­тель­ные числа друг с дру­гом или с по­ло­жи­тель­ны­ми.

1. Все от­ри­ца­тель­ные числа мень­ше всех по­ло­жи­тель­ных. Между ними на­хо­дит­ся ноль. То есть ноль мень­ше лю­бо­го по­ло­жи­тель­но­го числа, но боль­ше лю­бо­го от­ри­ца­тель­но­го.

По­че­му это так?

Если мы к числу при­бав­ля­ем по­ло­жи­тель­ное число, то число уве­ли­чит­ся; если ноль, то не из­ме­нит­ся; если вы­чтем по­ло­жи­тель­ное, то число умень­шит­ся. Но до­бав­ле­ние от­ри­ца­тель­но­го числа и озна­ча­ет вы­чи­та­ние.

2. Чем боль­ше по­ло­жи­тель­ное число, тем мень­ше про­ти­во­по­лож­ное ему от­ри­ца­тель­ное число.

На­при­мер, , по­это­му .

Это и по­нят­но, ведь если от­нять 20, то ре­зуль­тат будет мень­ше, чем если от­нять 10.

Если у числа не об­ра­щать вни­ма­ния на знак, то по­лу­ча­ю­ще­е­ся число мы на­зы­ва­ем мо­ду­лем.

У числа -23 и у 23 оди­на­ко­вые мо­ду­ли, 23.

Тогда про от­ри­ца­тель­ные числа можно ска­зать и так.

Из двух от­ри­ца­тель­ных чисел мень­ше то, у ко­то­ро­го боль­ше мо­дуль.

Вер­нем­ся к такой функ­ции чисел, как по­ря­док.

Когда мы едем по до­ро­ге, то через рав­ные про­ме­жут­ки нам встре­ча­ют­ся ки­ло­мет­ро­вые стол­бы с обо­зна­че­ни­ем прой­ден­но­го рас­сто­я­ния. В ма­те­ма­ти­ке мы сде­ла­ли ана­лог такой до­ро­ги – чис­ло­вой луч. Числа на луче со­от­вет­ству­ют точ­кам, и на­о­бо­рот.

«Одно число боль­ше дру­го­го» те­перь озна­ча­ет, что «одна точка пра­вее дру­гой». Чем пра­вее точка, тем боль­ше со­от­вет­ству­ю­щее ей число, мы это число на­зы­ва­ем ко­ор­ди­на­той (см. рис. 1).

Рис. 1. Чис­ло­вой луч

Те­перь, когда у нас есть от­ри­ца­тель­ные числа, мы можем рас­ши­рить нашу мо­дель. Вме­сто луча мы уже берем целую пря­мую и влево от нуля от­кла­ды­ва­ем от­ри­ца­тель­ные числа.

Пра­ви­ло «чем пра­вее точка, тем боль­ше число» со­хра­ня­ет­ся и для левой части пря­мой.

Точка с ко­ор­ди­на­той -5 пра­вее точки с ко­ор­ди­на­той -8. Это эк­ви­ва­лент­но тому, что .

Шкала улич­но­го тер­мо­мет­ра – при­мер, как такую чис­ло­вую пря­мую можно при­ме­нить в жизни (см. рис. 2).

Рис. 2. Тер­мо­метр

По­тре­ни­ру­ем­ся срав­ни­вать числа.

1.  25 641 и -25 642

Тут все про­сто: от­ри­ца­тель­ное число все­гда мень­ше по­ло­жи­тель­но­го.

2.  -25 641 и -25 642

Оба числа от­ри­ца­тель­ны. Зна­чит, нужно срав­нить их мо­ду­ли. У вто­ро­го числа мо­дуль боль­ше, зна­чит, само число мень­ше.

3. -75,47 и -75,53

4.  и 

Сна­ча­ла срав­ним мо­ду­ли этих чисел:

 и 

Раз­ло­жим на мно­жи­те­ли оба зна­ме­на­те­ля. Общий зна­ме­на­тель – это три трой­ки и одна пя­тер­ка. До­мно­жим у пер­вой дроби чис­ли­тель и зна­ме­на­тель на две трой­ки, а у вто­рой – на 5.

По­лу­ча­ем две дроби с оди­на­ко­вы­ми зна­ме­на­те­ля­ми. Счи­тать их не будем. Но чис­ли­тель пер­вой дроби боль­ше вто­ро­го.

Пер­вая дробь боль­ше.

Зна­чит:

И тогда:

Итак, под­ве­дем итог.

• От­ри­ца­тель­ные числа по­яв­ля­ют­ся как ин­стру­мент, упро­ща­ю­щий вы­чис­ле­ния.
• До­го­во­рен­ность про срав­не­ние этих чисел сле­ду­ю­щая:

1) Любое от­ри­ца­тель­ное число мень­ше лю­бо­го по­ло­жи­тель­но­го.

2) Ноль на­хо­дит­ся между всеми от­ри­ца­тель­ны­ми и всеми по­ло­жи­тель­ны­ми чис­ла­ми (боль­ше лю­бо­го от­ри­ца­тель­но­го и мень­ше лю­бо­го по­ло­жи­тель­но­го).

3) Из двух от­ри­ца­тель­ных чисел боль­ше то, у ко­то­ро­го мень­ше мо­дуль.

• Кроме того, что от­ри­ца­тель­ные числа упро­ща­ют вы­чис­ле­ния, в обыч­ной жизни им тоже нашли при­ме­не­ние.  На­при­мер, для упо­ря­до­чи­ва­ния, для обо­зна­че­ния тем­пе­ра­ту­ры по шкале Цель­сия, эта­жей ниже пер­во­го

источник конспекта — http://interneturok.ru/ru/school/matematika/6-klass/polozhitelnye-i-otricatelnye-chisla/sravnenie-chisel-2?seconds=0&chapter_id=1825

источник видео — http://www.youtube.com/watch?v=y2fR98kHaAM

источник презентации — http://5klass.net/zip/matematika/Sravnenie-chisel-6-klass.zip

Учеба в Studienkolleg в Германии. Сравнение математики в РФ и Германии / Хабр

Дисклеймер

Всё описанное здесь является лишь моей точкой зрения, основанной на проживании лишь в одной достаточно небольшой области восточной Германии.

Большую часть текста я хочу посвятить такому немецкому явлению как Studienkolleg, который принес мне больше негативных моментов, чем положительных. Также я затрону бытовые аспекты жизни в Германии, которые возможно будут вам интересны.

Studienkolleg — а по нашему Штудиенколлег

Что же такое Штудиенколлег?

Здесь я рекомендую прочесть самим, ибо инфы на эту тему в инете предостаточно, но все-таки дам очень краткое описание. В силу того, что обучение в российских школах (и насколько я знаю — в других странах СНГ тоже плюс-минус также) длится 11 лет, а в Германии 12 или 13, ребятам из стран СНГ надо проходить дополнительную школу в виде штудиенколлега.

В штудиенколлеге обычно 4 направления — T-Kurs (для поступления на технические специальности), W-Kurs (для экономических специальностей), G-Kurs (для гуманитариев), M-Kurs (в основном для медицинщиков и биологов). Учитесь год, у вас обычно 4-6 предметов, контрольные и так далее как обычно. В конце года сдаете главный экзамен. И на основании него поступаете в универ.

В моем штудиенколлеге был примерно такой же контингент

Почему штудиенколлег?

Как же я оказался в Штудиенколлеге?

Если кратко, то родители подталкивали меня к высшему образованию в Германии из-за потенциальной студенческой миграции в страну с лучшем уровнем жизни и возможности искать работу после Вуза в Германии на протяжении года. Я склонялся к образованию в России по причине хорошей технической и математической подготовки, на МИЭФе или Экономе Мгу, хотя также уже начинал думать, что программирование подойдет мне больше (ВМК МГУ или ИУ9 в бауманке). Но в итоге поехал в Германию. Перед поездкой сдал языковой экзамен и тест на способности (хотя я его таковым не считаю)(если интересно — TestDaF на 4544 и TestAS на (119/130)/(115/130) (инженерная часть)).

Дальше после ЕГЭ по профильной математике и русскому (практически не готовился, поэтому сдал на 86 и 91 соответственно), я с родителями поехал в Германию сдавать экзамены в выбранные Штудиенколлеги (Nordhausen, TU Berlin, Hannover, Muenchen, и тот, в котором в итоге учился (не называю, чтобы обойтись без имен)).

Поступил в итоге во все кроме Ганновера, где попал в лист ожидания из-за огромного количества абитуриентов.

Экзамены в Штудиенколлеги

Я сдавал экзамены на W-курс — математику и немецкий во всех штудиенколлегах кроме Мюнхена (там только немецкий). Немецкий был простой, в целом ничего интересного и сложного для знающего на уровень В2 язык человека.

А вот математика была интересной. Простейшие задания на уровень знания очень среднего российского школьника. Задания затрагивают немного пределы и интегралы, но на простейшем уровне. Во общем после экзаменов у меня сложилось неприятное подозрение насчет будущей учебы. Но в целом задания построены так, чтобы решить максимальное количество очень простых задач по планиметрии и алгебре 8 — 10 класса российской школы за ограниченное время. До сих пор не очень понимаю такую систему тестирования. Так что, если вы спокойно пишете пробники ЕГЭ даже на небольшие 80 баллов, вы уверенно сдадите эти тесты.

Да, я знаю, что есть штудиенколлеги, где дают более сложные задания (например Karlsruhe), но это все равно и близко не уровень сильного российского школьника с хорошей физмат базой.

Вот пример экзамена по математике в один из технических штудиенколлегов.

Первое впечатление

Большим плюсом оказалось наличие очень разных этносов. В моем классе учились ребята из Украины, Казахстана, Мексики, Колумбии, Венесуэлы, Китая, Вьетнама, Бразилии. Сразу стало заметно, что многие ребята из Латинской Америки даже не умеют решать квадратные или обычные линейные уравнения, что оказалось для меня сюрпризом. Но в целом группа была достаточно ровной, где лишь я и несколько ребят из стран СНГ достаточно сильно выделялись. Сразу скажу, это не бахвальство и я прекрасно знаю, что в России, Украине и Казахстане невероятно много студентов и школьников гораздо более умных, чем я. Но на контрасте с латиносами мы выглядели, как призеры Всероса по сравнению с обычными школьниками.

Люди

В целом ребята были очень дружелюбные и добрые, хоть и любящие выпить и весело отдохнуть. В целом никто не старался дополнительно учиться и в силу слабого материала большую часть времени люди либо ничего не делали, либо пили и отдыхали. По моему впечатлению, латиносы очень открыто относятся ко всем нациям и русские на самом деле на них достаточно похожи. Ребята из Китая и других Азиатских стран, наоборот, показались мне более закрытыми и не так легко идущими на контакт.

Учителя и администрация

Учителя немцы в целом произвели неплохое впечатление, кроме учителя немецкого, которая оказалась достаточно ярким последователем радикального феминизма и чрезмерно толерантных течений западного мира. С ней было действительно сложно найти общий язык и прийти к взаимопониманию. В принципе насколько я заметил, движение феминизма в Германии активно развито, хоть и не встречается на каждом шагу. Администрация тоже оставила приятные впечатления, прислушиваясь ко всем проблемам и нестандартным ситуациям.

Учеба

Это пожалуй будет самая длинная часть поста, потому что здесь мне есть много чем поделиться и попытаться понять, в чем же отличие нашей учебы от немецкой. Маленький дисклеймер: я учился на W-курсе, так как планировал поступать на бизнес-информатику (к счастью, не поступил). Поэтому у меня не было предметов по типу физики и химии, но я много общался с людьми с T-курса и примерно понимаю уровень и материал, который там давали.

Немецкий

В целом про этот предмет наверное не будет интересно читать пользователям Хабра, так что скажу кратко. В целом выглядит как урок английского в школе, изучение грамматики и разной более сложной лексики. В целом достаточно не сложно.

Английский

Так же очень легко, всякие грамматические тесты на уровень примерно B2 и презентации.

Sozialkunde

Обсуждение разной нынешней западной повестки, по типу загрязнения природы, равноправия между мужчинами и женщинами и улучшения прав однополых семей. Я бы не сказал, что нам навязывали какую то точку зрения, эти уроки скорее оставили впечатление жутко скучных занятий и непонимания, зачем это в принципе нужно.

Математика

Математика повторяла школьную программу 10-11 класса школы в РФ и немного затрагивала Вузовские темы. Немного затронули теорию множеств, но на очень поверхностном уровне. Дальше потратили много времени на изучение степеней, сокращения дробей и того, что такое логарифм (я серьезно). Дальше пошли уже многочлены и линейные уравнения (дали даже формулу бинома Ньютона, но не показали ее вывод и в целом не уделили ей практически никакого внимания). Дальше затронули немного системы уравнений и матрицы (в том числе формулу Крамера и RREF). Но поскольку не дали определения детерминанта, adjugate Matrix, инверсии, транспозиции, Вандермонда и много другого, оставалось немного странное впечатление. Дальше было немного пределов и интегралов, но на простом уровне (даже без Лопиталя).

Сразу скажу, что я спрашивал насчет математики другие курсы, и, например, на T-курсе математика была ненамного сложнее чем у нас, а там, по идее, готовят к поступлению на будущих инженеров и программистов. В целом, математика оставила максимально неприятное впечатление и на контрасте со своими знакомыми с 1 курса из ВШЭ и Бауманки (ИУ7), я чувствовал, что теряю время и потенциал изучать что-то полезное.

Примерно так выглядели задания на системы и матрицы

Итоги

Могу уверенно сказать, что 1 курс сильного экономического или технического направления в РФ окажется для вас гораздо более полезным занятием, пожалуй лишь за исключением отсутствия немецкого языка. В силу того, насколько я был разочарован в немецкой учебе — пришлось даже пить антидепрессанты, в конце года я вернулся в РФ и учусь сейчас в очень сильном российском ВУЗе на ПМИ (прикладная математика и информатика) — (да, на платке, чем я не горжусь, но даже так это выходит гораздо дешевле, чем жизнь в Германии, в силу того, что я москвич и мне не нужно платить здесь за квартиру).

Мой опыт обучения в штудиенколлеге оказался полезным с точки зрения понимания того, что экономика мне не интересна и я поступил на иную специальность уже в РФ, потеряв год в Германии (хотя он и дал мне очень многое). В момент учеба мне интересна и я с удовольствием учу C++, разную математику и в целом наслаждаюсь своей учебой всегда за исключением сессии.

Я буду рад вычитать в комментариях (если кто-то прокомментирует) ваше мнение на тему обучения и почитать opinions на тему такой слабой математики в Штудиенколлеге. Также мне будет интересно почитать про математику в вузах Германии на IT — специальностях. Мое мнение таково — если у вас есть возможность отучиться на Физтехе, Вышке, Бауманке, МГУ, ИТМО, СПбГУ, рекомендую это сделать, поскольку обучение в бакалавриате у вас будет длиться 4 года (а не 3, как в Германии) и вы успеете затронуть больше тем и более глубоко погрузиться в детали программирования или математики, чем в Германии. Ну и в целом IT-образование в России лично мне! больше нравится, чем в Германии. Если вы учитесь в других странах на IT-направлении, также можете поделиться своими впечатлениями от учебы там.

Если хотя бы один человек напишет в комментариях, что ему было бы интересно послушать о плюсах и минусах Германии в бытовом плане, я напишу пост об этом. Рад был поделиться своими впечатлениями и в заключение хочу лишь сказать, чтобы вы принимали решение насчет обучения в Германии в Штудиенколлеге или России в Вузе на основании своей индивидуальной ситуации и рассматривали этот пост лишь как попытку рассказать о впечатлениях, а не как четкое руководство к действию.

Живите и процветайте!🖖

Сравнение уровней успеваемости по математической компетентности: результаты для переменной пола

Введение

Образовательные процессы в настоящее время характеризуются однородностью и многомерностью, что затрудняет работу с разнообразными возможностями, потребностями и интересами в классе. Иногда также может отсутствовать диагностика, которая позволила бы изменить, индивидуализировать образовательные ответы, которые характерны для учащихся с высокими способностями и высокими способностями (García-Perales and Almeida, 2019).). Выявление талантов и работа над ними должны быть основной целью в развитом обществе, и обобщение процесса выявления и его нацеливание на все школьное население было бы интересным способом достижения этой цели. Это исследование представляет собой пример того, что в области математики. Этот процесс позволяет гибко подходить к различным ситуациям, основываясь на конкретных характеристиках учащегося, чтобы стимулировать когнитивные способности каждого учащегося на самом высоком уровне.

Математика важна, потому что она применима в повседневной жизни и для решения различных типов задач (Cázares et al., 2020), а также имеет междисциплинарные связи с другими частями учебной программы (Gilat and Amit, 2013). Это обобщение на рутинные повседневные контексты является фундаментальным аспектом включения в качестве ключевого навыка в образование (Méndez et al., 2015). В случае с математикой она включена в математическую компетенцию и базовые компетенции в области естественных наук и технологий. Математическая компетентность определяется как «способность учащихся формулировать, применять и интерпретировать математику в различных контекстах. Он включает в себя математические рассуждения и использование математических понятий, процедур, фактов и инструментов для описания, объяснения и прогнозирования различных явлений» (Ministerio de Educación y Formación Profesional, 2019)., п. 17). Это определение обеспечивает ключевой аспект оценки математики, измерения математических способностей в широком диапазоне контекстов, с целью подчеркнуть важность обобщения того, что было изучено, на широкий спектр ситуаций, знакомых или иных. Поиск конструктивного, целеустремленного, рефлексивного гражданства является фундаментальной предпосылкой образовательных процессов, аспектов, на которые преподавание математики оказывает сильное влияние (Организация экономического сотрудничества и развития, 2019 г.).б). Математические компетенции оценивались во всех шести выпусках Программы международной оценки учащихся (PISA) каждые три года с 2000 по 2018 год.

Оценки PISA являются основным ориентиром для оценки. Тот факт, что существует большая мировая выборка для тестов PISA, означает, что выводы чрезвычайно важны для разработки образовательной политики. Его концептуальная основа использовалась во многих исследованиях (García-Perales, 2014; Ferreira et al., 2017; Rodríguez-Mantilla et al., 2018; Fuentes and Renobell, 2019).; Сасон и др., 2020). К отличительным характеристикам PISA относятся (Ministerio de Educación y Formación Profesional, 2019): стремление направлять образовательную политику, интеграция концепции компетентности в оценивание, важная роль автономного обучения на протяжении всей жизни, регулярное развертывание и чувствительный международный охват. При интерпретации результатов по каждому элементу PISA использует теорию отклика элемента (IRT). В связи с этим ответы детей рассматриваются в соответствии с уровнем способностей ребенка к математической компетентности, иными словами, оценки успеваемости учащихся ориентированы на тип математических задач, которые они могут правильно решить (Ministerio de Educación y Formación Profesional, 2019).). Это означает, что можно определить уровни успеваемости, которые позволяют разместить каждого ребенка на непрерывной шкале компетентности для измеряемой конструкции (Roderer and Roebers, 2013), показывающей процент субъектов на каждом уровне вместе с их отличительными характеристиками, в данном случае для математическая компетентность. Эта методология использовалась с BECOMA On, инструментом в настоящем исследовании, в котором были установлены три уровня производительности на основе баллов.

Среди множества выводов PISA, касающихся математики, в отчетах подчеркивалось, что интерес учащихся к этой области и удовольствие от нее низки, и даже отмечалось наличие личных проблем, таких как тревога и неуверенность, особенно у девочек (Организация Экономическое сотрудничество и развитие, 2013 г. , Мизала и др., 2015 г., Организация экономического сотрудничества и развития, 2019 г.г). На протяжении всех оценок PISA мальчики всегда демонстрировали лучшие результаты по математической компетентности, чем девочки (Ministerio de Educación y Formación Profesional, 2019 г.), при этом пол был прогностическим фактором математических способностей (Farfán and Simon, 2017; Fuentes and Renobell, 2019; Palomares). -Руис и Гарсия-Пералес, 2020 г.). Биологические и социальные факторы могут действовать взаимосвязанным образом (Chamorro-Premuzic et al., 2009; Muelas, 2014), включая интеллектуальные способности (Schillinger et al., 2018), сложные математические рассуждения (Desco et al., 2011) и другие факторы. факторы индивидуального характера, влияющие на процесс обучения математике (Song et al., 2010; Marsh, Martin, 2011; Rodríguez, Guzman, 2018), школу (Carey et al., 2016; Dowker et al., 2016; Schillinger et al., 2018) и семьи (Pelegrina et al., 2002; Ferreira et al., 2017; Rodríguez-Mantilla et al. , 2018). Анализ математических способностей учащихся в зависимости от пола является одной из целей настоящего исследования.

Результаты тестов PISA 2012 года по математике (самого последнего, в котором предпочтение отдавалось математике) и тестов 2018 года (самого последнего оценивания) кратко изложены ниже. В PISA результаты учащихся ранжируются по семи уровням успеваемости: ниже уровня 1, 1, 2, 3, 4, 5 и 6. В PISA 2012 испанские мальчики набрали в среднем 492 балла, а испанские девочки — 476 баллов (Ministerio de Educación, Cultura y Deporte, 2014a). В PISA 2018 средний показатель испанских мальчиков — 485, а девочек — 478. В обоих случаях различия между полами были статистически значимыми (Ministerio de Educación y Formación Profesional, 2019).). При более внимательном изучении этих различий результаты для самых высоких уровней 5 и 6 выделяются; в PISA 2018 8% мальчиков и 5,50% девочек относились к одному из этих двух уровней. Другие исследования также указали на эти различия между полами в производительности и более высоких способностях (Llor et al. , 2012; García-Perales and Almeida, 2019; Ministryio de Educación y Formación Profesional, 2020; Palomares-Ruiz and García-Perales, 2020). . Напротив, 24,60% мальчиков и 24,80% девочек находились на самых низких уровнях — 1 и ниже 1 — без статистической значимости между полами (Ministerio de Educación y Formación Profesional, 2019).). Как показано на Рисунке 1, на более высоких уровнях успеваемости различия между полами становятся более значительными, при этом больше мальчиков, чем девочек, имеют более высокие уровни успеваемости по математике (что также наблюдается в среднем по ОЭСР). Это проблема, которая вызывает озабоченность по поводу потенциальных последствий для будущего академического и профессионального выбора.

Рисунок 1. Уровни успеваемости и гендер в PISA 2018 для Испании и ОЭСР. Источник: Министерство образования и профессионального образования (2019 г.).), п. 89.

Продолжая наблюдать за детьми с отличными результатами по математике, в PISA 2012 г. 8% испанских учащихся продемонстрировали отличные результаты (6,70% и 1,30% в двух группах с лучшими показателями), что соответствует цифрам предыдущих выпусков PISA по математике. навыков, в то время как средний показатель по ОЭСР составлял 9,30% и 3,30% в двух верхних группах (Instituto Nacional de Evaluación Educativa, 2013). В PISA 2018 6% и 1% испанских студентов попали в две лучшие группы, тогда как средний показатель по ОЭСР составлял 9% и 2% соответственно (Ministerio de Educación y Formación Professional, 2019; Организация экономического сотрудничества и развития, 2019a,b,c). Это поднимает фундаментальный вопрос. В Испании у нас нет высокоэффективных студентов? или наша собственная система не способна их идентифицировать и культивировать?

Что делает ученика способным к математике? PISA 2018, самая последняя версия, устанавливает следующие характеристики для достижения уровня 6 или выше по математическим навыкам (Ministerio de Educación y Formación Profesional, 2019)., п. 64):

«Они умеют формулировать понятия, обобщать и использовать информацию, основанную на их исследованиях и моделировать сложные проблемы, и они могут использовать свои знания в относительно нетипичных контекстах. Они могут одновременно связывать разные источники информации и представлений и гибко переключаться между ними. Студенты этого уровня обладают высоким уровнем математического мышления и рассуждений. Эти учащиеся могут применять это понимание, а также свое владение математическими операциями и символическими, формальными отношениями для разработки новых подходов и стратегий для решения новых ситуаций. Учащиеся на этом уровне могут обдумывать свои действия, точно формулировать и сообщать о своих действиях, а также думать о своих открытиях, интерпретациях, аргументах и ​​адаптации к новым ситуациям».

Другие исследования также влияют на концептуализацию наиболее математически способных детей (Geary and Brown, 1991; Greenes, 1997; Sriraman, 2003; Rotigel and Fello, 2004; Almeida et al. , 2008; Desco et al., 2011; Jaime и Гутьеррес, 2017 г.; Курназ, 2018 г.; Рамирес и Каньядас, 2018 г.). В области высших способностей стоит обратить особое внимание на женское население. Например, в Испании в 2018/19 учебном году процентная доля высокоспособных детей значительно различалась в зависимости от пола: 65,06% из них были мальчиками, а 34,9% — мальчиками.4% составляли девочки (Ministerio de Educación y Formación Profesional, 2020). Девочки относятся к группе повышенного риска среди высокоспособных, процессы идентификации более пагубны для них (Kerr, 2000; Landau, 2003; Jiménez, 2014) и изобилуют стереотипами (Bian et al., 2017). Кроме того, даже в настоящее время сохраняется неравенство в процессах социализации между полами (Hadjar et al., 2014; Ministryio de Educación y Formación Profesional, 2019), а возможности девочек иногда недооцениваются (Pomar et al., 2009).). ЮНЕСКО (2019, стр. 72) заявила, что «неблагоприятное положение девочек основано не на когнитивных способностях, а скорее на процессах социализации и обучения, в которых они растут, которые формируют их идентичность, убеждения, поведение и жизненный выбор».

Исследования математических способностей показывают, что мальчики, как правило, показывают лучшие результаты (Preckel et al., 2008; Llor et al., 2012; Instituto Nacional de Evaluación Educativa, 2013; Ministryio de Educación y Formación Profesional, 2019), несмотря на полов, получающих одинаковое преподавание математики с начала школьного обучения. Восприятие и отношение к математике особенно важны (Gonzalez-Pienda et al., 2012; Mato et al., 2014; Ministryio de Educación, Cultura y Deporte, 2014b; Preckel et al., 2008; Ministryio de Educación y Formación Profesional, 2019; Куэли и др., 2020 г.; Palomares-Ruiz and García-Perales, 2020), девочки могут проявлять тревогу и неуверенность в себе в этой области (Instituto Nacional de Evaluación Educativa, 2013; Rodríguez-Mantilla et al., 2018). При решении математических задач важно учитывать уровень внимания или успеваемость девочек (Boaler, 2016; Farfán and Simon, 2017; Hattie et al., 2017; Rodríguez and Guzmán, 2018; Cueli et al., 2020). а также другие мотивационные и эмоциональные факторы (Else-Quest et al., 2010; Rodríguez-Mantilla et al., 2018). Подготовка учителей и практика должны учитывать эти несоответствия между способностями и отношением к математике (Нортес и Нортес, 2013; Рико и др., 2014; Урсини и Рамирес-Меркадо, 2017). Эта переменная является ключевым фактором, определяющим успех обучения в любой учебной дисциплине. Чем более заинтересованы учащиеся и чем больше они считают изучение математики полезным источником знаний, тем лучше будет их успеваемость (Фигейредо и Гимарайнш, 2019 г.).). Это становится еще более важным при смене образовательных ступеней в условиях ухудшения отношения к обучению (Mato et al., 2014). Самоэффективность также влияет на развитие образования и является ключевой переменной, которую следует учитывать при индивидуальной адаптации учащихся в области математики (Ruiz, 2005; Zalazar et al., 2011; Rosário et al., 2012). Лучшее и более глубокое понимание этих поведенческих и мотивационных аспектов является важной задачей для преподавания математики.

Понимание аспектов, которые могут повлиять на образовательный путь мужчин и женщин, имеет ключевое значение и влияет на будущий академический и профессиональный выбор (Hadjar et al., 2014; ЮНЕСКО, 2019 г.).; Гарсия-Пералес и др., 2021). Чтобы ответить на вопрос, важно попытаться экстраполировать данные исследований; почему существует разница в выборе научной и технической карьеры между мужчинами и женщинами? Это исследование сосредоточено на математике, хотя та же проблема применима и к другим дисциплинам, таким как наука, технология и инженерия. Цель состоит в том, чтобы создать равную, справедливую образовательную систему, которая позволит всем учащимся соответствовать меняющимся требованиям глобализированного общества 21 века (Ryu et al., 2021), независимо от пола, поскольку в настоящее время в этих дисциплинах существует гендерный разрыв ( Кидзима и Сан, 2020 г.).

Цель этого исследования состояла в том, чтобы проанализировать результаты в BECOMA On от студентов в трех уровнях успеваемости по математике. Чтобы понять и осмыслить эти уровни производительности, результаты были изучены в зависимости от пола участников.

Материалы и методы

В исследовании использовалась ex post фактическая, описательная, количественная методология исследования с целью описания взаимосвязей, существующих между группами количественных данных из ряда модулирующих переменных.

Участники

Выборка исследования состояла из 3795 учащихся 5-х классов начальной школы в возрасте около 10-11 лет из 16 регионов Испании. Каждое региональное управление образования выбрало школы для участия в исследовании на добровольной основе в зависимости от готовности школ к участию и наличия у них подходящих технических средств для проведения исследования. Инструменты применялись к классным группам в их обычных классах с использованием онлайн-устройств. Распределение выборки по полу составило 2002 мальчика (52,75%) и 1793 девочки (47,25%).

Выборка была сгруппирована по уровням производительности. На основе результатов были установлены 3 иерархических уровня одинакового размера, где 1 — самый низкий, а 3 — самый высокий уровень производительности. Уровни для BECOMA On показаны в таблице 1.

Таблица 1. Уровни производительности в BECOMA On.

Средний уровень составил 1,97 ( SD = 0,82), с асимметрией 0,05, распределение уровней соответствовало симметричной кривой с эксцессом -1,50, платикуртическое распределение с отрицательным избыточным эксцессом.

Переменные

Математическая компетентность была основной переменной в этом исследовании. Это было измерено с помощью BECOMA On. Как упоминалось выше, математика играет ключевую роль в образовательных процессах, особенно из-за ее обобщения на повседневную жизнь субъектов, что является фундаментальным аспектом эффективного автономного развития в обществе. Другой используемой переменной был пол участников, мужской (M) или женский (F).

Инструмент

BECOMA On — это батарея, которая онлайн оценивает математические способности учащихся 5-х классов начальной школы. Он состоит из 30 заданий, распределенных по 7 оценочным тестам: математическая интерпретация (элементы 1-5; статистическое и вероятностное измерение), ментальная арифметика (элементы 6-11; арифметическое измерение), геометрические свойства (элементы 12 и 13; геометрическое измерение). , Логический числовой ряд (позиции 14-19; Арифметическая размерность), алгоритмы обнаружения (пункты 20 и 21; арифметическая размерность), условные единицы (пункты 22-27; величина и размерность пропорциональности) и логические ряды цифр (пункты 28-30; геометрическая размерность). При установлении содержания и показателей оценки для предметов в каждом измерении в качестве справочного материала использовался Королевский указ 126/2014 от 28 февраля, устанавливающий базовую учебную программу для начального образования (Ministerio de Educación, Cultura y Deporte, 2014c). Инструмент структурирован так, как показано в таблице 2.

Таблица 2. Структура прибора.

Каждое задание имеет возможную оценку 0 (неправильно), 1 (частично верно) или 2 (верно), что дает возможный общий минимальный балл 0 и возможный общий максимальный балл 60. Выполнение задания занимает 41 минуту. тест. С точки зрения статистической достоверности (Palomares-Ruiz and García-Perales, 2020) инструмент имел индекс надежности 0,83 с использованием альфа Кронбаха и индексы достоверности от 0,78 до 0,86 (содержание и структура). Индекс сложности (DI) для каждого пункта был следующим:

Как видно из Таблицы 3, батарея имела средний индекс сложности (DI = 0,45) и реагировала на различные уровни сложности. Пункт 28 был самым сложным (DI = 0,09), а пункт 13 — самым простым (DI = 0,75). Выбор элементов оценивался группой из 51 профессионала в области математики с разных уровней образования, что дало общий индекс достоверности для инструмента 0,81 и статистику Каппа 0,82.

Таблица 3. Индекс сложности заданий в BECOMA On.

Процедура

За месяц до периода сбора данных сотрудники каждой из участвующих школ прошли курс обучения, посвященный дифференциальным характеристикам батареи и тому, что они должны учитывать при ее применении, с инструкциями и временем контроля. Данные собирались в течение февраля 2019 года с помощью онлайн-приложения инструмента.

Было получено согласие родителей или опекунов каждого участвующего учащегося на их участие в исследовании, запрошенное от имени исследователей директором каждой школы. Впоследствии администрация образования в каждом испанском регионе вела список детей, имеющих разрешение семьи.

Результаты

Перед представлением результатов в соответствии с целями исследования описательная статистика представлена ​​для каждого элемента инструмента: среднее значение, стандартное отклонение, частоты и проценты.

Как видно из Таблицы 4, уровень сложности можно проанализировать по средним результатам по каждому пункту. Самыми легкими оказались предметы 4 ( М = 1,49, СО = 0,75), 5 ( М = 1,54, СО = 0,71), 7 ( М = 1,58, 9).0035 SD = 0,67), 13 ( M = 1,61, SD = 0,72) и 14 ( M = 1,63, SD = 0,65), а наиболее трудными заданиями были 11 ( M = 0,65). 0,74, SD = 0,84), 16 ( M = 0,81, SD = 0,77), 17 ( M = 0,80, SD = 0,76), 21 ( M = 0,82, SD .), 21 ( M = 0,82, SD .. = 0,89) и 28 ( M = 0,56, SD = 0,65). Среднее значение для комплекта батарей составило 34,83 ​​( SD = 9.69). На рис. 2 показан элемент с наименьшим уровнем сложности — номер 14, а на рис. 3 — элемент с наивысшей сложностью — номер 28.

Таблица 4. Описательная статистика позиций BECOMA On.

Рис. 2. Элемент 14, самый простой элемент в этом исследовании. Собственная работа авторов (2020).

Рисунок 3. Пункт 28, самый сложный пункт в инструменте в этом исследовании. Собственная работа авторов (2020).

С точки зрения асимметрии преобладали отрицательные баллы — 21 из 30 пунктов — другими словами, слева от среднего появилось больше значений. С точки зрения эксцесса почти все значения — 27 из 30 пунктов и общий балл — были отрицательными, платикуртическое распределение с более низкой концентрацией результатов вокруг среднего значения, интересный аспект при анализе различных уровней производительности в соответствии с результатами.

Результаты представлены на основе целей исследования, сначала результаты в BECOMA On для трех уровней производительности, а затем описательная статистика. После этого каждый уровень исследуется в отношении пола.

В таблице 5 показаны результаты BECOMA On для трех уровней производительности. Приведены частота и процентное соотношение для каждого уровня производительности. На первом уровне обучалось 1319 учащихся (34,76%), на втором уровне — 1263 (33,28%), на третьем уровне — 1213 (31,96%).

Таблица 5. Частота и процентное соотношение уровней производительности для каждого элемента ответа.

В таблице 5 приведены итоговые значения для каждого уровня и варианта ответа. В средних результатах по всем пунктам 15,45% учащихся находились на уровне 1 и набрали 0 баллов, 10,25% были на уровне 1 и набрали 1 балл и 9 баллов.0,06% были на уровне 1 и набрали 2 балла; 9,09% учащихся были на уровне 2 и набрали 0 баллов, 9,63% были на уровне 2 и набрали 1 балл, а 14,56% были на уровне 2 и набрали 2 балла; 3,99% учащихся были на уровне 3 и набрали 0 баллов, 6,97% были на уровне 3 и набрали 1 балл, а 21,01% были на уровне 3 и набрали 2 балла. Ответы учащихся на уровне 1 и 2 были более неустойчивыми и отражали явную разницу между уровнями. . Для определения статистически значимых различий в таблице 6 показаны средние значения, стандартные отклонения и результаты теста ANOVA.

Таблица 6. Тест ANOVA, сравнивающий уровни производительности.

Учащиеся 1-го уровня набрали в среднем 24,49 ( SD = 4,67), 2-го уровня средний балл составил 34,93 ( SD = 2,58), а 3-го уровня — 45,97 ( SD = 4,76). ). Учащиеся 3-го уровня имели более высокие средние баллы по всем пунктам. Кроме того, различия между уровнями были статистически значимыми по всем пунктам, p < 0,001, при этом учащиеся 3-го уровня набрали более высокие баллы. Чтобы завершить характеристику этих трех групп студентов, для сравнения между уровнями использовалась еще одна переменная, пол студентов.

Распределение по полу исходной выборки из 3795 учащихся: 2002 мальчика (52,75%) и 1793 девочки (47,25%). Средний балл по инструменту для мальчиков составил 35,18 ( SD = 10,08), а для девочек — 34,44 ( SD = 9,22), при p -Значение < 0,05. Чтобы более внимательно изучить значимость различий между полами, результаты были проанализированы в соответствии с каждым уровнем производительности. Частоты и проценты для каждого пола на каждом из трех уровней приведены ниже.

На уровне 1 показатели по каждому показателю различались незначительно (таблица 7): 23,12% респондентов составили мальчики, набравшие 0 баллов, 15,68% — мальчики, набравшие 1 балл, и 13,21% — мальчики, набравшие 2 балла; 21,33% ответов были девочки, набравшие 0 баллов, 13,80% — девочки, набравшие 1 балл, и 12,86% — девочки, набравшие 2 балла. Глядя на частоту 2 баллов для обоих полов, были различия. Больше мальчиков было на 2 балла по пунктам 15 (5,69% мальчиков и 3,26% девочек), 20 (17,44% мальчиков и 14,9% девочек).4%), 22 (25,78% мальчиков и 22,52% девочек) и 27 (17,66% мальчиков и 13,34% девочек). Больше девочек набрали 2 балла по пунктам 1 (20,55% мальчиков и 22,21% девочек), 7 (20,70% мальчиков и 23,28% девочек), 8 (12,66% мальчиков и 14,25% девочек) и 12 (23,43% мальчиков и 25,02% девочек). .

Таблица 7. Частота и процентное соотношение по полу учащихся с успеваемостью 1 уровня.

Для учащихся 2 уровня частота и процентное соотношение для каждого варианта ответа были следующими (Таблица 8):

Таблица 8. Частота и процентное соотношение по полу учащихся с успеваемостью 2 уровня.

На уровне 2 результаты были аналогичны результатам уровня 1 с точки зрения пола, с небольшими различиями между мальчиками и девочками. 13,53% ответов были мальчиками с 0 баллами, 14,98% — мальчиками с 1 баллом и 21,84% — мальчиками с 2 баллами; 13,78% девочек набрали 0 баллов, 13,95% — девочки набрали 1 балл и 21,91% — девочки набрали 3 балла. Глядя на частоту получения 2 баллов по каждому пункту, также были различия между полами. Больше мальчиков набрало 2 балла по 15 пунктам (мальчики 16,94% и девочки 9,74%), 17 (мальчики 8,71% и девочки 5,38%), 18 (мальчики 16,31% и девочки 12,67%) и 19 (мальчики 15,04% и девочки 11,80%). Больше девочек набрали 2 балла по пунктам 7 (35,79% мальчиков и 39,75% девочек), 8 (26,68% мальчиков и 30,64% девочек), 23 (21,06% мальчиков и 25,65% девочек) и 30 (22,33% мальчиков и 27,40% девочек). .

Для учащихся 3 уровня частота и процентное соотношение для каждого варианта ответа были следующими (Таблица 9):

Таблица 9. Частота и процентное соотношение учащихся с уровнем успеваемости 3 в разбивке по полу.

На уровне 3 разница между полами была больше, причем мальчики набирали больше баллов, чем девочки. 6,78% ответов были мальчиками с 0 баллами, 11,89% — мальчиками с 1 баллом и 37,38% — мальчиками с 2 баллами; В 5,70% случаев девушки набрали 0 баллов, в 9,91% — 1 балл, а в 28,33% — 2 балла. Судя по 2 баллам по каждому пункту, между полами были большие различия. Это было заметно по пунктам 15 (мальчики 39,57% и девочки 20,86%), 19 (мальчики 34,05% и девочки 20,61%), 22 (мальчики 53,01% и девочки 39%).0,32%) и 27 (44,44% мальчиков и 31,90% девочек). На этом уровне различия были меньше по пунктам 3 (мальчики 34,46% и девочки 29,51%), 26 (мальчики 23,99% и девочки 18,14%), 28 (мальчики 7,67% и девочки 6,92%), 29 (мальчики 25,47% и девочки). 23,50%) и 30 (юноши 39,24% и девушки 35,37%). Не было предметов, по которым девочки набрали 2 балла больше, чем мальчики.

После того, как частоты были установлены для каждого уровня в разбивке по полу, был проведен тест t для определения наличия статистически значимых различий в зависимости от пола. Результаты приведены в таблице 10.

Таблица 10. t — Тест по полу между уровнями эффективности 1, 2 и 3.

Как видно из таблицы 10, были статистически значимые различия при p < 0,05. Это значение было связано с неравной частотой между полами на уровне успеваемости 3, где было 680 мальчиков (17,92%) и 533 девочки (14,04%). На двух других уровнях, 1 и 2, результаты были более схожими: на уровень 1 было включено 686 (18,08%) мальчиков и 633 (16,68%) девочек, а на уровень 2 - 636 мальчиков (16,76%) и 627 девочек (16,52%). . Согласно статистике Министерства образования (Ministerio de Educación y Formación Profesional, 2020) по неуниверситетскому образованию в 2018/19 учебном году(самые последние доступные данные), из 35 494 учащихся, признанных высокоспособными, 23 092 мальчика (65,06%) и 12 402 девочки (34,94%). Это отражает сохраняющееся неравенство между полами в выявлении высокоспособных учащихся, при этом процесс диагностики наносит ущерб девочкам. Это указывает на неравенство в образовании и необходимость более глубокого изучения причинных факторов.

Обсуждение

Научно-технический прогресс общества требует высококвалифицированных специалистов (Frey and Osborne, 2017), поскольку существуют постоянные инновации и меняющиеся требования (Macià and Garreta, 2018). Школы играют основополагающую роль в развитии талантов учащихся (Mandelman et al., 2010). В самых последних испанских законах об образовании учитываются образовательные потребности, а удовлетворение потребностей учащихся и адаптация к ним с самого начала обучения в школе имеют основополагающее значение. Равенство и инновации способствуют качеству и социальному развитию (Организация экономического сотрудничества и развития, 2019 г.).а), а оценка и исследования помогают отслеживать их для разработки образовательной политики (Schleicher, 2018; Harju-Luukkainen et al. , 2020).

Это исследование было сосредоточено на анализе математических навыков в трех группах учащихся, определенных по успеваемости после применения BECOMA On, инструмента с высокими показателями надежности и достоверности. Понимание потенциала учащихся на этих трех уровнях представляет значительный социальный и образовательный интерес, а понимание сложности математических подходов и стратегий, которые они используют при решении задач, имеет основополагающее значение (Хайме и Гутьеррес, 2017). Первоначально результаты были ожидаемыми, учащиеся высшей ступени — 3 — продемонстрировали лучшие результаты и оценки, чем учащиеся 1 и 2 ступеней. Что интересно, так это наличие различных статистически значимых различий.

Чуть более трети, 1319 учащихся (34,76%), были определены как принадлежащие к уровню успеваемости 1, 1263 (33,28%) – к уровню 2 и 1213 (31,96%) – к уровню 3. Сравнивая результаты этих трех групп, статистически выявлены достоверные различия, p < 0,001; учащиеся 3-го уровня имели более высокие баллы по всем пунктам инструмента.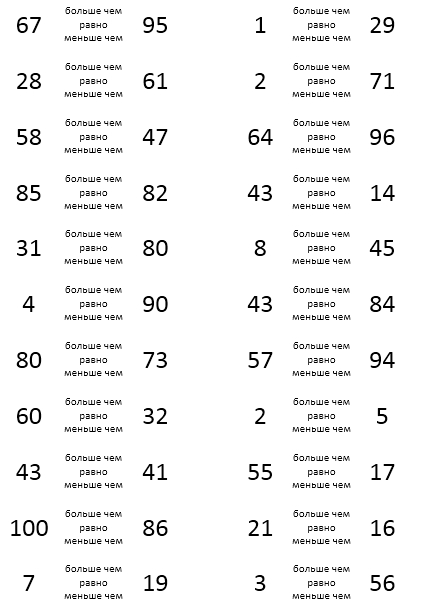 Учащиеся 3-го уровня оказались наиболее способными к математике. Важно рассмотреть процессы выявления этих высокоспособных учащихся. К сожалению, время от времени их потенциал, потребности и интересы игнорируются в процессе обучения и преподавания, а иногда возникают различные серьезные проблемы с адаптацией (Pomar et al., 2009).; Гарсия-Пералес и Алмейда, 2019 г.).

Чтобы завершить характеристику этих трех групп учащихся, уровни были сопоставлены в зависимости от пола учащихся. В исследовании 52,75% участвовавшей выборки составляли мальчики и 47,25% девочки. На уровнях производительности 1 и 2 было немного различий в производительности между полами, с различными различиями в пользу того или иного пола. Однако на уровне 3 различий было больше, и именно мальчики имели самые высокие баллы по всем пунктам. Мальчики на уровне 3 имели 6,78% ответов, набравших 0, 11,89 баллов.% с оценкой 1 и 37,38 % с оценкой 2. Для девочек на уровне 3 проценты составили 5,70 %, 9,91 % и 28,33 % для оценок 0, 1 и 2 соответственно. Это привело к статистически значимым различиям, p < 0,05, поскольку на уровне успеваемости 3 и выше было 680 мальчиков (17,92%) по сравнению с 533 девочками (14,04%). Это отражает сохраняющееся неравенство между полами в более высоких уровнях успеваемости по математике, которое также наблюдается в других исследованиях (Baye and Monseur, 2016; Hyde, 2016; Ministryio de Educación y Formación Profesional, 2019).), демонстрируя неравенство в образовании и необходимость глубокого изучения причинных факторов (Calvo, 2018).

Короче говоря, используемый инструмент является функциональным и оригинальным, поскольку он устанавливает взаимосвязь между оценкой и математическими и цифровыми навыками. Его тесная связь с испанской школьной программой для 5-го класса начального образования дает ему ценный практический компонент для использования в развитии образовательных практик. Выявление потребностей и потенциальных возможностей обучения, в данном случае для математики с использованием онлайн-оценки, является ключевым из-за инструментального и междисциплинарного характера математики, и это открывает интересный путь для обобщения и применения таких инструментов.

Заключение

Школы должны развивать образовательные практики, обеспечивающие инклюзивное качественное образование для всех (Franco et al., 2017; Arnaiz-Sánchez et al., 2018, 2020). Администрация образования должна обеспечить, чтобы все учащиеся достигли функционального и значимого обучения, уделяя приоритетное внимание поддержке существования равноправного, демократического школьного образования, адаптированного к потребностям и характеристикам каждого учащегося. Образовательная политика должна быть направлена ​​на достижение этой цели. В связи с этим важно учитывать все переменные, влияющие на процессы преподавания и обучения, включая пол учащихся (Хаджар и др., 2014 г.; Фарфан и Симон, 2017 г.; Паломарес-Руис и Гарсия-Пералес, 2020 г.), с с целью переосмысления действий, направленных на повышение академической успеваемости и продвижение инноваций в образовании.

Как отмечалось во введении, биологические факторы, такие как интеллект или определенные черты личности, и контекстуальные факторы, такие как стереотипы и сама семья, могут объяснить различия между полами в математических способностях, особенно на более высоких уровнях успеваемости. В связи с этим анализ контекстов, в которых социализируются мальчики и девочки, имеет основополагающее значение для изучения этих различий между полами (Hadjar et al., 2014; Mizala et al., 2015; Palomares-Ruiz and García-Perales, 2020). к этому следует подходить с разных точек зрения (Del Río et al., 2016). Кроме того, различия между полами подчеркивают необходимость переосмысления образовательных практик с точки зрения равенства и инноваций, пытаясь не допустить, чтобы математическое обучение вело к академической и профессиональной сегрегации (Cantoral et al., 2014). В связи с этим работа над навыками STEAM (наука, технология, инженерия, искусство и математика) может быть полезным подходом для продвижения совместного обучения и гендерного равенства в образовании (ЮНЕСКО, 2019 г.).; Ryu et al., 2021), включая неформальное образование (Juvera and Hernández-López, 2021), и могут быть распространены на учащихся с высокими способностями к математике (García-Perales and Almeida, 2019). Подготовка учителей для преподавания математики особенно важна (Monroy and Marroquín, 2020) и является ключевым аспектом преподавания и обучения в других областях STEAM (Román-Graván et al. , 2020; Hernández-Barco et al., 2021; Ortiz- Revilla and Greca, 2021), в котором женщины представлены недостаточно (Lehman et al., 2017; Botella et al., 2019).; Маккалоу, 2020).

Большая выборка, участвовавшая в этом исследовании, подчеркивает важность использования тестов способностей для диагностических процессов, в данном случае для математики. Обобщение конкретных видов деятельности для любого школьника, независимо от его способностей, означает запуск процесса учебной адаптации и индивидуализации (Díez, Jiménez, 2018; Torres, 2018). В настоящее время образовательные процессы характеризуются своей сложностью и многомерностью, с множеством факторов, которые могут оказывать влияние на преподавание и обучение в рамках преподавания математики (Palomares-Ruiz and García-Perales, 2020). По этой причине было бы целесообразно расширить переменные анализа в будущих исследованиях с помощью BECOMA On и включить такие переменные, как академическая успеваемость, восприятие учителями и учащимися интереса и мотивации учащихся к математике, а также то, насколько способные учащиеся обнаруживаются. Кроме того, будущие исследования будут стремиться распространить применение этого инструмента на другие образовательные уровни, при этом пол учащихся будет фундаментальной переменной. Распространение исследований этой переменной на другие уровни образования добавило бы веса результатам этого исследования. Кроме того, с использованием письменной версии этого инструмента будут предприняты попытки провести повторные исследования с повторяющимися измерениями, аналогичные тем, которые используются в других исследованиях (García-Perales et al., 2020, 2021). Выявление потенциала любого учащегося в области математики помогает предложить индивидуальный образовательный ответ, что является приоритетом инклюзивного высококачественного образования.

Заявление о доступности данных

Первоначальные материалы, представленные в исследовании, включены в статью/дополнительный материал, дальнейшие запросы можно направлять соответствующему автору/авторам.

Заявление об этике

Этическая экспертиза и одобрение не требовались для исследования с участием людей в соответствии с местным законодательством и институциональными требованиями. Перед началом исследования письменное информированное согласие на участие в данном исследовании было предоставлено областной администрацией каждой школы. Эти образовательные учреждения действительно требовали письменного информированного согласия от родителей. Мы обеспечили анонимность ответов и конфиденциальность всех собранных данных, а опубликованные результаты не содержали никакой информации, позволяющей идентифицировать школу.

Авторские взносы

RG разработала исследование, собрала и проанализировала данные и написала рукопись. AP внесла свой вклад в интерпретацию данных и написала, отредактировала и усовершенствовала рукопись. RG и AP принимали участие в отправке статьи в журнал. Оба автора внесли свой вклад в статью и одобрили представленную версию.

Финансирование

Исследование проводилось при финансовой поддержке Регионального правительства Кастилия-Ла-Манча (JCCM) и Европейского фонда регионального развития (FEDER) [Ссылка на проект/Код SBPLY/19/180501/000149]. Он также получил поддержку Национального института образовательных технологий и подготовки учителей (INTEF), Национального университета дистанционного образования (UNED) и Университета Кастилия-Ла-Манча (UCLM).

Конфликт интересов

Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.

Ссылки

Алмейда, Л.С., Гисанде, М.А., Прими, Р., и Лемос, Г.К. (2008). Contribuciones del factor general y de los factores específicos en la relación entre inteligencia y rendimiento escolar. Евро. Дж. Образ. Психол. 1, 5–16. doi: 10.30552/ejep.v1i3.13

Полный текст CrossRef | Google Scholar

Арнаис-Санчес П., Де Аро Р., Алькарас С. и Мирете-Руис А. Б. (2020). Школы, способствующие повышению успеваемости и успехам всех учащихся. Перед. Психол. 10:2920. doi: 10.3389/fpsyg.2019.02920

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Арнаис-Санчес П. , Де Аро Р. и Мирете А. Б. (2018). «Procesos de mejora e inclusión educativa en centros educativos de la Región de Murcia [Улучшение образования и процессы включения в образовательных центрах в регионе Мурсия]», в Inclsión y Mejora Educativa [Включение и улучшение образования] , редакторы JC Torrego, L. Rayón, Y. Muñoz и P. Gómez (Alcalá de Henares: Servicio Publicaciones Universidad), 271–281.

Google Scholar

Байе А. и Монсёр К. (2016). Гендерные различия в изменчивости и экстремальных показателях в международном контексте. Крупномасштабная оценка. Образовательный 4, 1–16. doi: 10.1186/s40536-015-0015-x

CrossRef Full Text | Google Scholar

Биан Л., Лесли С. Дж. и Кимпиан А. (2017). Гендерные стереотипы об интеллектуальных способностях возникают рано и влияют на интересы детей. Наука 355, 389–391. doi: 10.1126/science.aah6524

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Боалер, Дж. (2016). Математическое мышление: раскрытие потенциала учащихся с помощью творческой математики, вдохновляющих сообщений и инновационного обучения. Сан-Франциско, Калифорния: Джосси-Басс.

Google Scholar

Ботелла К., Руэда С., Лопес-Иньеста Э. и Марзал П. (2019). Гендерное разнообразие в дисциплинах STEM: многофакторная проблема. Энтропия 21, 1–17. doi: 10.3390/e21010030

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Кальво, Г. (2018). Las identidades де género Según лас у лос подростков. Percepciones, desigualdades у necesidades educativas. Контекст образования. Преподобный Образ. 21, 169–184. doi: 10.18172/con.3311

CrossRef Full Text | Google Scholar

Кантораль Р., Рейес-Гасперини Д. и Монтьель Г. (2014). Социоэпистемология, математика и реальность. Rev. Latinoamericana Etnomatemática 7, 91–116.

Google Scholar

Кэри Э., Хилл Ф., Дивайн А. и Сюч Д. (2016). Курица или яйцо? Направление связи между математической тревожностью и успеваемостью по математике. Перед. Психол. 6:1987. doi: 10.3389/fpsyg.2015.01987

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Касарес М. Дж., Паес Д. А. и Перес М. Г. (2020). Discusión teórica sobre las prácticas docentes como mediadoras para potencializar estrategias metacognitivas en la solucion de tareas matemáticas. Учеб. Математика 32, 221–240. doi: 10.24844/EM3201.10

Полный текст CrossRef | Google Scholar

Чаморро-Премузик Т., Кирога М. А. и Колом Р. (2009). Интеллектуальная компетентность и успеваемость: испанское исследование. Учиться. Индивид. Дифф. 19, 486–491. doi: 10.1016/j.lindif.2009.05.002

CrossRef Полный текст | Google Scholar

Куэли М., Аресес Д., Гарсия Т., Алвес Р. А. и Гонсалес-Кастро П. (2020). Внимание, тормозной контроль и ранние математические навыки у дошкольников. Псикотема 32, 237–244. doi: 10.7334/psicothema2019.225

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Дель Рио, М. Ф., Штрассер, К., и Суперреги, М. И. (2016). ¿Son las habilidades matemáticas un asunto de Género? Los estereotipos de género acerca de las matemáticas en niños y niñas de Kínder, sus familias y educadoras. Calidad Educación 45, 20–53. doi: 10.4067/S0718-45652016000200002

PubMed Abstract | Полный текст перекрестной ссылки | Академия Google

Деско, М., Навас-Санчес, Ф. Дж., Санчес-Гонсалес, Дж., Рейг, С., Роблес, О., Франко, К., и др. (2011). Математически одаренные подростки используют более обширные и более двусторонние области лобно-теменной сети, чем контрольные, во время исполнительных функций и задач на подвижное мышление. НейроИзображение 57, 281–292. doi: 10.1016/j.neuroimage.2011.03.063

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Диес, Л. П., и Хименес, Си Джей (2018). Influencia de la escolar organización en la educación de los alumnos de altas capacidades. Энсеньянса Учить. 36, 151–178. doi: 10.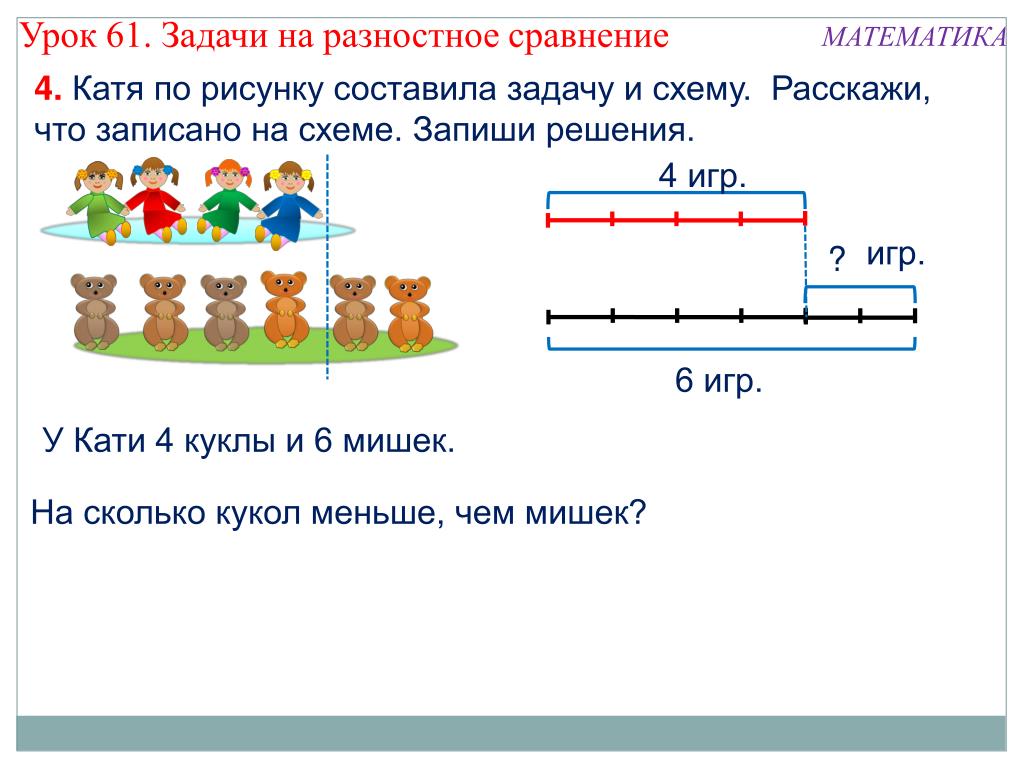 14201/et2018361151178

Полный текст CrossRef | Google Scholar

Даукер А., Саркар А. и Йен Лоой К. (2016). Математическая тревога: «Чему мы научились за 60 лет?». Перед. Психол. 7:508. doi: 10.3389/fpsyg.2016.00508

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Else-Quest, NM, Hyde, JS, and Linn, MC (2010). Межнациональные модели гендерных различий в математике: метаанализ. Псих. Бык. 136, 103–127. doi: 10.1037/a0018053

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Фарфан, Р. М., и Саймон, Г. (2017). Género у matemáticas: уна расследование кон niñas у niños Talento. Acta Sci. 19, 427–446.

Google Scholar

Феррейра А.С., Флорес И. и Касас-Новас Т. (2017). Introdução ao Estudo, Porque Melhoraram os Resultados PISA em Portugal?: Estudo Longitudinal e Comparado (2000-2015). Лиссабон: Fundação Francisco Manuel dos Santos.

Google Scholar

Фигейреду, М. , и Гимарайнш, Х. М. (2019). Relevância душ fatores motivacionais нос estilos де aprendizagem да Matemaìtica не iniìcio сделать ensino secundaìrio. Квадрант 28, 79–99.

Google Scholar

Франко В., Мело М., Сантос Г., Аполонио А. и Амарал Л. (2017). Национальная система раннего вмешательства как стратегия содействия инклюзивности и успеваемости в Португалии. Фронт. Психол. 8:1137. doi: 10.3389/fpsyg.2017.01137

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Фрей, К., и Осборн, М. (2017). Будущее занятости: насколько рабочие места подвержены компьютеризации? Техн. Прогноз. соц. Изменение 114, 254–280. doi: 10.1016/j.techfore.2016.08.019

Полный текст CrossRef | Google Scholar

Фуэнтес С. и Ренобелл В. (2019). La influencia del género en el aprendizaje matemático en España. Evidencias desde PISA. Искр. соц. Образовательный РАСЕ 13, 63–80. doi: 10.7203/RASE.13.1.16042

CrossRef Полный текст | Google Scholar

Гарсия-Пералес, Р. (2014). Diseño y Validación de Un Instrumento de Evaluación de la Competencia Matemática. Rendimiento Matematico де лос Alumnos Más Capaces. диссертация/магистерская диссертация. Мадрид: Национальный университет дистанционного образования (UNED).

Google Scholar

Гарсия-Пералес Р. и Алмейда Л. С. (2019). Programa de enriquecimiento para alumnado con alta capacidad: efectos positivos para el currículum. Коммуникар 60, 39–48. doi: 10.3916/C60-2019-04

CrossRef Полный текст | Google Scholar

Гарсия-Пералес, Р., Хименес-Фернандес, К., и Паломарес-Руис, А. (2020). Seguimiento де ип группа де выпускников у выпускников кон Альта Capacidad matemática. Rev. Расследование. Образовательный 38, 415–434. doi: 10.6018/rie.366541

Полный текст CrossRef | Google Scholar

Гарсия-Пералес Р., Хименес-Фернандес К. и Паломарес-Руис А. (2021). Elecciones académicas e Interes Vocacional en alumnado con alta capacidad matemática. Ensaio Avaliação e Políticas Públicas em Educação 29, 160–182. doi: 10.1590/S0104-40362020002802539

CrossRef Full Text | Google Scholar

Гири, округ Колумбия, и Браун, Южная Каролина (1991). Когнитивное дополнение: выбор стратегии и различия в скорости обработки данных у одаренных, нормальных и математически неполноценных детей. Дев. Психол. 27, 398–406. doi: 10.1037/0012-1649.27.3.398

CrossRef Полный текст | Google Scholar

Гилат, Т., и Амит, М. (2013). Изучение творческих способностей младших школьников: влияние моделирующей деятельности. ПНА 8, 51–59.

Google Scholar

Гонсалес-Пьенда Дж. А., Фернандес М. С., Суарес Н., Фернандес М. Э., Туэро Э., Гарсия Т. и др. (2012). Diferencias de género en actitudes hacia las matemáticas en la enseñanza obligatoria. Rev. Iberoamericana Psicol. Салуд 3, 55–73.

Google Scholar

Greenes, C. (1997). Оттачивание способностей математически перспективных. Матем. Учить. 90, 582–586.

Google Scholar

Хаджар А. , Кролак-Швердт С., Прием К. и Глок С. (2014). Гендерные и образовательные достижения. Учеб. Рез. 56, 117–125. doi: 10.1080/00131881.2014.898908

CrossRef Full Text | Google Scholar

Харью-Лууккайнен, Х., МакЭлвани, Н., и Станг, Дж. (редакторы) (2020). Мониторинг успеваемости учащихся в 21 веке. Перспективы европейской политики и стратегии оценки. Берлин: Springer International Publishing.

Google Scholar

Хэтти Дж., Фишер Д. и Фрей Н. (2017). Видимое обучение математике: что лучше всего подходит для оптимизации обучения учащихся. Таузенд-Оукс, Калифорния: Корвин.

Google Scholar

Эрнандес-Барко М., Каньяда-Каньяда Ф., Корбачо-Куэльо И. и Санчес-Мартин Дж. (2021). Исследовательское исследование взаимосвязи эмоций, самоэффективности и множественного интеллекта будущих учителей естественных наук. Перед. Образовательный 6:604791. doi: 10.3389/feduc.2021.604791

Полнотекстовая перекрестная ссылка | Google Scholar

Хайд, Дж. С. (2016). Пол и познание: пол и когнитивные функции. Курс. мнение Нейробиол. 38, 53–56. doi: 10.1016/j.conb.2016.02.007

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Национальный институт оценки образования (2013). PISA 2012: Informe Español. Том I: Результаты и контекст. Мадрид: Министерство образования, культуры и депортации.

Google Scholar

Хайме А. и Гутьеррес А. (2017). «Исследования, посвященные изучению высоких математических способностей», в Investigacioìn en Educacioìn Matemaìtica XXI , редакторы JM Munoz-Escolano, A. Arnal-Bailera, P. Beltraìn-Pellicer, ML Callejo и J. Carrillo (Сарагоса: SEIEM), 71–89.

Google Scholar

Хименес, К. (2014). El Desarrollo Del Talento: Educación y Alta Capacidad. Инаугурационный курс Академического курса 2014–2015 годов UNED. Мадрид: UNED.

Google Scholar

Ювера, Дж., и Эрнандес-Лопес, С. (2021). Пар в детстве и гендерный разрыв: предложение для неформального образования. ОБЗОР ЭДУ. Междунар. Образовательный Учиться. Ред. 9, 9–25. doi: 10.37467/gka-revedu.v9.2712

Полный текст CrossRef | Google Scholar

Керр, Б. (2000). «Сопровождение одаренных девушек и молодых женщин», в International Handbook of Giftedness and Talent , eds KM Heller, FJ Mönks, RJ Sternberg и RF Subotnik (Oxford, UK: Pergamon Press), 649–657.

Google Scholar

Кидзима Р. и Сун К.Л. (2020). «Женщины не должны сопротивляться»: использование дизайн-мышления для обретения творческой уверенности и интереса к STEAM. Междунар. J. Art Design Educ. 40, 66–81. doi: 10.1111/jade.12307

Полный текст CrossRef | Google Scholar

Курназ, А. (2018). Изучение влияния решения математических задач, математического мышления и пространственных способностей на математические достижения одаренных учащихся. Всемирная наука. Рез . 5, 37–43. doi: 10.20448/journal.510.2018.51.37.43

CrossRef Полный текст | Google Scholar

Ландау, Э. (2003). El valor de ser superdotado. Мадрид: Consejería de Educación.

Google Scholar

Леман, К. Дж., Сакс, Л. Дж., и Циммерман, Х. Б. (2017). Женщины, планирующие специализироваться в области компьютерных наук: кто они и что делает их уникальными? Дж. Вычисл. науч. Образовательный 26, 277–298. doi: 10.1080/08993408.2016.1271536

CrossRef Full Text | Google Scholar

Ллор Л., Феррандо М., Феррандис К., Эрнандес Д., Сайнс М., Прието М. Д. и др. (2012). Inteligencias Múltiples у Alta Habilidad. Аула Абиерта 40, 27–38.

Google Scholar

Масиа, М., и Гаррета, Дж. (2018). Accesibilidad y alfabetización digital: barreras para la integración de las TIC en la comunicación familia/escuela. Rev. Расследование. Образовательный 36, 239–257. doi: 10.6018/rie.36.1.2

CrossRef Полный текст | Google Scholar

Мандельман С. Д., Тан М., Альджугайман А. М. и Григоренко Э. Л. (2010). Интеллектуальная одаренность: экономические, политические, культурные и психологические соображения. Учиться. Индивид. Дифф. 20, 286–297.

Google Scholar

Марш, Х.В., и Мартин, А.Дж. (2011). Академическая самооценка и академические достижения: отношения и причинно-следственная связь. руб. Дж. Образ. Психол. 81, 59–77. doi: 10.1348/000709910X503501

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Мато, доктор медицинских наук, Эспиньейра, Э., и Чао, Р. (2014). Dimensión afectiva hacia la matemática: resultsados ​​de un análisis en educación primaria. Rev. Расследование. Образовательный 32, 57–72. doi: 10.6018/rie.32.1.164921

Полный текст CrossRef | Google Scholar

Маккалоу, Л. (2020). Пропорции женщин в лидерстве STEM в Академии в США. Учеб. науч. 10, 1–13. doi: 10.3390/educsci10010001

CrossRef Full Text | Google Scholar

Мендес Д., Мендес А. и Фернандес-Рио Ф. (2015). Análisis y valoración del proceso de incorporación de las Competencias Básicas en Educación Primaria. Rev. Расследование. Образовательный 33, 233–246. doi: 10.6018/rie.33.1.183841

CrossRef Full Text | Google Scholar

Ministryio de Educación, Cultura y Deporte (2014a). Marco General de la Evaluación de 3er curso de Educación Primaria. Мадрид: Министерство образования, культуры и депортации.

Google Scholar

Министерство образования, культуры и депортации (2014b). PISA 2012 Informe español. Результаты в контексте. Мадрид: Министерство образования, культуры и депортации.

Google Scholar

Ministryio de Educación, Cultura y Deporte (2014c). Реальный декрет 126/2014, де 28 де febrero, por el que se establece el currículo básico de la Educación Primaria. Boletín Oficial del Estado 52, 1–58.

Google Scholar

Министерство образования и профессионального образования (2019). PISA 2018. Programa para la Evaluación Internacional de los Estudiantes. Informe Español. Доступно в Интернете по адресу: https://cutt. ly/zr3uTgk (по состоянию на 25 сентября 2020 г.).

Google Scholar

Министерство образования и профессионального образования (2020). Datos Estadísticos Para Enseñanzas No Universitarias. Доступно в Интернете по адресу: https://cutt.ly/GgeQCdi (по состоянию на 6 октября 2020 г.).

Google Scholar

Мизала А., Мартинес Ф. и Мартинес С. (2015). Ожидания учителей начальной школы перед началом работы в отношении успеваемости учащихся: как на их убеждения влияет их тревожность по математике и пол учащегося. Учить. Учить. Образовательный 50, 70–78. doi: 10.1016/j.tate.2015.04.006

CrossRef Полный текст | Google Scholar

Монрой Д. и Маррокин Б. (2020). Didáctica де ла Matemática у су importancia ан лос profesores ан formación. Rev. Guatemalteca Educ. Супериор 3, 47–59. doi: 10.46954/revistages.v1i1.4

Полный текст CrossRef | Google Scholar

Муэлас, А. (2014). Influencia де ла переменная де personalidad ан эль rendimiento académico де лос estudiantes cuando finalizan ла Educación Secundaria Obligatoria (ESO) у comienzan Bachillerato. Христ. коммун. соц. 18, 115–126. doi: 10.5209/rev_HICS.2013.v18.44230

Полный текст CrossRef | Google Scholar

Нортес А. и Нортес Р. (2013). Formación inicial de maestros: un estudio en el dominio de las Maemáticas. Проф. Преподобный Куррик. Форма. проф. 17, 185–200.

Google Scholar

Организация экономического сотрудничества и развития (2013). Система оценки и анализа PISA 2012: математика, чтение, естественные науки, решение задач и финансовая грамотность. Париж: Издательство ОЭСР.

Google Scholar

Организация экономического сотрудничества и развития (2019a). Баланс между выбором школы и справедливостью: международная перспектива, основанная на PISA. Париж: Издательство ОЭСР.

Google Scholar

Организация экономического сотрудничества и развития (2019b). Оценка и аналитическая основа PISA 2018. Париж: Издательство ОЭСР.

Google Scholar

Организация экономического сотрудничества и развития (2019в). Результаты PISA 2018 (Том I): Что знают и умеют учащиеся. Париж: Издательство ОЭСР.

Google Scholar

Организация экономического сотрудничества и развития (2019d). Результаты PISA 2018 (Том II): где все учащиеся могут добиться успеха. Париж: Издательство ОЭСР.

Google Scholar

Ортис-Ревилла, Дж., и Грека, И.М. (2021). «Намерения заниматься наукой и инженерией среди учащихся начальных классов, участвующих в интегрированных мероприятиях STEAM», в 11-я Международная конференция по европейскому транснациональному образованию (ICEUTE 2020). Достижения в области интеллектуальных систем и вычислений , редакторы А. Эрреро, К. Камбра, Д. Урда, Дж. Седано, Х. Квинтиан и Э. Корчадо (Чам: Спрингер).

Google Scholar

Паломарес-Руис, А., и Гарсия-Пералес, Р. (2020). Успеваемость по математике и секс: способность прогнозировать самоэффективность, интерес и мотивацию к изучению математики. Перед. Психол. 11:1879. дои: 10. 3389/fpsyg.2020.01879

Реферат PubMed | Полный текст перекрестной ссылки | Google Scholar

Пелегрина С., Гарсия М. К. и Казанова П. Ф. (2002). Лос estilos educativos де лос падрес у ла компетентности académica де лос подростков. Infancia Aprendizaje 25, 147–168. doi: 10.1174/021037002317417796

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Помар К., Диас О., Санчес Т. и Фернандес М. (2009). Habilidades matemáticas yverbales: diferencias de género en una muestra de 6ş de Primaria y 1ş de ESO. Ред. Междунар. Faisca de Altas Capacidades 14, 14–26.

Google Scholar

Прекель Ф., Гетц Т., Пекрун Р. и Кляйне М. (2008). Гендерные различия у одаренных и учащихся со средними способностями: сравнение достижений девочек и мальчиков, самооценка, интерес и мотивация в математике. Подарок. Чайлд В. 52, 146–159. doi: 10.1177/0016986208315834

Полный текст CrossRef | Google Scholar

Рамирес Р. и Каньядас М. К. (2018). Nominación у atención дель Talento matemático пор parte дель доценте. UNO Rev. Didáctica de las Matemáticas 79, 23–30.

Google Scholar

Рико Л., Гомес П. и Каньядас М. (2014). Начальное математическое образование маэстрос де Примария в Испании, 1991–2010 годы. Рев. Образование. 363, 35–59. doi: 10.4438/1988-592X-RE-2012-363-169

Полный текст CrossRef | Google Scholar

Родерер, Т., и Роберс, К.М. (2013). Оценка успеваемости детей в тестах по математике и естественным наукам в течение учебного года: экспериментальное исследование. Электрон. Дж. Рез. Образовательный Психол. 11, 5–24. doi: 10.25115/ejrep.v11i29.1555

Полный текст CrossRef | Google Scholar

Родригес Д. и Гусман Р. (2018). Relación entre perfil motivacional y rendimiento académico en educación secundaria obligatoria. Estudios Sobre Educación 34, 199–217. doi: 10.15581/004.34.199-217

CrossRef Полный текст | Google Scholar

Родригес-Мантилья, Дж. М., Фернандес-Диас, М. Дж., и Ховер, Г. (2018). PISA 2015: прогнозы результатов исследований в Испании. Рев. Образовательный. 38, 75–102. doi: 10.4438/1988-592X-RE-2017-380-373

Полный текст CrossRef | Google Scholar

Роман-Граван П., Эрвас-Гомес К., Мартин-Падилья А. Х. и Фернандес-Маркес Э. (2020). Представления об использовании образовательной робототехники в начальной подготовке будущих учителей: исследование устойчивости STEAM среди учителей-женщин. Устойчивое развитие 12:4154. doi: 10.3390/su12104154

CrossRef Полный текст | Google Scholar

Росарио П., Лоуренсо А., Пайва О., Родригес А., Валле А. и Туэро-Эрреро Э. (2012). Predicción del rendimiento en matemáticas: efecto de переменных personales, socialeducativas y del contexto escolar. Псикотема 24, 289–295.

Google Scholar

Ротигель, Дж. В., и Фелло, С. (2004). Математически одаренные школьники: как мы можем удовлетворить их потребности. Подарок. Чайлд сегодня 27, 46–51. doi: 10.4219/gct-2004-150

Полный текст CrossRef | Google Scholar

Руис Ф. (2005). Influencia de la autoeficacia en el ámbito académico. Университет Досенсии. 1, 1–16. doi: 10.19083/ridu.1.33

Полный текст CrossRef | Google Scholar

Рю Дж., Ли Ю., Ким Ю., Гундар П., Ли Дж. и Юнг Дж. Ю. (2021). «STEAM в образовании для одаренных в Корее», в Справочник по развитию одаренности и талантов в Азиатско-Тихоокеанском регионе , изд. С. Р. Смит (Сингапур: Springer).

Google Scholar

Сэсон Х., Михальски Т. и Мевареч З. (2020). Содействие пониманию научного текста учащимися средней школы с помощью двух самостоятельно созданных «связывающих» методов опроса. Перед. Психол. 11:595745. doi: 10.3389/fpsyg.2020.595745

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Schillinger, F.L., Vogel, S.E., Diedrich, J., and Grabner, R.H. (2018). Математическая тревожность, интеллект и успеваемость по математике: результаты немецкой адаптации Сокращенной шкалы математической тревожности (AMAS-G). Учиться. Индивид. Дифф. 61, 109–119. doi: 10.1016/j.lindif.2017.11.014

CrossRef Полный текст | Google Scholar

Шлейхер, А. (2018). Мировой класс: как построить школьную систему 21-го века, сильные исполнители и успешные реформаторы в сфере образования. Париж: Издательство ОЭСР.

Google Scholar

Сонг Л.Дж., Хуанг Г., Пэн З., Лоу К., Вонг К. и Чен З. (2010). Дифференциальное влияние общих умственных способностей и эмоционального интеллекта на успеваемость и социальные взаимодействия. Разведка 38, 137–143. doi: 10.1016/j.intell.2009.09.003

Полный текст CrossRef | Google Scholar

Шрираман Б. (2003). Математическая одаренность, решение проблем и способность формулировать обобщения: опыт решения проблем четырех одаренных учеников. Дж. Второй. Подарок. Образовательный 14, 151–165. doi: 10.4219/jsge-2003-425

CrossRef Полный текст | Google Scholar

Торрес, Л.Л. (2018). Culturas de escola e excelência: Entre a integração de todos e distinção dos melhores. Искр. соц. Образовательный 11, 167–185. doi: 10.7203/RASE.10.1.9135

Полный текст CrossRef | Google Scholar

ЮНЕСКО (2019). Descifrar el Código: La Educación De Las Niñas en Ciencias, Tecnología, Ingeniería Y Matemáticas (STEM). Франция: ЮНЕСКО.

Google Scholar

Урсини, С., и Рамирес-Меркадо, член парламента (2017). Equidad, género y matemáticas en la escuela mexicana. Рев. Коломб. Образовательный 73, 213–234. doi: 10.17227/01203916.73rce211.232

Полнотекстовая перекрестная ссылка | Google Scholar

Залазар, М. Ф., Апарисио, М. М. Д., Рамирес, К. М., и Гарридо, С. Дж. (2011). Estudios Preliminares de Adaptación de la Escala de Fuentes de Autoeficacia para Matematicas. Rev. Аргентина Ciencias Comportamiento 3, 1–6.

Google Scholar

Гендерные различия в математической мотивации: дифференциальное влияние на успеваемость в начальном образовании MECD], 2016) не помогают нам с оптимизмом смотреть на преподавание и изучение этого предмета в нашей стране.

Результат теста по математике от мая 2015 года, в котором оценивались 37 205 из 414 276 15-летних учащихся в Испании, составил 486 баллов, что значительно ниже среднего показателя по ОЭСР (49 баллов).0 баллов. В рейтинге 36 стран-членов Испания находится на 26-м месте, и только 7,2% испанских школьников достигли высокого уровня успеваемости (5 и 6) по математике, что на 3,5 процентных пункта меньше, чем в среднем по ОЭСР (10,7%).

Эти результаты, кажется, отражают проблему, которая постоянно ставит под сомнение эффективность процессов преподавания и обучения математике. Мотивационные и эмоциональные переменные, которые включают в себя убеждения, эмоции и отношения, кажутся важными, когда дело доходит до полного понимания и объяснения результатов. На самом деле все указывает на то, что математические достижения связаны с такими переменными, как воспринимаемая компетентность и самоэффективность (Randhawa et al., 19).93; Пахарес и Грэм, 1999 г.; Фаст и др., 2010; Уильямс и Уильямс, 2010 г. ; Parker et al., 2014), интерес (Köller et al., 2001; Lee et al., 2014; Jansen et al., 2016) и беспокойство (Ashcraft, 2002; Ashcraft and Ridley, 2005; Lyons and Beilock, 2012; Рамирес и др., 2016).

В этом контексте, если мы посмотрим на результаты PISA 2015 (Ministerio de Educación Cultura y Deporte [MECD], 2016), разница в успеваемости по математике между мальчиками и девочками в возрасте 15 лет составляет в среднем 8 баллов в странах ОЭСР и 11 баллов в Европейском союзе (ЕС) в целом, причем мальчики набирают больше баллов, чем девочки. В Испании мальчики набрали на 16 баллов больше, чем девочки, что намного выше среднего показателя по ОЭСР. Различные метаанализы в 1970-е и 1980-е годы продемонстрировали небольшое преимущество мужчин в математике среди учащихся средних школ (Hyde et al., 1990; Hedges and Nowell, 1995), по крайней мере, в решении сложных задач. Однако это зависит от страны (Else-Quest et al., 2010; Mullis et al., 2012; Ministryio de Educación Cultura y Deporte [MECD], 2016), и более свежие данные свидетельствуют о том, что этот гендерный разрыв может исчезнуть (Hyde и др. , 2008; Хайд и Мерц, 2009; Линдберг и др., 2010).

Установлено, что убеждения и взгляды могут оказывать значительное влияние на решение о выборе профессиональной карьеры, связанной с математикой (Colbeck et al., 2001; Ceci and Williams, 2011; Sadler et al., 2012; Kanny et al., 2012; al., 2014; Legewie and DiPrete, 2014; Wang and Degol, 2017). Кроме того, женщины часто недопредставлены в программах STEM (наука, технология, инженерия и математика), особенно в инженерных, физических и вычислительных науках в западных университетах (например, Larivière et al., 2013; Hyde, 2014). Имея это в виду, важно включить эту тему в программу исследований педагогической психологии, чтобы полностью понять взаимодействие между мотивационными конструкциями и результатами каждой группы (девочек и мальчиков). Кроме того, исследования показывают, что гендерные различия в математических способностях минимальны в раннем детстве и не проявляются постоянно до среднего или позднего подросткового возраста (например, Lindberg et al. , 2010; Robinson and Lubienski, 2011). Настоящее исследование направлено на изучение аффективно-мотивационного аспекта учащихся последних лет начального образования, поскольку девочки могут терять мотивацию к математике по мере прохождения этой конкретной образовательной ступени.

Академическая мотивация и успеваемость по математике

Мотивационные исследования в области математики обращались к таким конструктам, как самоэффективность, которая указывает на суждения учащихся о своих способностях выполнять конкретные математические задачи и интерес к математике как положительный аффективный опыт в деятельности, связанной с математика. Как изложено в теории ожидания-ценности , как ожидания успеха, так и субъективные ценности, связанные с задачей, напрямую влияют на производительность, достижения, усилия и настойчивость (Wigfield and Eccles, 2000). Различные исследования показали, что воспринимаемая самоэффективность положительно влияет на успеваемость по математике (Randhawa et al. , 19).93; Пахарес и Грэм, 1999 г.; Стивенс и др., 2006 г.; Фаст и др., 2010; Уильямс и Уильямс, 2010 г.; Паркер и др., 2014). Точно так же интерес учащихся к математике связан с сильным предпочтением математического содержания, что выражается в устойчивой приверженности с течением времени и лучшей успеваемости (Köller et al., 2001; Hidi and Renninger, 2006; Lee et al., 2014; Jansen et al., 2014). al., 2016) как в детстве, так и в подростковом возрасте (Lepper et al., 2005; Aunola et al., 2006; Denissen et al., 2007; Viljaranta et al., 2009).).

Имеются также данные о том, что математическая тревожность негативно связана с успеваемостью, приводя к избеганию и уменьшению ресурсов рабочей памяти, необходимых для решения математических задач (Ashcraft, 2002; Ashcraft and Ridley, 2005; Lyons and Beilock, 2012; Ramirez et al. , 2016). Когда дело доходит до операционализации измерения математической тревожности, необходимо понимать нюансы исследования, а также тот факт, что с ней может быть связан весь спектр эмоциональных реакций (Goetz and Hall, 2013; Pekrun and Linnenbrink-Garcia, 2014). и влияют на успеваемость (Pekrun et al., 2014, 2017). По этой причине в этом исследовании мы отдельно рассматриваем негативные эмоции, связанные с математикой, и математическую тревогу. В соответствии с теория контрольной ценности эмоций достижения (Pekrun, 2006), предполагается, что учащиеся, которым нравится математика, сосредотачивают свое внимание на задачах, лучше используя стратегии глубокого обучения и, следовательно, получая лучшие результаты. Учащиеся, которым, например, скучно на уроках математики, уделяют меньше внимания и меньше используют стратегии обучения или используют более поверхностные стратегии, что приводит к снижению успеваемости (Pekrun, 2006; Pekrun et al., 2017; Putwain et al. , 2018).

Гендерные различия в математической мотивации

Исследования подтвердили гендерные различия, даже в начальном образовании, в самооценке, самоэффективности и интересе к математике, предполагая, что мальчики в целом имеют лучшие мотивационные профили в математике, чем девочки (Eccles et al. ., 1993; Kurtz-Costes et al., 2008). Изучение гендерных различий в математической мотивации на этих первых этапах обучения представляет особый интерес. Таким образом, можно максимально использовать потенциал студенток, улучшая гендерный баланс участия в будущих курсах STEM, которые были признаны критическим фильтром для высококвалифицированных и высокооплачиваемых рабочих мест.

Согласно предыдущим исследованиям (Fredricks and Eccles, 2002; Jacobs et al., 2002; Preckel et al., 2008; Else-Quest et al., 2010; Frenzel et al., 2010; Guo et al., 2015; Ganley and Lubienski, 2016), девочки сообщают о более низком уровне индивидуального интереса и воспринимаемой математической компетентности. Наиболее существенные различия наблюдаются у учащихся средних школ и университетов, а не у учащихся более низких уровней образования.

Демонстрируя необходимость изучения гендерных различий в академической мотивации, предыдущие исследования пришли к выводу, что, например, математическая самооценка может быть положительно связана с успеваемостью мальчиков, но может даже оказывать негативное влияние на успеваемость девочек (Yoon et al. , 1996). Также было показано, что влияние интереса на успеваемость по математике может быть несколько более важным для девочек, чем для мальчиков (Ganley and Lubienski, 2016). С этой точки зрения, хотя теория ожидаемой ценности не разрабатывает теоретической основы для рассмотрения гендерных различий, в частности, ее можно использовать для облегчения интерпретации дифференциального воздействия убеждений и ценностей в себе (Wigfield et al., 1991, 1997; Экклс и др., 1993).

С точки зрения гендерных различий, связанных с эмоциями, вызываемыми математикой, среди которых выделяются исследования математической тревожности, исследования указывают (хотя и с небольшой величиной эффекта) на существование более высоких показателей тревожности у девочек, чем у мальчиков, при выполнении задач, связанных с математическим мышлением (Hyde и др., 1990; Эльз-Квест и др., 2010). Предполагая возможность того, что эти различия начинаются уже в начальной школе (Yüksel-şahin, 2008; Griggs et al., 2013), исследования предполагают наличие более высокого уровня математической тревожности, а также более негативных чувств и установок у мальчиков, чем у девочек. (Hyde et al., 1990; Nagy et al., 2008; Goetz and Hall, 2013; Goetz et al., 2013; Bieg et al., 2015). В соответствии с принципами теории контрольной ценности исследования, посвященные разным воздействиям, показывают, что положительные эмоции, связанные с математикой, могут оказывать более выраженное влияние на целеустремленность девочек (Pinxten et al., 2014) и что уровень тревоги и отрицательных эмоций может не влияют на достижения девочек так негативно, как можно было бы ожидать (Goetz et al., 2013).

Исходя из этих соображений и помимо попытки проверить гендерные различия, основной целью данного исследования является анализ возможного дифференциального воздействия переменных, используемых для изучения математической мотивации, на успеваемость мальчиков и девочек в начальной школе. Во-первых, мы предполагаем, что будут статистически значимые различия в математической мотивации между мальчиками и девочками. Мы ожидаем, что модель мотивации мальчиков с точки зрения воспринимаемой компетентности и внутренней мотивации к математике будет более позитивной, чем у девочек (Fredricks and Eccles, 2002; Jacobs et al. , 2002; Preckel et al., 2008; Else- Quest et al., 2010; Frenzel et al., 2010; Guo et al., 2015; Ganley and Lubienski, 2016), а девочки проявляют больше негативных чувств и большей тревожности по отношению к математике, чем мальчики (Hyde et al. , 1990; Надь и др., 2008 г.; Гетц и др., 2013; Биг и др., 2015). Мы изучим объяснительный потенциал и различную распространенность представлений о компетентности и внутренней мотивации, а также негативные чувства и беспокойство по поводу успеваемости по математике у мальчиков и девочек, предполагая, что воспринимаемая компетентность будет влиять на академическую успеваемость в обоих случаях (Randhawa et al., 1993; Пахарес и Грэм, 1999; Стивенс и др., 2006; Фаст и др., 2010; Уильямс и Уильямс, 2010; Паркер и др., 2014). Мы также исследуем возможность того, что влияние внутренней мотивации на производительность будет более значительным, когда речь идет об объяснении достижений девочек, а не мальчиков (например, Yoon et al., 19).96; Гэнли и Лубенски, 2016). Наконец, мы также рассмотрим, является ли тревога более важной при объяснении мальчикам «по сравнению с девочками» математических успехов (например, Goetz et al., 2013).

Материалы и методы

Участники

Выборка состояла из 897 учащихся 13 государственных начальных школ испанской провинции Ла-Корунья. Половину (50,2%) составляли мальчики, а половину (49,8%) — девочки. Им было от 9 до 13 лет ( M = 10,77; SD 9).0036 = 0,69). Из общего числа 437 учащихся 5-го класса начального образования (223 мальчика и 213 девочек) и 460 учащихся 6-го класса начального образования (227 мальчиков и 233 девочки).

Инструменты

Для измерения отношения учащихся к математике мы использовали IAM ( Inventario de Acttitudes hacia las Matematicas/Инвентаризация отношения к математике ). Этот инструмент является результатом расширения Шкалы математического отношения Феннема-Шермана (FSS), разработанной Феннема и Шерманом (19).76). Это расширенная версия шкалы с некоторыми изменениями, адаптированная для испанского языка и включающая новые измерения, направленные на более точное измерение отношения и мотивации учащихся к математике (Сильва, 2005; Гонсалес-Пьенда и др. , 2012; Куэли и др. , 2014). В этом исследовании мы использовали следующие измерения IAM:

• Внутренняя мотивация к математике (четыре пункта; α = 0,72): это оценивает мотивацию к изучению и пониманию содержания математики для получения удовольствия и личного удовлетворения, которые приходят от работы. с этим типом контента (пример: «Я нахожу математику приятной и стимулирующей»).

• Воспринимаемая компетентность в математике (четыре пункта; α = 0,75): оценивает уровень уверенности в себе для обучения и получения хороших результатов по математике (пример пункта: «Я думаю, что могу решать еще более сложные математические задачи »).

• Негативные чувства, вызванные математикой (три пункта; α = 0,71): оценивает наличие и интенсивность грусти и беспокойства, вызванных учебой, домашним заданием или посещением уроков математики (пример пункта: «В математическом классе I я печален и несчастен»).

• Беспокойство по поводу математики (три пункта; α = 0,77): оценивает уровень страха и нервозности учащихся при выполнении математических тестов и заданий (пример пункта: «Я чувствую себя неловко и нервничаю из-за математики»).

Элементы в каждом измерении были в формате типа Лайкерта с пятью вариантами ответов от 1 (полностью неверно) до 5 (полностью верно).

Оценка успеваемости по математике была получена по итоговым школьным оценкам, которые учащиеся-участники получили по этому предмету. Были использованы следующие оценки: 1 = плохо, 2 = удовлетворительно, 3 = хорошо, 4 = очень хорошо, 5 = отлично.

Процедура

Данные были собраны во время школьных занятий персоналом, не относящимся к школе, с предварительного согласия руководства школы и учителей учащихся. До участия в исследовании учителя, учащиеся и родители (в зависимости от школьных правил) были проинформированы о содержании и порядке проведения исследования. Перед сбором данных, который проводился один раз, участникам напомнили о важности честных ответов на различные вопросы.

Данные о целевых переменных были собраны в соответствии с рекомендациями этических стандартов, установленных Комитетом по этике исследований и преподавания Университета Ла-Корунья и Хельсинкской декларацией. Конфиденциальность данных была обеспечена, а участие было добровольным, так что выход из исследования был возможен в любое время.

Анализ данных

В дополнение к описательному и корреляционному анализу для изучения гендерных различий в математической мотивации также использовался дисперсионный анализ (ANOVA). Пошаговый линейный регрессионный анализ был проведен для изучения прогностической способности мотивационных переменных в отношении достижений в математике между мальчиками и девочками. В обоих случаях предикторами были 9 переменных.0035 внутренняя мотивация , воспринимаемая компетентность , негативные чувства и тревога по поводу математики , при этом критериальной переменной является окончательная академическая оценка учащегося по математике. Во-первых, анализ был направлен на то, чтобы понять вклад каждой из переменных, добавленных в уравнение регрессии, когда дело дошло до прогнозирования математических результатов. Кроме того, мы хотели установить вес и конкретную значимость предикторных переменных в каждой выборке. Величину эффекта рассчитывали в соответствии с критериями Коэна (1988) классическая работа: d < 0,20 = недостоверный эффект; d ≥ 0,20 и d < 0,50 = небольшой эффект; д ≥ 0,50 и д < 0,80 = умеренный эффект; и d ≥ 0,80 = большой эффект.

Результаты

Анализ результатов сначала направлен на определение того, существуют ли существенные различия в внутренней мотивации , воспринимаемая компетентность , негативные чувства и математическая тревога по пол . После этого мы исследуем вклад этого набора аффективно-мотивационных переменных в академическую успеваемость студентов.

В таблице 1 показаны коэффициенты корреляции, а также описательная статистика центральной тенденции, распределения и дисперсии для переменных в этом исследовании. Учитывая корреляции, академические достижения по математике имели положительную, статистически значимую связь с внутренняя мотивация к математике ( r = 0,19 , p < 0,01) и воспринимаемая компетентность ( r = 0,28 , p < ). Тревога и негативные чувства по отношению к математике отрицательно ассоциировались с успеваемостью ( r = -0,29, p < 0,01 и r = -0,33, p < 0,01 соответственно).

Таблица 1. Средние значения, стандартные отклонения, асимметрия, эксцесс и корреляционная матрица.

Взаимосвязь между воспринимаемой компетентностью и отрицательными эмоциями и математической тревожностью была отрицательной и значимой ( r = -0,43, p < 0,01 и r = -0,49, p < 0,01 соответственно). Точно так же негативные чувства по отношению к математике и тревога значимо отрицательно коррелировали с внутренней мотивацией к математике ( r = -0,50, p < 0,01 и r = -0,49, p < 0,01 соответственно). Как и следовало ожидать, существовала значимая положительная связь между отрицательным отношением к математике и математической тревогой ( r = 0,47, p < 0,01).

Различия в мотивации к математике между мальчиками и девочками

Мы обнаружили статистически значимые различия в мотивации к математике между мальчиками и девочками в начальной школе с умеренным размером эффекта, хотя различия в успеваемости по математике были незначительными [ F _{( 1} , _{895 )} = 1,174, p = 0,279]. Девочки сообщили о более низких уровнях самоэффективности [ F _{( 1} , _{985 )} = 11,227; р < 0,01; η _р ² = 0,012; d = 0,71] и внутренняя мотивация [ F _{( 1} , _{895 )} = 6,522; р < 0,05; η _р ² = 0,007; d = 0,61] по математике, чем мальчики. С другой стороны, в то время как мальчики и девочки имели одинаковые уровни негативных чувств по отношению к математике [ F _{( 1} , _{895 )} = 1,272, p

0 = 0], более высокие показатели математической тревожности , чем у их одноклассников мужского пола [ F _{( 1} , _{895 )} = 11,018; р < 0,01; η _р ² = 0,012; д = 0,70].

Влияние мотивации на успеваемость по математике у девочек и мальчиков

Мы провели два идентичных пошаговых регрессионных анализа, один для выборки мальчиков ( n = 450; M _{возраст} = 10,70 = 10,70; SD 90,79; ) и один для девочек ( n = 447; М _{возраст} = 10,75; SD = 0,68) с целью определения прогностической ценности мотивационных переменных для успеваемости по математике в каждой выборке.

Как видно из таблицы 2, в группе мальчиков как негативные чувства, так и тревога, связанные с математикой, наряду с предполагаемой компетентностью в предмете, в значительной степени способствовали прогнозированию успеваемости [ F _{( 3} , _{446 )} = 36,914; p < 0,001], что объясняет почти 20% дисперсии ( R ² = 0,194) критериальной переменной.

Таблица 2. Объяснена дисперсия ( R ² ), изменение в R ² (Δ R ² ), коэффициенты регрессии ( β ) и Соселительный статистический значимость ( p <)] в прогнозировании успеваемости мальчиков и девочек по математике.

В группе девочек внутренняя мотивация, негативное отношение к математике и предполагаемая компетентность в предмете также были предикторами успеваемости по математике [ F _{( 3} , _{443 )} = 18,093; p < 0,001], хотя в этом случае процент объясняемой дисперсии был вдвое меньше, чем в выборке мальчиков ( R ² = 0,103).

Результаты анализов подтверждают объяснительный потенциал обоих негативные чувства к математике (β = -0,207; t = -4,156; p < 0,001 для мальчиков и β = -0,267; t = -5,087; p < 0,001 для девочек) и воспринимаемая компетентность (β = 0,162 ; t = 3,301; p < 0,001 для мальчиков и β = 0,225; t = 3,60; p 9035 у девочек) по математике. (см. Таблицу 2). В обеих выборках отрицательные чувства были связаны с плохой успеваемостью по математике, тогда как положительный коэффициент регрессии для воспринимаемой компетентности в предмете указывает, как отмечалось в предыдущих исследованиях, на положительную связь между этими типами убеждений и успеваемостью.

Результаты также указывают на некоторые отличительные аспекты, которые следует подчеркнуть. Во-первых, вклад математической тревожности был только объясняющим фактором для мальчиков (β = -0,192; t = -3,819; p < 0,001), тогда как внутренняя мотивация оказалась значимой переменной в объяснении успеваемости девочек. (β = -0,159; t = -2,667; p < 0,05). Отрицательный коэффициент регрессии этой переменной указывает на то, что для девочек приверженность математике по внутренним причинам может негативно сказаться на их успеваемости по этому предмету. Мы обсуждаем этот результат в свете теории контрольных значений Пекруна (2006).

Обсуждение и заключение

В соответствии с предыдущими исследованиями (Hyde et al., 1990; Else-Quest et al., 2010; Goetz et al., 2013; Bieg et al., 2015) мы подтверждаем, что девочки в Пятый и шестой классы начального образования сообщают о более высоком уровне математической тревожности, чем мальчики, в данном случае с умеренной величиной эффекта. Однако эти гендерные различия в тревожности по поводу математики нельзя перенести на другие негативные чувства или эмоции, такие как грусть или скука, как предполагалось в предыдущих исследованиях (Hyde et al., 19).90; Надь и др., 2008 г.; Гетц и Холл, 2013 г.; Гетц и др., 2013; Биг и др., 2015). Наши результаты также повторяют предыдущие исследования, показывая, что мальчики сообщают о большей внутренней мотивации и воспринимаемой компетентности в математике, чем девочки (Fredricks and Eccles, 2002; Jacobs et al., 2002; Preckel et al., 2008; Else-Quest et al., 2010; Frenzel et al., 2010; Louis and Mistele, 2012; Guo et al., 2015; Ganley and Lubienski, 2016), хотя их результаты в математике схожи (Skaalvik and Skaalvik, 2004; Else-Quest et al. , 2010; Линдберг и др., 2010).

В общих чертах, как и ожидалось, наши результаты подтверждают хорошо известное положительное влияние воспринимаемой самоэффективности на успеваемость по математике в школе (Zimmerman, 1995; Pajares and Graham, 1999; Valentine et al. , 2004; Fast et al. , 2010; Williams and Williams, 2010; Parker et al., 2014), обнаруженные как в стандартизированных тестах, так и, как в нашем случае, в оценках, выставляемых в классе (Randhawa et al., 1993; Fast et al., 2010; Grigg и др., 2018).

Кроме того, как предполагают различные точки зрения, наши результаты подчеркивают важность и влияние эмоций учащихся на их обучение и успеваемость. Было показано, что объяснительная сила негативных эмоций, связанных с математикой, даже важнее, чем часто цитируемая математическая тревога, когда дело доходит до объяснения результатов по этому предмету. Исследования эмоций в математике неоднократно сосредотачивались на математической тревожности, весьма вероятно, игнорируя большое количество различных эмоций, таких как грусть и скука, которые, как «горячее познание», могут указывать на путь обучения и успеха. Несмотря на то, что исследования показывают, что взаимосвязь между эмоциями и производительностью, как правило, имеет небольшой или умеренный эффект, возможно, что академические эмоции в конечном итоге оказывают значительное кумулятивное долгосрочное влияние на производительность. По этой причине мы не должны упускать из виду их роль в здоровье, субъективном благополучии, выборе и продолжении учебы или в обучении на протяжении всей жизни (Pekrun, 2006).

Различия в процентах дисперсии успеваемости, объясняемые мотивационными переменными, которые мы исследовали у мальчиков и девочек, указывают на необходимость поощрения исследований гендерных различий в академических эмоциях и мотивациях в целом и в математике в частности. В то время как негативные чувства, тревога и предполагаемая компетентность вместе объясняют почти 20% различий в успеваемости мальчиков по математике, объяснительная сила негативных чувств, компетентности и внутренней мотивации у девочек составляет практически половину этой разницы. Получение свода знаний, которые позволили бы нам охарактеризовать дифференциальные мотивационные профили в контексте достижений, позволило бы лучше приспособить аффективно-мотивационные вмешательства. Гендерный разрыв в когнитивных способностях может быть сокращен в долгосрочной перспективе за счет поощрения конкретного образовательного опыта на этих первых этапах формального образования (Ganley and Lubienski, 2016).

В этом исследовании было замечено, что успеваемость мальчиков, которые были более уверены в своих способностях, более мотивированы и больше интересовались математикой, снижалась в связи с появлением негативных чувств по отношению к математике, и были отмечены высокие показатели беспокойство. Тем не менее, и в соответствии с наблюдениями Goetz et al. (2013), наши результаты, по-видимому, демонстрируют, что, хотя девочки сообщали о более высоком уровне тревожности, на их успеваемость по математическим задачам и тестам это не повлияло так негативно, как можно было бы ожидать. Несоответствие между состоянием и чертой, выявленное исследователями в этих и других академических эмоциях (например, Porter et al., 2000; Frenzel et al., 2007; Bieg et al., 2013, 2014), предполагает, что гендерные различия, обнаруженные в математической тревожности, могут не учитываться. отражаться в повседневных процессах школьного обучения. На эмоциональные оценки могут сильно влиять субъективные убеждения, такие как ожидания или склонности к атрибуции. Общепринятая идея о том, что девочки считают себя менее компетентными в математике, может быть причиной ошибочной упреждающей оценки их математической тревожности (например, Skaalvik and Skaalvik, 2004; Ganley and Lubienski, 2016). Представления этих девочек о своих математических способностях вместе с гендерными стереотипами (Wigfield and Eccles, 2000; Pekrun, 2006; Thoman et al., 2013; Bieg et al., 2015) способствуют эмоциональной оценке, которая отличается от эмоций. действительно связаны с конкретными задачами или ситуациями. Вот почему, несмотря на то, что девочки проявляют более высокий уровень беспокойства по поводу математики, чем мальчики, эта переменная не является объясняющим фактором успеваемости девочек.

Что касается предпосылок теории контрольной ценности, негативные чувства, такие как грусть, несчастье и отчаяние, связанные с математическими задачами, безусловно, являются результатом модели низкого контроля с высокой ценностью, придаваемой успеху (Frenzel et al. , 2007; Биг и др., 2015). Включение внутренней мотивации в качестве отрицательного предиктора успеваемости девочек по математике следует понимать в этом контексте, характеризующемся низкой воспринимаемой компетентностью по данному предмету. Согласно теории Пекрун (2006), если отрицательные эмоции являются результатом слабого контроля в сочетании с высокой ценностью успеха, вовлеченность по внутренним причинам, указывающая на высокую ценность математики, может в конечном итоге привести к снижению успеваемости девочек, поскольку это может способствовать негативным чувствам в этой области.

Образовательные последствия

С точки зрения потенциала эмоций, связанных с классной комнатой, стоит предложить лонгитюдные, экспериментальные и интервенционные исследования для изучения предполагаемых причинно-следственных связей между дискретными эмоциями, как отрицательными (как мы сделали в этом исследовании), так и отрицательными. и положительные (наслаждение, надежда и благодарность среди прочего), и производительность. Помимо включения знаний о модерировании и опосредовании переменных академических эмоций и их происхождения в программу подготовки учителей, учителя должны также учитывать влияние стилей обучения на академические эмоции своих учеников и их роль в поощрении положительных эмоций и уменьшении отрицательных эмоций, связанных с класс.

С точки зрения наших результатов и в соответствии с Ganley and Lubienski (2016), математические вмешательства для девочек должны начинаться рано и конкретно касаться восприятия уверенности и контроля. С другой стороны, управление эмоциями, особенно тревогой, может быть чрезвычайно важным для математических вмешательств у мальчиков. Выявление и разработка стратегий обучения и планов вмешательства для улучшения аффективно-эмоционального опыта, связанного с процессом обучения, должны быть в образовательной и исследовательской повестке дня.

Ограничения

Помимо внутренних ограничений дизайна исследования, мы должны признать использование самоотчета для измерения эмоций и тот факт, что мальчики и девочки, безусловно, различаются по своим способностям и склонностям при описании своих эмоций (Bryant et al. ., 1996). Информация об эмоциях может быть особенно уязвима для социальной желательности или стереотипизации в таком контексте, как математика, которая воспринимается как мужская сфера.

Заявление о доступности данных

Наборы данных, созданные для этого исследования, доступны по запросу соответствующему автору.

Заявление об этике

Исследования с участием людей были рассмотрены и одобрены Комитетом по этике Университета Коруньи. Письменное информированное согласие на участие в этом исследовании было предоставлено законным опекуном/ближайшим родственником участников.

Вклад авторов

SR и IE внесли свой вклад в сбор данных, их анализ и написание рукописи. BR и AV внесли свой вклад в анализ данных и написание рукописи. ИП написал рукопись.

Финансирование

Работа выполнена при финансировании исследовательских проектов EDU2013-44062-P ​​(MINECO) и EDU2017-82984-P (MEIC).

Конфликт интересов

Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.

Ссылки

Ashcraft, MH (2002). Математическая тревога: личные, образовательные и когнитивные последствия. Курс. Реж. Психол. науч. 11, 181–185. doi: 10.1111/1467-8721.00196

Полный текст CrossRef | Google Scholar

Эшкрафт, М. Х., и Ридли, К. С. (2005). «Математическая тревога и ее когнитивные последствия», в Handbook of Mathematical Cognition , изд. Дж. И. Д. Кэмпбелл (Нью-Йорк, штат Нью-Йорк: Psychology Press), 315–327.

Google Scholar

Аунола К., Лескинен Э. и Нурми Дж. Э. (2006). Динамика развития между успеваемостью по математике, мотивацией задачи и целями учителей при переходе в начальную школу. Бр. Дж. Образ. Психол. 76, 21–40. doi: 10.1348/000709905X51608

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Биг М., Гетц Т. и Хаббард К. (2013). Могу ли я освоить его и имеет ли это значение? Внутрииндивидуальный анализ контрольно-ценностных предшественников черт характера и академических эмоций состояния. Учиться. Индивид. Отличаться. 28, 102–108. doi: 10.1016/j.lindif.2013.09.006

CrossRef Полный текст | Google Scholar

Биг М., Гетц Т. и Липневич А. А. (2014). То, что учащиеся думают, что они чувствуют, отличается от того, что они чувствуют на самом деле — академическая самооценка сглаживает несоответствие между чертами характера и эмоциональными самоотчетами учащихся. PLos One 9:e92563. doi: 10.1371/journal.pone.0092563

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Биг, М., Гетц, Т., Уолтер, И., и Холл, Северная Каролина (2015). Одобрение гендерных стереотипов по-разному предсказывает несоответствие личностного состояния девочек и мальчиков в математической тревожности. Перед. Психол. 6:1404. doi: 10.3389/fpsyg.2015.01404

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Брайант Ф. Б., Ярнольд П. Р. и Гримм Л. Г. (1996). К модели измерения интенсивности аффекта: трехфакторная структура. Дж. Рез. Перс. 30, 223–247. doi: 10.1006/jrpe.1996.0015

Полный текст CrossRef | Google Scholar

Сеси, С.Дж., и Уильямс, В.М. (2011). Понимание текущих причин недопредставленности женщин в науке. Проц. Натл. акад. науч. 108, 3157–3162. doi: 10.1073/pnas.1014871108

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Коэн, Дж. (1988). Статистический анализ мощности для поведенческих наук. Нью-Джерси: Лоуренс Эрлбаум.

Google Scholar

Колбек С.Л., Кабрера А.Ф. и Теренцини П.Т. (2001). Обучение профессиональной уверенности: связь методов преподавания, самовосприятия учащихся и пола. Ред. Высокий. Образовательный 24, 173–191. doi: 10.1353/rhe.2000.0028

CrossRef Full Text | Google Scholar

Куэли М., Гонсалес-Кастро П., Альварес Л., Гарсия Т. и Гонсалес-Пьенда Дж. А. (2014). Переменные afectivo-motivacionales y rendimiento en matemáticas: un análisis bidirectional. Искр. Мексика. Псикол. 31, 153–163.

Google Scholar

Дениссен, Дж. Дж. А., Зарретт, Н. Р., и Экклс, Дж. С. (2007). Мне нравится это делать, я умею и знаю, что умею: продольные связи между достижениями в предметной области, самооценкой и интересом. Детская разработка. 78, 430–447. doi: 10.1111/j.1467-8624.2007.01007.x

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Экклс Дж., Вигфилд А., Гарольд Р. Д. и Блюменфельд П. (1993). Возрастные и гендерные различия в восприятии себя и задач детьми в начальной школе. Ребенок Дев. 64, 830–847. doi: 10.1111/j.1467-8624.1993.tb02946.x ​​

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Else-Quest, NM, Hyde, JS, and Linn, MC (2010). Межнациональные модели гендерных различий в математике: метаанализ. Психолог. Бык. 136, 103–127. doi: 10.1037/a0018053

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Fast, L. A. , Lewis, J. L., Bryant, M. J., Bocian, K. A., Cardullo, R. A., Rettig, M., et al. (2010). Опосредует ли математическая самоэффективность влияние воспринимаемой среды в классе на результаты стандартизированного теста по математике? Дж. Образование. Психол. 102, 729–740. doi: 10.1037/a0018863

Полный текст CrossRef | Google Scholar

Феннема Э. и Шерман Дж. А. (1976). Шкалы отношения Феннема-Шермана к математике: инструменты, предназначенные для измерения отношения женщин и мужчин к изучению математики. Дж. Рез. Мат. Образовательный 7, 324–326. doi: 10.2307/748467

CrossRef Полный текст | Google Scholar

Фредрикс, Дж. А., и Экклс, Дж. С. (2002). Компетентность и ценностные убеждения детей с детства до подросткового возраста: траектории роста в двух областях мужского пола. Дев. Психол. 38, 519–533. doi: 10.1037/0012-1649.38.4.519

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Френцель А.С., Гетц Т. , Пекрун Р. и Ватт Х.М. (2010). Развитие интереса к математике в подростковом возрасте: влияние пола, семьи и школьного контекста. Дж. Рез. Адолеск 20, 507–537. doi: 10.1111/j.1532-7795

CrossRef Полный текст | Google Scholar

Френзель А.С., Пекрун Р. и Гетц Т. (2007). Воспринимаемая учебная среда и эмоциональные переживания учащихся: многоуровневый анализ занятий по математике. Учиться. Инстр. 17, 478–493. doi: 10.1016/j.learninstruc.2007.09.001

CrossRef Полный текст | Google Scholar

Гэнли, К.М., и Лубенски, С.Т. (2016). Уверенность в математике, интерес и производительность: изучение гендерных моделей и взаимных отношений. Учиться. Индивид. Отличаться. 47, 182–193. doi: 10.1016/j.lindif.2016.01.002

CrossRef Полный текст | Google Scholar

Гетц Т., Биг М., Людтке О., Пекрун Р. и Холл Н. К. (2013). Действительно ли девочки испытывают больше беспокойства по математике? Псих. науч. 24, 2079–2287. doi: 10. 1177/0956797613486989

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Гетц, Т., и Холл, Северная Каролина (2013). «Эмоции и достижения в классе», в International Guide to Student Achievement , eds J. Hattie and EM Anderman, (Нью-Йорк, штат Нью-Йорк: Routledge), 192–195.

Google Scholar

Гонсалес-Пьенда Дж. А., Фернандес-Куэли М., Гарсия Т., Суарес Н., Фернандес Э., Туэро-Эрреро Э. и др. (2012). Diferencias de género en actitudes hacia las matemáticas en la enseñanza obligatoria. Преподобный Ибероам. Псикол. Салуд. 3, 55–73.

Google Scholar

Григг С., Перера Х. Н., Макилвин П. и Светлефф З. (2018). Отношения между математической самоэффективностью, интересом, намерениями и достижениями: социальная когнитивная перспектива. Контемп. Образовательный Психол. 53, 73–86. doi: 10.1016/j.cedpsych.2018.01.007

CrossRef Полный текст | Google Scholar

Григгс, М.С., Римм-Кауфман, С.Е., Мерритт, Э. Г., и Паттон, К.Л. (2013). Отзывчивый подход в классе и тревожность и самоэффективность учеников пятого класса по математике и естественным наукам. Сх. Психол. Q. 28, 360–373. doi: 10.1037/spq0000026

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Guo, J., Parker, P.D., Marsh, H.W., and Morin, A.J. (2015). Достижения, мотивация и образовательный выбор: продольное исследование ожиданий и ценности с использованием мультипликативной точки зрения. Дев. Психол. 51, 1163–1176. doi: 10.1037/a0039440

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Хеджес, Л. В., и Ноуэлл, А. (1995). Половые различия в результатах умственных тестов, изменчивость и количество лиц с высокими баллами. Наука 269, 41–45. doi: 10.1126/science.7604277

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Хиди, С., и Реннингер, К.А. (2006). Четырехэтапная модель развития интереса. Учеб. Психол. 41, 111–127. doi: 10.1207/s15326985ep4102_4

CrossRef Full Text | Google Scholar

Хайд, Дж. С. (2014). Гендерные сходства и различия. год. Преподобный Психолог. 65, 373–398. doi: 10.1146/annurev-psych-010213-115057

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Хайд Дж. С., Феннема Э., Райан М., Фрост Л. А. и Хопп К. (1990). Гендерные сравнения математических установок и аффектов: метаанализ. Психолог. Женщины Q. 14, 299–324. doi: 10.1111/j.1471-6402.1990.tb00022.x

Полный текст CrossRef | Google Scholar

Хайд, Дж. С., Линдберг, С. М., Линн, М. К., Эллис, А. Б., и Уильямс, К. С. (2008). Гендерное сходство характеризует успеваемость по математике. Наука 321, 494–495. doi: 10.1126/science.1160364

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Хайд, Дж. С., и Мерц, Дж. Э. (2009). Гендерные, культурные и математические показатели. Проц. Натл. акад. науч. 106, 8801–8807. doi: 10.1073/pnas.0

5106

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Джейкобс Дж. Э., Ланца С., Осгуд Д. У., Экклс Дж. С. и Вигфилд А. (2002). Изменения в самооценке и ценностях детей: гендерные и предметные различия в классах с первого по двенадцатый. Ребенок Дев. 73, 509–527. doi: 10.1111/1467-8624.00421

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Янсен М., Людтке О. и Шредерс У. (2016). Доказательства положительной связи между интересом и достижениями: изучение различий между людьми и внутри человека в пяти областях. Контемп. Образовательный Психол. 46, 116–127. doi: 10.1016/j.cedpsych.2016.05.004

CrossRef Полный текст | Google Scholar

Канни, М. А., Сакс, Л. Дж., и Риггерс-Пил, Т. А. (2014). Расследование сорокалетних исследований STEM: как объяснения гендерного разрыва менялись с течением времени. J. Несовершеннолетние женщины. науч. англ. 20, 127–148. doi: 10.1615/JWomenMinorScienEng.2014007246

CrossRef Полный текст | Google Scholar

Келлер О., Баумерт Дж. и Шнабель К. (2001). Имеет ли значение интерес? Взаимосвязь между академическим интересом и достижениями в математике. Дж. Рез. Мат. Образовательный 32, 448–470. doi: 10.2307/749801

CrossRef Полный текст | Google Scholar

Курц-Костес Б., Роули С.Дж., Харрис-Бритт А. и Вудс Т.А. (2008). Гендерные стереотипы о математике и естественных науках, а также самооценка способностей в позднем детстве и раннем подростковом возрасте. Меррил Палмер. квартал. 54, 386–409. doi: 10.1007/s10212-014-0216-7

CrossRef Полный текст | Google Scholar

Ларивьер В., Ни К., Гинграс Ю., Кронин Б. и Сугимото К. Р. (2013). Библиометрия: глобальные гендерные различия в науке. Нац. Новости 504, 211–213. doi: 10.1038/504211a

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Lee, W. , Lee, M.J., and Bong, M. (2014). Тестирование интереса и самоэффективности как предикторов академической саморегуляции и успеваемости. Контемп. Образовательный Психол. 39, 86–99. doi: 10.1016/j.cedpsych.2014.02.002

CrossRef Полный текст | Google Scholar

Легеви, Дж., и ДиПрет, Т.А. (2014). Среда средней школы и гендерный разрыв в науке и технике. Соц. Образовательный 87, 259–280. doi: 10.1177/0038040714547770

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Леппер, М. Р., Хендерлонг Корпус, Дж., и Айенгар, С. С. (2005). Внутренние и внешние мотивационные ориентации в классе: возрастные различия и академические корреляты. Дж. Образование. Психол. 97, 184–196. doi: 10.1037/0022-0663.97.2.184

Полный текст CrossRef | Google Scholar

Линдберг С. М., Хайд Дж. С., Петерсен Дж. Л. и Линн М. К. (2010). Новые тенденции в гендерной и математической успеваемости: метаанализ. Психолог. Бык. 136, 1123–1135. doi: 10.1037/a0021276

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Луи, Р. А., и Мистеле, Дж. М. (2012). Различия в баллах и самоэффективности по полу учащихся по математике и естественным наукам. Междунар. J. Sci. Мат. Образовательный 10, 1163–1190. doi: 10.1007/s10763-011-9325-9

CrossRef Полный текст | Google Scholar

Лайонс И.М. и Бейлок С.Л. (2012). Когда математика причиняет боль: тревога по поводу математики предсказывает активацию болевой сети в предвкушении занятий математикой. PLos One 7:e48076. doi: 10.1371/journal.pone.0048076

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Ministryio de Educación Cultura y Deporte [MECD] (2016). PISA 2015. Programa Para la Evaluación Internacional de los Alumnos. Informe Español. Мадрид: Министерство образования, культуры и депортации..

Google Scholar

Муллис И. В., Мартин М. О., Фой П. и Арора А. (2012). Международные результаты TIMSS 2011 по математике. Амстердам: Международная ассоциация по оценке образовательных достижений.

Google Scholar

Nagy, G., Garrett, J., Trautwein, U., Cortina, K.S., Baumert, J., and Eccles, J. (2008). «Гендерный выбор курса средней школы как предвестник гендерной профессиональной карьеры: опосредующая роль самооценки и внутренней ценности», в Гендерные профессиональные результаты: продольные оценки индивидуальных, социальных и культурных влияний , под редакцией HMG Watt и JS Eccles, (Вашингтон, округ Колумбия: Американская психологическая ассоциация), 115–143. doi: 10.1037/11706-004

Полный текст CrossRef | Google Scholar

Пахарес Ф. и Грэм Л. (1999). Самоэффективность, конструкции мотивации и успеваемость по математике у поступающих в среднюю школу. Контемп. Образовательный Психол. 24, 124–139. дои: 10.1006/ceps.1998.0991

Реферат PubMed | Полный текст перекрестной ссылки | Google Scholar

Паркер, П. Д., Марш, Х. В., Чиаррочи, Дж., Маршалл, С., и Абдульджаббар, А. С. (2014). Сопоставление математической самоэффективности и самооценки как предикторов долгосрочных результатов достижений. Учеб. Психол. 34, 29–48. doi: 10.1080/01443410.2013.797339

CrossRef Полный текст | Google Scholar

Пекрун, Р. (2006). Теория контрольной ценности эмоций достижения: предположения, выводы и последствия для образовательных исследований и практики. Учеб. Психол. Ред. 18, 315–341. doi: 10.1007/s10648-006-9029-9

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Пекрун Р., Холл Н.К., Гетц Т. и Перри Р.П. (2014). Скука и успеваемость: проверка модели взаимной причинно-следственной связи. Дж. Образовательный. Психол. 106, 696–710. doi: 10.1037/a0036006

Полный текст CrossRef | Google Scholar

Пекрун Р., Лихтенфельд С., Марш Х.В., Мураяма К. и Гетц Т. (2017). Эмоции достижения и академическая успеваемость: лонгитюдные модели взаимных эффектов. Ребенок. Дев. 88, 1653–1670. doi: 10.1111/cdev.12704

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Пекрун, Р., и Линненбринк-Гарсия, Л. (редакторы) (2014). Международный справочник эмоций в образовании. Нью-Йорк, штат Нью-Йорк: Тейлор и Фрэнсис.

Google Scholar

Пинкстен М., Марш Х.В., Де Фрейн Б., Ван Ден Нортгейт В. и Ван Дамм Дж. (2014). Наслаждаетесь математикой или чувствуете себя компетентным в математике? Взаимное влияние на успеваемость по математике и предполагаемые затраты математических усилий. Бр. Дж. Образ. Психол. 84, 152–174. doi: 10.1111/bjep.12028

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Портер, Л. С., Марко, К. А., Шварц, Дж. Э., Нил, Дж. М., Шиффман, С., и Стоун, А. А. (2000). Гендерные различия в копинге: сравнение черт и сиюминутных оценок. J. Soc. клин. Психол. 19, 480–498. doi: 10.1521/jscp.2000.19.4.480

Полный текст CrossRef | Google Scholar

Прекель Ф. , Гетц Т., Пекрун Р. и Кляйне М. (2008). Гендерные различия у одаренных и учащихся со средними способностями: сравнение достижений девочек и мальчиков, самооценка, интерес и мотивация в математике. Подарок. Ребенок. Q. 52, 146–159. doi: 10.1177/0016986208315834

Полный текст CrossRef | Google Scholar

Putwain, D.W., Becker, S., Symes, W., and Pekrun, R. (2018). Взаимные отношения между академическим удовольствием студентов, скукой и достижениями во времени. Учиться. Инстр. 54, 73–81. doi: 10.1016/j.learninstruc.2017.08.004

CrossRef Full Text | Google Scholar

Рамирес Г., Чанг Х., Малони Э. А., Левин С. К. и Бейлок С. Л. (2016). О взаимосвязи между математической тревожностью и математическими достижениями в начальной школе: роль стратегий решения проблем. Дж. Эксп. Ребенок. Психол. 141, 83–100. doi: 10.1016/j.jecp.2015.07.014

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Рандхава Б.С., Бимер Дж. Э. и Лундберг И. (1993). Роль математической самоэффективности в структурной модели математических достижений. Дж. Образовательный. Психол. 85, 41–48. doi: 10.1037/0022-0663.85.1.41

CrossRef Полный текст | Google Scholar

Робинсон, Дж. П., и Лубенски, С. Т. (2011). Развитие гендерных разрывов в успеваемости по математике и чтению в начальной и средней школе: изучение прямых когнитивных оценок и рейтингов учителей. 900:35 утра. Образовательный Рез. J. 48, 268–302. doi: 10.3102/0002831210372249

CrossRef Full Text | Google Scholar

Сэдлер П.М., Соннерт Г., Хазари З. и Тай Р. (2012). Стабильность и изменчивость профессионального интереса к STEM в старшей школе: гендерное исследование. науч. Образовательный 96, 411–427. doi: 10.1002/sce.21007

Полный текст CrossRef | Google Scholar

Сильва, Э. Х. (2005). Действия Hacia эль Aprendizaje де лас Математикас. Tesis Doctoral no publicada, Университет Овьедо, Овьедо.

Google Scholar

Скаалвик Э. М. и Скаалвик С. (2004). Я-концепция и самоэффективность: тест внутренней/внешней системы координат модели и предсказания последующей мотивации и достижений. Психолог. Респ. 95, 1187–1202. doi: 10.2466/pr0.95.3f.1187-1202

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Стивенс Т., Оливарес А. и Хамман Д. (2006). Роль познания, мотивации и эмоций в объяснении разрыва в успеваемости по математике между латиноамериканскими и белыми учащимися. Латиноамериканец Дж. Бехав. науч. 28, 161–186. doi: 10.1177/0739986305286103

CrossRef Full Text | Google Scholar

Томан Д. Б., Смит Дж. Л., Браун Э. Р., Чейз Дж. и Ли Дж. Й. К. (2013). Помимо производительности: модель мотивационного опыта угрозы стереотипа. Учеб. Психол. Ред. 25, 211–243. doi: 10.1007/s10648-013-9219-1

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Валентайн Дж., Дюбуа Д. и Купер Х. (2004). Связь между уверенностью в себе и успеваемостью: метааналитический обзор. Учеб. Психол. 39, 111–133. doi: 10.1207/s15326985ep3902_3

CrossRef Full Text | Google Scholar

Вильяранта Дж., Леркканен М.К., Пойккеус А.М., Аунола К. и Нурми Дж.Э. (2009). Взаимосвязь между мотивацией задачи и успеваемостью по арифметике и грамотности в детском саду. Учиться. Инстр. 19, 335–344. doi: 10.1016/j.learninstruc.2008.06.011

CrossRef Full Text | Google Scholar

Ван, М. Т., и Дегол, Дж. Л. (2017). Гендерный разрыв в науке, технологиях, инженерии и математике (STEM): текущие знания, последствия для практики, политики и будущих направлений. Учеб. Психол. Ред. 29, 119–140. doi: 10.1007/s10648-015-9355-x

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Wigfield, A., Eccles, J., Mac Iver, D., Reuman, D., and Midgley, C. (1991). Переходы в раннем подростковом возрасте: изменения в самовосприятии детей в конкретной области и общей самооценке при переходе в неполную среднюю школу. Дев. Психол. 27, 552–565. doi: 10.1037/0012-1649.27.4.552

Полный текст CrossRef | Академия Google

Вигфилд, А., и Экклс, Дж. С. (2000). Теория ожидаемой ценности мотивации достижения. Контемп. Образовательный Психол. 25, 68–81. doi: 10.1006/ceps.1999.1015

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Wigfield, A., Eccles, J.S., Yoon, K.S., Harold, R.D., Arbreton, A., Freedman-Doan, K., et al. (1997). Изменения в представлениях детей о компетентности и субъективных ценностях задач в начальной школе: трехлетнее исследование. Дж. Образовательный. Психол. 89, 451–469. doi: 10.1037/0022-0663.89.3.451

Полный текст CrossRef | Google Scholar

Уильямс Т. и Уильямс К. (2010). Самоэффективность и успеваемость по математике: взаимный детерминизм в 33 странах. Дж. Образовательный. Психол. 102, 453–466. doi: 10.1037/a0017271

CrossRef Полный текст | Google Scholar

Юн, К.С., Экклс, Дж. С., и Вигфилд, А. (1996). «Я-концепция способностей, ценности и успеваемости: проверка причинно-следственных связей», в Ежегодное собрание Американской ассоциации исследований в области образования (Нью-Йорк, штат Нью-Йорк).

Google Scholar

Юксель-Шахин, Ф. (2008). Математическая тревожность среди учащихся 4-х и 5-х классов турецкой начальной школы. Междунар. Электрон. Дж. Матем. Образовательный 3, 179–192.

Google Scholar

Циммерман, Б. Дж. (1995). «Самоэффективность и развитие образования», в Самоэффективность в меняющихся обществах , ред. А. Бандура (Нью-Йорк, штат Нью-Йорк: издательство Кембриджского университета), 202–231. дои: 10.1017/CBO9780511527692.009

CrossRef Полный текст | Google Scholar

Сравнительные математические задачи

1. x + y = 15 

x – y = 24
Столбец A – (y)
Столбец B – (-5)

Столбец A, если число
больше
1. , если количество в столбце B больше
2. , если два количества равны
3. , если невозможно определить, какое количество больше
ш, у, х и г
Столбец B – 70
1. , если количество в столбце A больше
2. , если количество в столбце B больше
3. , если два количества равны
4. , если невозможно определить, какое количество больше
3. Затененные области на рисунке ниже составляют 65% площади всего круга. Каково значение d?
Столбец A – d 
Столбец B – 126 градусов
1. , если количество в столбце A больше 
2. , если количество в столбце B больше
3. , если два количества равны
4. , если невозможно определить, какое количество больше
4. Столбец A – площадь круга с радиусом 3
Столбец B – площадь полукруга радиусом 4
1. , если количество в столбце A больше
2. , если количество в столбце B больше
3. , если два количества равны
4. , если оно равно невозможно определить, какая величина больше
5. Сара вызвалась добровольцем с 9:27 утра. до 12:45
Ян вызвался добровольцем с 9:15 утра. до 12:32
Столбец A – количество времени, которое Сара добровольно вызвалась.
Столбец B — количество времени, которое Ян добровольно вызвался.
1. если количество в столбце А больше
2. если количество в столбце В больше
3. если два количества равны
4. если невозможно определить какое количество больше
6. Если 34% от 360 равно 7,5% от h, чему равно h
Столбец A – h
Столбец B – 1634
1. если количество в столбце A больше
2. если количество в столбце B больше
3. , если две величины равны
4. , если невозможно определить, какая величина больше
7. Столбец A – Доля 76 часов в неделю в день
1. если количество в столбце А больше
2. если количество в столбце Б больше
3. если два количества равны
4. если невозможно определить какое количество больше
8. Столбец А – ( x-y)
Столбец B – 0
1. , если количество в столбце A больше
2. , если количество в столбце B больше
3. , если два количества равны
4. , если невозможно определить, какое количество больше больше
9. Столбец А – 500% от 6
Столбец Б – 600% от 5
1. , если количество в столбце А больше равно
2. , если невозможно определить, какая величина больше
10. Если n>0,
Столбец A – 24/25 от n
Столбец B – 95% от n
1. , если количество в столбце A больше 
2. , если количество в столбце B больше 
3. , если две величины равны
4. , если невозможно определить, какая из величин больше
11. 5 составляет 2/3% от n количество в столбце A больше
1. если количество в столбце B больше
2. если две величины равны
3. если невозможно определить какая величина больше

1. уравнений дает  г 91 899 = -4,5. Поскольку -4,5 больше, чем -5, количество в столбце А больше.

2.  A:  Среднее значение может быть представлено как (360°)/5, что равно 72°. Поскольку 72° больше 70°, количество в столбце А больше.

3.  C:  Заштрихованная область представляет собой общий угол, который может быть представлен как 0,65 (360°) или 234°. Таким образом, незаштрихованная площадь, представляющая значение d, равна разности 360° и 234°, или 126°. Это значение такое же, как и для столбца B.

4.  A:  Площадь круга с радиусом 3 равна 9p. Площадь полукруга радиусом 4 равна половине 16п, а именно 8п. Таким образом, количество в столбце А больше.

5. A:  Количество времени, которое Сара предложила, составило 3 часа 18 минут. Количество времени, которое Ян вызвался добровольно, составило 3 часа 17 минут. Таким образом, количество Сары было больше.

6. B: Задача может быть смоделирована как 0,34(360) = 0,075 ч . Решение для ч дает ч = 1632, что меньше 1634. Таким образом, количество в столбце B больше.

7.  A:  Доля 76 часов в неделю может быть представлена ​​соотношением 76/168, что составляет примерно 45%. Доля 10 часов в сутках может быть представлена ​​соотношением 10/24, что составляет примерно 42%. Таким образом, количество в столбце А больше.

8. C:  Поскольку значения x и y одинаковы, разница будет равна 0. Таким образом, количества в столбцах A и B равны.

9. C: Значение для столбца A может быть записано как 5(6). Значение столбца B может быть записано как 6(5). Оба выражения равны 30, поэтому количества для столбцов A и B равны.

10. A: Количество, указанное для столбца A, может быть записано как 0,96 n , что больше, чем 0,95 n . Таким образом, количество для столбца А больше.

11. B: Задача может быть смоделирована как 5 = 0,667 n , где n  ~ 7,5. Поскольку 15 больше 7,5, количество в столбце B больше.

Как написать сочинение по математике для сравнения и сопоставления: описание каждого шага

CustomWritings. com

• Индивидуальная помощь в написании любых работ по более чем 80 дисциплинам.
• От 10 долларов США за страницу
• 100% оригинальные документы

Посетите сайт Одна бесплатная страница

Domyessay.net

• Индивидуальная и экономящая время помощь при написании.
• От 10 долларов США за страницу
• 326 экспертов-писателей в вашем распоряжении

Посетите сайт

Fastessay.com

• Хорошо написанные оригинальные документы вы можете получить всего за 2 часа.
• От 13,40 долл. США за страницу
• 9,62/10 уровень удовлетворенности клиентов

Посетите сайт

Thepensters.com

• Служба академической помощи, где вы можете выбрать своего собственного писателя.
• От 10 долларов США за страницу
• Полный контроль над вашим заказом

Посетите сайт

Codingpedia. org

• Помощь в программировании по более чем 10 предметам программирования или любой другой дисциплине STEM.
• От 29 долларов за страницу
• Оценка 8,5/10 от клиентов

Посетите сайт

Написание сравнительного эссе может показаться задачей, не требующей больших умственных способностей — в конце концов, вам просто нужно провести сравнение между двумя (или более) вещами. Что может быть проще? К сожалению, зачастую все гораздо менее прямолинейно. В средней и старшей школе сочинения такого типа, возможно, было легко писать, потому что вы в основном имели дело с конкретными, реальными объектами, понятиями и категориями вещей. Однако, когда дело доходит до математики, ситуация становится намного сложнее, поскольку математика является весьма абстрактной дисциплиной.

Ваши профессора могут попросить вас проанализировать и сравнить чрезвычайно абстрактные и расплывчатые идеи, правила и принципы. Чтобы сделать это, не совершая всевозможных ошибок, вы должны понимать все аспекты того, что вы делаете — и вы можете найти всю необходимую информацию в этом руководстве. Выполняйте все его шаги, и ваше следующее сопоставительное сочинение по математике не вызовет у вас никаких затруднений.

Как написать сочинение по математике для сравнения и сопоставления: подготовка к написанию

1. Выбор темы

Если ваш профессор еще не назначил вам тему или, по крайней мере, не ограничил ваш выбор, вам придется найти, сформулировать и исследовать тему самостоятельно. Хорошей новостью является то, что при написании эссе о сравнении и сопоставлении вам не нужно быть особенно изобретательным в этом отделе — вам просто нужно выбрать элементы, которые вы хотите проанализировать и сравнить друг с другом. При желании вы можете ограничить сравнение определенной областью — например, если вы пишете о развитии математической мысли в Европе и Азии, вы можете сосредоточиться на конкретном периоде истории и охватить только доминирующие школы, существовавшие в обоих регионах в то время. времени, не говоря уже о конкретных ученых.
Выбирая тему для эссе о сравнении и сопоставлении, было бы неплохо провести некоторое исследование, прежде чем брать на себя какие-либо обязательства. Довольно легко остановиться на теме только для того, чтобы обнаружить, что элементы, которые вы выбрали для сравнения, слишком неудобны для анализа рядом друг с другом. Например, вы можете обнаружить, что у них не так много точек соприкосновения, и вы просто не можете осмысленно сравнивать их. В других типах эссе обычно можно немного изменить тему, чтобы сделать ваше письмо более управляемым; однако в сравнительных и противопоставленных работах вам придется выбрать другую тему и начать заново. Поэтому убедитесь, что вы выбрали предметы, которые подходят друг другу.
В итоге вы должны получить что-то вроде этого:

• Математическая мысль в Индии и Китае в эпоху Нового времени;
• Пифагор и Блез Паскаль: их вклад в математическую мысль и влияние на нее;
• Математическая традиция в Азии и на Западе: сильные и слабые стороны;
• Математика и алгебра: различия и сходства.

2. Убедитесь, что сравнение имеет смысл

Написание эссе о сравнении и противопоставлении включает в себя больше, чем просто сопоставление двух концепций и последовательное обсуждение всех их сходств и различий. Если вы сделаете это, ваше эссе будет выглядеть бессвязным и дилетантским. Что превращает его из набора не связанных между собой точек в связное и связное целое, так это основная идея. Что доказывает ваше сравнение? Можно ли прийти к определенному выводу на основе вашего анализа? Убедитесь, что сравнение рассматриваемых предметов имеет смысл; в противном случае вам, возможно, придется изменить свою тему.

3. Мозговой штурм

Прежде чем приступить к дальнейшему изучению предметов, которые вы собираетесь сравнивать, вы должны систематизировать то, что вы уже знаете о них. Вы можете просто записать список всех их важных характеристик и то, как они сравниваются на их основе. Если у вас есть склонность к визуальному обучению, попробуйте диаграммы Венна — они представляют различия и сходства в удобной для понимания форме и могут привести вас к некоторым полезным выводам.
Постарайтесь придумать как можно больше пунктов и не заботьтесь об их актуальности на данном этапе — позже у вас будет возможность отбросить менее важные. Запишите, что вам следует исследовать: например, дополнительные критерии для сравнения и примеры для подтверждения определенных точек зрения.

4. Исследования

Все, что вы уже знаете по теме, вам придется собрать дополнительную информацию, прежде чем проводить какие-либо более глубокие сравнения.
Есть много способов найти источники этой информации: проконсультируйтесь со своим преподавателем и спросите, может ли он/она порекомендовать какие-либо соответствующие публикации, поговорите с библиотекарем или самостоятельно выполните поиск в библиотеке вашего колледжа. Однако, вероятно, наиболее многообещающим подходом было бы использование одной из многих онлайновых академических баз данных и поисковых систем — они включают информацию о тысячах научных журналов, книг и других публикаций и позволяют искать их в одном месте. Вы можете использовать общие, такие как Google Scholar и EBSCO, или взглянуть на более специализированные (например, arXiv.org или CiteSeerX).

Сначала выберите несколько ключевых слов, непосредственно относящихся к вашей теме, и посмотрите, что вы можете найти. Затем выберите несколько работ, которые содержат больше всего информации, и просмотрите разделы их библиографии (обратите внимание и на другие публикации тех же авторов). То, что вы найдете таким образом, должно быть более чем достаточно для завершения вашей работы.

5. Выбор наиболее подходящей конструкции

Это еще один вопрос, о котором следует подумать заранее. В противном случае вы можете обнаружить, что другая структура лучше соответствует вашей теме на полпути, и изменение вещей на этом этапе может занять очень много времени.

Существует три типичных структуры эссе для сравнения и противопоставления.
Пункт за пунктом
Вы выделяете наиболее важные критерии сравнения и анализируете позиции с этой точки зрения. Например, если вы сравните математические традиции разных цивилизаций, вы можете сначала сравнить, когда они ввели понятие нуля, перейти к идее отрицательных чисел и упомянуть несколько других важнейших математических открытий одно за другим.
В результате вы получаете хорошо структурированное сравнение, которое подробно анализирует каждый аспект рассматриваемых понятий и сразу же проводит все сравнения. Этот подход лучше всего использовать, когда у вас есть много моментов для обсуждения и вы не хотите, чтобы читатель запутался.
Блок за Блоком
Сначала вы описываете один предмет со всеми его характеристиками, затем переходите к следующему и делаете то же самое для него, обращая внимание читателя на то, что в них похоже и отличается. Этот подход лучше всего использовать, когда у вас есть только несколько важных моментов для обсуждения или вы хотите сначала описать один элемент, а затем использовать его в качестве фона для анализа другого.

Если у вас есть более двух элементов для сравнения или есть много разных критериев, которые вы хотите охватить, лучше избегайте этого метода, иначе ваш текст будет слишком явно разделен на несвязанные части.
Сходства/различия
Сначала вы описываете, что общего у исследуемых предметов, затем переходите к их различиям (или наоборот). Этот подход эффективен, когда вы хотите привлечь внимание к тому факту, что сравниваемые предметы очень разные, несмотря на многочисленные сходства (или, наоборот, очень похожи, несмотря на то, что в некоторых отношениях резко различаются).

Как написать сочинение по математике для сравнения и сопоставления: советы по написанию

1. Написание плана

Начните работу с написания плана. Это хорошее эмпирическое правило при работе с любым письменным заданием, но оно вдвойне полезно, когда вы пишете эссе со сравнением и сопоставлением, поскольку оно защищает вас от обширных переписываний и исправлений, которые могут вам понадобиться, если вы только начинаете писать.
Набросок — это больше, чем план, это скорее миниатюра всего вашего эссе. Вы записываете все его части и разделы, делаете краткие заметки о том, что вы собираетесь сказать, какие примеры использовать, как соединить отдельные части друг с другом, чтобы обеспечить плавное логическое течение. Вы можете быть настолько простыми или подробными, насколько хотите — здесь важно, чтобы это соответствовало вашим требованиям и работало для вашего стиля письма. Некоторые студенты пишут конспект настолько подробно, что его достаточно немного дополнить, чтобы он превратился в полноценное эссе.

2. Использование правильных переходных слов

Переходные слова и фразы используются для соединения отдельных частей вашего эссе, чтобы ваше письмо читалось естественно, без резких скачков с одной темы на другую. Некоторые из наиболее распространенных включают «пока», «однако», «в отличие от», «однако», «похоже», «аналогично», «по-другому» и так далее. Убедитесь, что вы всегда используете их в начале или в конце абзацев, чтобы подвести читателя к следующей мысли.

3. Не забывайте о подтверждающих доказательствах

Когда вы говорите о сходствах или различиях между обсуждаемыми вами предметами, вы не должны просто констатировать их как факты, какими бы очевидными они ни были. Когда вы что-то говорите, всегда подкрепляйте это примерами, свидетельствами из надежных изданий, статистикой и так далее. Старайтесь уделять относительно одинаковое количество внимания каждому пункту и каждому критерию сравнения.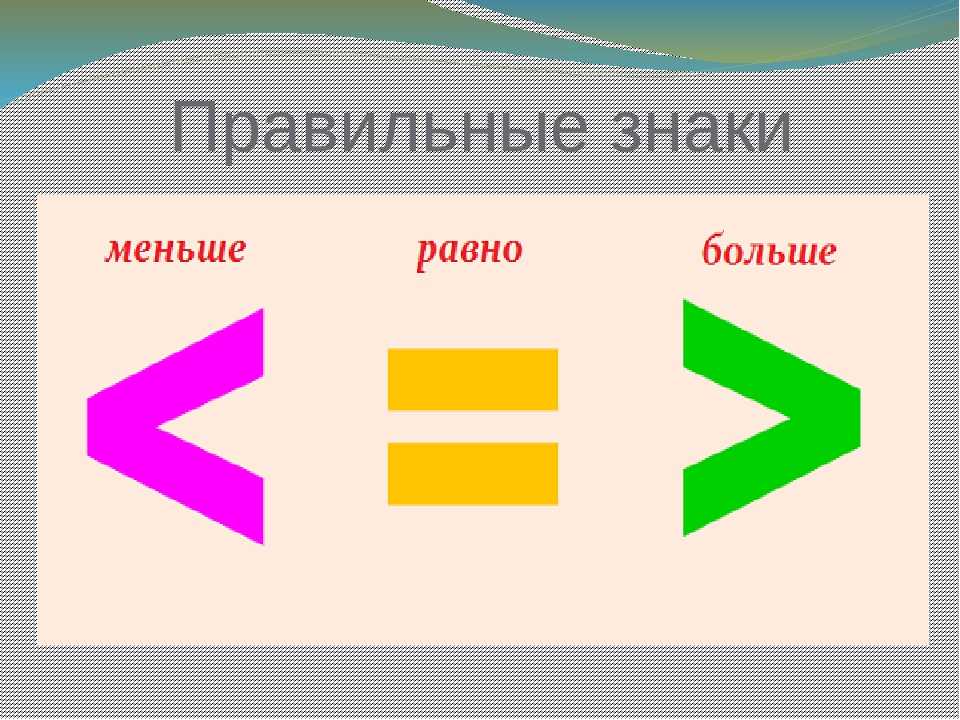 Для этого прикиньте, сколько абзацев вам придется написать и сколько слов вы сможете использовать в каждом из них.

4. Осветите только самые важные моменты

Вам не обязательно обсуждать абсолютно все о предметах, которые вы сравниваете. Эссе очень ограничено по объему, и если вы постараетесь сказать хотя бы пару слов о каждой мелочи, ваш анализ получится всесторонним, но крайне поверхностным. Лучшим решением будет выбрать несколько важных моментов и провести по ним подробное сравнение. Подумайте, какие из них докажут ваше видение даже без остальных доказательств, а какие можно смело отбросить.

Как написать сочинение по математике для сравнения и сопоставления: последние штрихи

1. Проверка грамматики и орфографии с помощью интерактивных программ проверки орфографии

Конечно, в Microsoft Word есть собственный встроенный инструмент проверки орфографии, и многие учащиеся считают, что его одного более чем достаточно, чтобы покрыть все их потребности в исправлении.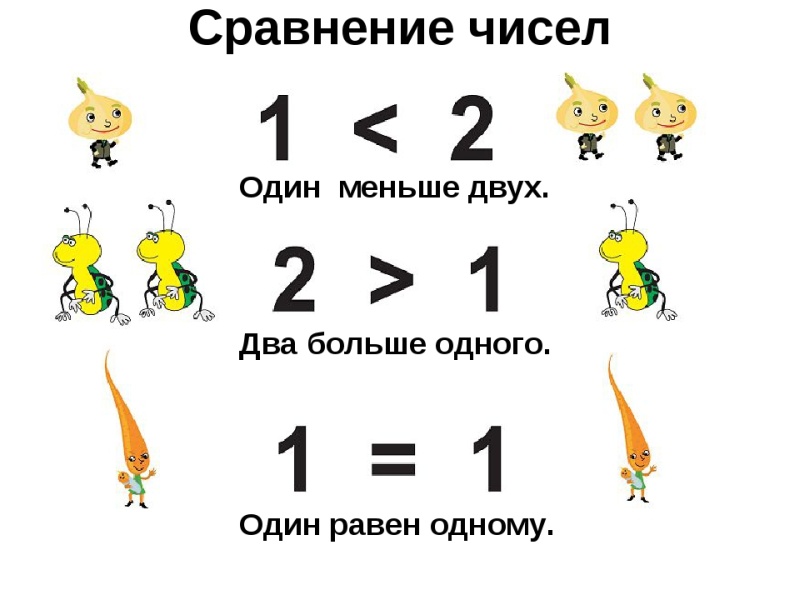 К сожалению, он крайне неадекватен для своей задачи и выявляет только самые основные ошибки, пропуская вполне очевидные промахи и возвращая многочисленные ложные срабатывания.
Некоторые онлайн-инструменты для проверки орфографии и грамматики (Grammarly, GrammarCheck, Scribens и другие) обладают гораздо большей функциональностью, поэтому попробуйте выбрать несколько и посмотреть, подходят ли они вам. Однако не слишком на них полагайтесь — ни один из них не заменит корректора-человека.

2. Несколько раз корректируйте свой текст

Человеческий мозг просто не устроен таким образом, чтобы он мог уделять внимание нескольким вещам одновременно. Если вы попытаетесь вычитать свое эссе с идеей поиска ошибок в целом, вы заметите некоторые из них, но они, вероятно, будут самыми очевидными. Если хотите копнуть глубже, пройдитесь по тексту несколько раз, каждый раз сосредотачиваясь на какой-то его части: грамматике, орфографии, структуре предложения, логических связях между предложениями и так далее. Если вы знаете, что особенно склонны к определенному типу ошибок, уделите особое внимание их выявлению.

3. Измените способ восприятия текста

Когда вы читаете написанный вами текст, вы ожидаете слишком многого. Внесите изменения, чтобы сломать это ожидание: прочитайте текст вслух — это позволит вам достаточно замедлиться, чтобы начать воспринимать отдельные слова, а не предложения. Прочитайте его в обратном порядке, предложение за предложением — таким образом, вы больше сосредоточитесь на структуре предложения, а не на общем потоке. Распечатайте его после того, как немного поиграетесь с типами и размерами шрифта — это поможет вам получить более свежий взгляд на то, что вы пишете.

4. Перепроверьте цифры

При написании эссе по математике вам почти наверняка придется включить в текст некоторые числа, цифры и формулы. Если это так, то не забудьте перепроверить каждое число, прежде чем сдавать работу. В математике небольшая ошибка в числах может резко изменить весь смысл, поэтому будьте к ним вдвойне осторожны.
Написать реферат по математике, конечно, может быть очень хлопотно, особенно если у вас нет опыта. Однако, даже если вы впервые пишете что-то подобное, вы можете добиться желаемых результатов, если внимательно будете следовать этому руководству и скрупулезно выполнять каждый шаг.

Исследователи Вандербильта находят ценность в сравнении нескольких стратегий преподавания и изучения математики

22 января 2021 г., 9:07

Как принципы когнитивной науки могут способствовать углублению математического образования? Группа исследователей из Колледжа образования и человеческого развития Пибоди Университета Вандербильта и Высшей школы образования Гарвардского университета изучила, как использование базового процесса обучения — сравнения — может привести к более высоким результатам по математике для школьников K-12, и проанализировала различные подходы к включение сравнения в учебную программу . Краткое изложение результатов исследования исследователей колледжа Пибоди Бетани Риттл-Джонсон и Келли Дуркин в сотрудничестве с Джоном Старом из Гарвардского университета было недавно опубликовано в декабрьском выпуске журнала Current Directions in Psychological Sciences за 2020 год.

Бетани Риттл-Джонсон (Университет Вандербильта) Келли Дуркин (Университет Вандербильта)

Когда дело доходит до выполнения математических процедур, студенты часто запоминают шаги, не понимая математических принципов, лежащих в основе каждого из них. Просьба к учащимся сравнить и обсудить несколько методов решения одной и той же проблемы стимулирует мышление более высокого порядка и требует от учащихся более глубокого понимания концепций. По словам исследовательской группы, сравнение — это естественный способ обучения людей, отметив, что, например, люди часто сравнивают продукты, чтобы решить, какой из них купить. Благодаря учебным программам и возможностям профессионального обучения исследователи помогли педагогам включить этот процесс естественного мышления в классы алгебры.

«Мы разработали высококачественные учебные материалы и учебные программы, чтобы помочь учителям использовать передовой опыт в области математического образования в своих классах», — сказали Бетани Риттл-Джонсон, Анита С. и Антонио М. Готто, заведующие кафедрой развития детей в Вандербильте. Университет. «Описания эффективной педагогической практики недостаточно; учителям нужны материалы и процедуры, чтобы поддержать их использование практики в их классах».

Анализируя прошлые исследования, команда также стремилась понять типы задач, которые учащиеся должны сравнивать. Они рассмотрели исследования по трем типам сравнения: сравнение нескольких правильных стратегий, сравнение типов проблем, которые можно спутать, и сравнение правильных и неправильных стратегий. Они обнаружили, что включение этих типов задач сравнения привело к большему концептуальному знанию и процедурной гибкости, чем контрольные группы.

Пример вопроса сравнения нескольких стратегий.

В дополнение к анализу типов задач для студентов, чтобы использовать стратегии сравнения, команда стремилась понять, когда в процессе обучения использовать сравнение. В частности, им было любопытно определить, следует ли откладывать методы сравнения до тех пор, пока учащиеся не поймут хотя бы один из методов. Первоначально группа обнаружила, что студенты лучше справлялись со сравнением правильных стратегий, когда имели некоторое представление об одной из стратегий. Однако позже команда обнаружила, что учащиеся могли эффективно использовать сравнение, чтобы найти сходства и различия между неизвестными стратегиями, хотя этот подход требовал большей поддержки со стороны преподавателей.

Наконец, исследовательская группа проанализировала методы сравнения методов обучения и оказала педагогам поддержку в использовании передового опыта в своих классах. Команда предлагает преподавателям сделать примеры ясными и наглядными для учащихся и представить оба решения одновременно. Кроме того, учащиеся лучше всего находили сходства и различия между стратегиями, когда преподаватели использовали хорошо понятную терминологию, жесты и визуальные подсказки. Более того, как только учащиеся определят сходства и различия, преподаватели должны использовать четкие вопросы-подсказки, чтобы стимулировать объяснение ключевых моментов и резюмировать основные моменты сравнения после размышлений учащихся. Исследователи подчеркивают необходимость в высококачественных, соответствующих стандартам учебных материалах и профессиональной поддержке обучения, чтобы оказать педагогам наилучшую поддержку при включении сравнения в учебную программу. Они разработали учебные материалы и учебные процедуры для поддержки сравнения и обсуждения нескольких стратегий по темам алгебры I.

Команда считает, что это только начало важного исследования стратегий сравнения и педагогики. Их работа способствовала дополнительным потенциальным исследовательским возможностям, таким как изучение влияния стратегий сравнения на отношение учащихся к математике или развитие способности учителей определять, когда их ученикам нужна дополнительная поддержка.

«Мы сосредоточились на обучении алгебре I и стремимся разработать учебные материалы для других математических тем, таких как геометрия, а также изучить дополнительные вспомогательные средства, которые могут потребоваться для содействия сравнению и обсуждению различных стратегий между разными учащимися», — объясняет Риттл-Джонсон.

Исследование «Как исследования в области когнитивных наук могут помочь улучшить образование? Случай сравнения нескольких стратегий для улучшения изучения и преподавания математики» был опубликован в выпуске Current Directions in Psychological Sciences за декабрь 2020 года. Учителя могут узнать больше о включении сравнения на веб-сайте проекта.

Ресурсы для пересмотренной математики TEKS

В апреле 2012 г. Совет по образованию штата (SBOE) принял изменения в учебнике по математике Texas Essential Knowledge and Skills (TEKS) для детского сада — 12 класс. На этой странице представлены ресурсы, которые помогут родителям и учителям перейти на пересмотренный курс TEKS по математике. для К-8, которые были реализованы в 2014-2015 гг.

 

Ресурсы для родителей

Вспомогательная информация : В этих документах содержится дополнительная информация о стандартах, взятых из документов параллельного сравнения TEKS, часто задаваемых вопросов и учителей.

Пересмотренный математический TEKS : Математические TEKS доступны онлайн.

Интерактивный математический глоссарий : (внешний источник):   Этот глоссарий был разработан для учителей, но может быть полезен родителям при изучении и понимании математической лексики, используемой в K-8 по математике TEKS. Каждый термин отображается в четырехквадрантной модели Фрайера, которая включает Мое определение , Ключевые характеристики , Пример и Непример.  

Сопоставительные документы TEKS : В этих документах представлено параллельное сравнение старых математических TEKS и текущих математических TEKS для курсов от детского сада до средней школы.

Параллельное сравнение TEKS по математике для детского сада (PDF, 625 КБ)

Параллельное сравнение TEKS по математике для 1 класса (PDF, 1207 КБ)

Параллельное сравнение TEKS по математике для 2 класса (PDF, 887 КБ)

Параллельное сравнение TEKS по математике для 3 класса (PDF, 702 КБ)

Параллельное сравнение TEKS по математике для 4 класса (PDF, 926 КБ)

Параллельное сравнение TEKS по математике для 5 класса (PDF, 711 КБ)

Параллельное сравнение TEKS по математике для 6 класса (PDF, 679 КБ) )

Параллельное сравнение TEKS по математике для 7 класса (PDF, 684 КБ)

Параллельное сравнение TEKS по математике для 8 класса (PDF, 737 КБ)

Параллельное сравнение TEKS по алгебре I (PDF, 1011 КБ) )

Алгебра II TEKS Наглядное сравнение (PDF, 1102 КБ)

Геометрия TEKS Наглядное сравнение (PDF, 728 КБ)

Параллельное сравнение TEKS PreCalculus (PDF, 491 КБ)

Параллельное сравнение математических моделей с приложениями TEKS (PDF, 494 КБ)

Расширенное количественное рассуждение TEKS Параллельное сравнение (PDF, 503 КБ)

Ресурсы для учителей

Вспомогательные документы и ресурсы 

Вспомогательная информация (внешний источник): В этих документах содержится дополнительная информация о стандартах, взятая из документов параллельного сравнения TEKS, часто задаваемых вопросов и учителей.

Видео «Учитель2Учитель» (внешний источник): потенциальные методы, стратегии и моменты, которые следует учитывать при изучении некоторых сложных тем в K – алгебре I по математике.

Вертикальные диаграммы выравнивания (внешний источник) : Вертикальные диаграммы выравнивания демонстрируют продвижение содержания математики в разных классах.    

Интерактивный математический глоссарий (сторонний источник): этот глоссарий помогает учителям изучить и понять математический словарь, используемый в классах K–8 TEKS. Каждый термин отображается в четырехквадрантной модели Фрайера, которая включает Мое определение , Ключевые характеристики , Пример и Не пример.  

Техас Ответ координационным центрам учебной программы (внешний источник): В этом документе основные знания и навыки Техаса (TEKS) организованы вокруг ключевых концептуальных идей, которые подчеркивают интеграцию концепций между направлениями/навыками и естественным образом ведут к математическим связям и мышление более высокого уровня.

TEKS с заявлениями «Такие как» (PDF, 638 КБ) : В этом документе показаны TEKS с формулировками типа «например», которые были удалены при втором чтении и окончательном принятии TEKS.

Обзор TEKS по математике : На этой странице представлена ​​информация о пересмотре и пересмотре TEKS по математике. Следующие списки включают лиц, назначенных SBOE для работы в комитетах по математике TEKS:

От детского сада до 5 класса (PDF, 67 КБ)

Классы 6–8 (PDF, 70 КБ)

Средняя школа (PDF, 71 КБ)

Курсы повышения квалификации

Учителя, которым нужна помощь, могут обратиться в службу поддержки по адресу [email protected].

The Revised Math TEKS (2012):  Цели участия — ознакомиться с вспомогательными документами, изучить, как использовать документы для улучшения общего обучения математике, а также исследовать вертикальное согласование математических концепций и процессов в рамках пересмотренная математика ТЭКС. Ниже приведены ссылки, по которым учителя могут записаться на следующие курсы: 

The Revised Math TEKS (2012) с подтверждающими документами	Revised Math TEKS: Module 1 (внешний источник)
The Revised Math TEKS (2012): применение стандартов математических процессов	Revised Math TEKS: Module 2 (внешний источник)
The Revised Math TEKS (2012): Завершение анализа пробелов	Revised Math TEKS: Module 3   (внешний источник)
The Revised Math TEKS (2012): Достижение свободного владения языком и профессионального мастерства	Пересмотренный математический TEKS: модуль 4 (внешний источник)

Ресурсы шлюза

 

Техас: Инициатива Algebra Ready (TXAR): Оценки ESTAR/MSTAR являются частью инициативы TXAR.

No related posts.