Формулы сокращённого умножения: таблица формул с примерами
Формулы сокращённого умножения используются для возведения чисел в степень, а также умножения этих чисел и различных выражений. Не редко такие формулы сокращающего умножения помогают вычислять примеры быстрее и компактней.
Нас ищут по таким запросам:
- Квадрат суммы;
- Формулы сокращённого умножения примеры;
- Все формулы сокращённого умножения;
- Формулы сокращённого умножения видео;
- Как быстро выучить формулы сокращённого умножения;
- Задание на формулы сокращённого умножения;
- Задание на формулы сокращённого умножения ВНО;
- Алгебра 7 класс формулы сокращённого умножения;
- Теорема Виета;
- Табличка сокращённого умножения;
- Тригонометрические формулы.
В этой статье рассмотрим самые популярные формулы сокращённого умножения. Затем сгруппируем формулы в табличку и рассмотрим некоторые примеры использования формул сокращающего умножения.
Таблица №1. Примеры использования формул сокращающего умножения для 7 класса
Как сократить формулы сокращённого умножения?
Квадрат суммы двух чисел:
В алгебре приведение целого выражения к стандартному виду многочлена осуществляется с помощью формул сокращённого умножения.
(a+b)2=(a+b)(a+b)=a2+2ab+b2=a2+ab+ab+b2=a2+2ab+b2 (квадрат суммы двух чисел)
Выражение (a+b)2 — это квадрат суммы чисел a и b. По определению степени выражение (a+b)2 представляет собой произведение двух многочленов (a+b)(a+b). Следовательно, из квадрата суммы мы можем сделать выводы, что
(a+b)2=(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2,
т. е. квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа.
е. квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа.
Из правила следует, что общая формула квадрата суммы, без промежуточных преобразований, будет выглядеть так:
(a+b)2=a2+2ab+b2
Многочлен a2+2ab+b2 называется разложением квадрата суммы.
Так как a и b обозначают любые числа или выражения, то правило даёт нам возможность сокращённым путём возводить в квадрат любое выражение, которое может быть рассмотрено как сумма двух слагаемых.
Пример. Возвести в квадрат выражение 3x2+2xy.
Решение: для того чтобы нам не производить лишних преобразований, воспользуемся формулой квадрата суммы двух чисел. У нас должна получиться сумма квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:
(3x2+2xy)2=(3x2)2+2(3x2 · 2xy)+(2xy)2
А сейчас, используя правило умножения и возведения в степень одночленов, упростим это выражение:
(3x2)2+2(3x2 · 2xy) + (2xy)2=9x4+12x3y+4x2y2
Квадрат разности двух чисел:
(a — b)2 = a2 — 2ab + b2 (квадрат разности двух чисел)
Выражение (a—b)2 — это квадрат разности чисел a и b. Выражение (a—b)2 представляет собой произведение двух многочленов (a—b)(a—b). Следовательно, из квадрата разности мы можем сделать выводы, что
Выражение (a—b)2 представляет собой произведение двух многочленов (a—b)(a—b). Следовательно, из квадрата разности мы можем сделать выводы, что
(a—b)2=(a—b)(a—b)=a2—ab—ab+b2=a2-2ab+b2,
т. е. квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа.
Из правила следует, что общая формула квадрата разности, без промежуточных преобразований, будет выглядеть так:
(a—b)2=a2-2ab+b2
Многочлен a2-2ab+b2 называется разложением квадрата разности.
Это правило применяется к сокращённому возведению в квадрат выражений, которые могут быть представлены как разность двух чисел.
Пример. Представьте квадрат разности двух чисел в виде трёхчлена:
(2a2-5ab2)2
Решение: используя формулу квадрата разности двух чисел находим:
(2a2-5ab2)2 = (2a2)2-2(2a2 · 5ab2)+(5ab2)2
Теперь преобразуем выражение в многочлен стандартного вида:
(2a2)2-2(2a2·5ab2)+(5ab2)2 =4a4— 20a3b2+25a2b4
Разность квадратов двух чисел
a2-b2=(a+b)(a-b) (разность квадратов двух чисел)
Выражение a2—b2 — это разность квадратов чисел a и b. Выражение a2—b2 представляет собой сокращённый способ умножения суммы двух чисел на их разность:
Выражение a2—b2 представляет собой сокращённый способ умножения суммы двух чисел на их разность:
(a +b)(a—b)=a2+ab—ab—b2=a2—b2,
т. е. произведение суммы двух чисел на их разность равно разности квадратов этих чисел.
Из правила следует, что общая формула разности квадратов выглядит так:
a2—b2=(a+b)(a —b)
Это правило применяется к сокращённому умножению таких выражений, которые могут быть представлены: одно — как сумма двух чисел, а другое — как разность тех же чисел.
Пример. Преобразуйте произведение в двучлен:
(5a2+3)(5a2-3)
Решение:
(5a2+3)(5a2-3)=(5a2)2-32=25a4-9
В примере мы применили формулу разности квадратов справа налево, то есть нам дана была правая часть формулы, а мы преобразовали её в левую:
(a+b)(a—b)=a2— b2
При решении практических примеров в алгебре зачастую применяют формулы сокращённого умножения с переставленными местами левыми и правыми частями. Это особенно удобно, когда имеет место разложение многочлена на множители. На практике первые три формулы применяются как слева направо, так и справа налево, в зависимости от конкретной ситуации.
Это особенно удобно, когда имеет место разложение многочлена на множители. На практике первые три формулы применяются как слева направо, так и справа налево, в зависимости от конкретной ситуации.
Формулы сокращённого умножения частенько называют тождествами сокращённого умножения. И здесь нет ничего удивительного, так как каждое равенство представляет собой тождество.
Сумма квадратов двух чисел бывает двух типов:
a2+b2=(a+bi)(a-bi)
OR.
(1) a2+b2=(a+b)2-2ab (сумма двух квадратов)
= a²+2ab+b²-2ab
= a²+b²
=> LHS = RHS
Значит доказали!
(2). a²+b² = (a-b)² +2ab
= a²-2ab+b²+2ab
=> LHS = RHS
Значит доказано!
Следовательно, a²+b²=(a+b)²-2ab
‘OR’
a²+b²=(a-b)²+2ab
Другие формулы сокращённого умножения:
(a+b-c)2=a2+b2+c2+2ab-2ac-2bc
Куб суммы двух чисел
(a+b)3=a3+3a2b+3ab2+b3 (куб суммы двух чисел)
Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго плюс куб второго числа.
(a+b)3 = a3+3a2b+3ab2+b3
Пример выражения:
a) (m+2n)3=m3+3·m2·2n+3·m·(2n)2+(2n)3=m3+6m2n+12mn2+8n3
б) (3x+2y)3=(3x)3+3·(3x)2·2y+3·3x·(2y)2+(2y)3=27x3+54x2y+36xy2+8y3
Куб разности двух чисел
(a-b)3=a3-3a2b+3ab2-b3 (куб разности двух чисел)
Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе число плюс утроенное произведение первого числа на квадрат второго числа минус куб второго числа.
(a-b)3=a3-3a2b+3ab2-b3
Пример выражения:
а) (2x–y)3=(2x)3-3·(2x)2·y +3·2x·y2–y3=8x3–12x2y+6xy2–y3
б) (x–3n)3=x3-3·x2·3n+3·x·(3n)2–(3n)3=x3–9x2n+27xn2–27n3
Сумма кубов двух чисел
a3 + b3 = (a + b)(a2 — ab + b2) (сумма кубов)
Сумма кубов двух чисел равна произведению суммы самих чисел на неполный квадрат их разности.
a3+b3 = (a+b)(a2–ab+b2)
Пример выражения:
a) 125 + 8x3 = 53 + (2x)3 = (5 + 2x)(52 — 5·2x + (2x)2) = (5 + 2x)(25 – 10x + 4x2)
б) (1 + 3m)(1 – 3m + 9m2) = 13 + (3m)3 = 1 + 27m3
Разность кубов двух чисел
a3 — b3 = (a — b)(a2 + ab + b2) (разность кубов)
Разность кубов двух чисел равна произведению разности самих чисел на неполный квадрат их суммы.
a3-b3 = (a-b)(a2+ab+b2)
Пример выражения:
а) 64с3 – 8 = (4с)3 – 23 = (4с – 2)((4с)2 + 4с·2 + 22) = (4с – 2)(16с2 + 8с + 4)
б) (3a – 5b)(9a2 + 15ab + 25b2) = (3a)3 – (5b)3 = 27a3 – 125b3
Формула для нахождения четвертой степени суммы двух чисел имеет вид:
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
Формула для нахождения четвертой степени разности двух чисел имеет вид:
(a — b)4 = a4 — 4a3b + 6a2b2 — 4ab3 + b4
Данные формулы сокращённого умножения доказываются путём раскрытия скобок и приведения подобных слагаемых.
Таблица формул сокращённого умножения для учеников 7 классов
Рассмотрим семь основных формул сокращённого умножения, которые изучают ученики на уроках алгебры в 7 классе:
Таблица формул сокращённого умножения
Произведение суммы двух чисел на их разность равно разности квадратов этих чисел:
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа:
Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого числа на второе плюс квадрат второго числа:
Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго плюс куб второго числа:
Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго числа:
Выражение в алгебре принято называть неполным квадратом разности. Если умножить сумму двух чисел на неполный квадрат разности этих чисел, то получим формулу суммы кубов.
Если умножить сумму двух чисел на неполный квадрат разности этих чисел, то получим формулу суммы кубов.
Сумма кубов двух чисел равна произведению суммы этих чисел на их неполный квадрат разности:
Выражение в алгебре, принято называть неполным квадратом суммы. Если умножить разность двух чисел на неполный квадрат суммы этих чисел, то получим формулу разности кубов.
Разность кубов двух чисел равна произведению разности этих чисел на их неполный квадрат суммы:
Группа формул: сумма степеней
Группа формул «Сумма степеней» составляет Таблицу 2. Эти формулы можно получить, выполняя вычисления в следующем порядке:
| (x + y)2 = (x + y)(x + y) , (x + y)3 = (x + y)2(x + y) , (x + y)4 = (x + y)3(x + y) |
Группу формул «сумма степеней» можно получить также с помощью треугольника Паскаля и с помощью бинома Ньютона, которым посвящены специальные разделы нашего справочника.
Таблица 2. – Сумма степеней
| Название формулы | Формула |
| Квадрат (вторая степень) суммы | (x + y)2 = x2 + 2xy + y2 |
| Куб (третья степень) суммы | (x + y)3 = x3 + 3x2y + 3xy2 + y3 |
| Четвертая степень суммы | (x + y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4 |
| Пятая степень суммы | (x + y)5 = x5 + 5x4y + 10x3y2 + 10x2y3 + 5xy4 + y5 |
| Шестая степень суммы | (x + y)6 = x6 + 6x5y + 15x4y2 + 20x3y3 + 15x2y4 + 6xy5 + y6 |
Общая формула для вычисления суммы
(x + y)n
с произвольным натуральным значением n рассматривается в разделе «Бином Ньютона» нашего справочника.
Разность степеней
Если в формулах из Таблицы 2 заменить y на – y , то мы получим группу формул «Разность степеней» (Таблица 3.):
Таблица 3. – Разность степеней
| Название формулы | Формула |
| Квадрат (вторая степень) разности | (x – y)2 = x2 – 2xy + y2 |
| Куб (третья степень) разности | (x – y)3 = x3 – 3x2y + 3xy2 – y3 |
| Четвертая степень разности | (x – y)4 = x4 – 4x3y + 6x2y2 – 4xy3 + y4 |
| Пятая степень разности | (x – y)5 = x |
| Шестая степень разности | (x – y)6 = x6 – 6x5y + 15x4y2 – 20x3y3 + 15x2y4 – 6xy5 + y6 |
Квадрат многочлена
Следующая формула применяется достаточно часто и называется «Квадрат многочлена»:
Квадрат многочлена формула
Что бы возвести многочлен в квадрат необходимо сложить его члены в квадрате и удвоенные произведения его членов попарно взятых.
Примеры квадрата многочлена
1. (1 + 2 + 3 + 4)2 =
12 + 22 + 32 + 42 + 2 • 1 • (2 + 3 + 4) + 23 • (3 + 4) + 2 • 3 • 4 =
1 + 4 + 9 + 16 + 2 • 1 • 9 + 2 • 2 • 7 + 24 =
30 + 18 + 28 + 24 = 100 ;
a = 1 ;
b = 2 ;
c = 3 ;
d = 4 ;
2. (2 + 3 + 4 + 5)2 =
22 + 32 + 42 + 52 + 2 • 2 • 3 + 2 • 2 • 4 + 2 • 2 • 5 + 2 • 3 • 4 + 2 • 3 • 5 + 2 • 4 • 5 =
4 + 9 + 16 + 25 + 12 + 16 + 20 + 24 + 30 + 40 = 196 ;
a = 2 ;
b = 3 ;
c = 4 ;
d = 5 ;
3. (5 + 6 + 7 + 8)2 =
52 + 62 + 72 + 82 + 2 • 5 • 6 + 2 • 5 • 7 + 2 • 5 • 8 + 2 • 6 • 7 + 2 • 6 • 8 + 2 • 7 • 8 =
25 + 36 + 49 + 64 + 60 + 70 + 80 + 84 + 96 + 112 = 676 ;
a = 5 ;
b = 6 ;
c = 7 ;
d = 8 ;
Куб трёхчлена
Следующая формула называется «Куб трёхчлена»:
(x + y + z)3 = x3 + y3 + z3 + 3x2y + 3x2z + 3xy2 + 3xz2 + 3y2z + 3yz2 + 6xyz
Советы
- Кубический многочлен является произведением трёх многочленов первой степени или произведением одного многочлена первой степени и неразлагаемого многочлена второй степени.
 3 + x + 1, у которых иррациональные корни, нельзя разложить на многочлены с целыми (рациональными) коэффициентами. Хотя такой многочлен может быть разложен по кубической формуле, он не разлагается как целый многочлен.
3 + x + 1, у которых иррациональные корни, нельзя разложить на многочлены с целыми (рациональными) коэффициентами. Хотя такой многочлен может быть разложен по кубической формуле, он не разлагается как целый многочлен.
Вместе с запросом «формулы сокращённого умножения» часто ищут:
| формулы сокращённого умножения 7 класс | формулы сокращённого умножения доказательство |
| формулы сокращённого умножения задания повышенной сложности | формулы сокращённого умножения словами |
| формулы сокращённого умножения примеры | формулы сокращённого умножения онлайн |
| формулы сокращённого умножения 7 класс контрольная работа | формулы сокращённого умножения примеры с дробями |
Формулы сокращённого умножения | О математике понятно
Формулы сокращённого умножения необходимы во всех разделах математики. От элементарной до высшей. Они применяются практически везде — в упрощении выражений, решении уравнений и неравенств, сокращении дробей, вычислении пределов, решении интегралов — список можно продолжать ещё долго…
От элементарной до высшей. Они применяются практически везде — в упрощении выражений, решении уравнений и неравенств, сокращении дробей, вычислении пределов, решении интегралов — список можно продолжать ещё долго…
Следовательно, нужно основательно разобраться с этими формулами. Понять, откуда они берутся, зачем они нужны, как их применять на практике и, самое главное, как их запомнить. А запомнить всё-таки придётся, да…
Поехали?
Квадрат суммы, квадрат разности, разность квадратов, куб суммы, куб разности, сумма кубов, разность кубов — что за звери?
Итак, вот они, формулы сокращённого умножения:
Эти семь формул — полный джентльменский набор. Последние две формулы (сумма и разность кубов) записаны не так как в большинстве учебников, а наоборот — справа налево. Это не просто так.) Любая формула в математике работает в обоих направлениях — как туда, так и обратно. Именно такая запись наиболее наглядно показывает, откуда берутся формулы сокращённого умножения.
Именно такая запись наиболее наглядно показывает, откуда берутся формулы сокращённого умножения.
Они берутся из… умножения. Вот ведь удивил, да?) Что ж, смотрите сами. Берём, например, самую первую формулу по списку:
(a+b)2 = (a+b)(a+b) = a2+ab+ba+b2 = a2+2ab+b2
Вот и все дела. Самое обычное перемножение скобок и приведение подобных. Именно так и получаются все формулы сокращённого умножения. Сокращённое умножение — потому, что в самих формулах нет раскрытия скобок и приведения подобных. Эти промежуточные действия сокращены. Сразу дан готовый результат. Пользуйтесь на здоровье!
Эти формулы надо знать наизусть. Без знания первых трёх формул, с квадратами, даже не мечтайте о тройке! Без всех остальных (с кубами) — о четвёрке и выше. Нет-нет, бросаться зубрить весь этот список прямо сейчас мы не будем.) Об этом позже. Пока просто знакомимся.)
Нет-нет, бросаться зубрить весь этот список прямо сейчас мы не будем.) Об этом позже. Пока просто знакомимся.)
Зачем нужны формулы сокращённого умножения?
Полезная вещь первая — самая очевидная. Это быстрое (т.е. сокращённое) умножение многих алгебраических выражений без промежуточных выкладок. Меньше выкладок — меньше и ошибок. Но это не самая главная полезная вещь! А вот вторая.
Дело в том, что вся математика строится на преобразованиях выражений. Вся! От школьной до высшей. Сообразил, что, где и как преобразовать и упростить — решил пример. Не сообразил — увы, не решил. Есть, допустим, выражение (a—b)(a+b). Как его можно преобразовать? Да просто тупо перемножить скобки и привести подобные. Не вопрос.) А вот что делать с a2–b2? Чему это равняется? Попробуй, догадайся! Только знания и спасают, да…
Сравним два равенства:
(a—b)(a+b) = a2–b2
и
a2–b2 = (a—b)(a+b)
Для математики эти два равенства абсолютно одинаковы. А вот для нас с вами — не совсем. Возьмём первую запись, слева направо:
А вот для нас с вами — не совсем. Возьмём первую запись, слева направо:
(a—b)(a+b) = a2–b2
Это самое обычное умножение скобок, не более того. Никаких принципиально новых возможностей. А теперь возьмём второй вариант того же равенства, справа налево:
a2–b2 = (a—b)(a+b)
А вот такая запись резко повышает уровень вашей математической культуры! Почему? Потому, что такая запись формулы, справа налево, — это разложение на множители! А разложение на множители — процедура поважнее простого умножения, да…) Сомневаетесь? Не надо. В соответствующей теме подробно расскажу.)
И такое разложение на множители имеет место быть во всех формулах сокращённого умножения! Почему? Давайте внимательно посмотрим на наш список. В левой части каждой формулы мы увидим перемножение скобок:
В левой части каждой формулы мы увидим перемножение скобок:
(a+b)2 = (a+b)(a+b) =…
(a-b)2 = (a-b)(a-b) = …
(a-b)(a+b) = …
(a+b)3 = (a+b)(a+b)(a+b) =…
и т.д.
Стало быть, левая часть каждой формулы разложена на множители, а вот правая часть — нет. Список, что приведён выше, — это, действительно, всего лишь сокращённое умножение. Но! Стоит только поменять местами левую и правую части каждой из формул, как тот же самый список становится формулами разложения на множители!
Для полного понимания перепишу этот список ещё разок, но справа налево. Вот так:
Такая обратная запись формул сокращённого умножения идеально подходит для разложения на множители многочленов, для сокращения алгебраических дробей и для решения самых разнообразных примеров. Но есть существенная проблема. Как их запомнить?
Запоминаем формулы сокращённого умножения! Секретные приёмы…
Начинаем с самого простого — запоминаем названия формул. Это совсем легко. Смотрим в таблицу и видим выражение (a+b)2. Или квадрат скобок. А в скобках что? Правильно, сумма! Стало быть, выражение (a+b)2 называется квадрат суммы. Аналогично, (a—b)2 называется квадрат разности. Элементарно, Ватсон!
Это совсем легко. Смотрим в таблицу и видим выражение (a+b)2. Или квадрат скобок. А в скобках что? Правильно, сумма! Стало быть, выражение (a+b)2 называется квадрат суммы. Аналогично, (a—b)2 называется квадрат разности. Элементарно, Ватсон!
С выражениями (a+b)3 и (a—b)3 всё то же самое — куб суммы и куб разности соответственно.
А как назвать a2–b2? «Одно выражение в квадрате минус другое выражение в квадрате?» Точно, но слишком уж длинно. Зато разность квадратов — и точно, и кратко!
Надеюсь, что названия сумма кубов и разность кубов у вас уже не вызовут недоумения?
А вот теперь начинается самое сложное — запоминание самих формул, со всеми этими выражениями. К сожалению, здесь тот самый случай, когда без механической памяти не обойтись. Это огорчает.
К сожалению, здесь тот самый случай, когда без механической памяти не обойтись. Это огорчает.
Однако здесь у нас с вами тайные знания! Эти знания помогут вам побыстрее сориентироваться во всех этих скобках, плюсах/минусах, квадратах/кубах, сведя механическую зубрёжку к минимуму. Читаем дальше и вникаем.
Итак, начинаем с квадрата суммы:
Просто медитировать, сверля формулу взглядом, будет недостаточно. Для лучшего запоминания настоятельно рекомендую выучить (да-да, именно выучить!) словесную формулировку:
Квадрат суммы двух выражений равен квадрату первого выражения ПЛЮС удвоенное произведение первого выражения на второе ПЛЮС квадрат второго выражения.
Эта мантра реально облегчает жизнь во многих разделах школьной математики! Да и в институте, при работе со всякими там пределами да интегралами, тоже. Ещё не раз вспомните эту формулировку добрым словом!)
Если вы запомнили квадрат суммы, то дальше будет проще. Можно включать логику и здравый смысл. Переходим к квадрату разности:
Можно включать логику и здравый смысл. Переходим к квадрату разности:
Сравните с квадратом суммы! Нашли отличие? Да! Перед удвоенным произведением появился минус. Ведь должен же он где-то появиться?! Перед a2 и b2 он появиться никак не может, ибо любое число в квадрате есть число положительное. Остаётся только серединка.) Для понимания рекомендую просто перемножить скобки сами на себя да привести подобные. И тогда у вас пропадут все вопросы.
В словесной расшифровке:
Квадрат разности двух выражений равен квадрату первого выражения МИНУС удвоенное произведение первого выражения на второе ПЛЮС квадрат второго выражения.
Разность квадратов:
Эта формула обычно и так легко запоминается. Единственное, можно случайно влепить в скобки два плюса или два минуса. Но тогда это уже будут квадрат суммы и квадрат разности. А это — совсем другие формулы…
А это — совсем другие формулы…
Итак:
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
Переходим к следующей группе формул — к сумме и разности кубов:
Приём для запоминания здесь следующий. В первых скобках (маленьких) знак совпадает со знаком в исходном выражении: плюс-плюс, минус-минус. А вот во вторых (больших) скобках — меняется на противоположный. Причём меняется не перед квадратами, а снова посерединке! Квадраты a2 и b2 — положительные!
Кстати, посмотрите внимательнее на большие скобки в каждой из формул и сравните с формулами квадрата суммы и квадрата разности!
Нашли отличия? Да! В кубах не хватает двойки посерёдке. Именно по этой причине выражения в больших скобках
a2+ab+b2
и
a2—ab+b2
часто называют неполным квадратом суммы/разности.
А теперь можно и шаблонные словесные формулировки из учебников привести:
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
Вот так. Слово «неполный» хорошо помогает не запутаться. Допустим, в тревожной боевой обстановке на контрольной или экзамене нахлынули сомнения — писать двойку в сумме/разности кубов или нет? Вот тут самое время вспомнить, что в кубах стоят неполные квадраты. А для полных квадратов есть свои формулы. Которые к кубам не имеют никакого отношения.
Остаётся последняя парочка — куб суммы и куб разности:
Эти две формулы встречаются в заданиях пореже предыдущих пяти, но знать их тоже не помешает, да. Претендуете на пятёрку? Тогда читаем дальше!
Итак, как запомнить куб суммы? Во-первых, все знаки в формуле — плюсы! Оно и естественно. Ведь мы же перемножаем только положительные выражения, так с какого перепугу минусам-то взяться? Первое и последнее слагаемые — чистые кубы первого и второго выражений. А вот по центру — утроенные произведения.
Ведь мы же перемножаем только положительные выражения, так с какого перепугу минусам-то взяться? Первое и последнее слагаемые — чистые кубы первого и второго выражений. А вот по центру — утроенные произведения.
Обратите внимание, как в формуле идут переменные a и b! Переменная a идёт по убыванию степени — сначала a3, потом a2, потом просто a (т.е. a1), а в последнем слагаемом буква a и вовсе исчезает, превращаясь в единичку или a0. Для полной ясности ситуации последнее слагаемое b3 я перепишу вот так:
b3 = 1∙b3 = a0∙b3
А вот переменная b — наоборот, идёт по возрастанию степени. От нуля и до тройки включительно: в первом слагаемом переменной b нет (т.е. она сидит в виде единички, или b0), во втором b1, в третьем b2, в четвёртом b3.
От нуля и до тройки включительно: в первом слагаемом переменной b нет (т.е. она сидит в виде единички, или b0), во втором b1, в третьем b2, в четвёртом b3.
Но и это ещё не всё! Смотрите-ка, какая интересная штука: сумма степеней a и b в каждом из слагаемых всегда равна трём! Например:
a3 = a3·b0 (3+0=3)
3a2b = 3a2b1 (2+1=3)
и так далее…
Такой порядок хорошо помогает не запутаться.)
Если вы уловили принцип запоминания куба суммы, то куб разности запомнится без проблем. Всё то же самое, только минусы надо правильно расставить. А это очень легко сообразить! Какая переменная у нас с минусом? Правильно, переменная b! Следовательно, в слагаемых, где b стоит в первой степени и в кубе — будет минус. Ибо любой минус в нечётной степени всегда даёт минус. А вот минус в квадрате (b2) даст плюс. И все дела.)
Всё то же самое, только минусы надо правильно расставить. А это очень легко сообразить! Какая переменная у нас с минусом? Правильно, переменная b! Следовательно, в слагаемых, где b стоит в первой степени и в кубе — будет минус. Ибо любой минус в нечётной степени всегда даёт минус. А вот минус в квадрате (b2) даст плюс. И все дела.)
Разумеется, изложенные выше советы — это не жёсткие правила математики. Это просто практические приёмы, помогающие более быстрому и комфортному запоминанию. Чисто для себя. Куда уж лучше, чем механическая зубрёжка, правда?)
Но, как ни крути, самый надёжный способ запомнить эти формулы — решать побольше примеров. Тогда весь этот перечень запомнится очень быстро. Сам собой, можно сказать.
Ну что, потренируемся?)
Примеры на формулы сокращённого умножения.
Начнём с самого простого — с прямого применения формул. Для разминки.)
Для разминки.)
Преобразовать в многочлен:
(5x+4y)2
Сразу видим квадрат скобок. А в скобках — сумму. Значит, работаем по самой первой формуле, вот этой:
Вспоминаем словесную формулировку: «Квадрат первого выражения…». За первое выражение у нас идёт 5x. Квадрат будет 25х2. Вот и пишем:
(5x+4y)2 = 25х2….
Идём дальше: «Плюс удвоенное произведение первого выражения на второе…». Удвоенное — это умножение на двойку. Первое выражение — это 5x, второе — это 4y. Продолжаем:
(5x+4y)2 = 25х2+2∙5x∙4y….
«Плюс квадрат второго выражения.» В роли второго выражения у нас 4y. Квадрат — это 16y2. Получим:
(5x+4y)2 = 25х2+2∙5x∙4y+16y2
Практически всё. Осталось «причесать» удвоенное произведение (перемножить 2∙5∙4) и получим окончательный ответ:
(5x+4y)2 = 25х2+40xy+16y2
Это было разминочное задание. А теперь примерчик посерьёзнее.
Разложить на множители:
4x2–20x+25
Что, внушает? Опять смотрим на наш список. Но не на тот, что в начале урока (для умножения), а на второй, для разложения на множители. Вот на этот:
Вот на этот:
Тут, разумеется, нашего выражения нет. Ну и что? Здесь важно понимать, что под буквами a и b может скрываться всё что угодно — и числа, и другие буквы, и более сложные выражения. Поэтому смотрим на список и ищем похожую формулу. И зацепкой будут степени переменной.
В нашем выражении есть x2 и просто x. Ясное дело, отбрасываем все формулы с кубами — у нас их явно нет. Далее выкидываем из рассмотрения формулу разности квадратов: там нет переменных в первой степени, только квадраты. А у нас — есть.
Остаются первые две формулы — квадрат суммы или квадрат разности. Уже проще, не так ли? Осталось сообразить, что в формуле квадрата суммы — только плюсы. А в нашем выражении в серединке стоит минус. Стало быть, похожая формула — это квадрат разности.
Но не факт, что квадрат разности сработает, совсем не факт… Наша задача — убедиться, что предложенное выражение 4x2–20x+25 точно соответствует квадрату разности. Только тогда у нас появится возможность записать и правую часть равенства (т.е. разложение на множители).
Только тогда у нас появится возможность записать и правую часть равенства (т.е. разложение на множители).
Для удобства я перепишу формулу и исходное выражение прямо одно под другим:
a2—2ab+b2 = (a—b)2
4x2–20x+25 = ….
Надо выяснить, что скрывается под буквами a и b в нашем выражении. Начинаем по порядочку — с самого первого слагаемого. Допустим, a2 — это 4x2. Тогда чему равно само а? Какое выражение в квадрате даёт 4x2? Очевидно, что 2х. Тогда a=2x. Есть! Первое выражение нашли.
А что может скрываться под b2. Ну, точно не 20х! Во-первых, икс уже в букве a сидит, а во-вторых, b2 должно быть с плюсом. А 20х у нас с минусом. Значит, под b2 скрывается число 25! Стало быть, b — это пятёрка!
Ну, точно не 20х! Во-первых, икс уже в букве a сидит, а во-вторых, b2 должно быть с плюсом. А 20х у нас с минусом. Значит, под b2 скрывается число 25! Стало быть, b — это пятёрка!
Итого: a=2x, b=5
Всё? Можно записывать разложение? Пока нет.
Нужна последняя, контрольная проверка по выражению 20х. Надо убедиться, что наши 20х точно соответствуют удвоенному произведению 2ab.
Итак, затаив дыхание составляем удвоенное произведение первого и второго выражений:
2ab = 2∙2x∙5 = 20x
Ура! Совпало! Значит, наше выражение — это действительно квадрат разности 2х и 5. Вот теперь можно со спокойной душой записывать ответ:
4x2–20x+25 = (2х-5)2
Идея ясна? Сначала ищем в списке похожую формулу, а затем сверяем с ней выражение, предложенное в задании, на полное соответствие. Если повезло и всё совпало, то записываем ответ. Если не повезло, то, значит, раскладывать надо как-то иначе.
Если повезло и всё совпало, то записываем ответ. Если не повезло, то, значит, раскладывать надо как-то иначе.
Это были самые простые примеры, для младшеньких. А теперь переместимся в старшие классы, с их синусами да логарифмами. Да-да, старшеньким формулы сокращённого умножения тоже бывают нужны!
Например, такое задание:
Упростить:
cos4x — 2cos2x∙sin2x + sin4x
Вся мощь тригонометрии слабо помогает в этом примере. Только алгебра седьмого класса и спасает, да…
Конечно, это выражение сильно смахивает на квадрат разности. Вот и пробуем применить эту формулу к нашему выражению! Что будет скрываться под буквами a и b? Конечно же, cos2x и sin2x. Удвоенное произведение, ясен перец, будет 2cos2x∙sin2x, как, собственно, в нашем выражении и записано. Смело сворачиваем нашего монстра в квадрат разности по формуле:
Удвоенное произведение, ясен перец, будет 2cos2x∙sin2x, как, собственно, в нашем выражении и записано. Смело сворачиваем нашего монстра в квадрат разности по формуле:
cos4x — 2cos2x∙sin2x + sin4x = (cos2x — sin2x)2
А вот теперь и тригонометрия в игру вступает! Что у нас в скобочках? У нас в скобочках косинус двойного угла!
cos2x — sin2x = cos2x
Вот вам и ответ:
cos4x — 2cos2x∙sin2x + sin4x = cos22x
Или такое задание:
Вычислить:
Пример не подарок, прямо скажем… Логарифмические формулы явно не катят, да и сами логарифмы ровно не считаются… Проверим на алгебру? Числитель явно намекает на применение формулы разности квадратов.
Вот этой: a2–b2 = (a-b)(a+b)
В роли a и b у нас логарифмы. Ну и что? Это формулу никак не портит, ибо законы алгебры работают во всей математике. Смело заменяем числитель дроби на произведение скобок и пишем:
А вот теперь и логарифмические формулы заработали! В первых скобках (разность) получается lg4, который и сокращается благополучно со знаменателем. А во вторых скобках (сумма) будет lg100. Что по свойствам логарифмов есть 2.
Конечно, подобные примеры в этом уроке легко решаются. Но на практике, когда ученик глубоко погружён в синусы/косинусы да логарифмы, разложение на множители просто не приходит в голову…
Посему практический совет:
Проверяем замороченные примеры на алгебру седьмого класса! В частности, на формулы сокращённого умножения.
И напоследок…
О типичном ляпе, который сразу же показывает блистательное отсутствие хоть какого-то понимания. Ляп настолько часто встречается, что хочется заявить громко:
Ляп настолько часто встречается, что хочется заявить громко:
И запомните это крепко-накрепко!
Формулы — штука жёсткая! Раз требуют удвоенного произведения 2ab, помимо чистых квадратов, значит спорить бессмысленно. Напишете такое на контрольной — будьте готовы получить заслуженную двойку! Такого не прощают. Вот так.
Наглядный пример на добрую память с квадратом суммы. Всё-таки картинки иногда проливают свет на очень многие волнующие вопросы. Нарисуем в тетрадке квадрат со стороной a+b. Можно по клеточкам. Допустим, для конкретики, a — это 4 клетки, a b — это 2 клетки.
Вот так:
Очевидно, площадь всего квадрата будет равна квадрату его стороны, т.е. как раз (a+b)2. В числах, безо всяких формул, это будет (4+2)2 = 62 = 36.
А теперь, глядя на картинку, соображаем: из чего складывается эта площадь? Правильно! Из большого (зелёного) квадрата площадью a2, маленького (жёлтого) квадратика площадью b2 и двух прямоугольников по ab площадью каждый.
Вот и получается: (a+b)2 = a2+ab+ab+b2 = a2+2ab+b2
Или, в числах, для a=4 и b=2:
(a+b)2 = a2+2ab+b2= 42+2∙4∙2+22 = 16+16+4 = 36
Вот и все дела.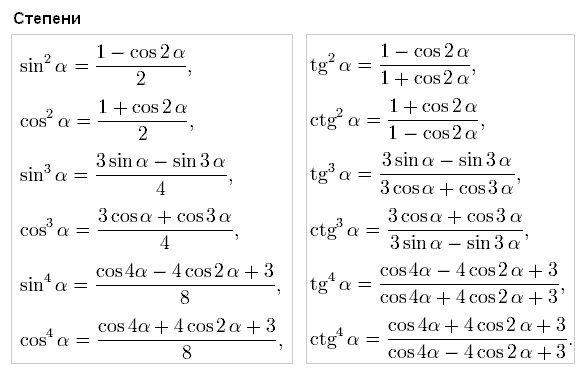 )
)
Упражнение для интересующихся: аналогичным образом доказать геометрически (т.е. через квадраты и прямоугольники) две другие формулы сокращённого умножения с квадратами — квадрат разности и разность квадратов. Попробуйте! Интересно.)
Ну что, порешаем?)
1. Преобразовать в многочлен стандартного вида:
(5a+1)2=
(3y-4)2=
(a-y3)2=
(a2+b2)2=
(3b-1)(3b+1)=
(x+7)(7-x)=
(3x+2)3=
Ответы (в беспорядке):
9b2 — 1
9y2-24y+16
27x3+18x2+36x+8
a4+2a2b2+b4
25a2+10a+1
49-x2
a2-2ay3+y6
Ну как, размялись? Получилось? Тогда продолжаем:
Разложить на множители:
16x2+8x+1 =
36x2y4-60xy2+25=
y2-100=
81a2-64x2y6=
27m3+8=
64x3-y6=
Ответы (в беспорядке):
(y-10)(y+10)
(4x-y2)(16x2+4xy2+y4)
(4x+1)2
(9a-8xy3)(9a+8xy3)
(6xy2-5)2
(3m+2)(9m2-6m+4)
И это получилось? Блеск! Значит, формулы сокращённого умножения на самом минимально необходимом уровне вы освоили. Можно браться за задания посерьёзнее.
Можно браться за задания посерьёзнее.
Что-то не срослось? Бывает… Возможно, проблема не в самих формулах, а в банальной арифметике — знаках, действиях со степенями. Повторите степени! Без отточенного навыка работы со степенями дальше идти нельзя. К сожалению…
А вообще, рецепт здесь простой — решать побольше заданий! Да-да! Задания этого урока — капля в море. Помогут, но не сильно. Маловато их… Берите любой учебник 7-го класса и решайте, решайте! До автоматизма. А сайт — ваш надёжный помощник! Тогда формулы сами собой и запомнятся. А труды окупятся. Проверено!)
Формулы сокращённого умножения кратко Арифметика
Привет, мой друг, тебе интересно узнать все про формулы сокращенного умножения, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое формулы сокращенного умножения , настоятельно рекомендую прочитать все из категории Арифметика.
При расчете алгебраических многочленов для упрощения вычислений используются формулы сокращенного умножения . Всего таких формул семь. Их все необходимо знать наизусть.
Всего таких формул семь. Их все необходимо знать наизусть.
Следует также помнить, что вместо a и b в формулах могут стоять как числа, так и любые другие алгебраические многочлены.
Разность квадратов
Разность квадратов двух чисел равна произведению разности этих чисел и их суммы.
Примеры:
Квадрат суммы
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.
Обратите внимание, что с помощью этой формулы сокращенного умножения легко находить квадраты больших чисел, не используя калькулятор или умножение в столбик. Поясним на примере:
Найти .
- Разложим 112 на сумму чисел, чьи квадраты мы хорошо помним.2
112 = 100 + 1 - Запишем сумму чисел в скобки и поставим над скобками квадрат.
- Воспользуемся формулой квадрата суммы:
Помните, что формула квадрат суммы также справедлива для любых алгебраических многочленов.
Предостережение!
Квадрат разности
Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе плюс квадрат второго числа.
Также стоит запомнить весьма полезное преобразование:
Формула выше доказывается простым раскрытием скобок:
Куб суммы
Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
Запомнить эту «страшную» на вид формулу довольно просто.
- Выучите, что в начале идет
- Два многочлена посередине имеют коэффициенты 3.
- Вспомним, что любое число в нулевой степени есть 1 . Об этом говорит сайт https://intellect.icu . (, ). Легко заметить, что в формуле идет понижение степени a и увеличение степени b. В этом можно убедиться:
Предостережение!
Куб разности
Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго.
Запоминается эта формула как и предыдущая, но только с учетом чередования знаков «+» и «-». Перед первым членом a3 стоит «+» (по правилам математики мы его не пишем). Значит, перед следующим членом будет стоять «-», затем опять «+» и т.д.
Сумма кубов
Не путать с кубом суммы!
Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.
Сумма кубов — это произведение двух скобок.
Разность кубов
Не путать с кубом разности!
Разность кубов равна произведению разности двух чисел на неполный квадрат суммы.
Будьте внимательны при записи знаков.
Применение формул сокращенного умножения
Следует помнить, что все формулы, приведенные выше, используется также и справа налево.
Многие примеры в учебниках рассчитаны на то, что вы с помощью формул соберете многочлен обратно.
Примеры:
Для чего нужны формулы сокращенного умножения?
Формулы сокращенного умножения применяются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют произвести вычисления более компактно и быстро.
Часто эти формулы позволяют произвести вычисления более компактно и быстро.
Цель использования формул сокращенного умножения — быстрое и краткое умножение и возведение выражений в степень. Однако, они приментюся не только для этого . Они широко применятся при сокращении выражений, сокращении дробей, разложении многочленов на множители.
Главной целью их применения развития умения абстрактного разбиение (синтеза и анализа) информации, развитие абстрактного и критического мышления
Как ты считаеешь, будет ли теория про формулы сокращенного умножения улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое формулы сокращенного умножения и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Арифметика
Из статьи мы узнали кратко, но емко про формулы сокращенного умножения
Сокращенное умножение: правила, формулы — Стоматология в Химках
B 2 математика
Знакомство с сокращенным умножением начинается впервые в седьмом классе. Тема непростая: нужно выучить наизусть много формул. Но зато вы сможете быстрее решать задачки без ошибок. Проверим?
Тема непростая: нужно выучить наизусть много формул. Но зато вы сможете быстрее решать задачки без ошибок. Проверим?
О чем эта статья:
Формулы сокращенного умножения
Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.
Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.
Как читать формулы сокращенного умножения
Учимся проговаривать формулы сокращенного выражения:
Разность квадратов двух выражений равна произведению их разности и их суммы.
Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго.
Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго.
Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.
Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.
Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.
Обучение на курсах по математике — дорога к хорошим оценкам в школе и высокому баллу на экзамене.
Доказательство формул сокращенного умножения
Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a 2 — b 2 = (a — b) * (a + b).
Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a — b) * (a + b) = a 2 — b 2 .
Важно знать, что разность квадратов не равна квадрату разности: a 2 — b 2 ≠ (a — b) 2 .
Докажем, что a 2 — b 2 = (a — b) * (a + b).
Используя искусственный метод, прибавим и отнимем одно и тоже a * b.
A 2 — b 2 = a 2 — b 2 + ab — ab
(a 2 — a * b) + (a * b — b 2 ) = a *(a — b) + b *(a — b)
Вынесем за скобки (a — b). a * (a — b) + b * (a — b) = (a — b) * (a + b)
Результат доказательства: a 2 — b 2 = (a — b) * (a + b)
Для того, чтобы доказать в обратную сторону: (a — b) * (a + b) = a 2 — b 2 , нужно раскрыть скобки: (a — b) * (a + b) = a * a + a * b — b * a — b * b = a 2 — b 2 .
Остальные ФСУ можно доказать аналогичным методом.
Дополнительные формулы сокращенного умножения
К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.
Бином Ньютона
Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:
Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:
ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.
Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
A n − b n = (a − b) * (a n-1 + a n-2 * b + a n-3 * b 2 + … + a * b n-2 + b n-1 ).
Для четных показателей можно записать так:
A 2*m − b 2*m = (a 2 − b 2 ) *(a 2*m−2 + a 2*m−4 * b 2 + a 2*m−6 * b 4 + … + b 2*m−2 ).
Для нечетных показателей:
A 2*m+1 − b 2*·m+1 = (a − b) * (a 2*m + a 2*m−1 * b + a 2*m−2 * b 2 + … + b 2*m ).
Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.
Решение задач
Давайте потренируемся и рассмотрим примеры с дробями.
Задание 1
Что сделать: вычислить квадрат произведения (55 + 10) 2 .
Как решаем: воспользуемся формулой квадрата суммы: (55 + 10) 2 = 55 2 + 2 * 55 * 10 + 10 2 = 3025 + 1100 + 100 = 4225.
Задание 2
Что сделать: упростить выражение 64 * с 3 – 8.
Как решаем: применим разность кубов: 64 * с 3 – 8 = (4 * с) 3 – 2 3 = (4 * с – 2)((4 * с) 2 + 4 * с * 2 + 2 2 ) = (4 * с – 2)(16 * с 2 + 8 * с + 4).
Задание 3
Что сделать: раскрыть скобки (7 * y — x) * (7 * y + x).
Как решаем:
Произведем умножение: (7 * y — x) * (7 * y + x) = 7 * y * 7 * y + 7 * y * x — x * 7 * y — x * x = 49 * y 2 + 7 * y * x — 7 * y * x — x 2 = 49 * y 2 — x 2 . Используем формулу сокращенного умножения: (7 * y — x) * (7 * y + x) = (7 * y) 2 — x 2 = 49 * y 2 — x 2 .
Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂
Используя искусственный метод, прибавим и отнимем одно и тоже a * b.
Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов a — b a b a 2 — b 2.
Skysmart. ru
08.07.2018 12:57:37
2018-07-08 12:57:37
Источники:
Https://skysmart. ru/articles/mathematic/formuly-sokrashennogo-umnozheniya
Номер №1090 — по Математике 6 класс: Виленкин Н. Я. » /> » /> .keyword { color: red; }
B 2 математика
2013г. Выбран Выбрать (готовое домашние задание из решебника) на Номер №1090 по учебнику Математика. 6 класс. Учебник для общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 30-е издание. Мнемозина, 2013г.
2019г. Выбран Выбрать Упражнение отсутствует в этой версии.
Условие
Проверьте равенство а — (-b) = а + b, если:
А) а = 18, b = 16; г) а = -4,8, b = 3,9;
Б) а = -2,3, b = -0,5; д) а = -5/7, b = 2/7;
В) а = 44, b = -7; е) а = -3 1/12, b = -2 5/12.
2013г. Выбран Выбрать (готовое домашние задание из решебника) на Номер №1090 по учебнику Математика. 6 класс. Учебник для общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 30-е издание. Мнемозина, 2013г.
2019г. Выбран Выбрать Упражнение отсутствует в этой версии.
Ответ на Номер 1090 из по Математике 6 класс Виленкин Н.
Otvetkin. info
14.03.2017 11:23:48
2017-03-14 11:23:48
Источники:
Https://otvetkin. info/reshebniki/6-klass/matematika/vilenkin/nomer-1090
Зачет по теме «Формулы сокращенного умножения» | Методическая разработка по алгебре (7 класс):
Опубликовано 17.01.2021 — 19:10 — Вехвиляйнен Юлия Алексеевна
Зачет по теме «Формулы сокращенного умножения» состоит из 3 блоков: теория, применение фсу, применение фсу в более сложных выражениях. Внизу каждого блока представлены критерии выставления отметки за блок. Материал содержит 2 файла, один из которых предназначен для подготовки к зачету, а второй — это бланк для проведения зачета.
Скачать:
Реклама
Подтяните оценки и знания с репетитором Учи.ру
За лето ребенок растерял знания и нахватал плохих оценок? Не беда! Опытные педагоги помогут вспомнить забытое и лучше понять школьную программу. Переходите на сайт и записывайтесь на бесплатный вводный урок с репетитором.
Вводный урок бесплатно, онлайн, 30 минут
Записаться >
Предварительный просмотр:
Зачет по теме «Формулы сокращенного умножения»
ФИ учащегося__________________________________________ класс_____ дата__________
1 блок «Теория»
№ | Теория | +/- | |
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражения плюс квадрат второго выражения. | |||
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражения плюс квадрат второго выражения. | |||
Разность квадратов двух выражений равна произведению суммы этих чисел и их разности. | |||
Сумма кубов двух выражений равна произведению суммы этих чисел и неполного квадрата их разности. | |||
Разность кубов двух выражений равна произведению разности этих чисел и неполного квадрата их суммы. | |||
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения. | |||
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения. | |||
Отметка за блок «Теория». Теория изложена без ошибок – ЗАЧЕТ (5), наличие ошибки – НЕЗАЧЕТ (2). | |||
2 блок «Практика»
№ | Используя формулы сокращенного умножения преобразуйте выражение в многочлен стандартного вида. | Баллы (0/1) |
Представьте многочлен в виде произведения многочленов или степени двучлена. | ||
а ) | ||
в) | ||
Отметка 5: безошибочное выполнение работы. Отметка 4: правильное выполнение не менее 80 % работы, при условии, что в каждом номере выполнено не менее половины заданий. Отметка 3: правильное выполнение не менее 50 % работы, при условии, что в каждом номере выполнено не менее половины заданий. Отметка 2 (НЕЗАЧЕТ): в остальных случаях. | ||
3 блок «Применение формул сокращенного умножения. Разложение многочлена на множители»
№ | Преобразуйте выражение в многочлен: | Баллы (0/1/2) |
Преобразуйте выражение в многочлен | ||
= | ||
Разложите многочлен на множители: | ||
х2 8х + 20 = | ||
(х + 3)( 4 – х)( 4 + х) + х2(х + 3) = | ||
Отметка 5: безошибочное выполнение работы. Отметка 4: правильное выполнение не менее 80 % работы, при условии, что в каждом номере выполнено не менее половины заданий. Отметка 3: правильное выполнение не менее 50 % работы, при условии, что в каждом номере выполнено не менее половины заданий. Отметка 2 (НЕЗАЧЕТ): в остальных случаях. | ||
Предварительный просмотр:
Зачет по теме «Формулы сокращенного умножения»
ФИ учащегося__________________________________________ класс_____ дата__________
1 блок «Теория»
№ | Запишите формулу и её словесную формулировку. | +/- | |
________________________________________(формула) Куб суммы двух выражений ______________________________________________ _____________________________________________________________________________ ______________________________________________________________________________________________________________________________________________________________ ___________________________________________________________________________________ | |||
________________________________________(формула) Квадрат разности двух выражений ______________________________________________ _____________________________________________________________________________ ______________________________________________________________________________________________________________________________________________________________ | |||
________________________________________(формула) Сумма кубов двух выражений ______________________________________________ _____________________________________________________________________________ ______________________________________________________________________________________________________________________________________________________________ | |||
________________________________________(формула) Разность кубов двух выражений ______________________________________________ _____________________________________________________________________________ ______________________________________________________________________________________________________________________________________________________________ | |||
________________________________________(формула) Разность квадратов двух выражений ______________________________________________ _____________________________________________________________________________ ___________________________________________________________________________________ | |||
________________________________________(формула) Квадрат суммы двух выражений ______________________________________________ _____________________________________________________________________________ ______________________________________________________________________________________________________________________________________________________________ | |||
________________________________________(формула) Куб разности двух выражений ______________________________________________ _____________________________________________________________________________ ______________________________________________________________________________________________________________________________________________________________ ___________________________________________________________________________________ | |||
Отметка за блок «Теория». Теория изложена без ошибок – ЗАЧЕТ (5), наличие ошибки – НЕЗАЧЕТ (2). | |||
2 блок «Практика»
№ | Используя формулы сокращенного умножения преобразуйте выражение в многочлен стандартного вида. | Баллы (0/1) |
Разложите многочлен на множители или представьте в виде степени двучлена. | ||
а ) | ||
в) | ||
Отметка 5: безошибочное выполнение работы. Отметка 4: правильное выполнение не менее 80 % работы, при условии, что в каждом номере выполнено не менее половины заданий. Отметка 3: правильное выполнение не менее 50 % работы, при условии, что в каждом номере выполнено не менее половины заданий. Отметка 2 (НЕЗАЧЕТ): в остальных случаях. | ||
3 блок «Применение формул сокращенного умножения. Разложение многочлена на множители»
№ | Преобразуйте выражение в многочлен: | Баллы (0/1/2) |
Преобразуйте выражение в многочлен | ||
= | ||
Разложите многочлен на множители: | ||
х2 8х + 20 = | ||
(х + 3)( 4 – х)( 4 + х) + х2(х + 3) = | ||
Отметка 5: безошибочное выполнение работы. Отметка 4: правильное выполнение не менее 80 % работы, при условии, что в каждом номере выполнено не менее половины заданий. Отметка 3: правильное выполнение не менее 50 % работы, при условии, что в каждом номере выполнено не менее половины заданий. Отметка 2 (НЕЗАЧЕТ): в остальных случаях. | ||
По теме: методические разработки, презентации и конспекты
Презентация «Формулы сокращенного умножения»
Данная презентация поможет в отработке навыков применения формул ….
урок в 7классе «Формулы сокращенного умножения»
урок-путешествие по формулам сокращенного умножения….
Формулы сокращенного умножения.Алгебра7 класс.
Тема «Формулы сокращенного умножения».Урок-пресс-конференция .Повторение и обобщение пройденного материала ….
Формулы сокращенного умножения
Конспект урока математики в 7 классе по теме «Формулы сокращенного умножения»…
Урок+презентация»Формулы сокращенного умножения «
Урок изучения нового материала. Сопровождается презентацией….
Сопровождается презентацией….
Зачет по теме «Формулы сокращенного умножения». 7 класс.
Работа позволит проверить, как усвоен учениками учебный материал по теме «Формулы сокращенного умножения» в 7 классе….
Зачет по теме «Формулы сокращенного умножения» 7 класс
Дифференцированный зачет по алгебре по теме «Формулы мокращенного умножения» 7 класс…
Поделиться:
Квадрат суммы и квадрат разности — формулы, правило квадрата и примеры решения
Для успешного решения математических задач часто бывает необходимо уметь преобразовывать созданные выражения. Для этого применяют базовые знания, формулы сокращённого умножения, в том числе, квадрат суммы и квадрат разности.
Они помогают упрощать громоздкие записи, более рационально подходить к приведению дробей к одному знаменателю, решению уравнений и задач по геометрии, тригонометрии, математическому анализу, физике, химии, экономическим дисциплинам и многим другим наукам.
Поэтому среди многих разделов математики школьная алгебра занимает базовую приоритетную позицию, дающую основы вычислений для смежных предметов.
Содержание
- Формула квадрата разности
- Примеры задач с решением
- Задача №1
- Задача №2
- Формула квадрата суммы и неполного квадрата суммы
- Примеры задач с решением
- Задача №3
- Задача №4
- Задача №5
- Задача №6
- Разность квадратов
- Пример задачи с решением
- Задача №7
Формула квадрата разности
Для получения формулы применяют правило умножения многочлена на многочлен: нахождение суммы произведений каждого слагаемого одной скобки на каждое слагаемое второй скобки, учитывая, что квадрат отрицательного числа равен квадрату положительного:
Если запомнить правило, то необходимость постоянно прописывать эту цепочку равенств исчезает.
Квадрат разности двух выражений равен сумме квадратов каждого из выражений без их удвоенного произведения:
Примеры задач с решением
Задача №1
Требуется возвести в квадрат разность (8x — 3y).
Решение.
При использовании формулы получается:
Ответ: 64x2 — 48xy + 9y2.
Задача №2
Упростить выражение:
b2 + 49 — (b — 7)2
Решение.
Ответ: 14b.
Формула квадрата суммы и неполного квадрата суммы
Также легко, как и в предыдущем случае, выводится эта формула:
Квадрат суммы двух выражений равен сумме квадратов каждого из них плюс их удвоенное произведение:
Многие школьники, начинающие знакомиться с этим материалом, часто теряют двойку во втором слагаемом правой части, получая
Однако, в этом случае, возникает неполный квадрат суммы (или разности), который на множестве действительных чисел не раскладывается на множители.
Обе формулы применяются не только для раскрытия скобок, но и для разложения на множители, что в свою очередь упрощает приведение к одному знаменателю, сокращение дробей, решение уравнений высоких степеней.
Примеры задач с решением
Задача №3
Преобразовать трёхчлен в квадрат двучлена:
28xy + 49x2 + 4y2
Решение.
Поскольку квадраты находятся на втором и третьем местах, поменяем слагаемые между собой и подготовим выражение для применения формулы:
Ответ: (7x + 2y)2.
Возведение во вторую степень суммы трёх и более слагаемых выполняется аналогично: необходимо возвести в квадрат каждый элемент, записать все возможные удвоенные произведения и сложить полученные результаты.
Правила возведения в степени более высоких порядков возникают, когда выполняется умножение одинаковых многочленов несколько раз.
Возможность выполнять возведение в квадрат больших чисел, не используя калькулятор, является одним из преимуществ сокращённого умножения.
Задача №4
Выполнить раскрытие скобок и упростить:
(x2 + 3x — 4y)2 — x4 — 9x2 — 16y2
Решение.
Ответ: 6x3 — 8x2 — 24xy.
Задача №5
Вычислить:
1032 + 1972
Решение.
Для каждого слагаемого применяется одно из правил возведения в квадрат, затем производится суммирование результатов:
Решая квадратные уравнения, вместо поиска дискриминанта выделяют полный (точный) квадрат среди слагаемых, расположенных в левой части. В правую сторону собираются оставшиеся элементы.
Задача №6
Решить уравнение:
x2 — 4x — 5 = 0
Решение.
Первые два слагаемых левой части полностью удовлетворяют формуле квадрата суммы. Соотнеся их с соответствующими элементами правила, определяют, прибавляют и вычитают третье, затем сворачивают в точный квадрат, остальные члены алгебраической суммы переносят в правую сторону:
Решениями исходного уравнения являются корни уравнений
Ответ: x = 5 или x = -1.
Разность квадратов
Ещё одной формулой сокращённого умножения является разность квадратов. Она получается при умножении суммы двух выражений на их разность.
Читается справа налево.
Разность квадратов двух выражений равна произведению разности этих выражений на их сумму:
Применение последней записи справа налево есть раскрытие скобок более удобным способом, чем простое умножение многочленов.
Разложение на множители позволяет судить о наличии целых или натуральных корней квадратного уравнения.
Пример задачи с решением
Задача №7
Сократить дробь:
Решение.
В числителе записан квадрат разности, а в знаменателе – разность квадратов двух выражений. Применяя соответствующие формулы, получается искомый результат:
Ответ: .
В большинстве случаев разницы, как сворачивать квадрат двучлена, не существует.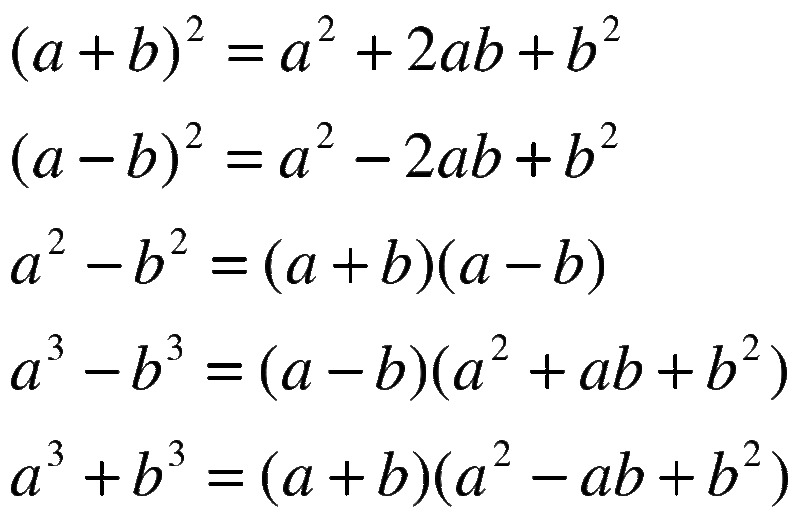 Однако в данной ситуации, благодаря выражению в знаменателе, на первое место лучше поставить , чтобы избежать игры с минусом при сокращении.
Однако в данной ситуации, благодаря выражению в знаменателе, на первое место лучше поставить , чтобы избежать игры с минусом при сокращении.
Онлайн калькуляторы помогают выполнять преобразования. Однако, поскольку формулы сокращённого умножения являются базовым материалом школьного курса, то лучше не просто получить результат, но и понять, каким образом к нему пришли.
Предыдущая
МатематикаДесятичный логарифм в математике — свойства, условия и примеры вычислений
Следующая
МатематикаПризнаки делимости чисел — правила и примеры решений
Сумма степеней положительных целых чисел — Пьер де Ферма (1601-1665), Франция
Автор(ы):
Джанет Бири (Университет Редлендс)
Пьер де Ферма, большую часть жизни проживший в Тулузе, Франция , был юристом, который проводил свободное время, занимаясь математикой. Как и Харриот, он никогда не публиковал свои работы, но намекал на них в письмах Марину Мерсенну, Жилю Персону де Робервалю и другим. Ферма известен тем, что сформулировал, но не доказал Великую теорему Ферма, которая, наконец, была доказана Эндрю Уайлсом в 1919 г.94.
Как и Харриот, он никогда не публиковал свои работы, но намекал на них в письмах Марину Мерсенну, Жилю Персону де Робервалю и другим. Ферма известен тем, что сформулировал, но не доказал Великую теорему Ферма, которая, наконец, была доказана Эндрю Уайлсом в 1919 г.94.
В письмах к Мерсенну и Робервалю в 1636 г. Ферма сформулировал следующие результаты об обобщенных треугольных числах (Махони, стр. 230-231):
Последняя сторона, умноженная на следующую большую, дает удвоенный треугольник. Последняя сторона, умноженная на треугольник следующей большей стороны, в три раза больше пирамиды. Последняя сторона, умноженная на пирамиду следующей большей стороны, дает в четыре раза больше треугольника. И так далее в той же последовательности до бесконечности.
Мы видели треугольные числа. Треугольные числа 1, 3, 6, 10, 15, 21, … являются суммами последовательных положительных целых чисел; пирамидальные числа 1, 4, 10, 20, 35, 56, … являются суммами последовательных треугольных чисел; треугольные числа (как назвал их Ферма) 1, 5, 15, 35, 70, 126, … являются суммами последовательных пирамидальных чисел; и так далее. Например, четвертое треугольное число 10 задается как 10 = 1 + 2 + 3 + 4, а третье пирамидальное число 10 задается как 10 = 1 + 3 + 6. Если мы обозначим n -е треугольное число через \(T_n,\) n -е пирамидальное число через \(P_n,\) и n -е треугольное число через \(TT_n,\), то мы можем перевести первые три предложения Ферма к следующим трем уравнениям в наших обозначениях: $$n(n + 1) = 2T_n, \ nT_{n + 1} = 3P_n, \ {\rm and}\ nP_{n + 1} = 4TT_n. $$
Например, четвертое треугольное число 10 задается как 10 = 1 + 2 + 3 + 4, а третье пирамидальное число 10 задается как 10 = 1 + 3 + 6. Если мы обозначим n -е треугольное число через \(T_n,\) n -е пирамидальное число через \(P_n,\) и n -е треугольное число через \(TT_n,\), то мы можем перевести первые три предложения Ферма к следующим трем уравнениям в наших обозначениях: $$n(n + 1) = 2T_n, \ nT_{n + 1} = 3P_n, \ {\rm and}\ nP_{n + 1} = 4TT_n. $$
Первое уравнение дает нам формулу $$T_n = {{n(n + 1)} \over 2}$$
для n -го треугольного числа или, что то же самое, сумма первых n целых положительных чисел. Этот результат, подставленный во второе уравнение, дает $$n\cdot{(n + 1)(n + 2) \over 2} = 3P_n\ {\rm or}\ P_n = {n(n + 1)( n + 2)\over 2 \cdot 3}$$
для n -го пирамидального числа. Наконец, этот последний результат, подставленный в третье уравнение, дает $$TT_n = {{n(n + 1)(n + 2)(n + 3)} \over {2 \cdot 3 \cdot 4}}$$
для n й треугольный номер.
В тех же письмах Ферма дал два намека на суммы степеней целых чисел. Во-первых, он написал следующую формулу для суммы четвертых степеней первых 93 } \over 3} — {n \over {30}}.$$
Было бы логично, если бы Ферма сообщил свою формулу для суммы четвертых степеней, потому что это была бы первая такая формула, которую он считал неизвестной ( Махони, стр. 232). В своем письме к Робервалю Ферма объяснил свое использование формул, описанных выше (Махони, стр. 231).
Все эти предложения, какими бы красивыми они ни были сами по себе, помогли мне в квадратуре, которую я рад, что вы оценили.
Биограф Ферма, Майкл Махони, утверждал, что, как и у Архимеда, результаты Ферма в «квадратурах» потребовали бы, чтобы у него были вербальные формулы для сумм степеней целых чисел (Махони, стр. 231-233). В частности, успех Ферма в вычислении определенного интеграла функции вида cx k потребовал бы, чтобы он описал формулу для суммы k -х степеней первых n положительных целых чисел. На самом деле было бы достаточно неравенства, подобного неравенству Архимеда, или предела, включающего только члены с показателем степени k + 1, поэтому мы не можем с уверенностью сказать, что у Ферма были формулы, отличные от той, которую он описал для суммы четвертых степеней.
На самом деле было бы достаточно неравенства, подобного неравенству Архимеда, или предела, включающего только члены с показателем степени k + 1, поэтому мы не можем с уверенностью сказать, что у Ферма были формулы, отличные от той, которую он описал для суммы четвертых степеней.
Основываясь на приведенных выше доказательствах, Махони предположил, что Ферма использовал следующий метод для получения сумм степеней (Махони, стр. 231-232). Будем считать, что Ферма уже знал или вывел формулы для сумм первых 9n k .$$
Если теперь мы подставим в наши формулы суммы первых n натуральных чисел и их квадратов и кубов, умножим обе части уравнения на 24 и упростим, то получим одно (или все) формул для сумм четвертых степеней, приведенных выше.
На самом деле Харриот написал символические формулы, подобные тем, что помечены как \(T_n,\) \(P_n,\) \(TT_n,\) и \(TP_n\) (Харриот, листы 108-109; или Бири и Стедалл, стр. 58). -61), но, как мы видели, он использовал другой метод для вывода своих формул для сумм степеней целых чисел. Этот метод, подробно описанный выше, был описан более кратко в книге Бири и Стедалла (стр. 19).-20).
Этот метод, подробно описанный выше, был описан более кратко в книге Бири и Стедалла (стр. 19).-20).
Упражнение 15: Покажите, как записать формулу Ферма для суммы первых n четвертых степеней как (рациональное) кратное n ( n + 1)(2 n + 1)/ 6.
Упражнение 16: Напишите формулу Ферма для треугольных чисел шестого порядка, 1, 7, 28, 84, … словами и символами, возможно, обозначив n треугольное число шестого порядка как T n 6 . Примечание: Треугольные числа второго порядка — это треугольные числа 1, 3, 6, 10, …; треугольные числа третьего порядка пирамидальные числа 1, 4, 10, 20, …; треугольные числа четвертого порядка — треугольные числа 1, 5, 15, 35, …; а треугольные числа пятого порядка — треугольные пирамидальные числа 1, 6, 21, 56, ….
Упражнение 17: Используйте вашу формулу для n треугольного числа шестого порядка T n 6 из упражнения 16 вместе с формулой для n th треугольно-пирамидальное число TP n (или T n 5 ) и уже выведенные четыре формулы для сумм первых n n целых положительных степеней, их четвертых степеней, кубов , чтобы вывести формулу суммы первых n пятых степеней.
Для решения этих упражнений щелкните здесь.
Джанет Бири (Университет Редлендса), «Суммы степеней положительных целых чисел — Пьер де Ферма (1601-1665), Франция», Convergence (июль 2010 г.), DOI: 10.4169/loci003284
Power Summations
Power Summations| Дом | Учитель | Родители | Глоссарий | О нас | |||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
© 2000-2005 Math.com. Все права защищены. Юридический Уведомления. Пожалуйста, ознакомьтесь с нашей Конфиденциальностью Политика. |
013: Сумма / суммы двух четвертых степеней
I. Сумма / Суммы биквадратов (Эта страница охватывает уравнения 1–9. )
)
- а 4 +b 4 = с 4 +d 4
- pq(p 2 +q 2 ) = rs(r 2 +s 2 )
- pq(p 2 -q 2 ) = rs(r 2 -s 2 )
- pq(p 2 +hq 2 ) = rs(r 2 +hs 2 )
- x 4 +y 4 = z 4 +nt 2
- x 4 +y 4 = z 4 +nt 4
- u 4 +nv 4 = (p 4 +nq 4 )w 2
- u 4 +nv 4 = x 4 +y 4 +nz 4
- u 4 +v 4 = x 4 +y 4 +nz 4
- a k +b k +c k = d k +e k +f k , k = 2,4
- a k +b k +c k = 2d k +e k , k = 2,4
- a k +b k +c k = d k +e k +f k , k = 2,3,4
- x 4 +y 4 +z 4 = 2(x 2 y 2 +x 2 z 2 +y 2 z 2 )-t 90
- x 4 +y 4 +z 4 = t 4
- x 4 +y 4 +z 4 = nt k
- v 4 +x 4 +y 4 +z 4 = nt k
- v k +x k +y k +z k = a к +b к +с к +d к , к = 2,4
- 2 (V 4 +x 4 +Y 4 +Z 4 ) = (V 2 +x 2 +Y 2 +Z 2 ) 2 +Z 2 ) 2 1 +Z 2 ) 2 111 +Z 2 )
- x 1 k +x 2 k +x 3 k +x 4 k +x 5 k = y 1 k +y 2 к +у 3 к , к = 1,2,3,4
- x 1 k +x 2 k +x 3 k +x 4 k +x 5 k = y 1 k +y 2 к +у 3 к +у 4 к +у 5 к , к = 1,2,68,4
- x 1 4 +x 2 4 +…x n 4 , n > 4
 Полиномы четвертой степени в степени k
Полиномы четвертой степени в степени k
I. Sum / Sums of biquadrates
Fourth powers are rather interesting since quite a number of situations seem to stop at эта степень. Например, уже известно, что решение P(x) = 0 в радикалах , вообще говоря, разрешимо только для степени k ≤ 4. Точно так же, используя метод Ферма, кажется, что решение P(x) = y 2 в рациональных числах и где P(x) имеет квадратный постоянный член, обычно разрешима только для k ≤ 4. Кроме того, в контексте диофантовых уравнений известны решения,
+C K = D K , и A K +B K = C K +D K
для K ≤ 4 и предоставлено (специальное чехление 3
для K ≤ 4, и это предполагаемо Расширенная гипотеза Эйлера
 Еще предстоит выяснить, так ли это на самом деле.
Еще предстоит выяснить, так ли это на самом деле.1. Форма: A 4 +B 4 = C 4 +D 4
Для базы данных Солн см. Результаты Jarek Wroblewski. Бесконечная последовательность полиномиальных тождеств может быть найдена с помощью эллиптической «кривой», обсуждаемой ниже, с наименьшей из них, имеющей 7-й градус. В красивой версии, представленной Джерардином, маленькие коэффициенты, используя только целые числа {1,2,3},
(a+3a 2 -2a 3 +a 5 +a 0 7 7 4 90 +a 2 -2a 4 -3a 5 +a 6 ) 4 =
(a-3a 2 -2a 3 +a 5 +a 7 ) 4 + (1+а 2 -2а 4 +3а 5 +а 6 ) 4
версия Чоудри0003
(A -A 3 -2A 5 +A ) 5 +(1 +A 2 -2A 6 +2A 7 +A 8 ) 7077070707070707070707070707070707070707077теля 7007070707070 7 + 8 ) 70707070 7 +71) +2A 7 . +(2A 3 +2A 4 -2A 7 ) 5 =
+(2A 3 +2A 4 -2A 7 ) 5 =
(A +3A 3 -2A 5 +A ) 5 +(1 +A ) 5 1 +(1 +A ) 5 1 +(1 +A ) 5 1 +(1 +A ) 2 -2а 6 -2а 7 +а 8 ) 5 + (-2а 3 +2а 4 +2а 7 )0070 5
что на самом деле хорошо для k = 1,5. Хотя существуют тождества для k = 6, неизвестны ни одного с такими малыми коэффициентами. ( Кто -то может найти один? )
J. Steggall
(A 3 +B) 4 +(1 +AD) 4 = (A 3 +D) . 4 + (1+ab) 4 ,
где d = 2ac-b и {a,b,c} должны удовлетворять квадратичному выражению в b , a 4 +3a 2 c-b 2 c+2abc 2 -2a 2 c 3 +1 = 0. elliptic curve,
elliptic curve,
z 2 = (1+a 4 )c+3a 2 c 2 -a 2 c 4
If we do the substitution a = (n+1)/(n-1), один раствор равен c = 9n 4 /(2n 8 -2n 6 +n 4 -2n 2 +2), из которых мы можем вычислить другие рациональные точки. Обратите внимание, что полученный квадрат после обратной замены имеет общий множитель с квадратом во втором альтернативном методе Эйлера для решения этого уравнения. Теорема ” (Пьезы)
Доказательство : в первом известном примере Giovanni Resta была форма
(M 2 N) 4 (x 4 +Y 4 ) = (MN) 6 (U 6 ) = (MN) 6 (U 6 1) = (MN) 6 (U 6 1) = (MN) 6 (U 6 ) = (MN) 6 (U 6 ) +v 6 ) (ур. 1)
1)
с примитивным решением {m,n} = {5, 73}; и {u,v,x,y} = {3, 4, 18, 31}. Уравнение 1 может быть упрощено как,
M 2 (x 4 +Y 4 ) = N 2 (U 6 +V 6 )
.0003 Следовательно, ситуация уменьшается до более легкой проблемы поиска, (x 4 +Y 4 ) (U 6 +V 6 ) = W 2 (eq.2) , где gcd(x,y) = 1 и gcd(u,v) = 1. Однако второй множитель также можно рассматривать как константу, так что это становится 25(193)(x 4 +y 4 ) = w 2 , что является эллиптической кривой. Начиная с известного {x, y} = {18, 31}, можно вычислить бесконечное число других рациональных точек. Следовательно, еще одно решение уравнения 1: {m,n} = {5, 228420709564570748140960777}; и {u,v,x,y} = {3, 4, 563280
и так далее, до бесконечности . Представляется весьма интересным, что в этой задаче фигурирует пифагорейская тройка {3, 4, 5}. Примечание : Компьютерный поиск, вероятно, может найти меньшие взаимно простые решения уравнения 2, хотя отношения u 3 y 2 -v 3 x 2 = 0 следует избегать, поскольку оно тривиально. ( END UPDATE .)
Представляется весьма интересным, что в этой задаче фигурирует пифагорейская тройка {3, 4, 5}. Примечание : Компьютерный поиск, вероятно, может найти меньшие взаимно простые решения уравнения 2, хотя отношения u 3 y 2 -v 3 x 2 = 0 следует избегать, поскольку оно тривиально. ( END UPDATE .)
2. Форма: PQ (P 2 +Q 2 ) = RS (R 2 +S 2 )
. a 4 +b 4 = c 4 +d 4 и pq(p 2 +q 2 ) = rs(r 2 +s 2) являются эквивалентными формами 1. Даны две пары пифагорейских троек:
(p 2 -q 2 ) 2 + (2pq) 2 = (с 2 + Q 2 ) 2 и
(R 2 -S 2 ) 2 + (2RS) 2 = (R 2 + (2RS) 2 = (R 2 + (2RS) 2 ) 2 + (2RS) 2 ) s 2 ) 2
которые определяют два прямоугольных треугольника, связанные с ними задачи нахождения: 1) равных произведений катета и гипотенузы или 2) равных произведений двух катетов,
(2pq) (p 2 +q 2 ) = (2rs)(r 2 + s 2 ) (уравнение 1)
(2pq) (стр. 2 -q 2 ) = (2RS) (R 2 -S 2 ) (уравнение 2)
2 -q 2 ) = (2RS) (R 2 -S 2 ) (уравнение 2)
, по сути, решает уравнение,
. (p+hq) 4 + (r-hs) 4 = (r+hs) 4 + (p-hq) 4
где h = 1 для первого, h = … -1 для второго, что можно доказать, расширив это уравнение. Решение Эйлера для первого случая включает решение простой эллиптической кривой y 2 = (а 3 -б)(б 3 -а). Чтобы получить это, дано,
PQ (P 2 +Q 2 ) = RS (R 2 +S 2 ) (уравнение 1)
Let {p, q,r,s} = {x, ay, bx, y}, чтобы получить
(a-b 3 )x 2 + (a 3 -b)y 2 3 0
3
или аналогичный,
y 2 /x 2 = (b 3 -a)/(a 3 -b)
1. Первый метод : Можно найти a,b такие, что приведенное выше становится квадратом. Эйлер, после ряда остроумных алгебраических преобразований, дал
Эйлер, после ряда остроумных алгебраических преобразований, дал
b = a(1+v), где v = 3(1-a 2 ) 3 /(1+10a 2 +a 4 +4a 6 )
, что даст 7 th градус решения в переменных {p,q,r,s}.
2. Второй метод : Предположим, что x = (a 3 -b). Затем нужно найти
y 2 = (a 3 -b)(b 3 -a)
. Но эта кривая имеет бесконечное число рациональных точек, еще одна из которых дается формулой +190a 4 -44a 6 +9a 8 )
это дает полизоль 13 th град к задаче и связан с задачей Стегалла. Отсюда можно найти другие рациональные точки и известны параметризации для степеней 7, 13, 19 и т. д. Подробнее об этом будет сказано позже. Другие Solns,
A. Gerardin
{P, Q, R, S} = {A 7 +A 5 -2A 3 +A, 3A 2 , A . 6 -2а 4 +а 2 +1, 3а 5 }
6 -2а 4 +а 2 +1, 3а 5 }
эквивалентно, но проще, чем Эйлера 7 й град. (Между прочим, это также было получено Суиннертоном-Дайером в его ранних работах в нежном возрасте 16 лет.)
Т. Хаяши
{p,q,r,s} = {2v 3 ( U 4 +2V 4 ), U 4 VW, 2UV 6 , UW (U 4 +2V 4 )}, если U 4 +3V 4 = W 2 2V 4 = W 2.
Простейшим нетривиальным решением является {u,v,w} = {1,2,7}, что дает {x 1 , x 2 , x 3 , x 4 } = {542, 103, 514, 359} so that x 1 4 +x 2 4 = x 3 4 +x 4 4 . Обратите внимание, что для исходного решения u 4 +3v 4 = w 2 последующие можно найти как
{u,v,w} = {a 4 -3b 40070 , 2abc, 12a 4 b 4 +c 4 }, если a 4 +3b 4 = c 2
, что является частным случаем тождества Лагранжа. Q. Любой полином решает u 4 +3v 4 = w 2 ?
Q. Любой полином решает u 4 +3v 4 = w 2 ?
3. Form: pq(p 2 -q 2 ) = rs(r 2 -s 2 )
Euler
If s = p уравнение сводится к решению p 2 = q 2 -qr+r 2 , два решения из которых
{p,q,r} = {u 2 +3v 2 , u 2 +2uv-3v 9 0,70071 +2uv-3v 4uv}
{p,q,r} = {u 2 +3v 2 , u 2 -2uv-3v 2 , u 2 +2uv-3v 2 }
Форма x 2 +xy+y 2 и ее эквивалент u 2 +3v 2 довольно часто появляются при работе с третьими степенями. Оказывается, это также играет значительную роль для 4-х степеней.
Л.Дж.Ландер
{p,q,r,s} = {v 5 -2v, v 5 +v, 77 -2v 4 +10, 1}
Используя это начальное решение, можно получить дополнительные сведения, используя общее тождество в разделе ff.
4. Форма: PQ (P 2 +HQ 2 ) = RS (R 2 +HS 2 )
На отзы к форме,
A 4 + B 4 = C 4 + D 4
, а также не решается,
A 4 + B 4 11 +
A 4 + B 4 4 + B 4 4 + B 4 4 + B 4 A 4 = D 4 + E 4 + F 4 J. Chernick IF PQ (P 2 + HQ 2 ) = RS (R 2 + HQ 2 ) = RS (R 2 + HQ 2 ) = RS (R 2 + HQ 2 ). hs 2 ), затем (p 2 -hq 2 ) к + (r 2 +hs 2 ) к + (-h) (к/2) (2rs) к 70 = 0 7 + 2109070 к 70 hq 2 ) k + (r 2 -hs 2 ) k + (-h) (k/2) (2pq) k , хотя личность Черника была установлена как h = -1. a 4 + b 4 + c 4 = d 4 + e 4 + f 4 разрешимо, одно из которых {a,b,c,d,e,f} = {7847, 21460, 3504, 21172, 10585, 7104} получено из наименьшего решения, 59 4 + 158 4 = 133 4 + 134 4 . См. также Форма 18 о том, как эта общая форма появляется в контексте Теоремы Круга Декарта 9.0016 . Пьеза Теорема : «Дано одно решение {p,q,r,s} для (p+hq) 4 + (r-hs) 4 4 4 + (p-hq) 4 или эквивалентно: pq(p 2 +hq 2 ) = rs(r 2 +hs 2 ), тогда можно найти последующие. Доказательство: (ab(a 2 +hb 2 )-cd(c 2 +hd 2 )) = (pq(02  Для h = 1 это означает, что система0071 = d 2 + e 2 — f 2
Для h = 1 это означает, что система0071 = d 2 + e 2 — f 2
a = m 3 pq 2 -3m 2 nqrs+2n 3 ps 2
b = q(m 3 q 2 -n 3 s 2 )
c = -2m 3 q 2 r+3mn 2 pqs-n 3 rs 2
d = s(m 3 q 2 -n 3 s 2 )
где {m, n} = {3p 2 +hq 2 , 3r 2 } Таким образом, если RHS = 0, то таким же будет и LHS.
Снова появляется форма x 2 +3y 2 . Это тождество подразумевается в методе, используемом Л. Дж. Ландером. Как уже упоминалось, многие полиномиальные решения для случая h = 1 уже были известны, и Синха заметил, что они имеют степень d = 7, 13, 19., 31, 37 или d = 6n+1, и спросили, происходит ли это только в том случае, если d простое число. В « нерешенных проблемах теории чисел » (2-е изд., Диофантовы уравнения , глава, стр. 141) Р. Гай упоминает, что это не обязательно так, поскольку существует d = 49, а Чоудри обнаружил d = 25. . Независимо этот автор обнаружил, что, используя приведенное выше тождество и начальное решение,
{p,q,r,s} = {-2(1+10v 2 +v 4 +4v 6 ) , в-17в 3 -17в 5 +V 7 , -2V (4 +V 2 +10V 4 +V 6 ), 1-17V 2 -17 В 4 +V 6 }
4 +V 6 } 9003 9003 9000 2 9000 2 9000 2 9007 9007 4 +V 6 } 4 +V 6 } 4 .
, и после удаления общих множителей он также дает 25-градусный полигон. На самом деле, путем разумной перестановки {p,q,r,s} можно найти 42-градусное -солнце, которое определенно не имеет формы d = 6n+1 и не кажется композицией 6 -градусные и 7-градусные полиномы.
5. Форма: x 4 +Y 4 = Z 4 +NT 2
DESBOVES
(A 2 +B 2 ) 70 4 (A . 2 -B 2 ) 4 = (2AB) 4 + 2 (A 4 -B 4 ) 2
С Уравнения a 2 + B 2
. = c k легко решается, это показывает, что x 4k +y 4 = z 4 +2t 2 имеет бесконечное число. растворов. (Или X 4 +Y 4 = Z 4K +2T 2 , поскольку это тривиально для решения 2AB = C K . )
)
E. Fauquembergue (также для X 4 + Y 4 = 1 +Z 2 )
(17p 2 -12PQ-13Q 2 ) 4 +(17P 2 +12PQ-13Q 2 ) +12PQ-13Q 2 ) +12PQ-13Q 2 ) +12PQ-13Q 2 ) +12PQ-13Q 2 ) (17p 2 -q 2 ) 4 + (289p 4 +14p 2 q 2 -239q 4 ) 2
. Чтобы избежать тривиального p = q , одно маленькое решение равно {p,q} = {11, 3}. Тождество Фокемберга зависит от единственного интегрального решения u 2 -2v 4 = -1 с {u,v} > 1, которое равно {u,v} = {239, 13}. Есть ли другие тождества, похожие по форме на это, еще неизвестно. Кстати, сделав третий член равным q 2 -17p 2 = ±1, это также решает x 4 +y 4 = z 2 +1. Поскольку Ферма доказал, что x 4 +y 4 = z 2 имеет не нетривиальное целочисленное решение, то это самое близкое близкое к промаху (точно так же, как существуют целочисленные решения для x 3 +y 3 = z 3 ±1, что также почти не соответствует последней теореме Ферма).
Поскольку Ферма доказал, что x 4 +y 4 = z 2 имеет не нетривиальное целочисленное решение, то это самое близкое близкое к промаху (точно так же, как существуют целочисленные решения для x 3 +y 3 = z 3 ±1, что также почти не соответствует последней теореме Ферма).
Примечание : Этот автор проверил x 4 +y 4 = z 2 ±1 и нашли много растворов для положительного случая, с наименьшим из них {x,y,z} = {5, 7, 55}. Напротив, вообще не было для отрицательного случая с {x,y} < 10 3 . Почему асимметрия? Для сравнения, существует примерно равное количество положительных целых чисел для x 3 +y 3 = z 3 ±1 ниже границы z.
(обновление от 3 января 2011 г.): Джим Каллен с помощью исчерпывающего компьютерного поиска показал, что нет решения для x 9.0070 4 +y 4 = z 2 -1 с {x,y} < 10 6 . Если таковой существует, с помощью модульных аргументов можно показать, что он имеет форму (10u) 4 + (10v) 4 = z 2 -1. Таблица решений вида (10x) 4 +(100y) 2 = z 2 -1 также приведена по ссылке.
Если таковой существует, с помощью модульных аргументов можно показать, что он имеет форму (10u) 4 + (10v) 4 = z 2 -1. Таблица решений вида (10x) 4 +(100y) 2 = z 2 -1 также приведена по ссылке.
6. Форма: x 4 +y 4 = z 4 +nt 4
710002
N. Elkies
(192m 8 -24m 4 -1) 4 + (192m 7 ) 4 = (192m 8 +24m 4 -1) 4 + 192M 4
или эквивалентно,
(192M 8 -24M 4 -1) 4 + (192M 7 ) 4 + (192M 7 ) 4 (192M 7 ) 4 + (192M 7 ) 4 + (192M 7 ) 4 + (192M 7 ) 4 + (192M 7 ) 4 + (192M 7 ) +24м 4 -1) 4 + 12(2м) 4
Это было найдено при рассмотрении почти промахов на кривой Ферма, x 4 +y 4 = z 4 . Три члена являются полиномами высокой степени, в то время как «избыток» является только квартикой, что обеспечивает очень хорошее приближение к кривой. Чтобы проиллюстрировать, для m = 2, это дает
Три члена являются полиномами высокой степени, в то время как «избыток» является только квартикой, что обеспечивает очень хорошее приближение к кривой. Чтобы проиллюстрировать, для m = 2, это дает
24576 4 + 48767 4 ≈ (49535.0000000000063 …) 4
Таким образом целое число.
7. Form: u 4 +nv 4 = (p 4 +nq 4 )w 2
R. Carmichael
Define { r,s} = {p 4 -nq 4 , p 4 +nq 4 }. Then,
(pm-2prs) 4 + n(qm+2qrs) 4 = (p 4 +nq 4 )(m 2 +16np 4 q 4 р 2 ) 2 , с M = P 8 +6NP 4 Q 4 +N 2 Q 8
См. Также Sophie Germain’s Identity .
. р 8 -4н 2 ,
(6пн 2 + PR) 4 + N (3P 4 N-R) 4 = (6PN 2 ) 4 + (PR) 4 + N (3P 4 N + R) 4 + N (3P 4 N + R) 4 + N (3P 4 N + R) 4 + N (3P 4 N + R) 4 + N (3P 4 N + R) 4 + N (3P 4 N + R) 4 + N (3P 4 .
(Обратите внимание, что если n = 0, тождество тривиально и не дает контрпримера к FLT для k = 4.) 4 = x 4 +y 4 +nz 4
Р. Норри
Определить r = p 8 -q 8 . Затем для Любая константа N ,
((2N + R) P 3 Q) 4 + (2NP 4 -Q 4 R) 4 = (2N -Q 4 R) 4 = (2N -Q 4 R) 4 = (2 -Q 4 R) 4 -Q 4 R) = (2 -Q 4 R) = (2 -Q 4 R) (2NP 4 -Q 4 . r)p 3 q) 4 + (2np 4 +q 4 r) 4 + n(2pqr) 4
r)p 3 q) 4 + (2np 4 +q 4 r) 4 + n(2pqr) 4
3 90 для любого числа p, 90 сумма/разность четырех рациональных четвертых степеней, как уже упоминалось в ч. Опять же, для n = 0 тождество тривиально. Может быть интересно спросить, для чего
n существует ли рациональное многозначное решение для x 4 +y 4 +z 4 = t 4 +n?
◄ Предыдущая страница Следующая страница ►
Суммы k-х степеней | Gowers’s Weblog
Недавно я выступал с докладом в школе в Лондоне, и мне пришлось задуматься о суммах k-х степеней, потому что я хотел показать людям разницу между непросветляющими и просветляющими доказательствами. (Моя задача заключалась в том, чтобы попытаться дать им некоторое представление о том, что такое доказательства и почему о них стоит беспокоиться.) В поезде вниз я понял, что существует очень простое общее рассуждение, которое можно использовать для получения формул для сумм k-я сила. Покопавшись в интернете, я не нашел именно этого метода, хотя нашел множество методов, близких к нему. Это должно быть где-то в литературе, так что, возможно, кто-нибудь может указать мне на ссылку. Но даже так, это стоит короткого поста.
Покопавшись в интернете, я не нашел именно этого метода, хотя нашел множество методов, близких к нему. Это должно быть где-то в литературе, так что, возможно, кто-нибудь может указать мне на ссылку. Но даже так, это стоит короткого поста.
Начну с дела. Я хочу сформулировать знакомый аргумент таким образом, чтобы его было легко обобщить так, как я хочу его обобщить. Позвольте быть прямоугольником, состоящим из всех целых точек таких, что и . Мы можем разбить на те точки, для которых и те точки, для которых . Количество точек первого рода равно , так как для каждой мы получаем возможности для . Количество точек второго рода равно , так как для каждой мы получаем возможности для . Поэтому и получаем знакомую формулу.
Теперь перейдем к сумме квадратов. На этот раз пусть будет множество точек с , и . Мы можем разбить на три множества, первое состоит из точек, для которых максимальна, вторая состоит из точек, для которых максимальна и не максимальна, а третья состоит из точек, для которых строго больше обоих и . Легко видеть, что количество точек в этих наборах равно
Легко видеть, что количество точек в этих наборах равно
и
,
соответственно. Это дает нам формулу
откуда получаем знакомую нам формулу суммы первых квадратов. Записав сумму первых степеней, мы также получим соотношение
Поразительный факт о суммах степеней заключается в том, что . Один из способов объяснить это можно найти в довольно красивой анимации, которую я наткнулся в результате поста Ричарда Грина в Google Plus. Другой исходит от продолжения подхода здесь.
На этот раз я возьму множество таких точек, что и находятся между 1 и n и и находятся между 1 и . Опять же, я разделю в соответствии с тем, какое из значений больше, выбирая первое, которое больше, когда есть ничья. Это дает мне четыре комплекта. Вот их размеры.
первый по величине: .
первый по величине: .
первый по величине: .
первый по величине: .
Эти размеры могут быть записаны как , и . Итак, мы получаем , что дает нам это.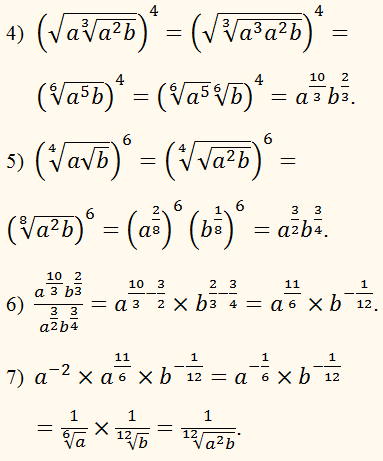 Это также дает нам своего рода объяснение этого факта: поскольку мы разлагаем на две равные части размера , а for мы разлагаем на четыре части, не все из которых имеют размер, но две ошибки компенсируются.
Это также дает нам своего рода объяснение этого факта: поскольку мы разлагаем на две равные части размера , а for мы разлагаем на четыре части, не все из которых имеют размер, но две ошибки компенсируются.
Чтобы убедиться, что это частичное, но не полное совпадение, я перейду к этому моменту. Я позволю быть набором таких точек, которые находятся между 1 и и находятся между 1 и . На этот раз расчеты следующие.
первый по величине: .
первый по величине: .
первый по величине: .
первый по величине: .
первый по величине: .
первый по величине: .
Складывая все это, мы находим, что . Из этого мы получаем, что
В общем, если мы используем этот метод для вычисления, когда нечетно, то (как и с другими методами) мы получаем связь между и ранее . Но что приятно в этом, так это то, что есть много отмен: все даже вносят нулевой вклад.
Действительно, если , то мы имеем множества, и их размеры равны , , , и так далее до
и далее то же самое, но с заменой всех знаков минус в этих линейных комбинациях знаками плюс. Складывая все это, мы получаем линейную комбинацию , , … , что равно , где если четно, а если нечетно. Когда мало, нам не нужно учитывать слишком много, поэтому формулы какое-то время остаются довольно приятными, прежде чем они станут отвратительными.
Складывая все это, мы получаем линейную комбинацию , , … , что равно , где если четно, а если нечетно. Когда мало, нам не нужно учитывать слишком много, поэтому формулы какое-то время остаются довольно приятными, прежде чем они станут отвратительными.
Обратите внимание, что довольно легко вычислить коэффициенты различных в приведенной выше линейной комбинации: они представляют собой просто суммы биномиальных коэффициентов. Несколько других методов требуют решения одновременных уравнений, хотя они обычно имеют треугольную форму, так что не так уж плохо.
Небольшое замечание: основная идея этого аргумента состоит в том, чтобы дискретизировать гораздо более простой непрерывный аргумент, который показывает, что . Этот аргумент состоит в том, чтобы взять -мерный куб, состоящий из всех точек, каждая из которых принадлежит интервалу, и разделить его на части в соответствии с наибольшей координатой. (Я называю этот аргумент геометрическим, потому что эти части представляют собой пирамиды с основаниями -кубами. ) В непрерывном случае нам не нужно беспокоиться о том, что произойдет, если существует более одной наибольшей координаты, поскольку это множество имеет нулевую меру. У каждой части есть мера, и есть части, а у куба есть мера, так что мы закончили.
) В непрерывном случае нам не нужно беспокоиться о том, что произойдет, если существует более одной наибольшей координаты, поскольку это множество имеет нулевую меру. У каждой части есть мера, и есть части, а у куба есть мера, так что мы закончили.
Второе замечание состоит в том, что известный мне ранее метод вычисления суммы th степеней заключается в использовании факта, который заслуживает того, чтобы называться естественным дискретным аналогом вышеизложенного. Определить быть. Это мы считаем дискретным аналогом . Затем мы делаем дискретный аналог дифференцирования, который заключается в том, чтобы посмотреть на , который равен . Это дискретный аналог того факта, что производная равна . Далее мы используем дискретный аналог фундаментальной теоремы исчисления, который заключается в утверждении, что для вывода этого . Это дает нам для каждого многочлен степени, которую мы можем легко суммировать, а именно , а затем, чтобы вычислить сумму первых степеней, мы записываем ее в виде линейной комбинации , суммируем все и упрощаем ответ. Это прекрасно работает, но вычисления немного сложнее, чем то, что я сделал выше, и доказательство слишком алгебраично, чтобы объяснить, почему ответы имеют довольно красивую форму. (Например, почему множитель суммы первых степеней всегда нечетен и не меньше 3? Из аргумента, который я приводил ранее в посте, это довольно легко следует по индукции.)
Это прекрасно работает, но вычисления немного сложнее, чем то, что я сделал выше, и доказательство слишком алгебраично, чтобы объяснить, почему ответы имеют довольно красивую форму. (Например, почему множитель суммы первых степеней всегда нечетен и не меньше 3? Из аргумента, который я приводил ранее в посте, это довольно легко следует по индукции.)
Нравится:
Нравится Загрузка…
Эта запись была опубликована 4 ноября 2014 г. в 22:18 и находится в рубрике Straight maths. Вы можете следить за любыми ответами на эту запись через ленту RSS 2.0. Вы можете оставить отзыв или вернуться со своего сайта.
Элементарный метод суммирования p-х степеней | by Ujjwal Singh
Вероятно, нет математика, который при первой же встрече не был бы очарован классической задачей суммирования первых n натуральных чисел, затем их квадраты, затем кубы и так далее. На самом деле суммирование натуральных чисел неизменно служит введением в арифметические прогрессии. Суммы квадратов и кубов натуральных чисел также относительно хорошо известны. В совокупности изучение этих сумм пробуждает аппетит к получению выражений в закрытой форме для рядов в целом, а также вызывает чувство признательности за то же самое.
Суммы квадратов и кубов натуральных чисел также относительно хорошо известны. В совокупности изучение этих сумм пробуждает аппетит к получению выражений в закрытой форме для рядов в целом, а также вызывает чувство признательности за то же самое.
К настоящему времени суммы p -я степень натуральных чисел была исчерпывающе изучена, и у нас есть выражения для них в замкнутой форме, данные формулой Фаульхабера. Однако мы не будем углубляться в это здесь. У этой статьи гораздо более скромные цели. Здесь мы будем исследовать альтернативную линию доказательства сумм степеней натуральных чисел. Альтернатива чему? Альтернатива широко используемым доказательствам, которые используют разницу между (p + 1)--ми степенями, чтобы найти сумму p -я степень натуральных чисел. Если вы хотите освежить в памяти то же самое, пожалуйста, посмотрите здесь — ссылка.
Напротив, мы будем полагаться на рассмотрение этих сумм как на сумму сумм (вместе с некоторыми перестановками) для получения наших результатов.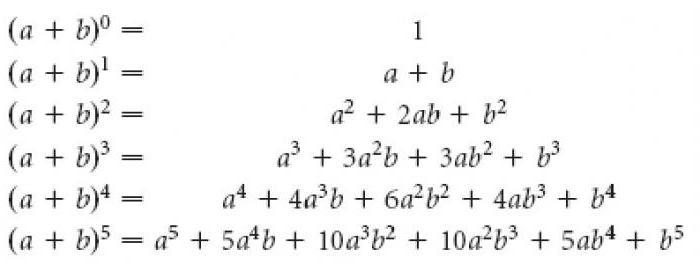 Эта статья структурирована следующим образом –
Эта статья структурирована следующим образом –
- Получение выражения для суммы натуральных чисел.
- Получение выражения для суммы квадратов натуральных чисел.
- Вычисление суммы кубов.
- Некоторые общие сведения о сумме p -х степеней натуральных чисел.
Ниже мы используем технику суммы сумм , чтобы получить известное выражение в закрытой форме для суммы первых n натуральных чисел. Тот же метод будет использоваться в последующих разделах для получения сумм для квадратов и кубов.
Сначала мы разбиваем каждое натуральное число таким образом —
Затем выполняем сложение по столбцам. Ясно, что первая колонка в сумме дает 9.0015 n , следующий за (n — 1) и так далее. Следовательно,
Значит доказано! Мы получили выражение для суммы первых n натуральных чисел. Далее идут квадраты …
Продолжая в том же духе, что и выше, мы сначала разбиваем наши слагаемые следующим образом —
Опять же, мы продолжаем сложение по столбцам. Сумма первого столбца дает (1 + 2 + … + n) , сумма второго столбца составляет (2 + 3 + … + n) и так далее.
Сумма первого столбца дает (1 + 2 + … + n) , сумма второго столбца составляет (2 + 3 + … + n) и так далее.
Используя формулу суммы натуральных чисел, получаем —
Снова применяя формулу суммы натуральных чисел —
Значит доказано! Теперь приступим к сумме кубов …
Продолжая описанную выше методику, сначала представим каждый куб в виде суммы квадратов —
Опять же, выполняя сложение по столбцам, получим —
Теперь, используя формула суммы квадратов натуральных чисел, получаем —
Применяя формулу суммы квадратов еще раз, получаем —
Теперь используем формулы суммы натуральных чисел и суммы квадратов натуральных чисел, чтобы получить —
Значит доказано! Таким образом, мы получили выражения в закрытой форме для суммы первых n натуральных чисел, суммы их квадратов и суммы их кубов.
Что дальше? Ясно, что мы можем продолжать применять описанную выше технику, чтобы получить выражения для сумм высших степеней. Но как насчет обобщения? Можем ли мы сказать что-нибудь о выражении для суммы p -я степень первых n натуральных чисел? Давайте посмотрим…
Но как насчет обобщения? Можем ли мы сказать что-нибудь о выражении для суммы p -я степень первых n натуральных чисел? Давайте посмотрим…
Прежде чем мы углубимся в выражение для суммы p -х степеней натуральных чисел, давайте сначала введем несколько удобных обозначений. Мы определяем —
Теперь, хотя мы можем не знать точное выражение для S_{p,n} (подчеркивание представляет нижний индекс), мы утверждаем следующее —
- S_{p,n} есть (p + 1) полином й степени от n .
- Старший коэффициент S_{p,n}, т. е. 9(p) составляет 1/2 .
Все вышесказанное переводится как —
Доказательство
Мы строим доказательство по индукции. То есть
- . Покажем, что утверждение (1) выполняется для S_{1,n}.
- Предположим, что утверждение верно для S_{p,n}.
- Используя вышеизложенное, мы получаем выражение для S_{p+1,n} и подтверждаем, что утверждение справедливо и для S_{p+1,n}.

Демонстрация истинности утверждения для S_{1,n}
Здесь,
Используя выражение для суммы натуральных чисел, получаем
Отсюда ясно, что
- S_{1,n} является многочленом порядка 2 (1+1) от n.
- Старший коэффициент равен 1/(1+1).
- Коэффициент следующего старшего члена (n) равен 1/2.
Следовательно, утверждение верно для S_{1,n}.
Предположим, что утверждение верно для S_{p,n}
Теперь предположим, что утверждение верно для суммы p-го степеней натуральных чисел. То есть
Доказательство утверждения для S_{p+1,n}
Для завершения процесса индукции мы должны доказать, что утверждение верно и для S_{p+1, n}. То есть от нас требуется вывести приведенные ниже
. Чтобы доказать вышесказанное, мы снова используем технику разложения суммы на сумму сумм. Помните,
- Для получения суммы натуральных чисел мы разбили каждое натуральное число на суммы единиц (например, 3 = 1 + 1 + 1), т.
 е. суммы нулевых степеней натуральных чисел.
е. суммы нулевых степеней натуральных чисел. - Для получения суммы квадратов натуральных чисел мы разложили каждый квадрат на суммы первых степеней (например, 3² = 3 + 3+ 3).
- Для получения суммы кубов натуральных чисел мы разложили каждый куб на суммы квадратов (например, 3³ = 3² + 3² + 3²).
Итак, как вы уже поняли, для суммирования (p+1)-й -й степени натуральных чисел мы разложим каждое слагаемое на сумму -й p-й -й степени.
Теперь, продолжая сложение по столбцам, получаем —
Теперь, используя выражение для S_{p,n} из (1), получаем —
Меняя порядок двойного суммирования, получаем
Снова расширяя S_{m,n} с помощью уравнения (1), мы получаем —
Теперь, произведя некоторые перестановки, мы получим
Более пристальный взгляд (который мы здесь пропустим) покажет, что все члены в скобках имеют степень меньше или равную p. то есть
Разлагая S_{p,n} с помощью уравнения (1), получаем —
Значит доказано! Процесс индукции успешно завершен.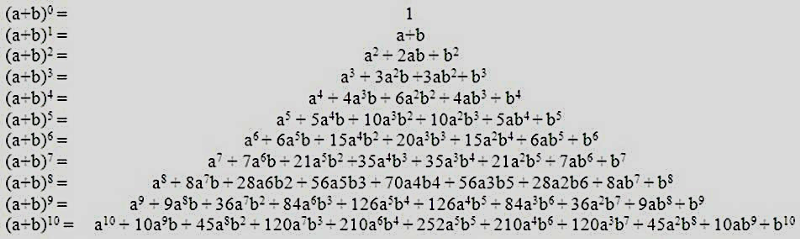
Итак, из вышеизложенного, хотя мы можем и не знать точное выражение для суммы p-й степеней, мы знаем несколько проницательных свойств того же самого! Надеюсь, вам понравилась статья и вы нашли ее информативной. В заключение приведем несколько выражений для S_{p,n}, которые вы можете использовать для перекрестной проверки общего результата, который мы только что доказали —
Сумма первых n членов ряда
Горячая математикаСумма членов последовательности называется серии .
Если последовательность является арифметика или же геометрический есть формулы для нахождения суммы первых н термины, обозначаемые С н , фактически не добавляя все термины.
(Обратите внимание, что последовательность не может быть ни арифметической, ни геометрической, и в этом случае вам нужно будет добавлять с помощью грубой силы или какой-либо другой стратегии.)
Сумма членов арифметической последовательности (арифметического ряда)
Чтобы найти сумму первых
н
члены арифметической прогрессии используют формулу,
С
н
знак равно
н
(
а
1
+
а
2
)
2
,
где
н
это количество терминов,
а
1
является первым термином и
а
н
это последний срок.
Пример 1:
Найдите сумму первых 20 члены арифметического ряда, если а 1 знак равно 5 а также а 20 знак равно 62 .
С 20 знак равно 20 ( 5 + 62 ) 2 С 20 знак равно 670
Пример 2:
Найдите сумму первых
40
члены арифметической прогрессии
2
,
5
,
8
,
11
,
14
,
⋯
Сначала найдите 40 й срок:
а 40 знак равно а 1 + ( н − 1 ) г знак равно 2 + 39( 3 ) знак равно 119
Затем найдите сумму:
С н знак равно н ( а 1 + а н ) 2 С 40 знак равно 40 ( 2 + 119) 2 знак равно 2420
Пример 3:
Найдите сумму:
∑ к знак равно 1 50 ( 3 к + 2 )
Первая находка а 1 а также а 50 :
а 1 знак равно 3 ( 1 ) + 2 знак равно 5 а 20 знак равно 3 ( 50 ) + 2 знак равно 152
Затем найдите сумму:
С к знак равно к ( а 1 + а к ) 2 С 50 знак равно 50 ( 5 + 152 ) 2 знак равно 3925
Сумма членов геометрического ряда (геометрического ряда)
Чтобы найти сумму первых
н
члены геометрической последовательности используют формулу,
С
н
знак равно
а
1
(
1
−
р
н
)
1
−
р
,
р
≠
1
,
где
н
это количество терминов,
а
1
является первым термином и
р
это
обыкновенное отношение
.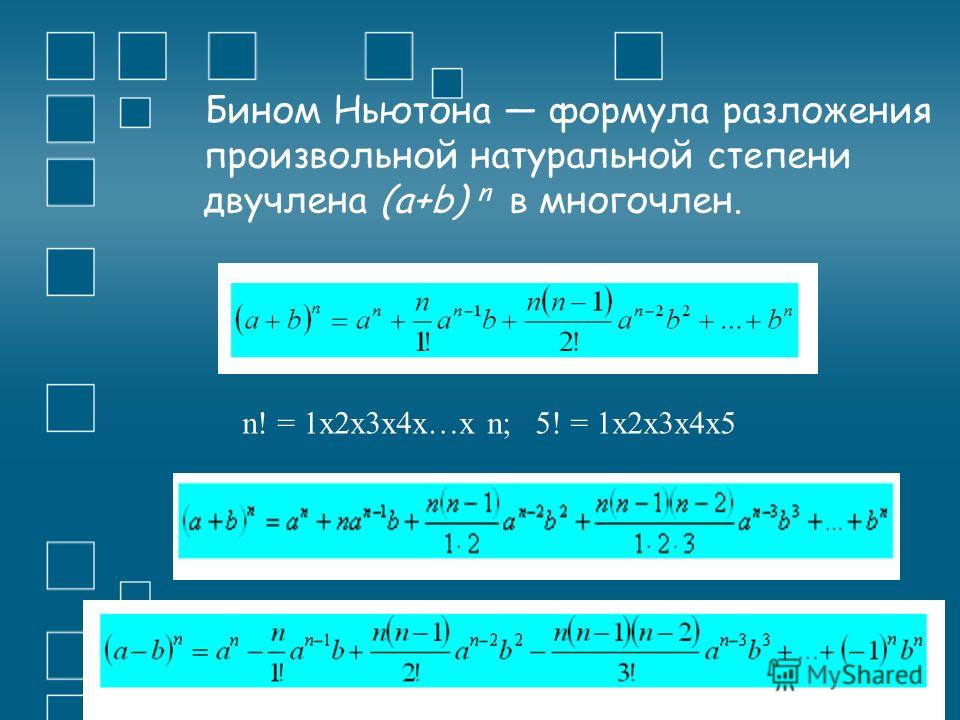
Пример 4:
Найдите сумму первых 8 членов геометрического ряда, если а 1 знак равно 1 а также р знак равно 2 .
С 8 знак равно 1 ( 1 − 2 8 ) 1 − 2 знак равно 255
Пример 5:
Находить
С
10
геометрического ряда
24
+
12
+
6
+
⋯
.
Сначала найдите р .
р знак равно р 2 р 1 знак равно 12 24 знак равно 1 2
Теперь найдите сумму:
С 10 знак равно 24 ( 1 − ( 1 2 ) 10 ) 1 − 1 2 знак равно 306964
Пример 6:
Оценивать.

 3 + x + 1, у которых иррациональные корни, нельзя разложить на многочлены с целыми (рациональными) коэффициентами. Хотя такой многочлен может быть разложен по кубической формуле, он не разлагается как целый многочлен.
3 + x + 1, у которых иррациональные корни, нельзя разложить на многочлены с целыми (рациональными) коэффициентами. Хотя такой многочлен может быть разложен по кубической формуле, он не разлагается как целый многочлен.








 . + п
. + п . + п 4
. + п 4  . + п 7
. + п 7  . + п 10
. + п 10 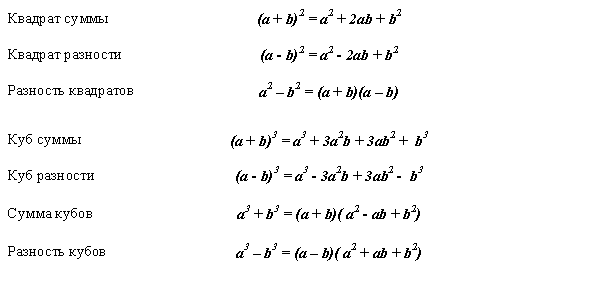
 е. суммы нулевых степеней натуральных чисел.
е. суммы нулевых степеней натуральных чисел.