Статистические критерии
Сравнение средних значений в двух группах
Критерий Стьюдента для двух выборок (t-test)
Предположение: выборки взяты из нормального распределения.
Нулевая гипотеза: средние двух генеральных совокупностей равны.
Варианты: есть два варианта критерия Стьюдента: для независимых выборок (в двух выборках содержатся значения показателя для разных объектов) и для связных выборок (в двух выборках содержатся значения показателя для одних и тех же объектов, например, в разные периоды времени). Пример использования критерия Стьюдента для независимых выборок: сравнение средних значений ВВП на душу населения в демократиях и автократиях. Пример использования критерия Стьюдента для связных выборок: сравнение средней заработной платы в одних и тех же регионах до экономической реформы и после нее.
Строго говоря, есть еще одно деление внутри критерия Стьюдента для независимых выборок: при условии, что дисперсии генеральных совокупностей, из которых взяты выборки, равны, и при условии, что эти дисперсии не равны.
Реализация в R:
Сравним средний уровень детской смертности в католических и протестантских кантонах Швейцарии (данные за 1888 год, встроенная в R база swiss). Предполагаем, что уровень смертности в католических и протестантских кантонах имеет нормальное распределение.
# переменная religion - по которой будем делить кантоны на 2 группы swiss$religion <- ifelse(swiss$Catholic > 50, "catholic", "protestant") # сам тест # через ~ указывается показатель, по которому делим наблюдения в базе на 2 группы t.test(data = swiss, Infant.Mortality ~ religion)
## ## Welch Two Sample t-test ## ## data: Infant.Mortality by religion ## t = 1.0863, df = 31.717, p-value = 0.2855 ## alternative hypothesis: true difference in means is not equal to 0 ## 95 percent confidence interval: ## -0.8620975 2.8310630 ## sample estimates: ## mean in group catholic mean in group protestant ## 20.55000 19.56552
Здесь p-value = 0.2855, значит, вероятность того, что наша нулевая гипотеза о равенстве средних верна (при условии имеющихся данных), равна 0.2855. На 5%-ном уровне значимости есть основания не отвергать нулевую гипотезу о равенстве средних значений (0.2855 > 0.05). Средний уровень детской смертности в католических и протестантских кантонах можно считать одинаковым.
Если вдруг в базе данных показатели, средние по которым нужно сравнить, просто находятся в двух разных столбцах, то t-test выглядит так:
# вместо векторов могут быть столбцы базы через $ set.seed(123) index.a <- rnorm(100, mean = 2, sd = 6) index.b <- rnorm(100, mean = 10, sd = 10) t.test(index.a, index.b)
## ## Welch Two Sample t-test ## ## data: index.a and index.b ## t = -5.7428, df = 156.59, p-value = 4.705e-08 ## alternative hypothesis: true difference in means is not equal to 0 ## 95 percent confidence interval: ## -8.577204 -4.186989 ## sample estimates: ## mean of x mean of y ## 2.542435 8.924532
Тут p-value = 4.705e-08, то есть почти 0. На 5%-ном уровне значимости есть основания отвергнуть нулевую гипотезу о равенстве средних значений.
Для связных выборок (парных показателей), в качестве аргумента функции t.test нужно дописать paired=TRUE).
Критерий Уилкоксона (Манна-Уитни) для двух групп
Предположение: выборки взяты не из нормального распределения (из какого – неизвестно).
Нулевая гипотеза: выборки взяты из одного и того же распределения (можно использовать как аналог t-test и говорить о равенстве средних двух независимых выборок, но изначально критерий Уилкоксона не об этом).
Варианты: как и в случае с критерием Стьюдента для двух выборок, есть вариант для независимых и связных выборок.
Реализация в R:
Сравним средний уровень детской смертности в католических и протестантских кантонах Швейцарии (данные за 1888 год, встроенная в R база swiss). Предполагаем, что уровень смертности в католических и протестантских кантонах имеет распределение, отличное от нормального.
Предполагаем, что уровень смертности в католических и протестантских кантонах имеет распределение, отличное от нормального.
# через ~ указывается показатель, по которому делим наблюдения в базе на 2 группы wilcox.test(data = swiss, Infant.Mortality ~ religion)
## Warning in wilcox.test.default(x = c(22.2, 20.2, 26.6, 23.6, 24.9, 21, ## 24.4, : cannot compute exact p-value with ties
## ## Wilcoxon rank sum test with continuity correction ## ## data: Infant.Mortality by religion ## W = 286.5, p-value = 0.5841 ## alternative hypothesis: true location shift is not equal to 0
Если вылезает предупреждение “не могу подсчитать точное p-значение при наличии повторяющихся наблюдений”, можно добавить аргумент exact=FALSE, что будет говорить R о том, что мы это понимаем, и не ждем от него втаком случае точного расчета p-value.
Случай с двумя столбцам:
wilcox.test(index.a, index.b)
## ## Wilcoxon rank sum test with continuity correction ## ## data: index.a and index.b ## W = 2923, p-value = 3.902e-07 ## alternative hypothesis: true location shift is not equal to 0
Сравнение средних значений в трех и более группах
ANOVA
ANOVA – analysis of variance, дисперсионный анализ.
Предположение:
выборки взяты из нормального распределения.Нулевая гипотеза: средние значения k генеральных совокупностей равны (где k – число исследуемых выборок).
Реализация в R:
Сравним средний вес цыплят в пяти группах – в зависимости от того, каким кормом их кормили (данные из встроенной в R базы chickwts). Предполагаем, что вес цыплят, относящихся к разным группам, имеет нормальное распределение.
anova.res <- aov(data = chickwts, weight ~ feed) # ANOVA, выдает сумму квадратов summary(anova.res) # все статистики + p-value
## Df Sum Sq Mean Sq F value Pr(>F) ## feed 5 231129 46226 15.37 5.94e-10 *** ## Residuals 65 195556 3009 ## --- ## Signif.codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Критерий Краскела-Уоллиса
Предположение: выборки взяты из распределения, отличного от нормального (из какого – неизвестно).
Нулевая гипотеза: выборки взяты из одного и того же распределения (можно говорить о равенстве средних k независимых выборок, но изначально критерий не об этом).
Реализация в R:
Сравним средний вес цыплят в пяти группах – в зависимости от того, каким кормом их кормили (данные из встроенной в R базы chickwts). Предполагаем, что вес цыплят, относящихся к разным группам, имеет распределение, отличное от нормального.
kruskal.test(data = chickwts, weight ~ feed)
## ## Kruskal-Wallis rank sum test ## ## data: weight by feed ## Kruskal-Wallis chi-squared = 37.343, df = 5, p-value = 5.113e-07
Таблицы распределений
Таблицы распределенийТаблицы распределений
В этом разделе представлены стандартные
таблицы функций распределения.
|
|
|
Все приведенные ниже распределения рассчитаны
с помощью функций STATISTICA BASIC и сверены с
другими опубликованными таблицами.
Стандартное нормальное (Z) распределение
Стандартное нормальное распределение используется при проверке различных гипотез, в том числе о среднем значении, о различии между двумя средними и о пропорциональности значений. Оно имеет среднее 0 и стандартное отклонение 1. На предыдущем рисунке динамически показана плотность распределения и соответствующие разным величинам значения вероятности. Дополнительную информацию о нормальном распределении и его использовании при статистической проверке гипотез можно найти в разделах Элементарные понятия статистики и Нормальное распределение.
Значения, приведенные в таблице, представляют
собой величину площади под стандартной
нормальной (гауссовой) кривой от 0 до
соответствующего z-значения, как показано на
следующем рисунке. Например, величина этой
площади между значениями 0 и 2. 36 показана в
ячейке, находящейся на пересечении строки 2.30
и столбца 0.06, и составляет 0.4909. Значение
площади между 0 и отрицательным значением
находится на пересечении строки и столбца,
которые в сумме соответствуют абсолютному
значению заданной величины. Например, площадь
под кривой от -1.3 до 0 равна площади под кривой
между 1.3 и 0, поэтому ее значение находится на
пересечении строки 1.3 и столбца 0.00 (и
составляет 0.4032).
36 показана в
ячейке, находящейся на пересечении строки 2.30
и столбца 0.06, и составляет 0.4909. Значение
площади между 0 и отрицательным значением
находится на пересечении строки и столбца,
которые в сумме соответствуют абсолютному
значению заданной величины. Например, площадь
под кривой от -1.3 до 0 равна площади под кривой
между 1.3 и 0, поэтому ее значение находится на
пересечении строки 1.3 и столбца 0.00 (и
составляет 0.4032).
| 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.0000 | 0.0040 | 0.0080 | 0.0120 | 0.0160 | 0. 0199 0199 |
0.0239 | 0.0279 | 0.0319 | 0.0359 |
| 0.1 | 0.0398 | 0.0438 | 0.0478 | 0.0517 | 0.0557 | 0.0596 | 0.0636 | 0.0675 | 0.0714 | 0.0753 |
| 0.2 | 0.0793 | 0.0832 | 0.0871 | 0.0910 | 0.0948 | 0.0987 | 0.1026 | 0.1064 | 0.1103 | 0.1141 |
| 0.3 | 0.1179 | 0.1217 | 0.1255 | 0.1293 | 0.1331 | 0.1368 | 0.1406 | 0.1443 | 0.1480 | 0.1517 |
| 0.4 | 0.1554 | 0. 1591 1591 |
0.1628 | 0.1664 | 0.1700 | 0.1736 | 0.1772 | 0.1808 | 0.1844 | 0.1879 |
| 0.5 | 0.1915 | 0.1950 | 0.1985 | 0.2019 | 0.2054 | 0.2088 | 0.2123 | 0.2157 | 0.2190 | 0.2224 |
| 0.6 | 0.2257 | 0.2291 | 0.2324 | 0.2357 | 0.2389 | 0.2422 | 0.2454 | 0.2486 | 0.2517 | 0.2549 |
| 0.7 | 0.2580 | 0.2611 | 0.2642 | 0.2673 | 0.2704 | 0.2734 | 0.2764 | 0.2794 | 0. 2823 2823 |
0.2852 |
| 0.8 | 0.2881 | 0.2910 | 0.2939 | 0.2967 | 0.2995 | 0.3023 | 0.3051 | 0.3078 | 0.3106 | 0.3133 |
| 0.9 | 0.3159 | 0.3186 | 0.3212 | 0.3238 | 0.3264 | 0.3289 | 0.3315 | 0.3340 | 0.3365 | 0.3389 |
| 1.0 | 0.3413 | 0.3438 | 0.3461 | 0.3485 | 0.3508 | 0.3531 | 0.3554 | 0.3577 | 0.3599 | 0.3621 |
| 1.1 | 0.3643 | 0.3665 | 0.3686 | 0.3708 | 0.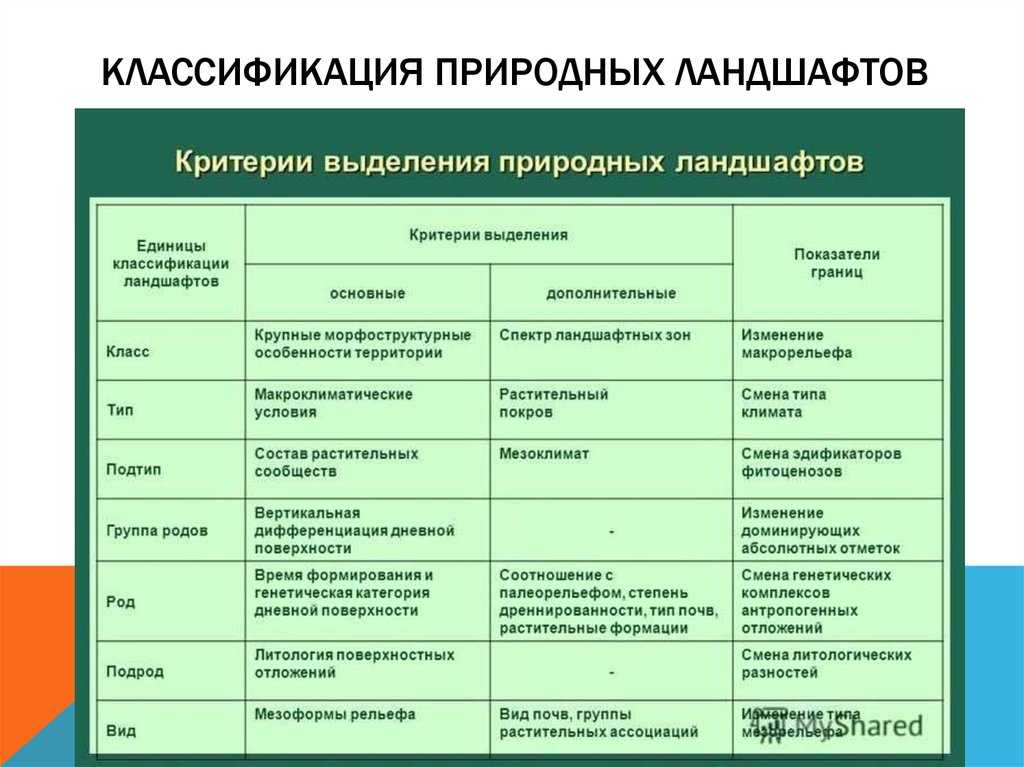 3729 3729 |
0.3749 | 0.3770 | 0.3790 | 0.3810 | 0.3830 |
| 1.2 | 0.3849 | 0.3869 | 0.3888 | 0.3907 | 0.3925 | 0.3944 | 0.3962 | 0.3980 | 0.3997 | 0.4015 |
| 1.3 | 0.4032 | 0.4049 | 0.4066 | 0.4082 | 0.4099 | 0.4115 | 0.4131 | 0.4147 | 0.4162 | 0.4177 |
| 1.4 | 0.4192 | 0.4207 | 0.4222 | 0.4236 | 0.4251 | 0.4265 | 0.4279 | 0.4292 | 0.4306 | 0.4319 |
| 1.5 | 0. 4332 4332 |
0.4345 | 0.4357 | 0.4370 | 0.4382 | 0.4394 | 0.4406 | 0.4418 | 0.4429 | 0.4441 |
| 1.6 | 0.4452 | 0.4463 | 0.4474 | 0.4484 | 0.4495 | 0.4505 | 0.4515 | 0.4525 | 0.4535 | 0.4545 |
| 1.7 | 0.4554 | 0.4564 | 0.4573 | 0.4582 | 0.4591 | 0.4599 | 0.4608 | 0.4616 | 0.4625 | 0.4633 |
| 1.8 | 0.4641 | 0.4649 | 0.4656 | 0.4664 | 0.4671 | 0.4678 | 0.4686 | 0. 4693 4693 |
0.4699 | 0.4706 |
| 1.9 | 0.4713 | 0.4719 | 0.4726 | 0.4732 | 0.4738 | 0.4744 | 0.4750 | 0.4756 | 0.4761 | 0.4767 |
| 2.0 | 0.4772 | 0.4778 | 0.4783 | 0.4788 | 0.4793 | 0.4798 | 0.4803 | 0.4808 | 0.4812 | 0.4817 |
| 2.1 | 0.4821 | 0.4826 | 0.4830 | 0.4834 | 0.4838 | 0.4842 | 0.4846 | 0.4850 | 0.4854 | 0.4857 |
| 2.2 | 0.4861 | 0.4864 | 0.4868 | 0. 4871 4871 |
0.4875 | 0.4878 | 0.4881 | 0.4884 | 0.4887 | 0.4890 |
| 2.3 | 0.4893 | 0.4896 | 0.4898 | 0.4901 | 0.4904 | 0.4906 | 0.4909 | 0.4911 | 0.4913 | 0.4916 |
| 2.4 | 0.4918 | 0.4920 | 0.4922 | 0.4925 | 0.4927 | 0.4929 | 0.4931 | 0.4932 | 0.4934 | 0.4936 |
| 2.5 | 0.4938 | 0.4940 | 0.4941 | 0.4943 | 0.4945 | 0.4946 | 0.4948 | 0.4949 | 0.4951 | 0.4952 |
2. 6 6 |
0.4953 | 0.4955 | 0.4956 | 0.4957 | 0.4959 | 0.4960 | 0.4961 | 0.4962 | 0.4963 | 0.4964 |
| 2.7 | 0.4965 | 0.4966 | 0.4967 | 0.4968 | 0.4969 | 0.4970 | 0.4971 | 0.4972 | 0.4973 | 0.4974 |
| 2.8 | 0.4974 | 0.4975 | 0.4976 | 0.4977 | 0.4977 | 0.4978 | 0.4979 | 0.4979 | 0.4980 | 0.4981 |
| 2.9 | 0.4981 | 0.4982 | 0.4982 | 0.4983 | 0.4984 | 0.4984 | 0. 4985 4985 |
0.4985 | 0.4986 | 0.4986 |
| 3.0 | 0.4987 | 0.4987 | 0.4987 | 0.4988 | 0.4988 | 0.4989 | 0.4989 | 0.4989 | 0.4990 | 0.4990 |
| В начало |
Распределение Стьюдента
Форма распределения Стьюдента зависит от числа
степеней свободы. На предыдущей картинке
показано, как при увеличении этого параметра
меняется форма распределения. О том, как
t-распределение используется при проверке
гипотез, можно прочитать в разделах t-критерий для
независимых выборок и t-критерий для
зависимых выборок в главе Основные
статистики и таблицы, а также в разделе Распределение
Стьюдента. Из приведенной ниже схемы видно, что
в верхней части таблицы приведены
вероятности получить значения, большие, чем
указаны в соответствующей ячейке. Критическое
значение, соответствующее вероятности 0.05
t-распределения с 6-ю степенями свободы, находится
на пересечении столбца 0.05 и строки 6: t(.05,6)
= 1.943180.
Критическое
значение, соответствующее вероятности 0.05
t-распределения с 6-ю степенями свободы, находится
на пересечении столбца 0.05 и строки 6: t(.05,6)
= 1.943180.
| df\p | 0.40 | 0.25 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.0005 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.324920 | 1.000000 | 3.077684 | 6.313752 | 12.70620 | 31.82052 | 63.65674 | 636.6192 |
| 2 | 0.288675 | 0.816497 | 1.885618 | 2.919986 | 4.30265 | 6.96456 | 9.92484 | 31. 5991 5991 |
| 3 | 0.276671 | 0.764892 | 1.637744 | 2.353363 | 3.18245 | 4.54070 | 5.84091 | 12.9240 |
| 4 | 0.270722 | 0.740697 | 1.533206 | 2.131847 | 2.77645 | 3.74695 | 4.60409 | 8.6103 |
| 5 | 0.267181 | 0.726687 | 1.475884 | 2.015048 | 2.57058 | 3.36493 | 4.03214 | 6.8688 |
| 6 | 0.264835 | 0.717558 | 1.439756 | 1.943180 | 2.44691 | 3.14267 | 3.70743 | 5.9588 |
| 7 | 0. 263167 263167 |
0.711142 | 1.414924 | 1.894579 | 2.36462 | 2.99795 | 3.49948 | 5.4079 |
| 8 | 0.261921 | 0.706387 | 1.396815 | 1.859548 | 2.30600 | 2.89646 | 3.35539 | 5.0413 |
| 9 | 0.260955 | 0.702722 | 1.383029 | 1.833113 | 2.26216 | 2.82144 | 3.24984 | 4.7809 |
| 10 | 0.260185 | 0.699812 | 1.372184 | 1.812461 | 2.22814 | 2.76377 | 3.16927 | 4.5869 |
| 11 | 0.259556 | 0. 697445 697445 |
1.363430 | 1.795885 | 2.20099 | 2.71808 | 3.10581 | 4.4370 |
| 12 | 0.259033 | 0.695483 | 1.356217 | 1.782288 | 2.17881 | 2.68100 | 3.05454 | 4.3178 |
| 13 | 0.258591 | 0.693829 | 1.350171 | 1.770933 | 2.16037 | 2.65031 | 3.01228 | 4.2208 |
| 14 | 0.258213 | 0.692417 | 1.345030 | 1.761310 | 2.14479 | 2.62449 | 2.97684 | 4.1405 |
| 15 | 0.257885 | 0.691197 | 1.340606 | 1. 753050 753050 |
2.13145 | 2.60248 | 2.94671 | 4.0728 |
| 16 | 0.257599 | 0.690132 | 1.336757 | 1.745884 | 2.11991 | 2.58349 | 2.92078 | 4.0150 |
| 17 | 0.257347 | 0.689195 | 1.333379 | 1.739607 | 2.10982 | 2.56693 | 2.89823 | 3.9651 |
| 18 | 0.257123 | 0.688364 | 1.330391 | 1.734064 | 2.10092 | 2.55238 | 2.87844 | 3.9216 |
| 19 | 0.256923 | 0.687621 | 1.327728 | 1.729133 | 2.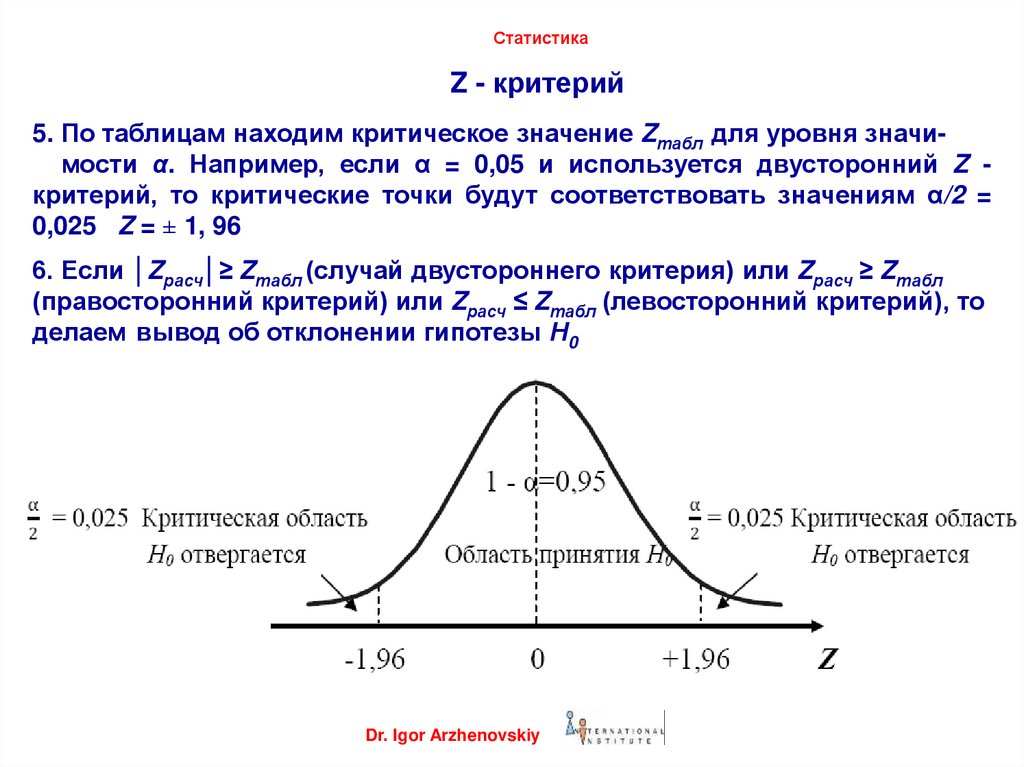 09302 09302 |
2.53948 | 2.86093 | 3.8834 |
| 20 | 0.256743 | 0.686954 | 1.325341 | 1.724718 | 2.08596 | 2.52798 | 2.84534 | 3.8495 |
| 21 | 0.256580 | 0.686352 | 1.323188 | 1.720743 | 2.07961 | 2.51765 | 2.83136 | 3.8193 |
| 22 | 0.256432 | 0.685805 | 1.321237 | 1.717144 | 2.07387 | 2.50832 | 2.81876 | 3.7921 |
| 23 | 0.256297 | 0.685306 | 1.319460 | 1.713872 | 2.06866 | 2. 49987 49987 |
2.80734 | 3.7676 |
| 24 | 0.256173 | 0.684850 | 1.317836 | 1.710882 | 2.06390 | 2.49216 | 2.79694 | 3.7454 |
| 25 | 0.256060 | 0.684430 | 1.316345 | 1.708141 | 2.05954 | 2.48511 | 2.78744 | 3.7251 |
| 26 | 0.255955 | 0.684043 | 1.314972 | 1.705618 | 2.05553 | 2.47863 | 2.77871 | 3.7066 |
| 27 | 0.255858 | 0.683685 | 1.313703 | 1.703288 | 2.05183 | 2.47266 | 2. 77068 77068 |
3.6896 |
| 28 | 0.255768 | 0.683353 | 1.312527 | 1.701131 | 2.04841 | 2.46714 | 2.76326 | 3.6739 |
| 29 | 0.255684 | 0.683044 | 1.311434 | 1.699127 | 2.04523 | 2.46202 | 2.75639 | 3.6594 |
| 30 | 0.255605 | 0.682756 | 1.310415 | 1.697261 | 2.04227 | 2.45726 | 2.75000 | 3.6460 |
| inf | 0.253347 | 0.674490 | 1.281552 | 1.644854 | 1.95996 | 2.32635 | 2.57583 | 3.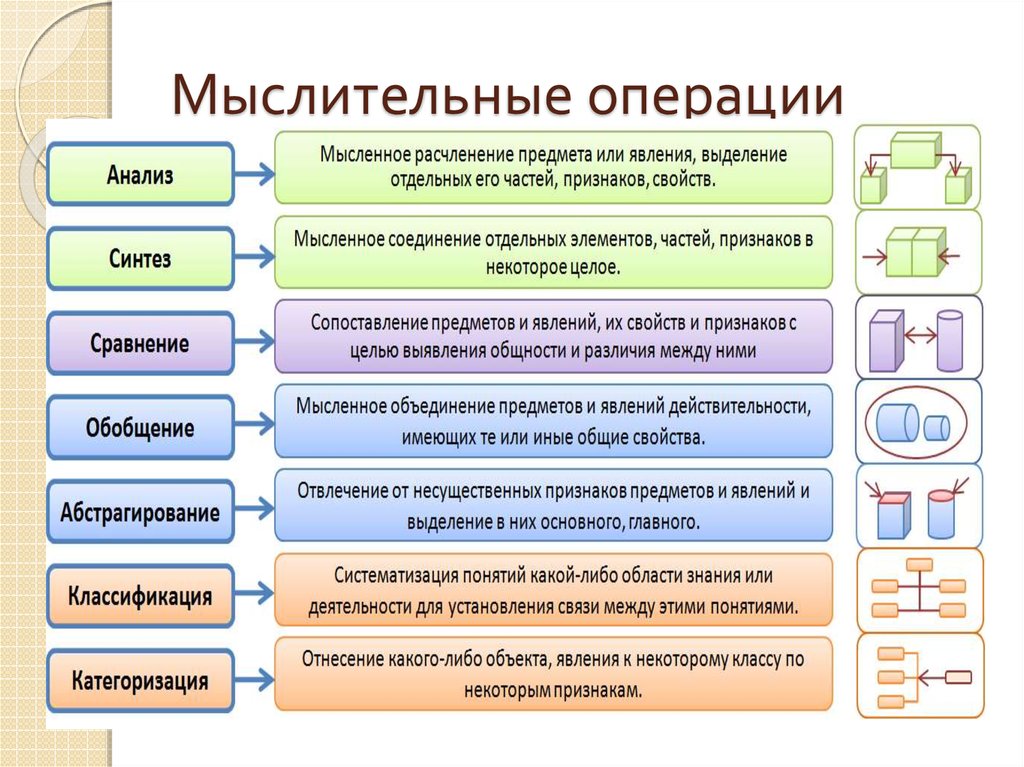 2905 2905 |
| В начало |
Хи-квадрат распределение
Как и в случае t-распределения Стьюдента, форма хи-квадрат
распределения определяется числом степеней
свободы. На предыдущем рисунке показана его
форма для различных степеней свободы (1, 2, 5, 10,
25 и 50). Примеры использования хи-квадрат
распределения для проверки гипотез можно
найти в разделах Статистики и
построение таблиц в главах Основные
статистики и таблицы и Нелинейное
оценивание, а также в разделе Хи-квадрат
распределение. В таблице приведены
критические значения хи-квадрат распределения с
заданным числом степеней свободы. Искомое
значение находится на пересечении столбца с
соответствующим значением вероятности и строки
с числом степеней свободы. Например, критическое
значение хи-квадрат распределения с 4-мя
степенями свободы для вероятности 0. 25
составляет 5.38527. Это означает, что площадь под
кривой плотности хи-квадрат распределения с 4-мя
степенями свободы справа от значения 5.38527
равна 0.25.
25
составляет 5.38527. Это означает, что площадь под
кривой плотности хи-квадрат распределения с 4-мя
степенями свободы справа от значения 5.38527
равна 0.25.
| df\area | .995 | .990 | .975 | .950 | .900 | .750 | .500 | .250 | .100 | .050 | .025 | .010 | .005 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.00004 | 0.00016 | 0.00098 | 0.00393 | 0.01579 | 0.10153 | 0.45494 | 1.32330 | 2.70554 | 3.84146 | 5.02389 | 6.63490 | 7.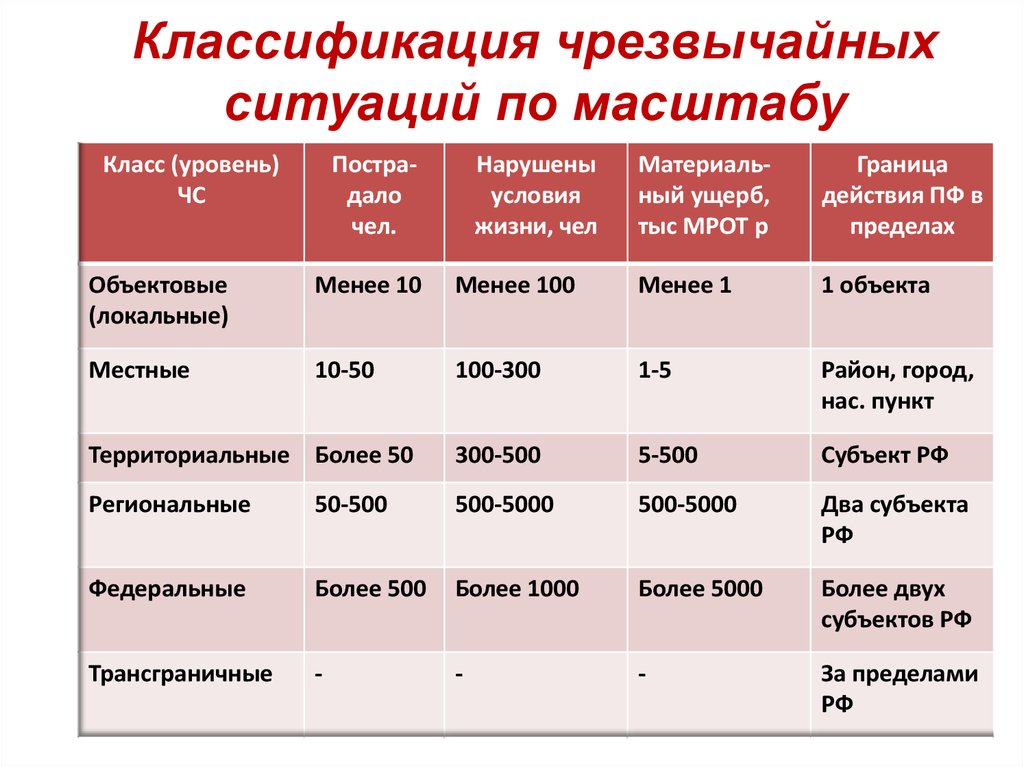 87944 87944 |
| 2 | 0.01003 | 0.02010 | 0.05064 | 0.10259 | 0.21072 | 0.57536 | 1.38629 | 2.77259 | 4.60517 | 5.99146 | 7.37776 | 9.21034 | 10.59663 |
| 3 | 0.07172 | 0.11483 | 0.21580 | 0.35185 | 0.58437 | 1.21253 | 2.36597 | 4.10834 | 6.25139 | 7.81473 | 9.34840 | 11.34487 | 12.83816 |
| 4 | 0.20699 | 0.29711 | 0.48442 | 0.71072 | 1.06362 | 1.92256 | 3.35669 | 5.38527 | 7.77944 | 9. 48773 48773 |
11.14329 | 13.27670 | 14.86026 |
| 5 | 0.41174 | 0.55430 | 0.83121 | 1.14548 | 1.61031 | 2.67460 | 4.35146 | 6.62568 | 9.23636 | 11.07050 | 12.83250 | 15.08627 | 16.74960 |
| 6 | 0.67573 | 0.87209 | 1.23734 | 1.63538 | 2.20413 | 3.45460 | 5.34812 | 7.84080 | 10.64464 | 12.59159 | 14.44938 | 16.81189 | 18.54758 |
| 7 | 0.98926 | 1.23904 | 1.68987 | 2.16735 | 2. 83311 83311 |
4.25485 | 6.34581 | 9.03715 | 12.01704 | 14.06714 | 16.01276 | 18.47531 | 20.27774 |
| 8 | 1.34441 | 1.64650 | 2.17973 | 2.73264 | 3.48954 | 5.07064 | 7.34412 | 10.21885 | 13.36157 | 15.50731 | 17.53455 | 20.09024 | 21.95495 |
| 9 | 1.73493 | 2.08790 | 2.70039 | 3.32511 | 4.16816 | 5.89883 | 8.34283 | 11.38875 | 14.68366 | 16.91898 | 19.02277 | 21.66599 | 23.58935 |
| 10 | 2.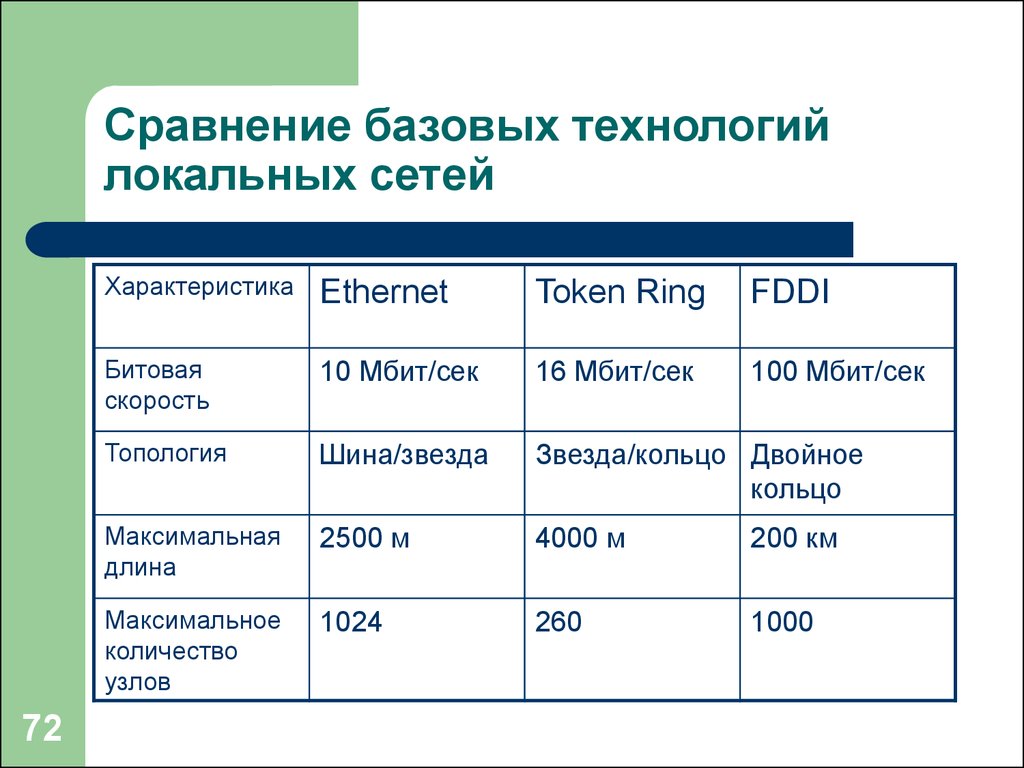 15586 15586 |
2.55821 | 3.24697 | 3.94030 | 4.86518 | 6.73720 | 9.34182 | 12.54886 | 15.98718 | 18.30704 | 20.48318 | 23.20925 | 25.18818 |
| 11 | 2.60322 | 3.05348 | 3.81575 | 4.57481 | 5.57778 | 7.58414 | 10.34100 | 13.70069 | 17.27501 | 19.67514 | 21.92005 | 24.72497 | 26.75685 |
| 12 | 3.07382 | 3.57057 | 4.40379 | 5.22603 | 6.30380 | 8.43842 | 11.34032 | 14.84540 | 18.54935 | 21. 02607 02607 |
23.33666 | 26.21697 | 28.29952 |
| 13 | 3.56503 | 4.10692 | 5.00875 | 5.89186 | 7.04150 | 9.29907 | 12.33976 | 15.98391 | 19.81193 | 22.36203 | 24.73560 | 27.68825 | 29.81947 |
| 14 | 4.07467 | 4.66043 | 5.62873 | 6.57063 | 7.78953 | 10.16531 | 13.33927 | 17.11693 | 21.06414 | 23.68479 | 26.11895 | 29.14124 | 31.31935 |
| 15 | 4.60092 | 5.22935 | 6.26214 | 7.26094 | 8.54676 | 11. 03654 03654 |
14.33886 | 18.24509 | 22.30713 | 24.99579 | 27.48839 | 30.57791 | 32.80132 |
| 16 | 5.14221 | 5.81221 | 6.90766 | 7.96165 | 9.31224 | 11.91222 | 15.33850 | 19.36886 | 23.54183 | 26.29623 | 28.84535 | 31.99993 | 34.26719 |
| 17 | 5.69722 | 6.40776 | 7.56419 | 8.67176 | 10.08519 | 12.79193 | 16.33818 | 20.48868 | 24.76904 | 27.58711 | 30.19101 | 33.40866 | 35.71847 |
| 18 | 6. 26480 26480 |
7.01491 | 8.23075 | 9.39046 | 10.86494 | 13.67529 | 17.33790 | 21.60489 | 25.98942 | 28.86930 | 31.52638 | 34.80531 | 37.15645 |
| 19 | 6.84397 | 7.63273 | 8.90652 | 10.11701 | 11.65091 | 14.56200 | 18.33765 | 22.71781 | 27.20357 | 30.14353 | 32.85233 | 36.19087 | 38.58226 |
| 20 | 7.43384 | 8.26040 | 9.59078 | 10.85081 | 12.44261 | 15.45177 | 19.33743 | 23.82769 | 28.41198 | 31.41043 | 34. 16961 16961 |
37.56623 | 39.99685 |
| 21 | 8.03365 | 8.89720 | 10.28290 | 11.59131 | 13.23960 | 16.34438 | 20.33723 | 24.93478 | 29.61509 | 32.67057 | 35.47888 | 38.93217 | 41.40106 |
| 22 | 8.64272 | 9.54249 | 10.98232 | 12.33801 | 14.04149 | 17.23962 | 21.33704 | 26.03927 | 30.81328 | 33.92444 | 36.78071 | 40.28936 | 42.79565 |
| 23 | 9.26042 | 10.19572 | 11.68855 | 13.09051 | 14. 84796 84796 |
18.13730 | 22.33688 | 27.14134 | 32.00690 | 35.17246 | 38.07563 | 41.63840 | 44.18128 |
| 24 | 9.88623 | 10.85636 | 12.40115 | 13.84843 | 15.65868 | 19.03725 | 23.33673 | 28.24115 | 33.19624 | 36.41503 | 39.36408 | 42.97982 | 45.55851 |
| 25 | 10.51965 | 11.52398 | 13.11972 | 14.61141 | 16.47341 | 19.93934 | 24.33659 | 29.33885 | 34.38159 | 37.65248 | 40.64647 | 44.31410 | 46.92789 |
| 26 | 11.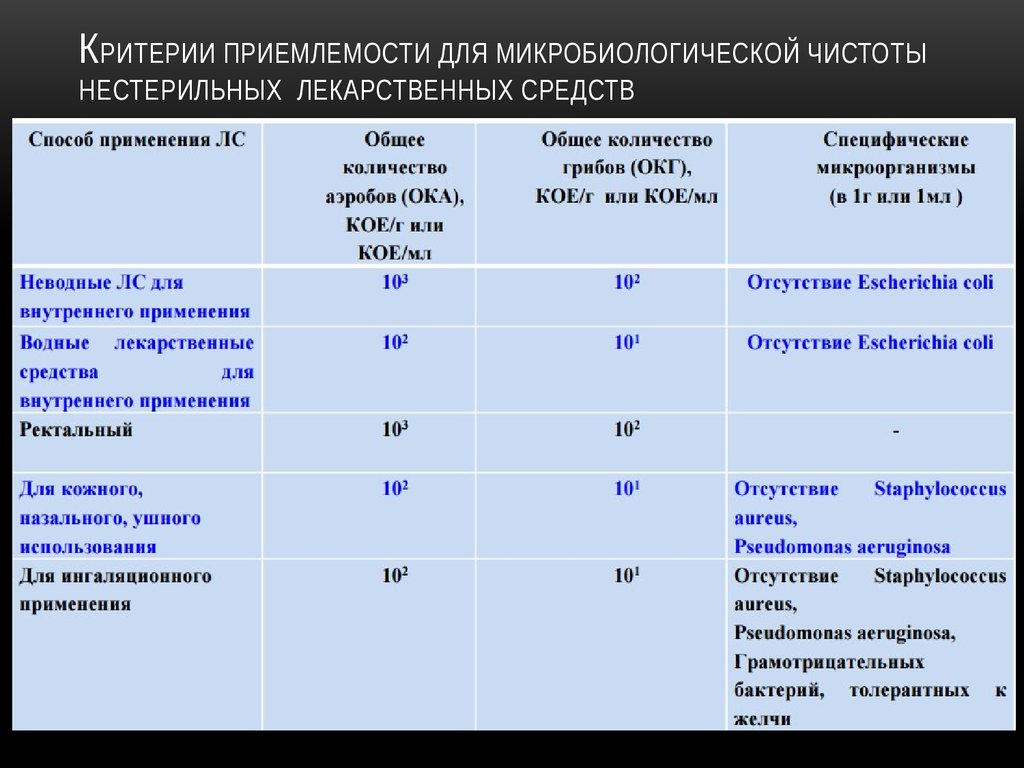 16024 16024 |
12.19815 | 13.84390 | 15.37916 | 17.29188 | 20.84343 | 25.33646 | 30.43457 | 35.56317 | 38.88514 | 41.92317 | 45.64168 | 48.28988 |
| 27 | 11.80759 | 12.87850 | 14.57338 | 16.15140 | 18.11390 | 21.74940 | 26.33634 | 31.52841 | 36.74122 | 40.11327 | 43.19451 | 46.96294 | 49.64492 |
| 28 | 12.46134 | 13.56471 | 15.30786 | 16.92788 | 18.93924 | 22.65716 | 27.33623 | 32.62049 | 37.91592 | 41.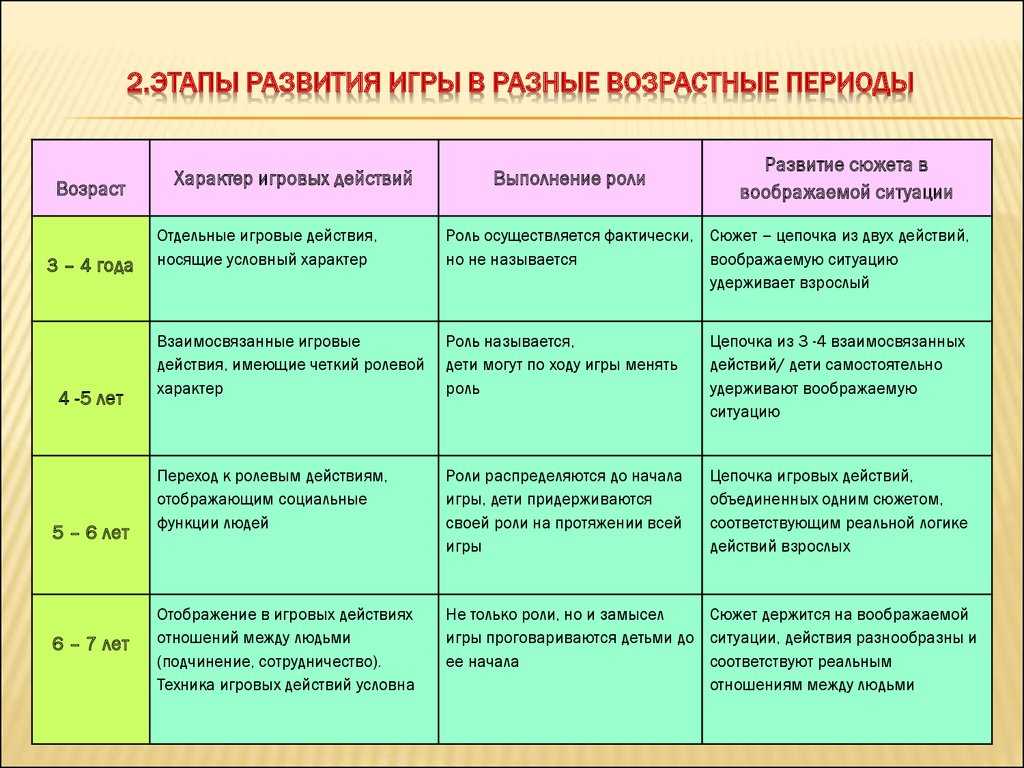 33714 33714 |
44.46079 | 48.27824 | 50.99338 |
| 29 | 13.12115 | 14.25645 | 16.04707 | 17.70837 | 19.76774 | 23.56659 | 28.33613 | 33.71091 | 39.08747 | 42.55697 | 45.72229 | 49.58788 | 52.33562 |
| 30 | 13.78672 | 14.95346 | 16.79077 | 18.49266 | 20.59923 | 24.47761 | 29.33603 | 34.79974 | 40.25602 | 43.77297 | 46.97924 | 50.89218 | 53.67196 |
| В начало |
F-распределение
F-распределение
является асимметричным и обычно используется
в дисперсионном анализе.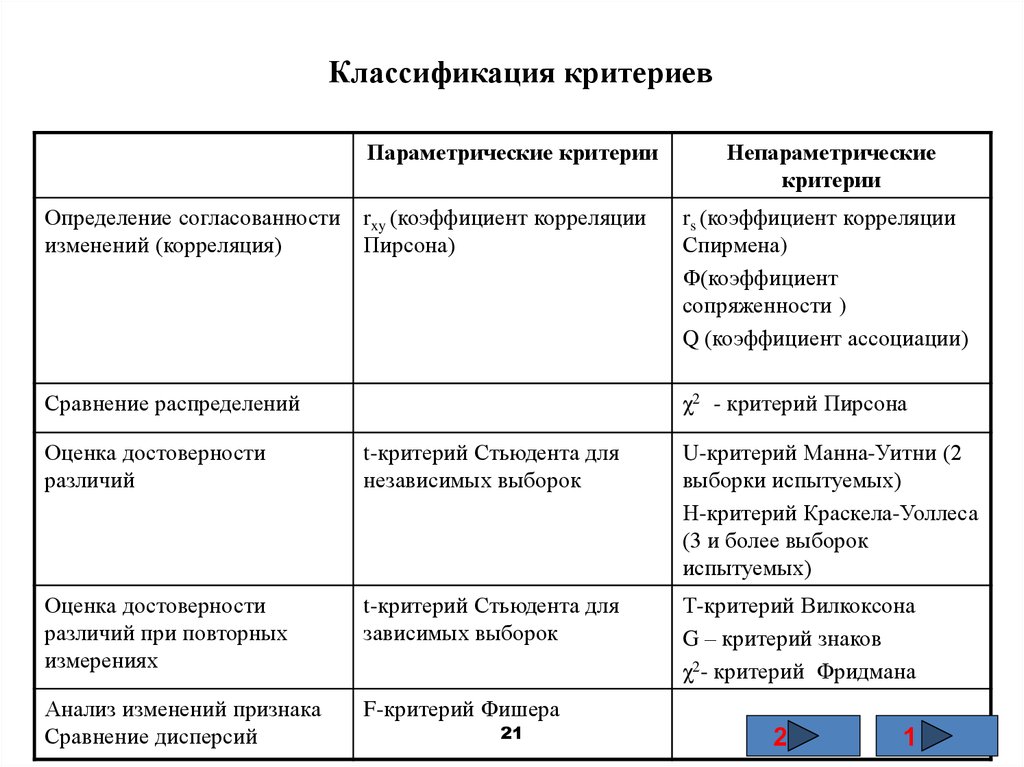 Такую
плотность распределения имеют величины,
являющиеся отношением двух величин, имющих хи-квадрат
распределение, при этом соответствующее
F-распределение определяется двумя значениями
числа степеней свободы. На показанной выше
иллюстрации показано распределение F(10,10)
. Первый индекс всегда соответствует числу
степеней свободы для числителя, и этот порядок
является существенным, поскольку F(10,12)
не равно F(12,10). В приведенных ниже таблицах
в столбце показано число степеней свободы
числителя, а в строке — число степней свободы для
знаменателя. В названии таблицы указано значение
вероятности. Например, критическое значение
F-распределения для вероятности .05 и степеней
свободы 10 и 12 находится на пересечении
столбца с значением 10 (числитель) и строки с
значением 12 (знаменатель) в таблице
«F-распределение для alpha=.05»: F(.05, 10, 12) =
2.
Такую
плотность распределения имеют величины,
являющиеся отношением двух величин, имющих хи-квадрат
распределение, при этом соответствующее
F-распределение определяется двумя значениями
числа степеней свободы. На показанной выше
иллюстрации показано распределение F(10,10)
. Первый индекс всегда соответствует числу
степеней свободы для числителя, и этот порядок
является существенным, поскольку F(10,12)
не равно F(12,10). В приведенных ниже таблицах
в столбце показано число степеней свободы
числителя, а в строке — число степней свободы для
знаменателя. В названии таблицы указано значение
вероятности. Например, критическое значение
F-распределения для вероятности .05 и степеней
свободы 10 и 12 находится на пересечении
столбца с значением 10 (числитель) и строки с
значением 12 (знаменатель) в таблице
«F-распределение для alpha=.05»: F(.05, 10, 12) =
2.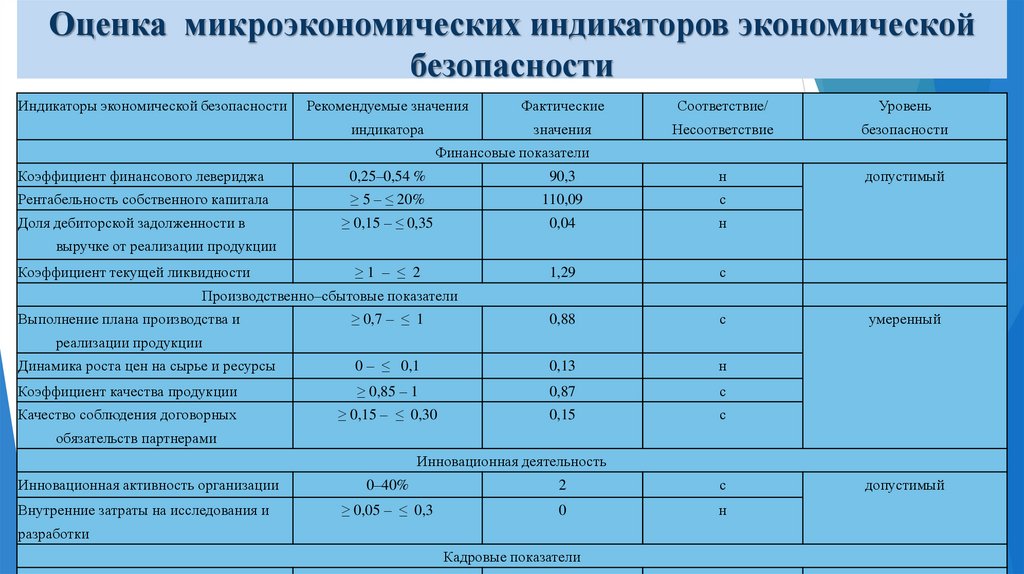 7534.
7534.
F-распределение для alpha=.10 .
| df2/df1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 | 20 | 24 | 30 | 40 | 60 | 120 | INF |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 39.86346 | 49.50000 | 53.59324 | 55.83296 | 57.24008 | 58.20442 | 58.90595 | 59.43898 | 59.85759 | 60. 19498 19498 |
60.70521 | 61.22034 | 61.74029 | 62.00205 | 62.26497 | 62.52905 | 62.79428 | 63.06064 | 63.32812 |
| 2 | 8.52632 | 9.00000 | 9.16179 | 9.24342 | 9.29263 | 9.32553 | 9.34908 | 9.36677 | 9.38054 | 9.39157 | 9.40813 | 9.42471 | 9.44131 | 9.44962 | 9.45793 | 9. 46624 46624 |
9.47456 | 9.48289 | 9.49122 |
| 3 | 5.53832 | 5.46238 | 5.39077 | 5.34264 | 5.30916 | 5.28473 | 5.26619 | 5.25167 | 5.24000 | 5.23041 | 5.21562 | 5.20031 | 5.18448 | 5.17636 | 5.16811 | 5.15972 | 5.15119 | 5.14251 | 5.13370 |
| 4 | 4.54477 | 4. 32456 32456 |
4.19086 | 4.10725 | 4.05058 | 4.00975 | 3.97897 | 3.95494 | 3.93567 | 3.91988 | 3.89553 | 3.87036 | 3.84434 | 3.83099 | 3.81742 | 3.80361 | 3.78957 | 3.77527 | 3.76073 |
| 5 | 4.06042 | 3.77972 | 3.61948 | 3.52020 | 3.45298 | 3.40451 | 3.36790 | 3. 33928 33928 |
3.31628 | 3.29740 | 3.26824 | 3.23801 | 3.20665 | 3.19052 | 3.17408 | 3.15732 | 3.14023 | 3.12279 | 3.10500 |
| 6 | 3.77595 | 3.46330 | 3.28876 | 3.18076 | 3.10751 | 3.05455 | 3.01446 | 2.98304 | 2.95774 | 2.93693 | 2.90472 | 2.87122 | 2.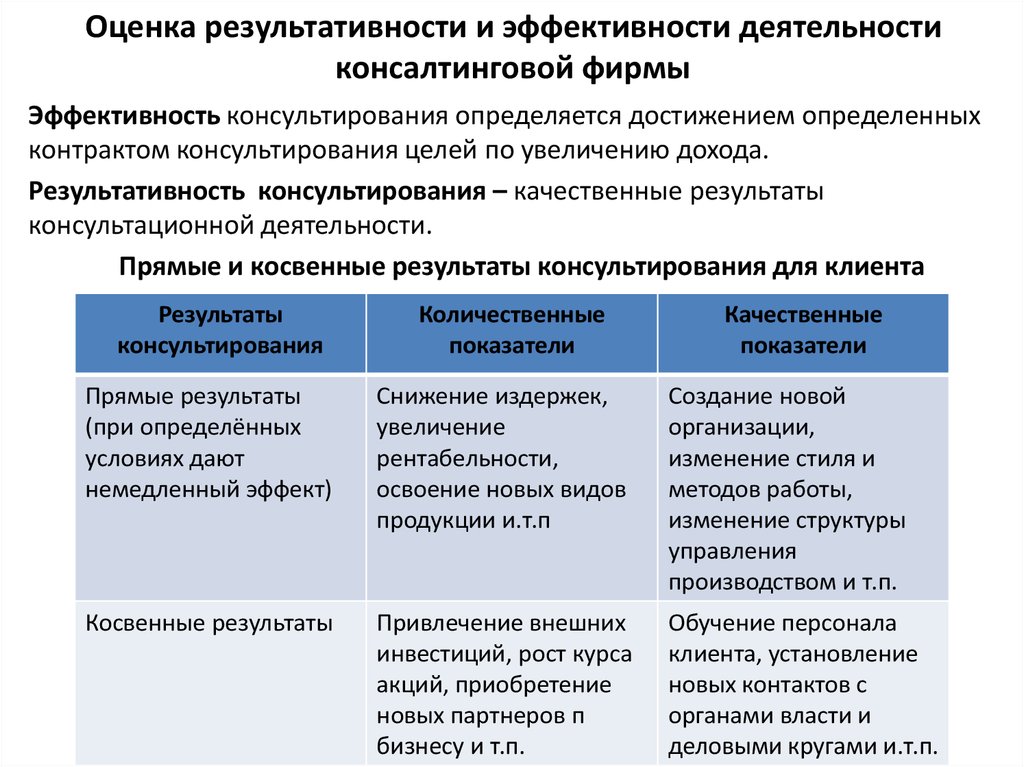 83634 83634 |
2.81834 | 2.79996 | 2.78117 | 2.76195 | 2.74229 | 2.72216 |
| 7 | 3.58943 | 3.25744 | 3.07407 | 2.96053 | 2.88334 | 2.82739 | 2.78493 | 2.75158 | 2.72468 | 2.70251 | 2.66811 | 2.63223 | 2.59473 | 2.57533 | 2.55546 | 2.53510 | 2.51422 | 2.49279 | 2. 47079 47079 |
| 8 | 3.45792 | 3.11312 | 2.92380 | 2.80643 | 2.72645 | 2.66833 | 2.62413 | 2.58935 | 2.56124 | 2.53804 | 2.50196 | 2.46422 | 2.42464 | 2.40410 | 2.38302 | 2.36136 | 2.33910 | 2.31618 | 2.29257 |
| 9 | 3.36030 | 3.00645 | 2.81286 | 2.69268 | 2. 61061 61061 |
2.55086 | 2.50531 | 2.46941 | 2.44034 | 2.41632 | 2.37888 | 2.33962 | 2.29832 | 2.27683 | 2.25472 | 2.23196 | 2.20849 | 2.18427 | 2.15923 |
| 10 | 3.28502 | 2.92447 | 2.72767 | 2.60534 | 2.52164 | 2.46058 | 2.41397 | 2.37715 | 2.34731 | 2.32260 | 2.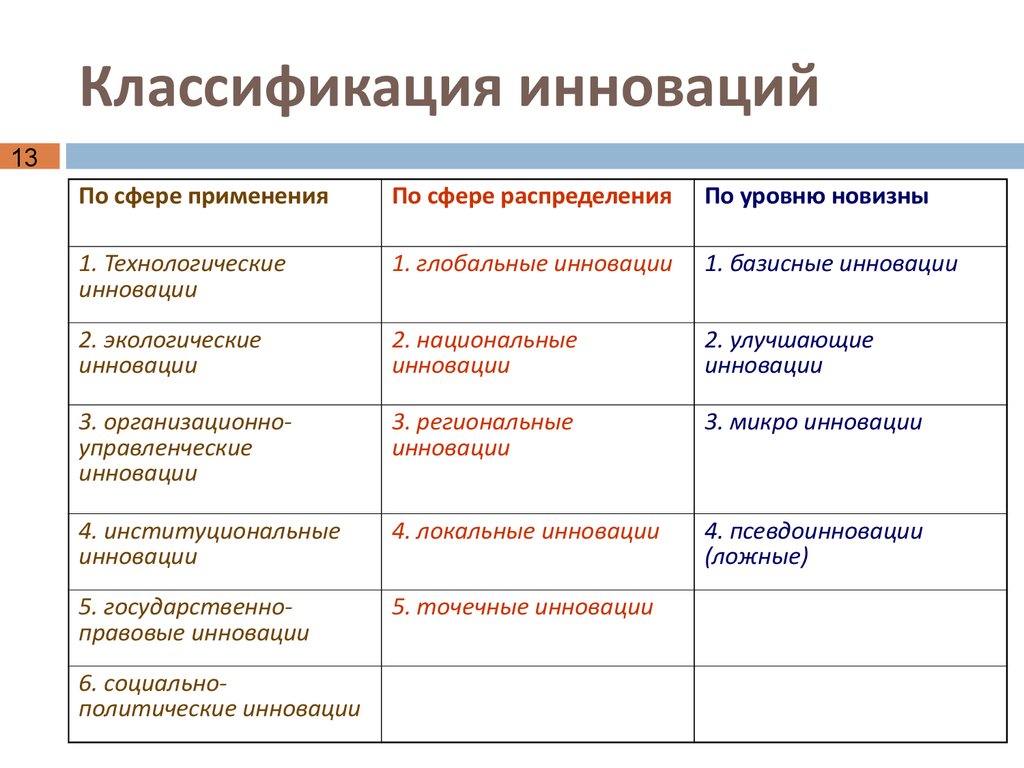 28405 28405 |
2.24351 | 2.20074 | 2.17843 | 2.15543 | 2.13169 | 2.10716 | 2.08176 | 2.05542 |
| 11 | 3.22520 | 2.85951 | 2.66023 | 2.53619 | 2.45118 | 2.38907 | 2.34157 | 2.30400 | 2.27350 | 2.24823 | 2.20873 | 2.16709 | 2.12305 | 2.10001 | 2.07621 | 2.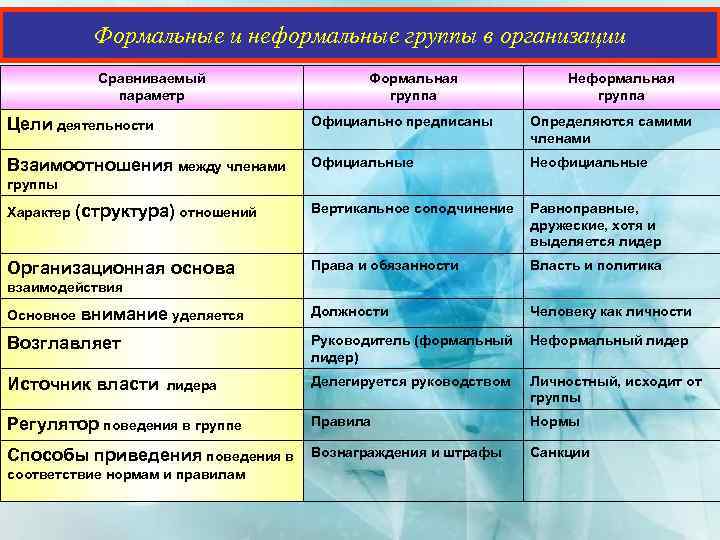 05161 05161 |
2.02612 | 1.99965 | 1.97211 |
| 12 | 3.17655 | 2.80680 | 2.60552 | 2.48010 | 2.39402 | 2.33102 | 2.28278 | 2.24457 | 2.21352 | 2.18776 | 2.14744 | 2.10485 | 2.05968 | 2.03599 | 2.01149 | 1.98610 | 1.95973 | 1.93228 | 1.90361 |
| 13 | 3.13621 | 2.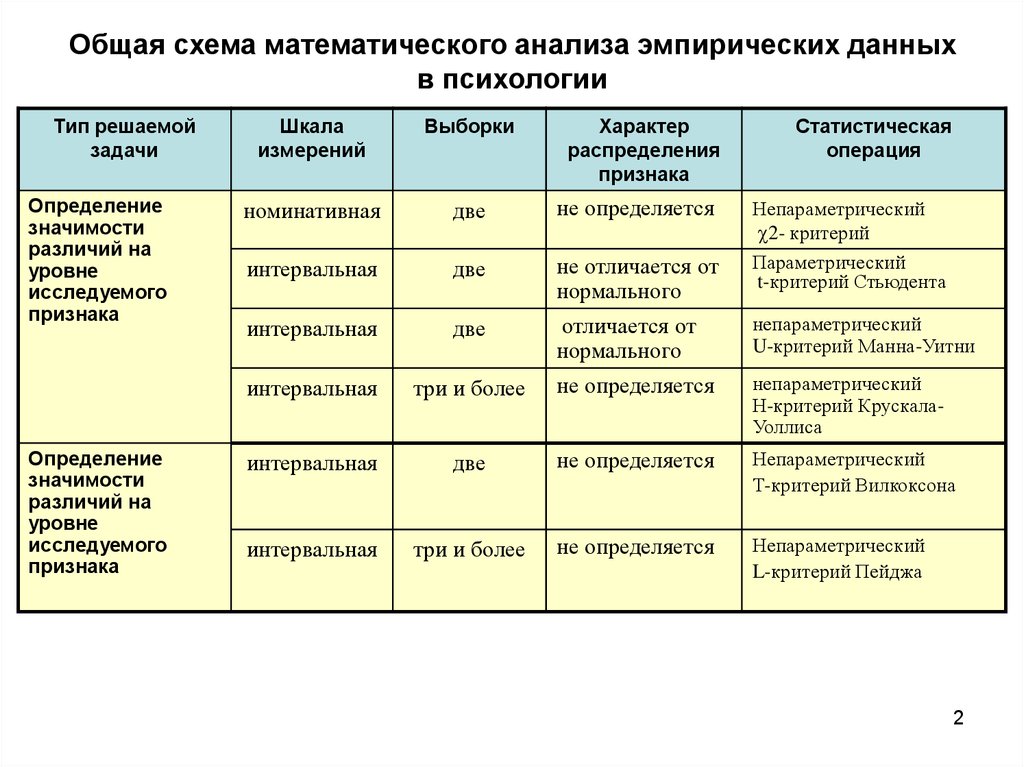 76317 76317 |
2.56027 | 2.43371 | 2.34672 | 2.28298 | 2.23410 | 2.19535 | 2.16382 | 2.13763 | 2.09659 | 2.05316 | 2.00698 | 1.98272 | 1.95757 | 1.93147 | 1.90429 | 1.87591 | 1.84620 |
| 14 | 3.10221 | 2.72647 | 2.52222 | 2.39469 | 2.30694 | 2.24256 | 2.19313 | 2.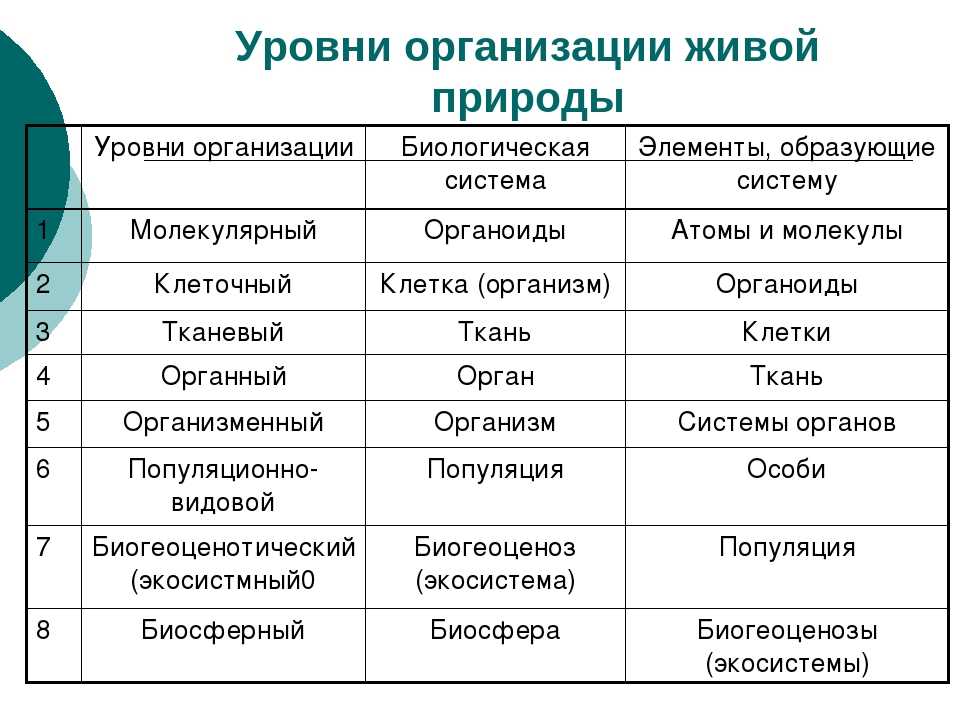 15390 15390 |
2.12195 | 2.09540 | 2.05371 | 2.00953 | 1.96245 | 1.93766 | 1.91193 | 1.88516 | 1.85723 | 1.82800 | 1.79728 |
| 15 | 3.07319 | 2.69517 | 2.48979 | 2.36143 | 2.27302 | 2.20808 | 2.15818 | 2.11853 | 2.08621 | 2.05932 | 2.01707 | 1.97222 | 1.92431 | 1. 89904 89904 |
1.87277 | 1.84539 | 1.81676 | 1.78672 | 1.75505 |
| 16 | 3.04811 | 2.66817 | 2.46181 | 2.33274 | 2.24376 | 2.17833 | 2.12800 | 2.08798 | 2.05533 | 2.02815 | 1.98539 | 1.93992 | 1.89127 | 1.86556 | 1.83879 | 1.81084 | 1.78156 | 1.75075 | 1. 71817 71817 |
| 17 | 3.02623 | 2.64464 | 2.43743 | 2.30775 | 2.21825 | 2.15239 | 2.10169 | 2.06134 | 2.02839 | 2.00094 | 1.95772 | 1.91169 | 1.86236 | 1.83624 | 1.80901 | 1.78053 | 1.75063 | 1.71909 | 1.68564 |
| 18 | 3.00698 | 2.62395 | 2.41601 | 2.28577 | 2.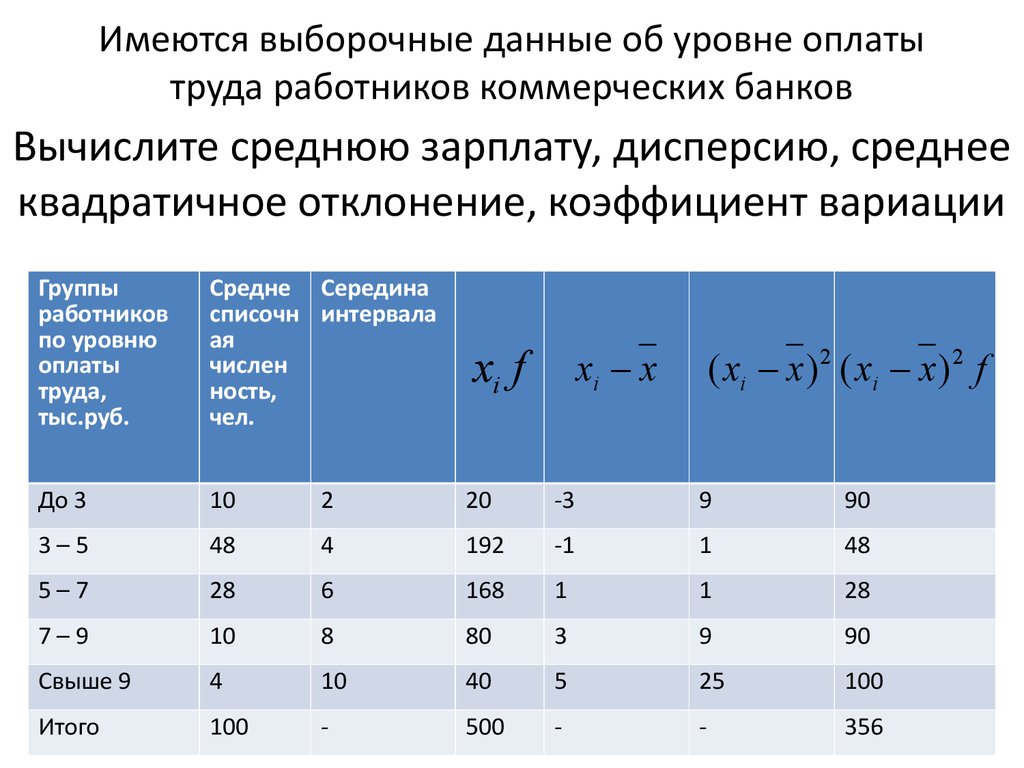 19583 19583 |
2.12958 | 2.07854 | 2.03789 | 2.00467 | 1.97698 | 1.93334 | 1.88681 | 1.83685 | 1.81035 | 1.78269 | 1.75371 | 1.72322 | 1.69099 | 1.65671 |
| 19 | 2.98990 | 2.60561 | 2.39702 | 2.26630 | 2.17596 | 2.10936 | 2.05802 | 2.01710 | 1.98364 | 1.95573 | 1. 91170 91170 |
1.86471 | 1.81416 | 1.78731 | 1.75924 | 1.72979 | 1.69876 | 1.66587 | 1.63077 |
| 20 | 2.97465 | 2.58925 | 2.38009 | 2.24893 | 2.15823 | 2.09132 | 2.03970 | 1.99853 | 1.96485 | 1.93674 | 1.89236 | 1.84494 | 1.79384 | 1.76667 | 1.73822 | 1.70833 | 1. 67678 67678 |
1.64326 | 1.60738 |
| 21 | 2.96096 | 2.57457 | 2.36489 | 2.23334 | 2.14231 | 2.07512 | 2.02325 | 1.98186 | 1.94797 | 1.91967 | 1.87497 | 1.82715 | 1.77555 | 1.74807 | 1.71927 | 1.68896 | 1.65691 | 1.62278 | 1.58615 |
| 22 | 2.94858 | 2. 56131 56131 |
2.35117 | 2.21927 | 2.12794 | 2.06050 | 2.00840 | 1.96680 | 1.93273 | 1.90425 | 1.85925 | 1.81106 | 1.75899 | 1.73122 | 1.70208 | 1.67138 | 1.63885 | 1.60415 | 1.56678 |
| 23 | 2.93736 | 2.54929 | 2.33873 | 2.20651 | 2.11491 | 2.04723 | 1.99492 | 1.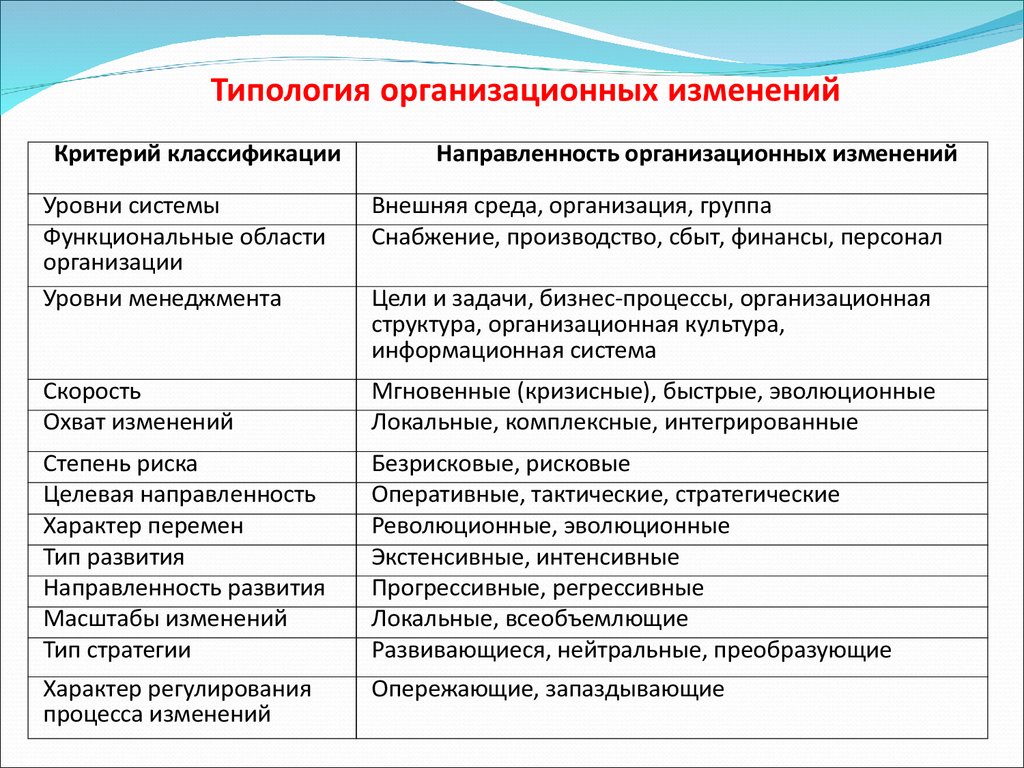 95312 95312 |
1.91888 | 1.89025 | 1.84497 | 1.79643 | 1.74392 | 1.71588 | 1.68643 | 1.65535 | 1.62237 | 1.58711 | 1.54903 |
| 24 | 2.92712 | 2.53833 | 2.32739 | 2.19488 | 2.10303 | 2.03513 | 1.98263 | 1.94066 | 1.90625 | 1.87748 | 1.83194 | 1.78308 | 1.73015 | 1. 70185 70185 |
1.67210 | 1.64067 | 1.60726 | 1.57146 | 1.53270 |
| 25 | 2.91774 | 2.52831 | 2.31702 | 2.18424 | 2.09216 | 2.02406 | 1.97138 | 1.92925 | 1.89469 | 1.86578 | 1.82000 | 1.77083 | 1.71752 | 1.68898 | 1.65895 | 1.62718 | 1.59335 | 1.55703 | 1.51760 |
| 26 | 2. 90913 90913 |
2.51910 | 2.30749 | 2.17447 | 2.08218 | 2.01389 | 1.96104 | 1.91876 | 1.88407 | 1.85503 | 1.80902 | 1.75957 | 1.70589 | 1.67712 | 1.64682 | 1.61472 | 1.58050 | 1.54368 | 1.50360 |
| 27 | 2.90119 | 2.51061 | 2.29871 | 2.16546 | 2.07298 | 2.00452 | 1.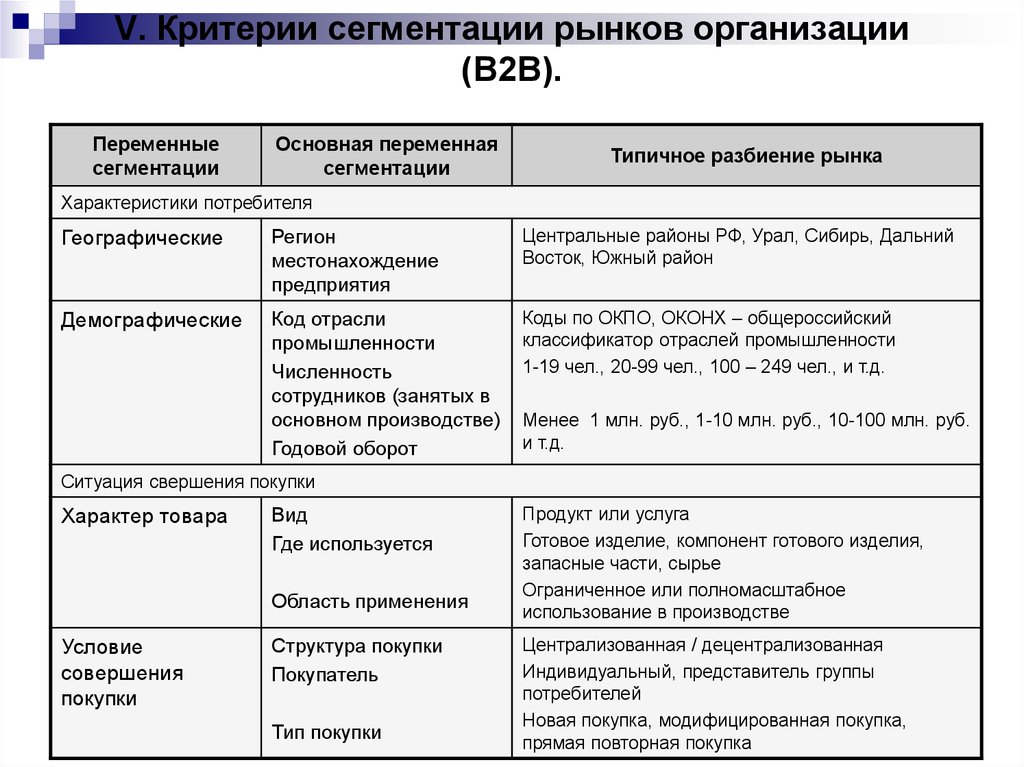 95151 95151 |
1.90909 | 1.87427 | 1.84511 | 1.79889 | 1.74917 | 1.69514 | 1.66616 | 1.63560 | 1.60320 | 1.56859 | 1.53129 | 1.49057 |
| 28 | 2.89385 | 2.50276 | 2.29060 | 2.15714 | 2.06447 | 1.99585 | 1.94270 | 1.90014 | 1.86520 | 1.83593 | 1.78951 | 1.73954 | 1. 68519 68519 |
1.65600 | 1.62519 | 1.59250 | 1.55753 | 1.51976 | 1.47841 |
| 29 | 2.88703 | 2.49548 | 2.28307 | 2.14941 | 2.05658 | 1.98781 | 1.93452 | 1.89184 | 1.85679 | 1.82741 | 1.78081 | 1.73060 | 1.67593 | 1.64655 | 1.61551 | 1.58253 | 1.54721 | 1.50899 | 1.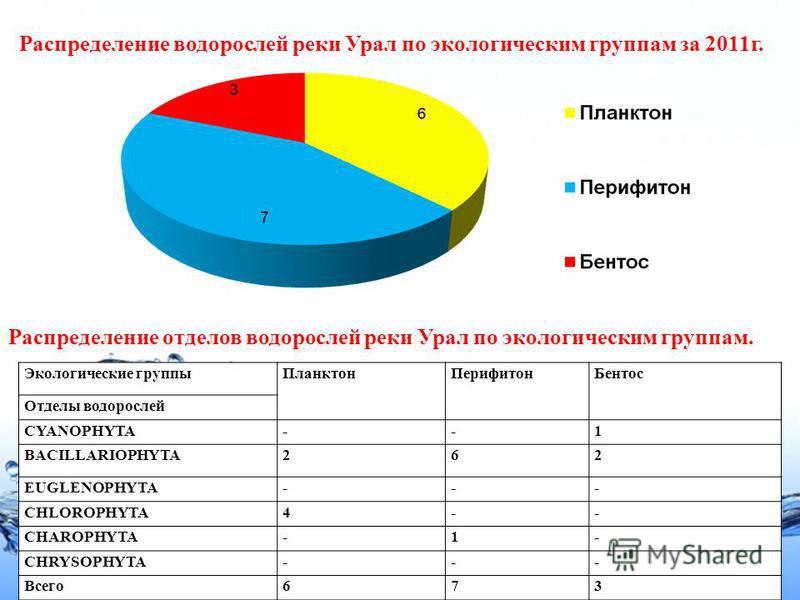 46704 46704 |
| 30 | 2.88069 | 2.48872 | 2.27607 | 2.14223 | 2.04925 | 1.98033 | 1.92692 | 1.88412 | 1.84896 | 1.81949 | 1.77270 | 1.72227 | 1.66731 | 1.63774 | 1.60648 | 1.57323 | 1.53757 | 1.49891 | 1.45636 |
| 40 | 2.83535 | 2.44037 | 2.22609 | 2.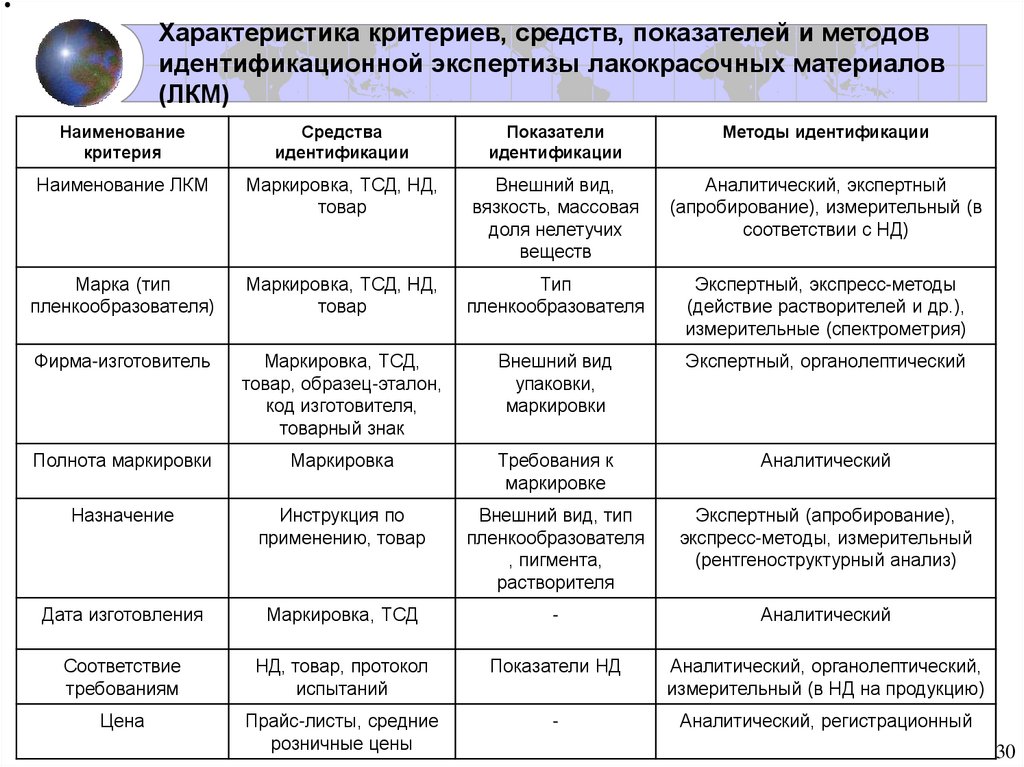 09095 09095 |
1.99682 | 1.92688 | 1.87252 | 1.82886 | 1.79290 | 1.76269 | 1.71456 | 1.66241 | 1.60515 | 1.57411 | 1.54108 | 1.50562 | 1.46716 | 1.42476 | 1.37691 |
| 60 | 2.79107 | 2.39325 | 2.17741 | 2.04099 | 1.94571 | 1.87472 | 1.81939 | 1.77483 | 1.73802 | 1. 70701 70701 |
1.65743 | 1.60337 | 1.54349 | 1.51072 | 1.47554 | 1.43734 | 1.39520 | 1.34757 | 1.29146 |
| 120 | 2.74781 | 2.34734 | 2.12999 | 1.99230 | 1.89587 | 1.82381 | 1.76748 | 1.72196 | 1.68425 | 1.65238 | 1.60120 | 1.54500 | 1.48207 | 1.44723 | 1.40938 | 1. 36760 36760 |
1.32034 | 1.26457 | 1.19256 |
| inf | 2.70554 | 2.30259 | 2.08380 | 1.94486 | 1.84727 | 1.77411 | 1.71672 | 1.67020 | 1.63152 | 1.59872 | 1.54578 | 1.48714 | 1.42060 | 1.38318 | 1.34187 | 1.29513 | 1.23995 | 1.16860 | 1.00000 |
| В начало |
F-распределение для
alpha=.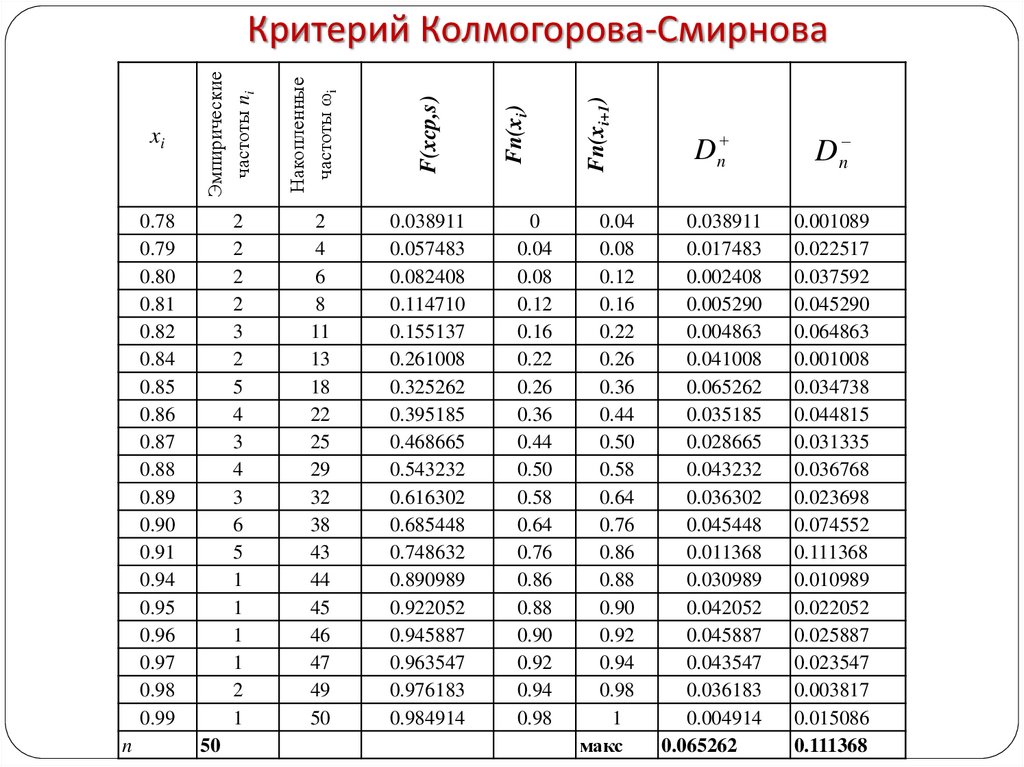 05 .
05 .
| df2/df1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 | 20 | 24 | 30 | 40 | 60 | 120 | INF |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 161.4476 | 199.5000 | 215.7073 | 224.5832 | 230.1619 | 233.9860 | 236.7684 | 238.8827 | 240.5433 | 241.8817 | 243.9060 | 245. 9499 9499 |
248.0131 | 249.0518 | 250.0951 | 251.1432 | 252.1957 | 253.2529 | 254.3144 |
| 2 | 18.5128 | 19.0000 | 19.1643 | 19.2468 | 19.2964 | 19.3295 | 19.3532 | 19.3710 | 19.3848 | 19.3959 | 19.4125 | 19.4291 | 19.4458 | 19.4541 | 19.4624 | 19.4707 | 19.4791 | 19.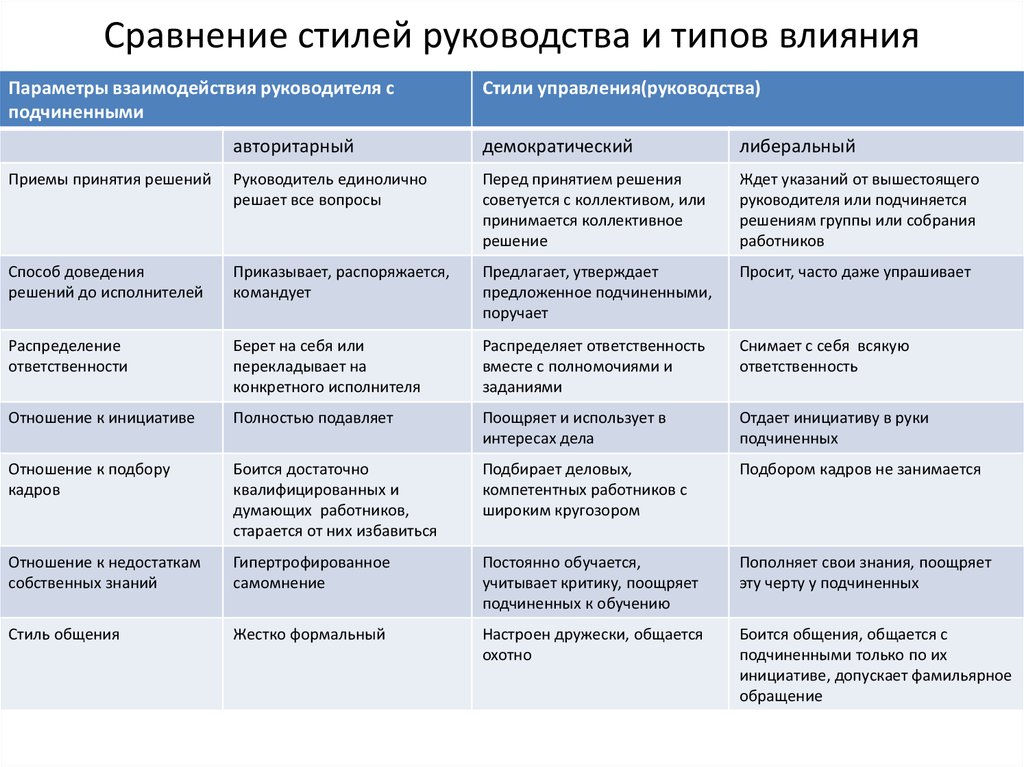 4874 4874 |
19.4957 |
| 3 | 10.1280 | 9.5521 | 9.2766 | 9.1172 | 9.0135 | 8.9406 | 8.8867 | 8.8452 | 8.8123 | 8.7855 | 8.7446 | 8.7029 | 8.6602 | 8.6385 | 8.6166 | 8.5944 | 8.5720 | 8.5494 | 8.5264 |
| 4 | 7.7086 | 6.9443 | 6.5914 | 6.3882 | 6. 2561 2561 |
6.1631 | 6.0942 | 6.0410 | 5.9988 | 5.9644 | 5.9117 | 5.8578 | 5.8025 | 5.7744 | 5.7459 | 5.7170 | 5.6877 | 5.6581 | 5.6281 |
| 5 | 6.6079 | 5.7861 | 5.4095 | 5.1922 | 5.0503 | 4.9503 | 4.8759 | 4.8183 | 4.7725 | 4.7351 | 4.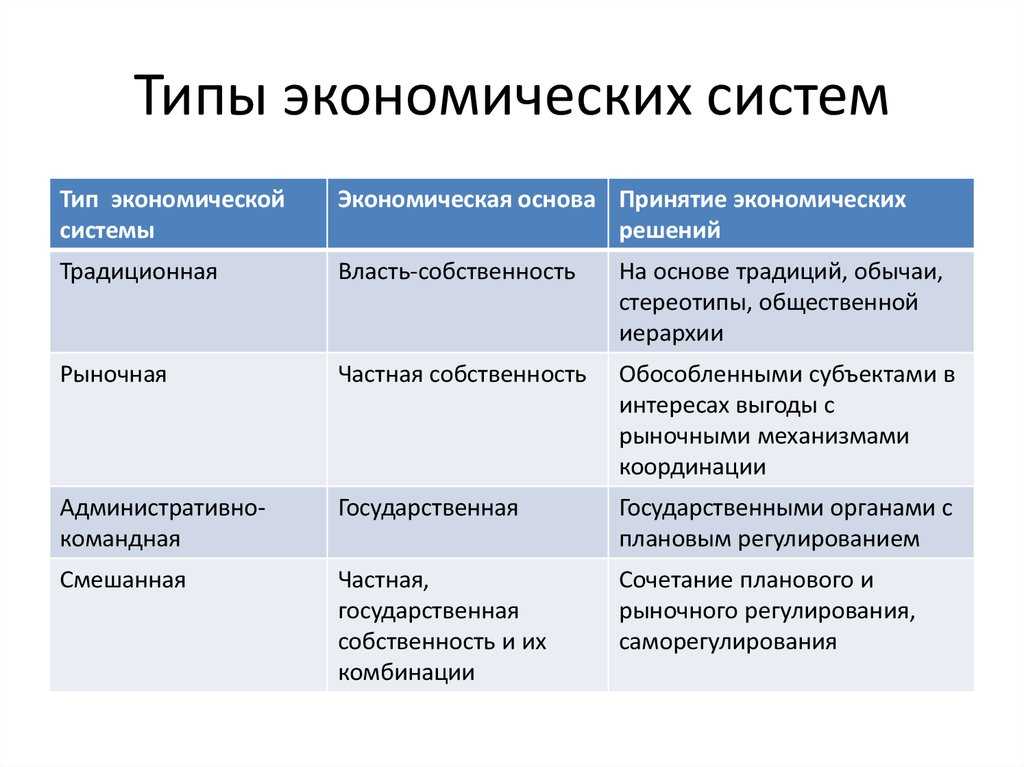 6777 6777 |
4.6188 | 4.5581 | 4.5272 | 4.4957 | 4.4638 | 4.4314 | 4.3985 | 4.3650 |
| 6 | 5.9874 | 5.1433 | 4.7571 | 4.5337 | 4.3874 | 4.2839 | 4.2067 | 4.1468 | 4.0990 | 4.0600 | 3.9999 | 3.9381 | 3.8742 | 3.8415 | 3.8082 | 3.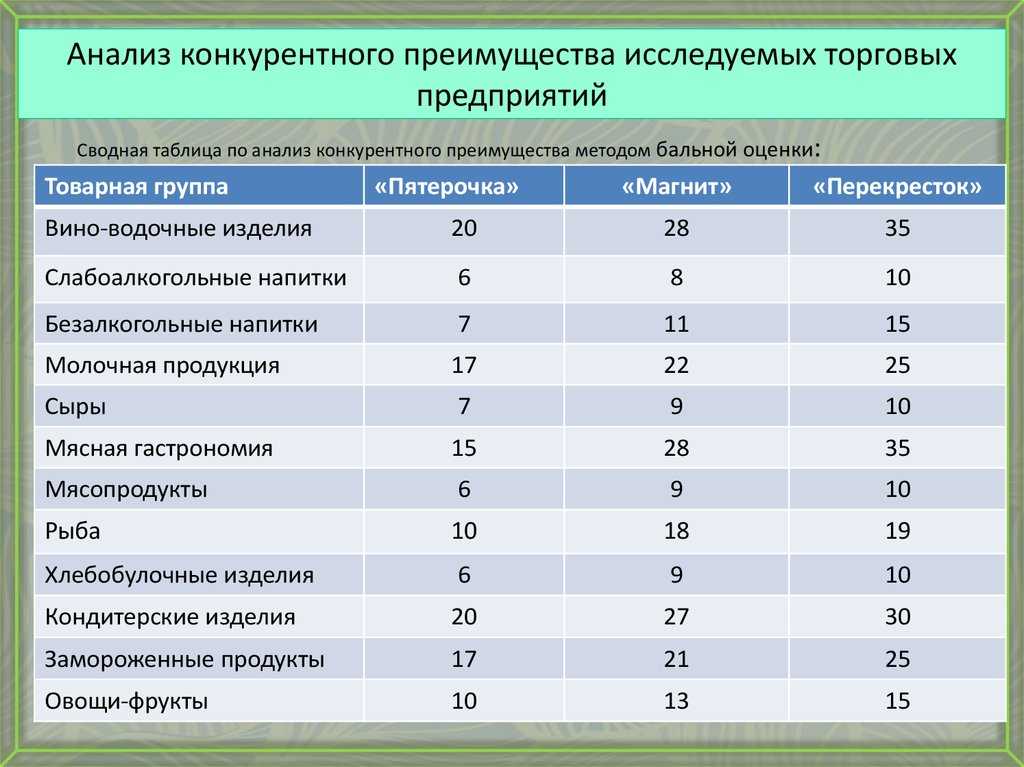 7743 7743 |
3.7398 | 3.7047 | 3.6689 |
| 7 | 5.5914 | 4.7374 | 4.3468 | 4.1203 | 3.9715 | 3.8660 | 3.7870 | 3.7257 | 3.6767 | 3.6365 | 3.5747 | 3.5107 | 3.4445 | 3.4105 | 3.3758 | 3.3404 | 3.3043 | 3.2674 | 3.2298 |
| 8 | 5.3177 | 4.4590 | 4. 0662 0662 |
3.8379 | 3.6875 | 3.5806 | 3.5005 | 3.4381 | 3.3881 | 3.3472 | 3.2839 | 3.2184 | 3.1503 | 3.1152 | 3.0794 | 3.0428 | 3.0053 | 2.9669 | 2.9276 |
| 9 | 5.1174 | 4.2565 | 3.8625 | 3.6331 | 3.4817 | 3.3738 | 3.2927 | 3.2296 | 3. 1789 1789 |
3.1373 | 3.0729 | 3.0061 | 2.9365 | 2.9005 | 2.8637 | 2.8259 | 2.7872 | 2.7475 | 2.7067 |
| 10 | 4.9646 | 4.1028 | 3.7083 | 3.4780 | 3.3258 | 3.2172 | 3.1355 | 3.0717 | 3.0204 | 2.9782 | 2.9130 | 2.8450 | 2.7740 | 2.7372 | 2. 6996 6996 |
2.6609 | 2.6211 | 2.5801 | 2.5379 |
| 11 | 4.8443 | 3.9823 | 3.5874 | 3.3567 | 3.2039 | 3.0946 | 3.0123 | 2.9480 | 2.8962 | 2.8536 | 2.7876 | 2.7186 | 2.6464 | 2.6090 | 2.5705 | 2.5309 | 2.4901 | 2.4480 | 2.4045 |
| 12 | 4. 7472 7472 |
3.8853 | 3.4903 | 3.2592 | 3.1059 | 2.9961 | 2.9134 | 2.8486 | 2.7964 | 2.7534 | 2.6866 | 2.6169 | 2.5436 | 2.5055 | 2.4663 | 2.4259 | 2.3842 | 2.3410 | 2.2962 |
| 13 | 4.6672 | 3.8056 | 3.4105 | 3.1791 | 3.0254 | 2.9153 | 2.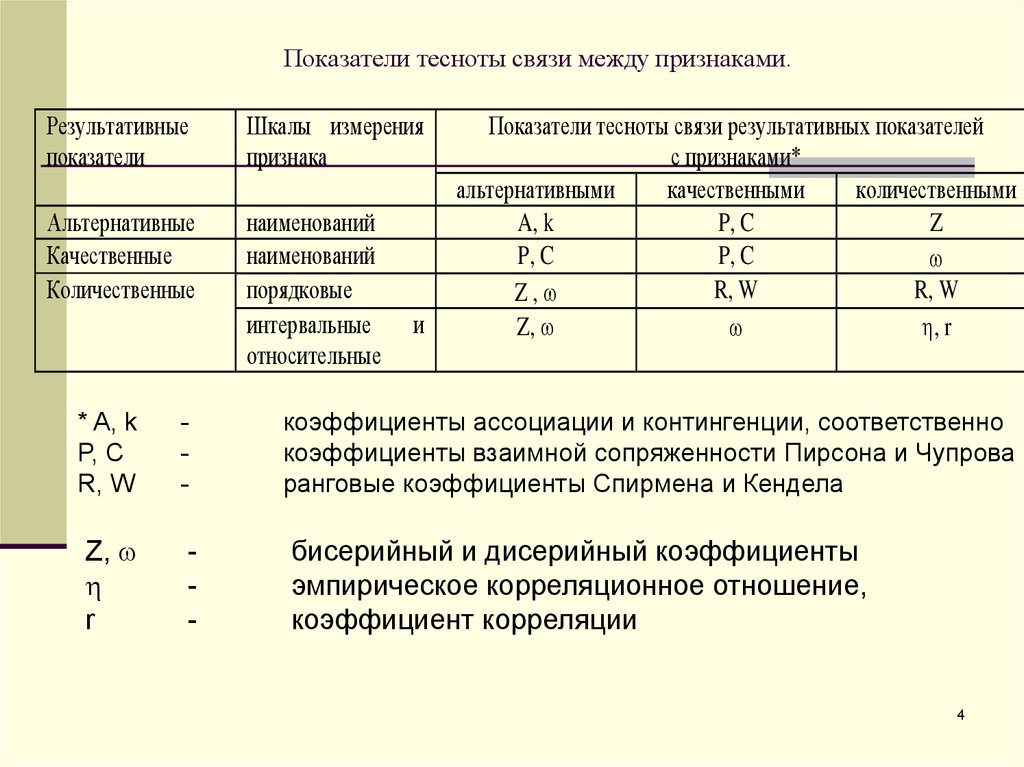 8321 8321 |
2.7669 | 2.7144 | 2.6710 | 2.6037 | 2.5331 | 2.4589 | 2.4202 | 2.3803 | 2.3392 | 2.2966 | 2.2524 | 2.2064 |
| 14 | 4.6001 | 3.7389 | 3.3439 | 3.1122 | 2.9582 | 2.8477 | 2.7642 | 2.6987 | 2.6458 | 2.6022 | 2.5342 | 2.4630 | 2.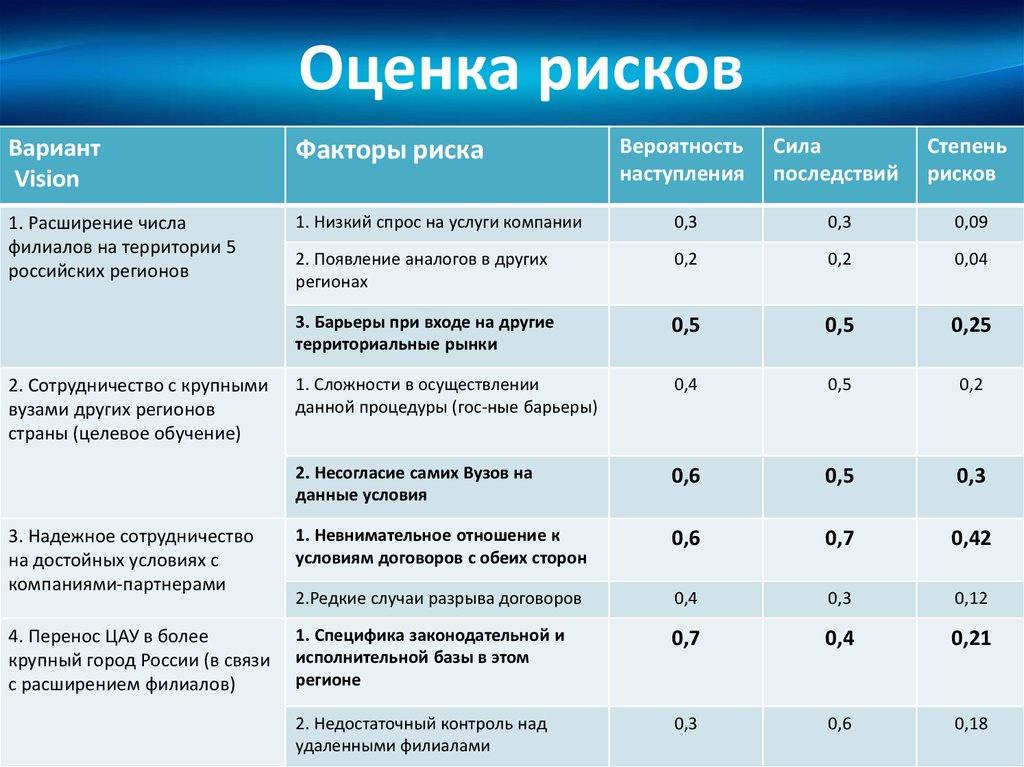 3879 3879 |
2.3487 | 2.3082 | 2.2664 | 2.2229 | 2.1778 | 2.1307 |
| 15 | 4.5431 | 3.6823 | 3.2874 | 3.0556 | 2.9013 | 2.7905 | 2.7066 | 2.6408 | 2.5876 | 2.5437 | 2.4753 | 2.4034 | 2.3275 | 2.2878 | 2.2468 | 2.2043 | 2.1601 | 2.1141 | 2. 0658 0658 |
| 16 | 4.4940 | 3.6337 | 3.2389 | 3.0069 | 2.8524 | 2.7413 | 2.6572 | 2.5911 | 2.5377 | 2.4935 | 2.4247 | 2.3522 | 2.2756 | 2.2354 | 2.1938 | 2.1507 | 2.1058 | 2.0589 | 2.0096 |
| 17 | 4.4513 | 3.5915 | 3.1968 | 2.9647 | 2.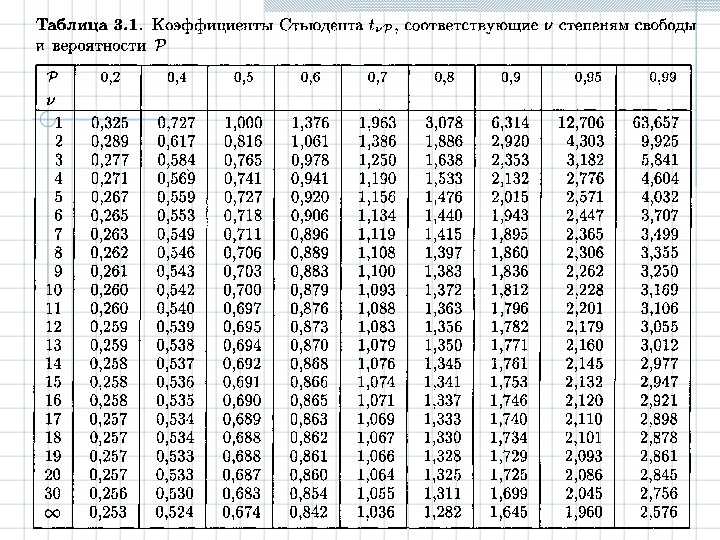 8100 8100 |
2.6987 | 2.6143 | 2.5480 | 2.4943 | 2.4499 | 2.3807 | 2.3077 | 2.2304 | 2.1898 | 2.1477 | 2.1040 | 2.0584 | 2.0107 | 1.9604 |
| 18 | 4.4139 | 3.5546 | 3.1599 | 2.9277 | 2.7729 | 2.6613 | 2.5767 | 2.5102 | 2.4563 | 2.4117 | 2. 3421 3421 |
2.2686 | 2.1906 | 2.1497 | 2.1071 | 2.0629 | 2.0166 | 1.9681 | 1.9168 |
| 19 | 4.3807 | 3.5219 | 3.1274 | 2.8951 | 2.7401 | 2.6283 | 2.5435 | 2.4768 | 2.4227 | 2.3779 | 2.3080 | 2.2341 | 2.1555 | 2.1141 | 2.0712 | 2.0264 | 1.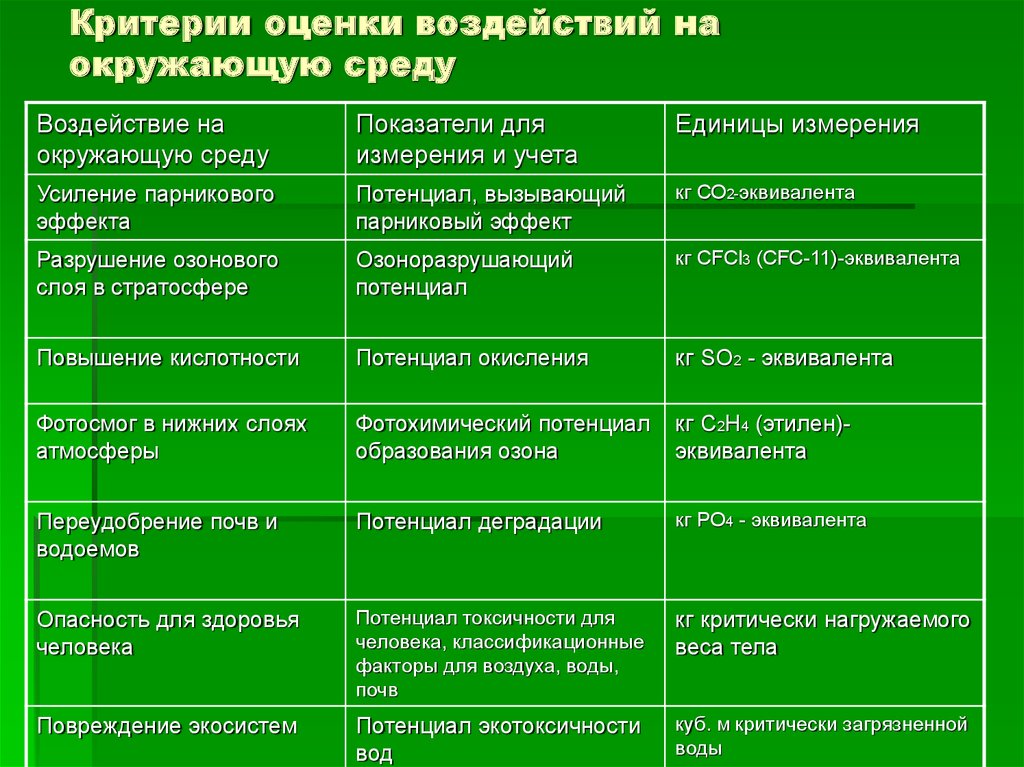 9795 9795 |
1.9302 | 1.8780 |
| 20 | 4.3512 | 3.4928 | 3.0984 | 2.8661 | 2.7109 | 2.5990 | 2.5140 | 2.4471 | 2.3928 | 2.3479 | 2.2776 | 2.2033 | 2.1242 | 2.0825 | 2.0391 | 1.9938 | 1.9464 | 1.8963 | 1.8432 |
| 21 | 4.3248 | 3.4668 | 3.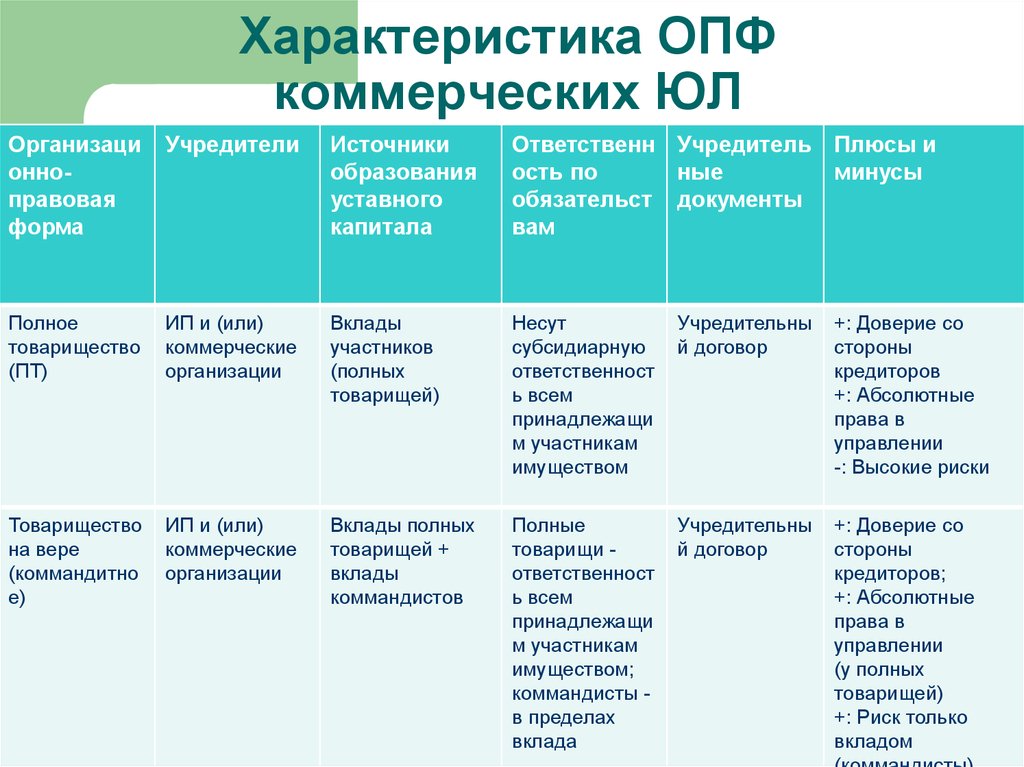 0725 0725 |
2.8401 | 2.6848 | 2.5727 | 2.4876 | 2.4205 | 2.3660 | 2.3210 | 2.2504 | 2.1757 | 2.0960 | 2.0540 | 2.0102 | 1.9645 | 1.9165 | 1.8657 | 1.8117 |
| 22 | 4.3009 | 3.4434 | 3.0491 | 2.8167 | 2.6613 | 2.5491 | 2.4638 | 2.3965 | 2. 3419 3419 |
2.2967 | 2.2258 | 2.1508 | 2.0707 | 2.0283 | 1.9842 | 1.9380 | 1.8894 | 1.8380 | 1.7831 |
| 23 | 4.2793 | 3.4221 | 3.0280 | 2.7955 | 2.6400 | 2.5277 | 2.4422 | 2.3748 | 2.3201 | 2.2747 | 2.2036 | 2.1282 | 2.0476 | 2.0050 | 1. 9605 9605 |
1.9139 | 1.8648 | 1.8128 | 1.7570 |
| 24 | 4.2597 | 3.4028 | 3.0088 | 2.7763 | 2.6207 | 2.5082 | 2.4226 | 2.3551 | 2.3002 | 2.2547 | 2.1834 | 2.1077 | 2.0267 | 1.9838 | 1.9390 | 1.8920 | 1.8424 | 1.7896 | 1.7330 |
| 25 | 4.2417 | 3. 3852 3852 |
2.9912 | 2.7587 | 2.6030 | 2.4904 | 2.4047 | 2.3371 | 2.2821 | 2.2365 | 2.1649 | 2.0889 | 2.0075 | 1.9643 | 1.9192 | 1.8718 | 1.8217 | 1.7684 | 1.7110 |
| 26 | 4.2252 | 3.3690 | 2.9752 | 2.7426 | 2.5868 | 2.4741 | 2. 3883 3883 |
2.3205 | 2.2655 | 2.2197 | 2.1479 | 2.0716 | 1.9898 | 1.9464 | 1.9010 | 1.8533 | 1.8027 | 1.7488 | 1.6906 |
| 27 | 4.2100 | 3.3541 | 2.9604 | 2.7278 | 2.5719 | 2.4591 | 2.3732 | 2.3053 | 2.2501 | 2.2043 | 2.1323 | 2.0558 | 1. 9736 9736 |
1.9299 | 1.8842 | 1.8361 | 1.7851 | 1.7306 | 1.6717 |
| 28 | 4.1960 | 3.3404 | 2.9467 | 2.7141 | 2.5581 | 2.4453 | 2.3593 | 2.2913 | 2.2360 | 2.1900 | 2.1179 | 2.0411 | 1.9586 | 1.9147 | 1.8687 | 1.8203 | 1.7689 | 1.7138 | 1. 6541 6541 |
| 29 | 4.1830 | 3.3277 | 2.9340 | 2.7014 | 2.5454 | 2.4324 | 2.3463 | 2.2783 | 2.2229 | 2.1768 | 2.1045 | 2.0275 | 1.9446 | 1.9005 | 1.8543 | 1.8055 | 1.7537 | 1.6981 | 1.6376 |
| 30 | 4.1709 | 3.3158 | 2.9223 | 2.6896 | 2.5336 | 2.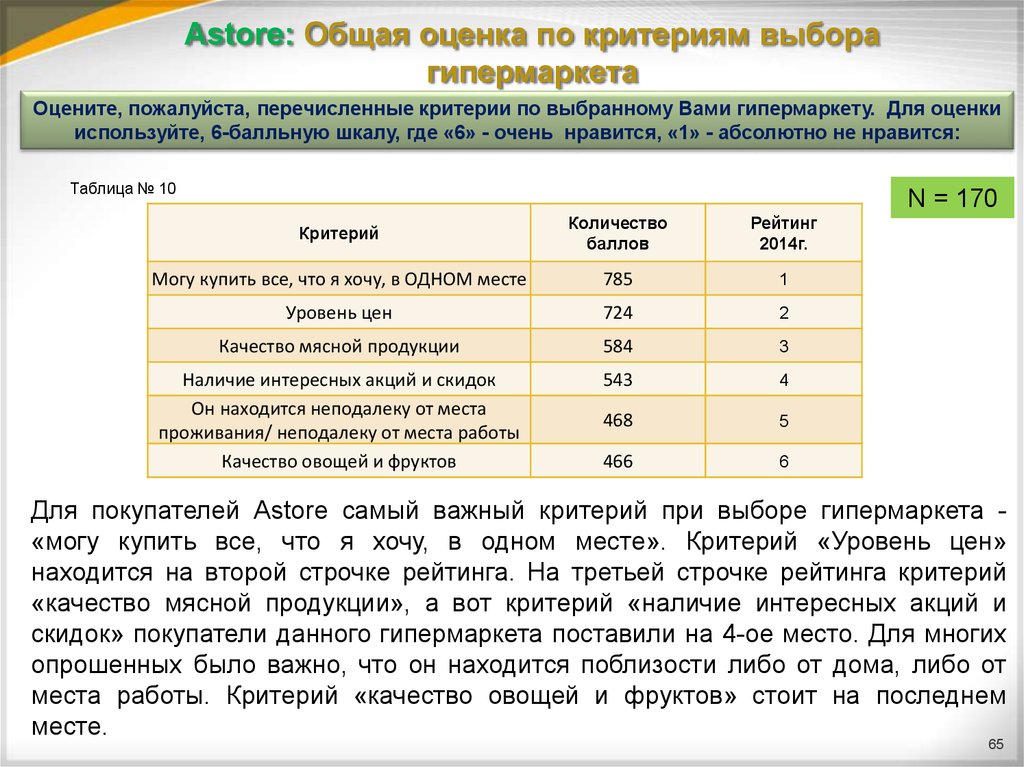 4205 4205 |
2.3343 | 2.2662 | 2.2107 | 2.1646 | 2.0921 | 2.0148 | 1.9317 | 1.8874 | 1.8409 | 1.7918 | 1.7396 | 1.6835 | 1.6223 |
| 40 | 4.0847 | 3.2317 | 2.8387 | 2.6060 | 2.4495 | 2.3359 | 2.2490 | 2.1802 | 2.1240 | 2.0772 | 2. 0035 0035 |
1.9245 | 1.8389 | 1.7929 | 1.7444 | 1.6928 | 1.6373 | 1.5766 | 1.5089 |
| 60 | 4.0012 | 3.1504 | 2.7581 | 2.5252 | 2.3683 | 2.2541 | 2.1665 | 2.0970 | 2.0401 | 1.9926 | 1.9174 | 1.8364 | 1.7480 | 1.7001 | 1.6491 | 1.5943 | 1. 5343 5343 |
1.4673 | 1.3893 |
| 120 | 3.9201 | 3.0718 | 2.6802 | 2.4472 | 2.2899 | 2.1750 | 2.0868 | 2.0164 | 1.9588 | 1.9105 | 1.8337 | 1.7505 | 1.6587 | 1.6084 | 1.5543 | 1.4952 | 1.4290 | 1.3519 | 1.2539 |
| inf | 3.8415 | 2.9957 | 2.6049 | 2.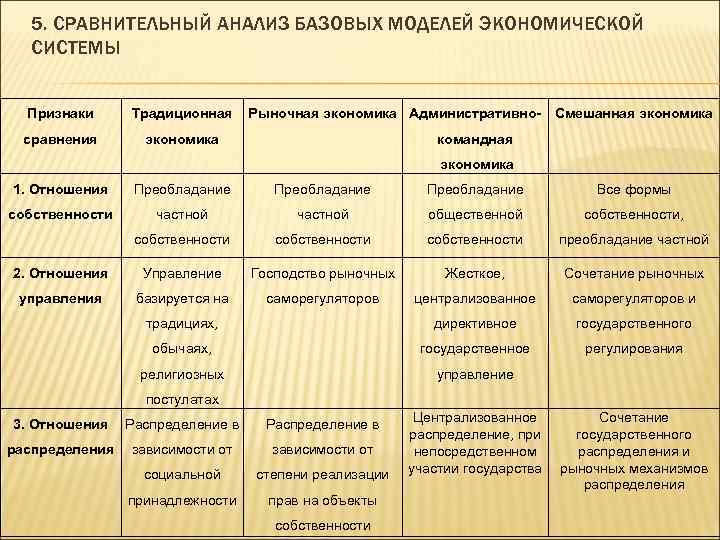 3719 3719 |
2.2141 | 2.0986 | 2.0096 | 1.9384 | 1.8799 | 1.8307 | 1.7522 | 1.6664 | 1.5705 | 1.5173 | 1.4591 | 1.3940 | 1.3180 | 1.2214 | 1.0000 |
| В начало |
F-распределение для alpha=.025 .
| df2/df1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 | 20 | 24 | 30 | 40 | 60 | 120 | INF |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 647. 7890 7890 |
799.5000 | 864.1630 | 899.5833 | 921.8479 | 937.1111 | 948.2169 | 956.6562 | 963.2846 | 968.6274 | 976.7079 | 984.8668 | 993.1028 | 997.2492 | 1001.414 | 1005.598 | 1009.800 | 1014.020 | 1018.258 |
| 2 | 38.5063 | 39.0000 | 39.1655 | 39.2484 | 39.2982 | 39. 3315 3315 |
39.3552 | 39.3730 | 39.3869 | 39.3980 | 39.4146 | 39.4313 | 39.4479 | 39.4562 | 39.465 | 39.473 | 39.481 | 39.490 | 39.498 |
| 3 | 17.4434 | 16.0441 | 15.4392 | 15.1010 | 14.8848 | 14.7347 | 14.6244 | 14.5399 | 14.4731 | 14.4189 | 14.3366 | 14.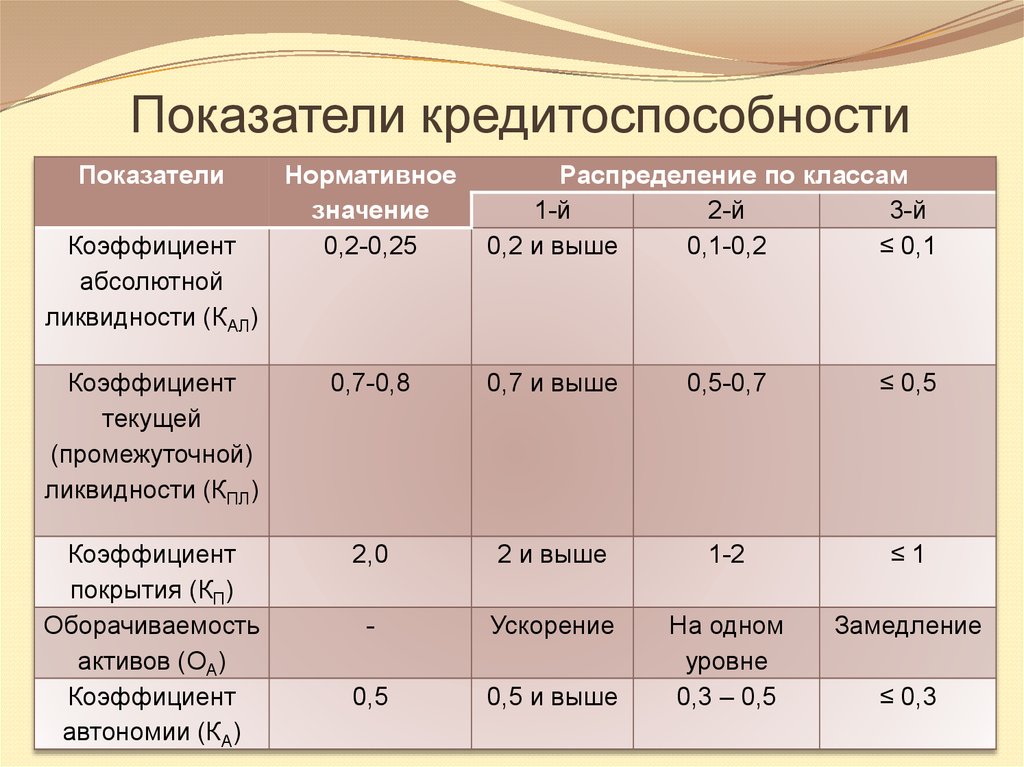 2527 2527 |
14.1674 | 14.1241 | 14.081 | 14.037 | 13.992 | 13.947 | 13.902 |
| 4 | 12.2179 | 10.6491 | 9.9792 | 9.6045 | 9.3645 | 9.1973 | 9.0741 | 8.9796 | 8.9047 | 8.8439 | 8.7512 | 8.6565 | 8.5599 | 8.5109 | 8.461 | 8.411 | 8.360 | 8. 309 309 |
8.257 |
| 5 | 10.0070 | 8.4336 | 7.7636 | 7.3879 | 7.1464 | 6.9777 | 6.8531 | 6.7572 | 6.6811 | 6.6192 | 6.5245 | 6.4277 | 6.3286 | 6.2780 | 6.227 | 6.175 | 6.123 | 6.069 | 6.015 |
| 6 | 8.8131 | 7.2599 | 6.5988 | 6. 2272 2272 |
5.9876 | 5.8198 | 5.6955 | 5.5996 | 5.5234 | 5.4613 | 5.3662 | 5.2687 | 5.1684 | 5.1172 | 5.065 | 5.012 | 4.959 | 4.904 | 4.849 |
| 7 | 8.0727 | 6.5415 | 5.8898 | 5.5226 | 5.2852 | 5.1186 | 4.9949 | 4.8993 | 4.8232 | 4.7611 | 4. 6658 6658 |
4.5678 | 4.4667 | 4.4150 | 4.362 | 4.309 | 4.254 | 4.199 | 4.142 |
| 8 | 7.5709 | 6.0595 | 5.4160 | 5.0526 | 4.8173 | 4.6517 | 4.5286 | 4.4333 | 4.3572 | 4.2951 | 4.1997 | 4.1012 | 3.9995 | 3.9472 | 3.894 | 3.840 | 3.784 | 3. 728 728 |
3.670 |
| 9 | 7.2093 | 5.7147 | 5.0781 | 4.7181 | 4.4844 | 4.3197 | 4.1970 | 4.1020 | 4.0260 | 3.9639 | 3.8682 | 3.7694 | 3.6669 | 3.6142 | 3.560 | 3.505 | 3.449 | 3.392 | 3.333 |
| 10 | 6.9367 | 5.4564 | 4.8256 | 4.4683 | 4.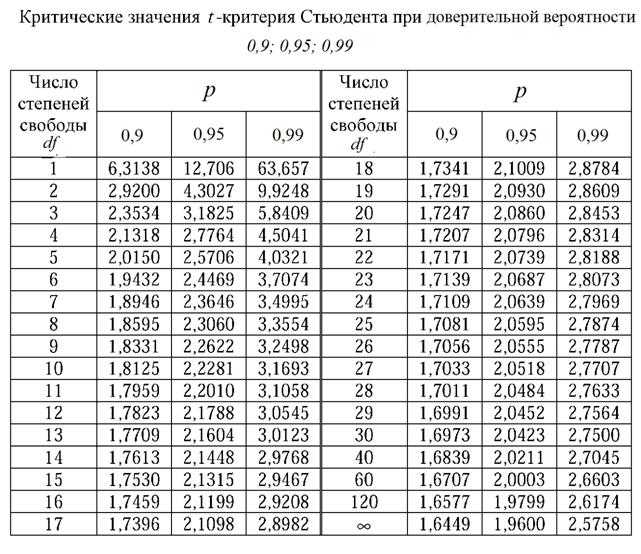 2361 2361 |
4.0721 | 3.9498 | 3.8549 | 3.7790 | 3.7168 | 3.6209 | 3.5217 | 3.4185 | 3.3654 | 3.311 | 3.255 | 3.198 | 3.140 | 3.080 |
| 11 | 6.7241 | 5.2559 | 4.6300 | 4.2751 | 4.0440 | 3.8807 | 3.7586 | 3.6638 | 3.5879 | 3.5257 | 3. 4296 4296 |
3.3299 | 3.2261 | 3.1725 | 3.118 | 3.061 | 3.004 | 2.944 | 2.883 |
| 12 | 6.5538 | 5.0959 | 4.4742 | 4.1212 | 3.8911 | 3.7283 | 3.6065 | 3.5118 | 3.4358 | 3.3736 | 3.2773 | 3.1772 | 3.0728 | 3.0187 | 2.963 | 2.906 | 2.848 | 2. 787 787 |
2.725 |
| 13 | 6.4143 | 4.9653 | 4.3472 | 3.9959 | 3.7667 | 3.6043 | 3.4827 | 3.3880 | 3.3120 | 3.2497 | 3.1532 | 3.0527 | 2.9477 | 2.8932 | 2.837 | 2.780 | 2.720 | 2.659 | 2.595 |
| 14 | 6.2979 | 4.8567 | 4.2417 | 3.8919 | 3. 6634 6634 |
3.5014 | 3.3799 | 3.2853 | 3.2093 | 3.1469 | 3.0502 | 2.9493 | 2.8437 | 2.7888 | 2.732 | 2.674 | 2.614 | 2.552 | 2.487 |
| 15 | 6.1995 | 4.7650 | 4.1528 | 3.8043 | 3.5764 | 3.4147 | 3.2934 | 3.1987 | 3.1227 | 3.0602 | 2.9633 | 2. 8621 8621 |
2.7559 | 2.7006 | 2.644 | 2.585 | 2.524 | 2.461 | 2.395 |
| 16 | 6.1151 | 4.6867 | 4.0768 | 3.7294 | 3.5021 | 3.3406 | 3.2194 | 3.1248 | 3.0488 | 2.9862 | 2.8890 | 2.7875 | 2.6808 | 2.6252 | 2.568 | 2.509 | 2.447 | 2.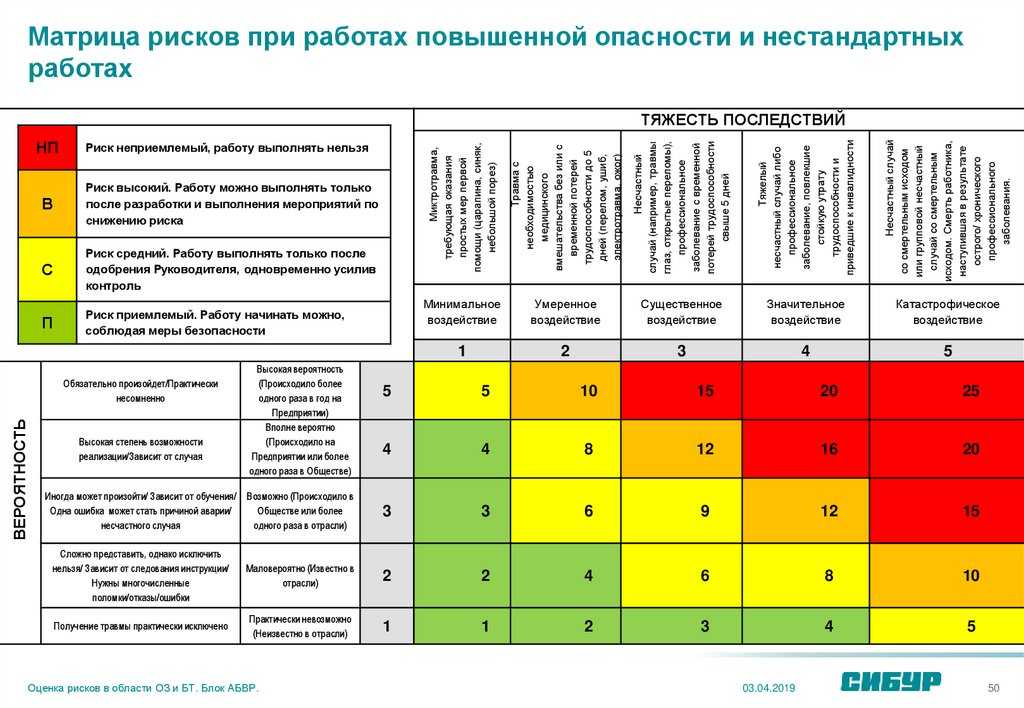 383 383 |
2.316 |
| 17 | 6.0420 | 4.6189 | 4.0112 | 3.6648 | 3.4379 | 3.2767 | 3.1556 | 3.0610 | 2.9849 | 2.9222 | 2.8249 | 2.7230 | 2.6158 | 2.5598 | 2.502 | 2.442 | 2.380 | 2.315 | 2.247 |
| 18 | 5.9781 | 4.5597 | 3.9539 | 3.6083 | 3. 3820 3820 |
3.2209 | 3.0999 | 3.0053 | 2.9291 | 2.8664 | 2.7689 | 2.6667 | 2.5590 | 2.5027 | 2.445 | 2.384 | 2.321 | 2.256 | 2.187 |
| 19 | 5.9216 | 4.5075 | 3.9034 | 3.5587 | 3.3327 | 3.1718 | 3.0509 | 2.9563 | 2.8801 | 2.8172 | 2.7196 | 2. 6171 6171 |
2.5089 | 2.4523 | 2.394 | 2.333 | 2.270 | 2.203 | 2.133 |
| 20 | 5.8715 | 4.4613 | 3.8587 | 3.5147 | 3.2891 | 3.1283 | 3.0074 | 2.9128 | 2.8365 | 2.7737 | 2.6758 | 2.5731 | 2.4645 | 2.4076 | 2.349 | 2.287 | 2.223 | 2.156 | 2.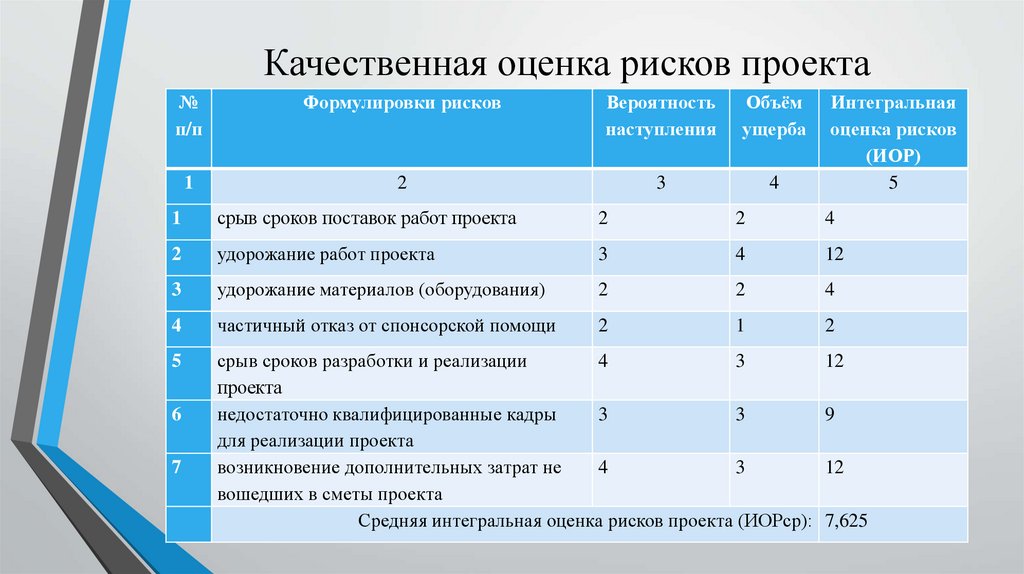 085 085 |
| 21 | 5.8266 | 4.4199 | 3.8188 | 3.4754 | 3.2501 | 3.0895 | 2.9686 | 2.8740 | 2.7977 | 2.7348 | 2.6368 | 2.5338 | 2.4247 | 2.3675 | 2.308 | 2.246 | 2.182 | 2.114 | 2.042 |
| 22 | 5.7863 | 4.3828 | 3.7829 | 3.4401 | 3. 2151 2151 |
3.0546 | 2.9338 | 2.8392 | 2.7628 | 2.6998 | 2.6017 | 2.4984 | 2.3890 | 2.3315 | 2.272 | 2.210 | 2.145 | 2.076 | 2.003 |
| 23 | 5.7498 | 4.3492 | 3.7505 | 3.4083 | 3.1835 | 3.0232 | 2.9023 | 2.8077 | 2.7313 | 2.6682 | 2.5699 | 2. 4665 4665 |
2.3567 | 2.2989 | 2.239 | 2.176 | 2.111 | 2.041 | 1.968 |
| 24 | 5.7166 | 4.3187 | 3.7211 | 3.3794 | 3.1548 | 2.9946 | 2.8738 | 2.7791 | 2.7027 | 2.6396 | 2.5411 | 2.4374 | 2.3273 | 2.2693 | 2.209 | 2.146 | 2.080 | 2.010 | 1. 935 935 |
| 25 | 5.6864 | 4.2909 | 3.6943 | 3.3530 | 3.1287 | 2.9685 | 2.8478 | 2.7531 | 2.6766 | 2.6135 | 2.5149 | 2.4110 | 2.3005 | 2.2422 | 2.182 | 2.118 | 2.052 | 1.981 | 1.906 |
| 26 | 5.6586 | 4.2655 | 3.6697 | 3.3289 | 3.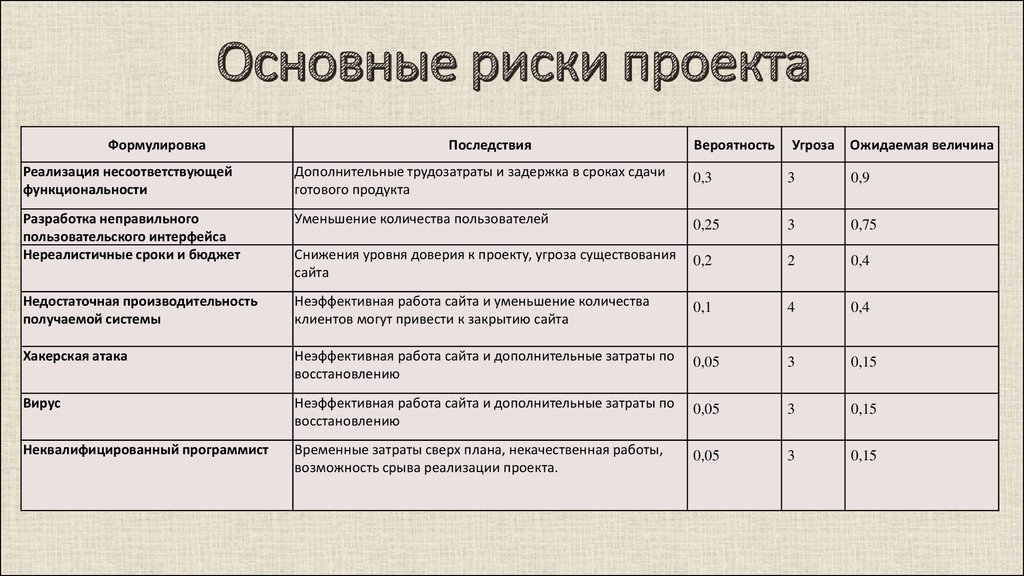 1048 1048 |
2.9447 | 2.8240 | 2.7293 | 2.6528 | 2.5896 | 2.4908 | 2.3867 | 2.2759 | 2.2174 | 2.157 | 2.093 | 2.026 | 1.954 | 1.878 |
| 27 | 5.6331 | 4.2421 | 3.6472 | 3.3067 | 3.0828 | 2.9228 | 2.8021 | 2.7074 | 2.6309 | 2.5676 | 2.4688 | 2. 3644 3644 |
2.2533 | 2.1946 | 2.133 | 2.069 | 2.002 | 1.930 | 1.853 |
| 28 | 5.6096 | 4.2205 | 3.6264 | 3.2863 | 3.0626 | 2.9027 | 2.7820 | 2.6872 | 2.6106 | 2.5473 | 2.4484 | 2.3438 | 2.2324 | 2.1735 | 2.112 | 2.048 | 1.980 | 1.907 | 1. 829 829 |
| 29 | 5.5878 | 4.2006 | 3.6072 | 3.2674 | 3.0438 | 2.8840 | 2.7633 | 2.6686 | 2.5919 | 2.5286 | 2.4295 | 2.3248 | 2.2131 | 2.1540 | 2.092 | 2.028 | 1.959 | 1.886 | 1.807 |
| 30 | 5.5675 | 4.1821 | 3.5894 | 3.2499 | 3.0265 | 2.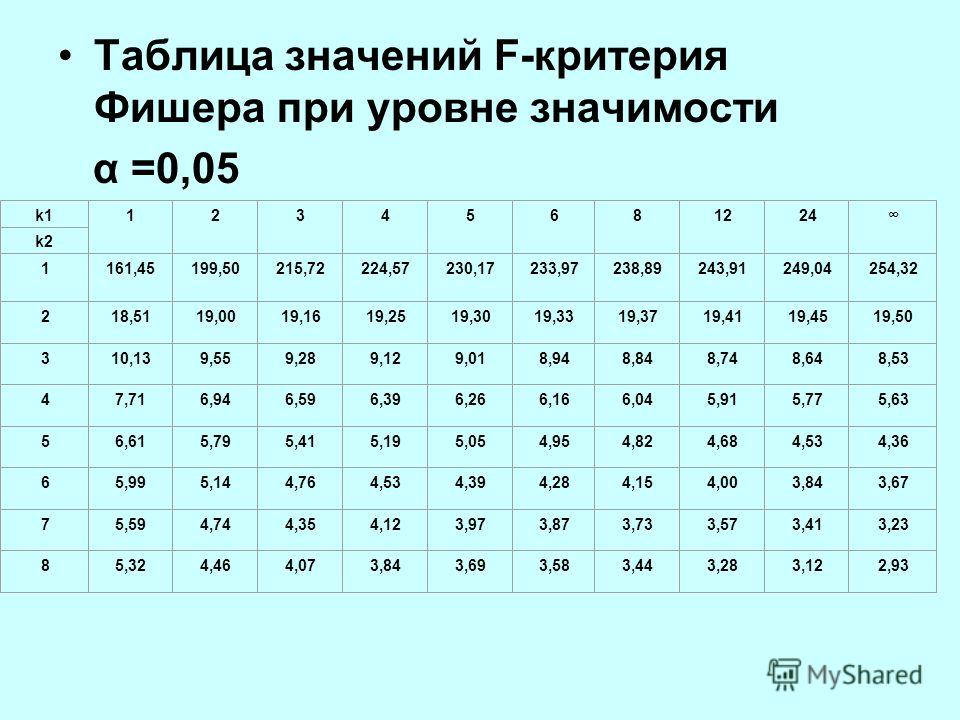 8667 8667 |
2.7460 | 2.6513 | 2.5746 | 2.5112 | 2.4120 | 2.3072 | 2.1952 | 2.1359 | 2.074 | 2.009 | 1.940 | 1.866 | 1.787 |
| 40 | 5.4239 | 4.0510 | 3.4633 | 3.1261 | 2.9037 | 2.7444 | 2.6238 | 2.5289 | 2.4519 | 2.3882 | 2.2882 | 2.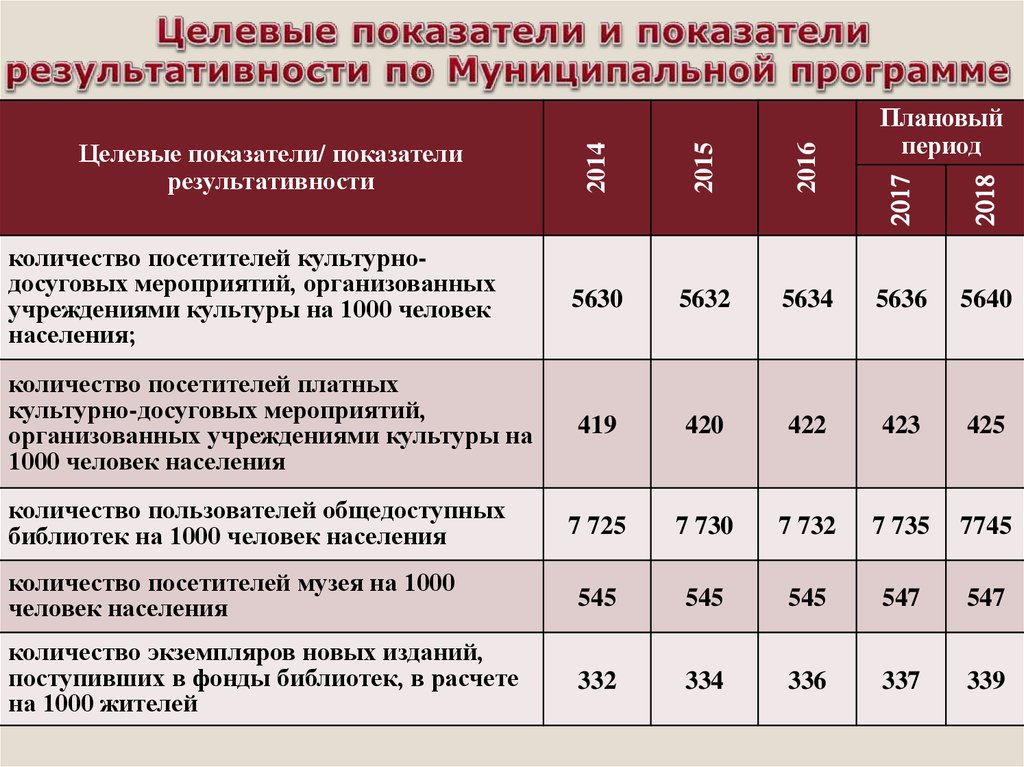 1819 1819 |
2.0677 | 2.0069 | 1.943 | 1.875 | 1.803 | 1.724 | 1.637 |
| 60 | 5.2856 | 3.9253 | 3.3425 | 3.0077 | 2.7863 | 2.6274 | 2.5068 | 2.4117 | 2.3344 | 2.2702 | 2.1692 | 2.0613 | 1.9445 | 1.8817 | 1.815 | 1.744 | 1.667 | 1.581 | 1. 482 482 |
| 120 | 5.1523 | 3.8046 | 3.2269 | 2.8943 | 2.6740 | 2.5154 | 2.3948 | 2.2994 | 2.2217 | 2.1570 | 2.0548 | 1.9450 | 1.8249 | 1.7597 | 1.690 | 1.614 | 1.530 | 1.433 | 1.310 |
| inf | 5.0239 | 3.6889 | 3.1161 | 2.7858 | 2.5665 | 2.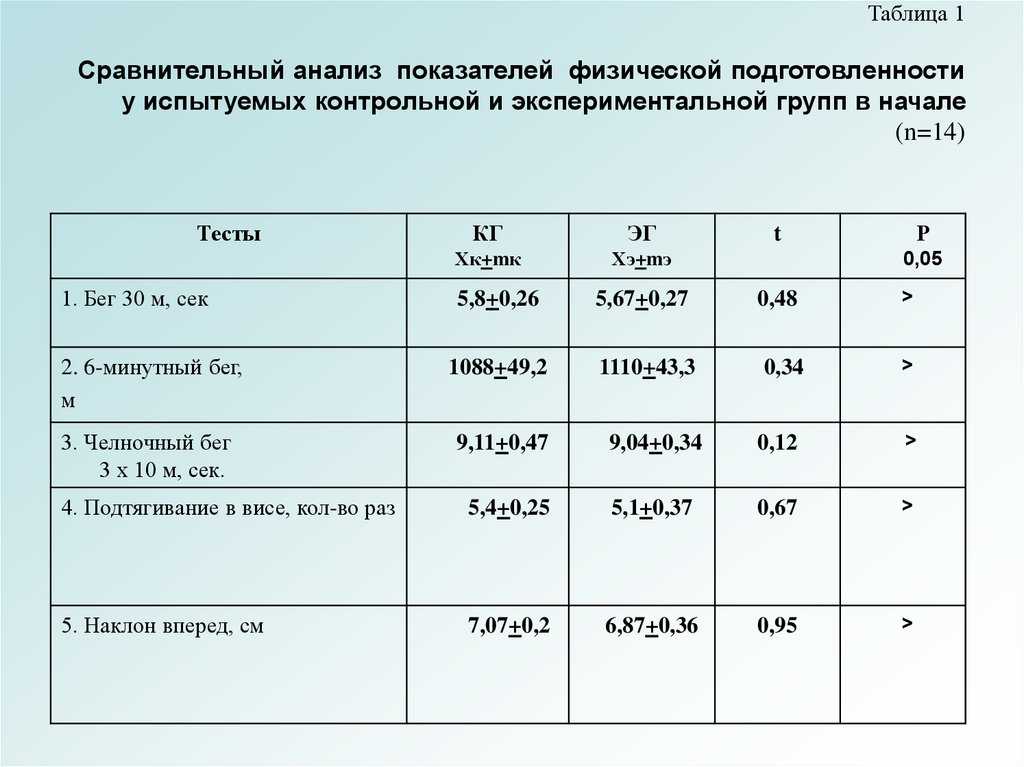 4082 4082 |
2.2875 | 2.1918 | 2.1136 | 2.0483 | 1.9447 | 1.8326 | 1.7085 | 1.6402 | 1.566 | 1.484 | 1.388 | 1.268 | 1.000 |
| В начало |
F-распределение для alpha=.01 .
| df2/df1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 | 20 | 24 | 30 | 40 | 60 | 120 | INF |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4052..png) 181 181 |
4999.500 | 5403.352 | 5624.583 | 5763.650 | 5858.986 | 5928.356 | 5981.070 | 6022.473 | 6055.847 | 6106.321 | 6157.285 | 6208.730 | 6234.631 | 6260.649 | 6286.782 | 6313.030 | 6339.391 | 6365.864 |
| 2 | 98.503 | 99.000 | 99.166 | 99.249 | 99.299 | 99.333 | 99. 356 356 |
99.374 | 99.388 | 99.399 | 99.416 | 99.433 | 99.449 | 99.458 | 99.466 | 99.474 | 99.482 | 99.491 | 99.499 |
| 3 | 34.116 | 30.817 | 29.457 | 28.710 | 28.237 | 27.911 | 27.672 | 27.489 | 27.345 | 27.229 | 27.052 | 26.872 | 26. 690 690 |
26.598 | 26.505 | 26.411 | 26.316 | 26.221 | 26.125 |
| 4 | 21.198 | 18.000 | 16.694 | 15.977 | 15.522 | 15.207 | 14.976 | 14.799 | 14.659 | 14.546 | 14.374 | 14.198 | 14.020 | 13.929 | 13.838 | 13.745 | 13.652 | 13.558 | 13. 463 463 |
| 5 | 16.258 | 13.274 | 12.060 | 11.392 | 10.967 | 10.672 | 10.456 | 10.289 | 10.158 | 10.051 | 9.888 | 9.722 | 9.553 | 9.466 | 9.379 | 9.291 | 9.202 | 9.112 | 9.020 |
| 6 | 13.745 | 10.925 | 9.780 | 9.148 | 8. 746 746 |
8.466 | 8.260 | 8.102 | 7.976 | 7.874 | 7.718 | 7.559 | 7.396 | 7.313 | 7.229 | 7.143 | 7.057 | 6.969 | 6.880 |
| 7 | 12.246 | 9.547 | 8.451 | 7.847 | 7.460 | 7.191 | 6.993 | 6.840 | 6.719 | 6.620 | 6.469 | 6. 314 314 |
6.155 | 6.074 | 5.992 | 5.908 | 5.824 | 5.737 | 5.650 |
| 8 | 11.259 | 8.649 | 7.591 | 7.006 | 6.632 | 6.371 | 6.178 | 6.029 | 5.911 | 5.814 | 5.667 | 5.515 | 5.359 | 5.279 | 5.198 | 5.116 | 5.032 | 4.946 | 4.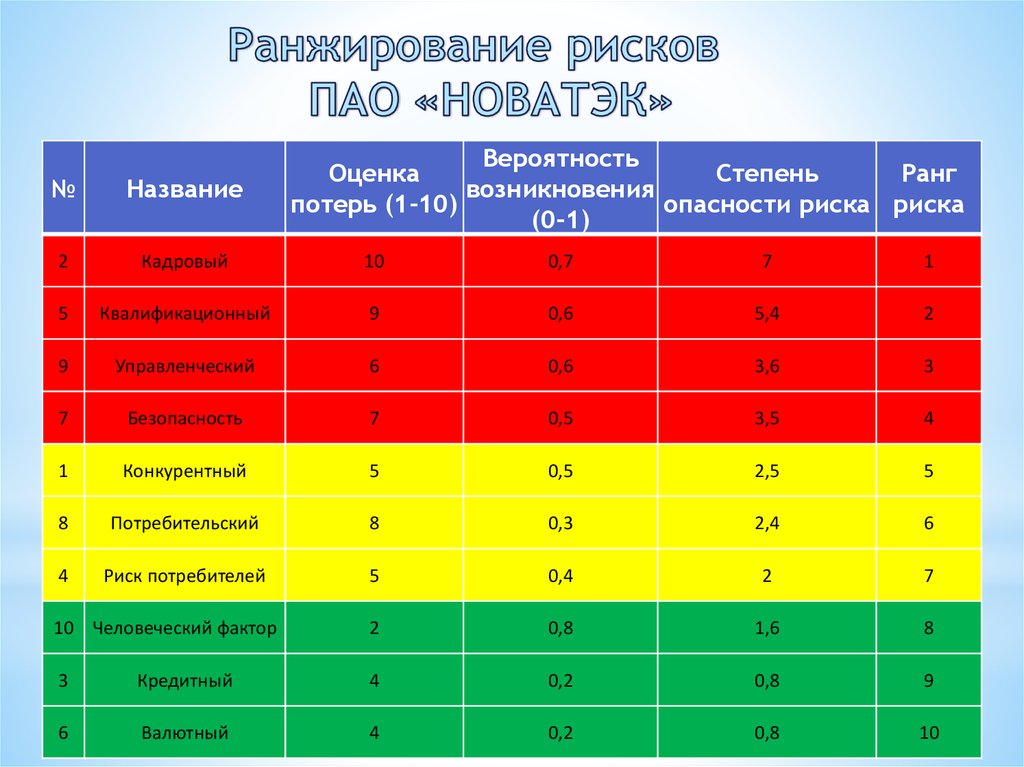 859 859 |
| 9 | 10.561 | 8.022 | 6.992 | 6.422 | 6.057 | 5.802 | 5.613 | 5.467 | 5.351 | 5.257 | 5.111 | 4.962 | 4.808 | 4.729 | 4.649 | 4.567 | 4.483 | 4.398 | 4.311 |
| 10 | 10.044 | 7.559 | 6.552 | 5.994 | 5.636 | 5.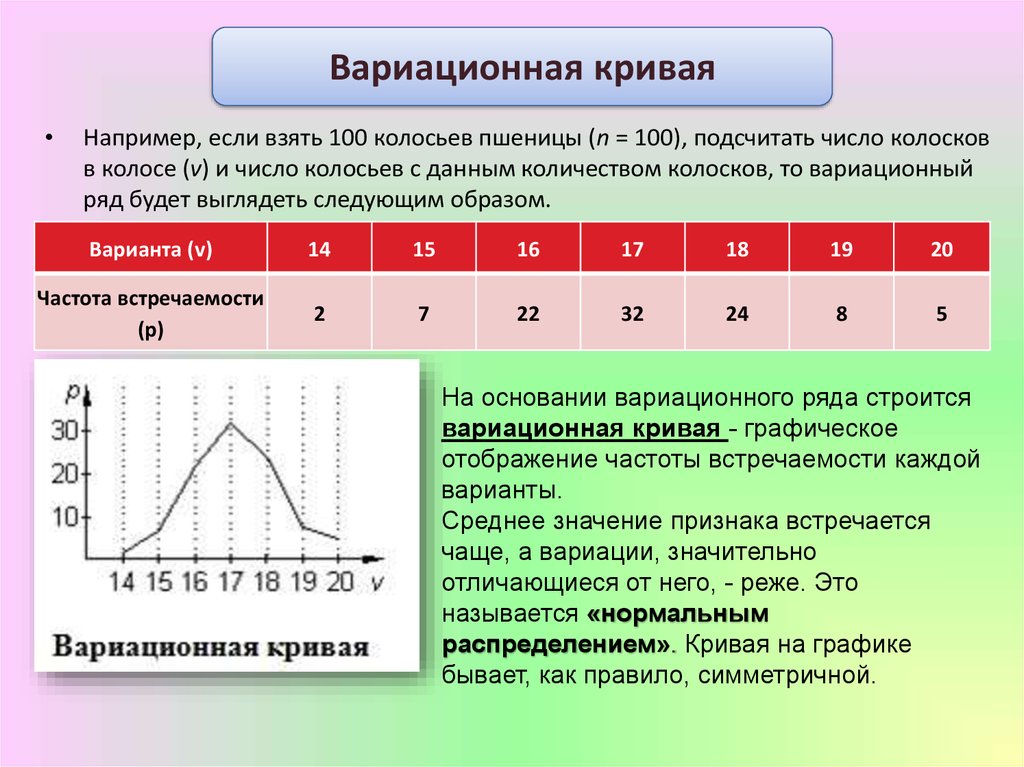 386 386 |
5.200 | 5.057 | 4.942 | 4.849 | 4.706 | 4.558 | 4.405 | 4.327 | 4.247 | 4.165 | 4.082 | 3.996 | 3.909 |
| 11 | 9.646 | 7.206 | 6.217 | 5.668 | 5.316 | 5.069 | 4.886 | 4.744 | 4.632 | 4.539 | 4.397 | 4.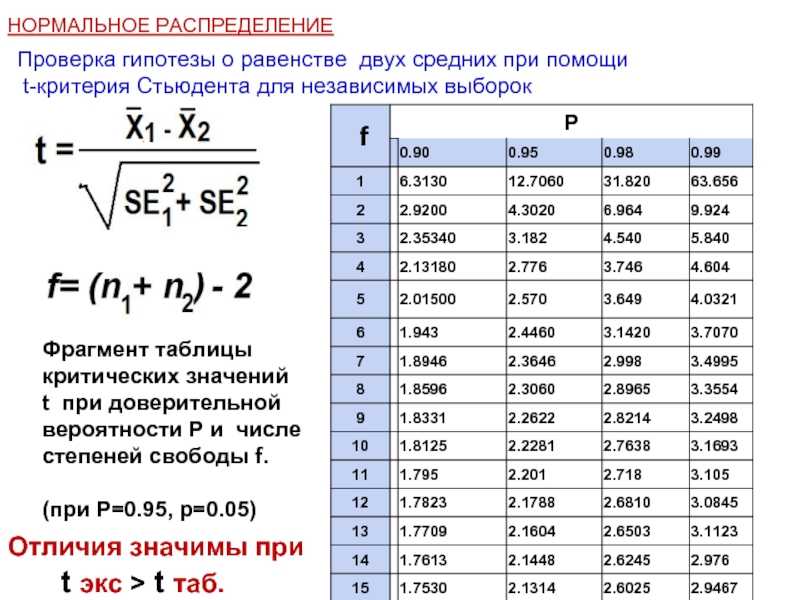 251 251 |
4.099 | 4.021 | 3.941 | 3.860 | 3.776 | 3.690 | 3.602 |
| 12 | 9.330 | 6.927 | 5.953 | 5.412 | 5.064 | 4.821 | 4.640 | 4.499 | 4.388 | 4.296 | 4.155 | 4.010 | 3.858 | 3.780 | 3.701 | 3.619 | 3.535 | 3.449 | 3. 361 361 |
| 13 | 9.074 | 6.701 | 5.739 | 5.205 | 4.862 | 4.620 | 4.441 | 4.302 | 4.191 | 4.100 | 3.960 | 3.815 | 3.665 | 3.587 | 3.507 | 3.425 | 3.341 | 3.255 | 3.165 |
| 14 | 8.862 | 6.515 | 5.564 | 5.035 | 4.695 | 4.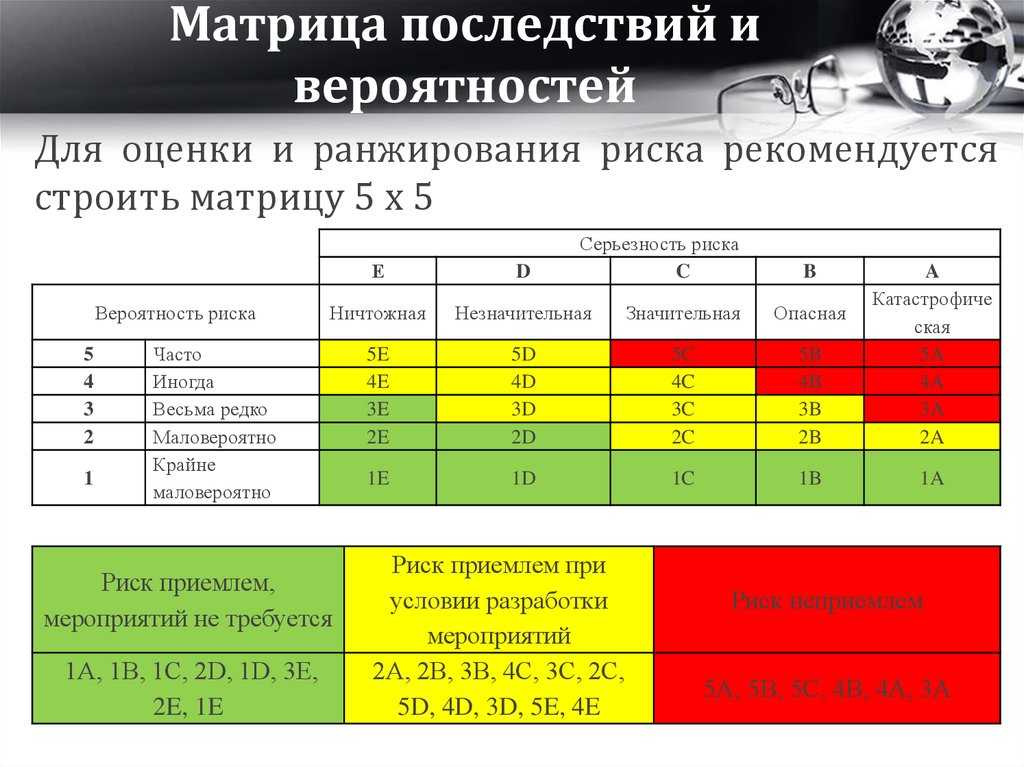 456 456 |
4.278 | 4.140 | 4.030 | 3.939 | 3.800 | 3.656 | 3.505 | 3.427 | 3.348 | 3.266 | 3.181 | 3.094 | 3.004 |
| 15 | 8.683 | 6.359 | 5.417 | 4.893 | 4.556 | 4.318 | 4.142 | 4.004 | 3.895 | 3.805 | 3.666 | 3.522 | 3.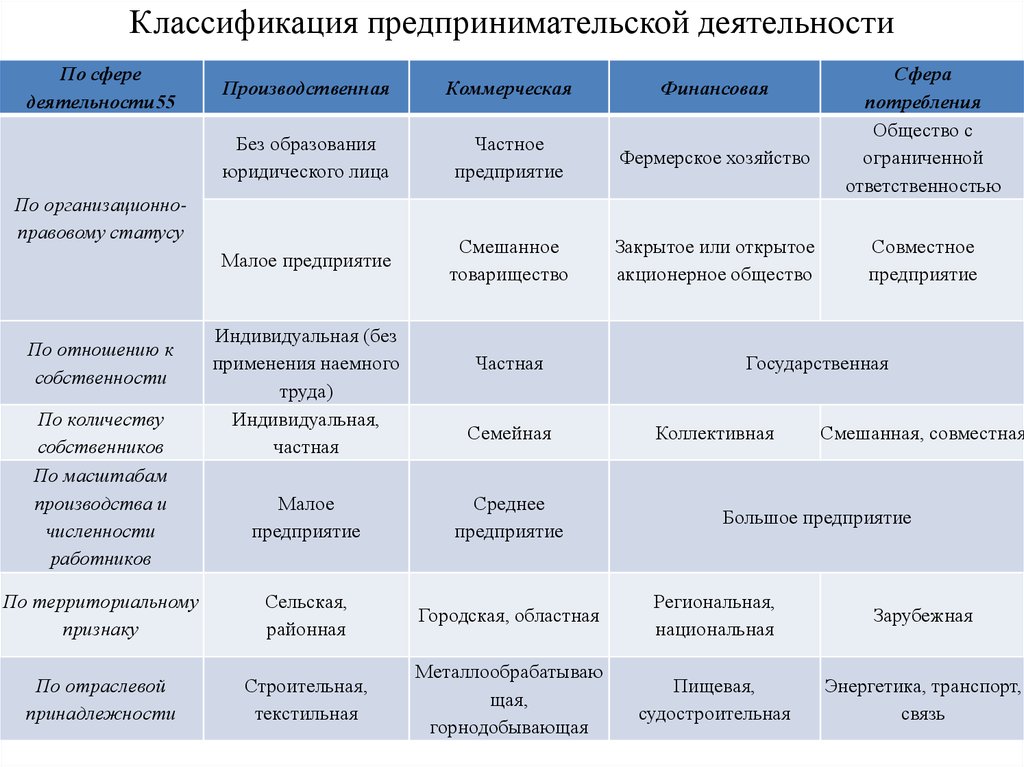 372 372 |
3.294 | 3.214 | 3.132 | 3.047 | 2.959 | 2.868 |
| 16 | 8.531 | 6.226 | 5.292 | 4.773 | 4.437 | 4.202 | 4.026 | 3.890 | 3.780 | 3.691 | 3.553 | 3.409 | 3.259 | 3.181 | 3.101 | 3.018 | 2.933 | 2.845 | 2. 753 753 |
| 17 | 8.400 | 6.112 | 5.185 | 4.669 | 4.336 | 4.102 | 3.927 | 3.791 | 3.682 | 3.593 | 3.455 | 3.312 | 3.162 | 3.084 | 3.003 | 2.920 | 2.835 | 2.746 | 2.653 |
| 18 | 8.285 | 6.013 | 5.092 | 4.579 | 4.248 | 4. 015 015 |
3.841 | 3.705 | 3.597 | 3.508 | 3.371 | 3.227 | 3.077 | 2.999 | 2.919 | 2.835 | 2.749 | 2.660 | 2.566 |
| 19 | 8.185 | 5.926 | 5.010 | 4.500 | 4.171 | 3.939 | 3.765 | 3.631 | 3.523 | 3.434 | 3.297 | 3.153 | 3.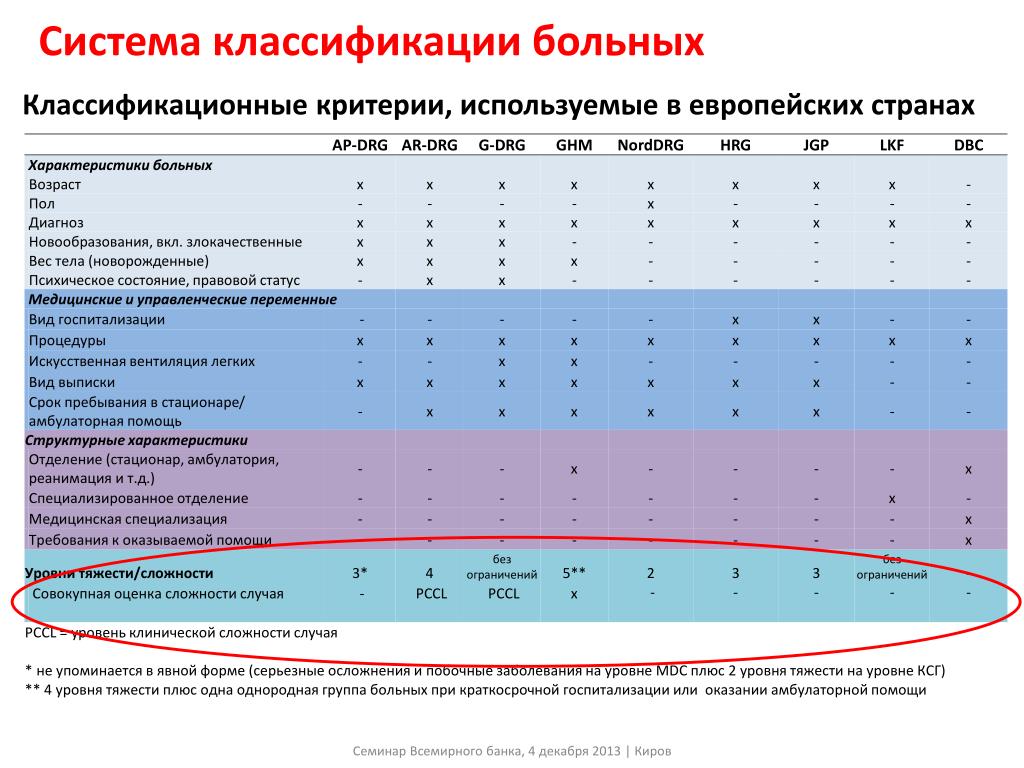 003 003 |
2.925 | 2.844 | 2.761 | 2.674 | 2.584 | 2.489 |
| 20 | 8.096 | 5.849 | 4.938 | 4.431 | 4.103 | 3.871 | 3.699 | 3.564 | 3.457 | 3.368 | 3.231 | 3.088 | 2.938 | 2.859 | 2.778 | 2.695 | 2.608 | 2.517 | 2.421 |
| 21 | 8.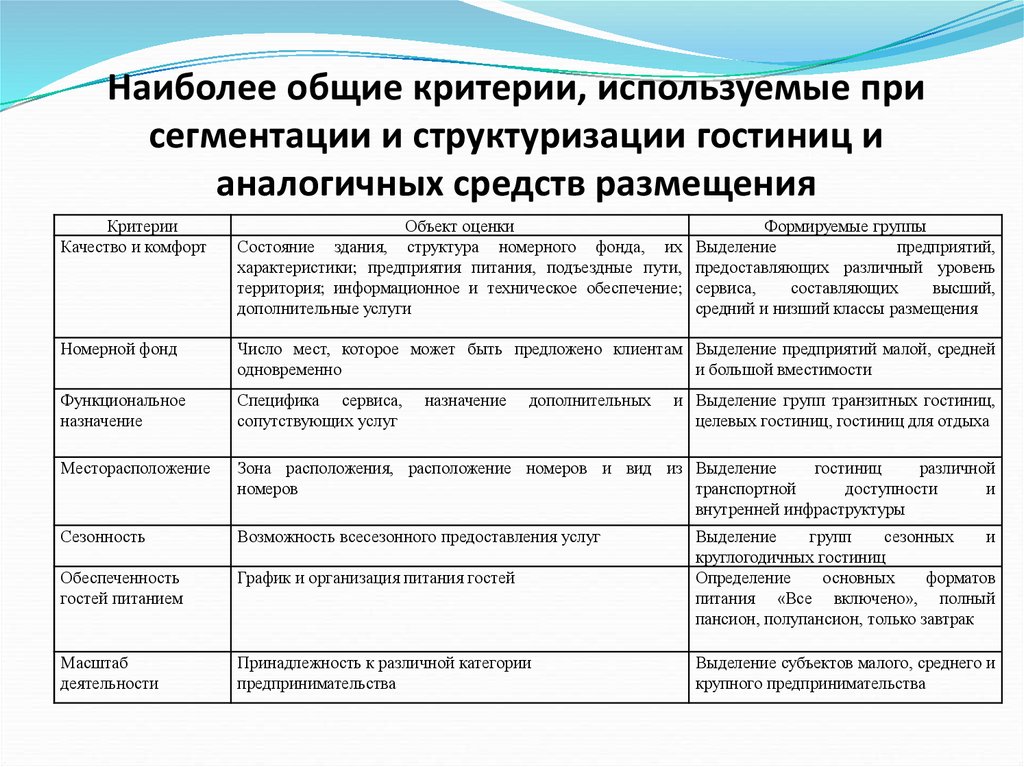 017 017 |
5.780 | 4.874 | 4.369 | 4.042 | 3.812 | 3.640 | 3.506 | 3.398 | 3.310 | 3.173 | 3.030 | 2.880 | 2.801 | 2.720 | 2.636 | 2.548 | 2.457 | 2.360 |
| 22 | 7.945 | 5.719 | 4.817 | 4.313 | 3.988 | 3.758 | 3.587 | 3.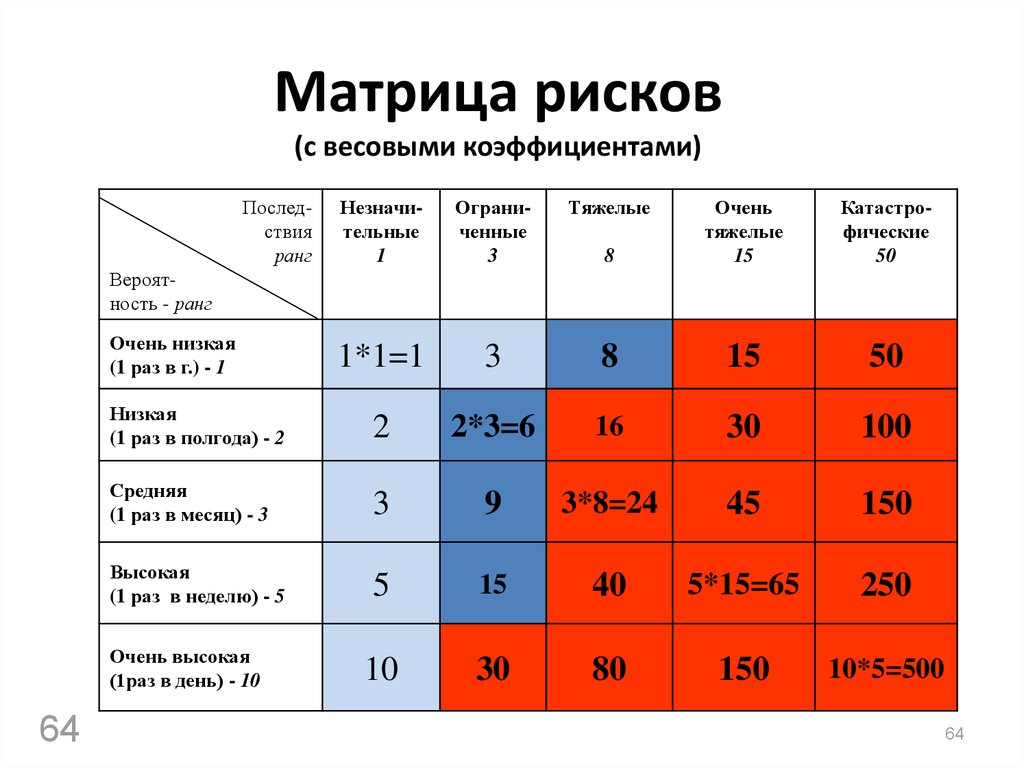 453 453 |
3.346 | 3.258 | 3.121 | 2.978 | 2.827 | 2.749 | 2.667 | 2.583 | 2.495 | 2.403 | 2.305 |
| 23 | 7.881 | 5.664 | 4.765 | 4.264 | 3.939 | 3.710 | 3.539 | 3.406 | 3.299 | 3.211 | 3.074 | 2.931 | 2.781 | 2.702 | 2. 620 620 |
2.535 | 2.447 | 2.354 | 2.256 |
| 24 | 7.823 | 5.614 | 4.718 | 4.218 | 3.895 | 3.667 | 3.496 | 3.363 | 3.256 | 3.168 | 3.032 | 2.889 | 2.738 | 2.659 | 2.577 | 2.492 | 2.403 | 2.310 | 2.211 |
| 25 | 7.770 | 5.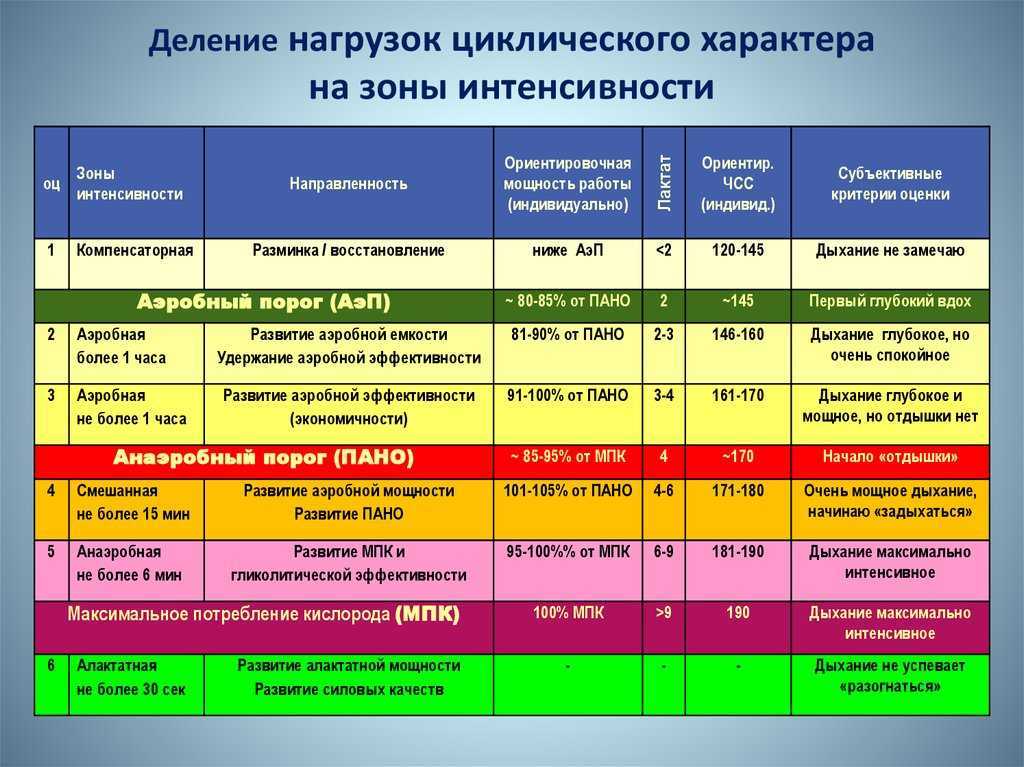 568 568 |
4.675 | 4.177 | 3.855 | 3.627 | 3.457 | 3.324 | 3.217 | 3.129 | 2.993 | 2.850 | 2.699 | 2.620 | 2.538 | 2.453 | 2.364 | 2.270 | 2.169 |
| 26 | 7.721 | 5.526 | 4.637 | 4.140 | 3.818 | 3.591 | 3.421 | 3.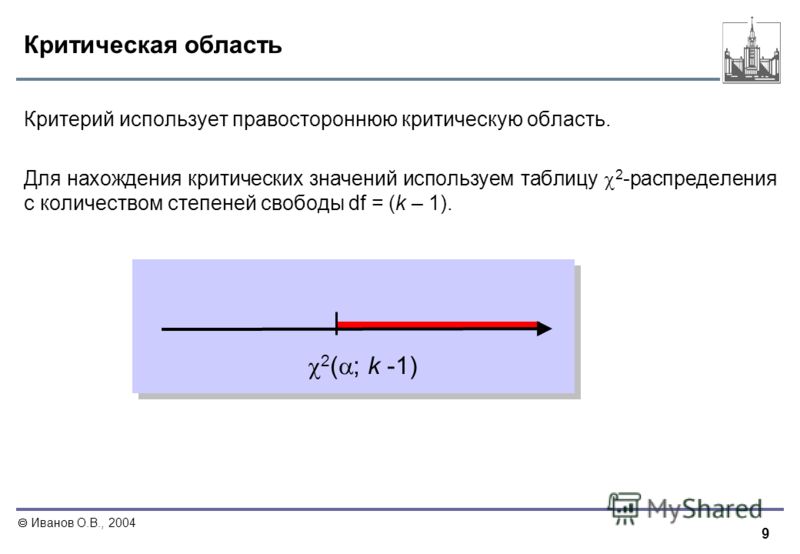 288 288 |
3.182 | 3.094 | 2.958 | 2.815 | 2.664 | 2.585 | 2.503 | 2.417 | 2.327 | 2.233 | 2.131 |
| 27 | 7.677 | 5.488 | 4.601 | 4.106 | 3.785 | 3.558 | 3.388 | 3.256 | 3.149 | 3.062 | 2.926 | 2.783 | 2.632 | 2.552 | 2. 470 470 |
2.384 | 2.294 | 2.198 | 2.097 |
| 28 | 7.636 | 5.453 | 4.568 | 4.074 | 3.754 | 3.528 | 3.358 | 3.226 | 3.120 | 3.032 | 2.896 | 2.753 | 2.602 | 2.522 | 2.440 | 2.354 | 2.263 | 2.167 | 2.064 |
| 29 | 7.598 | 5. 420 420 |
4.538 | 4.045 | 3.725 | 3.499 | 3.330 | 3.198 | 3.092 | 3.005 | 2.868 | 2.726 | 2.574 | 2.495 | 2.412 | 2.325 | 2.234 | 2.138 | 2.034 |
| 30 | 7.562 | 5.390 | 4.510 | 4.018 | 3.699 | 3.473 | 3.304 | 3.173 | 3. 067 067 |
2.979 | 2.843 | 2.700 | 2.549 | 2.469 | 2.386 | 2.299 | 2.208 | 2.111 | 2.006 |
| 40 | 7.314 | 5.179 | 4.313 | 3.828 | 3.514 | 3.291 | 3.124 | 2.993 | 2.888 | 2.801 | 2.665 | 2.522 | 2.369 | 2.288 | 2. 203 203 |
2.114 | 2.019 | 1.917 | 1.805 |
| 60 | 7.077 | 4.977 | 4.126 | 3.649 | 3.339 | 3.119 | 2.953 | 2.823 | 2.718 | 2.632 | 2.496 | 2.352 | 2.198 | 2.115 | 2.028 | 1.936 | 1.836 | 1.726 | 1.601 |
| 120 | 6.851 | 4. 787 787 |
3.949 | 3.480 | 3.174 | 2.956 | 2.792 | 2.663 | 2.559 | 2.472 | 2.336 | 2.192 | 2.035 | 1.950 | 1.860 | 1.763 | 1.656 | 1.533 | 1.381 |
| inf | 6.635 | 4.605 | 3.782 | 3.319 | 3.017 | 2.802 | 2.639 | 2.511 | 2.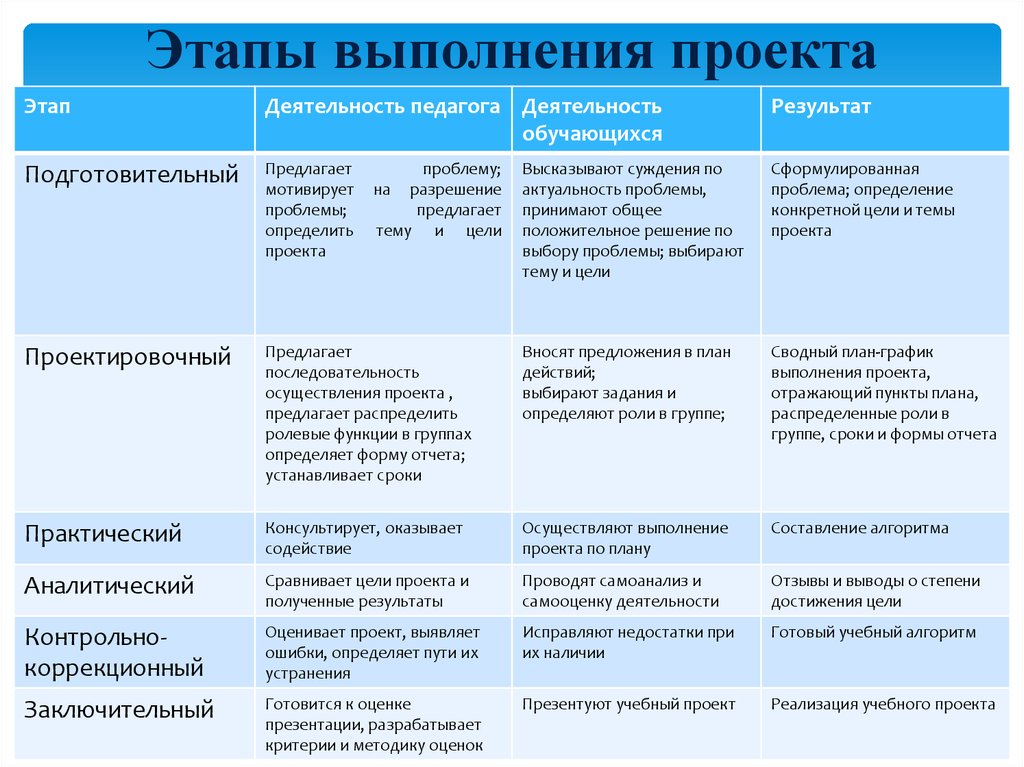 407 407 |
2.321 | 2.185 | 2.039 | 1.878 | 1.791 | 1.696 | 1.592 | 1.473 | 1.325 | 1.000 |
| В начало |
Все права на материалы электронного учебника принадлежат компании StatSoft
Закон нормального распределения
Значение для исследований в области физической культуры и спорта (ФКиС)
Нормальное распределение случайной величины (гауссово распределение, распределение Гаусса, распределение Гаусса-Лапласа) – одно из непрерывных распределений, имеющее основополагающую роль в математической статистике. Причинами это являются:
- Многие эмпирические распределения можно успешно описать с помощью нормального закона распределения.
 Это чаще всего происходит в тех случаях, когда на показатель оказывает влияние большое число случайных факторов. При этом действие каждого фактора незначительно. Примерами показателей, которые распределяются по нормальному закону являются: рост, сила мышц, результаты в беге, прыжках, метаниях и др.
Это чаще всего происходит в тех случаях, когда на показатель оказывает влияние большое число случайных факторов. При этом действие каждого фактора незначительно. Примерами показателей, которые распределяются по нормальному закону являются: рост, сила мышц, результаты в беге, прыжках, метаниях и др. - Нормальное распределение обладает рядом благоприятных математических свойств, обеспечивших его широкое применение в статистике.
- Корректное использование критериев проверки статистических гипотез предполагает знание закона распределения экспериментальных данных. Так, например, использование t – критерия Стьюдента и F-критерия Фишера требует нормального распределения экспериментальных данных.
- Большинство экспериментальных распределений, полученных при исследованиях в области физической культуры и спорта может быть описано с помощью нормального распределения.
Однако в природе и в области ФКиС встречаются экспериментальные распределения, для описания которых модель нормального распределения малопригодна.
Более подробно о методах статистической обработки данных рассказано в книгах:
- Факторный анализ в педагогических исследованиях в области физической культуры и спорта
- Компьютерная обработка данных экспериментальных исследований
- Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта
История изучения нормального распределения
Блез Паскаль и Пьер Ферма
Первые исследования по теории вероятностей проводили математик, механик, физик Блез Паскаль и математик Пьер Ферма в середине XVII века. Эти исследования выполнялись по просьбе Шевалье де Мере, азартного игрока в кости, который пытался понять природу выигрыша. В дальнейшем эти исследования заложили основы теории вероятностей (Дж. Гласс, Дж. Стэнли, 1976).
Якоб Бернулли
Дальнейшее развитие теория вероятностей получила в XVIII веке. В 1713 году была опубликована книга швейцарского математика Якоба Бернулли «Искусство предположений». В этой книге был рассмотрен ряд вопросов теории вероятностей. Якоб Бернулли ввёл значительную часть современных понятий теории вероятностей, а также изложил правила подсчёта вероятности для сложных событий и дал первый вариант «закона больших чисел», разъясняющего, почему частота события в серии испытаний не меняется хаотично, а в некотором смысле стремится к своему предельному теоретическому значению (то есть вероятности).
В этой книге был рассмотрен ряд вопросов теории вероятностей. Якоб Бернулли ввёл значительную часть современных понятий теории вероятностей, а также изложил правила подсчёта вероятности для сложных событий и дал первый вариант «закона больших чисел», разъясняющего, почему частота события в серии испытаний не меняется хаотично, а в некотором смысле стремится к своему предельному теоретическому значению (то есть вероятности).
Джеймс Стирлинг
В последствии (в 1730 г.) шотландский математик Джеймс Стирлинг опубликовал формулу, аппроксимирующую произведение первых n чисел. Это позволило упростить решение ряда задач, которые встречаются в теории вероятностей. Однако все еще эти задачи оставались трудно разрешимыми.
Абрахам де Муавр
Эту задачу решил английский математик Абрахам де Муавр. В работе «Доктрина случайностей», которая была издана в 1738 году он привел формулу, аппроксимирующую биномиальное распределение события, вероятность которого была равна 0,5 (рис. 1). То есть он нашел уравнение кривой, проходящей через точки графика, изображенного на рис. 1. Эта была формула, которую впоследствии стали называть формулой нормального распределения вероятностей. Появление формулы нормального распределения значительно упростило расчеты вероятностей событий.
1). То есть он нашел уравнение кривой, проходящей через точки графика, изображенного на рис. 1. Эта была формула, которую впоследствии стали называть формулой нормального распределения вероятностей. Появление формулы нормального распределения значительно упростило расчеты вероятностей событий.
Пьер-Симон де Лаплас
В начале XIX века (в 1812 г.) французский математик, механик, физик и астроном Пьер-Симон де Лаплас обобщил результаты А. Муавра для произвольного биномиального распределения.
Рис.1. Биномиальное распределениеКарл Фридрих Гаусс
Одновременно с П. Лапласом в 1809 году немецкий математик, механик, физик и астроном Карл Фридрих Гаусс в сочинении «Теория движения небесных тел» использовал формулу нормального распределения для описания случайных ошибок, возникающих в результате многократных измерений движений небесных тел. К.Ф. Гаусс внес настолько большой вклад в разработку теории нормального распределения, что впоследствии это распределение стали назвать гауссово распределение или распределение Гаусса-Лапласса.
Адольф Кетле
В начале ХХ века бельгийский математик, астроном и социолог Адольф Кетле одним из первых применил нормальный закон распределения случайной величины к анализу биологических и социальных процессов. Изучая распределение солдат американской армии по росту, Адольф Кетле обратил внимание, что распределение роста подчиняется нормальному закону. Он писал: «…Человеческий рост, изменяющийся, по-видимому, самым случайным образом, тем не менее подчиняется самым точным законам, и эта особенность свойственна не только росту, она проявляется также в весе, силе, быстроте передвижений человека, во всех его физических … и нравственных способностях. Этот великий принцип… разнообразящий проявление человеческих способностей…кажется нам одним из самых удивительных законов мира» (А.Кетле, 1911).
В настоящее время нормальное распределение широко используется в биологии, медицине, экономике и других областях науки.
Формула нормального распределения
Формула, описывающая нормальный закон распределения случайной величины, имеет следующий вид:
где: μ — генеральное среднее арифметическое; σ — генеральное стандартное отклонение, е — основание натуральных логарифмов, приблизительно равное 2,719, π — число, приблизительно равное 3,142; xi — конкретное значение признака.
Пусть Вас не пугает эта формула. Сейчас мы с ней разберемся. Для начала давайте посмотрим, как выглядит график, построенный на основе этой формулы. Зададим значения μ=0 и σ=1. Хочу заметить, что μ и σ — это просто числа. Их еще называют параметрами распределения. Поэтому критерии, в формулу расчета которых входят параметры распределения называют параметрическими. Например, параметрическим критерием является t-критерий Стьюдента. В формулу расчета критерия Стьюдента входят параметры μ и σ. Кривая нормального распределения вероятностей имеет вид (рис.2).
Рис.2. График плотности вероятностей нормального распределения при μ=0 и σ=1.
Если мы поменяем параметры, то получим следующее. Изменение параметра μ будет сдвигать график вдоль оси Х. Например при μ=3 график сместится вправо вдоль оси Х (рис.3).
Рис.3. График плотности вероятностей нормального распределения при μ=3 и σ=1.Если мы оставим μ=0 , а изменим параметр σ, например σ=3, то получим распределение с большим размахом (рис. 4).
4).
Свойства нормального распределения
- Нормальная кривая имеет колокообразную форму, симметричную относительно точки x=µ, с точками перегиба, абсциссы которых отстоят от µ на ± σ.
- Нормальное распределение полностью определятся двумя параметрами: значением генерального среднего (µ) и генерального стандартного отклонения (σ).
- Медиана и мода нормального распределения совпадают и равны µ.
- Коэффициенты асимметрии и эксцесса нормального распределения равны нулю.
Нормированное отклонение
В области математической статистики важное место занимает нормированное отклонение (t) – показатель, представляющий отклонение той или иной варианты от средней величины, отнесенное к значению стандартного отклонения. Нормированное отклонение рассчитывает по формуле:
Нормированное отклонение позволяет установить, на сколько «сигм» отклоняются варианты от среднего значения. Например, необходимо определить насколько «сигм» отклоняется значение роста человека, равное 180 см от среднего, если среднее арифметическое равно 170 см, а «сигма», то есть стандартное отклонение равно 10 см. Подставив эти значения в формулу, получим: t= (180-170)/10 = 1.
Например, необходимо определить насколько «сигм» отклоняется значение роста человека, равное 180 см от среднего, если среднее арифметическое равно 170 см, а «сигма», то есть стандартное отклонение равно 10 см. Подставив эти значения в формулу, получим: t= (180-170)/10 = 1.
Ответ: значение роста человека, равное 180 см отклоняется от среднего на одну «сигму».
Нормированное нормальное распределение
Рис.5. Нормированное нормальное распределение роста мужчин с параметрами: µ=0; σ = 1.Формула нормального распределения описывает целое семейство кривых, зависящих от двух параметров μ и σ, которые могут принимать любые значения. Поэтому возможно бесконечно много нормально распределенных совокупностей.
Чтобы избежать неудобств, связанных с расчетами для каждого конкретного случая в до компьютерную эпоху было предложено использовать нормированное (стандартное) нормальное распределение, для которого были составлены подробные таблицы. Нормированное нормальное распределение имеет параметры: µ=0; σ = 1 (рис. 1, 5). Это распределение получается, если пронормировать нормально распределенную величину Х по формуле: U= (X-μ)/σ.
1, 5). Это распределение получается, если пронормировать нормально распределенную величину Х по формуле: U= (X-μ)/σ.
Для нормированного нормального распределения характерно, что в интервал µ±σ попадают 68 % всех результатов, в интервал µ±2σ попадают 95% всех результатов, в интервал µ±3σ попадают 99 % всех результатов.
В области физической культуры и спорта эти закономерности используют для разработки системы оценок. Так, В.М. Зациорским (рис. 6) предложено использовать следующую систему оценок результатов. Если результат, показанный спортсменом, попал в интервал от -2σ до -1σ — он получает низкую оценку (Рассчитать, в какой интервал попадает результат можно при помощи нормированного отклонения. Это описано выше). Если результат попал в интервал от -1σ до -0,5σ — оценка ниже средней. Средний результат соответствует интервалу от -0,5σ до -0,5σ, результат, получивший оценку выше среднего — от 0,5 до 1σ. Высокий результат попадает в интервал от 1σ до 2σ.
Критерии согласия
Чтобы проверить, соответствует ли распределение нормальному закону, существует много методов.
Можно использовать свойства нормального распределения (равенство среднего, моды и медианы).
Однако более точные результаты дают критерии согласия. В зависимости от объема выборки (n) следует использовать различные критерии:
- если объем выборки небольшой (n = 10) – критерий Шапиро – Уилки;
- если объем выборки более 40 — критерий хи-квадрат и критерий Колмогорова-Смирнова.
- в статистическом пакете Statgraphics Centurion существует специальная опция — критерии проверки нормальности распределения. В этой опции есть 4 критерия, посредством которых можно сделать вывод о соответствии эмпирического распределения нормальному закону.
Литература
- Высшая математика и математическая статистика: учебное пособие для вузов / Под общ.
 ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с. - Гласс Дж., Стенли Дж. Статистические методы в педагогике и психологии.- М.: Прогресс, 1976.-495 с.
- Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
- Кетле А. (1835) Социальная физика, или опыт исследования о развитии человеческих способностей. Т.1, 1911.- С. 38-39.
- Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.
“История одного обмана” или “Требования к распределению в t-тесте” | by Stats&Data ninja
Почему все говорят, что для t-критерия нужны нормальные данные??
Последний год я прособеседовал несколько десятков аналитиков, и каждый раз при ответе на казалось бы простой вопрос я получал столько же простой, но неверный ответ.
Обычно я спрашивал примерно так: “В каких ситуациях (тип метрики, ее распределение) какой стат-тест будешь использовать?”.
Большинство аналитиков отвечало (спойлер: неправильно 😩): “В случае нормального распределения у метрики стоит использовать t-test, в обратном случае — тест Манна-Уитни (U-критерий)”.
Если зайти на википедию, то увидим что она также врет (по крайней мере на момент написания статьи). Игнорирование факта, что это ложь, может принести вред бизнесу — об этим ниже есть специальный раздел.
Хороший вопрос: откуда пошло заблуждение про нормальность выборок? Я решил поизучать его 🕵🏻♂️. Например, если мы откроем на вики английскую версию статьи про t-критерий, то во втором абзаце увидим правильные слова (под статистикой там подразумевается среднее по выборке) ❤:
A t-test is the most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known.
When the scaling term is unknown and is replaced by an estimate based on the data, the test statistics (under certain conditions) follow a Student’s t distribution.
Обратимся к оригинальной статье Стьюдента. Госсет (реальное имя Стьюдента) говорит, что в экспериментах всегда 2 неизвестные сущности — форма распределения и ее параметры (например, среднее). На малых выборках форму распределения понять сложно, поэтому Студент предполагает что лучше считать его нормальным. При этом, он использует формулу для доверительного интервала выборочного среднего (ЦПТ), и не говорит, что выборка обязательно должна быть из нормального распределения. Доказательство текущего нестрогого вида ЦПТ (через теорему Леви) появилось уже позже, возможно именно поэтому в статье вообще говорится про нормальность выборок.
Картинка 1. Скриншот из статьи на википедии про t-тестА вот статья про t-тест на русской википедии гласит, как показано слева (на момент написания статьи). Скорее всего, это неверный перевод с английской версии статьи — перепутали выборку и статистику. В тексте про критерий Уэлча (мы поговорим про него ниже) также допущена эта ошибка. BTW, в английской версии статьи про t-распределение (не про критерий) также допущена ошибка про нормальность данных. Источник номер раз — вики!
Скорее всего, это неверный перевод с английской версии статьи — перепутали выборку и статистику. В тексте про критерий Уэлча (мы поговорим про него ниже) также допущена эта ошибка. BTW, в английской версии статьи про t-распределение (не про критерий) также допущена ошибка про нормальность данных. Источник номер раз — вики!
Карпов в своем курсе сказал, что в случае размера выборок меньше 30 данные должны быть нормальными. И, хотя при больших выборках сказано, что нормальность необязательна, а в блоке про ЦПТ отдельным шагом показано, что распределение может быть любым, все же это может быть источником №2. Но Карпову респект 💕.
На вполне достоверном сайте machinelearning.ru также неверно указано это требование (источник №3). Известный русско-язычный блог про R — источник №4.
Ну и конечно я не ожидал оплошностей от основателей ExpF 😭 (источник №5). В этой статье (на медиуме она кстати уже удалена), хотя посыл и выводы верные, есть следующие неточности:
- “Но мы не можем его использовать на изначальных данных.
 Ненормальное распределение даст большой дисбаланс в среднее и шум (дисперсия) сделает неточным результат применения критерия” — сам t-критерий устроен так, что всегда даст точный результат (FPR при верной H0), и уровень дисперсии может оказать влияние разве что на чувствительность.
Ненормальное распределение даст большой дисбаланс в среднее и шум (дисперсия) сделает неточным результат применения критерия” — сам t-критерий устроен так, что всегда даст точный результат (FPR при верной H0), и уровень дисперсии может оказать влияние разве что на чувствительность. - “данные далеки от нормального распределения, следовательно, посчитать на нем среднее значение проблемно — очень сильно влияет длинный хвост из значений” — это совсем непонятное выражение, т.к. среднее значение — это детерминированная функция, и длина хвоста на нее не влияет, тем более если форма распределения исторически одна и та же.
Чтобы ответить на этот вопрос, давай поймем, как вообще работает t-критерий (критерий Стьюдента).
Большинство стат-тестов работает так — рассчитывает по выборке статистику (в узком смысле статистика это любая функция, которая переводит выборку в скаляр, например: среднее, максимальный элемент или средне-квадратичная ошибка) и сравнивает его с табличными значениями. Чтобы определить стат-значимость, нужно заранее понимать форму распределения этой статистики и уметь считать для каждой точки этого распределения соотвествующий p-value (площадь под графиком от точки до конца распределения ко всей площади ).
Чтобы определить стат-значимость, нужно заранее понимать форму распределения этой статистики и уметь считать для каждой точки этого распределения соотвествующий p-value (площадь под графиком от точки до конца распределения ко всей площади ).
В случае стандартного нормального распределения статистики (среднее 0, дисперсия 1): p-value = 0.05 при z-статистике равной 1.96. T-критерий назван так потому, что использует t-распределение статистики. Отличие от z-теста в том, что t-распределение принимает еще 1 параметр — степень свободы.
Допустим наша метрика — доход с пользователя за период. Нас, как бизнес, в основном интересует среднее (ARPU) значение этой метрики, потому что именно оно участвует в бизнес-моделях и юнит-экономике. Так вот, значения поюзерной метрики (user revenue в нашем случае) — это выборка, а ее среднее (ARPU) — это как раз статистика. Что мы можем сказать о распределении ARPU?
Доходы пользователей — случайные величины из одного и того же распределения, необязательно нормального. При условии, что пользователи независимы, существует центральная предельная теорема, говорящая нам о том, что среднее значение метрики по достаточно большой выборке пользователей будет иметь нормальное распределение. Именно это и использует z-критерий (сравнивая значения z-оценки с точками на этом распределении), и именно распределение средних и должно быть нормальным для t-теста. Это важный результат, который стоит помнить:
При условии, что пользователи независимы, существует центральная предельная теорема, говорящая нам о том, что среднее значение метрики по достаточно большой выборке пользователей будет иметь нормальное распределение. Именно это и использует z-критерий (сравнивая значения z-оценки с точками на этом распределении), и именно распределение средних и должно быть нормальным для t-теста. Это важный результат, который стоит помнить:
Никакого условия на распределение самой метрики в ЦПТ нет, поэтому не стоит требовать нормальность от для входные данных z- и t-тестов.
Как теперь свести полученный результат к t-критерию? В z-статистике в знаменателе используется стандартная ошибка среднего, рассчитанная через стандартное отклонение генеральной совокупности, которое мы на самом деле не знаем. Однако, мы можем оценить его по выборке через среднеквадратичное отклонение. Распределение полученной статистики и является распределением Стьюдента (об этом рассказывал еще Карпов в своем курсе статистики). В целом, оно очень похоже на нормальное распределение, но с чуть более широкими хвостами (увеличение дисперсии как раз объясняется тем, что вместо известного параметры мы подставляем его выборочную оценку).
Распределение полученной статистики и является распределением Стьюдента (об этом рассказывал еще Карпов в своем курсе статистики). В целом, оно очень похоже на нормальное распределение, но с чуть более широкими хвостами (увеличение дисперсии как раз объясняется тем, что вместо известного параметры мы подставляем его выборочную оценку).
Как мы уже выяснили, нормальным должно быть распределение среднего значения метрики в группе. Стоп-стоп, что❓❓ Среднее это же одно число, какое распределение❗❓
Код 1. Проверка распределения выборочного среднегоДа, среднее — это случайная величина, посчитанная лишь по выборке от всех возможных пользователей. Если через какое-то время взять другую выборку (новые пользователи), или даже для тех же пользователей посчитать среднее еще раз, оно окажется отличным. Каждый раз оно семплируется из неизвестного распределения, и мы лишь делаем догадки о его форме в случае ЦПТ (и t-теста). Если мы не знаем, можем ли считать его нормальным, то можем оценить это по одной нашей выборке, превратив ее во много выборок и посчитав среднее для всех. Так мы получим распределение, предполагая, что оно примерное совпадает с распределением среднего генеральной совокупности. Этот метод и называется бутстрап, код для него слева в gist’е.
Так мы получим распределение, предполагая, что оно примерное совпадает с распределением среднего генеральной совокупности. Этот метод и называется бутстрап, код для него слева в gist’е.
Вопрос, который может возникнуть — а как такое может быть, ведь согласно ЦПТ распределение должно стремиться к нормальному? На самом деле существует много факторов, благодаря которым такое может случиться, но два из них основные. Во-первых, ЦПТ требует чтобы все значения в выборке были i.i.d., т.е. одинаковы и независимо распределены. В случае сетевого эффекта, наши юниты (например пользователи) будут влиять друг на друга, соответственно предположения будут нарушены.
Во-вторых, ЦПТ это асимптотический метод, для формального равенства требуется бесконечно большая выборка, чего не встретишь в реальных задачах. Поэтому такая проблема может воспроизвестись на малых выборках (видимо именно это имел ввиду Карпов). Кстати, в той же статье Госсет поднимал вопрос о границах малой и большой выборок, чтобы считать среднее нормально распределенным.
Самое интересное в статье — это размеры выборок. Он брал 3000 измерений пальцев преступников. Далее делил их на 750 выборок по 4 элемента, внутри каждой выборки считал среднее и смотрел, как эти 750 значений распределены вокруг реального среднего (по всем 3000 измерениям). Нет, тут нет опечатки. Он правда использовал выборки по четыре юнита. Даже на таких выборках можно работать с t-критерием!
Важно найти, на каком размере выборок именно в твоих задачах и метриках распределение выборочного среднего становится похожим на нормальное. Скорость схождения к нормальному распределению описывается через неравенство Берри — Эссеена (расстояние убывает обратно-пропорционально корню из размера выборки). Так что если выборка не удовлетворяет требованиям t-теста и хочется увеличить ее размер, лучше сразу делать это на пару порядков.
Тест Манна-Уитни учит делать тот же Карпов. И в статье на вики про t-тест написано следующее: “При несоблюдении этих условий [нормальность выборок] при сравнении выборочных средних должны использоваться аналогичные методы непараметрической статистики, среди которых наиболее известными являются U-критерий Манна — Уитни” .
Давай подробнее разберем, почему я считаю его почти неприменимым (точнее применимым лишь для небольшого типа задач). Во-первых, если ты хочешь один тест на все случаи в жизни, тебе стоит знать что на тех же нормальных данных он менее мощный чем t-критерий (правда несильно, на 5%). Это грозит бизнесу найти меньше возможностей.
Во-вторых, сам тест не всегда робастен и точен относительно p-value (ошибки первого рода). Если распределение состоит из большого количества повторяющихся значений (и еще во многих кейсах), то это критерий сходит с ума и выдает весьма странные результаты.
В-третьих, есть важный момент, который кстати указали в своей статье ExpF (и Карпов на Матемаркетинге — выбросы могут быт неслучайны (это можно проверить на исторических данных), и в таком случае удалять их нельзя! Если удалить, можно посчитать положительным тест с отрицательным в реальности эффектом на средний чек. Например, предположим что у нас половина клиентов нам не платят, а верхний персентиль имеет средний чек в несколько миллионов. Если в таргетной группе мы сменим нижняя половина начнет нам приносить по 1 рубля, а в верхнем персентиле AOV упадет в несколько раз, то скорее всего средний доход упадет. При этом, при удалении верхнего персентиля как выбросы, мы получим положительный эффект в тесте.
Если в таргетной группе мы сменим нижняя половина начнет нам приносить по 1 рубля, а в верхнем персентиле AOV упадет в несколько раз, то скорее всего средний доход упадет. При этом, при удалении верхнего персентиля как выбросы, мы получим положительный эффект в тесте.
Ну и главное — как объяснить бизнесу результаты критерия? Он сравнивает то, что сравнивает. Т.е. не среднее и не медиану, как многие думают, а ранги в объединенной выборке. Можно придумать примеры, когда эти ранги могут быть разнонаправленными со средними значениями. Какой в таком случае репортить аплифт? Это же касается и любых трансформаций данных, таких как логарифмирование, Бокс-Кокс и тд.
Кстати, многие используют непараметрические критерии в анализе, при этом считают sample size/MDE/мощность через формулу для t-теста. Так конечно же делать нельзя, ведь считать данные величины нужно способом, соответствующим используемому при анализе методу расчета значимости. Например, можно использовать бутстрап из библиотеки от facebook.
В отличие от нормальности выборок, у t-критерия есть гораздо более важные требования к распределениям. Например, неравенство дисперсий в двух выборках (несоблюдения гомогенности). Давай наглядно продемонстрирую тебе.
Картинка 3. Вывод для t-распределенияДля одной выборки t-критерий выглядит так, как показано на картинке в первой формуле. На самом деле это не совсем t-распределение, поскольку в классическом варианте оно обязует и числитель, и каждый член суммы в знаменателе (дисперсия — это сумма) иметь стандартное нормально распределение N(0,1). Чтобы его получить, во второй формуле мы делим и числитель, и знаменатель на фактор масштаба (обрати внимание, в нем используется неизвестный параметр дисперсии генеральной совокупности, а не выборочное SE, но это не важно).
Теперь рассмотрим кейс сравнения средних двух выборок. В общем случае после деления на фактор масштаба каждое из слагаемых в среднеквадратичном отклонении не стандартизируется, соотвественно распределение знаменателя уже не Хи-квадрат. И если в случае равных размеров выборки мы можем использовать pooled variance объединенной выборки (тем самым свести это к кейсу одной выборки), то при неравных дисперсиях и размеров выборки мы получаем проблему Беренца-Фишера, которая до недавнего времени считалась нерешаемой в строгом виде. Потом решение нашли, но оно малопопулярное и сложное и все используют способ, описанный ниже.
И если в случае равных размеров выборки мы можем использовать pooled variance объединенной выборки (тем самым свести это к кейсу одной выборки), то при неравных дисперсиях и размеров выборки мы получаем проблему Беренца-Фишера, которая до недавнего времени считалась нерешаемой в строгом виде. Потом решение нашли, но оно малопопулярное и сложное и все используют способ, описанный ниже.
Стандартом для таких кейсов является тест Уэлча (на картинке слева), идея которого проста — дисперсия разницы равна сумме дисперсий. А вот степень свободы для такого теста называет pooled sample size и считается (найдешь по ссылке выше) по сложной формуле , о которой стоит знать следующее — она возвращает нецелую cлучайную величину, к чему t-распределение конечно не готово. Но все же, тест Уэлча отдает вполне релевантные результаты, и можно по дефолту использовать его в независимости от размеров выборок и дисперсий (это лучше, чем вначале делать тест на гомогенность для выборка между критериями Сьюдента и Уэлча). К сожалению, иногда этот тест сильно неточен, особенно если большая по размеру выборка имеет меньшую дисперсию.
К сожалению, иногда этот тест сильно неточен, особенно если большая по размеру выборка имеет меньшую дисперсию.
Надеюсь, ты и так это знаешь, но в зависимых выборках используется другая дисперсия (разностей для каждой пары).
На самом деле, в отличии от Стъюдента, некоторые статистические тесты действительно требуют нормальное распределение данных. Например, в проверке гомогенности дисперсий, которую упоминал в прошлом разделе📊. Используемый тут и в регрессиях F-тест требует нормальности. Как и t-тест, он также имеет непараметрические альтернативы (тест Левена и тест Бартлетта), которые также имеют свои недостатки. Требующая нормальности выборок ANOVA не так чувствительна к нарушению этого правила, но все же имеет слегка завышенный FPR в этом случае.
Как ты уже понял, существует правило ✍️: если распределение удовлетворяет условиям наиболее строгих параметрических тестов (кстати обычно они самые простые в вычислении и интерпретации), то лучше использовать именно их.
Регрессия требует нормальности лишь для остатков, а это может выполняться при любом распределении зависимых и независимых переменных (более того, форма распределения никак не влияет на нормальность остатков) при условии выполнения других пунктов из теоремы Гаусса-Маркова. Проще можно объяснить это условие так — Y должен быть нормальным на каждом уровне X.
Проще можно объяснить это условие так — Y должен быть нормальным на каждом уровне X.
А вот дов-интервалы и стат-значимости коэффициентов регрессии можно посчитать только при нормальных выборках (об этом будет отдельная статья).
Напоследок, держи эту статью. И до скорых (возможно очень) встреч!
Проверка гипотезы о нормальном распределении по критерию Пирсона. Подробный пример решения
Критерий согласия Пирсона:Проверить гипотезу о нормальном распределении по критерию Пирсона. Уровень значимости α=0.05. Данные разбить на 6 интервалов.
Решение находим с помощью калькулятора. Ширина интервала составит:
Xmax — максимальное значение группировочного признака в совокупности.
Xmin — минимальное значение группировочного признака.
Определим границы группы.
| Номер группы | Нижняя граница | Верхняя граница |
| 1 | 43 | 45. 83 83 |
| 2 | 45.83 | 48.66 |
| 3 | 48.66 | 51.49 |
| 4 | 51.49 | 54.32 |
| 5 | 54.32 | 57.15 |
| 6 | 57.15 | 60 |
Одно и тоже значение признака служит верхней и нижней границами двух смежных (предыдущей и последующей) групп.
Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
| 43 | 43 — 45.83 | 1 |
| 48.5 | 45.83 — 48.66 | 1 |
| 49 | 48.66 — 51.49 | 1 |
| 49 | 48.66 — 51.49 | 2 |
| 49.5 | 48.66 — 51.49 | 3 |
| 50 | 48.66 — 51.49 | 4 |
| 50 | 48.66 — 51.49 | 5 |
| 50.5 | 48.66 — 51.49 | 6 |
| 51.5 | 51.49 — 54.32 | 1 |
51. 5 5 | 51.49 — 54.32 | 2 |
| 52 | 51.49 — 54.32 | 3 |
| 52 | 51.49 — 54.32 | 4 |
| 52 | 51.49 — 54.32 | 5 |
| 52 | 51.49 — 54.32 | 6 |
| 52 | 51.49 — 54.32 | 7 |
| 52 | 51.49 — 54.32 | 8 |
| 52 | 51.49 — 54.32 | 9 |
| 52.5 | 51.49 — 54.32 | 10 |
| 52.5 | 51.49 — 54.32 | 11 |
| 53 | 51.49 — 54.32 | 12 |
| 53 | 51.49 — 54.32 | 13 |
| 53 | 51.49 — 54.32 | 14 |
| 53.5 | 51.49 — 54.32 | 15 |
| 54 | 51.49 — 54.32 | 16 |
| 54 | 51.49 — 54.32 | 17 |
| 54 | 51.49 — 54.32 | 18 |
| 54.5 | 54.32 — 57.15 | 1 |
| 54.5 | 54.32 — 57.15 | 2 |
55. 5 5 | 54.32 — 57.15 | 3 |
| 57 | 54.32 — 57.15 | 4 |
| 57.5 | 57.15 — 59.98 | 1 |
| 57.5 | 57.15 — 59.98 | 2 |
| 58 | 57.15 — 59.98 | 3 |
| 58 | 57.15 — 59.98 | 4 |
| 58.5 | 57.15 — 59.98 | 5 |
| 60 | 57.15 — 59.98 | 6 |
| Группы | № совокупности | Частота fi |
| 43 — 45.83 | 1 | 1 |
| 45.83 — 48.66 | 2 | 1 |
| 48.66 — 51.49 | 3,4,5,6,7,8 | 6 |
| 51.49 — 54.32 | 9,10,11,12,13,14,15, 16,17,18,19,20,21, 22,23,24,25,26 | 18 |
| 54.32 — 57.15 | 27,28,29,30 | 4 |
| 57.15 — 59.98 | 31,32,33,34,35,36 | 6 |

| Группы | xi | Кол-во, fi | xi * fi | Накопленная частота, S | |x — xср|*f | (x — xср)2*f | Частота, fi/n |
| 43 — 45.83 | 44.42 | 1 | 44.42 | 1 | 8.88 | 78.91 | 0.0278 |
| 45.83 — 48.66 | 47.25 | 1 | 47.25 | 2 | 6.05 | 36.64 | 0.0278 |
| 48.66 — 51.49 | 50.08 | 6 | 300.45 | 8 | 19.34 | 62.33 | 0.17 |
| 51.49 — 54.32 | 52.91 | 18 | 952.29 | 26 | 7.07 | 2.78 | 0.5 |
| 54.32 — 57.15 | 55.74 | 4 | 222.94 | 30 | 9.75 | 23.75 | 0.11 |
| 57.15 — 59.98 | 58.57 | 6 | 351.39 | 36 | 31.6 | 166.44 | 0.17 |
| 36 | 1918. 73 73 | 82.7 | 370.86 | 1 |
Показатели центра распределения.
Средняя взвешенная
Мода
Мода — наиболее часто встречающееся значение признака у единиц данной совокупности.
где x0 – начало модального интервала; h – величина интервала; f2 –частота, соответствующая модальному интервалу; f1 – предмодальная частота; f3 – послемодальная частота.
Выбираем в качестве начала интервала 51.49, так как именно на этот интервал приходится наибольшее количество.
Наиболее часто встречающееся значение ряда – 52.8
Медиана
Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше.
В интервальном ряду распределения сразу можно указать только интервал, в котором будут находиться мода или медиана. Медиана соответствует варианту, стоящему в середине ранжированного ряда.
 Медианным является интервал 51.49 — 54.32, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).
Медианным является интервал 51.49 — 54.32, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).Таким образом, 50% единиц совокупности будут меньше по величине 53.06
Показатели вариации.
Абсолютные показатели вариации.
Размах вариации — разность между максимальным и минимальным значениями признака первичного ряда.
R = Xmax — Xmin
R = 60 — 43 = 17
Среднее линейное отклонение — вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности.
Каждое значение ряда отличается от другого не более, чем на 2.3
Дисперсия — характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
Несмещенная оценка дисперсии — состоятельная оценка дисперсии.
Среднее квадратическое отклонение.
Каждое значение ряда отличается от среднего значения 53.
 3 не более, чем на 3.21
3 не более, чем на 3.21Оценка среднеквадратического отклонения.
Относительные показатели вариации.
К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение.
Коэффициент вариации — мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.
Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять.
Линейный коэффициент вариации или Относительное линейное отклонение — характеризует долю усредненного значения признака абсолютных отклонений от средней величины.
Проверка гипотез о виде распределения.
1. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.
где pi — вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону
Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа
где s = 3.
 21, xср = 53.3
21, xср = 53.3Теоретическая (ожидаемая) частота равна ni = npi, где n = 36
| Интервалы группировки | Наблюдаемая частота ni | x1 = (xi-x)/s | x2 = (xi+1-x)/s | Ф(x1) | Ф(x2) | Вероятность попадания в i-й интервал, pi = Ф(x2) — Ф(x1) | Ожидаемая частота, 36pi | Слагаемые статистики Пирсона, Ki |
| 43 — 45.83 | 1 | -3.16 | -2.29 | -0.5 | -0.49 | 0.01 | 0.36 | 1.14 |
| 45.83 — 48.66 | 1 | -2.29 | -1.42 | -0.49 | -0.42 | 0.0657 | 2.37 | 0.79 |
| 48.66 — 51.49 | 6 | -1.42 | -0.56 | -0.42 | -0.21 | 0.21 | 7.61 | 0.34 |
| 51.49 — 54.32 | 18 | -0.56 | 0. 31 31 | -0.21 | 0.13 | 0.34 | 12.16 | 2.8 |
| 54.32 — 57.15 | 4 | 0.31 | 1.18 | 0.13 | 0.38 | 0.26 | 9.27 | 3 |
| 57.15 — 59.98 | 6 | 1.18 | 2.06 | 0.38 | 0.48 | 0.0973 | 3.5 | 1.78 |
| 36 | 9.84 |
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения χ2 и заданным значениям s, k (число интервалов), r=2 (параметры xcp и s оценены по выборке).

Kkp = 7.81473; Kнабл = 9.84
Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл > Kkp, поэтому есть основания отвергать основную гипотезу. Данные выборки распределены не по нормальному закону.
Перейти к онлайн решению своей задачи
Пример №2. Используя критерий Пирсона, при уровне значимости 0.05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X с эмпирическим распределением выборки объема n = 200.
Решение находим с помощью калькулятора.
Таблица для расчета показателей.
| xi | Кол-во, fi | xi·fi | Накопленная частота, S | (x-x)·f | (x-x)2·f | (x-x)3·f | Частота, fi/n |
| 5 | 15 | 75 | 15 | 114.45 | 873.25 | -6662.92 | 0. 075 075 |
| 7 | 26 | 182 | 41 | 146.38 | 824.12 | -4639.79 | 0.13 |
| 9 | 25 | 225 | 66 | 90.75 | 329.42 | -1195.8 | 0.13 |
| 11 | 30 | 330 | 96 | 48.9 | 79.71 | -129.92 | 0.15 |
| 13 | 26 | 338 | 122 | 9.62 | 3.56 | 1.32 | 0.13 |
| 15 | 21 | 315 | 143 | 49.77 | 117.95 | 279.55 | 0.11 |
| 17 | 24 | 408 | 167 | 104.88 | 458.33 | 2002.88 | 0.12 |
| 19 | 20 | 380 | 187 | 127.4 | 811.54 | 5169.5 | 0.1 |
| 21 | 13 | 273 | 200 | 108.81 | 910.74 | 7622.89 | 0.065 |
| 200 | 2526 | 800.96 | 4408.62 | 2447.7 | 1 |

Средняя взвешенная
Показатели вариации.
Абсолютные показатели вариации.
Размах вариации — разность между максимальным и минимальным значениями признака первичного ряда.
R = Xmax — Xmin
R = 21 — 5 = 16
Дисперсия — характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
Несмещенная оценка дисперсии — состоятельная оценка дисперсии.
Среднее квадратическое отклонение.
Каждое значение ряда отличается от среднего значения 12.63 не более, чем на 4.7
Оценка среднеквадратического отклонения.
Проверка гипотез о виде распределения.
1. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.
где n*i — теоретические частоты:
Вычислим теоретические частоты, учитывая, что:
n = 200, h=2 (ширина интервала), σ = 4.
 7, xср = 12.63
7, xср = 12.63| i | xi | ui | φi | n*i |
| 1 | 5 | -1.63 | 0,1057 | 9.01 |
| 2 | 7 | -1.2 | 0,1942 | 16.55 |
| 3 | 9 | -0.77 | 0,2943 | 25.07 |
| 4 | 11 | -0.35 | 0,3752 | 31.97 |
| 5 | 13 | 0.0788 | 0,3977 | 33.88 |
| 6 | 15 | 0.5 | 0,3503 | 29.84 |
| 7 | 17 | 0.93 | 0,2565 | 21.85 |
| 8 | 19 | 1.36 | 0,1582 | 13.48 |
| 9 | 21 | 1.78 | 0,0804 | 6.85 |
Χ2=
| i | ni | n*i | ni-n*i | (ni-n*i)2 | (ni-n*i)2/n*i |
| 1 | 15 | 9. 01 01 | -5.99 | 35.94 | 3.99 |
| 2 | 26 | 16.55 | -9.45 | 89.39 | 5.4 |
| 3 | 25 | 25.07 | 0.0734 | 0.00539 | 0.000215 |
| 4 | 30 | 31.97 | 1.97 | 3.86 | 0.12 |
| 5 | 26 | 33.88 | 7.88 | 62.14 | 1.83 |
| 6 | 21 | 29.84 | 8.84 | 78.22 | 2.62 |
| 7 | 24 | 21.85 | -2.15 | 4.61 | 0.21 |
| 8 | 20 | 13.48 | -6.52 | 42.53 | 3.16 |
| 9 | 13 | 6.85 | -6.15 | 37.82 | 5.52 |
| ∑ | 200 | 200 | 22.86 |

Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения «хи-квадрат» и заданным значениям σ, k = 9, r=2 (параметры xcp и σ оценены по выборке).
Kkp(0.05;6) = 12.59159; Kнабл = 22.86
Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл > Kkp, поэтому есть основания отвергать основную гипотезу. Данные выборки распределены не по нормальному закону. Другими словами, эмпирические и теоретические частоты различаются значимо.
Пример 2. Используя критерий Пирсона, при уровне значимости 0.05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X с эмпирическим распределением выборки объема n = 200.
Решение.
Таблица для расчета показателей.
| xi | Кол-во, fi | xi·fi | Накопленная частота, S | (x-x)·f | (x-x)2·f | (x-x)3·f | Частота, fi/n |
0. 3 3 | 6 | 1.8 | 6 | 5.77 | 5.55 | -5.34 | 0.03 |
| 0.5 | 9 | 4.5 | 15 | 6.86 | 5.23 | -3.98 | 0.045 |
| 0.7 | 26 | 18.2 | 41 | 14.61 | 8.21 | -4.62 | 0.13 |
| 0.9 | 25 | 22.5 | 66 | 9.05 | 3.28 | -1.19 | 0.13 |
| 1.1 | 30 | 33 | 96 | 4.86 | 0.79 | -0.13 | 0.15 |
| 1.3 | 26 | 33.8 | 122 | 0.99 | 0.0375 | 0.00143 | 0.13 |
| 1.5 | 21 | 31.5 | 143 | 5 | 1.19 | 0.28 | 0.11 |
| 1.7 | 24 | 40.8 | 167 | 10.51 | 4.6 | 2.02 | 0.12 |
| 1.9 | 20 | 38 | 187 | 12.76 | 8.14 | 5.19 | 0.1 |
| 2.1 | 8 | 16.8 | 195 | 6. 7 7 | 5.62 | 4.71 | 0.04 |
| 2.3 | 5 | 11.5 | 200 | 5.19 | 5.39 | 5.59 | 0.025 |
| 200 | 252.4 | 82.3 | 48.03 | 2.54 | 1 |
Средняя взвешенная
Показатели вариации.
Абсолютные показатели вариации.
Размах вариации — разность между максимальным и минимальным значениями признака первичного ряда.
R = Xmax — Xmin
R = 2.3 — 0.3 = 2
Дисперсия — характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
Несмещенная оценка дисперсии — состоятельная оценка дисперсии.
Среднее квадратическое отклонение.
Каждое значение ряда отличается от среднего значения 1.26 не более, чем на 0.49
Оценка среднеквадратического отклонения.

Проверка гипотез о виде распределения.
1. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.
где n*i — теоретические частоты:
Вычислим теоретические частоты, учитывая, что:
n = 200, h=0.2 (ширина интервала), σ = 0.49, xср = 1.26
| i | xi | ui | φi | n*i |
| 1 | 0.3 | -1.96 | 0,0573 | 4.68 |
| 2 | 0.5 | -1.55 | 0,1182 | 9.65 |
| 3 | 0.7 | -1.15 | 0,2059 | 16.81 |
| 4 | 0.9 | -0.74 | 0,3034 | 24.76 |
| 5 | 1.1 | -0.33 | 0,3765 | 30.73 |
| 6 | 1.3 | 0.0775 | 0,3977 | 32.46 |
| 7 | 1.5 | 0.49 | 0,3538 | 28.88 |
| 8 | 1. 7 7 | 0.89 | 0,2661 | 21.72 |
| 9 | 1.9 | 1.3 | 0,1691 | 13.8 |
| 10 | 2.1 | 1.71 | 0,0909 | 7.42 |
| 11 | 2.3 | 2.12 | 0,0422 | 3.44 |
Χ2=
| i | ni | n*i | ni-n*i | (ni-n*i)2 | (ni-n*i)2/n*i |
| 1 | 6 | 4.68 | -1.32 | 1.75 | 0.37 |
| 2 | 9 | 9.65 | 0.65 | 0.42 | 0.0435 |
| 3 | 26 | 16.81 | -9.19 | 84.53 | 5.03 |
| 4 | 25 | 24.76 | -0.24 | 0.0555 | 0.00224 |
| 5 | 30 | 30. 73 73 | 0.73 | 0.53 | 0.0174 |
| 6 | 26 | 32.46 | 6.46 | 41.75 | 1.29 |
| 7 | 21 | 28.88 | 7.88 | 62.07 | 2.15 |
| 8 | 24 | 21.72 | -2.28 | 5.2 | 0.24 |
| 9 | 20 | 13.8 | -6.2 | 38.41 | 2.78 |
| 10 | 8 | 7.42 | -0.58 | 0.34 | 0.0454 |
| 11 | 5 | 3.44 | -1.56 | 2.42 | 0.7 |
| ∑ | 200 | 200 | 12.67 |
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения «хи-квадрат» и заданным значениям σ, k = 11, r=2 (параметры xcp и σ оценены по выборке).

Kkp(0.05;8) = 15.50731; Kнабл = 12.67
Наблюдаемое значение статистики Пирсона не попадает в критическую область: Кнабл нормальное распределение.
Параметрические критерии проверки статистических гипотез
Наиболее распространенным параметрическим критерием является критерий t-Стъюдента. Его используют для проверки гипотезы о равенстве двух генеральных средних. Как видно из рисунка 18, две выборки могут быть извлечены из одной генеральной совокупности и в этом случае у выборочных средних одна общая генеральная средняя, или же эти выборки принадлежат разным совокупностям и, следовательно, генеральные средние отличаются.
Рисунок 18. Гипотезы о равенстве
Критерий Стъюдента можно использовать при условии, если
Несоблюдение этих условий может привести к некорректным результатам.
СЛУЧАЙ 1. Выборки независимые.
В этом случае нулевая гипотеза Н(0) звучит так:
две генеральные средние равны
или — две выборки извлечены из одной генеральной совокупности
или — две совокупности имеют одинаковое распределение
В
медицинских задачах гипотеза может
быть сформулирована, например, таким
образом: содержание гемоглобина у
городских и сельских жителей одинаково
(подразумевая, что одинаково его
распределение).
Проверяемый t-критерий вычисляется по формуле
(11)
где – выборочные средние
m1, m2 — стандартные ошибки средних значений сравниваемых выборок.
Находим по таблице tкритдля заданного α и числа степеней свободы
f =n1 + n2 – 2 (12)
Если │tвыч │< tкрит то принимается Н(0) (нет аргументов, чтобы ее отвергнуть)
Если │ tвыч│≥ tкрит то принимается Н(1) и делается заключение
о наличии статистически значимых
различий между генеральными средними
значениями на соответствующем уровне
значимости.
Условие равенства двух генеральных дисперсий проверяется по критерию Фишера, который равен отношению большей выборочной дисперсии к меньшей:
(13)
Fкрит находится по таблице (Приложение 7) для заданного α и числа степеней свободы
f1=n1-1 и f2=n2-1 (14)
Если Fвыч≥ Fкрит , то гипотеза о равенстве генеральных дисперсий отвергается
Если Fвыч< Fкрит, то принимается нулевая гипотеза о равенстве.
Пример. По данным из таблицы 14 определить,
отличается ли при себорее содержание
связанного холестерина крови (мг%) от
нормы, если известно, что концентрация
холестерина имеет нормальное
распределение, а дисперсии в двух
совокупностях одинаковы. Таблица 14. Данные к примеру
Решение: Вычислим средние значения для двух выборок: Несмотря на то,
что две выборочные средние отличаются,
не исключена возможность, что генеральные
средние равны. Н(0): среднее значение связанного холестерина в крови при себорее не отличается от нормы Н(1): среднее значение связанного холестерина в крови при себорее отличается от нормы Гипотезы будем проверять на уровне значимости α=0,05. Результаты вычислений представлены в таблице 15. Таблица15. Итоги проверки гипотезы
Определим Fкрит по таблице (Приложение 7) для f1=8 и f2=7 Fкрит=3,73 Т. Определим tкрит для α=0,05 и числа степеней свободы в двух группах f=n1+n2-2=9+8-2=15 Из таблицы (Приложение 2) получаем двусторонний tкрит=2,13 т.к.│tвыч│> tкрит (20,8>2,13) – то принимается альтернативная гипотеза. Вывод: Содержание связанного холестерина в крови при себорреи статистически значимо отличается от нормы с вероятностью не менее 95%. |
СЛУЧАЙ 2. Выборки зависимые
Для сравнения
двух зависимых выборок или выборок с
попарно связанными вариантами проверяют гипотезу
о равенстве нулю среднего значения их попарных
разностей. Такая задача возникает, когда имеются
данные об изменении интересующего
признака у каждого пациента. Например,
если группа пациентов получала изучаемый
метод лечения, и у каждого пациента
измерялось значение признака до и после
лечения. В данном случае предстоит
проверить нулевую гипотезу о равенстве
нулю изменений этого признака в результате
получения терапии.
Такая задача возникает, когда имеются
данные об изменении интересующего
признака у каждого пациента. Например,
если группа пациентов получала изучаемый
метод лечения, и у каждого пациента
измерялось значение признака до и после
лечения. В данном случае предстоит
проверить нулевую гипотезу о равенстве
нулю изменений этого признака в результате
получения терапии.
При подобных исследованиях все наблюдения можно представить в виде n-пар измерений (например, до и после)
Для каждой пары вычисляется разность di, где i=1, n
Для полученного ряда вычисляется среднее и среднеквадратичное отклонение
Далее вычисляется значение критерия Стъюдента
(15)
Проверка гипотезы
производится по таблицам распределения
Стьюдента (Приложение
2) для
выбранного уровня значимости и числа
степеней свободы f=
п-1.
Если │tвыч │< tкрит то принимается Н(0)
Если │ tвыч│≥ tкрит то принимается Н(1) и делается заключение о наличии статистически значимых различий между генеральными средними значениями «до» и «после».
Пример. В группе из 6 человек изучалось влияние пробежки на ЧСС (уд/мин). В результате опыта получилось 2 ряда ЧСС: первый – до пробежки, второй – после пробежки: Таблица 16. ЧСС до и после пробежки
Изменяется
ли ЧСС после пробежки? Необходимо
оценить статистическую значимость
полученных результаты, если известно,
что ЧСС имеет нормальное распределение. Для наглядности представим данные в следующей таблице 17: Таблица 17. Изменения ЧСС x1i(до пробежки) х2i(после пробежки) di(разница ЧСС) 65 77 12 75 82 7 68 65 3 80 90 10 75 85 10 62 75 13 Ср. знач.=70,8 Ср. знач.=79 Ср. знач.= 8,2 Несмотря
на то, что средние значения ЧСС до и
после пробежки отличаются, не исключена
возможность, что в генеральной
совокупности пробежка не повлияет на
ЧСС. Поэтому выдвигаем гипотезы: Н(0): после пробежки ЧСС в среднем не меняется Н(1): после пробежки ЧСС в среднем меняется Гипотезы будем проверять на уровне значимости α=0,05. Результаты вычислений представлены в таблице 18. Таблица 18. Результаты проверки гипотезы
Определим
по таблице Стьюдента (Приложение
2)
для α=0,05 и числа
степеней свободы f=n—1=5
двусторонний tкрит = 2,57. │tвыч │> tкрит – следовательно принимается Н(1). Вывод: изменение ЧСС после пробежки статистически значимо с вероятностью не менее 95%. |
Контрольное задание 5:
На каком уровне значимости можно утверждать, что содержание сахара в крови лиц основной и контрольной групп одинаково
Таблица 19. Данные к заданию
Сахар в крови, г/л | t0,05 | t0,01 | tвыч | |
Основная группа | 2,262 | 3,25 | 3,11 | |
Контрольная группа |
По данным из таблицы 20 сформулируйте нулевую и альтернативную гипотезы.
 Какая из гипотез будет принята.
Какая из гипотез будет принята.
Таблица 20. Данные к заданию
Аплитуда ЭЭГ | фон | альфа | р |
гипервентилляция | 0,05 | 7,5% |
Goodness-of-Fit
Что такое Goodness-of-Fit?
Термин «доброподгонка» относится к статистическому тесту, который определяет, насколько хорошо выборочные данные соответствуют распределению из совокупности с нормальным распределением. Проще говоря, он выдвигает гипотезу о том, является ли выборка искаженной или представляет данные, которые вы ожидаете найти в реальной совокупности.
Качество соответствия устанавливает несоответствие между наблюдаемыми значениями и теми, которые ожидаются от модели в случае нормального распределения. Существует несколько методов определения степени соответствия, включая хи-квадрат.
Существует несколько методов определения степени соответствия, включая хи-квадрат.
Ключевые выводы
- Качество соответствия — это статистический тест, который пытается определить, соответствует ли набор наблюдаемых значений тем, которые ожидаются в рамках применимой модели.
- Они могут показать вам, соответствуют ли данные вашей выборки ожидаемому набору данных из генеральной совокупности с нормальным распределением.
- Существует несколько типов тестов согласия, но наиболее распространенным является тест хи-квадрат.
- Тест хи-квадрат определяет, существует ли связь между категориальными данными.
- Критерий Колмогорова-Смирнова определяет, происходит ли выборка из определенного распределения генеральной совокупности.
Понимание качества подгонки
Критерии согласия — это статистические методы, которые делают выводы о наблюдаемых значениях. Например, вы можете определить, действительно ли группа выборки репрезентативна для всего населения. Таким образом, они определяют, как фактические значения связаны с прогнозируемыми значениями в модели. При использовании в процессе принятия решений тесты на соответствие облегчают прогнозирование тенденций и закономерностей в будущем.
Таким образом, они определяют, как фактические значения связаны с прогнозируемыми значениями в модели. При использовании в процессе принятия решений тесты на соответствие облегчают прогнозирование тенденций и закономерностей в будущем.
Как отмечалось выше, существует несколько типов тестов согласия. К ним относятся тест хи-квадрат, который является наиболее распространенным, а также тест Колмогорова-Смирнова и тест Шапиро-Уилка. Тесты обычно проводятся с использованием компьютерного программного обеспечения. Но статистики могут проводить эти тесты, используя формулы, адаптированные к конкретному типу теста.
Чтобы провести тест, вам нужна определенная переменная, а также предположение о том, как она распределяется. Вам также нужен набор данных с четкими и явными значениями, например:
- Наблюдаемые значения, полученные из набора фактических данных
- Ожидаемые значения, полученные на основе сделанных предположений
- Общее количество категорий в наборе
Критерии согласия обычно используются для проверки нормальности остатков или для определения того, собраны ли две выборки из идентичных распределений.
Особые указания
Чтобы интерпретировать критерий согласия, статистикам важно установить альфа-уровень, например, значение p для критерия хи-квадрат. Значение p относится к вероятности получения результатов, близких к крайним значениям наблюдаемых результатов. Это предполагает, что нулевая гипотеза верна. Нулевая гипотеза утверждает, что между переменными нет взаимосвязи, а альтернативная гипотеза предполагает, что взаимосвязь существует. 92/E_i χ2=i=1∑k(Oi−Ei)2/Ei
Тест хи-квадрат, также известный как тест хи-квадрат на независимость, представляет собой метод статистического вывода, который проверяет обоснованность утверждения, сделанного о совокупности на основе случайной выборки.
Используется исключительно для данных, разделенных на классы (бины), и требует достаточного размера выборки для получения точных результатов. Но это не указывает на тип или интенсивность отношений. Например, он не делает вывод, является ли отношение положительным или отрицательным.
Чтобы вычислить хи-квадрат согласия, установите желаемый альфа-уровень значимости. Итак, если ваш уровень достоверности составляет 95% (или 0,95), то альфа равна 0,05. Затем определите категориальные переменные для проверки, а затем определите утверждения гипотезы об отношениях между ними.
Переменные должны быть взаимоисключающими, чтобы можно было пройти тест хи-квадрат на независимость. И критерий согласия хи не следует использовать для непрерывных данных.
Тест Колмогорова-Смирнова (К-С)
Д знак равно Максимум 1 ≤ я ≤ Н ( Ф ( Д я ) − я − 1 Н , я Н − Ф ( Д я ) ) D=\max\limits_{1\leq i\leq N}\bigg(F(Y_i)-\frac{i-1}{N},\frac{i}{N}-F(Y_i)\bigg) D=1≤i≤Nmax(F(Yi)−Ni−1,Ni−F(Yi))
Названный в честь российских математиков Андрея Колмогорова и Николая Смирнова, критерий Колмогорова-Смирнова (К-С) представляет собой статистический метод, который определяет, относится ли выборка к определенному распределению в популяции.
Этот тест, который рекомендуется для больших выборок (например, более 2000), является непараметрическим. Это означает, что он не зависит от какого-либо дистрибутива. Цель состоит в том, чтобы доказать нулевую гипотезу, которая является выборкой нормального распределения.
Как и хи-квадрат, он использует нулевую и альтернативную гипотезы и альфа-уровень значимости. Null указывает, что данные следуют определенному распределению внутри совокупности, а альтернатива указывает, что данные не подчиняются определенному распределению внутри совокупности. Альфа используется для определения критического значения, используемого в тесте. Но в отличие от критерия хи-квадрат, критерий Колмогорова-Смирнова применим к непрерывным распределениям. 9{N} \frac {( 2i — 1 )}{ N } [\ln F ( Y_i ) + \ln ( 1 — F ( Y_ {N + 1 — i} ) ) ] S=∑i=1NN(2i−1)[lnF(Yi)+ln(1−F(YN+1−i))]
Критерий Андерсона-Дарлинга (AD) является разновидностью критерия KS, но придает больший вес хвостам распределения. Критерий K-S более чувствителен к различиям, которые могут возникнуть ближе к центру распределения, в то время как критерий AD более чувствителен к вариациям, наблюдаемым в хвостах. Поскольку риск хвоста и идея «толстых хвостов» широко распространены на финансовых рынках, тест AD может дать больше возможностей для финансового анализа.
92},
W=∑i=1n(xi−xˉ)2(∑i=1nai(x(i))2,
Критерий K-S более чувствителен к различиям, которые могут возникнуть ближе к центру распределения, в то время как критерий AD более чувствителен к вариациям, наблюдаемым в хвостах. Поскольку риск хвоста и идея «толстых хвостов» широко распространены на финансовых рынках, тест AD может дать больше возможностей для финансового анализа.
92},
W=∑i=1n(xi−xˉ)2(∑i=1nai(x(i))2,
Критерий Шапиро-Уилка (S-W) определяет, соответствует ли выборка нормальному распределению. Тест проверяет нормальность только при использовании выборки с одной переменной непрерывных данных и рекомендуется для небольших размеров выборки до 2000.
В тесте Шапиро-Уилка используется вероятностный график, называемый графиком QQ, который отображает два набора квантилей по оси Y, расположенных от наименьшего к наибольшему. Если каждый квантиль получен из одного и того же распределения, ряд графиков будет линейным.
График QQ используется для оценки дисперсии. Используя дисперсию графика QQ вместе с оценочной дисперсией населения, можно определить, принадлежит ли выборка нормальному распределению. Если отношение обеих дисперсий равно или близко к 1, можно принять нулевую гипотезу. Если значение значительно ниже 1, оно может быть отклонено.
Если отношение обеих дисперсий равно или близко к 1, можно принять нулевую гипотезу. Если значение значительно ниже 1, оно может быть отклонено.
Как и упомянутые выше тесты, этот использует альфу и формирует две гипотезы: нулевую и альтернативную. Нулевая гипотеза утверждает, что выборка исходит из нормального распределения, тогда как альтернативная гипотеза утверждает, что выборка не исходит из нормального распределения.
Пример согласия
Вот гипотетический пример, показывающий, как работает критерий согласия.
Предположим, что небольшой общественный спортзал работает исходя из предположения, что самая высокая посещаемость приходится на понедельник, вторник и субботу, средняя посещаемость — на среду и четверг, а самая низкая посещаемость — на пятницу и воскресенье. Исходя из этих предположений, в тренажерном зале каждый день работает определенное количество сотрудников, которые регистрируют участников, убирают помещения, предлагают услуги по обучению и проводят занятия.
Но спортзал не работает в финансовом отношении, и владелец хочет знать, верны ли эти предположения о посещаемости и уровне укомплектования персоналом. Владелец решает подсчитывать количество посетителей спортзала каждый день в течение шести недель. Затем они могут сравнить предполагаемую посещаемость тренажерного зала с наблюдаемой посещаемостью, используя, например, критерий согласия хи-квадрат.
Теперь, когда у них есть новые данные, они могут определить, как лучше управлять тренажерным залом и повысить прибыльность.
Что означает качество прилегания?
Goodness-of-Fit — это проверка статистической гипотезы, используемая для проверки того, насколько точно наблюдаемые данные отражают ожидаемые данные. Тесты согласия могут помочь определить, соответствует ли выборка нормальному распределению, связаны ли категориальные переменные или случайные выборки относятся к одному и тому же распределению.
Почему важна точность прилегания?
Тесты согласия помогают определить, соответствуют ли наблюдаемые данные ожидаемым. Решения могут быть приняты на основе результатов проведенной проверки гипотезы. Например, розничный торговец хочет знать, какие товары нравятся молодежи. Розничный продавец опрашивает случайную выборку пожилых и молодых людей, чтобы определить, какой продукт предпочтительнее. Используя хи-квадрат, они определяют, что с 95% уверенности, существует связь между продуктом А и молодыми людьми. Основываясь на этих результатах, можно определить, что эта выборка представляет собой популяцию молодых людей. Розничные маркетологи могут использовать это для реформирования своих кампаний.
Решения могут быть приняты на основе результатов проведенной проверки гипотезы. Например, розничный торговец хочет знать, какие товары нравятся молодежи. Розничный продавец опрашивает случайную выборку пожилых и молодых людей, чтобы определить, какой продукт предпочтительнее. Используя хи-квадрат, они определяют, что с 95% уверенности, существует связь между продуктом А и молодыми людьми. Основываясь на этих результатах, можно определить, что эта выборка представляет собой популяцию молодых людей. Розничные маркетологи могут использовать это для реформирования своих кампаний.
Что такое критерий согласия в тесте хи-квадрат?
Проверка хи-квадрат на наличие отношений между категориальными переменными и на то, представляет ли выборка целое. Он оценивает, насколько точно наблюдаемые данные отражают ожидаемые данные или насколько хорошо они соответствуют.
Как вы проводите тест на пригодность?
Тест на пригодность состоит из различных методов тестирования. Цель теста поможет определить, какой метод использовать. Например, если цель состоит в том, чтобы проверить нормальность на относительно небольшой выборке, может подойти тест Шапиро-Уилка. Если необходимо определить, была ли выборка получена из определенного распределения внутри совокупности, будет использоваться критерий Колмогорова-Смирнова. В каждом тесте используется своя уникальная формула. Однако у них есть общие черты, такие как нулевая гипотеза и уровень значимости.
Цель теста поможет определить, какой метод использовать. Например, если цель состоит в том, чтобы проверить нормальность на относительно небольшой выборке, может подойти тест Шапиро-Уилка. Если необходимо определить, была ли выборка получена из определенного распределения внутри совокупности, будет использоваться критерий Колмогорова-Смирнова. В каждом тесте используется своя уникальная формула. Однако у них есть общие черты, такие как нулевая гипотеза и уровень значимости.
Итог
Критерии согласия определяют, насколько хорошо выборочные данные соответствуют ожиданиям от совокупности. Из выборочных данных собирается наблюдаемое значение и сравнивается с рассчитанным ожидаемым значением с использованием меры несоответствия. Существуют различные тесты гипотез согласия в зависимости от того, какой результат вы ищете.
Выбор правильного критерия согласия во многом зависит от того, что вы хотите знать о выборке, и от того, насколько она велика. Например, если вы хотите узнать, соответствуют ли наблюдаемые значения категориальных данных ожидаемым значениям категориальных данных, используйте хи-квадрат. Если вы хотите узнать, соответствует ли небольшая выборка нормальному распределению, может оказаться полезным тест Шапиро-Уилка. Существует множество тестов, позволяющих определить соответствие.
Если вы хотите узнать, соответствует ли небольшая выборка нормальному распределению, может оказаться полезным тест Шапиро-Уилка. Существует множество тестов, позволяющих определить соответствие.
Три распределения экстремальных значений: вводный обзор
1
1Введение
Статистика экстремальных значений предлагает мощный набор инструментов для физиков-теоретиков. Но это своего рода ящик для инструментов, который нельзя упустить до того, как с ним познакомишься — возможно, немного похоже на смартфон. Он касается статистики экстремальных явлений и призван ответить на такие вопросы, как «если бы самый сильный сигнал, который я наблюдал за последний час, имел значение x , каким должен быть самый сильный сигнал, если измерять его в течение ста часов?» Кроме того, если я разделю этот сточасовой интервал на сто часовых интервалов, каким будет статистическое распределение самого сильного сигнала в каждом часовом интервале?
Именно последнему вопросу посвящен этот мини-обзор.
В литературе по статистике экстремальных значений недостатка нет, см., например, [1–5] или просто google термин. Мы находим его используемым в связи со спиновыми стеклами и неупорядоченными системами [6], в связи с 1/f-шумом [7], в связи с оптикой [8], в связи с разрушением [9] или модели расслоения [10], в диффузионных процессах [11] и т. д. Примеров из разных областей физики предостаточно.
Итак, у новичка, увидевшего потребность в этом инструменте, недостатка в материалах нет. Проблема в том, что не так просто проникнуться литературой, которая часто написана на довольно математическом языке, для проникновения в который нужно потрудиться. Цель этого мини-обзора — представить теорию и основные результаты, касающиеся распределений экстремальных значений, в простой и компактной форме. Мы не представим ничего нового. Более длинный, широкий и подробный обзор статистики экстремальных значений Fortin и Clusel [12] или Majumdar et al. представляют именно это [13]. У нас есть статистическое распределение p(x) и связанная с ним кумулятивная вероятность
У нас есть статистическое распределение p(x) и связанная с ним кумулятивная вероятность
P(x)=∫−∞xp(x′)dx′,(1)
– вероятность найти число, меньшее или равное x . Мы берем N чисел из этого распределения и записываем наибольшее из N чисел. Мы повторяем эту процедуру M раз и тем самым получаем M наибольших чисел, по одному на каждую последовательность. Каково распределение этих M наибольших чисел в пределе, когда M→∞, что затем определяет распределение экстремальных значений ?
Получается, что в зависимости от p(x) распределение экстремальных значений будет иметь одну из трех функциональных форм:
• Кумулятивная вероятность Вейбулла <0,1 для u≥0, (2)
, где мы предполагаем α>0. Обратите внимание, что Φ(−∞)=0. Соответствующее распределение экстремальных значений Вейбулла:
ϕ(u)={α(−u)α−1e−(−u)αfor u<0,0for u≥0. (3)
(3)
• Фреше кумулятивная вероятность
Φ(u)={0for u≤0,e−u−αfor u>0.(4)
Также здесь мы предполагаем α>0. Обратите внимание, что Φ(∞)=1. Распределение экстремальных значений Фреше:
ϕ(u)={0for u≤0,αu−α−1e−u−αfor u>0.(5)
• Кумулятивная вероятность Gumbel
Φ(u) =e−e−u,(6)
, где −∞ ϕ(u)=e−u−e−u.(7) Вопросы заключаются в следующем: 1. какие классы распределений p(x) приводят к какому из трех экстремальных значений дистрибутивы и 2. какая связь между x и u в каждом случае? Оказывается, что. • распределения, где p(x)=0 при x>x0 и p(x)∼(x0−x)α−1 при x→x0−, см. формулу. 10, приводят к распределению экстремальных значений Вейбулла , • распределениям, где p(x)∼x−α−1 при x→∞, см. • и распределениям, где p(x) падает быстрее любого степенного закона при x→∞, см. уравнение. 53 приводят к распределению экстремальных значений Гамбеля. Кроме того, мы найдем это. • для распределения экстремальных значений Вейбулла u дается через x в уравнении. 13, • для распределения экстремальных значений Фреше, u, заданное через x в уравнении. 27, • для распределения экстремальных значений Гамбеля u дается через x в уравнениях 51 и 43. Мы суммируем эти результаты в Таблице I. Резюме основных результатов. Дальнейшее обсуждение будет построено на следующем соотношении. Мы рисуем N чисел из распределения вероятностей p(x): x1,x2,⋯,xN. Вероятность того, что все N чисел меньше или равны значению x , равна Prob[x1≤x,x2≤x,⋯,xN≤x]=[∫−∞xp(x′)dx ′]N=P(x)N,(8) , где P(x) — кумулятивная вероятность 1. Вместо традиционного подхода (см., например, [10]) к этому вопросу, основанного на критерии устойчивости Фреше, Фишера и Типпета [1], я буду основывать все обсуждение на соотношении limN→∞(1+xN)=ex.(9) Я считаю, что это более простой и интуитивно понятный способ. 2 Здесь мы рассматриваем распределения вероятностей p(x), имеющие вид ) , где b положительный. Отметим, что 0<α<1 приводит к расходящейся плотности вероятности при x→x0−. Кроме того, отметим, что α=1 подразумевает, что p(x) приближается к константе, когда x→x0−, что, например, имеет место в случае равномерного распределения. Соответствующая кумулятивная вероятность равна P(x)={1for x≥x0,1−b(x0−x)αfor x→x0−. Кумулятивная вероятность экстремального значения для N выборок определяется выражением P(x )N=[1−b(x0−x)α]N, (12) для x→x0−. Мы вводим изменение переменной x−x0=,u(bN)1/α(13) , где читатель должен заметить, что b определяется исходным распределением 10. Тогда уравнение 12 принимает вид P(x )N=[1−(−u)αN]N.(14) В пределе N→∞ это становится Φ(u)=limN→∞P(x)N=e−(−u )α,(15) для отрицательных и . Следовательно, мы имеем, что Φ(u)={e−(−u)αfor u<0,1for u≥0, (16) , что является кумулятивной вероятностью Вейбулла, справедливо для всех значений u , хотя мы знаем только поведение p(x) вблизи x0. Плотность вероятности Вейбулла определяется как обратите внимание, что распределение Вейбулла напоминает растянутую экспоненту. Мы выражаем кумулятивную вероятность Вейбулла через исходную переменную x , используя уравнение 13, Φ(u)=Φ((bN)1/α(x−x0))=e−Nb(x0−x)α=Φ˜(x).(18) Отсюда в терминах исходная переменная x , распределение экстремальных значений Вейбулла принимает вид ϕ˜(x)=dΦ˜(x)dx=Nbα(−x)α−1e−Nb(x0−x)α. 2.1 Теперь разработаем конкретный пример. Предположим, что p(x) задается как p(x)={0for x<0,α(1−x)α−1for 0≤x≤1,0for x>1, (20) т. е. b=1 и x0=1 в уравнении 10. Тогда кумулятивная вероятность равна P(x)={0for x<0,1−(1−x)αfor 0≤x≤1,1for x>1.(21) Из уравнения 19 и имеем, что ϕ˜(x)=Nα(1−x)α−1e−N(1−x)α.(22) Покажем распределение 20 с α=3 вместе с соответствующим экстремумом распределения значений для N = 100 и N = 1000, уравнение. РИСУНОК 1 . (A) Кривая, имеющая максимум при x=0, представляет собой распределение вероятностей 20 с α=3. Кривая с максимумом посередине — это ϕ˜(x), уравнение 22 с N=100, а кривая с максимумом справа – это ϕ˜(x) с N=1000. (B) Показанные здесь гистограммы основаны на данных согласно распределению вероятностей 20 с α=3. Гистограмма с максимумом слева показывает все сгенерированные данные. Гистограмма с максимумом в середине показывает наибольшее число среди каждой последовательности чисел длиной 100, а гистограмма с максимумом справа показывает наибольшее число среди каждой последовательности чисел длиной 1000. Мы сгенерировали 107 последовательностей для обоих случаев. Использование генератора случайных чисел для получения номеров IID 1 r равномерно распределены на единичном интервале, мы можем стохастически генерировать числа, распределенные в соответствии с плотностью вероятности p(x), заданной в 20. x=1−r1/α, (23) , где мы также использовали, что r можно заменить 1−r в 21. Мы генерируем последовательность последовательности чисел, использующие этот алгоритм, каждая последовательность имеет длину Н . Затем мы определяем наибольшее значение в каждой последовательности. Мы выбрали N=100 и N=1000, в каждом случае создавая 107 таких последовательностей. Гистограммы, основанные на самих случайных числах и экстремальных значениях для каждой последовательности длиной 100 или 1000, показаны на рисунке 1В. Эту цифру следует сравнить с фигурой 1А. Распределение Вейбулла, уравнение 17 широко используется в связи с прочностью материала [15]. Это не случайно. Рассмотрим цепь. Каждое звено в цепи может выдерживать нагрузку до определенного значения, выше которого оно выходит из строя. Это максимальное значение распределяется в соответствии с некоторым распределением вероятностей. 3 Теперь предположим, что распределение вероятностей p(x) ведет себя как как P(x)=1−bx−α для x→∞. (25) Кумулятивная вероятность экстремального значения для N выборок определяется выражением P(x)N=[1−bx−α ]N,(26) для x→∞. x=(bN)1/αu, (27) , где b исходит из исходного распределения 24. Теперь мы подставим это изменение переменных в уравнение. 26 найти P(x)N=[1−b((bN)1/α u)−α]N=[1−u−αN]N.(28) В пределе N→∞ , это становится Φ(u)=limN→∞P(x)N=e−u−α, (29) , где u≥0 определяется уравнением 27. Мы видим, что Φ(u)→0 при u→0+. Кроме того, при u<0 функция уже не является вещественной. Следовательно, мы определяем Φ(u)=0 при u<0. Суммарная вероятность последующего экстремального значения определяется как Φ(u)={0for u≤0,e−u−αfor u>0, (30) , что является кумулятивной вероятностью Фреше. Плотность вероятности Фреше определяется как вероятность с точки зрения исходной переменной x с использованием уравнения. 27, Φ(u)=Φ(x(bN)1/α)=e−Nx−α=Φ˜(x). Следовательно, через исходную переменную x Распределение экстремальных значений Фреше принимает вид ϕ˜(x)=dΦ˜(x)dx=Nαx−α−1e−Nx−α.(33) 3.1 Рассмотрим распределение P(x)={0for x≤1,1−x−αfor x>1.(35) Используя уравнение 33, мы находим соответствующее распределение экстремальных значений Фреше равным ϕ˜(x)=Nαx−α−1e−Nx−α, (36) , действительным для всех x>1. Мы показываем p(x) и соответствующий ϕ˜(x) для α=3 и N=100 и N=1000 на рисунке 2A. РИСУНОК 2 . (A) Кривая, имеющая максимум при x=1, представляет собой распределение вероятностей 34 с α=3. Кривая с максимумом посередине — это ϕ˜(x), уравнение 36 с N=100, а кривая с максимумом справа – это ϕ˜(x) с N=1000. (B) Показанные здесь гистограммы основаны на данных согласно распределению вероятностей 34 с α=3. Для сравнения с численными результатами мы генерируем числа, распределенные согласно 34, путем решения уравнения P(x)=r, где r получается из равномерного распределения на единичном интервале. Из уравнения 35, мы получаем x=r−1/α. (37) Мы генерируем последовательность чисел, используя этот алгоритм, группируя их вместе в последовательности N=100 или N=1000. Мы генерируем 107 таких последовательностей. Гистограммы, основанные на самих случайных числах, сгенерированных с помощью уравнения. 37, а крайние значения для каждой последовательности длиной 100 или 1000 мы показываем на рисунке 2B. 4 Теперь предположим, что у нас есть распределение вероятностей, которое принимает вид f′(x)=df(x)/dx. У нас есть x0 — любое число, положительное или отрицательное, а f(x) — возрастающая функция x . Позже мы введем достаточный критерий, наложенный на p(x), чтобы получить распределение Гамбеля, см. 53. Этот критерий эквивалентен тому, что f(x) удовлетворяет limx→∞ddx(1f′(x))=0.(39) Этому критерию, например, удовлетворяет любой полином f(x). (40) ≤x0. Кумулятивная вероятность экстремального значения для N выборок определяется выражением P(x)N=[1−e−f(x)]N,(41) для x>x0. Введем замену переменной u˜=f(x)−f(xN), (42) , где xN определяется как P(xN)=1−1N.(43) Хотя xN определяется числом 43, мы можем интерпретировать его значение. f(xN)=lnN. (44) Теперь определим ∆x=x−xN. (45) Затем разложим f(x) вокруг xN, f( x)=f(xN+∆x)=∑n=0∞f(n)(xN)n!∆xn,(46) , где f(n)(x)=dnf(x)/dxn. Если теперь мы установим Δx=1f′(xN), (47) так, чтобы член первого порядка в разложении стал постоянным при увеличении N , мы получим, что f′(xN)Δx+∑n=2∞f(n)(xN)n!Δxn=1+∑n=2∞f(n)(xN)n!f′(xN)n.(48) Следовательно, если имеем, что limN→∞f(n)(xN)f′(xN)n=0,(49) для n≥2, то в этом пределе найдем f (x)=f(xN)+f′(xN)Δx=f(xN)+u, (50) , где мы определяем u=f′(xN)Δx=Np(xN)(x−xN ).(51) Здесь мы использовали уравнения (40) и (44). 4.1 Если мы объединим уравнение. 49 для n=2 с уравнениями 38 и 40, мы находим limN→∞f′′(xN)f′(xN)2=limN→∞ddx[1−P(x)p(x)]x=xN=0, (52) , что эквивалентно limx→∞ddx[1−P(x)p(x)]=0.(53) Уравнение 53, эквивалентное уравнению 39, на самом деле является достаточным условием для того, чтобы 49 выполнялось для всех n>1. Мы можем показать это по индукции. Имеем, что f(n+1)(x)f′(x)n+1=1f′(x) ddx(f(n)(x)f′(x)n)+f(n)( x)f′(x)n+2.(54) Если выполнено условие 52, то есть когда приведенное выше выражение равно нулю в пределе x→∞ при n=2, мы также имеем, что limN→∞f(3)(x)f′(x)3=0,(55) , так как оба члена в правой части уравнения 54 равны нулю в этом пределе. Теперь мы предполагаем уравнение. 49 для некоторого n>3. limN→∞f(n+1)(xN)f′(xN)n+1=0, (56) снова из-за обоих членов в правой части уравнения. 54 равны нулю в этом пределе. Это завершает доказательство. 4.2 Теперь мы объединим уравнение. 42 с уравнением. 41, чтобы найти P(x)N=[1−e−u−f(xN)]N=[1−e−u−lnN]N=[1−e−uN]N.(57) В пределе N→∞ это становится Φ(u)=limN→∞P(x)N=e−e−u, (58) , что равно кумулятивной вероятности Гамбеля. Здесь −∞ ϕ(u)=dΦ(u)du=e−u−e−u. (59) Мы выражаем кумулятивную вероятность Гамбеля через исходную переменную x , используя уравнение . 51, Φ(u)=Φ(Np(xN)(x−xN))=e−e−Np(xN)(x−xN)=Φ˜(x).(60) Следовательно, в условия исходной переменной x , распределение экстремальных значений Гамбеля принимает вид . 4.3 Вот пример: гауссиана. Гауссова плотность вероятности определяется как p(x)=e−x2/2σ2πσ , (62) , где σ — квадрат стандартного отклонения. Кумулятивная вероятность равна P(x)=12[1+erf(x2σ)],(63) , где erf(z) — функция ошибок. Для проверки того, что гауссиана порождает экстремальное распределение Гумбеля, воспользуемся достаточным условием 53, limx→∞ddx[1−P(x)p(x)]=limx→∞π2σex2/2σx[1−erf(x2σ)]=0.(64) Гауссова кумулятивная вероятность в уравнении 63 имеет асимптотическую форму P(x)=1−σ2πe−x2/2σx, (65) для больших x . Определим xN, решая уравнение 43, используя эту асимптотическую форму. Находим xN=σW(N22π), (66) , где W(z) — W-функция Ламберта, также известная как логарифм произведения, которая является решением уравнения W(z)exp[W(z )]=г. Np(xN)=1σW(N22π),(67) при подстановке выражения для x=xN, уравнение 66 в уравнение. 62. Таким образом, теперь мы можем выразить переменную u в кумулятивной вероятности Гумбеля 57 через переменные x , σ и N , используя уравнение. 51, u=x 1σW(N22π)−W(N22π).(68) На рисунке 3A показано распределение Гаусса и соответствующее распределение Гамбеля для σ=1, N=100 и N=1000. Мы находим, что x100=2,375 и x1000=3,115. Это доверительные интервалы для 99% и 99,9%. РИСУНОК 3 . (A) Распределение Гаусса и соответствующее распределение Гамбеля для σ=1, N=100 и N=1000. (B) Показанные здесь гистограммы основаны на данных, сгенерированных с помощью алгоритма Бокса-Мюллера, который выдает числа, распределенные по гауссовской схеме. Мы показываем на рисунке 3B гистограмму, основанную на числах, распределенных согласно распределению Гаусса с использованием алгоритма Бокса-Мюллера [14]. Эти числа были сгруппированы в наборы из N=100 или N=1000 элементов. Я сгенерировал 107 таких наборов. На рисунке показаны два экстремальных распределения для двух размеров наборов. Эту цифру следует сравнить с фигурой 3А. В отличие от двух других распределений экстремальных значений, мы видим видимые расхождения между рассчитанными распределениями Гамбеля на рисунке 3A и гистограммами экстремальных значений на рисунке 3B. Кроме того, мы видим, что гистограмма для N=1000 ближе к рассчитанному распределению Гамбеля, чем гистограмма для N=100. 5 Мы суммируем основные результаты, представленные в этом мини-обзоре, в Таблице I. , Раздел 2. Это, однако, легко решить: просто преобразовать x→−x . В остальном представленная здесь история довольно полна. Однако следует сделать одно замечание. При выводе распределения экстремальных значений Гамбеля, раздел 4, мы определили переменную xN в уравнении. 43. Прежде всего, xN, определенный в уравнении. 43 можно рассчитать за любой кумулятивной вероятности P(x), и у него есть интерпретация, делающая его очень полезным. Плотность вероятности для наибольшего из N чисел, полученных с использованием распределения вероятностей p(x), определяется как pN(x)=dP(x)Ndx=NP(x)N−1p(x). Рассчитываем среднее значение кумулятивной вероятности P(x) для экстремального значения на основе N отсчетов, 〈P(x)〉=∫−∞∞P(x)pN(x)dx= ∫01PNdP=NN+1=1−1N+1 .(70) Для больших N , мы можем записать это как 〈P(x)〉=P(xN)=1−1N,(71) , используя здесь уравнение 43. Следовательно, мы можем интерпретировать xN как значение x , соответствующее среднему доверительному интервалу наибольшего наблюдаемого значения в последовательностях из N чисел. По сути, это типичный размер экстремального значения для выборки размером N . Автор подтверждает, что является единственным автором этой работы и одобрил ее публикацию. Эта работа была частично поддержана Исследовательским советом Норвегии через схему финансирования Центров передового опыта, номер проекта 262644. финансовые отношения, которые могут быть истолкованы как потенциальный конфликт интересов. Я благодарю Эйвинда Беринга, Астрид де Вейн, Х. Джорджа, Э. Хентшеля, Срутарши Прадхана и Итамара Прокачча за многочисленные интересные дискуссии по этой теме. 1 Переменные IID. Независимые и одинаково распределенные случайные величины — терминология, используемая в некоторых сообществах. 1. Гамбель Э.Дж. Статистика экстремумов . Нью-Йорк: издательство Колумбийского университета (1958). Google Scholar 2. Дэвид Х.А. Статистика заказов . 2-е изд. Нью-Йорк: Уайли (1981). Google Scholar 3. Галамбос Дж. Асимптотическая теория статистики экстремального порядка . Малабар, Флорида: Кригер (1987). Google Scholar 4. Эмбрехтс П., Клюппельберг С., Микош Т. Моделирование экстремальных явлений для страхования и финансов . Берлин: Спрингер (1997). Google Scholar 5. Google Scholar 6. Bouchaud J-P, Mézard M. Классы универсальности для статистики экстремальных значений. J Физико-математическое поколение (1997). 30 :7997. doi:10.1088/0305-4470/30/23/004 CrossRef Full Text | Google Scholar 7. Антал Т., Дроз М., Дьёрдьи Г., Рац З. Шум 1/f и статистика экстремальных значений. Phys Rev Letter (2001 г.). 87 :240601. doi:10.1103/physrevlett.87.240601 PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar 8. Randoux S, Suret P. Экспериментальные доказательства статистики экстремальных значений в рамановских волоконных лазерах. Доп. письмо (2012 г.). 37 :500. doi:10.1364/OL.37.000500 Полный текст CrossRef | Google Scholar 9. Талони А., Водрет М., Костантини Г., Заппери С. Влияние размера на разрушение микро- и наноразмерных материалов. CrossRef Full Text | Google Scholar 10. Hansen A, Hemmer PC, Pradhan S. Модель пучка волокон . Берлин: Wiley VCH (2015). Google Scholar 11. Пал А., Элиазар И., Реувени С. Первый пассаж при рестарте с ответвлением. Phys Rev Letter (2019 г.). 122 :020602. doi:10.1103/PhysRevLett.122.020602 CrossRef Full Text | Google Scholar 12. Фортин Дж.-Й., Клюзель М. Применение статистики экстремальных значений в физике. J Phys Math Theor (2015). 48 :183001. doi:10.1088/1751-8113/48/18/183001 CrossRef Full Text | Google Scholar 13. Маджумдар С.Н., Пал А., Шер Г. Статистика экстремальных значений коррелированных случайных величин: педагогический обзор. Phys Rep (2020) 840 :1. doi:10.1016/j.physrep.2019.10.005 Полный текст CrossRef | Google Scholar 14. Google Scholar 15. Ринне Х. Распределение Вейбулла . Бока-Ратон: CRC Press (2008). Google Scholar 16. Corless RM, Gonnet GH, Hare DEG, Jeffrey DJ, Knuth DE. О функции Ламберта. Adv Comput Math (1996) 5 : 329–59. doi:10.1007/BF02124750 Полный текст CrossRef | Google Scholar 17. Зарфати Л., Баркай Э., Кесслер Д.А. Точное приближение статистики экстремальных значений (2020 г.). архив: 2006.13677. Google Scholar . 2012 авг; 90 (8): 2750-3. doi: 10.2527/jas.2011-4634.
Epub 2012 9 марта. Дж. К. Бейли 1 , Л. О. Тедески, Э. Д. Мендес, Дж. Э. Сойер, Г. Э. Карстенс Принадлежности JC Bailey et al.
J Anim Sci.
2012 авг. . 2012 авг; 90 (8): 2750-3. doi: 10.2527/jas.2011-4634.
Epub 2012 9 марта. Дж. К. Бейли 1 , Л. О. Тедески, Э. Д. Мендес, Дж. Э. Сойер, Г. Э. Карстенс Приемы пищи представляют собой группы событий посещения кормления (BV), которые отличаются от следующего приема пищи более продолжительным интервалом без кормления по сравнению с интервалами без кормления в рамках приема пищи. Использование смешанных моделей распределения для определения критериев анализа поведения животных. Йейтс, член парламента, Толкамп Б.Дж., Олкрофт, ди-джей, Кириазакис И. Влияние кормления цельными семенами хлопка и продуктами из семян хлопка на продуктивность и характеристики туши откормочного мясного скота. Крэнстон Дж. Дж., Ривера Дж. Д., Гальян М. Л., Браширс М. М., Брукс Дж. К., Маркхэм К. Э., Макбет Л. Дж., Кребил К. Р.
Крэнстон Дж. Дж. и соавт.
J Anim Sci. 2006 г., август; 84 (8): 2186-99. doi: 10.2527/jas.2005-669.
J Anim Sci. 2006.
PMID: 16864881
Клиническое испытание. Оценка высушенного зерна тритикале после перегонки с растворимыми веществами в качестве заменителя зерна ячменя и ячменного силоса в рационах для откорма на откормочных площадках. Wierenga KT, McAllister TA, Gibb DJ, Chaves AV, Okine EK, Beauchemin KA, Oba M.
Wierenga KT, et al.
J Anim Sci. 2010 г., сен; 88 (9): 3018-29. doi: 10.2527/jas.2009-2703. Epub 2010 21 мая.
J Anim Sci. 2010.
PMID: 20495119
Клиническое испытание. Влияние расхождения в остаточном потреблении корма на пищевое поведение, метаболические показатели крови и особенности состава тела у растущих телок мясного направления. Келли А.К., МакГи М., Крюс Д.Х. младший, Фэйи А.Г., Уайли А.Р., Кенни Д.А.
Келли А.К. и др.
J Anim Sci. 2010 Январь; 88 (1): 109-23. doi: 10.2527/jas.2009-2196. Epub 2009 9 октября.
J Anim Sci. 2010.
PMID: 19820067 Мука из рыжика и сырой глицерин в качестве кормовых добавок для выращивания ремонтных мясных телок. Мориэль П., Найигихугу В., Каппеллоцца Б.И., Гонсалвес Э.П., Кралл Дж.М., Фоулке Т., Каммак К.М., Хесс Б.В.
Мориэль П. и др.
J Anim Sci. 2011 декабрь; 89 (12): 4314-24. doi: 10.2527/jas.2010-3630. Epub 2011 5 августа.
J Anim Sci. 2011.
PMID: 21821818
Клиническое испытание. Посмотреть все похожие статьи Влияние лечения поливалентной вакциной против BRD и темперамента на производительность и реакцию пищевого поведения на контрольную стимуляцию BVDV1b у мясных бычков. Смит П., Карстенс Г., Раньян С., Ридпат Дж., Сойер Дж., Херринг А.
Смит П. и др.
Животные (Базель). 2021 19 июля; 11 (7): 2133. дои: 10.3390/ani11072133.
Животные (Базель). 2021.
PMID: 34359261
Бесплатная статья ЧВК. Характеристика особенностей пищевого поведения бычков с дивергентным остаточным потреблением корма, потребляющих высококонцентрированный рацион. Парсонс И.Л., Джонсон Дж.Р., Кайзер В.К., Тедески Л.О., Карстенс Г.Э.
Парсонс И.Л. и соавт.
J Anim Sci. 2020 1 июля; 98 (7): skaa189. дои: 10.1093/jas/skaa189.
J Anim Sci. 2020.
PMID: 32589744
Бесплатная статья ЧВК. Влияние 3-нитрооксипропанола на продукцию кишечного метана, ферментацию рубца и кормовое поведение у мясного скота, получающего рацион с высоким содержанием фуража или зерна1. Kim SH, Lee C, Pechtl HA, Hettick JM, Campler MR, Pairis-Garcia MD, Beauchemin KA, Celi P, Duval SM.
Ким С.Х. и др.
J Anim Sci. 2019 2 июля; 97 (7): 2687-2699. дои: 10.1093/jas/skz140.
J Anim Sci. 2019.
PMID: 31115441
Бесплатная статья ЧВК. Влияние темперамента по прибытии на откормочную площадку и типа породы на эффективность роста, кормовое поведение и стоимость туши у откормочных телок. Олсон К.А., Карстенс Г.Э., Херринг А.Д., Хейл Д.С., Кайзер В.К., Миллер Р.К.
Олсон К.А. и соавт.
J Anim Sci. 2019 3 апреля; 97 (4): 1828-1839. дои: 10.1093/jas/skz029.
J Anim Sci. 2019.
PMID: 30689930
Бесплатная статья ЧВК. Оценка активных сухих дрожжей в рационах откормочных бычков-I: влияние на характеристики кормления, структуру роста и характеристики туши1. Crossland WL, Jobe JT, Ribeiro FRB, Sawyer JE, Callaway TR, Tedeschi LO.
Кроссленд В.Л. и др.
J Anim Sci. 2019 1 марта; 97 (3): 1335-1346. дои: 10.1093/jas/skz007.
J Anim Sci. 2019.
PMID: 30657913
Бесплатная статья ЧВК. Просмотреть все статьи «Цитируется по» Определение мощности и объема выборки Автор: Лиза Салливан, доктор философии Профессор биосатистики Школа общественного здравоохранения Бостонского университета Критически важным аспектом любого исследования является определение соответствующего размера выборки для ответа на вопрос исследования. Исследования должны быть разработаны таким образом, чтобы в них участвовало достаточное количество участников, чтобы адекватно ответить на вопрос исследования. Исследования с недостаточным или чрезмерно большим числом участников являются расточительными с точки зрения времени участников и исследователей, ресурсов для проведения оценок, аналитических усилий и так далее. Эти ситуации также можно рассматривать как неэтичные, поскольку участники могли подвергаться риску в рамках исследования, которое не смогло ответить на важный вопрос. Исследования, которые намного больше, чем они должны быть, чтобы ответить на вопросы исследования, также являются расточительными. Представленные здесь формулы позволяют оценить необходимый размер выборки на основе статистических критериев. После завершения этого модуля студент сможет: Модуль доверительных интервалов предоставил методы оценки доверительных интервалов для различных параметров (например, μ , p, ( μ 1 — μ 2 ), μ d , (p 1 -p 2 )). Доверительные интервалы для каждого параметра имеют следующий общий вид: Оценка точки + Погрешность В модуле по доверительным интервалам мы вывели формулу доверительного интервала для μ как На практике мы используем стандартное отклонение выборки для оценки стандартного отклонения генеральной совокупности. Точечная оценка среднего значения генеральной совокупности является средним значением выборки, а предел погрешности равен При планировании исследований мы хотим определить размер выборки, необходимый для обеспечения того, чтобы погрешность была достаточно малой, чтобы быть информативной. Например, предположим, что мы хотим оценить средний вес студенток колледжа. Мы проводим исследование и получаем 95% доверительный интервал следующим образом: 125 + 40 фунтов, или от 85 до 165 фунтов. Допустимая погрешность в доверительном интервале одной выборки для μ может быть записана следующим образом: . Наша цель — определить размер выборки n, который гарантирует, что погрешность « E » не превышает заданного значения. Мы можем взять приведенную выше формулу и с помощью некоторой алгебры найти n : Сначала умножьте обе части уравнения на квадратный корень из n . Затем вычеркните квадратный корень из n из числителя и знаменателя в правой части уравнения (поскольку любое число, деленное само на себя, равно 1). Остается: Теперь разделите обе части на «Е» и вычеркните «Е» из числителя и знаменателя в левой части. Это оставляет: Наконец, возведите в квадрат обе части уравнения, чтобы получить: Эта формула генерирует размер выборки n , необходимый для того, чтобы погрешность E не превышала заданного значения. Чтобы найти n , мы должны ввести « Z «, « σ, и E Иногда трудно оценить σ . Когда мы используем приведенную выше формулу размера выборки (или одну из других формул, которые мы представим в следующих разделах), мы планируем исследование для оценки неизвестного среднего значения конкретной переменной результата в популяции. Маловероятно, что мы узнаем стандартное отклонение этой переменной. При расчете размера выборки исследователи часто используют значение стандартного отклонения из предыдущего исследования или исследования, проведенного в другой, но сопоставимой популяции. Вычисление размера выборки не является применением статистического вывода, и поэтому разумно использовать соответствующую оценку стандартного отклонения. Оценка может быть получена из другого исследования, о котором сообщалось в литературе; некоторые исследователи проводят небольшое пилотное исследование для оценки стандартного отклонения. Формула дает минимальный размер выборки, чтобы гарантировать, что погрешность доверительного интервала не превысит E . При планировании исследований исследователи также должны учитывать отсев или выбывание из-под наблюдения. Приведенная выше формула дает количество участников, необходимых для полных данных, чтобы гарантировать, что погрешность в доверительном интервале не превышает E . В следующих разделах мы проиллюстрируем, как проблема истощения решается в исследованиях по планированию, на примерах. В исследованиях, в которых планируется оценить среднее значение непрерывной переменной исхода в отдельной популяции, формула для определения размера выборки приведена ниже: , где Z — значение стандартного нормального распределения, отражающее уровень достоверности, который будет использоваться (например, Z = 1,96 для 95%), σ — стандартное отклонение переменной результата, а E — желаемое значение. допустимая погрешность. Приведенная выше формула генерирует минимальное количество субъектов, необходимое для обеспечения того, чтобы погрешность в доверительном интервале для μ не превышала Е . Пример 1: Исследователь хочет оценить среднее систолическое артериальное давление у детей с врожденными пороками сердца в возрасте от 3 до 5 лет. Сколько детей должно быть включено в исследование? Исследователь планирует использовать 95% доверительный интервал (т.е. Чтобы гарантировать, что 95% доверительный интервал оценки среднего систолического артериального давления у детей в возрасте от 3 до 5 лет с врожденным пороком сердца находится в пределах 5 единиц от истинного среднего значения, необходима выборка размером 62. [ Примечание : Мы всегда округляем; формулы размера выборки всегда генерируют минимальное количество субъектов, необходимое для обеспечения заданной точности.] Если бы мы предположили, что стандартное отклонение равно 15, размер выборки был бы n=35. Исследователь хочет оценить средний вес детей при рождении в срок (примерно 40 недель беременности) у матерей в возрасте 19 лет и младше. Средняя масса тела при рождении доношенных детей от матерей в возрасте 20 лет и старше составляет 3510 граммов при стандартном отклонении 385 граммов. Сколько женщин в возрасте 19 лет и младше должно быть включено в исследование, чтобы гарантировать, что оценка среднего веса при рождении их младенцев с доверительным интервалом 95% имеет погрешность, не превышающую 100 граммов? Попробуйте проработать расчет, прежде чем смотреть на ответ. Ответ В исследованиях, план которых заключается в оценке доли успешных результатов в дихотомической переменной результата (да/нет) в одной популяции, формула для определения размера выборки: , где Z — значение из стандартного нормального распределения, отражающее уровень достоверности, который будет использоваться (например, Z = 1,96 для 95%), а E — желаемая погрешность. Пример 2: Исследователь хочет оценить долю первокурсников своего университета, которые в настоящее время курят сигареты (т. е. распространенность курения). Сколько первокурсников должно быть вовлечено в исследование, чтобы гарантировать, что оценка 95% доверительного интервала доли курящих первокурсников находится в пределах 5% от истинной доли? Поскольку у нас нет информации о доле курящих первокурсников, мы используем 0,5 для оценки размера выборки следующим образом: Чтобы гарантировать, что оценка 95% доверительного интервала доли курящих первокурсников находится в пределах 5% от истинной доли, необходима выборка размером 385. Предположим, что аналогичное исследование было проведено 2 года назад и обнаружило, что распространенность курения среди первокурсников составила 27%. Если исследователь считает, что это разумная оценка распространенности спустя 2 года, ее можно использовать для планирования следующего исследования. Используя эту оценку p, какой размер выборки необходим (при условии, что снова 9Будет использоваться доверительный интервал 5%, и мы хотим такой же уровень точности)? Ответ Пример 3: Исследователь хочет оценить распространенность рака молочной железы среди женщин в возрасте от 40 до 45 лет, проживающих в Бостоне. Сколько женщин должно быть вовлечено в исследование, чтобы оценка была точной? Национальные данные свидетельствуют о том, что у 1 из 235 женщин диагностируют рак молочной железы к 40 годам. Это соответствует доле 0,0043 (0,43%) или распространенности 43 на 10 000 женщин. Предположим, исследователь хочет, чтобы оценка была в пределах 10 на 10 000 женщин с 95% уверенности. Выборка размером n = 16 448 гарантирует, что оценка 95% доверительного интервала распространенности рака молочной железы находится в пределах 0,10 (или в пределах 10 женщин на 10 000) от его истинного значения. Это ситуация, когда исследователи могут решить, что выборка такого размера невозможна. Предположим, что исследователи сочли, что выборка размером 5000 будет разумной с практической точки зрения. Как точно мы можем оценить распространенность при размере выборки n=5000? Напомним, что формула доверительного интервала для оценки распространенности: . Предполагая, что распространенность рака молочной железы в выборке будет близка к таковой, основанной на национальных данных, мы ожидаем, что предел погрешности будет примерно равен следующему: Таким образом, при n=5000 женщин можно ожидать, что 95% доверительный интервал будет иметь погрешность 0,0018 (или 18 на 10 000). Исследователи должны решить, будет ли это достаточно точным, чтобы ответить на исследовательский вопрос. В исследованиях, в которых планируется оценить разницу в средних значениях между двумя независимыми популяциями, ниже приводится формула для определения размера выборки в каждой группе сравнения: , где n i — требуемый размер выборки в каждой группе (i = 1,2), Z — значение стандартного нормального распределения, отражающее уровень достоверности, который будет использоваться, а E — желаемая погрешность. σ снова отражает стандартное отклонение переменной результата. Если имеются данные о вариабельности исхода в каждой группе сравнения, можно рассчитать Sp и использовать его в формуле размера выборки. Однако чаще бывает так, что данные о вариабельности исхода доступны только для одной группы, часто не получавшей лечения (например, плацебо-контроль) или не подвергавшейся воздействию. При планировании клинического испытания нового препарата или процедуры часто доступны данные из других испытаний, в которых участвовало плацебо или активная контрольная группа (т. е. стандартное лекарство или лечение, назначенное для изучаемого состояния). Стандартное отклонение переменной исхода, измеренное у пациентов, отнесенных к группе плацебо, контрольной группе или группе, не подвергавшейся воздействию, можно использовать для планирования будущих испытаний, как показано ниже. Обратите внимание, что формула для размера выборки генерирует оценки размера выборки для выборок одинакового размера. Если планируется исследование, в котором будет назначено разное количество пациентов или разное количество пациентов будет составлять группы сравнения, то можно использовать альтернативные формулы. Пример 4: Исследователь хочет запланировать клиническое испытание для оценки эффективности нового препарата, предназначенного для повышения уровня холестерина ЛПВП («хорошего» холестерина). План состоит в том, чтобы зарегистрировать участников и случайным образом назначить им либо новый препарат, либо плацебо. Холестерин ЛПВП будет измеряться у каждого участника через 12 недель назначенного лечения. Основываясь на предыдущем опыте подобных испытаний, исследователь ожидает, что 10% всех участников будут потеряны для последующего наблюдения или выпадут из исследования в течение 12 недель. А 95% доверительный интервал будет оцениваться для количественной оценки разницы средних уровней ЛПВП между пациентами, принимающими новый препарат, по сравнению с плацебо. Размер выборки рассчитывается следующим образом: Основная проблема заключается в определении вариабельности интересующего исхода (σ), в данном случае стандартного отклонения холестерина ЛПВП. Чтобы спланировать это исследование, мы можем использовать данные Framingham Heart Study. У участников, присутствовавших на седьмом обследовании в рамках исследования «Потомство» и не получавших лечения от высокого уровня холестерина, стандартное отклонение холестерина ЛПВП составляет 17,1. Мы будем использовать это значение и другие входные данные для расчета размеров выборки следующим образом: Образцы размером n 1 = 250 и n 2 = 250 гарантируют, что 95% доверительный интервал для разницы средних уровней ЛПВП будет иметь погрешность не более 3 единиц. Опять же, эти размеры выборки относятся к количеству участников с полными данными. N (число для регистрации) * (% оставшихся) = желаемый размер выборки Следовательно, N (число для регистрации) = желаемый размер выборки/(% оставшихся) Н = 500/0,90 = 556 Если они ожидают 10% отсева, исследователи должны зарегистрировать 556 участников. Это обеспечит N = 500 с полными данными в конце испытания. Пример 5: Исследователь хочет сравнить две программы диеты для детей, страдающих ожирением. Одна диета — это диета с низким содержанием жиров, а другая — диета с низким содержанием углеводов. План состоит в том, чтобы зачислить детей и взвесить их в начале исследования. Затем каждому ребенку будет случайным образом назначена либо диета с низким содержанием жиров, либо диета с низким содержанием углеводов. Размер выборки рассчитывается следующим образом: Опять же проблема заключается в определении вариабельности интересующего результата (σ), здесь стандартное отклонение в фунтах, потерянных за 8 недель. Чтобы спланировать это исследование, исследователи используют данные опубликованного исследования у взрослых. Предположим, в одном таком исследовании сравнивались одни и те же диеты у взрослых, и в каждой диетической группе участвовало 100 человек. Теперь мы используем это значение и другие входные данные для вычисления размеров выборки: Образцы размером n 1 = 56 и n 2 = 56 гарантируют, что 95% доверительный интервал для разницы в весе, потерянном между диетами, будет иметь погрешность не более 3 фунтов. Опять же, эти размеры выборки относятся к количеству детей с полными данными. Следователи ожидают 20% отсева. Чтобы гарантировать, что общий размер выборки 112 будет доступен через 8 недель, исследователь должен набрать больше участников, чтобы учесть отсев. N (число для регистрации) * (% оставшихся) = желаемый размер выборки Следовательно, N (число для регистрации) = желаемый размер выборки/(% оставшихся) Н = 112/0,80 = 140 В исследованиях, в которых планируется оценить среднюю разницу непрерывного результата на основе сопоставленных данных, формула для определения размера выборки приведена ниже: , где Z — значение стандартного нормального распределения, отражающее уровень достоверности, который будет использоваться (например, Z = 1,9). В исследованиях, где планируется оценить разницу в пропорциях между двумя независимыми популяциями (т. е. оценить разницу в риске), формула для определения размера выборки, необходимой в каждой группе сравнения, выглядит следующим образом: , где n i — размер выборки, требуемый в каждой группе (i = 1,2), Z — значение из стандартного нормального распределения, отражающее уровень достоверности, который будет использоваться (например, Z = 1,96 для 95%), и E — желаемая погрешность. р 1 и р 2 — доли успехов в каждой группе сравнения. Опять же, здесь мы планируем исследование для получения 95% доверительного интервала для разницы в неизвестных пропорциях, и формула для оценки необходимых размеров выборки требует р 1 и стр 2 . Подобно ситуации с двумя независимыми выборками и непрерывным результатом в верхней части этой страницы, может случиться так, что будут доступны данные о доле успехов в одной группе, обычно не получавшей лечения (например, плацебо-контроль) или не подвергавшейся воздействию. . Если это так, то известная пропорция может быть использована как для p 1 и p 2 в приведенной выше формуле. Формула, показанная выше, генерирует оценки размера выборки для выборок одинакового размера. Если планируется исследование, в котором будет назначено разное количество пациентов или разное количество пациентов будет составлять группы сравнения, то можно использовать альтернативные формулы. Пример 6: Исследователь хочет оценить влияние курения во время беременности на преждевременные роды. Нормальная беременность длится примерно 40 недель, а преждевременные роды происходят до 37 недель. В отчете Национальной статистики естественного движения населения за 2005 год указано, что примерно 12% младенцев в Соединенных Штатах рождаются преждевременно. 5 Исследователь планирует собрать данные посредством просмотра медицинской документации и создать 95% доверительный интервал для разницы в доле младенцев, родившихся недоношенными у женщин, которые курили во время беременности, по сравнению с теми, кто не курил. Сколько женщин должно быть включено в исследование, чтобы гарантировать, что 95% доверительный интервал для разницы в пропорциях имеет погрешность не более 4%? Размер выборки (т. е. количество женщин, которые курили и не курили во время беременности) можно рассчитать с помощью приведенной выше формулы. Выборки размером n 1 = 508 женщин, которые курили во время беременности, и n 2 = 508 женщин, которые не курили во время беременности, гарантируют, что 95% доверительный интервал для разницы в доле преждевременных родов будет иметь запас погрешность не более 4%. Является ли здесь проблемой истощение? Ответ В модуле по проверке гипотез для средних и долей мы представили методы для средних, пропорций, различий в средних и различий в пропорциях. В то время как каждый тест включал детали, которые были специфичны для интересующего результата (например, непрерывный или дихотомический) и количества групп сравнения (одна, две, более двух), в каждом тесте были общие элементы. Например, в каждой проверке гипотезы могут быть допущены две ошибки. Здесь мы представляем формулы для определения размера выборки, необходимой для обеспечения высокой мощности теста. Вычисления размера выборки зависят от уровня значимости, aα, желаемой мощности теста (эквивалентной 1-β), изменчивости результата и размера эффекта. Величина эффекта представляет собой разницу в интересующем параметре, которая представляет собой клинически значимую разницу. Подобно погрешности в приложениях доверительного интервала, размер эффекта определяется на основе клинических или практических критериев, а не статистических критериев. Понятие статистической мощности может быть трудно понять. Прежде чем представить формулы для определения размеров выборки, необходимых для обеспечения высокой мощности в тесте, мы сначала обсудим мощность с концептуальной точки зрения. Предположим, мы хотим проверить следующие гипотезы при aα = 0,05: H 0 : μ = 90 по сравнению с H 1 : μ ≠ 90. и Если нулевая гипотеза верна, можно наблюдать любое среднее значение выборки, показанное на рисунке ниже; все возможно под H 0 : μ = 90. Когда мы устанавливаем решающее правило для нашей проверки гипотезы, мы определяем критические значения на основе α = 0,05 и двустороннего теста. Когда мы проводим проверки гипотез, мы обычно стандартизируем данные (например, преобразуем в Z или t), а критические значения являются соответствующими значениями из распределения вероятностей, используемого в тесте. Чтобы облегчить интерпретацию, мы продолжим это обсуждение с в отличие от Z. Критические значения для двустороннего теста с α = 0,05 составляют 86,06 и 9.3,92 (эти значения соответствуют -1,96 и 1,96 соответственно по шкале Z), поэтому правило принятия решения следующее: Отклонить H 0 , если < 86,06 или если > 93,92. Область отторжения показана в конце рисунка ниже. Область отклонения для теста H 0 : μ = 90 по сравнению с H 1 : μ ≠ 90 при α = 0,05 . Площади на двух концах кривой представляют вероятность ошибки типа I, α = 0,05. Теперь предположим, что альтернативная гипотеза H 1 верна (т. е. μ ≠ 90) и что истинное среднее на самом деле равно 94. На рисунке ниже показано распределение выборочного среднего при нулевой и альтернативной гипотезах. значения выборочного среднего показаны по горизонтальной оси. Распределение Under H 0 : μ = 90 и Under H 1 : μ = 94 Если истинное среднее значение равно 94, то альтернативная гипотеза верна. В нашем тесте мы выбрали α = 0,05 и отвергли H 0 , если наблюдаемое среднее значение выборки превышает 93,92 (на данный момент основное внимание уделяется верхнему хвосту области отклонения). Критическое значение (93,92) указано вертикальной линией. Вероятность ошибки II рода обозначается β, а β = P(Не отвергать H 0 | H 0 ложно), т. е. вероятность не отвергнуть нулевую гипотезу, если нулевая гипотеза верна. β показан на рисунке выше как площадь под самой правой кривой (H 1 ) слева от вертикальной линии (где мы не отбрасываем H 0 ). Обратите внимание, что β и мощность связаны с α, изменчивостью результата и величиной эффекта. Из рисунка выше видно, что произойдет с β и мощностью, если мы увеличим α. Предположим, например, что мы увеличиваем α до α=0,10. Верхнее критическое значение будет равно 92,56 вместо 93,92. Вертикальная линия сдвинется влево, увеличивая α, уменьшая β и увеличивая мощность. Хотя лучшим тестом является тест с более высокой мощностью, не рекомендуется увеличивать α как средство увеличения мощности. Тем не менее, существует прямая связь между α и мощностью (с увеличением α увеличивается и мощность). β и мощность также связаны с изменчивостью исхода и величиной эффекта. Величина эффекта — это разница в интересующем параметре (например, μ), которая представляет собой клинически значимую разницу. Рисунок — Распределение Under H 0 : μ = 90 и Under H 1 : μ = 98. Обратите внимание, что мощность намного выше, когда разница между средним значением H 0 больше, чем H 1 (т. е. 90 против 98). Статистический тест с гораздо большей вероятностью отклонит нулевую гипотезу в пользу альтернативы, если истинное среднее значение равно 9.8, чем если бы истинное среднее равно 94. Обратите также внимание на то, что в этом случае распределение в нулевой и альтернативной гипотезах мало перекрывается. Если наблюдается выборочное среднее значение 97 или выше, очень маловероятно, что оно получено из распределения, среднее значение которого равно 90. При планировании исследований большинство людей принимают во внимание мощность 80 % или 90 % (точно так же, как мы обычно используем 95 % в качестве доверительного уровня для оценок доверительного интервала). Входные данные для формул размера выборки включают желаемую мощность, уровень значимости и размер эффекта. Величина эффекта выбирается для представления клинически значимого или практически важного различия в интересующем параметре, как мы проиллюстрируем. Формулы, которые мы приводим ниже, дают минимальный размер выборки, гарантирующий, что проверка гипотезы будет иметь заданную вероятность отклонения нулевой гипотезы, когда она ложна (т. е. указанную мощность). В исследованиях, в которых планируется провести проверку гипотезы, сравнивая среднее значение непрерывной переменной исхода в одной популяции с известным средним значением, представляют интерес следующие гипотезы: H 0 : μ = μ 0 и H 1 : μ ≠ μ 0 , где μ 0 — известное среднее значение (например, исторический контроль). Формула для определения размера выборки, чтобы гарантировать, что тест имеет заданную мощность, приведена ниже: , где α — выбранный уровень значимости, а Z 1-α/2 — значение стандартного нормального распределения, ниже которого находится 1-α/2. Например, если α=0,05, то 1-α/2 = 0,975 и Z=1,960. ES — размер эффекта , определяемый следующим образом: , где μ 0 — среднее значение по H 0 , μ 1 — среднее значение по H 1 , а σ — стандартное отклонение интересующего результата. Числитель размера эффекта, абсолютное значение разницы средних | мк 1 — μ 0 | представляет то, что считается клинически значимым или практически важным различием в средних значениях. Подобно проблеме, с которой мы столкнулись при планировании исследований для оценки доверительных интервалов, иногда бывает сложно оценить стандартное отклонение. Пример 7: Исследователь предполагает, что у людей без диабета уровень глюкозы в крови натощак, фактор риска ишемической болезни сердца, выше у тех, кто выпивает не менее 2 чашек кофе в день. Планируется поперечное исследование для оценки среднего уровня глюкозы в крови натощак у людей, выпивающих не менее двух чашек кофе в день. Средний уровень глюкозы в крови натощак у людей без диабета составляет 95,0 мг/дл со стандартным отклонением 9.0,8 мг/дл. 7 Если средний уровень глюкозы в крови у людей, которые пьют не менее 2 чашек кофе в день, составляет 100 мг/дл, это может иметь клиническое значение. Размер эффекта рассчитывается как: . Величина эффекта представляет собой значимую разницу в среднем для генеральной совокупности — здесь 95 против 100, или 0,51 единицы стандартного отклонения отличается. Теперь мы подставляем размер эффекта и соответствующие значения Z для выбранных α и мощности, чтобы вычислить размер выборки. Таким образом, размер выборки n=31 гарантирует, что двусторонний тест с α =0,05 имеет мощность 80% для обнаружения разницы в 5 мг/дл в среднем уровне глюкозы в крови натощак. В запланированном исследовании участников попросят голодать в течение ночи и сдать образец крови для анализа уровня глюкозы. Основываясь на предыдущем опыте, исследователи предполагают, что 10% участников не будут голодать или откажутся следовать протоколу исследования. N (число для регистрации) * (% следования протоколу) = желаемый размер выборки Следовательно, N (число для регистрации) = желаемый размер выборки/(% оставшихся) Н = 31/0,90 = 35. В исследованиях, в которых планируется выполнить проверку гипотезы, сравнивая долю успешных результатов в дихотомической переменной исхода в одной популяции с известной пропорцией, представляют интерес следующие гипотезы: против , где p 0 — известная пропорция (например, исторический контроль). Формула для определения размера выборки для обеспечения заданной мощности теста приведена ниже: , где α — выбранный уровень значимости, а Z 1-α/2 — значение стандартного нормального распределения, ниже которого находится 1-α/2. 1-β — выбранная мощность, Z 1-β – значение из стандартного нормального распределения, в котором 1-β находится ниже него, а ES – величина эффекта, определяемая следующим образом: , где p 0 — пропорция по H 0 , а p 1 — пропорция по H 1 . Пример 8: Недавний отчет Фрамингемского исследования сердца показал, что 26% людей, не страдающих сердечно-сосудистыми заболеваниями, имели повышенный уровень холестерина ЛПНП, определяемый как ЛПНП > 159.мг/дл. 9 Исследователь предполагает, что более высокая доля пациентов с сердечно-сосудистыми заболеваниями в анамнезе будет иметь повышенный уровень холестерина ЛПНП. Сколько пациентов необходимо обследовать, чтобы убедиться, что мощность теста составляет 90 % для выявления 5 % разницы в пропорции с повышенным холестерином ЛПНП? Будет использован двусторонний тест с уровнем значимости 5%. Сначала мы вычисляем размер эффекта: Теперь мы подставляем размер эффекта и соответствующие значения Z для выбранных α и мощности, чтобы вычислить размер выборки. Выборка размером n = 869 гарантирует, что двусторонний тест с α = 0,05 имеет 90-процентную мощность для выявления 5-процентной разницы в доле пациентов с сердечно-сосудистыми заболеваниями в анамнезе, у которых повышен уровень холестерина ЛПНП. Производитель медицинского оборудования производит имплантируемые стенты. В процессе производства примерно 10% стентов признаются бракованными. Производитель хочет проверить, превышает ли доля дефектных стентов 10%. Если в процессе получается более 15% дефектных стентов, необходимо предпринять корректирующие действия. Поэтому производитель хочет, чтобы тест имел 90% мощность для обнаружения разницы в пропорциях этой величины. Сколько стентов необходимо оценить? Для своих расчетов используйте двусторонний тест с уровнем значимости 5%. (Проведите вычисления самостоятельно, прежде чем смотреть ответ.) Ответ В исследованиях, в которых планируется выполнить проверку гипотезы, сравнивая средние значения непрерывной переменной результата в двух независимых выборках, представляют интерес следующие гипотезы: против , где μ 1 и μ 2 — средние значения в двух сравниваемых популяциях. , где n i — размер выборки, требуемый в каждой группе (i = 1,2), α — выбранный уровень значимости, а Z 1-α /2 — значение из стандартного нормального распределения, содержащего 1-α /2 под ним, а 1- β – выбранная мощность и Z 1-β — это значение стандартного нормального распределения, которое ниже на 1-β. ES — размер эффекта, определяемый как: где | μ 1 — μ 2 | является абсолютным значением разницы в средних значениях между двумя группами, ожидаемой согласно альтернативной гипотезе, H 1 . σ — стандартное отклонение интересующего результата. Напомним из модуля «Проверка гипотез», что, когда мы проводили проверку гипотез, сравнивая средние значения двух независимых групп, мы использовали Sp, объединенную оценку общего стандартного отклонения, как меру изменчивости результата. Sp вычисляется следующим образом: Если имеются данные о вариабельности исхода в каждой группе сравнения, можно рассчитать Sp и использовать его для создания размеров выборки. Также обратите внимание, что приведенная выше формула позволяет получить оценки размера выборки для выборок одинакового размера. Если планируется исследование, в котором будет назначено разное количество пациентов или разное количество пациентов будет составлять группы сравнения, то можно использовать альтернативные формулы (см. Пример 9: Исследователь планирует клиническое испытание для оценки эффективности нового препарата, предназначенного для снижения систолического артериального давления. План состоит в том, чтобы зарегистрировать участников и случайным образом назначить им либо новый препарат, либо плацебо. Систолическое артериальное давление будет измеряться у каждого участника через 12 недель назначенного лечения. Основываясь на предыдущем опыте проведения подобных испытаний, исследователь ожидает, что 10% всех участников будут потеряны для последующего наблюдения или выпадут из исследования. Если новый препарат показывает снижение среднего систолического артериального давления на 5 единиц, это будет клинически значимым снижением. Сколько пациентов должно быть включено в исследование, чтобы гарантировать, что мощность теста составляет 80% для обнаружения этой разницы? Будет использован двусторонний тест с уровнем значимости 5%. Для расчета размера эффекта необходима оценка вариабельности систолического артериального давления. Анализ данных Framingham Heart Study показал, что стандартное отклонение систолического артериального давления составило 19,0. Это значение можно использовать для планирования испытания. Размер эффекта: Теперь мы подставляем размер эффекта и соответствующие значения Z для выбранных α и мощности, чтобы вычислить размер выборки. Выборки размером n 1 = 232 и n 2 = 232 гарантируют, что проверка гипотезы будет иметь 80%-ную мощность для обнаружения разницы в 5 единиц среднего систолического артериального давления у пациентов, получающих новый препарат, по сравнению с пациентами прием плацебо. Однако исследователи предположили, что уровень отсева составляет 10% (в обеих группах), и чтобы обеспечить общий размер выборки в 232 человека, им необходимо учесть отсев. N (число для регистрации) * (% оставшихся) = желаемый размер выборки Следовательно, N (число для регистрации) = желаемый размер выборки/(% оставшихся) N = 232/0,90 = 258. Исследователь должен зарегистрировать 258 участников, которым случайным образом будет назначено либо новое лекарство, либо плацебо. Исследователь планирует исследование для оценки связи между потреблением алкоголя и средним баллом среди выпускников колледжей. План состоит в том, чтобы классифицировать учащихся как сильно пьющих или не употребляющих 5 или более порций алкоголя в обычный день употребления алкоголя в качестве критерия злоупотребления алкоголем. Средние средние баллы будут сравниваться между учащимися, классифицированными как сильно пьющие, и учащимися, не использующими двух независимых выборок для проверки материального положения. Предполагается, что стандартное отклонение среднего балла составляет 0,42, а значимая разница в среднем балле (по отношению к употреблению алкоголя) составляет 0,25 единицы. Сколько выпускников колледжей должно быть зачислено в исследование, чтобы гарантировать, что мощность теста составляет 80%, чтобы обнаружить разницу в 0,25 единицы в средних баллах? Используйте двусторонний тест с уровнем значимости 5%. Ответ В исследованиях, в которых планируется выполнить проверку гипотезы о средней разнице в непрерывной переменной результата на основе сопоставленных данных, представляют интерес следующие гипотезы: против , где μ d — средняя разница в популяции. Формула для определения размера выборки для обеспечения заданной мощности теста приведена ниже: , где α — выбранный уровень значимости, а Z 1-α/2 — значение из стандартного нормального распределения, имеющего 1-α/2 ниже него, 1-β — выбранная степень, а Z 1-β — значение из стандартного нормального распределения, содержащее 1-β ниже него, а ES представляет собой величину эффекта, определяемую следующим образом: , где μ d — средняя разность, ожидаемая при альтернативной гипотезе, H 1 , а σ d — стандартное отклонение разница в результате (например, разница, основанная на измерениях во времени, или разница между подобранными парами). Пример 10: Исследователь хочет оценить эффективность лечения иглоукалыванием для уменьшения боли у пациентов с хроническими мигренозными головными болями. План состоит в том, чтобы зарегистрировать пациентов, которые страдают от мигрени. Каждому будет предложено оценить тяжесть боли, которую он испытывает при следующей мигрени, прежде чем будет назначено какое-либо лечение. Боль будет регистрироваться по шкале от 1 до 100, где более высокие баллы указывают на более сильную боль. Затем каждый пациент проходит курс лечения иглоукалыванием. При следующей мигрени (после лечения) каждого пациента снова попросят оценить тяжесть боли. Разница в боли будет рассчитана для каждого пациента. Будет проведена двусторонняя проверка гипотезы при α = 0,05, чтобы оценить, существует ли статистически значимая разница в показателях боли до и после лечения. Сколько пациентов должно быть вовлечено в исследование, чтобы гарантировать, что тест имеет мощность 80% для обнаружения разницы в 10 единиц по шкале боли? Предположим, что стандартное отклонение в оценках различий составляет приблизительно 20 единиц. Сначала вычислите размер эффекта: Затем подставьте размер эффекта и соответствующие значения Z для выбранных α и мощности, чтобы вычислить размер выборки. Выборка размером n = 32 пациента с мигренью гарантирует, что двусторонний тест с α = 0,05 имеет мощность 80% для определения средней разницы в 10 баллов в боли до и после лечения, при условии, что все 32 пациента завершили лечение. . В исследованиях, в которых планируется провести проверку гипотез, сравнивая долю успешных результатов в двух независимых выборках, представляют интерес следующие гипотезы: H 0 : p 1 = p 2 по сравнению с H 1 : p 1 ≠ p 2 , где p 1 и p 2 — доли в двух сравниваемых популяциях. Формула для определения размеров выборки для обеспечения заданной мощности теста приведена ниже: , где n i — размер выборки, требуемый в каждой группе (i = 1,2), α — выбранный уровень значимости, а Z 1-α/2 — значение из стандартного нормального распределения, содержащего 1-α /2 ниже него, а 1-β — это выбранная степень, а Z 1-β — это значение из стандартного нормального распределения, содержащее 1-β ниже него. , где |p 1 — p 2 | — абсолютное значение разницы в пропорциях между двумя группами, ожидаемое при альтернативной гипотезе, H 1 , а p — общая пропорция, основанная на объединении данных из двух сравниваемых групп (p можно вычислить, взяв среднее пропорций в двух сравниваемых группах, предполагая, что группы будут примерно одинакового размера). Пример 11: Исследователь выдвинул гипотезу о том, что заболеваемость гриппом среди учащихся, которые регулярно посещают спортивные сооружения, выше, чем среди их сверстников, которые этого не делают. Исследование будет проводиться весной. Каждого учащегося спросят, регулярно ли он посещал спортивный комплекс в течение последних 6 месяцев и болел ли он гриппом. Будет проведена проверка гипотезы для сравнения доли учащихся, которые регулярно посещали спортивные сооружения и заболели гриппом, с долей учащихся, которые не посещали спортивные сооружения и заболели гриппом. Сначала мы вычисляем величину эффекта, подставляя доли учащихся в каждой группе, у которых ожидается развитие гриппа, p 1 = 0,46 (т. р=0,41 (т.е. (0,46+0,35)/2): Теперь мы подставляем размер эффекта и соответствующие значения Z для выбранных α и мощности, чтобы вычислить размер выборки. Образцы размером n 1 = 324 и n 2 =324 гарантирует, что проверка гипотезы будет иметь мощность 80% для выявления 30%-ной разницы в доле учащихся, заболевших гриппом, между теми, кто регулярно и не посещает спортивные сооружения. Донорский кал? Действительно? Clostridium difficile (также называемый «C. difficile» или «C. diff.») представляет собой вид бактерий, который можно обнаружить в толстой кишке человека, хотя его численность контролируется другой нормальной флорой толстой кишки. Терапия антибиотиками иногда уменьшает нормальную флору в толстой кишке до такой степени, что C. difficile процветает и вызывает инфекцию с симптомами, варьирующимися от диареи до опасного для жизни воспаления толстой кишки. Заболевание, вызванное C. difficile, чаще всего поражает пожилых людей в больницах или учреждениях длительного ухода и обычно возникает после применения антибиотиков. В последние годы инфекции, вызванные C. difficile, стали более частыми, более тяжелыми и труднее поддающимися лечению. По иронии судьбы C. difficile сначала лечат путем прекращения приема антибиотиков, если они все еще назначаются. Если это не помогло, инфекцию лечили переходом на другой антибиотик. Однако лечение другим антибиотиком часто не излечивает инфекцию C. Ответ Определение надлежащего дизайна исследования важнее, чем статистический анализ; плохо спланированное исследование никогда нельзя спасти, в то время как плохо проанализированное исследование можно проанализировать повторно. В следующей таблице приведены формулы размера выборки для каждого описанного здесь сценария. Формулы организованы по предлагаемому анализу, оценке доверительного интервала или проверке гипотезы. Ситуация Размер образца до Оценка доверительного интервала Размер выборки для проверки гипотез Непрерывный результат, Один образец: CI для µ, H 0 : µ = µ 0 Непрерывный результат, Два независимых образца: CI для ( μ 1 — μ 2 ), H 0 : μ 1 = мк 2 Непрерывный результат, Два совпадающих образца: ДИ для μ d , H 0 : μ d = 0 Дихотомический исход, Один образец: CI для p , H 0 : p = p 0 Дихотомический исход, Два независимых образца: CI для (p 1 -p 2 ) , H 0 : p 1 = p 2 Исследователь хочет оценить средний вес детей при рождении в срок (примерно 40 недель беременности) у матерей в возрасте 19 лет и младше. Чтобы гарантировать, что оценка 95% доверительного интервала среднего веса при рождении находится в пределах 100 граммов от истинного среднего значения, необходима выборка размера 57. При планировании исследования исследователь должен учитывать тот факт, что у некоторых женщин возможны преждевременные роды. Если женщины включаются в исследование во время беременности, то необходимо будет включить более 57 женщин, чтобы после исключения преждевременно родивших 57 женщин с информацией о результатах были доступны для анализа. Например, если у 5% женщин ожидаются преждевременные роды (т. N (количество участников) * (% оставшихся) = желаемый размер выборки N (0,95) = 57 N = 57/0,95 = 60. Предположим, что аналогичное исследование было проведено 2 года назад и обнаружило, что распространенность курения среди первокурсников составила 27%. Если исследователь считает, что это разумная оценка распространенности спустя 2 года, ее можно использовать для планирования следующего исследования. Используя эту оценку p, какой размер выборки необходим (при условии, что снова будет использоваться 95% доверительный интервал, и мы хотим такой же уровень точности)? Чтобы гарантировать, что оценка 95% доверительного интервала доли курящих первокурсников находится в пределах 5% от истинной доли, необходима выборка размером 303. Производитель медицинского оборудования производит имплантируемые стенты. В процессе производства примерно 10% стентов признаются бракованными. Производитель хочет проверить, превышает ли доля дефектных стентов 10%. Если в процессе получается более 15% дефектных стентов, необходимо предпринять корректирующие действия. Поэтому производитель хочет, чтобы тест имел мощность 90% для обнаружения разницы в пропорциях этой величины. Сколько стентов необходимо оценить? Для своих расчетов используйте двусторонний тест с уровнем значимости 5%. Затем подставьте размер эффекта и соответствующие значения z для выбранной альфы и мощности, чтобы вычислить размер выборки. Размер выборки из 364 стентов гарантирует, что двусторонний тест с α = 0,05 имеет мощность 90% для обнаружения разницы в 0,05 или 5% в доле произведенных дефектных стентов. Исследователь планирует исследование для оценки связи между потреблением алкоголя и средним баллом среди выпускников колледжей. План состоит в том, чтобы классифицировать учащихся как сильно пьющих или не употребляющих 5 или более порций алкоголя в обычный день употребления алкоголя в качестве критерия злоупотребления алкоголем. Средние средние баллы будут сравниваться между учащимися, классифицированными как сильно пьющие, и учащимися, не использующими двух независимых выборок для проверки материального положения. Предполагается, что стандартное отклонение среднего балла составляет 0,42, а значимая разница в среднем балле (по отношению к употреблению алкоголя) составляет 0,25 единицы. Сколько выпускников колледжей должно быть зачислено в исследование, чтобы гарантировать, что мощность теста составляет 80%, чтобы обнаружить разницу в 0,25 единицы в средних баллах? Используйте двусторонний тест с уровнем значимости 5%. Сначала вычислите размер эффекта. Теперь подставьте размер эффекта и соответствующие значения z для альфы и мощности, чтобы вычислить размер выборки. Размеры выборки из n i = 44 сильно пьющих и 44, которые выпивают менее пяти порций алкоголя в обычный день употребления алкоголя, гарантируют, что проверка гипотезы имеет 80%-ную мощность для обнаружения разницы в 0,25 единицы в средних средних баллах. Сначала мы вычисляем размер эффекта, подставляя пропорции пациентов, которые, как ожидается, будут излечены при каждом лечении, p 1 = 0,6 и p 2 = 0,9, и общую пропорцию, p = 0,75: Теперь мы подставляем размер эффекта и соответствующие значения Z для выбранных a и мощности, чтобы вычислить размер выборки. Образцы размера n 1 =33 и n 2 =33 гарантирует, что проверка гипотезы будет иметь 80% мощности для обнаружения этой разницы в доле пациентов, излеченных от C. Фактически, исследователи зачислили по 38 человек в каждую группу, чтобы учесть отсев. Тем не менее, исследование было остановлено после промежуточного анализа. Из 16 пациентов в группе инфузии у 13 (81%) диарея, связанная с C. difficile, разрешилась после первой инфузии. Остальным 3 пациентам была проведена повторная инфузия фекалий от другого донора с разрешением у 2 пациентов. Разрешение инфекции C. difficile произошло только у 4 из 13 пациентов (31%), получавших антибиотик ванкомицин. Распределение частиц данного материала по размерам является важным параметром анализа в процессах контроля качества и исследовательских приложениях, поскольку многие другие свойства продукта напрямую связаны с ним. Распределение частиц по размерам влияет на свойства материала, такие как текучесть и поведение при транспортировке (для сыпучих материалов), реакционная способность, абразивность, растворимость, поведение при экстракции и реакции, вкус, прессуемость и многое другое. Анализ распределения частиц по размерам является установленной процедурой во многих лабораториях. В зависимости от материала пробы и объема исследования для этой цели используются различные методы. К ним относятся лазерная дифракция (LD), динамическое рассеяние света (DLS), динамический анализ изображений (DIA) или ситовой анализ. Обычно анализируют суспензии, эмульсии и сыпучие материалы, в исключительных случаях также аэрозоли (распылители). Обладая глубоким пониманием сильных и слабых сторон каждого метода, Microtrac предлагает непревзойденный ассортимент технологий для анализа гранулометрического состава. Наши специалисты будут рады помочь найти правильное решение для вашего приложения. Обзор продукцииСвяжитесь с нами! Большинство образцов представляют собой так называемые полидисперсные системы, что означает наличие частиц не одного размера, а разного размера. Ниже показан простой пример. Here, a mixture of grinding balls has been separated by size: 5 mm, 10 mm, 15 mm and 40 mm: уравнение. 24 приводят к распределению экстремальных значений Фреше ,
уравнение. 24 приводят к распределению экстремальных значений Фреше ,  Наша задача — вычислить предел Prob[x1≤x,x2≤x,⋯,xN≤x] =P(x)N→Φ(u) при N→∞, и что такое u=u(x) при приближении к этому пределу.
Наша задача — вычислить предел Prob[x1≤x,x2≤x,⋯,xN≤x] =P(x)N→Φ(u) при N→∞, и что такое u=u(x) при приближении к этому пределу. 2Класс Вейбулла
 (11)
(11) Это верно для α<1. Однако в дикой природе гораздо чаще встречается α≥1.
Это верно для α<1. Однако в дикой природе гораздо чаще встречается α≥1. 2.1Вейбулл: Пример
 19 на фиг. 1А.
19 на фиг. 1А. Мы делаем это, обращая выражение P(x)=r, где кумулятивная вероятность равна 21. Следовательно, мы имеем
Мы делаем это, обращая выражение P(x)=r, где кумулятивная вероятность равна 21. Следовательно, мы имеем Когда цепочка загружена, это будет ссылка с наименьший порог отказа , который сломается первым, что приведет к сбою цепочки в целом. Следовательно, распределение прочности ансамбля цепей является распределением экстремальных значений, но относительно наименьшего, а не наибольшего значения. Сила связи должна быть положительным числом. Следовательно, распределение силы связи обрывается при нуле или некотором положительном значении. Распределение вблизи этого значения отсечки должно вести себя как степенной закон на расстоянии от отсечки, например, из-за разложения Тейлора вокруг отсечки. Соответствующее распределение экстремальных значений, которое является распределением силы цепи, должно быть распределением Вейбулла.
Когда цепочка загружена, это будет ссылка с наименьший порог отказа , который сломается первым, что приведет к сбою цепочки в целом. Следовательно, распределение прочности ансамбля цепей является распределением экстремальных значений, но относительно наименьшего, а не наибольшего значения. Сила связи должна быть положительным числом. Следовательно, распределение силы связи обрывается при нуле или некотором положительном значении. Распределение вблизи этого значения отсечки должно вести себя как степенной закон на расстоянии от отсечки, например, из-за разложения Тейлора вокруг отсечки. Соответствующее распределение экстремальных значений, которое является распределением силы цепи, должно быть распределением Вейбулла. 3Класс Фреше
 Введем переменную замену
Введем переменную замену (32)
(32) 3.1Фреше: Пример
 Гистограмма с максимумом слева показывает все сгенерированные данные. Гистограмма с максимумом в середине показывает наибольшее число среди каждой последовательности чисел длиной 100, а гистограмма с максимумом справа показывает наибольшее число среди каждой последовательности чисел длиной 1000. Для каждой длины последовательности было сгенерировано 107 таких последовательностей.
Гистограмма с максимумом слева показывает все сгенерированные данные. Гистограмма с максимумом в середине показывает наибольшее число среди каждой последовательности чисел длиной 100, а гистограмма с максимумом справа показывает наибольшее число среди каждой последовательности чисел длиной 1000. Для каждой длины последовательности было сгенерировано 107 таких последовательностей. Эту цифру следует сравнить с фигурой 2А.
Эту цифру следует сравнить с фигурой 2А. 4Класс Гамбеля
 Мы делаем это в заключении, см. уравнение. 71. Из уравнения. 40 мы получаем, что
Мы делаем это в заключении, см. уравнение. 71. Из уравнения. 40 мы получаем, что
4.1 Достаточный критерий для класса Гумбеля
 Тогда мы имеем, что
Тогда мы имеем, что 4.2Возврат к выводу
 (61)
(61) 4.3 Пример: гауссиана
 Для больших аргументов он приближается к натуральному логарифму, W(z)→log(z) при z→∞ [16]. Это дает нам
Для больших аргументов он приближается к натуральному логарифму, W(z)→log(z) при z→∞ [16]. Это дает нам Здесь σ=1. Гистограмма с максимумом слева показывает все сгенерированные данные. Гистограмма с максимумом посередине показывает наибольшее число среди каждой последовательности чисел длиной 100, а гистограмма с крайним справа максимумом показывает наибольшее число среди каждой последовательности чисел длиной 1000. Для каждой длины последовательности было сгенерировано 107 таких последовательностей.
Здесь σ=1. Гистограмма с максимумом слева показывает все сгенерированные данные. Гистограмма с максимумом посередине показывает наибольшее число среди каждой последовательности чисел длиной 100, а гистограмма с крайним справа максимумом показывает наибольшее число среди каждой последовательности чисел длиной 1000. Для каждой длины последовательности было сгенерировано 107 таких последовательностей. Это связано с очень медленной сходимостью, вызванной W-функциями Ламберта. Медленная сходимость типична для распределений экстремальных значений Гамбеля. Эта медленная сходимость была проанализирована и недавно исправлена с помощью умного использования методов масштабирования [17].
Это связано с очень медленной сходимостью, вызванной W-функциями Ламберта. Медленная сходимость типична для распределений экстремальных значений Гамбеля. Эта медленная сходимость была проанализирована и недавно исправлена с помощью умного использования методов масштабирования [17]. 5Заключительные замечания
 ( 69)
( 69) Вклад авторов
Финансирование

Благодарности
Сноски
ССЫЛКИ
 Коулз С. Введение в статистическое моделирование экстремальных явлений . Берлин: Спрингер (2001).
Коулз С. Введение в статистическое моделирование экстремальных явлений . Берлин: Спрингер (2001). Nat Rev Mater (2018). 3 :211–24. doi:10.1038/s41578-018-0029-4
Nat Rev Mater (2018). 3 :211–24. doi:10.1038/s41578-018-0029-4 Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Численные рецепты . 3-е изд. Кембридж: Издательство Кембриджского университета (2007).
Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Численные рецепты . 3-е изд. Кембридж: Издательство Кембриджского университета (2007). Техническое примечание: Оценка бимодальных моделей распределения для определения критерия приема пищи у телок, получающих рацион с высоким содержанием зерна

принадлежность

Авторы
принадлежность
Абстрактный
 Самый длинный интервал без кормления, который считается частью приема пищи, определяется как критерий приема пищи. Цель этого исследования состояла в том, чтобы определить, какая комбинация двух функций плотности вероятности [(PDF): нормального Гаусса (G), Вейбулла (W), логарифмически-нормального, гамма и Гумбеля], используемая в бимодальной модели распределения, лучше всего соответствовала данных о перерывах между кормлениями, собранных у мясных телок. Признаки пищевого поведения (всего 572 627 событий BV) были измерены у 119 животных.телки получали рацион с высоким содержанием зерна (3,08 Мкал ME/кг сухого вещества) с использованием системы GrowSafe в течение 66 дней. Частота и продолжительность событий БВ в среднем составляли 75 ± 15 событий/сутки и 73,0 ± 22,3 мин/сутки соответственно. Бимодальные комбинации PDF были приспособлены к длинам интервалов, преобразованным в log(10) между событиями BV для каждого животного, с использованием пакета R mixdist (2.13). Информационный критерий Акаике (AIC) использовался для оценки соответствия 25 бимодальных комбинаций PDF.
Самый длинный интервал без кормления, который считается частью приема пищи, определяется как критерий приема пищи. Цель этого исследования состояла в том, чтобы определить, какая комбинация двух функций плотности вероятности [(PDF): нормального Гаусса (G), Вейбулла (W), логарифмически-нормального, гамма и Гумбеля], используемая в бимодальной модели распределения, лучше всего соответствовала данных о перерывах между кормлениями, собранных у мясных телок. Признаки пищевого поведения (всего 572 627 событий BV) были измерены у 119 животных.телки получали рацион с высоким содержанием зерна (3,08 Мкал ME/кг сухого вещества) с использованием системы GrowSafe в течение 66 дней. Частота и продолжительность событий БВ в среднем составляли 75 ± 15 событий/сутки и 73,0 ± 22,3 мин/сутки соответственно. Бимодальные комбинации PDF были приспособлены к длинам интервалов, преобразованным в log(10) между событиями BV для каждого животного, с использованием пакета R mixdist (2.13). Информационный критерий Акаике (AIC) использовался для оценки соответствия 25 бимодальных комбинаций PDF. Модель PDF с наименьшим значением AIC была выбрана как наиболее подходящая для каждого человека. Анализ χ(2) выбранного наилучшего распределения PDF среди особей показал, что 78,2% телок, лучше всего подходящих, имели модели G-W или W-W PDF. Оценки вероятности правдоподобия рассчитывались по среднему отклонению AIC каждой модели от стандартной модели G-G. Оценка вероятности вероятности G-W была выше (P = 0,001), чем комбинация W-W (0,9).97 против 0,727). Наш анализ показал, что модель G-W статистически лучше подходит и, скорее всего, является лучшим подходом для определения критерия приема пищи у мясных телок, получающих рацион с высоким содержанием зерна.
Модель PDF с наименьшим значением AIC была выбрана как наиболее подходящая для каждого человека. Анализ χ(2) выбранного наилучшего распределения PDF среди особей показал, что 78,2% телок, лучше всего подходящих, имели модели G-W или W-W PDF. Оценки вероятности правдоподобия рассчитывались по среднему отклонению AIC каждой модели от стандартной модели G-G. Оценка вероятности вероятности G-W была выше (P = 0,001), чем комбинация W-W (0,9).97 против 0,727). Наш анализ показал, что модель G-W статистически лучше подходит и, скорее всего, является лучшим подходом для определения критерия приема пищи у мясных телок, получающих рацион с высоким содержанием зерна. Похожие статьи
 Йейтс, член парламента, и соавт.
Дж Теор Биол. 2001 г., 7 декабря; 213(3):413-25. doi: 10.1006/jtbi.2001.2425.
Дж Теор Биол. 2001.
PMID: 11735288
Йейтс, член парламента, и соавт.
Дж Теор Биол. 2001 г., 7 декабря; 213(3):413-25. doi: 10.1006/jtbi.2001.2425.
Дж Теор Биол. 2001.
PMID: 11735288

Цитируется


Типы публикаций
термины MeSH
Определение мощности и размера выборки
Определение мощности и размера выборки Этот модуль будет посвящен формулам, которые можно использовать для оценки размера выборки, необходимой для получения оценки доверительного интервала с заданным пределом погрешности (точности) или для обеспечения того, чтобы проверка гипотезы имела высокую вероятность обнаружения значимой разницы в параметр.
Этот модуль будет посвящен формулам, которые можно использовать для оценки размера выборки, необходимой для получения оценки доверительного интервала с заданным пределом погрешности (точности) или для обеспечения того, чтобы проверка гипотезы имела высокую вероятность обнаружения значимой разницы в параметр. Однако во многих исследованиях размер выборки определяется финансовыми или логистическими ограничениями. Например, предположим, что предлагается провести исследование для оценки нового скринингового теста на синдром Дауна. Предположим, что скрининговый тест основан на анализе образца крови, взятого у женщин на ранних сроках беременности. Для оценки свойств скринингового теста (например, чувствительности и специфичности) каждой беременной женщине будет предложено сдать образец крови и дополнительно пройти амниоцентез. Амниоцентез включен в качестве золотого стандарта, и планируется сравнить результаты скринингового теста с результатами амниоцентеза. Предположим, что сбор и обработка образца крови стоит 250 долларов на участника, а амниоцентез — 9 долларов.00 с участника. Одни только эти финансовые ограничения могут существенно ограничить число женщин, которые могут быть зачислены. Точно так же, как важно учитывать как статистическую, так и клиническую значимость при интерпретации результатов статистического анализа, также важно взвешивать как статистические, так и логистические аспекты при определении размера выборки для исследования.
Однако во многих исследованиях размер выборки определяется финансовыми или логистическими ограничениями. Например, предположим, что предлагается провести исследование для оценки нового скринингового теста на синдром Дауна. Предположим, что скрининговый тест основан на анализе образца крови, взятого у женщин на ранних сроках беременности. Для оценки свойств скринингового теста (например, чувствительности и специфичности) каждой беременной женщине будет предложено сдать образец крови и дополнительно пройти амниоцентез. Амниоцентез включен в качестве золотого стандарта, и планируется сравнить результаты скринингового теста с результатами амниоцентеза. Предположим, что сбор и обработка образца крови стоит 250 долларов на участника, а амниоцентез — 9 долларов.00 с участника. Одни только эти финансовые ограничения могут существенно ограничить число женщин, которые могут быть зачислены. Точно так же, как важно учитывать как статистическую, так и клиническую значимость при интерпретации результатов статистического анализа, также важно взвешивать как статистические, так и логистические аспекты при определении размера выборки для исследования.
 Обратите внимание, что существует альтернативная формула для оценки среднего значения непрерывного результата в одной популяции, и она используется, когда размер выборки мал (n<30). Он включает значение из t-распределения, а не из стандартного нормального распределения, чтобы отразить желаемый уровень достоверности. При расчете размера выборки мы используем приведенную здесь формулу для большой выборки. [Примечание: результирующий размер выборки может быть небольшим, и на этапе анализа необходимо использовать соответствующую формулу доверительного интервала.]
Обратите внимание, что существует альтернативная формула для оценки среднего значения непрерывного результата в одной популяции, и она используется, когда размер выборки мал (n<30). Он включает значение из t-распределения, а не из стандартного нормального распределения, чтобы отразить желаемый уровень достоверности. При расчете размера выборки мы используем приведенную здесь формулу для большой выборки. [Примечание: результирующий размер выборки может быть небольшим, и на этапе анализа необходимо использовать соответствующую формулу доверительного интервала.] Погрешность настолько широка, что доверительный интервал неинформативен. Чтобы быть информативным, исследователь может захотеть, чтобы погрешность не превышала 5 или 10 фунтов (это означает, что 95% доверительный интервал будет иметь ширину (от нижнего до верхнего предела) 10 или 20 фунтов). Чтобы определить необходимый размер выборки, исследователь должен указать желаемую погрешность . Важно отметить, что это не статистический вопрос, а клинический или практический. Например, предположим, что мы хотим оценить средний вес при рождении младенцев, рожденных матерями, которые курили сигареты во время беременности. Вес при рождении младенцев явно имеет гораздо более ограниченный диапазон, чем вес студенток колледжа. Следовательно, мы, вероятно, хотели бы создать доверительный интервал для среднего веса при рождении, который имеет погрешность, не превышающую 1 или 2 фунта.
Погрешность настолько широка, что доверительный интервал неинформативен. Чтобы быть информативным, исследователь может захотеть, чтобы погрешность не превышала 5 или 10 фунтов (это означает, что 95% доверительный интервал будет иметь ширину (от нижнего до верхнего предела) 10 или 20 фунтов). Чтобы определить необходимый размер выборки, исследователь должен указать желаемую погрешность . Важно отметить, что это не статистический вопрос, а клинический или практический. Например, предположим, что мы хотим оценить средний вес при рождении младенцев, рожденных матерями, которые курили сигареты во время беременности. Вес при рождении младенцев явно имеет гораздо более ограниченный диапазон, чем вес студенток колледжа. Следовательно, мы, вероятно, хотели бы создать доверительный интервал для среднего веса при рождении, который имеет погрешность, не превышающую 1 или 2 фунта.

 Пилотное исследование обычно включает небольшое количество участников (например, n = 10), которые отбираются по принципу удобства, а не методом случайной выборки. Данные участников пилотного исследования можно использовать для расчета стандартного отклонения выборки, которое служит хорошей оценкой σ в формуле размера выборки. Независимо от того, как получена оценка изменчивости исхода, она всегда должна быть консервативной (т. е. настолько большой, насколько это разумно), чтобы результирующий размер выборки не был слишком мал.
Пилотное исследование обычно включает небольшое количество участников (например, n = 10), которые отбираются по принципу удобства, а не методом случайной выборки. Данные участников пилотного исследования можно использовать для расчета стандартного отклонения выборки, которое служит хорошей оценкой σ в формуле размера выборки. Независимо от того, как получена оценка изменчивости исхода, она всегда должна быть консервативной (т. е. настолько большой, насколько это разумно), чтобы результирующий размер выборки не был слишком мал.
 Z=1,96) и хочет погрешность в 5 единиц. Стандартное отклонение систолического артериального давления неизвестно, но исследователи провели поиск литературы и обнаружили, что стандартное отклонение систолического артериального давления у детей с другими пороками сердца составляет от 15 до 20. Чтобы оценить размер выборки, мы рассматриваем больший стандарт. отклонение для получения наиболее консервативного (наибольшего) размера выборки.
Z=1,96) и хочет погрешность в 5 единиц. Стандартное отклонение систолического артериального давления неизвестно, но исследователи провели поиск литературы и обнаружили, что стандартное отклонение систолического артериального давления у детей с другими пороками сердца составляет от 15 до 20. Чтобы оценить размер выборки, мы рассматриваем больший стандарт. отклонение для получения наиболее консервативного (наибольшего) размера выборки. Поскольку оценки стандартного отклонения были получены в результате исследований детей с другими пороками сердца, было бы целесообразно использовать большее стандартное отклонение и запланировать исследование с участием 62 детей. Выбор меньшего размера выборки потенциально может дать оценку доверительного интервала с большей погрешностью.
Поскольку оценки стандартного отклонения были получены в результате исследований детей с другими пороками сердца, было бы целесообразно использовать большее стандартное отклонение и запланировать исследование с участием 62 детей. Выбор меньшего размера выборки потенциально может дать оценку доверительного интервала с большей погрешностью. p — доля успехов в популяции. Здесь мы планируем исследование для создания 95% доверительный интервал для неизвестной доли населения, p . Уравнение для определения размера выборки для определения p, кажется, требует знания p, но очевидно, что это круговой аргумент, потому что если бы мы знали долю успехов в популяции, то исследование было бы не нужно! Что нам действительно нужно, так это приблизительное значение p или ожидаемое значение. Диапазон p составляет от 0 до 1, и, следовательно, диапазон p(1-p) составляет от 0 до 1. Значение p, которое максимизирует p(1-p), равно p=0,5. Следовательно, если нет доступной информации для аппроксимации p, то можно использовать p = 0,5 для получения наиболее консервативного или наибольшего размера выборки.
p — доля успехов в популяции. Здесь мы планируем исследование для создания 95% доверительный интервал для неизвестной доли населения, p . Уравнение для определения размера выборки для определения p, кажется, требует знания p, но очевидно, что это круговой аргумент, потому что если бы мы знали долю успехов в популяции, то исследование было бы не нужно! Что нам действительно нужно, так это приблизительное значение p или ожидаемое значение. Диапазон p составляет от 0 до 1, и, следовательно, диапазон p(1-p) составляет от 0 до 1. Значение p, которое максимизирует p(1-p), равно p=0,5. Следовательно, если нет доступной информации для аппроксимации p, то можно использовать p = 0,5 для получения наиболее консервативного или наибольшего размера выборки.
 Размер выборки рассчитывается следующим образом:
Размер выборки рассчитывается следующим образом: Обратите внимание, что вышеизложенное основано на предположении, что распространенность рака молочной железы в Бостоне аналогична общенациональной. Это может быть или не быть разумным предположением. Фактически, целью настоящего исследования является оценка распространенности в Бостоне. Исследовательская группа при участии клинических исследователей и специалистов по биостатистике должна тщательно оценить последствия выбора размера выборки n = 5000, n = 16 448 или любого промежуточного размера.
Обратите внимание, что вышеизложенное основано на предположении, что распространенность рака молочной железы в Бостоне аналогична общенациональной. Это может быть или не быть разумным предположением. Фактически, целью настоящего исследования является оценка распространенности в Бостоне. Исследовательская группа при участии клинических исследователей и специалистов по биостатистике должна тщательно оценить последствия выбора размера выборки n = 5000, n = 16 448 или любого промежуточного размера. Напомним из модуля о доверительных интервалах, что, когда мы генерировали оценку доверительного интервала для разницы в средних, мы использовали Sp, объединенную оценку общего стандартного отклонения, в качестве меры изменчивости результата (на основе объединения данных). , где Sp вычисляется следующим образом:
Напомним из модуля о доверительных интервалах, что, когда мы генерировали оценку доверительного интервала для разницы в средних, мы использовали Sp, объединенную оценку общего стандартного отклонения, в качестве меры изменчивости результата (на основе объединения данных). , где Sp вычисляется следующим образом:
 Исследователь хотел бы, чтобы погрешность была не более 3 единиц. Сколько пациентов следует набрать в исследование?
Исследователь хотел бы, чтобы погрешность была не более 3 единиц. Сколько пациентов следует набрать в исследование? Исследователи предположили, что коэффициент отсева (или отсева) составляет 10% (в обеих группах). Чтобы гарантировать, что общий размер выборки в 500 человек будет доступен через 12 недель, исследователь должен набрать больше участников, чтобы учесть отсев.
Исследователи предположили, что коэффициент отсева (или отсева) составляет 10% (в обеих группах). Чтобы гарантировать, что общий размер выборки в 500 человек будет доступен через 12 недель, исследователь должен набрать больше участников, чтобы учесть отсев. Каждый ребенок будет соблюдать назначенную диету в течение 8 недель, после чего его снова взвесят. Количество потерянных килограммов будет подсчитано для каждого ребенка. Основываясь на данных, полученных в ходе испытаний диеты у взрослых, исследователь ожидает, что 20% всех детей не завершат исследование. А 95% доверительный интервал будет рассчитан для количественной оценки разницы в весе, потерянном между двумя диетами, и исследователь хотел бы, чтобы погрешность не превышала 3 фунтов. Сколько детей должно быть привлечено к исследованию?
Каждый ребенок будет соблюдать назначенную диету в течение 8 недель, после чего его снова взвесят. Количество потерянных килограммов будет подсчитано для каждого ребенка. Основываясь на данных, полученных в ходе испытаний диеты у взрослых, исследователь ожидает, что 20% всех детей не завершат исследование. А 95% доверительный интервал будет рассчитан для количественной оценки разницы в весе, потерянном между двумя диетами, и исследователь хотел бы, чтобы погрешность не превышала 3 фунтов. Сколько детей должно быть привлечено к исследованию? В исследовании сообщалось о стандартном отклонении веса, потерянного за 8 недель на диете с низким содержанием жиров, на 8,4 фунта, и стандартном отклонении веса, потерянного за 8 недель на диете с низким содержанием углеводов, на 7,7 фунта. Эти данные можно использовать для оценки общего стандартного отклонения потери веса следующим образом:
В исследовании сообщалось о стандартном отклонении веса, потерянного за 8 недель на диете с низким содержанием жиров, на 8,4 фунта, и стандартном отклонении веса, потерянного за 8 недель на диете с низким содержанием углеводов, на 7,7 фунта. Эти данные можно использовать для оценки общего стандартного отклонения потери веса следующим образом: 6 для 95%), E — желаемая погрешность, а σ d — стандартное отклонение разностных оценок. Чрезвычайно важно, чтобы стандартное отклонение 90 140 90 234 разности 90 235 90 141 баллов (например, разница, основанная на измерениях во времени или разница между подобранными парами) использовалась здесь для надлежащей оценки размера выборки.
6 для 95%), E — желаемая погрешность, а σ d — стандартное отклонение разностных оценок. Чрезвычайно важно, чтобы стандартное отклонение 90 140 90 234 разности 90 235 90 141 баллов (например, разница, основанная на измерениях во времени или разница между подобранными парами) использовалась здесь для надлежащей оценки размера выборки. Чтобы оценить размер выборки, нам нужны приблизительные значения p 1 и p 2 . Значения p 1 и p 2 , которые максимизируют размер выборки, составляют p 1 = p 2 = 0,5. Таким образом, если нет доступной информации для аппроксимации p 1 и p 2 , то можно использовать 0,5 для получения наиболее консервативных или самых больших размеров выборки.
Чтобы оценить размер выборки, нам нужны приблизительные значения p 1 и p 2 . Значения p 1 и p 2 , которые максимизируют размер выборки, составляют p 1 = p 2 = 0,5. Таким образом, если нет доступной информации для аппроксимации p 1 и p 2 , то можно использовать 0,5 для получения наиболее консервативных или самых больших размеров выборки. Заинтересованные читатели могут увидеть Fleiss для более подробной информации. 4
Заинтересованные читатели могут увидеть Fleiss для более подробной информации. 4  Национальные данные свидетельствуют о том, что 12% младенцев рождаются недоношенными. Мы будем использовать эту оценку для обеих групп при расчете размера выборки.
Национальные данные свидетельствуют о том, что 12% младенцев рождаются недоношенными. Мы будем использовать эту оценку для обеих групп при расчете размера выборки. Первая называется ошибкой типа I и относится к ситуации, когда мы ошибочно отвергаем H 0 , хотя на самом деле это правда. На первом этапе любой проверки гипотезы мы выбираем уровень значимости α и α = P (ошибка типа I) = P (отклонение H 0 | H 0 верно). Поскольку мы намеренно выбираем малое значение для α, мы контролируем вероятность совершения ошибки первого рода. Второй тип ошибки называется ошибкой типа II и определяется как вероятность того, что мы не отвергнем H 0 , когда она ложна. Вероятность ошибки II рода обозначается β, и β = P(ошибка II рода) = P(Не отвергать H 0 | H 0 ложно). При проверке гипотез мы обычно ориентируемся на мощность, которая определяется как вероятность того, что мы отклоним H 0 , когда она ложна, т. е. мощность = 1-β = P(Reject H 0 | H 0 ложна). ). Мощность — это вероятность того, что тест правильно отвергнет ложную нулевую гипотезу. Хороший тест — это тест с низкой вероятностью совершения ошибки типа I (т.
Первая называется ошибкой типа I и относится к ситуации, когда мы ошибочно отвергаем H 0 , хотя на самом деле это правда. На первом этапе любой проверки гипотезы мы выбираем уровень значимости α и α = P (ошибка типа I) = P (отклонение H 0 | H 0 верно). Поскольку мы намеренно выбираем малое значение для α, мы контролируем вероятность совершения ошибки первого рода. Второй тип ошибки называется ошибкой типа II и определяется как вероятность того, что мы не отвергнем H 0 , когда она ложна. Вероятность ошибки II рода обозначается β, и β = P(ошибка II рода) = P(Не отвергать H 0 | H 0 ложно). При проверке гипотез мы обычно ориентируемся на мощность, которая определяется как вероятность того, что мы отклоним H 0 , когда она ложна, т. е. мощность = 1-β = P(Reject H 0 | H 0 ложна). ). Мощность — это вероятность того, что тест правильно отвергнет ложную нулевую гипотезу. Хороший тест — это тест с низкой вероятностью совершения ошибки типа I (т. е. малое α) и высокой мощностью (т. е. малым β, высокой мощностью).
е. малое α) и высокой мощностью (т. е. малым β, высокой мощностью). Предположим, что для проверки гипотез мы выбираем выборку размером n = 100. Для этого примера предположим, что стандартное отклонение результата равно σ=20. Мы вычисляем среднее значение выборки, а затем должны решить, предоставляет ли среднее значение выборки свидетельство в поддержку альтернативной гипотезы или нет. Это делается путем вычисления тестовой статистики и сравнения тестовой статистики с соответствующим критическим значением. Если нулевая гипотеза верна (µ=90), то мы, вероятно, выберем выборку, среднее значение которой близко к 90. Однако также можно выбрать выборку, среднее значение которой много больше или много меньше 90. Вспомним из центральной предельной теоремы (см. стр. 11 модуля «Вероятность»), что при больших n (здесь n=100 достаточно велико) распределение выборочных средних приблизительно нормально со средним значением
Предположим, что для проверки гипотез мы выбираем выборку размером n = 100. Для этого примера предположим, что стандартное отклонение результата равно σ=20. Мы вычисляем среднее значение выборки, а затем должны решить, предоставляет ли среднее значение выборки свидетельство в поддержку альтернативной гипотезы или нет. Это делается путем вычисления тестовой статистики и сравнения тестовой статистики с соответствующим критическим значением. Если нулевая гипотеза верна (µ=90), то мы, вероятно, выберем выборку, среднее значение которой близко к 90. Однако также можно выбрать выборку, среднее значение которой много больше или много меньше 90. Вспомним из центральной предельной теоремы (см. стр. 11 модуля «Вероятность»), что при больших n (здесь n=100 достаточно велико) распределение выборочных средних приблизительно нормально со средним значением
 Эта концепция обсуждалась в модуле «Проверка гипотез».
Эта концепция обсуждалась в модуле «Проверка гипотез». Мощность определяется как 1-β = P(Отклонить H 0 | H 0 неверно) и показана на рисунке как площадь под самой правой кривой (H 1 ) справа от вертикальной линии ( где мы отбрасываем H 0 ).
Мощность определяется как 1-β = P(Отклонить H 0 | H 0 неверно) и показана на рисунке как площадь под самой правой кривой (H 1 ) справа от вертикальной линии ( где мы отбрасываем H 0 ). На приведенном выше рисунке графически показаны α, β и мощность, когда разница среднего значения при нулевой гипотезе по сравнению с альтернативной гипотезой составляет 4 единицы (т. е. 90 против 94). На рисунке ниже показаны те же компоненты для ситуации, когда среднее значение по альтернативной гипотезе равно 98.
На приведенном выше рисунке графически показаны α, β и мощность, когда разница среднего значения при нулевой гипотезе по сравнению с альтернативной гипотезой составляет 4 единицы (т. е. 90 против 94). На рисунке ниже показаны те же компоненты для ситуации, когда среднее значение по альтернативной гипотезе равно 98. На предыдущем рисунке для H 0 : µ = 90 и H 1 : µ = 94, если мы наблюдали выборочное среднее значение 93, например, было бы не так ясно, произошло ли оно из распределения, среднее значение которого равно 90, или из распределения, среднее значение которого равно 94.
На предыдущем рисунке для H 0 : µ = 90 и H 1 : µ = 94, если мы наблюдали выборочное среднее значение 93, например, было бы не так ясно, произошло ли оно из распределения, среднее значение которого равно 90, или из распределения, среднее значение которого равно 94. При планировании исследований исследователи снова должны учитывать отсев или выпадение из-под наблюдения. Формулы, показанные ниже, позволяют получить необходимое количество участников с полными данными, и мы проиллюстрируем, как решается проблема отсева в исследованиях по планированию.
При планировании исследований исследователи снова должны учитывать отсев или выпадение из-под наблюдения. Формулы, показанные ниже, позволяют получить необходимое количество участников с полными данными, и мы проиллюстрируем, как решается проблема отсева в исследованиях по планированию. 1-β — выбранная степень, а Z 1-β — значение стандартного нормального распределения, ниже которого находится 1-β. Оценки размера выборки для проверки гипотез часто основаны на достижении 80% или 90% мощности. Значения Z 1-β для этих популярных сценариев приведены ниже:
1-β — выбранная степень, а Z 1-β — значение стандартного нормального распределения, ниже которого находится 1-β. Оценки размера выборки для проверки гипотез часто основаны на достижении 80% или 90% мощности. Значения Z 1-β для этих популярных сценариев приведены ниже: При расчете размера выборки исследователи часто используют значение стандартного отклонения из предыдущего исследования или исследования, проведенного в другой, но сопоставимой популяции. Независимо от того, как получена оценка изменчивости исхода, она всегда должна быть консервативной (т. е. настолько большой, насколько это разумно), чтобы результирующий размер выборки не был слишком мал.
При расчете размера выборки исследователи часто используют значение стандартного отклонения из предыдущего исследования или исследования, проведенного в другой, но сопоставимой популяции. Независимо от того, как получена оценка изменчивости исхода, она всегда должна быть консервативной (т. е. настолько большой, насколько это разумно), чтобы результирующий размер выборки не был слишком мал. Сколько пациентов должно быть включено в исследование, чтобы гарантировать, что мощность теста составляет 80% для обнаружения этой разницы? Будет использован двусторонний тест с уровнем значимости 5%.
Сколько пациентов должно быть включено в исследование, чтобы гарантировать, что мощность теста составляет 80% для обнаружения этой разницы? Будет использован двусторонний тест с уровнем значимости 5%. Таким образом, в исследование будет включено в общей сложности 35 участников, чтобы гарантировать, что 31 человек будет доступен для анализа (см. ниже).
Таким образом, в исследование будет включено в общей сложности 35 участников, чтобы гарантировать, что 31 человек будет доступен для анализа (см. ниже). Числитель величины эффекта, абсолютное значение разницы в пропорциях |p 1 -p 0 |, снова представляет то, что считается клинически значимой или практически важной разницей в пропорциях.
Числитель величины эффекта, абсолютное значение разницы в пропорциях |p 1 -p 0 |, снова представляет то, что считается клинически значимой или практически важной разницей в пропорциях.
 Формула для определения размера выборки, чтобы убедиться, что тест имеет заданную мощность:
Формула для определения размера выборки, чтобы убедиться, что тест имеет заданную мощность: Однако чаще бывает так, что данные о вариабельности исхода доступны только для одной группы, обычно не получавшей лечения (например, плацебо-контроль) или не подвергавшейся воздействию. При планировании клинического испытания нового препарата или процедуры часто доступны данные из других испытаний, в которых могло участвовать плацебо или активная контрольная группа (т. е. стандартное лекарство или лечение, назначенное для изучаемого состояния). Стандартное отклонение переменной исхода, измеренное у пациентов, отнесенных к группе плацебо, контрольной группе или группе, не подвергавшейся воздействию, можно использовать для планирования будущих испытаний, как показано на рисунке.
Однако чаще бывает так, что данные о вариабельности исхода доступны только для одной группы, обычно не получавшей лечения (например, плацебо-контроль) или не подвергавшейся воздействию. При планировании клинического испытания нового препарата или процедуры часто доступны данные из других испытаний, в которых могло участвовать плацебо или активная контрольная группа (т. е. стандартное лекарство или лечение, назначенное для изучаемого состояния). Стандартное отклонение переменной исхода, измеренное у пациентов, отнесенных к группе плацебо, контрольной группе или группе, не подвергавшейся воздействию, можно использовать для планирования будущих испытаний, как показано на рисунке. Howell 3 для получения более подробной информации).
Howell 3 для получения более подробной информации).




 ES – размер эффекта, определяемый следующим образом:
ES – размер эффекта, определяемый следующим образом:  В течение обычного года примерно 35% учащихся болеют гриппом. Исследователи считают, что увеличение заболеваемости гриппом на 30% среди тех, кто регулярно посещал спортивные сооружения, было бы клинически значимым. Сколько студентов должно быть зачислено в исследование, чтобы мощность теста составила 80% для обнаружения этой разницы в пропорциях? Будет использован двусторонний тест с уровнем значимости 5%.
В течение обычного года примерно 35% учащихся болеют гриппом. Исследователи считают, что увеличение заболеваемости гриппом на 30% среди тех, кто регулярно посещал спортивные сооружения, было бы клинически значимым. Сколько студентов должно быть зачислено в исследование, чтобы мощность теста составила 80% для обнаружения этой разницы в пропорциях? Будет использован двусторонний тест с уровнем значимости 5%.
 difficile. Имеются спорадические сообщения об успешном лечении путем введения фекалий здоровых доноров в двенадцатиперстную кишку пациентов, страдающих C. difficile. (Юк!) Это восстанавливает нормальную микробиоту в толстой кишке и противодействует чрезмерному росту C. diff. Эффективность этого подхода была проверена в рандомизированном клиническом исследовании, опубликованном в New England Journal of Medicine (январь 2013 г.). Исследователи планировали случайным образом назначать пациентов с рецидивирующей инфекцией C. difficile либо на антибактериальную терапию, либо на дуоденальное введение донорских фекалий. Чтобы оценить необходимый размер выборки, исследователи предположили, что вливание фекалий будет успешным 90% времени, а антибактериальная терапия будет успешной в 60% случаев. Сколько испытуемых потребуется в каждой группе, чтобы мощность исследования составила 80 % при уровне значимости α = 0,05?
difficile. Имеются спорадические сообщения об успешном лечении путем введения фекалий здоровых доноров в двенадцатиперстную кишку пациентов, страдающих C. difficile. (Юк!) Это восстанавливает нормальную микробиоту в толстой кишке и противодействует чрезмерному росту C. diff. Эффективность этого подхода была проверена в рандомизированном клиническом исследовании, опубликованном в New England Journal of Medicine (январь 2013 г.). Исследователи планировали случайным образом назначать пациентов с рецидивирующей инфекцией C. difficile либо на антибактериальную терапию, либо на дуоденальное введение донорских фекалий. Чтобы оценить необходимый размер выборки, исследователи предположили, что вливание фекалий будет успешным 90% времени, а антибактериальная терапия будет успешной в 60% случаев. Сколько испытуемых потребуется в каждой группе, чтобы мощность исследования составила 80 % при уровне значимости α = 0,05? Важнейшим компонентом дизайна исследования является определение соответствующего размера выборки. Размер выборки должен быть достаточно большим, чтобы адекватно ответить на вопрос исследования, но не слишком большим, чтобы охватить слишком много пациентов, когда было бы достаточно меньшего числа. Определение соответствующего размера выборки включает в себя статистические критерии, а также клинические или практические соображения. Определение размера выборки требует командной работы; специалисты по биостатистике должны тесно сотрудничать с исследователями-клиницистами, чтобы определить размер выборки, которая позволит решить интересующий вопрос исследования с достаточной точностью или мощностью для получения клинически значимых результатов.
Важнейшим компонентом дизайна исследования является определение соответствующего размера выборки. Размер выборки должен быть достаточно большим, чтобы адекватно ответить на вопрос исследования, но не слишком большим, чтобы охватить слишком много пациентов, когда было бы достаточно меньшего числа. Определение соответствующего размера выборки включает в себя статистические критерии, а также клинические или практические соображения. Определение размера выборки требует командной работы; специалисты по биостатистике должны тесно сотрудничать с исследователями-клиницистами, чтобы определить размер выборки, которая позволит решить интересующий вопрос исследования с достаточной точностью или мощностью для получения клинически значимых результатов. А., Фостер Г., Викерс П. Девочки-подростки и их дети: достижение оптимального веса при рождении. Прибавка массы тела во время беременности и исход беременности с точки зрения срока беременности при родах и массы тела при рождении: сравнение между подростками до 16 лет и взрослыми женщинами. Ребенок: уход, здоровье и развитие. 2001 г.; 27(2):163-171.
А., Фостер Г., Викерс П. Девочки-подростки и их дети: достижение оптимального веса при рождении. Прибавка массы тела во время беременности и исход беременности с точки зрения срока беременности при родах и массы тела при рождении: сравнение между подростками до 16 лет и взрослыми женщинами. Ребенок: уход, здоровье и развитие. 2001 г.; 27(2):163-171. Курение сигарет и риск рака предстательной железы у мужчин среднего возраста. Эпидемиология рака, биомаркеры и профилактика. 2003 г.; 12: 604-609.
Курение сигарет и риск рака предстательной железы у мужчин среднего возраста. Эпидемиология рака, биомаркеры и профилактика. 2003 г.; 12: 604-609. Ответ на вопрос о массе тела при рождении — стр. 3
 Средняя масса тела при рождении доношенных детей от матерей в возрасте 20 лет и старше составляет 3510 граммов при стандартном отклонении 385 граммов. Сколько женщин 19в возрасте лет и младше должны быть включены в исследование, чтобы гарантировать, что оценка 95% доверительного интервала средней массы тела при рождении их младенцев имеет погрешность, не превышающую 100 граммов?
Средняя масса тела при рождении доношенных детей от матерей в возрасте 20 лет и старше составляет 3510 граммов при стандартном отклонении 385 граммов. Сколько женщин 19в возрасте лет и младше должны быть включены в исследование, чтобы гарантировать, что оценка 95% доверительного интервала средней массы тела при рождении их младенцев имеет погрешность, не превышающую 100 граммов? е. 95% будут рожать в срок), тогда необходимо зарегистрировать 60 женщин, чтобы гарантировать, что 57 родят в срок. Количество женщин, которые должны быть зачислены, N, рассчитывается следующим образом:
е. 95% будут рожать в срок), тогда необходимо зарегистрировать 60 женщин, чтобы гарантировать, что 57 родят в срок. Количество женщин, которые должны быть зачислены, N, рассчитывается следующим образом: Ответ Курение первокурсников — Страница 4
 Обратите внимание, что этот размер выборки существенно меньше, чем оцененный выше. Наличие некоторой информации о величине доли в совокупности всегда будет давать размер выборки, меньший или равный размеру, основанному на доле в совокупности, равной 0,5. Однако оценка должна быть реалистичной.
Обратите внимание, что этот размер выборки существенно меньше, чем оцененный выше. Наличие некоторой информации о величине доли в совокупности всегда будет давать размер выборки, меньший или равный размеру, основанному на доле в совокупности, равной 0,5. Однако оценка должна быть реалистичной. Ответ на проблему с медицинским устройством — стр. 7

Ответ на алкоголь и средний балл — Страница 8

Ответ на донорские фекалии — Страница 8
 diff. инфузией фекалий по сравнению с антибактериальной терапией.
diff. инфузией фекалий по сравнению с антибактериальной терапией. Распределение частиц по размерам: Анализаторы частиц :: Microtrac

Microtrac MRB предлагает продукты для всех технологий анализа размера частиц. Методы определения гранулометрического состава
 Распределение частиц по размерам показывает процент частиц определенного размера (или в определенном интервале размеров). Эти интервалы также называют размерными классами или фракциями.
Распределение частиц по размерам показывает процент частиц определенного размера (или в определенном интервале размеров). Эти интервалы также называют размерными классами или фракциями. 5 mm 10 mm 15 mm 40 mm
Количественное определение теперь может быть выполнено несколькими способами:
- взвешивание: Каждая фракция содержит 190 г образца или 25% от общего количества или веса. Эти значения также соответствуют доле общего объема, поскольку массу и объем можно трактовать эквивалентно, при условии, что плотность не меняется с размером частиц.
- подсчет: Всего выборка состоит из 573 объектов, распределенных по четырем фракциям. Поскольку есть только одна сфера диаметром 40 мм, теперь это составляет всего 0,2% от общего количества, а не 25%, как при распределении по массе.
 С другой стороны, 490 сфер диаметром 5 мм имеют долю 85,5%.
С другой стороны, 490 сфер диаметром 5 мм имеют долю 85,5%.
Таким образом, в зависимости от типа оценки (количество или масса/объем) для одного и того же образца получается очень разное распределение частиц по размерам.
Некоторые анализаторы размера частиц обеспечивают числовое распределение (динамический анализ изображения), другие – распределение по массе (сетчатый анализ) или объемное распределение частиц по размеру (лазерная дифракция). При наличии подходящей модели распределения могут быть преобразованы друг в друга. Одним из особых случаев является динамическое рассеяние света, в котором очень часто сообщается о распределении частиц по размерам на основе интенсивности. Это означает, что различные размеры представлены в соответствии с их вкладом в общую интенсивность рассеяния. Это приводит к сильному представлению крупных частиц, поскольку интенсивность рассеяния уменьшается с размером в 106 раз9.0005
Представление результатов гранулометрического состава
Гранулометрический состав может быть представлен либо в табличной, либо в графической форме. В таблице ниже показано это для мелющих шаров. Количество в каждой фракции обозначается буквой р, индекс 0 означает «количественный», индекс 3 означает «массовый или объемный».
В таблице ниже показано это для мелющих шаров. Количество в каждой фракции обозначается буквой р, индекс 0 означает «количественный», индекс 3 означает «массовый или объемный».
| Размер | Масса | П 3 | Номер | П 0 |
| 5 мм | 190 г | 25 % | 490 | 85,5 % |
| 10 мм | 190 г | 25 % | 64 | 11,2 % |
| 15 мм | 190 г | 25 % | 18 | 3,1 % |
| 40 мм | 190 г | 25 % | 1 | 0,2 % | Всего | 760 г | 100 % | 573 | 100 % |
Таким образом, описательным способом представления распределения частиц по размерам является гистограмма, где ширина столбца соответствует нижнему или верхнему пределу класса размера, а высота столбца соответствует количеству в этом классе размера . В технологии измерения частиц принято генерировать кумулятивное распределение из значений, зависящих от класса. Для этого величины в каждом классе измерений суммируются, начиная с наименьшей дроби. Это дает кривую, которая непрерывно увеличивается от 0 % до 100 %, «кумулятивную кривую». Как определяется кумулятивная кривая для ситового анализа, показано на рисунке 2. Кумулятивное распределение частиц по размерам обозначено буквой Q. Каждое значение Q(x) указывает количество пробы, состоящей из частиц меньше размера x. Поскольку это количество, которое пройдет через гипотетическое сито с размером ячеек x, такой тип распределения частиц по размерам также называется «процентным прохождением»9.0005
В технологии измерения частиц принято генерировать кумулятивное распределение из значений, зависящих от класса. Для этого величины в каждом классе измерений суммируются, начиная с наименьшей дроби. Это дает кривую, которая непрерывно увеличивается от 0 % до 100 %, «кумулятивную кривую». Как определяется кумулятивная кривая для ситового анализа, показано на рисунке 2. Кумулятивное распределение частиц по размерам обозначено буквой Q. Каждое значение Q(x) указывает количество пробы, состоящей из частиц меньше размера x. Поскольку это количество, которое пройдет через гипотетическое сито с размером ячеек x, такой тип распределения частиц по размерам также называется «процентным прохождением»9.0005
Иногда фракции также суммируются, начиная с наибольшего размера частиц. Результирующее распределение частиц по размерам представляет собой кривую, которая падает от 100% до 0%. Это обозначается 1-Q и является зеркальным отражением Q-кривой. Распределение 1-Q указывает для каждого значения x процент выборки, превышающий x. Распределение называется «удержанным в процентах», так как оно указывает, какая часть общего образца будет задержана конкретным ситом.
Распределение называется «удержанным в процентах», так как оно указывает, какая часть общего образца будет задержана конкретным ситом.
Кумулятивное распределение (красный) представляет собой сумму отдельных дробей
Параметры, полученные из анализа распределения частиц по размерам
Многие статистические параметры могут быть получены из распределения частиц по размерам. Кумулятивное распределение особенно подходит для этой цели. Среди наиболее важных параметров, безусловно, процентили. Они указывают в каждом случае величину х, ниже которой находится определенное количество пробы. Таким образом, процентили отвечают, например, на вопросы «Меньше какого размера находятся 10% мельчайших частиц?» или «Выше какого размера 5% самых крупных частиц?» Процентили можно считывать непосредственно с кривой Q или 1-Q.
Процентили обозначаются буквой d, за которой следует значение в %. Таким образом, d10 = 83 мкм, d50 = 330 мкм и d90 = 1600 мкм означает, что 10 % образца меньше 83 мкм, 50 % меньше 330 мкм и 90 % меньше 1600 мкм. Альтернативные обозначения: x10/50/90 или D 0,1/0,5/0,9. Величина d50 также называется «медианой», и она делит распределение частиц по размерам на равные количества «более мелких» и «крупных» частиц. Обычно d10, d50 и d90 указываются для распределения частиц по размерам.
Альтернативные обозначения: x10/50/90 или D 0,1/0,5/0,9. Величина d50 также называется «медианой», и она делит распределение частиц по размерам на равные количества «более мелких» и «крупных» частиц. Обычно d10, d50 и d90 указываются для распределения частиц по размерам.
Это позволяет легко охарактеризовать среднюю или центральную точку распределения, а также верхнюю и нижнюю границы тремя значениями. Эта спецификация не всегда полезна, но обычно дает хороший обзор. Может быть определено любое количество значений процентиля, например. d16, d84, d95, d99 и т. д. Однако следует также обратить внимание на то, достаточна ли чувствительность метода измерения для надежного определения процентилей, близких к 0 % или близких к 100 %. Значение d100 четко не определено и поэтому не имеет смысла. Если 100% частиц имеют размер < 2 мм, то это также верно для всех больших значений x, которые также являются значениями d100.
На этом рисунке показано, как можно считывать процентили непосредственно из кумулятивной кривой.
Процентили, такие как d10, d50, d90, могут быть получены непосредственно из кумулятивной кривой
Средние значения (или средний размер частиц) также могут быть рассчитаны из табличных значений. Это делается путем умножения количества в каждом классе измерения на класс измерения среднего размера и суммирования отдельных значений. Существуют различные методы расчета среднего значения, некоторые из них описаны в ISO 9.276-2. Чтобы также охарактеризовать ширину распределения, можно использовать стандартное отклонение от среднего значения или значение размаха. Это рассчитывается как (d90 — d10) / d50. Чем шире распределение, тем больше стандартное отклонение и диапазон.
Значение x, при котором распределение плотности достигает максимума (или наиболее часто используемый класс измерения), называется размером моды. Распределения частиц по размерам с несколькими максимальными значениями в распределении плотности называются мультимодальными (или бимодальными, тримодальными и т. д.).
д.).
Особым вопросом при анализе распределения частиц по размерам является определение частиц слишком большого и меньшего размера. Это небольшие порции частиц, которые значительно больше или значительно меньше, чем основная масса образца. На кумулятивной кривой наличие переразмера или недоразмера проявляется ступенькой, в распределении плотности — небольшим вторым пиком (вторым максимумом) вне фактического распределения. Этот завышенный или заниженный размер лучше всего характеризуется значениями Q или 1-Q при подходящем размере x.
В приведенном ниже примере показано распределение частиц по размерам с запасом по размеру 5 %. Здесь 95 % частиц имеют размер менее 1 мм, примеси имеют размер от 1 до 1,25 мм. Это можно количественно определить как Q3(1 мм) = 95% или 1-Q3(1 мм) = 5%. Этот пример также показывает, что добавление большего размера увеличивает средний размер частиц, в то время как медиана остается неизменной. В качестве альтернативы наличие негабарита также может быть описано увеличением d95.
Гранулометрический состав мономодального материала (красный) в виде кривых Q3 и q3. Если добавить 5 % частиц размером 1–1,25 мм, это приводит к бимодальному распределению. 10 % и 50 % процентили остаются неизменными, среднее значение и стандартное отклонение увеличиваются. Негабарит лучше всего характеризуется d95 или Q3 на 1 мм
Microtrac MRB Продукция и контакты
Компания Microtrac предлагает широкий спектр инновационных анализаторов частиц и технологий для анализа распределения частиц по размерам. Наши специалисты знают сильные и слабые стороны каждого метода и будут рады помочь найти правильное решение для вашего приложения.
Анализ распределения частиц по размерам – часто задаваемые вопросы
Что такое распределение частиц по размерам?
Распределение частиц по размерам порошка, гранулята, суспензии или эмульсии показывает частоту частиц определенного размера в образце. Таким образом, это статистическая концепция. На практике проценты указываются на размерный интервал (дробь) или используются кумулятивные значения, в которых дроби складываются в порядке возрастания или убывания размера.
На практике проценты указываются на размерный интервал (дробь) или используются кумулятивные значения, в которых дроби складываются в порядке возрастания или убывания размера.
Какие методы используются для измерения гранулометрического состава?
Существует множество методов определения гранулометрического состава образца. Какой из них подходит для конкретного образца, зависит от диапазона размеров частиц и свойств материала. Обычно используемыми методами являются ситовой анализ, лазерная дифракция, динамическое светорассеяние и анализ изображений.
Почему важно распределение частиц по размерам?
Гранулометрический состав является важным критерием качества многих продуктов, а также сырья. На многие свойства материалов влияет распределение частиц по размерам. К ним относятся, например, текучесть, площадь поверхности, свойства транспортировки, поведение при экстракции и растворении, реакционная способность, абразивность и даже вкус.
Что означают d10, d50 и d90 в гранулометрическом составе?
d10, d50 и d90 являются так называемыми процентильными значениями. Это статистические параметры, которые можно считать непосредственно из кумулятивного распределения частиц по размерам. Они указывают размер, ниже которого находится 10%, 50% или 90% всех частиц.
Это статистические параметры, которые можно считать непосредственно из кумулятивного распределения частиц по размерам. Они указывают размер, ниже которого находится 10%, 50% или 90% всех частиц.
В чем разница между мономодальным и бимодальным распределением частиц по размерам?
Найден размер моды, при котором частотное распределение достигает максимума. Если частотное распределение имеет только один максимум, такое распределение называется мономодальным, если оно имеет два максимума, оно называется бимодальным распределением. Распределение частиц по размерам с большим количеством максимумов называется мультимодальным.
Как указывается ширина распределения частиц по размерам?
Ширина распределения частиц по размерам является важным статистическим свойством. Если все частицы одинакового размера, распределение называется монодисперсным. Однако чаще всего мы имеем дело с полидисперсными системами. Ширина распределения может быть задана, например, стандартным отклонением от среднего значения (средний размер частиц) или значением SPAN (d90-d10)/d50.
Статистическая мощность и ее значение
Опубликован в 16 февраля 2021 г. по Прита Бхандари. Отредактировано 19 августа 2022 г.
Статистическая мощность или чувствительность — это вероятность того, что тест значимости обнаружит эффект, когда он действительно существует.
Истинный эффект — это реальная ненулевая связь между переменными в совокупности. На эффект обычно указывает реальная разница между группами или корреляция между переменными.
Высокая мощность в исследовании указывает на большую вероятность того, что тест обнаружит истинный эффект. Низкая мощность означает, что ваш тест имеет лишь небольшой шанс обнаружить истинный эффект или что результаты, вероятно, будут искажены случайной и систематической ошибкой.
Мощность в основном зависит от размера выборки, размера эффекта и уровня значимости. Анализ мощности можно использовать для определения необходимого размера выборки для исследования.
Содержание
- Почему мощность имеет значение в статистике?
- Что такое анализ мощности?
- Другие факторы, влияющие на мощность
- Как увеличить мощность?
- Часто задаваемые вопросы о статистической мощности
Наличие достаточной статистической мощности необходимо для того, чтобы делать точные выводы о населении, используя выборочные данные.
При проверке гипотез вы начинаете с нулевой и альтернативной гипотез: нулевой гипотезы об отсутствии эффекта и альтернативной гипотезы об истинном эффекте (вашего фактического исследовательского прогноза).
Цель состоит в том, чтобы собрать достаточно данных из выборки, чтобы статистически проверить, можете ли вы обоснованно отвергнуть нулевую гипотезу в пользу альтернативной гипотезы.
Пример: Нулевая и альтернативная гипотезы Ваш исследовательский вопрос касается того, может ли времяпрепровождение на природе сдерживать стресс у выпускников колледжей. Вы перефразируете это в нулевую и альтернативную гипотезу.
- Нулевая гипотеза: Проведение 10 минут ежедневно на свежем воздухе в естественной среде не влияет на стресс у недавних выпускников колледжей.
- Альтернативная гипотеза: Проведение 10 минут в день на свежем воздухе в естественной среде уменьшит симптомы стресса у недавних выпускников колледжей.
Всегда есть риск сделать одну из двух ошибок при интерпретации результатов исследования:
- Ошибка типа I : отклонение нулевой гипотезы об отсутствии эффекта, когда она действительно верна.
- Ошибка типа II : не отвергать нулевую гипотезу об отсутствии эффекта, когда она на самом деле ложна.
- Ошибка типа I : вы делаете вывод, что ежедневное 10-минутное пребывание на природе снижает стресс, хотя на самом деле это не так.
- Ошибка типа II : вы заключаете, что ежедневные 10 минут на природе не влияют на стресс, хотя на самом деле это так.

Мощность — это вероятность избежать ошибки второго рода. Чем выше статистическая мощность теста, тем ниже риск совершения ошибки второго рода.
Мощность обычно устанавливается на 80%. Это означает, что если в 100 различных исследованиях с мощностью 80% будут обнаружены истинные эффекты, то только 80 из 100 статистических тестов действительно обнаружат их.
Если вы не обеспечите достаточную мощность, ваше исследование вообще не сможет обнаружить истинный эффект. Это означает, что такие ресурсы, как время и деньги, тратятся впустую, и может быть даже неэтично собирать данные от участников (особенно в клинических испытаниях).
С другой стороны, слишком большая мощность означает, что ваши тесты очень чувствительны к истинным эффектам, включая очень маленькие. Это может привести к нахождению статистически значимых результатов с очень малой полезностью в реальном мире.
Чтобы сбалансировать эти плюсы и минусы низкой и высокой статистической мощности, вы должны использовать анализ мощности, чтобы установить соответствующий уровень.
Что такое анализ мощности?
Анализ мощности — это расчет, который помогает определить минимальный размер выборки для вашего исследования.
Анализ мощности состоит из четырех основных компонентов. Если вы знаете или имеете оценки для любых трех из них, вы можете рассчитать четвертый компонент.
- Статистическая мощность: вероятность того, что тест обнаружит эффект определенного размера, если таковой имеется, обычно устанавливается на уровне 80% или выше.
- Размер выборки: минимальное количество наблюдений, необходимое для наблюдения эффекта определенного размера с заданным уровнем мощности.
- Уровень значимости (альфа) : максимальный риск отклонения истинной нулевой гипотезы, которую вы готовы принять, обычно устанавливается на уровне 5%.
- Ожидаемый размер эффекта: стандартизированный способ выражения величины ожидаемого результата вашего исследования, обычно основанный на аналогичных исследованиях или экспериментальном исследовании.

Перед началом исследования можно использовать анализ мощности для расчета минимального размера выборки для желаемого уровня мощности и значимости, а также ожидаемого размера эффекта.
Традиционно уровень значимости устанавливается равным 5 %, а желаемый уровень мощности — 80 %. Это означает, что вам нужно только выяснить ожидаемый размер эффекта, чтобы рассчитать размер выборки из анализа мощности.
Чтобы рассчитать размер выборки или выполнить анализ мощности, используйте онлайн-инструменты или статистическое программное обеспечение, такое как G*Power.
Объем выборки
Размер выборки положительно связан с мощностью. Небольшая выборка (менее 30 единиц) может иметь только низкую мощность, в то время как большая выборка имеет большую мощность.
Увеличение размера выборки увеличивает мощность, но только до определенного предела. Когда у вас достаточно большая выборка, каждое наблюдение, добавленное к выборке, лишь незначительно увеличивает мощность. Это означает, что сбор большего количества данных увеличит время, затраты и усилия вашего исследования, но не принесет гораздо большей пользы.
Это означает, что сбор большего количества данных увеличит время, затраты и усилия вашего исследования, но не принесет гораздо большей пользы.
Дизайн вашего исследования также связан с мощностью и размером выборки:
- В дизайне внутри субъектов каждый участник тестируется на всех видах лечения в рамках исследования, поэтому индивидуальные различия не будут неравномерно влиять на результаты различных видов лечения.
- В дизайне между субъектами каждый участник принимает участие только в одном лечении, поэтому с разными участниками в каждом лечении есть вероятность, что индивидуальные различия могут повлиять на результаты.
Внутренний дизайн более мощный, поэтому требуется меньшее количество участников. В дизайне между субъектами требуется больше участников, чтобы установить отношения между переменными.
Уровень значимости
Уровень значимости исследования – это вероятность ошибки первого рода, обычно она составляет 5 %. Это означает, что ваши результаты должны иметь менее 5% вероятности того, что они будут выполнены при нулевой гипотезе, чтобы считаться статистически значимыми.
Это означает, что ваши результаты должны иметь менее 5% вероятности того, что они будут выполнены при нулевой гипотезе, чтобы считаться статистически значимыми.
Уровень значимости коррелирует с мощностью: увеличение уровня значимости (например, с 5% до 10%) увеличивает мощность. Когда вы уменьшаете уровень значимости, ваш критерий значимости становится более консервативным и менее чувствительным к обнаружению истинных эффектов.
Исследователи должны сбалансировать риски совершения ошибок типа I и II, учитывая степень риска, на который они готовы пойти, делая ложноположительный вывод по сравнению с ложноотрицательным заключением.
Размер эффекта
Величина эффекта — это величина различия между группами или отношения между переменными. Это указывает на практическую значимость открытия.
В то время как исследования с высокой мощностью могут помочь вам обнаружить средние и большие эффекты в исследованиях, исследования с низкой мощностью могут выявить только большие.
Чтобы определить ожидаемую величину эффекта, вы выполняете систематический обзор литературы, чтобы найти аналогичные исследования. Вы сужаете список релевантных исследований только теми, которые манипулируют временем, проведенным на природе, и используют стресс в качестве основного показателя.
Для пяти исследований, соответствующих этим критериям, вы берете каждую из сообщаемых величин эффекта и вычисляете среднюю величину эффекта. Вы принимаете это среднее значение в качестве ожидаемого размера эффекта.
При использовании данных из выборок для выводов о популяциях всегда возникает некоторая ошибка выборки. Это означает, что всегда существует несоответствие между наблюдаемым размером эффекта и истинным размером эффекта. Величина эффекта в исследовании может варьироваться в зависимости от случайных факторов, ошибки измерения или естественной изменчивости выборки.
Маломощные исследования обычно выявляют истинные эффекты только тогда, когда они являются большими в исследовании. Это означает, что в маломощном исследовании любой наблюдаемый эффект с большей вероятностью будет усилен несвязанными факторами.
Если маломощные исследования являются нормой в определенной области, такой как неврология, наблюдаемые размеры эффекта будут постоянно преувеличивать или переоценивать истинные эффекты.
Получение отзывов о языке, структуре и форматировании
Профессиональные редакторы вычитывают и редактируют вашу статью, уделяя особое внимание:
- Академический стиль
- Расплывчатые предложения
- Грамматика
- Согласованность стиля
См. пример
Другие факторы, влияющие на мощность
Помимо четырех основных компонентов, при определении мощности необходимо учитывать и другие факторы.
Изменчивость
Изменчивость характеристик совокупности влияет на мощность вашего теста. Высокая дисперсия населения снижает мощность.
Высокая дисперсия населения снижает мощность.
Другими словами, использование совокупности, которая принимает широкий диапазон значений переменной, снизит чувствительность вашего теста, а использование совокупности, в которой переменная распределена относительно узко, повысит чувствительность теста.
Использование достаточно конкретной совокупности с определенными демографическими характеристиками может снизить разброс интересующей переменной и улучшить мощность.
Пример: сведение к минимуму изменчивости Стресс — это переменная, которая широко варьирует среди всего населения Соединенных Штатов. Но та же самая переменная может иметь более узкое распределение (принимать меньший диапазон значений) в конкретной и четко определенной совокупности, например, среди женщин с окончанием колледжа в возрасте до 25 лет. Низкая изменчивость уровней стресса повысит эффективность теста в вашем исследовании стресса.Ошибка измерения
Ошибка измерения — это разница между истинным значением и наблюдаемым или записанным значением чего-либо. Измерения могут быть настолько точными, насколько точны инструменты и исследователи, которые их измеряют, поэтому некоторая ошибка присутствует почти всегда.
Измерения могут быть настолько точными, насколько точны инструменты и исследователи, которые их измеряют, поэтому некоторая ошибка присутствует почти всегда.
Чем выше ошибка измерения в исследовании, тем ниже статистическая мощность теста. Ошибка измерения может быть случайной или систематической:
- Случайные ошибки непредсказуемы и неравномерно изменяют измерения из-за случайных факторов (например, изменения настроения могут повлиять на ответы в опросе, или плохой день может привести к неправильной записи наблюдений исследователями).
- Систематические ошибки влияют на данные предсказуемым образом при переходе от одного измерения к другому (например, неправильно откалиброванное устройство будет постоянно записывать неточные данные, или проблемные вопросы опроса могут привести к предвзятым ответам).
Как увеличить мощность?
Поскольку многие аспекты исследования прямо или косвенно влияют на мощность, существуют различные способы ее повышения. В то время как некоторые из них обычно могут быть реализованы, другие являются дорогостоящими или требуют компромисса с другими важными соображениями.
В то время как некоторые из них обычно могут быть реализованы, другие являются дорогостоящими или требуют компромисса с другими важными соображениями.
Увеличение размера эффекта. Чтобы увеличить ожидаемый эффект в эксперименте, вы можете более широко манипулировать независимой переменной (например, провести 1 час вместо 10 минут на природе), чтобы увеличить влияние на зависимую переменную (уровень стресса). Это не всегда возможно, потому что существуют ограничения на то, насколько могут отличаться результаты эксперимента.
Увеличить размер выборки. Основываясь на расчетах размера выборки, у вас может быть место для увеличения размера выборки при значительном повышении мощности. Но есть момент, когда увеличение размера выборки может не дать достаточно высоких преимуществ.
Увеличить уровень значимости. Хотя это делает тест более чувствительным к обнаружению истинных эффектов, это также увеличивает риск совершения ошибки типа I.
Уменьшить погрешность измерения. Повышение точности и правильности ваших измерительных устройств и процедур снижает изменчивость, повышая надежность и мощность. Использование нескольких измерений или методов, известных как триангуляция, также может помочь уменьшить систематическую погрешность исследования.
Используйте односторонний тест вместо двустороннего. При использовании теста t или теста z односторонний тест имеет более высокую мощность. Однако односторонний тест следует использовать только тогда, когда есть веские основания ожидать эффекта в определенном направлении (например, одна средняя оценка будет выше, чем другая), потому что он не сможет обнаружить эффект в определенном направлении. другое направление. Напротив, двусторонний тест способен обнаружить эффект в любом направлении.
- Что такое статистическая мощность? org/Answer»>
- Что такое статистическая значимость?
Статистическая значимость — это термин, используемый исследователями, чтобы заявить, что маловероятно, что их наблюдения могли произойти при нулевой гипотезе статистического теста. Значимость обычно обозначается p -значением или значением вероятности.

Статистическая значимость произвольна — она зависит от порога или значения альфа, выбранного исследователем. Самый распространенный порог — 9.0140 p < 0,05, что означает, что данные, вероятно, будут встречаться менее чем в 5% случаев при нулевой гипотезе.
Когда значение p падает ниже выбранного альфа-значения, мы говорим, что результат теста статистически значим.
- Что такое силовой анализ?
Анализ мощности — это расчет, который помогает определить минимальный размер выборки для вашего исследования. Он состоит из четырех основных компонентов. Если вы знаете или имеете оценки для любых трех из них, вы можете рассчитать четвертый компонент.
- Статистическая мощность : вероятность того, что тест обнаружит эффект определенного размера, если таковой имеется, обычно устанавливается на уровне 80% или выше.

- Размер выборки : минимальное количество наблюдений, необходимое для наблюдения эффекта определенного размера с заданным уровнем мощности.
- Уровень значимости (альфа) : максимальный риск отклонения истинной нулевой гипотезы, которую вы готовы принять, обычно устанавливается на уровне 5%.
- Ожидаемый размер эффекта : стандартизированный способ выражения величины ожидаемого результата вашего исследования, обычно основанный на аналогичных исследованиях или экспериментальном исследовании.
- Статистическая мощность : вероятность того, что тест обнаружит эффект определенного размера, если таковой имеется, обычно устанавливается на уровне 80% или выше.
- Как повысить статистическую мощность?
Существуют различные способы повышения мощности:
- Увеличьте размер потенциального эффекта, более сильно манипулируя независимой переменной,
- Увеличить размер выборки,
- Увеличить уровень значимости (альфа),
- Уменьшите ошибку измерения за счет повышения точности и правильности ваших измерительных устройств и процедур,
- Используйте односторонний тест вместо двустороннего для тестов t и тестов z .

В статистике мощность относится к вероятности того, что проверка гипотезы обнаружит истинный эффект, если таковой имеется. Статистически мощный тест с большей вероятностью отклонит ложноотрицательный результат (ошибка типа II).
Если вы не обеспечите достаточную мощность в своем исследовании, вы не сможете обнаружить статистически значимый результат, даже если он имеет практическое значение. Ваше исследование может не дать ответа на ваш исследовательский вопрос.

 55000 19.56552
55000 19.56552 542435 8.924532
542435 8.924532 a and index.b
## W = 2923, p-value = 3.902e-07
## alternative hypothesis: true location shift is not equal to 0
a and index.b
## W = 2923, p-value = 3.902e-07
## alternative hypothesis: true location shift is not equal to 0 codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Это чаще всего происходит в тех случаях, когда на показатель оказывает влияние большое число случайных факторов. При этом действие каждого фактора незначительно. Примерами показателей, которые распределяются по нормальному закону являются: рост, сила мышц, результаты в беге, прыжках, метаниях и др.
Это чаще всего происходит в тех случаях, когда на показатель оказывает влияние большое число случайных факторов. При этом действие каждого фактора незначительно. Примерами показателей, которые распределяются по нормальному закону являются: рост, сила мышц, результаты в беге, прыжках, метаниях и др.