Текстовые задачи на движение – легко! Алгоритм решения и успех на ЕГЭ
Смотри видео «Текстовые задачи на ЕГЭ по математике».
Почему текстовые задачи относятся к простым?
Во-первых, все такие задачи решаются по единому алгоритму, о котором мы вам расскажем. Во-вторых, многие из них однотипны — это задачи на движение или на работу. Главное — знать к ним подход.
Внимание! Чтобы научиться решать текстовые задачи, вам понадобится всего три-четыре часа самостоятельной работы, то есть два-три занятия. Всё, что нужно, — это здравый смысл плюс умение решать квадратное уравнение. И даже формулу для дискриминанта мы вам напомним, если вдруг забыли.
Прежде чем перейти к самим задачам — проверьте себя.
Запишите в виде математического выражения:
- на больше ;
- в пять раз больше ;
- на меньше, чем ;
- меньше в раза;
- на меньше, чем ;
- частное от деления на в полтора раза больше ;
- квадрат суммы и равен ;
- составляет процентов от ;
- больше на процентов.
Пока не напишете — в ответы не подглядывайте! 🙂
Казалось бы, на первые три вопроса ответит и второклассник. Но почему-то у половины выпускников они вызывают затруднения, не говоря уже о вопросах и . Из года в год мы, репетиторы, наблюдаем парадоксальную картину: ученики одиннадцатого класса долго думают, как записать, что « на больше ». А в школе в этот момент они «проходят» первообразные и интегралы 🙂
Итак, правильные ответы:
больше, чем . Разница между ними равна пяти. Значит, чтобы получить большую величину, надо к меньшей прибавить разницу.
больше, чем , в пять раз. Значит, если умножить на , получим .
меньше, чем . Разница между ними равна . Чтобы получить меньшую величину, надо из большей вычесть разницу.
меньше, чем . Значит, если из большей величины вычтем разницу, получим меньшую.
На всякий случай повторим терминологию:
Сумма — результат сложения двух или нескольких слагаемых.
Разность — результат вычитания.
Произведение — результат умножения двух или нескольких множителей.
Частное — результат деления чисел.
Мы помним, что .
Если принять за , то на процентов больше, то есть .
Начнем мы с задач на движение. Они часто встречаются в вариантах ЕГЭ. Здесь всего два правила:
- Все эти задачи решаются по одной-единственной формуле: , то есть расстояние скорость время. Из этой формулы можно выразить скорость или время .
- В качестве переменной удобнее всего выбирать скорость. Тогда задача точно решится!
Для начала очень внимательно читаем условие. В нем все уже есть. Помним, что текстовые задачи на самом деле очень просты.
. Из пункта в пункт , расстояние между которыми км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт на часа позже автомобилиста.
Ответ дайте в км/ч.
Что здесь лучше всего обозначить за ? Скорость велосипедиста. Тем более, что ее и надо найти в этой задаче. Автомобилист проезжает на километров больше, значит, его скорость равна .
Нарисуем таблицу. В нее сразу можно внести расстояние — и велосипедист, и автомобилист проехали по км. Можно внести скорость — она равна и для велосипедиста и автомобилиста соответственно. Осталось заполнить графу «время».
Его мы найдем по формуле: . Для велосипедиста получим , для автомобилиста .
Эти данные тоже запишем в таблицу.
Вот что получится:
| велосипедист | |||
| автомобилист |
Остается записать, что велосипедист прибыл в конечный пункт на часа позже автомобилиста. Позже — значит, времени он затратил больше. Это значит, что на четыре больше, чем , то есть
Решаем уравнение.
Приведем дроби в левой части к одному знаменателю.
Первую дробь домножим на , вторую — на .
Если вы не знаете, как приводить дроби к общему знаменателю (или — как раскрывать скобки, как решать уравнение…), подойдите с этим конкретным вопросом к вашему учителю математики и попросите объяснить. Бесполезно говорить учительнице: «Я не понимаю математику» — это слишком абстрактно и не располагает к ответу. Учительница может ответить, например, что она вам сочувствует. Или, наоборот, даст какую-либо характеристику вашей личности. И то и другое неконструктивно.
А вот если вы зададите конкретный вопрос: «Как приводить дроби к одному знаменателю?» или «Как раскрывать скобки?» — вы получите нужный вам конкретный ответ. Вам ведь необходимо в этом разобраться! Если педагог занят, договоритесь о времени, когда вы можете с ним (или с ней) встретиться, чтобы получить консультацию. Используйте ресурсы, которые у вас под рукой!
Получим:
Разделим обе части нашего уравнения на .
В результате уравнение станет проще. Но почему-то многие учащиеся забывают это делать, и в результате получают сложные уравнения и шестизначные числа в качестве дискриминанта.
Умножим обе части уравнения на . Получим:
Раскроем скобки и перенесем всё в левую часть уравнения:
Мы получили квадратное уравнение. Напомним, что квадратным называется уравнение вида . Решается оно стандартно — сначала находим дискриминант по формуле , затем корни по формуле
В нашем уравнении , , .
Найдем дискриминант и корни:
, .
Ясно, что не подходит по смыслу задачи — скорость велосипедиста не должна быть отрицательной.
Ответ: .
Следующая задача — тоже про велосипедиста.
2. Велосипедист выехал с постоянной скоростью из города в город , расстояние между которыми равно км. На следующий день он отправился обратно со скоростью на км/ч больше прежней. По дороге он сделал остановку на часа. В результате он затратил на обратный путь столько же времени, сколько на путь из в .
Найдите скорость велосипедиста на пути из в . Ответ дайте в км/ч.
Пусть скорость велосипедиста на пути из в равна . Тогда его скорость на обратном пути равна . Расстояние в обеих строчках таблицы пишем одинаковое — километров. Осталось записать время. Поскольку , на путь из в велосипедист затратит время , а на обратный путь время .
| туда | |||
| обратно |
На обратном пути велосипедист сделал остановку на часа и в результате затратил столько же времени, сколько на пути из в . Это значит, что на обратном пути он крутил педали на часа меньше.
Значит, на три меньше, чем . Получается уравнение:
Как и в предыдущей задаче, сгруппируем слагаемые:
Точно так же приводим дроби к одному знаменателю:
Разделим обе части уравнения на
Напомним — если вам непонятны какие-либо действия при решении уравнений, обращайтесь к учительнице! Показывайте конкретную строчку в решении задачи и говорите: «Пожалуйста, объясните, как это делать».
Для нее такое объяснение — дело пятнадцати минут, а вы наконец научитесь решать уравнения, что очень важно для сдачи ЕГЭ по математике.
Умножим обе части уравнения на , раскроем скобки и соберем все в левой части.
Находим дискриминант. Он равен .
Найдем корни уравнения:
. Это вполне правдоподобная скорость велосипедиста. А ответ не подходит, так как скорость велосипедиста должна быть положительна.
Ответ: .
Следующий тип задач — когда что-нибудь плавает по речке, в которой есть течение. Например, теплоход, катер или моторная лодка. Обычно в условии говорится о собственной скорости плавучей посудины и скорости течения. Собственной скоростью называется скорость в неподвижной воде.
При движении по течению эти скорости складываются. Течение помогает, по течению плыть — быстрее.
Скорость при движении по течению равна сумме собственной скорости судна и скорости течения.
А если двигаться против течения? Течение будет мешать, относить назад.
Теперь скорость течения будет вычитаться из собственной скорости судна.
3. Моторная лодка прошла против течения реки км и вернулась в пункт отправления, затратив на обратный путь на часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна км/ч. Ответ дайте в км/ч.
Пусть скорость лодки в неподвижной воде равна .
Тогда скорость движения моторки по течению равна , а скорость, с которой она движется против течения .
Расстояние и в ту, и в другую сторону одинаково и равно км.
Занесем скорость и расстояние в таблицу.
Заполняем графу «время». Мы уже знаем, как это делать. При движении по течению , при движении против течения , причем на два часа больше, чем .
| по течению | |||
| против течения |
Условие « на два часа больше, чем «» можно записать в виде:
Составляем уравнение:
и решаем его:
Приводим дроби в левой части к одному знаменателю:
Раскрываем скобки:
Делим обе части на , чтобы упростить уравнение:
Умножаем обе части уравнения на
Вообще-то это уравнение имеет два корня: и (оба этих числа при возведении в квадрат дают ).
Но конечно же, отрицательный ответ не подходит — скорость лодки должна быть положительной.
Ответ: .
4. Теплоход проходит по течению реки до пункта назначения км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна км/ч, стоянка длится часов, а в пункт отправления теплоход возвращается через часов после отплытия из него. Ответ дайте в км/ч.
Снова обозначим за скорость течения. Тогда скорость движения теплохода по течению равна , скорость его движения против течения равна . Расстояния — и туда, и обратно — равны км.
Теперь графа «время».
Поскольку , время движения теплохода по течению равно , которое теплоход затратил на движение против течения, равно .
| по течению | |||
| против течения |
В пункт отправления теплоход вернулся через часов после отплытия из него.
Стоянка длилась часов, следовательно, часов теплоход плыл — сначала по течению, затем против.
Значит,
Прежде всего разделим обе части уравнения на . Оно станет проще!
Мы не будем подробно останавливаться на технике решения уравнения. Всё уже понятно — приводим дроби в левой части к одному знаменателю, умножаем обе части уравнения на , получаем квадратное уравнение . Поскольку скорость течения положительна, получаем: .
Ответ: .
Наверное, вы уже заметили, насколько похожи все эти задачи. Текстовые задачи хороши еще и тем, что ответ легко проверить с точки зрения здравого смысла. Ясно, что если вы получили скорость течения, равную километров в час — задача решена неверно.
5. Баржа в вышла из пункта в пункт , расположенный в км от . Пробыв в пункте час минут, баржа отправилась назад и вернулась в пункт в . Определите (в км/час) скорость течения реки, если известно, что собственная скорость баржи равна км/ч.
Пусть скорость течения равна .
Тогда по течению баржа плывет со скоростью , а против течения со скоростью .
Сколько времени баржа плыла? Ясно, что надо из вычесть , а затем вычесть время стоянки. Обратите внимание, что час минут придется перевести в часы: час минут часа. Получаем, что суммарное время движения баржи (по течению и против) равно часа.
| по течению | |||
| против течения |
Возникает вопрос — какой из пунктов, или , расположен выше по течению? А этого мы никогда не узнаем! 🙂
Да и какая разница — ведь в уравнение входит сумма , равная .
Итак,
Решим это уравнение. Число в правой части представим в виде неправильной дроби: .
Приведем дроби в левой части к общему знаменателю, раскроем скобки и упростим уравнение. Получим:
Работать с дробными коэффициентами неудобно! Если мы разделим обе части уравнения на и умножим на , оно станет значительно проще:
Поскольку скорость течения положительна, .
Ответ: 2.
Еще один тип текстовых задач в вариантах ЕГЭ по математике — это задачи на работу.
Благодарим за то, что пользуйтесь нашими публикациями. Информация на странице «Текстовые задачи на движение – легко! Алгоритм решения и успех на ЕГЭ» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена: 08.05.2023
Решения задач
|
|
Тридцать четвертый Математический праздник (19 февраля 2023 года)
Решения в формате PDF
Рабочие критерии проверки:
— классический Математический праздник
— «Математический праздник в Математической вертикали»
Тридцать третий Математический праздник (27 февраля 2022 года)
Решения в формате PDF
Рабочие критерии проверки:
— «классический» Математический праздник
(6 класс и 7 класс)
— «Математический праздник в Математической вертикали»
(6 класс и 7 класс)
Тридцать второй Математический праздник (18 апреля 2021 года)
Решения в формате PDF
Рабочие критерии проверки:
6 класс,
7 класс
«Математический праздник в Математической вертикали»:
6 класс, 7 класс
Рабочие критерии проверки:
6 класс,
7 класс
Тридцать первый Математический праздник (09 февраля 2020 года)
Решения в формате PDF
Рабочие критерии проверки:
6 класс,
7 класс
«Математический праздник в Математической вертикали»:
6 класс, 7 класс
Тридцатый Математический праздник (17 февраля 2019 года)
Решения в формате PDF
Рабочие критерии проверки:
6 класс,
7 класс
Двадцать девятый Математический праздник (18 февраля 2018 года)
Решения в формате PDF
Рабочие критерии проверки:
6 класс,
7 класс
Двадцать восьмой Математический праздник (19 февраля 2017 года)
Решения в формате PDF
Рабочие критерии проверки:
6 класс,
7 класс
Двадцать седьмой Математический праздник (21 февраля 2016 года)
Решения в формате PDF
Рабочие критерии проверки:
6 класс,
7 класс
Двадцать шестой Математический праздник (15 февраля 2015 года)
Решения в формате PDF
Рабочие критерии проверки:
6 класс,
7 класс
Двадцать пятый Математический праздник (16 февраля 2014 года)
Решения в формате PDF (555 К, 12 страниц)
Рабочие критерии проверки:
6 класс,
7 класс
Двадцать четвёртый Математический праздник (17 февраля 2013 года)
Решения в формате PDF (308 К, 12 страниц)
Рабочие критерии проверки:
6 класс, 7 класс
Двадцать третий Математический праздник (19 февраля 2012 года)
Решения в формате PDF (486 К, 12 страниц)
Рабочие критерии проверки:
6 класс, 7 класс
Двадцать второй Математический праздник (13 февраля 2011 года)
Решения в формате PDF (141 К, 16 страниц)
Рабочие критерии проверки:
6 класс, 7 класс
Двадцать первый Математический праздник (14 февраля 2010 года)
Решения в формате PDF (96 К, 12 страниц)
Двадцатый Математический праздник (15 февраля 2009 года)
Решения в формате PDF (102 К, 12 страниц)
Девятнадцатый Математический праздник (17 февраля 2008 года)
Решения в формате PDF (132 К, 8 страниц)
Восемнадцатый Математический праздник (11 февраля 2007 года)
6 класс
7 класс
Решения в формате PDF (98 Кб, 8 страниц)
Семнадцатый Математический праздник (12 февраля 2006 года)
6 класс
7 класс
Решения в формате PDF (551 Кб, 8 страниц)
Шестнадцатый Математический праздник (13 февраля 2005 года)
6 класс
7 класс
Решения в формате PDF (217 Кб, 8 страниц)
Пятнадцатый Математический праздник (15 февраля 2004 года)
6 класс
7 класс
Решения в формате PDF (214 Кб, 7 страниц)
Четырнадцатый Математический праздник (16 февраля 2003 года)
6 класс
7 класс
Решения в формате PDF (214 Кб, 8 страниц)
Тринадцатый Математический праздник (17 февраля 2002 года)
6 класс
7 класс
Решения в формате PDF (131 Кб, 8 страниц)
Двенадцатый Математический праздник (18 февраля 2001 года)
6 класс
7 класс
Решения в формате PDF (183 Кб, 4*2 страниц)
Одиннадцатый Математический праздник (13 февраля 2000 года)
6 класс
7 класс
Решения в формате PDF (88 Кб, 6 страниц)
Десятый Математический праздник (21 февраля 1999 года)
6 класс
7 класс
Дата последнего изменения: 02 апреля 2023 года
| источник | крайний срок | отправленных решения (*) | |||
|---|---|---|---|---|---|
| — 2020 — | |||||
Математический журнал, Vol. 92, №4, окт. 2019 | 1 марта 2020 г. | 2078 | |||
| Математический журнал колледжа, Vol. 50, № 4, сен 2019 | 15 марта 2020 г. | 1157, 1159 | |||
| Математический журнал, Vol. 92, № 5, декабрь 2019 г. | 1 мая 2020 г. | 2082 | |||
| Математический журнал колледжа, Vol. 50, № 5, ноябрь 2019 г. | 15 мая 2020 г. | 1161 | |||
| Математический журнал, Vol. 93, №1, февраль 2020 г. | 1 июля 2020 г. | 2086 | |||
| Математический журнал колледжа, Vol. 51, № 1, янв. 2020 г. | 15 июля 2020 г. | 1167 | |||
| Математический журнал колледжа, Vol. 51, № 2, март 2020 г. | 15 июля 2020 г. | 1175 | |||
Математический журнал, Vol.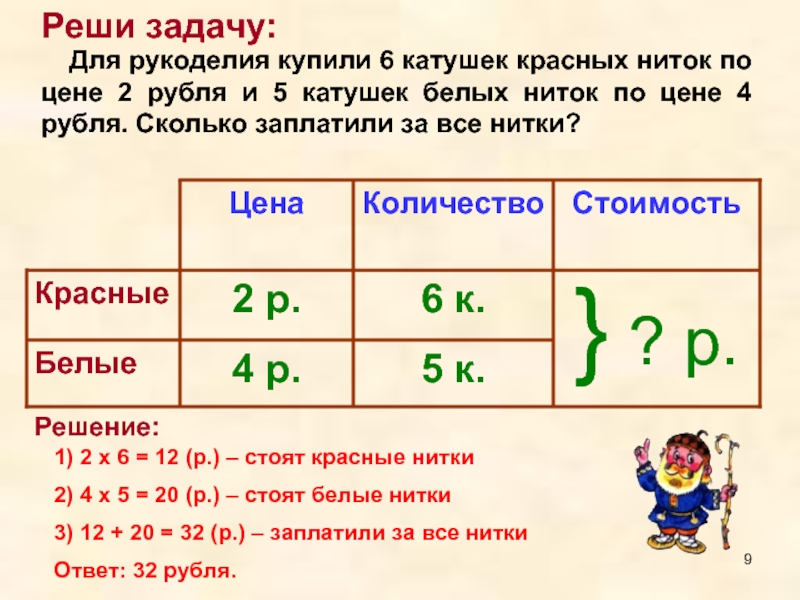 93, №2, апр 2020 | 1 сентября 2020 г. | 2094 | |||
| Математический журнал, Vol. 93, №3, май 2020 г. | 1 ноября 2020 г. | 2098 | |||
| Математический журнал колледжа, Vol. 51, № 3, май 2020 г. | 15 ноября 2020 г. | 1176 | |||
| — 2021 — | |||||
| Математический журнал, Vol. 93, №4, окт 2020 | 1 марта 2021 г. | 2103 | |||
| Математический журнал колледжа, Vol. 51, № 4, сен 2020 | 15 марта 2021 г. | 1183 | |||
| Математический журнал, Vol. 93, № 5, декабрь 2020 г. | 1 мая 2021 г. | 2106, 2107 | |||
| Математический журнал колледжа, Vol. 51, № 5, декабрь 2020 г. | 15 мая 2021 г. | 1186 | |||
Математический журнал, Vol. 94, №1, февраль 2021 г. | 1 июля 2021 г. | 2111 | |||
| Математический журнал колледжа, Vol. 52, № 1, янв 2021 | 15 июля 2021 г. | 1192, 1194 | |||
| Математический журнал, Vol. 94, №2, апр 2021 | 1 сентября 2021 г. | 2118 | |||
| Математический журнал колледжа, Vol. 52, № 2, март 2021 г. | 15 сентября 2021 г. | 1200 | |||
| Математический журнал, Vol. 94, №3, апр 2021 | 1 ноября 2021 г. | 2123 | |||
| Математический журнал колледжа, Vol. 52, № 3, май 2021 | 15 ноября 2021 г. | 1203 | |||
| Математический журнал колледжа, Vol. 52, № 3, май 2021 г. (исправления) | |||||
| — 2022 — | |||||
Математический журнал, Vol. 94, №4, окт 2021 | 1 марта 2022 г. | 2128 | |||
| Математический журнал колледжа, Vol. 52, № 4, сен 2021 | 15 марта 2022 г. | 1210 | |||
| Математический журнал, Vol. 94, № 5, декабрь 2021 г. | 1 мая 2022 г. | 2133 | |||
| Математический журнал колледжа, Vol. 52, № 5, ноябрь 2021 г. | 15 мая 2022 г. | 1214 | |||
| Математический журнал, Vol. 95, №1, янв 2022 | 1 июля 2022 г. | 2137 | |||
| Математический журнал колледжа, Vol. 53, № 1, янв. 2022 г. | 15 июля 2022 г. | 1218 | |||
| Математический журнал, Vol. 95, № 2, апрель 2022 г. | 1 сентября 2022 г. | 2141 | |||
Математический журнал колледжа, Vol. 53, № 2, март 2022 г. | 15 сентября 2022 г. | 1223 | |||
| Математический журнал, Vol. 95, №3, июнь 2022 г. | 1 ноября 2022 г. | 2147, 2149 | |||
| Математический журнал колледжа, Vol. 53, № 3, май 2022 | 15 ноября 2022 г. | 1227 | |||
| — 2023 — | |||||
| Математический журнал, Vol. 95, №4, окт 2022 | 1 марта 2023 г. | 2154 | |||
| Математический журнал колледжа, Vol. 53, № 4, сен 2022 | 15 марта 2023 г. | 1233 | |||
| Математический журнал, Vol. 95, № 5, декабрь 2022 г. | 1 мая 2023 г. | 2159 | |||
| Математический журнал колледжа, Vol. 53, № 5, ноябрь 2022 г. | 15 мая 2023 г. | 1237 | |||
Математический журнал, Vol. 96, №1, март 2023 г. | 1 июля 2023 г. | 2161 | |||
| Математический журнал колледжа, Vol. 54, № 1, февраль 2023 г. | 15 июля 2023 г. | ||||
| Математический журнал, Vol. 96, № 2, апрель 2023 г. | 1 сентября 2023 г. | ||||
| Математический журнал колледжа, Vol. 54, № 2, апр 2023 | 15 сентября 2023 г. | ||||
6 советов по обучению математике Навыки решения задач
У учащихся все больше беспокоит умение решать задачи, особенно сложные, многоступенчатые. Данные показывают, что учащимся труднее решать текстовые задачи, чем при вычислениях, поэтому решение задач следует рассматривать отдельно от вычислений.
Почему?
Подумайте об этом. Когда мы на пути к новому пункту назначения и подключаем наше местоположение к карте на нашем телефоне, он сообщает нам, по какой полосе двигаться, и показывает нам любые объезды или столкновения, иногда даже жужжание наших часов, чтобы напомнить нам повернуть. Когда я испытываю это как водитель, мне не нужно думать. Я могу думать о том, что буду готовить на ужин, не обращая особого внимания на то, что меня окружает, кроме как следовать этим указаниям. Если бы меня снова попросили пойти туда, я бы не смог вспомнить и снова обратился бы за помощью.
Если мы сможем переключиться на предоставление учащимся стратегий, которые требуют от них думать, вместо того, чтобы оказывать им слишком большую поддержку на протяжении всего пути к ответу, мы сможем дать им возможность научиться читать карту и иметь несколько способов попасть туда.
Вот шесть способов, с помощью которых мы можем начать позволять учащимся думать так, чтобы они могли снова и снова решать сложные задачи, прокладывая свой собственный путь к решению.
1. Связать решение проблем с чтением
Когда мы можем напомнить учащимся, что у них уже есть много навыков понимания и стратегий, которые они могут легко использовать при решении математических задач, это может уменьшить беспокойство, связанное с математической задачей. Например, предоставление им стратегий для практики, таких как визуализация, разыгрывание проблемы с помощью математических инструментов, таких как счетчики или блоки с основанием 10, рисование быстрого наброска проблемы, пересказ истории своими словами и т. д., может действительно помочь. использовать навыки, которые у них уже есть, чтобы сделать задачу менее сложной.
Мы можем разбить эти навыки на отдельные короткие уроки, чтобы у учащихся был набор стратегий, которые они могли бы попробовать самостоятельно. Вот пример якорной диаграммы, которую они могут использовать для визуализации. Разбивка понимания на конкретные навыки может повысить самостоятельность учащихся и помочь учителям быть более целенаправленными в своих инструкциях по решению проблем.
Это позволяет учащимся обрести уверенность и разрушить барьеры между чтением и математикой, чтобы увидеть, что у них уже есть так много сильных сторон, которые можно применить для решения любых задач.
2. Не заставляйте учащихся выбирать конкретную операцию
Может возникнуть соблазн предложить учащимся искать определенные слова, которые могут означать определенную операцию. Это может быть вполне успешным даже в детском саду и первом классе, но точно так же, как когда наша карта указывает нам, куда идти, это ограничивает учеников от того, чтобы они стали глубокими мыслителями. Срок его действия также истекает, когда они переходят в старшие классы, где эти слова могут встречаться в задаче несколько раз, создавая еще большую путаницу, когда учащиеся пытаются следовать правилу, которое может существовать не в каждой задаче.
Мы можем поощрять различные способы решения проблем вместо того, чтобы сначала выбирать операцию. В первом классе в задаче может быть сказано: «У Джослин 13 мягких игрушек, а у Джордана — 17.
Сколько еще у Джордана?» Некоторые учащиеся могут выбрать вычитание, но многие учащиеся могут просто считать, чтобы найти промежуточную сумму. Если мы скажем им, что «сколько еще» означает вычесть, мы полностью избавим их от размышлений о проблеме, позволив им действовать на автопилоте, не решая проблему по-настоящему и не используя свои навыки понимания для ее визуализации.
3. Пересмотрите «представительство»
Слово «представительство» может ввести в заблуждение. Кажется, что-то делать после процесса решения. Когда учащиеся думают, что им нужно сразу перейти к решению, они могут не осознавать, что им нужен промежуточный шаг, чтобы иметь возможность сначала поддержать свое понимание того, что на самом деле происходит в задаче.
Использование опорной диаграммы, подобной одной из этих (младший класс, старший класс), может помочь учащимся выбрать представление, которое наиболее точно соответствует тому, что они визуализируют в своем воображении. Как только они сделают набросок, это может дать им более четкое представление о различных способах решения проблемы.
Подумайте об этой задаче: «Варуш отправился с семьей в путешествие к бабушке. До него было 710 миль. По дороге туда по очереди ехали три человека. Его мама проехала 214 миль. Его отец проехал 358 миль. Остальные вела его старшая сестра. Сколько миль проехала его сестра?
Если бы мы показали этому студенту якорную диаграмму, он, вероятно, выбрал бы числовую прямую или ленточную диаграмму, чтобы помочь им понять, что происходит.
Если мы скажем учащимся, что они всегда должны рисовать квадраты с основанием 10 на диаграмме разрядности, это не обязательно соответствует концепции этой задачи. Когда мы просим студентов соответствовать нашему образу мышления, мы лишаем их практики критического мышления и иногда в процессе сбиваем их с толку.
4. Дайте время на обдумывание
Иногда мы, педагоги, можем чувствовать спешку, чтобы добраться до всех и всего, что требуется. При решении сложной задачи учащимся нужно время, чтобы просто сидеть с проблемой и бороться с ней, возможно, даже оставить ее и вернуться к ней через некоторое время.
Это может означать, что нам нужно давать им меньше проблем, но углубляться в те проблемы, которые мы им даем. Мы также можем ускорить время обработки, если предусмотрим совместную работу и время для общения с коллегами по задачам решения проблем.
5. Задавайте вопросы, которые позволяют учащимся думать
Вопросы или подсказки во время решения задач должны быть очень открытыми, чтобы стимулировать мышление. Попросив учащегося перечитать проблему или подумать о том, какие инструменты или ресурсы помогут ему ее решить, вы сможете заставить их попробовать что-то новое, но не завладеть их мышлением.
Эти навыки также можно использовать в разных материалах, и учащимся будет напоминать: «Хорошие читатели и математики перечитывают».
6. Спиралевидные понятия, чтобы учащиеся часто использовали навыки решения проблем
Когда учащимся не нужно переключать передачи между понятиями, они на самом деле не используют глубокие навыки решения проблем.