Дискретная математика, комбинаторика, теория чисел
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
 c c |
| ||
22/07/12 |
| ||
| |||
| EtCetera |
| |||
28/04/09 |
| |||
| ||||
| main.c |
| ||
22/07/12 |
| ||
| |||
| EtCetera |
| |||
28/04/09 |
| |||
| ||||
| main.c |
| ||
22/07/12 |
| ||
| |||
| EtCetera |
| |||
28/04/09 |
| |||
| ||||
| main.c |
| ||
560 |
| ||
| |||
| main.c |
| ||
22/07/12 |
| ||
| |||
| EtCetera |
| |||
28/04/09 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 9 ] |
Модераторы: Модераторы Математики, Супермодераторы
Онлайн калькулятор: Код Хаффмана
УчебаИнформатика
Построение кода Хаффмана для таблицы вероятностей.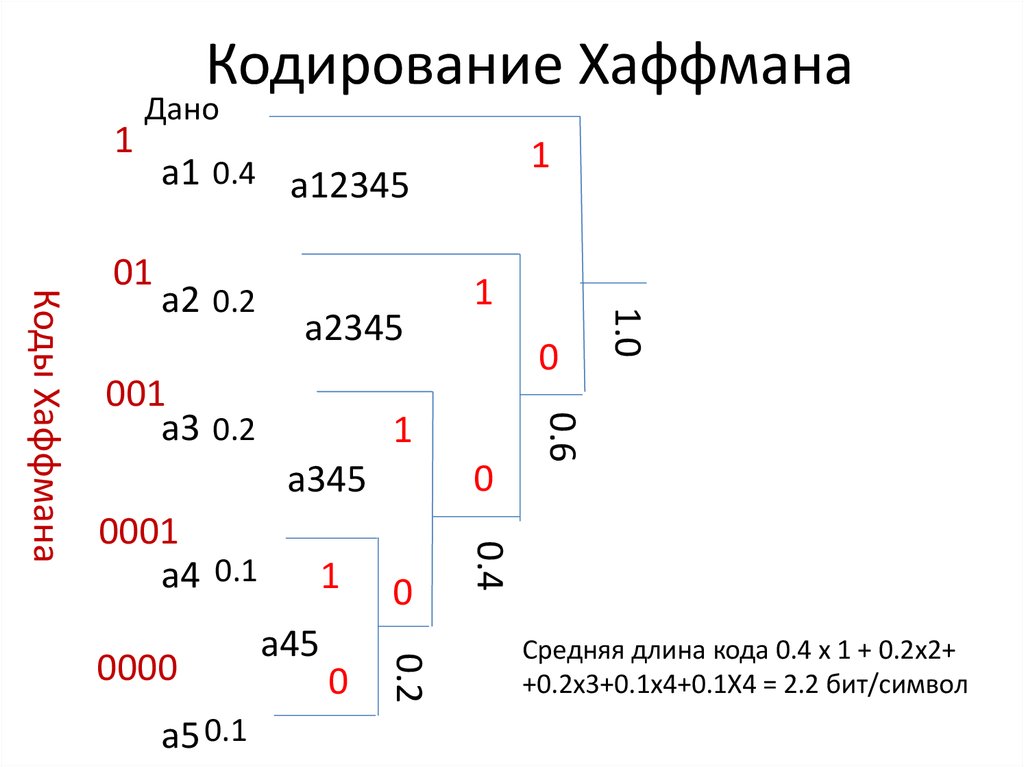
Вот калькулятор, который рассчитывает коды Хаффмана для заданной вероятности символов.
Немного теории под калькулятором.
Код Хаффмана
Таблица вероятности символов
| Имя | Значение | ||
|---|---|---|---|
51020501001000
Таблица вероятности символов
Значение
Импортировать данныеОшибка импорта
Данные
Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: Lorem ipsum;50.5
Загрузить данные из csv файла
Точность вычисления
Знаков после запятой: 2
Средняя длина символа
Энтропия
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Инвертировать 0 и 1
Небольшой отрывок из Википедии.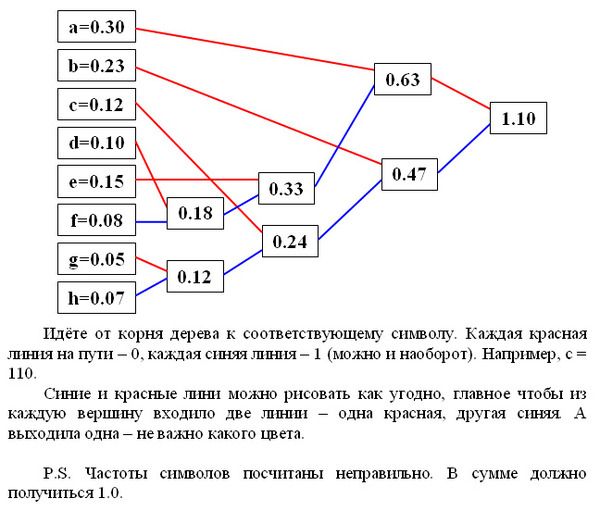
Алгоритм Хаффмана — адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. В настоящее время используется во многих программах сжатия данных.
Этот метод кодирования состоит из двух основных этапов:
Построение оптимального кодового дерева.
Построение отображения код-символ на основе построенного дерева.
Идея алгоритма состоит в следующем: зная вероятности символов в сообщении, можно описать процедуру построения кодов переменной длины, состоящих из целого количества битов. Символам с большей вероятностью ставятся в соответствие более короткие коды. Коды Хаффмана обладают свойством префиксности (т. е. ни одно кодовое слово не является префиксом другого), что позволяет однозначно их декодировать.
Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости символов в сообщении.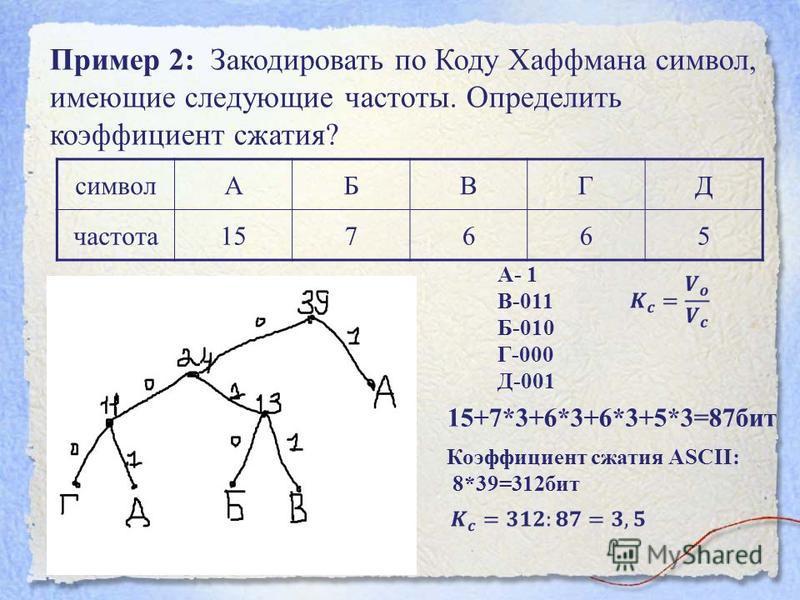 Далее на основании этой таблицы строится дерево кодирования Хаффмана (Н-дерево).
Далее на основании этой таблицы строится дерево кодирования Хаффмана (Н-дерево).
- Символы входного алфавита образуют список свободных узлов. Каждый лист имеет вес, который может быть равен либо вероятности, либо количеству вхождений символа в сжимаемое сообщение.
- Выбираются два свободных узла дерева с наименьшими весами.
- Создается их родитель с весом, равным их суммарному весу.
- Родитель добавляется в список свободных узлов, а два его потомка удаляются из этого списка.
- Одной дуге, выходящей из родителя, ставится в соответствие бит 1, другой — бит 0.
- Шаги, начиная со второго, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева.
Этот процесс можно представить как построение дерева, корень которого — символ с суммой вероятностей объединенных символов, получившийся при объединении символов из последнего шага, его n0 потомков — символы из предыдущего шага и т. д.
д.
Чтобы определить код для каждого из символов, входящих в сообщение, мы должны пройти путь от корня до листа дерева, соответствующего текущему символу, накапливая биты при перемещении по ветвям дерева (первая ветвь в пути соответствует младшему биту). Полученная таким образом последовательность битов является кодом данного символа, записанным в обратном порядке.
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Код Хаффмана для последовательности символов
- • Построение таблицы частот
- • Формула Шеннона
- • Частная условная энтропия
- • Условная энтропия
- • Раздел: Информатика ( 59 калькуляторов )
алгоритм Информатика код код Хаффмана Компьютеры теория информации Хаффман Шеннон энтропия
PLANETCALC, Код Хаффмана
Timur2020-11-03 14:19:30
жадных алгоритмов — Длина кратчайшего кодового слова в кодировке Хаффмана
спросил
Изменено 4 года, 2 месяца назад
Просмотрено 1к раз
$\begingroup$
При кодировании Хаффмана, если один символ встречается более 1/3 времени, гарантируется ли наличие хотя бы одного символа, кодовое слово которого имеет длину 1?
Я подумал о двух случаях, когда это может быть правдой, но это не совсем доказательства —
Случай 1: Есть только один символ, который встречается более 1/3 времени. В этом случае хорошая схема кодирования Хаффмана гарантирует, что этот символ соответствует односимвольной кодировке, потому что нет конкурирующих символов. Несмотря на то, что могут быть символы, которые встречаются с высокой вероятностью (но все же меньше 0,33), они должны иметь длину больше 1, чтобы гарантировать беспрефиксный характер кодирования.
В этом случае хорошая схема кодирования Хаффмана гарантирует, что этот символ соответствует односимвольной кодировке, потому что нет конкурирующих символов. Несмотря на то, что могут быть символы, которые встречаются с высокой вероятностью (но все же меньше 0,33), они должны иметь длину больше 1, чтобы гарантировать беспрефиксный характер кодирования.
Случай 2: Несколько символов встречаются более 33% времени. Можно также сделать более сильное утверждение, что в этом случае таких характеров может быть не более 2. Это можно дополнительно разделить на случаи, когда 1) в схеме кодирования всего 2 символа и 2) когда в схеме более 2 символов. В случае 1) оба символа могут соответствовать односимвольной схеме кодирования (0 и 1 для каждого соответственно). В случае 2) не более 1 из 2 широко распространенных/частых символов должен иметь кодировку длины 1 (поскольку мы рассматриваем хорошую схему кодирования Хаффмана), в то время как другие символы n-1 имеют длину не менее 2
Боюсь, это неправильный подход.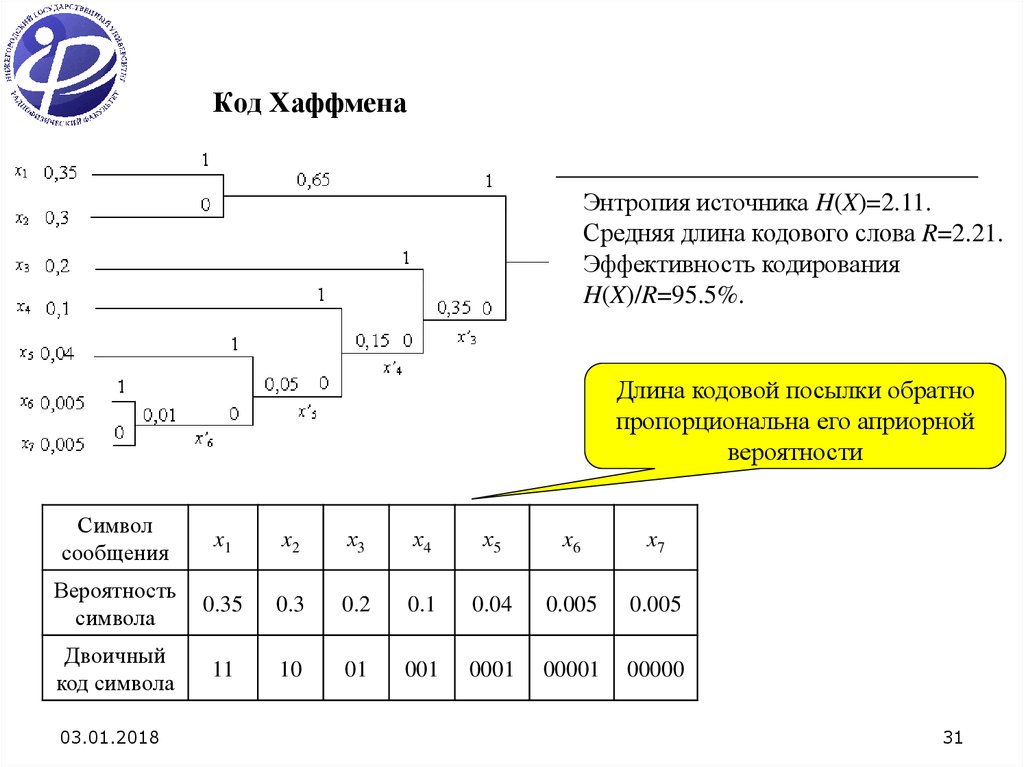 Может ли кто-нибудь помочь мне?
Может ли кто-нибудь помочь мне?
- жадные алгоритмы
- Хаффман-кодирование
$\endgroup$
$\begingroup$
Рассмотрим распределение $\Pr[a]=0,34,\Pr[b]=\Pr[c]=\Pr[d]=0,22$.
Алгоритм Хаффмана сначала объединит (скажем) $c$ и $d$, чтобы создать символ $cd$ с вероятностью $0,44$. Затем он объединит $a$ и $b$, чтобы создать символ $ab$ с вероятностью $0,56$. Наконец, он объединит оставшиеся символы.
Таким образом, все кодовые слова имеют длину 2.
Вы можете проверить, что тот же пример работает до $\Pr[a] = 0,4$ (нам нужно $\Pr[a] \leq 2\Pr[b] = (2 /3)(1-\Pr[a])$). Что если $\Pr[a] > 0,4$? Рассмотрим момент, когда алгоритм Хаффмана объединяет $a$ с некоторым символом $X$ (который может состоять из нескольких исходных символов). Если $a$ и $X$ — единственные символы, то $a$ будет закодирован символом длины 1. В противном случае существует какой-то другой символ $Y$ с вероятностью не менее $\max(\Pr[a] ,\Pr[X]) > 0,4$. Мы видим, что $a,X,Y$ должны быть единственными оставшимися символами, и, кроме того, $\Pr[a] > \Pr[X]$ (иначе было бы 3 символа, вероятность которых превышает 0,4).
Мы видим, что $a,X,Y$ должны быть единственными оставшимися символами, и, кроме того, $\Pr[a] > \Pr[X]$ (иначе было бы 3 символа, вероятность которых превышает 0,4).
Предположим, что $Y$ получен слиянием двух других символов $Z,W$. В этот момент, поскольку сам $X$ или одна из его составляющих не были объединены, мы должны иметь $\Pr[X] \geq \max(\Pr[Z],\Pr[W]) \geq \Pr[ г]/2$. Но $\Pr[Y] > 0,4$ и, следовательно, $\Pr[X] > 0,2$, поэтому суммы вероятностей больше 1. Это противоречие показывает, что $Y$ — исходный символ, поэтому в этом случае имеется кодовое слово длины 1.
В заключение, порог гарантированного кодового слова длины 1 равен 0,4.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
жадных алгоритмов — Задача о кодовом слове Хаффмана
спросил
Изменено 2 года, 1 месяц назад
Просмотрено 131 раз
$\begingroup$
При кодировании Хаффмана, при каких обстоятельствах длина кодового слова каждого символа быть равным? (предположим, что количество символов равно степени 2)
Я думаю, что если все частоты символов одинаковы, то длина кодового слова всех символов будет одинаковой.
Удивительно, но если есть два символа, у которых разница между частотой двух символов составляет $2$, а частота других равна, то длина кодового слова всех символов будет одинаковой.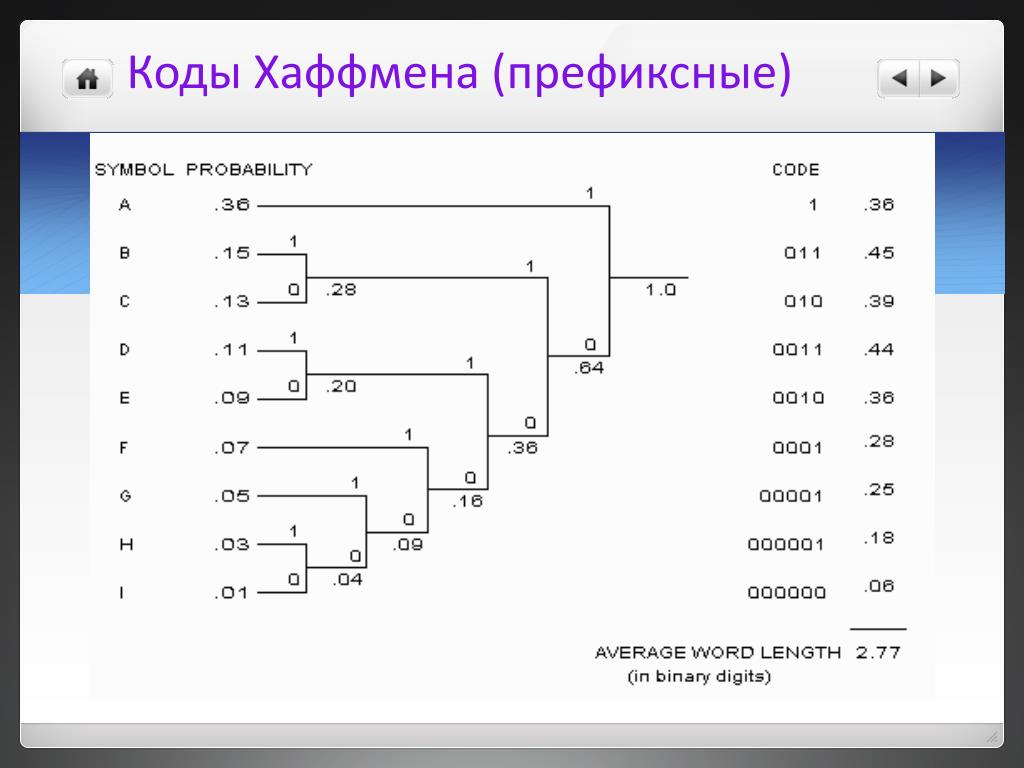

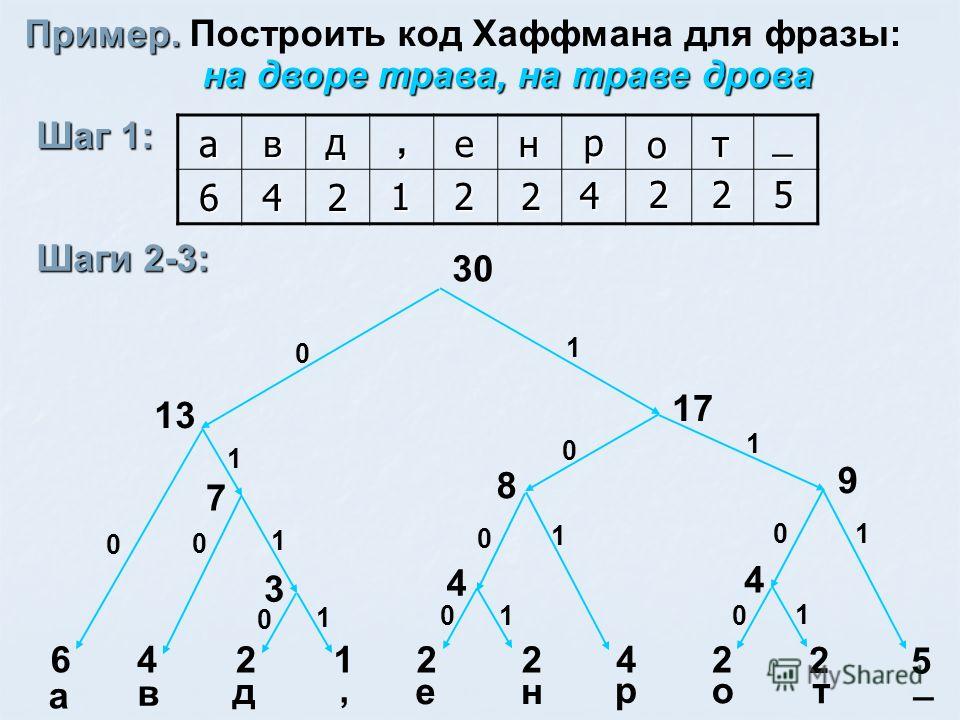 А вот на второй вопрос я ответить затрудняюсь. Просьба хотя бы дать наводку.
А вот на второй вопрос я ответить затрудняюсь. Просьба хотя бы дать наводку. 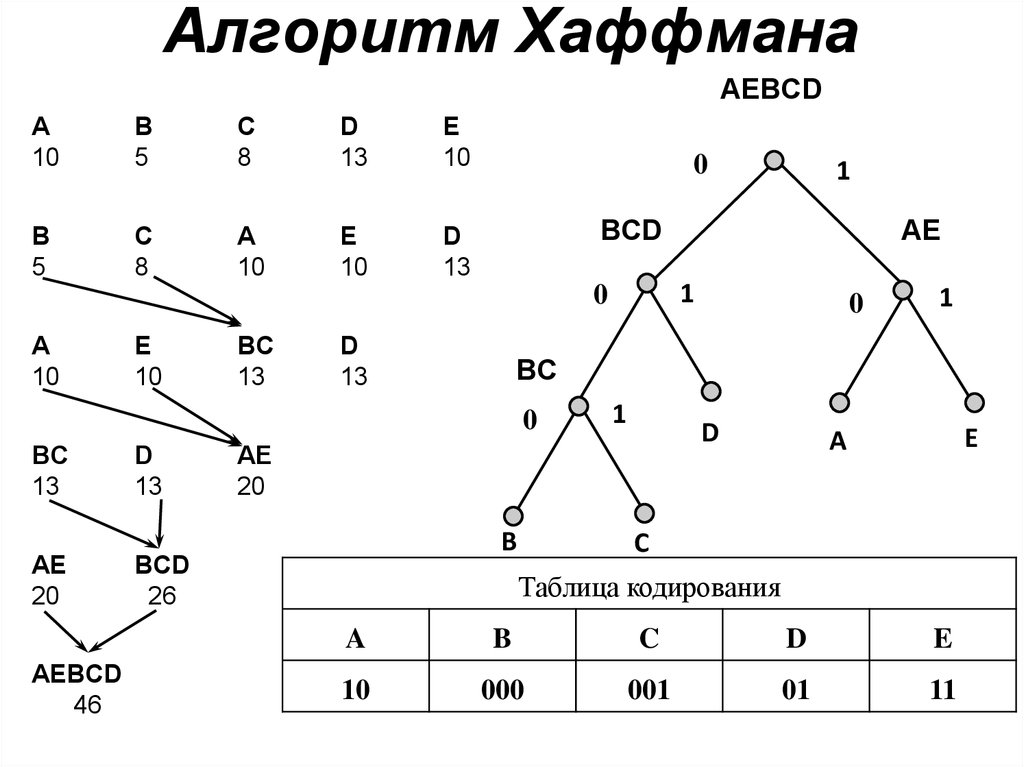


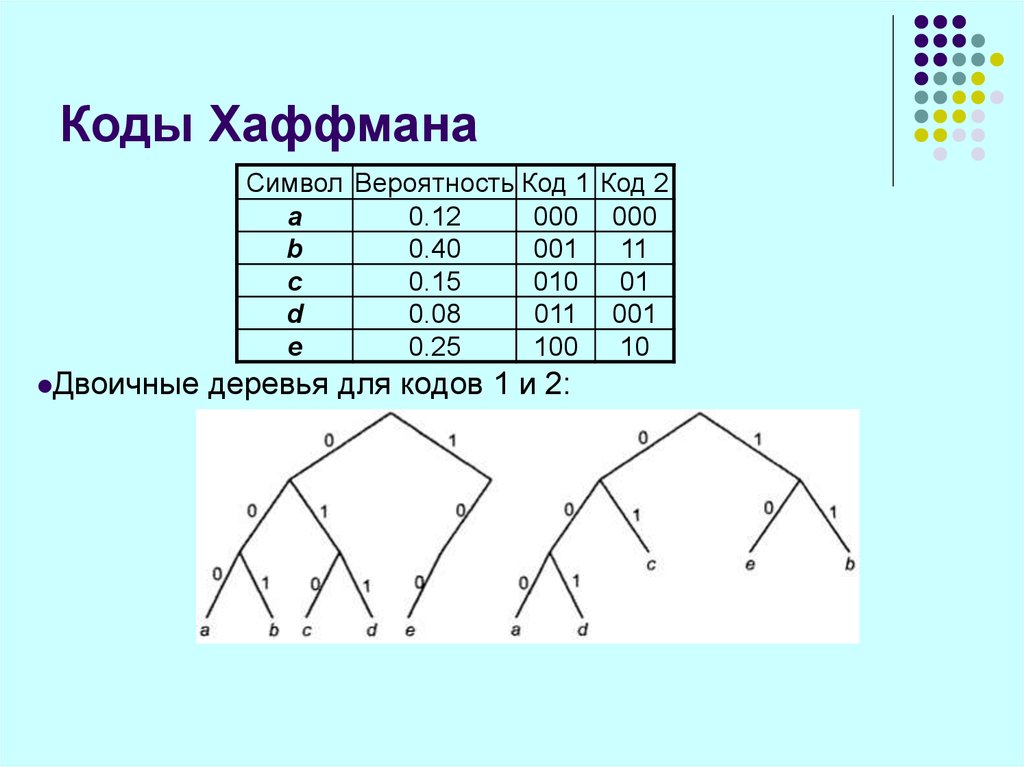 12.2012, 17:08
12.2012, 17:08  12.2012, 17:36
12.2012, 17:36  12.2012, 20:45
12.2012, 20:45 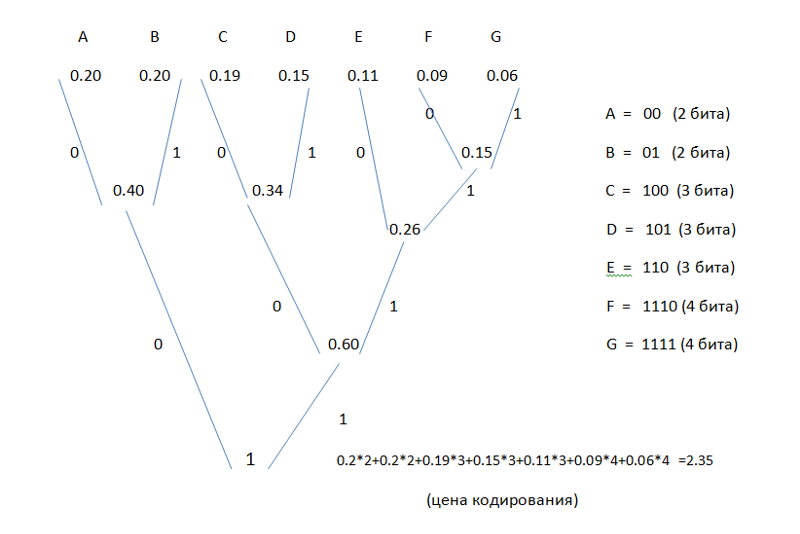 12.2012, 21:28
12.2012, 21:28