Mathway | Популярные задачи
Популярные задачи
Элемент. математикаОсновы алгебрыАлгебраТригонометрияОсновы мат. анализаМатематический анализКонечная математикаЛинейная алгебраХимияPhysics
| Рейтинг | Тема | Задача | Форматированная задача |
|---|---|---|---|
| 1 | Решить, используя обратную матрицу | x+2y=1 , 4x+5y=13 | , |
| 2 | Перемножить матрицы | [[1/( квадратный корень из 17),-4/( квадратный корень из 17)]][[1/( квадратный корень из 17)],[-4/( квадратный корень из 17)]] | |
| 3 | Найти область определения | x+y=3 | |
| 4 | Найти область определения | x-y=3 | |
| 5 | Найти область определения | y=-2x+3 | |
| 6 | Найти область определения | y=2x+1 | |
| 7 | Записать в виде векторного равенства | x=x^2+9x+3 , x=x+2 | , |
| 8 | Найти область определения | y=2x | |
| 9 | Найти область определения | y=-3x | |
| 10 | Найти область определения | y=3x-2 | |
| 11 | Найти область определения | y=4x | |
| 12 | Найти область определения | 3x+2y=6 | |
| 13 | Trovare la 5×5 Matrice Identità | 5 | |
| 14 | Trovare la 6×6 Matrice Identità | 6 | |
| 15 | Trovare la 4×4 Matrice Identità | 4 | |
| 16 | Решить, используя обратную матрицу | 2x+y=-2 , x+2y=2 | , |
| 17 | Решить, используя обратную матрицу | 4x+4=y , y=6x | , |
| 18 | Решить, используя обратную матрицу | 4x+2=5y-3 , y=3x-1 | , |
| 19 | Найти степенное множество | (3,4) | |
| 20 | Вычислить | кубический корень из 216 | |
| 21 | Найти степенное множество | (1,3) | |
| 22 | Найти область определения | 3x-2y=12 | |
| 23 | Найти область определения | y=5x+2 | |
| 24 | Найти область определения | y=2x-3 | |
| 25 | Найти область определения | y=2x-4 | |
| 26 | Найти область определения | y=2x+5 | |
| 27 | Найти область определения | y=1/2x | |
| 28 | Найти область определения | y=1/2x-3 | |
| 29 | Найти область определения | y=2/3x-2 | |
| 30 | Найти область определения | x=2y | |
| 31 | Найти область определения | x-2y=2 | |
| 32 | Найти область определения | x-2y=6 | |
| 33 | Найти область определения | 2y+x | |
| 34 | Найти область определения | 2x+y=0 | |
| 35 | Найти область определения | y=5x+6 | |
| 36 | Найти область определения | y=x+3 | |
| 37 | Solve Using a Matrix by Elimination | y=4x+3x-2 , y=6 | , |
| 38 | Проверить линейную зависимость | B={[[-10,2],[5,-2. 5]]} 5]]} | |
| 39 | Сложение | [[2,4],[6,-4]]+[[-3,-7],[20,10]] | |
| 40 | Проверить линейную зависимость | B={[[-1,2],[0,-2.5]]} | |
| 41 | Перемножить матрицы | [[0,0,1,1],[1,0,1,0],[0,0,0,1],[0,1,0,0]][[0,0,1,1],[1,0,1,0],[0,0,0,1],[0,1,0,0]] | |
| 42 | Найти область определения | y=5x | |
| 43 | Найти область определения | y=7x | |
| 44 | Найти область определения | y=-x-2 | |
| 45 | Найти область определения | y=x-2 | |
| 46 | Найти область определения | y=x-3 | |
| 47 | Привести матрицу к ступенчатому виду по строкам | [[4,-3,1,0],[1,0,-2,0],[-2,1,1,0]] | |
| 48 | Записать в виде векторного равенства | x+y+z=2 , 4x+5y+z=12 , 2x=-4 | , , |
| 49 | Найти определитель | [[0,-1,a],[3,-a,1],[1,-2,3]] | |
| 50 | Найти область определения | y=-x+2 | |
| 51 | Найти определитель | [[2,5,0],[1,0,-3],[2,-1,2]] | |
| 52 | Найти определитель | [[7,5,0],[4,5,8],[0,-1,5]] | |
| 53 | Найти обратный элемент | [[1,-3,0,-2],[3,-12,-2,-6],[-2,10,2,5],[-1,6,1,3]] | |
| 54 | Найти обратный элемент | [[1,2,3],[2,5,7],[3,7,9]] | |
| 55 | Привести матрицу к ступенчатому виду по строкам | [[0,1,5,-4],[1,4,3,-2],[2,7,1,-2]] | |
| 56 | Привести матрицу к ступенчатому виду по строкам | [[1,1,0],[1,0,1],[1,0,1],[2,1,0],[2,1,0]] | |
| 57 | Привести матрицу к ступенчатому виду по строкам | [[1,2,3],[4,5,6],[7,8,9]] | |
| 58 | Привести матрицу к ступенчатому виду по строкам | [[7,8]] | |
| 59 | Найти область определения | 2x+y=1 | |
| 60 | Записать в виде векторного равенства | 2x+y=-2 , x+2y=2 | , |
| 61 | Найти область определения | x-2y=4 | |
| 62 | Найти область определения | x-y=-1 | |
| 63 | Найти область определения | x+y=5 | |
| 64 | Найти область определения | x=-3y-8 | |
| 65 | Найти область определения | x=-2y-8 | |
| 66 | Найти область определения | x+y=6 | |
| 67 | Найти область определения | x+y=4 | |
| 68 | x+2y=4 | ||
| 69 | Найти область определения | x+y | |
| 70 | Найти область определения | y=7x+9 | |
| 71 | Найти область определения | y=1/2x-5 | |
| 72 | Найти область определения | y=1/2x+2 | |
| 73 | Найти область определения | y=1/2x+3 | |
| 74 | Найти область определения | x-y=-3 | |
| 75 | Найти область определения | x-y=4 | |
| 76 | Найти область определения | y=-2x | |
| 77 | Найти область определения | y=-2x+1 | |
| 78 | Найти область определения | y=2^(x+9) | |
| 79 | Найти область определения | y=10-x^2 | |
| 80 | Найти область определения | y=2x-6 | |
| 81 | Найти область определения | y=-2x-3 | |
| 82 | Найти область определения | y=3x-8 | |
| 83 | Найти область определения | y=3x | |
| 84 | Найти область определения | y=-3x+1 | |
| 85 | Найти область определения | y=4x+3 | |
| 86 | Найти область определения | y=3x-4 | |
| 87 | Найти область определения | y=4x-2 | |
| 88 | Найти область определения | y=-6x | |
| 89 | Найти область определения | y=x-4 | |
| 90 | Найти область определения | 7 корень четвертой степени из 567y^4 | |
| 91 | Найти область определения | c=5/9*(f-32) | |
| 92 | Найти область определения | f=9/5c+32 | |
| 93 | Вычислить | квадратный корень из 4 | |
| 94 | Привести матрицу к ступенчатому виду по строкам | [[-6,7],[2,6],[-4,1]] | |
| 95 | Найти собственные значения | [[2,1],[3,2]] | |
| 96 | Найти собственные значения | [[4,0,1],[2,3,2],[49,0,4]] | |
| 97 | Найти степенное множество | A=(2,3,4,5) | |
| 98 | Найти мощность | (2,1) | |
| 99 | Решить, используя обратную матрицу | -3x-4y=2 , 8y=-6x-4 | , |
| 100 | Решить, используя обратную матрицу | 2x-5y=4 , 3x-2y=-5 | , |
«Калькулятор матриц» (Koliuzhnov Viacheslav), «Решение матриц» (DragoN) и Matrix Calculator (страница 2)
«Решение матриц» (DragoN)
Знакомство
Собрались изучать высшую математику? Тогда вам никак нельзя обойти стороной матрицы и приложение «Решение матриц», выпущенное разработчиком с ником DragoN. Ведь оно с легкостью позволяет выполнять самые распространенные действия над матрицами.
Ведь оно с легкостью позволяет выполнять самые распространенные действия над матрицами.
Приложение «Решение матриц» позволяет осуществлять следующие действия:
- Вычислять определитель 3-4 порядка;
- Решать уравнения методом Крамера и матричным способом;
- Складывать матрицы 2 x 2, 3 x 3, 4 x 4;
- Умножать матрицы на число;
- Умножать матрицы на матрицу;
- Возводить матрицу в квадрат.
рекомендации
Начало работы
Интерфейс матричного калькулятора «Решение матриц» представлен в виде очень необычного вертикального меню. На нем располагаются «кнопки» с доступными функциями по преобразованию матриц (я насчитал таких аж семь штук), а также ссылки на официальную группу в социальной сети ВКонтакте и оценки/отзывы в Google Play.
Программа умеет находить определитель (детерминант), складывать матрицы, умножать матрицу на число, умножать матрицу на матрицу, возводить матрицу в квадрат. Их решение осуществляется с помощью двух наиболее распространенных методов: матричного и Крамера.
Их решение осуществляется с помощью двух наиболее распространенных методов: матричного и Крамера.
Выбираем необходимое действие и переходим в подменю. Там нам необходимо установить размер матрицы и непосредственно ввести ее.
К сожалению, в большинстве действий размерность матрицы ограничивается четырьмя строками и четырьмя столбцами. Правда, при обучении по программе бакалавриата в среднестатистическом вузе большая размерность нам не пригодится, хотя бывают и исключения.
Кстати, перед вводом примера отображается разобранный пример, то есть метод решения.
Более серьезным недостатком приложения «Решение матриц», по моему мнению, является неудобная клавиатура, которая не позволяет быстро переходить к рядом стоящему элементу. Лишь нажатие клавиши «Enter» сможет опустить нас на строчку ниже.
Ответ программа выдает в расписанном виде, хотя совершаемые действия никак не подписываются. Интерфейс и меню с ответами не масштабируются, поэтому на планшетах с низким разрешением экрана могут возникать различные проблемы, как минимум элементы отображаются очень мелким шрифтом.
Кстати, в отличие от вышерассмотренного приложения и многих других, здесь есть генератор случайных значений. Благодаря ему можно создать уникальный пример, решить его вручную и уже затем через калькулятор. Это будет полезно студентам, которые учатся решать матрицы.
Тестирование
| Версия приложения | |
| Размер дистрибутива | |
| Размер приложения в установленном виде | |
| Потребление ОЗУ |
К функционированию приложения «Решение матриц» у меня нет претензий, так как калькулятор работает исправно и неплохо нагружает мобильное устройство.
Выводы
В целом, «Решение матриц» – это неплохой матричный калькулятор. Он прост в использовании, содержит необычный интерфейс и предлагает несколько методов решения матриц. Правда, программа не умеет совершать определенные операции, например, возводить матрицу в третью степень или транспонировать ее. Есть и проблемы с удобством ввода данных.
Он прост в использовании, содержит необычный интерфейс и предлагает несколько методов решения матриц. Правда, программа не умеет совершать определенные операции, например, возводить матрицу в третью степень или транспонировать ее. Есть и проблемы с удобством ввода данных.
С другой стороны, функциональность программы не ограничена, а сама она является бесплатной. Платой за это стала реклама, которую можно отключить за $1.99.
Скачать приложение «Решение матриц» Скачать приложение «Решение матриц Pro» | |
| Разработчик | DragoN. |
| Стоимость | «Решение матриц» – бесплатно, «Решение матриц Pro» – $1.99. |
| Требования | Для OC Android 4.0 и новее. |
Подпишитесь на наш канал в Яндекс. Дзен или telegram-канал @overclockers_news — это удобные способы следить за новыми материалами на сайте. С картинками, расширенными описаниями и без рекламы.
Дзен или telegram-канал @overclockers_news — это удобные способы следить за новыми материалами на сайте. С картинками, расширенными описаниями и без рекламы.
Quick-R: Матричная алгебра
Большинство методов на этом веб-сайте фактически описывают программирование матриц. Он глубоко встроен в язык R. В этом разделе будут просто рассмотрены операторы и функции, специально предназначенные для линейной алгебры. Прежде чем продолжить, вы, возможно, захотите просмотреть разделы о типах данных и операторах.
Matrix facilites
В следующих примерах A и B являются матрицами, а x и b — это векторы.
| Оператор или функция | Описание |
| А * Б | Поэлементное умножение |
| А %*% В | Умножение матриц |
| А %о% В | Внешний продукт. АБ’ АБ’ |
| перекрестный(A,B) перекрестный(A) | A’B и A’A соответственно. |
| т(А) | Транспонировать |
| диаг(х) | Создает диагональную матрицу с элементами x по главной диагонали |
| диаг.(А) | Возвращает вектор, содержащий элементы главной диагонали |
| диаг(к) | Если k является скаляром, создается единичная матрица размера k x k. Иди разберись. |
| решить(А, б) | Возвращает вектор x в уравнении b = Ax (т. е. A -1 b ) |
| решить(А) | Инверсия A , где A — квадратная матрица.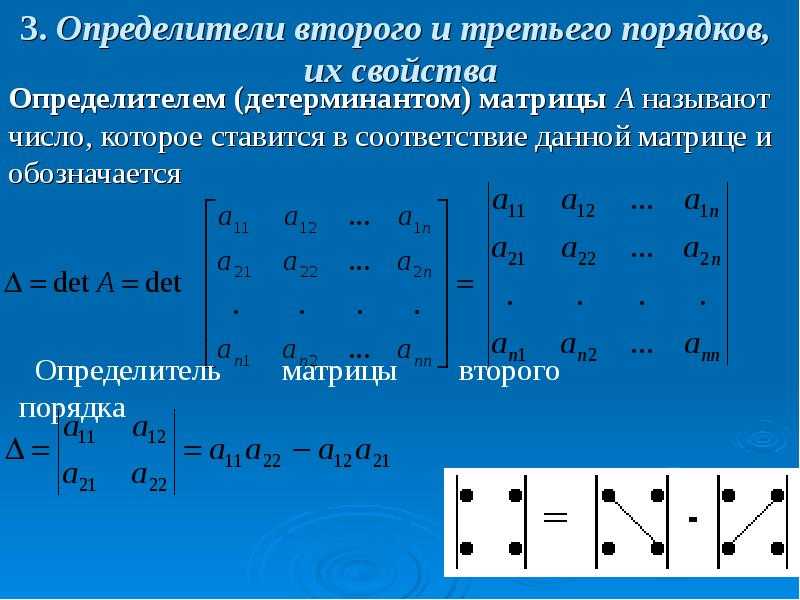 |
| джинв(А) | Обобщенный алгоритм Мура-Пенроуза, обратный A . ginv(A) требует загрузки пакета MASS . |
| y<-собственный (A) | y$val — собственные значения A y$vec — собственные векторы А |
| у<-свд(А) | Однозначное разложение A . y$d = вектор, содержащий сингулярные числа A y$u = матрица со столбцами, содержащими левые сингулярные векторы A y$v = матрица со столбцами, содержащими правые сингулярные векторы А |
| R <- хол(А) | Факторизация Холецкого A . Возвращает верхний треугольный коэффициент, такой что R’R = A . Возвращает верхний треугольный коэффициент, такой что R’R = A . |
| у <- qr(A) | QR-разложение A . y$qr имеет верхний треугольник, содержащий разложение, и нижний треугольник, содержащий информацию о разложении Q. y$rank — ранг A. y$qraux вектор, который содержит дополнительную информацию о Q. y$pivot содержит информацию об используемой стратегии поворота. |
| cbind(A,B,…) | Объединить матрицы(векторы) по горизонтали. Возвращает матрицу. |
| rbind(A,B,…) | Объединить матрицы(векторы) по вертикали. Возвращает матрицу. |
| ряд Среднее(А) | Возвращает вектор средних значений строки. |
| рядСумм(А) | Возвращает вектор сумм строк. |
| colMeans(A) | Возвращает вектор средних значений столбца. |
| столбцы(A) | Возвращает вектор сумм столбцов. |
Эмуляция Matlab
Пакет Matlab содержит функции-оболочки и переменные, используемые для наилучшей репликации вызовов функций MATLAB. Это может помочь при переносе приложений и кода MATLAB на R.
Идем дальше
Пакет Matrix содержит функции, расширяющие R для поддержки очень плотных или разреженных матриц. Он обеспечивает эффективный доступ к BLAS (базовым подпрограммам линейной алгебры), Lapack (плотная матрица), TAUCS (разреженная матрица) и UMFPACK (разреженная матрица) рутины.
Для практики
Попробуйте выполнить некоторые упражнения по матричной алгебре в этом курсе по введению в статистику с помощью R. {-1}A−1 для обозначения обращения матрицы в уравнении, на практике мы фактически не инвертируем матрицу. Вместо этого мы решаем систему линейных уравнений. Позвольте мне сначала пояснить это утверждение. Рассмотрим решение для x\mathbf{x}x в 9{-1}A−1 полностью путем непосредственного решения системы линейных уравнений.
{-1}A−1 для обозначения обращения матрицы в уравнении, на практике мы фактически не инвертируем матрицу. Вместо этого мы решаем систему линейных уравнений. Позвольте мне сначала пояснить это утверждение. Рассмотрим решение для x\mathbf{x}x в 9{-1}A−1 полностью путем непосредственного решения системы линейных уравнений.
Так почему и когда один подход лучше другого? У Джона Кука есть запись в блоге на эту тему, и хотя на нее часто ссылаются, в ней мало подробностей. Например, Кук утверждает, что «Решение системы является более точным в численном отношении, чем выполнение матричного умножения», но не дает никаких объяснений или доказательств.
Цель этого поста состоит в том, чтобы расширить , почему вычислительное уравнение. 222 явно нежелательно. Как всегда, ответ кроется в деталях.
LU-разложение
Прежде чем сравнивать обращение матриц с решением линейной системы, нам нужно поговорить о мощной операции, которая используется в обоих вычислениях: разложении снизу-вверх. Не стесняйтесь пропустить этот раздел, если вы знакомы с этим материалом.
Не стесняйтесь пропустить этот раздел, если вы знакомы с этим материалом.
Разложение LU использует исключение Гаусса для преобразования полной линейной системы в верхнетреугольную систему путем применения линейных преобразований слева. Это похоже на разложение QR без ограничения, что левая матрица ортогональна. Оба разложения можно использовать для решения линейных систем и инвертирующих матриц, но я сосредоточусь на LU-разложении, потому что, по крайней мере, насколько я понимаю, оно обычно предпочтительнее на практике. 9{\mathbf{L}_2 \mathbf{L}_1 \mathbf{A}}. \тег{3} ⎣⎢⎡×××××××××⎦⎥⎤A→⎣⎢⎡×00××××××⎦⎥⎤L1A→⎣ ⎢⎡×00××0×××⎦⎥⎤L2L1A.(3)
На iii-м преобразовании алгоритм вводит n−in-in-i нулей ниже диагональ путем вычитания кратных (i−1)(i-1)(i−1)-й строки из строк под ней (i+1,…,ni+1, \dots, ni+1,…, н).
Давайте рассмотрим пример, который во многом заимствован из (Trefethen & Bau III, 1997). Рассмотрим матрицу
A=[211433879].(4)
\mathbf{A} = \begin{bmatrix} 2 & 1 & 1 \\ 4 & 3 & 3 \\ 8 & 7 & 9\end{bматрица}. \тег{4}
A=⎣⎢⎡248137139⎦⎥⎤.(4)
\тег{4}
A=⎣⎢⎡248137139⎦⎥⎤.(4)
Во-первых, мы хотим ввести нули ниже левого верхнего 222. Трефетен и Бау выбрали числа в A\mathbf{A}A разумно для удобного устранения. А именно, A0,1=2A0,0A_{0,1} = 2 A_{0,0}A0,1=2A0,0 и A0,2=4A0,0A_{0,2} = 4 A_{0, 0}А0,2=4А0,0. Мы можем представить это исключение в виде нижней треугольной матрицы L1\mathbf{L}_1L1 как:
L1A=[100−210−401][211433879]=[211011035].(5) \mathbf{L}_1 \mathbf{A} = \begin{bmatrix} 1 & 0 & 0 \\ -2 & 1 & 0 \\ -4 & 0 & 1 \end{bmatrix} \begin{bmatrix} 2 & 1&1\4&3&3\8&7&9\end{bmatrix} = \begin{bmatrix} 2 & 1 & 1 \\ 0 & 1 & 1 \\ 0 & 3 & 5 \end{bmatrix}. \тег{5} L1A=⎣⎢⎡1−2−4010001⎦⎥⎤⎣⎢⎡248137139⎦⎥⎤=⎣⎢⎡200113115⎦⎥⎤ .(5)
Теперь нам просто нужно исключить 333 в A2,1A_{2,1}A2,1, что мы можем сделать с помощью другой линейной карты:
L2L1A=[1000100−31][211011035]= [211011002].(6)
\mathbf{L}_2 \mathbf{L}_1 \mathbf{A} =
\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -3 & 1 \end{bmatrix}
\begin{bmatrix} 2 & 1 & 1 \\ 0 & 1 & 1 \\ 0 & 3 & 5 \end{bmatrix}
знак равно
\begin{bmatrix} 2 & 1 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 2 \end{bmatrix}. \тег{6}
L2L1A=⎣⎢⎡10001−3001⎦⎥⎤⎣⎢⎡200113115⎦⎥⎤=⎣⎢⎡200110112⎦⎥⎤ .(6) 9{-1}. \тег{8}
L=L1−1…Ln−1−1Ln−1−1.(8)
\тег{6}
L2L1A=⎣⎢⎡10001−3001⎦⎥⎤⎣⎢⎡200113115⎦⎥⎤=⎣⎢⎡200110112⎦⎥⎤ .(6) 9{-1}. \тег{8}
L=L1−1…Ln−1−1Ln−1−1.(8)
Как оказалось, общая формула для Li\mathbf{L}_iLi такова, что вычисление обратной величины тривиально : мы просто отрицаем значения ниже диагонали. Подробности см. в главе 202020 (Trefethen & Bau III, 1997).
Сколько операций с плавающей запятой (flops) требуется для вычисления разложения LU? Вы можете найти более подробные доказательства в другом месте, но вот простая геометрическая интуиция, предоставленная Трефетеном и Бау. Для iii-й строки в A\mathbf{A}A мы должны оперировать n−in — in−i столбцов. Таким образом, для каждой из n-1n-1n-1 итераций алгоритма мы имеем сложность, которая составляет (n-i)×(n-i)(n-i) \times (n-i)(n-i)×(n- я). Мы можем представить это как пирамиду вычислений (рис. 111). 93 \quad \text{флопс}. \тег{9} ∼32n3flops.(9)
Решение линейной системы
Теперь поговорим об использовании LU-разложения для решения линейной системы. Пусть A∖b\mathbf{A} \setminus \mathbf{b}A∖b обозначает вектор x\mathbf{x}x, который решает Ax=b\mathbf{A x} = \mathbf{b}Ax= б. Как вычислить x\mathbf{x}x без , используя обратную матрицу? Стандартный метод заключается в использовании LU-разложения A\mathbf{A}A, а затем решении двух простых систем уравнений:
Пусть A∖b\mathbf{A} \setminus \mathbf{b}A∖b обозначает вектор x\mathbf{x}x, который решает Ax=b\mathbf{A x} = \mathbf{b}Ax= б. Как вычислить x\mathbf{x}x без , используя обратную матрицу? Стандартный метод заключается в использовании LU-разложения A\mathbf{A}A, а затем решении двух простых систем уравнений:
Ax=b,LUx=b,(LU разложение)L∖b=y,(прямая подстановка) U∖y=x (обратная замена)⇓LUx=Ly=b.(10) \begin{выровнено} \mathbf{Ax} &= \mathbf{b}, \\ \mathbf{LUx} &= \mathbf{b}, && \text{(разложение LU)} \\ \mathbf{L} \setminus \mathbf{b} &= \mathbf{y}, && \text{(прямая подстановка)} \\ \mathbf{U} \setminus \mathbf{y} &= \mathbf{x}, && \text{(обратная замена)} \\ &\Кнопка «Стрелка вниз \\ \mathbf{LUx} &= \mathbf{Ly} = \mathbf{b}. \end{выровнено} \tag{10} AxLUxL∖bU∖yLUx=b,=b,=y,=x,⇓=Ly=b.(LU разложение)(прямая подстановка)(обратная подстановка)(10)
Почему легко найти y\mathbf{y}y и x\mathbf{x}x относительно L\mathbf{L}L и U\mathbf{U}U соответственно? Потому что это нижнетреугольные и верхнетреугольные матрицы соответственно. Например, рассмотрите решение для y\mathbf{y}y выше:
Например, рассмотрите решение для y\mathbf{y}y выше:
[1ℓ2,11⋮…⋱ℓn−1,1……1ℓn,1……ℓn,n−11][y1y2⋮yn−1yn]= [b1b2⋮bn−1bn](11) \begin{bmatrix} 1 \\ \ell_{2,1} и 1 \\ \vdots & \dots & \ddots \\ \ell_{n-1,1} & \dots & \dots & 1 \\ \ell_{n,1} & \dots & \dots & \ell_{n,n-1} & 1 \end{bmatrix} \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_{n-1} \\ y_n \end{bmatrix} знак равно \begin{bmatrix} b_1\b_2\\vdots\b_{n-1}\b_n \end{bmatrix} \тег{11} ⎣⎢⎢⎢⎢⎢⎢⎡1ℓ2,1⋮ℓn−1,1ℓn,11………⋱……1ℓn,n−11⎦⎥⎥⎥⎥⎥⎥ ⎤⎣⎢⎢⎢⎢⎢⎢⎡y1y2⋮yn−1yn⎦⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎢⎡b1b2⋮bn−1 bn⎦⎥⎥⎥⎥⎥⎥⎤(11)
Для каждого значения yiy_iyi мы имеем
yi=bi-ℓi,1y1-⋯-ℓi,i-1yi-1.(12) y_i = b_i — \ell_{i,1} y_1 — \dots — \ell_{i,i-1} y_{i-1}. \тег{12} yi=bi−ℓi,1y1−⋯−ℓi,i−1yi−1.(12)
Решение для y\mathbf{y}y таким способом называется прямой подстановкой , потому что мы вычисляем y1y_1y1 и затем вперед подставляем значение в следующую строку и так далее. Затем мы можем запустить обратную замену на матрице верхнего треугольника, то есть начиная с нижней строки и двигаясь вверх, чтобы найти x\mathbf{x}x.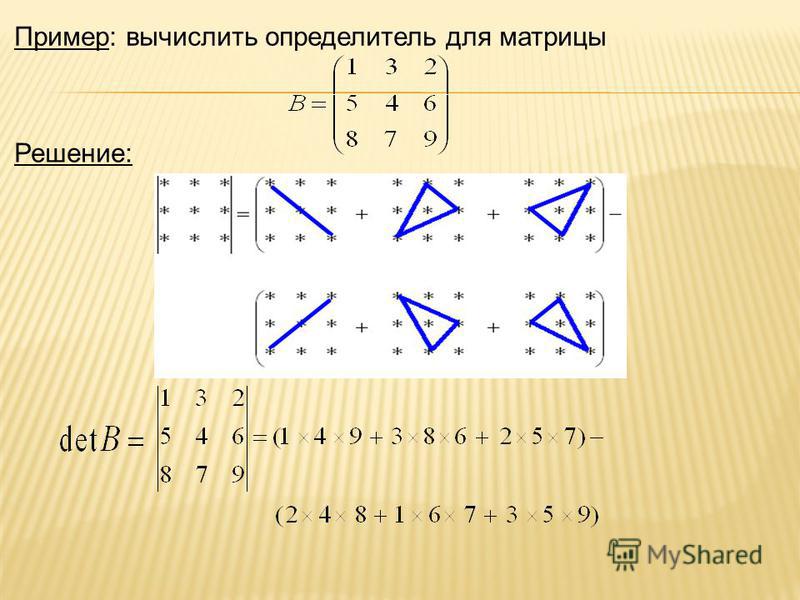 93 \quad \text{флопс.} \tag{18}
∼2n3flops.(18)
93 \quad \text{флопс.} \tag{18}
∼2n3flops.(18)
Как мы видим, обращение матрицы для решения Ax=b\mathbf{Ax} = \mathbf{b}Ax=b примерно в три раза дороже, чем непосредственное вычисление x\mathbf{x} Икс. Уже одно это является оправданием для утверждения, что, если у вас нет веских причин, лучше напрямую найти x\mathbf{x}x.
Численные ошибки и обусловленность
Как мы увидим, решение линейной системы с использованием обратной матрицы также может быть менее точным. Однако, прежде чем обсуждать это, давайте рассмотрим несколько концепций, связанных с численными методами. Рассмотрим функцию 9 даже не основано на значении, близком к истинному вводу xxx. Итак, ∣Δx∣\left| \Delta x \right|∣Δx∣ называется обратной ошибкой.
Например, представьте, что мы приближаем 2\sqrt{2}2 к 1,41,41,4. Прямая ошибка — это абсолютная разница между 1.41.41.4 и 2\sqrt{2}2. Поскольку 1,96=1,4\sqrt{1,96} = 1,41,96=1,4, обратная ошибка представляет собой абсолютную разницу между 222 и 1,961,961,96.
Наконец, мы говорим, что задача y=f(x)y = f(x)y=f(x) является хорошо обусловленной , если небольшое изменение xxx приводит к небольшому изменению yyy, и плохо обусловленной в противном случае . Это часто измеряется цифрой 9.{-1} \rВерт. \тег{21} κ(A)=∥A∥∥A−1∥.(21)
212121 — это просто отношение наибольшего сингулярного числа к наименьшему,
κ(A)=λ1λn.(21) \ каппа (\ mathbf {A}) = \ гидроразрыва {\ lambda_1} {\ lambda_n}. \тег{21} κ(A)=λnλ1.(21)
Доказательство см. в этом ответе StackExchange. Другими словами, плохо обусловленная матрица — это матрица с большим разбросом сингулярных значений. Интуитивно это неудивительно, поскольку матрицы с резким спадом своих сингулярных значений связаны со многими другими неустойчивостями, например, в системах управления.
Точность
Вернемся к основному потоку. Вторая проблема с инверсией матриц заключается в том, что она может быть менее точной. Пусть xLU\mathbf{x}_{\texttt{LU}}xLUобозначает вектор, вычисленный непосредственно с помощью разложения LU, и пусть xinv\mathbf{x}_{\texttt{inv}}xinv обозначает вектор, который решается по inv(A)×b\text{inv}(\mathbf{A}) \times \mathbf{b}inv(A)×b, где inv(A)\text{inv}(\mathbf{A}) inv(A) вычисляется с использованием разложения LU, как обсуждалось выше. Теперь представьте, что мы вычислили обратную матрицу 9{-1} \право| \влево| \mathbf{b} \right|, \tag{22}
∣b-Axinv∣≤γn∣A∣∣∣∣A-1∣∣∣∣b∣,(22)
Теперь представьте, что мы вычислили обратную матрицу 9{-1} \право| \влево| \mathbf{b} \right|, \tag{22}
∣b-Axinv∣≤γn∣A∣∣∣∣A-1∣∣∣∣b∣,(22)
, где γn\gamma_nγn — небольшой постоянный коэффициент, учитывающий такие вещи, как машинная точность. Для xLU\mathbf{x}_{\texttt{LU}}xLU эта оценка равна
∣b−AxLU∣≤γn∣L∣∣U∣∣xLU∣.(23) \влево| \mathbf{b} — \mathbf{A} \mathbf{x}_{\texttt{LU}} \right| \leq \textcolor{#8e7cc3}{\gamma_n \left| \mathbf{L} \право| \влево| \mathbf{U} \право|} \лево| \mathbf{x}_{\texttt{LU}} \right|. \тег{23} ∣b−AxLU∣≤γn∣L∣∣U∣∣xLU∣.(23) 9{-1} \право| \влево| \mathbf{b} \right|∣∣∣A−1∣∣∣∣b∣. Таким образом, подход с обращением матриц может иметь значительно большую обратную ошибку, чем прямое решение для x\mathbf{x}x, если матрица A\mathbf{A}A плохо обусловлена.
Тем не менее, прямая ошибка между обращением матрицы и прямым решением может быть намного ближе, чем ожидалось, для хорошо обусловленных задач, как утверждают (Druinsky & Toledo, 2012). Таким образом, на практике, если вы заботитесь только об прямой ошибке, народная мудрость о том, что никогда не следует инвертировать матрицу, может слишком сильно подчеркнуть этот момент. Я не обсуждаю здесь ограничения на ошибки переадресации, но подробности см. в этом сообщении StackExchange.
Таким образом, на практике, если вы заботитесь только об прямой ошибке, народная мудрость о том, что никогда не следует инвертировать матрицу, может слишком сильно подчеркнуть этот момент. Я не обсуждаю здесь ограничения на ошибки переадресации, но подробности см. в этом сообщении StackExchange.
На мой взгляд, результат все тот же: решение системы линейных уравнений путем обращения матрицы обычно менее точно, чем непосредственное решение системы.
Численные эксперименты
Я провел пару простых численных экспериментов, чтобы проверить результаты, описанные выше.
Во-первых, давайте посмотрим, быстрее ли на практике вычисление x\mathbf{x}x напрямую, чем с помощью обращения матриц. Для увеличения nnn я провел следующий эксперимент: сгенерировал матрицу A\mathbf{A}A и вектор b\mathbf{b}b. Затем найдите x\mathbf{x}x, используя np.linalg.solve(A, b) и np.linalg.inv(A) @ b . Я провел каждый эксперимент 101010 раз и записал среднее время выполнения (рис. 222). Как и ожидалось, непосредственное вычисление x\mathbf{x}x выполняется быстрее. Хотя абсолютная разница в секундах здесь незначительна, легко представить, что она имеет большее значение в крупномасштабных задачах обработки данных.
222). Как и ожидалось, непосредственное вычисление x\mathbf{x}x выполняется быстрее. Хотя абсолютная разница в секундах здесь незначительна, легко представить, что она имеет большее значение в крупномасштабных задачах обработки данных.
Рис. 2. Среднее время выполнения для вычисления x\mathbf{x}x в Ax=b\mathbf{Ax} = \mathbf{b}Ax=b по 101010 испытаниям и увеличению размерности матрицы nnn с использованием как матричной инверсии, так и линейный решатель.
Теперь давайте исследуем прямую и обратную ошибку для хорошо и плохо обусловленных задач. Я сгенерировал две матрицы Aw\mathbf{A}_wAw и Ai\mathbf{A}_iAi следующим образом:
x = np.random.normal(n) # Хорошо обусловленный A и результирующий b. Aw = np.random.normal (размер = (n, n)) чб = Ав @ х # Плохо обусловленный A и результирующий b. ягнята = np.power (np.linspace (0, 1, n), б) inds = np.argsort (ягнята) [:: -1] ягнята = ягнята [инды] Q = орто_группа.rvs (dim = n) Ai = Q @ np.diag (ягнята) @ QT би = Аи @ х
Другими словами, хорошо обусловленная матрица — это просто матрица полного ранга, каждый элемент которой взят из N(0,1)\mathcal{N}(0, 1)N(0,1). Для плохо обусловленной матрицы я сгенерировал матрицу с резко затухающими сингулярными значениями. Скорость затухания контролируется основанием экспоненты
Для плохо обусловленной матрицы я сгенерировал матрицу с резко затухающими сингулярными значениями. Скорость затухания контролируется основанием экспоненты b . Как мы видим (рис. 333), как прямые, так и обратные ошибки относительно малы и близки друг к другу, когда матрица хорошо обусловлена. Однако, когда матрица плохо обусловлена, прямые и обратные ошибки увеличиваются, примерно как функция скорости затухания для сингулярных значений.
Рис. 3. (Верхний ряд) Прямая и обратная ошибки для xinv\mathbf{x}_{\texttt{inv}}xinv и xLU\mathbf{x}_{\texttt{LU}}xLU на лунке -условная матрица. (Нижний ряд) Прямые и обратные ошибки для xinv\mathbf{x}_{\texttt{inv}}xinv и xLU\mathbf{x}_{\texttt{LU}}xLU на плохо обусловленных матрицах. Сингулярные значения затухают относительно к различным экспоненциальным основаниям (внизу слева).
Сводка
При решении x\mathbf{x}x в Ax=b\mathbf{Ax} = \mathbf{b}Ax=b всегда быстрее и часто точнее решать систему линейных уравнений напрямую , а не инвертировать A\mathbf{A}A и выполнять левое умножение на b\mathbf{b}b.