Определитель матрицы второго и третьего порядков и правила вычисления
Матрица содержит в себе векторы-столбцы. Они по-разному ориентированы в пространстве. Характеристикой этого расположения и того матричного преобразования, которое может дать матрица, выступает определитель матрицы.
Содержание
Определитель матрицы 2×2
Пусть дана квадратная матрица второго порядка:
A=\begin{pmatrix} a_{11}& a_{12}\\ a_{21}& a_{22} \end{pmatrix}
Определителем (или детерминантом) второго порядка, соответствующим данной матрице, называется число a_{11}a_{22}-a_{12}a_{21}.
Определитель второго порядка записывается так:
detA=\begin{vmatrix} a_{11}& a_{12}\\ a_{21}& a_{22} \end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}
Геометрический смысл определителя
Если нам дана квадратная матрица
A=\begin{pmatrix} a_{11}& a_{12}\\ a_{21}& a_{22} \end{pmatrix}
То первый столбец дает нам координаты одного вектора, а второй столбец чисел — координаты второго вектора.
Начало данных векторов — в точке начала координат.
Тогда определитель матрица дает нам площадь параллелограмма, построенного на данных векторах.
Рассмотрим на примере
Пусть нам дана матрица с координатами:
A=\begin{pmatrix} 3& 1\\ 1& 2 \end{pmatrix}
Нарисуем координатную плоскость и отметим на ней данные векторы.
Векторы и
Где у вектора \overline{a} координаты (3; 1), а у вектора \overline{b} координаты (2; 1).
Теперь построим на этих векторах параллелограмм, считая, что векторы a и b его стороны. Получим:
Параллелограмм на векторах и
Площадь данного параллелограмма и будет являться определителем матрицы. Площадь данного параллелограмма S_{ABCD}=5. И определитель матрицы:
detA=\begin{vmatrix} 3& 1\\ 1& 2 \end{vmatrix}=3 \cdot 2-1 \cdot 1=6-1=5
Однако, обычно в линейной алгебре говорят не о площади параллелограмма, а о матричном преобразовании. То есть о том, в какую фигуру матрица преобразует единичный квадрат, построенный на единичных векторах.
Насколько она ее масштабирует в пространстве. То есть вот из такого квадрата (синий цвет) матричное преобразование делает параллелограмм с определенной площадью (отмечено красным цветом), равной по модулю определителю матрицы.
Матричное преобразование площади определитель матрицы
Однако иногда определитель матрицы может быть отрицательным числом. В этом случае площадь фигуры, построенной на векторах матрицы, будет равна модулю данного числа, а знак минус означает, что ориентация данной фигуры отрицательна.
Геометрический смысл определителя матрицы
Определитель показывает какой будет площадь единичного квадрата при матричном преобразовании. Она будет равна площади параллелограмма, который будет построен на векторах-столбцах матрицы. Первый столбец матрицы дает нам координаты первого вектора, а второй столбец — координаты второго вектора.
Можно расширить геометрический смысл матрицы и на матрицы другого размера.
Таким образом, определитель матрицы 1×1 дает длину вектора, 2×2 — площадь параллелограмма, 3×3 — объем параллелепипеда, а nxn — объем n-мерного параллелепипеда.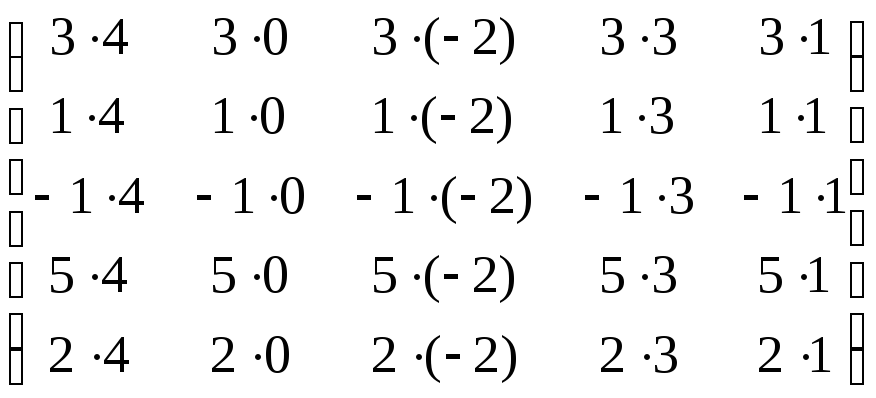
2=0
Ответ: 0
Определитель третьего порядка
Пусть дана квадратная матрица третьего порядка:
A=\begin{pmatrix} a_{11}& a_{12} & a_{13}\\ a_{21}& a_{22} & a_{23} \\ a_{31}& a_{32} & a_{33} \end{pmatrix}
Определителем (или детерминантом) третьего порядка, соответствующим данной матрице, называется число:
a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{33}a_{21}-a_{11}a_{23}a_{32}
Определитель третьего порядка будет:
detA=\begin{vmatrix} a_{11}& a_{12} & a_{13}\\ a_{21}& a_{22} & a_{23} \\ a_{31}& a_{32} & a_{33}\end{vmatrix}= \\ =a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{33}a_{21}-a_{11}a_{23}a_{32}
Правило треугольников
При вычислении определителей третьего порядка удобно пользоваться правилом треугольников (правилом Саррюса). Это правило проиллюстрируем на схеме:
Правило треугольников или правило Саррюса
Как пользоваться правилом треугольника:
На схеме есть две картинки — красная и синяя, красная картинка дает нам три положительных слагаемых в формуле определителя третьего порядка, а синяя — три отрицательных.
Умножаем так — сначала умножаем элементы матрицы по главной диагонали потом в вершинах одного треугольника и в вершинах другого треугольника: . Все полученные множители складываем.
Теперь обратимся к синей картинке. Тут мы начинаем сначала перемножать элементы по побочной диагонали: , а потом элементы в вершинах двух треугольников: и . Полученные множители записываем в формулу со знаком минус.
Примеры на вычисление определителя третьего порядка
a) Вычислить определитель матрицы:
A=\begin{pmatrix} 2& 3 & 4\\ 6& 5 & 7 \\ 9& 0& 8 \end{pmatrix}
Решение:
det A=\begin{vmatrix} 2& 3 & 4\\ 6& 5 & 7 \\ 9& 0 & 8 \end{vmatrix}=2 \cdot 5 \cdot 8+ 3 \cdot 7 \cdot 9+6\cdot 0 \cdot 4 — 4 \cdot 5 \cdot 9 — 3 \cdot 6 \cdot 8 — 7 \cdot 0 \cdot 2=80+189+0-180-144-0=-55
Ответ: det A=-55
б) Вычислить определитель матрицы 3×3:
A=\begin{pmatrix} 2& 3 & 1\\ 1& -5 & 6\\ 2& -3& 4 \end{pmatrix}
Решение:
Используем формулу определителя третьего порядка
det B=\begin{vmatrix} 2& 3 & 1\\ 1& -5 & 6\\ 2& -3& 4 \end{vmatrix}=2 \cdot (-5) \cdot 4+ 3 \cdot 6 \cdot 2+1\cdot 1 \cdot (-3) — 1 \cdot (-5) \cdot 2 — 2 \cdot 6 \cdot (-3) — 3 \cdot 1 \cdot 4=-40+36-3+10+36-12=27
Ответ: det B=27
в) Вычислите определитель единичной матрицы 3×3.
Решение:
Единичная матрица 3×3 имеет вид:
A=\begin{pmatrix} 1& 1 & 1\\ 1& 1 & 1\\ 1& 1& 1 \end{pmatrix}
Используем формулу определителя третьего порядка
det A=\begin{vmatrix} 1& 1 & 1\\ 1& 1 & 1\\ 1& 1& 1 \end{vmatrix}=1 \cdot 1 \cdot 1+ 1 \cdot 1 \cdot 1+1\cdot 1 \cdot 1 — 1 \cdot 1 \cdot 1 — 1 \cdot 1 \cdot 1 — 1 \cdot 1 \cdot 1=1+1+1-1-1-1=0
Действительно, в столбцах единичной матрицы три совпадающих вектора, на которых невозможно построить объемную фигуру, объем которой и определяет определитель матрицы третьего порядка. Поэтому мы и получили число 0.
Вообще говоря, любая матрица с одинаковыми строками и столбцами дает определитель, равный нулю. Можете проверить самостоятельно.
Ответ: 0
Разложение определителя по строке или столбцу, а также его свойства, миноры и дополнения элементов определителя рассмотрим далее.
Функция МОПРЕД — Служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще.
..Меньше
В этой статье описаны синтаксис формулы и использование MDETERM в Microsoft Excel.
Описание
Возвращает определитель матрицы (матрица хранится в массиве).
Синтаксис
МОПРЕД(массив)
Аргументы функции МОПРЕД описаны ниже.
Замечания
-
Массив может быть задан как интервал ячеек, например A1:C3, как массив констант, например {1;2;3:4;5;6:7;8;9}, как имя для интервала или массива.
-
Функция МОПРЕД возвращает значение ошибки #ЗНАЧ! в случаях, указанных ниже.
org/ListItem»>
Определитель матрицы — это число, вычисляемое на основе значений элементов массива. Для массива A1:C3, состоящего из трех строк и трех столбцов, определитель вычисляется следующим образом:
МОПРЕД(A1:C3)
равно A1*(B2*C3-B3*C2) + A2*(B3*C1-B1*C3) + A3*(B1*C2-B2*C1)
-
Определители матриц обычно используются при решении систем уравнений с несколькими неизвестными.
-
Функция МОПРЕД производит вычисления с точностью примерно 16 значащих цифр, что может в некоторых случаях приводить к незначительным ошибкам. Например, определитель сингулярной матрицы отличается от нуля на 1E-16.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel.
Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Данные |
Данные |
Данные |
|
1 |
3 |
8 |
5 |
|
1 |
3 |
6 |
1 |
|
1 |
1 |
1 |
0 |
|
7 |
3 |
10 |
2 |
|
Формула |
Описание |
Результат |
|
|
=МОПРЕД(A2:D5) |
Определитель приведенной выше матрицы. |
88 |
|
|
=МОПРЕД({3;6;1:1;1;0:3;10;2}) |
Определитель матрицы, представленной в виде массива констант. |
1 |
|
|
=МОПРЕД({3;6:1;1}) |
Определитель матрицы в массиве констант. |
-3 |
|
|
=МОПРЕД({1;3;8;5:1;3;6;1}) |
Возвращает сообщение об ошибке, так как массив имеет разное количество строк и столбцов. |
#ЗНАЧ! |
Собственные значения и собственные векторы матриц 3 на 3
Собственные значения и собственные векторы матриц 3 на 3Так же, как матрицы 2 на 2 могут представлять преобразования плоскости, матрицы 3 на 3 могут представлять преобразования трехмерного пространства. Картина более сложная, но, как и в случае 2 на 2, наши лучшие идеи приходят от нахождения собственных векторов матрицы: то есть тех векторов, направление которых преобразование оставляет неизменным.
Если ненулевое {\bf e} является собственным вектором матрицы A 3 на 3, то
А\,{\bf е}=\лямбда \,{\bf е}
для некоторого скаляра \lambda . Этот скаляр называется собственным значением A.
Это может быть переписано
А\,{\bf е}=\лямбда \,I\,{\bf е},
и в свою очередь как
\влево(А\,-\лямбда \,I\вправо)\,{\bf e}={\bf 0}.
Как и в случае 2 на 2, матрица A-\lambda \,I должна быть вырожденной. Тогда мы еще раз спрашиваем: при каких значениях \lambda A-\lambda \,I является сингулярным? То есть значения, удовлетворяющие характеристическому уравнению
\text{det}\left(A-\lambda \,I\right)\,=\,0?
Рассмотрим пример
\left(\begin{array}{ccc}-2&-4&2\\-2&1&2\\4&2&5\end{массив}\right).
Характеристическое уравнение
\text{det}\left(\begin{array}{ccc}-2-\lambda &-4&2\\-2&1-\lambda &2\\4&2&5-\lambda \end{array}\right)=0 .
Раскрывая определитель,
\влево(-2-\лямбда\вправо)[\влево(1-\лямбда\вправо)\влево(5-\лямбда\вправо)-2\умножить на 2]+4[\влево(-2\вправо) )\times \left(5-\lambda\right)-4\times 2]+2[\left(-2\right)\times 2-4\left(1-\lambda\right)]=0. 9{2}-\лямбда-30\вправо)=\влево(\лямбда-3\вправо)\влево(\лямбда+5\вправо)\влево(\лямбда-6\вправо),
это означает, что собственные значения равны 3, -5 и 6.
Теперь приступаем к решению
\left(\begin{array}{ccc}-2-\lambda &-4&2\\-2&1-\lambda &2\\4&2&5-\lambda \end{array}\right)\left(\begin{array }{c}X\\Y\\Z\конец{массив}\right)=\left(\begin{массив}{c}0\\0\\0\end{массив}\right)
для каждого собственного значения \lambda .
Теперь каждая такая система будет иметь бесконечно много решений, потому что если {\bf e} является собственным вектором, то и любой кратен {\bf e}. Таким образом, наша стратегия будет заключаться в том, чтобы попытаться найти собственный вектор с X = 1, а затем, при необходимости, увеличить его. (Если такого собственного вектора нет, мы знаем, что X на самом деле должно быть равно нулю, и вместо этого мы ищем собственный вектор с Y = 1 и так далее.)
Собственный вектор, соответствующий собственному значению 3
В случае \lambda =3 имеем
\left(\begin{array}{ccc}-5&-4&2\\-2&-2&2\\4&2&2\end{массив}\right)\left(\begin{array}{c}X\\Y\ \Z\end{массив}\right)=\left(\begin{array}{c}0\\0\\0\end{массив}\right).
Установка X=1 дает, как и наши первые два уравнения,
-5-4Y+2Z=0,
-2-2Y+2Z=0.
Вычитание первого из второго:
3+2Г=0,
и, таким образом, Y=-\frac{3}{2}.
Подставляя обратно во второе уравнение,
-2+3+2Z=0,
что дает Z=-\frac{1}{2}.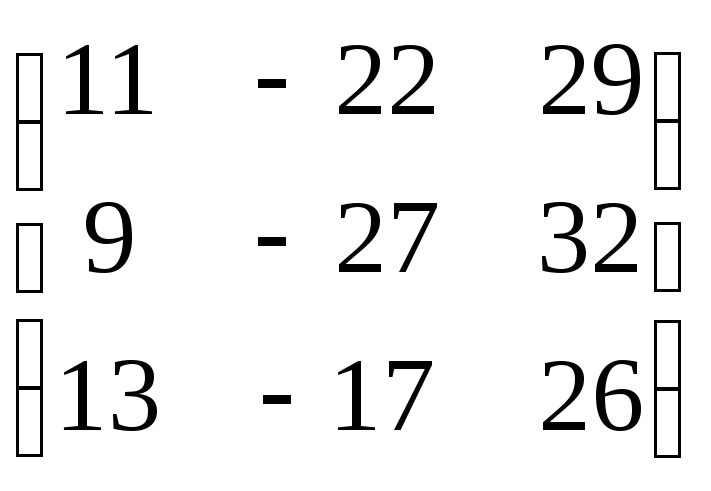
Проверяя третье уравнение,
4-3-1=0,
который работает. Это дает нам собственный вектор
\left(1,-\frac{3}{2},-\frac{1}{2}\right).
Для удобства мы можем увеличить масштаб в 2 раза, чтобы получить
\влево(2,-3,-1\вправо).
Собственный вектор, соответствующий собственному значению -5
В случае \lambda =-5 имеем
\left(\begin{массив}{ccc}3&-4&2\\-2&6&2\\4&2&10\end{массив}\right)\left(\begin{массив}{c}X\\Y\\Z\ конец {массив}\справа)=\влево(\начало{массив}{с}0\\0\\0\конец{массив}\справа).
Установка X=1 дает, как и наши первые два уравнения,
3-4Y+2Z=0,
-2+6Y+2Z=0.
Вычитание первого из второго:
-5+10Y=0,
и, таким образом, Y=\frac{1}{2}.
Подставляя обратно во второе уравнение,
-2+3+2Z=0,
что дает Z=-\frac{1}{2}.
Проверяя третье уравнение,
4+1-5=0,
который работает. Это дает нам собственный вектор
\left(1,-\frac{1}{2},\frac{1}{2}\right).
Еще раз, мы можем масштабироваться в 2 раза, чтобы получить
\влево(2,-1,1\вправо).
Собственный вектор, соответствующий собственному значению 6
В случае \lambda =6 имеем
\left(\begin{array}{ccc}-8&-4&2\\-2&-5&2\\4&2&-1\end{массив}\right)\left(\begin{array}{c}X\\ Y\\Z\end{массив}\right)=\left(\begin{array}{c}0\\0\\0\end{массив}\right).
Установка X=1 дает, как и наши первые два уравнения,
-8-4Y+2Z=0,
-2-5Y+2Z=0.
Вычитание первого из второго:
6-Y=0,
и, таким образом, Y=6.
Подставляя обратно во второе уравнение,
-2-30+2Z=0,
давая Z=16.
Проверяя третье уравнение,
4+12-16=0,
который работает. Это дает нам собственный вектор
\влево(1,6,16\вправо).
Общие Соображения
В общем, собственные значения реальной матрицы 3 на 3 могут быть
(i) три различных действительных числа, как здесь;
(ii) три действительных числа с повторениями;
(iii) одно действительное число и два сопряженных недействительных числа.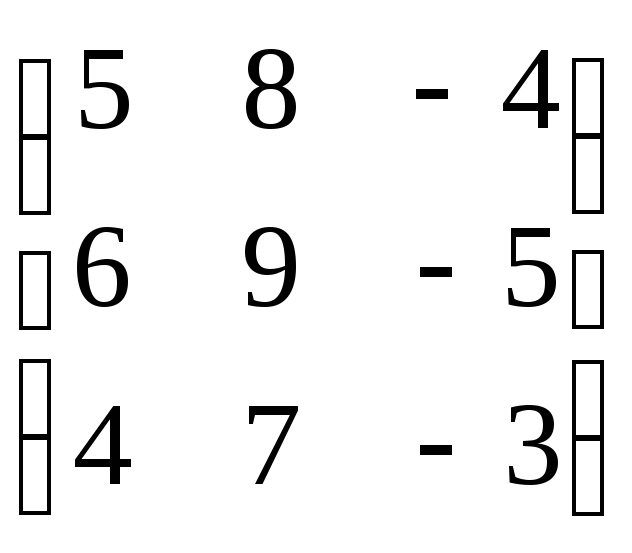
Геометрическая интерпретация преобразования зависит от того, что из вышеперечисленного верно: первое будет включать растяжение в трех направлениях собственного вектора, третье — вращение и растяжение вдоль своей оси, а второе — обычно один из нескольких типов трехмерного изображения. сдвиг. Однако мы оставляем эти детали на данный момент.
Еще одним важным применением собственных значений и собственных векторов является диагонализация, и именно к ней мы сейчас и обратимся.
Создано с помощью пакета ExportAsWebPage в Wolfram Mathematica 7.0
Определители матриц 2 на 2 и 3 на 3
Привет. Этот пост посвящен теме линейной алгебры вычисления определителей матриц 2 на 2 и 3 на 3. В этом посте будут рассмотрены формулы, а не метод кофакторов. Метод кофакторов при вычислении определителей будет в другом посте.
Введение
Определитель матрицы — это число. Сам по себе он не имеет большого применения, но влияет на множество результатов в математической области линейной алгебры.
Обозначение определителя матрицы A часто обозначается как \(\text{det}(A)\). Иногда вместо квадратных скобок, подобных этим [ ], у вас будут вертикальные черточки (как абсолютные значения), обозначающие определитель матрицы. Вот пример определителя 3 на 3:
\[\displaystyle \text{A} = \begin{vmatrix} a & d & g \\ b & e & h\\ c & f & i \\ \end{vmatrix} \]
Вычисление определителей 2 на 2 и 3 на 3
Существует альтернативный и более простой способ вычисления определителей для матриц 2 на 2 и 3 на 3. У нас есть формулы и средства памяти для вычисления таких определителей. Они не работают для матриц более высокой размерности, таких как 4 на 4 или матрица 1000 на 1000.
Два на два Определяющий случай
Предположим, что квадратная матрица A 2 на 2 имеет вид:
\[\displaystyle \text{A} = \begin{bmatrix} а & b \\ c & d \\ \end{bmatrix} \]
Определитель A равен \(\text{det}(A) = ad — bc\).
Учитывая квадратную матрицу A 2 на 2 формы, как указано выше, и определитель отличен от нуля, тогда обратная матрица A:
9{-1} = \dfrac{1}{\text{det}(A)}\begin{bmatrix} d & -b \\ -c & a \\ \end{bmatrix} \, = \, \dfrac{ 1}{(ad — bc)}\begin{bmatrix} d & -b \\ -c & a \\ \end{bmatrix} \]
Записи \(a\) и \(d\) переключаются, а записи \(b\) и \(c\) меняют знаки. Кроме того, вы видите, почему определитель должен быть ненулевым. Математическая полиция будет преследовать вас, если вы разделите на ноль!
Три на три Определяющий случай
Формула для вычисления определителя матрицы 3 на 3 сложнее, чем для случая 2 на 2, но она не слишком сложна, как только вы ее поймете.
Предположим, что матрица A имеет вид:
\[\displaystyle \text{A} = \begin{bmatrix} a & b & c \\ d & e & f\\ e & f & g \\ \ end{bmatrix} \]
Чтобы вычислить определитель 3 на 3, мы добавим еще один столбец a,b,c и еще один столбец d,e,f справа от A.
Рисунок ниже поможет проиллюстрировать это.
«Трудная» часть
Объяснять словами несколько долго. Если вы хотите увидеть (и краткое изложение) приведенных ниже шагов, обратитесь к изображению ниже.
Источник ссылки на изображение: http://thejuniverse.org/PUBLIC/LinearAlgebra/LOLA/detDef/special.html
Начиная с верхнего левого \(a\) элемента, мы проводим нисходящую правую диагональную линию к получите один из шести терминов, который равен \(aei\). Затем от записи \(b\) в строке 1 столбца 2 проведите еще одну нисходящую правую диагональную линию, чтобы получить терм \(bfg\). Продолжайте от \(c\) в строке 1, столбце 3 и до того же, чтобы получить \(cdh\).
(Напомним, что строка 1 — это верхняя строка матрицы, а столбец 1 — крайний левый вертикальный столбец.)
Пока у нас есть \(aei + bfg + cdh\).
Чтобы получить последние три члена, мы проделываем аналогичную процедуру, но начинаем сверху справа и идем вниз влево.