принцип, теорема и примеры решения задач
Содержание:
- Историческая справка
- Принцип метода Гаусса
- Примеры решения систем уравнений
Историческая справка
Метод Гаусса был предложен известнейшим немецким математиком Карлом Фридрихом Гауссом (1777 — 1855) и является одним из наиболее универсальных методов решения СЛАУ. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении задачи, расширенная матрица системы с помощью элементарных преобразований над ее строками приводится к ступенчатому виду. Далее последовательно находятся все неизвестные, начиная снизу вверх.
Принцип метода Гаусса
Метод Гаусса включает в себя прямой (приведение
расширенной матрицы к ступенчатому виду, то есть получение нулей под
главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы.
Прямой ход и называется
методом Гаусса, обратный — методом Гаусса-Жордана, который отличается от первого только последовательностью исключения
переменных.
Метод Гаусса идеально подходит для решения систем содержащих больше трех линейных уравнений, для решения систем уравнений, которые не являются квадратными (чего не скажешь про метод Крамера и матричный метод). То есть метод Гаусса — наиболее универсальный метод для нахождения решения любой системы линейных уравнений, он работает в случае, когда система имеет бесконечно много решений или несовместна.
Примеры решения систем уравнений
Пример
Задание. Решить СЛАУ $\left\{\begin{array}{l} 2 x_{1}+x_{2}+x_{3}=2 \\ x_{1}-x_{2}=-2 \\ 3 x_{1}-x_{2}+2 x_{3}=2 \end{array}\right.$ методом Гаусса.
Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее
строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса
(сделаем нули выше главной диагонали).
$$\tilde{A}=A \mid B=\left(\begin{array}{rrr|r} 2 & 1 & 1 & 2 \\ 1 & -1 & 0 & -2 \\ 3 & -1 & 2 & 2 \end{array}\right) \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 2 & 1 & 1 & 2 \\ 3 & -1 & 2 & 2 \end{array}\right)$$
Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей — три первых:
$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 3 & 1 & 6 \\ 0 & 2 & 2 & 8 \end{array}\right)$$
Все элементы третьей строки делим на два (или, что тоже самое, умножаем на $\frac{1}{2}$ ):
$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 3 & 1 & 6 \\ 0 & 1 & 1 & 4 \end{array}\right)$$
Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:
$$\tilde{A} \sim\left(\begin{array}{ccc|c} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 3 & 1 & 6 \end{array}\right)$$
От третьей строки отнимаем вторую, умноженную на 3:
$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 0 & -2 & -6 \end{array}\right)$$
Умножив третью строку на $\left(-\frac{1}{2}\right)$ , получаем:
$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 0 & 1 & 3 \end{array}\right)$$
Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю.
Начнем с элементов третьего столбца. Надо обнулить элемент $a_{23}$, для этого от второй строки отнимем третью:
$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 3 \end{array}\right)$$
Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:
$$\tilde{A} \sim\left(\begin{array}{ccc|c} 1 & 0 & 0 & -1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 3 \end{array}\right)$$
Полученной матрице соответствует система
$\left\{\begin{array}{l}x_{1}+0 \cdot x_{2}+0 \cdot x_{3}=-1 \\ 0 \cdot x_{1}+x_{2}+0 \cdot x_{3}=1 \\ 0 \cdot x_{1}+0 \cdot x_{2}+x_{3}=3\end{array}\right.$ или $\left\{\begin{array}{l} x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3 \end{array}\right.$
Ответ. $\left\{\begin{array}{l}
x_{1}=-1 \\
x_{2}=1 \\
x_{3}=3
\end{array}\right.
$
Читать дальше: однородные СЛАУ. Фундаментальная система решений.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Примеры решения системы линейных алгебраических уравнений 3-его порядка методом Гаусса, пример № 1
СЛАУ 3-его порядка:
1 —
2 —
3 —
4 —
5 —
6 —
7 —
8 —
9 —
10 —
11 —
12
Условие
|
Решение системы линейных алгебраических уравнений методом Гаусс
Для проверки ответов можете воспользоваться нашим онлайн сервисом —
Решение системы линейных уравнений методом Гаусса.
Все действия описанные в данном разделе не противоречат правилам обращения с матрицами и являются
элементарными преобразованиями матрицы.
Если после изучения
примеров решения задач
у Вас останутся вопросы, то Вы всегда можете задать их на
форуме, и не забывайте про наши
онлайн калькуляторы для
решения задач по математике и другим предметам!
Перепишем систему линейных алгебраических уравнений в матричную форму. Получится матрица 3 × 4, слева от разделительной линии стоят коэффициенты при переменных, а справа стоят свободные члены.
Проведём следующие действия:
- Из строки № 2 вычтем строку № 1 умноженную на 3 (Строка 2 — 3 × строка 1)
- Из строки № 3 вычтем строку № 1 (Строка 3 — строка 1)
Получим:
Проведём следующие действия:
- Строку № 2 умножим на -1 (Строка 2 = -1 × строка 2 )
- Из строки № 3 вычтем строку № 2 (Строка 3 — строка 1)
Получим:
Проведём следующие действия:
- Строку № 3 умножим на -1 (Строка 3 = -1 × строка 3 )
- Из строки № 2 вычтем строку № 3 умноженную на 2 (Строка 2 — 2 × строка 3)
- Из строки № 1 вычтем строку № 3 умноженную на 3 (Строка 1 — 3 × строка 3)
Получим:
Проведём следующие действия:
- Из строки № 1 вычтем строку № 2 умноженную на 2 (Строка 1 — 2 × строка 2)
Получим:
В левой части матрицы по главной диагонали остались одни единицы.
х1 = -4
х2 = -13
х3 = 11
Вы поняли, как решать? Нет?
Другие примеры
Игра исключения Гаусса: Введение в линейную алгебру | Бретт Берри | Math Hacks
Переход от алгебры к стране матриц 🎉
Подпишитесь на Math Hacks в InstagramC исповедь: я люблю линейную алгебру. Ладно, может, это и не очень похоже на признание, но мне это нравится! Во многом из-за того, что линейная алгебра не похожа на остальную математику, она кажется загадкой.
Это может звучать безумно, но выслушайте меня.
Эта новая страна матриц и векторов может показаться пугающей, и на то есть веские причины: новые обозначения, новые правила, новые свойства. Все немного по-другому. Но, возможно, рассматривая это как головоломку, вы сможете преодолеть это новое препятствие в обозначениях.
Готовы попробовать?
Я считаю, что лучше всего начать с линейной алгебры с решения систем уравнений , потому что вы, вероятно, уже изучили это.
Помните методы замены и исключения?? Они звонят в колокол? Если нет, вы можете освежить свою память здесь. 🙂
Сегодня мы собираемся применить новый подход к решению систем уравнений, используя метод под названием Исключение Гаусса.
Что такое исключение Гаусса??
Исключение Гаусса — это метод, при котором мы переводим наши уравнения в матрицу и используем матрицу для решения системы (т.е. находим решения для каждой переменной, которые делают все уравнения верными).
Сегодня я шаг за шагом проведу вас через упрощенный пример (числа хорошо работают, так что шагов гораздо меньше!). Если вам нужен более подробный пример, посмотрите мой учебник на YouTube по исключению Гаусса ниже ⬇
Нажмите здесь, чтобы подписаться на «Математические лайфхаки» на YouTube 🎥Как и в случае с карточной игрой путем перетасовки и раздачи карт, начало нашей игры «Исключение по Гауссу» начинается с преобразования наших уравнений в матрицу.
Вот система, которую мы собираемся решить:
Самое первое, что вам нужно понять, это то, что в нашей системе много скрытой информации.
Красным цветом я добавлю нули и единицы заполнителя.
Далее мы отделим всю важную числовую информацию от посторонних символов. Теперь, выделенное красным цветом, вы найдете всю важную информацию, с которой мы будем работать:
Нам нужно переписать приведенные выше числовые значения в виде матрицы. Мы опустим буквы, знаки равенства и символы сложения (но не символы минус!) и просто напишем числа в точном порядке и в тех строках, в которых они указаны выше.
После этого мы добавим большие квадратные скобки, чтобы сгруппировать их вместе. Это наша матрица:
Как и в любой игре, мы должны соблюдать несколько правил:
- Вы можете поменять местами любые две строки
- Вы можете умножать или делить любую строку на значение
- Вы можете складывать или вычитать вместе любые две строки
*Примечание: вы можете комбинировать эти правила одним ходом.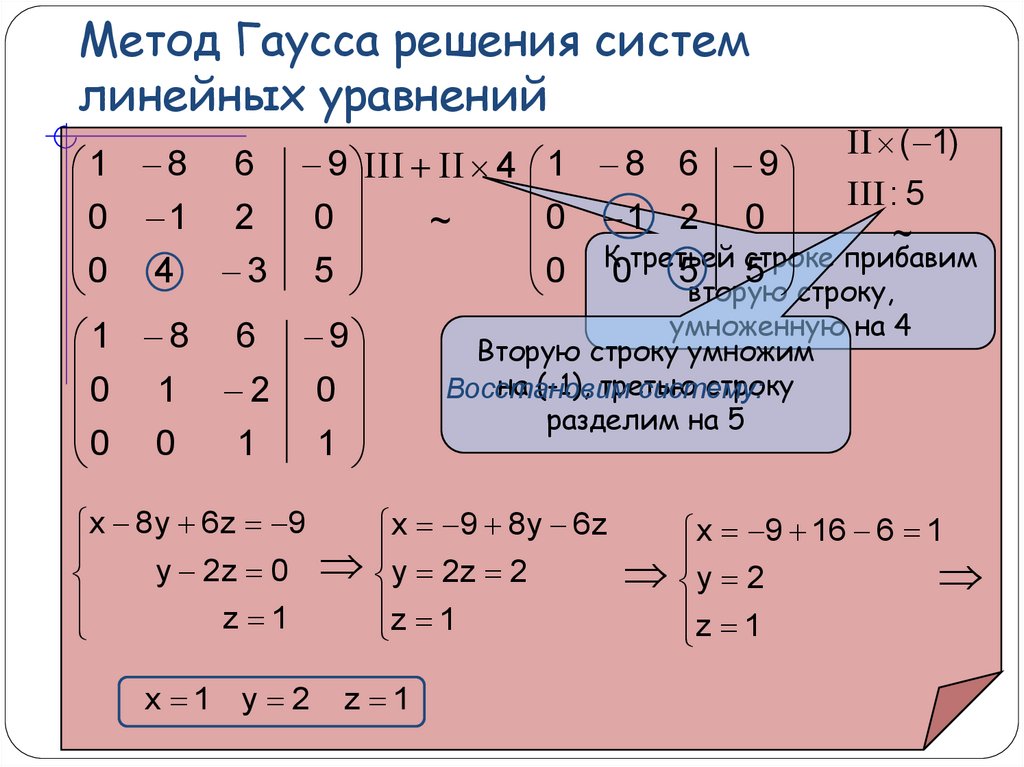
Не беспокойтесь, если это пока не совсем понятно. Вы увидите, как они работают, когда мы будем работать с нашим примером.
Вы выигрываете, когда ваша матрица выглядит так:
Где символы # представляют собой любые числа, а остальная часть матрицы имеет нули во всех позициях, кроме диагональных. это называется Форма эшелона с уменьшенным рядом.
Начните с матрицы, которую вы создали на этапе настройки. Теперь мы собираемся использовать правила, чтобы довести эту матрицу до финиша!
Начальная матрицаХод 1: Поменять местами первую и вторую строки
Есть много разных способов привести эту матрицу в выигрышную форму, но я думаю, что самый простой способ начать — это поменять местами первую и вторую строки. Таким образом, мы получаем 1 в первой позиции первой строки и 0 в первой позиции второй строки.
Ход 2: прибавьте -2 раза ко второй строке к третьей строке
Одна вещь, которую нам разрешено делать, это использовать несколько правил вместе в одном шаге.
В этом шаге мы умножим -2 на вторую строку и добавим эти продукты в третью строку. Это оставит вторую строку без изменений, но поможет нам получить ноль во второй позиции третьей строки.
Ход 3: Разделить третью строку на -3
Далее мы просто разделим третью строку на -3, чтобы получить 1 в третьей позиции третьей строки.
Движение 4: добавьте -2 раза к третьему ряду ко второму ряду
Теперь, когда у нас есть все нули в нижнем левом углу, окруженные диагональю 1, мы готовы начать работать над получением нулей в позициях над единицами.
👉 Но прежде чем мы это сделаем, я хочу сделать небольшое примечание: наша матрица в настоящее время находится в форме эшелона из строк. В этой форме вы можете перевести свою матрицу обратно в набор уравнений, если хотите, и легко сможете найти x, y и z. Сегодня мы работаем над преобразованием нашего уравнения в уменьшил форму эшелона строк , что означает, что мы хотим получить нули в позициях над единицами.
Часто в линейной алгебре вас будут просить работать до сокращенной формы эшелона строк, поскольку это самая простая форма для чтения ответа.
Часто в линейной алгебре вас будут просить работать до сокращенной формы эшелона строк, поскольку это самая простая форма для чтения ответа.Хорошо, вернемся к нашей математике. В следующем шаге мы умножим -2 на третью строку и добавим ее ко второй строке, чтобы получить 0 в третьей позиции строки 2.
Ход 5: добавить третью строку к первой строке
Далее , мы просто добавим третью строку к первой, поскольку -1 + 1 = 0, что поможет нам получить 0 в третьей позиции первой строки.
Движение 6: прибавим -2 раза ко второй строке к первой строке
Наконец, мы добавим -2 раза ко второй строке к первой строке, чтобы получить ноль во второй позиции первой строки.
Осталось только прочитать ответ! Для этого просто переведите свою матрицу обратно в набор уравнений, и вы увидите, что нашли решения для x, y и z.
Отбросив все нулевые члены, вы получите:
Это означает, что точка пересечения в трехмерном пространстве, где пересекаются три плоскости, находится в точке (-1,2,-3).
Помните, что вы всегда можете проверить свое решение, подставив значения обратно в исходные уравнения.
Все в порядке, вы также можете решить системы 3×3 с хорошей олевой алгеброй 😉
- Проверьте математические хакеры на YouTube для получения более практических учебников по математике , покрывающие популярные темы из алгебры, тригонометрии, предварительной оценки и сочетание с новыми сочетанием. видео добавляются каждую неделю.
- Если вам нужна дополнительная помощь с устранением Гаусса , я расскажу о совершенно другой и немного более сложной проблеме в видеоуроке, ссылка на который находится вверху этого поста.
- Вы можете найти ряд интересных математических тем и задач прямо здесь, на Medium, просто нажмите кнопку «Подписаться»!
Спасибо, что присоединились ко мне!
— Бретт
для получения обновлений и математического вдохновения следите за Бреттом в социальных сетях:
Instagram | Фейсбук | Twitter
Метод оптимизации распределенного Гаусса-Ньютона в глобальном поиске и его интеграция с методом рандомизированного максимального правдоподобия для количественной оценки неопределенности производительности пласта | Журнал SPE
Пропустить пункт назначения навигации
11 мая 2018 г.
Чаохуэй Чен;
Гохуа Гао;
Жуйцзян Ли;
Ричард Цао;
Тяньхун Чен;
Йерун С. Винк;
Пол ГелдербломSPE J. 23 (05): 1496–1517.
Номер бумаги: SPE-182639-PA
https://doi.org/10.2118/182639-PA
История статьи
Получено:
27 февраля 2017 г.
Принято:
28 декабря 2017 г.
Подключенный контент
Относится к: Интеграция распределенного метода Гаусса-Ньютона с рандомизированным методом максимального правдоподобия для количественной оценки неопределенности производительности коллектора
Цитирование
Чен, Чаохуэй, Гао, Гохуа, Ли, Жуйцзянь, Цао, Ричард, Чен, Тяньхун, Винк, Джероэн С.
и Пол Гелдерблом. «Метод оптимизации распределенного Гаусса-Ньютона с глобальным поиском и его интеграция с методом рандомизированного максимального правдоподобия для количественной оценки неопределенности производительности резервуара».
Скачать файл цитаты:
- Ris (Zotero)
- Менеджер ссылок
- EasyBib
- Подставки для книг
- Менделей
- Бумаги
- КонецПримечание
- РефВоркс
- Бибтекс
Расширенный поиск
Хотя можно применять традиционные алгоритмы оптимизации вместе с методом рандомизированного максимального правдоподобия (RML) для создания нескольких условных реализаций, стоимость вычислений высока. В этой статье представлен новый метод расширения возможностей глобального поиска метода распределенной оптимизации Гаусса-Ньютона (DGN) и его интеграции с методом RML для синхронного создания нескольких реализаций, обусловленных производственными данными.
RML генерирует выборки из приближенных апостериорных значений путем минимизации большого ансамбля возмущенных целевых функций, в которых наблюдаемые данные и априорные средние значения неопределенных параметров модели были искажены гауссовским шумом. Вместо того, чтобы выполнять эту минимизацию изолированно, используя большие наборы симуляций для оценки конечно-разностных аппроксимаций градиентов, используемых для оптимизации каждой возмущенной реализации, мы используем параллельную реализацию, в которой результаты симуляции распределяются между различными задачами минимизации всякий раз, когда эти результаты помогают сходятся к глобальному минимуму конкретной задачи минимизации. Чтобы улучшить совместное использование результатов, мы снижаем точность конечно-разностных аппроксимаций для градиентов с более широко разнесенными результатами моделирования. Чтобы избежать захвата локальных оптимумов, был разработан новый метод расширения возможностей глобального поиска алгоритма DGN, который легко интегрируется с формулировкой RML.
Таким образом, мы можем улучшить качество условных реализаций RML, которые выбирают приблизительную апостериорную вероятность.
Предлагаемый рабочий процесс сначала проверяется на игрушечной задаче, а затем применяется к нетрадиционному объекту реального месторождения. Численные результаты показывают, что новый метод очень эффективен по сравнению с традиционными методами. Сотни реализаций с обусловленными данными могут быть сгенерированы параллельно в течение 20–40 итераций. Стоимость вычислений (использование центрального процессора) значительно снижается по сравнению с традиционным подходом RML.
Тематические исследования реальных месторождений включают исследование сопоставления с историей для получения реализаций с сопоставлением с историей с помощью предлагаемого метода и количественную оценку неопределенности прогнозирования добычи с использованием этих обусловленных моделей. Все обусловленные модели генерируют прогнозы добычи, которые согласуются с реальными данными добычи как в период сопоставления с историей, так и в период слепого тестирования.