Умножение графиков: Методы графического сложения, вычитания.

4.2. Умножение и деление графиков

Изучим правила перемножения и деления графиков функций. Рассмотрим как построить график суперпозиции двух функций. Приведем некоторые примеры.

Произведение. Пусть известны графики двух функций и . Построим график функции . Для этого изобразим на одном чертеже графики функций, входящих в произведение. Затем проведем ряд вертикальных прямых, пересекающих графики этих функций, и пометим на них точки, ординаты которых равны произведению ординат перемножаемых функций. При этом, если ордината одной их функций, входящих в произведение равна нулю, т.е. ее график пересекает ось , то и ордината произведения будет равна нулю, т.е. график будет пересекать ось при том же значении абсциссы. Если ордината одной их функций или равна , то ордината произведения этих функций будет раположена на графике другой функции. Если перемножаются ординаты одного знака (либо обе ординаты имеют знак » «, либо обе ординаты имеют знак » «), то произведение будет положительно.

Если в произведение входят ординаты разных знаков (одна ордината имеет знак » «, а другая » «), то их произведение будет отрицательно. Соединяя полученные точки плавной кривой, получим эскиз графика функции (см. рис. ).

Например (см. рис. 21), при имеем , , значит .

Рис. 21. Графики функций , и .

Пример 10. Построить график функции .

Решение. График функций и нам известны. График — бисектрисса первого и третьего координатных углов, а график изображен на рис. 22. Заметим, что функция — нечётная и — нечётная, поэтому их произведение — чётная функция. Следовательно, достаточно построить график только для , а затем симметрично отобразить на полуплоскость . Заметим также, что поскольку , то произведение , т.е. график не выходит за пределы линий и .

Итак, пусть . В точках , где произведение равно нулю, следовательно в этих точках график пересекает ось .

Удобно также отметить точки, в которых , поскольку при график попадает на прямую , а при — на прямую .

Проведя вертикальные прямые через точки , …, и перемножая соответствующие ординаты функций и , получим график функции (см. рис. 22).

Рис. 22. Графики функций , и .

Частное. Теперь, зная графики функций и изобразим график функции . Если знаменатель дроби отличен от нуля: , то при делении графиков совершаются действия, аналогичные действиям при умножении графиков. А именно, изображаются графики и , проводится ряд вертикальных прямых, пересекающих эти графики, отмечаются точки, ординаты которых равны , полученные точки соединяются плавной линией (см. рис. 23).

Рис. 23. Графики функций , и .

Точки, в которых заслуживают особого внимания, поскольку в этих точках функция не существует.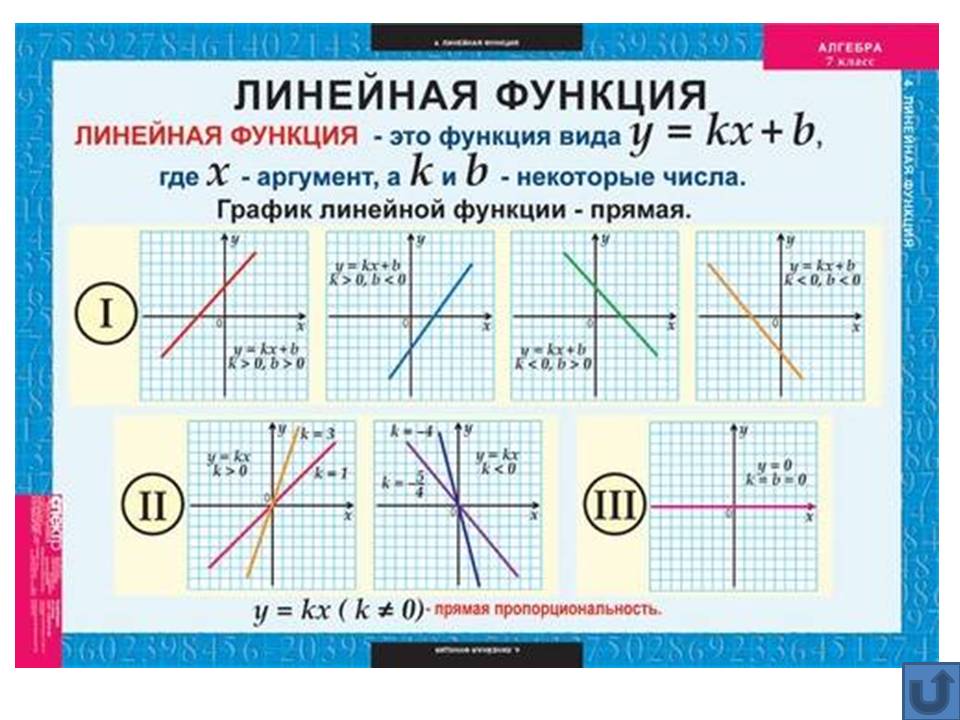 В окрестнотях точек, в которых знаменатель функция может вести себя по разному. Рассмотрим возможные варианты.

Пусть при ( ). Возможны два случая: или .

При функция неограниченно возрастает или убывает в окрестности точки . В этом случае, нужно обратить внимание на знак частного при и при . Рассмотрим, например, правую окрестность, т.е. точки , которые больше : . Если при , достаточно близких к , таких, что частное , то график функции будет уходить вверх, прижимаясь справа к прямой , но не пересекая её. Если же , то график будет идти вниз, прижимаясь справа к прямой (см. рис. 23).

Аналогично поведет себя график и в левой окрестности, т.е. при (только прижиматься к прямой график будет слева) (см. рис. 23).

Ситуацию когда и и можно тщательно изучить только пользуясь теорией пределов, однако в некоторых случаях можно определить поведение функции исходя из графиков и и в этом случае.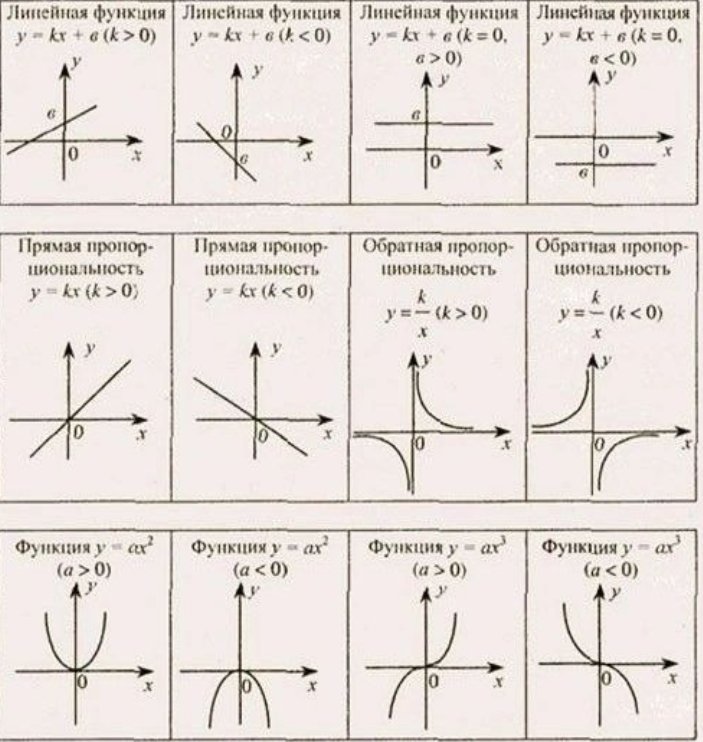

Отметим также, что для построения частного можно перемножить графики и .

Замечание. При построении графиков произведения и частного двух функций полезно помнить, что если обе функции и чётные или обе нечётные, то и произведение и частное будет чётной функцией. Если же одна из функций или нечётная, а другая чётная, то их произведение и частное будет нечётной функцией.

Пример 11. 3 Построить график функции .

Решение. Используя рис. 2 и таблицу 1 изобразим графики функций и (см. рис. 24).

Функции определена и непрерывна во всех точках, за исключением нуля.

Заметим, что — четная функция, причем при , функция тоже четная, причем для всех . Поэтому функция график будет симметричен относительно оси и расположен выше оси .

Построим график при . Проведем вертикальные линии, проходящие через точки , , , и отметим на них значение частного функций и . Так при будем иметь , при получим и т.д.

Замечая, что при знаменатель дроби обращаетя в нуль, а числитель отличен от нуля (равен единице), и учитывая, что для всех (значит, и в любой окрестности точки ) получим, что график рассматриваемой функции при будет уходить вверх, прижимаясь справа к оси .

Рис. 24. Графики функций , и .

Соединяя отмеченные точки и рисуя график функции в промежетке от до уходящим вверх и приближающимся справа к оси , получим график функции при . В силу четности рассматриваемой функции, слева от оси изображаем кривую, симметричную кривой справа от оси , получаем искомый график (см. рис. 24).

растяжение и сжатие, параллельный перенос, общее уравнение синусоиды, тангенцоиды

1. Растяжение и сжатие графиков тригонометрических функций по оси OX
2. Растяжение и сжатие графиков тригонометрических функций по оси OY
3. Параллельный перенос графиков тригонометрических функций по оси OX
4. Параллельный перенос графиков тригонометрических функций по оси OY
5. Общее уравнение синусоиды
6. Общее уравнение тангенцоиды
7. Примеры

Общие принципы преобразования графиков функций изучались нами в главе 8, (см.

§47, §48, §50 справочника для 8 класса). В этом параграфе мы рассмотрим особенности тригонометрических функций при использовании этих преобразований.

п.1. Растяжение и сжатие графиков тригонометрических функций по оси

OX

Общие принципы растяжения и сжатия графиков по оси OX:

При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(px),\ \ p\gt 1 $$ график второй функции сжимается в p раз по оси OX по сравнению с графиком первой функции.

При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(\frac{x}{p}),\ \ p\gt 1 $$ график второй функции растягивается в p раз по оси OX по сравнению с графиком первой функции.

Эти принципы справедливы и для тригонометрических функций.
Тригонометрические функции являются периодическими: синус и косинус с периодом 2π, тангенс и котангенс – с периодом π. Получаем следствие общих принципов:

При сравнении двух тригонометрических функций $$ y_1=f(x),\ \ y_2=f(px),\ \ p\gt 1 $$ период второй функции уменьшается в

p раз: $$ T_2=\frac{T_1}{p} $$

При сравнении двух тригонометрических функций $$ y_1=f(x),\ \ y_2=f(\frac{x}{p}),\ \ p\gt 1 $$ период второй функции увеличивается в p раз: $$ T_2=pT_1 $$

Например:

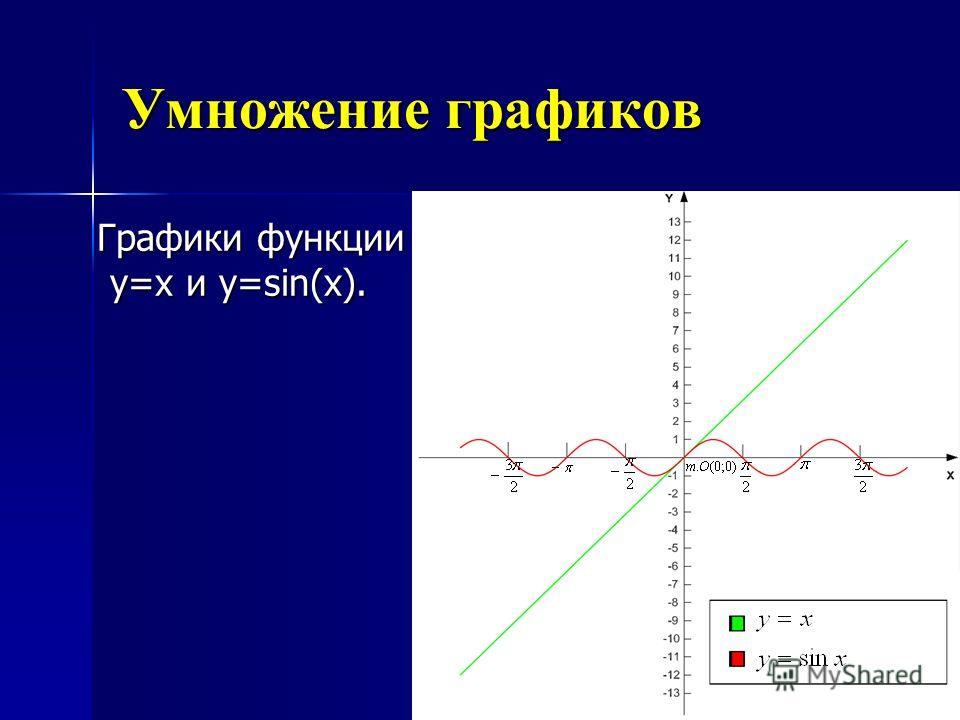
Построим в одной системе координат три графика: $$ f(x)=sinx,\ \ g(x)=sin2x,\ \ h(x)=sin\frac{x}{2} $$
Период колебаний функции \(g(x)=sin2x\) в 2 раза меньше: \(T_g=\frac{2\pi}{2}=\pi\).
Период колебаний функции \(h(x)=sin\frac{x}{2}\) в 2 раза больше: \(T_h=2\cdot 2\pi=4\pi\).

п.2. Растяжение и сжатие графиков тригонометрических функций по оси

OY

Общие принципы растяжения и сжатия графиков по оси OY:

При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=Af(x),\ \ A\gt 1 $$ график второй функции растягивается в A раз по оси OY по сравнению с графиком первой функции.

Общий принцип сжатия графиков:

При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=\frac{1}{A}f(x),\ \ A\gt 1 $$ график второй функции сжимается в A раз по оси OY по сравнению с графиком первой функции.

Эти принципы справедливы и для тригонометрических функций.
Т.к. для графиков синуса и косинуса (синусоиды) характерна амплитуда колебаний, то также говорят, что:

• умножение на параметр \(A\gt 1\) увеличивает амплитуду колебаний в \(A\) раз;
• деление на параметр \(A\gt 1\) уменьшает амплитуду колебаний в \(A\) раз.

Например:

1) Построим в одной системе координат три графика: $$ f(x)=cosx,\ \ g(x)=2cosx,\ \ h(x)=\frac{1}{2}cosx $$
Умножение на \(A=2\) увеличивает амплитуду колебаний в 2 раза.
Область значений функции \(g(x)=2cosx:\ y\in[-2;2]\). График растягивается по оси

OY.
Деление на \(A=2\) уменьшает амплитуду колебаний в 2 раза. Область значений функции \(h(x)=\frac12 cosx:\ y\in\left[-\frac12; \frac12\right]\). График сжимается по оси OY.

2) Теперь построим $$ f(x)=tgx,\ \ g(x)=2tgx,\ \ h(x)=\frac{1}{2}tgx $$
В этом случае хорошей иллюстрацией растяжения по оси OY при умножении и сжатия по оси OY при делении на \(A=2\) служит поведение функции при \(x=\frac\pi4\). $$ f\left(\frac\pi4\right)=tg\left(\frac\pi4\right)=1,\ \ g\left(\frac\pi4\right)=2tg\left(\frac\pi4\right)=2,\ \ h\left(\frac\pi4\right)=\frac12 tg\left(\frac\pi4\right)=\frac12 $$ Аналогично – для любого другого значения аргумента x.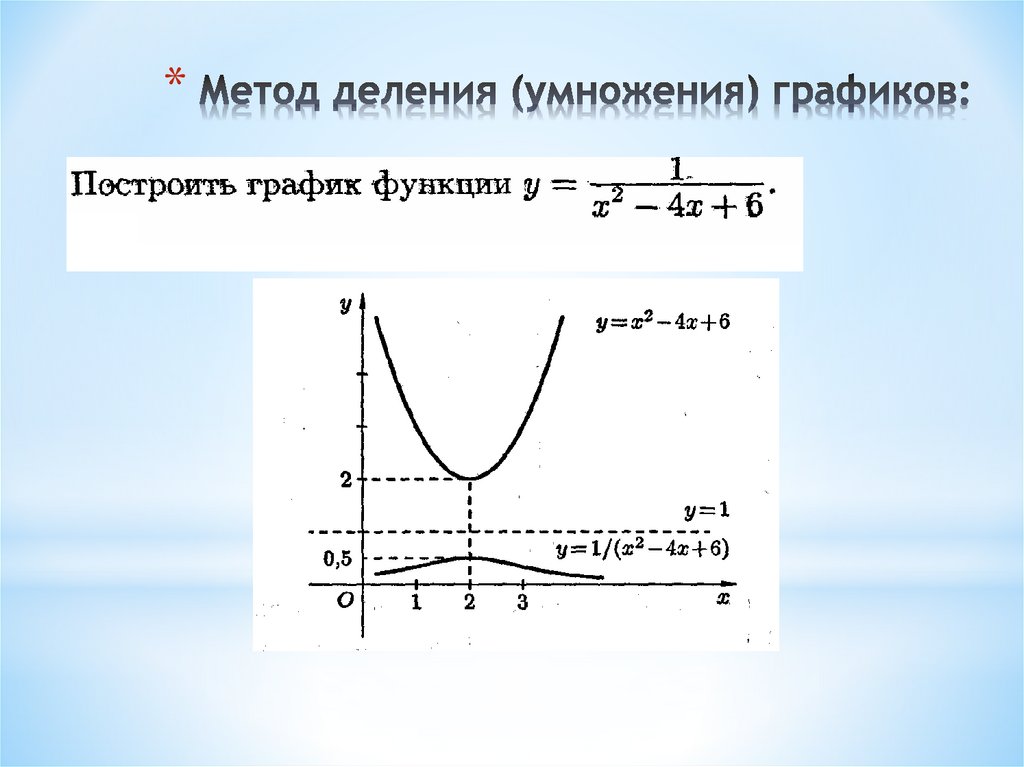

п.3. Параллельный перенос графиков тригонометрических функций по оси

OX

Общие принципы переноса по оси OX:

При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(x+a),\ \ a\gt 0 $$ график второй функции смещается влево на

a по оси OX по сравнению с графиком первой функции.

При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(x-a),\ \ a\gt 0 $$ график второй функции смещается вправо на a по оси OX по сравнению с графиком первой функции.

Эти принципы справедливы и для тригонометрических функций.
При этом параметр x называют начальной фазой колебаний.
При сравнении двух тригонометрических функций \(y_1=f(x)\) и \(y_2=f(x\pm a)\) говорят, что у второй функции сдвиг по фазе равен \(\pm a\).

Например:

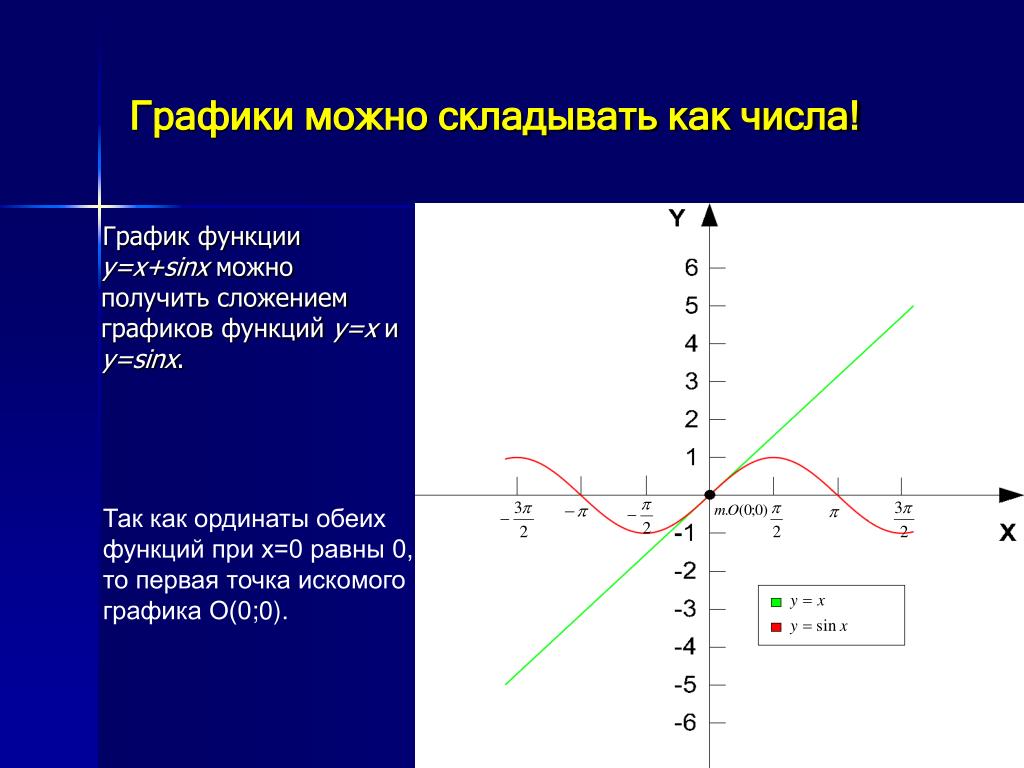
1) Построим в одной системе координат три графика: $$ f(x)=sinx,\ \ g(x)=sin\left(x+\frac\pi4\right),\ \ h(x)=sin\left(x-\frac\pi4\right) $$
Функция \(g(x)=sin\left(x+\frac\pi4\right)\) сдвинута на \(\frac\pi4\) влево по сравнению с \(f(x)\)
Функция \(h(x)=sin\left(x-\frac\pi4\right)\) сдвинута на \(\frac\pi4\) вправо по сравнению с \(f(x)\)

п.

4. Параллельный перенос графиков тригонометрических функций по оси OY

Общие принципы переноса по оси OY:

При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(x)+a,\ \ a\gt 0 $$ график второй функции смещается вверх на a по оси OY по сравнению с графиком первой функции.

При сравнении графиков двух функций $$ y_1=f(x),\ \ y_2=f(x)-a,\ \ a\gt 0 $$ график второй функции смещается вниз на a по оси OY по сравнению с графиком первой функции.

Эти принципы справедливы и для тригонометрических функций.

Например:

1) Построим в одной системе координат три графика: $$ f(x)=sinx,\ \ g(x)=sinx+1,\ \ h(x)=sinx-1 $$
Функция \(g(x)=sinx+1\) сдвинута на 1 вверх по сравнению c \(f(x)\)
Функция \(h(x)=sinx-1\) сдвинута на 1 вниз по сравнению с \(f(x)\)

п.5. Общее уравнение синусоиды

Синусоида – плоская кривая, которая задается в прямоугольной системе координат уравнением: $$ y(x)=Asin(cx+d)+B $$ где
A — амплитуда, характеризует растяжение графика по оси OY
B – вертикальный сдвиг, характеризует сдвиг графика по оси OY (вверх/вниз)
c — циклическая частота, характеризует период колебаний и растяжение графика по оси OX
d- начальная фаза, характеризует сдвиг графика по оси OX(влево/вправо)

График \(y(x)=Acos(cx+d)+B\) также называют синусоидой. Термин «косинусоида» употребляется относительно редко.
Поскольку график косинуса получается из графика синуса сдвигом по фазе на π/2 влево, вводить термин «косинусоида» излишне.

Например:

Построим график \(g(x)=3sin\left(2x+\frac\pi2\right)-1\)
По сравнению с \(f(x)=sinx\):

• \(A=3\) — график растянут по оси OY в 3 раза
• \(c=2\) — период меньше в 2 раза T=π, график сжат в 2 раза по оси OX
• \(d=\frac\pi2\) – начальная фаза положительная, график сдвинут на \(\frac{\pi}{2\cdot 2}=\frac\pi4\) влево
• \(B=-1\) — график сдвинут по оси OY на 1 вниз

п.6. Общее уравнение тангенцоиды

Tангенцоидa – плоская кривая, которая задается в прямоугольной системе координат уравнением: $$ y(x)=Atg(cx+d)+B $$ где
A — амплитуда, характеризует растяжение графика по оси OY
B – вертикальный сдвиг, характеризует сдвиг графика по оси OY (вверх/вниз)
c — циклическая частота, характеризует период колебаний и растяжение графика по оси OX
d- начальная фаза, характеризует сдвиг графика по оси OX(влево/вправо)

График \(y(x)=Actg(cx+d)+B\) также называют тангенцоидой.

Например:

Построим график \(g(x)=\frac12 tg\left(\frac{x}{2}-\frac\pi3\right)+1\)
По сравнению с \(f(x)=tgx\):

• \(A=\frac12\) — график сжат по оси OY в 2 раза
• \(c=\frac12\) — период больше в 2 раза T=2π, расстояние между асимптотами 2π, график растянут в 2 раза по оси OX
• \(d=-\frac\pi3\) – начальная фаза отрицательная, график сдвинут на \(\frac{\pi}{3\cdot 1/2}=\frac{2\pi}{4}\) вправо
• \(B=1\) — график сдвинут по оси OY на 1 вверх

п.7. Примеры

Пример 1.Постройте в одной системе координат графики: $$ f(x)=sinx,\ \ g(x)=-sinx,\ \ h(x)=cosx $$ Найдите сдвиг по фазе для \(g(x)\) и \(h(x)\) в сравнении с \(f(x)\).

Сдвиг по фазе удобно определять по главной арке синусоиды.
Для \(f(x)=sin⁡x\) главная арка определена на отрезке \(0\leq x\leq \pi\)
Для \(g(x)=-sin⁡x\) главная арка определена на отрезке \(-\pi\leq x\leq 0\), т.е. сдвинута на π влево от \(f(x)\).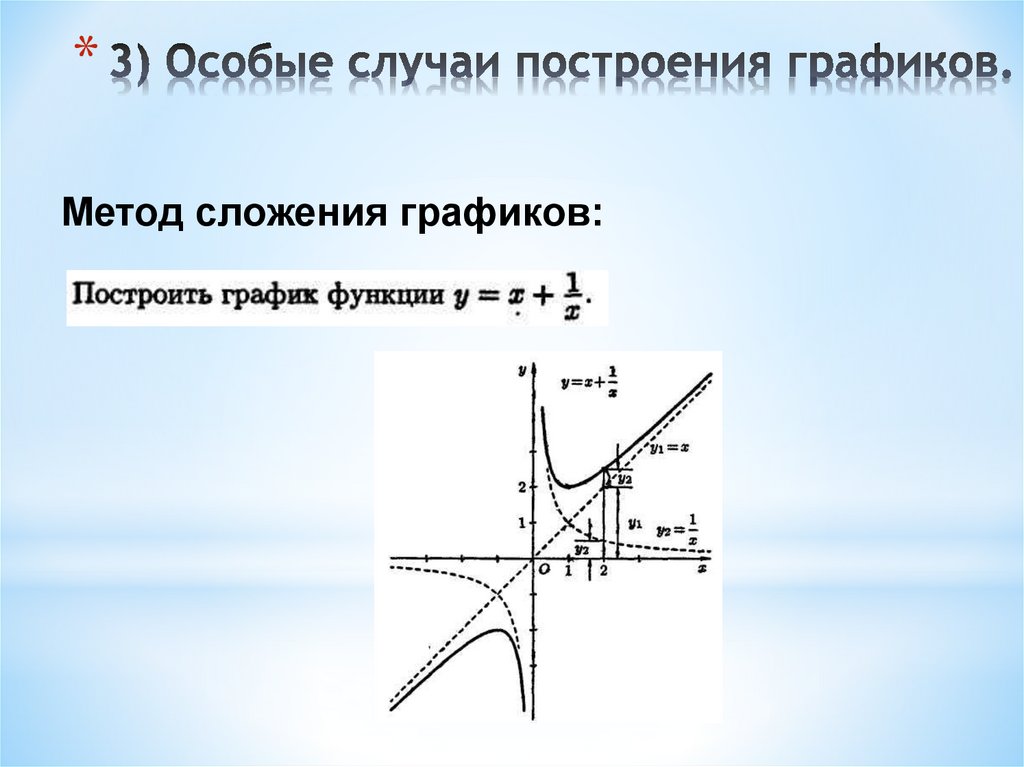 Это означает, что: $$ f(x)=g(x+\pi),\ \ sin⁡x=-sin⁡(x+\pi) $$ Для \(h(x)=cos⁡x\) главная арка определена на отрезке \(-\frac\pi2\leq x\leq \frac\pi2\), т.е. сдвинута на \(\frac\pi2\) влево от \(f(x)\). Это означает, что: $$ f(x)=h\left(x+\frac\pi2\right),\ \ sinx=cos\left(x+\frac\pi2\right) $$

Пример 2. Найдите наименьшие положительные периоды функций:
a) \(y=sin5x\)
Период синуса \(2\pi\) уменьшается в 5 раз. Получаем: \(T=\frac{2\pi}{5}\)

б) \(y=cos\pi x\)
Период косинуса \(2\pi\) уменьшается в \(\pi\) раз. Получаем: \(T=\frac{2\pi}{\pi}=2\)

в) \(y=tg\frac{x}{4}\)
Период тангенса \(\pi\) увеличивается в 4 раза. Получаем: \(T=4\pi\)

г) \(y=tg\left(2x+\frac{\pi}{3}\right)\)
Период тангенса \(\pi\) уменьшается в 2 раза. Получаем: \(T=\frac\pi2\)

Пример 3. Используя правила преобразования графиков функций, постройте график $$ f(x)=2ctg\left(3x+\frac\pi6\right) $$ По сравнению с \(g(x)=tg⁡x\):

• \(A=2\) — график растянут по оси OY в 2 раза
• \(c=3\) — период меньше в 3 раза \(T=\frac\pi3\), расстояние между асимптотами \(\frac\pi3\), график сжат в 3 раза по оси OX
• \(d=-\frac\pi6\) – начальная фаза положительная, график сдвинут на \(\frac{\pi}{6\cdot 3}=\frac{\pi}{18}\) влево

Расположение нулей: $$ tg\left(3x+\frac\pi6\right)=0\Rightarrow 3x+\frac\pi6=\pi k\Rightarrow 3x=-\frac\pi6+\pi k\Rightarrow x =-\frac{\pi}{18}+\frac{\pi k}{3} $$ Вертикального сдвига нет, нули расположены на оси OX.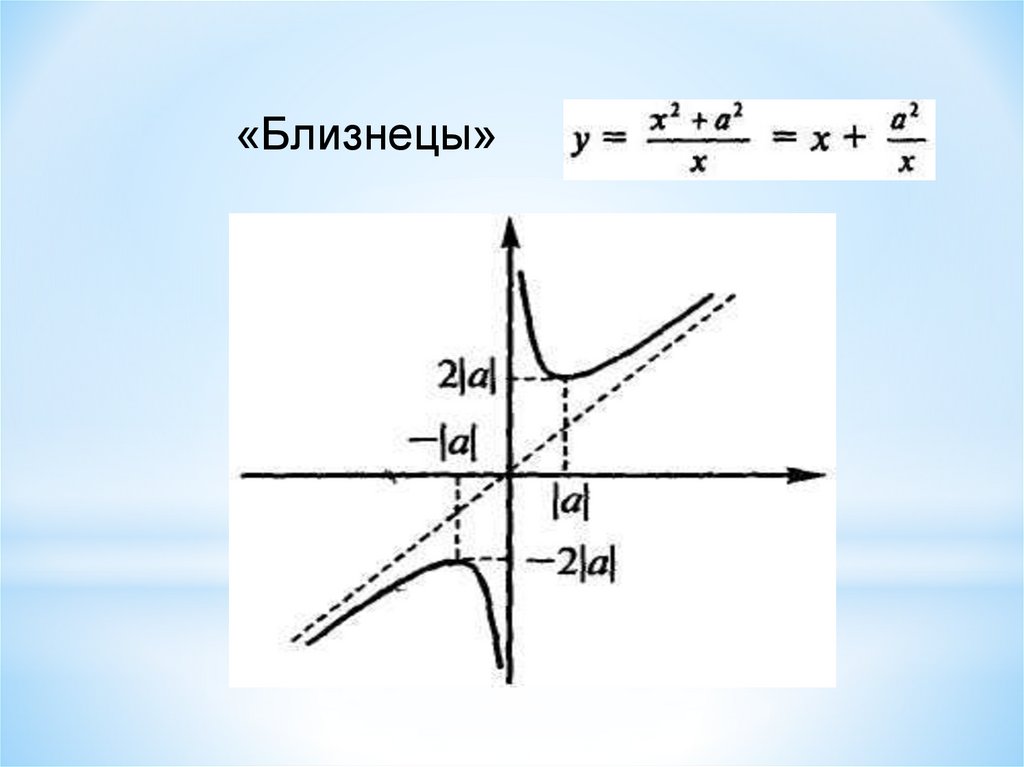
Расположение асимптот: $$ 3x+\frac\pi6\ne\frac\pi2+\pi k\Rightarrow 3x\ne\frac\pi3+\pi k\Rightarrow x\ne\frac\pi9+\frac{\pi k}{3} $$ Пересечение главной ветви с осью OY: \(x=0,\ y=2tg\frac\pi6=\frac{2}{\sqrt{3}}\)
С учетом периода \(\frac\pi3\) получаем семейство дополнительных точек для построения графика \(\left(\frac{\pi k}{3}; \frac{2}{\sqrt{3}}\right)\).

Пример 4. Определите графически, сколько корней имеет уравнение на отрезке: a) \(sinx=sin2x\) при \(0\leq x\leq 3\pi\)

Ответ: 7 корней

б) \(cos\frac{x}{2}=cos2x\) при \(-2\pi\leq x\leq 2\pi\)

Ответ: 7 корней

The Graph Grid Игра и видео об умножении

 

Когда дело доходит до объяснения основ умножения, многие дети погружаются в чан фактов об умножении и просят запомнить их, не имея абсолютно никакого представления о том, что такое умножение на самом деле. о.

Определение — отличное место для начала, и с этой игрой на умножение графической сетки ваши ученики быстро поймут, что означает !

Возьмите эти несколько принадлежностей, и вы уже в пути:

1. Прежде всего, поместите лист миллиметровой бумаги между двумя или более детьми. Вы можете скачать нашу диаграмму здесь или использовать свою собственную (дополнительную информацию см. ниже).

2. Учащиеся один за другим бросают пару игральных костей. (Эти 10-гранные игральные кости очень крутые! Мне нравится этот набор из 100 многогранных игральных костей.)  

3.  Учащиеся смотрят на два выпавших числа и составляют сетку. Например, если ученик выбрасывает 3 и 4, он рисует сетку, состоящую из 3 в высоту и 4 в ширину или 4 в высоту и 3 в ширину. После этого на ячейку наносят номер и ответ. Если учащиеся не знают ответа, они могут посчитать квадраты. Это очень хорошо, так как это действие помогает детям понять, что умножение — это площадь и многократное сложение!

4. Учащиеся раскрашивают свою сетку и/или помещают внутрь свои инициалы. Игроки по очереди бросают кости и строят сетки.

5. Игра продолжается до тех пор, пока один из игроков не выкинет число, равное сетке, которую нельзя нарисовать на бумаге. Если игроков более двух, игра продолжается до тех пор, пока каждый игрок не выкинет два неподходящих числа.

6. Учащиеся подсчитывают количество клеток в сетке, чтобы определить победителя. У победителя больше всего квадратов!

Хотите увидеть игру?

,

 

 

Примечания:  Вы можете использовать более распространенные 6-гранные кости, или вы можете инвестировать в некоторые 9- и 12-гранные кости. Они идеально подходят для этой игры. Вы можете найти их здесь.

Вы можете использовать миллиметровку, которая есть у вас дома, но будьте осторожны: количество клеток на миллиметровке может значительно изменить продолжительность вашей игры! Мы предлагаем использовать эту бесплатную миллиметровку PDF 25X25.

Для начинающих вы можете рассмотреть эту миллиметровую бумагу PDF 20X20 или даже эту миллиметровую бумагу PDF 15X15.

А для расширенного обучения мы представляем вам:

Это задание по математике с массивом даст учащимся больше времени для практики умножения. Учащиеся бросают кости и перечисляют все различные сетки (или семейства фактов), которые можно составить, используя эти два числа. Повторите 15 раз, затем обведите на бумаге все различные сетки, перекрывая семейства фактов. Раскрасьте свои сетки, и у вас получится произведение искусства, достойное холодильника! Для более полного объяснения: Художественное задание «Умножение массива».

Если понимание умножения уже освоено, то пришло время перейти к этой супер веселой соревновательной версии Войны умножения! Ваши ученики забудут, что они практикуют свои таблицы умножения в кратчайшие сроки!

 

Получайте удовольствие!
 

 

Умножение графа | Semantic Scholar

• DOI: 10.1007/BF01162967
• Идентификатор корпуса: 186238657

 @article{Sabidussi1959GraphM,
  title={Умножение графика},
  автор={Герт Сабидусси},
  журнал={Mathematische Zeitschrift},
  год = {1959},
  объем = {72},
  страницы = {446-457}
} 

• Г. Сабидусси
• Опубликовано в 1959 году
• Математика
• Mathematische Zeitschrift

View on Springer

Базовый размер, метрическая размерность

6 вариантов графов и другие варианты графов 73

Р. Бейли, П. Кэмерон

Математика

2011

Базовый размер группы перестановок и метрическая размерность графа — это два из ряда связанных параметров групп, графов, когерентных конфигураций и ассоциативных схем. Они были…

Энергия симплициального комплекса

Об определяющем числе и метрической размерности графов

• Дж. Касерес, Д. Гарихо, М. Л. Пуэртас, К. Сеара

• Математика, информатика

  3 Электрон. Дж. Комб.

• 2010

Приведены новые доказательства и результаты по определению количества деревьев и декартовых произведений графов, а также установлены некоторые нижние оценки на разницу между двумя параметрами.

Полные вращения в графах Кэли

• М. Хайдеманн, Наусика Марлин, С. Перенн

• Математика

  Eur. Дж. Комб.

• 2001

Некоторые асимметрии графа с потенциальными алгебраическими симметриями, фигурирующие в его определении как графа Кэли на группе, связаны между собой.

Почти оптимальные нижние границы регулярных разрешающих опровержений формул Цейтина для всех графов постоянной степени

Эта статья мотивирована поиском точной сложности разрешающего опровержения формул Цейтина. Доказано, что размер любого регулярного резолютивного опровержения формулы Цейтина…

Асимметричные раскраски произведений графов и орграфов

• И. Броер, В. Имрих, Р. Калиновски, М. Пилсняк

• Математика

  Дискрет. заявл. Мат.

• 2019

Вычисление направленного декартова разложения ориентированного графа из его неориентированного разложения за линейное время

• C. Crespelle, E. Thierry

• Информатика, математика 9002 Discret. Мат.

• 2015

Алгоритм линейного времени для вычисления простого разложения ориентированного графа с учетом декартова произведения

• C. Crespelle, E. Thierry, Thomas Lambert

• CO 9003CO 9003 CO 9003 CO 90, математика 003

• 2013

В этой статье разрабатывается первый алгоритм с линейным временем для вычисления простого разложения орграфа G относительно декартова произведения, а также дается новый взгляд на связи между направленной и неориентированной версиями декартова произведения графов.

ЗАМЕЧАНИЕ О РЕБЕРНОЙ СВЯЗИМОСТИ ДЕКРАТОВЫХ ПРОИЗВЕДЕНИЙ ГРАФОВ

Аннотация Основная цель данной статьи — установить условия, необходимые и достаточные для того, чтобы реберная связность декартова произведения двух графов равнялась сумме …

О РЕБЕРНОЙ СВЯЗИМОСТИ ДЕкартова произведения графов

• C.

  No related posts.