ОглавлениеПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДАВВЕДЕНИЕ ЧАСТЬ 1. ОБЩАЯ ТЕОРИЯ 1.1.1. Понятие случайной величины. 1.1.2. Интегральная функция распределения случайной величины. 1.1.3. Функция плотности вероятности. 1.1.4. Дискретные случайные величины. 1.1.5. Математическое ожидание и высшие моменты случайной величины. § 1.2. Понятие статистической гипотезы 1.2.2. Простые и сложные гипотезы. § 1.3. Основные черты существующей методики проверки статистических гипотез 1.3.2. Общая методика проверки статистических гипотез. 1.3.3. Принципы выбора критической области. 1.3.4. Количество наблюдений, необходимых при заданных вероятностях a и b. 1.3.5. Проверка гипотезы как выбор между двумя возможными действиями. ГЛАВА 2. ПОСЛЕДОВАТЕЛЬНАЯ ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ. ОБЩИЕ ВОПРОСЫ § 2.2. Последствия выбора конкретной методики последовательной проверки 2.2.2. Функция среднего числа наблюдений последовательного критерия.  § 2.3. Принципы, на которых основывается выбор последовательного критерия 2.3.2. Требования, предъявляемые к оперативной характеристике. 2.3.3. Функция среднего числа наблюдений как основа для выбора последовательного критерия. § 2.4. Проверка простой гипотезы Н0 при единственной конкурирующей гипотезе Н1 2.4.2. Эффективность существующей методики проверки гипотез, рассматриваемой как частный случай последовательного критерия. ГЛАВА 3. ПОСЛЕДОВАТЕЛЬНЫЙ КРИТЕРИЙ ОТНОШЕНИЙ ВЕРОЯТНОСТЕЙ ДЛЯ ПРОВЕРКИ ПРОСТОЙ ГИПОТЕЗЫ Н0 ПРОТИВ ЕДИНСТВЕННОЙ КОНКУРИРУЮЩЕЙ ГИПОТЕЗЫ Н1 § 3.1. Определение последовательного критерия отношений вероятностей § 3.2. Основные соотношения между величинами a, b, A и B § 3.3. Определение постоянных A и B на практике § 3.5. Среднее число наблюдений последовательного критерия отношений вероятностей § 3.6. Выигрыш в числе наблюдений при использовании последовательного критерия отношений вероятностей вместо обычной процедуры проверки § 3.  7. Нижняя граница вероятности того, что последовательный критерий окончится при числе наблюдений, меньшем или равном заданному числу 7. Нижняя граница вероятности того, что последовательный критерий окончится при числе наблюдений, меньшем или равном заданному числу§ 3.8. Усечение процедуры последовательного анализа § 3.9. Увеличение среднего числа наблюдений, обусловленное заменой точных значений A(a,b) и B(a,b) на … ГЛАВА 4. ОСНОВЫ ТЕОРИИ ПОСЛЕДОВАТЕЛЬНЫХ КРИТЕРИЕВ ДЛЯ ПРОСТЫХ И СЛОЖНЫХ ГИПОТЕЗ ОТНОСИТЕЛЬНО МНОЖЕСТВА КОНКУРИРУЮЩИХ ГИПОТЕЗ 4.1.2. Проверка простой гипотезы при односторонних конкурирующих гипотезах. 4.1.3. Проверка простой гипотезы в случае, когда на конкурирующие величины неизвестных параметров не накладывается никаких ограничений. 4.1.4. Применение общей методики к проверке среднего значения нормального распределения с известной дисперсией. § 4.2. Проверка сложных гипотез 4.2.2. Описание методики проверки в общем случае. 4.2.3. Применение общей методики к проверке среднего значения нормального распределения с неизвестной дисперсией (последовательный t-критерий). 4.  2.4. Частный класс задач, рассмотренный Гиршиком. 2.4. Частный класс задач, рассмотренный Гиршиком.ЧАСТЬ II. ПРИЛОЖЕНИЕ ОБЩЕЙ ТЕОРИИ К ЧАСТНЫМ СЛУЧАЯМ ГЛАВА 5. КРИТЕРИЙ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ (ПРИЕМОЧНАЯ ПРОВЕРКА ПАРТИИ ИЗДЕЛИЙ, В КОТОРОЙ КАЖДОЕ ИЗДЕЛИЕ ОТНЕСЕНО К ОДНОЙ ИЗ ДВУХ КАТЕГОРИЙ) § 5.2. Допускаемый риск, связанный с принятием неправильных решений § 5.3. Последовательный критерий отношения вероятностей, соответствующий величинам … 5.3.3. Графический метод проведения контроля. § 5.4. Оперативная характеристика критерия L(p) § 5.5. Среднее число наблюдений критерия § 5.6. Группировка наблюдений 5.6.2. Влияние группировки на оперативную характеристику и среднее число наблюдений; верхние и нижние границы для них. § 5.7. Усеченный критерий ГЛАВА 6. КРИТЕРИЙ ДЛЯ РАЗНОСТИ МЕЖДУ СРЕДНИМИ ЗНАЧЕНИЯМИ ДВУХ БИНОМИАЛЬНЫХ РАСПРЕДЕЛЕНИЙ (ДВОЙНАЯ ДИХОТОМИЯ) § 6.4. Последовательный критерий для гипотезы … 6.4.1. Допускаемый риск, связанный с принятием неверных решений.  6.4.2. Последовательный критерий отношения вероятностей, соответствующий величинам u0, u1, a и b. 6.4.3. Кривая оперативной характеристики критерия. 6.4.4. Среднее число наблюдений, требуемых в критерии. 6.4.6. Наблюдения, осуществляемые группами. ГЛАВА 7. ПРОВЕРКА ТОГО, ЧТО СРЕДНЕЕ ЗНАЧЕНИЕ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ С ИЗВЕСТНЫМ СРЕДНИМ КВАДРАТИЧЕСКИМ ОТКЛОНЕНИЕМ НЕ ПРЕВЫШАЕТ ЗАДАННОЙ ВЕЛИЧИНЫ § 7.2. Допускаемый риск, связанный с неправильным решением § 7.3. Последовательный критерий отношений вероятностей, соответствующий величинам … § 7.4. Кривая оперативной характеристики критерия § 7.6. Среднее число необходимых наблюдений в критерии ГЛАВА 8. ПРОВЕРКА ТОГО, ЧТО СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ НЕ ПРЕВЫШАЕТ ЗАДАННОГО ЗНАЧЕНИЯ § 8.2. Допускаемый риск принятия неверного решения § 8.3. Последовательный критерий отношений вероятностей, соответствующий величинам … § 8.4. Оперативная характеристика критерия § 8.  5. Среднее число наблюдений в критерии 5. Среднее число наблюдений в критерииГЛАВА 9. ПРОВЕРКА ТОГО, ЧТО СРЕДНЕЕ ЗНАЧЕНИЕ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ С ИЗВЕСТНОЙ ДИСПЕРСИЕЙ РАВНО ОПРЕДЕЛЕННОЙ ВЕЛИЧИНЕ § 9.2. План последовательной проверки, удовлетворяющий заданным требованиям ЧАСТЬ III. ПРОБЛЕМА МНОГОЗНАЧНЫХ РЕШЕНИЙ И ОЦЕНКИ ГЛАВА 10. ВЫБОР ГИПОТЕЗЫ ИЗ МНОЖЕСТВА ВЗАИМНО ИСКЛЮЧАЮЩИХ ДРУГ ДРУГА ГИПОТЕЗ (МНОГОЗНАЧНОЕ РЕШЕНИЕ) § 10.2. Основные черты последовательного критерия для выбора гипотезы из множества взаимно исключающих друг друга гипотез § 10.3. Последствия выбора любого частного способа последовательной выборочной проверки § 10.4. Принципы выбора плана последовательной выборки 10.4.2. Функция риска, связанная с данным способом проверки. 10.4.3. Функция риска и среднее число наблюдений как основа для выбора плана последовательной выборки. 10.4.4. Использование некоторых простых весовых функций. 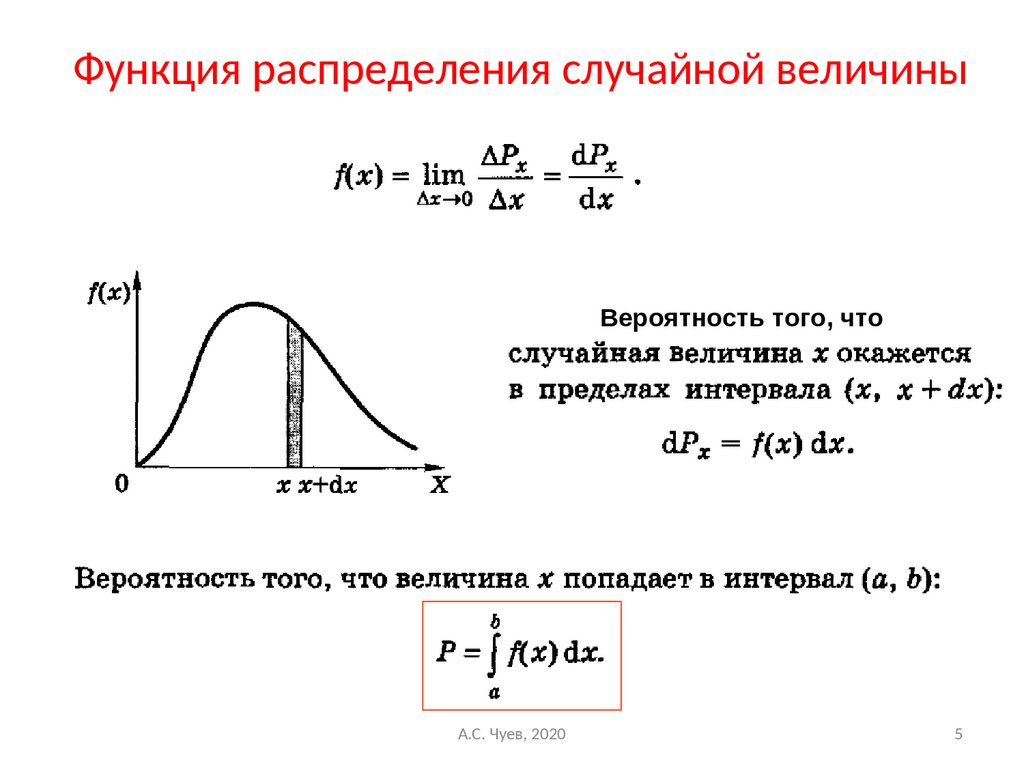 § 10.5. Обсуждение специального класса планов последовательной выборки ГЛАВА 11. ПРОБЛЕМА ПОСЛЕДОВАТЕЛЬНОЙ ОЦЕНКИ § 11.1. Принципы современной теории оценок интервалами или множествами § 11.2. Постановка задачи о последовательной оценке посредством интервалов или множеств § 11.3. Специальный класс способов последовательной оценки ПРИЛОЖЕНИЯ П.1. Доказательство того, что с вероятностью, равной единице, последовательный критерий отношений вероятностей рано или поздно закончится П.2. Верхняя и нижняя границы оперативной характеристики последовательного критерия П.2.3. Определение верхней и нижней границ для оперативной характеристики. П.2.4. Расчет … для биномиального распределения П.2.5. Вычисление … для нормального распределения. П.3. Верхняя и нижняя границы для функции среднего числа наблюдений последовательного критерия отношений вероятностей П.4. Вывод точных формул для оперативной характеристики и функции среднего числа наблюдений в случае, когда z может принимать только конечное число значений, кратных постоянному числу П.  5. Характеристическая функция и высшие моменты величины n 5. Характеристическая функция и высшие моменты величины nП.5.2. Вывод точной формулы для случая, когда z может принимать только конечное число значений, кратных некоторому постоянному числу. П.6. Приближенное распределение величины n для случая, когда z распределена по нормальному закону П.7. Эффективность последовательного критерия отношений вероятностей П.8. Определение оптимальной весовой функции w(O) в некоторых специальных случаях проверки простых гипотез без ограничения возможных конкурирующих значений параметров П.8.2. Приложение к проверке средних значений независимых нормально распределенных случайных величин с известными дисперсиями. П.9. Определение оптимальных весовых функций … в некоторых специальных случаях проверки сложных гипотез П.9.2. Применение к проверке среднего значения нормального распределения с неизвестной дисперсией (последовательный t-критерий). ДОПОЛНЕНИЯ. АСИМПТОТИЧЕСКИЕ МИНИМАКСНЫЕ РЕШЕНИЯ ЗАДАЧ ПОСЛЕДОВАТЕЛЬНЫХ ТОЧЕЧНЫХ ОЦЕНОК ДИФФЕРЕНЦИРОВАНИЕ ПОД ЗНАКОМ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ В ОСНОВНОМ ТОЖДЕСТВЕ ПОСЛЕДОВАТЕЛЬНОГО АНАЛИЗА НЕКОТОРЫЕ УТОЧНЕНИЯ ГРАНИЦ ДЛЯ СРЕДНЕГО ЧИСЛА НАБЛЮДЕНИЙ В ПОСЛЕДОВАТЕЛЬНОМ КРИТЕРИИ ОТНОШЕНИЙ ВЕРОЯТНОСТЕЙ ОПТИМАЛЬНЫЙ ХАРАКТЕР ПОСЛЕДОВАТЕЛЬНОГО КРИТЕРИЯ ОТНОШЕНИЙ ВЕРОЯТНОСТЕЙ ОСНОВНЫЕ ИДЕИ ОБЩЕЙ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ |
Дифференциальное и интегральное исчисления для втузов, т.
 2 Дифференциальное и интегральное исчисления для втузов, т.2
2 Дифференциальное и интегральное исчисления для втузов, т.2
ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА XIII.  (n) = f(x) (n) = f(x)§ 18. Некоторые типы дифференциальных уравнений второго порядка, приводимых к уравнениям первого порядка. Задача о второй космической скорости § 19. Графический метод интегрирования дифференциального уравнения второго порядка § 20. Линейные однородные уравнения. Определения и общие свойства § 21. Линейные однородные уравнения второго порядка с постоянными коэффициентами § 22. Линейные однородные уравнения n-го порядка с постоянными коэффициентами § 23. Неоднородные линейные уравнения второго порядка § 24. Неоднородные линейные уравнения второго порядка с постоянными коэффициентами § 25. Неоднородные линейные уравнения высших порядков § 26. Дифференциальное уравнение механических колебаний § 27. Свободные колебания. Векторное и комплексное изображение гармонических колебаний § 28. Вынужденные колебания § 29. Системы обыкновенных дифференциальных уравнений § 30. Системы линейных дифференциальных уравнений с постоянными коэффициентами § 31.  Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки§ 32. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера § 33. Разностный метод приближенного решения дифференциальных уравнений, основанный на применении формулы Тейлора.. Метод Адамса § 34. Приближенный метод интегрирования систем дифференциальных уравнений первого порядка Упражнения к главе XIII ГЛАВА XIV. КРАТНЫЕ ИНТЕГРАЛЫ § 2. Вычисление двойного интеграла § 3. Вычисление двойного интеграла (продолжение) § 4. Вычисление площадей и объемов с помощью двойных интегралов § 5. Двойной интеграл в полярных координатах § 6. Замена переменных в двойном интеграле (общий случай) § 7. Вычисление площади поверхности § 9. Момент инерции площади плоской фигуры § 10. Координаты центра масс площади плоской фигуры § 11. Тройной интеграл § 12. Вычисление тройного интеграла § 13. Замена переменных в тройном интеграле § 14.  Момент инерции и координаты центра масс тела Момент инерции и координаты центра масс тела§ 15. Вычисление интегралов, зависящих от параметра Упражнения к главе XIV ГЛАВА XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ § 2. Вычисление криволинейного интеграла § 3. Формула Грина § 4. Условия независимости криволинейного интеграла от пути интегрирования § 5. Поверхностный интеграл § 6. Вычисление поверхностного интеграла § 7. Формула Стокса § 9. Оператор Гамильтона. Некоторые его применения Упражнения к главе XV ГЛАВА XVI. РЯДЫ § 1. Ряд. Сумма ряда § 2. Необходимый признак сходимости ряда § 3. Сравнение рядов с положительными членами § 4. Признак Даламбера § 5. Признак Коши § 6. Интегральный признак сходимости ряда § 7. Знакочередующиеся ряды. Теорема Лейбница § 8. Знакопеременные ряды. Абсолютная и условная сходимость § 9. Функциональные ряды § 10. Мажорируемые ряды § 11. Непрерывность суммы ряда § 12. Интегрирование и дифференцирование рядов § 13.  Степенные ряды. Интервал сходимости Степенные ряды. Интервал сходимости§ 14. Дифференцирование степенных рядов § 15. Ряды по степеням x-a § 16. Ряды Тейлора и Маклорена § 17. Примеры разложения функций в ряды § 18. Формула Эйлера § 19. Биномиальный ряд § 20. Разложение функции ln(1+x) в степенной ряд. Вычисление логарифмов § 21. Вычисление определенных интегралов с помощью рядов § 22. Интегрирование дифференциальных уравнений с помощью рядов § 23. Уравнение Бесселя § 24. Ряды с комплексными членами § 25. Степенные ряды с комплексной переменной § 26. Решение дифференциального уравнения первого порядка методом последовательных приближений (метод итераций) § 27. Доказательство существования решения дифференциального уравнения. Оценка погрешности при приближенном решении § 28. Теорема единственности решения дифференциального уравнения Упражнения к главе XVI ГЛАВА XVII. РЯДЫ ФУРЬЕ § 2. Примеры разложения функций в ряды Фурье § 3. Одно, замечание о разложении периодической функции в ряд Фурье § 4.  Ряды Фурье для четных и нечетных функций Ряды Фурье для четных и нечетных функций§ 5. Ряд Фурье для функции с периодом 2l § 6. О разложении непериодической функции в ряд Фурье § 7. Приближение в среднем заданной функции с помощью тригонометрического многочлена § 8. Интеграл Дирихле § 9. Сходимость ряда Фурье в данной точке § 10. Некоторые достаточные условия сходимости ряда Фурье § 11. Практический гармонический анализ § 12. Ряд Фурье в комплексной форме § 13. Интеграл Фурье § 14. Интеграл Фурье в комплексной форме § 15. Ряд Фурье по ортогональной системе функций § 16. Понятие о линейном функциональном пространстве. Аналогия между разложением функций в ряд Фурье и разложением векторов Упражнения к главе XVII ГЛАВА XVIII. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ § 1. Основные типы уравнений математической физики § 2. Вывод уравнения колебаний струны. Формулировка краевой задачи. Вывод уравнений электрических колебаний в проводах § 3. Решение уравнения колебаний струны методом разделения переменных (методом Фурье) § 4.  Уравнение распространения тепла в стержне. Формулировка краевой задачи Уравнение распространения тепла в стержне. Формулировка краевой задачи§ 5. Распространение тепла в пространстве § 6. Решение первой краевой задачи для уравнения теплопроводности методом конечных разностей § 7. Распространение тепла в неограниченном стержне § 8. Задачи, приводящие к исследованию решений уравнения Лапласа. Формулировка краевых задач § 9. Уравнение Лапласа в цилиндрических координатах. Решение задачи Дирихле для кольца с постоянными значениями искомой функции на внутренней и внешней окружностях § 10. Решение задачи Дирихле для круга § 11. Решение задачи Дирихле методом конечных разностей Упражнения к главе XVIII ГЛАВА XIX. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ И НЕКОТОРЫЕ ЕГО ПРИЛОЖЕНИЯ § 1. Начальная функция и ее изображение § 2. Изображение функций … § 3. Изображение функции с измененным масштабом независимой переменной. Изображение функций sin at, cos at § 4. Свойство линейности изображения § 5. Теорема смещения § 6. Изображение функций … § 7.  Дифференцирование изображения Дифференцирование изображения§ 8. Изображение производных § 9. Таблица некоторых изображений § 10. Вспомогательное уравнение для данного дифференциального уравнения § 11. Теорема разложения § 12. Примеры решения дифференциальных уравнений и систем дифференциальных уравнений операционным методом § 13. Теорема свертывания § 14. Дифференциальные уравнения механических колебаний. Дифференциальные уравнения теории электрических цепей § 15. Решение дифференциального уравнения колебаний § 16. Исследование свободных колебаний § 17. Исследование механических и электрических колебаний в случае периодической внешней силы § 18. Решение уравнения колебаний в случае резонанса § 19. Теорема запаздывания § 20. Дельта-функция и ее изображение Упражнения к главе XIX ГЛАВА XX. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ § 1. Случайное событие. Относительная частота случайного события. Вероятность события. Предмет теории вероятностей § 2.  Классическое определение вероятности и непосредственный подсчет вероятностей Классическое определение вероятности и непосредственный подсчет вероятностей§ 3. Сложение вероятностей. Противоположные случайные события § 4. Умножение вероятностей независимых событий § 5. Зависимые события. Условная вероятность. Полная вероятность § 6. Вероятность гипотез. Формула Байеса § 7. Дискретная случайная величина. Закон распределения дискретной случайной величины § 8. Относительная частота и вероятность относительной частоты при повторных испытаниях § 9. Математическое ожидание дискретной случайной величины § 10. Дисперсия. Среднеквадратичное отклонение. Понятие о моментах § 11. Функции от случайных величин § 12. Непрерывная случайная величина. Плотность распределения непрерывной случайной величины. Вероятность попадания случайной величины в заданный интервал § 13. Функция распределения, или интегральный закон распределения. Закон равномерного распределения вероятностей § 14. Числовые характеристики непрерывной случайной величины § 15.  Нормальный закон распределения. Математическое ожидание нормального распределения Нормальный закон распределения. Математическое ожидание нормального распределения§ 16. Дисперсия и среднеквадратичное отклонение случайной величины, подчиненной нормальному закону распределения § 17. Вероятность попадания значения случайной величины в заданный интервал. Функция Лапласа. Интегральная функция распределения для нормального закона § 18. Вероятное (срединное) отклонение или срединная ошибка § 19. Выражение нормального закона распределения через срединное отклонение. Приведенная функция Лапласа § 20. Правило трех сигм. Шкала вероятностей распределения ошибок § 21. Среднеарифметическая ошибка § 22. Мера точности. Соотношение между характеристиками распределения ошибок § 23. Двумерная случайная величина § 24. Нормальный закон распределения на плоскости § 25. Вероятность попадания двумерной случайной величины в прямоугольник со сторонами, параллельными главным осям рассеивания, при нормальном законе распределения § 26. Вероятность попадания двумерной случайной величины в эллипс рассеивания § 27.  Задачи математической статистики. Статистический материал Задачи математической статистики. Статистический материал§ 28. Статистический ряд. Гистограмма § 29. Определение подходящего значения измеряемой величины § 30. Определение параметров закона распределения. Теорема Ляпунова. Теорема Лапласа Упражнения к главе XX ГЛАВА XXI. МАТРИЦЫ. МАТРИЧНАЯ ЗАПИСЬ СИСТЕМ И РЕШЕНИЙ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ § 1. Линейные преобразования. Матрица § 2. Общие определения, связанные с понятием матрицы § 3. Обратное преобразование § 4. Действия над матрицами. Сложение матриц § 5. Преобразование вектора в другой вектор с помощью матрицы § 6. Обратная матрица § 7. Нахождение матрицы, обратной данной § 8. Матричная запись системы линейных уравнений § 9. Решение системы линейных уравнений матричным методом § 10. Ортогональные отображения. Ортогональные матрицы § 11. Собственный вектор линейного преобразования § 12. Матрица линейного преобразования, при котором базисные векторы являются собственными векторами § 13.  Преобразование матрицы линейного преобразования при переходе от одного базиса к другому Преобразование матрицы линейного преобразования при переходе от одного базиса к другому§ 14. Квадратичные формы и их преобразования § 15. Ранг матрицы. Существование решений системы линейных уравнений § 16. Дифференцирование и интегрирование матриц § 17. Матричная запись системы дифференциальных уравнений и решений системы дифференциальных уравнений с постоянными коэффициентами § 18. Матричная запись линейного уравнения n-го порядка § 19. Решение систем линейных дифференциальных уравнений с переменными коэффициентами методом последовательных приближений с использованием матричной записи Упражнения к главе XXI ПРИЛОЖЕНИЯ |
4.9: Ожидаемое значение как интеграл
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 10165
- Кайл Зигрист
- Университет Алабамы в Хантсвилле via Random Services
\(\newcommand{\var}{\text{var}}\) \(\newcommand{\sd}{\text{sd}}\) \(\newcommand{\cov}{\text{cov}} \) \(\newcommand{\cor}{\text{cor}}\) \(\renewcommand{\P}{\mathbb{P}}\) \(\newcommand{\E}{\mathbb{E} }\) \(\newcommand{\R}{\mathbb{R}}\) \(\newcommand{\N}{\mathbb{N}}\) \(\newcommand{\bs}{\boldsymbol}\ )
Во вводном разделе мы определили математическое ожидание отдельно для дискретного, непрерывного и смешанного распределений, используя функции плотности.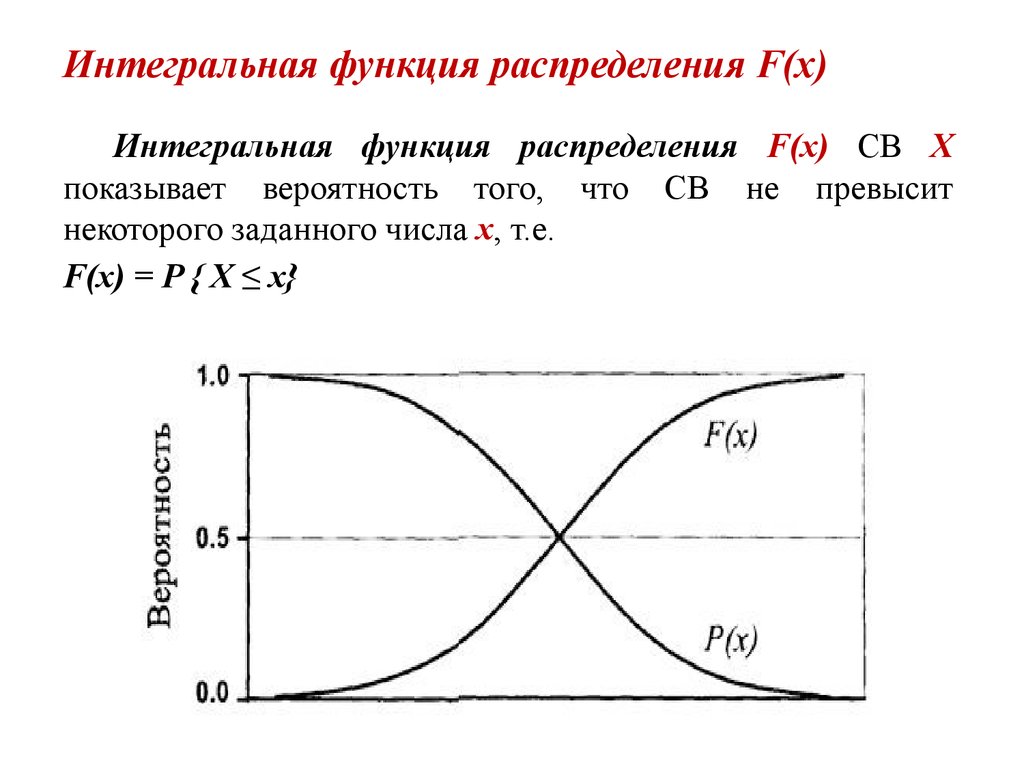 В разделе о дополнительных свойствах мы показали, как можно унифицировать эти определения, сначала определив ожидаемое значение для неотрицательных случайных величин в терминах функции распределения с правой стороны. Однако, безусловно, лучшее и наиболее элегантное определение ожидаемой ценности — это интеграл по отношению к лежащей в основе вероятностной мере. Это определение и обзор свойств ожидаемой ценности являются целями этого раздела. Никаких доказательств не требуется (будете рады узнать), так как все результаты следуют из общей теории интегрирования. Однако, чтобы понять экспозицию, вам необходимо просмотреть расширенные разделы по интегралу в отношении положительной меры и свойств интеграла. Если вы новичок в изучении вероятностей или не интересуетесь подробностями этого предмета с точки зрения теории меры, вы можете смело пропустить этот раздел.
В разделе о дополнительных свойствах мы показали, как можно унифицировать эти определения, сначала определив ожидаемое значение для неотрицательных случайных величин в терминах функции распределения с правой стороны. Однако, безусловно, лучшее и наиболее элегантное определение ожидаемой ценности — это интеграл по отношению к лежащей в основе вероятностной мере. Это определение и обзор свойств ожидаемой ценности являются целями этого раздела. Никаких доказательств не требуется (будете рады узнать), так как все результаты следуют из общей теории интегрирования. Однако, чтобы понять экспозицию, вам необходимо просмотреть расширенные разделы по интегралу в отношении положительной меры и свойств интеграла. Если вы новичок в изучении вероятностей или не интересуетесь подробностями этого предмета с точки зрения теории меры, вы можете смело пропустить этот раздел.
Определения
Как обычно, нашей отправной точкой является случайный эксперимент, смоделированный вероятностным пространством \( (\Omega, \mathscr{F}, \P) \). n \), мы предполагаем, что \( S \) измерима по Лебегу, и мы переводим \( \mathscr{S} \) в \( \sigma \)-алгебру измеримой по Лебегу подмножества \( S \). Как отмечалось выше, вот теоретико-мерное определение:
n \), мы предполагаем, что \( S \) измерима по Лебегу, и мы переводим \( \mathscr{S} \) в \( \sigma \)-алгебру измеримой по Лебегу подмножества \( S \). Как отмечалось выше, вот теоретико-мерное определение:
Если \( X \) является случайной величиной с действительным знаком в вероятностном пространстве, ожидаемое значение \( X \) определяется как интеграл от \( X \) по \( \P \), в предположении, что интеграл существует: \[ \E(X) = \int_\Omega X \, d\P \]
Рассмотрим, как поэтапно определяется интеграл, но теперь с использованием обозначений теории вероятностей.
Пусть \(S\) обозначает опорное множество \(X\), так что \(S\) является измеримым подмножеством \(\R\).
- Если \( S \) конечно, то \( \E(X) = \sum_{x \in S} x \, \P(X = x) \). 9- \) обозначают положительную и отрицательную части \( X \).
- Если \( A \in \mathscr{F} \), то \( \E(X; A) = \E\left(X \bs{1}_A \right) \), предполагая, что ожидаемое значение на право есть.
Таким образом, как и в случае с интегралами в целом, ожидаемое значение может существовать как число в \( \R \) (в этом случае \( X \) является интегрируемым ), может существовать как \( \infty \) или \ ( -\infty \) или может не существовать. Что касается части (а), случайная величина с конечным набором значений в \( \R \) является 9-\право) \lt\infty\).
Что касается части (а), случайная величина с конечным набором значений в \( \R \) является 9-\право) \lt\infty\).
Наша следующая цель — переформулировать основные теоремы и свойства интегралов, но в обозначении вероятности. Если не указано иное, предполагается, что все случайные величины имеют действительные значения.
Основные свойства
Линейные свойства
Возможно, наиболее важными и основными свойствами являются линейные свойства . Часть (a) является аддитивным свойством , а часть (b) является свойством масштабирования .
Предположим, что \( X \) и \( Y \) являются случайными величинами, ожидаемые значения которых существуют, и что \( c \in \R \). Затем
- \( \E(X + Y) = \E(X) + \E(Y) \), если правая часть не имеет вида \( \infty — \infty \).
- \( \Е(сХ) = с\Е(Х)\)
Таким образом, часть (a) выполняется, если хотя бы одно из математических ожиданий справа конечно, или оба равны \( \infty \), или оба равны \( -\infty \). Что исключено, так это два случая, когда одно ожидаемое значение равно \( \infty \), а другое — \(-\infty \), и это то, что подразумевается под неопределенной формой \( \infty — \infty \) .
Что исключено, так это два случая, когда одно ожидаемое значение равно \( \infty \), а другое — \(-\infty \), и это то, что подразумевается под неопределенной формой \( \infty — \infty \) .
Равенство и порядок
Следующий набор свойств касается равенства и порядка. Во-первых, ожидаемое значение случайной величины в нулевом наборе равно 0.
Если \( X \) — случайная величина, а \( A \) — событие с \( \P(A) = 0 \). Тогда \( \Е(Х; А) = 0 \).
Случайные величины, которые эквивалентны, имеют одинаковое ожидаемое значение
Если \( X \) — случайная величина, ожидаемое значение которой существует, и \( Y \) — случайная величина с \( \P(X = Y) = 1 \), то \( \E(X) = \E(Y) \).
Наш следующий результат — положительное свойство ожидаемого значения.
Предположим, что \( X \) является случайной величиной и \( \P(X \ge 0) = 1 \). Тогда
- \( \E(X) \ge 0 \)
- \( \E(X) = 0 \) тогда и только тогда, когда \( \P(X = 0) = 1 \).

Итак, если \( X \) неотрицательная случайная величина, то \( \E(X) \gt 0 \) тогда и только тогда, когда \( \P(X \gt 0) \gt 0 \). Следующим результатом является возрастающее свойство математического ожидания, возможно, самое важное свойство после линейности.
Предположим, что \( X, Y \) — случайные величины, ожидаемые значения которых существуют, и что \( \P(X \le Y) = 1 \). Тогда
- \( \E(X) \le \E(Y) \)
- За исключением случая, когда оба ожидаемых значения равны \( \infty \) или оба \( -\infty \), \( \E(X) = \E(Y) \) тогда и только тогда, когда \( \P( Х = Y) = 1 \).
Итак, если \( X \le Y \) с вероятностью 1, то, за исключением двух упомянутых случаев, \( \E(X) \lt \E(Y) \) тогда и только тогда, когда \( \P(X \lt Y) \gt 0 \). Следующий результат абсолютное значение неравенства .
Предположим, что \( X \) — случайная величина, ожидаемое значение которой существует. Затем
- \( \left| \E(X) \right| \le \E \left(\left| X \right| \right) \)
- Если \( \E(X) \) конечно, то равенство имеет место в (а) тогда и только тогда, когда \( \P(X \ge 0) = 1 \) или \( \P(X \le 0) = 1 \).

Замена переменных и функции плотности
Теорема о замене переменных
Предположим теперь, что \( X \) является общей случайной величиной в вероятностном пространстве \((\Omega, \mathscr F, \P)\), принимающие значения в измеримом пространстве \( (S, \mathscr{S}) \). Напомним, что распределение вероятностей \( X \) является вероятностной мерой \( P \) на \( (S, \mathscr{S}) \), заданной \( P(A) = \P(X \in A) \) для \( A \in \mathscr{S} \). Это частный случай новой положительной меры, индуцированной данной положительной мерой и измеримой функцией. Если \(g: S \to \R\) измерима, то \(g(X) \) является случайной величиной с действительным знаком. Следующий результат показывает, как вычислить ожидаемое значение \(g(X)\) как интеграл по отношению к распределению \(X\), и известен как замена переменных теорема.
Если \( g: S \to \R \) измеримо, то при условии, что ожидаемое значение существует, \[\E\left[g(X)\right] = \int_S g(x) \, dP( x) \]
Таким образом, используя исходное определение и теорему о замене переменных, а также указывая переменные явно для акцента, мы имеем \[ \E\left[g(X)\right] = \int_\Omega g\ left[X(\omega)\right] \, d\P(\omega) = \int_S g(x) \, dP(x)\]
Теорема Радона-Никодима
Предположим теперь \( \mu \ ) является положительной мерой на \((S,\mathscr{S})\), и что распределение \(X\) абсолютно непрерывно относительно \(\mu\). Напомним, что это означает, что из \( \mu(A) = 0 \) следует \( P(A) = \P(X \in A) = 0 \) для \( A \in \mathscr{S} \). К Теорема Радона-Никодима , названная в честь Иоганна Радона и Отто Никодима, \( X \) имеет функцию плотности вероятности \( f \) по отношению к \( \mu \). То есть \[ P(A) = \P(X \in A) = \int_A f \, d\mu, \quad A \in \mathscr{S} \] В этом случае мы можем записать ожидаемое значение от \( g(X) \) как интеграл по функции плотности вероятности.
Напомним, что это означает, что из \( \mu(A) = 0 \) следует \( P(A) = \P(X \in A) = 0 \) для \( A \in \mathscr{S} \). К Теорема Радона-Никодима , названная в честь Иоганна Радона и Отто Никодима, \( X \) имеет функцию плотности вероятности \( f \) по отношению к \( \mu \). То есть \[ P(A) = \P(X \in A) = \int_A f \, d\mu, \quad A \in \mathscr{S} \] В этом случае мы можем записать ожидаемое значение от \( g(X) \) как интеграл по функции плотности вероятности.
Если \( g: S \to \R \) измеримо, то при условии, что ожидаемое значение существует, \[ \E\left[g(X)\right] = \int_S g f \, d\mu \]
Опять же, задавая явно переменные для акцента, мы имеем следующую цепочку интегралов: \[ \E\left[g(X)\right] = \int_\Omega g\left[X(\omega)\right] \, d\P(\omega) = \int_S g(x) \, dP(x) = \int_S g(x) f(x) \, d\mu(x)\]
Имеются два критически важных Особые случаи.
Дискретные распределения
Предположим сначала, что \((S, \mathscr S, \#)\) является пространством с дискретной мерой , так что \( S \) счетно, \( \mathscr{S} = \ mathscr{P}(S) \) — это совокупность всех подмножеств \( S \), а \( \# \) — считающая мера на \( (S, \mathscr S) \). Таким образом, \(X\) имеет дискретное распределение на \(S\), и это распределение всегда абсолютно непрерывно относительно \(\#\). В частности, \( \#(A) = 0 \) тогда и только тогда, когда \( A = \emptyset \) и, конечно, \( \P(X \in \emptyset) = 0 \). Функция плотности вероятности \( f \) от \( X \) по отношению к \( \# \), как мы знаем, просто \( f(x) = \P(X = x) \) для \( х \в S\). Более того, интегралы по \( \# \) являются суммами, так что \[ \E\left[g(X)\right] = \sum_{x \in S} g(x) f(x) \] при условии что ожидаемое значение существует. Существование в этом случае означает, что либо сумма положительных членов конечна, либо сумма отрицательных членов конечна, так что сумма имеет смысл (и, в частности, не зависит от порядка добавления членов). Специализируясь далее, если \( X \) сам по себе является вещественным и \( g = 1 \), мы имеем \[ \E(X) = \sum_{x \in S} x f(x) \], который был нашим исходным определение ожидаемой стоимости в дискретном случае. 9n \) для некоторого \( n \in \N_+ \), \(\mathscr S\) есть \(\sigma\)-алгебра измеримых по Лебегу подмножеств \(S\), а \( \lambda_n \ ) является мерой Лебега на \( (S, \mathscr S) \).
Таким образом, \(X\) имеет дискретное распределение на \(S\), и это распределение всегда абсолютно непрерывно относительно \(\#\). В частности, \( \#(A) = 0 \) тогда и только тогда, когда \( A = \emptyset \) и, конечно, \( \P(X \in \emptyset) = 0 \). Функция плотности вероятности \( f \) от \( X \) по отношению к \( \# \), как мы знаем, просто \( f(x) = \P(X = x) \) для \( х \в S\). Более того, интегралы по \( \# \) являются суммами, так что \[ \E\left[g(X)\right] = \sum_{x \in S} g(x) f(x) \] при условии что ожидаемое значение существует. Существование в этом случае означает, что либо сумма положительных членов конечна, либо сумма отрицательных членов конечна, так что сумма имеет смысл (и, в частности, не зависит от порядка добавления членов). Специализируясь далее, если \( X \) сам по себе является вещественным и \( g = 1 \), мы имеем \[ \E(X) = \sum_{x \in S} x f(x) \], который был нашим исходным определение ожидаемой стоимости в дискретном случае. 9n \) для некоторого \( n \in \N_+ \), \(\mathscr S\) есть \(\sigma\)-алгебра измеримых по Лебегу подмножеств \(S\), а \( \lambda_n \ ) является мерой Лебега на \( (S, \mathscr S) \). Распределение \( X \) абсолютно непрерывно относительно \( \lambda_n \), если из \( \lambda_n(A) = 0 \) следует \( \P(X \in A) = 0 \) для \( A \in \mathscr{S} \). Если это так, то функция плотности вероятности \(f\) от \(X\) имеет свой обычный смысл. Таким образом, \[ \E\left[g(X)\right] = \int_S g(x) f(x) \, d\lambda_n(x)\] при условии, что ожидаемое значение существует. Когда \( g \) — типично хорошая функция, этот интеграл сводится к обычному \ ( n \)-мерному интегралу Римана исчисления. Специализируясь далее, если \( X \) само является вещественным и \(g = 1 \), то \[ \E(X) = \int_S x f(x) \, dx \], что было нашим исходным определением ожидаемого значения в непрерывном случае.
Распределение \( X \) абсолютно непрерывно относительно \( \lambda_n \), если из \( \lambda_n(A) = 0 \) следует \( \P(X \in A) = 0 \) для \( A \in \mathscr{S} \). Если это так, то функция плотности вероятности \(f\) от \(X\) имеет свой обычный смысл. Таким образом, \[ \E\left[g(X)\right] = \int_S g(x) f(x) \, d\lambda_n(x)\] при условии, что ожидаемое значение существует. Когда \( g \) — типично хорошая функция, этот интеграл сводится к обычному \ ( n \)-мерному интегралу Римана исчисления. Специализируясь далее, если \( X \) само является вещественным и \(g = 1 \), то \[ \E(X) = \int_S x f(x) \, dx \], что было нашим исходным определением ожидаемого значения в непрерывном случае.
Свойства обмена
В этом подразделе мы рассмотрим свойства, которые позволяют обменивать математическое ожидание и другие операции: пределы последовательностей, бесконечные суммы и интегралы. Мы снова предполагаем, что случайные величины действительны, если не указано иное.
Пределы
Наш первый набор результатов сходимости касается взаимозаменяемости ожидаемого значения и пределов. Начнем с версии математического ожидания леммы Фату , названной в честь Пьера Фату. Его полезность связана с тем, что на случайные величины не делается никаких предположений, кроме того, что они неотрицательны.
Начнем с версии математического ожидания леммы Фату , названной в честь Пьера Фату. Его полезность связана с тем, что на случайные величины не делается никаких предположений, кроме того, что они неотрицательны.
Предположим, что \( X_n \) является неотрицательной случайной величиной для \( n \in \N_+ \). Тогда \[ \E\left( \liminf_{n \to \infty} X_n \right) \le \liminf_{n \to \infty} \E(X_n) \]
Наш следующий набор результатов дает условия для обмен ожидаемой стоимостью и лимитами.
Предположим, что \( X_n \) является случайной величиной для каждого \( n \in \N_+ \). тогда \[ \E\left(\lim_{n \to \infty} X_n\right) = \lim_{n \to \infty} \E\left(X_n\right) \] в каждом из следующих случаев:
- \( X_n \) неотрицательно для каждого \( n \in \N_+ \) и \( X_n \) возрастает в \( n \).
- \( \E(X_n) \) существует для каждого \( n \in \N_+ \), \( \E(X_1) \gt -\infty \), и \( X_n \) возрастает в \( н\).
- \( \E(X_n) \) существует для каждого \( n \in \N_+ \), \( \E(X_1) \lt \infty \), и \( X_n \) убывает в \( n \).

- \( \lim_{n \to \infty} X_n \) существует, и \( \left|X_n\right| \le Y \) для \( n \in \N \), где \( Y \) неотрицательная случайная величина с \( \E(Y) \lt \infty \).
- \( \lim_{n \to \infty} X_n \) существует, и \( \left|X_n\right| \le c \) для \( n \in \N \), где \( c \) положительная постоянная.
Утверждения о случайных величинах в приведенной выше теореме (неотрицательность, возрастание, существование предела и т. д.) должны выполняться только с вероятностью 1. Часть (a) — это теорема о монотонной сходимости , один из наиболее важных результатов сходимости и в некотором смысле существенным для определения интеграла в первую очередь. Части (b) и (c) являются небольшими обобщениями теоремы о монотонной сходимости. В частях (a), (b) и (c) обратите внимание, что \( \lim_{n \to \infty} X_n \) существует (с вероятностью 1), хотя предел может быть \( \infty \) в части (а) и (б) и \( -\infty \) в части (в) (с положительной вероятностью). Часть (d) — 9Теорема 0058 о доминирующей сходимости , еще один из наиболее важных результатов сходимости. Иногда ее также называют теоремой о мажорируемой сходимости Лебега в честь Анри Лебега. Часть (e) является следствием теоремы об ограниченной сходимости и известна как теорема об ограниченной сходимости .
Часть (d) — 9Теорема 0058 о доминирующей сходимости , еще один из наиболее важных результатов сходимости. Иногда ее также называют теоремой о мажорируемой сходимости Лебега в честь Анри Лебега. Часть (e) является следствием теоремы об ограниченной сходимости и известна как теорема об ограниченной сходимости .
Бесконечный ряд
Наши следующие результаты включают замену ожидаемого значения и бесконечной суммы, поэтому эти результаты обобщают основное свойство аддитивности ожидаемого значения. 9\infty \E(X; A_n) \]
Конечно, предыдущая теорема применима, в частности, если \( X \) неотрицательно.
Интегралы
Предположим, что \( (T, \mathscr{T}, \mu) \) является \( \sigma \)-пространством с конечной мерой и что \( X_t \) является вещественной случайной величиной для каждого \( t \in T \). Таким образом, мы можем думать, что \( \left\{X_t: t \in T\right\} \) — это стохастический процесс, индексированный \( T \). Мы предполагаем, что \( (\omega, t) \mapsto X_t(\omega) \) измерима как функция из пространства произведений \( (\Omega \times T, \mathscr{F} \otimes \mathscr{T }) \) в \( \R \). Наш следующий результат включает замену ожидаемого значения и интеграла и является следствием теоремы Фубини, названной в честь Гвидо Фубини.
Наш следующий результат включает замену ожидаемого значения и интеграла и является следствием теоремы Фубини, названной в честь Гвидо Фубини.
В приведенных выше предположениях \[ \E\left[\int_T X_t \, d\mu(t)\right] = \int_T \E\left(X_t\right) \, d\mu(t) \] в каждом из следующих случаев:
- \( X_t \) неотрицательно для каждого \( t \in T \).
- \(\int_T \E\left(\left|X_t\right|\right) \, d\mu(t) \lt \infty \)
Теорема Фубини фактически утверждает, что два приведенных выше повторных интеграла равны объединенному интегралу \[ \int_{\Omega \times T} X_t(\omega) \, d(\P \otimes \mu)(\omega, t) \ ] где, конечно, \( \P \otimes \mu \) — мера произведения на \( (\Omega \times T, \mathscr{F} \otimes \mathscr{T}) \). Однако нас обычно интересует оценка повторного интеграла выше слева с точки зрения повторного интеграла справа. Часть (a) представляет собой версию ожидаемой стоимости 9{a+1}}, \quad x \in [1, \infty) \] где \( a \gt 0 \) — параметр формы . Распределение Парето изучается в более общем виде в главе, посвященной специальным распределениям.
Распределение Парето изучается в более общем виде в главе, посвященной специальным распределениям.
Предположим, что \( X \) имеет распределение Парето с параметром формы \( a \). Найти \( \E(X)\) в следующих случаях:
- \(0 \lt a \le 1\)
- \( а \gt 1 \)
- \(\infty\)
- \( \frac{a}{a — 1} \)
Откройте специальный симулятор распределения и выберите распределение Парето. Измените параметр формы и обратите внимание на форму функции плотности вероятности и положение среднего значения. Для различных значений параметра запустите эксперимент 1000 раз и сравните среднее значение выборки со средним значением распределения. 9\infty \P(X \ge k) \). Мы видели этот результат ранее в разделе о дополнительных свойствах ожидаемого значения, но теперь мы можем понять доказательство в терминах замены суммы и ожидаемого значения.
Эта страница под названием 4.9: Expected Value as an Integral распространяется под лицензией CC BY 2. 0 и была создана, изменена и/или курирована Кайлом Зигристом (Random Services) с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
0 и была создана, изменена и/или курирована Кайлом Зигристом (Random Services) с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Кайл Зигрист
- Лицензия
- СС BY
- Версия лицензии
- 2,0
- Теги
- источник@http://www.
 randomservices.org/random
randomservices.org/random
- источник@http://www.
11.3 Вероятность
Возможно, вы имеете хотя бы элементарное представление о дискретная вероятность , которая измеряет вероятность «события», когда существует конечное число возможностей. Например, если выпадает обычный шестигранный кубик. выпало, вероятность выпадения любого конкретного числа составляет $1/6$. В В общем, вероятность события — это количество способов, которыми событие может произойти, деленное на количество способов, которыми может произойти «что угодно».
В качестве более сложного примера рассмотрим случай двух шестигранный кубик. Кости физически различны, что означает, что бросок 2–5 отличается от броска 5–2; каждый в равной степени вероятное событие из 36 вариантов, при которых кости могут выпасть, поэтому у каждого есть вероятность $1/36$.
Самые интересные события не так просты. Более интересным является
вероятность выпадения определенной суммы из возможностей 2
до 12. Ясно, что неверно, что все суммы равновероятны:
единственный способ выбросить 2 — это выбросить 1–1, хотя есть много способов
выбросьте 7. Поскольку количество возможностей довольно мало, и
поскольку закономерность быстро становится очевидной, легко увидеть, что
вероятности различных сумм:
$$\выравнивание{
P(2) =P(12) &=1/36\cr
P(3) = P(11) &= 2/36\cr
P(4) =P(10) &= 3/36\cr
Р(5) =Р(9) &= 4/36\кр
P(6) =P(8) &= 5/36\cr
Р(7) &=6/36\кр
}$$
Здесь мы используем $P(n)$ для обозначения «вероятности выпадения $n$».
Поскольку мы правильно учли все возможности, сумма
все эти вероятности $36/36=1$; вероятность того, что сумма
одно из значений от 2 до 12 равно 1, потому что других вариантов нет.
Ясно, что неверно, что все суммы равновероятны:
единственный способ выбросить 2 — это выбросить 1–1, хотя есть много способов
выбросьте 7. Поскольку количество возможностей довольно мало, и
поскольку закономерность быстро становится очевидной, легко увидеть, что
вероятности различных сумм:
$$\выравнивание{
P(2) =P(12) &=1/36\cr
P(3) = P(11) &= 2/36\cr
P(4) =P(10) &= 3/36\cr
Р(5) =Р(9) &= 4/36\кр
P(6) =P(8) &= 5/36\cr
Р(7) &=6/36\кр
}$$
Здесь мы используем $P(n)$ для обозначения «вероятности выпадения $n$».
Поскольку мы правильно учли все возможности, сумма
все эти вероятности $36/36=1$; вероятность того, что сумма
одно из значений от 2 до 12 равно 1, потому что других вариантов нет.
Изучение вероятности связано с более сложными вопросами, такими как
хорошо; например, предположим, что два игральных кубика бросают много раз. На
средняя, какая сумма выйдет? На языке вероятности это
средний называется ожидаемое значение суммы. Сначала это немного вводит в заблуждение, так как не говорит
нам чего «ожидать» при броске двух игральных костей, но что мы ожидаем
будет долгосрочное среднее значение. {12} iP(i)$. В то время
фактическое среднее значение большого количества бросков не будет ровно 7,
среднее значение должно быть близко к 7, когда количество бросков
большой. Оборачивая это, если среднее значение не близко к 7, мы
следует подозревать, что кости не справедливы.
9nx_iP(x_i)$. Ожидаемое значение
также называется означает .
{12} iP(i)$. В то время
фактическое среднее значение большого количества бросков не будет ровно 7,
среднее значение должно быть близко к 7, когда количество бросков
большой. Оборачивая это, если среднее значение не близко к 7, мы
следует подозревать, что кости не справедливы.
9nx_iP(x_i)$. Ожидаемое значение
также называется означает .
Когда число возможных значений для $X$ конечно, мы говорим, что $X$
является дискретной случайной величиной. Во многих приложениях вероятности
число возможных значений случайной величины очень велико,
возможно, даже бесконечно. Чтобы иметь дело с бесконечным случаем, нам понадобится
другой подход, и, поскольку речь идет о сумме, она не должна
совершенно удивительно, что интеграция оказывается полезным
инструмент. Тогда оказывается, что даже при числе возможностей
большим, но конечным, часто легче сделать вид, что число
бесконечно. Предположим, например, что дротик брошен в дротик
доска. Поскольку мишень для дротиков состоит из конечного числа атомов,
в каком-то смысле существует только конечное число мест, куда может попасть дротик. {13/2} f(x)\,dx.$$
Конечно, мы могли бы также вычислять вероятности, которые не имеют смысла.
в контексте игральных костей, таких как вероятность того, что
$X$ находится в диапазоне от 4 до $5,8$.
$\квадрат$
92/2}\, дх =
{1\над А} А = 1,
$$
поэтому $g$ — это функция плотности вероятности. Оказывается, очень
полезным и называется стандартная нормальная плотность вероятности
функция или
более неформально кривая нормального распределения , дающая начало
к стандартному нормальному распределению . См. график на рис. 11.3.2.
колоколообразной кривой.
$\квадрат$
{13/2} f(x)\,dx.$$
Конечно, мы могли бы также вычислять вероятности, которые не имеют смысла.
в контексте игральных костей, таких как вероятность того, что
$X$ находится в диапазоне от 4 до $5,8$.
$\квадрат$
92/2}\, дх =
{1\над А} А = 1,
$$
поэтому $g$ — это функция плотности вероятности. Оказывается, очень
полезным и называется стандартная нормальная плотность вероятности
функция или
более неформально кривая нормального распределения , дающая начало
к стандартному нормальному распределению . См. график на рис. 11.3.2.
колоколообразной кривой.
$\квадрат$
Рисунок 11.3.2. Колокольная кривая.
Мы показали, что $A$ — некоторое конечное число, не вычисляя его; мы не может вычислить его с помощью методов, которые у нас есть. С помощью некоторых методами многомерного исчисления можно показать, что $\ds A=\sqrt{2\pi}$. 9\inftyxf(x)\,dx$, при условии, что интеграл сходится. $\квадрат$
Когда среднее значение существует, оно уникально, так как является результатом
явный расчет. \infty f(x)\,dx=1$. В центре масс
интерпретация, этот интеграл представляет собой полную массу балки, т.е.
всегда 1, когда $f$ является функцией плотности вероятности.
9Д=
{1\over\sqrt{2\pi}}.
$$
Их сумма равна 0, что является средним значением.
$\квадрат$
\infty f(x)\,dx=1$. В центре масс
интерпретация, этот интеграл представляет собой полную массу балки, т.е.
всегда 1, когда $f$ является функцией плотности вероятности.
9Д=
{1\over\sqrt{2\pi}}.
$$
Их сумма равна 0, что является средним значением.
$\квадрат$
Хотя среднее значение очень полезно, обычно недостаточно информации.
правильно оценить ситуацию. Например, предположим, что мы могли бы
изготовить 11-гранную матрицу с гранями, пронумерованными от 2 до 12, поэтому
что каждая грань с одинаковой вероятностью выпадет вниз, когда кость
свернутый. Значение броска — это значение на этой нижней грани. Роллинг
кубик дает тот же диапазон значений, что и бросок двух обычных игральных костей,
но теперь каждое значение встречается с вероятностью $1/11$. Ожидаемое значение
рулона
$$ {2\более 11} + {3\более 11} + \cdots + {12\более 11} = 7.$$
Среднее не различает эти два случая, хотя, конечно, они
достаточно разный.
92/2}\,дх=
0+{1\over\sqrt{2\pi}}\sqrt{2\pi}=1.
$$
Тогда стандартное отклонение равно $\ds \sqrt{1}=1$.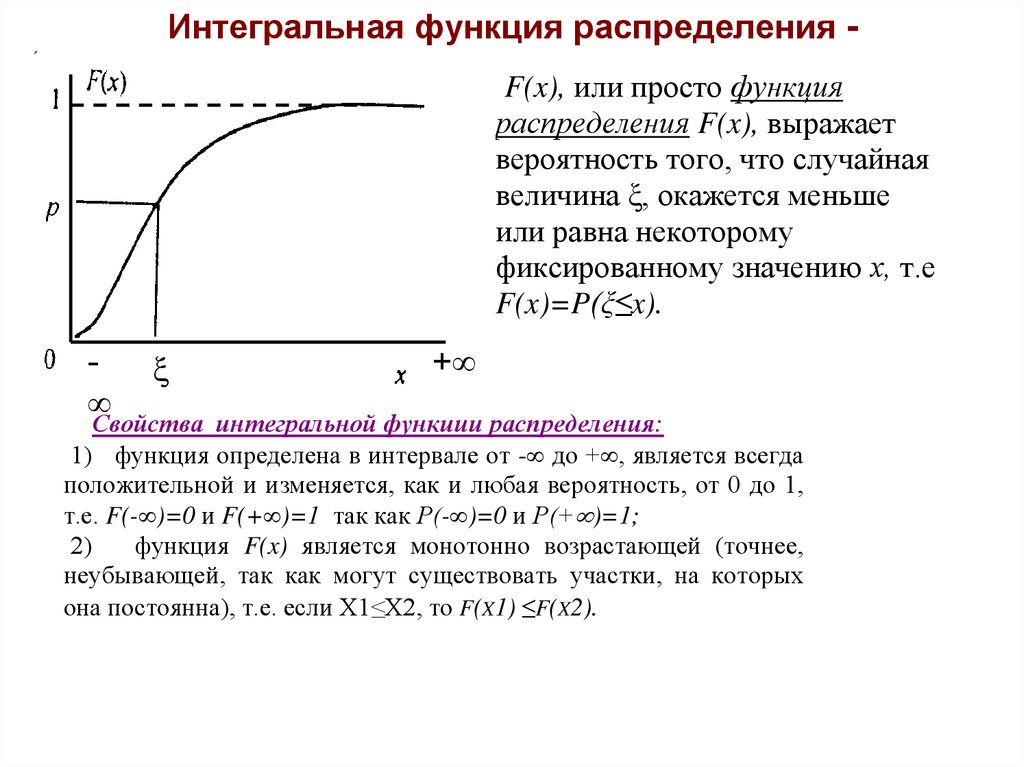 $\квадрат$
$\квадрат$
Пример 11.3.9
Вот простой пример, показывающий, как эти идеи могут быть реализованы.
полезный. Предположим, известно, что в долгосрочной перспективе 1 из каждых 100
микросхемы компьютерной памяти, выпускаемые определенным заводом-изготовителем,
неисправен, если производственный процесс работает правильно. Предполагать
Наугад выбирают 1000 чипов, 15 из них бракованные. Этот
больше, чем «ожидаемое» число (10), но настолько ли оно, что мы
следует подозревать, что что-то пошло не так в производстве
процесс? Нас интересует вероятность того, что различные числа
возникают бракованные чипы; распределение вероятностей дискретно: существует
может быть только целое число дефектных чипов. Но (при разумных
предположения) распределение очень близко к нормальному
дистрибутив, а именно этот:
$$
f(x)={1\over\sqrt{2\pi}\sqrt{1000(0,01)(0,9{10,5} f(x)\,dx \приблизительно 0,126$, что больше,
конечно, но все же мало, даже для «наиболее вероятного» исхода.
Самый полезный вопрос в большинстве случаев таков: насколько вероятно, что
количество дефектных чипов «далеко от» среднего? Например,
насколько вероятно или маловероятно, что количество дефектных чипов
отличается на 5 или более от ожидаемого значения 10? Это
вероятность того, что количество бракованных чипов меньше 5 или
больше 15, а именно
$$
\ int_ {- \ infty} ^ {5} f (x) \, dx + \ int_ {15} ^ {\ infty} f (x) \, dx \ приблизительно 0,11.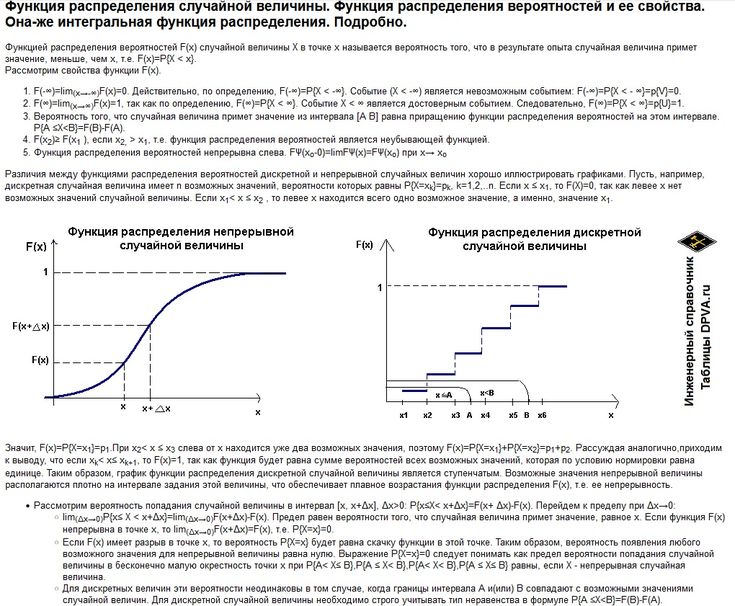





 randomservices.org/random
randomservices.org/random