Метод математической индукции примеры: Метод математической индукции: пример решения с объяснением

Содержание

11. Метод математической индукции

Во многих разделах математики приходится доказывать истинность утверждения, зависящего от , т. е. истинность высказывания P(N) Для «NÎN (для любого NÎN P(N) Верно).

Часто это удается доказать Методом математической индукции.

В основе этого метода лежит принцип математической индукции. Обычно он выбирается в качестве одной из аксиом арифметики и, следовательно, принимается без доказательства. Согласно принципу математической индукции предложение P(N) считается истинным для всех натуральных значений переменной, если выполнены два условия:

1. Предложение P(N) истинно для N = 1.

2. Из предложения, что P(N) истинно для N = K (K — Произвольное натуральное число) следует, что оно истинно для N = K + 1.

Под методом математической индукции понимают следующий способ доказательства

1. Проверяют истинность утверждения для N = 1 – база индукции.

2. Предполагают, что утверждение верно для N = K – Индуктивное предположение.

3. Доказывают, что тогда оно верно и для N = K + 1 индуктивный переход.

Иногда предложение P(N) оказывается верным не для всех натуральных N, а начиная с некоторого для N = N0. В этом случае в базе индукции проверяется истинность P(N) при N = N0.

Пример 1. Пусть . Доказать, что

1. База индукции: при N = 1 по определению S1 = 1 и по формуле получаем один результат. Утверждение верно.

2. Индуктивное предположение. Пусть N = k и .

3. Индуктивный переход. Пусть N = k + 1. Докажем, что .

Действительно, в силу индуктивного предположения

Преобразуем это выражение

Индуктивный переход доказан.

Замечание. Полезно записать, что дано (индуктивное предположение) и что нужно доказать!

Пример 2. Доказать

1. База индукции. При N = 1, утверждение, очевидно, верно.

2. Индуктивное предположение. Пусть N = K и

3. Индуктивный переход. Пусть N = K + 1. Докажем:

Действительно, возведем правую сторону в квадрат как сумму двух чисел:

Используя индуктивное предположение и формулу суммы арифметической прогрессии: , получим

Пример 3. Доказать неравенство

для .

1. Базой индукции в этом случае является проверка истинности утверждения для , т. е. необходимо проверить неравенство . Для этого достаточно возвести неравенство в квадрат: или 63 < 64 – неравенство верно.

2. Пусть неравенство верно для , т. е.

3. Пусть , докажем:

Используем предположение индукции

Зная как должна выглядеть правая сторона в доказываемом неравенстве выделим эту часть

Остается установить, что лишний множитель не превосходит единицы. Действительно,

Пример 4. Доказать, что при любом натуральном число оканчивается цифрой .

1. Наименьшее натуральное , с которого справедливо утверждение, равно . .

2. Пусть при число оканчивается на . Это означает, что это число можно записать в виде , где – какое-то натуральное число. Тогда .

3. Пусть . Докажем, что оканчивается на . Используя полученное представление, получим

Последнее число имеет ровно единиц.

Задачи.

1. Доказать, что при каждом верны равенства

1) .

2) .

3) .

4) .

5) .

6) .

7) .

8) .

9) .

10).

2. Доказать, что при любом .

1) кратно .

2) кратно .

3) кратно .

4) кратно .

5) кратно .

6) кратно 19.

3. Доказать справедливость следующих неравенств для всех натуральных .

1) .

2) .

3) .

4) .

5) .

4. Доказать, что при любом натуральном верно неравенство

1) .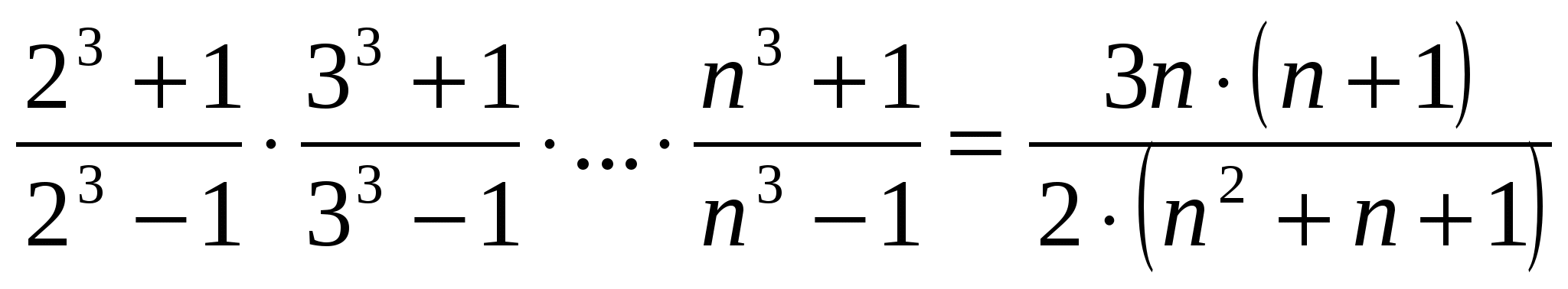 2) .

5. Доказать равенство для любого

1) ,

(в левой части содержится корней).

2) .

6. Пусть – произвольные неотрицательные числа, причем

Доказать, что .

7. Доказать неравенство Бернулли

8.Пусть – произвольные положительные числа, причем

. Доказать, что .

< Предыдущая		Следующая >

Алгебра Метод математической индукции

Материалы к уроку

Конспект урока

Пусть дана последовательность а энное, в которой первый член равен четырем, а с индексом эн плюс один равно сумме а энного, два эн и три.

Попытаемся задать ее формулой энного члена.

Вычислим первые несколько членов последовательности:

Первый член равен четырем; второй член равен сумме четырех, два умноженного на один и три и равен девяти; третий член равен сумме девяти, два умноженного на два и три и равен шестнадцати.

Значит, последовательность начинается так: четыре, девять, шестнадцать.

Естественно предположить, что эту последовательность можно задать формулой а энное равно квадрату суммы эн и один. Формула верна для любых эн, равных единице, двум, трем. Однако, как бы долго мы ни продолжали вычисления, они не дают оснований утверждать, что эта формула верна при любом натуральном эн. Поэтому мы воспользуемся специальным методом рассуждений. Предположим, что формула верна при эн равном ка, то есть а с индексом ка равно квадрату суммы ка и один, и докажем, что она верна и при эн равном ка плюс один, то есть, что а с индексом ка плюс один равно квадрату суммы ка и два.

По условию: а с индексом ка плюс один равно сумме а с индексом ка плюс два ка плюс три. Заменив а с индексом ка на квадрат суммы ка и один,…… Выполним преобразования и получим квадрат суммы ка и два.

Значит, а с индексом ка плюс один будет равно квадрату суммы ка и два. Это означает, что если формула верна для эн равного ка, то она верна и для ка плюс один.

Мы убедились, что формула верна и для эн равного один плюс один, то есть для эн равного двум. Из того, что формула верна для эн равного двум, следует, что формула верна и для эн равного два плюс один, то есть для трех. Из справедливости формулы для эн равного трем вытекает ее справедливость и для эн равного три плюс один, то есть для четырех и так далее.

Ясно, что, строя такую цепочку рассуждений, мы дойдем до любого натурального числа. Значит, формула а энное равно квадрат суммы эн и один верна при любом натуральном эн, то есть последовательность можно задать этой формулой.

Примененный метод доказательства называется методом математической индукции. Он основан на следующем положении, которое известно под названием «принцип математической индукции»:

Утверждение о том, что некоторый факт имеет место при любом натуральном эн, верно, если выполняются два условия. Первое условие: утверждение верно при эн равном единице. Второе условие: из справедливости утверждения для эн равного ка следует его справедливость для эн равного ка плюс один.

Доказательство утверждения методом математической индукции состоит из двух частей. Сначала проверяют его справедливость при эн равном единице. Затем, предположив, что утверждение верно при эн равном ка, доказывают, что оно верно и при эн равном ка плюс один.

Рассмотрим примеры применения метода математической индукции.

Первый пример. При решении некоторых задач из геометрии и механики, Архимедом была выведена следующая формула… Докажем ее справедливость.

При эн равном единице формула верна……

Допустим, что эта формула верна и для эн равного ка…

Докажем, что отсюда следует ее справедливость и для эн равного ка плюс один…

Имеем следующее преобразование…………

Разложив на множители квадратный трехчлен два ка квадрат плюс семь ка плюс шесть, получим произведение линейных множителей, первый из которых равен сумме ка и два, второй равен сумме два ка и три.

Отсюда мы получили равенство…

Таким образом, мы доказали справедливость формулы Архимеда.

Пример второй. Докажем, что при любом натуральном эн сумма пятнадцати в степени эн и шести кратна семи.

При эн равном единице, утверждение верно, так как сумма будет равна двадцати одному.

Допустим, что утверждение верно и при эн равном ка, то есть сумма пятнадцати в степени ка и шести кратна семи, и докажем, что из этого следует его справедливость и для эн равного ка плюс один, то есть сумма пятнадцати в степени ка плюс один и шести также кратна семи.

Имеем следующее преобразование………………………

В полученной сумме каждое слагаемое кратно семи, значит, и сумма пятнадцати в степени эн и шести при любом натуральном ка кратна семи. В силу принципа математической индукции утверждение доказано.

Остались вопросы по теме? Наши репетиторы готовы помочь!

Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитораОставить заявку на подбор

Математическая индукция — Темы предварительного исчисления

Темы в

ПРЕДВАРИТЕЛЬНАЯ РАБОТА

Содержание | Дом

Принцип математической индукции

НАТУРАЛЬНЫЕ ЧИСЛА счетные числа: 1, 2, 3, 4 и т.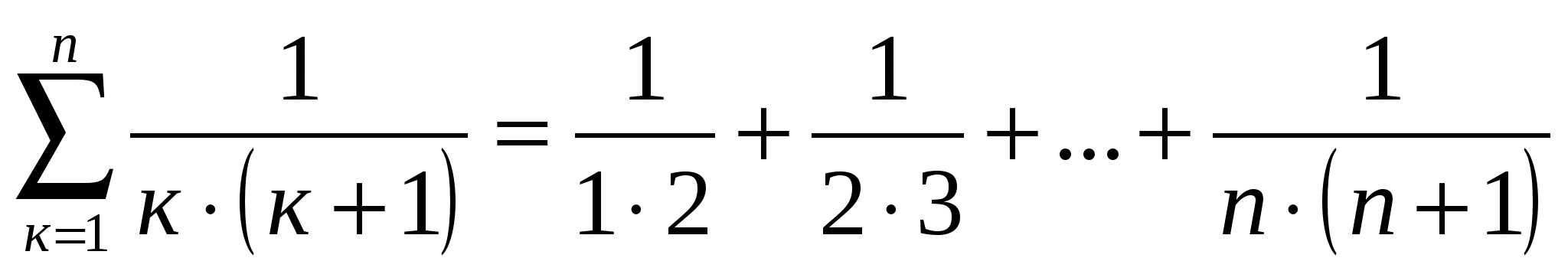 д. Математическая индукция — это метод доказательства утверждения (теоремы или формулы), которое утверждается о каждое натуральное число.

Под «каждым» или «всем» натуральными числами мы подразумеваем любое, которое назовем.

Например,

1 + 2 + 3 + . . . + н = ½ н ( н + 1).

Это утверждает, что сумма последовательных чисел от 1 до n задается формулой справа. Мы хотим доказать, что это будет верно для n = 1, n = 2, n = 3 и так далее. Теперь мы можем проверить формулу для любого

заданного числа , скажем, n = 3:

1 + 2 + 3 = ½ · 3 · 4 = 6

— это правда. Это верно и для n = 4:

1 + 2 + 3 + 4 = ½ · 4 · 5 = 10.

Но как нам доказать это правило для каждого значения n ?

Метод доказательства следующий. Мы показываем, что , если утверждение — правило — истинно для любого конкретного числа k (например, 104), то оно также будет истинным для следующего за ним числа k + 1 (например, 105). Затем мы показываем, что утверждение будет верным для 1. Отсюда следует, что утверждение будет верным для 2. Следовательно, оно будет верным для 3. Оно будет верным для любого натурального числа, которое мы назовем.

Это называется принципом математической индукции.

Если

	1)	, когда утверждение истинно для натурального числа n = k , , то оно также будет истинным для его преемника, н = к + 1;

и

	2)	утверждение верно для n = 1;

то утверждение будет верным для любого натурального числа n .

Чтобы доказать утверждение по индукции, мы должны доказать части 1) и 2) выше.

Гипотеза шага 1) — » Утверждение верно для n = k » — называется предположением индукции или гипотезой индукции. это то, что мы предполагают , когда мы доказываем теорему по индукции.

Пример 1. Докажите, что сумма первых n натуральных чисел задается следующей формулой:

1 + 2 + 3 + . . . + п

n ( n + 1)
2

Доказательство . Мы выполним шаги 1) и 2) выше. Во-первых, предположим , что формула верна для n = k ; то есть будем считать:

1 + 2 + 3 + . . . + к

к ( к + 1)
2

. (1)

Это предположение индукции. Предполагая это, мы должны доказать, что формула верна для ее преемника, n = k + 1.

То есть мы должны показать:

1 + 2 + 3 + . . . + ( к + 1)

( к + 1)( к + 2)
2

. (2)

Для этого мы просто добавим следующий член ( k + 1) в обе стороны предположения индукции, строка (1):

Это строка (2), которую мы хотели показать в первую очередь.

Далее мы должны показать, что формула верна для n = 1. Имеем:

1 = ½ · 1 · 2

— это правда. Теперь мы выполнили оба условия принципа математической индукции. Таким образом, формула верна для любого натурального числа.

(В приложении к арифметике мы прямо устанавливаем эту формулу.)

Пример 2. Докажите, что это правило показателей верно для любого натурального числа n :

( аб ) ^н = а

н б ^н16 .

Доказательство . Опять же, мы начинаем с , предполагая, что верно для 9.0015 n = k ; то есть принимаем:

( аб ) ^к = а ^к б ^к . . . . . . . . (3)

При таком предположении мы должны показать, что правило верно для его преемника, n = ( k + 1). Мы должны показать:

( аб ) ^{к + 1} = a ^{к + 1} б ^{к + 1} . . . . . . . (4)

(При использовании математической индукции учащийся всегда должен писать именно то, что должно быть показано.)

Теперь, учитывая предположение, строка (3), как мы можем получить из нее строку (4)?

Просто умножив обе стороны линии (3) на

ab :

( аб ) ^к аб	=	а ^к б ^к аб

	=	а ^к а б ^к б

так как порядок множителей не имеет значения,

	=	а ^{к + 1} б ^{к + 1} .

Это линия (4), которую мы хотели показать.

Итак, мы показали, что если теорема верна для любого конкретного натурального числа k , то она также верна для следующего за ним числа k + 1,

Далее мы должны показать, что правило верно для n = 1; то есть тот

( аб ) ¹ = а ¹ б ¹ .

Но ( аб ) ¹ = аб ; и a ¹ b ¹ = ab .

Таким образом, это правило верно для любого натурального числа n .

Пример 3. Сумма последовательных кубов. Докажите этот замечательный факт арифметики:

1 ³ + 2 ³ + 3 ³ + . . . + n ³ = (1 + 2 + 3 + . . . + n ) ² .

«Сумма n последовательных кубов равна квадрату
суммы первых n чисел. »

Другими словами, согласно Примеру 1:

1 ³ + 2 ³ + 3 ³ + . . . + п ³

n ²( n + 1)²
4

Доказательство . Для удобства сумму до n будем обозначать через S ( n ). Предположим, что формула верна для n = k ; то есть тот

С ( к )	=	к ²( к + 1)² 4	(1)

Теперь мы должны показать, что формула верна и для н = к + 1; что

S ( к + 1)	=	( к + 1)²( к + 2)² 4	(2)

для этого, добавьте следующий куб к с ( K ), линия (1):

9 S 0
S6 (
S 0
S 0
S 0.	=	S ( к ) + ( к + 1) ³

	=	к ²( к + 1)² 4	+ ( к + 1) ³

	=	к ²( к + 1)² + 4( к + 1)³ 4

	=	( k + 1)²[ k ² + 4( k + 1)] 4

— принимая ( k + 1) ² как общий множитель,
9007 90
=	( к + 1)²( к ² + 4 к + 4) 4

	=	( к + 1)²( к + 2)² 4

Это линия (2), которую мы хотели показать.

Наконец, мы должны показать, что формула верна для n = 1.

1 ³	=	1² · 2² 4

1	=	1 · 4 4

— это правда. Таким образом, формула верна для любого натурального числа.

В Приложении к Арифметике мы прямо показываем, что это верно.

Задача 1. В соответствии с принципом математической индукции доказать утверждение, которое утверждается о каждом натуральном числе 9.0015 n , нужно доказать две вещи.

а) Что первое?

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).

Если утверждение верно для n = k , то оно будет верно и для его преемника, k + 1.

б) Что такое второе?

Утверждение верно для н = 1.

c) Часть a) содержит предположение индукции. Что это такое?

Утверждение верно для n = k .

Задача 2. Пусть S ( n ) = 2 n − 1. Вычислить

а) S ( к ) = 2 к — 1

б) S ( к + 1) = 2( к + 1) − 1 = 2 k + 2 − 1 = 2 k + 1

Задача 3. Сумма первых n нечетных чисел равна n-му квадрату .

1 + 3 + 5 + 7 + . . . + (2 н — 1) = н ² .

а) Чтобы доказать, что с помощью математической индукции, какой будет индукция
а) предположение?

Утверждение верно для n = к :

1 + 3 + 5 + 7 + . . . + (2 к — 1) = к ² .

б) На основании этого предположения, что мы должны показать?

Утверждение верно для его преемника, k + 1:

1 + 3 + 5 + 7 + . . . + (2 к — 1) + 2 к + 1 = ( к + 1)².

c) Покажи это.

При добавлении 2 k + 1 к обеим частям предположения индукции:

1 + 3 + 5 + 7 + . . . + (2 к — 1) + 2 к + 1	=	к ² + 2 к + 1

	=	( к + 1) ²

г) Чтобы завершить доказательство с помощью математической индукции, что мы должны показать?

Утверждение верно для n = 1.

д) Покажите это.

1 = 1 ²

Задача 4. Докажите методом математической индукции:

Если мы обозначим эту сумму как S ( n ), то предположим, что формула верна для n = k ; то есть предположим

С ( к )

к
2 к + 1

Теперь покажите, что формула верна для n = k + 1; то есть показать:

С ( к + 1)

к + 1
2 к + 3

Начало:

С ( к + 1)	=	S ( k ) + следующих членов, чей знаменатель является произведением следующих нечетных чисел.

	=

	=

	=

	=

	=

Далее,

Формула верна для n = 1:

Следовательно, это верно для всех натуральных чисел.

Содержание | Дом

Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.

Вопросы или комментарии?

Электронная почта: [email protected]

Математическая индукция

В этом разделе мы рассматриваем утверждения, которые включают некоторую форму «… истинно для каждого целого числа». Например,

Это последовательности утверждений, и мы будем использовать рекурсивную технику, чтобы доказать их, потому что мы не можем доказать истинность такого утверждения, показывая, что оно истинно для каждого буквального целого числа (их бесконечно много, так что это невозможный). Вместо этого принцип математической индукции говорит нам, что мы может доказать, что утверждения, подобные этим, верны, если мы делаем это правильно. Этот раздел поможет нам узнать, как это сделать.

Подраздел

Определение 4.3.1. Математическая индукция.

Чтобы доказать, что утверждение \(P(n)\) истинно для всех целых чисел \(n\ge 0\text{,}\), мы используем принцип математической индукции . Процесс состоит из двух основных шагов:

Базовый шаг: Докажите, что \(P(0)\) верно.
Индуктивный шаг: предположим, что \(P(k)\) истинно для некоторого значения \(k \ge 0\), и покажем, что \(P(k+1)\) истинно.

Видео/Ответ.

Обычная аналогия для индукции — представить бесконечную лестницу. Сначала вы ставите ногу на нижнюю ступеньку. Если вы сможете подняться с \(k\)-й ступени на \(k+1\)-ю ступеньку, вы сможете подниматься вечно.

Пример 4.3.2.

Модель индукции всегда будет иметь следующую структуру:

Доказательство.

Доказательство математической индукцией.

Базовый шаг. [здесь вы доказываете, что \(P(0)\) верно]
Индуктивный шаг. Предположим, что \(P(k)\) истинно для некоторого \(k\ge 0\) [явно скажите, что это за утверждение. Это называется индуктивной гипотезой ]. Мы покажем, что \(P(k+1)\) верно.
[здесь вы фактически доказываете, что \(P(k+1)\) верно. Вы должны использовать индуктивную гипотезу. Если вы этого не сделали, вы где-то ошиблись]

Пример 4.3.3.

Докажите, что \(\ds 1 + 2 + 3 + \dots + n = \frac{n(n+1)}{2}\text{.}\)

92\) для \(n > 4\)

Видео/Ответ.

Пример 4.3.7.

Что не так со следующим «доказательством» того, что все лошади одного цвета?

Доказательство по индукции:

Базовый шаг: утверждение \(P(1)\) — это утверждение «одна лошадь того же цвета, что и она сама». Это совершенно верно.
Шаг индукции: предположим, что \(P(k)\) верно для некоторого целого числа \(k\text{.}\) То есть любая группа из \(k\) лошадей имеет одинаковую окраску.
Рассмотрим группу из \(k+1\) лошадей. Давайте выстроим их в ряд. Если мы посмотрим на первые \(k\) лошадей, наша индукционная гипотеза говорит нам, что они одного цвета. Точно так же, если мы посмотрим на последние \(k\) лошадей, они тоже будут одного цвета. Это показывает, что все \(k+1\) лошадей одного цвета.

Таким образом, по математической индукции все лошади одного цвета.

Подраздел

Следующее определение говорит «сильная индукция», и я следую соглашению почти всех книг по дискретной математике, определяя это собственным именем. Эти две концепции на самом деле не очень отличаются, как мы увидим ниже.

Определение 4.3.8. Сильная индукция.

Принцип сильной математической индукции подобен так называемой слабой индукции, за исключением того, что вместо доказательства \(P(k) \to P(k+1)\text{,}\) мы предполагаем, что \(P( m)\) верно для всех значений \(m\), таких что \(0 \le m \le k\text{,}\), и мы показываем, что следующее утверждение \(P(k+1)\ текст{,}\) верно.

Пример 4.3.9.

Пусть \(P(n)\) будет утверждением, что «почтовые расходы в \(n\) центов могут быть сформированы с использованием только 4-х и 7-центовых марок». Докажите, что \(P(n)\) верно для \(n\ge 18\text{.}\)

Видео/Ответ.

Вот другой подход к проблеме. Если мы можем составить \(18, 19, 20, \точек k\) почтовых марок, используя марки в четыре и семь центов, то для почтовых расходов \(k+1\) центов мы просто притворимся, что вы просили на четыре цента меньше. ! \(k+1 -4 = k-3\text{.}\) Гарантируется, что мы сможем оплатить почтовые расходы по предположению индукции. Представьте, что вы ставите эти марки на пакет. Тогда все, что нам нужно, это приклеить одну четырехцентовую марку, и все готово!

Раствор.

Вот один из способов решения проблемы. Начните с демонстрации того, что мы можем сделать основу, посмотрим, сможем ли мы найти закономерность, а затем проведем формальное доказательство:

\(\displaystyle 18 = 7\cdot2 + 4\cdot1\)
\(\displaystyle 19 = 7\cdot1 + 4\cdot3\)
\(\displaystyle 20 = 7\cdot0 + 4\cdot5\)
\(\displaystyle 21 = 7\cdot3 + 4\cdot0\)
\(\displaystyle 22 = 7\cdot2 + 4\cdot2\)
\(\displaystyle 23 = 7\cdot1 + 4\cdot4\)
\(\displaystyle 24 = 7\cdot0 + 4\cdot6\)
\(\displaystyle 25 = 7\cdot3 + 4\cdot1\)
\(\displaystyle 26 = 7\cdot2 + 4\cdot3\)
\(\displaystyle 27 = 7\cdot1 + 4\cdot5\)
\(\displaystyle 28 = 7\cdot0 + 4\cdot7\)

Вы заметили закономерность? Потратьте пару минут, чтобы подумать об этом, затем давайте сделаем доказательство.

Доказательство.

Базовый шаг: Мы можем сформировать 18-центовую почтовую марку, используя две 7-центовые и одну 4-центовую марку.

Индуктивный шаг: Предположим, что можно сформировать почтовые расходы для всех значений от 18 центов до \(k\) центов. Теперь нас просят сформировать \(k+1\) центов. мы знаем, что можем образовать \(k\) центов, поэтому без ограничения общности предположим, что для этого требуется \(s\) марок по 7 центов и \(t\) марок по 4 цента. То есть:

\begin{уравнение*} к = 7с + 4т \end{уравнение*}

Теперь, если \(s \ge 1\text{,}\), то мы можем сделать следующее, прибавив единицу к обеим сторонам двумя разными способами:

\begin{уравнение*} к+1 = 7с + 4т — 7 + 8 \end{уравнение*}

Объединяя подобные термины, мы имеем

\begin{уравнение*} k+1 = 7(s-1) + 4(t+2) \end{уравнение*}

Если, с другой стороны, \(s=0\text{,}\), то нам нужно добавить единицу другим способом:

\begin{уравнение*} к+1 = 7с + 4т + 21 — 20 \end{уравнение*}

или, объединяя подобные термины:

\begin{уравнение*} k+1 = 7(s+3) + 4(t-5) \end{уравнение*}

Таким образом, по индуктивной гипотезе, если мы можем сформировать \(k\) центов, я могу сформировать \(k+1\) центов почтовых расходов.

Таким образом, по математической индукции все почтовые расходы, превышающие или равные 18, могут быть сформированы с использованием марок номиналом 4 и 7 центов.

Пример 4.3.10.

Докажите, что каждое натуральное число имеет двоичное представление, т. е. является либо степенью двойки, либо суммой различных степеней двойки.

Видео/Ответ.

Мы разделяем «слабую» и «сильную» индукцию, но на самом деле это одно и то же. Просто когда удобно показать \(P(k) \to P(k+1)\text{,}\), мы пишем меньше слов для нашей индуктивной гипотезы. Потому что, если нам не нужно использовать тот факт, что \(P(m)\) истинно для всех \(1 \le m \le k\text{,}\), то мы просто опускаем это. Математики ленивы.

Подраздел Компьютерный уголок

При разработке алгоритмов вы будете использовать математическую индукцию. Возьмем пример сортировки набора данных. Чтобы доказать правильность алгоритма, вам нужно:

Существует правильный базовый вариант. В нашем примере — может сортировать набор из одного элемента)
Предположим, что алгоритм работает для \(n\) объектов. Он может сортировать набор из \(n\) объектов
Покажите, что если у вас есть больший набор из еще одного объекта, \(n+1\) объектов, ваш алгоритм правильно сортирует эти новые элементы с предыдущими \(n\) элементами. Он может сортировать набор с \(n+1\) объектами. Следовательно, алгоритм правильный. 92 = \frac{n(n+1)(2n+1)}{6}\) верно для всех целых чисел \(n\ge 1\text{.}\)
5.
Что не так со следующим «доказательством» «факта» того, что \(n+3 = n+7\) для всех значений \(n\) (кроме, конечно, того, что то, что оно пытается доказать, ложно? )?
Доказательство.
Пусть \(P(n)\) будет утверждением, что \(n + 3 = n + 7\text{.}\) Мы докажем, что \(P(n)\) верно для всех \(n \ in \N\text{.}\) Предположим для индукции, что \(P(k)\) истинно. То есть \(k+3 = k+7\text{.}\) Мы должны показать, что \(P(k+1)\) верно. Теперь, поскольку \(k + 3 = k + 7\text{,}\), добавьте 1 к обеим сторонам. Это дает \(k + 3 + 1 = k + 7 + 1\text{.}\) Перегруппировка \((k+1) + 3 = (k+1) + 7\text{.}\) Но это просто \(P(k+1)\text{.}\) Таким образом, по принципу математической индукции \(P(n)\) верно для всех \(n \in \N\text{.}\)
Раствор.
Единственная проблема в том, что мы так и не установили базовый вариант. Конечно, когда \(n = 0\text{,}\) \(0+3 \ne 0+7\text{.}\)
6.
Доказательство предыдущей задачи не работает. Но если мы изменим «факт», мы сможем получить рабочее доказательство. Докажите, что \(n + 3 \lt n + 7\) для всех значений \(n \in \N\text{.}\). Вы можете сделать это доказательство с помощью алгебры (без индукции), но цель этого упражнения состоит в том, чтобы выписать корректное индукционное доказательство.
Решение.
Доказательство.
Пусть \(P(n)\) будет утверждением, что \(n + 3 \lt n + 7\text{. }\) Мы докажем, что \(P(n)\) истинно для всех \(n \in \N\text{.}\) Во-первых, обратите внимание, что выполняется базовый случай: \(0+3 \lt 0+7\text{.}\) Теперь предположим для индукции, что \(P(k)\) правда. То есть \(k+3 \lt k+7\text{.}\) Мы должны показать, что \(P(k+1)\) верно. Теперь, поскольку \(k + 3 \lt k + 7\text{,}\), добавьте 1 к обеим сторонам. Это дает \(k + 3 + 1 \lt k + 7 + 1\text{.}\) Перегруппировка \((k+1) + 3 \lt (k+1) + 7\text{.}\) Но это просто \(P(k+1)\text{.}\) Таким образом, по принципу математической индукции \(P(n)\) верно для всех \(n \in \N\text{.}\ )
7.
Найдите ошибку в следующем «доказательстве» того «факта», что \(n \lt 100\) для каждого \(n \in \N\text{.}\)
Доказательство.
Пусть \(P(n)\) будет утверждением \(n \lt 100\text{.}\) Мы докажем, что \(P(n)\) верно для всех \(n \in \N\text {.}\) Сначала мы устанавливаем базовый случай: когда \(n = 0\text{,}\) \(P(n)\) верно, потому что \(0 \lt 100\text{.}\) Теперь для индуктивного шага предположим, что \(P(k)\) верно. 2 + n\) нечетно? 92 + n\) четно для всех натуральных чисел
.
10.
Используйте индукцию, чтобы доказать, что если \(n\) человек пожимают друг другу руки, то общее количество рукопожатий равно \(\frac{n(n-1)}{2}\text{.}\)
Решение.
Доказательство.
Пусть \(P(n)\) будет утверждением «когда \(n\) человек пожимают друг другу руки, всего происходит \(\frac{n(n-1)}{2}\) рукопожатий ».
Базовый случай: когда \(n=2\text{,}\) будет одно рукопожатие и \(\frac{2(2-1)}{2} = 1\text{.}\) Таким образом \ (P(2)\) верно.
Индуктивный случай: предположим, что \(P(k)\) верно для произвольного \(k\ge 2\) (что количество рукопожатий среди \(k\) людей равно \(\frac{k(k-1) }{2}\text{.}\) Что произойдет, если появится \(k+1\)-й человек? Сколько будет новых рукопожатий? Новый человек должен пожать руку всем присутствующим, то есть \( k\) новых рукопожатий. Таким образом, общее количество теперь равно \(\frac{k(k-1)}{2} + k = \frac{(k+1)k}{2}\text{,}\) как нужно
Следовательно, по принципу математической индукции \(P(n)\) истинно для всех \(n \ge 2\text{. }\) 9k) + \log(a) = k\log(a) + \log(a) \end{уравнение*}
с последним равенством в силу индуктивного предположения. Но это упрощается до \((k+1) \log(a)\text{,}\), устанавливая \(P(k+1)\text{.}\). Поэтому по принципу математической индукции \(P (n)\) верно для всех \(n \ge 2\text{.}\)
12.
Пусть \(f_1, f_2,\ldots, f_n\) — дифференцируемые функции. Докажите по индукции, что
\begin{уравнение*} (f_1 + f_2 + \cdots + f_n)’ = f_1′ + f_2′ + \cdots + f_n’ \end{уравнение*}
Вы можете принять \((f+g)’ = f’ + g’\) для любых дифференцируемых функций \(f\) и \(g\text{.}\) (на самом деле вам не нужно знать исчисление уметь это делать).
Подсказка.
Вы можете принять базовый вариант. Для индуктивного случая сгруппируйте все функции, кроме последней, как одну сумму функций, затем примените обычное правило суммы производных, а затем индуктивную гипотезу.
13.
Напомним, что \(F_n\) – это \(n\)-е число Фибоначчи, определенное в примере 4. 1.5.
Докажите методом математической индукции, что \(F_0 + F_1 + F_2 + \cdots + F_{n} = F_{n+2} — 1\text{.}\)
Решение.
Доказательство.
Пусть \(P(n)\) будет утверждением «\(F_0 + F_1 + F_2 + \cdots + F_{n} = F_{n+2} — 1\text{.}\)»
Базовый шаг: если \(n = 0\), то \(F_0 = 0\), тогда как \(F_{n+2} — 1 = 1 — 1 = 0\), значит, базовый шаг верен.
Индуктивный шаг: Предположим, что \(P(k)\) верно для некоторого целого числа \(k \ge 0\text{.}\) То есть \(F_0 + F_1 + F_2 + \cdots + F_{k} = F_{k+2} — 1\text{.}\) Теперь рассмотрим
\начать{выровнять*} \amp ~ F_0 + F_1 + F_2 + \dots F_k + F_{k+1}\amp\\ \amp= ( F_{k+2} — 1 ) + F_{k+1} \amp \text{по предположению индукции}\\ \amp= F_{k+2} + F_{k+1} — 1 \amp\\ \amp= F_{k+3} — 1 \amp \text{по рекурсивному определению} \конец{выравнивание*}
, таким образом, \(P(k+1)\) верно.
Следовательно, по математической индукции \(F_0 + F_1 + F_2 + \cdots + F_{n} = F_{n+2} — 1\) для всех натуральных чисел.
14.
Докажите, что \(F_0 + F_2 + F_4 + \cdots + F_{2n} = F_{2n+1} — 1\), где \(F_n\) — \(n\)-е число Фибоначчи.
Решение.
Доказательство.
Пусть \(P(n)\) будет утверждением \(F_0 + F_2 + F_4 + \cdots + F_{2n} = F_{2n+1} — 1\text{.}\) Мы покажем, что \( P(n)\) верно для всех \(n \ge 0\text{.}\) Во-первых, базовый случай прост, потому что \(F_0 = 0\) и \(F_1 = 1\), поэтому \(F_0 = F_1 — 1\text{.}\) Теперь рассмотрим индуктивный случай. Предположим, что \(P(k)\) верно, то есть предположим, что \(F_0 + F_2 + F_4 + \cdots + F_{2k} = F_{2k+1} — 1\text{.}\) Чтобы установить \ (P(k+1)\) работаем слева направо:
\начать{выровнять*} \amp F_0 + F_2 + \cdots + F_{2k} + F_{2k+2} \amp\\ \amp = F_{2k+1} — 1 + F_{2k+2} \amp \text{по предположению индукции} \\ \amp = F_{2k+1} + F_{2k+2} — 1 \amp\\ \amp = F_{2k+3} — 1 \amp \text{по рекурсивному определению} \end{выравнивание*}
Следовательно, \(F_0 + F_2 + F_4 + \cdots + F_{2k+2} = F_{2k+3} — 1\text{,}\), что означает \(P(k+1)\) . Поэтому по принципу математической индукции \(P(n)\) верно для всех \(n \ge 0\text{.}\)
15.
Докажите, используя сильную индукцию, что каждое натуральное число является либо числом Фибоначчи, либо может быть записано как сумма различных чисел Фибоначчи.
Решение.
Доказательство.
Пусть \(P(n)\) будет утверждением, что \(n\) является либо числом Фибоначчи суммы различных чисел Фибоначчи
Базовый шаг: для \(n=0\text{,}\) мы имеем, что \(0 = F_0\) является числом Фибоначчи.
Индуктивный шаг: предположим, что существует целое число \(k \ge 0\), такое что \(P(m)\) верно для всех \(0\le m \le k\text{.}\) То есть , \(m\) является либо числом Фибоначчи, либо суммой различных чисел Фибоначчи. Теперь рассмотрим следующее число, \(k+1\text{:}\)
.
Случай 1: Если \(k+1\) является числом Фибоначчи, то мы закончили.
Случай 2: Если \(k+1\) не является числом Фибоначчи, то пусть \(F_m\) будет наибольшим числом Фибоначчи, меньшим чем \(k+1\text{. }\), так как \(k+1 — F_m \le k\), то по предположению индукции \(k+1 — F_m\) есть сумма различных чисел Фибоначчи.
Добавление \(F_m\) к этой сумме дает нам \(k+1 — F_m + F_m = k+1\), которое затем представляет собой сумму различных чисел Фибоначчи.
Таким образом, по индукции каждое натуральное число является либо числом Фибоначчи суммы различных чисел Фибоначчи.
16.
Докажите методом математической индукции, что \(F_1 + F_3 + F_5 + \dots + F_{2n -1} = F_{2n}\text{,}\), где \(F_n\) — это \(n\) число Фибоначчи.
Решение.
Доказательство.
Пусть \(P(n)\) будет оператором «\(F_1 + F_3 + F_5 + \dots + F_{2n -1} = F_{2n}\)»
Базовый шаг: если \(n =1\), то \(F_1 =1\) и \(F_{2\cdot 1} = 1\), так что \(P(1)\) верно.
Индуктивный шаг: предположим, что \(P(k)\) верно для некоторого целого числа \(k\ge 1\text{.}\), то есть \(F_1 + F_3 + F_5 + \dots + F_{2k — 1} = F_{2k}\) и рассмотрим:
\начать{выровнять*} \amp F_1 + F_3 + F_5 + \dots + F_{2k -1} + F_{2(k+1) — 1}\amp \\ \amp = F_1 + F_3 + F_5 + \dots + F_{2k -1} + F_{2k+1} \amp \\ \amp = F_{2k} + F_{2k+1} \amp \text{по предположению индукции} \\ \amp = F_{2k+2} \amp \text{по рекурсивному определению}\\ \amp = F_{2(k+1)}\amp \end{выравнивание*} 92 = F_n \cdot F_{n+1}\text{,}\), где \(F_n\) — \(n\)-е число Фибоначчи.
Подсказка.
\(F_{k+1}\left(F_{k} + F_{k+1}\right) = F_{k+1}F_{k+2} \)
18.
Докажите, что существует строго возрастающая последовательность \(a_1, a_2, a_3, \ldots\) чисел (не обязательно целых) такая, что \(a_n \lt 100\) для всех \(n \in \N\text{ .}\) (Под строго возрастающим мы подразумеваем \(a_n \lt a_{n+1}\) для всех \(n\text{.}\). Таким образом, каждый член должен быть больше предыдущего.)
Решение.
Доказательство.
Пусть \(P(n)\) будет утверждением «существует строго возрастающая последовательность \(a_1, a_2, \ldots, a_n\) с \(a_n \lt 100\text{.}\)». Мы докажем \(P(n)\) истинно для всех \(n \ge 1\text{.}\) Сначала мы установим базовый случай: \(P(1)\) говорит, что существует единственное число \(a_1\ ) с \(a_1 \lt 100\text{.}\) Это верно – возьмем \(a_1 = 0\text{.}\) Теперь для индуктивного шага предположим, что \(P(k)\) верно. То есть существует строго возрастающая последовательность \(a_1, a_2, a_3, \ldots, a_k\) с \(a_k \lt 100\text{.
No related posts.