Минус косинус: Чему равен косинус минус п/4 и синус минус п/6?

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значение
sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значение sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы 88 град.

Разность косинус минус синус / синус

Размер:

3.58 MB

Длительность:

03:54

Качество:

320 kbps

Добавлено:

2019-03-25

Жанр:

Easy Listening

Другие песни исполнителя

Возможно, вам понравятся также:

01

минус — Звезда — бэк.

минус

07:01

02

минус — Песня о хороших людях

минус

02:25

03

минус — голос

минус

02:58

04

Минус — Весна идёт

Минус

04:20

05

Минус — I Can

Минус

04:26

06

Минус — Звезда по имени Солнце

Минус

03:00

07

минус — лишь ты умеешь так любить

минус

03:57

08

минус — от Freeteam

минус

04:09

09

минус — клевый

минус

08:12

10

минус — Школа любимая

минус

03:32

11

Минус — С басами [224] [3. 58]

Минус

03:57

12

Минус — Cyarice

Минус

03:11

13

Минус — Абсалям

Минус

03:43

14

минус — Гитара и бит 120 bpm *лирика*

минус

02:24

15

минус — белым снегом

минус

03:36

16

минус — Ты самая лучшая на свете-весна 2012

минус

03:39

17

Минус — 123

Минус

02:36

18

минус — О сердце

минус

07:11

19

Минус — Выше жарче

Минус

02:52

20

Минус — Надарую квіти

Минус

03:08

21

минус — круто

минус

02:10

22

Минус — От героев былых времен

Минус

02:57

23

МИНУС — Три белых коня

МИНУС

01:53

24

минус — лирическая

минус

03:00

25

Минус — Минусовка для репа

Минус

02:03

26

МИНУС — Jingle Bells 2

МИНУС

05:17

27

минус — осенний блюз

минус

03:24

28

Минус — Ритм моего сердца

Минус

04:25

29

минус — 3

минус

01:30

30

минус — ломай меня полностью

минус

02:45

31

Минус — Улыбка

Минус

02:27

32

Минус — Mercedes Rhythm

Минус

02:50

Как найти отрицательный косинус

Все математические ресурсы ACT

14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept

ACT Math Help » Тригонометрия » косинус » Как найти отрицательный косинус

Если и , каково значение ?

Возможные ответы:

Правильный ответ:

Объяснение:

На основе этих данных мы можем составить небольшой треугольник, который выглядит так:

Это потому, что .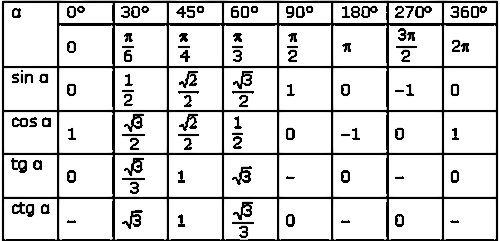

Теперь это означает, что должно быть равно. (Напомним, что функция косинуса во втором квадранте отрицательна.) Теперь ищем:

 или . Это косинус опорного угла:

Глядя на наш маленький треугольник выше, мы видим, что косинус   равен .

Сообщить об ошибке

Чему равен косинус угла, образованного между началом и точкой, если этот угол образован с одной стороной угла, начинающейся на оси, а затем вращающейся против часовой стрелки до ? Округлить до сотых.

Возможные ответы:

Правильный ответ:

Объяснение:

Вспомните, что когда вы вычисляете тригонометрическую функцию для такого тупого угла, вы всегда используете -ось в качестве исходной точки для вашего угла. (Поэтому он называется «угол отсчета».)  

Теперь проще всего представить это так, будто вы рисуете маленький треугольник в третьем квадранте декартовой плоскости. Это будет выглядеть так:

Итак, сначала нужно вычислить гипотенузу. Это можно сделать с помощью теоремы Пифагора, , где и  – длины катетов треугольника и  длина гипотенузы. Преобразовав уравнение для решения, вы получите:

Подставив полученные значения:

Итак, косинус угла равен:

 или, для ваших данных, .

Это примерно . Округление, это . Однако, поскольку  находится в третьем квадранте, ваше значение должно быть отрицательным: .

Сообщить об ошибке

Чему равен косинус угла, образованного между началом и точкой, если этот угол образован с одной стороной угла, начинающейся на оси, а затем вращающейся против часовой стрелки до ? Округлить до сотых.

Возможные ответы:

Правильный ответ:

Объяснение:

Вспомните, что когда вы вычисляете тригонометрическую функцию для такого тупого угла, вы всегда используете -ось в качестве исходной точки для вашего угла. (Поэтому он называется «угол отсчета».) Теперь проще всего думать об этом, как будто вы рисуете маленький треугольник во втором квадранте декартовой плоскости. Это будет выглядеть так:

Итак, сначала нужно вычислить гипотенузу:

Итак, косинус угла равен:

 или, для ваших данных, .

Это примерно . Округление, это . Однако, поскольку  находится во втором квадранте, ваше значение должно быть отрицательным: .

Сообщить об ошибке

Чему равен косинус угла между началом и точкой с точностью до ? Допустим вращение против часовой стрелки.

Возможные ответы:

Правильный ответ:

Объяснение:

Если нужно достичь точки , то мы можем представить себе прямоугольный треугольник со сторонами  и , и гипотенузой . Теорема Пифагора говорит нам об этом, поэтому мы подключаем и находим, что:

Таким образом,

Теперь SOHCAHTOA говорит нам об этом, поэтому мы знаем, что:

Таким образом, наш косинус приблизительно равен . Однако, поскольку мы находимся в третьем квадранте, косинус должен быть отрицательным! Следовательно, наш истинный косинус равен .

Сообщить об ошибке

Чему равен косинус угла, образованного на сетке между линией от начала координат до  и осью x?

Возможные ответы:

Правильный ответ:

Объяснение:

Если нужно достичь точки , то мы можем представить себе прямоугольный треугольник со сторонами  и , и гипотенузой . Теорема Пифагора говорит нам об этом, поэтому мы подключаем и находим, что:

Таким образом, .

Теперь SOHCATOA  говорит нам об этом, поэтому мы знаем, что:

Таким образом, наш косинус приблизительно равен . Однако, поскольку мы находимся во втором квадранте, косинус должен быть отрицательным! Следовательно, наш истинный косинус равен .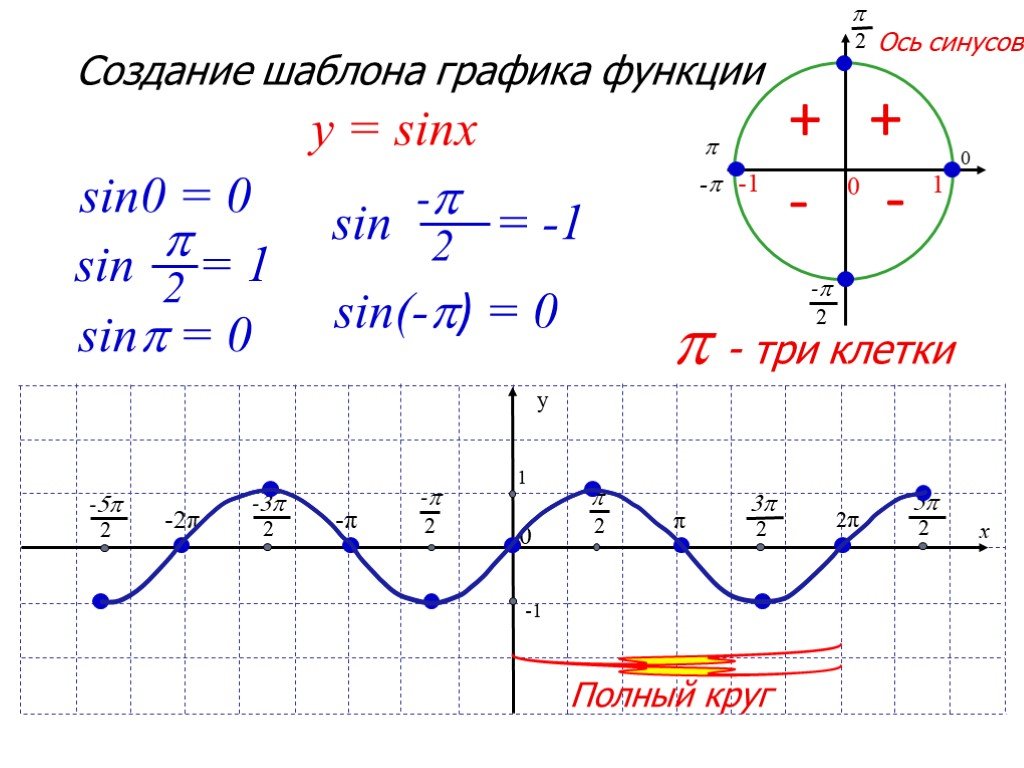

Сообщить об ошибке

Уведомление об авторских правах

Все математические ресурсы ACT

14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept

машинное обучение — интерпретация подобия отрицательного косинуса

Задай вопрос

спросил

Изменено 2 года, 8 месяцев назад

Просмотрено 35 тысяч раз

$\begingroup$

Мой вопрос может быть глупым. Так что заранее извиняюсь.

Я пытался использовать модель GLOVE, предварительно обученную Стэнфордской группой НЛП (ссылка). Однако я заметил, что мои результаты подобия показали некоторые отрицательные числа.

Это сразу же побудило меня взглянуть на файл данных word-vector. По-видимому, значения в векторах слов могли быть отрицательными. Это объяснило, почему я увидел отрицательные косинусные сходства.

Я привык к понятию косинусного подобия частотных векторов, значения которых ограничены в [0, 1]. Я точно знаю, что скалярное произведение и функция косинуса могут быть положительными или отрицательными, в зависимости от угла между векторами. Но мне действительно трудно понять и интерпретировать это отрицательное косинусное сходство.

Например, если у меня есть пара слов, дающая сходство -0,1, они менее похожи, чем другая пара, у которой сходство равно 0,05? Как насчет сравнения сходства -0,9 с 0,8?

Или мне просто посмотреть на абсолютное значение минимальной разности углов от $n\pi$? Абсолютное значение баллов?

Большое спасибо.

  • машинное обучение
  • word2vec
  • косинусное сходство

$\endgroup$

4

$\begingroup$

Пусть два вектора $a$ и $b$, угол $θ$ получается скалярным произведением и нормой векторов:

$$ cos(\theta) = \frac{a \cdot b}{ ||а|| \cdot ||b||} $$

Поскольку значение $cos(\theta)$ находится в диапазоне $[-1,1]$ :

  • Значение $-1$ будет указывать на сильно противоположные векторы
  • $0$ независимых (ортогональных) векторов
  • $1$ подобных (положительно коллинеарных) векторов. Промежуточные значения используется для оценки степени сходства.

Пример : Пусть два пользователя $U_1$ и $U_2$, и $sim(U_1, U_2)$ сходство между этими двумя пользователями в соответствии с их предпочтениями в кино:

  • $sim(U_1, U_2) = 1$, если у двух пользователей одинаковые вкусы (или если $U_1 = U_2$)
  • $sim(U_1, U_2) = 0$, если мы не находим корреляции между двумя пользователями, т.е. если они не видели обычных фильмов
  • $sim(U_1, U_2) = -1$, если у пользователей разные вкусы, т.е. если бы они оценивали одни и те же фильмы по-разному 92)) шалунья =-1 макс = 1 return(((dot_product/anorm*bnorm)-minx)/(maxx-minx)) }

    (код Python)

     def cos_sim(a, b):
    """Принимает 2 вектора a, b и возвращает косинусное сходство в соответствии с
к определению скалярного произведения"""
    dot_product = np.dot (а, б)
    norm_a = np.linalg.norm(a)
    norm_b = np.linalg.norm(b)
    возврат dot_product / (норма_а * норма_б)
Минкс = -1
макс = 1
cos_sim(строка1, строка2)- minx)/(maxx-minx)
```

    $\endgroup$

    1

    $\begingroup$

    Косинусное сходство аналогично корреляции Пирсона, но без вычитания средних значений. Таким образом, вы можете сравнить относительную силу сходства двух косинусов, взглянув на абсолютные значения, точно так же, как вы бы сравнили абсолютные значения двух корреляций Пирсона.

    $\endgroup$

    $\begingroup$

    Верно то, что косинусное сходство между частотными векторами не может быть отрицательным, поскольку количество слов не может быть отрицательным, но с вложением слов (таким как перчатка) вы можете иметь отрицательные значения. 9д. Затем запустите оптимизатор, который попытается подтолкнуть два похожих вектора v1 и v2 ближе друг к другу или развести два непохожих вектора v3 и v4 дальше друг от друга (согласно некоторому расстоянию, скажем, косинусу). Вы выполняете эту оптимизацию для достаточного количества итераций, и в конце у вас есть вложения слов с единственным критерием, что похожие слова имеют более близкие векторы, а непохожие векторы находятся дальше друг от друга.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *