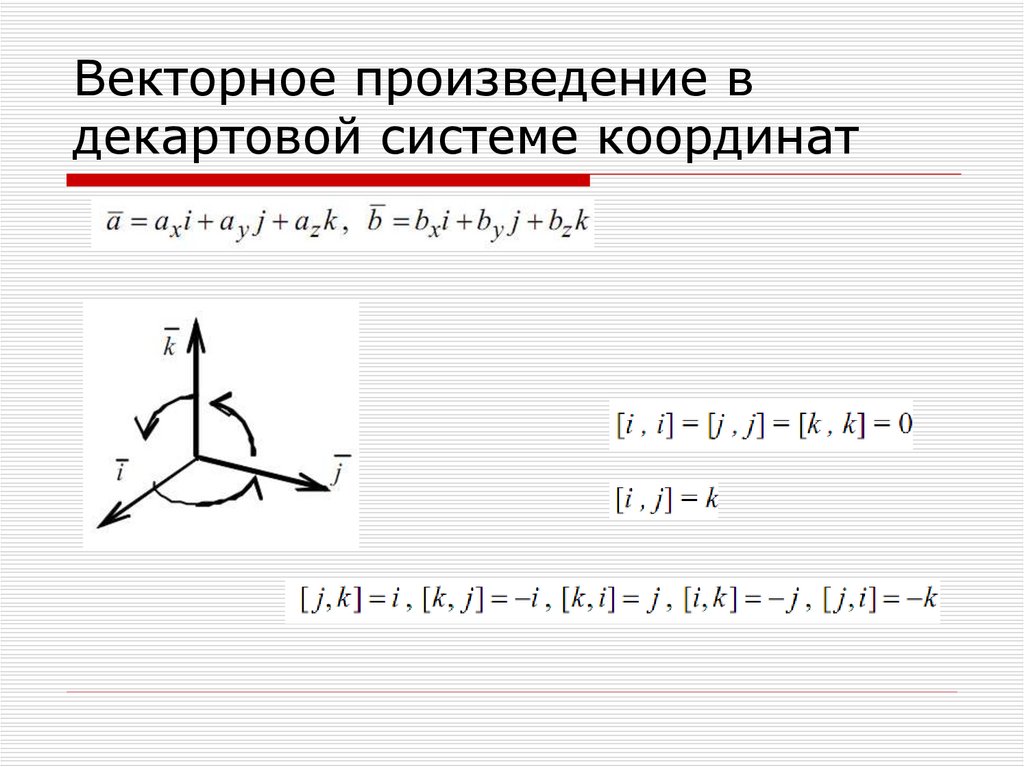
Векторное произведение векторов в координатах формула: формула, примеры, свойства, геометрический смысл

Содержание

Как найти векторное произведение?

Векторное произведение векторов , заданных в ортонормированном базисе , выражается формулой:

В верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем их в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ».

Данный определитель всегда раскрываем по первой строке, что продемонстрировано выше. Что получается в результате раскрытия определителя? В результате получается ВЕКТОР. А как иначе? Векторное произведение – это же вектор:

Задача 51

Найти векторное произведение векторов и его длину.

Решение: Задача состоит из двух частей: во-первых, необходимо найти само векторное произведение (вектор), а во-вторых – его длину.

1) Найдём векторное произведение:

В результате получен вектор или .

Выполним проверку: по определению, вектор должен быть ортогонален векторам . Ортогональность векторов, как мы помним, проверяется с помощью скалярного произведения:

– если получилось хотя бы одно число, отличное от нуля, ищите ошибку в раскрытии определителя.

2) Вычислим длину векторного произведения. Используем простейшую формулу для вычисления длины вектора:

Ответ:

Аналогичный пример для самостоятельного решения:

Задача 52

Даны векторы . Найти и вычислить .

Будьте внимательны!

Огонь камина в самом разгаре, и самое время добавить живительный геометрический смысл в наши задачи:

Задача 53

Даны вершины треугольника . Найти его площадь.

Решение: Алгоритм решения, думаю, многие уже представляют. Сначала найдём векторы:

Затем векторное произведение:

Вычислим его длину:

Формулы площадей параллелограмма и треугольника, само собой, остаются те же:

Ответ:

В рассмотренной задаче было не обязательно выбирать стороны , существует ещё два варианта. Решение допустимо провести через векторы либо . Желающие могут проверить, что во всех трёх случаях получится один и тот же ответ. …Почему именно эти стороны? Мысленно представьте или изобразите на черновике этот треугольник.

Еще одна важная особенность состоит в том, что в задачах на нахождение площади фигуры порядок векторов не имеет значения. Действительно, если находить , то получим противоположно направленный вектор , но формула вычисления длины вектора всё равно «съест» эти минусы. Заметьте, что такую перестановку нельзя делать в Задачах 51-52, поскольку там требовалось найти вполне конкретный вектор.

Задача 54

Вычислить площадь параллелограмма, построенного на векторах , если

Самостоятельно. Решение и ответ в конце книги.

И в заключение параграфа обещанная задача:

Задача 55

Проверить, будут ли коллинеарны следующие векторы пространства:

а)

б)

Решение: проверка основана на упомянутом ранее факте: если векторы коллинеарны, то их векторное произведение равно нулевому вектору: .

а) Найдём векторное произведение:

Таким образом, векторы не коллинеарны.

б) Найдём векторное произведение:

Значит,

Ответ: а) не коллинеарны, б)

Вот, пожалуй, и все основные сведения о векторном произведении векторов.

1.10.1. Смешанное произведение векторов

1.9.2. Свойства векторного произведения

| Оглавление |

Автор: Aлeксaндр Eмeлин

Векторное произведение | Компьютерная графика

Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Векторное произведение не обладает свойствами коммутативности и ассоциативности (является антикоммутативным) и, в отличие от скалярного произведения векторов, является вектором. Широко используется во многих технических и физических приложениях. Например, момент импульса и сила Лоренца математически записываются в виде векторного произведения. Векторное произведение полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.

Определить векторное произведение можно по-разному, и теоретически, в пространстве любой размерности n можно вычислить произведение n-1 векторов, получив при этом единственный вектор, перпендикулярный к ним всем. Но если произведение ограничить нетривиальными бинарными произведениями с векторным результатами, то традиционное векторное произведение определено только в трёхмерном и семимерном пространствах. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства.

В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности».

Определение:
Векторным произведением вектора a на вектор b в пространстве R³ называется вектор c, удовлетворяющий следующим требованиям:
длина вектора c равна произведению длин векторов a и b на синус угла φ между ними:
|c|=|a||b|sin φ;
вектор c ортогонален каждому из векторов a и b;
вектор c направлен так, что тройка векторов abc является правой;
в случае пространства R7 требуется ассоциативность тройки векторов a,b,c.
Обозначение:
c=[ab]=[a,b]=a × b

Рис. 1. Площадь параллелограмма равна модулю векторного произведения

Геометрические свойства векторного произведения:
Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулю их векторного произведения.

Модуль векторного произведения [ab] равняется площади S параллелограмма, построенного на приведённых к общему началу векторах a и b (см. рис.1).

Если e — единичный вектор, ортогональный векторам a и b и выбранный так, что тройка a,b,e — правая, а S — площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:
[a, b]=S e

Рис.2. Объём параллелепипеда при использовании векторного и скалярного произведения векторов; пунктирные линии показывают проекции вектора c на a × b и вектора a на b × c, первым шагом является нахождение скалярных произведений

Если c — какой-нибудь вектор, π — любая плоскость, содержащая этот вектор, e — единичный вектор, лежащий в плоскости π и ортогональный к c,g— единичный вектор, ортогональный к плоскости π и направленный так, что тройка векторов ecg является правой, то для любого лежащего в плоскости π вектора a справедлива формула:
[a, c]=Pr_ea•|c|g
где Pr_ea проекция вектора e на a
|c|-модуль вектора с

При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c. Такое произведение трех векторов называется смешанным.
V=|a•(b×c)|
На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:
V=a×b•c=a•b×c

Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов также, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны.

Выражение для векторного произведения в декартовых координатах
Если два вектора a и b определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
a=(a_x,a_y,a_z)
b=(b_x,b_y,b_z)
а система координат правая, то их векторное произведение имеет вид
[a, b]=(a_yb_z-a_zb_y,a_zb_x-a_xb_z,a_xb_y-a_yb_x)
Для запоминания этой формулы :
[a,b]_i=∑ε_ijka_jb_k
где ε_ijk— символ Леви-Чивиты.

12.4 Перекрестное произведение

Еще одна полезная операция: по двум векторам найти третий (ненулевой!) вектор перпендикулярно первым двум. Их конечно бесконечное множество таких векторов разной длины. Тем не менее, давайте найдем его. Предположим, что $\ds {\bf A}=\langle a_1,a_2,a_3\rangle$ и $\ds {\bf B}=\langle b_1,b_2,b_3\rangle$. Мы хотим найти вектор $\ds {\bf v} = \langle v_1,v_2,v_3\rangle$ с ${\bf v}\cdot{\bf A}={\bf v}\cdot{\bf B}=0$, или $$\выравнивание{ a_1v_1+a_2v_2+a_3v_3&=0,\кр b_1v_1+b_2v_2+b_3v_3&=0.\cr }$$ Умножьте первое уравнение на $\ds b_3$, а второе на $\ds a_3$ и вычесть, чтобы получить $$\выравнивание{ b_3a_1v_1+b_3a_2v_2+b_3a_3v_3&=0\кр a_3b_1v_1+a_3b_2v_2+a_3b_3v_3&=0\кр (a_1b_3-b_1a_3)v_1 + (a_2b_3-b_2a_3)v_2&=0\cr }$$ Конечно, это уравнение с двумя переменными имеет много решений; а особенно легко увидеть $\ds v_1=a_2b_3-b_2a_3$, $\ds v_2=b_1a_3-a_1b_3$. Замена обратно на любой из исходных уравнения и решение для $\ds v_3$ дает $\ds v_3=a_1b_2-b_1a_2$.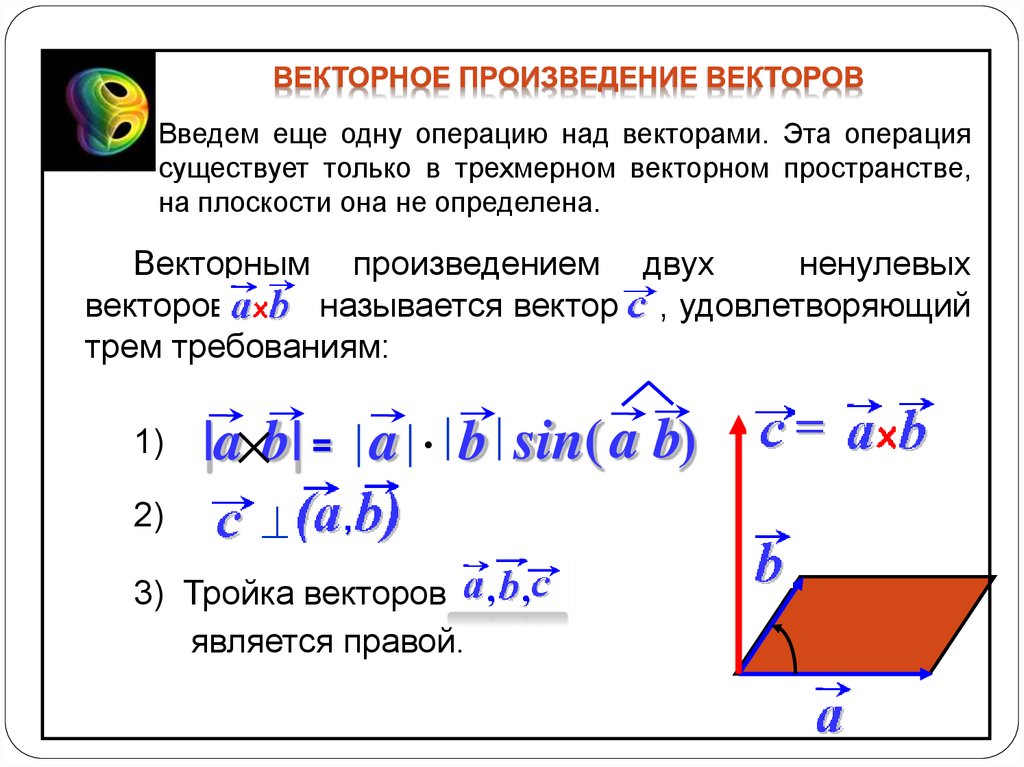

Этот конкретный ответ на проблему, оказывается, имеет некоторые хорошие свойства, и он удостоился имени: перекрестное произведение : $$ {\bf A}\times{\bf B} = \langle a_2b_3-b_2a_3,b_1a_3-a_1b_3,a_1b_2-b_1a_2\rangle. $$ Хотя в этом векторе есть хороший шаблон, он может быть немного сложно запомнить; вот удобная мнемоника. Определитель матрицы два на два равен $$\left|\matrix{a&b\cr c&d\cr}\right|=ad-cb.$$ Это распространяется на определитель матрицы три на три: $$\выравнивание{ \left|\matrix{x&y&z\cr а_1&а_2&а_3\кр b_1&b_2&b_3\cr}\right|&=x\left|\matrix{a_2&a_3\cr b_2&b_3\cr}\right|-y\left|\matrix{a_1&a_3\cr b_1&b_3\cr}\right|+z\left|\matrix{a_1&a_2\cr b_1&b_2\cr}\право|\cr &=x(a_2b_3-b_2a_3)-y(a_1b_3-b_1a_3)+z(a_1b_2-b_1a_2)\cr &=x(a_2b_3-b_2a_3)+y(b_1a_3-a_1b_3)+z(a_1b_2-b_1a_2).\cr} $$ Каждая из матриц два на два формируется удалением верхней строки и один столбец матрицы три на три; вычитание середины термин также необходимо запомнить. Здесь не место превозносить использование определителя; достаточно сказать, что детерминанты необычайно полезно и важно.

Здесь мы хотим использовать его просто как мнемонический прием. Вы могли заметить, что три выражения в круглые скобки в последней строке — это в точности три координаты перекрестный продукт; замена $x$, $y$, $z$ на $\bf i$, $\bf j$, $\bf k$ дает нам $$\выравнивание{ \left|\matrix{{\bf i}&{\bf j}&{\bf k}\cr а_1&а_2&а_3\кр b_1&b_2&b_3\cr}\право| &=(a_2b_3-b_2a_3){\bf i}-(a_1b_3-b_1a_3){\bf j}+(a_1b_2-b_1a_2){\bf к}\кр &=(a_2b_3-b_2a_3){\bf i}+(b_1a_3-a_1b_3){\bf j}+(a_1b_2-b_1a_2){\bf к}\кр &=\лангл a_2b_3-b_2a_3,b_1a_3-a_1b_3,a_1b_2-b_1a_2\rangle\cr &={\bf A}\times{\bf B}.\cr} $$

Пример 12.4.1 Предположим, что ${\bf A}=\langle 1,2,3\rangle$, ${\bf B}=\langle 4,5,6\угол$. затем $$\выравнивание{ {\bf A}\times{\bf B}&=\left|\matrix{{\bf i}&{\bf j}&{\bf k}\cr 1&2&3\кр 4&5&6\cr}\право|\cr &=(2\cdot 6-5\cdot 3){\bf i}+(4\cdot 3-1\cdot 6){\bf j}+ (1\cdot 5-4\cdot 2){\bf k}\cr &=-3{\bf i}+6{\bf j}-3{\bf k}\cr &=\langle -3, 6, -3\rangle\cr }$$ Немного потренировавшись, вы обнаружите, что избавляться от промежуточные шаги, переходя непосредственно от матрицы $3\times3$ к обычная векторная форма.

2\theta\cr |{\bf A}\times{\bf B}|&=|{\bf A}||{\bf B}|\sin\theta\cr }$$ Таким образом, величина ${\bf A}\times{\bf B}$ очень похожа на точку товар. В частности, обратите внимание, что если $\bf A$ параллелен $\bf B$, угол между ними равен нулю, поэтому $\sin\theta=0$, поэтому $|{\bf A}\times{\bf B}|=0$, и аналогично, если они антипараллельны, $\sin\theta=0$ и $|{\bf A}\times{\bf B}|=0$. Наоборот, если $|{\bf A}\times{\bf B}|=0$ и $|{\bf A}|$ и $|{\bf B}|$ не равны нулю, должно быть так, что $\sin\theta=0$, поэтому $\bf A$ параллелен или антипараллелен $\bf B$.

Вот любопытный факт по этому поводу количество, которое впоследствии оказывается весьма полезным: Даны два векторы, мы можем сложить их хвост к хвосту и сформировать параллелограмм, как на рисунке 12.4.1. высота параллелограмма $h$ равна $|{\bf A}|\sin\theta$, а основание равно $|{\bf B}|$, поэтому площадь параллелограмм $|{\bf A}||{\bf B}|\sin\theta$, в точности равно величине $|{\bf A}\times{\bf B}|$.

Рисунок 12. 4.1. Параллелограмм.

А как насчет направления перекрестного произведения? Примечательно, что существует простое правило, описывающее направление. Давайте посмотрим на простой пример: пусть ${\bf A}=\langle a,0,0\rangle$, ${\bf B}=\langle б, в, 0\угол$. Если векторы поставить хвостами в начале координат, $\bf A$ лежит вдоль оси $x$, а $\bf B$ лежит в плоскости $x$-$y$, поэтому мы знаем, что перекрестный продукт будет указывать либо вверх, либо вниз. Крест продукт $$\выравнивание{ {\bf A}\times {\bf B}=\left|\matrix{{\bf i}&{\bf j}&{\bf k}\cr а&0&0\кр b&c&0\cr}\right| &=\лангл 0,0,ac\угол.\cr} $$ Как и было предсказано, это вектор, направленный вверх или вниз, в зависимости от знак $ac$. Предположим, что $a>

0$, поэтому знак зависит только от $c$: если $c>0$, $ac>0$ и вектор направлен вверх; если $c0$, то вектор указывает вниз, а если $a0$ и $c>0$ или $a

Хотя с вычислительной точки зрения довольно сложно увидеть, как это работает для любых двух начальных векторов, правило, по сути, тем же. Расположите $\bf A$ и $\bf B$ хвост к хвосту. Плоскость, в которой $\bf A$ и $\bf B$ можно рассматривать с двух сторон; посмотреть на это со стороны для которого $\bf A$ должен вращаться против часовой стрелки, чтобы достичь $\bf B$; тогда вектор ${\bf A}\times{\bf B}$ указывает на вас.

Это правило обычно называют правило правой руки . Представьте, что вы помещаете пятку правой руки в точку, где находятся решки. соединены так, чтобы ваши слегка согнутые пальцы указывали направление вращение из $\bf A$ в $\bf B$. Затем ваш большой палец указывает на направление векторного произведения ${\bf A}\times{\bf B}$.

Одним из непосредственных следствий этих фактов является то, что ${\bf A}\times{\bf B}\not={\bf B}\times{\bf A}$, потому что два перекрестные произведения указывают в противоположном направлении. С другой стороны, поскольку $$ |{\bf A}\times{\bf B}|=|{\bf A}||{\bf B}|\sin\theta =|{\bf B}||{\bf A}|\sin\theta=|{\bf B}\times{\bf A}|, $$ длины двух перекрестных произведений равны, поэтому мы знаем, что ${\bf A}\times{\bf B}=-({\bf B}\times{\bf A})$.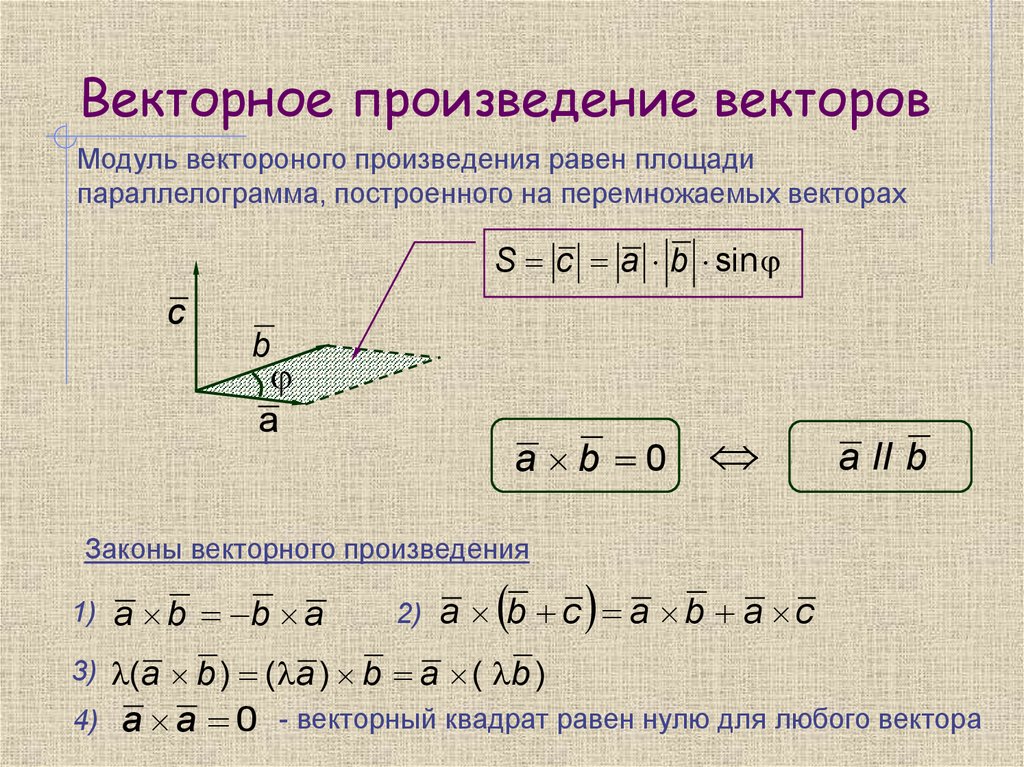

Перекрестное произведение имеет некоторые знакомые свойства, которые будут пригодится позже, поэтому мы перечислим их здесь. Как и в случае скалярного произведения, они могут быть доказано выполнением соответствующих вычислений по координатам, после чего мы можем иногда избежать таких вычислений, используя характеристики.

Теорема 12.4.2 Если ${\bf u}$, ${\bf v}$ и ${\bf w}$ — векторы, а $a$ — вещественное число, затем

1. ${\bf u}\times({\bf v}+{\bf w}) = {\bf u}\times{\bf v}+{\bf u}\times{\bf w}$

2. $({\bf v}+{\bf w})\times{\bf u} = {\bf v}\times{\bf u}+{\bf w}\times{\bf u}$

3. $(a{\bf u})\times{\bf v}=a({\bf u}\times{\bf v}) = {\ bf и} \ раз (a {\ bf v}) $

4. ${\bf u}\cdot({\bf v}\times{\bf w}) = ({\bf u}\times{\bf v})\cdot{\bf w}$

5. ${\bf u}\times({\bf v}\times{\bf w}) = ({\ bf u} \ cdot {\ bf w}) {\ bf v} — ({\ bf u} \ cdot {\ bf v}) {\ bf w} $ $\qed$

Вы можете использовать Sage для вычисления перекрестных произведений.

Пример 12.4.1 Найдите векторное произведение $\langle 1,1,1\rangle$ и $\лэнгл 1,2,3\рангл$. (отвечать)

Пример 12.4.2 Найдите векторное произведение $\langle 1,0,2\rangle$ и $\лангле -1,-2,4\рангл$. (отвечать)

Пример 12.4.3 Найдите векторное произведение $\langle -2,1,3\rangle$ и $\лэнгл 5,2,-1\рангл$. (отвечать)

Пример 12.4.4 Найдите векторное произведение $\langle 1,0,0\rangle$ и $\лэнгл 0,0,1\рангл$. (отвечать)

Пример 12.4.5 Два вектора ${\bf u}$ и ${\bf v}$ разделены угол $\pi/6$, а $|{\bf u}|=2$ и $|{\bf v}|=3$. Находить $|{\bf u}\times{\bf v}|$. (отвечать)

Пример 12.4.6 Два вектора ${\bf u}$ и ${\bf v}$ разделены угол $\pi/4$, а $|{\bf u}|=3$ и $|{\bf v}|=7$. Находить $|{\bf u}\times{\bf v}|$. (отвечать)

Пример 12.4.7 Найдите площадь параллелограмма с вершинами $(0,0)$, $(1,2)$, $(3,7)$ и $(2,5)$. (отвечать)

Пример 12.4.8 Найдите площадь параллелограмма с вершинами $(0,-1)$, $(3,4)$, $(1,6)$ и $(-2,1)$. (отвечать)

Пример 12.4.9 Найдите площадь треугольника с вершинами $(2,0,0)$, $(1,3,4)$, и $(-2,-1,1)$. (отвечать)

Пример 12.4.10 Найдите площадь треугольника с вершинами $(2,-2,1)$, $(-3,2,3)$, и $(3,3,-2)$. (отвечать)

Пример 12.4.11 Найдите и объясните значение $({\bf i} \times {\bf j}) \times {\bf k}$ и $({\bf i} + {\bf j}) \times ({\bf i} — {\bf j})$.

Пример 12.4.12 Докажите, что для всех векторов ${\bf u}$ и ${\bf v}$ $({\bf u}\times{\bf v})\cdot{\bf v}=0$.

Пример 12.4.13 Докажите теорему 12.4.2.

Пример 12.4.14 Определим тройное произведение трех векторов ${\bf x}$, ${\bf y}$ и ${\bf z}$, чтобы быть скаляром ${\bf x} \cdot ({\bf y} \times {\bf z})$. Докажите, что три вектора лежат в одной плоскости тогда и только тогда, когда их тройное произведение равно нулю. Убедитесь, что $\langle 1, 5, -2 \rangle$, $\langle 4, 3, 0 \rangle$ и $\langle 6, 13, -4 \rangle$ копланарный.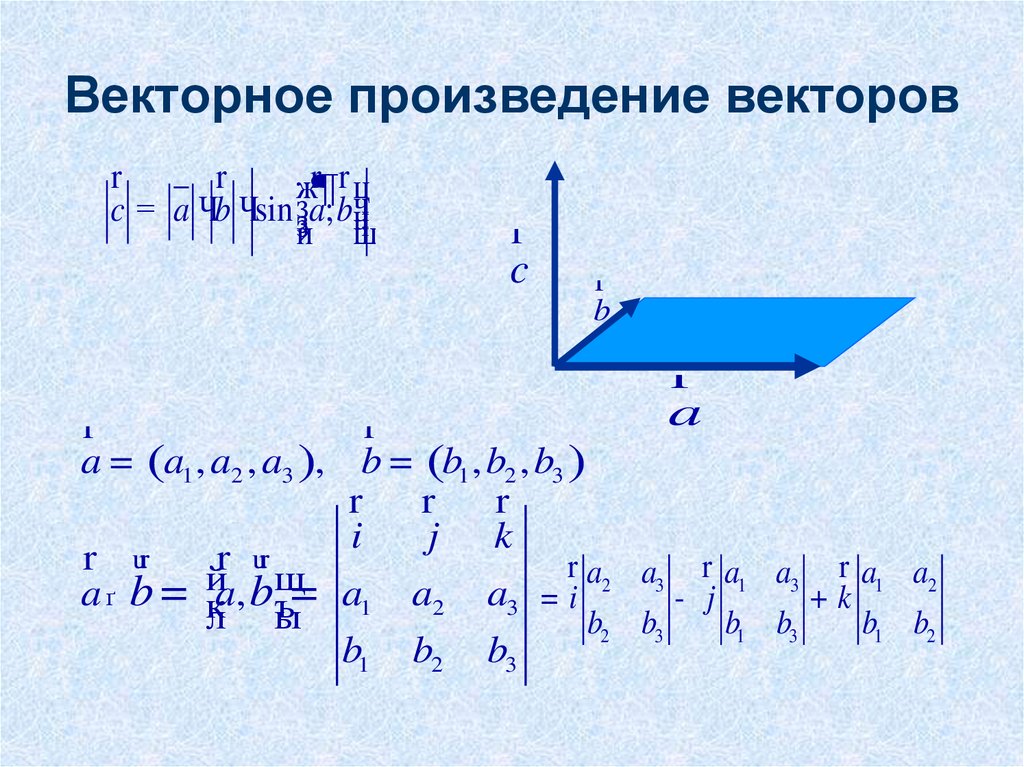

17.2: Векторное произведение (перекрестное произведение)

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 24530

Питер Дурмашкин
Массачусетский технологический институт через MIT OpenCourseWare

Пусть $\overrightarrow{\mathbf{A}}$ и $\overrightarrow{\mathbf{B}}$ — два вектора. Поскольку любые два непараллельных вектора образуют плоскость, мы обозначаем угол θ как угол между векторами $\overrightarrow{\mathbf{A}}$ и $\overrightarrow{\mathbf{B}}$ как показано на рисунке 17.2. Величина векторного произведения $\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}$ векторов $\overrightarrow{\mathbf{A}}$ и \ (\overrightarrow{\mathbf{B}}\) определяется как произведение величины векторов $\overrightarrow{\mathbf{A}}$ и $\overrightarrow{\mathbf{B}}$ с синусом угла θ между двумя векторами,

\[|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|=|\overrightarrow{\mathbf{A}}||\overrightarrow{\mathbf{B}}| \sin (\theta) \номер\]

Угол θ между векторами ограничен значениями $0 \leq \theta \leq \pi$, гарантирующими, что $\sin (\theta) \geq 0$.

Рис. 17.2. Геометрия векторного произведения.

Направление векторного произведения определяется следующим образом. Векторы $\overrightarrow{\mathbf{A}}$ и $\overrightarrow{\mathbf{B}}$ образуют плоскость. Рассмотрим направление, перпендикулярное этой плоскости. Есть две возможности: мы выберем одну из этих двух (показанную на рис. 17.2) в качестве направления векторного произведения \(\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}\ ), используя соглашение, которое обычно называют «правилом правой руки».

Правило правой руки для направления векторного произведения

Первый шаг — перерисовать векторы $\overrightarrow{\mathbf{A}} \text { и } \overrightarrow{\mathbf{B}}$ так, чтобы хвосты соприкасаются. Затем нарисуйте дугу, начиная с вектора $\overrightarrow{\mathbf{A}}$ и заканчивая вектором $\overrightarrow{\mathbf{B}}$. Согните правые пальцы так же, как дуга. Большой палец правой руки указывает направление векторного произведения $\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}$ (рис. 17.3).

Рисунок 17.3 Правило правой руки.

Вы должны помнить, что направление векторного произведения $\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}$ перпендикулярно плоскости, образованной $\overrightarrow{\mathbf{ A}} \text { и } \overrightarrow{\mathbf{B}}$. Мы можем дать геометрическую интерпретацию величины векторного произведения, записав величину как

\[|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|=|\overrightarrow{\ mathbf{A}}|(|\overrightarrow{\mathbf{B}}| \sin \theta) \nonumber \]

Векторы $\overrightarrow{\mathbf{A}} \text { и } \overrightarrow{\mathbf{B}}$ образуют параллелограмм. Площадь параллелограмма равна произведению высоты на основание, что является величиной векторного произведения. На рис. 17.4 показаны два разных изображения высоты и основания параллелограмма. Как показано на рис. 17.4а, член $|\overrightarrow{\mathbf{B}}| \sin \theta$ является проекцией вектора $\overrightarrow{\mathbf{B}}$ в направлении перпендикулярно вектору $\overrightarrow{\mathbf{B}}$ Мы могли бы также записать величину векторного произведения как

\[|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|=(|\overrightarrow{\mathbf{A}}| \sin\theta)|\overrightarrow{\mathbf {Б}}| \nonumber \]

Член $|\overrightarrow{\mathbf{A}}| \sin \theta$ является проекцией вектора $\overrightarrow{\mathbf{A}}$ в перпендикулярном направлении вектору $\overrightarrow{\mathbf{B}}$, как показано на рис. 17.4(b). Векторное произведение двух векторов, параллельных (или антипараллельных) друг другу, равно нулю, поскольку угол между векторами равен 0 (или $\pi$) и $\sin (0)=0$ ( или $\sin (\pi)=0$). Геометрически два параллельных вектора не имеют уникальной компоненты, перпендикулярной их общему направлению.

Рис. 17.4 Проекция (a) $\overrightarrow{\mathbf{B}}$ перпендикулярно $\overrightarrow{\mathbf{A}}$, (b) $\overrightarrow{\mathbf{A }}$ перпендикулярно $\overrightarrow{\mathbf{B}}$

Свойства векторного произведения

(1) Векторное произведение является антикоммутативным, поскольку изменение порядка векторов меняет направление вектора произведение по правилу правой руки:

\[\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=-\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{ А}} \номер\]

(2) Векторное произведение вектора $c \overrightarrow{\mathbf{A}}$, где $c$ — скаляр, на вектор $\overrightarrow{\mathbf{B}}$ равно

\[c \overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=c(\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}) \nonumber \]

Аналогично,

\[\overrightarrow{\mathbf{A}} \times c \overrightarrow{\mathbf{B}}=c(\overrightarrow{\mathbf{A}} \times \overrightarrow{ \mathbf{B}}) \номер \]

(3) Векторное произведение суммы двух векторов $\overrightarrow{\mathbf{A}} \text { и } \overrightarrow{\mathbf{B}}$ на вектор $\overrightarrow{\ mathbf{C}}$ равно

\[(\overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{B}}) \times \overrightarrow{\mathbf{C}}=\overrightarrow{\mathbf {A}} \times \overrightarrow{\mathbf{C}}+\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}} \nonumber \]

Аналогично,

\[\overrightarrow {\mathbf{A}} \times(\overrightarrow{\mathbf{B}}+\overrightarrow{\mathbf{C}})=\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B} }+\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{C}} \nonumber \]

Векторное разложение и векторное произведение: декартовы координаты

Сначала вычислим, что величина векторного произведения единичных векторов $\hat{\mathbf{i}}$ и $\hat{\mathbf{j} }$:

\[|\hat{\mathbf{i}} \times \hat{\mathbf{j}}|=|\hat{\mathbf{i}} \| \ шляпа {\ mathbf {j}} | \sin (\pi / 2)=1 \nonumber \]

, потому что единичные векторы имеют величину $|\hat{\mathbf{i}}|=|\hat{\mathbf{j}}|=1\ ) и \(\sin (\pi / 2)=1$. По правилу правой руки направление $\hat{\mathbf{i}} \times \hat{\mathbf{j}}$ находится в $+\hat{\mathbf{k}}$ как показано на рисунке 17.5. Таким образом, $\ hat{\mathbf{i}} \times \hat{\mathbf{j}}=\hat{\mathbf{k}}$.

Рис. 17.5 Векторное произведение $\hat{\mathbf{i}} \times \hat{\mathbf{j}}$

Заметим, что то же правило применяется к единичным векторам в направлениях y и z,

\[\ шляпа {\ mathbf {j}} \ раз \ шляпа {\ mathbf {k}} = \ шляпа {\ mathbf {i}}, \ четырехъядерная \ шляпа {\ mathbf {k}} \ раз \ шляпа { \mathbf{i}}=\hat{\mathbf{j}} \nonumber \]

По антикоммутативному свойству (1) векторного произведения

\[\hat{\mathbf{j}} \ раз \ шляпа {\ mathbf {i}} = — \ шляпа {\ mathbf {k}}, \ четырехъядерная \ шляпа {\ mathbf {i}} \ раз \ шляпа {\ mathbf {k}} = — \ шляпа {\ mathbf{j}} \номер \]

Векторное произведение единичного вектора $\hat{\mathbf{i}}$ на самого себя равно нулю, поскольку два единичных вектора параллельны друг другу, $(\sin (0)=0)$ ,

\[|\hat{\mathbf{i}} \times \hat{\mathbf{i}}|=|\hat{\mathbf{i}}||\hat{\mathbf{i}}| \sin (0)=0 \nonumber \]

Векторное произведение единичного вектора $\hat{\mathbf{j}}$ на себя и единичный вектор $\hat{\mathbf{k}} $ с самим собой также равны нулю по той же причине,

\[|\hat{\mathbf{j}} \times \hat{\mathbf{j}}|=0, \quad|\hat{\mathbf{ k}} \times \hat{\mathbf{k}}|=0 \nonumber \]

Имея в виду эти свойства, мы можем теперь построить алгебраическое выражение для векторного произведения через компоненты. Выберем декартову систему координат с вектором $\overrightarrow{\mathbf{B}}$, указывающим вдоль положительной оси x с положительной x-компонентой $B_{x}$. Тогда векторы $\overrightarrow{\mathbf{A}} \text { и } \overrightarrow{\mathbf{B}}$ можно записать как

\[\overrightarrow{\mathbf{A}}=A_{ x} \hat{\mathbf{i}}+A_{y} \hat{\mathbf{j}}+A_{z} \hat{\mathbf{k}} \nonumber \]

\[\overrightarrow{\mathbf{B}}=B_{x} \hat{\mathbf{i}} \nonumber \]

соответственно. Векторное произведение в векторных компонентах равно

\[\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=\left(A_{x} \hat{\mathbf{i}}+A_ {y} \hat{\mathbf{j}}+A_{z} \hat{\mathbf{k}}\right) \times B_{x} \hat{\mathbf{i}} \nonumber \]

Это становится

\[\begin{align}
\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}} &=\left(A_{x} \hat{\mathbf{i} } \times B_{x} \hat{\mathbf{i}}\right)+\left(A_{y} \hat{\mathbf{j}} \times B_{x} \hat{\mathbf{i} }\right)+\left(A_{z} \hat{\mathbf{k}} \times B_{x} \hat{\mathbf{i}}\right) \\
&=A_{x} B_{x}(\hat{\mathbf{i}} \times \hat{\mathbf{i}})+A_{y} B_{x}(\hat{\mathbf{j }} \times \hat{\mathbf{i}})+A_{z} B_{x}(\hat{\mathbf{k}} \times \hat{\mathbf{i}}) \\
&= -A_{y} B_{x} \hat{\mathbf{k}}+A_{z} B_{x} \hat{\mathbf{j}}
\end{aligned} \nonumber \]

Вектор компонентное выражение для векторного произведения легко обобщается для произвольных векторов }}+A_{z} \hat{\mathbf{k}} \nonumber \]

\[\overrightarrow{\mathbf{B}}=B_{x} \hat{\mathbf{i}}+B_{y} \hat{\mathbf{j}}+B_{z} \hat{\ mathbf{k}} \nonumber \]

, чтобы получить

\[\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=\left(A_{y} B_{z}- A_{z} B_{y}\right) \hat{\mathbf{i}}+\left(A_{z} B_{x}-A_{x} B_{z}\right) \hat{\mathbf{ j}}+\left(A_{x} B_{y}-A_{y} B_{x}\right) \hat{\mathbf{k}} \nonumber \]

Векторное разложение и векторное произведение: цилиндрическое Координаты

Вспомним цилиндрическую систему координат, показанную на рис. 17.6. Мы выбрали два направления: радиальное и тангенциальное в плоскости и перпендикулярное к плоскости направление.

Рис. 17.6. Цилиндрические координаты

. Единичные векторы расположены под прямым углом друг к другу, поэтому по правилу правой руки векторное произведение единичных векторов определяется соотношениями

\[\hat{\mathbf{r}} \ times \hat{\boldsymbol{\theta}}=\hat{\mathbf{k}} \nonumber \]

\[\hat{\boldsymbol{\theta}} \times \hat{\mathbf{k}} =\hat{\mathbf{r}} \nonumber \]

\[\hat{\mathbf{k}} \times \hat{\mathbf{r}}=\hat{\boldsymbol{\theta}} \ nonumber \]

Поскольку векторное произведение удовлетворяет условию $\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=-\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf {A}}$ у нас также есть

\[\hat{\boldsymbol{\theta}} \times \hat{\mathbf{r}}=-\hat{\mathbf{k}} \nonumber \]

\[\hat{\mathbf{ k}} \times \hat{\boldsymbol{\theta}}=-\hat{\mathbf{r}} \nonumber \]

\[\hat{\mathbf{r}} \times \hat{\mathbf {k}}=-\hat{\boldsymbol{\theta}} \nonumber \]

Наконец

\[\hat{\mathbf{r}} \times \hat{\mathbf{r}}=\hat {\boldsymbol{\theta}} \times\hat{\boldsymbol{\theta}}=\hat{\mathbf{k}} \times\hat{\mathbf{k}}=\overrightarrow{\mathbf{0} } \номер\]

Пример 17. 1 Произведения векторов

Для двух векторов $\overrightarrow{\mathbf{A}}=2 \hat{\mathbf{i}}+-3 \hat{\mathbf{j}}+7 \ шляпа {\ mathbf {k}} $ и \ (\ overrightarrow {\ mathbf {B}} = 5 \ шляпа {\ mathbf {i}} + \ шляпа {\ mathbf {j}} + 2 \ шляпа {\ mathbf{k}}\), найдите $\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}$.

Решение:

\[\begin{align}
\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}} &=\left(A_{y} B_{z}-A_{ z} B_{y}\right) \hat{\mathbf{i}}+\left(A_{z} B_{x}-A_{x} B_{z}\right) \hat{\mathbf{j} }+\left(A_{x} B_{y}-A_{y} B_{x}\right) \hat{\mathbf{k}} \\
&=((-3)(2)-(7)(1)) \шляпа{\mathbf{i}}+((7)(5)-(2)(2)) \шляпа{\mathbf{ j}}+((2)(1)-(-3)(5)) \шляпа{\mathbf{k}} \\
&=-13 \шляпа{\mathbf{i}}+31 \шляпа{ \mathbf{j}}+17 \hat{\mathbf{k}}
\end{aligned} \nonumber \]

Пример 17.2 Закон синусов

Для треугольника, показанного на рис. 17.7а, докажите закон синусов, $|\overrightarrow{\mathbf{A}}| / \sin \alpha=|\overrightarrow{\mathbf{B}}| / \sin \beta=|\overrightarrow{\mathbf{C}}| / \sin\gamma$, используя векторное произведение.

Рисунок 17.7 (b) Векторный анализ

Решение. Рассмотрим площадь треугольника, образованного тремя векторами $\overrightarrow{\mathbf{A}}, \overrightarrow{\mathbf{B}}$ и $\overrightarrow {\mathbf{C}}$, где $\overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{B}}+\overrightarrow{\mathbf{C}}=0$ (рис. 17.7б). ). Поскольку $\overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{B}}+\overrightarrow{\mathbf{C}}=0$, мы имеем это $0=\overrightarrow{\mathbf{ A}} \times(\overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{B}}+\overrightarrow{\mathbf{C}})=\overrightarrow{\mathbf{A}} \times \overrightarrow {\mathbf{B}}+\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{C}}$. Таким образом, $\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=-\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{C}}$ или $ |\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|=|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{C}}|$. Из рисунка 17.7b видно, что $|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|=|\overrightarrow{\mathbf{A}}||\overrightarrow{\mathbf{ B}}| \sin \gamma$ и $|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{C}}|=|\overrightarrow{\mathbf{A}}||\overrightarrow {\mathbf{C}}|\sin\бета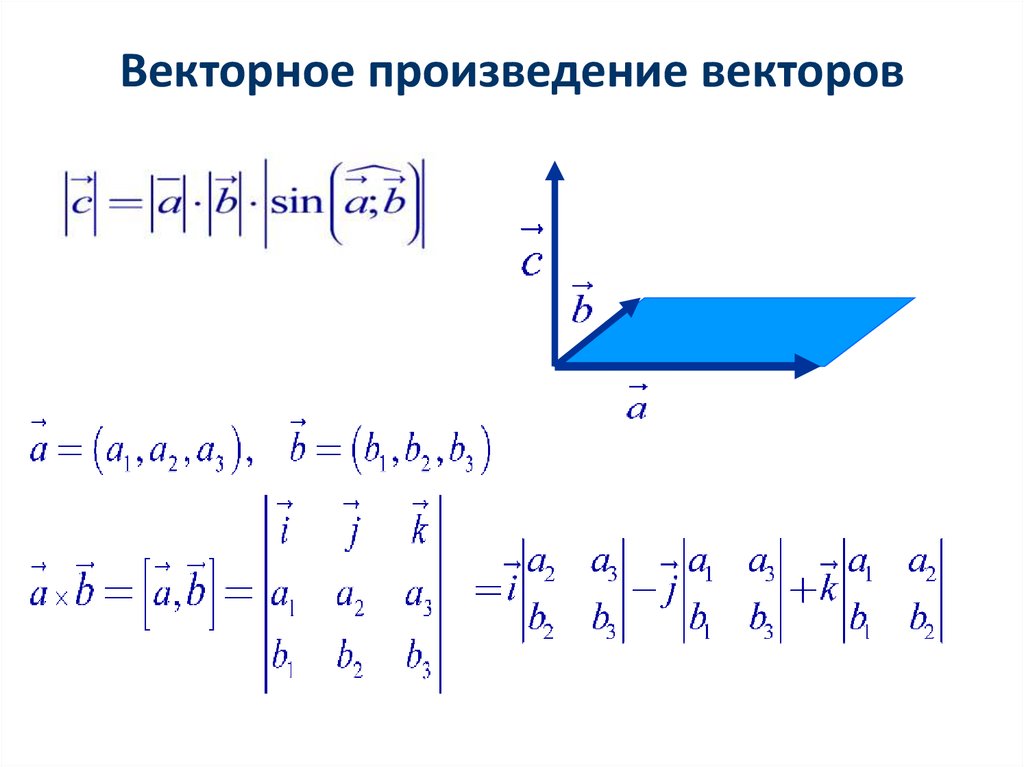$. Следовательно, }| \sin \beta\), и, следовательно, $|\overrightarrow{\mathbf{B}}| / \sin \beta=|\overrightarrow{\mathbf{C}}| / \sin \gamma$. Аналогичный аргумент показывает, что $|\overrightarrow{\mathbf{B}}| / \sin \beta=|\overrightarrow{\mathbf{A}}| / \sin \alpha$ доказывает закон синусов.

Пример 17.3. Единичная нормаль

Найдите единичный вектор, перпендикулярный $\overrightarrow{\mathbf{A}}=\hat{\mathbf{i}}+\hat{\mathbf{j}}-\hat {\mathbf{k}}$ и $\overrightarrow{\mathbf{B}}=-2 \шляпа{\mathbf{i}}-\шляпа{\mathbf{j}}+3 \шляпа{\mathbf {к}}$.

Решение: векторное произведение $\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}$ перпендикулярно обоим $\overrightarrow{\mathbf{A}} \text { и } \overrightarrow{\mathbf{B}}$. Следовательно, единичные векторы $\hat{\mathbf{n}}=\pm \overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}} /|\overrightarrow{\mathbf{A}} \ времена \overrightarrow{\mathbf{B}}|$ перпендикулярны обоим $\overrightarrow{\mathbf{A}} \text {и} \overrightarrow{\mathbf{B}}$. Сначала вычисляем

\[\begin{align}
\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}} &=\left(A_{y} B_{z}-A_{z} B_{ y}\right) \hat{\mathbf{i}}+\left(A_{z} B_{x}-A_{x} B_{z}\right) \hat{\mathbf{j}}+\left (A_{x} B_{y}-A_{y} B_{x}\right) \hat{\mathbf{k}} \\
&=((1)(3)-(-1)(-1 )) \ шляпа {\ mathbf {i}} + ((-1) (2) — (1) (3)) \ шляпа {\ mathbf {j}} + ((1) (- 1) — (1) (2)) \шляпа{\mathbf{k}} \\
&=2 \шляпа{\mathbf{i}}-5 \шляпа{\mathbf{j}}-3 \шляпа{\mathbf{k}}
\end{aligned} \nonumber \]

Теперь вычисляем магнитуду 9{1 / 2} \nonumber \]

Пример 17.4 Объем параллелепипеда

Покажите, что объем параллелепипеда с ребрами, образованными векторами $\overrightarrow{\mathbf{A}}, \overrightarrow{\mathbf {B}}, \text { и }$ $\overrightarrow{\mathbf{C}}$ задается как $\overrightarrow{\mathbf{A}} \cdot(\overrightarrow{\mathbf{B} } \times \overrightarrow{\mathbf{C}})$.

Решение: Объем параллелепипеда равен площади основания, умноженной на высоту. Если основание образовано векторами $\overrightarrow{\mathbf{B}} \text { и } \overrightarrow{\mathbf{C}}$, то площадь основания определяется величиной $ \overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}}$. Вектор $\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}}=|\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}}| \hat{ \mathbf{n}}$, где $\hat{\mathbf{n}}$ — единичный вектор, перпендикулярный основанию (рис. 17.8).

Рисунок 17.8 Пример 17.4

Проекция вектора $\overrightarrow{\mathbf{A}}$ вдоль направления $\hat{\mathbf{n}}$ дает высоту параллелепипеда. Эта проекция задается скалярным произведением $\overrightarrow{\mathbf{A}}$ на единичный вектор и равна $\overrightarrow{\mathbf{A}} \cdot \hat{\mathbf{ п}}=\текст {высота}$. Следовательно,

\[\overrightarrow{\mathbf{A}} \cdot(\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}})=\overrightarrow{\mathbf{A}} \cdot (|\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}}|) \hat{\mathbf{n}}=(|\overrightarrow{\mathbf{B}} \times \overrightarrow{ \mathbf{C}}|) \overrightarrow{\mathbf{A}} \cdot \hat{\mathbf{n}}=(\text {площадь})(\text {высота})=(\text {объем} ) \номер\]

Пример 17. 5. Разложение вектора

Пусть $\overrightarrow{\mathbf{A}}$ — произвольный вектор, а $\hat{\mathbf{n}}$ — единичный вектор направление. Покажите, что \mathbf{n}} \times \overrightarrow{\mathbf{A}}) \times \hat{\mathbf{n}}\)

Решение: пусть $\overrightarrow{\mathbf{A}}=A_{ \|} \hat{\mathbf{n}}+A_{\perp} \hat{\mathbf{e}}$, где $A_{\|}$ — компонент $\overrightarrow{\mathbf{ A}}$ в направлении $\hat{\mathbf{n}}, \hat{\mathbf{e}}$ — это направление проекции $\overrightarrow{\mathbf{A}} $ в плоскости, перпендикулярной $\hat{\mathbf{n}}$, а $A_{\perp}$ является компонентой $\overrightarrow{\mathbf{A}}$ в направление \ (\ шляпа {\ mathbf {e}} \). Поскольку $\hat{\mathbf{e}} \cdot \hat{\mathbf{n}}=0$, мы имеем, что $\overrightarrow{\mathbf{A}} \cdot \hat{\mathbf{ n}}=A_{\|}$. Обратите внимание, что

\[\hat{\mathbf{n}} \times \overrightarrow{\mathbf{A}}=\hat{\mathbf{n}} \times\left(A \hat{\mathbf{n}}+ A_{\perp} \hat{\mathbf{e}}\right)=\hat{\mathbf{n}} \times A_{\perp} \hat{\mathbf{e}}=A_{\perp}( \hat{\mathbf{n}} \times \hat{\mathbf{e}}) \nonumber \]

Единичный вектор $\hat{\mathbf{n}} \times \hat{\mathbf{e }}$ лежит в плоскости, перпендикулярной $\hat{\mathbf{n}}$, а также перпендикулярно $\hat{\mathbf{e}}$. Поэтому $(\hat{\mathbf{n}} \times \hat{\mathbf{e}}) \times \hat{\mathbf{n}}$ также является единичным вектором, параллельным $\ hat{\mathbf{e}}$ (по правилу правой руки. Итак, $(\hat{\mathbf{n}} \times \overrightarrow{\mathbf{A}}) \times \hat{\mathbf{ n}}=A_{\perp}\hat{\mathbf{e}}$, таким образом,

\[\overrightarrow{\mathbf{A}}=A_{\|} \hat{\mathbf{n}}+A_{\perp} \hat{\mathbf{e}}=(\overrightarrow{\mathbf {A}} \cdot \hat{\mathbf{n}}) \hat{\mathbf{n}}+(\hat{\mathbf{n}} \times \overrightarrow{\mathbf{A}}) \times \ шляпа {\ mathbf {n}} \ не число \]

Эта страница под названием 17.2: Vector Product (Cross Product) распространяется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Петром Дурмашкиным (MIT OpenCourseWare) посредством исходного содержимого, которое было отредактировано для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или страница
Автор
Петр Доурмашкин
Лицензия
CC BY-NC-SA
Версия лицензии
4,0
Программа OER или Publisher
MIT OpenCourseWare
Показать оглавление
нет
Метки
1. перекрестное произведение
2. источник@https://ocw.
  No related posts.