Множества,их элементы,поджмножества
Определение 1
В математике совокупности объектов, объединяющие ряд объектов называют множество. Данное понятие является первичным, значит, к более простым понятиям оно не сводится.
Термин множество употребляется тогда, когда речь идет о нечисловых множествах. Например, говорят о множестве диагоналей многоугольника, о множестве точек на координатной прямой, о множестве прямых, проходящих через точку.
Предметы или объекты, образующие данное множество, называются его элементами. Например, число $6$ будет являться элементом множества натуральных чисел, а число $0,9$ не будет являться элементом множества натуральных чисел.
Виды множеств
Множества могут быть конечными и бесконечными, пустыми.
Определение 2
Конечным называют множество, состоящее из конечного числа элементов, но при этом конечное множество может иметь любое количество элементов.
Среди конечных множеств выделяют множество, не имеющее ни одного элемента. Такое множество называется пустым множеством.
Такое множество называется пустым множеством.
Определение 3
Множество, не являющееся конечным, называют бесконечным множеством.
Подмножества
Если некоторое множество не является пустым, то из него можно выделить другие множества, которые будут являться его частями.
Например, из множества натуральных чисел можно выделить множество четных.
В математике часть множества называют — подмножество. Говорят, что множество является подмножеством другого, если каждый элемент подмножества является одновременно и элементом большего множества.
Обозначение множеств, подмножеств и их элементов
Чаще всего множества обозначаются латинскими буквами- $A, B, C , D, X, Y, Z, W$ и Т.Д.
Элементы множеств обозначаются строчными буквами $a,b,c,d,x,y,z$ и Т.Д.
Записать принадлежность некоторого элемента к некоторому множеству, например то, что некоторой элемент $a$ будет входить в множество $A$ математически можно так: $a\in A$. Прочитать данную запись можно так: a принадлежит множеству $A$.
Прочитать данную запись можно так: a принадлежит множеству $A$.
Если же некоторый элемент, например, $b$ не принадлежит множеству $B$, то это записывается так: $b\notin B$.Читают эту запись так: $b$ не принадлежит множеству $B$
Например, если обозначить множество целых чисел за $A$, что тогда можно записать: $3\in A$, $7,5\notin B$
Пустое множество в математике обозначают так: $ᴓ$
Для обозначения того, что множество $B$ является подмножеством множества $A$, используют обозначение: Знак $\subset $ обозначает включение одного множества в другое множество.
Пример 1
Определить какие элементы из перечисленных $12,38,54,79,934$ будут входить в множество $A$- чисел кратных $3$.
Решение: По условию множество $A$ содержит в себе элементы, каждый из которых должен быть кратным, т.е. делится без остатка на $3.$ Значит для того чтобы определить будут ли заданные числа являться элементами множества $A$ нам надо проверить какие из них будут делится на $3$ без остатка, какие нет.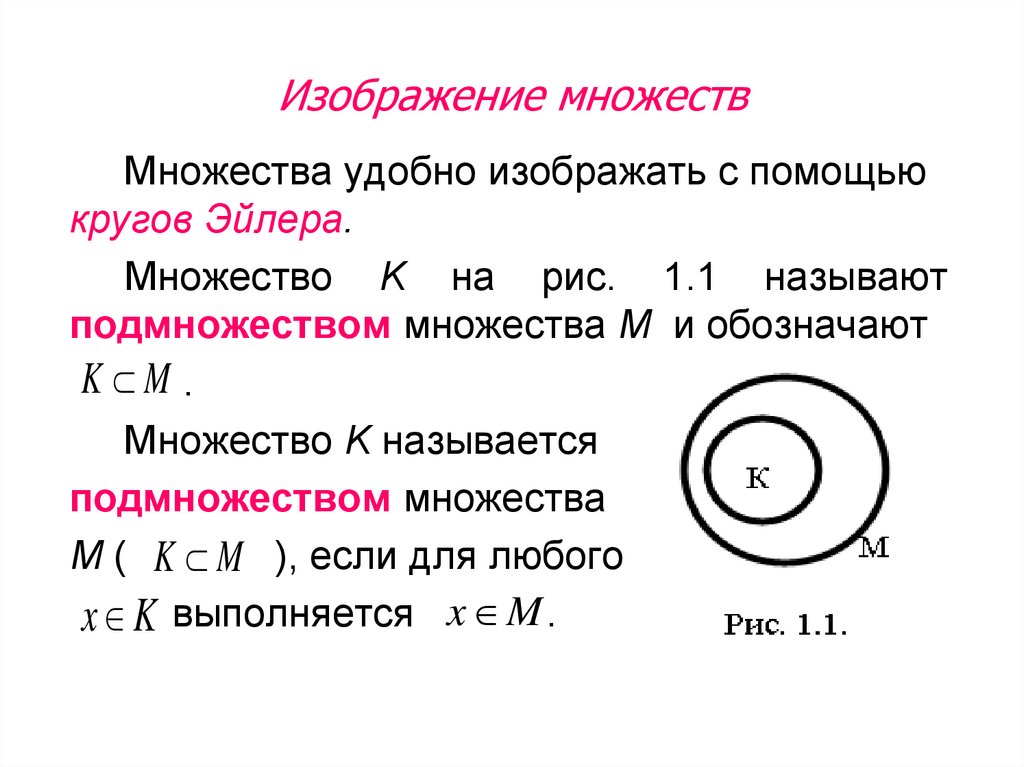
Вспомним признак делимости на $3$: Если сумма цифр, входящих в состав числа делится на $3$, то число делится на $3$ без остатка.
$12$ делится на $3$, т.к. сумма цифр числа $12$ равна $3$
число $38$ на $3$ без остатка делится не будет, т.к. сумма цифр $3+8=11$ не делится на $3$ без остатка
аналогично т.к. суммы цифр числа $54$ равна $9$ доказываем, что на $3$ оно делится, в число $74$ на $3$ делится не будет, т.к. сумма цифр равна $11.$
Найдем сумму цифр числа $934: 9+3+4=16$, число $16$ не кратно $3$ ,значит и число $934$ на $3$ без остатка делится не будет
Теперь сделаем вывод, какие числа будут являться элементами множества $A$:
\[38\notin А, 74\notin А,934\notin А ; 12\in A,\ {\rm :\ }54\in A.\]
Способы задания множеств
Существует два глобально различных способа задания множеств.
Первый заключается в том, что множество задается указанием всех его элементов. В таком случае говорят, что множество задано перечислением всех своих элементов или списком своих элементов. Перечислением элементов можно задать только конечные множества и при небольшом количестве элементов, входящих в него
В таком случае говорят, что множество задано перечислением всех своих элементов или списком своих элементов. Перечислением элементов можно задать только конечные множества и при небольшом количестве элементов, входящих в него
Конечные множества с небольшим количеством элементов обычно записывают в фигурных скобках $\left\{a,b,c\right\}$
При таком способе задания множеств говорят, что множество задано перечислением его элементов.
Второй способ задания множеств применим как для конечных. так и для бесконечных множеств. Он заключается в том, что указывается свойство, которым обладает каждый элемент данного множества — множество задают описанием, т.е. указав его характеристическое свойство, т. е свойство, которым обладают все элементы этого множества и не обладают никакие другие объекты.
Пример 2
Например, с помощью описания можно задать такие множество натуральных чисел от $1$ до $9$ включительно. Характеристическим свойством, т. е. свойством, которым обладают все элементы этого множества для данных элементов будет являться то, что все они являются натуральными числами и каждое из них не меньше $1$ и не больше $9$. Перечислением указанное множество можно задать следующим образом:
Перечислением указанное множество можно задать следующим образом:
$A=\left\{1\ ,2\ ,3,4,5,6,7,8,9\right\}$
Равенство множеств
Множества равны в том случае, если равны их элементы. При этом если множества состоят из одних и тех же элементов, но записанных в разном порядке то эти множества различны, хотя и равны.
Пример 3
Например, рассмотрим множества
$A=\left\{1\ ,2\ ,3,4,5,6,7,8,9\right\}$
$B=\left\{9,8,7,6,5,4,3,2,1\right\}$
Эти множества будут, состоят из равных элементов, значит, они будут равны, но при этом элементы расположены в разном порядке, т.е. множества различны
Пересечение множеств
Если даны два множества, то можно образовать новое множество, составленное из общих элементов этих множеств.
Пример 4
Например, рассмотрим два множества:
$A=\left\{1\ ,2,3,4,5\right\}$
$B=\left\{9,7,5,3,\right\}$
Общей частью этих множеств будет множество $C=\left\{3,5,\right\}$
Математически это можно обозначить так: $А\cap B=\left\{3,5\right\}$
Пересечением множеств $A$ и $B$ называется новое множество, содержащее те и только те элементы, которые входят одновременно и в множество $A$ и в множество $B$.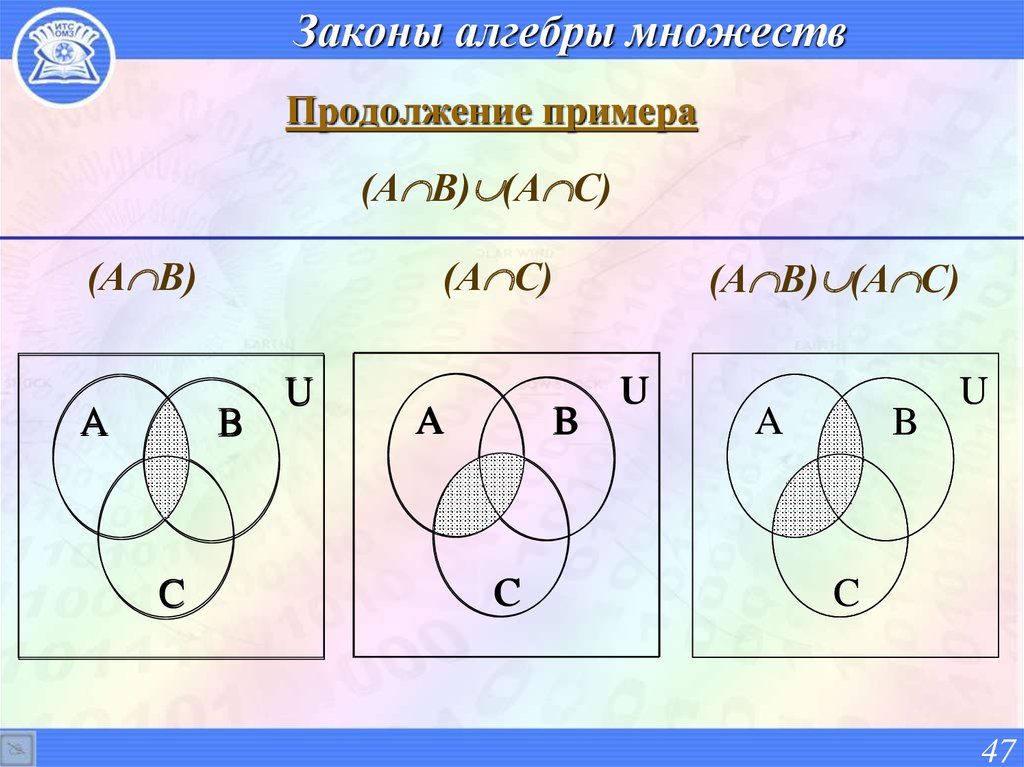
Объединение множеств
Из двух множеств $A$ и $B$ можно образовать новое множество, объединяя все элементы множества $A$ и все элементы множества $B$
Математически это можно обозначить так:$\ А\ \cup B$
Объединением множеств $A$ и $B$ называется новое множество$\ А\ \cup B$, состоящее из тех и только из тех элементов, которые входят хотя бы в одно из множеств $A$ или $B$.
Разность множеств
Разностью двух множеств $A$ и $B$ называют такое множество, в которое входят все элементы из множества $A$, не принадлежащие множеству $B$.
Python и теория множеств / Хабр
В Python есть очень полезный тип данных для работы с множествами – это set. Об этом типе данных, примерах использования, и небольшой выдержке из теории множеств пойдёт речь далее.
Следует сразу сделать оговорку, что эта статья ни в коем случае не претендует на какую-либо математическую строгость и полноту, скорее это попытка доступно продемонстрировать примеры использования множеств в языке программирования Python.
- Множество
- Множества в Python
- Хешируемые объекты
- Свойства множеств
- Принадлежность множеству
- Мощность множества
- Перебор элементов множества
- Отношения между множествами
- Равные множества
- Непересекающиеся множества
- Подмножество и надмножество
- Операции над множествами
- Объединение множеств
- Добавление элементов в множество
- Пересечение множеств
- Разность множеств
- Удаление элементов из множества
- Симметрическая разность множеств
- Заключение
- Полезные ссылки
Множество
Множество – это математический объект, являющийся набором, совокупностью, собранием каких-либо объектов, которые называются элементами этого множества. Или другими словами:
Множество – это не более чем неупорядоченная коллекция уникальных элементов.
Что значит неупорядоченная? Это значит, что два множества эквивалентны, если содержат одинаковые элементы.
Элементы множества должны быть уникальными, множество не может содержать одинаковых элементов. Добавление элементов, которые уже есть в множестве, не изменяет это множество.
Множества, состоящие из конечного числа элементов, называются конечными, а остальные множества – бесконечными. Конечное множество, как следует из названия, можно задать перечислением его элементов. Так как темой этой статьи является практическое использование множеств в Python, то я предлагаю сосредоточиться на конечных множествах.
Множества в Python
Множество в Python можно создать несколькими способами. Самый простой – это задать множество перечислением его элементов в фигурных скобках:
fruits = {"banana", "apple", "orange"} Единственное ограничение, что таким образом нельзя создать пустое множество. Вместо этого будет создан пустой словарь:
Вместо этого будет создан пустой словарь:
wrong_empty_set = {}
print(type(wrong_empty_set))
# Вывод
<class "dict">Для создания пустого множества нужно непосредственно использовать set():
correct_empty_set = set() print(type(correct_empty_set)) # Вывод <class "set">
Также в set() можно передать какой-либо объект, по которому можно проитерироваться (Iterable):
color_list = ["red", "green", "green", "blue", "purple", "purple"]
color_set = set(color_list)
print(color_set)
# Вывод (порядок может быть другим):
{"red", "purple", "blue", "green"}Ещё одна возможность создания множества – это использование set comprehension. Это специальная синтаксическая конструкция языка, которую иногда называют
numbers = [1, 2, 2, 2, 3, 3, 4, 4, 5, 6]
# Единственное отличие со списковыми включениями - это
# использование фигурных скобок вместо квадратных
even_numbers = {
number for number in numbers
if number % 2 == 0
}
print(even_numbers)
# Вывод (порядок может быть другим):
{2, 4, 6}Хешируемые объекты
Существует ограничение, что элементами множества (как и ключами словарей) в Python могут быть только так называемые хешируемые (Hashable) объекты. Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари – это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (int, float, str, bool, и т.д.) – хешируемые. Неизменяемые коллекции, например tuple, являются хешируемыми, если хешируемы все их элементы.
Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари – это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (int, float, str, bool, и т.д.) – хешируемые. Неизменяемые коллекции, например tuple, являются хешируемыми, если хешируемы все их элементы.
# Множество кортежей (tuple)
records = {
("Москва", 17_200_000),
("Санкт-Петербург", 5_400_000),
("Новосибирск", 1_600_000),
("Москва", 17_200_000),
}
for city, population in records:
print(city)
# Вывод (порядок может быть другим):
Москва
Новосибирск
Санкт-ПетербургОбъекты пользовательских классов являются хешируемыми по умолчанию. Но практического смысла чаще всего в этом мало из-за того, что сравнение таких объектов выполняется по их адресу в памяти, т.е. невозможно создать два «равных» объекта.
class City:
def __init__(self, name: str):
self. name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}
name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}Скорее всего мы предполагаем, что объекты City("Moscow") должны быть равными, и следовательно в множестве cities должен находиться один объект.
Этого можно добиться, если определить семантику равенства для объектов класса City:
class City:
def __init__(self, name: str):
# Атрибут name не должен изменяться, пока объект существует
# Для простоты пометим этот атрибут как внутренний
self._name = name
def __hash__(self) -> int:
""" Хеш от объекта
"""
return hash((self._name, self.__class__))
def __eq__(self, other) -> bool:
""" Определяем семантику равентсва (оператор ==)
"""
if not isinstance(other, self. __class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'
__class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'Чтобы протокол хеширования работал без явных и неявных логических ошибок, должны выполняться следующие условия:
- Хеш объекта не должен изменяться, пока этот объект существует
- Равные объекты должны возвращать одинаковый хеш
moscow = City("Moscow")
moscow_again = City("Moscow")
print(moscow == moscow_again and hash(moscow) == hash(moscow_again))
# Вывод:
True
# Теперь множество городов работает более логично и интуитивно
cities = {City("Moscow"), City("Kazan"), City("Moscow")}
print(cities)
# Вывод (порядок может быть другим):
{City("Kazan"), City("Moscow")}Свойства множеств
Тип set в Python является подтипом Collection
- Определена операция проверки принадлежности элемента множеству
- Можно получить количество элементов в множестве
- Множества являются iterable-объектами
Принадлежность множеству
Проверить принадлежит ли какой-либо объект множеству можно с помощью оператора in. Это один из самых распространённых вариантов использования множеств. Такая операция выполняется в среднем за
Это один из самых распространённых вариантов использования множеств. Такая операция выполняется в среднем за O(1) с теми же оговорками, которые существуют для хеш-таблиц.
tremendously_huge_set = {"red", "green", "blue"}
if "green" in tremendously_huge_set:
print("Green is there!")
else:
print("Unfortunately, there is no green...")
# Вывод:
Green is there!
if "purple" in tremendously_huge_set:
print("Purple is there!")
else:
print("Unfortunately, there is no purple...")
# Вывод:
Unfortunately, there is no purple... Мощность множества
Мощность множества – это характеристика множества, которая для конечных множеств просто означает количество элементов в данном множестве. Для бесконечных множеств всё несколько сложнее.
even_numbers = {i for i in range(100) if i % 2 == 0}
# Мощность множества
cardinality = len(even_numbers)
print(cardinality)
# Вывод:
50Перебор элементов множества
Как уже было отмечено выше, множества поддерживают протокол итераторов, таким образом любое множество можно использовать там, где ожидается iterable-объект.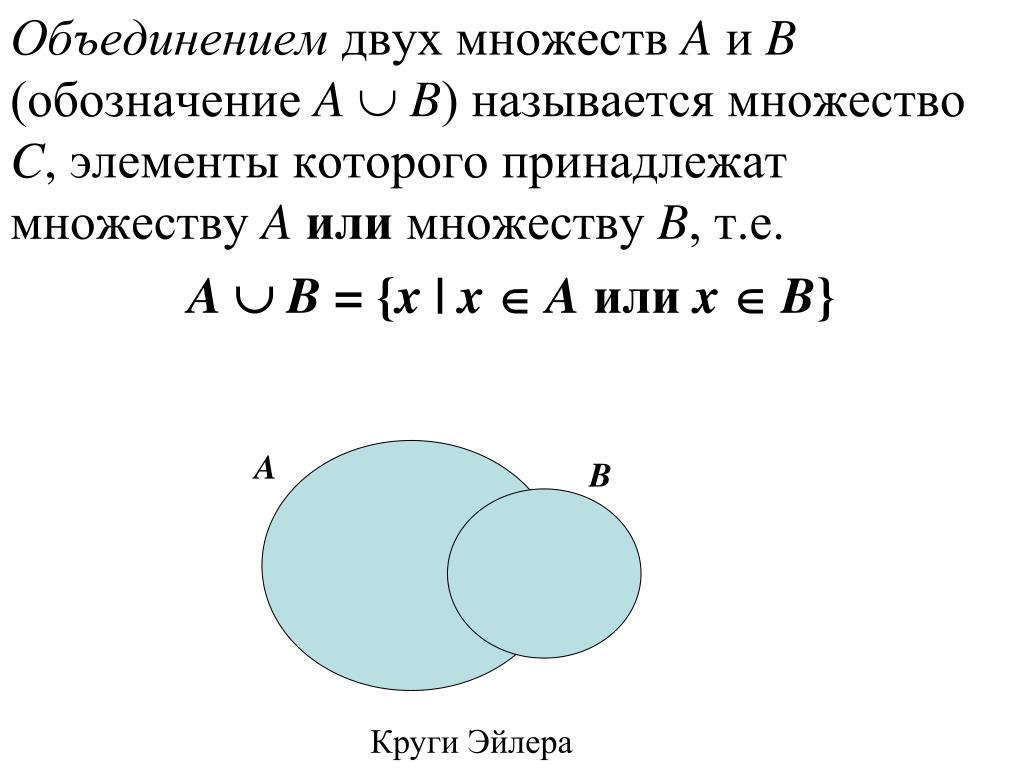
colors = {"red", "green", "blue"}
# Элементы множества можно перебрать с помощью цикла for
for color in colors:
print(color)
# Вывод (порядок может быть другим):
red
green
blue
# Множества можно использовать там, где ожидается iterable-объект
color_counter = dict.fromkeys(colors, 1)
print(color_counter)
# Вывод (порядок может быть другим):
{"green": 1, "red": 1, "blue": 1}Отношения между множествами
Между множествами существуют несколько видов отношений, или другими словами взаимосвязей. Давайте рассмотрим возможные отношения между множествами в этом разделе.
Равные множества
Тут всё довольно просто – два множества называются равными, если они состоят из одних и тех же элементов. Как следует из определения множества, порядок этих элементов не важен.
my_fruits = {"banana", "apple", "orange", "orange"}
your_fruits = {"apple", "apple", "banana", "orange", "orange"}
print(my_fruits == your_fruits)
# Вывод:
TrueНепересекающиеся множества
Если два множества не имеют общих элементов, то говорят, что эти множества не пересекаются.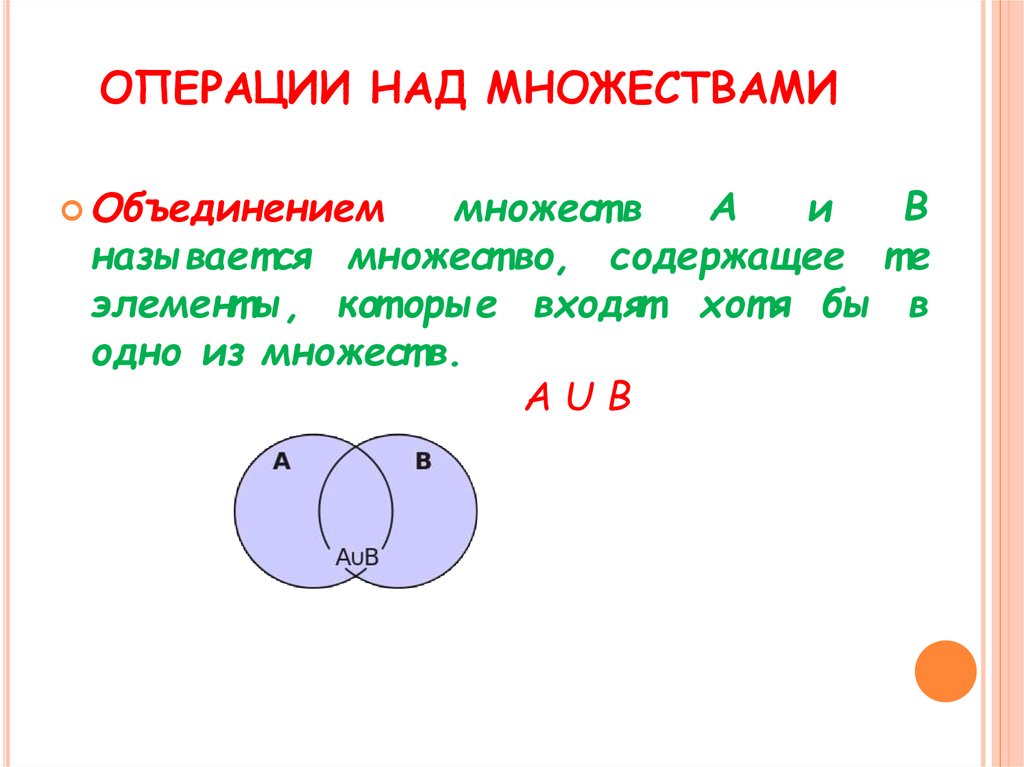 Или другими словами, пересечение этих множеств является пустым множеством.
Или другими словами, пересечение этих множеств является пустым множеством.
even_numbers = {i for i in range(10) if i % 2 == 0}
odd_numbers = {i for i in range(10) if i % 2 == 1}
# Очевидно, что множества чётных и нечётных чисел не пересекаются
if even_numbers.isdisjoint(odd_numbers):
print("Множества не пересекаются!")
# Вывод:
Множества не пересекаются!Подмножество и надмножество
Подмножество множества S – это такое множество, каждый элемент которого является также и элементом множества S. Множество S в свою очередь является надмножеством исходного множества.
# Множество чисел Фибоначчи меньших 100
fibonacci_numbers = {0, 1, 2, 3, 34, 5, 8, 13, 21, 55, 89}
# Множество натуральных чисел меньших 100
natural_numbers = set(range(100))
# Множество чисел Фибоначчи является подмножеством множества
# натуральных чисел
if fibonacci_numbers.issubset(natural_numbers):
print("Подмножество!")
# Вывод:
Подмножество!
# В свою очередь множество натуральных чисел является
# надмножеством множества чисел Фибоначчи
if natural_numbers. issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество!
issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество!Пустое множество является подмножеством абсолютно любого множества.
empty = set()
# Методы issubset и issuperset могут принимать любой iterable-объект
print(
empty.issubset(range(100))
and empty.issubset(["red", "green", "blue"])
and empty.issubset(set())
)
# Вывод:
TrueСамо множество является подмножеством самого себя.
natural_numbers = set(range(100))
if natural_numbers.issubset(natural_numbers):
print("Подмножество!")
# Вывод:
Подмножество!Операции над множествами
Рассмотрим основные операции, опредяляемые над множествами.
Объединение множеств
Объединение множеств – это множество, которое содержит все элементы исходных множеств. В Python есть несколько способов объединить множества, давайте рассмотрим их на примерах.
my_fruits = {"apple", "orange"}
your_fruits = {"orange", "banana", "pear"}
# Для объединения множеств можно использовать оператор `|`,
# оба операнда должны быть объектами типа set
our_fruits = my_fruits | your_fruits
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
# Также можно использовать ментод union. # Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
# Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}Добавление элементов в множество
Добавление элементов в множество можно рассматривать как частный случай объединения множеств за тем исключением, что добавление элементов изменяет исходное множество, а не создает новый объект. Добавление одного элемента в множество работает за O(1).
colors = {"red", "green", "blue"}
# Метод add добаляет новый элемент в множество
colors.add("purple")
# Добавление элемента, который уже есть в множестве, не изменяет
# это множество
colors.add("red")
print(colors)
# Вывод (порядок может быть другим):
{"red", "green", "blue", "purple"}
# Метод update принимает iterable-объект (список, словарь, генератор и т.п.)
# и добавляет все элементы в множество
numbers = {1, 2, 3}
numbers. update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}
update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}Пересечение множеств
Пересечение множеств – это множество, в котором находятся только те элементы, которые принадлежат исходным множествам одновременно.
def is_prime(number: int) -> bool:
""" Возвращает True, если number - это простое число
"""
assert number > 1
return all(number % i for i in range(2, int(number**0.5) + 1))
def is_fibonacci(number: int) -> bool:
""" Возвращает True, если number - это число Фибоначчи
"""
assert number > 1
a, b = 0, 1
while a + b < number:
a, b = b, a + b
return a + b == number
# Множество простых чисел до 100
primes = set(filter(is_prime, range(2, 101)))
# Множество чисел Фибоначчи до 100
fibonacci = set(filter(is_fibonacci, range(2, 101)))
# Множество простых чисел до 100, которые одновременно являются
# числами Фибоначчи
prime_fibonacci = primes.intersection(fibonacci)
# Или используя оператор `&`, который определён для множеств
prime_fibonacci = fibonacci & primes
print(prime_fibonacci)
# Вывод (порядок может быть другим):
{2, 3, 5, 13, 89}При использовании оператора & необходимо, чтобы оба операнда были объектами типа set. Метод
Метод intersection, в свою очередь, принимает любой iterable-объект. Если необходимо изменить исходное множество, а не возращать новое, то можно использовать метод intersection_update, который работает подобно методу intersection, но изменяет исходный объект-множество.
Разность множеств
Разность двух множеств – это множество, в которое входят все элементы первого множества, не входящие во второе множество.
i_know: set = {"Python", "Go", "Java"}
you_know: dict = {
"Go": 0.4,
"C++": 0.6,
"Rust": 0.2,
"Java": 0.9
}
# Обратите внимание, что оператор `-` работает только
# для объектов типа set
you_know_but_i_dont = set(you_know) - i_know
print(you_know_but_i_dont)
# Вывод (порядок может быть другим):
{"Rust", "C++"}
# Метод difference может работать с любым iterable-объектом,
# каким является dict, например
i_know_but_you_dont = i_know.difference(you_know)
print(i_know_but_you_dont)
# Вывод:
{"Python"}Удаление элементов из множества
Удаление элемента из множества можно рассматривать как частный случай разности, где удаляемый элемент – это одноэлементное множество. Следует отметить, что удаление элемента, как и в аналогичном случае с добавлением элементов, изменяет исходное множество. Удаление одного элемента из множества имеет вычислительную сложность
Следует отметить, что удаление элемента, как и в аналогичном случае с добавлением элементов, изменяет исходное множество. Удаление одного элемента из множества имеет вычислительную сложность O(1).
fruits = {"apple", "orange", "banana"}
# Удаление элемента из множества. Если удаляемого элемента
# нет в множестве, то ничего не происходит
fruits.discard("orange")
fruits.discard("pineapple")
print(fruits)
# Вывод (порядок может быть другим):
{"apple", "banana"}
# Метод remove работает аналогично discard, но генерирует исключение,
# если удаляемого элемента нет в множестве
fruits.remove("pineapple") # KeyError: "pineapple"Также у множеств есть метод differenсe_update, который принимает iterable-объект и удаляет из исходного множества все элементы iterable-объекта. Этот метод работает аналогично методу difference, но изменяет исходное множество, а не возвращает новое.
numbers = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
even_numbers_under_100 = (i for i in range(1, 101) if i % 2 == 0)
numbers. , также существует два специальных метода –
, также существует два специальных метода – symmetric_difference и symmetric_difference_update. Оба этих метода принимают iterable-объект в качестве аргумента, отличие же состоит в том, что symmetric_difference возвращает новый объект-множество, в то время как symmetric_difference_update изменяет исходное множество.non_positive = {-3, -2, -1, 0}
non_negative = range(4)
non_zero = non_positive.symmetric_difference(non_negative)
print(non_zero)
# Вывод (порядок может быть другим):
{-1, -2, -3, 1, 2, 3}
# Метод symmetric_difference_update изменяет исходное множество
colors = {"red", "green", "blue"}
colors.symmetric_difference_update(["green", "blue", "yellow"])
print(colors)
# Вывод (порядок может быть другим):
{"red", "yellow"}
Заключение
Я надеюсь, мне удалось показать, что Python имеет очень удобные встроенные средства для работы с множествами. На практике это часто позволяет сократить количество кода, сделать его выразительнее и легче для восприятия, а следовательно и более поддерживаемым. Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
Полезные ссылки
Множества (Статья на Википедии)
Документация по типу set
Iterable-объекты (Глоссарий Python)
Hashable-объекты (Глоссарий Python)
Sets in Python
Set Theory: the Method To Database Madness
Докажите что множества равны
Алгебра 8 класс. Контрольная работа КР-1 Множества и операции над ними для УМК Мерзляк, Поляков (УГЛУБЛЕННОЕ изучение) + ОТВЕТЫ. Цитаты из пособия «Алгебра 8 класс Самостоятельные и контрольные работы» (авт. Мерзляк, Полонский, Рабинович и др., изд-во «Вентана-Граф») использованы в учебных целях.
Контрольная работа № 1 по алгебре в 8 классе (угл.)
КР-1 Множества и операции над ними
Тема. Множества и операции над ними. Вариант 1.
1. Задайте с помощью перечисления элементов множество A = <>.
2. Запишите все подмножества множества делителей числа 7.
3. Какие из приведённых утверждений являются верными:
4. Какие из приведённых утверждений являются верными:
5. На фирме работает 29 человек. Из них 15 человек знают немецкий язык, 21 — английский и 8 человек знают оба языка. Сколько работников фирмы не знают ни одного из этих языков?
6. Докажите, что множества А и В равны.
7. Докажите, что множество чисел вида , где n е N, счётно.
8. Множество А содержит 25 элементов. Каких подмножеств этого множества больше: с чётным количеством элементов или с нечётным количеством элементов?
ОТВЕТЫ на Контрольную № 1
ВАРИАНТ 1.
№ 1. A = <2, -7>
№ 2. A = <1, -1, 7, -7>
№ 3. 1) не верно, 2) не верно, 3) не верно, 4) не верно
№ 4. 1) верно, 2) не верно, 3) не верно, 4) верно, 5) верно, 6) верно.
№ 5. Ответ: 1 человек
№ 6. А = В, если их объединение и пересечение совпадает. A ∪ B = . A ∩ B =.
А = В, если их объединение и пересечение совпадает. A ∪ B = . A ∩ B =.
№ 7. При n = 1 ⇒ 1/2; при n = 2 ⇒ 1/4; при n = 3 ⇒ 1/6 и так далее. Все элементы множества различны и образуют числовую последовательность. Значит, счётно.
№ 8. 1 и 25 (начало и конец) — нечетные числа. Значит, нечетных будет больше.
ВАРИАНТ 2.
№ 1. A = <4, -6>
№ 2. A = <1, -1, 5, -5>
№ 3. 1) не верно, 2) не верно, 3) не верно, 4) не верно
№ 4. 1) не верно, 2) верно, 3) верно, 4) верно, 5) не верно, 6) не верно.
№ 5. Ответ: 5 человек
№ 6. C = D, если их объединение и пересечение совпадает. C ∪ D = . C ∩ D =.
№ 7. При k = 1 ⇒ 1/3; при k = 2 ⇒ 1/6; при k = 3 ⇒ 1/9 и так далее. Все элементы множества различны и образуют числовую последовательность. Значит, счётно.
№ 8. 1 и 27 (начало и конец) — нечетные числа. Значит, нечетных будет больше.
1 и 27 (начало и конец) — нечетные числа. Значит, нечетных будет больше.
Алгебра 8 класс. Контрольная работа № 1 «Множества и операции над ними» для УМК Мерзляк, Поляков (УГЛУБЛЕННОЕ изучение) + ОТВЕТЫ. Цитаты из пособия «Алгебра 8 класс Самостоятельные и контрольные работы» (авт. Мерзляк, Полонский, Рабинович и др., изд-во «Вентана-Граф») использованы в учебных целях.
Очень часто в задачах по дискретной математике, а именно в теории множеств, требуется доказать равенство множеств. Напомним, что равенство множеств $M=N$ означает выполнение взаимного включения, то есть $Msubseteq N$ и $Nsubseteq M$. Следовательно, для доказательства равенства $M=N$ множеств $M, N$ нужно показать выполнение этих включений. Делать это можно различными способами:
- по определению теоретико-множественных операций;
- с помощью законов алгебры множеств;
- построением диаграмм Эйлера-Венна;
- построением таблиц принадлежности;
- используя индикаторные функции.

Продемонстрируем каждый из этих способов на конкретном примере.
Доказать равенство множеств:
$$left(Acap B
ight)ackslash C=left(Aackslash C
ight)cap left(Backslash C
ight)$$
1. Равенство двух множеств $M=N$ эквивалентно двум включениям $Msubseteq N, Nsubseteq M$.
Докажем, что $left(Acap B
ight)ackslash Csubseteq left(Aackslash C
ight)cap left(Backslash C
ight)$. Пусть $xin left(Acap B
ight)ackslash C$, тогда по определению разности множеств $xin left(Acap B
ight)$ и $x
otin C$. По определению пересечения множеств $xin left(Acap B
ight)$ тогда и только тогда, когда $xin A$ и $xin B$. Так как $xin A$ и $x
otin C$, то $xin Aackslash C$. Так как $xin B$ и $x
otin C$, то $xin Backslash C$. По определению пересечения получаем, что $xin left(Aackslash C
ight)cap left(Backslash C
ight)$. Что доказывает то, что $left(Acap B
ight)ackslash Csubseteq left(Aackslash C
ight)cap left(Backslash C
ight)$.
Докажем, что $left(Aackslash C
ight)cap left(Backslash C
ight)subseteq left(Acap B
ight)ackslash C$. Пусть $xin left(Aackslash C
ight)cap left(Backslash C
ight)$, тогда по определению пересечения множеств $xin left(Aackslash C
ight)$ и $xin left(Backslash C
ight)$. По определению разности множеств $xin A$, $x
otin C$ и $xin B, x
otin C$. По определению пересечения получаем, что $xin left(Acap B
ight) и x
otin C$, то есть $xin left(Acap B
ight)ackslash C$. Что доказывает то, что $left(Aackslash C
ight)cap left(Backslash C
ight)subseteq left(Acap B
ight)ackslash C$. Из доказанных включений следует, что $Aleft(Acap B
ight)ackslash C=left(Aackslash C
ight)cap left(Backslash C
ight)$.
2. Докажем справедливость соотношения $left(Acap B
ight)ackslash C=left(Aackslash C
ight)cap left(Backslash C
ight)$, используя основные законы алгебры множеств.
Операцию разность $Xackslash Y$ произвольных множеств $X, Y$ можно записать, как $Xackslash Y=Xcap overline$. Тогда для левой части данного соотношения $left(Acap B
Тогда для левой части данного соотношения $left(Acap B
ight)ackslash C=Acap Bcap overline$. Для правой части: $left(Aackslash C
ight)cap left(Backslash C
ight)=Acap overlinecap Bcap overline=Acap Bcap overline$. Видим, что левая и правая части в результате преобразований совпали $Acap Bcap overline=Acap Bcap overline$. Соотношение верно.
3. Видим, что диаграммы множеств $left(Acap B
ight)ackslash C$ и $left(Aackslash C
ight)cap left(Backslash C
ight)$ полностью совпадают, значит, равенство $left(Acap B
ight)ackslash C=left(Aackslash C
ight)cap left(Backslash C
ight)$ верно.
4. Построим таблицу принадлежности для левой и правой частей данного равенства $left(Acap B
ight)ackslash C=left(Aackslash C
ight)cap left(Backslash C
ight)$.
egin <|c|c|>hline A & B & C & Acap B & left(Acap B
ight)ackslash C & Aackslash C & Backslash C & left(Aackslash C
ight)cap left(Backslash C
ight) \ hline 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \ hline 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \ hline 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 \ hline 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \ hline 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \ hline 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \ hline 1 & 1 & 0 & 1 & 1 & 1 & 1 & 1 \ hline 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \ hline end
Видим, что $left(Acap B
ight)ackslash C=left(Aackslash C
ight)cap left(Backslash C
ight)=left(00000010
ight)$.
5. Докажем справедливость соотношения $left(Acap B
ight)ackslash C=left(Aackslash C
ight)cap left(Backslash C
ight)$ с помощью индикаторных функций. Индикаторная функция для левой части соотношения:
$$ <chi >_<left(Acap B
ight)ackslash C>left(x
ight)=<chi >_left(x
ight)-<chi >_left(x
ight)<chi >_Cleft(x
ight)=<chi >_Aleft(x
ight)<chi >_Bleft(x
ight)-<chi >_Aleft(x
ight)<chi >_Bleft(x
ight)<chi >_Cleft(x
ight)=<chi >_Aleft(x
ight)<chi >_Bleft(x
ight)cdot left(1-<chi >_Cleft(x
ight)
ight)$$ Индикаторная функция для правой части: $$<chi >_<left(Aackslash C
ight)cap left(Backslash C
ight)>left(x
ight)=<chi >_<left(Aackslash C
ight)>left(x
ight)<chi >_<left(Backslash C
ight)>left(x
ight)=left(<chi >_Aleft(x
ight)-<chi >_Aleft(x
ight)<chi >_Cleft(x
ight)
ight)left(<chi >_Bleft(x
ight)-<chi >_Bleft(x
ight)<chi >_Cleft(x
ight)
ight)=<chi >_Aleft(x
ight)<chi >_Bleft(x
ight)-<chi >_Aleft(x
ight)<chi >_Bleft(x
ight)<chi >_Cleft(x
ight)-<chi >_Aleft(x
ight)<chi >_Bleft(x
ight)<chi >_Cleft(x
ight)+<chi >_Aleft(x
ight)<chi >_Bleft(x
ight)<chi >_Cleft(x
ight)=<chi >_Aleft(x
ight)<chi >_Bleft(x
ight)-<chi >_Aleft(x
ight)<chi >_Bleft(x
ight)<chi >_Cleft(x
ight)=<chi >_Aleft(x
ight)<chi >_Bleft(x
ight)left(1-<chi >_Cleft(x
ight)
ight). $$ Видим, что индикаторные функции обеих частей совпали $$<chi >_Aleft(x
$$ Видим, что индикаторные функции обеих частей совпали $$<chi >_Aleft(x
ight)<chi >_Bleft(x
ight)cdot left(1-<chi >_Cleft(x
ight)
ight)=<chi >_Aleft(x
ight)<chi >_Bleft(x
ight)cdot left(1-<chi >_Cleft(x
ight)
ight).$$ Соотношение верно.
Универсальное множество. Дополнение множества
Если А и В два множества, состоящие из одних и тех же элементов, и не содержат никаких других элементов, то говорят, что множества равны: А = В.
Если каждый элемент множества А является в то же время элементом множества В, то множество А называют подмножеством, или частью, множества В. Это отношение записывается так: А В или В А.
На рис. 2.1 дана иллюстрация этого определения с помощью так называемых диаграмм Венна (диаграмма Венна – это замкнутая линия, внутри которой расположены элементы данного множества, а снаружи – элементы, не принадлежащие этому множеству).
Приведем примеры подмножеств:
множество жителей Самары является подмножеством множества жителей России;
множество всех квадратов есть подмножество множества всех прямоугольников;
множество Z всех целых чисел есть подмножество множества R всех действительных чисел.
Если одновременно А В, а В А, то эти множества равны: А = В.
Отметим, что каждое непустое множество имеет, по крайней мере, два подмножества: пустое множество и само множество.
Пусть дано какое-либо множество Е. Тогда, если рассматриваются все возможные подмножества данного множества, его называют универсальным множеством. На диаграммах Венна прямоугольник как раз и символизирует это универсальное множество.
Например, рассмотрим множество книг в университетской библиотеке. В него входят подмножества научных, художественных книг, книг по искусству и т.д. Научные в свою очередь тоже можно разбить на подмножества книг по математике, физике, химии и т. д. То есть множество всех книг – это универсальное множество, содержащее в себе различные подмножества книг.
д. То есть множество всех книг – это универсальное множество, содержащее в себе различные подмножества книг.
Рассмотрим другой пример. Пусть универсальное множество Е состоит из трех элементов: <a; b; c>. Перечислим все подмножества Е: <a>, <b>, <c>, <a, b>, <a, c>, <b, c>, <a, b, c>, <>. Их всего 8, т.е. 2 3 . Не трудно доказать, что если элементов будет n, то подмножеств будет 2 n .
Пусть множество А есть некоторое подмножества универсального множества Е. Тогда множество , состоящее из элементов множестваЕ, не принадлежащих множеству А, называется дополнением множества А до универсального множества Е (рис. 2.2).
Например, если Е = <целые числа>, А = <четные числа>, то = <нечетные числа>.
3.
 . Операции над множествами
. Операции над множествамиСуммой, или объединением, двух множеств А и В называется множество
элементы которого с С принадлежат либо А, либо В, либо принадлежат и А и В.
Данное определение можно распространить на случай произвольного конечного или бесконечного числа множеств.
На рис. 3.1 показана диаграмма Венна объединения двух (а) и трех (б) множеств.
►Пример 3.1.Заданы числовые множестваА= <3, 5, 7, 13>иВ= <2, 4, 5, 7, 9>. Найти множествоС=АВ. Показать решение с помощью диаграмм Венна.
Решение. Множество С состоит из всех элементов входящих в множество А или множество В. Союз «или» здесь не разделительный, то есть не исключается возможность одновременной принадлежности некоторых элементов и множеству А и множеству В. Итак,
Изобразим С=АВс помощью диаграммы Венна (рис. 3.2). Для наглядности множества показаны вместе с элементами. ◄
3.2). Для наглядности множества показаны вместе с элементами. ◄
Произведением, или пересечением, двух множеств А и В называется множество
элементы которого с С принадлежат одновременно и А и В.
Данное определение также можно распространить на случай произвольного конечного или бесконечного числа множеств.
На рис. 3.3 показана диаграмма Венна пересечения двух (а) и трех (б) множеств.
►Пример 3.2.По условиям примера 3.1 найти множество
Решение. Множество С состоит из всех элементов входящих одновременно как в А, так и в В. Как видно из рис. 3.2 такими элементами являются 5 и 7. Следовательно
►Пример 3.3. Пусть А = <1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72>– множество натуральных делителей числа 72, а В = <1, 2, 3, 6, 9, 18, 27, 54>– множество натуральных делителей числа 54. Тогда множество С = <1, 2, 3, 6, 9, 18>является пересечением множеств А и В, а числа, входящие в множество С, являются делителями для 72 и 54. Наибольший элемент множества С, то есть 18, называется наибольшим общим делителем чисел 54 и 72. ◄
Наибольший элемент множества С, то есть 18, называется наибольшим общим делителем чисел 54 и 72. ◄
Следует отметить, что пересечение нескольких непустых множеств может быть пустым множеством.
Термин «пересечение» по существу геометрического происхождения. Например, если прямая и плоскость не параллельны, то их пересечением является точка.
Разностью двух множеств А и В называется множество
состоящее из элементов, принадлежащих множеству А, но не принадлежащих множествуВ.
Разность между множеством А и множеством В часто называется дополнением множества В до множества А.
►Пример 3.4. Пусть заданы множества А = <3, 5, 7, 13>и В = <2, 4, 5, 7, 9>. Тогда разности этих множеств будут иметь вид:
Введение понятия множества в 8-м классе
Ключевые слова: множество,
пустое множество,
конечные и бесконечные множества,
числовые множества
Множества в школьной математике ведут себя
примерно так же, как обитатели леса: мы их почти
не видим, но знаем, что они есть.
В классах с углубленным изучением математики
основные понятия теории множеств
рассматриваются достаточно подробно. Например, в
[1] им посвящена глава "Элементы теории
множеств". Ученик, изучивший эту главу, сможет
лучше ориентироваться в других разделах
математики.
Для обычного класса такую подготовку провести
трудно, даже если содержание упомянутой главы
значительно сократить. Слишком много новых
терминов, чисто абстрактных рассуждений и
специфической символики. Да и количество часов
по программе не позволяет вводить
дополнительную тему. Но если ученика
математического класса можно сравнить с опытным
охотником, который уверенно идет по лесу, то
ученику обычного класса нужен хотя бы
определенный минимум знаний по теории множеств,
чтобы не заблудиться в трех соснах.
В обычных классах множества только изредка
упоминаются. Чтобы сильные ученики смогли, тем не
менее, овладеть нужными знаниями, возможно,
например, изучать элементы теории множеств на
факультативных занятиях. Но все-таки по
возможности основные сведения должны получить
все дети.
Но все-таки по
возможности основные сведения должны получить
все дети.
Решительный шаг в этом направлении сделан в
последнем издании учебника по алгебре для 8
класса [5]. В прежних изданиях в разделе
"Квадратные корни" назывались основные
числовые множества (натуральные числа, целые,
рациональные, действительные). Вводился знак
принадлежности. Сейчас к этому добавилось
определение подмножества (и знак включения).
Говорится о взаимно однозначном соответствии
между точками на прямой и действительными
числами.
В теме "Неравенства" помимо рассмотрения
числовых промежутков введен параграф
"Пересечение и объединение множеств". Если
раньше данным терминам уделялось немного
внимания при рассмотрении промежутков, то теперь
ученик сможет более детально ознакомиться с
операциями над множествами. С недавних пор
появился новый предмет "Теория вероятностей и
статистика". Как раз в курсе теории вероятностей
для 8 класса [6] при изучении алгебры событий
говорится о правиле суммы и произведения,
демонстрируются в качестве иллюстраций круги
Эйлера. Нам представляется, что если ученик к
этому времени будет знать, что такое вообще
объединение и пересечение множеств (а не только
для числовых множеств), то и в теории
вероятностей объединение, пересечение событий
этот ученик встретит как своих знакомых.
Нам представляется, что если ученик к
этому времени будет знать, что такое вообще
объединение и пересечение множеств (а не только
для числовых множеств), то и в теории
вероятностей объединение, пересечение событий
этот ученик встретит как своих знакомых.
Но хотелось бы отметить, что само понятие
множества в [5]подробно не обсуждается.
По-видимому, авторы учебника допускают, что
интуитивно ученик понимает это слово, первый раз
встречаясь со словами "множество натуральных
чисел" и т.д. Практика показывает, что это не так.
У детей в первую очередь срабатывает реакция на
названия "натуральные", "целые" и т.д. Они
стараются их не перепутать, особенно
"рациональные", "иррациональные",
"действительные". Хотя предварительные
сведения об этих числах встречаются уже в 6
классе, все равно для некоторых детей они
оказываются трудными: во-первых, сами названия
непростые, во-вторых, использование этих
названия не так уж часто.
А смысл слова "множество" отходит при этом на
второй план, некоторые дети автоматически
связывают его со словом "много". Показателен
вопрос, который растерянно задала мне одна
восьмиклассница: "Как же множество может быть
пустым? Ведь это же - множество!" Иногда путают
слова "множество" и "количество". Скажем,
когда детям нужно было привести пример
множества, я в одной тетради прочитала:
"Расстояние от Москвы до Петербурга". Поэтому
для того, чтобы слово "множество" как
математический термин хоть немного стало
понятным, нужно как можно больше примеров и их
обсуждения. Ученик должен привыкнуть к новому
термину. Это произойдет только тогда, когда он
начнет самостоятельно использовать его в своей
речевой деятельности, пускай и в самых простых
ситуациях. И только потом можно переходить к
следующим темам, например, изучать пересечение и
объединение множеств.
Чтобы понятие множества более органично
воспринималось детьми, я посвящала ему отдельный
урок в теме "Неравенства". На следующем уроке
вводилось определение подмножества,
рассматривалось число подмножеств конечного
множества. Затем изучались операции над
множествами, Эти уроки предшествовали занятиям
по теории вероятностей.
На следующем уроке
вводилось определение подмножества,
рассматривалось число подмножеств конечного
множества. Затем изучались операции над
множествами, Эти уроки предшествовали занятиям
по теории вероятностей.
Учитывая состав класса, я старалась
максимально доходчиво вводить новые термины, но
при этом стремилась не перегружать учащихся
формальными выкладками, а добиваться понимания
общих сведений. У меня было два восьмых класса. В
одном, гимназическом, занимаются дети с более
широким кругозором, они более восприимчивы к
тому, что касается истории математики, к
проблемам современной науки. На уроке в этом
классе я приводила больше примеров с
бесконечными множествами. Стараясь не
перегружать учеников дополнительной
терминологией, я показывала им интересные
примеры со взаимно однозначным соответствием
между множествами, которые иллюстрируют
поразительный факт - часть может быть такой же,
как целое. Слово "мощность" при этом намеренно
старалась не называть. Мне кажется, что хотя бы на
интуитивном уровне главная идея этих примеров
детям все равно будет понятна.
Слово "мощность" при этом намеренно
старалась не называть. Мне кажется, что хотя бы на
интуитивном уровне главная идея этих примеров
детям все равно будет понятна.
В другом классе ученики не такие
подготовленные. Им, скажем, сложно было
воспринимать даже само слово "множество",
потому что они с трудом могли настроиться на то,
что это математический термин, а не обычное слово
"множество", то есть "много". Поэтому для них я
готовила больше простых конкретных примеров.
В презентации я использовала тот образ
множества, который предложил Н.Н. Лузин:
"Представим прозрачную непроницаемую оболочку,
нечто вроде закрытого прозрачного мешка.
Предположим, что внутри этой оболочки заключены
все элементы данного множества и что, кроме них,
внутри оболочки никаких других предметов не
находится"[1].
Тем самым мы фиксируем элементы данного
множества, а оболочка показывает, что они собраны
в одно множество. Когда мы записываем множество с
помощью фигурных скобок, именно эти скобки
подчеркивают, что данные элементы составляют
множество.
Когда мы записываем множество с
помощью фигурных скобок, именно эти скобки
подчеркивают, что данные элементы составляют
множество.
Поэтому на слайдах некоторые множества
изображены как будто помещенными в прозрачные
шары.
В данной статье представлен материал к уроку
"Введение понятия множества".
Ключевые слова: "Множество, элемент
множества, пустое множество, конечные и
бесконечные множества".
В 70-х годах ХIX века немецкий математик Г. Кантор
создал новую область математики - теорию
бесконечных множеств. Через несколько
десятилетий почти вся математика была
перестроена на теоретико-множественной основе.
Понятия теории множеств отражают наиболее
общие свойства математических объектов.
Мы только начинаем знакомиться с множествами.
(Слайд 3)
Множество - неопределяемое понятие в
математике. С неопределяемыми понятиями мы уже
встречались, например, в геометрии (прямая и
точка). Множество можно представить себе как
совокупность некоторых элементов.
Множество можно представить себе как
совокупность некоторых элементов.
Например, можно говорить о множестве цветов,
которые растут на клумбе около нашей школы. Или о
множестве точек на плоскости. Элементы множества
могут быть любыми!
(Слайд 4)
Рассмотрим множество, которое состоит из
чисел 1, 2, 3, 4, 5. Обозначим это множество А.
Используется такая запись: А={1, 2, 3, 4, 5}. Число 1 -
элемент данного множества. Можно сказать и так:
"1 принадлежит множеству А". Есть специальный
значок принадлежности: 1А Тот факт, что, скажем, число 7 не
принадлежит множеству А, записываем следующим
образом: 7А.
Говоря о множестве А, мы просто перечисляли его
элементы. Иногда это отнимает много времени.
Иногда вообще такое перечисление невозможно.
Рассмотрим множество всех положительных чисел.
Пусть это множество В. С одной стороны, мы не в
состоянии перечислить все элементы множества В,
их бесконечно много, но, с другой стороны, мы
понимаем, о каком множестве идет речь: с
положительными числами мы хорошо знакомы - это
числа, которые больше нуля. Записываем данное
множество так: В={x|x>0}.
Записываем данное
множество так: В={x|x>0}.
(Слайд 5 )
Дополнительные вопросы. Существует ли в этом
множестве наибольший элемент? Приведите примеры
элементов этого множества, которые меньше 1; 0,1;
0,01; 0,001. Существует ли наименьший элемент этого
множества? Будет ли принадлежать этому множеству
число 0?
На этом примере показано, что мы можем задать
множество, описав самое важное свойство его
элементов (оно называется характеристическим
свойством множества). По этому свойству можно
точно понять, из каких элементов состоит данное
множество. Если нам удается это свойство
сформулировать, то не нужно тратить время на
перечисление элементов множества. Указав
множество цветов, растущих на школьной клумбе, мы
не обязаны перечислять все цветы. Мы только
указали, где они находятся.
Таким образом, множества могут быть заданы
по-разному. Самое главное, чтобы было понятно,
какие именно элементы принадлежат данному
множеству, а какие не принадлежат. Элементы могут
быть любые, их порядок не важен.
Элементы могут
быть любые, их порядок не важен.
(Слайд 6)
Если два множества состоят из одних и тех же
элементов, мы их считаем равными. Пусть множество
М состоит из элементов: квадрат, трапеция,
пятиугольник, круг, треугольник. Множество Р:
круг, квадрат, треугольник, пятиугольник,
трапеция. Будут ли множества М и Р равны? Ответ
поясните.
Отметим, что здесь мы обсуждаем множество
именно как математическое понятие. Но ведь в
нашем обычной речи тоже встречается слово
"множество"! Важно их не перепутать.
"Математическое" множество вовсе не обязано
состоять из большого количества элементов.
Множество может содержать и всего один элемент.
Например, пусть множество D состоит из моей птицы
Чир. И даже может быть так, что в множестве вообще
нет никаких элементов!
(Слайд 7)
Множество, в котором нет ни одного элемента,
называется пустым множеством. Обозначение: . Например,
множество говорящих рыб - пустое. Пустым будет
множество корней уравнения 0х=3. Или, например,
множество параллелограммов, в которых все углы
острые.
Обозначение: . Например,
множество говорящих рыб - пустое. Пустым будет
множество корней уравнения 0х=3. Или, например,
множество параллелограммов, в которых все углы
острые.
О некоторых множествах трудно сразу сказать,
пусты ли они или нет. Например, знаменитая
проблема Ферма была решена только в 90-х годах ХХ
века: было доказано, что не существует
натуральных чисел n, больших двух, при которых
уравнение xn+yn=zn имеет
целочисленные положительные решения, то есть
множество таких n пусто.
Приведите сами примеры различных пустых
множеств.
Среди всех множеств выделяют конечные
множества и бесконечные.
(Слайд 8)
В конечном множестве число его элементов
всегда можно выразить определенным числом
(иногда, правда, это число не так-то просто найти).
Приведем несколько примеров.
- Множество из 4 элементов: M={a;b;c;d}
- Множество цифр.
 Это множество из 10 элементов
(назовите их!).
Это множество из 10 элементов
(назовите их!). - Множество букв русского алфавита. Сколько в нем элементов?
- Множество всех тигров, живущих на Земле. К сожалению, тигров на Земле осталось очень мало. Экологи постоянно следят за их численностью.
(Слайд 9)
Рассмотрим множество, состоящее из гласных букв. Сколько в нем элементов?
Будет ли это множество равно множеству, состоящему из цифр?
А в некоторых случаях даже представить себе
конечность множества нелегко. Вычислительная
техника стремительно развивается. Компьютер
отвечает на наши повседневные вопросы очень
быстро, иногда нам кажется, что мгновенно. И
действительно, объем информации, которую может
обрабатывать современный компьютер, громадно.
Однако и возможности компьютера ограничены, то
есть конечны. В начале ХХI века стали заметны
серьезные проблемы. Оказалось, что есть
несколько принципиальных (непреодолимых)
барьеров: атомная структура вещества,
ограничение скорости света, туннельный эффект и
проблема отвода тепла (перегрев процессора). Современный процессор по своим размерам
постепенно приближается к атому! Но меньше атома
процессор быть уже не сможет. А сейчас самая
передовая технология дает отличие от размеров
атома всего на три порядка! По прогнозам ученых, к
2017 году при аналогичных методах развития
наступит предел - процессор уже нельзя сделать
меньше.
Современный процессор по своим размерам
постепенно приближается к атому! Но меньше атома
процессор быть уже не сможет. А сейчас самая
передовая технология дает отличие от размеров
атома всего на три порядка! По прогнозам ученых, к
2017 году при аналогичных методах развития
наступит предел - процессор уже нельзя сделать
меньше.
Перед человечеством встали задачи, которые можно решить с помощью существующих компьютеров только теоретически. В реальности на их решение потребуется время, сравнимое со временем существования Вселенной [3].
Математики и другие ученые предлагают ответы на то, как обойти эти барьеры и ищут новые решения.
В истории математики было много случаев, когда
вновь созданная теория воспринималась сначала
слишком искусственной, а потом приобретала
важнейшее практическое значение. Так было и с
теорией бесконечных множеств. А сейчас теория
множеств - это "каркас современной математики,
она не всегда хорошо видна, но обеспечивает
прочность всей конструкции" [4].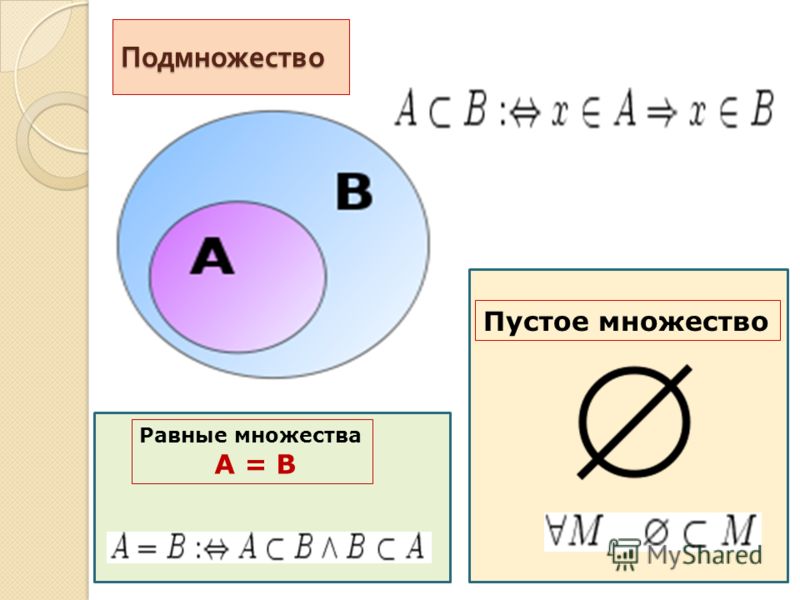
(Слайд 10)
Бесконечные множества. В них количество элементов выразить конечным числом невозможно.
Примеры бесконечных множеств:
- Множество всех положительных чисел.
- Множество всех точек на прямой.
- Множество всех треугольников.
- Множество всех фигур на плоскости.
(Слайд 11)
Нам уже известны самые важные числовые множества: N, Z, Q, R. Мы знаем, что натуральные числа - часть целых, целые числа составляют часть рациональных, рациональные - часть действительных. Как называются действительные числа, которые не рациональны?
Пусть даны числа 28; -15; 0,9; .
Запишите для каждого числа, принадлежит ли оно множествам N, Z, Q, R.
Попробуйте привести примеры множеств из
геометрии, которые можно было бы
проиллюстрировать аналогичной диаграммой (см.
слайд: одно множество - часть другого).
(Слайд 12)
Мы уже знакомы с понятием "числовые промежутки". Это тоже множества.
Рассмотрим некоторые из них . Назовите несколько чисел, принадлежащих промежутку (5;8). Принадлежит ли этому промежутку число 8? Число 7,999? А можно ли назвать число из этого промежутка, которое больше 7,999? Есть ли на промежутке (5;8) самое большое число? Самое маленькое число?
Как вы думаете, сколько всего действительных чисел на промежутке (5;8)? Сколько на нем целых чисел? Назовите их.
Аналогичные вопросы можно рассмотреть для промежутков [5;8], [5;8).
В мире бесконечного мы встречаем много
удивительного. Например, мы рассмотрели совсем
небольшие, казалось бы, промежутки, а
действительных чисел на них бесконечно много!
Вспомним известный нам график - гиперболу. Что
удивительного в гиперболе? А то, что она,
приближаясь к осям координат, никогда не
пересекает их. Но становится к ним все ближе и
ближе! Как это возможно? Математики на это дали
ответ (правда, далеко не сразу). Можно сравнить
это настойчивое стремление с тем, как человек все
время стремится к идеалу, но никогда его не
достигает, а стремиться нужно!
Можно сравнить
это настойчивое стремление с тем, как человек все
время стремится к идеалу, но никогда его не
достигает, а стремиться нужно!
Другой удивительный пример из мира бесконечного. Мы привыкли к тому, что часть всегда меньше целого. А с бесконечными множествами иногда получаем другую картину. Рассмотрим натуральные числа и четные числа. Казалось бы, раз четные числа - это только часть натуральных, то четных должно быть меньше. А получается, что их столько же, сколько и натуральных!
(Слайд 13)
Допустим, что в фантастической гостинице
(аналогичный пример приведен в [1]) бесконечно
много номеров, все они заняты гостями из разных
галактик - значит, этих гостей столько же,
сколько номеров, то есть столько же, сколько
натуральных чисел. И приезжает еще много гостей,
нужно их разместить. А ведь все номера заняты, что
же делать? Директор очень вежливо просит прежних
постояльцев перейти в другие номера: если у
прежнего гостя был номер 1, то этот гость
переходит в номер 2, номер 2 - в номер 4, то есть все
прежние номера меняются на номера, в два раза
большие. Тогда освобождаются все нечетные
номера! И их бесконечно много! Гостиница готова к
приему новых туристов. А в четных номерах живут
постояльцы, которых столько же, сколько
натуральных чисел. С другой стороны, если новые
туристы быстро уедут, то прежние могут вернуться
в свои номера. И тогда получается, что четные
числа благополучно "размещаются" по номерам
1,2,3:. Таким образом, мы установили взаимно
однозначное соответствие между множеством
натуральных чисел и множеством четных чисел.
Четных чисел и натуральных - одинаковое
количество.
Тогда освобождаются все нечетные
номера! И их бесконечно много! Гостиница готова к
приему новых туристов. А в четных номерах живут
постояльцы, которых столько же, сколько
натуральных чисел. С другой стороны, если новые
туристы быстро уедут, то прежние могут вернуться
в свои номера. И тогда получается, что четные
числа благополучно "размещаются" по номерам
1,2,3:. Таким образом, мы установили взаимно
однозначное соответствие между множеством
натуральных чисел и множеством четных чисел.
Четных чисел и натуральных - одинаковое
количество.
(Слайд 14)
Похожим образом можно показать, что количество
точек на промежутке (5; 8) такое же, что и на всей
прямой. Изменим форму промежутка так, чтобы
получилась дуга, полуокружность (но без
граничных точек А и В) - эта дуга изображена на
слайде. Пусть О - центр окружности, АВ - диаметр.
Нашу прямую (обозначим ее СD) расположим так,
чтобы она была параллельна АВ. Из точки О можно
провести бесконечно много прямых, которые будут
пересекать дугу, и при этом каждая из этих прямых
пересечет нашу прямую СD. Можно представить себе,
что каждая точка дуги "переезжает" в точку на
прямой CD (по прямой, идущей из т. О и пересекающей
СD - пути "переезда" изображены на слайде
стрелками). И наоборот: для каждой точки прямой СD
есть соответствующая на дуге. Таким образом,
точек на дуге и на всей прямой - одинаковое
количество, а, значит, оно будет одинаковым и для
промежутка, и для прямой.
Из точки О можно
провести бесконечно много прямых, которые будут
пересекать дугу, и при этом каждая из этих прямых
пересечет нашу прямую СD. Можно представить себе,
что каждая точка дуги "переезжает" в точку на
прямой CD (по прямой, идущей из т. О и пересекающей
СD - пути "переезда" изображены на слайде
стрелками). И наоборот: для каждой точки прямой СD
есть соответствующая на дуге. Таким образом,
точек на дуге и на всей прямой - одинаковое
количество, а, значит, оно будет одинаковым и для
промежутка, и для прямой.
Дополнительные вопросы.
Почему нужно было расположить прямую CD параллельно АВ? Укажите прямую, которая пройдет через точку О, но не пересечет дугу. Не забудьте, что мы рассматриваем дугу без концов!
Более трудный вопрос. Можно ли аналогичным
образом устроить "переезд" точек для [5; 8], [5; 8)?
Замечаем, что "мешают" граничные точки. С теми
ребятами, кого заинтересует эта задача, мы
обсудим ее на факультативном занятии.
Для всех множеств (и конечных, и бесконечных), мы должны научиться определять, какие элементы принадлежат данному множеству, а какие нет.
(Слайд 15)
Рассмотрим два множества, А и В. Пусть множество А состоит из параллелограмма, трапеции, треугольника, квадрата. Множество В состоит из круга, квадрата, треугольника, пятиугольника, трапеции.
- Назовите общие элементы этих множеств.
- Какие элементы множества А не принадлежат множеству В?
- Какие элементы множества В не принадлежат множеству А?
- Назовите элементы, которые входят хотя бы в одно из данных множеств.
(Слайд 16)
Итак, мы познакомились с понятием множества,
говорили об элементах множества. Узнали, что есть
пустое множество. Множества бывают конечные и
бесконечные. На следующих уроках мы узнаем о том,
что с множествами можно производить некоторые
действия (как и с числами - этим они немножко
похожи друг на друга). Будем и дальше изучать
множества! Они нам помогут лучше разобраться с
другими задачами.
Будем и дальше изучать
множества! Они нам помогут лучше разобраться с
другими задачами.
Литература.
- Виленкин Н.Я. Рассказы о множествах. - М.: Наука, 1965.
- Виленкин Н.Я.и др. Алгебра для 9 класса. - М.: Просвещение, 1996.
- Губайловский В. Наука будущего. Классические и квантовые компьютеры. //"Новый мир", 2011, №7.
- Жарковская Н.А. Георг Кантор и теория множеств. //"Курсор. Международный математический конкурс-игра "Кенгуру"". 2011, выпуск 5
- Макарычев Ю.Н. и др. Алгебра. 8 класс.- 19-е изд. - М.: Просвещение, 2011.
- Тюрин Ю.Н. и др. Теория вероятностей и статистика, - Москва, МЦНМО, 2008.
Математика. 5 класс: 21, 22. Множества
21, 22. Множества
Это надо знать
Множество - это совокупность объектов, рассматриваемая как одно целое.
Объекты, составляющие данное множество, называются его элементами.
Пример
Множество домов на данной улице, множество натуральных чисел, множество учеников класса и т. д.
Множества обозначаются заглавными латинскими буквами, а их элементы – строчными. Запись a ∈ R означает, что элемент а принадлежит множеству R , то есть а является элементом множества R . В противном случае, когда а не принадлежит множеству R , пишут a ∉ R .
Пример
N – множество натуральных чисел,
N = {1, 2, 3, 4,…};
Два множества А и В называются равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А .
Говорят, что множество А содержится в множестве В) или множество А является подмножеством множества В, если каждый элемент множества А одновременно является элементом множества В.
Пример
А={0, 1, 2, 3}, В={0, 1}, B ⊂ A .
Объединение множеств А и В ( пишется А ∪ В ) есть множество элементов, каждый из которых принадлежит либо А , либо В.
Пример
А={К, А, Т, Я}, В={К, О, С, Т, Я},
A ∪ B={К, А, Т, Я, О, С}
Пересечение множеств А и В ( пишется А ∩ В ) есть множество элементов, каждый из которых принадлежит и А , и В.
Пример
А={К, А, Т, Я}, В={К, О, С, Т, Я},
A ∩ B ={К, Т, Я}.
Разность множеств А и В ( пишется А – В ) есть множество элементов, которые принадлежат множеству А , но не принадлежат множеству В. Это множество называется также дополнением множества В относительно множества А.
Пример
А={К, А, Т, Я}, В={К, О, С, Т, Я},
А - В={A}, В - А ={О, С}.
Видеоурок
Видео к уроку 21Видео к уроку 22
Задачи для решения
№1. (1 уровень) Собралось 5 охотников и 8 рыбаков, а всего 10 человек. Может ли быть такая ситуация? Объясните ситуацию с помощью различных моделей.
№2. (1 уровень) Группа студентов 25 человек отправилась на отдых, среди них 18 волейболистов и 12 теннисистов. Сколько студентов играют и в волейбол, и в теннис?
№3. (2 уровень) В магазине «Канцтовары» в первой половине дня 30 человек покупали школьные тетради. 19 человек покупали тетради «в клеточку», 18 человек покупали тетради «в линейку». Были ли среди 30 покупателей те, которые покупали тетради двух видов (в клетку и линейку)? Если да, то, сколько таких покупателей было?
№4. (2 уровень) В классе 24 ученика, из них 12 учащихся занимаются танцами, 16 учащихся занимаются в различных спортивных секциях и 5 учеников класса не занимаются танцами и не посещают спортивные секции. Сколько учащихся класса, посещающие спортивные секции, занимаются еще и танцами?
(2 уровень) В классе 24 ученика, из них 12 учащихся занимаются танцами, 16 учащихся занимаются в различных спортивных секциях и 5 учеников класса не занимаются танцами и не посещают спортивные секции. Сколько учащихся класса, посещающие спортивные секции, занимаются еще и танцами?
№5. (3 уровень) Группа студентов изучает английский и французский языки, причем, английский язык изучает 15 человек, французский – 12 человек. Оба языка изучают 7 человек. Сколько учащихся в группе по изучению иностранных языков?
№6. (3уровень) В группе туристов из 100 человек 70 человек знают английский язык, 45 –знают немецкий язык, и 23 человека знают оба языка. Сколько туристов в группе не знают ни английского, ни немецкого языков?
№7. (4 уровень) По контрольной работе по математике 8 баллов получили 48 учащихся 11классов одной из школ города Минска, а по физике -37 учащихся, по русскому языку - 42 ученика. По математике или физике -75 учащихся, по математике или русскому языку- 76 учащихся, по физике или по русскому языку - 66 учеников. По всем трем предметам 8 баллов получили 4 учащихся. Сколько учащихся получили хотя бы одну «восьмерку»?
По всем трем предметам 8 баллов получили 4 учащихся. Сколько учащихся получили хотя бы одну «восьмерку»?
№8. (4 уровень) В оздоровительном лагере 70 ребят старших отрядов. Из них 27 занимаются в драмкружке, 32 изготавливают поделки, 22 увлекаются спортом. В драмкружке 10 ребят изготавливают поделки, в кружке по изготовлению поделок 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок, и кружок по изготовлению поделок. Сколько ребят не изготавливают поделки, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?
№9. (5 уровень) Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Хватит ли 20 –ти велосипедов в прокатном пункте лагеря для ребят, которые не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?
№10. (5 уровень) В предварительном туре школьной олимпиады по математике принимало участие 40 учащихся 5-х классов, которым предложили решить три задачи: №1, №2, №3. Задачу №1 правильно решили 19 учащихся, №2 – 18 учащихся, №3 также 19 учащихся. Задачи №1и №2 решили 7 человек, задачи №2 и №3 - 9 человек, задачи №1и №3 - 7 человек, ни одной задачи не решили 3 ученика. Сколько учеников решили все задачи? Сколько учащихся решили только две задачи? Сколько учащихся решили по одной задаче?
(5 уровень) В предварительном туре школьной олимпиады по математике принимало участие 40 учащихся 5-х классов, которым предложили решить три задачи: №1, №2, №3. Задачу №1 правильно решили 19 учащихся, №2 – 18 учащихся, №3 также 19 учащихся. Задачи №1и №2 решили 7 человек, задачи №2 и №3 - 9 человек, задачи №1и №3 - 7 человек, ни одной задачи не решили 3 ученика. Сколько учеников решили все задачи? Сколько учащихся решили только две задачи? Сколько учащихся решили по одной задаче?
Домашнее задание
Для тренировки можете перейти на страницу Множества.
К уроку 21 (на 30.09)
1. Р – множество натуральных чисел, больших семи и меньших четырнадцати. Выясните, какие из чисел 13,10, 5, 7, 14 ему принадлежат, а какие не принадлежат. Ответ запишите, используя знаки и .
2. Перечислите элементы следующих множеств:
А– множество нечетных однозначных чисел;
В– множество натуральных чисел, меньших или равных 20;
С– множество двузначных чисел, делящихся на 10.
3. Изобразите при помощи кругов отношения между множествами А, В и С, если известно, что:
1)АВ и ВС,
2) АВ, С пересекается с В, но не пересекается с А,
3) А, В и С пересекаются, но ни одно не является подмножеством другого.
К уроку 22 (на 01.10)
1. Восьмого марта в кино пришло 100 ребят. На приключенческий фильм было продано 87 билетов, а на комедию — 63. Сколько ребят посмотрели и тот фильм, и другой? (Каждый посмотрел по меньшей мере один из фильмов.)
2. В классе 29 человек. 15 из них занимаются в музыкальном кружке, 21 — в математическом. Сколько человек посещают оба кружка, если известно, что только Вовочка не ходит ни в один из двух кружков?
Главная страница
Подписаться на: Сообщения (Atom)
МНОЖЕСТВ ТЕОРИЯ • Большая российская энциклопедия
МНО́ЖЕСТВ ТЕО́РИЯ, раздел математики, в котором изучаются свойства множеств, преим. бесконечных. Понятие множества, или совокупности, принадлежит к числу исходных математич. понятий; оно формально не определяется, но может быть пояснено при помощи примеров. Так, можно говорить о множестве всех книг, составляющих данную библиотеку, множестве всех точек данной линии, множестве всех решений данного уравнения. Книги данной библиотеки, точки данной линии, решения данного уравнения являются элементами соответствующего множества. Чтобы определить множество, достаточно указать характеристич. свойство его элементов, т. е. такое свойство, которым обладают все элементы этого множества и только они. Может случиться, что данным свойством не обладает вообще ни один объект; тогда говорят, что это свойство определяет пустое множество. То, что данный объект $x$ есть элемент множества $M$, записывают как $x∈М$.
бесконечных. Понятие множества, или совокупности, принадлежит к числу исходных математич. понятий; оно формально не определяется, но может быть пояснено при помощи примеров. Так, можно говорить о множестве всех книг, составляющих данную библиотеку, множестве всех точек данной линии, множестве всех решений данного уравнения. Книги данной библиотеки, точки данной линии, решения данного уравнения являются элементами соответствующего множества. Чтобы определить множество, достаточно указать характеристич. свойство его элементов, т. е. такое свойство, которым обладают все элементы этого множества и только они. Может случиться, что данным свойством не обладает вообще ни один объект; тогда говорят, что это свойство определяет пустое множество. То, что данный объект $x$ есть элемент множества $M$, записывают как $x∈М$.
Если каждый элемент множества $A$ является в то же время элементом множества $B$, то множество $A$ называется подмножеством множества $B$. Это записывают как $A⊂B$ или $B⊃A$. Подмножеством данного множества $B$ является и само множество $B$. Если $A⊂B$ и $A⊃B$, то множества $А$ и $B$ называют равными и пишут $A=B$. Пустое множество, по определению, считают подмножеством любого множества. Всякое непустое подмножество $A$ данного множества $B$, отличное от всего множества $B$, называют правильной частью последнего (вместо символа включения $⊂$ иногда используют символ включения $⊆$; в этом случае запись $A⊂B$ означает, что $A$ есть правильная часть $B$).
Это записывают как $A⊂B$ или $B⊃A$. Подмножеством данного множества $B$ является и само множество $B$. Если $A⊂B$ и $A⊃B$, то множества $А$ и $B$ называют равными и пишут $A=B$. Пустое множество, по определению, считают подмножеством любого множества. Всякое непустое подмножество $A$ данного множества $B$, отличное от всего множества $B$, называют правильной частью последнего (вместо символа включения $⊂$ иногда используют символ включения $⊆$; в этом случае запись $A⊂B$ означает, что $A$ есть правильная часть $B$).
Мощность множеств
Первым вопросом, возникшим в применении к бесконечным множествам, был вопрос о возможности их сравнения между собой. Ответ на этот и близкие вопросы дал в кон. 1870-х гг. Г. Кантор, основавший М. т. как математич. науку. Возможность сравнительной оценки множеств опирается на понятие взаимно однозначного соответствия между двумя множествами. Пусть каждому элементу множества $A$ поставлен в соответствие с помощью к.-л. правила или закона некоторый определённый элемент множества $B$; если при этом каждый элемент множества $B$ оказывается поставленным в соответствие одному и только одному элементу множества $A$, то говорят, что между множествами $A$ и $B$ установлено взаимно однозначное соответствие. Между двумя конечными множествами можно установить взаимно однозначное соответствие тогда и только тогда, когда оба множества состоят из одинакового числа элементов. Обобщая этот факт, определяют эквивалентность или равномощность двух бесконечных множеств как возможность установить между ними взаимно однозначное соответствие.
Пусть каждому элементу множества $A$ поставлен в соответствие с помощью к.-л. правила или закона некоторый определённый элемент множества $B$; если при этом каждый элемент множества $B$ оказывается поставленным в соответствие одному и только одному элементу множества $A$, то говорят, что между множествами $A$ и $B$ установлено взаимно однозначное соответствие. Между двумя конечными множествами можно установить взаимно однозначное соответствие тогда и только тогда, когда оба множества состоят из одинакового числа элементов. Обобщая этот факт, определяют эквивалентность или равномощность двух бесконечных множеств как возможность установить между ними взаимно однозначное соответствие.
Ещё до создания М. т. Б. Больцано владел, с одной стороны, вполне точно сформулированным понятием взаимно однозначного соответствия, с др. стороны, считал несомненным существование бесконечностей разл. ступеней; однако он не только не сделал взаимно однозначное соответствие основой установления равносильности множеств, но решительно возражал против этого. Больцано останавливало то, что бесконечное множество может находиться во взаимно однозначном соответствии со своей правильной частью. Напр., если каждому натуральному числу $n$ поставить в соответствие натуральное число $2n$, то получается взаимно однозначное соответствие между множеством всех натуральных и множеством всех чётных чисел. Вместо того чтобы в применении к бесконечным множествам отказаться от положения, состоящего в том, что часть меньше целого, Больцано отказался от взаимной однозначности как критерия равномощности. В каждом бесконечном множестве $M$ имеется правильная часть, равномощная всему множеству $M$, тогда как ни в одном конечном множестве такой правильной части не существует.
стороны, считал несомненным существование бесконечностей разл. ступеней; однако он не только не сделал взаимно однозначное соответствие основой установления равносильности множеств, но решительно возражал против этого. Больцано останавливало то, что бесконечное множество может находиться во взаимно однозначном соответствии со своей правильной частью. Напр., если каждому натуральному числу $n$ поставить в соответствие натуральное число $2n$, то получается взаимно однозначное соответствие между множеством всех натуральных и множеством всех чётных чисел. Вместо того чтобы в применении к бесконечным множествам отказаться от положения, состоящего в том, что часть меньше целого, Больцано отказался от взаимной однозначности как критерия равномощности. В каждом бесконечном множестве $M$ имеется правильная часть, равномощная всему множеству $M$, тогда как ни в одном конечном множестве такой правильной части не существует. Поэтому наличие правильной части, равномощной целому, можно принять за определение бесконечного множества.
Поэтому наличие правильной части, равномощной целому, можно принять за определение бесконечного множества.
Для двух бесконечных множеств $A$ и $B$ возможны следующие 3 случая: либо в $A$ есть правильная часть, равномощная $B$, но в $B$ нет правильной части, равномощной $A$; либо, наоборот, в $B$ есть правильная часть, равномощная $A$, а в $A$ нет правильной части, равномощной $B$; либо, наконец, в $A$ есть правильная часть, равномощная $B$, и в $B$ есть правильная часть, равномощная $A$. Доказывается, что в 3-м случае множества $A$ и $B$ равномощны (теорема Кантора – Бернштейна). В 1-м случае говорят, что мощность множества $A$ больше мощности множества $B$, во 2-м – что мощность множества $B$ больше мощности множества $A$. Формально возможный 4-й случай – в $A$ нет правильной части, равномощной $B$, а в $B$ нет правильной части, равномощной $A$, – в действительности для бесконечных множеств осуществиться не может.
Ценность понятия мощности множества связана с существованием неравномощных бесконечных множеств. Напр., множество всех подмножеств данного множества $M$ имеет мощность бо́льшую, чем множество $M$. Множество, равномощное множеству всех натуральных чисел, называется счётным множеством. Мощность счётных множеств есть наименьшая мощность, которую может иметь бесконечное множество; всякое бесконечное множество содержит счётную правильную часть. Кантор доказал, что множество всех рациональных и даже всех алгебраических чисел счётно, тогда как множество всех действительных чисел несчётно. Из этого следует, в частности, доказательство существования т. н. трансцендентных чисел, т. е. действительных чисел, не являющихся корнями никакого алгебраич. уравнения с целыми коэффициентами (и даже несчётность множества таких чисел). Мощность множества всех действительных чисел называется мощностью континуума. Множеству всех действительных чисел равномощны множество всех подмножеств счётного множества, множество всех комплексных чисел и, следовательно, множество всех точек плоскости, а также множество всех точек $n$-мерного пространства при любом $n$. Кантор высказал гипотезу о том, что всякое множество, состоящее из действительных чисел, либо конечно, либо счётно, либо равномощно множеству всех действительных чисел; по поводу этой гипотезы и о связанных с нею результатах см. Континуум-гипотеза, Континуума проблема.
Мощность множества всех действительных чисел называется мощностью континуума. Множеству всех действительных чисел равномощны множество всех подмножеств счётного множества, множество всех комплексных чисел и, следовательно, множество всех точек плоскости, а также множество всех точек $n$-мерного пространства при любом $n$. Кантор высказал гипотезу о том, что всякое множество, состоящее из действительных чисел, либо конечно, либо счётно, либо равномощно множеству всех действительных чисел; по поводу этой гипотезы и о связанных с нею результатах см. Континуум-гипотеза, Континуума проблема.
Отображения множеств
В М. т. понятие функции, геометрич. понятие отображения или преобразования фигуры приводят к общему понятию отображения одного множества в другое. Пусть даны два множества $X$ и $Y$ и каждому элементу $x∈X$ поставлен в соответствие некоторый определённый элемент $y=f(x)$ множества $Y$; тогда говорят, что имеется отображение множества $X$ в множество $Y$ или что имеется функция, аргумент $x$ которой пробегает множество $X$, а значения $y$ принадлежат множеству $Y$; при этом для каждого данного $x∈X$ элемент $y=f(x)$ множества $Y$ называется образом элемента $x$ при данном отображении или значением данной функции для данного значения $x$ её аргумента. 3$, то тем самым будет установлено отображение множества $X$ в себя.
3$, то тем самым будет установлено отображение множества $X$ в себя.
3) Пусть $X$ – множество всех действительных чисел; если для каждого $x∈X$ положить $y=f(x)=\text {arctg}$ $x$, то этим будет установлено отображение множества $X$ в интервал $(-π/2, π/2)$.
Взаимно однозначное соответствие между двумя множествами $X$ и $Y$ есть такое отображение множества $X$ в множество $Y$, при котором каждый элемент множества $Y$ является образом одного и только одного элемента множества $X$. Отображения примеров 2) и 3) взаимно однозначны, примера 1) – нет.
Операции над множествами
Суммой, или объединением, конечного или бесконечного множества множеств называется множество всех тех элементов, каждый из которых есть элемент хотя бы одного из данных множеств-слагаемых. Объединение множеств $A$ и $B$ обозначается $A∪B$. Пересечением любого конечного или бесконечного множества множеств называется множество всех элементов, принадлежащих всем данным множествам. Пересечение множеств $A$ и $B$ обозначается $A∩B$. Пересечение непустых множеств может быть пустым. Разностью между множеством $B$ и множеством $A$ называется множество всех элементов из $B$, не являющихся элементами из $A$; эта разность обозначается $BA$; разность между множеством $B$ и его частью $A$ называется дополнением множества $A$ в множестве $B$ и обозначается .
Пересечение множеств $A$ и $B$ обозначается $A∩B$. Пересечение непустых множеств может быть пустым. Разностью между множеством $B$ и множеством $A$ называется множество всех элементов из $B$, не являющихся элементами из $A$; эта разность обозначается $BA$; разность между множеством $B$ и его частью $A$ называется дополнением множества $A$ в множестве $B$ и обозначается .
Операции сложения и пересечения множеств обладают ассоциативностью и коммутативностью. Операция пересечения, кроме того, обладает дистрибутивностью по отношению к сложению и вычитанию. Если эти операции производить над множествами, являющимися подмножествами одного и того же множества $M$, то и результат будет подмножеством множества $M$. Указанным свойством не обладает т. н. внешнее умножение множеств, внешним произведением множеств $X$ и $Y$ или прямым произведением множеств $X$ и $Y$ называется множество $X×Y$ всевозможных пар $(x, y)$, где $x∈X, y∈Y$. X$, что в случае конечных множеств согласуется с умножением и возведением в степень натуральных чисел. Аналогично определяется сумма мощностей как мощность суммы попарно непересекающихся множеств с заданными мощностями.
X$, что в случае конечных множеств согласуется с умножением и возведением в степень натуральных чисел. Аналогично определяется сумма мощностей как мощность суммы попарно непересекающихся множеств с заданными мощностями.
Упорядоченные множества
В данном множестве $X$ можно установить порядок, т. е. определить для некоторых пар $x′, x″$ элементов этого множества к.-л. правило предшествования (следования), выражаемое словами элемент $x′$ предшествует элементу $x″$ (или, что то же, элемент $x″$ следует за элементом $x'$ ), что записывается $x′≺x″$; при этом предполагается, что для данного отношения порядка выполнено условие транзитивности, т. е. если $x≺x′$ и $x′≺x″$, то $x≺x″$. Множество, рассматриваемое вместе с к.-л. установленным в нём порядком, называется частично упорядоченным множеством; иногда – упорядоченным множеством. Однако чаще упорядоченным множеством называется частично упорядоченное множество, в котором порядок удовлетворяет следующим дополнит. требованиям (линейного порядка): 1) никакой элемент не предшествует самому себе; 2) из всяких двух разл. элементов $x, x′$ один предшествует другому, т. е. если $x≠x′$, то или $x≺x′$, или $x″≺x$.
Однако чаще упорядоченным множеством называется частично упорядоченное множество, в котором порядок удовлетворяет следующим дополнит. требованиям (линейного порядка): 1) никакой элемент не предшествует самому себе; 2) из всяких двух разл. элементов $x, x′$ один предшествует другому, т. е. если $x≠x′$, то или $x≺x′$, или $x″≺x$.
Примеры.
1) Любое множество, элементами которого являются некоторые множества $x$, является частично упорядоченным по включению, если считать, что $x≺x′$, если $x⊂x′$.
2) Любое множество функций $f$, определённых на числовой прямой, становится частично упорядоченным, если считать, что $f_1≺f_2$, тогда и только тогда, когда для каждого действительного числа $x$ справедливо неравенство $f_1(x)⩽f_2(x)$.
3) Любое множество действительных чисел линейно упорядочено, если считать, что меньшее из двух чисел предшествует большему.
Два упорядоченных множества называются подобными, или имеющими один и тот же порядковый тип, если между ними можно установить взаимно однозначное соответствие, сохраняющее порядок. Элемент упорядоченного множества называется первым, если он предшествует всем остальным элементам; аналогично определяется и последний элемент. Напр., в упорядоченном множестве всех действительных чисел нет ни первого, ни последнего элемента; в упорядоченном множестве всех неотрицательных чисел нуль есть первый элемент, а последнего элемента нет; в упорядоченном множестве всех действительных чисел $x$, удовлетворяющих неравенствам $a⩽x⩽b$, число $a$ есть первый элемент, $b$ – последний.
Упорядоченное множество называется вполне упорядоченным, если оно само и всякое его правильное подмножество имеют первый элемент. Порядковые типы вполне упорядоченных множеств называются порядковыми, или ординальными, числами. Если вполне упорядоченное множество конечно, то его порядковое число есть натуральное число. Порядковый тип бесконечного вполне упорядоченного множества называется трансфинитным числом.
Если вполне упорядоченное множество конечно, то его порядковое число есть натуральное число. Порядковый тип бесконечного вполне упорядоченного множества называется трансфинитным числом.
Точечные множества
Теория точечных множеств, т. е. множеств, элементами которых являются действительные числа (точки числовой прямой), а также точки многомерных пространств, основана Г. Кантором, который ввёл понятие предельной точки множества и связанные с ним понятия замкнутого множества и пр. Развитие теории точечных множеств привело к понятиям метрического пространства и топологического пространства, изучением которых занимается общая топология. Самостоятельно существует дескриптивная теория множеств, основанная франц. математиком Р. Бэром и А. Лебегом в связи с классификацией разрывных функций (1905). Дескриптивная теория множеств началась с изучения и классификации т. н. борелевских множеств ($B$-множеств). Борелевские множества определяются как множества, которые могут быть построены, отправляясь от замкнутых множеств, применением операций объединения и пересечения в любых комбинациях, но каждый раз к конечному или к счётному множеству множеств. Дальнейшее развитие дескриптивной теории множеств осуществлялось преим. рус. и польск. математиками, особенно московской математич. школой, созданной Н. Н. Лузиным (П. С. Александров, А. Н. Колмогоров, М. А. Лаврентьев, П. С. Новиков, М. Я. Суслин). Александров доказал (1916), что всякое бесконечное несчётное борелевское множество имеет мощность континуума. Аппарат этого доказательства был применён Суслиным для построения теории т. н. $A$-множеств, охватывающих как частный случай борелевские или $B$-множества, считавшиеся до того единственными множествами, которые могут встретиться в математич.
н. борелевских множеств ($B$-множеств). Борелевские множества определяются как множества, которые могут быть построены, отправляясь от замкнутых множеств, применением операций объединения и пересечения в любых комбинациях, но каждый раз к конечному или к счётному множеству множеств. Дальнейшее развитие дескриптивной теории множеств осуществлялось преим. рус. и польск. математиками, особенно московской математич. школой, созданной Н. Н. Лузиным (П. С. Александров, А. Н. Колмогоров, М. А. Лаврентьев, П. С. Новиков, М. Я. Суслин). Александров доказал (1916), что всякое бесконечное несчётное борелевское множество имеет мощность континуума. Аппарат этого доказательства был применён Суслиным для построения теории т. н. $A$-множеств, охватывающих как частный случай борелевские или $B$-множества, считавшиеся до того единственными множествами, которые могут встретиться в математич. анализе. Суслин показал, что множество, дополнительное к $A$-множеству $M$, является само $A$-множеством только в том случае, когда множество $M$ – борелевское (дополнение к борелевскому множеству всегда есть борелевское множество). При этом оказалось, что $A$-множества совпадают с непрерывными образами множества всех иррациональных чисел. Теория $A$-множеств в течение нескoльких лет оставалась в центре внимания дескриптивной теории множеств до того, как Лузин пришёл к общему определению проективных множеств, которые могут быть получены, отправляясь от множества всех иррациональных чисел при помощи повторного применения операций вычитания и непрерывного отображения. К теории $A$-множеств и проективных множеств относятся также работы Новикова и др. Дескриптивная теория множеств тесно связана с исследованиями по основаниям математики (с вопросами эффективной определимости математич.
анализе. Суслин показал, что множество, дополнительное к $A$-множеству $M$, является само $A$-множеством только в том случае, когда множество $M$ – борелевское (дополнение к борелевскому множеству всегда есть борелевское множество). При этом оказалось, что $A$-множества совпадают с непрерывными образами множества всех иррациональных чисел. Теория $A$-множеств в течение нескoльких лет оставалась в центре внимания дескриптивной теории множеств до того, как Лузин пришёл к общему определению проективных множеств, которые могут быть получены, отправляясь от множества всех иррациональных чисел при помощи повторного применения операций вычитания и непрерывного отображения. К теории $A$-множеств и проективных множеств относятся также работы Новикова и др. Дескриптивная теория множеств тесно связана с исследованиями по основаниям математики (с вопросами эффективной определимости математич. объектов и разрешимости математич. проблем).
объектов и разрешимости математич. проблем).
Роль теории множеств в развитии математики
Влияние М. т. на развитие совр. математики очень велико. Прежде всего М. т. явилась фундаментом ряда математич. дисциплин, напр. теории функций действительного переменного, общей топологии, общей алгебры, функционального анализа. Теоретико-множественные методы применяются и в классич. разделах математики. Напр., они широко применяются в качественной теории дифференциальных уравнений, вариационном исчислении, теории вероятностей. М. т. оказала глубокое влияние на понимание самого предмета математики, в частности, таких её разделов, как геометрия. Только М. т. позволила отчётливо сформулировать понятие изоморфизма систем объектов, заданных вместе со связывающими их отношениями, и привела к пониманию того, что каждая математич. теория в её чистой абстрактной форме изучает ту или иную систему объектов лишь с точностью до изоморфизма, т. е. может быть без всяких изменений перенесена на любую систему объектов, изоморфную той, для изучения которой теория была первоначально создана. В вопросах обоснования математики, т. е. создания строгого, логически безупречного построения математич. теорий, следует иметь в виду, что сама М. т. нуждается в обосновании применяемых в ней методов рассуждения. Более того, все логич. трудности, связанные с понятием бесконечности, при переходе на точку зрения общей М. т. приобретают бо́льшую отчётливость.
теория в её чистой абстрактной форме изучает ту или иную систему объектов лишь с точностью до изоморфизма, т. е. может быть без всяких изменений перенесена на любую систему объектов, изоморфную той, для изучения которой теория была первоначально создана. В вопросах обоснования математики, т. е. создания строгого, логически безупречного построения математич. теорий, следует иметь в виду, что сама М. т. нуждается в обосновании применяемых в ней методов рассуждения. Более того, все логич. трудности, связанные с понятием бесконечности, при переходе на точку зрения общей М. т. приобретают бо́льшую отчётливость.
Равные множества — определение, свойства, различия, примеры
Равные множества — это множества в теории множеств, в которых число элементов одинаково и все элементы равны. Это концепция равенства множеств. Прежде чем вдаваться в детали понятия равных множеств, давайте вспомним значение множеств. Набор — это четко определенный набор объектов, таких как буквы, числа, люди, фигуры и т. д. Они обычно обозначаются заглавной буквой и фигурными скобками '{}'.
Набор — это четко определенный набор объектов, таких как буквы, числа, люди, фигуры и т. д. Они обычно обозначаются заглавной буквой и фигурными скобками '{}'.
Мы изучаем различные типы множеств в теории множеств. В этой статье мы рассмотрим концепцию равных множеств, ее определение и их свойства. Мы также поймем разницу между равными множествами и эквивалентными множествами с помощью примеров для лучшего понимания.
| 1. | Что такое равные множества? |
| 2. | Равные множества Определение |
| 3. | Свойства равных множеств |
| 4. | Разница между равными и эквивалентными наборами |
| 5. | Часто задаваемые вопросы о равных наборах |
Что такое равные множества?
Равные множества определяются как множества, имеющие одинаковую мощность и все равные элементы. Другими словами, два или более множества называются равными множествами, если они состоят из одних и тех же элементов и из одного и того же числа элементов. Например, установите A = {1, 2, 3, 4, 5} и B = {1, 2, 3, 4, 5}. Тогда говорят, что множества A и B равны, так как их элементы одинаковы и имеют одинаковую мощность.
Другими словами, два или более множества называются равными множествами, если они состоят из одних и тех же элементов и из одного и того же числа элементов. Например, установите A = {1, 2, 3, 4, 5} и B = {1, 2, 3, 4, 5}. Тогда говорят, что множества A и B равны, так как их элементы одинаковы и имеют одинаковую мощность.
Теперь два набора называются неравными, если все элементы в двух наборах не одинаковы, а наборы, содержащие одинаковое количество элементов, называются эквивалентными наборами. Например, если А = {1, 2, 3, 4, 5}, С = {2, 4, 6, 7, 9} и D = {2, 5, 6} . Множества A и C имеют одинаковое количество элементов, но все элементы не равны. Следовательно, множества A и C эквивалентны. Теперь множества A и D имеют разную мощность и элементы тоже не равны. Следовательно, множества A и D являются неравными множествами. Равные и эквивалентные множества можно понять по количеству элементов и подобию элементов двух множеств.
Определение равных множеств
Если все элементы двух или более наборов равны и количество элементов также равно, то наборы называются равными наборами. Для обозначения равных множеств используется обозначение '=', т. е. если множества A и B равны, то пишется A = B. Мы знаем, что порядок элементов в множествах не имеет значения. Итак, если A = {a, b, c, d} и B = {b, a, d, c}, то множества A и B равны, потому что они имеют одни и те же элементы, а порядок элементов не влияет на результат. равенство множеств.
Для обозначения равных множеств используется обозначение '=', т. е. если множества A и B равны, то пишется A = B. Мы знаем, что порядок элементов в множествах не имеет значения. Итак, если A = {a, b, c, d} и B = {b, a, d, c}, то множества A и B равны, потому что они имеют одни и те же элементы, а порядок элементов не влияет на результат. равенство множеств.
Представление равных множеств с помощью диаграммы Венна
Теперь представим равные множества на диаграмме Венна. Диаграмма Венна, приведенная ниже, показывает два равных множества A и B с одинаковым количеством элементов и равными элементами, т. е. A = {11, 17, 38} = B.
Свойства равных множеств
Теперь мы поняли значение равных множеств. Далее мы изучим некоторые из его важных свойств, которые помогают понять и идентифицировать их:
- Порядок элементов не влияет на равенство двух наборов.
- Равные множества имеют одинаковую мощность, то есть имеют одинаковое количество элементов.

- Если два множества являются подмножествами друг друга, то используется обозначение множества: A ⊆ B и B ⊆ A, и эти два множества равны. А = В.
- Равные множества должны иметь все равные элементы.
- Силовое множество равных множеств также имеет одинаковое кардинальное число.
- Равные и эквивалентные множества обладают одинаковым свойством равного числа элементов.
- Все равные множества являются эквивалентными множествами, но обратное неверно.
Разница между равными и эквивалентными множествами
В приведенной ниже таблице показаны сходства и различия между равными и эквивалентными наборами:
| Равные наборы | Эквивалентные наборы |
|---|---|
| Если все элементы равны в двух или более наборах, то они равны. | Если количество элементов одинаково в двух или более наборах, то они эквивалентны. |
| Равные множества имеют одинаковую мощность | Эквивалентные наборы имеют одинаковую мощность. |
| У них одинаковое количество элементов. | У них одинаковое количество элементов. |
| Символ, используемый для обозначения одинаковых наборов, — «=» | Для обозначения эквивалентных наборов используется символ ~ или ≡ |
| Все равные наборы являются эквивалентными наборами. | Эквивалентные наборы могут быть или не быть равными. |
| Элементы должны быть одинаковыми. | Элементы не обязательно должны быть одинаковыми. |
Важные свойства равных множеств
- Равные множества эквивалентны, но эквивалентные множества не обязательно должны быть равными.
- Наборы с одинаковыми элементами равны.
- Если два множества являются подмножествами друг друга, то они равны.
Связанные темы
- Наборы формул
- Набор операций
- Непересекающиеся наборы
- А штуцер В
- А перекресток В
Часто задаваемые вопросы о равных наборах
Что такое равные множества в математике?
Равные множества — это наборы в математике, в которых количество элементов одинаково и все элементы равны. Равные множества определяются как множества, имеющие одинаковую мощность и все равные элементы.
Равные множества определяются как множества, имеющие одинаковую мощность и все равные элементы.
В чем разница между равными и эквивалентными наборами?
Разница между равными и эквивалентными множествами заключается только в различии элементов. Если все элементы равны в двух или более наборах, то они равны, но в эквивалентных наборах элементы не обязательно должны быть одинаковыми, но количество элементов должно быть одинаковым.
Как определить равные множества?
Для определения равных наборов все элементы наборов должны быть равными, а количество элементов должно быть одинаковым.
Как доказать, что два множества равны?
Чтобы доказать равенство двух множеств, мы можем доказать, что они являются подмножествами друг друга. Другой способ показать равные множества, мы можем проверить равенство элементов и их кардинальность.
Что такое равные и неравные множества?
Два или более множества называются равными множествами, если они состоят из одних и тех же элементов и одного и того же количества элементов. Если какое-либо из этих условий не выполняется, то множества неравны, т. е. если множества не равны, то . они называются неравными множествами.
Если какое-либо из этих условий не выполняется, то множества неравны, т. е. если множества не равны, то . они называются неравными множествами.
Эквивалентные наборы равны наборам?
Все эквивалентные наборы не являются равными наборами. Эквивалентные множества равны, только если все элементы множеств равны.
Какое обозначение множества используется для равных множеств?
Символ, используемый для представления одинаковых наборов, — '='. Обозначение набора, используемое для представления множества A и множества B, которые равны, равно A = B.
Равные и эквивалентные множества – определение, объяснение, примеры и часто задаваемые вопросы
Даже если равные и эквивалентные множества звучат так, как будто нет большой разницы между ними. Это два похожих понятия, да, но между ними есть небольшая разница, которая отличает их обоих.
Но прежде чем мы разделим на равные и эквивалентные множества, давайте разберемся, что такое кардинальность. Кардинальность — это количество элементов внутри набора. Теперь это важно, потому что это поможет нам понять разницу между равными и эквивалентными множествами.
Кардинальность — это количество элементов внутри набора. Теперь это важно, потому что это поможет нам понять разницу между равными и эквивалентными множествами.
Равные и эквивалентные наборы — это термины, используемые для обозначения некоторой связи между двумя наборами. Вы можете думать об этом как о каком-то сравнении. Например, как бы вы сравнили яблоки с апельсинами, но если нет стандарта, по которому мы можем их сравнивать, то установить что-либо будет очень сложно. Если бы мы сравнили их по количеству, то могли бы сказать, что яблок больше, чем апельсинов, или наоборот. Или можно сказать, что яблок и апельсинов одинаковое количество.
Точно так же, если бы мы сравнивали два набора, мы могли бы использовать количество элементов в качестве стандарта для сравнения.
Посмотрим, как это делается.
Определить равные множества
Чтобы понять значение равного множества, равное множество определяется как два множества, имеющие одинаковые элементы. Два множества A и B могут быть равны только при условии, что каждый элемент множества A является также элементом множества B. Кроме того, если два множества являются подмножествами друг друга, то они называются равными множествами.
Два множества A и B могут быть равны только при условии, что каждый элемент множества A является также элементом множества B. Кроме того, если два множества являются подмножествами друг друга, то они называются равными множествами.
Продолжая наш вышеприведенный пример, если бы мы сравнили одну корзину апельсинов с другой корзиной апельсинов, и если количество апельсинов одинаково в обеих корзинах, то говорят, что это пример для равных наборов.
равные наборы
. Равный набор может быть представлен:
P = Q
P ⊂ Q и Q ⊂ P что если обсуждавшееся выше условие не выполняется, то множество считается неравным.
Уточним, если две корзины содержат неравное количество апельсинов или если одна корзина содержит яблоки, а другая содержит такое же количество апельсинов, то такие случаи называются примерами неравных наборов.
Неравные множества представлены как
P ≠ Q
Определить эквивалентные множества
Значение эквивалентных множеств в математике имеет два определения.
Эквивалентные множества Определение 1. Предположим, что два множества A и B имеют одинаковую мощность, тогда существует целевая функция от множества A до B.
Эквивалентные множества Определение 2. Предположим, что два множества A и B считаются эквивалентными только в том случае, если они имеют одинаковую мощность, то есть n(A) = n(B).
Таким образом, чтобы оставаться или быть эквивалентными, множества должны иметь одинаковую мощность.
Другими словами, если есть корзина с яблоками и корзина с апельсинами, то если они одного и того же числа, мы можем назвать их в качестве примера для эквивалентных наборов.
Это условие означает, что между элементами, принадлежащими обоим наборам, должно быть однозначное соответствие. В этом контексте условие «один к одному» подразумевает, что для каждого элемента в наборе A существует элемент в наборе B, пока и набор A, и набор B не будут исчерпаны.
В этом контексте условие «один к одному» подразумевает, что для каждого элемента в наборе A существует элемент в наборе B, пока и набор A, и набор B не будут исчерпаны.
Таким образом, в общем случае можно утверждать, что два набора остаются эквивалентными друг другу, если только количество элементов в обоих наборах остается равным. Наборы не обязательно должны содержать одни и те же элементы, иначе они остаются подмножествами друг друга.
Примеры равных и эквивалентных множеств
Пример равных множеств
Если мы рассматриваем числа для обозначения элементов двух множеств, то мы можем понимать равные и эквивалентные множества следующим образом.
Давайте разберемся с равными множествами на примере:
Если M = {1, 3, 9, 5, −7} и N = {5, −7, 3, 1, 9,}, то можно сказать, что M = N. Следует отметить, что независимо от того, сколько раз элемент повторяется в конкретном наборе, этот элемент учитывается только один раз. Кроме того, следует отметить, что порядок элементов для определенного набора не имеет значения. Таким образом, с точки зрения кардинального числа равные множества могут быть сформулированы следующим образом:
Кроме того, следует отметить, что порядок элементов для определенного набора не имеет значения. Таким образом, с точки зрения кардинального числа равные множества могут быть сформулированы следующим образом:
Если P = Q, то n(P) = n(Q) и для любого x ∈ P также x ∈ Q.
Пример эквивалентного набора
Если S = {x : x, где x считается положительным целым числом} и T = {d : d, где x считается натуральным числом}, тогда S быть эквивалентным T.
Таким образом, можно утверждать, что эквивалентное множество — это просто множество с равным числом элементов. Однако наборы не обязательно должны иметь одни и те же элементы, но должны состоять из одинакового количества элементов.
Разберем эквивалентные множества на примерах
Если A = {1,−7,200011000,55} и B = {1,2,3,4}, то A эквивалентно B.

Если Набор G: {Свитер, Рукавицы, Шарф, Куртка} и Набор H: {Яблоки, Бананы, Персики, Виноград}, можно заметить, что и Набор G, и Набор H содержат словесные элементы в разных категориях и имеют одинаковые номера элементов, то есть четыре.
Теперь нам ясно, что такое равные и эквивалентные множества. Теперь давайте расширим наши знания, чтобы учесть несколько интересных фактов об отношениях между равными и эквивалентными множествами. Они упоминаются как важные указатели ниже.
Важные моменты, которые следует помнить об эквивалентных множествах
Все нулевые множества считаются эквивалентными друг другу.
Не все бесконечные множества остаются эквивалентными друг другу. Например, эквивалентный набор всех действительных чисел и эквивалентный набор целых чисел.

Если утверждается, что P и Q являются двумя множествами такими, что P равно Q, то есть (P = Q). Этот пример означает, что два равных множества всегда будут оставаться эквивалентными, но обратное эквивалентному множеству может оставаться верным, а может и не быть.
Равный набор может быть эквивалентным набором, но эквивалентный набор не обязательно должен быть равным набором.
Равенство множеств — определение и примеры
Множества — одно из самых фундаментальных понятий в математике. Мы уже обсуждали базовую классификацию наборов на предыдущих уроках. Теперь давайте рассмотрим одну из самых важных операций над множествами — Set Equality.
В этой статье объясняется концепция равенства множеств, чтобы помочь вам лучше понять их.
Два множества называются равными, если они содержат одни и те же элементы и имеют одинаковую мощность. Эта концепция известна как равенство множеств.
Эта концепция известна как равенство множеств.
В этой статье мы рассмотрим следующие темы:
- Что такое установленное равенство?
- Как показать, что два набора равны?
- Свойства равных множеств.
- Примеры
- Практические задачи
Что такое равенство множеств?
Когда юные энтузиасты математики впервые погружаются в изучение множеств, они часто спрашивают: «Что такое равенство множеств?» Итак, давайте разберемся с этим вопросом.
Набор Равенство — это термин, который используется для обозначения равенства двух наборов. Любые два множества, конечные или бесконечные, равны, если они содержат одни и те же элементы.
Рассмотрим два множества, A и B. Эти два множества равны только тогда и только тогда, когда каждый элемент множества A также существует в множестве B. Порядок элементов двух множеств не имеет значения, пока элементы одинаковый. Давайте рассмотрим следующие два набора, A и B, чтобы понять это утверждение.
Давайте рассмотрим следующие два набора, A и B, чтобы понять это утверждение.
A = {1, 2, 3, 4}
B = {2, 4, 1, 3}
Наблюдая за двумя множествами A и B, становится очевидным, что хотя два множества A и B различны , они содержат одни и те же элементы.
Еще один фактор, который следует учитывать при анализе равенства множеств, заключается в том, что два равных множества также имеют одинаковый размер множества, т. е. одинаковую мощность. Следовательно, пока два множества имеют одинаковые элементы и одинаковую мощность, они будут классифицироваться как равные множества.
Давайте решим пример, чтобы понять эту концепцию.
Пример 1
Определите, какие из следующих множеств являются равными множествами:
(i) A = {55, 32, 77, 1} и B = {1, 32, 55, 77}
(ii) X = {x : x — простое число и 2 (iii) S = {2, 4, 6, 8} и T = { 2, 4, 6} Решение (i) Чтобы определить равенство множества, мы должны рассмотреть две вещи; установить элементы и установить кардинальность. |A| = 4 А, |Б| = 4 Итак, |А| = |В| Оба множества A и B состоят из одних и тех же элементов: 1, 32, 55 и 7. Следовательно, множества A и B равны. (ii) Чтобы определить равенство множеств, давайте сначала упростим множество X. X = {x : x — простое число и 2 Итак, X = {3, 5, 7} Теперь найдем кардинальность. |Х| = 3 А, |Y| = 3 Итак, |Х| = |Y| Кроме того, оба набора содержат одни и те же элементы: 3, 5 и 7. Следовательно, множества X и Y равны. (iii) Чтобы определить равенство множеств, давайте сначала рассчитаем кардинальность. |С| = 4 А, |Т| = 3 Как |S| ≠ |Т| Таким образом, два множества, S и T, не равны. В предыдущих уроках мы обсуждали важность диаграмм Венна и способы их использования для изображения различных операций. Для этого рассмотрим два множества, A и B. Пусть множество A = {2, 6, 8} и множество B = {6, 8, 2}. Их представление через диаграмму Венна выглядит следующим образом: Поскольку эти множества равны, то их пересечение будет следующим: A ∩ B = {2, 6, 8} Следовательно, = A = B Что показывает, что множества A и B равны. Предположим, у вас есть коллекция данных, включающая несколько наборов. Мы уже рассмотрели, как вы собираетесь классифицировать эти наборы. Но что, если некоторые наборы идентичны? Как вы будете идентифицировать эти идентичные или равные наборы? Чтобы ответить на эти вопросы, нам нужно понять, как определить, что два множества равны. Чтобы показать, что два множества равны, оба множества должны быть подмножествами друг друга. Ранее мы упоминали, что они должны быть подмножеством друг друга, чтобы два множества были равны. Математически это можно выразить следующим образом: Если A ⊆ B И B ⊆ A Тогда A = B Если это условие подмножеств не выполняется, то два множества не равны множествам . Давайте решим следующие примеры, чтобы понять эту идентификацию. Пример 2 Пусть множество A = {3, 6, 9, 12} и множество B = {9, 12, 6, 3}. Оцените, равны ли два набора или нет. Решение Чтобы оценить, равны ли множества, мы применим изложенную выше концепцию подмножеств. Элементы A — 3, 6, 9 и 12. Элементы B — 9, 12, 6 и 3. Ясно, что A ⊆ B А также B ⊆ A Следовательно, A = B Следовательно, два множества A и B равны. Пример 3 Пусть X = {x : x — четное число и 4 Решение Чтобы определить равенство множеств, мы сначала упростим эти множества. Набор А можно переписать как: A = {6, 8} Набор B можно переписать как: B = {6, 8} Теперь применим концепцию подмножеств. Элементы A 6 и 8. Элементы B также 6 и 8. Ясно, что A ⊆ B А также, B ⊆ A Отсюда, = B Следовательно, два множества A и B равны. Теперь мы решим несколько примеров, объединяющих понятия подмножеств и кардинальности, чтобы определить равенство множеств. Пример 4 Если установить A = {1, 3, 5, 7, 9} и установить B = {x : x нечетное число и 1≤x<11}, то определить, являются ли два множества равны. Решение Чтобы определить равенство множеств, мы сначала упростим множества. Множество B можно переписать как: B = {1, 3, 5, 7, 9} Теперь оценим их мощность. |А| = 5 А, |В| = 5 Итак, |А| = |В| Это доказывает, что два набора равны. Теперь оценим равенство множеств через подмножества. Элементами множества А являются 1, 3, 5, 7 и 9. Элементами множества В являются 1, 3, 5, 7 и 9. As A ⊆ B , B ⊆ A Следовательно, A = B Следовательно, два множества A и B равны. Чтобы еще больше укрепить понимание и концепцию множественного равенства, рассмотрите следующие практические задачи. (i) A = {10, 20, 30} и B = {20, 10} ii, X = {1) (2) 133, 144} и B = {144, 122, 133} Два множества A и B равны , если они состоят из одних и тех же элементов. Два множества A и B эквивалентны , если \(n(A)\)= \(n(B)\). Другими словами, два множества эквивалентны, если они имеют одинаковое количество элементов. Определите, являются ли следующие пары наборов равными, эквивалентными или и тем, и другим Решение Иногда коллекция может содержать не все элементы набора. Например, у Криса есть три альбома Мадонны. Хотя коллекция Криса представляет собой набор, мы также можем сказать, что это подмножество из большего набора всех альбомов Мадонны. Подмножество множества \(A\) — это другое множество, которое содержит только элементы из множества \(A\), но может не содержать все элементы \(A\). Если \(B\) является подмножеством \(A,\), мы пишем \(B \subseteq A\) Правильное подмножество - это подмножество, которое не идентично исходному набору - оно содержит меньше элементы. Если \(B\) является правильным подмножеством \(A\), мы пишем \(B \subset A\) Рассмотрим эти три набора \(A=\) множество всех четных чисел\(\quad B=\{2,4,6\} \quad C=\{2,3,4, 6\}\) Здесь \(B \подмножество A\), так как каждый элемент \(B\) также является четным числом, поэтому является элементом \(A\). Более формально мы могли бы сказать \(B \subset A\), поскольку если \(x \in B,\), то \(x \in A\) Также верно, что \(B \subset C\ ). \(C\) не является подмножеством \(A\), поскольку \(C\) содержит элемент 3 , который не содержится в \(A\) Предположим, набор содержит пьесы «Много шума из ничего», «Макбет» и «Сон в летнюю ночь». Подмножеством какого большого множества может быть это? Решение Здесь может быть много возможных ответов. Одним из них будет набор пьес Шекспира. Это также подмножество всех когда-либо написанных пьес. Это также подмножество всей британской литературы. Набор \(A=\{1,3,5\} .\) Подмножеством какого большого набора может быть этот набор? Есть несколько ответов: Множество всех нечетных чисел меньше 10. Множество всех нечетных чисел. Множество всех целых чисел. Множество всех действительных чисел. Один из способов получить интуитивное представление о подмножествах — попытаться перечислить все различные подмножества определенного множества. Давайте рассмотрим несколько примеров малых множеств и определим все их подмножества. Перечислите все подмножества для следующих наборов: а. Пустой набор \(\emptyset\) b. {а} в. {м, п} д. {x, y, z} Решение а. Поскольку в пустом множестве нет элементов, единственным подмножеством пустого множества \(\emptyset\) является само пустое множество. б. Множество {a} имеет два подмножества: само множество {a}, а также пустое множество \(\emptyset\) c. Множество {m, n} имеет четыре подмножества: пустое множество \(\emptyset\), {m}, {n} и {m, n} d. Множество {x, y, z} имеет восемь подмножеств: пустое множество \(\emptyset\), {x}, {y}, {z}, {x, y}, {x, z}, {y, г} и {х, у, г} Здесь есть несколько вещей, на которые стоит обратить внимание. Набор из тыс. элементов имеет 2 тыс. различных подмножеств. Эта страница под заголовком 2.2: Сравнение наборов распространяется по лицензии CC BY-SA, ее автор, ремикширование и/или куратор — Дэвид Липпман (The OpenTextBookStore) . Равные множества в теории множеств — это те, в которых количество элементов/чисел/символов одинаково. Что такое равный набор; рассмотрим, есть ли у нас два набора, скажем, X и Y. Наборы X и Y называются равными, если количество их элементов равно плюс соответствующие элементы также одинаковы. Элементами могут быть любые цифры, изображения, алфавиты, символы и т. д. Например, если P = {a, e, i, u} и Q = {a, e, i, u}, тогда P и Q являются равными множествами, так как они имеют одинаковое количество элементов, а также элементы равны. Согласно определению, которое мы прочитали выше, два множества P и Q объявляются равными, если они содержат одни и те же элементы. Это означает, что каждый элемент P является элементом Q и каждый элемент Q является элементом P. Другими словами, можно считать, что если множества P и Q равны, то в терминах математической записи пишется P = Q. В данном конкретном типе множества порядок элементов не имеет значения. Различные типы множеств в теории множеств: пустое множество, конечное множество, одноэлементное множество, равное, непересекающееся множество, эквивалентное множество, подмножества, степенное множество, универсальное множество, надмножество, бесконечное множество и т. д. Среди этих множеств мы обсуждаем, в частности, равное. Количество различных элементов, присутствующих в данном наборе (скажем, X), называется количественным числом набора и обозначается n(X). Если X = набор букв в слове TESTBOOK. То есть X = {T, E, S, T, B, O, O, K} Следовательно, мощность множества равна n(X) = 8. С точки зрения мощности множества изображаются равными, если они имеют одинаковую мощность плюс все элементы равны. То есть, если у нас есть два множества, такие как X и Y, и мощность множества X равна n (X) = a, где «a» обозначает количество элементов множества. Тогда множества называются равными, если: n(X) = n(Y) и a∈X, a∈Y также, Тогда X = Y Большинство отношений между множествами, отношениями и функциями можно интерпретировать с помощью диаграмм, известных как диаграммы Венна. Диаграммы Венна включают прямоугольники и замкнутые изогнутые окружности. Форма прямоугольника — это универсальное множество, а его подмножества — замкнутые круги. Диаграмма Венна, иллюстрирующая равные множества, показана ниже: Диаграмма Венна, показанная выше, включает два равных множества P и Q, поскольку имеется одинаковое количество компонентов с одинаковыми элементами, т. В предыдущих заголовках мы читали об определении, символе и мощности вместе с диаграммой Венна. Двигаясь вперед, давайте проверим важные свойства, относящиеся к одному и тому же: В фундаментальной теории множеств мы можем рассматривать два множества как эквивалентные, равные или неравные друг другу. Узнайте больше о пересечении множеств здесь. Давайте перейдем к некоторому примеру с равными множествами, чтобы понять концепции, которые мы прочитали в предыдущих разделах. Решено Пример 1: Даны три множества; U = {2, 3, 5, 7, 11}, V = {3, 5, 2, 7, 11} и S = {2, 11, 19, 22, 51}. Проверьте, равны ли заданные множества или нет. Решение: Даны U = {2, 3, 5, 7, 11}, V = {3, 5, 2, 7, 11} и S = {2, 11, 19, 22, 51}. Рассмотрим множество U = {2, 3, 5, 7, 11} и V = {3, 5, 2, 7, 11} Два множества имеют одинаковое количество элементов, и все они равны. Следовательно, множества равны. Теперь проверим U = {2, 3, 5, 7, 11}, V = {3, 5, 2, 7, 11} и S = {2, 11, 19, 22, 51} Для трех наборов количество элементов одинаково, отсюда следуют следующие выводы: U =V U, V и S эквивалентны множествам согласно условию. Прочтите эту статью о дополнении набора. Решено Пример 2: Представленные наборы равны или эквивалентны: Y={a,e,3} Z={Янвь,Февраль,Март} Решение: Дано Y={a,e,3 } и Z={Янвь,Февраль,Март} Наборы эквивалентны, так как количество элементов одинаково, но не идентично. Решенный Пример 3: Данные множества B = {p, q, a, d} и C = {a, d, c, 9} неравнодоказательны. Решение: Множество B = {p, q, a, d} и C = {a, d, c, 9} не равны, так как элементы не равны, несмотря на то, что количество элементов одинаково. Решенный пример 4: Если aN = {ax : x∈N}, то 2N ∩ 5N равно Понятие: Вычисление: Дано: aN = {ax : x∈N} ⇒ 2N = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20….} ⇒ 5N = {5, 10, 15, 20, 25….} Отсюда 2N ∩ 5N = {10, 20 ….} ∴ 2N ∩ 5N = 10N Решенный пример 5: Если A = {x | x 2 – 2x – 3 = 0} и B = {y | у 2 – 4у – 5 = 0}. Тогда найдите A ∪ (A ∩ B)? Понятие: Для любых двух множеств A и B имеем а) A ∪ B = {x | x ∈ A или B} б) A ∩ B = {y | y ∈ A и B} Расчет: Здесь A = {x | x 2 – 2x – 3 = 0}, что может быть представлено в форме реестра как: A = {-1, 3}. Аналогично, B = {y | y 2 – 4y – 5 = 0} может быть представлено в списке как: B = {-1, 5}. Пусть C = (A ∩ B) = {-1}. ⇒ A ∪ C = {-1, 3} Решено Пример 6. Концепция: Если A, B и C являются подмножествами набора X. Затем Коммутативное свойство: A ⋃ B = B ⋃ A Ассоциативное свойство: (A ⋃ B B ⋃ . ) ∪ C = A ⋃ (B ⋃ C) Распределительное свойство: A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) или A ⋂ (B ⋃ C) = (A ⋂ B ) ⋃ (A ⋂ C) Некоторые другие свойства I. A ∪ A = A, и A ∩ A = A II. А ∩ (А ∪ В) = А, А ∪ (А ∩ В) = А III. (А ∩ В) ∪ С = (А ∩ С) ∪ (В ∩ С) IV. (A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C) V. (A ⋃ B)' = A' ⋂ B' и (A ⋂ B)' = A' ⋃ B' VI. (A’)’ = A Расчет: 2. Л.В.С = А' ∪ (А ∪ В) = А ∪ В B') ⋃ A' = (A ∪ B) ⋃ A' = A ∪ B Итак, вариант 2 правильный. 3. Л.В.С = A' ∪ (B ∪ C) П.Г.С = (C' ∩ B)' ∩ A' = ((C')' ⋃ B) ⋂ A' = (C ⋂ B) ⋂ A' Таким образом, вариант 3 неверен. Решено Пример 7: Если A = {x : 0 ≤ x ≤ 2} и B = {y; y — простое число}, то чему равно A ∩ B? Понятие: Простые числа = Число, которое делится только на само на себя и на 1 {г; у — простое число} A = (0, 1, 2) и B = (2, 3, 5, 7, 11, 13, 17, 19, …..) Итак, исходя из вышеизложенного, общее число между A и B равно 2. ⇒ A ∩ B = {2} Решено Пример 8. Если A, B и C являются подмножествами заданного множества, то какое из следующих соотношений не является правильным? Понятие: Если A, B и C являются подмножествами множества X. Тогда I. A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) II. A ∪ A = A, A ∩ (A ∪ B) = A, A ∪ (A ∩ B) = A и A ∩ A = A III. IV. (A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C) Расчет: ⇒ A ∪ (A ∩ B) = (A ∪ A) ∩ (A ∪ B) = A ∩ (A ∪ B) = A — (Используя свойство I и II) Итак, вариант 1 неверен. ⇒ A ∩ (A ∪ B) = (A ∩ A) ∪ (A ∩ B) = A ∪ (A ∩ B) = A — (Используя свойства I и II) Итак, вариант 2 верен. ⇒ (A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C) — (Используя свойство III) Итак, вариант 3 верен. ⇒ (A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C) — (Используя свойство IV) Итак, вариант 4 верен. Решено Пример 9: Какое из следующих утверждений верно для любых двух множеств A и B? I. \({\left( {A \cup B} \right)’} = A’ \cap B’\) II. \({\left( {A \cap B} \right)’} = A’ \cup B’\) III. \(\left( {A – B} \right) = A \cap B’\) Понятие: 1. Закон Де-Моргана: Для любых двух множеств A и B имеем \({\left( {A \cup B} \right)'} = A' \cap B '\) и \({\left( {A \cap B} \right)'} = A' \cup B'\) 2. Решенный пример 10. Если A ∩ B = A, то найти значение A ∪ B. Понятие: Объединение множеств: Объединение двух заданных множеств – это множество, содержащее те элементы, которые находятся либо в A, либо в B, либо в обоих. Объединение множеств A и B, обозначаемое A U B Пересечение множеств: Пересечение двух заданных множеств — это наибольшее множество, содержащее все элементы, общие для обоих множеств. Пересечение множеств A и B, обозначенное A ∩ B Формула: A ∪ B = A + B – A ∩ B Расчет: Дано: A ∩ B = A 5 Найти Как мы знаем, A ∪ B = A + B – A ∩ B ⇒ A ∪ B = A + B – A ∴ A ∪ B = B Мы надеемся, что приведенная выше статья поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. В.1 Как мы определяем равный набор? Ответ 1 Два заданных набора считаются равными тогда и только тогда, когда все компоненты, присутствующие в обоих наборах, абсолютно одинаковы. Q.2 Что такое эквивалентный набор? Ответ 2 Два множества считаются эквивалентными, если в них одинаковое количество элементов. В.3. Каковы основные различия между равными и эквивалентными наборами? Ответ 3 Основное различие между равными и эквивалентными множествами заключается в том, что элементы в равных типах множеств идентичны, тогда как элементы не обязательно должны быть одинаковыми для эквивалентных множеств. Q.4 Какое обозначение множества используется для равных множеств? Ответ 4 Для обозначения равенства множеств используется символ «=». В.5 Что такое пример равного множества? Ответ 5 Пример равенства множеств: P={a,e,3}, Q={a,e,3} Тогда P=Q согласно условиям равенства множеств. Q.6 Как доказать, что два набора равны? Ответ 6 Два заданных множества могут быть равны тогда и только тогда, когда каждый элемент одного множества является также элементом второго множества. В дополнение к этому, если два множества являются подмножествами друг друга, они считаются равными. Поиск Задача 1. Решение: Оба учащегося использовали правильные обозначения. Наборы из задачи 1: равны , и мы пишем X = Y. Знак равенства (=) используется для демонстрации равенства. Давайте рассмотрим еще несколько примеров равенства множеств. Пример 1. Наборы A и B равны? Решение: А = {1, 3, 5, 7} В = {3, 7, 1, 5} Внимательно изучите эти наборы, чтобы убедиться, что они равны. Ответ: A = B Поскольку A и B содержат одинаковое количество элементов, и элементы в обоих одинаковы, мы говорим, что A равно B , и мы пишем A = B . Порядок, в котором элементы появляются в наборе, не важен. Пример 2. Наборы X и Y равны? Решение: X = {а, е, я, о, и} Y = {и, о, я, е, а} Внимательно изучите эти наборы, чтобы убедиться, что они равны . Ответ: X = Y Поскольку X и Y содержат одинаковое количество элементов, мы пишем X = . Помните, что порядок, в котором элементы появляются в наборе, не важен. Пример 3. Решение: P = {яблоки, апельсины, бананы, груши} Q = {апельсины, груши, яблоки} Внимательно изучите эти наборы, чтобы убедиться, что они не равны . Ответ: P ≠ Q С P и Q не содержат точно тех же элементов, мы говорим, что P не равны Q, и WE wy 88. 888888888 годы 8. Q . Пример 4: пусть R — множество всех целых чисел меньше 5, и пусть S = {4, 2, 0, 3, 1}. Наборы R и S одинаковы? Решение: R = {целые числа < 5} S = {4, 2, 0, 3, 1} Внимательно изучите эти наборы, чтобы убедиться, что они равны. Ответ: R = S Пример 5. Какие из следующих наборов равны? Ответ: C = G и F = K В примере 5, эти наборы не равны: D ≠ H и E h. не равный? Резюме: Два набора равны, если они имеют одинаковое количество элементов и их элементы одинаковы. Порядок, в котором элементы появляются в наборе, не важен. Указания: Прочтите каждый вопрос ниже. Выберите свой ответ, нажав на его кнопку. Обратная связь по вашему ответу представлена в ОКНО РЕЗУЛЬТАТЫ. Если вы допустили ошибку, обдумайте свой ответ еще раз, а затем выберите другую кнопку. P = {понедельник, вторник, среда, четверг, пятница} ОКНО РЕЗУЛЬТАТОВ: H = {5, 2, 1, 4, 3, 6} ОКНО РЕЗУЛЬТАТОВ: ОКНО РЕЗУЛЬТАТОВ:  Мощность множеств A и B:
Мощность множеств A и B: Равные множества также можно представить с помощью диаграммы Венна, а их отношение можно изобразить с помощью операции пересечения.
Равные множества также можно представить с помощью диаграммы Венна, а их отношение можно изобразить с помощью операции пересечения. Подмножество — это дочерний набор, содержащий все или некоторые элементы родительского набора. Символ ⊆ используется для обозначения подмножества.
Подмножество — это дочерний набор, содержащий все или некоторые элементы родительского набора. Символ ⊆ используется для обозначения подмножества.

Ответы
Предыдущий урок | Главная страница | Следующий урок 2.2: Сравнение множеств — Математика LibreTexts
Равные и эквивалентные
 Мы пишем A = B.
Мы пишем A = B. Пример 1
 Однако они эквивалентны, потому что оба имеют 4 элемента.
Однако они эквивалентны, потому что оба имеют 4 элемента. Подмножество
Пример 2

Пример 3
Попробуйте сейчас 1

Пример 4
 Во-первых, обратите внимание, что каждое множество имеет себя как подмножество. Кроме того, пустое множество является подмножеством любого возможного множества. Наконец, вы видели, что произошло, когда наборы увеличились в размерах? Для каждого нового элемента набора — 0, 1, 2, 3 — количество подмножеств удваивается — 1, 2, 4, 8. Эта закономерность сохраняется для наборов любого размера, поэтому мы можем придумать формулу для предсказания количество подмножеств для данного множества.
Во-первых, обратите внимание, что каждое множество имеет себя как подмножество. Кроме того, пустое множество является подмножеством любого возможного множества. Наконец, вы видели, что произошло, когда наборы увеличились в размерах? Для каждого нового элемента набора — 0, 1, 2, 3 — количество подмножеств удваивается — 1, 2, 4, 8. Эта закономерность сохраняется для наборов любого размера, поэтому мы можем придумать формулу для предсказания количество подмножеств для данного множества. Определение: количество подмножеств набора
Знать определение, символ, диаграмму Венна, примеры здесь
 Здесь набор представляет собой хорошо описанную группу объектов (букв, чисел, людей, форм и т. д.) и обычно обозначается заглавной буквой с элементами, помещенными в фигурные скобки «{}». Элементы, записанные в наборе, могут быть в любой форме, но не могут повторяться. Все элементы множества в математике выражаются строчными буквами в случае алфавитов. В этой статье мы постараемся узнать о равных множествах с помощью определения, символа, кардинальности, диаграммы Венна, за которыми следуют свойства, сравнение с эквивалентными множествами и решенные примеры для того же, чтобы понять концепции.
Здесь набор представляет собой хорошо описанную группу объектов (букв, чисел, людей, форм и т. д.) и обычно обозначается заглавной буквой с элементами, помещенными в фигурные скобки «{}». Элементы, записанные в наборе, могут быть в любой форме, но не могут повторяться. Все элементы множества в математике выражаются строчными буквами в случае алфавитов. В этой статье мы постараемся узнать о равных множествах с помощью определения, символа, кардинальности, диаграммы Венна, за которыми следуют свойства, сравнение с эквивалентными множествами и решенные примеры для того же, чтобы понять концепции. Равные наборы

Символ равных множеств
Мощность равных множеств

Диаграмма Венна равных множеств
 е. P = {2, 7, r} = Q.
е. P = {2, 7, r} = Q. Свойства равных множеств
Равные множества против эквивалентных множеств
 Хорошо знакомый с определением, обозначениями и диаграммой Венна для равенства множеств, давайте перейдем к сравнению между равными и эквивалентными множествами.
Хорошо знакомый с определением, обозначениями и диаграммой Венна для равенства множеств, давайте перейдем к сравнению между равными и эквивалентными множествами. Равные наборы Равные наборы Условие: Все компоненты в заданных множествах равны. Условие: Количество компонентов в данных наборах одинаковое. Мощность: мощности множеств равны. Мощность: заданные множества имеют одинаковую мощность. Количество элементов: идентичные Количество элементов: идентичные Символ: символ, используемый для обозначения равных множеств, '=' Символ: символ, используемый для обозначения эквивалентных множеств, ~ или ≡ Пример: X = {1, 13, -9, 23, 7} и Y = {23, 7, 13, 1, -9}, тогда X = Y Пример: Если P = {1, −21, 2110, 75} и Q = {2, 4, 6, 8}, то P эквивалентно Q. Элементы: элементы должны быть идентичными для равенства множеств. 
Элементы: элементы не обязательно должны быть одинаковыми для эквивалентных наборов. Равные множества — это своего рода эквивалентные множества. Эквивалентные наборы могут быть или не быть равными по своей природе. Решенные примеры на равных множествах


2 получить
 Если A, B и C являются подмножествами универсального множества, то какое из следующих утверждений неверно? Где A’ — дополнение A.
Если A, B и C являются подмножествами универсального множества, то какое из следующих утверждений неверно? Где A’ — дополнение A. 
L.H.S ≠ R.H.S (А ∩ В) ∪ С = (А ∩ С) ∪ (В ∩ С)
(А ∩ В) ∪ С = (А ∩ С) ∪ (В ∩ С) A – B = {c | c ∈ A и c ∉ B} = A ∩ B'
A – B = {c | c ∈ A и c ∉ B} = A ∩ B'5 A ∪ B
 Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам. Часто задаваемые вопросы о равном наборе

Еще на testbook.com
Непересекающийся набор: Знайте определение, символы, шаги для идентификации здесь, используя диаграммы Венна и примеры! Установить разницу: узнать определение, свойства, связь, разницу на примерах Многоугольники: определение, классификация, формулы с изображениями и примерами Четырехугольник: значение, классификация, формулы и примеры решения Производные правила и правила дифференцирования с доказательством и формулой Задать уроки равенства
Форма поиска
 Миссис Глоссер попросила свой класс написать набор основных цветов, используя запись реестра. Она получила два разных ответа от двух разных студентов, как показано ниже. Кто из учащихся использовал правильную запись?
Миссис Глоссер попросила свой класс написать набор основных цветов, используя запись реестра. Она получила два разных ответа от двух разных студентов, как показано ниже. Кто из учащихся использовал правильную запись? Студент Обозначение Эдуардо X = {красный, желтый, синий} Энджи Y = {синий, красный, желтый} 
 Наборы P и Q равны?
Наборы P и Q равны?
C = {1, 2, 3} D = {а, д, я, о, у} E = {2, 4, 6, 8, 10} F = {Джон, Джейн, Джо} G = {2, 3, 1} H = {о, е, а, у, и} J = {2, 4, 6, 8} K = {Джейн, Джо, Джон} 
Упражнения 1. Какой из следующих наборов равен набору P?
W = {Четверг, Пятница, Суббота, Воскресенье, Понедельник}
X = {Вторник, Среда, Четверг, Пятница, Суббота}
Y = {Четверг, Пятница, Понедельник, Вторник, Среда}
Все над.
2. 
Какой из следующих наборов не равен набору H?
M = {3, 2, 1, 4, 5, 6}
Q = {4, 1, 6, 2, 7, 3}
D = {1, 2, 6, 4, 5 , 3}
Ничего из вышеперечисленного.
3. Пусть M = {0, 2, 4, 6, 8, 10} и N = {четные числа < 10}. Какие из следующих утверждений является верным?
M — бесконечное множество.
M = N
M ≠ N
Все вышеперечисленное.
4. 

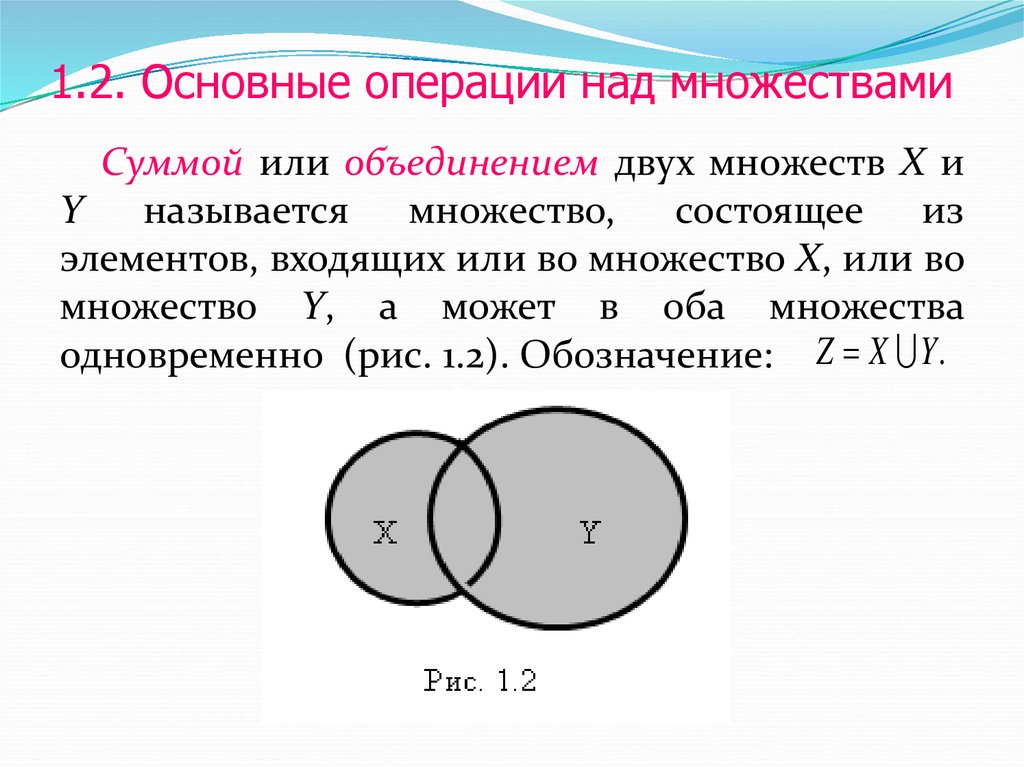
 name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}
name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}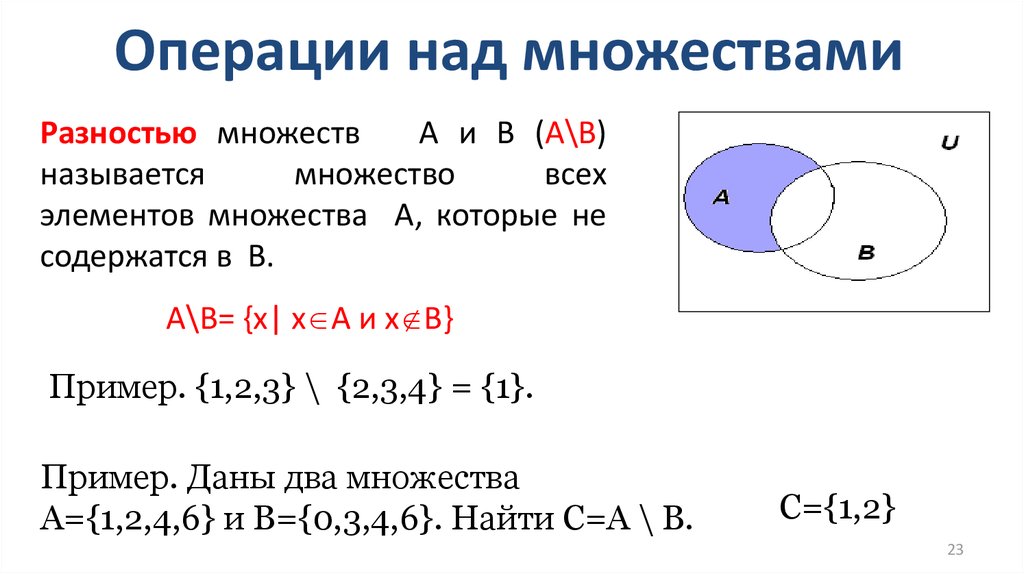 __class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'
__class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")' issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество!
issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество! # Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
# Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"} update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}
update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9} , также существует два специальных метода –
, также существует два специальных метода –  Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.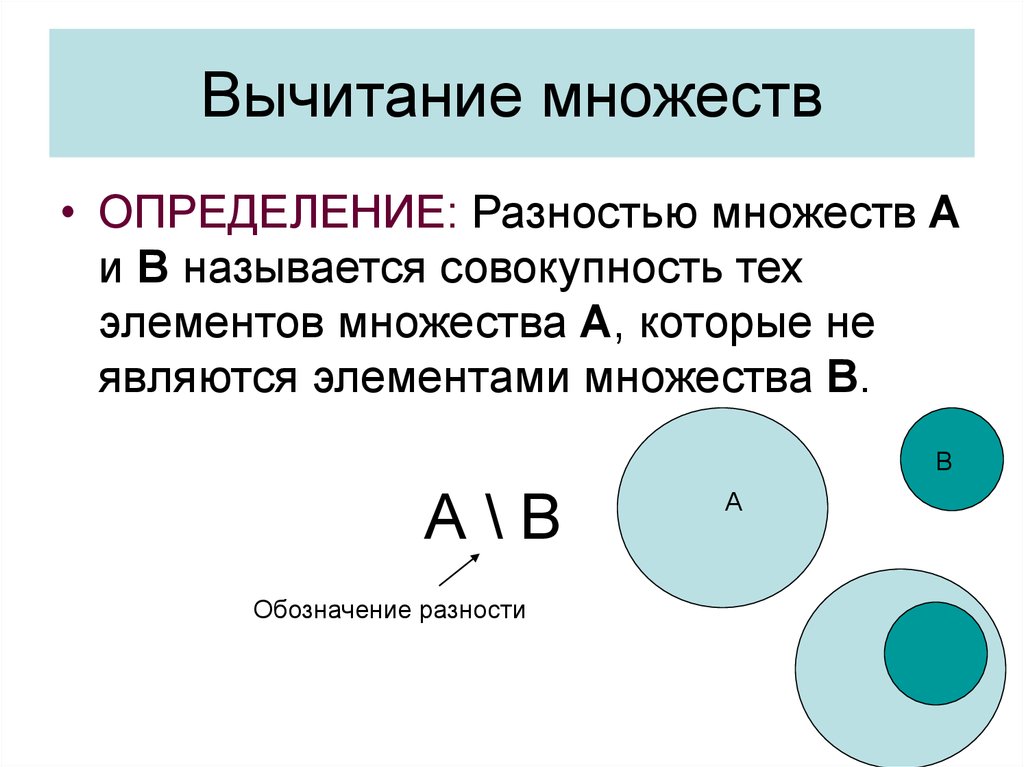
 А = В, если их объединение и пересечение совпадает. A ∪ B = . A ∩ B =.
А = В, если их объединение и пересечение совпадает. A ∪ B = . A ∩ B =. 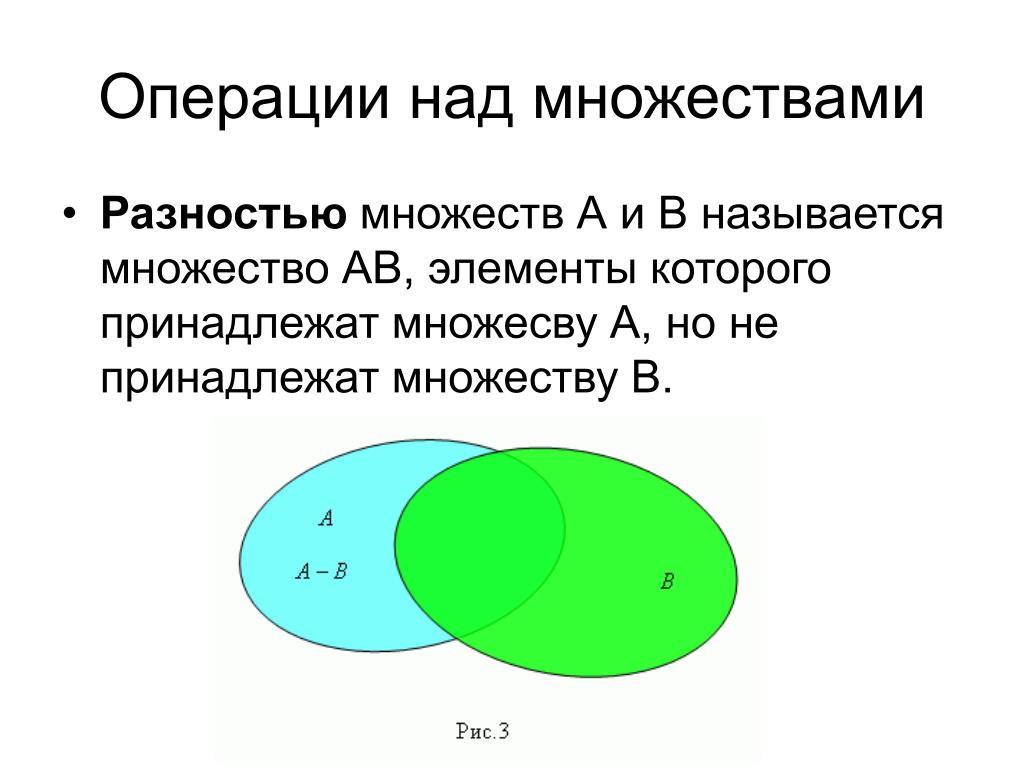 1 и 27 (начало и конец) — нечетные числа. Значит, нечетных будет больше.
1 и 27 (начало и конец) — нечетные числа. Значит, нечетных будет больше.
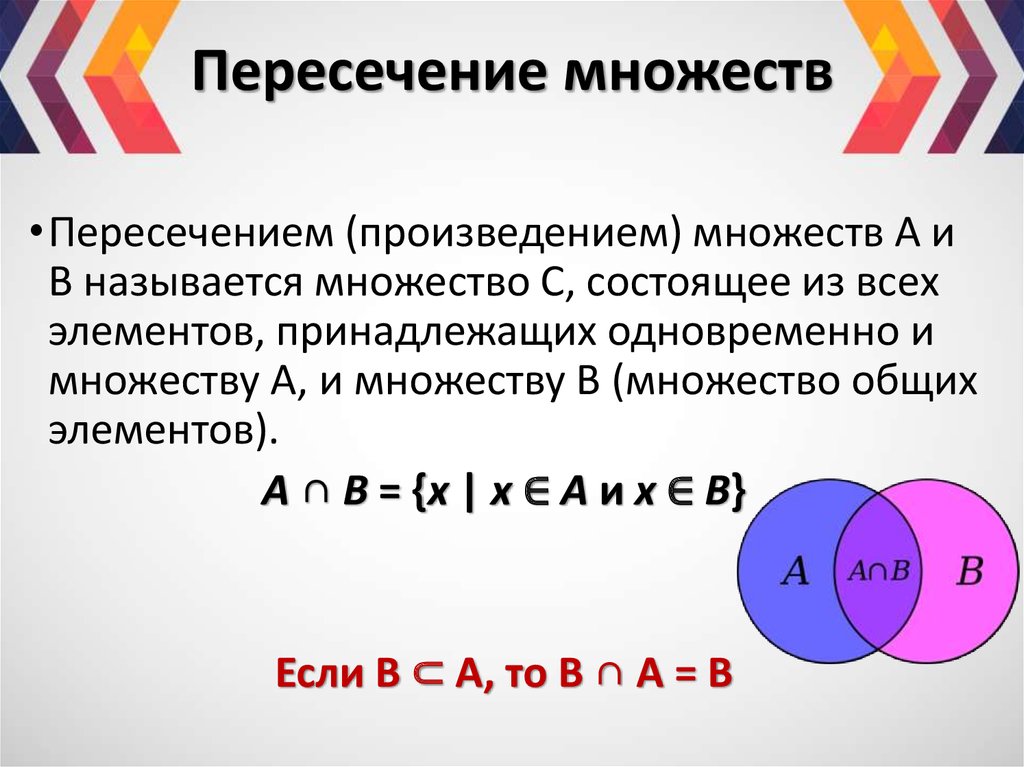
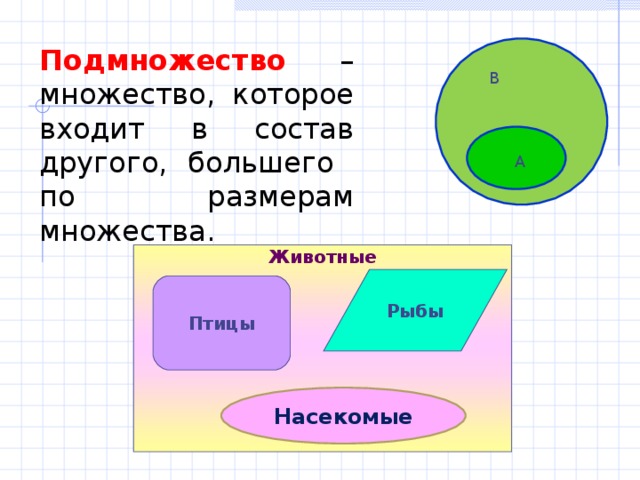 Тогда для левой части данного соотношения $left(Acap B
Тогда для левой части данного соотношения $left(Acap B
 $$ Видим, что индикаторные функции обеих частей совпали $$<chi >_Aleft(x
$$ Видим, что индикаторные функции обеих частей совпали $$<chi >_Aleft(x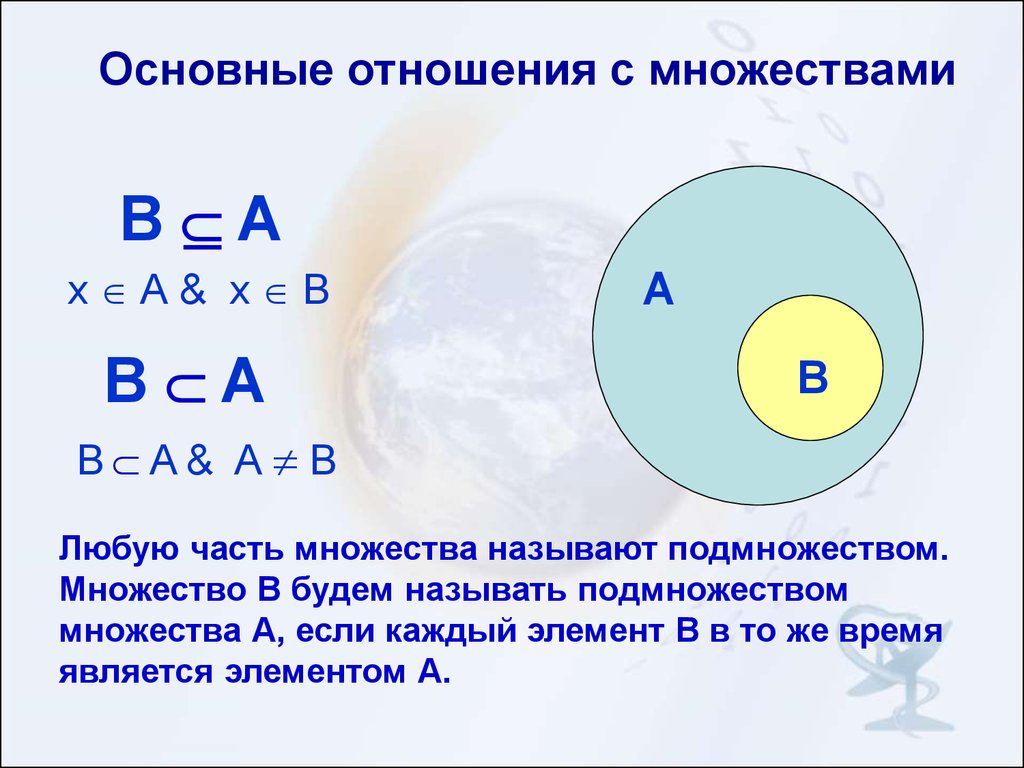
 д. То есть множество всех книг – это универсальное множество, содержащее в себе различные подмножества книг.
д. То есть множество всех книг – это универсальное множество, содержащее в себе различные подмножества книг. . Операции над множествами
. Операции над множествами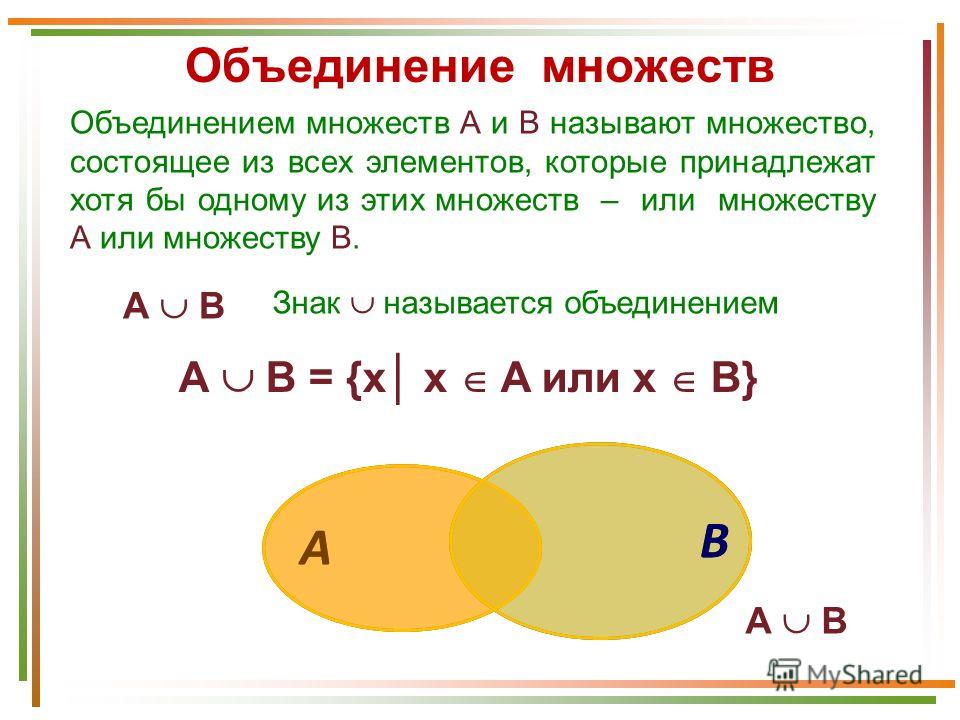 3.2). Для наглядности множества показаны вместе с элементами. ◄
3.2). Для наглядности множества показаны вместе с элементами. ◄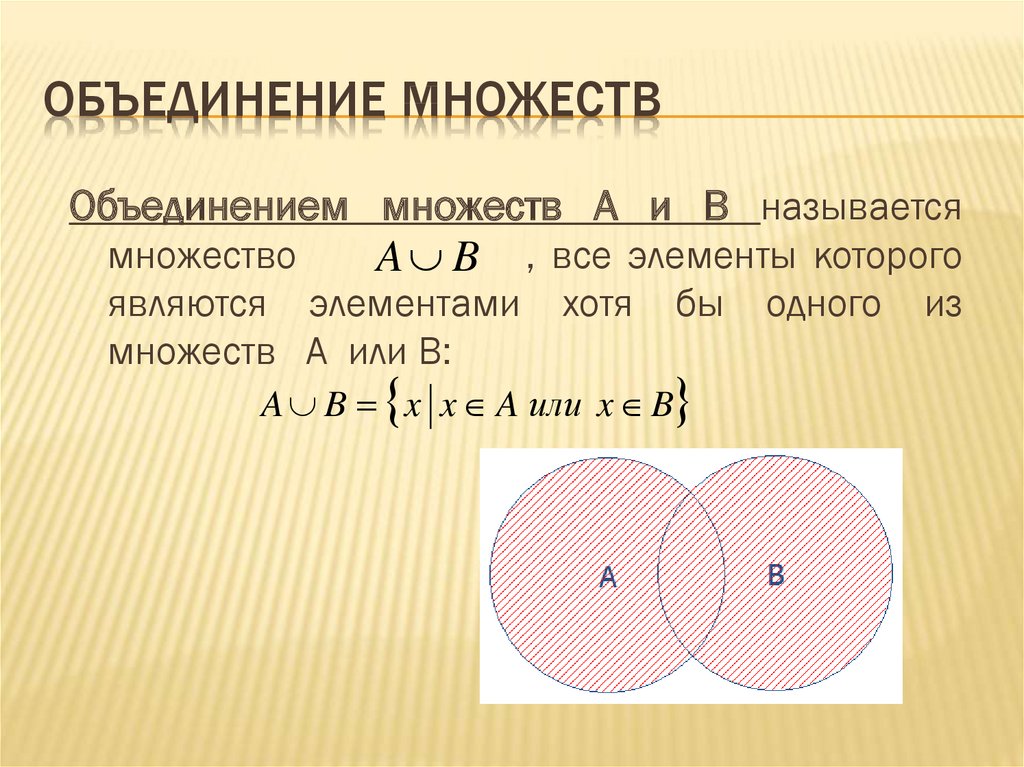 Наибольший элемент множества С, то есть 18, называется наибольшим общим делителем чисел 54 и 72. ◄
Наибольший элемент множества С, то есть 18, называется наибольшим общим делителем чисел 54 и 72. ◄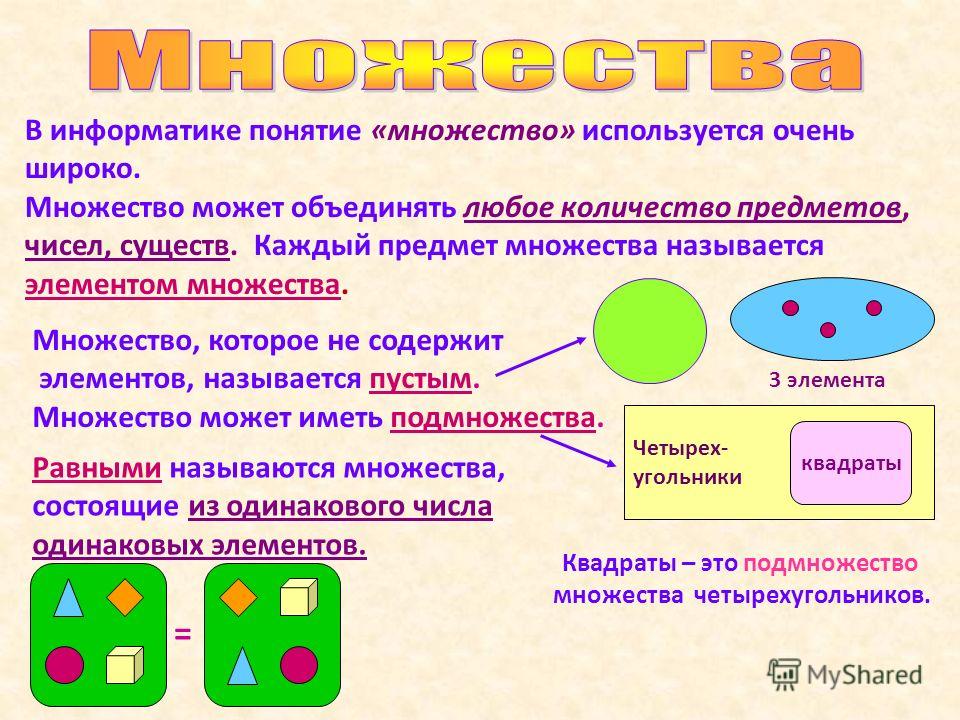
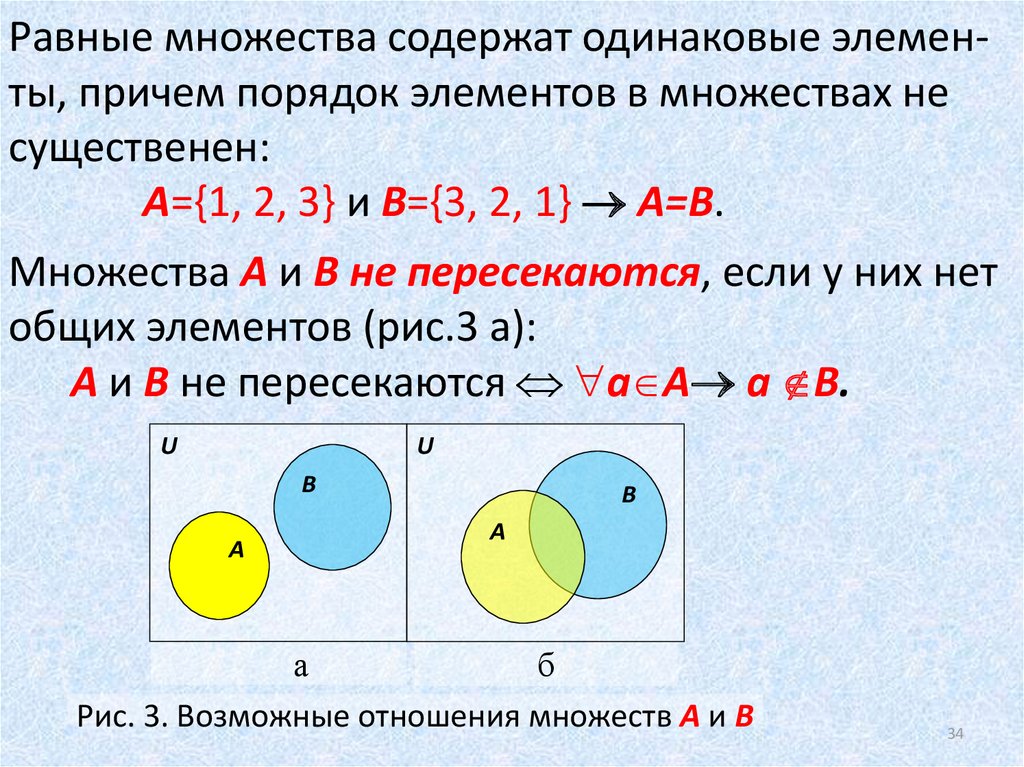 Но все-таки по
возможности основные сведения должны получить
все дети.
Но все-таки по
возможности основные сведения должны получить
все дети. Нам представляется, что если ученик к
этому времени будет знать, что такое вообще
объединение и пересечение множеств (а не только
для числовых множеств), то и в теории
вероятностей объединение, пересечение событий
этот ученик встретит как своих знакомых.
Нам представляется, что если ученик к
этому времени будет знать, что такое вообще
объединение и пересечение множеств (а не только
для числовых множеств), то и в теории
вероятностей объединение, пересечение событий
этот ученик встретит как своих знакомых.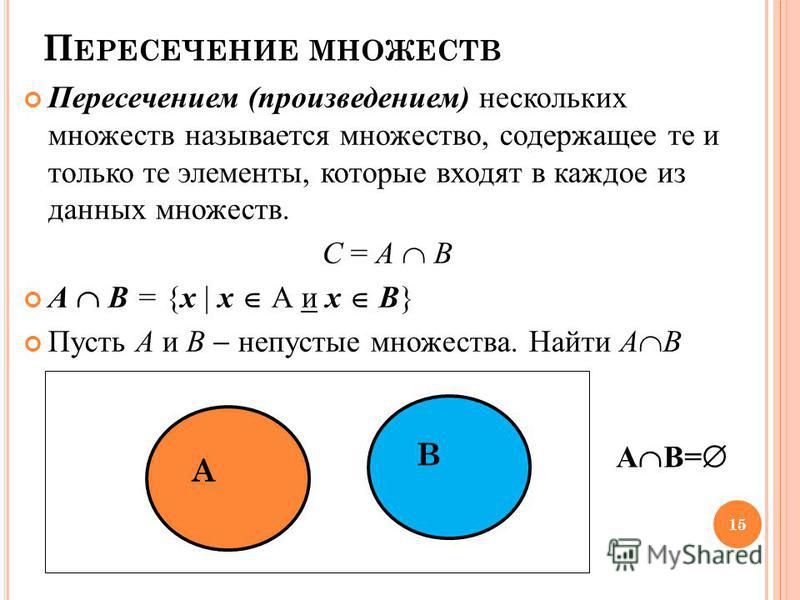
 На следующем уроке
вводилось определение подмножества,
рассматривалось число подмножеств конечного
множества. Затем изучались операции над
множествами, Эти уроки предшествовали занятиям
по теории вероятностей.
На следующем уроке
вводилось определение подмножества,
рассматривалось число подмножеств конечного
множества. Затем изучались операции над
множествами, Эти уроки предшествовали занятиям
по теории вероятностей. Слово "мощность" при этом намеренно
старалась не называть. Мне кажется, что хотя бы на
интуитивном уровне главная идея этих примеров
детям все равно будет понятна.
Слово "мощность" при этом намеренно
старалась не называть. Мне кажется, что хотя бы на
интуитивном уровне главная идея этих примеров
детям все равно будет понятна.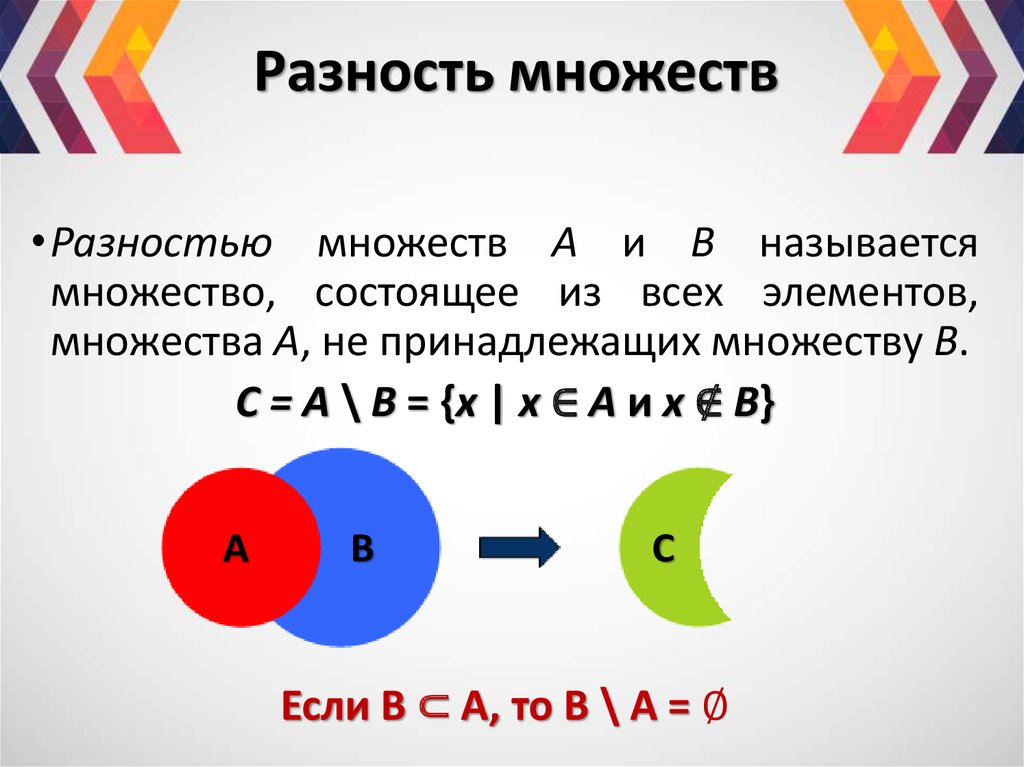 Когда мы записываем множество с
помощью фигурных скобок, именно эти скобки
подчеркивают, что данные элементы составляют
множество.
Когда мы записываем множество с
помощью фигурных скобок, именно эти скобки
подчеркивают, что данные элементы составляют
множество. Множество можно представить себе как
совокупность некоторых элементов.
Множество можно представить себе как
совокупность некоторых элементов. Записываем данное
множество так: В={x|x>0}.
Записываем данное
множество так: В={x|x>0}. Элементы могут
быть любые, их порядок не важен.
Элементы могут
быть любые, их порядок не важен.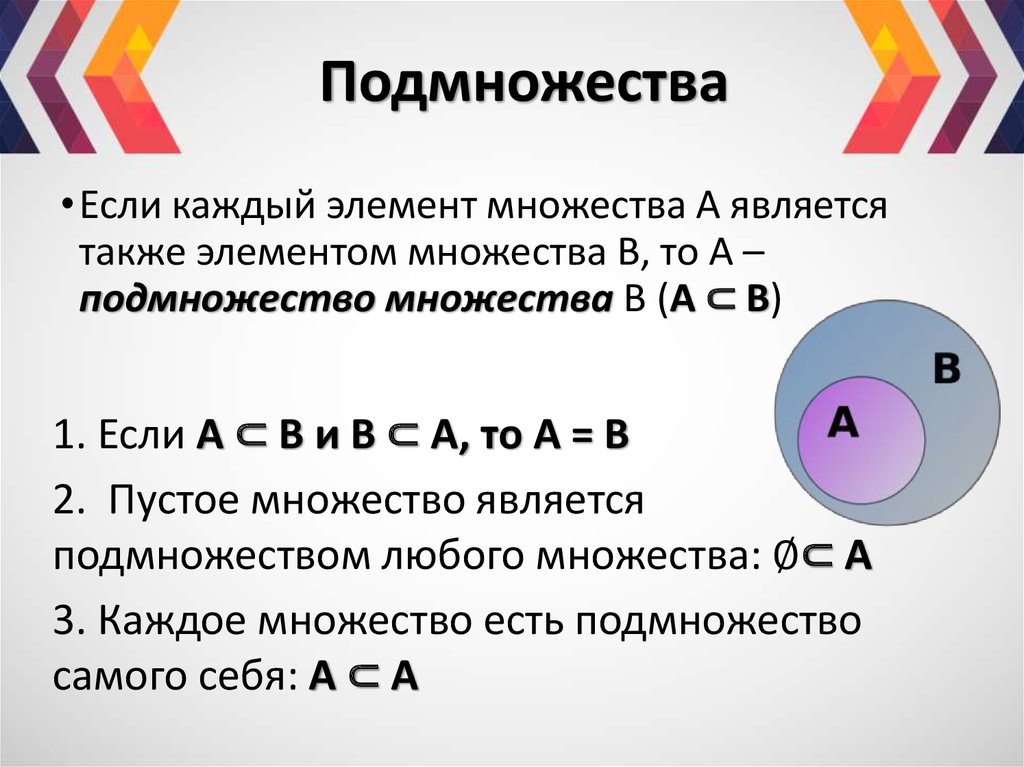 Обозначение: . Например,
множество говорящих рыб - пустое. Пустым будет
множество корней уравнения 0х=3. Или, например,
множество параллелограммов, в которых все углы
острые.
Обозначение: . Например,
множество говорящих рыб - пустое. Пустым будет
множество корней уравнения 0х=3. Или, например,
множество параллелограммов, в которых все углы
острые. Это множество из 10 элементов
(назовите их!).
Это множество из 10 элементов
(назовите их!).