Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
В выпуклом четырехугольнике ABCD AB=9.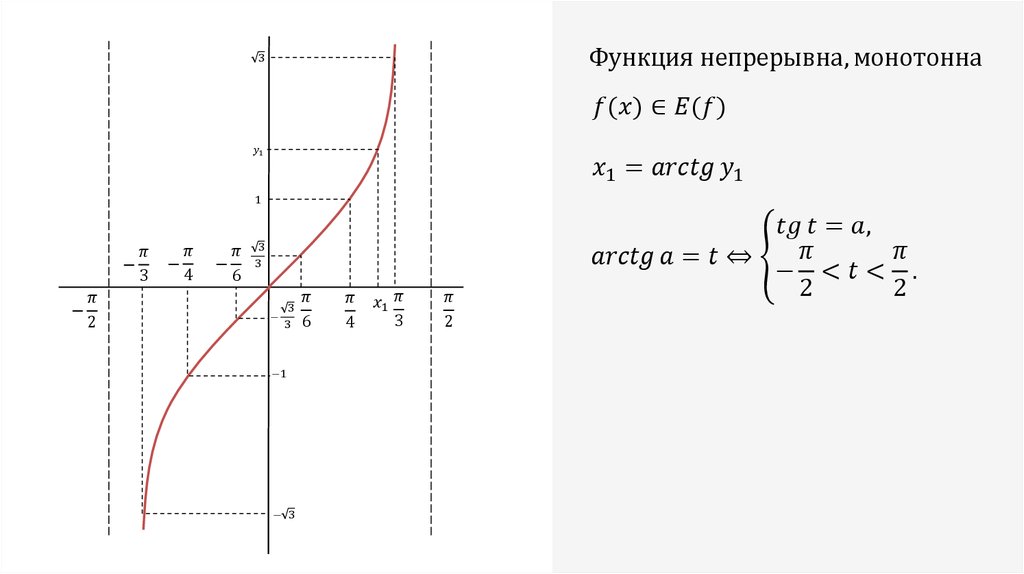 ..
..
сокращенное ионное уравнение реакции Ba(2+) + SO4(2-) = BaSO4 соответствует взаимодействию
Карандаш совмещенс главной оптической осью тонкой собирающей линзы ,его длина равна фокусному расстоянию линзы f=12см середина карандаша находиться на расстоянии 2f от линзы.расчитайте длину
Решено
Какие свойства фенола лежат в основе его применения
Камертон, прикрепленный к резонансному ящику,…
Пользуйтесь нашим приложением
Чему равен arctg 3. Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса. Разложение в ряд
Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
И для тех, кто «очень даже…»)
К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4 ! Да-да.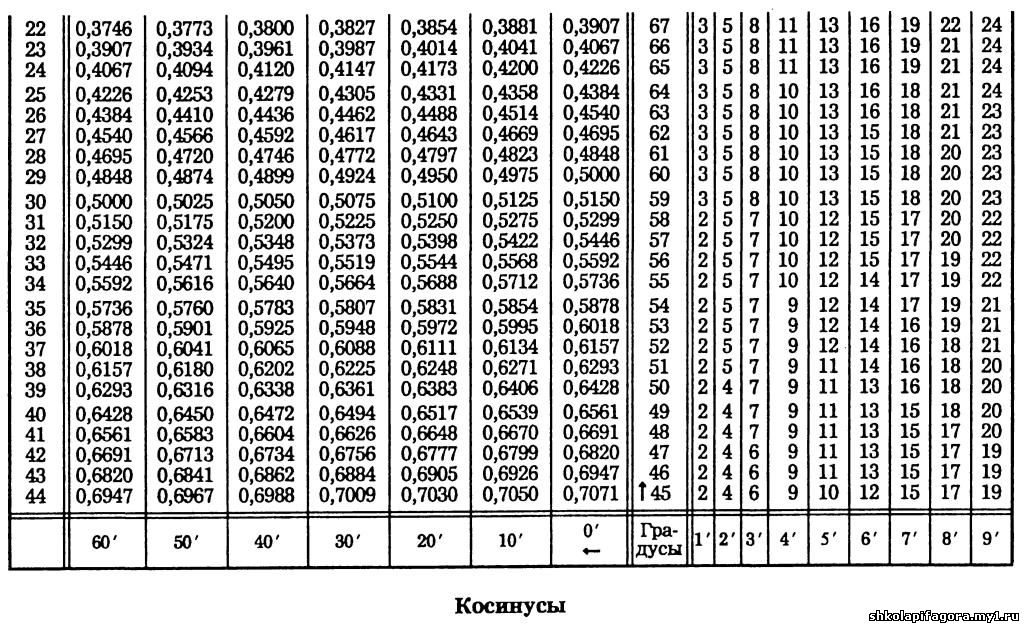 Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc sin 0,4
угол, синус которого равен 0,4
Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.
Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов. ) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно —
Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.
А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку:
arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов . Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:arcsin 0,5 = 30°
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус… Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да…) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.
Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно.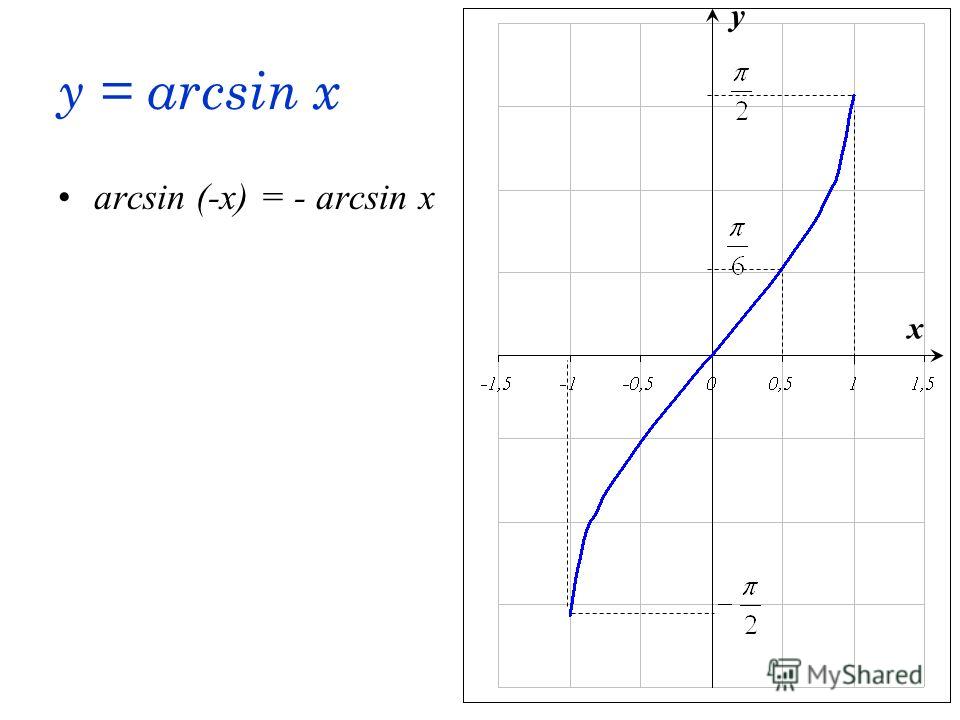 Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Вот и всё.
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
С примерами 7 — 9 проблема? Ну да, есть там некоторая хитрость.)
Все эти примеры, с 1-го по 9-й, тщательно разобраны по полочкам в Разделе 555. Что, как и почему. Со всеми тайными ловушками и подвохами. Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
Учимся — с интересом!)
можно познакомиться с функциями и производными.
Эта статья про нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса данного числа. Сначала мы внесем ясность, что называется значением арксинуса, арккосинуса, арктангенса и арккотангенса. Дальше получим основные значения этих аркфункций, после чего разберемся, как находятся значения арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса. Наконец, поговорим про нахождение арксинуса числа, когда известен арккосинус, арктангенс или арккотангенс этого числа, и т.п.
Навигация по странице.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Сначала стоит разобраться, что вообще такое «значение арксинуса, арккосинуса, арктангенса и арккотангенса ».
Таблицы синусов и косинусов, а также тангенсов и котангенсов Брадиса позволяют найти значение арксинуса, арккосинуса, арктангенса и арккотангенса положительного числа в градусах с точностью до одной минуты. Здесь стоит оговориться, что нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса отрицательных чисел можно свести к нахождению значений соответствующих аркфункций положительных чисел, обратившись к формулам arcsin, arccos, arctg и arcctg противоположных чисел вида arcsin(−a)=−arcsin a
, arccos(−a)=π−arccos a
, arctg(−a)=−arctg a
и arcctg(−a)=π−arcctg a
.
Здесь стоит оговориться, что нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса отрицательных чисел можно свести к нахождению значений соответствующих аркфункций положительных чисел, обратившись к формулам arcsin, arccos, arctg и arcctg противоположных чисел вида arcsin(−a)=−arcsin a
, arccos(−a)=π−arccos a
, arctg(−a)=−arctg a
и arcctg(−a)=π−arcctg a
.
Разберемся с нахождением значений арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам Брадиса. Будем это делать на примерах.
Пусть нам требуется найти значение арксинуса 0,2857
. Находим это значение в таблице синусов (случаи, когда это значение отсутствует в таблице, разберем ниже). Ему соответствует синус 16
градусов 36
минут. Следовательно, искомым значением арксинуса числа 0,2857
является угол 16
градусов 36
минут.
Часто приходится учитывать и поправки из трех справа столбцов таблицы. К примеру, если нам нужно найти арксинус 0,2863
. По таблице синусов это значение получается как 0,2857
плюс поправка 0,0006
, то есть, значению 0,2863
соответствует синус 16
градусов 38
минут (16
градусов 36
минут плюс 2
минуты поправки).
Если же число, арксинус которого нас интересует, отсутствует в таблице и даже не может быть получено с учетом поправок, то в таблице нужно отыскать два наиболее близких к нему значения синусов, между которыми данное число заключено. Например, мы ищем значение арксинуса числа 0,2861573
. Этого числа нет в таблице, с помощью поправок это число тоже не получить. Тогда находим два наиболее близких значения 0,2860
и 0,2863
, между которыми исходное число заключено, этим числам соответствуют синусы 16
градусов 37
минут и 16
градусов 38
минут. Искомое значение арксинуса 0,2861573
заключено между ними, то есть, любое из этих значений угла можно принять в качестве приближенного значения арксинуса с точностью до 1
минуты.
Абсолютно аналогично находятся и значения арккосинуса, и значения арктангенса и значения арккотангенса (при этом, конечно, используются таблицы косинусов, тангенсов и котангенсов соответственно).
Нахождение значения arcsin через arccos, arctg, arcctg и т.
 п.
п.Например, пусть нам известно, что arcsin a=−π/12 , а нужно найти значение arccos a . Вычисляем нужное нам значение арккосинуса: arccos a=π/2−arcsin a=π/2−(−π/12)=7π/12 .
Куда интереснее обстоит дело, когда по известному значению арксинуса или арккосинуса числа a требуется найти значение арктангенса или арккотангенса этого числа a или наоборот. Формул, задающих такие связи, мы, к сожалению, не знаем. Как же быть? Разберемся с этим на примере.
Пусть нам известно, что арккосинус числа a равен π/10 , и нужно вычислить значение арктангенса этого числа a . Решить поставленную задачу можно так: по известному значению арккосинуса найти число a , после чего найти арктангенс этого числа. Для этого нам сначала потребуется таблица косинусов, а затем – таблица тангенсов.
Угол π/10
радиан – это угол 18
градусов, по таблице косинусов находим, что косинус 18
градусов приближенно равен 0,9511
, тогда число a
в нашем примере есть 0,9511
.
Осталось обратиться к таблице тангенсов, и с ее помощью найти нужное нам значение арктангенса 0,9511
, оно приближенно равно 43
градусам 34
минутам.
Эту тему логически продолжает материал статьи вычисление значений выражений, содержащих arcsin, arccos, arctg и arcctg .
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- И. В. Бойков, Л. Д. Романова. Сборникк задач для подготовки к ЕГЭ, часть 1, Пенза 2003.
- Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.
 — 96 с.: ил. ISBN 5-7107-2667-2
— 96 с.: ил. ISBN 5-7107-2667-2
Урок и презентация на темы: «Арксинус. Таблица арксинусов. Формула y=arcsin(x)»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Программная среда «1С: Математический конструктор 6.1»
Решаем задачи по геометрии. Интерактивные задания на построение в пространстве
Что будем изучать:
1. Что такое арксинус?
2. Обозначение арксинуса.
3. Немного истории.
4. Определение.
6. Примеры.
Что такое арксинус?
Ребята, мы с вами уже научились решать уравнения для косинуса, давайте теперь научимся решать подобные уравнения и для синуса. Рассмотрим sin(x)= √3/2. Для решения этого уравнения требуется построить прямую y= √3/2 и посмотреть: в каких точках она пересекает числовую окружность. Видно, что прямая пересекает окружность в двух точках F и G.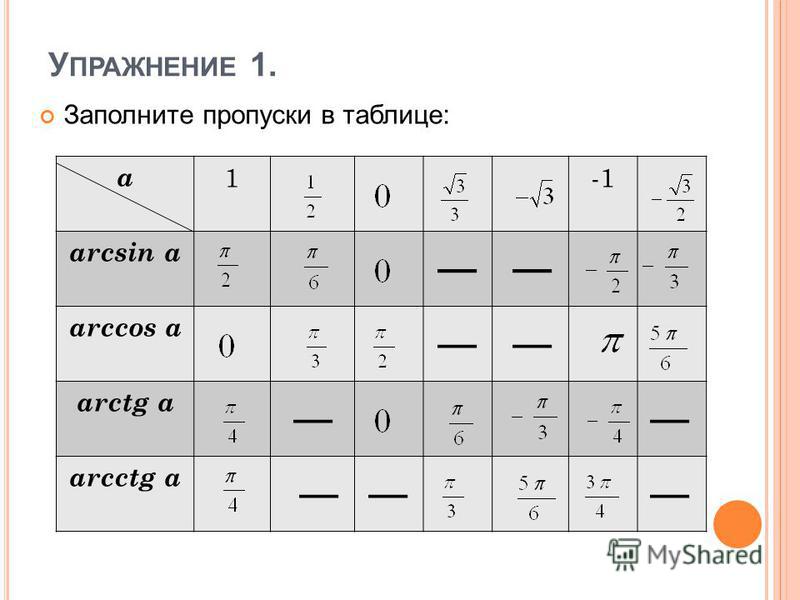 Эти точки и будут решением нашего уравнения. Переобозначим F как x1, а G как x2. Решение этого уравнения мы уже находили и получили: x1= π/3 + 2πk,
Эти точки и будут решением нашего уравнения. Переобозначим F как x1, а G как x2. Решение этого уравнения мы уже находили и получили: x1= π/3 + 2πk,
а x2= 2π/3 + 2πk.
Решить данное уравнение довольно просто, но как решить, например, уравнение
sin(x)= 5/6. Очевидно, что это уравнение будет иметь также два корня, но какие значения будут соответствовать решению на числовой окружности? Давайте внимательно посмотрим на наше уравнение sin(x)= 5/6.
Решением нашего уравнения будут две точки: F= x1 + 2πk и G= x2 + 2πk,
где x1 – длина дуги AF, x2 – длина дуги AG.
Заметим: x2= π — x1, т.к. AF= AC — FC, но FC= AG, AF= AC — AG= π — x1.
Но, что это за точки?
Столкнувшись с подобной ситуацией, математики придумали новый символ – arcsin(x). Читается, как арксинус.
Тогда решение нашего уравнения запишется так: x1= arcsin(5/6), x2= π -arcsin(5/6).
И решение в общем виде: x= arcsin(5/6) + 2πk и x= π — arcsin(5/6) + 2πk.
Арксинус — это угол (длина дуги AF, AG) синус, которого равен 5/6.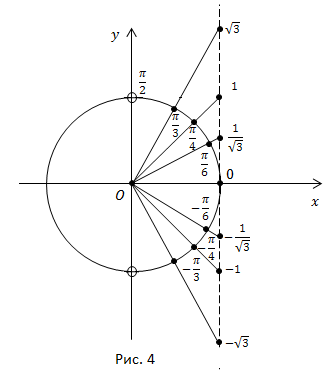
Немного истории арксинуса
История происхождения нашего символа совершенно такая же, как и у arccos. Впервые символ arcsin появляется в работах математика Шерфера и известного французского ученого Ж.Л. Лагранжа. Несколько ранее понятие арксинус рассматривал Д. Бернули, правда записывал его другими символами.
Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга). Это вполне согласуется со смыслом понятия: arcsin x — это угол (а можно сказать и дуга), синус которого равен x.
Определение арксинуса
Если |а|≤ 1, то arcsin(a) – это такое число из отрезка [- π/2; π/2], синус которого равен а.
Если |а|≤ 1, то уравнение sin(x)= a имеет решение: x= arcsin(a) + 2πk и
x= π — arcsin(a) + 2πk
Перепишем:
x= π — arcsin(a) + 2πk = -arcsin(a) + π(1 + 2k).
Ребята, посмотрите внимательно на два наших решения. Как думаете: можно ли их записать общей формулой? Заметим, что если перед арксинусом стоит знак «плюс», то π умножается на четное число 2πk, а если знак «минус», то множитель — нечетный 2k+1.
С учётом этого, запишем общую формула решения для уравнения sin(x)=a:
Есть три случая, в которых предпочитают записывать решения более простым способом:
sin(x)=0, то x= πk,
sin(x)=1, то x= π/2 + 2πk,
sin(x)=-1, то x= -π/2 + 2πk.
Для любого -1 ≤ а ≤ 1 выполняется равенство: arcsin(-a)=-arcsin(a).
Напишем таблицу значений косинуса наоборот и получим таблицу для арксинуса.
Примеры
1. Вычислить: arcsin(√3/2).
Решение: Пусть arcsin(√3/2)= x, тогда sin(x)= √3/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= π/3, т.к. sin(π/3)= √3/2 и –π/2 ≤ π/3 ≤ π/2.
Ответ: arcsin(√3/2)= π/3.
2. Вычислить: arcsin(-1/2).
Решение: Пусть arcsin(-1/2)= x, тогда sin(x)= -1/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= -π/6, т.к. sin(-π/6)= -1/2 и -π/2 ≤-π/6≤ π/2.
Ответ: arcsin(-1/2)=-π/6.
3. Вычислить: arcsin(0).
Решение: Пусть arcsin(0)= x, тогда sin(x)= 0. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: значит x= 0, т.к. sin(0)= 0 и — π/2 ≤ 0 ≤ π/2.
Ответ: arcsin(0)=0.
По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: значит x= 0, т.к. sin(0)= 0 и — π/2 ≤ 0 ≤ π/2.
Ответ: arcsin(0)=0.
4. Решить уравнение: sin(x) = -√2/2.
x= arcsin(-√2/2) + 2πk и x= π — arcsin(-√2/2) + 2πk.
Посмотрим в таблице значение: arcsin (-√2/2)= -π/4.
Ответ: x= -π/4 + 2πk и x= 5π/4 + 2πk.
5. Решить уравнение: sin(x) = 0.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(0) + 2πk и x= π — arcsin(0) + 2πk. Посмотрим в таблице значение: arcsin(0)= 0.
Ответ: x= 2πk и x= π + 2πk
6. Решить уравнение: sin(x) = 3/5.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(3/5) + 2πk и x= π — arcsin(3/5) + 2πk.
Ответ: x= (-1) n — arcsin(3/5) + πk.
7. Решить неравенство sin(x)
Решение: Синус — это ордината точки числовой окружности. Значит: нам надо найти такие точки, ордината которых меньше 0.7. Нарисуем прямую y=0.7. Она пересекает числовую окружность в двух точках. Неравенству y
Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk
Неравенству y
Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk
Задачи на арксинус для самостоятельного решения
1) Вычислить: а) arcsin(√2/2), б) arcsin(1/2), в) arcsin(1), г) arcsin(-0.8).
2) Решить уравнение: а) sin(x) = 1/2, б) sin(x) = 1, в) sin(x) = √3/2, г) sin(x) = 0.25,
д) sin(x) = -1.2.
3) Решить неравенство: а) sin (x)> 0.6, б) sin (x)≤ 1/2.
Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.
Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.
Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.
Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию.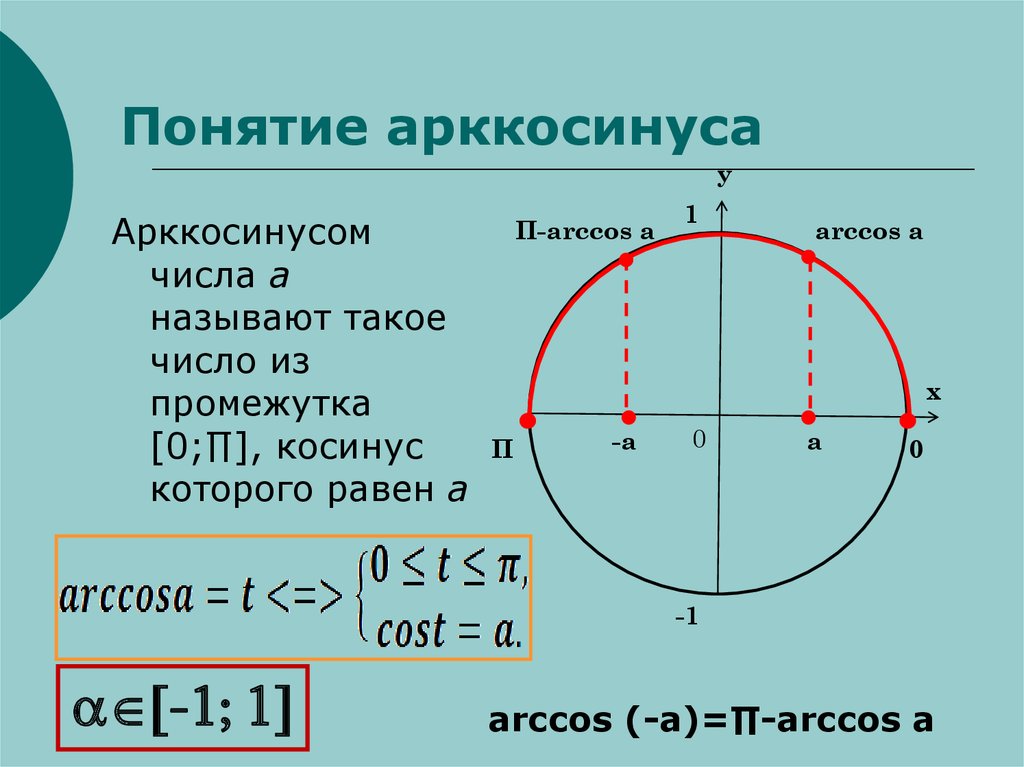 График имеет вид асимметричной кривой, проходящей через центр координат.
График имеет вид асимметричной кривой, проходящей через центр координат.
Свойства арксинуса:
Если сопоставить графики sin и arcsin , у двух тригонометрических функций можно найти общие закономерности.
Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
Рассмотрим функцию арккосинуса более подробно:
- Функция определена на отрезке [-1; 1].
- ОДЗ для arccos — .
- График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
- Y = 0 при x = 1.
- Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
Возможно, школьникам покажется излишним такое «подробное» изучение «арков».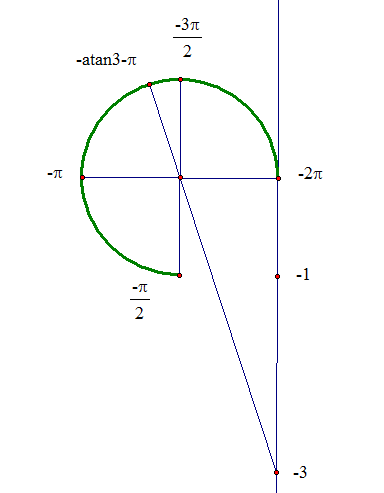 Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.
Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.
Задание 1. Укажите функции изображенные на рисунке.
Ответ: рис. 1 – 4, рис.2 — 1.
В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.
Арктангенс
Arctg числа a – это такое значение угла α, что его тангенс равен а.
Если рассмотреть график арктангенса, можно выделить следующие свойства:
- График бесконечен и определен на промежутке (- ∞; + ∞).
- Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
- Y = 0 при x = 0.
- Кривая возрастает на всей области определения.

Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
Свойства функции арккотангенса:
- Интервал определения функции – бесконечность.
- Область допустимых значений – промежуток (0; π).
- F(x) не является ни четной, ни нечетной.
- На всем своем протяжении график функции убывает.
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2. Соотнести график и форму записи функции.
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Ответ: рис. 1 – 1, рис. 2 – 4.
Тригонометрические тождества arcsin, arcos, arctg и arcctg
Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.
Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.
Также существуют соотношения для arctg и arcctg:
Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла.
Примеры решения задач
Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.
При решении первого типа задач необходимо придерживаться следующего плана действий:
При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.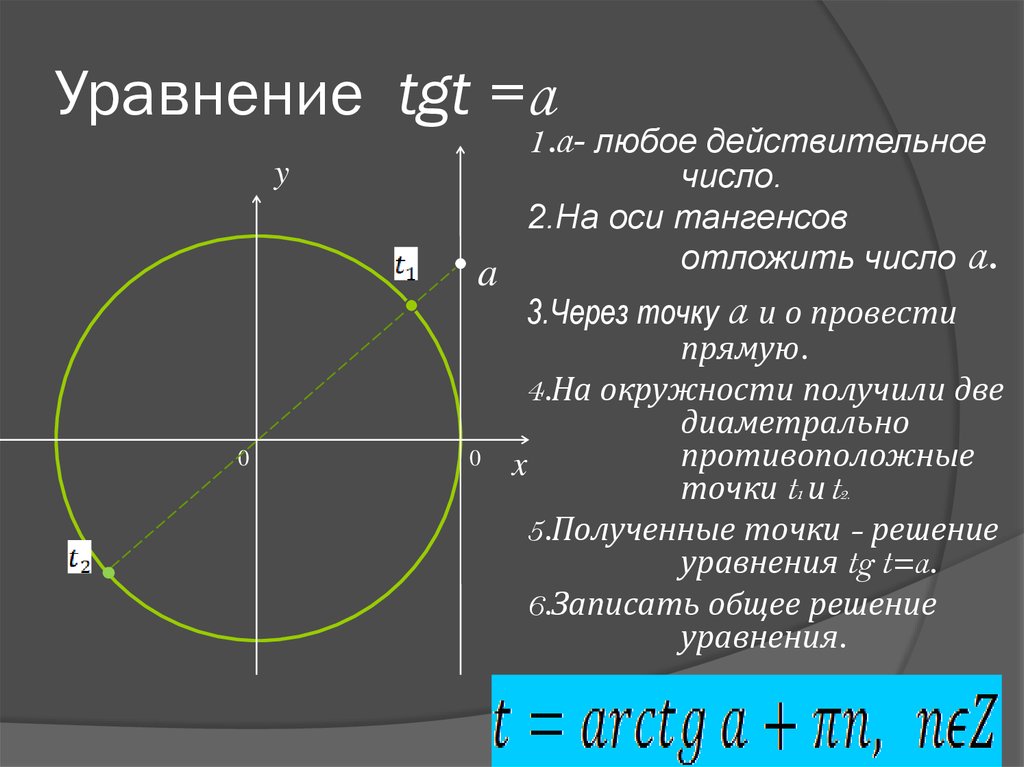
Допустим в ЕГЭ необходимо найти ответ для уравнения типа:
Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.
Если вспомнить формулу arcsin (sin α) = α , то можно свести поиск ответов к решению системы из двух уравнений:
Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.
Арктангенс (y = arctg
x
) — это функция, обратная к тангенсу (x = tg
y
tg(arctg
x)
= x
arctg(tg
x)
= x
Арктангенс обозначается так:
.
График функции арктангенс
График функции y = arctg x
График арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом ,
на котором функция монотонна. Такое определение называют главным значением арктангенса.
Такое определение называют главным значением арктангенса.
Арккотангенс, arcctg
Арккотангенс (y = arcctg
x
) — это функция, обратная к котангенсу (x = ctg
y
). Он имеет область определения и множество значений .
ctg(arcctg
x)
= x
arcctg(ctg
x)
= x
Арккотангенс обозначается так:
.
График функции арккотангенс
График функции y = arcctg x
График арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккотангенса.
Четность
Функция арктангенс является нечетной:
arctg(-
x)
=
arctg(-tg arctg
x)
=
arctg(tg(-arctg
x))
=
— arctg
x
Функция арккотангенс не является четной или нечетной:
arcctg(-
x)
=
arcctg(-ctg arcctg
x)
=
arcctg(ctg(π-arcctg
x))
=
π — arcctg
x ≠ ± arcctg
x
.
Свойства — экстремумы, возрастание, убывание
Функции арктангенс и арккотангенс непрерывны на своей области определения, то есть для всех x
. (см. доказательство непрерывности). Основные свойства арктангенса и арккотангенса представлены в таблице.
(см. доказательство непрерывности). Основные свойства арктангенса и арккотангенса представлены в таблице.
| y = arctg x | y = arcctg x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Множество значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы, минимумы | нет | нет |
| Нули, y = 0 | x = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
| — | π | |
| 0 |
Таблица арктангенсов и арккотангенсов
В данной таблице представлены значения арктангенсов и арккотангенсов, в градусах и радианах, при некоторых значениях аргумента.
| x | arctg x | arcctg x | ||
град._5.jpg) | рад. | град. | рад. | |
| — ∞ | — 90° | — | 180° | π |
| — | — 60° | — | 150° | |
| — 1 | — 45° | — | 135° | |
| — | — 30° | — | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 1 | 45° | 45° | ||
| 60° | 30° | |||
| + ∞ | 90° | 0° | 0 | |
≈ 0,5773502691896258
≈ 1,7320508075688772
Формулы
Формулы суммы и разности
при
при
при
при
при
при
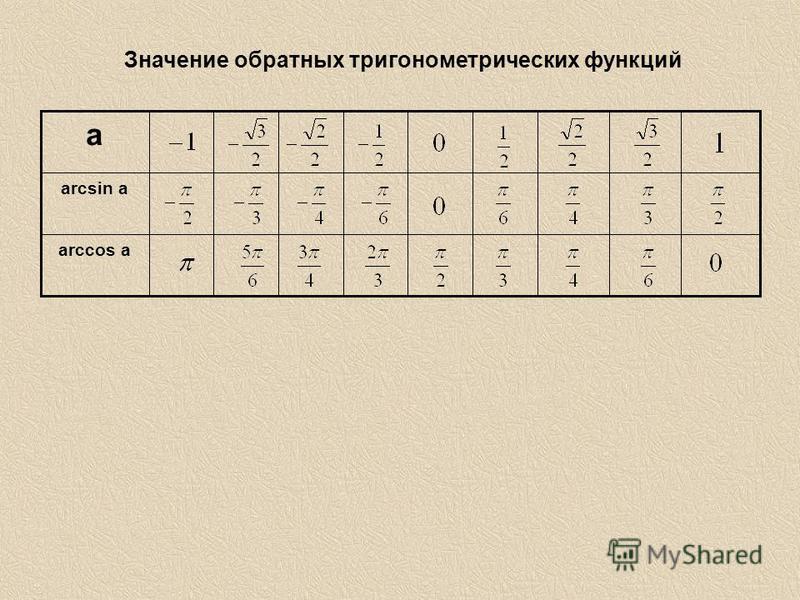
Выражения через логарифм, комплексные числа
,
.
Выражения через гиперболические функции
Производные
См. Вывод производных арктангенса и арккотангенса > > >
Производные высших порядков :
Пусть .
Тогда производную n-го порядка арктангенса можно представить одним из следующих способов:
;
.
Символ означает мнимую часть стоящего следом выражения.
См. Вывод производных высших порядков арктангенса и арккотангенса > > >
Там же даны формулы производных первых пяти порядков.
Аналогично для арккотангенса. Пусть .
Тогда
;
.
Интегралы
Делаем подстановку x = tg
t
и интегрируем по частям:
;
;
;
Выразим арккотангенс через арктангенс:
.
Разложение в степенной ряд
При |x| ≤ 1
имеет место следующее разложение:
;
.
Обратные функции
Обратными к арктангенсу и арккотангенсу являются тангенс и котангенс , соответственно.
Следующие формулы справедливы на всей области определения:
tg(arctg
x)
= x
ctg(arcctg
x)
= x
.
Следующие формулы справедливы только на множестве значений арктангенса и арккотангенса:
arctg(tg
x)
= x
при
arcctg(ctg
x)
= x
при .
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Расчёт арктангенса онлайн калькулятор. Получить угол зная значение тангенса угла.
Арктангенс(y = arctg(x)) – это обратная тригонометрическая функция к тангенсу x = tg(y). Область определения -∞ ≤ x ≤ +∞ и множество значений -π/2 ≤ y ≤ +π/2.
| arctg(0) = 0° | arctg(-1.732050808) = 120° | arctg(1.732050808) = 240° |
| arctg(0.01745506493) = 1° | arctg(-1.664279482) = 121° | arctg(1.804047755) = 241° |
| arctg(0.03492076949) = 2° | arctg(-1.600334529) = 122° | arctg(1.880726465) = 242° |
| arctg(0.05240777928) = 3° | arctg(-1.539864964) = 123° | arctg(1.962610506) = 243° |
arctg(0. 06992681194) = 4° 06992681194) = 4° | arctg(-1.482560969) = 124° | arctg(2.050303842) = 244° |
| arctg(0.08748866353) = 5° | arctg(-1.428148007) = 125° | arctg(2.144506921) = 245° |
| arctg(0.1051042353) = 6° | arctg(-1.37638192) = 126° | arctg(2.246036774) = 246° |
| arctg(0.1227845609) = 7° | arctg(-1.327044822) = 127° | arctg(2.355852366) = 247° |
| arctg(0.1405408347) = 8° | arctg(-1.279941632) = 128° | arctg(2.475086853) = 248° |
| arctg(0.1583844403) = 9° | arctg(-1.234897157) = 129° | arctg(2.605089065) = 249° |
| arctg(0.1763269807) = 10° | arctg(-1.191753593) = 130° | arctg(2.747477419) = 250° |
| arctg(0.1943803091) = 11° | arctg(-1.150368407) = 131° | arctg(2.904210878) = 251° |
| arctg(0.2125565617) = 12° | arctg(-1.110612515) = 132° | arctg(3.077683537) = 252° |
arctg(0. 2308681911) = 13° 2308681911) = 13° | arctg(-1.07236871) = 133° | arctg(3.270852618) = 253° |
| arctg(0.2493280028) = 14° | arctg(-1.035530314) = 134° | arctg(3.487414444) = 254° |
| arctg(0.2679491924) = 15° | arctg(-1) = 135° | arctg(3.732050808) = 255° |
| arctg(0.2867453858) = 16° | arctg(-0.9656887748) = 136° | arctg(4.010780934) = 256° |
| arctg(0.3057306815) = 17° | arctg(-0.9325150861) = 137° | arctg(4.331475874) = 257° |
| arctg(0.3249196962) = 18° | arctg(-0.9004040443) = 138° | arctg(4.704630109) = 258° |
| arctg(0.3443276133) = 19° | arctg(-0.8692867378) = 139° | arctg(5.144554016) = 259° |
| arctg(0.3639702343) = 20° | arctg(-0.8390996312) = 140° | arctg(5.67128182) = 260° |
| arctg(0.383864035) = 21° | arctg(-0.8097840332) = 141° | arctg(6.313751515) = 261° |
arctg(0. 4040262258) = 22° 4040262258) = 22° | arctg(-0.7812856265) = 142° | arctg(7.115369722) = 262° |
| arctg(0.4244748162) = 23° | arctg(-0.7535540501) = 143° | arctg(8.144346428) = 263° |
| arctg(0.4452286853) = 24° | arctg(-0.726542528) = 144° | arctg(9.514364454) = 264° |
| arctg(0.4663076582) = 25° | arctg(-0.7002075382) = 145° | arctg(11.4300523) = 265° |
| arctg(0.4877325886) = 26° | arctg(-0.6745085168) = 146° | arctg(14.30066626) = 266° |
| arctg(0.5095254495) = 27° | arctg(-0.6494075932) = 147° | arctg(19.08113669) = 267° |
| arctg(0.5317094317) = 28° | arctg(-0.6248693519) = 148° | arctg(28.63625328) = 268° |
| arctg(0.5543090515) = 29° | arctg(-0.600860619) = 149° | arctg(57.28996163) = 269° |
| arctg(0.5773502692) = 30° | arctg(-0.5773502692) = 150° | arctg(∞) = 270° |
arctg(0. 600860619) = 31° 600860619) = 31° | arctg(-0.5543090515) = 151° | arctg(-57.28996163) = 271° |
| arctg(0.6248693519) = 32° | arctg(-0.5317094317) = 152° | arctg(-28.63625328) = 272° |
| arctg(0.6494075932) = 33° | arctg(-0.5095254495) = 153° | arctg(-19.08113669) = 273° |
| arctg(0.6745085168) = 34° | arctg(-0.4877325886) = 154° | arctg(-14.30066626) = 274° |
| arctg(0.7002075382) = 35° | arctg(-0.4663076582) = 155° | arctg(-11.4300523) = 275° |
| arctg(0.726542528) = 36° | arctg(-0.4452286853) = 156° | arctg(-9.514364454) = 276° |
| arctg(0.7535540501) = 37° | arctg(-0.4244748162) = 157° | arctg(-8.144346428) = 277° |
| arctg(0.7812856265) = 38° | arctg(-0.4040262258) = 158° | arctg(-7.115369722) = 278° |
| arctg(0.8097840332) = 39° | arctg(-0.383864035) = 159° | arctg(-6.313751515) = 279° |
arctg(0. 8390996312) = 40° 8390996312) = 40° | arctg(-0.3639702343) = 160° | arctg(-5.67128182) = 280° |
| arctg(0.8692867378) = 41° | arctg(-0.3443276133) = 161° | arctg(-5.144554016) = 281° |
| arctg(0.9004040443) = 42° | arctg(-0.3249196962) = 162° | arctg(-4.704630109) = 282° |
| arctg(0.9325150861) = 43° | arctg(-0.3057306815) = 163° | arctg(-4.331475874) = 283° |
| arctg(0.9656887748) = 44° | arctg(-0.2867453858) = 164° | arctg(-4.010780934) = 284° |
| arctg(1) = 45° | arctg(-0.2679491924) = 165° | arctg(-3.732050808) = 285° |
| arctg(1.035530314) = 46° | arctg(-0.2493280028) = 166° | arctg(-3.487414444) = 286° |
| arctg(1.07236871) = 47° | arctg(-0.2308681911) = 167° | arctg(-3.270852618) = 287° |
| arctg(1.110612515) = 48° | arctg(-0.2125565617) = 168° | arctg(-3.077683537) = 288° |
arctg(1.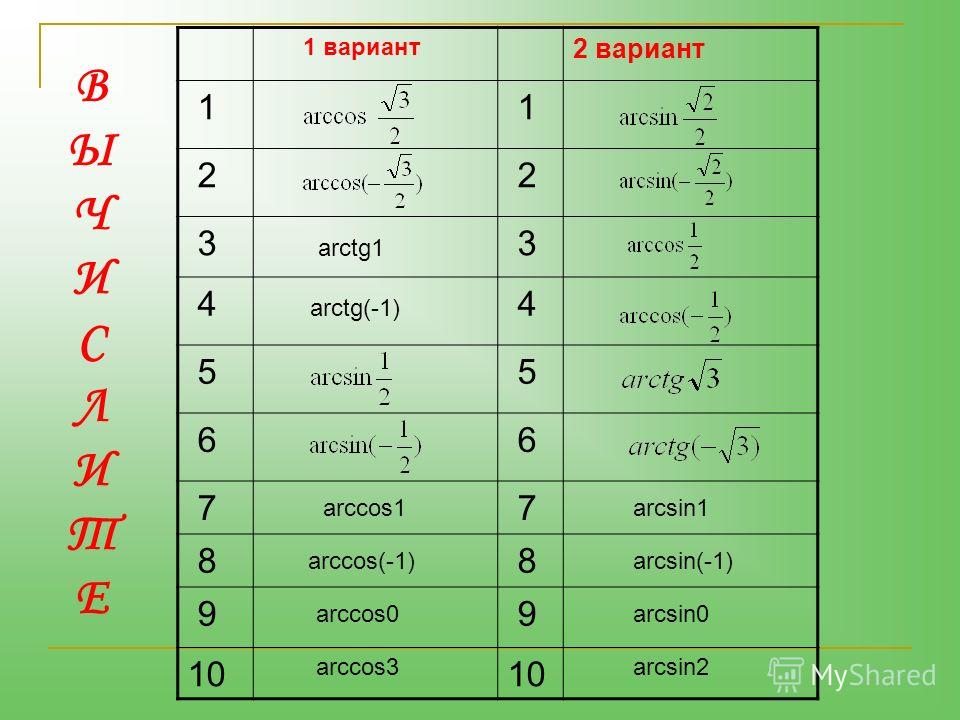 150368407) = 49° 150368407) = 49° | arctg(-0.1943803091) = 169° | arctg(-2.904210878) = 289° |
| arctg(1.191753593) = 50° | arctg(-0.1763269807) = 170° | arctg(-2.747477419) = 290° |
| arctg(1.234897157) = 51° | arctg(-0.1583844403) = 171° | arctg(-2.605089065) = 291° |
| arctg(1.279941632) = 52° | arctg(-0.1405408347) = 172° | arctg(-2.475086853) = 292° |
| arctg(1.327044822) = 53° | arctg(-0.1227845609) = 173° | arctg(-2.355852366) = 293° |
| arctg(1.37638192) = 54° | arctg(-0.1051042353) = 174° | arctg(-2.246036774) = 294° |
| arctg(1.428148007) = 55° | arctg(-0.08748866353) = 175° | arctg(-2.144506921) = 295° |
| arctg(1.482560969) = 56° | arctg(-0.06992681194) = 176° | arctg(-2.050303842) = 296° |
| arctg(1.539864964) = 57° | arctg(-0.05240777928) = 177° | arctg(-1.962610506) = 297° |
arctg(1.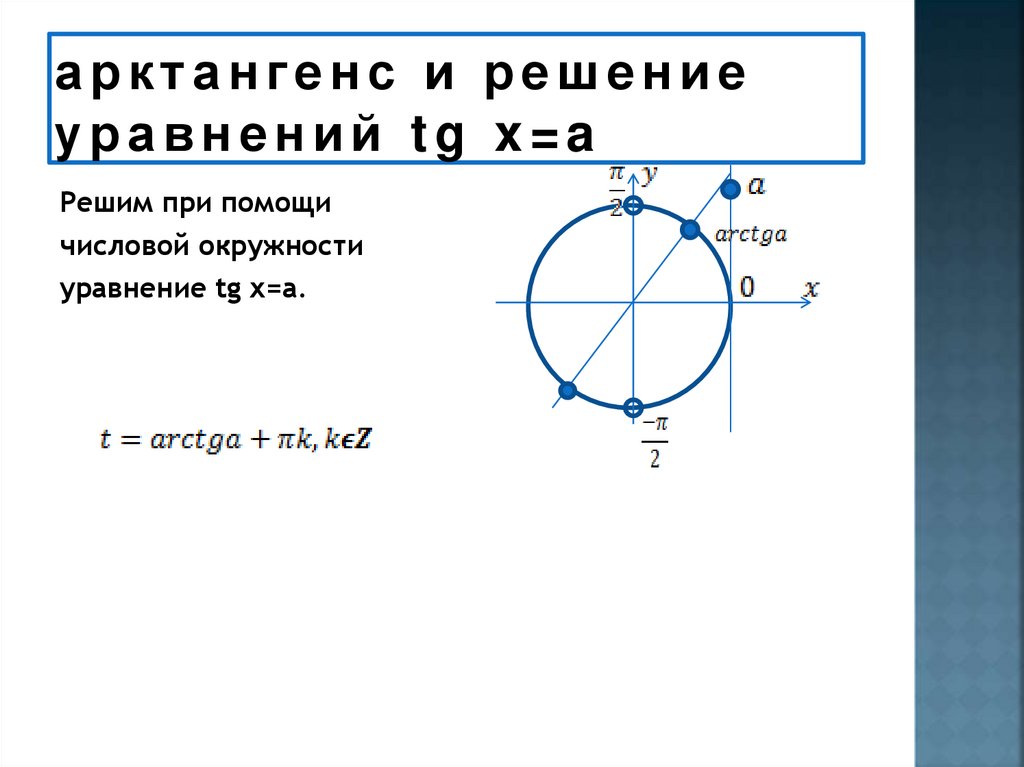 600334529) = 58° 600334529) = 58° | arctg(-0.03492076949) = 178° | arctg(-1.880726465) = 298° |
| arctg(1.664279482) = 59° | arctg(-0.01745506493) = 179° | arctg(-1.804047755) = 299° |
| arctg(1.732050808) = 60° | arctg(0) = 180° | arctg(-1.732050808) = 300° |
| arctg(1.804047755) = 61° | arctg(0.01745506493) = 181° | arctg(-1.664279482) = 301° |
| arctg(1.880726465) = 62° | arctg(0.03492076949) = 182° | arctg(-1.600334529) = 302° |
| arctg(1.962610506) = 63° | arctg(0.05240777928) = 183° | arctg(-1.539864964) = 303° |
| arctg(2.050303842) = 64° | arctg(0.06992681194) = 184° | arctg(-1.482560969) = 304° |
| arctg(2.144506921) = 65° | arctg(0.08748866353) = 185° | arctg(-1.428148007) = 305° |
| arctg(2.246036774) = 66° | arctg(0.1051042353) = 186° | arctg(-1.37638192) = 306° |
arctg(2. 355852366) = 67° 355852366) = 67° | arctg(0.1227845609) = 187° | arctg(-1.327044822) = 307° |
| arctg(2.475086853) = 68° | arctg(0.1405408347) = 188° | arctg(-1.279941632) = 308° |
| arctg(2.605089065) = 69° | arctg(0.1583844403) = 189° | arctg(-1.234897157) = 309° |
| arctg(2.747477419) = 70° | arctg(0.1763269807) = 190° | arctg(-1.191753593) = 310° |
| arctg(2.904210878) = 71° | arctg(0.1943803091) = 191° | arctg(-1.150368407) = 311° |
| arctg(3.077683537) = 72° | arctg(0.2125565617) = 192° | arctg(-1.110612515) = 312° |
| arctg(3.270852618) = 73° | arctg(0.2308681911) = 193° | arctg(-1.07236871) = 313° |
| arctg(3.487414444) = 74° | arctg(0.2493280028) = 194° | arctg(-1.035530314) = 314° |
| arctg(3.732050808) = 75° | arctg(0.2679491924) = 195° | arctg(-1) = 315° |
| arctg(4.010780934) = 76° | arctg(0. 2867453858) = 196° 2867453858) = 196° | arctg(-0.9656887748) = 316° |
| arctg(4.331475874) = 77° | arctg(0.3057306815) = 197° | arctg(-0.9325150861) = 317° |
| arctg(4.704630109) = 78° | arctg(0.3249196962) = 198° | arctg(-0.9004040443) = 318° |
| arctg(5.144554016) = 79° | arctg(0.3443276133) = 199° | arctg(-0.8692867378) = 319° |
| arctg(5.67128182) = 80° | arctg(0.3639702343) = 200° | arctg(-0.8390996312) = 320° |
| arctg(6.313751515) = 81° | arctg(0.383864035) = 201° | arctg(-0.8097840332) = 321° |
| arctg(7.115369722) = 82° | arctg(0.4040262258) = 202° | arctg(-0.7812856265) = 322° |
| arctg(8.144346428) = 83° | arctg(0.4244748162) = 203° | arctg(-0.7535540501) = 323° |
| arctg(9.514364454) = 84° | arctg(0.4452286853) = 204° | arctg(-0.726542528) = 324° |
| arctg(11.4300523) = 85° | arctg(0. 4663076582) = 205° 4663076582) = 205° | arctg(-0.7002075382) = 325° |
| arctg(14.30066626) = 86° | arctg(0.4877325886) = 206° | arctg(-0.6745085168) = 326° |
| arctg(19.08113669) = 87° | arctg(0.5095254495) = 207° | arctg(-0.6494075932) = 327° |
| arctg(28.63625328) = 88° | arctg(0.5317094317) = 208° | arctg(-0.6248693519) = 328° |
| arctg(57.28996163) = 89° | arctg(0.5543090515) = 209° | arctg(-0.600860619) = 329° |
| arctg(∞) = 90° | arctg(0.5773502692) = 210° | arctg(-0.5773502692) = 330° |
| arctg(-57.28996163) = 91° | arctg(0.600860619) = 211° | arctg(-0.5543090515) = 331° |
| arctg(-28.63625328) = 92° | arctg(0.6248693519) = 212° | arctg(-0.5317094317) = 332° |
| arctg(-19.08113669) = 93° | arctg(0.6494075932) = 213° | arctg(-0.5095254495) = 333° |
| arctg(-14.30066626) = 94° | arctg(0. 6745085168) = 214° 6745085168) = 214° | arctg(-0.4877325886) = 334° |
| arctg(-11.4300523) = 95° | arctg(0.7002075382) = 215° | arctg(-0.4663076582) = 335° |
| arctg(-9.514364454) = 96° | arctg(0.726542528) = 216° | arctg(-0.4452286853) = 336° |
| arctg(-8.144346428) = 97° | arctg(0.7535540501) = 217° | arctg(-0.4244748162) = 337° |
| arctg(-7.115369722) = 98° | arctg(0.7812856265) = 218° | arctg(-0.4040262258) = 338° |
| arctg(-6.313751515) = 99° | arctg(0.8097840332) = 219° | arctg(-0.383864035) = 339° |
| arctg(-5.67128182) = 100° | arctg(0.8390996312) = 220° | arctg(-0.3639702343) = 340° |
| arctg(-5.144554016) = 101° | arctg(0.8692867378) = 221° | arctg(-0.3443276133) = 341° |
| arctg(-4.704630109) = 102° | arctg(0.9004040443) = 222° | arctg(-0.3249196962) = 342° |
| arctg(-4.331475874) = 103° | arctg(0. 9325150861) = 223° 9325150861) = 223° | arctg(-0.3057306815) = 343° |
| arctg(-4.010780934) = 104° | arctg(0.9656887748) = 224° | arctg(-0.2867453858) = 344° |
| arctg(-3.732050808) = 105° | arctg(1) = 225° | arctg(-0.2679491924) = 345° |
| arctg(-3.487414444) = 106° | arctg(1.035530314) = 226° | arctg(-0.2493280028) = 346° |
| arctg(-3.270852618) = 107° | arctg(1.07236871) = 227° | arctg(-0.2308681911) = 347° |
| arctg(-3.077683537) = 108° | arctg(1.110612515) = 228° | arctg(-0.2125565617) = 348° |
| arctg(-2.904210878) = 109° | arctg(1.150368407) = 229° | arctg(-0.1943803091) = 349° |
| arctg(-2.747477419) = 110° | arctg(1.191753593) = 230° | arctg(-0.1763269807) = 350° |
| arctg(-2.605089065) = 111° | arctg(1.234897157) = 231° | arctg(-0.1583844403) = 351° |
| arctg(-2.475086853) = 112° | arctg(1. 279941632) = 232° 279941632) = 232° | arctg(-0.1405408347) = 352° |
| arctg(-2.355852366) = 113° | arctg(1.327044822) = 233° | arctg(-0.1227845609) = 353° |
| arctg(-2.246036774) = 114° | arctg(1.37638192) = 234° | arctg(-0.1051042353) = 354° |
| arctg(-2.144506921) = 115° | arctg(1.428148007) = 235° | arctg(-0.08748866353) = 355° |
| arctg(-2.050303842) = 116° | arctg(1.482560969) = 236° | arctg(-0.06992681194) = 356° |
| arctg(-1.962610506) = 117° | arctg(1.539864964) = 237° | arctg(-0.05240777928) = 357° |
| arctg(-1.880726465) = 118° | arctg(1.600334529) = 238° | arctg(-0.03492076949) = 358° |
| arctg(-1.804047755) = 119° | arctg(1.664279482) = 239° | arctg(-0.01745506493) = 359° |
Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса, таблица arctg
В данной статье рассматриваются вопросы нахождения значений арксинуса, арккосинуса, арктангенса и арккотангенса заданного числа. Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.
Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».
Определения арксинуса, арккосинуса, арктангенса и арккотангенса числа помогут разобраться в вычислении заданных функций. Значение тригонометрических функций угла равняется числу a, тогда автоматически считается величиной этого угла. Если a – число, тогда это и есть значение функции.
Для четкого понимания рассмотрим пример.
Если имеем арккосинус угла равного π3, то значение косинуса отсюда равно 12 по таблице косинусов. Данный угол расположен в промежутке от нуля до пи, значит, значение арккосинуса 12 получим π на 3. Такое тригонометрическое выражение записывается как arcos(12)=π3.
Величиной угла может быть как градус, так и радиан.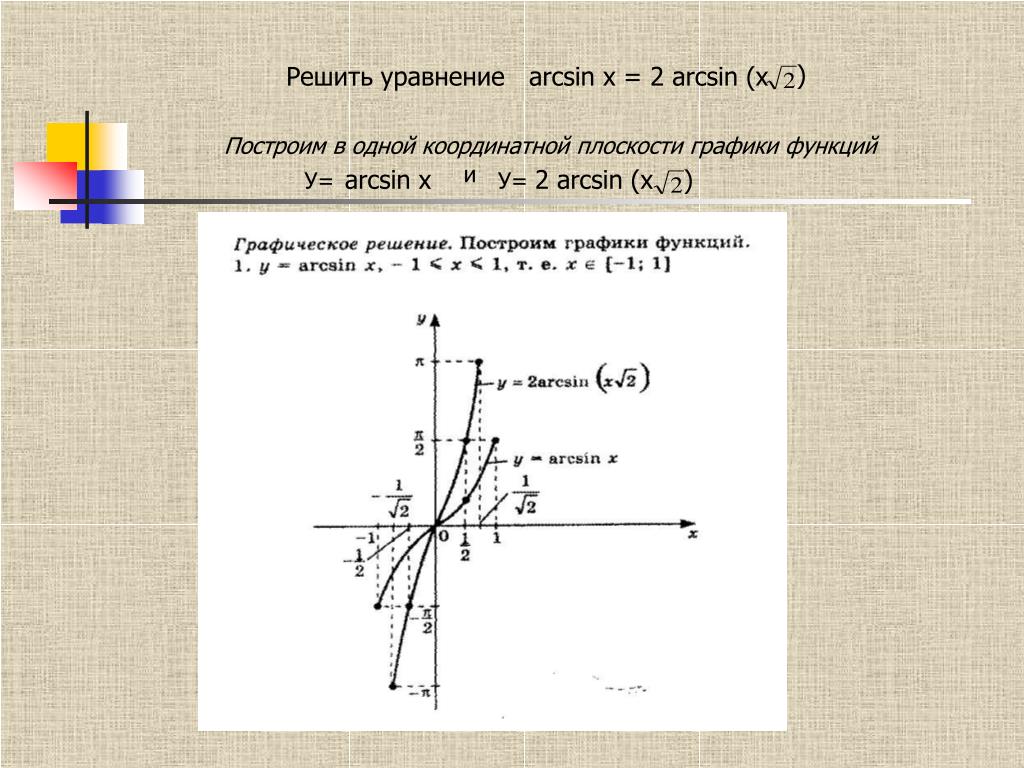 Значение угла π3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 12 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид arccos12=60°
Значение угла π3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 12 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид arccos12=60°
Основные значения arcsin, arccos, arctg и arctg
Благодаря таблице синусов, косинусов, тангенсов и котангенсов, мы имеет точные значения угла при 0, ±30, ±45, ±60, ±90, ±120, ±135, ±150, ±180 градусов. Таблица достаточно удобна и из нее можно получать некоторые значения для аркфункций, которые имеют название как основные значения арксинуса, арккосинуса, арктангенса и арккотангенса.
Таблица синусов основных углов предлагает такие результаты значений углов:
sin(-π2)=-1, sin(-π3)=-32, sin(-π4)=-22, sin(-π6)=-12,sin 0 =0, sinπ6=12, sinπ4=22, sinπ3=32, sinπ2=1
Учитывая их, можно легко высчитать арксинус числа всех стандартных значений, начиная от -1 и заканчивая 1, также значения от –π2 до +π2 радианов, следуя его основному значению определения. Это и является основными значениями арксинуса.
Это и является основными значениями арксинуса.
Для удобного применения значений арксинуса занесем в таблицу. Со временем придется выучить эти значения, так как на практике приходится часто к ним обращаться. Ниже приведена таблица арксинуса с радианным и градусным значением углов.
| α | -1 | -32 | -22 | -12 | 0 | 12 | 22 | 32 | |
| arcsin αкак угол | в радианах
| -π2 | -π3 | -π4 | -π6 | 0 | π6 | π4 | π3 |
| в градусах | -90° | -60° | -45° | -30° | 0° | 30° | 45° | 60° | |
| arcsin α как число | -π2 | -π3 | -π4 | -π6 | 0 | π6 | π4 | π3 | |
Для получения основных значений арккосинуса необходимо обратиться к таблице косинусов основных углов. Тогда имеем:
Тогда имеем:
cos 0=1, cos π6=32 , cos π4=22, cos π3=12, cosπ2=0,cos2π3=-12, cos3π4=-22, cos5π6=-32, cosπ=-1
Следуя из таблицы, находим значения арккосинуса:
arccos (-1)=π, arccos (-32)=5π6, arcocos (-22)=3π4, arccos-12=2π3, arccos 0 =π2, arccos 12=π3, arccos 22=π4, arccos32=π6, arccos 1 =0
Таблица арккосинусов.
| α | -1 | -32 | -22 | -12 | 0 | 12 | 22 | 32 | 1 | |
| arccos αкак угол | в радианах
| π | 5π6 | 3π4 | 2π3 | π2 | π3 | π4 | π6 | 0 |
| в градусах | 180° | 150° | 135° | 120° | 90° | 60° | 45° | 30° | 0° | |
| arccos α как число | π | 5π6 | 3π4 | 2π3 | π2 | π3 | π4 | π6 | 0 | |
Таким же образом, исходя из определения и стандартных таблиц, находятся значения арктангенса и арккотангенса, которые изображены в таблице арктангенсов и арккотангенсов ниже.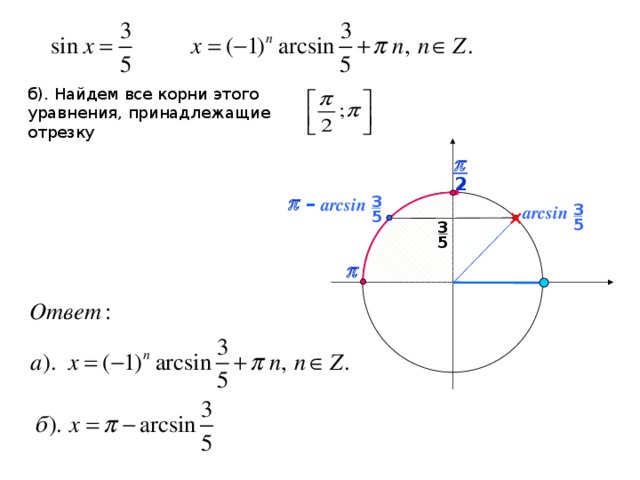
| α | -3 | -1 | -33 | 0 | 33 | 1 | 3 | |
| arctg aкак угол | в радианах | -π3 | -π4 | -π6 | 0 | π6 | π4 | π3 |
| в градусах | -60° | -45° | -30° | 0° | 30° | 45° | 60° | |
| arctg a как число | -π3 | -π4 | -π6 | 0 | π6 | π4 | π3 | |
Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
arcsin, arccos, arctg и arcctg
Для точного значения arcsin, arccos, arctg и arcctg числа а необходимо знать величину угла. Об этом сказано в предыдущем пункте. Однако, точное значении функции нам неизвестно. Если необходимо найти числовое приближенное значение аркфункций, применяют таблицу синусов, косинусов, тангенсов и котангенсов Брадиса.
Такая таблица позволяет выполнять довольно точные вычисления, так как значения даются с четырьмя знаками после запятой. Благодаря этому числа выходят точными до минуты. Значения arcsin, arccos, arctg и arcctg отрицательных и положительных чисел сводится к нахождению формул arcsin, arccos, arctg и arcctg противоположных чисел вида arcsin(-α)=-arcsin α, arccos(-α)=π-arccos α, arctg(-α)=-arctg α, arcctg(-α)=π-arcctg α.
Рассмотрим решение нахождения значений arcsin, arccos, arctg и arcctg с помощью таблицы Брадиса.
Если нам необходимо найти значение арксинуса 0,2857, ищем значение, найдя таблицу синусов. Видим, что данному числу соответствует значение угла sin 16 градусов и 36 минут. Значит, арксинус числа 0,2857 – это искомый угол в 16 градусов и 36 минут. Рассмотрим на рисунке ниже.
Правее градусов имеются столбцы называемые поправки. При искомом арксинусе 0,2863 используется та самая поправка в 0,0006, так как ближайшим числом будет 0,2857. Значит, получим синус 16 градусов 38 минут и 2 минуты, благодаря поправке. Рассмотрим рисунок с изображением таблицы Брадиса.
Рассмотрим рисунок с изображением таблицы Брадиса.
Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.
Таким образом находятся значения arcsin, arccos, arctg и arcctg.
Нахождение значения arcsin, arccos, arctg и arcctg
Чтобы найти арксинус через известный арккосинус данного числа, нужно применить тригонометрические формулы arcsin α+arccos α=π2, arctg α+arcctg α=π2 (не обходимо просмотреть тему формул суммы арккосинуса и арксинуса, суммы арктангенса и арккотангенса).
При известном arcsin α= -π12 необходимо найти значение arccos α, тогда необходимо вычислить арккосинус по формуле:
arccos α=π2−arcsin α=π2−(−π12)=7π12.
Если необходимо найти значение арктангенса или арккотангенса числа a с помощью известного арксинуса или арккосинуса, необходимо производить долгие вычисления, так как стандартных формул нет. Рассмотрим на примере.
Если дан арккосинус числа а равный π10, а вычислить арктангенс данного числа поможет таблица тангенсов. Угол π10 радиан представляет собой 18 градусов, тогда по таблице косинусов видим, что косинус 18 градусов имеет значение 0,9511, после чего заглядываем в таблицу Брадиса.
При поиске значения арктангенса 0,9511 определяем, что значение угла имеет 43 градуса и 34 минуты. Рассмотрим по таблице ниже.
Фактически, таблица Брадиса помогает в нахождении необходимого значения угла и при значении угла позволяет определить количество градусов.
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
определение, формула, таблица, график, свойства
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel. ru Математика Обратная тригонометрическая функция: Арктангенс (arctg)
ru Математика Обратная тригонометрическая функция: Арктангенс (arctg)
- Определение
- График арктангенса
- Свойства арктангенса
- Таблица арктангенсов
Определение
Арктангенс (arctg или arctan) – это обратная тригонометрическая функция.
Арктангенс x определяется как функция, обратная к тангенсу x, где x – любое число (x∈ℝ).
Если тангенс угла у равен х (tg y = x), значит арктангенс x равняется y:
arctg x = tg-1 x = y, причем -π/2<y<π/2
Примечание: tg-1x означает обратный тангенс, а не тангенс в степени -1.
Например:
arctg 1 = tg-1 1 = 45° = π/4 рад
График арктангенса
Функция арктангенса пишется как y = arctg (x). График в общем виде выглядит следующим образом:
Свойства арктангенса
Ниже в табличном виде представлены основные свойства арктангенса с формулами.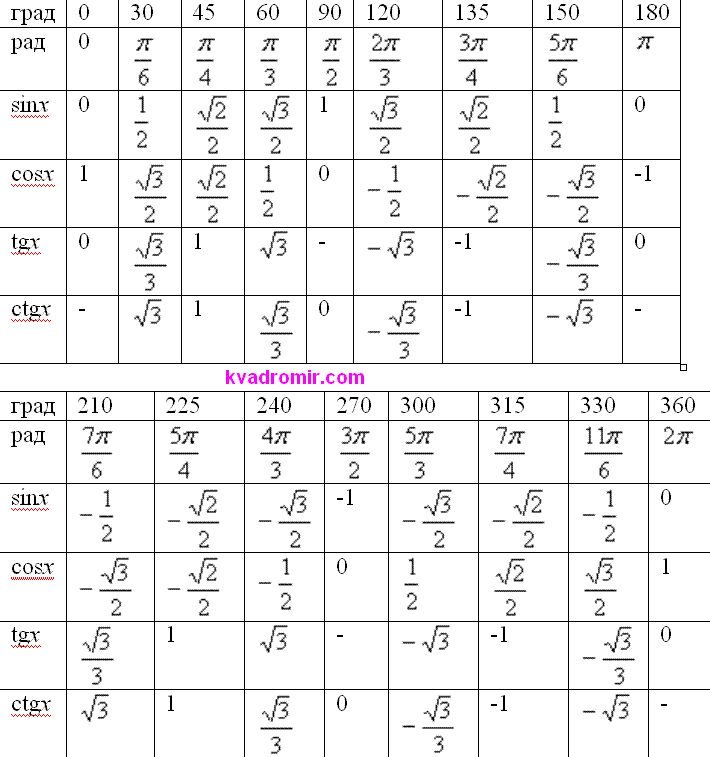
| Свойство | Формула |
| Тангенс арктангенса | tg (arctg x) = x |
| Арктангенс отрицательного числа | arctg (-x) = -arctg x |
| Сумма арктангенсов | ru/wp-content/uploads/2020/02/arctg-summa-exc.png" class="stbSkipLazy aligncenter size-full" width="420" height="910" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arctg-summa-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/02/arctg-summa-exc.png" class="stbSkipLazy aligncenter size-full" width="420" height="910" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arctg-summa-exc.png" />»> |
| Разность арктангенсов | ru/wp-content/uploads/2020/02/arctg-raznost-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/02/arctg-raznost-exc.png" class="stbSkipLazy aligncenter size-full" width="420" height="948" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arctg-raznost-exc.png" />»> |
| Синус арктангенса | ru/wp-content/uploads/2020/02/arktangets-formuly-exc-1.png" class="stbSkipLazy aligncenter size-full" width="180" height="366" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arktangets-formuly-exc-1.png" />»> |
| Косинус арктангенса | png" class="stbSkipLazy aligncenter size-full" width="180" height="372" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arktangets-formuly-exc-6.png" />»> |
| Арктангенс дроби | ru/wp-content/uploads/2020/02/arktangets-formuly-exc-7.png" />»> |
| Арктангенс из арксинуса | png" />»> |
| Производная арктангенса | |
| Неопределенный интеграл арктангенса | ru/wp-content/uploads/2020/02/arktangets-formuly-exc-5.png" class="stbSkipLazy aligncenter size-full" width="320" height="670" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arktangets-formuly-exc-5.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/02/arktangets-formuly-exc-5.png" class="stbSkipLazy aligncenter size-full" width="320" height="670" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arktangets-formuly-exc-5.png" />»> |
microexcel.ru
Таблица арктангенсов
| arctg x (°) | arctg x (рад) | x |
| -90° | -π/2 | -∞ |
| 565°» data-order=»-71.565°»>-71.565° | -1.2490 | -3 |
| -63.435° | -1.1071 | -2 |
| -60° | -π/3 | -√3 |
| -45° | -π/4 | -1 |
| -30° | -π/6 | -1/√3 |
| 565°» data-order=»-26.565°»>-26.565° | -0.4636 | -0.5 |
| 0° | 0 | 0 |
| 26.565° | 4636″ data-order=»0.4636″>0.4636 | 0.5 |
| 30° | π/6 | 1/√3 |
| 45° | π/4 | 1 |
| 60° | π/3 | √3 |
| 435°» data-order=»63.435°»>63.435° | 1.1071 | 2 |
| 71.565° | 1.2490 | 3 |
| 90° | π/2 | ∞ |
microexcel.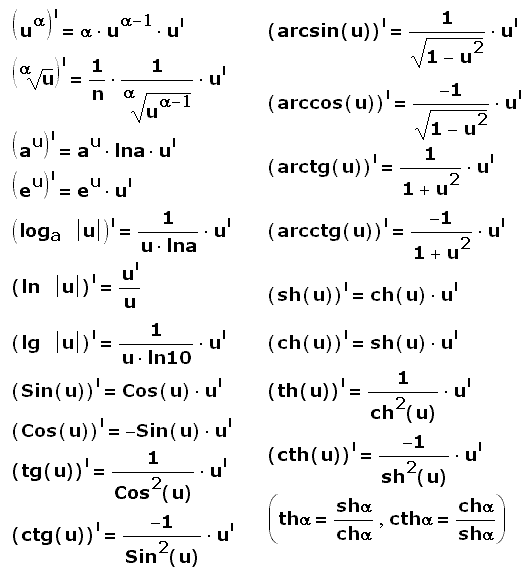 ru
ru
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Где на окружности находится arctg 1 3.
 Урок «Арктангенс и арккотангенс. Решение уравнений tgx = а, ctgx = a». Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс
Урок «Арктангенс и арккотангенс. Решение уравнений tgx = а, ctgx = a». Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенсРанее по программе учащиеся получили представление о решении тригонометрических уравнений, ознакомились с понятиями арккосинуса и арксинуса, примерами решений уравнений cos t = a и sin t = a. В этом видеоуроке рассмотрим решение уравнений tg x = a и ctg x = a.
В начале изучения данной темы рассмотрим уравнения tg x = 3 и tg x = — 3. Если уравнение tg x = 3 будем решать с помощью графика, то увидим, что пересечение графиков функций y = tg x и y = 3 имеет бесконечное множество решений, где x = x 1 + πk. Значение x 1 — это координата x точки пересечения графиков функций y = tg x и y = 3. Автор вводит понятие арктангенса: arctg 3 это число, tg которого равен 3, и это число принадлежит интервалу от -π/2 до π/2. Используя понятие арктангенса, решение уравнения tg x = 3 можно записать в виде x = arctg 3 + πk.
По аналогии решается уравнение tg x = — 3. По построенным графикам функций y = tg x и y = — 3 видно, что точки пересечения графиков, а следовательно, и решениями уравнений, будет x = x 2 + πk. С помощью арктангенса решение можно записать как x = arctg (- 3) + πk. На следующем рисунке увидим, что arctg (- 3) = — arctg 3.
По построенным графикам функций y = tg x и y = — 3 видно, что точки пересечения графиков, а следовательно, и решениями уравнений, будет x = x 2 + πk. С помощью арктангенса решение можно записать как x = arctg (- 3) + πk. На следующем рисунке увидим, что arctg (- 3) = — arctg 3.
Общее определение арктангенса выглядит следующим образом: арктангенсом а называется такое число из промежутка от -π/2 до π/2, тангенс которого равен а. Тогда решением уравнения tg x = a является x = arctg a + πk.
Автор приводит пример 1. Найти решение выражения arctg.Введем обозначения: арктангенс числа равен x, тогда tg x будет равен данному числу, где x принадлежит отрезку от -π/2 до π/2. Как в примерах в предыдущих темах, воспользуемся таблицей значений. По этой таблице тангенсу данного числа соответствует значение x = π/3. Запишем решение уравнения арктангенс заданного числа равен π/3, π/3 принадлежит и интервалу от -π/2 до π/2.
Пример 2 — вычислить арктангенс отрицательного числа. Используя равенство arctg (- a) = — arctg a, введем значение x. Аналогично примеру 2 запишем значение x, которое принадлежит отрезку от -π/2 до π/2. По таблице значений найдем, что x = π/3, следовательно, — tg x = — π/3. Ответом уравнения будет — π/3.
Аналогично примеру 2 запишем значение x, которое принадлежит отрезку от -π/2 до π/2. По таблице значений найдем, что x = π/3, следовательно, — tg x = — π/3. Ответом уравнения будет — π/3.
Рассмотрим пример 3. Решим уравнение tg x = 1. Запишем, что x = arctg 1 + πk. В таблице значению tg 1 соответствует значение x = π/4, следовательно, arctg 1 = π/4. Подставим это значение в исходную формулу x и запишем ответ x = π/4 + πk.
Пример 4: вычислить tg x = — 4,1. В данном случае x = arctg (- 4,1) + πk. Т.к. найти значение arctg в данном случае нет возможности, ответ будет выглядеть как x = arctg (- 4,1) + πk.
В примере 5 рассматривается решение неравенства tg x > 1. Для решения построим графики функций y = tg x и y = 1. Как видно на рисунке, эти графики пересекаются в точках x = π/4 + πk. Т.к. в данном случае tg x > 1, на графике выделим область тангенсоиды, которая находится выше графика y = 1, где x принадлежит интервалу от π/4 до π/2. Ответ запишем как π/4 + πk
Далее рассмотрим уравнение ctg x = a. На рисунке изображены графики функций у = ctg x, y = a, y = — a, которые имеют множество точек пересечения. Решения можно записать как x = x 1 + πk, где x 1 = arcctg a и x = x 2 + πk, где x 2 = arcctg (- a). Отмечено, что x 2 = π — x 1 . Из этого следует равенство arcctg (- a) = π — arcctg a. Далее дается определение арккотангенса: арккотангенсом а называется такое число из промежутка от 0 до π, котангенс которого равен а. Решение уравнения сtg x = a записывается в виде: x = arcctg a + πk.
На рисунке изображены графики функций у = ctg x, y = a, y = — a, которые имеют множество точек пересечения. Решения можно записать как x = x 1 + πk, где x 1 = arcctg a и x = x 2 + πk, где x 2 = arcctg (- a). Отмечено, что x 2 = π — x 1 . Из этого следует равенство arcctg (- a) = π — arcctg a. Далее дается определение арккотангенса: арккотангенсом а называется такое число из промежутка от 0 до π, котангенс которого равен а. Решение уравнения сtg x = a записывается в виде: x = arcctg a + πk.
В конце видеоурока делается еще один важный вывод — выражение ctg x = a можно записать в виде tg x = 1/a, при условии, что a не равно нулю.
ТЕКСТОВАЯ РАСШИФРОВКА:
Рассмотрим решение уравнений tg х = 3 и tg х= — 3. Решая первое уравнение графически, мы видим, что графики функций у = tg х и у = 3 имеют бесконечно много точек пересечения, абсциссы которых запишем в виде
х = х 1 + πk, где х 1 — это абсцисса точки пересечения прямой у = 3 с главной ветвью тангенсоиды (рис.1), для которой было придумано обозначение
arctg 3 (арктангенс трех).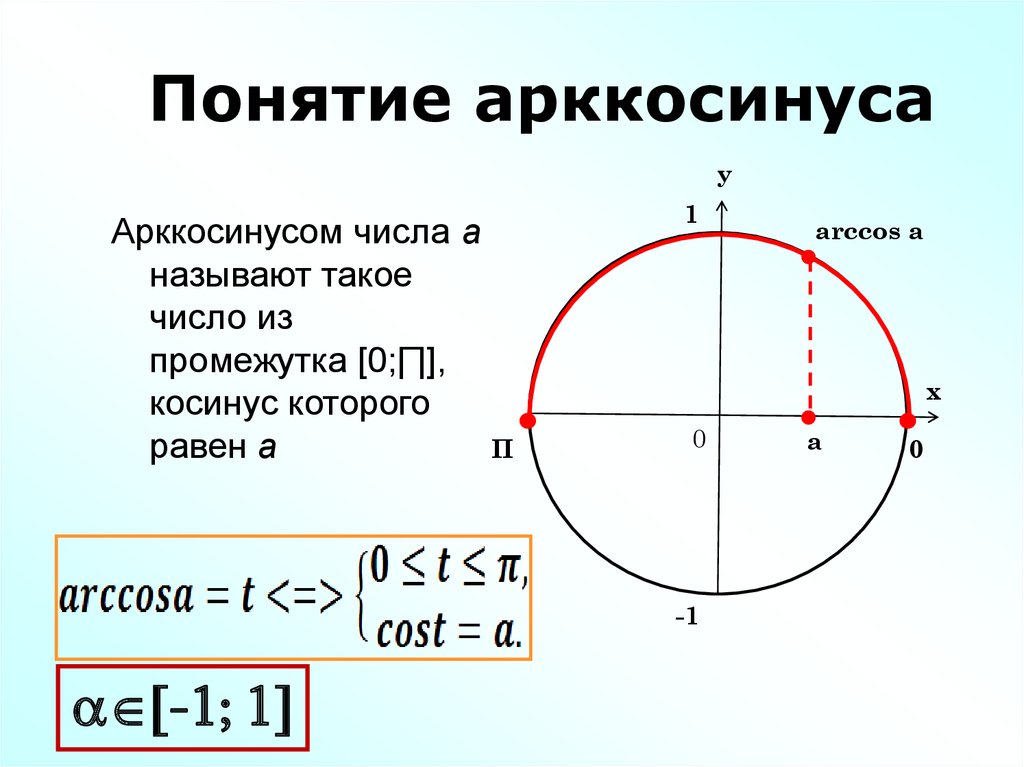
Как же понимать arctg 3?
Это число, тангенс которого равен 3 и это число принадлежит интервалу (- ;). Тогда все корни уравнения tg х = 3 можно записать формулой х = arctg 3+πk.
Аналогично решение уравнения tg х = — 3 можно записать в виде х = х 2 + πk, где х 2 — это абсцисса точки пересечения прямой у = — 3 с главной ветвью тангенсоиды (рис.1), для которой было придумано обозначение arctg(-3) (арктангенс минус трех). Тогда все корни уравнения можно записать формулой: х = arctg(-3)+ πk. По рисунку видно, что arctg(- 3)= — arctg 3.
Сформулируем определение арктангенса. Арктангенсом а называется такое число из промежутка (-;), тангенс которого равен а.
Часто используют равенство: arctg(-а) = -arctg а, которое справедливо для любого а.
Зная определение арктангенса, сделаем общий вывод о решении уравнения
tg х= a: уравнение tg х = a имеет решение х = arctg а + πk.
Рассмотрим примеры.
ПРИМЕР 1.Вычислить arctg.
Решение. Пусть arctg = х, тогда tgх = и хϵ (- ;). Показать таблицу значений Следовательно, х =, так как tg = и ϵ (- ;).
Показать таблицу значений Следовательно, х =, так как tg = и ϵ (- ;).
Итак, arctg =.
ПРИМЕР 2. Вычислить arctg (-).
Решение. Используя равенство arctg(- а) = — arctg а, запишем:
arctg(-) = — arctg . Пусть — arctg = х, тогда — tgх = и хϵ (- ;). Следовательно, х =, так как tg = и ϵ (- ;). Показать таблицу значений
Значит — arctg=- tgх= — .
ПРИМЕР 3. Решить уравнение tgх = 1.
1. Запишем формулу решений: х = arctg 1 + πk.
2. Найдем значение арктангенса
так как tg = . Показать таблицу значений
Значит arctg1= .
3. Поставим найденное значение в формулу решений:
ПРИМЕР 4. Решить уравнение tgх = — 4,1(тангенс икс равно минус четыре целые одна десятая).
Решение. Запишем формулу решений: х = arctg (- 4,1) + πk.
Вычислить значение арктангенса мы не можем, поэтому решение уравнения оставим в полученном виде.
ПРИМЕР 5. Решить неравенство tgх 1.
Решение. Будем решать графически.
- Построим тангенсоиду
у= tgх и прямую у = 1(рис. 2). Они пересекаются в точках вида х = + πk.
2). Они пересекаются в точках вида х = + πk.
2. Выделим промежуток оси икс, на котором главная ветвь тангенсоиды расположена выше прямой у = 1, так как по условию tgх 1. Это интервал (;).
3. Используем периодичность функции.
Своийство 2. у=tg х — периодическая функция с основным периодом π.
Учитывая периодичность функции у= tgх, запишем ответ:
(;). Ответ можно записать в виде двойного неравенства:
Перейдем к уравнению ctg х = a. Представим графическую иллюстрацию решения уравнения для положительного и отрицательного а (рис.3).
Графики функций у= ctg х и у =а а также
у= ctg х и у=-а
имеют бесконечно много общих точек, абсциссы которых имеют вид:
х = х 1 + , где х 1 — это абсцисса точки пересечения прямой у =а с главной ветвью тангенсоиды и
х 1 = arcсtg а;
х = х 2 + , где х 2 — это абсцисса точки пересечения прямой
у = — а с главной ветвью тангенсоиды и х 2 = arcсtg (- а).
Заметим, что х 2 = π — х 1 . Значит, запишем важное равенство:
arcсtg (-а) = π — arcсtg а.
Сформулируем определение: арккотангенсом а называется такое число из интервала (0;π), котангенс которого равен а.
Решение уравнения ctg х = a записываются в виде: х = arcсtg а + .
Обратим внимание, что уравнение ctg х = a можно преобразовать к виду
tg х = , за исключение, когда а = 0.
Эта статья про нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса данного числа. Сначала мы внесем ясность, что называется значением арксинуса, арккосинуса, арктангенса и арккотангенса. Дальше получим основные значения этих аркфункций, после чего разберемся, как находятся значения арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса. Наконец, поговорим про нахождение арксинуса числа, когда известен арккосинус, арктангенс или арккотангенс этого числа, и т.п.
Навигация по странице.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Сначала стоит разобраться, что вообще такое «значение арксинуса, арккосинуса, арктангенса и арккотангенса ».
Таблицы синусов и косинусов, а также тангенсов и котангенсов Брадиса позволяют найти значение арксинуса, арккосинуса, арктангенса и арккотангенса положительного числа в градусах с точностью до одной минуты. Здесь стоит оговориться, что нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса отрицательных чисел можно свести к нахождению значений соответствующих аркфункций положительных чисел, обратившись к формулам arcsin, arccos, arctg и arcctg противоположных чисел вида arcsin(−a)=−arcsin a , arccos(−a)=π−arccos a , arctg(−a)=−arctg a и arcctg(−a)=π−arcctg a .
Разберемся с нахождением значений арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам Брадиса. Будем это делать на примерах.
Пусть нам требуется найти значение арксинуса 0,2857
. Находим это значение в таблице синусов (случаи, когда это значение отсутствует в таблице, разберем ниже). Ему соответствует синус 16
градусов 36
минут. Следовательно, искомым значением арксинуса числа 0,2857
является угол 16
градусов 36
минут.
Часто приходится учитывать и поправки из трех справа столбцов таблицы. К примеру, если нам нужно найти арксинус 0,2863
. По таблице синусов это значение получается как 0,2857
плюс поправка 0,0006
, то есть, значению 0,2863
соответствует синус 16
градусов 38
минут (16
градусов 36
минут плюс 2
минуты поправки).
Если же число, арксинус которого нас интересует, отсутствует в таблице и даже не может быть получено с учетом поправок, то в таблице нужно отыскать два наиболее близких к нему значения синусов, между которыми данное число заключено. Например, мы ищем значение арксинуса числа 0,2861573
. Этого числа нет в таблице, с помощью поправок это число тоже не получить. Тогда находим два наиболее близких значения 0,2860
и 0,2863
, между которыми исходное число заключено, этим числам соответствуют синусы 16
градусов 37
минут и 16
градусов 38
минут. Искомое значение арксинуса 0,2861573
заключено между ними, то есть, любое из этих значений угла можно принять в качестве приближенного значения арксинуса с точностью до 1
минуты.
Абсолютно аналогично находятся и значения арккосинуса, и значения арктангенса и значения арккотангенса (при этом, конечно, используются таблицы косинусов, тангенсов и котангенсов соответственно).
Нахождение значения arcsin через arccos, arctg, arcctg и т.п.
Например, пусть нам известно, что arcsin a=−π/12 , а нужно найти значение arccos a . Вычисляем нужное нам значение арккосинуса: arccos a=π/2−arcsin a=π/2−(−π/12)=7π/12 .
Куда интереснее обстоит дело, когда по известному значению арксинуса или арккосинуса числа a требуется найти значение арктангенса или арккотангенса этого числа a или наоборот. Формул, задающих такие связи, мы, к сожалению, не знаем. Как же быть? Разберемся с этим на примере.
Пусть нам известно, что арккосинус числа a
равен π/10
, и нужно вычислить значение арктангенса этого числа a
. Решить поставленную задачу можно так: по известному значению арккосинуса найти число a
, после чего найти арктангенс этого числа. Для этого нам сначала потребуется таблица косинусов, а затем – таблица тангенсов.
Угол π/10
радиан – это угол 18
градусов, по таблице косинусов находим, что косинус 18
градусов приближенно равен 0,9511
, тогда число a
в нашем примере есть 0,9511
.
Осталось обратиться к таблице тангенсов, и с ее помощью найти нужное нам значение арктангенса 0,9511
, оно приближенно равно 43
градусам 34
минутам.
Эту тему логически продолжает материал статьи вычисление значений выражений, содержащих arcsin, arccos, arctg и arcctg .
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.
 ; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3. - И. В. Бойков, Л. Д. Романова. Сборникк задач для подготовки к ЕГЭ, часть 1, Пенза 2003.
- Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2
Урок и презентация на темы: «Арксинус. Таблица арксинусов. Формула y=arcsin(x)»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Программная среда «1С: Математический конструктор 6.1»
Решаем задачи по геометрии. Интерактивные задания на построение в пространстве
Что будем изучать:
1. Что такое арксинус?
2. Обозначение арксинуса.
3. Немного истории.
4. Определение.
6.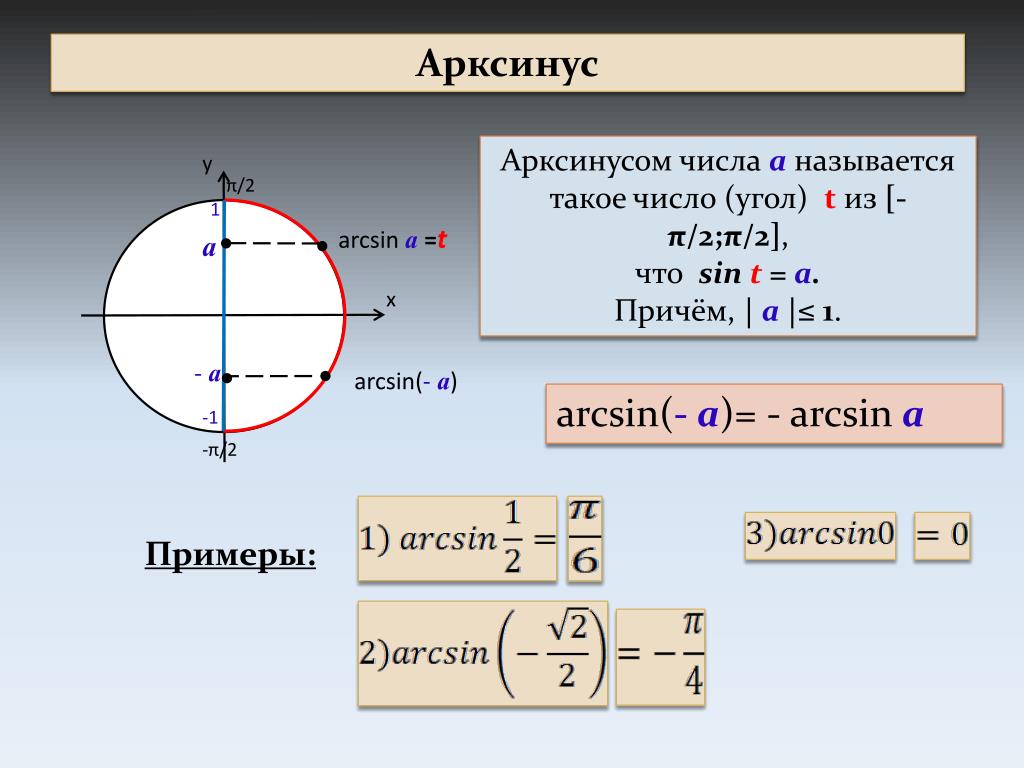 Примеры.
Примеры.
Что такое арксинус?
Ребята, мы с вами уже научились решать уравнения для косинуса, давайте теперь научимся решать подобные уравнения и для синуса. Рассмотрим sin(x)= √3/2. Для решения этого уравнения требуется построить прямую y= √3/2 и посмотреть: в каких точках она пересекает числовую окружность. Видно, что прямая пересекает окружность в двух точках F и G. Эти точки и будут решением нашего уравнения. Переобозначим F как x1, а G как x2. Решение этого уравнения мы уже находили и получили: x1= π/3 + 2πk,
а x2= 2π/3 + 2πk.
Решить данное уравнение довольно просто, но как решить, например, уравнение
sin(x)= 5/6. Очевидно, что это уравнение будет иметь также два корня, но какие значения будут соответствовать решению на числовой окружности? Давайте внимательно посмотрим на наше уравнение sin(x)= 5/6.
Решением нашего уравнения будут две точки: F= x1 + 2πk и G= x2 + 2πk,
где x1 – длина дуги AF, x2 – длина дуги AG.
Заметим: x2= π — x1, т.к. AF= AC — FC, но FC= AG, AF= AC — AG= π — x1.
Но, что это за точки?
Столкнувшись с подобной ситуацией, математики придумали новый символ – arcsin(x). Читается, как арксинус.
Тогда решение нашего уравнения запишется так: x1= arcsin(5/6), x2= π -arcsin(5/6).
И решение в общем виде: x= arcsin(5/6) + 2πk и x= π — arcsin(5/6) + 2πk.
Арксинус — это угол (длина дуги AF, AG) синус, которого равен 5/6.
Немного истории арксинуса
История происхождения нашего символа совершенно такая же, как и у arccos. Впервые символ arcsin появляется в работах математика Шерфера и известного французского ученого Ж.Л. Лагранжа. Несколько ранее понятие арксинус рассматривал Д. Бернули, правда записывал его другими символами.
Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга). Это вполне согласуется со смыслом понятия: arcsin x — это угол (а можно сказать и дуга), синус которого равен x.
Определение арксинуса
Если |а|≤ 1, то arcsin(a) – это такое число из отрезка [- π/2; π/2], синус которого равен а.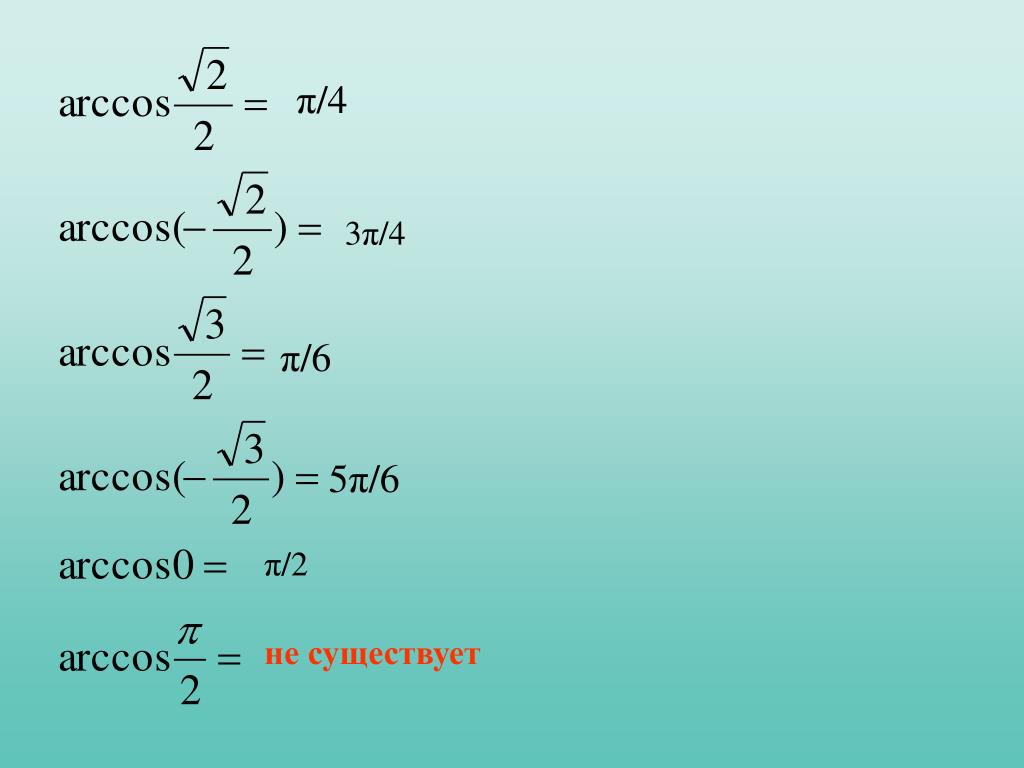
Если |а|≤ 1, то уравнение sin(x)= a имеет решение: x= arcsin(a) + 2πk и
x= π — arcsin(a) + 2πk
Перепишем:
x= π — arcsin(a) + 2πk = -arcsin(a) + π(1 + 2k).
Ребята, посмотрите внимательно на два наших решения. Как думаете: можно ли их записать общей формулой? Заметим, что если перед арксинусом стоит знак «плюс», то π умножается на четное число 2πk, а если знак «минус», то множитель — нечетный 2k+1.
С учётом этого, запишем общую формула решения для уравнения sin(x)=a:
Есть три случая, в которых предпочитают записывать решения более простым способом:
sin(x)=0, то x= πk,
sin(x)=1, то x= π/2 + 2πk,
sin(x)=-1, то x= -π/2 + 2πk.
Для любого -1 ≤ а ≤ 1 выполняется равенство: arcsin(-a)=-arcsin(a).
Напишем таблицу значений косинуса наоборот и получим таблицу для арксинуса.
Примеры
1. Вычислить: arcsin(√3/2).
Решение: Пусть arcsin(√3/2)= x, тогда sin(x)= √3/2.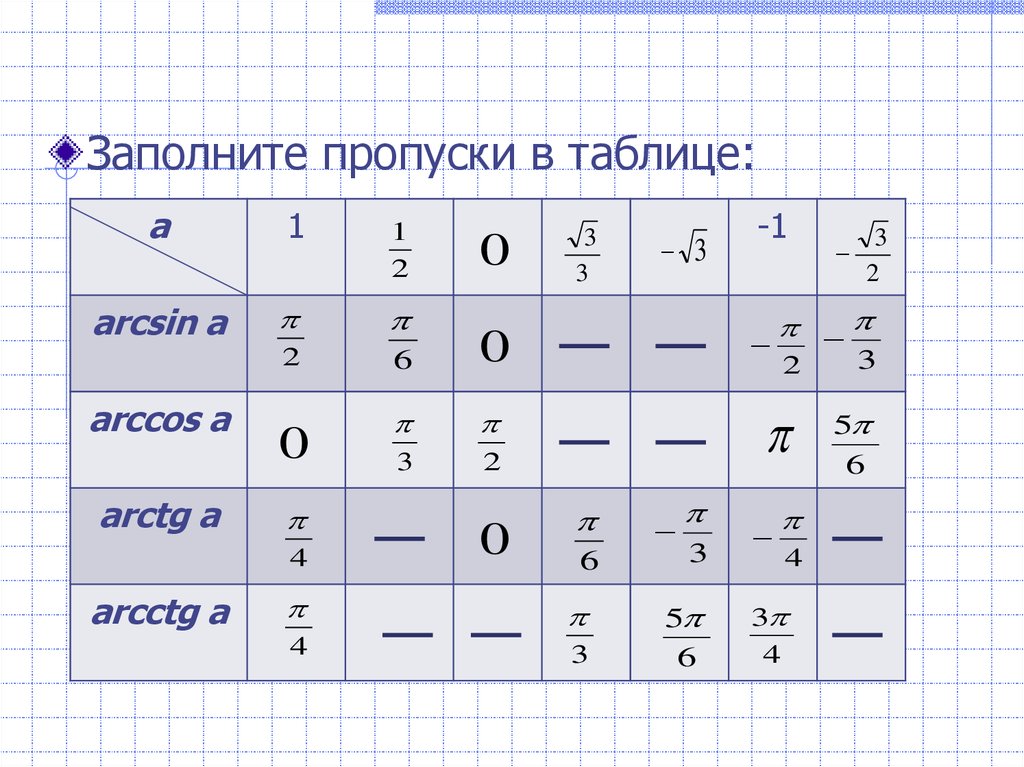 По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= π/3, т.к. sin(π/3)= √3/2 и –π/2 ≤ π/3 ≤ π/2.
По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= π/3, т.к. sin(π/3)= √3/2 и –π/2 ≤ π/3 ≤ π/2.
Ответ: arcsin(√3/2)= π/3.
2. Вычислить: arcsin(-1/2).
Решение: Пусть arcsin(-1/2)= x, тогда sin(x)= -1/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= -π/6, т.к. sin(-π/6)= -1/2 и -π/2 ≤-π/6≤ π/2.
Ответ: arcsin(-1/2)=-π/6.
3. Вычислить: arcsin(0).
Решение: Пусть arcsin(0)= x, тогда sin(x)= 0. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: значит x= 0, т.к. sin(0)= 0 и — π/2 ≤ 0 ≤ π/2.
Ответ: arcsin(0)=0.
4. Решить уравнение: sin(x) = -√2/2.
x= arcsin(-√2/2) + 2πk и x= π — arcsin(-√2/2) + 2πk.
Посмотрим в таблице значение: arcsin (-√2/2)= -π/4.
Ответ: x= -π/4 + 2πk и x= 5π/4 + 2πk.
5. Решить уравнение: sin(x) = 0.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(0) + 2πk и x= π — arcsin(0) + 2πk. Посмотрим в таблице значение: arcsin(0)= 0.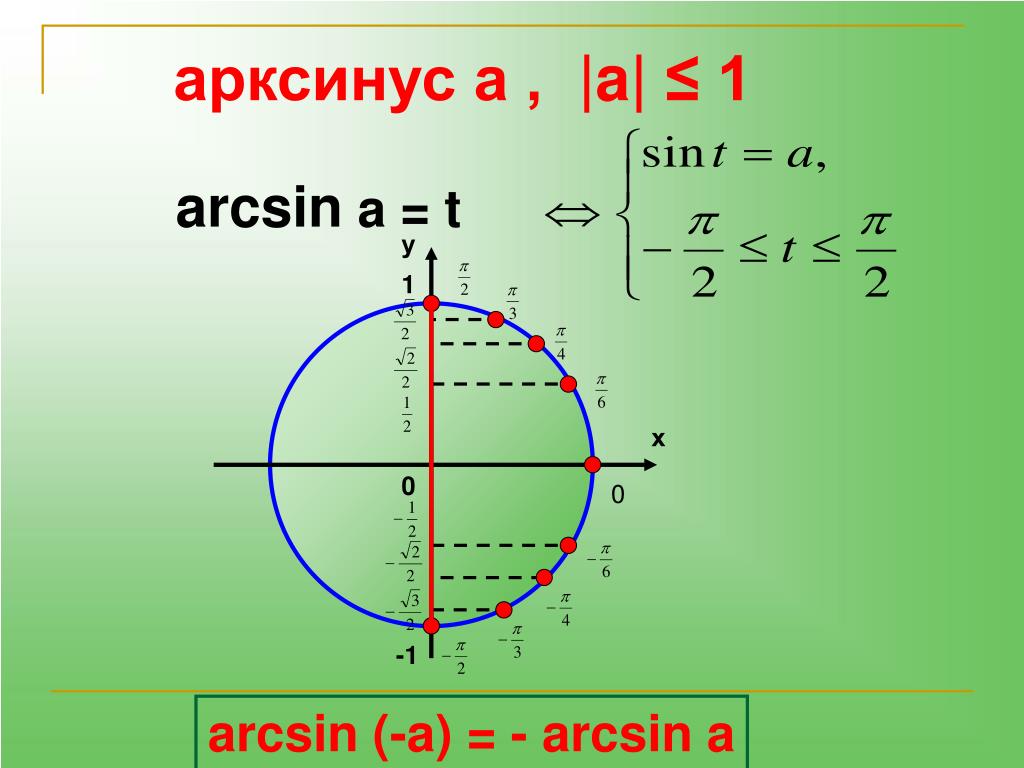
Ответ: x= 2πk и x= π + 2πk
6. Решить уравнение: sin(x) = 3/5.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(3/5) + 2πk и x= π — arcsin(3/5) + 2πk.
Ответ: x= (-1) n — arcsin(3/5) + πk.
7. Решить неравенство sin(x)
Решение: Синус — это ордината точки числовой окружности. Значит: нам надо найти такие точки, ордината которых меньше 0.7. Нарисуем прямую y=0.7. Она пересекает числовую окружность в двух точках. Неравенству y
Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk
Задачи на арксинус для самостоятельного решения
1) Вычислить: а) arcsin(√2/2), б) arcsin(1/2), в) arcsin(1), г) arcsin(-0.8).
2) Решить уравнение: а) sin(x) = 1/2, б) sin(x) = 1, в) sin(x) = √3/2, г) sin(x) = 0.25,
д) sin(x) = -1.2.
3) Решить неравенство: а) sin (x)> 0.6, б) sin (x)≤ 1/2.
Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом.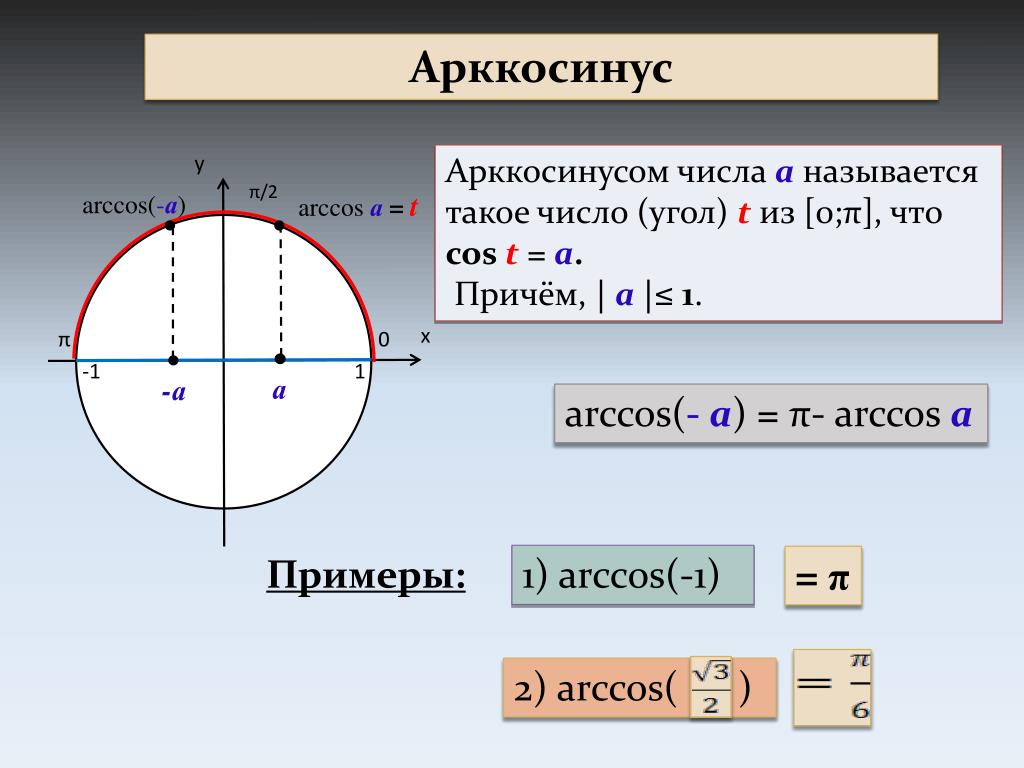 Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.
Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.
Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.
Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.
Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат.
Свойства арксинуса:
Если сопоставить графики sin и arcsin , у двух тригонометрических функций можно найти общие закономерности.
Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
Рассмотрим функцию арккосинуса более подробно:
- Функция определена на отрезке [-1; 1].

- ОДЗ для arccos — .
- График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
- Y = 0 при x = 1.
- Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.
Задание 1. Укажите функции изображенные на рисунке.
Ответ: рис. 1 – 4, рис.2 — 1.
В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.
Арктангенс
Arctg числа a – это такое значение угла α, что его тангенс равен а.
Если рассмотреть график арктангенса, можно выделить следующие свойства:
- График бесконечен и определен на промежутке (- ∞; + ∞).
- Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
- Y = 0 при x = 0.
- Кривая возрастает на всей области определения.
Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
Свойства функции арккотангенса:
- Интервал определения функции – бесконечность.
- Область допустимых значений – промежуток (0; π).
- F(x) не является ни четной, ни нечетной.
- На всем своем протяжении график функции убывает.
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2. Соотнести график и форму записи функции.
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Ответ: рис. 1 – 1, рис. 2 – 4.
Тригонометрические тождества arcsin, arcos, arctg и arcctg
Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.
Также существуют соотношения для arctg и arcctg:
Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла.
Примеры решения задач
Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.
При решении первого типа задач необходимо придерживаться следующего плана действий:
При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.
Допустим в ЕГЭ необходимо найти ответ для уравнения типа:
Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.
Если вспомнить формулу arcsin (sin α) = α , то можно свести поиск ответов к решению системы из двух уравнений:
Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.
{-1} (\frac{4}{3})$.Однако, как на самом деле вычислить это?
Я не думаю, что это $\frac{1}{\tan(\theta)}$ = $\frac{\cos(\theta)}{\sin(\theta)}$, потому что это просто кажется странным и больше похоже на котангенс.
Где я ошибся?
Спасибо,
комплексный анализ алгебра предварительное исчисление геометрия комплексные числа
$\endgroup$
6 9{-1}\theta$ можно интерпретировать двояко.
Как обратная функция — это известно как $\arctan\frac43$ и означает угол, тангенс которого равен $\frac43$. Для большинства значений (включая ваше) нет другого способа записать его, кроме записи десятичной аппроксимации, полученной с помощью калькулятора или подобного. $\arctan\frac43\прибл.0,9272952180\cdots$
В качестве обратной функции — это известно как котангенс, и вы дали правильное определение, например. $\cot\theta=\frac{\cos\theta}{\sin\theta}$. 9{-1}\theta$ зарезервировано для первого значения.
$\endgroup$
$\begingroup$
$\texttt{Метод Ньютона-Рапсона}$ дает хорошее приближение $\displaystyle{~\left(~\mbox{начиная с}\ 1 = \tan\left(\,{\pi \over 4}\,\right) ~\right)}$ с $\color{#f00 }{\underline{3}}$ итераций: $$ \left\lbrace\begin{массив}{rcl} \displaystyle{r_{0}} & \displaystyle{=} & \displaystyle{1} \\[1 мм] \displaystyle{r_{n + 1}} & \displaystyle{=} & \displaystyle{r_{n} + {4 \over 3}\,\cos^{2}\left(\, r_{n}\,\right) — {1 \over 2}\,\sin\left(\, 2r_{n}\,\right)\,\qquad n \geq 0} \конец{массив}\право.
 {-5}\ \%
$$
{-5}\ \%
$$Обратите внимание, что $\displaystyle{{4 \over 3} > {\pi \over 4}}$. По этой причине нашим начальным значением было $\displaystyle{1 = \tan\left(\,{\pi \over 4}\,\right)}$.
$\endgroup$
$\begingroup$
Во-первых, это угол в $\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)$ и $\tan \theta = \dfrac{4} {3}$. Часто вас просят найти что-то вроде $\sin\theta $ для $0 < \theta < \dfrac{\pi}{2}$. Имея это в виду, у вас есть: 9{-1} 4/3$. Очевидно, вы не поймете этого, составив дробь из $\frac 1{\tan 4/3}$. Вы были правы, что были сбиты с толку --- это не имело бы никакого гребаного смысла.
Итак… вы, вероятно, спрашиваете, как сделать , чтобы вычислить $\arctan 4/3$? Ну стандартного пути нет. Вы пользуетесь таблицами или калькулятором. Легко видеть, что это также будет угол $x$, так что $\sin x = 4/5$ и $\cos x = 3/5$.
Что бы это ни было.

=====
Как вычислить? 9{-1} 4/3$.
Как посчитать эти углы без калькулятора? Вы не знаете. Это угол при основании прямоугольного треугольника с основанием 3 и высотой 4. что бы это ни было.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите
Зарегистрироваться через Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
97} — \cdots$$Однако это можно использовать только для $x>1$ (и аналогичный ряд для $x < 1$ не включает $\pi$!)
Единственный другой способ получить $ \pi$ в «ответе» означало бы признать, что $\arctan(x)$ может равняться $\theta + n\cdot\pi$ (где $n = 0, \pm1,2,3,.
 .. $).
.. $).Итак, $\arctan(1/3) = 0,322 +n\cdot\pi = (0,102 + n)\cdot\pi$ (где $n = 0, \pm1,2,3,…$).
Не очень удовлетворительно.
$\endgroup$
$\begingroup$ 96}{231}} \tag 4$$
Используя приведенные выше формулы, вы получите $\frac{139}{432}$, $\frac{250}{777}$, $\frac{20806}{ 64665}$, $\frac{19593}{60895}$, которые составляют $\приблизительно 0,3217592593$, $\приблизительно 0,3217503218$, $\приблизительно 0,3217505606$, $\приблизительно 0,3217505542$, в то время как «точное» значение будет $\приблизительно 0,3217505544$.
$\endgroup$
$\begingroup$
Не забывайте, что вы можете построить его. Геометрическое решение также является решением.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Калькулятор — arctan(4/3) — Solumaths
Арктан, расчет онлайн
Сводка:
Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
arctan онлайн
Описание:
Функция arctan является обратной функцией касательная функция, это вычисляет арктангенс числа онлайн .
- Расчет арктангенса
- Пределы арктангенса Пределы арктангенса существуют при `-oo` (минус бесконечность) и `+oo` (плюс бесконечность):
Чтобы вычислить арктангенс числа , просто введите число и примените арктанг функция.
Например, чтобы вычислить арктангенс следующего числа 10, введите arctan(`10`), или сразу 10, если кнопка arctan уже появляется, возвращается результат 1.
 4711276743.
92)`.
4711276743.
92)`.- Функция арктангенса имеет предел в `-oo`, который равен `pi/2`.
- Функция арктангенса имеет предел в `+oo`, который равен `-pi/2`.
- `lim_(x->-oo)arctan(x)=pi/2`
- `lim_(x->+oo)arctan(x)=-pi/2`
- Таблица замечательных значений
- Арккосинус : arccos.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. - Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
- Упрощение калькулятора: упрощение. Калькулятор, который может упростить алгебраическое выражение онлайн.
- Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
- Касательная: рыжевато-коричневая. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
- Что такое arctan?
- График арктангенса
- Свойства арктангенса, связи с тригонометрическими функциями, интеграл и производная арктангенса
- Калькулятор арктангенса – как пользоваться
-
cot(x) = 1/tan(x), так что котангенс в основном является обратной величиной тангенса, или, другими словами, мультипликативным обратным - arctan(x) — угол, тангенс которого равен x
- Синус:
sin(arctan(x)) = x / √(1 + x²) - Косинус:
cos(arctan(x)) = 1 / √(1 + x²) - Тангенс:
tan(arctan(x)) = x -
arctan(x) = π/2 - arccot(x) -
арктан(-х) = -арктан(х) - arcsin(x)
= arctg(x / √(1 - x²)) - интеграл от arctan:
∫arctan(x) dx = x arctan(x) - (1/2) ln(1 + x²) + C - производная от arctan:
d/dx arctan(x) = 1/(1 + x²), где x ≠ -i, i -
arctan(x) + arctan(1/x) = π/2, для x > 0 иarctan(x) + arctan(1/x) = -π/2, для x < 0 - tan(π / 2) = ∞ ⇒ arctan(∞) = π/2
- тангенс (π / 3) = √3 ⇒ арктангенс (√3) = π/3
- тангенс (0) = 0 ⇒ арктангенс (0) = 0
- arctan(-x) = -arctan(x), для всех x ∈ R
- tan (arctan x) = x, для всех действительных чисел x
- arctan (tan x) = x, для x ∈ (-π/2, π/2)
- arctan(1/x) = π/2 — arctan(x) = arccot(x), если x > 0 или,
arctan(1/x) = — π/2 — arctan(x) = arccot(x) — π, если x < 0 9{2}+1}дз\) - π/4 = 4 арктангенса (1/5) — арктангенса (1/239)
- π/4 = арктангенс (1/2) + арктангенс (1/3)
- π/4 = 2 арктангенса (1/2) — арктангенса (1/7)
- π/4 = 2 арктангенса (1/3) + арктангенса (1/7)
- π/4 = 8 арктан (1/10) — 4 арктан (1/515) — арктан (1/239)
- π/4 = 3 арктангенса (1/4) + арктангенса (1/20) + арктангенса (1/1985)
- тангенс (тангенс -1 х) = х, для всех действительных чисел х
- tan -1 x + tan -1 y = tan -1 [(x + y)/(1 — xy)], когда xy < 1
загар -1 x — tan -1 y = tan -1 [(x — y)/(1 + xy)], когда xy > -1 - У нас есть 3 формулы для 2tan -1 x
2tan -1 x = sin -1 (2x / (1+x 2 )), когда |x| ≤ 1
2tan -1 x = cos -1 ((1-x 2 ) / (1+x 2 )), когда x ≥ 0
2tan -1 x = tan -1 (2x / (1-x 2 )), когда -1 < x < 1 - желтовато-коричневый -1 (-x) = -tan -1 x, для всех x ∈ R
- загар -1 (1/x) = кроватка -1 х, когда х > 0
- tan -1 x + cot -1 x = π/2, когда x ∈ R
- tan -1 (tan x) = x, только когда x ∈ R — {x : x = (2n + 1) (π/2), где n ∈ Z}
т. е. tan -1 (tan x) = x, только если x НЕ является нечетным кратным π/2. В противном случае tan -1 (tan x) не определен.
е. tan -1 (tan x) = x, только если x НЕ является нечетным кратным π/2. В противном случае tan -1 (tan x) не определен. - При x = ∞, y = π/2
- Когда x = √3, y = π/3
- Когда х = 0, у = 0
- Когда x = -√3, y = -π/3
- Когда x = -∞, y = -π/2
- Калькулятор Arctan
- Тригонометрические функции
- Тригонометрическая таблица
- Грех кост тан
- Arctan также может быть записан как arctan x или tan -1 x. Однако тангенс -1 х не равен (тангенс х) -1 = 1 / тангенс х = кроватка х.
- Основная формула для арктангенса задается как θ = арктангенс (перпендикуляр / основание).
- Производная арктангенса равна d/dx(tan -1 x) = 1/(1+x 2 ).

- Интеграл от arctan равен ∫tan -1 x dx = x tan -1 x — ½ ln |1+x 2 | + С
| arctan(`-1`) | `3*pi/4` |
| arctan(`-sqrt(3)/3`) | `5*pi/6` | 6 arctan (`-sqrt(3)`) | `2*pi/3` |
| arctan(`0`) | `0` |
| arctan(`sqrt(3)`) | `/3` |
| arctan(`1`) | `pi/4` |
| arctan(`sqrt(3)/3`) | `pi/6` |
Syntax :
arctan(x) , x — число. 92)`
Предельный арктангенс :
Калькулятор пределов позволяет вычислять пределы функции арктангенса.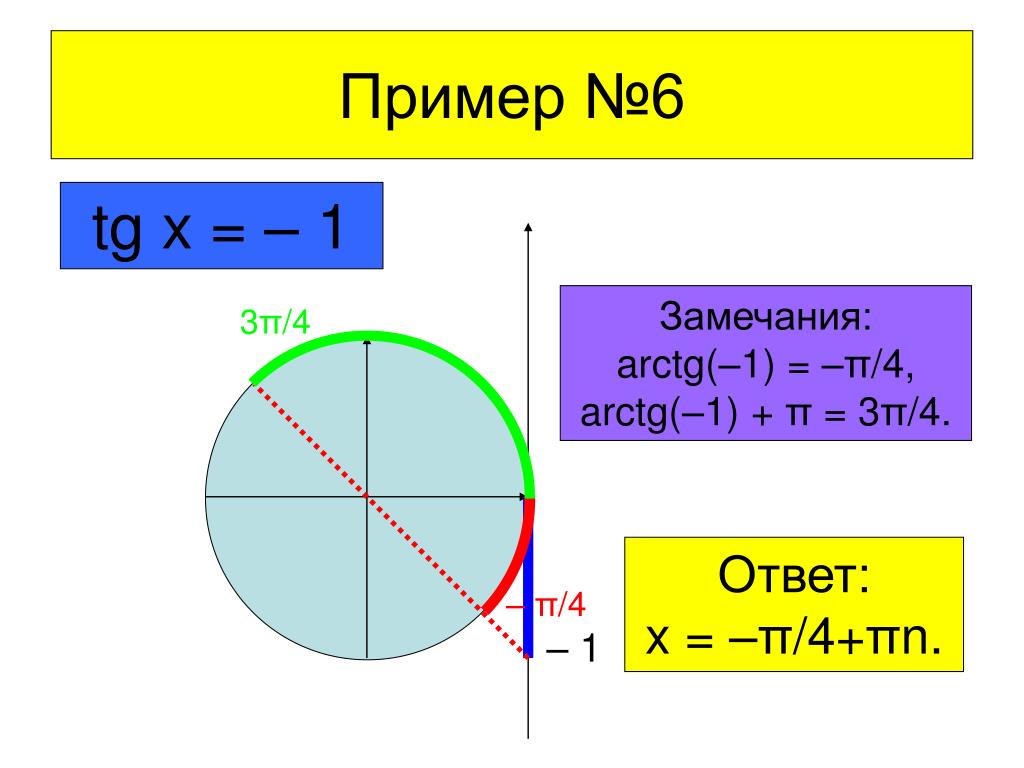
предел арктангенса(x) is limit(`»arctan»(x)`)
Обратная функция арктангенса :
обратная функция арктангенса представляет собой функцию тангенса, отмеченную тангенсом.
Графический арктангенс :
Графический калькулятор может отображать функцию арктангенса в интервале ее определения.
Свойство функции арктангенс:
Функция арктангенса является нечетной функцией.
Расчет онлайн с арктангенсом (арктангенсом)
См. также
Список связанных калькуляторов:
Тригонометрические функции | Вещественные функции
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найдите точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек (45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы | 45 | |
| 33 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | желтовато-коричневый (пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найдите точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | соз(210) | |
| 52 | Найти точное значение | сек (60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | желтовато-коричневый ((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | грех((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | грех((2pi)/3) | |
| 88 | Найти точное значение | желтовато-коричневый ((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найдите точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Калькулятор арктангенса.
 Найдите обратную сторону тангенса
Найдите обратную сторону тангенсаСоздано Ханной Памула, кандидатом наук
Отредактировано Bogna Szyk и Jack Bowater
Последнее обновление: 15 августа 2021 г.
Содержание:Используйте этот калькулятор арктангенса, чтобы быстро найти арктангенс. Ищете ли вы простой ответ на вопрос «что такое арктан?» или вас интересует интеграл или производная от arctan, вы пришли в нужное место. Ниже вы также найдете график арктангенса, а также четкую таблицу с часто используемыми значениями, такими как арктангенс (1) и арктангенс (0). Кроме того, вы можете просто ввести интересующее вас значение в этот инструмент, и вы найдете ответ в мгновение ока.
Заинтересованы в более сложной тригонометрии? Проверьте наши калькуляторы закона синусов и закона косинусов, если вам нужно решить треугольники.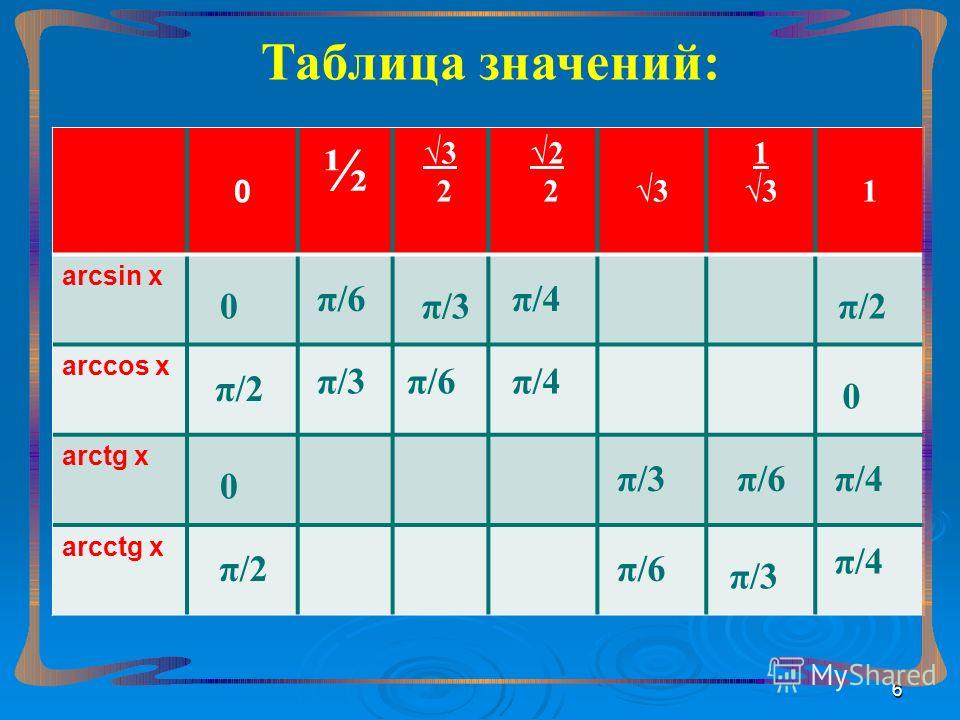
Что такое арктан?
Арктангенс является обратной функцией тангенса. Проще говоря, мы используем arctan, когда хотим найти угол, для которого известно значение тангенса.
Однако, строго говоря, поскольку тангенс является периодической тригонометрической функцией, у него нет обратной функции. Тем не менее, мы можем определить обратную функцию, если ограничим область определения интервалом, где функция монотонна. Обычно выбираемый интервал -π/2 < y < π/2 называется главным значением и в то же время является диапазоном функции арктангенса.
| Сокращение | Определение | Домен арктана x | Диапазон обычных основных значений |
|---|---|---|---|
| арктан(х) тан -1 х, атан | х = тангенс (у) | все действительные числа R | -π/2 < y < π/2 -90° < y < 90° |
Использование условного обозначения tan -1 x может привести к путанице в отношении разницы между арктангенсом и котангенсом. Оказывается, arctg и cot на самом деле разные вещи:
Оказывается, arctg и cot на самом деле разные вещи:
Надеемся, что теперь вы не сомневаетесь, что арктан и котан разные. Чтобы избежать дальнейших недоразумений, вы можете используйте арктангенс(х), а не тангенс -1 х нотация .
Диаграмма арктангенса
Ограничивая область определения функции главного тангенса, мы получаем арктангенс, который находится исключительно в диапазоне от −π/2 до π/2 радиан. Однако областью определения функции арктангенса являются все действительные числа. Тогда график выглядит следующим образом:
| График | Часто используемые значения | |||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||
Как создается этот арктический график? Отражая тангенс (x) в диапазоне (-π/2 π/2) через линию y = x. Вы также можете посмотреть на это как на перестановку горизонтальной и вертикальной осей:
Свойства арктангенса, отношения с тригонометрическими функциями, интеграл и производная от арктангенса
Соотношения в тригонометрии имеют решающее значение для более глубокого понимания этой темы. Изучение прямоугольного треугольника с длинами сторон 1 и x — хорошая отправная точка, если вы хотите найти отношения между арктангенсом и основными тригонометрическими функциями:
Другие полезные соотношения с арктангенсом:
Первое уравнение легко доказать из свойств прямоугольного треугольника с длинами сторон 1 и x, так как мы прекрасно знаем, что сумма углов в треугольнике равна 180°.
Вычитая прямой угол, равный 90°, мы получаем два непрямых угла, которые в сумме должны давать 9.0°. Таким образом, мы можем записать углы как arctan(x) и arctan(1/x).
Калькулятор арктангенса – как пользоваться
Это действительно один из наших самых простых в использовании калькуляторов! Просто введите номер, который вы хотите найти арктангенса . Поскольку домен arctan состоит из действительных чисел, вам не нужно слишком беспокоиться. Допустим, мы хотим найти арктангенс 1. Просто введите число, и калькулятор арктангенса отобразит результат . Как мы и ожидали, арктангенс числа 1 равен 45°. Этот калькулятор арктангенса работает и наоборот, то есть как стандартный калькулятор тангенса — введите угол во второе поле, и появится тангенс этого угла.
Hanna Pamuła, кандидат PhD
Y = Arctan (x)
Проверьте 19 аналогичные калькуляторы тригонометрии 📐
Arccosarcsincofunction… 16 еще
Арктан — Формула, график, идентичности, домен и диапазон
в Тригонометрии, 434334333333333 годы, .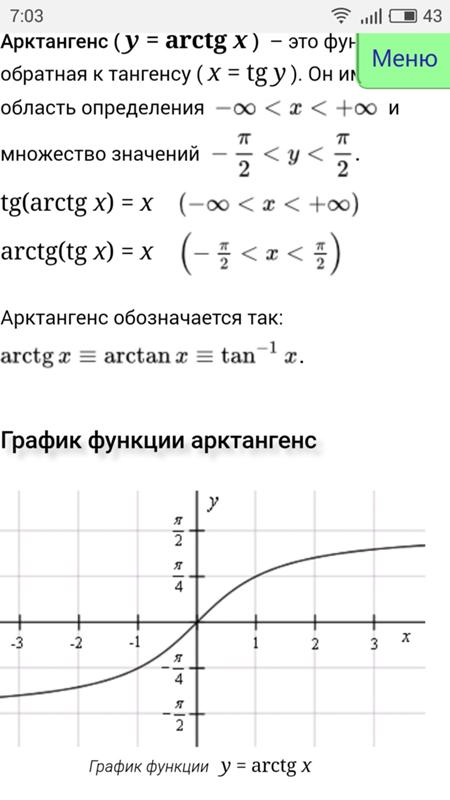 относится к функции арктангенса. Обратные тригонометрические функции обычно сопровождаются приставкой — дуга. Математически мы представляем функцию арктангенса или арктангенса как тангенс -1 х или арктангенс(х). Так как тригонометрических функций всего шесть, то и обратных тригонометрических функций тоже шесть, а именно sin -1 х, кос -1 х, тан -1 х, косек -1 х, сек -1 х, и кроватка -1 х.
относится к функции арктангенса. Обратные тригонометрические функции обычно сопровождаются приставкой — дуга. Математически мы представляем функцию арктангенса или арктангенса как тангенс -1 х или арктангенс(х). Так как тригонометрических функций всего шесть, то и обратных тригонометрических функций тоже шесть, а именно sin -1 х, кос -1 х, тан -1 х, косек -1 х, сек -1 х, и кроватка -1 х.
Arctan (tan -1 x) не то же самое, что 1/tan x. Это означает, что обратная тригонометрическая функция не является обратной величиной соответствующей тригонометрической функции. Цель arctan — найти значение неизвестного угла, используя значение тригонометрического отношения тангенса. Навигация, физика и инженерия широко используют функцию арктангенса. В этой статье мы узнаем о нескольких аспектах загара 9.1389 -1 x, включая область определения, диапазон, график и интеграл, а также значение производной.
| 1. | Что такое Арктан? |
| 2. | Арктан Формула |
| 3. | Арктанские личности |
| 4. | Домен Арктана и Диапазон |
| 5. | Свойства функции Arctan |
| 6. | Диаграмма Арктана |
| 7. | Производное арктана |
| 8. | Интеграл арктана |
| 9. | Часто задаваемые вопросы по Arctan |
Что такое Арктан?
Арктан – одна из важных обратных тригонометрических функций. В прямоугольном треугольнике тангенс угла определяет отношение перпендикуляра и основания, то есть «перпендикуляр/основание». Напротив, арктангенс отношения «перпендикуляр / основание» дает нам значение соответствующего угла между основанием и гипотенузой. Таким образом, arctan является обратной функцией tan.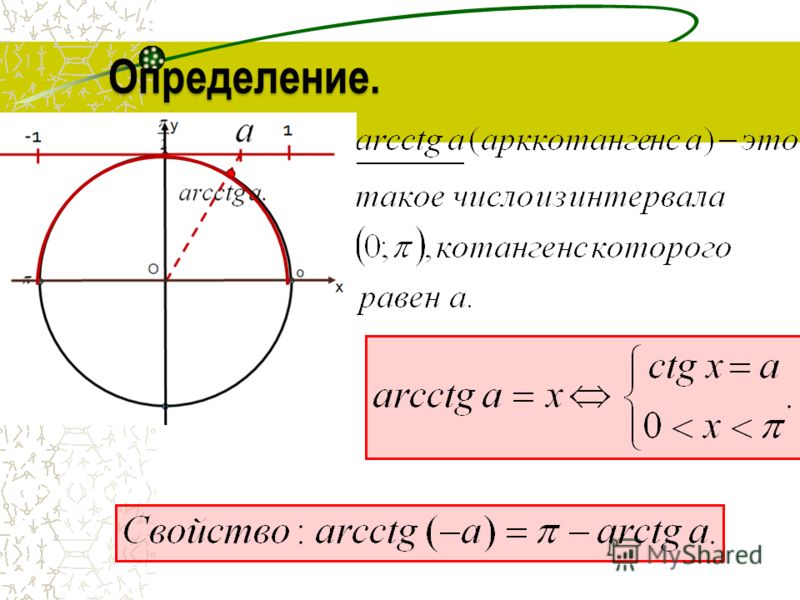
Если тангенс угла θ равен x, то есть x = tan θ, то θ = arctan(x). Ниже приведены некоторые примеры, которые могут помочь нам понять, как работает функция arctan:
Предположим, у нас есть прямоугольный треугольник. Пусть θ будет углом, значение которого необходимо определить. Мы знаем, что тангенс θ будет равен отношению перпендикуляра к основанию. Следовательно, тангенс θ = Перпендикуляр/Основание. Чтобы найти θ, мы будем использовать функцию арктангенса: θ = тангенс -1 [Перпендикуляр/База].
Арктан Формула
Как обсуждалось выше, основная формула арктангенса дается следующим образом: арктангенс (перпендикуляр/основание) = θ, где θ — угол между гипотенузой и основанием прямоугольного треугольника. Мы используем эту формулу для арктангенса, чтобы найти значение угла θ в градусах или радианах.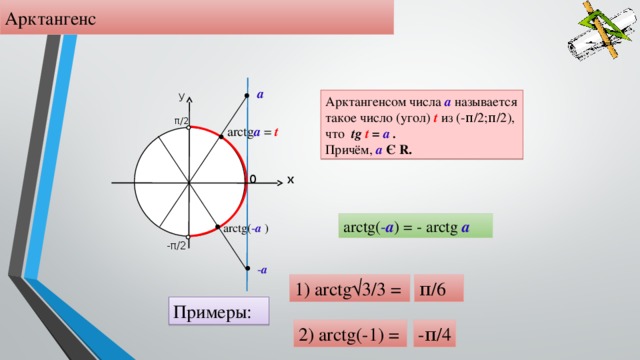 Мы также можем записать эту формулу как θ = тангенс -1 [Перпендикуляр/Основание].
Мы также можем записать эту формулу как θ = тангенс -1 [Перпендикуляр/Основание].
Идентичности Арктана
Существует несколько формул арктангенса, тождеств и свойств арктангенса, которые помогают решать как простые, так и сложные суммы по обратной тригонометрии. Некоторые из них приведены ниже:
У нас также есть некоторые формулы арктангенса для числа π. Они приведены ниже.
Как применять формулу Arctan x?
Мы можем получить более глубокое понимание применения формулы арктангенса с помощью следующих примеров:
Пример : В прямоугольном треугольнике ABC, если основание треугольника составляет 2 единицы, а высота треугольника 3 единицы. Найдите угол основания.
Найдите угол основания.
Решение:
Чтобы найти: угол при основании
Используя формулу арктангенса, мы знаем,
⇒ θ = арктангенс (3 ÷ 2) = арктангенс (1,5) 90 152
⇒ θ = 56,3 °
Ответ: Угол равен 56,3 ° .
Арктан Домен и Диапазон
Все тригонометрические функции, включая tan (x), имеют отношение «многие к одному». Однако обратная функция может существовать только в том случае, если она имеет взаимно-однозначное отношение и отношение. По этой причине домен tan x должен быть ограничен, иначе не может существовать обратное. Другими словами, тригонометрическая функция должна быть ограничена своей основной ветвью, поскольку нам нужно только одно значение.
Домен tan x ограничен (-π/2, π/2). Значения, при которых cos(x) = 0, были исключены. Диапазон тангенса (x) — это все действительные числа. Мы знаем, что область определения и область значений тригонометрической функции преобразуются в область значений и область определения обратной тригонометрической функции соответственно.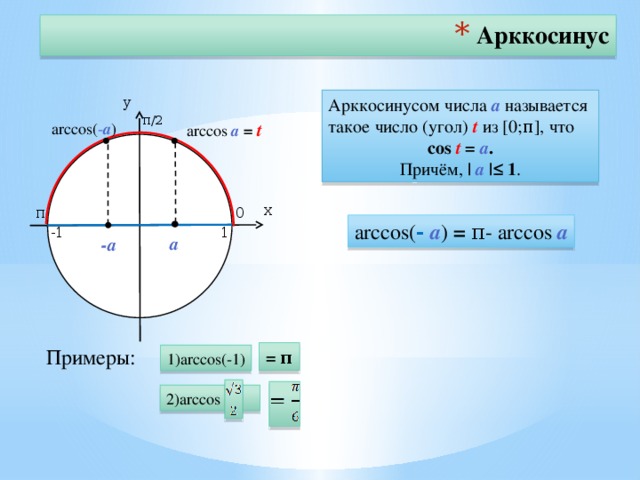 Таким образом, мы можем сказать, что домен tan -1 x состоит из всех действительных чисел, а диапазон равен (-π/2, π/2). Интересно отметить тот факт, что мы можем распространить функцию арктангенса на комплексные числа. В таком случае доменом arctan будут все комплексные числа.
Таким образом, мы можем сказать, что домен tan -1 x состоит из всех действительных чисел, а диапазон равен (-π/2, π/2). Интересно отметить тот факт, что мы можем распространить функцию арктангенса на комплексные числа. В таком случае доменом arctan будут все комплексные числа.
Таблица Arctan
Любой угол, выраженный в градусах, также может быть преобразован в радианы. Для этого мы умножаем значение градуса на коэффициент π/180°. Кроме того, функция арктангенса принимает действительное число в качестве входных данных и выводит соответствующее уникальное значение угла. В приведенной ниже таблице указаны значения арктангенса для некоторых действительных чисел. Их также можно использовать при построении графика арктангенса.
| х | арктан(х) (°) | арктан(х) (рад) |
|---|---|---|
| -∞ | -90° | -π/2 |
| -3 | -71,565° | -1,2490 |
| -2 | -63,435° | -1. 1071 1071 |
| -√3 | -60° | -π/3 |
| -1 | -45° | -π/4 |
| -1/√3 | -30° | -π/6 |
| -1/2 | -26,565° | -0,4636 |
| 0 | 0° | 0 |
| 1/2 | 26,565° | 0,4636 |
| 1/√3 | 30° | №/6 |
| 1 | 45° | №/4 |
| √3 | 60° | №/3 |
| 2 | 63,435° | 1.1071 |
| 3 | 71,565° | 1,2490 |
| ∞ | 90° | №/2 |
Арктан х Свойства
Ниже приведены некоторые полезные тождества арктангенса, основанные на свойствах функции арктангенса. Эти формулы можно использовать для упрощения сложных тригонометрических выражений, тем самым облегчая решение задач.
Арктан График
Мы знаем, что домен arctan равен R (все действительные числа), а диапазон равен (-π/2, π/2). Чтобы построить график арктангенса, мы сначала определим несколько значений y = arctan(x). Используя уже известные значения специальных углов, получаем на графике следующие точки:
Используя их, мы можем построить график арктангенса.
Арктан производный
Чтобы найти производную арктангенса, мы можем использовать следующий алгоритм.
Пусть y = arctan x
Беря тангенс с обеих сторон, получаем x
Теперь, продифференцировав обе части и используя цепное правило, мы получим
Sec 2 Y DY/DX = 1
⇒ DY/DX = 1/с 2 Y
В соответствии с тригонометрической идентичностью мы имеем SEC 2 Y = 1 + TAN 2 Y
dy/dx = 1 / (1 + tan 2 y)
При подстановке,
Таким образом, d(arctan x) / dx = 1 / (1 + x 2 )
Интеграл арктана x
Интеграл от арктангенса является первообразной функции арктангенса. Интегрирование по частям используется для вычисления интеграла арктангенса.
Интегрирование по частям используется для вычисления интеграла арктангенса.
Здесь f(x) = tan -1 x, g(x) = 1
Формула имеет вид ∫f(x)g(x)dx = f(x) ∫g(x)dx — ∫[d(f(x))/dx × ∫g(x) dx] dx
После подстановки значений и решения выражения получаем интеграл от arctan как
∫tan -1 x dx = x tan -1 x — ½ ln |1+x 2 | + C
где C – постоянная интегрирования.
Статьи по теме:
Важные замечания по Arctan
Часто задаваемые вопросы по Arctan
Что такое функция арктангенса в тригонометрии?
Функция Arctan обратна функции тангенса. Обычно его обозначают как arctan x или tan -1 x. Основная формула для определения значения арктангенса: θ = тангенс -1 (перпендикуляр/основание).
Является ли Арктан инверсией Тан?
Да, арктан противоположен загару. Он может определить значение угла в прямоугольном треугольнике, используя функцию касательной. Tan -1 x будет существовать только в том случае, если мы ограничим область определения функции тангенса.
Арктан и кроватка — это одно и то же?
Арктан и детская кроватка не одно и то же. Обратной функцией тангенса является арктангенс, определяемый как тангенс -1 x. Однако котангенс является обратной функцией тангенса. То есть (загар х) -1 = 1 / детская кроватка x
То есть (загар х) -1 = 1 / детская кроватка x
Какова формула арктана?
Основная формула арктангенса может быть представлена как θ = тангенс -1 (Перпендикуляр/Основание). Здесь θ — угол между гипотенузой и основанием прямоугольного треугольника.
Что такое производное арктана?
Производную арктангенса можно вычислить, применяя концепции подстановки и цепного правила. Таким образом, d(arctan x)/dx = 1/(1 + x 2 ), x ≠ i, -i.
Как рассчитать интеграл арктангенса?
Нам придется использовать интегрирование по частям, чтобы найти значение интеграла от арктангенса. Это значение задается как ∫tan -1 x dx = x tan -1 x — ½ ln |1+x 2 | + C.
Что такое Арктан Бесконечности?
Мы знаем, что значение тангенса (π/2) = sin(π/2) / cos (π/2) = 1 / 0 = ∞. Таким образом, мы можем сказать, что arctan(∞) = π/2.
Каков предел арктангенса х, когда х приближается к бесконечности?
Значение arctan приближается к π/2, когда x приближается к бесконечности.

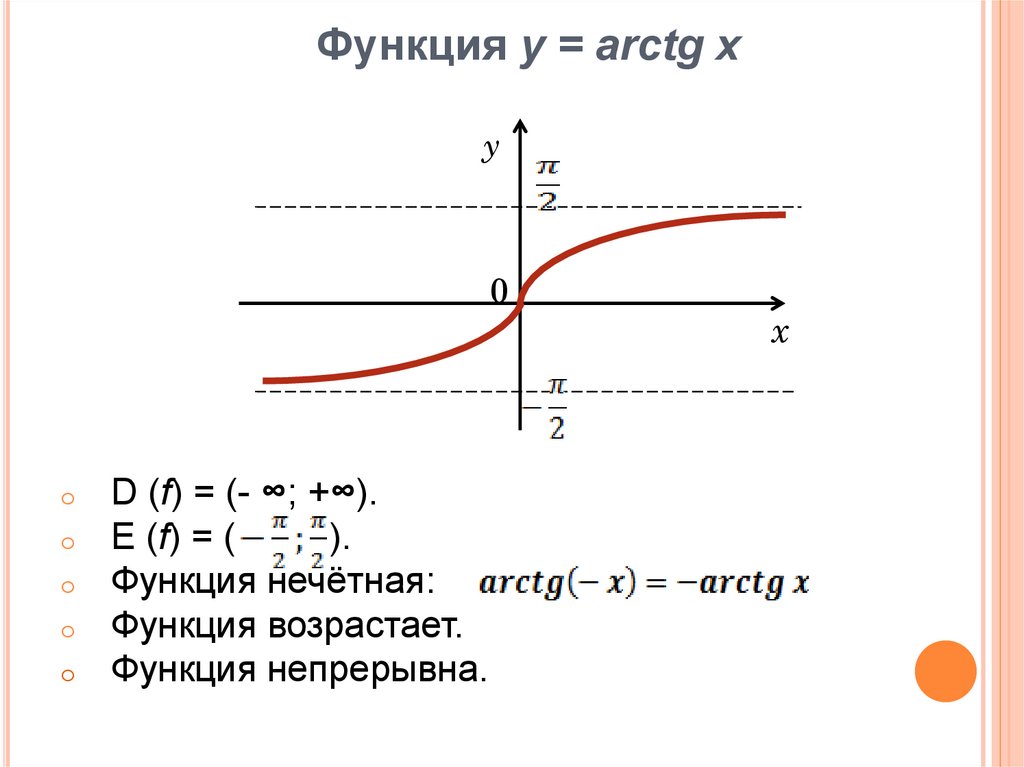 — 96 с.: ил. ISBN 5-7107-2667-2
— 96 с.: ил. ISBN 5-7107-2667-2
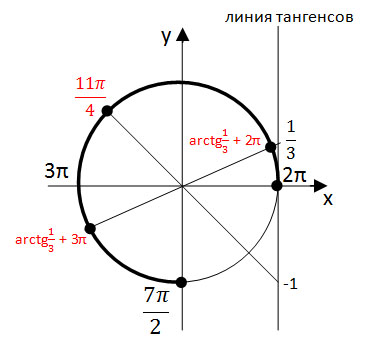 ; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
 {-5}\ \%
$$
{-5}\ \%
$$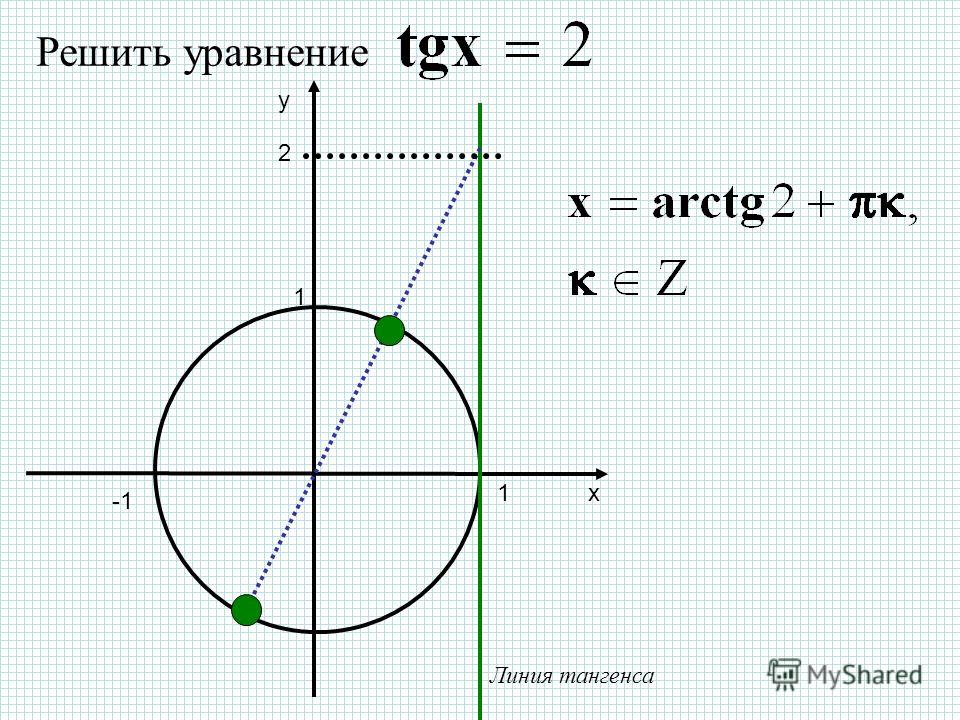
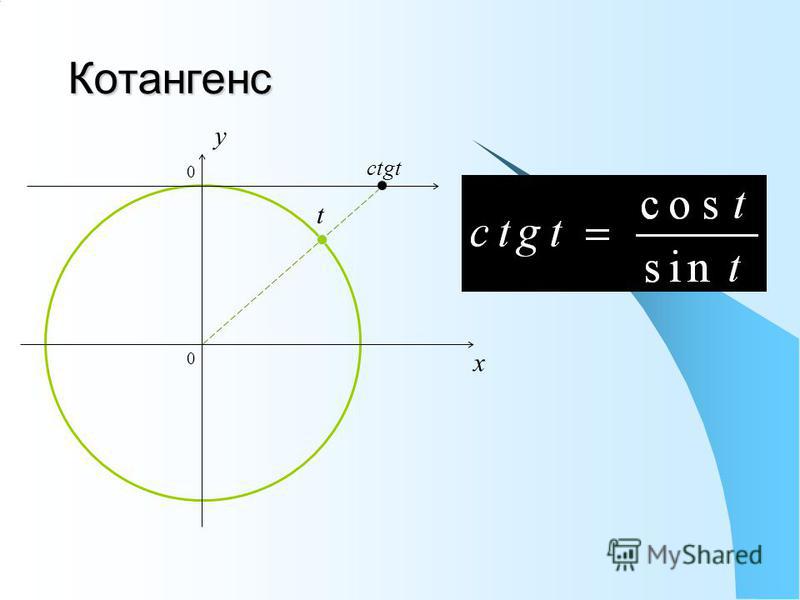 .. $).
.. $).
 4711276743.
92)`.
4711276743.
92)`.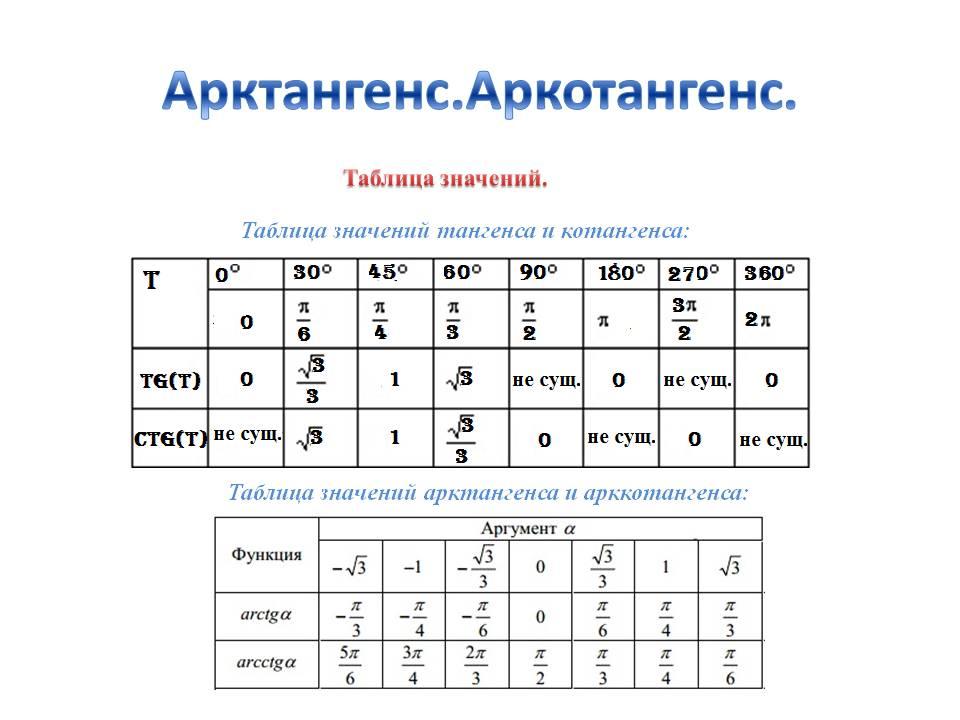 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения.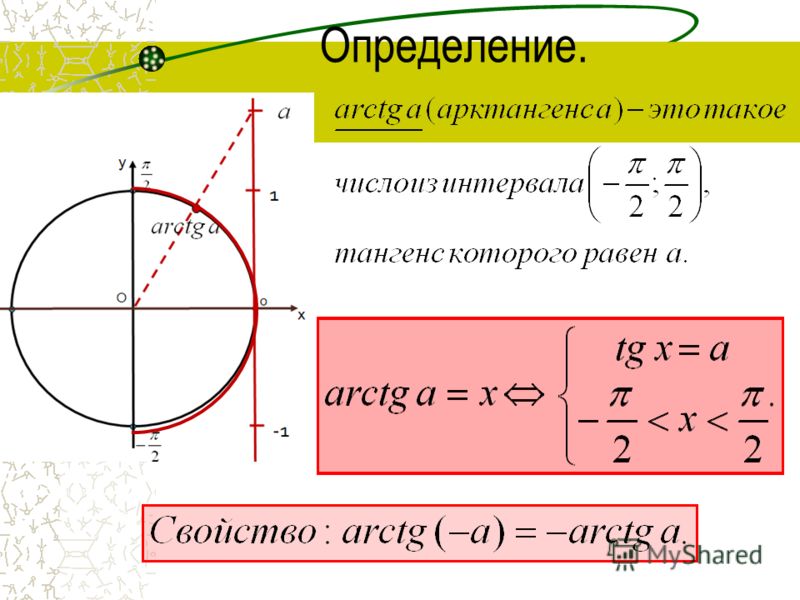 1071
1071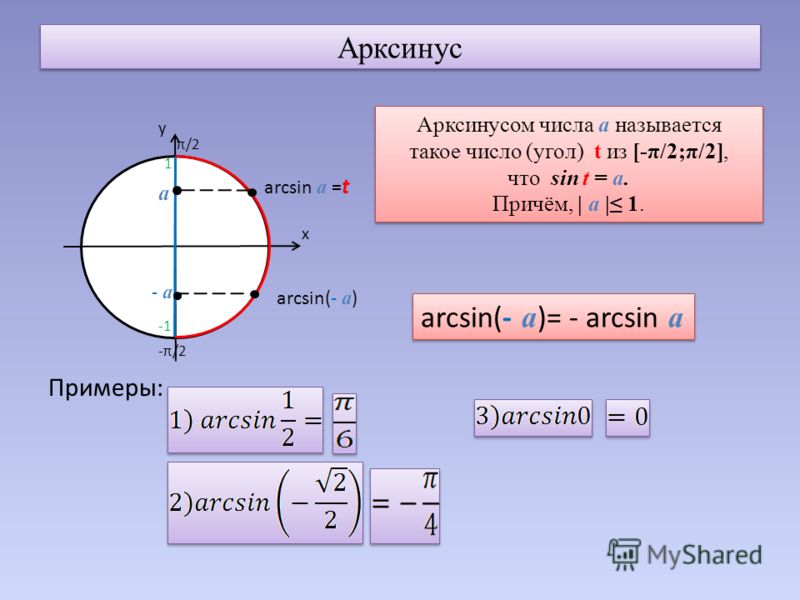 1071
1071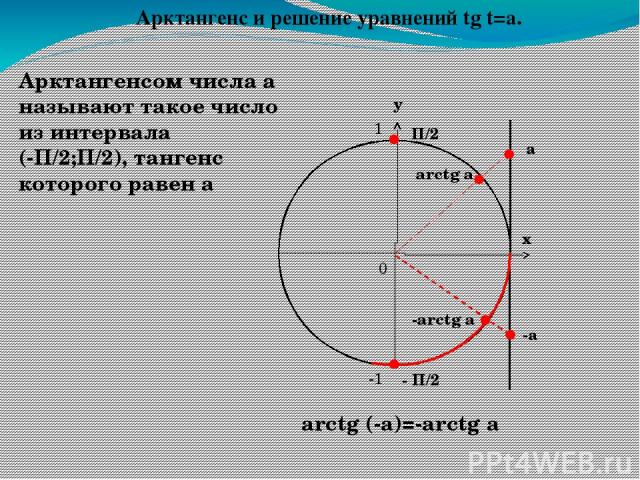 Вычитая прямой угол, равный 90°, мы получаем два непрямых угла, которые в сумме должны давать 9.0°. Таким образом, мы можем записать углы как arctan(x) и arctan(1/x).
Вычитая прямой угол, равный 90°, мы получаем два непрямых угла, которые в сумме должны давать 9.0°. Таким образом, мы можем записать углы как arctan(x) и arctan(1/x).