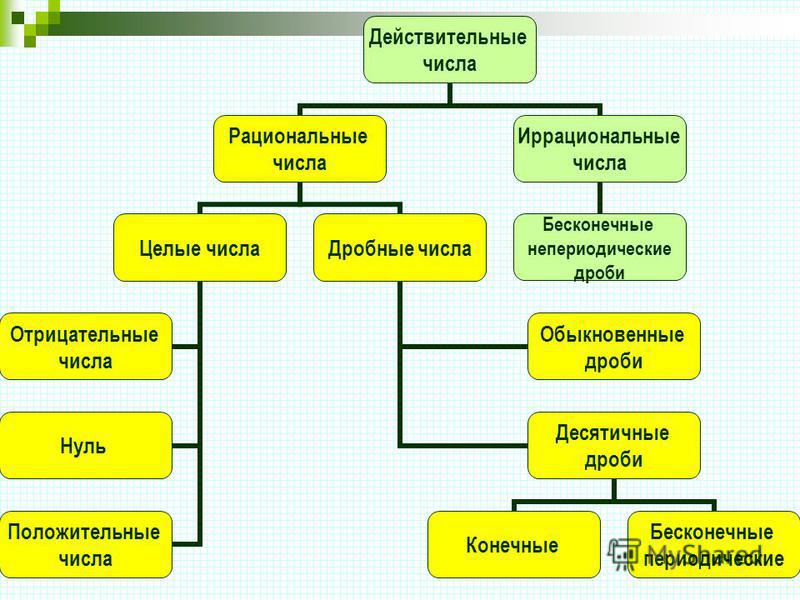
натуральный, рациональный, иррациональный, действительные числа, комплексный
Понимание чисел, особенно натуральных чисел, является одним из старейших математических «умений». Многие цивилизации, даже современные, приписывали числам некие мистические свойства ввиду их огромной важности в описании природы. Хотя современная наука и математика не подтверждают эти «волшебные» свойства, значение теории чисел неоспоримо.
Исторически сначала появилось множество натуральных чисел, затем довольно скоро к ним добавились дроби и положительные иррациональные числа. Ноль и отрицательные числа были введены после этих подмножеств множества действительных чисел. Последнее множество, множество комплексных чисел, появилось только с развитием современной науки.
В современной математике числа вводят не в историческом порядке, хотя и в довольно близком к нему.
Натуральные числа $\mathbb{N}$
Множество натуральных чисел часто обозначается как
$\mathbb{N}=\lbrace 1,2,3,4. .. \rbrace $, и часто его дополняют нулем, обозначая $\mathbb{N}_0$.
.. \rbrace $, и часто его дополняют нулем, обозначая $\mathbb{N}_0$.
В $\mathbb{N}$ определены операции сложения (+) и умножения ($\cdot$) со следующими свойствами для любых $a,b,c\in \mathbb{N}$:
1. $a+b\in \mathbb{N}$, $a\cdot b \in \mathbb{N}$ множество $\mathbb{N}$ замкнуто относительно операций сложения и умножения
2. $a+b=b+a$, $a\cdot b=b\cdot a$ коммутативность
3. $(a+b)+c=a+(b+c)$, $(a\cdot b)\cdot c=a\cdot (b\cdot c)$ ассоциативность
4. $a\cdot (b+c)=a\cdot b+a\cdot c$ дистрибутивность
5. $a\cdot 1=a$ является нейтральным элементом для умножения
Поскольку множество $\mathbb{N}$ содержит нейтральный элемент для умножения, но не для сложения, добавление нуля к этому множеству обеспечивает включение в него нейтрального элемента для сложения.
Кроме этих двух операций, на множестве $\mathbb{N}$ определены отношения «меньше» ($
1. $a b$ трихотомия
2. если $a\leq b$ и $b\leq a$, то $a=b$ антисимметрия
3. если $a\leq b$ и $b\leq c$, то $a\leq c$ транзитивность
4.
5. если $a\leq b$, то $a\cdot c\leq b\cdot c$
Целые числа $\mathbb{Z}$
Примеры целых чисел:
$1, -20, -100, 30, -40, 120…$
Решение уравнения $a+x=b$, где $a$ и $b$ — известные натуральные числа, а $x$ — неизвестное натуральное число, требует введения новой операции — вычитания(-). Если существует натуральное число $x$, удовлетворяющее этому уравнению, то $x=b-a$. Однако, это конкретное уравнение не обязательно имеет решение на множестве $\mathbb{N}$, поэтому практические соображения требуют расширения множества натуральных чисел таким образом, чтобы включить решения такого уравнения. Это приводит к введению множества целых чисел: $\mathbb{Z}=\lbrace 0,1,-1,2,-2,3,-3…\rbrace$.
Поскольку $\mathbb{N}\subset \mathbb{Z}$, логично предположить, что введенные ранее операции $+$ и $\cdot$ и отношения $
1. $0+a=a+0=a$ существует нейтральный элемент для сложения
Свойство 5. :
:
5. если $0\leq a$ и $0\leq b$, то $0\leq a\cdot b$
Множество $\mathbb{Z} $ замкнуто также и относительно операции вычитания, то есть $(\forall a,b\in \mathbb{Z})(a-b\in \mathbb{Z})$.
Рациональные числа $\mathbb{Q}$
Примеры рациональных чисел:
$\frac{1}{2}, \frac{4}{7}, -\frac{5}{8}, \frac{10}{20}…$
Теперь рассмотрим уравнения вида
$a\cdot x=b$, где $a$ и $b$ — известные целые числа, а $x$ — неизвестное. Чтобы решение было возможным, необходимо ввести операцию деления ($:$), и решение приобретает вид $x=b:a$, то есть $x=\frac{b}{a}$. Опять возникает проблема, что $x$ не всегда принадлежит $\mathbb{Z}$, поэтому множество целых чисел необходимо расширить. Таким образом вводится множество рациональных чисел $\mathbb{Q}$ с элементами $\frac{p}{q}$, где $p\in \mathbb{Z}$ и $q\in \mathbb{N}$. Множество $\mathbb{Z}$ является подмножеством, в котором каждый элемент $q=1$, следовательно $\mathbb{Z}\subset \mathbb{Q}$ и операции сложения и умножения распространяются и на это множество по следующим правилам, которые сохраняют все вышеперечисленные свойства и на множестве $\mathbb{Q}$:
$\frac{p-1}{q_1}\cdot \frac{p_2}{q_2}=\frac{p_1\cdot p_2}{q_1\cdot q_2}$
Деление вводится таким образом:
$\frac{p_1}{q_1}:\frac{p_2}{q_2}=\frac{p_1}{q_1}\cdot \frac{q_2}{p_2}$
На множестве $\mathbb{Q}$ уравнение $a\cdot x=b$ имеет единственное решение для каждого $a\neq 0$ (деление на ноль не определено). {-1}$:
{-1}$:
$(\forall a\in \mathbb{Q}\setminus\lbrace 0\rbrace)(\exists \frac{1}{a})(a\cdot \frac{1}{a}=\frac{1}{a}\cdot a=1)$
Порядок множества $\mathbb{Q}$ можно расширить таким образом:
Множество $\mathbb{Q}$ имеет одно важное свойство: между любыми двумя рациональными числами находится бесконечно много других рациональных чисел, следовательно, не существует двух соседних рациональных чисел, в отличие от множеств натуральных и целых чисел.
Иррациональные числа $\mathbb{I}$
Примеры иррациональных чисел:
$\sqrt{2} \approx 1.41422135…$
$\pi \approx 3.1415926535…$
Ввиду того, что между любыми двумя рациональными числами находится бесконечно много других рациональных чисел, легко можно сделать ошибочный вывод, что множество рациональных чисел настолько плотное, что нет необходимости в его дальнейшем расширении. Даже Пифагор в свое время сделал такую ошибку. Однако, уже его современники опровергли этот вывод при исследовании решений уравнения
$x\cdot x=2$ ($x^2=2$) на множестве рациональных чисел. 2=a$, где $a$ — известное рациональное число, а $x$ — неизвестное, не всегда имеет решение на множестве рациональных чисел, и опять возникает необходимость в расширении множества. Возникает множество иррациональных чисел, и такие числа как $\sqrt{2}$, $\sqrt{3}$, $\pi$… принадлежат этому множеству.
2=a$, где $a$ — известное рациональное число, а $x$ — неизвестное, не всегда имеет решение на множестве рациональных чисел, и опять возникает необходимость в расширении множества. Возникает множество иррациональных чисел, и такие числа как $\sqrt{2}$, $\sqrt{3}$, $\pi$… принадлежат этому множеству.
Действительные числа $\mathbb{R}$
Объединением множеств рациональных и иррациональных чисел является множество действительных чисел. Поскольку $\mathbb{Q}\subset \mathbb{R}$, снова логично предположить, что введенные арифметические операции и отношения сохраняют свои свойства на новом множестве. Формальное доказательство этого весьма сложно, поэтому вышеупомянутые свойства арифметических операций и отношения на множестве действительных чисел вводятся как аксиомы. В алгебре такой объект называется полем, поэтому говорят, что множество действительных чисел является упорядоченным полем.
Для того, чтобы определение множества действительных чисел было полным, необходимо ввести дополнительную аксиому, различающую множества
$\mathbb{Q}$ и $\mathbb{R}$.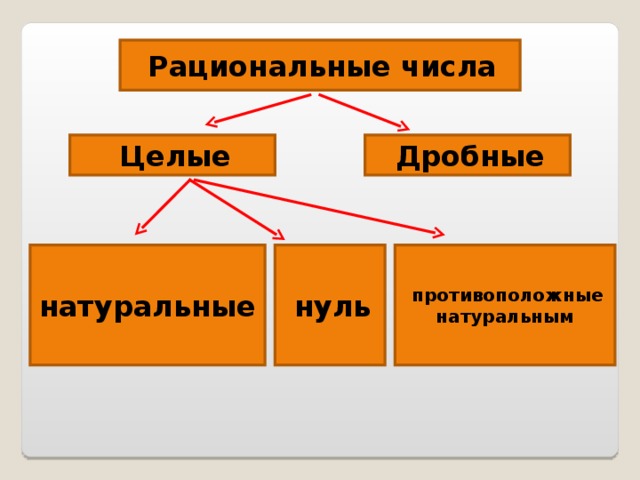 2=-1$. Расширение множества $\mathbb{R}$ на множество $\mathbb{C}$ позволяет определить квадратный корень из отрицательных чисел, что и послужило причиной введения множества комплексных чисел.
Также легко показать, что подмножество множества $\mathbb{C}$, заданное как $\mathbb{C}_0=\lbrace (a,0)|a\in \mathbb{R}\rbrace$, удовлетворяет всем аксиомам для действительных чисел, следовательно $\mathbb{C}_0=\mathbb{R}$, или $R\subset\mathbb{C}$.
2=-1$. Расширение множества $\mathbb{R}$ на множество $\mathbb{C}$ позволяет определить квадратный корень из отрицательных чисел, что и послужило причиной введения множества комплексных чисел.
Также легко показать, что подмножество множества $\mathbb{C}$, заданное как $\mathbb{C}_0=\lbrace (a,0)|a\in \mathbb{R}\rbrace$, удовлетворяет всем аксиомам для действительных чисел, следовательно $\mathbb{C}_0=\mathbb{R}$, или $R\subset\mathbb{C}$.
Алгебраическая структура множества $\mathbb{C}$ относительно операций сложения и умножения имеет следующие свойства:
1. коммутативность сложения и умножения
2. ассоциативность сложения и умножения
3. $0+i0$ — нейтральный элемент для сложения
4. $1+i0$ — нейтральный элемент для умножения
5. умножение дистрибутивно по отношению к сложению
6. существует единственный обратный элемент как для сложения, так и для умножения.
Урок 15. действительные числа — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №15. Действительные числа.
Действительные числа.
Перечень вопросов, рассматриваемых в теме
1) множество иррациональных чисел;
2) множество рациональных чисел;
3) правила выполнения действий с бесконечными десятичными дробями;
4)определение бесконечно убывающей геометрической прогрессии.
Глоссарий по теме
Рациональные числа – это такие числа, которые можно записать в виде обыкновенной дроби , где m — целое число, n — натуральное число , обозначаются буквой Q.
Иррациональные числа— это действительные числа, которые нельзя представить в виде обыкновенной дроби. Иррациональное число может быть представлено в виде бесконечной непериодической дроби, т.е. числа после запятой в записи данного числа не повторяются.
Дробные числа – это числа, которые можно записать в виде обыкновенной дроби.
Все основные действия над рациональными числами сохраняются и для действительных чисел (переместительный, сочетательный и распределительный законы, правила сравнения, правила раскрытия скобок и т.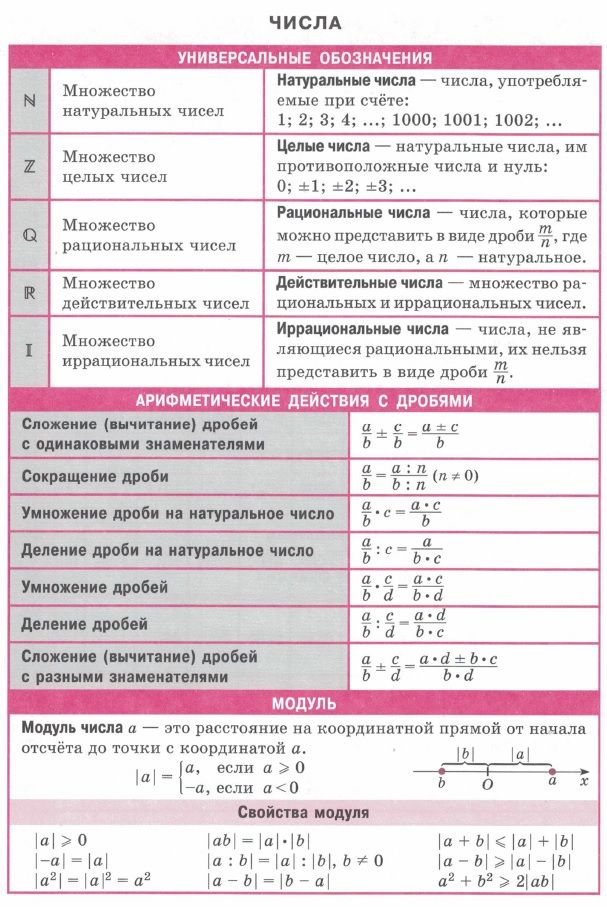 д.).
д.).
Арифметические операции над действительными числами обычно заменяются операциями над их приближениями.
Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Все числа, которые мы изучаем в школе, называются действительными числами. Они образуют множество действительных чисел, которые принято обозначать латинской буквой R.
В свою очередь все действительные числа можно разделить на 2 группы: рациональные числа и иррациональные числа.
Рациональные числа – это такие числа, которые можно записать в виде обыкновенной дроби , где m —целое число, n — натуральное число , обозначаются буквой Q.
Пример: -3; -0,5; .
Иррациональные числа— это действительные числа, которые нельзя представить в виде обыкновенной дроби. Иррациональное число может быть представлено в виде бесконечной непериодической дроби, т.е. числа после запятой в записи данного числа не повторяются.
Пример: π=3,141592…; 0, 113456… .
Рациональные числа, в свою очередь, можно разделить на 2 вида – это целые числа и дробные числа.
Дробные числа – это числа, которые можно записать в виде обыкновенной дроби.
Целые же числа можно разделить еще на несколько групп: отрицательные целые числа, нуль и положительные (натуральные) целые числа.
На числовой оси (Ох) между целыми числами будут находиться дробные иррациональные числа. Все вместе они будут представлять собой множество действительных чисел, R.
Обратите внимание, что все основные действия над рациональными числами сохраняются и для действительных чисел (переместительный, сочетательный и распределительный законы, правила сравнения, правила раскрытия скобок и т.д.).
Арифметические операции над действительными числами обычно заменяются операциями над их приближениями.
Числа 4; 4,2; 4,28 и т.д. являются последовательными приближениями значений суммы
.
Пусть это последовательные приближения действительного числа у с точностью до 1, до 0,1, до 0,01 и т.д. Тогда погрешность приближения как угодно близко приближается к нулю.
при или
Читается «модуль разности у и стремится к нулю при n, стремящемся к бесконечности» или «предел модуля разности у и при n, стремящемся к бесконечности, равен нулю»
Т.е. если при или
Модуль действительного числа у обозначается как |у| и определяется так же, как и модуль рационально числа:
.
А теперь давайте вспомним, что такое геометрическая прогрессия.
Рассмотрим квадрат со стороной, равной 1. Нарисуем ещё один квадрат, сторона которого равна половине первого квадрата, затем ещё один, сторона которого – половина второго, потом следующий и т.д. Каждый раз сторона нового квадрата равна половине предыдущего (Рисунок 1).
Рисунок 1
В результате, мы получили последовательность сторон квадратов образующих геометрическую прогрессию со знаменателем .
И, что очень важно, чем больше мы будем строить таких квадратов, тем меньше будет сторона квадрата. Например,
n=15, ;
n=20, ;
n=21, .
Т.е. с возрастанием номера n члены прогрессии приближаются к нулю.
Рассмотрим ещё один пример. Равносторонний треугольник со стороной равной 1см. Построим следующий треугольник с вершинами в серединах сторон 1-го треугольника, по теореме о средней линии треугольника – сторона 2-го равна половине стороны первого, сторона 3-го – половине стороны 2-го и т.д. Опять получаем последовательность длин сторон треугольников. (рисунок 2)
(рисунок 2)
Рисунок 2
Если рассмотреть геометрическую прогрессию с отрицательным знаменателем.
То, опять, с возрастанием номера n члены прогрессии приближаются к нулю.
Обратим внимание на знаменатели этих последовательностей. Везде знаменатели были меньше 1 по модулю.
Можно сделать вывод: геометрическая прогрессия будет бесконечно убывающей, если модуль её знаменателя меньше 1.
Определение:
Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы.
Используя данное определение можно решить вопрос о том, является ли геометрическая прогрессия бесконечно убывающей или нет.
Рассмотрим квадрат со стороной, равной 1. Разделим его пополам, одну из половинок ещё пополам и т.д. площади всех полученных прямоугольников при этом образуют бесконечно убывающую геометрическую прогрессию: (Рисунок 3)
Рисунок 3
Сумма площадей всех полученных таким образом прямоугольников будет равна площади 1-го квадрата и равна 1.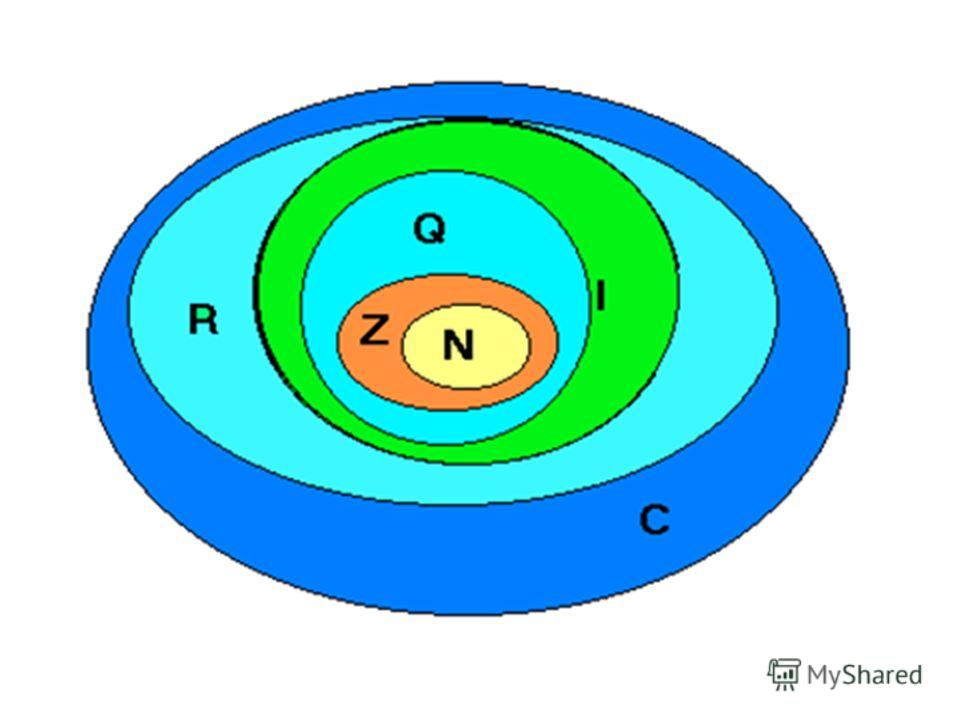
Но в левой части этого равенства – сумма бесконечного числа слагаемых.
Рассмотрим сумму n первых слагаемых.
По формуле суммы n первых членов геометрической прогрессии, она равна
Если n неограниченно возрастает, то
или . Поэтому , т.е. .
Сумма бесконечно убывающей геометрической прогрессии есть предел последовательности
Например, для прогрессии , где ,
имеем
Так как то
Сумму бесконечно убывающей геометрической прогрессии можно находить по формуле
Примеры и разборы решений заданий тренировочного модуля
Пример 1:
Воспользуемся калькулятором:
Найдем значение данного выражения с точностью до единиц.
Округлим полученные результаты до десятых:
Тогда получаем:
Найдем значение данного выражения с точностью до десятых.
Округлим полученные результаты до сотых:
3
Тогда получаем:
Найдем значение данного выражения с точностью до сотых.
Округлим полученные результаты до тысячных:
32
Тогда получаем:
и т.д.
Пример 2.
Давайте выясним, является ли последовательность бесконечно убывающей геометрической прогрессией, если она задана формулой:
а) ; б)
Решение:
. Найдем q.
;;
Следовательно, данная геометрическая прогрессия является бесконечно убывающей.
б)
Следовательно, данная последовательность не является бесконечно убывающей геометрической прогрессией.
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.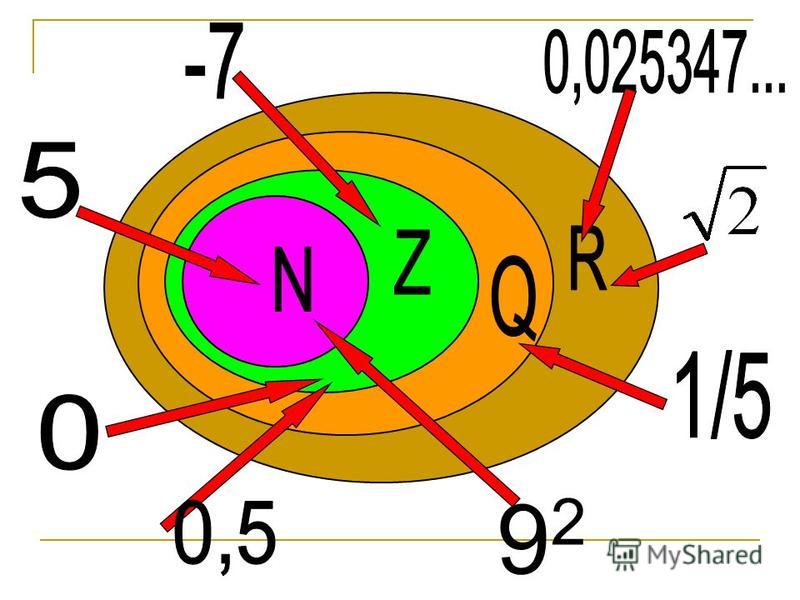 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град.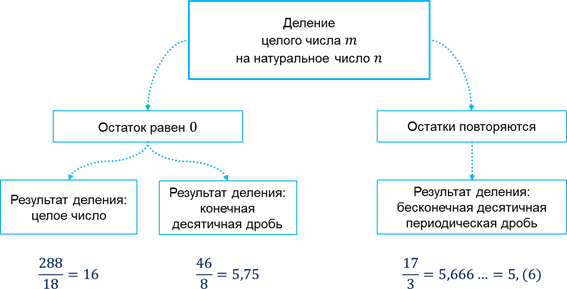 ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град.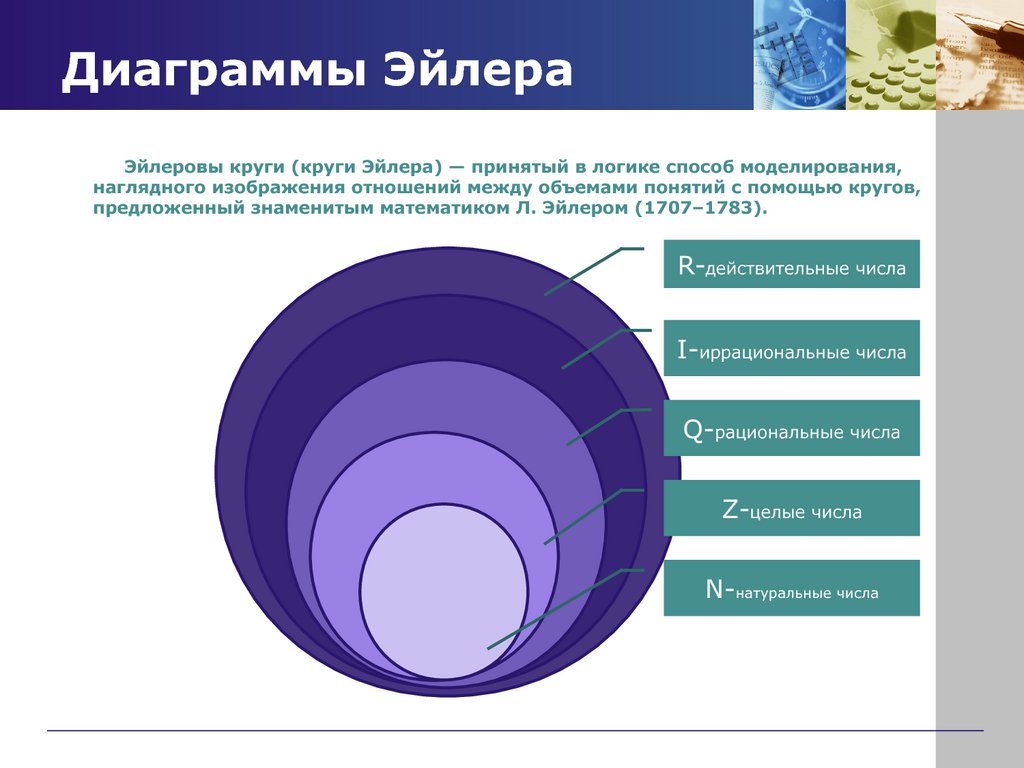 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Чем отличается натуральное число от целого
Математика
Это числа, которые используются при счете: 1, 2, 3. и т.д.
Ноль не является натуральным.
Натуральные числа принято обозначать символом N.
Целые числа. Положительные и отрицательные числа
Два числа отличающиеся друг от друга только знаком, называются противоположными, например, +1 и -1, +5 и -5. Знак «+» обычно не пишут, но предполагают, что перед числом стоит «+». Такие числа называются положительными. Числа, перед которыми стоит знак «-«, называются отрицательными.
Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.
Рациональные числа
Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.
Иррациональные числа
Бесконечная непериодическая дробь называется иррациональным числом. Например:
Множество иррациональных чисел обозначается J.
Действительные числа
Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.
Действительные числа обозначаются символом R.
Округление чисел
Рассмотрим число 8,759123. . Округлить до целой части означает записать лишь ту часть числа, которая находится до запятой. Округлить до десятых означает записать целую часть и после запятой одну цифру; округлить до сотых — после запятой две цифры; до тысячных — три цифры и т.д.
Числа: натуральные, целые, рациональные, иррациональные, действительные
Натуральные числа определение – это целые положительные числа. Натуральные числа используют для счета предметов и многих иных целей. Вот эти числа:
Это натуральный ряд чисел.
Ноль натуральное число? Нет, ноль не является натуральным числом.
Сколько натуральных чисел существует? Существует бесконечное множество натуральных чисел.
Каково наименьшее натуральное число? Единица — это наименьшее натуральное число.
Каково наибольшее натуральное число? Его невозможно указать, ведь существует бесконечное множество натуральных чисел.
Сумма натуральных чисел есть натуральное число.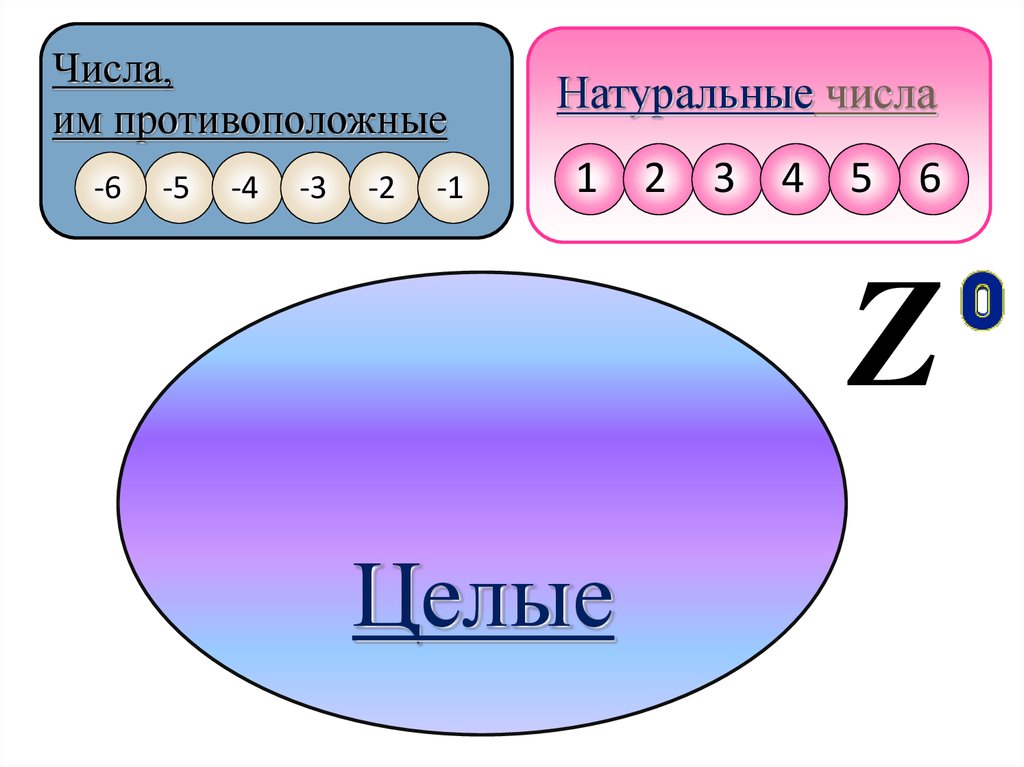 Итак, сложение натуральных чисел a и b:
Итак, сложение натуральных чисел a и b:
с — это всегда натуральное число.
Произведение натуральных чисел есть натуральное число. Итак, произведение натуральных чисел a и b:
с — это всегда натуральное число.
Разность натуральных чисел Не всегда есть натуральное число. Если уменьшаемое больше вычитаемого, то разность натуральных чисел есть натуральное число, иначе — нет.
Частное натуральных чисел Не всегда есть натуральное число. Если для натуральных чисел a и b
где с — натуральное число, то это значит, что a делится на b нацело. В этом примере a — делимое, b — делитель, c — частное.
Делитель натурального числа — это натуральное число, на которое первое число делится нацело.
Каждое натуральное число делится на единицу и на себя.
Простые натуральные числа делятся только на единицу и на себя. Здесь имеется ввиду делятся нацело. Пример, числа 2; 3; 5; 7 делятся только на единицу и на себя. Это простые натуральные числа.
Единицу не считают простым числом.
Числа, которые больше единицы и которые не являются простыми, называют составными. Примеры составных чисел:
Единицу не считают составным числом.
Множество натуральных чисел составляют единица, простые числа и составные числа.
Множество натуральных чисел обозначается латинской буквой N.
Свойства сложения и умножения натуральных чисел:
переместительное свойство сложения
сочетательное свойство сложения
переместительное свойство умножения
сочетательное свойство умножения
распределительное свойство умножения
Целые числа
Целые числа — это натуральные числа, ноль и числа, противоположные натуральным.
Числа, противоположные натуральным — это целые отрицательные числа, например:
Множество целых чисел обозначается латинской буквой Z.
Рациональные числа
Рациональные числа — это целые числа и дроби.
Любое рациональное число может быть представлено в виде периодической дроби. Примеры:
Из примеров видно, что любое целое число есть периодическая дробь с периодом ноль.
Любое рациональное число может быть представлено в виде дроби m/n, где m целое число,n натуральное число. Представим в виде такой дроби число 3,(6) из предыдущего примера:
Другой пример: рациональное число 9 может быть представлено в виде простой дроби как 18/2 или как 36/4.
Ещё пример: рациональное число -9 может быть представлено в виде простой дроби как -18/2 или как -72/8.
Множество рациональных чисел обозначается латинской буквой Q.
Подробнее о рациональных числах в разделе Рациональные числа.
Иррациональные числа
Иррациональные числа — это бесконечные непериодические десятичные дроби. Примеры:
Реальные числа и целые числа 2022
Математики разработали системы для определения того, как определенное число отличается от другого. Как и другие понятия, категории номеров перекрываются. Поскольку действительные числа включают в себя все рациональные числа, такие как целые числа, они имеют сходные характеристики, такие как использование целых чисел и построение на числовой строке. Следовательно, ключевым отличием является то, что реальные числа являются общей классификацией, а целые — подмножеством, которое характеризуется целыми числами, которые могут иметь отрицательные свойства.
Следовательно, ключевым отличием является то, что реальные числа являются общей классификацией, а целые — подмножеством, которое характеризуется целыми числами, которые могут иметь отрицательные свойства.
Что такое реальные цифры?
Реальные числа — это значения, которые вы можете найти на числовой строке, которая обычно выражается как геометрическая горизонтальная линия, где выбранная точка функционирует как «начало». Те, которые падают с правой стороны, обозначаются как положительные, а те, что слева, отрицательны. Описание «настоящего» было представлено Рене Декарт, известным математиком и философом в 17 веке. В частности, он установил разницу между реальными корнями полиномов и их мнимыми корнями.
Реальные числа включают целые, целые, естественные, рациональные и иррациональные числа:
- Целые числа
Целые числа — это положительные числа, которые не имеют дробных частей и десятичных точек, поскольку они представляют целые объекты без фрагментов или кусков.
- Целые
Целые числа — это целые числа, которые включают отрицательную сторону числовой линии.
- Естественные числа
Также известные как подсчет чисел, натуральные числа похожи на целые числа, но нуль не включается, поскольку ничто не может быть по существу подсчитано как «0».
- Рациональное число
Что касается его происхождения, Пифагор, древнегреческий математик, провозгласил, что все числа являются рациональными. Рациональные числа — это частные или дробные числа двух целых чисел. Где p и q — оба целых числа, а q не эквивалентен нулю, p / q — рациональное число. Например, 3/5 — это рациональное число, но 3/0 — нет.
- Иррациональные числа
Студент Пифагора, Гиппас не согласился с тем, что все цифры были рациональными. Через геометрию он доказал, что некоторые числа иррациональны. Например, квадратный корень из двух, который равен 1.41, не может быть выражен как дробь; следовательно, он иррационален. К сожалению, действительность рациональных чисел не была принята последователями Пифагора. Это привело к тому, что Гиппас утонул в море, которое, как говорили, было наказанием богов за это время.
К сожалению, действительность рациональных чисел не была принята последователями Пифагора. Это привело к тому, что Гиппас утонул в море, которое, как говорили, было наказанием богов за это время.
Что такое целые числа?
Из латинского слова «integer», которое переводится как «целое» или «нетронутое», эти числа не имеют дробных или десятичных компонентов, как целые числа. Числа включают положительные натуральные числа или числа подсчета и их негативы. Например, -3, -2, -1, 0, -1, 2, 3 являются целыми числами. Обычная иллюстрация — равномерно распределенные числа на бесконечной числовой линии с нулем, которая не является ни положительной, ни отрицательной, посередине. Следовательно, положительные результаты больше отрицательных.
Что касается его истории, следующие учетные записи отслеживают, как были применены целые числа:
- В 200 г. до Р.Х. отрицательные числа были сначала представлены красными стержнями в Древнем Китае.
- Примерно в 630 году А. Д.
 , отрицательные числа были использованы для представления долга в Индии.
, отрицательные числа были использованы для представления долга в Индии. - Арбермут Хольст, немецкий математик, вводил целые числа в 1563 году как система в дополнение и умножение. Он разработал систему как ответ на растущее число кроликов и слонов, на которых он экспериментировал.
Ниже приведены характеристики целых чисел:
- положительный
Числа в правой части числовой линии положительны, и они часто представляют собой более высокую ценность их отрицательных копий.
- отрицательный
Числа в левой части числовой линии часто рассматриваются как меньшее стандартное значение их положительных аналогов.
- нейтральный
Центр числовой линии, нуль — это целое число, которое не является ни положительным, ни отрицательным.
- Без фрагментов
Подобно целым числам, целые числа не имеют десятичных точек и дробей.
Разница между реальными числами и целыми числами
Объем реальных чисел и целых чисел
Реальные числа включают целые числа, рациональные, иррациональные, естественные и целые числа. С другой стороны, область целых чисел в основном касается целых чисел, которые являются отрицательными и положительными. Следовательно, действительные числа более общие.
С другой стороны, область целых чисел в основном касается целых чисел, которые являются отрицательными и положительными. Следовательно, действительные числа более общие.
Фракции
Реальные числа могут включать в себя такие фракции, как рациональные и иррациональные числа. Однако дроби не могут быть целыми числами.
Свойство с наименьшей границей
Реальные числа имеют свойство с наименьшим верхним пределом, которое также известно как «полнота». Это означает, что линейный набор действительных чисел имеет подмножества с супремумальными качествами. Напротив, целые числа не обладают свойством наименьшей верхней границы.
Архимедовое имущество
Архимедовое свойство, являющееся предположением о том, что существует натуральное число, равное или большее любого действительного числа, может быть применено к действительным числам. Напротив, Архимедовое свойство не может быть применено к целым числам.
Реальные числа — это своеобразное поле, которое является существенной алгебраической структурой, в которой определены арифметические процессы. Напротив, целые числа не рассматриваются как поле.
Напротив, целые числа не рассматриваются как поле.
Счетный
В качестве набора действительные числа несчетны, а целые числа являются счетными.
Символы действительных чисел и целых чисел
Реальные числа обозначаются как «R», а набор целых чисел — «Z». N. Bourbaki, группа французских математиков 1930-х годов, указала «Z» на немецкое слово «Zahlen», что означает число или целые числа.
Происхождение слова для реальных чисел и целых чисел
Реальные числа обозначают вещественные корни многочленов, а целое число — латинское слово, «целое», поскольку они не включают десятичные числа и дроби.
Реальные числа против целых чисел
Резюме действительных чисел против целых чисел
- На числовой строке могут отображаться как действительные числа, так и целые числа.
- Целые числа — это подмножество вещественных чисел.
- Целые числа имеют отрицательные числа.
- В качестве набора реальные числа имеют более общий масштаб по сравнению с целыми числами.

- В отличие от целых чисел, действительные числа могут содержать дроби и десятичные точки.
- Свойства наименее связанного, архимедова и поля обычно применимы к действительным числам, но не к целым числам.
- В отличие от действительных чисел, целые числа являются строго счетными.
- «R» означает действительные числа, а «Z» — для целых чисел.
Рекомендуем
Различия между арабским и фарси
Разница между вашим и вами
Разница между CIF и FOB
Рекомендуем
Различия между ADA и IDEA
ADA против IDEA Чтобы иметь порядок и порядочность, законы создаются. Первый закон, когда-либо написанный, — это 10 заповедей. Создатель считал законы необходимыми, чтобы избежать хаоса и конфликтов между Его людьми. Если законы не соблюдаются, эквивалентное наказание будет исполнено по закону. В нашем мире сегодня больше и
Разница между переговорами и арбитражем
Переговоры против Арбитража Арбитраж и переговоры — это две формы процессов, связанных с разрешением споров между двумя сторонами. Эти две формы урегулирования споров являются частью соответствующих мер разрешения споров (также известных как ДОПОГ), используемых в качестве альтернативы судебному разбирательству или судебному разбирательству. Случаи отставания в
Эти две формы урегулирования споров являются частью соответствующих мер разрешения споров (также известных как ДОПОГ), используемых в качестве альтернативы судебному разбирательству или судебному разбирательству. Случаи отставания в
Числовые множества N,Z,Q,R
Текст 1. Числовые множества
N = {1; 2; 3; …; n; …} – множество всех натуральных чисел.
Z = {… — 3; — 2; — 1; 0; 1; 2; 3; …} – множество всех целых чисел. Q = { (m∈Z, n∈ N)} – множество всех рациональных чисел.
R – множество всех действительных чисел.
N ⊂ Z ⊂ Q ⊂ R
Задание 1. 1) Смотрите, слушайте и повторяйте текст 1.
2) Читайте текст. 3) Пишите текст. 4) Выучите текст.
Задание 2. 1)Смотрите, слушайте и повторяйте:
1 – натуральное число.
1, 2, 3, … , n, … – натуральные числа.
N= {1; 2; 3; …; n; …} – множество всех натуральных чисел.
1∈ N, 2∈N, 0∉N, – 2 ∉ N.
2) Читайте. 3) Пишите. 4) Ответьте на вопросы:
а) Какой буквой обозначают множество всех натуральных чисел?
б) Какое множество обозначают буквой N? в) Какое самое маленькое натуральное число? г) Какое самое большое натуральное число? д) Сумма двух натуральных чисел – натуральное число? е) Разность двух натуральных чисел – тоже натуральное число?
Задание 3. 1)Смотрите, слушайте и повторяйте:
1)Смотрите, слушайте и повторяйте:
-2 – целое число.
2; 0; 2 – целые числа.
Z = {… — 3; — 2; — 1; 0; 1; 2; 3; …} – множество всех целых чисел.
1∈ Z, — 1∈Z, 0∈Z, ½∉Z.
2) Читайте. 3) Пишите. 4) Ответьте на вопросы: а) Какой буквой обозначают множество всех целых чисел? б) Какое множество обозначают буквой Z? в) Разность двух целых чисел – целое число? г) Частное двух целых чисел – тоже целое число?
Задание 4. 1) Смотрите, слушайте и повторяйте:
½ рациональное число.
3½; ⅔; 1,215; 0; — 7 рациональные числа.
Числа вида (m∈Z, n∈N) это рациональные числа. Рациональные числа можно записать в виде (m∈ Z, n∈N). Q = { (m∈Z, n∈N)} – множество всех рациональных чисел.
-1⅔∈Q; 6,723∈Q; 5∈Q; 3 (корень из трёх)∉Q.
2) Читайте. 3) Пишите. 4) Ответьте на вопросы: а) Какой буквой обозначают множество всех рациональных чисел? б) Какое множество обозначают буквой Q? в) Какие числа называют рациональными? г) Почему числа -1⅔; 6,723; 5 – рациональные?
Задание 5. 1) Смотрите, слушайте и повторяйте:
1) Смотрите, слушайте и повторяйте:
Если число нельзя записать в виде (m∈Z, n∈N), то это
иррациональное число. 3 = 1, 73205…; — 2 = — 1,41421…;
е = 2,71828…; π (пи) = 3,14159…– иррациональные числа.
Иррациональные числа – бесконечные непериодические
десятичные дроби.
Рациональные и иррациональные числа образуют множество всех действительных чисел R.
2) Читайте. 3) Пишите. 4) Ответьте на вопросы: а) Какой буквой обозначают множество всех действительных чисел? б) Какое множество обозначают буквой R? в) Какие числа образуют
множество R? г) Какие из следующих чисел действительные: 0; 5⅜;
-9,02; — ; − ; е; 10; 12,5?
Задание 6. Рассмотрите схему и опишите её:
√3
-√2
π
Задание 7. Поставьте знак Ѓ или ∉:
-2 … Z 4 16 … Z π …R – … R
0 … N 3 …Q – … Q 0,175 … Q
100 … N 5,5 …Q − …R е … R
Задание 8. Выпишите: 1) рациональные числа; 2) иррациональные числа:
Выпишите: 1) рациональные числа; 2) иррациональные числа:
25 ; 17 ;
3
; 0; – 6; — 2 ; 3,6; 0,6666… ; 0,313131… ;
7
0,272272227… ; 5 .
Задание 9. Выполните действия:
1) N ∩ Z; 2) N U Z; 3) Q ∩ Z; 4) Z U Q; 5) N U R; 6)R∩N;
7) N ∩ Q; 8) R∩ Q; 9) Q U R; 10) Z ∩ Q.
Задание 10. Ответьте на вопросы:
1) Чему равно пересечение множеств рациональных и иррациональных чисел?
2) Чему равно объединение множеств рациональных и иррациональных чисел?
Задание 11. Назовите несколько элементов множества:
1) натуральных чисел; 2) положительных чисел; 3) отрицательных
чисел; 4) целых чисел; 5) рациональных чисел; 6) иррациональных чисел; 7) действительных чисел; 8) недействительных чисел.
Задание 12. Скажите, верны или нет следующие утверждения.
Приведите примеры.
1) Целые числа состоят из натуральных чисел, нуля и чисел,
противоположных натуральным. 2) Рациональные числа состоят из
p
целых чисел и дробей вида
, где р – целое, q – натуральное. q
3) Рациональные числа – это бесконечные периодические десятичные дроби. 4) Иррациональные числа – это бесконечные непериодические десятичные дроби. 5) Действительные числа – это бесконечные десятичные дроби. 6) Квадратный корень из рационального числа всегда иррациональное число.
Слова и словосочетания:
натуральное число действительное число целое число периодическая дробь рациональное число десятичная дробь иррациональное число
Материал взят из книги Начальный курс по математике для студентов-иностранцев подготовительных факультетов (Т.А. Полевая)
Рациональные и иррациональные числа доклад, проект
8 класс
Рациональные, иррациональные, действительные числа.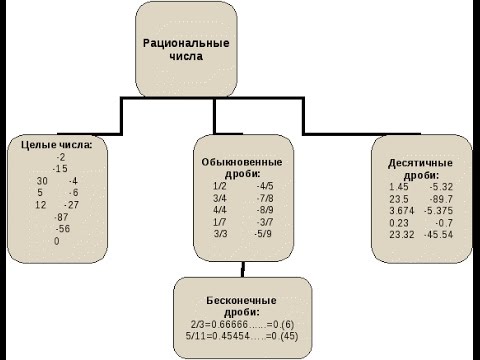 Числовые множества.
Числовые множества.
План
Множество
Натуральные числа
Целые числа
Рациональные числа
Рациональные числа в виде дроби
Преобразование обыкновенной дроби в десятичную
Иррациональные числа
Действительные числа
Выберите правильные утверджения
Сравните
Вычислите
Сравните
Множество
Понятие “множество” принадлежит к одному из первичных понятий математики. Множество можно представить как савокупность некоторых предметов, объединенных по некоторым свойствам.
Пример : множество учеников отдельного класса, множество букв алфавита, множество точек на прямой.
Предметы, из которых состоит множество, называются ее элементами.
Пример: Петя из 5-А класса; электрочайник — элемент множества кухонной техники.
Что такое число и натуральные числа
Математика изучает количественные отношенния и пространственные формы реального мира, для которых основным измерением является число. Понятие “число” появилось тогда, когда люди отделили его от реальных объектов и их особенностей.
Понятие “число” появилось тогда, когда люди отделили его от реальных объектов и их особенностей.
Натуральные числа– числа, которые используют при счете предметов. Натуральных чисел бесконечное количество. Их записывають с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Значит, с помощью десяти цифр можно записать числа, которые используют при счете предметов , в некоторую савокупность. Такие числа образуют множество натуральных чисел. А сами числа называють ее элементами.
Термин “натуральное число” происходит от латинского слова NATURA – природа. Обозначают это множество – N.
N={ 1, 2, 3 …} – это бесконечное множество.
То, что число принадлежит или не принадлежит множеству натуральных чисел, записывают так:-15 N, 10 € N
N
1 2 3 4
Целые числа
При сложении и умножении натуральных чисел всегда получают натуральное число. При этом при их вычитании не всегда получают натуральное число.
При этом при их вычитании не всегда получают натуральное число.
Пример: 13-15=-2, 10-10=0; числа -2 и 0 не натуральные.
Чтобы всегда выполнялось действие вычитание, ввели отрицательные числа и 0.
Множество натуральных чисел расширили до множества целых чисел.
+1, +2, +3…
-1, -2, -3, 0…
Что такое целые числа
Термин “целое число” происходит от немецкого слова Zahlen — считать; обозначается буквою Z.
Z= { … -3, -2, -1, 0, 1, 2 …} – это бесконечное множество.
Пример: -205 N, але -205 Z, 2055 N, 2055 Z.
Целые числа – это натуральные числа, им противоположные числа и 0.
Если к множеству N присоединить число 0 , то получим новое множество, которое називают множеством неотрицательных целых чисел и записывают Z+ ={ 0, 1, 2, … }
N
1 2 3 4 5
Z
-2 -1 0 1 2 3 4 5
Рациональные числа
При сложении, умножении, вычитании целых чисел всегда получают целое число. Однако при делении двух целых чисел не всегда получают целое число.
Однако при делении двух целых чисел не всегда получают целое число.
Пример: 20:6=3 (ост. 2), то есть деление чисел 20 і 6 невозможно выполнить в множестве целых чисел.
Если расширить множество целых чисел, дополнив его дробными, то в этом расширенном множестве будут выполняться четыре арифметических действия.
Мы пришли к такому числовому множеству, в котором содержатся все целые и дробные (положительные и отрицательные) числа. Его называють множеством рациональных чисел.
Термин “рациональное число” происходит от
латинского слова Ratio – отношение (частное).
Множество рациональных чисел обозначают– Q.
Рациональные числа в виде дроби
Число, которое можно представить в виде дроби , где m – целое число, n – натуральное, называется рациональным числом .
Любое рациональное число можно разными способами представить в виде дроби.
Пример: ; ;
Среди равных дробей всегда можно найти дробь, знаменатель которой наименший. Такая дробь называется несокротимой.
Такая дробь называется несокротимой.
Примером множества рациональных чисел будет
множество : А={ 20; -5,2; -1; 0; 3; 8,4…}
Некоторые элементы этого множества принадлежат только множеству рациональных чисел, однако есть и такие, которые приналежат множеству целых и натуральних чисел.
-1 Q; -1 N; -1 Z; 20 Q; 20 Z; 20 N.
Рациональные числа. Преоразование обыкновенной дроби в десятичную
Для преоразование обыкновенной дроби в десятичную, используют действие деление m:n. Таким образом,
При этом бывают случаи, когда деление 1) заканчивается через несколько шагов; 2) повторяются через несколько шагов; 3) преоразовывается в бесконечное повторение одной и то же самой савокупности цифр. То, что при делении повторяется один и тот же остаток и одни и те же числа в частном, называють периодичностью дроби, а савокупность цифр, что повторяется, называють периодом дроби. В записи периодичних десятичных дробей период пишут один раз, взявши его в круглые скобки.
В записи периодичних десятичных дробей период пишут один раз, взявши его в круглые скобки.
Запись читают так:
0 целых 3 в периоде; мінус 0 целых 81 в периоде; 0 цілих 58 сотих и 3 у периоде.
Рациональные числа. Переобразование обыкновенной дроби в десятичную.
Каждую дробь , де m Z , n N , можно представить в виде конечной десятичной дроби или в виде бесконечной периодической десятичной дроби.
Кождую конечную десятичную дробь можно записать в виде бесконечной дроби, приписывая справа бесконечное количество нулей. 2,7=2,7000…=2,7(0).
N
1 2 3 4 5
Z
-2 -1 0 1 2 3 4 5
Q
-2,5 -2 -1 0 1 2 3 4 5
Иррациональные числа
Уже пифагорийцы знали, что квадрат гипотенузы равен сумме квадратов катетов. Знали, что когда сторона квадрата равна 1, то его диагональ должна выражаться таким числом, квадрат которого равен 2. А среди рациональных чисел такого числа не существует. Они не догадались ввести иррациональные числа и сделали вывод: если сторона квадрата 1, то длина его диагонали не равна никакому числу!!! ТО есть, существуют отрезки, которые не имеют длины!!! Это привело к кризису математической науки, который длился много столетий, пока ученые не ввели иррациональные числа. Значит, иррациональные числа – бесконечные непериодические десятичные
Знали, что когда сторона квадрата равна 1, то его диагональ должна выражаться таким числом, квадрат которого равен 2. А среди рациональных чисел такого числа не существует. Они не догадались ввести иррациональные числа и сделали вывод: если сторона квадрата 1, то длина его диагонали не равна никакому числу!!! ТО есть, существуют отрезки, которые не имеют длины!!! Это привело к кризису математической науки, который длился много столетий, пока ученые не ввели иррациональные числа. Значит, иррациональные числа – бесконечные непериодические десятичные
дроби. √2≈1,41421356… π≈3,1415926…
Бесконечные десятичные дроби
периодические непериодические
Рациональные числа иррациональные числа
Действительные числа
Множество всех рациональных и иррациональных чисел називают множеством действительных чисел. Множество обозначають буквой R , от английского слова Real, немецкого Reel – действительный. Некоторые элементы этого множества принадлежат лишь множеству действительных чисел, однако есть такие, которые приналежат множеству рациональных чисел.
Множество обозначають буквой R , от английского слова Real, немецкого Reel – действительный. Некоторые элементы этого множества принадлежат лишь множеству действительных чисел, однако есть такие, которые приналежат множеству рациональных чисел.
Тогда,N Z Q R.Поскольку каждая точка числовой прямой определяет некоторое действительное число и, наоборот, каждое действительное число имеет место на числовой прямой, то множество действительных чисел R образуют числовую прямую.
N
1 2 3 4 …
Z
-2 -1 0 1 2 3 4 …
Q
-2 -1 0 1 2 3 4 …
R
-∞ -2 -1 0 1 2 3 4 +∞
Выберите правильные утверджения
мм
Сравните
>
>
Вычислите
Сравните
>
>
>
Набор чисел (Действительные, целые, рациональные, натуральные и иррациональные числа)
В этом разделе мы дадим краткое, но более содержательное введение в понятия наборов чисел, причем набор действительных чисел является наиболее важным, и обозначается через $$\mathbb{R}$$.
Но сначала, чтобы перейти к действительным числам, мы начнем с множества натуральных чисел.
Натуральные числа $$\mathbb{N}$$
Натуральные числа – это числа, которые с незапамятных времен использовались для счета. В большинстве стран они переняли арабские цифры, названные так потому, что арабы привезли их в Европу, но они были изобретены в Индии.
Множество натуральных чисел обозначается как $$\mathbb{N}$$; Итак:
$$$\mathbb{N}=\{1,2,3,4,5,6\ldots\}$$$
Натуральные числа характеризуются двумя свойствами:
- Число 1 равно первое натуральное число и каждое натуральное число образуется путем прибавления 1 к предыдущему.
- Когда мы вычитаем или делим два натуральных числа, результат не обязательно является натуральным числом, поэтому мы говорим, что натуральные числа не замыкаются при выполнении этих двух операций. Натуральные числа замкнуты только при сложении и умножении, т. е. сложение или умножение двух натуральных чисел всегда приводит к другому натуральному числу.

Целые числа $$\mathbb{Z}$$
Когда возникает необходимость отличать одни значения от других по эталонной позиции, в игру вступают отрицательные числа. Например, когда от уровня 0 (уровень моря) мы различаем выше уровня моря или глубокого моря. Или в случае отрицательных или положительных температур. То есть мы можем быть на высоте 700м, $$+700$$, или нырнуть на 10м в глубину, $$-10$$, а может быть около 25 градусов $$+25$$, или 5 градусов ниже 0, $$-5$$.
Для обозначения отрицательных чисел мы добавляем знак минус перед числом.
Короче говоря, набор, образованный отрицательными целыми числами, числом ноль и положительными целыми числами (или натуральными числами), называется набором целых чисел.
Они обозначаются символом $$\mathbb{Z}$$ и могут быть записаны как:
$$$\mathbb{Z}=\{\ldots,-2,-1,0,1,2 ,\ldots\}$$$
Представим их на числовой прямой следующим образом:
Важным свойством целых чисел является то, что они замкнуты относительно сложения, умножения и вычитания, то есть любого сложения, вычитания и умножения из двух целых чисел получается другое целое число. Обратите внимание, что частное двух целых чисел, например $$3$$ и $$7$$, не обязательно является целым числом. Таким образом, множество не замыкается при делении.
Обратите внимание, что частное двух целых чисел, например $$3$$ и $$7$$, не обязательно является целым числом. Таким образом, множество не замыкается при делении.
Рациональные числа $$\mathbb{Q}$$
Рациональные числа — это числа, которые можно представить как деление двух целых чисел. Множество рациональных чисел обозначается как $$\mathbb{Q}$$, поэтому:
$$$\mathbb{Q}=\Big\{\dfrac{p}{q} \ | \ p,q \in\mathbb{Z} \Big\}$$$
Результатом рационального числа может быть целое число ($$-\dfrac{8}{4}=-2$$) или десятичное ($$\dfrac{6}{5}=1,2$$) число, положительное или отрицательное. Кроме того, среди десятичных дробей есть два разных типа: один с ограниченным количеством цифр, который называется точной десятичной дробью ($$\dfrac{88}{25}=3,52$$), а другой с неограниченным количеством цифр. цифр, которые называются повторяющимися десятичными числами ($$\dfrac{5}{9}=0,5555\ldots=0,\widehat{5}$$).
Мы называем их повторяющимися десятичными дробями, потому что некоторые цифры в десятичной части повторяются снова и снова. Если только повторяющиеся цифры начинаются с десятого, мы называем их чистыми повторяющимися десятичными знаками ($6,8888\ldots=6,\widehat{8}$$), в противном случае мы называем их смешанными повторяющимися десятичными знаками ($3,415626262\ldots=3,415\). широкий{62}$$).
Если только повторяющиеся цифры начинаются с десятого, мы называем их чистыми повторяющимися десятичными знаками ($6,8888\ldots=6,\widehat{8}$$), в противном случае мы называем их смешанными повторяющимися десятичными знаками ($3,415626262\ldots=3,415\). широкий{62}$$).
Обратите внимание, что каждое целое число является рациональным числом, поскольку, например, $$5=\dfrac{5}{1}$$; следовательно, $$\mathbb{Z}$$ является подмножеством $$\mathbb{Q}$$. Точно так же каждое натуральное число также является целым числом, в частности положительным целым числом. Таким образом имеем:
$$$\mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}$$$
Рациональные числа замкнуты не только относительно сложения, умножения и вычитания, но и деления (кроме $ $0$$).
Иррациональные числа $$\mathbb{I}$$
Мы видели, что любое рациональное число может быть представлено как целое, десятичное или точное десятичное число.
Однако не все десятичные числа являются точными или повторяющимися десятичными числами, и поэтому не все десятичные числа могут быть выражены в виде доли двух целых чисел.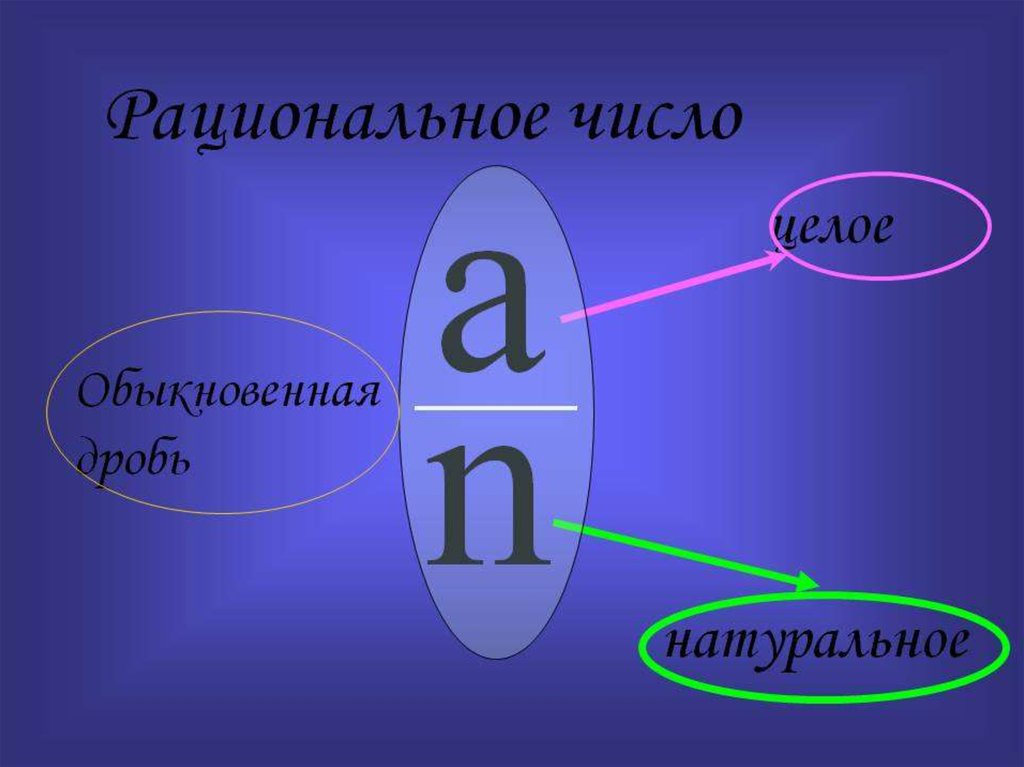
Эти десятичные числа, которые не являются ни точными, ни повторяющимися десятичными числами, характеризуются бесконечными непериодическими десятичными цифрами, т. е. никогда не заканчивающимися и не повторяющимися.
Обратите внимание, что множество иррациональных чисел является дополнительным к множеству рациональных чисел.
Некоторыми примерами иррациональных чисел являются $$\sqrt{2},\pi,\sqrt[3]{5},$$ и, например, $$\pi=3,1415926535\ldots$$ получается из отношения между длина окружности и ее диаметр.
Действительные числа $$\mathbb{R}$$
Множество, состоящее из рациональных и иррациональных чисел, называется множеством действительных чисел и обозначается как $$\mathbb{R}$$.
Таким образом, мы имеем:
$$$\mathbb{R}=\mathbb{Q}\cup\mathbb{I}$$$
И рациональные, и иррациональные числа являются действительными числами.
Одним из наиболее важных свойств действительных чисел является то, что их можно представить в виде точек на прямой линии.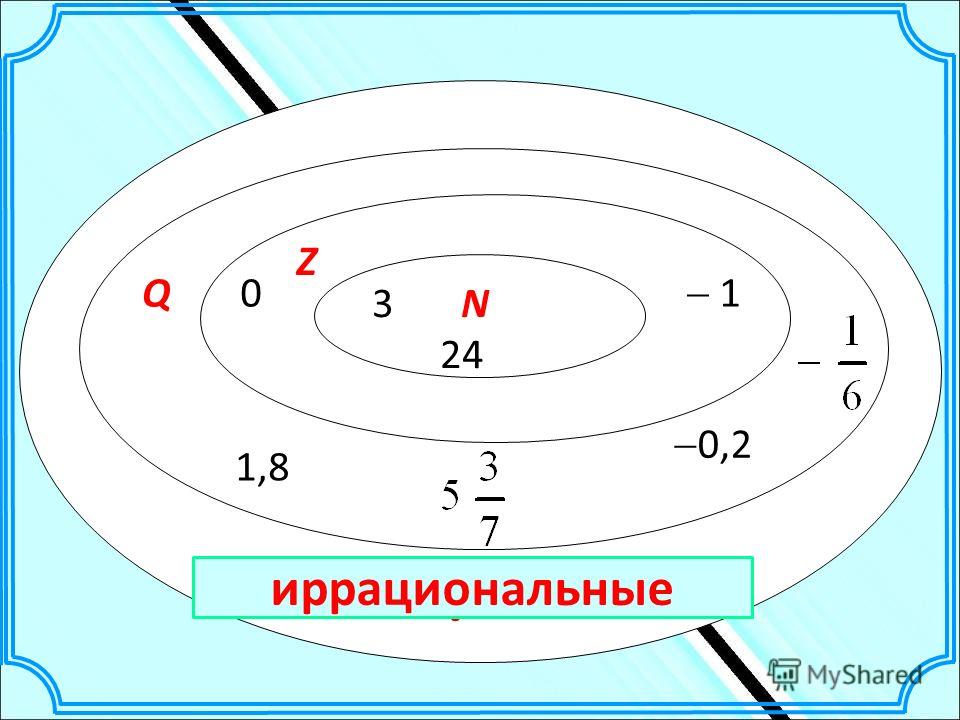 Мы выбираем точку, называемую источником, для представления $$0$$ и другую точку, обычно справа, для представления $$1$$.
Мы выбираем точку, называемую источником, для представления $$0$$ и другую точку, обычно справа, для представления $$1$$.
Соответствие между точками на прямой и действительными числами возникает естественным образом; другими словами, каждая точка на прямой представляет одно действительное число, и каждое действительное число имеет одну точку на прямой. Мы называем это реальной линией. На следующем рисунке вы можете увидеть пример:
Разница между рациональными и иррациональными числами
Математика — это не что иное, как игра чисел. Число — это арифметическое значение, которое может быть объектом, словом или символом, представляющим величину, имеющую множество значений при подсчете, измерении, маркировке и т. д. Числа могут быть целыми, целыми числами, натуральными числами, действительными числами. или комплексные числа. Действительные числа далее делятся на рациональные и иррациональные числа. Рациональные числа — это целые числа, которые могут быть выражены в виде x/y, где и числитель, и знаменатель — целые числа, тогда как иррациональные числа — это те числа, которые не могут быть выражены дробью. В этой статье мы обсудим рациональные числа, иррациональные числа, примеры рациональных и иррациональных чисел, разницу между иррациональными и рациональными числами и т. д.
В этой статье мы обсудим рациональные числа, иррациональные числа, примеры рациональных и иррациональных чисел, разницу между иррациональными и рациональными числами и т. д.
Рациональные числа
Термин «отношение» произошел от слова «отношение», которое означает сравнение любых двух величин, представленных в более простой форме дроби. Число считается рациональным числом, если оно может быть выражено в виде a/b, где a (числитель) и b (знаменатель) являются целыми числами. Знаменатель рационального числа — натуральное число (ненулевое число). Целые числа, дроби, в том числе смешанные дроби, повторяющиеся десятичные дроби, конечные десятичные дроби и т. д. — все они подпадают под категорию рациональных чисел.
Иррациональные числа
Число считается иррациональным, если оно не может быть просто преобразовано в любую часть натурального числа и целого числа. Десятичное расширение иррациональных чисел не является ни конечным, ни повторяющимся. К иррациональным числам относятся сурды и специальные числа, такие как π. Наиболее распространенной формой иррационального числа является пи (π). Сурд — это несовершенный квадрат или куб, который нельзя упростить дальше, чтобы удалить квадратный или кубический корень.
К иррациональным числам относятся сурды и специальные числа, такие как π. Наиболее распространенной формой иррационального числа является пи (π). Сурд — это несовершенный квадрат или куб, который нельзя упростить дальше, чтобы удалить квадратный или кубический корень.
Примеры рациональных и иррациональных чисел
Некоторые примеры рациональных чисел
Число 4 можно записать в виде 4/1, где 4 и 1 — целые числа.
0,25 также может быть записано как 1/4 или 25/100, и все конечные десятичные дроби являются рациональными числами.
√64 — рациональное число, поскольку его можно упростить до 8, которое также является частным 8/1.
0,888888 является рациональным числом, потому что оно повторяется в природе.
Некоторые примеры иррациональных чисел
3/0 — иррациональное число со знаменателем, равным нулю.

π — иррациональное число, имеющее значение 3,142, неповторяющееся и бесконечное по своей природе.
√3 — иррациональное число, так как его нельзя упростить дальше.
0,21211211 является иррациональным числом, поскольку оно не повторяется и не заканчивается по своей природе.
Важная разница между рациональными числами и иррациональными числами представлена ниже в табличной форме.
Рациональные номера | Иррациональные числа |
. Числа, которые могут быть представлены как at -in -ably. | Числа, которые не могут быть представлены в виде отношения двух чисел, то есть в форме a/b, называются иррациональными числами. |
Рациональное число включает только те десятичные дроби, которые конечны и повторяются по своей природе. | К иррациональным числам относятся все те числа, которые являются непрерывными или неповторяющимися по своей природе. |
Рациональные числа состоят из чисел, являющихся полными квадратами, таких как 4, 9, 16, 25 и т.д. | |
И числитель, и знаменатель рациональных чисел являются целыми числами, в которых знаменатель рациональных чисел не равен нулю. | Иррациональные числа не могут быть представлены в дробной форме. |
Пример: 5/3 = 1,66, 1/7 = 0,1428 .. | Пример: √7, √17 |
Как классифицировать Rational Rational?
Давайте теперь изучим, как идентифицировать рациональные и иррациональные числа на основе приведенных ниже примеров.
Как мы знаем, рациональные числа могут быть выражены дробью, и она включает в себя все целые числа, дроби и повторяющиеся десятичные дроби.
Рациональные числа можно идентифицировать при следующих условиях:
Иррациональные числа — это числа, которые не являются рациональными числами. Иррациональные числа могут быть представлены в десятичной форме, но не в дробях, что означает, что иррациональные числа не могут быть выражены как отношение двух целых чисел.
рациональные числа имеют бесконечные неповторяющиеся цифры после запятой.
Ниже приведены некоторые примеры рациональных и иррациональных чисел.
[Изображение будет загружено в ближайшее время]
Решенные примеры
1. Найдите любые 4 рациональных числа между 2/5 и 1/2.
Решение: Чтобы найти 5 рациональных чисел между -⅖ и ½, мы сначала сделаем одинаковыми знаменатели.
Следовательно, -⅖ = (2 * 10) / (5 * 10) = 20/50
И, ½ = (1 * 25) / (2 * 25) = 25/50
4 рациональное число между ⅖ и ½.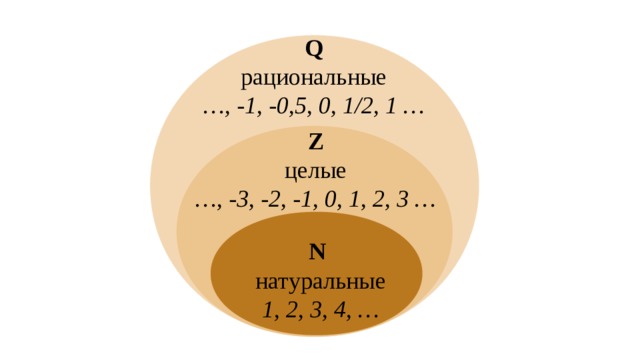 = 5 рациональных чисел от 20/50 до 25/50.
= 5 рациональных чисел от 20/50 до 25/50.
Следовательно, 4 рациональных числа между -⅖ и ½ — это 21/50, 22/50, 23/50 и 24/50.
2. Какое из приведенных ниже чисел не является иррациональным числом?
\[\sqrt{7}\] , \[\sqrt{5}\] , \[\sqrt{16}\] , \[\sqrt{11}\]
Решение: 16 — полный квадрат то есть \[\sqrt{16}\] = 4, что является рациональным числом
Как мы знаем, квадратный корень из простых чисел является иррациональным числом. 7, 5 и 11 — простые числа. Следовательно, единственное число, которое не является иррациональным, это \[\sqrt{16}\].
Время викторины
1. Какое из следующих чисел является иррациональным?
21/99
\ [\ sqrt {100} \]
\ [\ sqrt {36/3} \]
2/94
99999999999999999999999999999999999999999999999999999999999999999999999999999969999969999999999699.
- 9
2/94
669 2 . Квадратный корень из 225
Рациональное число
Иррациональное число
3. Какое из следующих чисел является рациональным?
¼
3.7
.25
1.2314
4. 9.0 is a
Rational number
Irrational number
Facts
Hippassus introduced irrational numbers when attempting to запишите квадратный корень из 2 в форме дроби (думается, используя геометрию).
 Он доказал, что квадратный корень из 2 нельзя записать в виде дроби, поэтому он иррационален.
Он доказал, что квадратный корень из 2 нельзя записать в виде дроби, поэтому он иррационален.
Типы чисел. Различие и классификация
Можете ли вы представить, какой была бы ваша жизнь, если бы у вас не было способа представить возраст, вес, дни рождения, время, счет, банковские счета и номера телефонов? Десять математических цифр (от 0 до 9) используются для определения всех этих величин.
Числа — это строки цифр, используемые для представления количества. Величина числа указывает на размер количества. Он может быть как большим, так и маленьким. Они существуют в разных формах, таких как 3, 999, 0,351, 2/5 и т. д.
Типы чисел в математике
Точно так же, как разные члены семьи живут в разных домах, разные числа относятся к одной семье, но имеют разные типы. Со временем различные комбинации из десяти цифр были отнесены к различным типам чисел. Эти образцы чисел отличаются друг от друга из-за различных представлений и свойств.
Натуральные числа
Натуральные числа или счетные числа — это самые основные типы чисел, которые вы впервые узнали в детстве.
 Они начинаются с 1 и идут до бесконечности, т. е. 1, 2, 3, 4, 5, 6 и так далее. Их также называют положительными целыми числами. В установленной форме они могут быть записаны как:
Они начинаются с 1 и идут до бесконечности, т. е. 1, 2, 3, 4, 5, 6 и так далее. Их также называют положительными целыми числами. В установленной форме они могут быть записаны как:{1, 2, 3, 4, 5, …}
Натуральные числа представлены символом N .
Целые числа
Целые числа — это набор натуральных чисел, включая ноль. Это означает, что они начинаются с 0 и доходят до 1, 2, 3 и т. д., т. е.
{0, 1, 2, 3, 4, 5, …}
Целые числа представлены символом W .
Целые числа
Целые числа представляют собой множество всех целых чисел и отрицательных чисел натуральных чисел. Они содержат все числа, лежащие между отрицательной бесконечностью и положительной бесконечностью. Они могут быть положительными, нулевыми или отрицательными, но не могут быть записаны в виде десятичной или дробной части. Целые числа могут быть записаны в заданной форме как
{…, -3, -2, -1, 0, 1, 2, 3, …}
Можно сказать, что все целые числа и натуральные числа являются целыми числами, но не все целые числа являются натуральными числами или целыми числами.

Символ Z представляет целые числа.
Дроби
Дробь представляет части целого куска. Его можно записать в виде a/b , где a и b — целые числа, а b никогда не может быть равно 0. Все дроби — рациональные числа, но не все рациональные числа — дроби. .
Далее дроби преобразуются в правильные и неправильные дроби. Неправильные дроби — это те, в которых числитель больше знаменателя, а в правильных функциях верно обратное, то есть знаменатель больше числителя. Примерами правильных дробей являются 3/7 и 99/101, а 7/3 и 101/99 — неправильные дроби. Это означает, что неправильные дроби всегда больше 1.
Все завершающие и повторяющиеся десятичные дроби можно записать в виде дробей. Вы можете записать завершающую десятичную дробь 1,25 как 125/100 = 5/4. Повторяющееся десятичное число 0,3333 можно записать как 1/3.
Рациональные числа
Вы можете записывать рациональные числа в виде дробей. Слово «рациональный» происходит от слова «отношение», поскольку рациональные числа — это отношения двух целых чисел.
 Например, 0,7 — рациональное число, потому что его можно записать как 7/10. Другими примерами рациональных чисел являются -1/3, 2/5, 99/100, 1,57 и т. д.
Например, 0,7 — рациональное число, потому что его можно записать как 7/10. Другими примерами рациональных чисел являются -1/3, 2/5, 99/100, 1,57 и т. д.Рассмотрим рациональное число p/q , где p и q — два целых числа. Здесь числитель p может быть любым целым числом (положительным или отрицательным), но знаменатель q никогда не может быть 0, так как дробь не определена. Кроме того, если q = 1, то дробь является целым числом.
Символ Q обозначает рациональные числа.
Иррациональные числа
Иррациональные числа нельзя записать в виде дроби, т. е. их нельзя записать в виде отношения двух целых чисел. Вот несколько примеров иррациональных чисел: √2, √5, 0,353535…, π и так далее. Вы можете видеть, что цифры в иррациональных числах продолжаются до бесконечности без повторяющегося шаблона.
Символ Q обозначает иррациональные числа.
Вещественные числа
Вещественные числа — это совокупность всех рациональных и иррациональных чисел.
 Сюда входят все числа, которые можно записать в десятичной форме. Все целые числа являются действительными числами, но не все действительные числа являются целыми числами. Действительные числа включают в себя все целые числа, целые числа, дроби, повторяющиеся десятичные дроби, завершающие десятичные дроби и так далее.
Сюда входят все числа, которые можно записать в десятичной форме. Все целые числа являются действительными числами, но не все действительные числа являются целыми числами. Действительные числа включают в себя все целые числа, целые числа, дроби, повторяющиеся десятичные дроби, завершающие десятичные дроби и так далее.Символ R представляет действительные числа.
Воображаемые числа
Числа, отличные от действительных чисел, являются мнимыми или комплексными числами. Когда мы возводим в квадрат мнимое число, он дает отрицательный результат, что означает, что это квадратный корень из отрицательного числа, например, √-2 и √-5. Когда мы возводим эти числа в квадрат, результаты равны -2 и -5. Квадратный корень из отрицательной единицы представлен буквой i , т.е.
i = √-1
Пример 1
Чему равен квадратный корень из -16? Запишите свой ответ в терминах воображаемого числа 9.0339 и .
Решение
- Шаг 1: Запишите форму квадратного корня.

√(-16)
- Шаг 2: Разделить -1.
√(16 × -1)
- Шаг 3: Разделение квадратных корней.
√(16) × √(-1)
- Шаг 4: Извлеките квадратный корень.
4 × √(-1)
- Шаг 5: Запишите в виде i.
4 i
Иногда вы получаете воображаемое решение уравнений.
Пример 2
Решение уравнения,
x 2 + 2 = 0
Раствор
- Шаг 1: Принимайте константную территорию на другую сторону.
x 2 = -2
- Шаг 2: Извлеките квадратный корень из обеих сторон.
√ х 2 = +√-2 или -√-2
- Шаг 3: Решить.
x = √ (2) × √ (-1)
x = +√2 I или -√2 I
- .
 В исходном уравнении и посмотрите, получим ли мы 0.
В исходном уравнении и посмотрите, получим ли мы 0.
x 2 + 2
( + √2 I ) 2 + 2 = -2 + 2 = 0 (As9 I + 2 = -2 + 2 = 0 (AS = √-1 и квадрат I равно -1)
(-2 I ) 2 + 2 = -2 + 2 = 0 (AS I = √ -1 и квадрат I —1)
То, что их имя «воображаемое», не означает, что они бесполезны. У них много приложений. Одним из величайших применений мнимых чисел является их использование в электрических цепях. Расчеты тока и напряжения выполняются в терминах мнимых чисел. Эти числа также используются в сложных математических вычислениях. В некоторых местах мнимое число также представлено буквой 9.0339 и .
Комплексные числа
Мнимое число объединяется с действительным числом для получения комплексного числа. Он представлен как a + bi , где действительная часть и b являются комплексной частью комплексного числа.
 Действительные числа лежат на числовой прямой, а комплексные — на двумерной плоской плоскости.
Действительные числа лежат на числовой прямой, а комплексные — на двумерной плоской плоскости.Как и мнимые числа, комплексные числа тоже не бесполезны. Они используются во многих приложениях, таких как «Сигналы и системы» и «Преобразование Фурье».
Простые и составные числа
Простые и составные числа противоположны друг другу. Простые числа — это тип целых чисел без делителей, кроме самих себя и 1, например, 2, 3, 5, 7 и так далее. Число 4 не является простым числом, потому что оно делится на 2. Точно так же 12 также не является простым числом, потому что оно делится на 2, 3 и 4. Таким образом, 4 и 12 являются примерами составных чисел.
Трансцендентные числа
Числа, которые никогда не могут быть нулем (или корнем) полиномиального уравнения с рациональными коэффициентами, называются трансцендентными числами. Не все иррациональные числа являются трансцендентными числами, но все трансцендентные числа являются иррациональными числами.

Классификация чисел
Семейство чисел, которое мы видели выше, также может быть классифицировано по разным категориям. Это похоже на то, что в семье 20 человек, но они живут в двух общих семейных домах по 10 человек в каждом, что означает, что 10 человек живут в одном доме. Мы можем сказать, что два или более типов чисел могут подпадать под одну категорию.
Дискретные и непрерывные числа
Типы счетных чисел называются дискретными числами, а типы чисел, которые нельзя посчитать, называются непрерывными числами. Все натуральные числа, целые числа, целые числа и рациональные числа дискретны. Это связано с тем, что каждое их множество счетно. Множество действительных чисел слишком велико и не может быть сосчитано, поэтому оно классифицируется как непрерывное число. Если мы случайным образом возьмем два ближайших действительных числа, между ними все равно будет бесконечно больше действительных чисел; следовательно, их нельзя сосчитать.
Наборы чисел
Числа также можно классифицировать в виде наборов.
 Каждый тип числа является подмножеством другого типа числа. Например, натуральные числа являются подмножеством целых чисел. Точно так же целые числа являются подмножеством целых чисел. Множество рациональных чисел содержит все целые числа и дроби. Наборы рациональных чисел и иррациональных чисел образуют действительные числа. Действительные числа подпадают под комплексные числа с мнимой частью как 0. Мы можем классифицировать эти числа в иерархической таблице следующим образом:
Каждый тип числа является подмножеством другого типа числа. Например, натуральные числа являются подмножеством целых чисел. Точно так же целые числа являются подмножеством целых чисел. Множество рациональных чисел содержит все целые числа и дроби. Наборы рациональных чисел и иррациональных чисел образуют действительные числа. Действительные числа подпадают под комплексные числа с мнимой частью как 0. Мы можем классифицировать эти числа в иерархической таблице следующим образом:Натуральные числа могут быть сведены к четным, нечетным, простым, взаимно простым, составным числам и числам с полным квадратом.
Обучение рациональным числам: десятичные дроби и др.
Математика — это гораздо больше, чем просто числа. Он включает в себя формы, логику, символы, пространства и широкие практики, такие как критическое мышление и внимание к точности, а также широкое применение во всем, от физики до физического воспитания.
 Но спросите кого-нибудь, что такое математика, и вы почти всегда услышите ответ, включающий номера . Они часто являются нашим введением в математику и важным способом найти математику в реальном мире.
Но спросите кого-нибудь, что такое математика, и вы почти всегда услышите ответ, включающий номера . Они часто являются нашим введением в математику и важным способом найти математику в реальном мире.Так что же такое число?
Ответить на этот вопрос непросто. Например, не всегда было известно, как писать и выполнять арифметические действия с нулевыми или отрицательными величинами. Понятие числа развивалось на протяжении тысячелетий и, по крайней мере, апокрифически, стоило жизни одному древнему математику.
Натуральные, целые и целые числа
Наиболее распространенные числа, с которыми мы сталкиваемся — от ограничений скорости до серийных номеров — это натуральные числа . Это счетные числа, которые начинаются с 1, 2 и 3 и продолжаются бесконечно. Если вместо этого мы начнем считать с 0, набор чисел вместо этого будет называться целыми числами .
Хотя это стандартные термины, это также возможность рассказать о том, что математика, в конечном счете, является человеческим делом.
 Разные люди могут давать этим наборам разные имена, иногда даже меняя, какое из них они называют 9.0339 натуральный а какой называют целым ! Откройте его своим ученикам: как бы они назвали набор чисел 1, 2, 3…? Какое новое имя они дали бы ему, если бы включили 0?
Разные люди могут давать этим наборам разные имена, иногда даже меняя, какое из них они называют 9.0339 натуральный а какой называют целым ! Откройте его своим ученикам: как бы они назвали набор чисел 1, 2, 3…? Какое новое имя они дали бы ему, если бы включили 0?Целое число Числа (или просто целое число ) также расширяют целые числа до своих противоположностей: …–3, –2, –1, 0, 1, 2, 3…. Обратите внимание, что 0 единственное число, противоположным которому является само себя.
Рациональные числа и многое другое
Дальнейшее расширение понятия числа приводит нас к рациональные числа . Название не имеет ничего общего с осмысленностью чисел, хотя оно дает возможность обсудить ELA на уроке математики и показать, как одно слово может иметь много разных значений в языке, и важность точности в языке в математике. Скорее, слово рациональное связано со словом, находящимся в первых пяти буквах: ratio .

Рациональное число — это любое число, которое может быть записано как отношение двух целых чисел, например \(\frac{1}{2}\), \(\frac{783}{62,450}\) или \ (\фракция{-25}{5}\). Обратите внимание, что, хотя отношения всегда могут быть выражены в виде дробей, они также могут отображаться по-разному. Например, \(\frac{3}{1}\) обычно записывается как просто \(3\), дробь \(\frac{1}{4}\) часто записывается как \(0,25\) и можно написать \(-\frac{1}{9}\) как повторяющееся десятичное число \(-0,111\)….
Любое число, которое не может быть записано как рациональное число, достаточно логично называется иррациональным числом . И вся категория всех этих чисел, или другими словами, все числа, которые могут быть изображены на числовой прямой, называются действительными числами . Иерархия действительных чисел выглядит примерно так:
Важным свойством, применимым к действительным, рациональным и иррациональным числам, является число 9.
 0421 свойство плотности . В нем говорится, что между любыми двумя действительными (или рациональными, или иррациональными) числами всегда есть другое действительное (или рациональное, или иррациональное) число. Например, между 0,4588 и 0,4589 существует число 0,45887 и бесконечно много других. Итак, вот все возможные действительные числа:
0421 свойство плотности . В нем говорится, что между любыми двумя действительными (или рациональными, или иррациональными) числами всегда есть другое действительное (или рациональное, или иррациональное) число. Например, между 0,4588 и 0,4589 существует число 0,45887 и бесконечно много других. Итак, вот все возможные действительные числа:Вещественные числа: Рациональные
Ключевой стандарт: понимать рациональное число как отношение двух целых чисел и точки на числовой прямой. (6 класс)
Рациональные числа: Любое число, которое можно записать как отношение (или дробь) двух целых чисел, является рациональным числом. Студенты часто спрашивают, являются ли дроби рациональными числами? Ответ положительный, но дроби составляют большую категорию, которая также включает целые числа, конечные десятичные дроби, повторяющиеся десятичные дроби и дроби.
- Целое число можно представить в виде дроби, присвоив ему знаменатель, равный единице, поэтому любое целое число является рациональным числом.
 \(6=\frac{6}{1}\)\(0=\frac{ 0}{1}\)\(-4=\frac{-4}{1}\) или \(\frac{4}{-1}\) или \(-\frac{4}{1}\ )
\(6=\frac{6}{1}\)\(0=\frac{ 0}{1}\)\(-4=\frac{-4}{1}\) или \(\frac{4}{-1}\) или \(-\frac{4}{1}\ ) - , завершающее десятичное число , может быть записано как дробь с использованием свойств разрядного значения. Например, 3,75 = три и семьдесят пять сотых или \(3\frac{75}{100}\), что равно неправильной дроби \(\frac{375}{100}\).
- Повторяющееся десятичное число всегда можно записать в виде дроби с помощью алгебраических методов, которые выходят за рамки этой статьи. Однако важно понимать, что любое десятичное число с одной или несколькими цифрами, которое повторяется вечно, например \(2.111\)… (которое можно записать как \(2.\overline{1}\)) или \( 0,8890\)… (или \(0.\overline{890}\)), является рациональным числом. Распространенный вопрос: «Являются ли повторяющиеся десятичные дроби рациональными числами?» Ответ — да!
Целые числа: Счетные числа (1, 2, 3,…), их противоположности (–1, –2, –3,.
 ..) и 0 являются целыми числами. Распространенной ошибкой учащихся 6–8 классов является предположение, что целые числа относятся к отрицательным числам. Точно так же многие студенты задаются вопросом, являются ли десятичные дроби целыми числами? Это верно только тогда, когда десятичная дробь оканчивается на «.000…», например, 3.000…, что равно 3. (Технически это также верно, когда десятичная дробь оканчивается на «.9).99…», так как 0,999… = 1. Это не особенно часто встречается, но число 3 на самом деле может быть записано как 2,999….)
..) и 0 являются целыми числами. Распространенной ошибкой учащихся 6–8 классов является предположение, что целые числа относятся к отрицательным числам. Точно так же многие студенты задаются вопросом, являются ли десятичные дроби целыми числами? Это верно только тогда, когда десятичная дробь оканчивается на «.000…», например, 3.000…, что равно 3. (Технически это также верно, когда десятичная дробь оканчивается на «.9).99…», так как 0,999… = 1. Это не особенно часто встречается, но число 3 на самом деле может быть записано как 2,999….)Целые числа: Нуль и положительные целые числа
Натуральные числа: Также называемые счетными числами, этот набор включает все целые числа, кроме нуля (1, 2, 3,…)
Вещественные числа: иррациональные
Ключ стандарт: Знай, что есть числа, которые не являются рациональными (8 класс)
Иррациональные числа: Любое действительное число, которое нельзя записать в виде дроби, является иррациональным числом.
 Эти числа включают непрерывающиеся неповторяющиеся десятичные знаки, например \(\pi\), 0,45445544455544445555… или \(\sqrt{2}\). Любой квадратный корень, не являющийся полным корнем, является иррациональным числом. Например, \(\sqrt{1}\) и \(\sqrt{4}\) рациональны, потому что \(\sqrt{1}=1\) и \(\sqrt{4}=2\), но \(\sqrt{2}\) и \(\sqrt{3}\) иррациональны. Все четыре числа обозначают точки на числовой прямой, но не все они могут быть записаны в виде целочисленных отношений. 92+3=0\) (решение которого равно \(\pm\sqrt{3}i\)).
Эти числа включают непрерывающиеся неповторяющиеся десятичные знаки, например \(\pi\), 0,45445544455544445555… или \(\sqrt{2}\). Любой квадратный корень, не являющийся полным корнем, является иррациональным числом. Например, \(\sqrt{1}\) и \(\sqrt{4}\) рациональны, потому что \(\sqrt{1}=1\) и \(\sqrt{4}=2\), но \(\sqrt{2}\) и \(\sqrt{3}\) иррациональны. Все четыре числа обозначают точки на числовой прямой, но не все они могут быть записаны в виде целочисленных отношений. 92+3=0\) (решение которого равно \(\pm\sqrt{3}i\)).В каком-то смысле комплексные числа отмечают «конец» чисел, хотя математики постоянно изобретают новые способы описания и представления чисел. Числа также можно абстрагировать различными способами, включая математические объекты, такие как матрицы и множества. Поощряйте своих учеников быть математиками! Как бы они описали число, которое не входит в число типов, показанных здесь? Почему ученый или математик может попытаться это сделать?
***
Ищете учебную программу по математике, которая повысит уверенность учащихся в математике и поможет учащимся использовать рациональные и иррациональные числа? Изучите HMH Into Math , наше основное математическое решение для классов K–8.

2.1 Рациональные и иррациональные числа | Рациональные и иррациональные числа
2.1 Наборы чисел
Набор — это набор объектов, которые имеют что-то общее. Набор может быть группой вещей, которые мы используем вместе, или которые имеют сходные свойства. Числа могут быть организованы в наборы номеров . В предыдущем лет вы узнали о следующих наборах чисел:
- Натуральные числа — положительные счетные числа.
- Целые числа — это положительные счетные числа плюс ноль.
- Целые числа — это целые числа плюс отрицательные числа счета.
Мы можем использовать нотацию набора для записи этих наборов с помощью символов:
В последующие годы вы узнаете больше о системе обозначений.
Набор чисел Набор чисел — это группа чисел со схожими свойствами.

натуральные числа Множество натуральных чисел включает все положительные счетные числа.
целые числа Набор целых чисел включает все положительные счетные числа и ноль.
целое число Набор целых чисел включает все отрицательные счетные числа, ноль и все положительные счетные числа.
В этой главе вы узнаете о множестве чисел, называемых рациональными числами . Рациональное число любое число, которое можно записать в виде такой, что а также являются целыми числами и . В системе обозначений пишем:
В системе обозначений символ означает «такой, что». Символ означает «является элементом». Следовательно, означает » является элементом множества целых чисел».
Любые числа, не входящие в множество рациональных чисел, называются иррациональные числа .
 Этот
множество чисел иногда также называют множеством нерациональных чисел. Вы узнаете больше об иррациональном
числа далее в этой главе.
Этот
множество чисел иногда также называют множеством нерациональных чисел. Вы узнаете больше об иррациональном
числа далее в этой главе.рациональные числа Множество рациональных чисел включает все числа, которые можно записать в виде такой, что а также являются целыми числами и .
иррациональные числа Иррациональные числа – это все числа, не входящие в множество рациональное число. Набор также можно назвать нерациональными числами.
На следующей диаграмме показаны взаимосвязи между наборами номеров, рассмотренными выше.
2.2 Рациональные числа
Целые числа
Все целые числа являются рациональными числами. Это потому, что любое целое число можно записать в виде дроби с как знаменатель. Вот несколько примеров:
Обыкновенные дроби
Все обыкновенные дроби являются рациональными числами. В предыдущие годы вы узнали, что обыкновенная дробь записывается в форма:
, где числитель и знаменатель — целые числа.

В правильных дробях числитель меньше знаменателя. Вот несколько примеров:
В неправильных дробях числитель больше знаменателя. Вот несколько примеров:
Смешанные числа
Все смешанные числа являются рациональными числами. В предыдущие годы вы узнали, что смешанное число состоит из целого числа и правильная дробь. Вы также научились записывать смешанные числа в виде неправильных дробей. Этот же метод можно использовать для положительных и отрицательных смешанных чисел. Вот несколько примеров:
\начать{выравнивать} 2\frac{3}{4} & =\frac{11}{4}\\ 15\frac{7}{8} & = \frac{127}{8}\\ 100\frac{1}{100} & = \frac{101}{100} \\ -5\frac{3}{20}& =\frac{-103}{20}\\ -50\frac{9}{10}& =\frac{-509}{10} \end{выравнивание}
Числа, записанные в десятичной системе счисления
Все завершающие десятичные дроби являются рациональными числами. В конце десятичной дроби цифры, которые приходят после десятичной точки заканчиваются.
 В прошлом году вы научились преобразовывать числа, записанные в десятичной системе счисления, в
обыкновенные дроби. Вот несколько примеров:
В прошлом году вы научились преобразовывать числа, записанные в десятичной системе счисления, в
обыкновенные дроби. Вот несколько примеров:\begin{массив}{rcl} 0,8 & = \ гидроразрыва {8} {10} = & \ гидроразрыва {4} {5} \\ 2.5 & = \frac{25}{10} = & \frac{5}{2} \\ 0,12 & = \frac{12}{100} = & \frac{3}{25} \\ 4.08 & = \frac{408}{100} = & \frac{102}{25} \\ 0,025 & = \frac{25}{1000} = & \frac{1}{40} \конец{массив}
Все повторяющиеся десятичные дроби являются рациональными числами. В повторяющемся десятичном числе одна или несколько десятичных цифр повторять в том же шаблоне навсегда. Если повторяются только одна или две цифры, мы пишем точку над повторяющимися цифрами. Если повторяются более двух цифр, мы пишем точку над первой и последней цифрами повторяющегося рисунка. Вот некоторые примеры:
\начать{выравнивать} 0,3333333 \ldots & = 0.\dot{3} \\ 0,1555555 \ldots & = 0,1\dot{5} \\ 10.
 27272727 \ldots & = 10.\dot{2}\dot{7} \\
2,578578578 \ldots & = 2.\dot{5}7\dot{8} \\
15,32656565 \ldots & = 15,32\dot{6}\dot{5}
\end{выравнивание}
27272727 \ldots & = 10.\dot{2}\dot{7} \\
2,578578578 \ldots & = 2.\dot{5}7\dot{8} \\
15,32656565 \ldots & = 15,32\dot{6}\dot{5}
\end{выравнивание}Повторяющиеся десятичные дроби можно записать в виде обыкновенных дробей.
завершающая десятичная дробь В завершающей десятичной дроби цифры, идущие после запятой, идут к концу.
повторяющееся десятичное число В повторяющемся десятичном числе одна или несколько десятичных цифр повторяются по одному и тому же шаблону навсегда.
Рабочий пример 2.1: Написание повторяющиеся десятичные дроби в виде обыкновенных дробей (метод 1)
Запись как обыкновенная дробь.
Шаг 1: Запишите число как сумму его целого числа и его десятичной дроби.
Шаг 2: Запишите десятичную дробь в виде правильной дроби. Повторяющиеся цифры являются числителем.
 в знаменателе число 9повторяется столько раз, сколько цифр в числителе.
в знаменателе число 9повторяется столько раз, сколько цифр в числителе.Числитель должен быть 15. Он состоит из двух цифр.
Следовательно, знаменатель должен быть равен 99.Шаг 3: Найдите простейшую форму дроби из шага 2.
Шаг 4: Перепишите шаг 1, но теперь используйте десятичную дробь как правильную дробь. Добавьте целое число и дробная часть.
\начать{выравнивать} &2+\фракция{5}{33} \\ =&\frac{2}{1}\times\frac{33}{33}+\frac{5}{33}\\ =&\frac{66}{33}+\frac{5}{33} \\ =&\фракция{71}{33} \end{выравнивание}Этот метод работает, только если нет неповторяющихся цифр после запятой.
Рабочий пример 2.2: Написание повторяющиеся десятичные дроби в виде обыкновенных дробей (метод 2)
Запись как обыкновенная дробь.
Шаг 1: Запишите повторяющийся шаблон не менее трех раз.
 Пусть это будет равно
. Обозначьте уравнение как (1).
Пусть это будет равно
. Обозначьте уравнение как (1).Шаг 2: Умножьте выписанное десятичное число на число, кратное десяти. Начните с 10, затем попробуйте 100, затем 1000 и так далее. на. Вы должны получить одинаковые цифры после десятичная точка, как в уравнении (1). Вы также должны получить повторяющиеся цифры до десятичной точки.
Начать с 10:
\начать{выравнивать} 10 \times 2.151515 \ldots &= 10 \times x \\ 21,51515 \ldots &= 10x \\ \end{выравнивание}Цифры после запятой не такие, как в уравнении (1), а только цифра 1 повторяющиеся цифры стоят перед запятой.
Теперь попробуйте 100:
\начать{выравнивать} 100 \times 2.151515 \ldots &= 100 \times x \\ 215,1515 \ldots &= 100x \\ \end{выравнивание}Цифры после запятой такие же, как в уравнении (1), и появляются обе повторяющиеся цифры 15. до десятичной точки.

Шаг 3: Обозначьте уравнение из шага 2 как (2). Вычтите уравнение (1) из уравнения (2).
\начать{выравнивать} 2.151515 \ldots &= x \phantom{00000}(1) \\ 215,1515 \ldots &= 100x \фантом{00}(2) \end{выравнивание}:
\начать{выравнивать} 215,1515 \ldots — 2,151515 \ldots &= 100x — x \\ 213 &= 99x \\ \end{выравнивание}Шаг 4: Решите уравнение из шага 3.
\начать{выравнивать} 213 &= 99x \\ \frac{213}{99} &= \frac{99x}{99}\\ х&=\фракция{213}{99} \\ &= \фракция{71}{33} \end{выравнивание}Если после запятой стоит неповторяющаяся цифра, перед этим умножьте уравнение (1) на 10. вы продолжаете с шага 2.
Упражнение 2.1. Запишите повторяющиеся десятичные дроби как обычные дроби
Каждую из следующих повторяющихся десятичных дробей запишите в виде обыкновенных дробей.
\начать{выравнивать} &4+\фракция{2}{9}\\ =&\фракция{36+2}{9}\\ =&\фракция{38}{9} \end{выравнивание}
\начать{выравнивать} &33+\фракция{3}{9}\\ =&\фракция{297+3}{9}\\ =&\фракция{300}{9} \end{выравнивание}
После запятой стоит неповторяющаяся цифра, поэтому вам нужно умножить уравнение (1) на 10, прежде чем вы получаете значения, которые вы можете вычесть.

У вас все еще нет повторяющейся цифры перед запятой, поэтому умножьте на 100.
Повторяющиеся цифры теперь одинаковы только в уравнениях (2) и (3), поэтому вы вычитаете (2) из (3).
\начать{выравнивать} 100x-10x&=2,22222-0,22222 \\ 90x&=2 \\ \фракция{90x}{90}&=\фракция{2}{90}\\ \следовательно, x&=\frac{1}{45} \end{выравнивание}
Проценты
Все проценты являются рациональными числами. Процент – это дробь, знаменатель которой равен 100, и где записывается только числитель, за которым следует символ процента. В прошлом году вы научились конвертировать процентов к обыкновенным дробям. Вот несколько примеров:
процент Процент – это дробь, знаменатель которой равен 100, а где записывается только числитель, за которым следует символ процента.
Квадратный корень
Квадратный корень числа — это множитель числа, который при умножении на себя дает количество.
 Рациональны только квадратные корни, имеющие целые числа, завершающие десятичные дроби или обыкновенные дроби.
числа. Вот примеры квадратных корней, являющихся рациональными числами:
Рациональны только квадратные корни, имеющие целые числа, завершающие десятичные дроби или обыкновенные дроби.
числа. Вот примеры квадратных корней, являющихся рациональными числами:квадратный корень Квадратный корень числа — это множитель числа, который при умноженный сам на себя, дает число.
Упражнение 2.2. Докажите, что числа рациональны
Докажите, что каждое из следующих чисел является рациональным числом.
Помните, что рациональное число — это любое число, которое можно записать в виде такой, что а также являются целыми числами и .
2.
 3 Иррациональные числа
3 Иррациональные числаИррациональные числа нельзя записать в виде такой, что а также являются целыми числами и .
Иррациональные числа не имеют точных значений. Примеры иррациональных чисел:
- десятичные числа, которые имеют бесконечное количество десятичных цифр, из которых ни одна не повторяется, например
- квадратных корней, не имеющих целых чисел, заканчивающихся десятичными или обыкновенными дробями в качестве ответов (корней), для пример .
Упражнение 2.3. Классифицируйте числа как рациональные или иррациональное
Классифицируйте каждое из следующих чисел как рациональное или иррациональное.
Рациональное число:
, а целые числа являются рациональными числами.Рациональное число:
Проценты — это рациональные числа.Рациональное число:
Целые числа являются рациональными числами.
Иррациональное число:
Десятичные числа, которые не заканчиваются и не повторяются, являются иррациональными числами.Рациональное число:
Смешанные числа — это рациональные числа.Иррациональное число:
не имеет целого числа, заканчивающегося десятичным или обычным дробь как ее корень (или ответ).Рациональное число:
Повторяющиеся десятичные дроби — это рациональные числа.Рациональное число:
Целые числа являются рациональными числами.Рациональный номер:
Рациональное число:
Конечные десятичные дроби — это рациональные числа.
Рациональное число:
Повторяющиеся десятичные дроби — это рациональные числа.Иррациональное число:
не имеет целого числа, заканчивающегося десятичным или обыкновенная дробь как ее корень.Иррациональное число:
Десятичные числа, которые не заканчиваются и не повторяются, являются иррациональными числами.Иррациональное число:
не имеет целого числа, заканчивающегося десятичным или обычным дробь как ее корень.Рациональный номер:
2,4 Пи ( )
Пи — пример иррационального числа.
 Он представлен символом
. Он представляет различные отношения в круге. Вы должны быть знакомы с
следующие размеры круга:
Он представлен символом
. Он представляет различные отношения в круге. Вы должны быть знакомы с
следующие размеры круга:Для любого круга пи представляет следующие отношения:
Пи не имеет фиксированного значения. Чтобы использовать его в расчетах, округлим до 3,142 или .
Пи Пи есть постоянное отношение длины окружности к диаметру любого круга.
Рабочий пример 2.3: Подтверждение значения
Окружность внизу имеет длину окружности ( ) из и площадь ( ) из .
- Рассчитать отношение длины окружности к диаметру ( ).
- Вычислить отношение площади к квадрату радиуса ( ).
- Что ваши ответы говорят вам о ценности ?
Шаг 1: Рассчитайте отношение длины окружности к диаметру.
\начать{выравнивать} &\ гидроразрыва {C} {d} \\ =&\frac{62,832 \text{ см}}{2 \times 10 \text{ см}} \\ =&\frac{62,832 \text{ см}}{20 \text{ см}} \\ =&3. 1416
\end{выравнивание}
92} \\
=&3.1416
\end{выравнивание}
1416
\end{выравнивание}
92} \\
=&3.1416
\end{выравнивание}Шаг 3. Укажите, что ответы говорят вам о ценности .
Оба коэффициента используются при расчете стоимости , и ответы те же 3.1416. Это подтверждает, что значение близко к 3,1416.
Упражнение 2.4. Вычисление значения
Для каждого из следующих кругов рассчитайте значение до четырех знаков после запятой. 92} \\ =&3.1415 \end{выравнивание}
Для круга ниже, а также .
\начать{выравнивать} \pi&=\frac{C}{d} \\ &=\фракция{14.14\; \текст м}{2\умножить на 2,25\; \текст м} \\ &=\фракция{14.14\; \текст м}{4.5\; \текст м} \\ &=3,1422 \end{выравнивание}
2.5 Резюме
- Набор чисел — это группа чисел со схожими свойствами.

- Множество натуральных чисел включает в себя все положительные счетные числа.
- Набор целых чисел включает в себя все положительные счетные числа и ноль.
- Набор целых чисел включает все отрицательные счетные числа, ноль и все положительные счетные числа.
- Множество рациональных чисел включает все числа, которые можно записать в виде такой, что а также являются целыми числами и .
- Рациональные числа:
- целых чисел
- обыкновенные дроби
- смешанные числа
- завершающие десятичные дроби
- повторяющиеся десятичные дроби
- процентов
- квадратных корней, которые имеют целые числа, заканчивая десятичными или обыкновенными дробями в качестве ответов.
- Иррациональные числа (или нерациональные числа) — это все числа, не входящие в множество рациональных
числа.

- Следующие числа являются иррациональными:
- десятичные числа, содержащие бесконечное количество десятичных цифр, из которых ни одна не повторяется
- квадратных корней, не имеющих целых чисел, заканчивающихся десятичными или обыкновенными дробями в качестве корней.
- Пи ( ) — постоянное отношение длины окружности к диаметру любой окружности.
Количество чисел: бесконечная странность | Вишеш Хемани, доктор философии.
Сколько существует чисел каждого типа? Могут ли две бесконечности быть равны? Может ли одна бесконечность быть больше другой бесконечности?
Строка Действительных Чисел Иерархия Действительных ЧиселСколько существует натуральных чисел (1, 2, 3, …)? Существует ли наибольшее такое число? Приходят ли в конце концов к остановке дискретные точки натуральных чисел на числовой прямой?
Чтобы ответить на эти вопросы, давайте воспользуемся забавной и мощной логической техникой, называемой доказательством от противного (или доведение до абсурда , что в переводе с латыни означает доведение до абсурда). В таком доказательстве мы предполагаем, что утверждение верно. Затем мы делаем вывод из предполагаемого истинного утверждения, следуя логическим шагам, и обнаруживаем, что вывод неверен/абсурден/противоречив. Это должно означать, что утверждение, которое считалось истинным, ложно. Исходное утверждение было доказано ложным от противного.
В таком доказательстве мы предполагаем, что утверждение верно. Затем мы делаем вывод из предполагаемого истинного утверждения, следуя логическим шагам, и обнаруживаем, что вывод неверен/абсурден/противоречив. Это должно означать, что утверждение, которое считалось истинным, ложно. Исходное утверждение было доказано ложным от противного.
Для разминки докажем от противного, что не существует наибольшего натурального числа. Предположим, что существует натуральное число, назовем его L, которое больше всех других натуральных чисел. Тогда, поскольку натуральные числа замкнуты при сложении (т. е. добавление двух натуральных чисел дает еще одно натуральное число), число, полученное прибавлением 1 к L, назовем его М, также является натуральным числом. И M больше, чем L (например, потому что это одна точка справа от L на числовой прямой). Но это противоречит исходному предположению, что L — наибольшее натуральное число. Так что это предположение, должно быть, было неверным, и мы доказали, что не существует наибольшего натурального числа.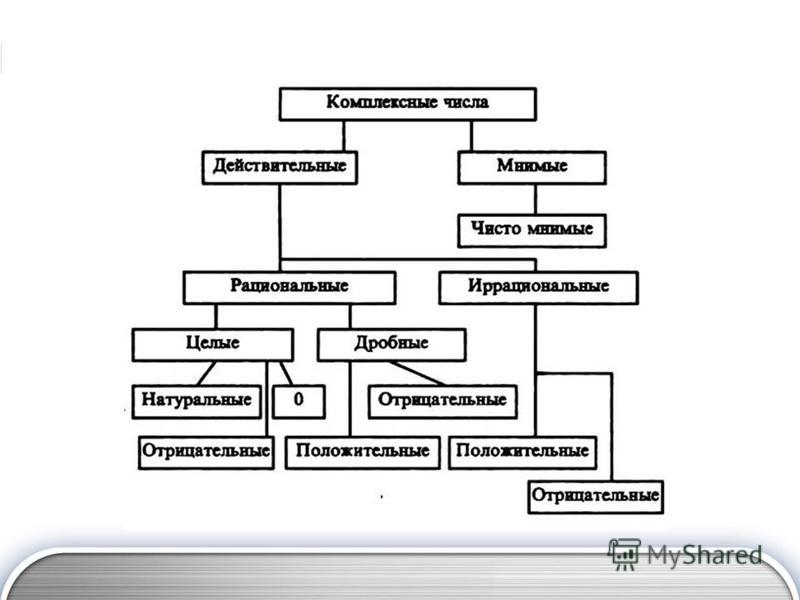 Натуральные числа неограниченно выше . Точки натуральных чисел на числовой прямой простираются до бесконечности вправо. Существует бесконечных натуральных чисел.
Натуральные числа неограниченно выше . Точки натуральных чисел на числовой прямой простираются до бесконечности вправо. Существует бесконечных натуральных чисел.
Множество целых чисел — это множество натуральных чисел и нуля. Означает ли это, что целых чисел на 1 больше, чем натуральных? Нет!
Каждое натуральное число соответствует ровно одному уникальному целому числу (например, 1 -> 0, 2 -> 1, 3 -> 2, … другими словами, n -> n-1). И нет оставшихся целых чисел, которые не отображаются на натуральное число. это называется однозначное соответствие между натуральными числами и целыми числами. Когда такое взаимно-однозначное соответствие существует между двумя бесконечными множествами, это означает, что два бесконечных множества имеют одинаковое количество элементов. Количество целых чисел равно количеству натуральных чисел, оба множества бесконечны, хотя натуральные числа являются правильным подмножеством целых чисел!
Соответствие 1:1 между натуральными и целыми числами Еще один способ представить взаимно-однозначное соответствие между набором чисел и натуральными числами состоит в том, что набор чисел можно перечислить (начиная с индекса 1), ничего не оставив выходит в наборе.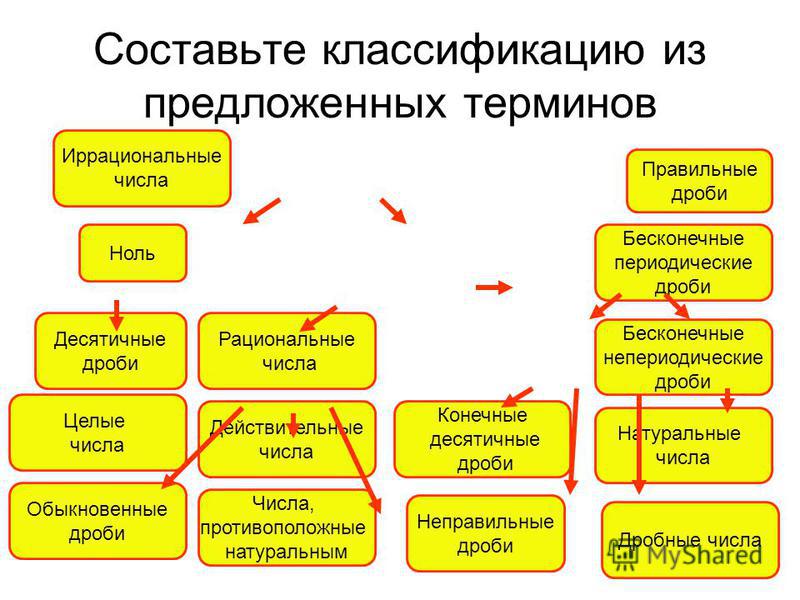 Такое перечисление для целых чисел было бы следующим:
Такое перечисление для целых чисел было бы следующим:
- 0
- 1
- 2
- …
Целые числа состоят из всех целых чисел (0, 1, 2, 3, …) и не дробных отрицательных чисел (-1, -2, -3 , …). Наверняка целых чисел больше, чем целых чисел (возможно, где-то в два раза больше, чтобы учесть отрицательное целое число для каждого натурального числа)? Нет!
На самом деле количество целых чисел равно количеству натуральных чисел! Как это может быть? Это должно быть потому, что существует однозначное соответствие между целыми и натуральными числами. Вот перечисление всех целых чисел, которое устанавливает это соответствие:
- 0
- 1
- -1
- 2
- -2
- …
Точное соответствие состоит в том, что нечетное натуральное число ‘o’ соответствует ровно одному уникальному неположительному числу ‘о’)/2 (то есть 1 -> 0, 3 -> -1, 5 -> -2, …). А четное натуральное число «e» соответствует ровно одному уникальному целому положительному «e»/2 (то есть 2 -> 1, 4 -> 2, 6 -> 3, …). Количество целых чисел равно количеству натуральных чисел, оба набора бесконечны, хотя натуральные числа являются правильным подмножеством целых чисел!
Количество целых чисел равно количеству натуральных чисел, оба набора бесконечны, хотя натуральные числа являются правильным подмножеством целых чисел!
Рациональные числа состоят из целых и дробных чисел в форме p/q (где p, q — целые числа и q ≠ 0). Сколько существует рациональных чисел? Бесконечный, конечно. Вы можете ясно видеть это по тому факту, что как раз между 0 и 1 находится бесконечно много рациональных чисел вида 1/2, 1/3, 1/4 и так далее. Кажется, что рациональных чисел должно быть бесконечно больше, чем целых, верно? Опять неправильно!
На самом деле существует однозначное соответствие между натуральными и рациональными числами, что приводит к неожиданному выводу, что количество рациональных чисел равно количеству целых чисел ! Детали переписки немного сложны, поэтому я просто дам вам ее почувствовать. Вы можете перечислить все рациональные числа в порядке возрастания суммы числителя и знаменателя, пропуская любое ранее увиденное число.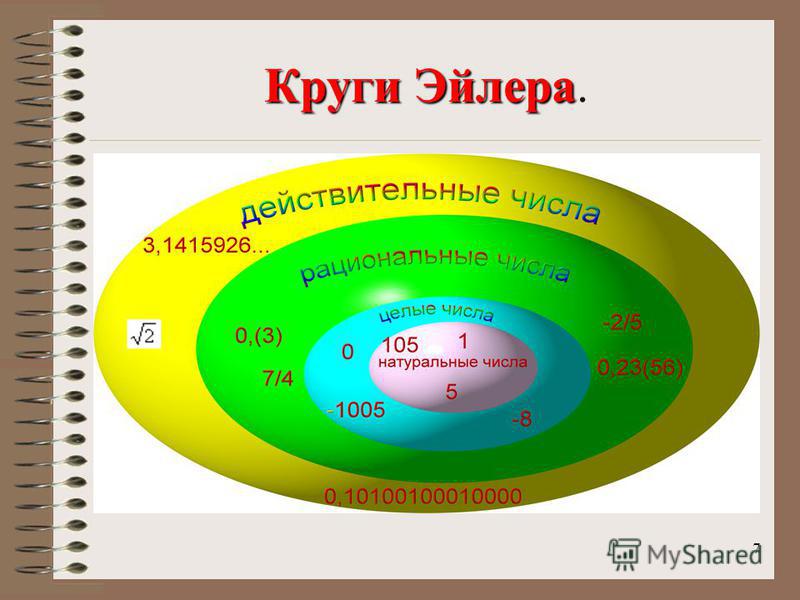 Итак, для суммы 1 у нас есть рациональное число 0/1 или 0. Для суммы 2 у нас есть рациональное число 1/1 или 1. Для суммы 3 у нас есть два рациональных числа: 1/2 и 2. /1 или 2. Для суммы 4 у нас есть следующие ранее неизвестные рациональные числа: 1/3, 3. Для суммы 5 у нас есть 1/4, 2/3, 3/2, 4. И так далее . Когда у нас есть четко определенное перечисление, учитывающее все рациональные числа, у нас есть однозначное соответствие между натуральными числами и рациональными числами.
Итак, для суммы 1 у нас есть рациональное число 0/1 или 0. Для суммы 2 у нас есть рациональное число 1/1 или 1. Для суммы 3 у нас есть два рациональных числа: 1/2 и 2. /1 или 2. Для суммы 4 у нас есть следующие ранее неизвестные рациональные числа: 1/3, 3. Для суммы 5 у нас есть 1/4, 2/3, 3/2, 4. И так далее . Когда у нас есть четко определенное перечисление, учитывающее все рациональные числа, у нас есть однозначное соответствие между натуральными числами и рациональными числами.
Пусть это усвоится. Хотя существует бесконечно много рациональных чисел между любыми двумя последовательными целыми числами, количество рациональных чисел по-прежнему равно количеству целых чисел. Этот кажущийся нелогичным результат связан с тем, что у нас нет достаточной интуиции для бесконечности. Хотя целые числа кажутся менее плотными, чем рациональные числа на числовой прямой, тот факт, что целые числа не ограничены, позволяет нам отображать каждое целое число ровно в одно уникальное рациональное число, не заканчивая целые числа и не пропуская ни одного рационального числа.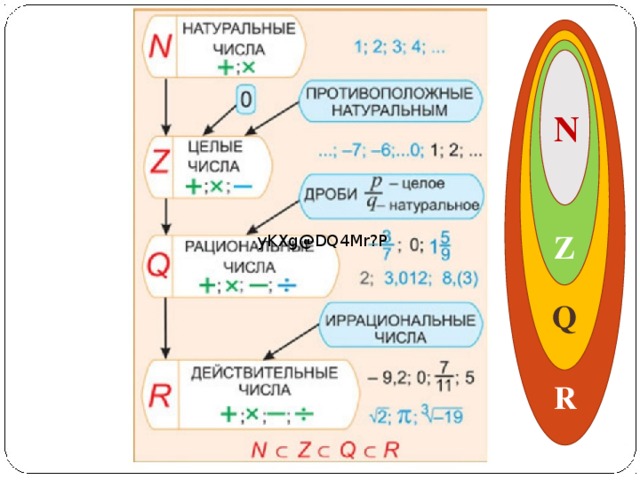
Иррациональные числа — это действительные числа, которые не являются рациональными. Десятичное представление иррационального числа имеет бесконечное количество цифр после запятой без бесконечно повторяющегося шаблона.
Сколько существует иррациональных чисел? Бесконечный, ничего удивительного в этом нет. К настоящему времени мы, вероятно, ожидаем, что количество иррациональных чисел будет таким же, как количество рациональных чисел (которое, в свою очередь, совпадает с количеством натуральных чисел). Но иррациональные люди опровергнут это ожидание. Количество иррациональных чисел на самом деле больше, чем количество рациональных чисел. Вот случай, когда одна бесконечность больше другой бесконечности! Мы можем доказать это от противного: предположим, что иррациональные числа можно полностью перечислить, а затем найдем иррациональное, которого нет в перечислении.
Вот набросок доказательства. Рассмотрим следующее произвольное перечисление иррациональных чисел (подробности перечисления не важны, лишь бы было перечисление):
1: 3,141…
2: 1,414…
3: 2,718…
4: …
Теперь построим еще одно иррациональное число особым образом. Его первая десятичная цифра будет на 1 больше, чем первая десятичная цифра первого числа в перечислении, что дает 0,2… Так что это число будет явно отличаться от первого числа. Его вторая десятичная цифра будет на 1 больше, чем вторая десятичная цифра второго числа в перечислении, что даст 0,22… Так что это число будет явно отличаться от второго числа. Его третья десятичная цифра будет на 1 больше, чем третья десятичная цифра третьего числа в перечислении, что дает 0,229.… Так что это число явно будет отличаться от третьего числа. И так далее для всех десятичных цифр до бесконечности. Это иррациональное число отличается от всех иррациональных чисел в перечислении. Таким образом, иррациональные числа нельзя перечислить, не пропустив хотя бы одно иррациональное число. Это означает, что не может быть однозначного соответствия с натуральными числами, и иррациональных чисел больше, чем натуральных (и, следовательно, иррациональных чисел больше, чем рациональных).
Его первая десятичная цифра будет на 1 больше, чем первая десятичная цифра первого числа в перечислении, что дает 0,2… Так что это число будет явно отличаться от первого числа. Его вторая десятичная цифра будет на 1 больше, чем вторая десятичная цифра второго числа в перечислении, что даст 0,22… Так что это число будет явно отличаться от второго числа. Его третья десятичная цифра будет на 1 больше, чем третья десятичная цифра третьего числа в перечислении, что дает 0,229.… Так что это число явно будет отличаться от третьего числа. И так далее для всех десятичных цифр до бесконечности. Это иррациональное число отличается от всех иррациональных чисел в перечислении. Таким образом, иррациональные числа нельзя перечислить, не пропустив хотя бы одно иррациональное число. Это означает, что не может быть однозначного соответствия с натуральными числами, и иррациональных чисел больше, чем натуральных (и, следовательно, иррациональных чисел больше, чем рациональных).
Пусть это впитается. Эти странные иррациональные числа, с которыми вы, вероятно, не слишком часто сталкивались в своей жизни, их гораздо больше, чем знакомые целые и рациональные числа. На самом деле их бесконечно много. Если вы закроете глаза и наугад выберете точку на числовой прямой, вы, скорее всего, выберете иррациональное число!
Эти странные иррациональные числа, с которыми вы, вероятно, не слишком часто сталкивались в своей жизни, их гораздо больше, чем знакомые целые и рациональные числа. На самом деле их бесконечно много. Если вы закроете глаза и наугад выберете точку на числовой прямой, вы, скорее всего, выберете иррациональное число!
Мы видели, что бесконечные множества могут быть довольно нелогичными. Давайте вспомним некоторые из этих странностей и насладимся ими:
- Бесконечное множество (например, целые числа) и бесконечное собственное подмножество множества (например, натуральные числа) могут иметь одинаковое количество элементов. На самом деле все следующие бесконечные множества имеют одинаковое количество элементов: натуральные числа, целые числа, целые числа, четные числа, нечетные числа, простые числа и т. д.
- Более плотное бесконечное множество (в геометрическом представлении множества) может иметь то же количество элементов, что и менее плотное бесконечное множество.


 , отрицательные числа были использованы для представления долга в Индии.
, отрицательные числа были использованы для представления долга в Индии.




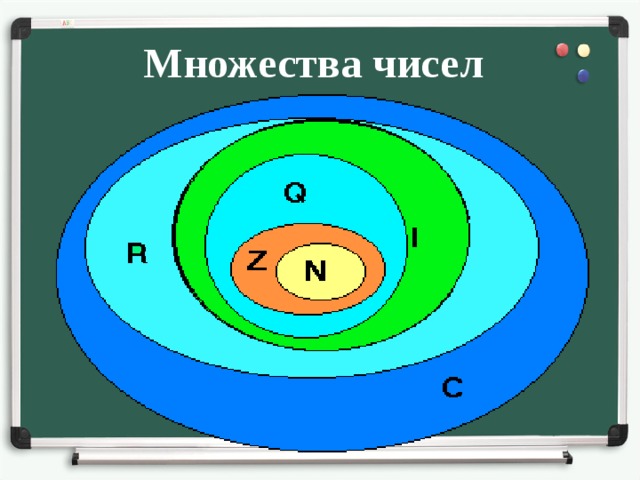 Он доказал, что квадратный корень из 2 нельзя записать в виде дроби, поэтому он иррационален.
Он доказал, что квадратный корень из 2 нельзя записать в виде дроби, поэтому он иррационален.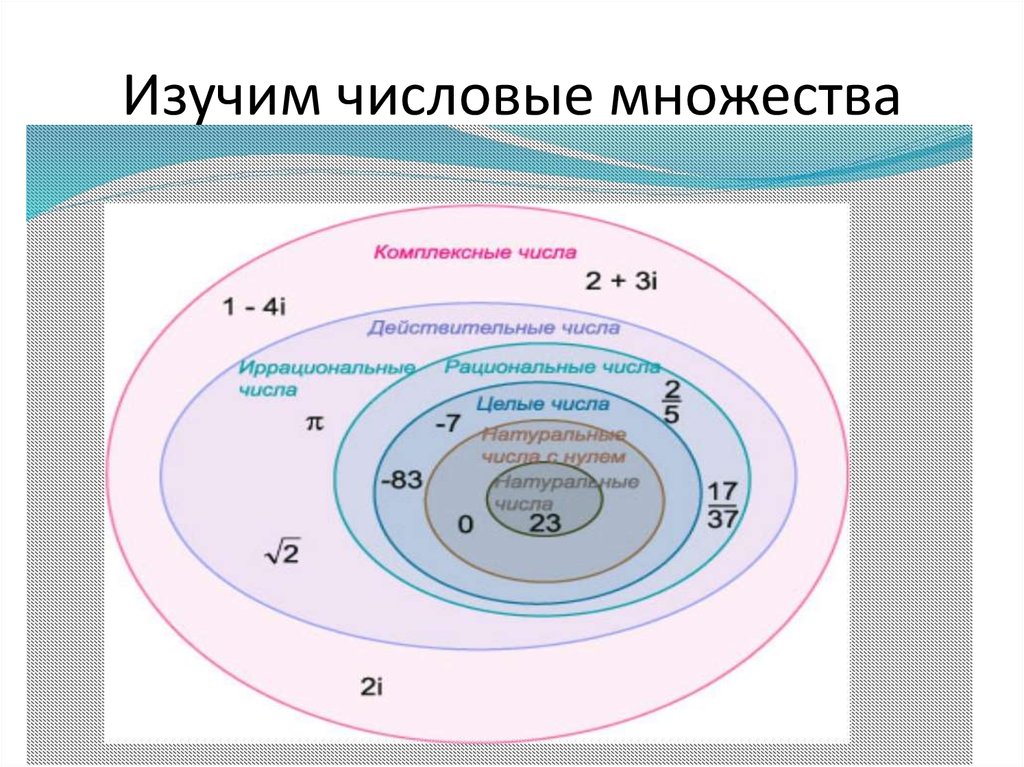 Они начинаются с 1 и идут до бесконечности, т. е. 1, 2, 3, 4, 5, 6 и так далее. Их также называют положительными целыми числами. В установленной форме они могут быть записаны как:
Они начинаются с 1 и идут до бесконечности, т. е. 1, 2, 3, 4, 5, 6 и так далее. Их также называют положительными целыми числами. В установленной форме они могут быть записаны как:
 Например, 0,7 — рациональное число, потому что его можно записать как 7/10. Другими примерами рациональных чисел являются -1/3, 2/5, 99/100, 1,57 и т. д.
Например, 0,7 — рациональное число, потому что его можно записать как 7/10. Другими примерами рациональных чисел являются -1/3, 2/5, 99/100, 1,57 и т. д.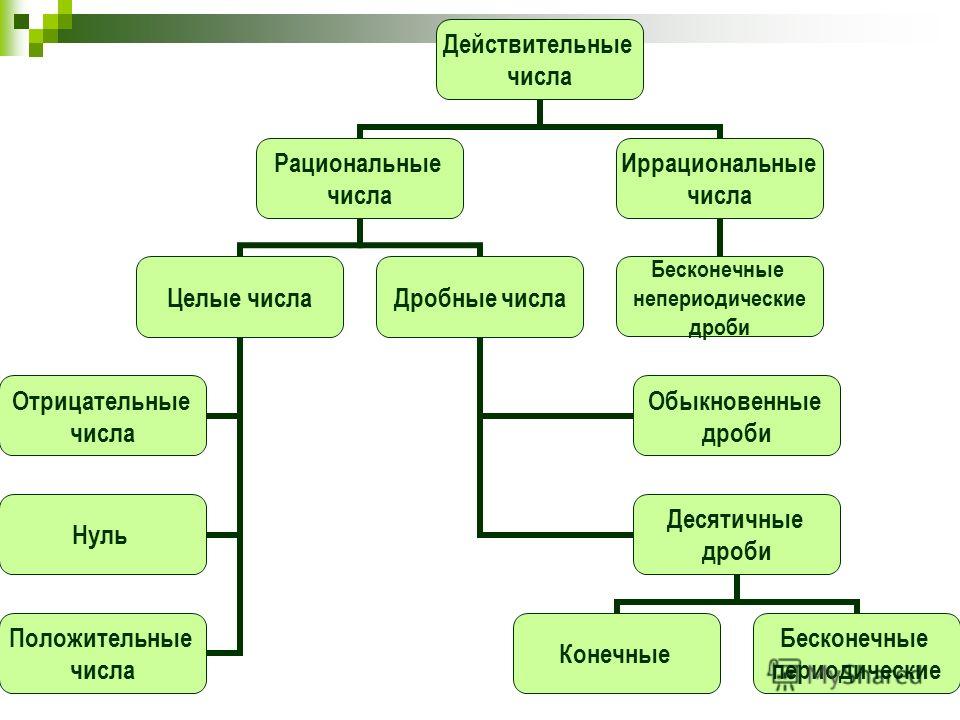 Сюда входят все числа, которые можно записать в десятичной форме. Все целые числа являются действительными числами, но не все действительные числа являются целыми числами. Действительные числа включают в себя все целые числа, целые числа, дроби, повторяющиеся десятичные дроби, завершающие десятичные дроби и так далее.
Сюда входят все числа, которые можно записать в десятичной форме. Все целые числа являются действительными числами, но не все действительные числа являются целыми числами. Действительные числа включают в себя все целые числа, целые числа, дроби, повторяющиеся десятичные дроби, завершающие десятичные дроби и так далее.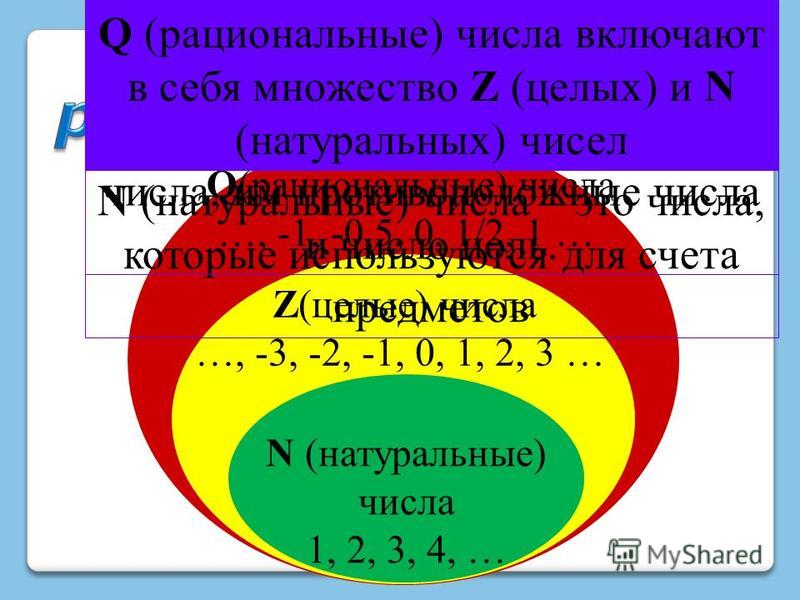
 В исходном уравнении и посмотрите, получим ли мы 0.
В исходном уравнении и посмотрите, получим ли мы 0. 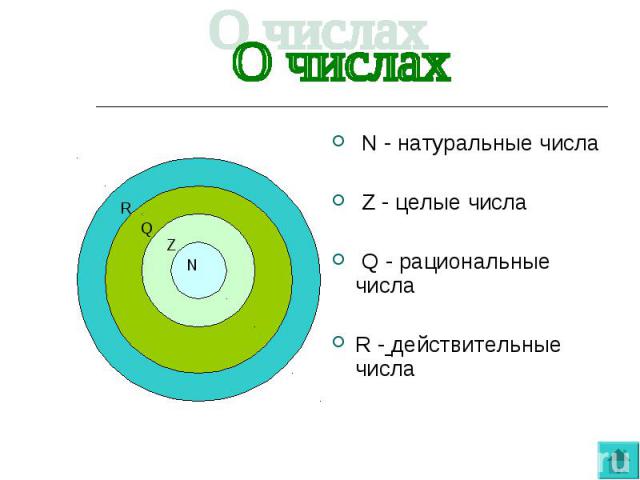 Действительные числа лежат на числовой прямой, а комплексные — на двумерной плоской плоскости.
Действительные числа лежат на числовой прямой, а комплексные — на двумерной плоской плоскости.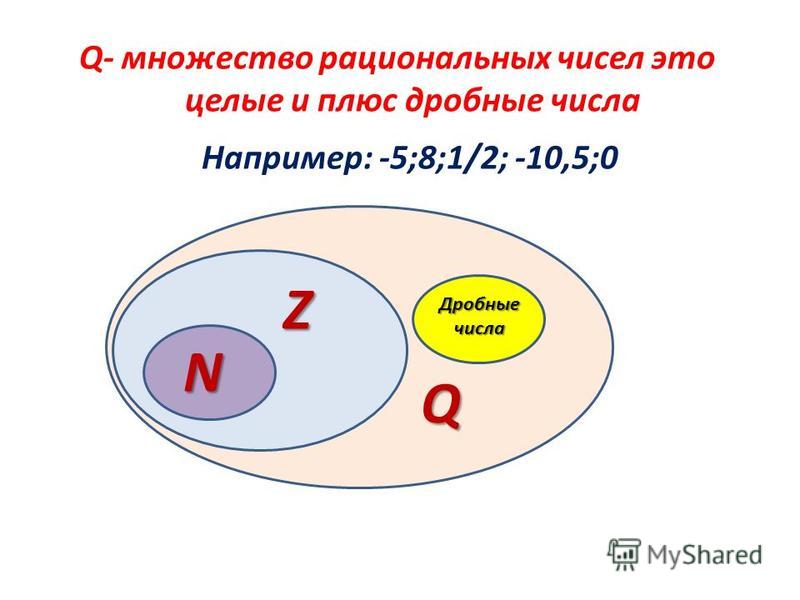
 Каждый тип числа является подмножеством другого типа числа. Например, натуральные числа являются подмножеством целых чисел. Точно так же целые числа являются подмножеством целых чисел. Множество рациональных чисел содержит все целые числа и дроби. Наборы рациональных чисел и иррациональных чисел образуют действительные числа. Действительные числа подпадают под комплексные числа с мнимой частью как 0. Мы можем классифицировать эти числа в иерархической таблице следующим образом:
Каждый тип числа является подмножеством другого типа числа. Например, натуральные числа являются подмножеством целых чисел. Точно так же целые числа являются подмножеством целых чисел. Множество рациональных чисел содержит все целые числа и дроби. Наборы рациональных чисел и иррациональных чисел образуют действительные числа. Действительные числа подпадают под комплексные числа с мнимой частью как 0. Мы можем классифицировать эти числа в иерархической таблице следующим образом: Но спросите кого-нибудь, что такое математика, и вы почти всегда услышите ответ, включающий номера . Они часто являются нашим введением в математику и важным способом найти математику в реальном мире.
Но спросите кого-нибудь, что такое математика, и вы почти всегда услышите ответ, включающий номера . Они часто являются нашим введением в математику и важным способом найти математику в реальном мире. Разные люди могут давать этим наборам разные имена, иногда даже меняя, какое из них они называют 9.0339 натуральный а какой называют целым ! Откройте его своим ученикам: как бы они назвали набор чисел 1, 2, 3…? Какое новое имя они дали бы ему, если бы включили 0?
Разные люди могут давать этим наборам разные имена, иногда даже меняя, какое из них они называют 9.0339 натуральный а какой называют целым ! Откройте его своим ученикам: как бы они назвали набор чисел 1, 2, 3…? Какое новое имя они дали бы ему, если бы включили 0?
 0421 свойство плотности . В нем говорится, что между любыми двумя действительными (или рациональными, или иррациональными) числами всегда есть другое действительное (или рациональное, или иррациональное) число. Например, между 0,4588 и 0,4589 существует число 0,45887 и бесконечно много других. Итак, вот все возможные действительные числа:
0421 свойство плотности . В нем говорится, что между любыми двумя действительными (или рациональными, или иррациональными) числами всегда есть другое действительное (или рациональное, или иррациональное) число. Например, между 0,4588 и 0,4589 существует число 0,45887 и бесконечно много других. Итак, вот все возможные действительные числа: \(6=\frac{6}{1}\)\(0=\frac{ 0}{1}\)\(-4=\frac{-4}{1}\) или \(\frac{4}{-1}\) или \(-\frac{4}{1}\ )
\(6=\frac{6}{1}\)\(0=\frac{ 0}{1}\)\(-4=\frac{-4}{1}\) или \(\frac{4}{-1}\) или \(-\frac{4}{1}\ )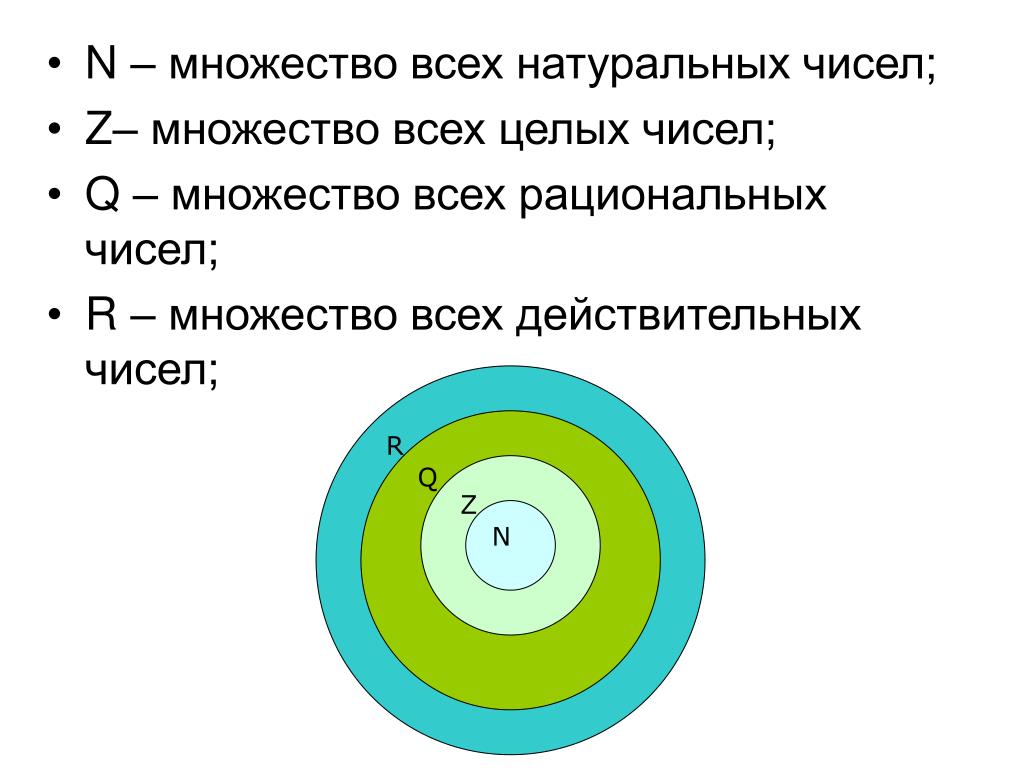 ..) и 0 являются целыми числами. Распространенной ошибкой учащихся 6–8 классов является предположение, что целые числа относятся к отрицательным числам. Точно так же многие студенты задаются вопросом, являются ли десятичные дроби целыми числами? Это верно только тогда, когда десятичная дробь оканчивается на «.000…», например, 3.000…, что равно 3. (Технически это также верно, когда десятичная дробь оканчивается на «.9).99…», так как 0,999… = 1. Это не особенно часто встречается, но число 3 на самом деле может быть записано как 2,999….)
..) и 0 являются целыми числами. Распространенной ошибкой учащихся 6–8 классов является предположение, что целые числа относятся к отрицательным числам. Точно так же многие студенты задаются вопросом, являются ли десятичные дроби целыми числами? Это верно только тогда, когда десятичная дробь оканчивается на «.000…», например, 3.000…, что равно 3. (Технически это также верно, когда десятичная дробь оканчивается на «.9).99…», так как 0,999… = 1. Это не особенно часто встречается, но число 3 на самом деле может быть записано как 2,999….) Эти числа включают непрерывающиеся неповторяющиеся десятичные знаки, например \(\pi\), 0,45445544455544445555… или \(\sqrt{2}\). Любой квадратный корень, не являющийся полным корнем, является иррациональным числом. Например, \(\sqrt{1}\) и \(\sqrt{4}\) рациональны, потому что \(\sqrt{1}=1\) и \(\sqrt{4}=2\), но \(\sqrt{2}\) и \(\sqrt{3}\) иррациональны. Все четыре числа обозначают точки на числовой прямой, но не все они могут быть записаны в виде целочисленных отношений. 92+3=0\) (решение которого равно \(\pm\sqrt{3}i\)).
Эти числа включают непрерывающиеся неповторяющиеся десятичные знаки, например \(\pi\), 0,45445544455544445555… или \(\sqrt{2}\). Любой квадратный корень, не являющийся полным корнем, является иррациональным числом. Например, \(\sqrt{1}\) и \(\sqrt{4}\) рациональны, потому что \(\sqrt{1}=1\) и \(\sqrt{4}=2\), но \(\sqrt{2}\) и \(\sqrt{3}\) иррациональны. Все четыре числа обозначают точки на числовой прямой, но не все они могут быть записаны в виде целочисленных отношений. 92+3=0\) (решение которого равно \(\pm\sqrt{3}i\)).

 Этот
множество чисел иногда также называют множеством нерациональных чисел. Вы узнаете больше об иррациональном
числа далее в этой главе.
Этот
множество чисел иногда также называют множеством нерациональных чисел. Вы узнаете больше об иррациональном
числа далее в этой главе.
 В прошлом году вы научились преобразовывать числа, записанные в десятичной системе счисления, в
обыкновенные дроби. Вот несколько примеров:
В прошлом году вы научились преобразовывать числа, записанные в десятичной системе счисления, в
обыкновенные дроби. Вот несколько примеров: 27272727 \ldots & = 10.\dot{2}\dot{7} \\
2,578578578 \ldots & = 2.\dot{5}7\dot{8} \\
15,32656565 \ldots & = 15,32\dot{6}\dot{5}
\end{выравнивание}
27272727 \ldots & = 10.\dot{2}\dot{7} \\
2,578578578 \ldots & = 2.\dot{5}7\dot{8} \\
15,32656565 \ldots & = 15,32\dot{6}\dot{5}
\end{выравнивание} в знаменателе число 9повторяется столько раз, сколько цифр в числителе.
в знаменателе число 9повторяется столько раз, сколько цифр в числителе. Пусть это будет равно
. Обозначьте уравнение как (1).
Пусть это будет равно
. Обозначьте уравнение как (1).

 Рациональны только квадратные корни, имеющие целые числа, завершающие десятичные дроби или обыкновенные дроби.
числа. Вот примеры квадратных корней, являющихся рациональными числами:
Рациональны только квадратные корни, имеющие целые числа, завершающие десятичные дроби или обыкновенные дроби.
числа. Вот примеры квадратных корней, являющихся рациональными числами: 3 Иррациональные числа
3 Иррациональные числа

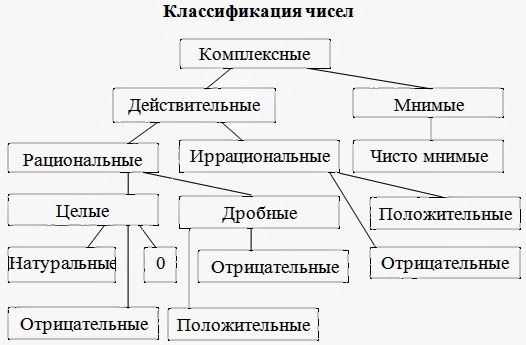 Он представлен символом
. Он представляет различные отношения в круге. Вы должны быть знакомы с
следующие размеры круга:
Он представлен символом
. Он представляет различные отношения в круге. Вы должны быть знакомы с
следующие размеры круга: 1416
\end{выравнивание}
92} \\
=&3.1416
\end{выравнивание}
1416
\end{выравнивание}
92} \\
=&3.1416
\end{выравнивание}