Как выполнить множественную линейную регрессию в Excel
Множественная линейная регрессия — это метод, который мы можем использовать для понимания взаимосвязи между двумя или более независимыми переменными и переменной отклика .
В этом руководстве объясняется, как выполнить множественную линейную регрессию в Excel.
Примечание. Если у вас есть только одна независимая переменная, вам следует вместо этого выполнить простую линейную регрессию .
Пример: множественная линейная регрессия в ExcelПредположим, мы хотим знать, влияет ли количество часов, потраченных на учебу, и количество сданных подготовительных экзаменов на балл, который студент получает на определенном вступительном экзамене в колледж.
Чтобы исследовать эту взаимосвязь, мы можем выполнить множественную линейную регрессию, используя часы обучения и подготовительные экзамены, взятые в качестве объясняющих переменных, и экзаменационный балл в качестве переменной ответа.
Выполните следующие шаги в Excel, чтобы провести множественную линейную регрессию.
Шаг 1: Введите данные.
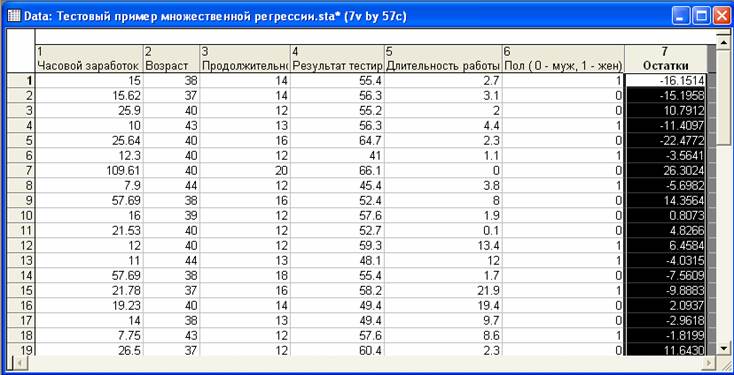
Введите следующие данные для количества часов обучения, сданных подготовительных экзаменов и результатов экзаменов, полученных для 20 студентов:
Шаг 2: Выполните множественную линейную регрессию.
В верхней ленте Excel перейдите на вкладку « Данные » и нажмите « Анализ данных».Если вы не видите эту опцию, вам необходимо сначала установить бесплатный пакет инструментов анализа .
Как только вы нажмете « Анализ данных», появится новое окно. Выберите «Регрессия» и нажмите «ОК».
Для Input Y Range заполните массив значений для переменной ответа. Для Input X Range заполните массив значений для двух независимых переменных. Установите флажок рядом с Метки , чтобы Excel знал, что мы включили имена переменных во входные диапазоны. В поле Выходной диапазон выберите ячейку, в которой должны отображаться выходные данные регрессии. Затем нажмите ОК .
В поле Выходной диапазон выберите ячейку, в которой должны отображаться выходные данные регрессии. Затем нажмите ОК .
Автоматически появится следующий вывод:
Шаг 3: Интерпретируйте вывод.
Вот как интерпретировать наиболее релевантные числа в выводе:
R-квадрат: 0,734.Это известно как коэффициент детерминации. Это доля дисперсии переменной отклика, которая может быть объяснена объясняющими переменными. В этом примере 73,4% вариаций в экзаменационных баллах можно объяснить количеством часов обучения и количеством сданных подготовительных экзаменов.
Стандартная ошибка: 5,366.Это среднее расстояние, на которое наблюдаемые значения отходят от линии регрессии. В этом примере наблюдаемые значения отклоняются от линии регрессии в среднем на 5,366 единицы.
Ф: 23,46.Это общая F-статистика для регрессионной модели, рассчитанная как MS регрессии / остаточная MS.
Значение F: 0,0000.Это p-значение, связанное с общей статистикой F. Он говорит нам, является ли регрессионная модель в целом статистически значимой. Другими словами, он говорит нам, имеют ли объединенные две объясняющие переменные статистически значимую связь с переменной отклика. В этом случае p-значение меньше 0,05, что указывает на то, что независимые переменные количество часов обучения и сданных подготовительных экзаменов вместе имеют статистически значимую связь с экзаменационным баллом .
P-значения. Отдельные p-значения говорят нам, является ли каждая независимая переменная статистически значимой. Мы можем видеть, что изученные часы статистически значимы (p = 0,00), в то время как пройденные подготовительные экзамены (p = 0,52) не являются статистически значимыми при α = 0,05. Поскольку сданные подготовительные экзамены не являются статистически значимыми, мы можем принять решение удалить их из модели.
Коэффициенты: коэффициенты для каждой независимой переменной говорят нам о среднем ожидаемом изменении переменной отклика при условии, что другая независимая переменная остается постоянной. Например, ожидается, что за каждый дополнительный час, потраченный на учебу, средний экзаменационный балл увеличится на 5,56 при условии, что количество сданных подготовительных экзаменов останется неизменным.
Вот еще один способ подумать об этом: если учащийся А и учащийся Б сдают одинаковое количество подготовительных экзаменов, но учащийся А учится на один час больше, то ожидается, что учащийся А получит результат на 5,56 балла выше, чем учащийся Б.
Мы интерпретируем коэффициент для перехвата как означающий, что ожидаемая оценка экзамена для студента, который учится ноль часов и сдает нулевые подготовительные экзамены, составляет 67,67 .
Расчетное уравнение регрессии: мы можем использовать коэффициенты из выходных данных модели, чтобы создать следующее расчетное уравнение регрессии:
экзаменационный балл = 67,67 + 5,56*(часы) – 0,60*(подготовительные экзамены)
Мы можем использовать это оценочное уравнение регрессии, чтобы рассчитать ожидаемый балл экзамена для учащегося на основе количества часов, которые он изучает, и количества подготовительных экзаменов, которые он сдает.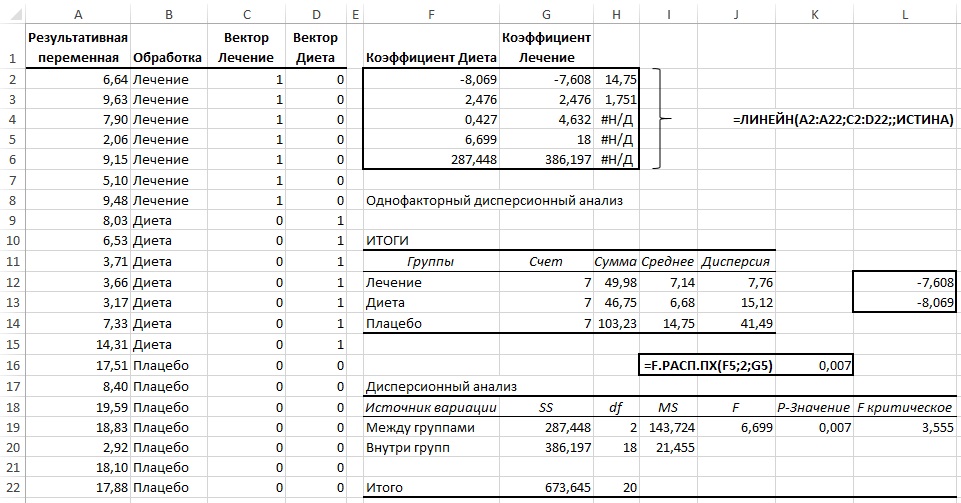 Например, студент, который занимается три часа и сдает один подготовительный экзамен, должен получить 83,75 балла:
Например, студент, который занимается три часа и сдает один подготовительный экзамен, должен получить 83,75 балла:
экзаменационный балл = 67,67 + 5,56*(3) – 0,60*(1) = 83,75
Имейте в виду, что, поскольку пройденные подготовительные экзамены не были статистически значимыми (p = 0,52), мы можем решить удалить их, поскольку они не улучшают общую модель. В этом случае мы могли бы выполнить простую линейную регрессию, используя только часы изучения в качестве независимой переменной.
С результатами этого простого линейного регрессионного анализа можно ознакомиться здесь .
Дополнительные ресурсыПосле выполнения множественной линейной регрессии есть несколько предположений, которые вы можете проверить, в том числе:
1. Тестирование на мультиколлинеарность с помощью VIF .
2. Тестирование на гетеродескедастичность с помощью теста Бреуша-Пагана .
3. Проверка нормальности с использованием графика QQ .
Проверка нормальности с использованием графика QQ .
Как запустить множественную регрессию в Excel за 5 шагов • BUOM
Формулы и математические уравнения — это исключительные инструменты, которые помогают людям из всех отраслей получить представление о будущих результатах, что позволяет им делать более обоснованные прогнозы на основе данных. Одним из таких инструментов является метод множественной регрессии, представляющий собой формулу, которую вы можете использовать в Excel для оптимизации получаемой информации в упрощенной и доступной форме. Изучение этого измерения может помочь вам применить свои собственные бизнес-потребности. В этой статье мы обсудим, что такое множественная регрессия, рассмотрим причины, почему ее полезно использовать, и узнаем, как измерить формулу в Excel.
Что такое множественная регрессия?
Множественная регрессия или множественная линейная регрессия — это математический метод, использующий несколько независимых переменных для статистического прогнозирования результата зависимой переменной. Вы можете использовать эту технику, чтобы отвечать на важные бизнес-вопросы, принимать реалистичные финансовые решения и выполнять другие операции, управляемые данными.
Вы можете использовать эту технику, чтобы отвечать на важные бизнес-вопросы, принимать реалистичные финансовые решения и выполнять другие операции, управляемые данными.
Одной из основных целей использования множественной линейной регрессии является определение линейной связи между независимыми переменными и зависимой переменной. Независимые переменные — это элементы, которые вы изменяете и контролируете в ходе анализа, и эти изменения влияют на изменение зависимой переменной.
Какова формула множественной регрессии?
Формула множественной регрессии выглядит следующим образом:
Программы для Windows, мобильные приложения, игры — ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале — Подписывайтесь:)
Y = ß0 + ß1×1 + ß2×2 + … + ßpxp
Вот элементы этого уравнения:
Y: эта цифра представляет собой зависимую переменную.
x1, x2 и xp: эти элементы представляют собой независимые переменные.
ß0: представляет собой значение Y, когда каждая независимая переменная равна нулю.

ß1, ß2 и ßp: они представляют собой оценочные коэффициенты регрессии, которые описывают изменение зависимой переменной относительно изменения независимой переменной на одну единицу.
Зачем запускать множественную регрессию в Excel?
Существует несколько причин запуска множественной регрессии в Excel, например:
Улучшенные прогнозные данные. Основная причина запуска множественной регрессии в Excel — получение более полных сведений о прогнозируемом целевом объекте. Когда есть несколько переменных, которые вы можете включать и выключать из уравнения, вы можете получить более точное описание конечного результата.
Улучшенное решение проблем: этот метод полезен для решения проблем, поскольку он предоставляет информацию для оценки того, дают ли конкретные переменные положительные или отрицательные результаты. Если результат неблагоприятный, может стать проще определить проблему и внедрить новые переменные для ее решения.
Улучшенное принятие решений: успешное выполнение формулы множественной регрессии дает вам необходимые данные для принятия более обоснованных решений.
 Это гарантирует, что вы сможете сделать выбор или правильно настроить параметры для получения желаемых результатов.
Это гарантирует, что вы сможете сделать выбор или правильно настроить параметры для получения желаемых результатов.Создание моделей визуализации. Вы можете реализовать данные, полученные в результате множественного регрессионного анализа, в визуальное представление этой информации. Независимо от того, используете ли вы диаграмму или график, возможность визуализации данных может облегчить понимание для вас и ваших коллег.
Упрощенный процесс вычислений: Преимущество использования множественной регрессии в Excel заключается в том, что программа интуитивно понятна и позволяет выполнять различные сложные уравнения упрощенным способом. Вы можете найти такую же простоту доступа при расчете или внесении изменений в формулу множественной регрессии.
Выявление аномалий или выбросов. Когда вы запускаете формулу множественной регрессии, вы можете лучше оценить аномалии или выбросы в ваших данных. Оттуда вы можете определить, что означают эти выбросы, как они влияют на ваши результаты, имеют ли они какое-либо значение и почему они могли произойти.

Определение относительного влияния: метод множественной регрессии полезен для определения относительного влияния одной переменной на другую. Это может помочь вам определить, насколько релевантна переменная для достижения надлежащего результата, и сможете ли вы извлечь выгоду из использования более значимой переменной.
Применение в различных сценариях. Множественная регрессия имеет универсальное применение, что позволяет использовать ее для различных сценариев и ситуаций. Это делает его довольно доступным методом, который люди из любой отрасли или сектора бизнеса могут использовать для получения осмысленной информации о своих инициативах и целях.
Как запустить множественную регрессию в Excel
Вот пять шагов, которые помогут вам запустить метод множественной регрессии в Excel:
1. Активируйте пакет инструментов анализа данных
После того, как вы откроете Excel, первым делом убедитесь, что пакет инструментов анализа данных активен. Вы можете сделать это, выполнив следующие действия:
Вы можете сделать это, выполнив следующие действия:
Перейдите на вкладку «Данные».
Если вы не видите вкладку «Данные», включите ее, перейдя в меню «Файл».
Нажмите «Параметры».
Нажмите «Надстройки» на левой панели заполненного окна.
Нажмите «Перейти», который находится рядом с опцией «Управление: надстройки», расположенной в нижней части окна.
Когда появится новое окно, установите флажок «AnalysisToolPak» и нажмите «ОК», чтобы включить надстройку.
2. Введите свои основные данные
Следующим шагом является ввод основных данных вручную. Вы также можете открыть файл данных для автоматического ввода информации в лист Excel. Обязательно расположите данные в соседних столбцах и поместите метки в первую строку каждого столбца.
3. Введите зависимые данные
Третий шаг — выбрать вкладку «Данные», а затем выбрать параметр «Анализ данных» в группе «Анализ». Когда окно «Регрессия» заполнится, добавьте зависимые данные в поле «Входной диапазон Y». Затем выделите столбец данных на листе Excel.
Затем выделите столбец данных на листе Excel.
4. Введите свои независимые данные
В том же окне введите свои независимые переменные в поле «Входной X-диапазон». Затем выделите несколько независимых столбцов данных на листе. Убедитесь, что ваши независимые столбцы переменных данных расположены рядом друг с другом.
5. Проведите анализ
Наконец, выберите предпочтительные параметры в области «Остатки». Если вы хотите создать визуализированный вывод, выберите параметры «Графики с линейным соответствием» и «Остаточные графики». Затем нажмите кнопку «ОК», чтобы создать множественный регрессионный анализ в Excel. При необходимости вы можете внести коррективы в уравнение и переменные.
Обратите внимание, что ни одна из компаний, упомянутых в этой статье, не связана с компанией Indeed.
Похожие записи
10 обязательных навыков няни в резюме (с примером резюме)
Как стать писателем-анималистом (плюс обязанности и зарплата)
25 рабочих мест для новаторов (с обязанностями и средней зарплатой)
Структура анализа конкурентов: определение, преимущества и типы
Узнайте о том, как стать косметологом
Как стать консультантом по зависимостям за 6 шагов (с советами)
Множественная регрессия EXCEL
Множественная регрессия EXCEL Колин Кэмерон, факультет экономики, Университет. из
Калифорния
— Дэвис
Колин Кэмерон, факультет экономики, Университет. из
Калифорния
— Дэвис - Множественная регрессия с использованием надстройки анализа данных.
- Интерпретация статистики регрессии.
- Интерпретация таблицы ANOVA (часто это пропускается).
- Интерпретация таблицы коэффициентов регрессии.
- Доверительные интервалы для параметров наклона.
- Проверка статистической значимости коэффициентов
- Проверка гипотезы о параметре наклона.
- Проверка общей значимости регрессоров.
- Предсказание y заданных значений регрессоров.
- Ограничения Excel.
Основным дополнением является F-тест на общую пригодность.
МНОЖЕСТВЕННАЯ РЕГРЕССИЯ С ИСПОЛЬЗОВАНИЕМ НАДПОЛНЕНИЯ АНАЛИЗА ДАННЫХ
 Excel
2007: Доступ и активация
Надстройка анализа данных
Excel
2007: Доступ и активация
Надстройка анализа данных Используемые данные находятся в файле carsdata.xls
. Затем мы создаем новую переменную в ячейках C2:C6, размер домохозяйства в кубе.
как
регрессор.
Затем в ячейке C1 введите заголовок CUBED HH SIZE.
(Оказывается, что
для этих данных в квадрате HH SIZE коэффициент равен точно 0,0.
используется куб).
Ячейки электронной таблицы A1:C6 должны выглядеть так:
У нас есть регрессия с перехватом и регрессоры HH SIZE и РАЗМЕР В КУБАХ
Модель регрессии населения: y = β 1 + β 2 x 2 + β 3 x 3 + u
Предполагается, что ошибка u независима с постоянной дисперсией
(гомоскедастический) — см. ОГРАНИЧЕНИЯ EXCEL внизу.
Мы хотим оценить линию регрессии: y =
б 1 + б 2 х 2 + б 3 х 3
Мы делаем это с помощью надстройки анализа данных и регрессии.
Единственное изменение по сравнению с регрессией с одной переменной заключается в включении более
один столбец в диапазоне ввода X.
Обратите внимание, однако, что регрессоры должны быть в смежных столбцах.
(здесь столбцы B и C).
Если это не так в исходных данных, то столбцы должны быть
скопировано, чтобы получить регрессоры в смежных столбцах.
Нажимаем OK получаем
- Таблица статистики регрессии
- Таблица дисперсионного анализа
- Таблица коэффициентов регрессии.
ИНТЕРПРЕТАЦИЯ СТАТИСТИЧЕСКОЙ ТАБЛИЦЫ РЕГРЕССИИ
Это следующий вывод. Наибольший интерес представляет R Square.
| | | Пояснение |
| Несколько R | 0,895828 | R = квадратный корень из R 2 |
| Квадрат R | 0,802508 | Р 2 |
| Регулируемый квадрат R | 0,605016 | Скорректированный R 2 используется, если более одной переменной x |
| Стандартная ошибка | 0,444401 | Это примерная оценка стандартного отклонения ошибка ты |
| Наблюдения | 5 | Количество наблюдений, использованных в регрессии (n) |
Выше приведены общие показатели соответствия:
R 2 = 0,8025
Корреляция между y и y-шляпой
0,8958
(при возведении в квадрат дает 0,8025 ).
Скорректировано R 2 = R 2 —
(1-R 2 )*(к-1)/(н-к)
= 0,8025 — 0,1975 * 2/2 = 0,6050.
Стандартная ошибка здесь относится к предполагаемому стандартному отклонению
из
термин ошибки u.
Иногда ее называют стандартной ошибкой регрессии. Это равно
sqrt(SSE/(n-k)).
Не следует путать со стандартной ошибкой самого y (от
описательной статистики) или со стандартными ошибками регрессии
коэффициенты
нижеприведенный.
R 2 = 0,8025 означает, что
80,25% вариации y
ИНТЕРПРЕТАЦИЯ ТАБЛИЦЫ ANOVA
Дана таблица ANOVA. Это часто пропускают.
| | дф | нержавеющая сталь | МС | Ф | Значение F |
| Регрессия | 2 | 1. 6050 6050 | 0,8025 | 4.0635 | 0,1975 |
| Остаток | 2 | 0,3950 | 0,1975 | | |
| Итого | 4 | 2,0 | | | |
Таблица ANOVA (дисперсионный анализ) разбивает сумму квадраты на его составляющие.
Общая сумма квадратов
= остаточная (или ошибочная) сумма квадратов + регрессионная (или объясненная) сумма
квадратов.
Таким образом Σ я (у я — убар) 2 = Σ i (y i — yhat i ) 2 + Σ i (yhat i — ybar) 2
где yhat i — это предсказанное значение y i от линии регрессии
ybar – это выборочное среднее y.
Например:
R 2 = 1 — Остаточная СС / Общая СС (общая
формула R 2 )
= 1 —
0,3950 / 1,6050 (из данных таблицы ANOVA)
«=»
0,8025 (что равно R 2 , приведенным в таблице статистики регрессии).
Столбец с пометкой F дает общий F-критерий H0: β
В стороне: Excel вычисляет F это как:
F = [Регрессия SS/(k-1)] / [Остаточное SS/(n-k)] = [1,6050/2] /
[0,39498/2]
= 4,0635.
Столбец с пометкой значимость F имеет связанное P-значение.
С
0,1975 > 0,05, мы не отвергаем H0 на уровне значимости 0,05.
Примечание. Значение F в целом = FОБР(F, k-1, n-k), где k
количество регрессоров, включая перехват.
Здесь FINV(4,0635,2,2) = 0,1975.
ИНТЕРПРЕТАЦИЯ КОЭФФИЦИЕНТОВ РЕГРЕССИИ ТАБЛИЦА
Наиболее интересными выходными данными регрессии является следующая таблица
коэффициенты
и связанный вывод:
| | Коэффициент | Св. ошибка ошибка | т Стат | P-значение | Нижний 95% | Верхний 95% |
| Перехват | 0,89655 | 0,76440 | 1.1729 | 0,3616 | -2,3924 | 4,1855 |
| РАЗМЕР НВ | 0,33647 | 0,42270 | 0,7960 | 0,5095 | -1,4823 | 2.1552 |
| КУБИЧЕСКИЙ РАЗМЕР HH | 0,00209 | 0,01311 | 0,1594 | 0,8880 | -0,0543 | 0,0585 |
Пусть β j обозначает коэффициент населенности j-го регрессор (перехват, РАЗМЕР HH и РАЗМЕР В КУБАХ HH).
Тогда
- Столбец « Коэффициент » дает оценки методом наименьших квадратов β j .

- Столбец « Стандартная ошибка » содержит стандартные ошибки (т.е. оцененный стандартное отклонение) оценок методом наименьших квадратов b j β и .
- Столбец « t Stat » дает вычисленную t-статистику для H0: β j = 0 против
Ha: β j ≠ 0,
- Столбец « P-значение » дает p-значение для теста H0: β j = 0 против
Ha: β j ≠ 0..
- Столбцы «Нижние 95%» и «Верхние 95%» определяют 95%
доверительный интервал
для β j .

Обратите внимание, что это значение p для двустороннего теста. Для одностороннего теста разделите это p-значение на 2 (также проверяя знак t-Stat).
y = 0,8966 + 0,3365*x + 0,0021*z
CO ИНТЕРВАЛЫ NFIDENCE ДЛЯ КОЭФФИЦИЕНТЫ НАКЛОНА
95% доверительный интервал для коэффициента наклона β 2 взят из Вывод в Excel (-1,4823, 2.1552).
Excel вычисляет это как
б 2 ± t_.025(3) × se(б 2 )
= 0,33647 ± TОБР(0,05, 2) × 0,42270
= 0,33647 ± 4,303 × 0,42270
= 0,33647 ± 1,8189
= (-1,4823,
2.1552).
Например, чтобы найти 99% доверительные интервалы: в диалоговом окне Регрессия поле (в поле Данные Надстройка анализа),
установите флажок «Уровень достоверности» и установите уровень 99%.
ПРОВЕРКА ГИПОТЕЗЫ О НУЛЕВОМ КОЭФФИЦИЕНТЕ НАКЛОНА («ПРОВЕРКА СТАТИСТИЧЕСКИХ ЗНАЧЕНИЕ»)
Расчетная стандартная ошибка коэффициента HH SIZE составляет 0,4227,
t-статистика
0,7960 и p-значение 0,5095.
Следовательно, он статистически незначим на уровне значимости α =
0,05 при р > 0,05.
Коэффициент CUBED HH SIZE оценил стандартную ошибку в
0,0131,
t-статистика 0,1594 и p-значение 0,8880.
Следовательно, он статистически незначим на уровне значимости α =
0,05 при р > 0,05.
Есть 5 наблюдений и 3 регрессора (перехват и x), поэтому мы
использовать
т(5-3)=т(2).
Например, для РАЗМЕРА ЧЧ p = =TDРАСП(0,796,2,2) = 0,5095.
ПРОВЕРКА ГИПОТЕЗЫ ПО ПАРАМЕТРУ РЕГРЕССИИ
Здесь мы проверяем, имеет ли HH SIZE коэффициент β 2 = 1,0.
Пример: H0: β 2 = 1,0 против
Ha: β 2 ≠ 1,0 при значимости
уровень α = 0,05.
Затем
t = (b 2 — H0 значение β 2 ) / (стандартное
ошибка b 2 )
= (0,33647 — 1,0) / 0,42270
= -1,569.
Использование метода p-значения
- p-значение = СТЬЮДРАСП(1,569, 2, 2) = 0,257.
 [Здесь n=5 и k=3, поэтому
n-k=2].
[Здесь n=5 и k=3, поэтому
n-k=2]. - Не отклонять нулевое значение гипотеза на уровне 0,05, поскольку значение p > 0,05.
- Мы вычислили t = -1,569
- Критическое значение t_.025(2) = TINV(0.05,2) = 4.303. [Здесь n=5 и k=3, поэтому n-k=2].
- Так что не отклоняйте нуль гипотеза на уровне 0,05, поскольку t = |-1,569| < 4,303.
ОБЩАЯ ПРОВЕРКА ЗНАЧИМОСТИ ПАРАМЕТРОВ РЕГРЕССИИ
Тестируем H0: β 2 = 0 и β 3 =
0 по сравнению с Ha: по крайней мере один из β 2 и β 3 не соответствует
равен нулю.
Из таблицы ANOVA статистика F-критерия равна 4,0635 с p-значением
0,1975.
Поскольку p-значение не меньше 0,05, мы не отклоняем нулевое значение.
гипотеза
что параметры регрессии равны нулю на уровне значимости 0,05.
93 =
64.
йхат =
б 1 + б 2 х 2 + б 3 х 3 = 0,88966 + 0,3365 × 4 + 0,0021 × 64
= 2,37006
ОГРАНИЧЕНИЯ EXCEL
Excel ограничивает количество регрессоров (только до 16 регрессоров). ??).
??).
Excel требует, чтобы все переменные регрессора находились в соседних
столбцы.
Возможно, вам придется переместить столбцы, чтобы убедиться в этом.
например Если регрессоры находятся в столбцах B и D, вам нужно скопировать как минимум
один из столбцов B и D так, чтобы они были рядом друг с другом.
Стандартные ошибки Excel, а также t-статистика и p-значения основаны на
предположение, что ошибка независима с постоянной дисперсией
(гомоскедастический).
Excel не предоставляет альтернатив, таких как гетероскедастический или устойчивый.
устойчивые к автокорреляции стандартные ошибки, t-статистика и p-значения.
Более специализированное программное обеспечение, такое как STATA, EVIEWS, SAS, LIMDEP, PC-TSP,
… необходим.
Для получения дополнительной информации об использовании Excel см.
http://cameron.econ.ucdavis.edu/excel/excel.html
Регрессионный анализ Excel | Реальная статистика с использованием Excel.
 тыс. независимых переменных.
тыс. независимых переменных. Свойство 1 :
Доказательство. Доказательство такое же, как и для свойства 1 регрессионного анализа.
Свойство 2 : где R — коэффициент множественной корреляции (определенный в определении 1 множественной корреляции) Регрессионный анализ, соответственно, и их доказательства аналогичны.
Наблюдение : Из свойства 2 и второго утверждения свойства 3,
, которое является многомерной версией свойства 1 основных понятий корреляции.
Собственность 3 :
Свойство 4 : MS RES — это непредвзятая оценка, где находится дисперсия по ошибке
. Матрицы, ковариационная матрица B может быть оценена как
В частности, диагональ C = [ c ij ] содержит дисперсию b j , поэтому стандартная ошибка j может быть выражена как 2 j
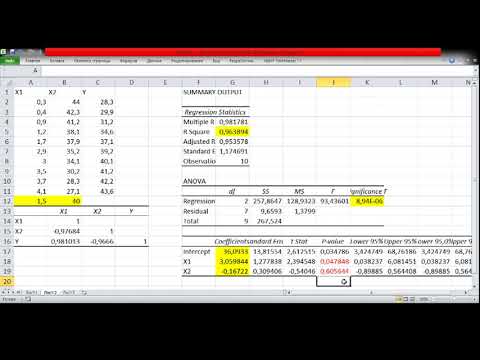
Пример 1 : Рассчитать коэффициенты линейной регрессии и их стандартные ошибки для данных в Примере 1 метода наименьших квадратов для множественной регрессии (повторяется ниже на рисунке с использованием матричных методов.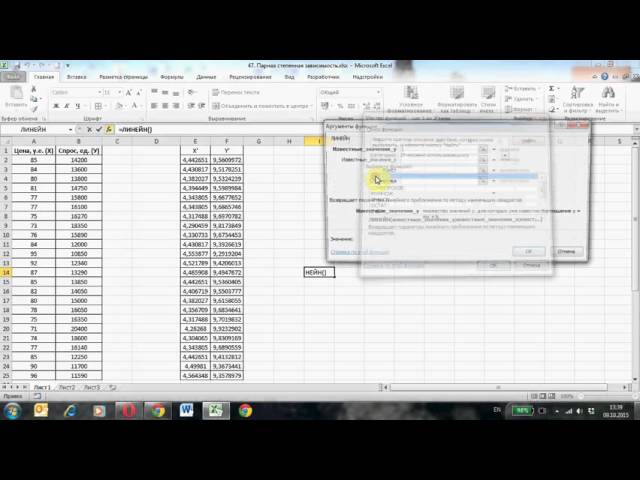
Рисунок 1 – Создание линии регрессии с использованием матричных методов
Результат показан на рисунке 1. Диапазон E4:G14 содержит матрицу проектирования X , а диапазон I4:I14 содержит Y . Матрица ( X T X ) -1 в диапазоне E17:G19 может быть рассчитана с использованием формулы массива
= MINVERSE(MMULT(TRANSPOSE(E4:G14),E4:G14))
Согласно свойству 1 множественной регрессии с использованием матриц вектор коэффициентов равен 9.0626 B (в диапазоне K4:K6) можно рассчитать по формуле массива:
=ММНОЖ(E17:G19,ММНОЖ(ТРАНСП(E4:G14),I4:I14))
Прогнозируемые значения Y , т. е. Y -шляпа, можно затем рассчитать с помощью формулы массива
=МУМНОЖ(E4:G14,K4:K6)
Стандартную ошибку каждого из коэффициентов в B можно рассчитать следующим образом. Сначала вычислите массив членов ошибки E (диапазон O4:O14), используя формулу массива I4:I14 – M4:M14.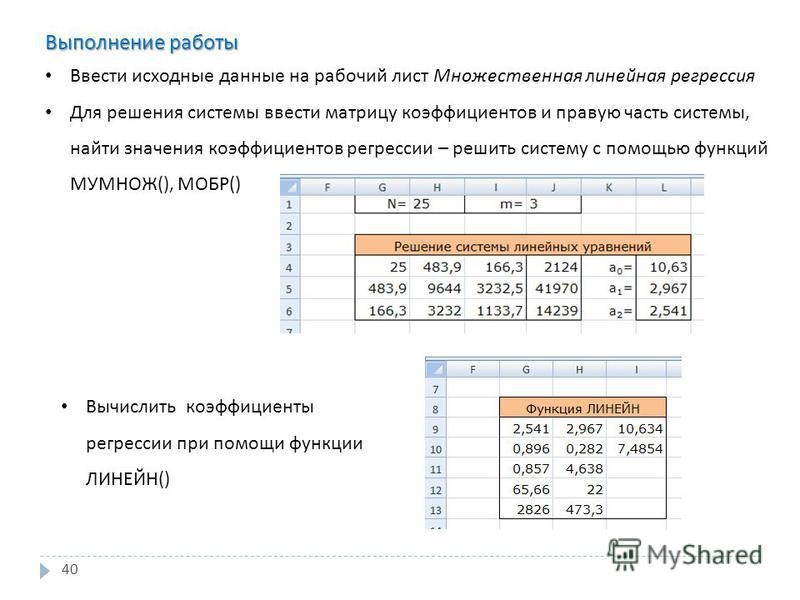 Тогда, как и в случае простой регрессии SS RES = DEVSQ (O4: O14) = 277,36, DF RES = N — K — 1 = 2 — 1 = 8 и МС 66663.s
Тогда, как и в случае простой регрессии SS RES = DEVSQ (O4: O14) = 277,36, DF RES = N — K — 1 = 2 — 1 = 8 и МС 66663.s
Из наблюдения, следующего за свойством 4, следует, что MS Res ( X T X ) -1 является ковариационной матрицей для диагональных коэффициентов, поэтому стандартная ошибка коэффициентов. В частности, стандартная ошибка перехвата b 0 (в ячейке К9) выражается формулой =КОРЕНЬ(I17), стандартная ошибка цветового коэффициента b 1 (в ячейке К10) выражается формулой =КОРЕНЬ(J18) , а стандартная ошибка коэффициента качества b 2 (в ячейке К11) выражается формулой =КОРЕНЬ(К19).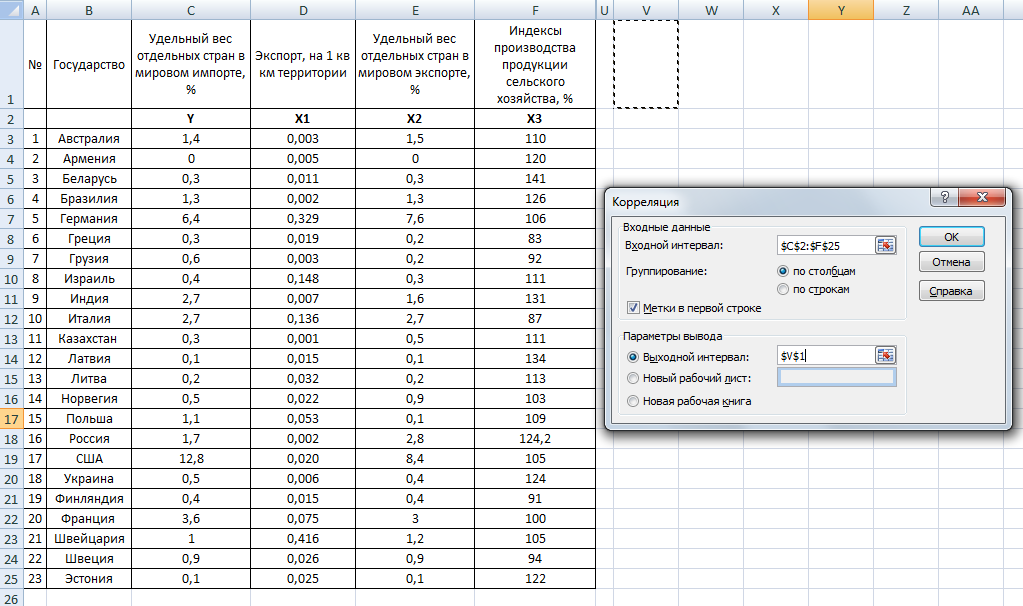
Функции Excel: Функции НАКЛОН, ПЕРЕМЕЩЕНИЕ, СТЕЙКС и ПРОГНОЗ не работают для множественной регрессии, но функции ТРЕНД и ЛИНЕЙН поддерживают множественную регрессию, как и инструмент анализа данных регрессии.
TREND работает точно так же, как описано в методе наименьших квадратов, за исключением того, что второй параметр R2 теперь будет содержать данные для всех независимых переменных.
ЛИНЕЙН работает так же, как и в случае простой линейной регрессии, за исключением того, что вместо использования области 5 × 2 для выходных данных требуется область 5 × 90 626 k 90 629, где 90 626 k 90 629 = количество независимых переменных + 1. Таким образом, для модели с тремя независимыми переменными вам нужно выделить пустую область 5 × 4. Как и раньше, вам нужно вручную добавить соответствующие метки для ясности.
Инструмент анализа данных Regression работает точно так же, как и в случае простой линейной регрессии, за исключением того, что для каждой из независимых переменных создаются дополнительные диаграммы.
Пример 2 : Мы возвращаемся к примеру 1 множественной корреляции, анализируя модель, в которой уровень бедности может быть оценен как линейная комбинация уровня младенческой смертности, доли белого населения и уровня насильственных преступлений ( на 100 000 человек).
We need to find the parameters b 0 , b 1 and such that
Poverty (predicted) = b 0 + b 1 ∙ Infant + b 2 ∙ Белый + b 3 ∙ Криминал.
Мы иллюстрируем, как использовать ТРЕНД и ЛИНЕЙН на рисунке 2.
Рисунок 2 – ТРЕНД и ЛИНЕЙН для данных в примере 1 ) и процент бедности, прогнозируемый, когда младенческая смертность, доля белых в населении и уровень преступности соответствуют указанным (диапазон G6:J8). Выделив диапазон J6:J8, вводим формулу массива =TREND(B4:B53,C4:E53,G6:I8). Как видно из рисунка 2, модель предсказывает уровень бедности в 12,87%, когда младенческая смертность составляет 7,0, белые составляют 80% населения, а насильственные преступления составляют 400 на 100 000 человек.
На рис. 2 также показаны выходные данные функции ЛИНЕЙН после того, как мы выделим заштрихованный диапазон h23:K17 и введем =ЛИНЕЙН(B4:B53,C4:E53,ИСТИНА,ИСТИНА). Заголовки столбцов b 1 , b 2 , b 3 и точка пересечения относятся только к первым двум строкам (обратите внимание на порядок коэффициентов). Остальные три строки содержат по два значения в каждой, помеченные слева и справа.
Таким образом, мы видим, что линия регрессии равна
Бедность = 0,437 + 1,279∙ Младенческая смертность + 0,0363 ∙ Белые + 0,00142 ∙ Преступность
Здесь Бедность представляет прогнозируемое значение. Мы также видим, что R Square равен 0,337 (т. е. 33,7% дисперсии уровня бедности объясняется моделью), стандартная ошибка оценки составляет 2,47 и т. д.
Мы также можем использовать инструмент анализа данных регрессии, чтобы получить результат, показанный на рисунке 3.
Рисунок 3. Выходные данные инструмента регрессионного анализа данных
Выходные данные инструмента регрессионного анализа данных
Поскольку значение p = 0,00026 < 0,05 = α , мы заключаем, что регрессионная модель хорошо подходит; то есть существует только 0,026% вероятность получить такую высокую корреляцию (0,58) при условии, что нулевая гипотеза верна.
Обратите внимание, что значения p для всех коэффициентов, за исключением коэффициента детской смертности, превышают 0,05. Это означает, что мы не можем отвергнуть гипотезу о том, что они равны нулю (и поэтому могут быть исключены из модели). Это подтверждается и тем, что 0 лежит в промежутке между нижними 95% и верхние 95% (т.е. 95% доверительный интервал) для каждого из этих коэффициентов.
Если мы повторно запустим инструмент регрессионного анализа данных только с использованием переменной младенческой смертности, мы получим результаты, показанные на рис. 4.
= 4,27 + 1,23 ∙ Младенческая смертность хорошо соответствует данным (значение p = 1,96E-05 < 0,05).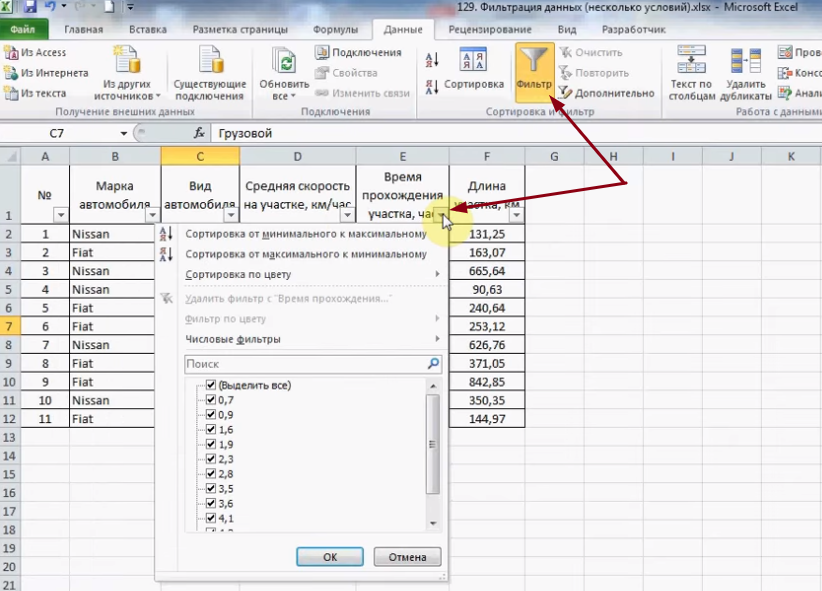 Мы также видим, что оба коэффициента значимы. Самое главное мы видим, что R Square равен 31,9%, что ненамного меньше значения R Square 33,7%, которое мы получили из более крупной модели (на рис. 3). Все это указывает на то, что переменные White и Crime не вносят большого вклада в модель и могут быть исключены.
Мы также видим, что оба коэффициента значимы. Самое главное мы видим, что R Square равен 31,9%, что ненамного меньше значения R Square 33,7%, которое мы получили из более крупной модели (на рис. 3). Все это указывает на то, что переменные White и Crime не вносят большого вклада в модель и могут быть исключены.
Дополнительную информацию о том, как проверить, можно ли исключить независимые переменные из модели, см. в разделе Проверка значимости дополнительных переменных в регрессионной модели.
Нажмите здесь, чтобы увидеть альтернативный способ определения того, подходит ли регрессионная модель.
Пример 3 : Определите, подходит ли регрессионная модель для данных из примера 1 метода наименьших квадратов для множественной регрессии, используя инструмент регрессионного анализа данных.
Результаты анализа представлены на рисунке 5.
Рисунок 5. Выходные данные инструмента анализа данных регрессии
регрессионная модель Прайса = 1,75 + 4,90 ∙ Цвет + 3,76 ∙ Качество хорошо подходит для данных. Обратите внимание, что все коэффициенты значимы. То, что R квадрат = 0,85, указывает на то, что модель охватывает большую часть изменчивости цены.
Обратите внимание, что все коэффициенты значимы. То, что R квадрат = 0,85, указывает на то, что модель охватывает большую часть изменчивости цены.
Наблюдение : Мы можем рассчитать все записи в анализе данных регрессии на рисунке 5, используя формулы Excel следующим образом:
Дисперсионный анализ
- SS T = DEVSQ(C4:C14)
- SS Reg = DEVSQ(M4:M14) из рисунка 3 метода наименьших квадратов для множественной регрессии
- нержавеющая сталь рез = G16-G14
- . Все остальные записи можно рассчитать аналогично тому, как мы рассчитали значения ANOVA для примера 1 проверки соответствия линии регрессии (см. рис. 1 на этой веб-странице).
Коэффициенты (в третьей таблице) — показываем, как считать поля перехвата; поля цвета и качества аналогичны
- Коэффициент и стандартная ошибка могут быть рассчитаны, как показано на рисунке 3 метода наименьших квадратов для множественной регрессии
- т Стат = F19/G19
- P-значение = T.
 DIST.2T(ABS(h29),F15)
DIST.2T(ABS(h29),F15) - Нижний 95% = F19-T.INV.2T(0,05,F15)*G19
- Верхние 95% = F19+T.ОБР.2T(0,05,F15)*G19
Остальные выходные данные регрессионного анализа данных показаны на рис. 6. 9Рисунок 6. Остатки/процентили выходных данных регрессии В частности, записи для Наблюдения 1 можно рассчитать следующим образом:
- Прогнозируемая цена =F19+A4*F20+B4*F21 (из рисунка 5)
- Остатки =C4-F26
- Стандартные остатки =G26/СТАНДОТКЛОН.S(G26:G36)
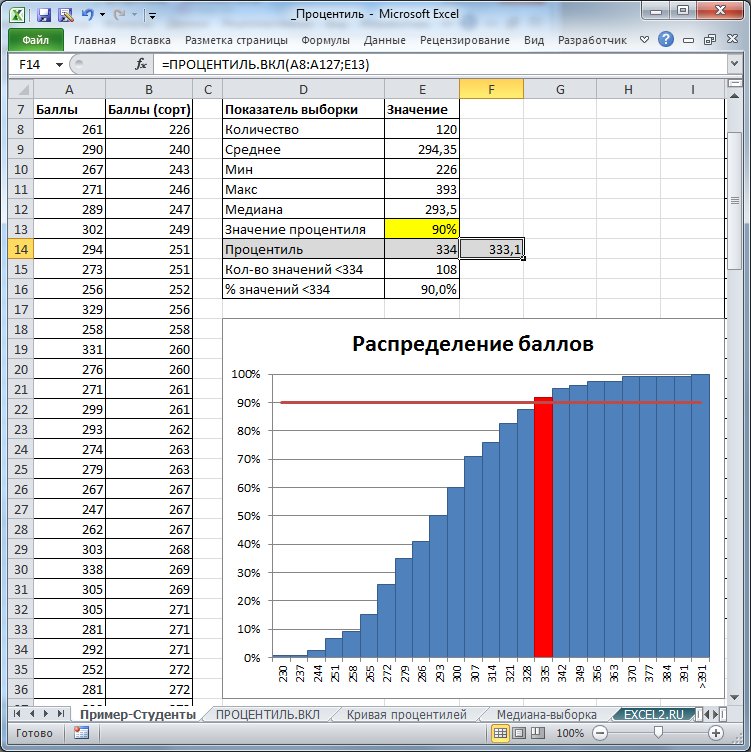
Вероятностный выход
- Процентиль: ячейка J26 содержит формулу =100/(2*E36), ячейка J27 содержит формулу =J26+100/E36 (аналогично для ячеек с J28 по J36)
- Цена: это просто значения цен в диапазоне C4:C14 (из рисунка 5) в отсортированном порядке. Например. формула дополнительного массива =QSORT(C4:C14) может быть помещена в диапазон K26:K36.
Наконец, инструмент анализа данных создает следующие диаграммы рассеяния.
График нормальной вероятности
- На этом графике показана зависимость процентиля от цены из выходных данных таблицы на рис.
 6. Этот график используется для определения того, соответствуют ли данные нормальному распределению. Может быть полезно добавить линию тренда, чтобы увидеть, соответствуют ли данные прямой линии. Это можно сделать, щелкнув график и выбрав Layout > Analysis|Trendline и выбрав Linear Trendline .
6. Этот график используется для определения того, соответствуют ли данные нормальному распределению. Может быть полезно добавить линию тренда, чтобы увидеть, соответствуют ли данные прямой линии. Это можно сделать, щелкнув график и выбрав Layout > Analysis|Trendline и выбрав Linear Trendline . - Играет ту же роль, что и сюжет QQ. Фактически, за исключением масштаба, он генерирует тот же график, что и график QQ, созданный дополнительным инструментом анализа данных (переключение осей).
Рисунок 7 – График нормальной вероятности
График на рисунке 7 показывает, что данные разумно соответствуют нормальному предположению.
Графики остатков
- Для каждой независимой переменной создается один график. Для примера 2 генерируются два графика: цвет по сравнению с остатками и качество по сравнению с остатками.
- Эти графики используются для определения того, соответствуют ли данные предположениям о линейности и однородности дисперсии.
 Для выполнения предположения об однородности дисперсии каждый график должен отображать случайный набор точек. Если появляется определенная форма точек или если вертикальный разброс точек не является постоянным на горизонтальных интервалах одинаковой длины, то это указывает на нарушение предположения об однородности дисперсий.
Для выполнения предположения об однородности дисперсии каждый график должен отображать случайный набор точек. Если появляется определенная форма точек или если вертикальный разброс точек не является постоянным на горизонтальных интервалах одинаковой длины, то это указывает на нарушение предположения об однородности дисперсий. - Для выполнения допущения о линейности остатки должны иметь среднее значение 0, на что указывает приблизительно равный разброс точек выше и ниже оси x.
Рисунок 8. Графики остатков
График цветовых остатков на рисунке 8 показывает приемлемое соответствие линейности и однородности предположений о дисперсии. График Quality Residual немного менее точен, но для такого небольшого числа точек выборки он подходит неплохо.
Два графика на рисунке 9показать явные проблемы. К счастью, они не основаны на данных Примера 3.
Рисунок 9 – Графики остатков, демонстрирующие нарушение предположений
график больше, чем слева. Это явный признак того, что дисперсии не являются однородными. Для диаграммы справа точки не кажутся случайными, а также несколько точек находятся ниже оси x (что указывает на нарушение линейности). Диаграмма на рис. 10 идеально соответствует тому, что нам нужно: случайное распределение точек с одинаковым числом точек выше и ниже оси x.
Это явный признак того, что дисперсии не являются однородными. Для диаграммы справа точки не кажутся случайными, а также несколько точек находятся ниже оси x (что указывает на нарушение линейности). Диаграмма на рис. 10 идеально соответствует тому, что нам нужно: случайное распределение точек с одинаковым числом точек выше и ниже оси x.
Рисунок 10. Остатки, предположения о линейности и дисперсии
Графики линейной аппроксимации
- Для каждой независимой переменной создается один график. Для примера 3 генерируются два графика: один для цвета и один для качества. Для каждой диаграммы наблюдаемые значения y (Цена) и прогнозируемые значения y наносятся на график относительно наблюдаемых значений независимой переменной.
Рисунок 11 – Графики аппроксимации для Примера 3
Наблюдение : Результаты примера 3 могут быть представлены следующим образом:
Множественный регрессионный анализ был использован для проверки того, действительно ли определенные характеристики в значительной степени предсказывают цену бриллиантов.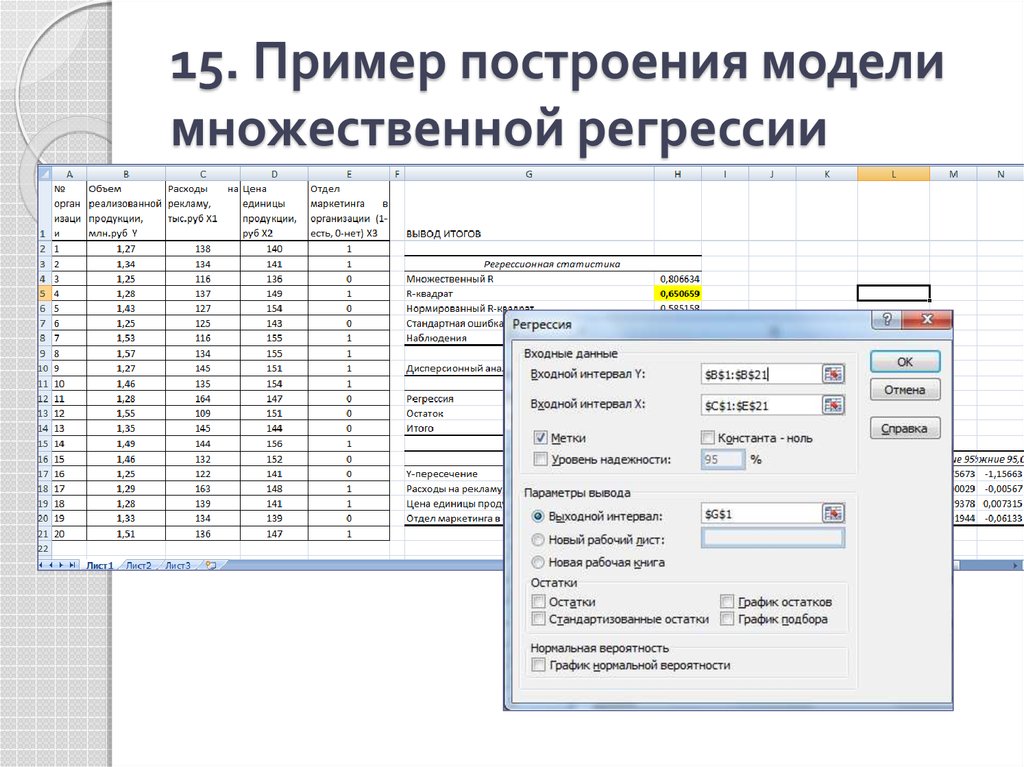


 Это гарантирует, что вы сможете сделать выбор или правильно настроить параметры для получения желаемых результатов.
Это гарантирует, что вы сможете сделать выбор или правильно настроить параметры для получения желаемых результатов.


 [Здесь n=5 и k=3, поэтому
n-k=2].
[Здесь n=5 и k=3, поэтому
n-k=2].  DIST.2T(ABS(h29),F15)
DIST.2T(ABS(h29),F15) 6. Этот график используется для определения того, соответствуют ли данные нормальному распределению. Может быть полезно добавить линию тренда, чтобы увидеть, соответствуют ли данные прямой линии. Это можно сделать, щелкнув график и выбрав Layout > Analysis|Trendline и выбрав Linear Trendline .
6. Этот график используется для определения того, соответствуют ли данные нормальному распределению. Может быть полезно добавить линию тренда, чтобы увидеть, соответствуют ли данные прямой линии. Это можно сделать, щелкнув график и выбрав Layout > Analysis|Trendline и выбрав Linear Trendline . Для выполнения предположения об однородности дисперсии каждый график должен отображать случайный набор точек. Если появляется определенная форма точек или если вертикальный разброс точек не является постоянным на горизонтальных интервалах одинаковой длины, то это указывает на нарушение предположения об однородности дисперсий.
Для выполнения предположения об однородности дисперсии каждый график должен отображать случайный набор точек. Если появляется определенная форма точек или если вертикальный разброс точек не является постоянным на горизонтальных интервалах одинаковой длины, то это указывает на нарушение предположения об однородности дисперсий.