Распределения Пуассона. Решение задач
Дискретная случайная величина Х имеет закон распределения Пуассона, если вероятности ее возможных значений
вычисляется по формуле Пуассона, где a=np<10. Как правило, Пуассоновское распределение касается вероятности появления благоприятного события в большом количестве экспериментов, если в одном — вероятность успешного завершения стремится к нулю.
В табличной форме этот закон распределения имеет вид
Условие нормировки для пуассоновского закона распределения запишется следующим образом
Построим образующую функцию вероятностей для приведенного закона
Она принимает достаточно простой компактный вид
Воспользовавшись зависимостями для определения математического ожидания М (Х) и дисперсии D (X) через производные от образующей функции в единице, получим их простые зависимости
1. Математическое ожидание определяется по формуле
2. Имея вторую производную от образующей функции в единице
находят дисперсию
Среднее квадратическое отклонение вычисляем через квадратный корень из дисперсии
Следовательно, для пуассоновского закона распределения вероятностей математическое ожидание и дисперсия равны произведению количества опытов на вероятность благоприятной события
На практике, если математическое ожидание и дисперсия близкие по значению то принимают гипотезу, что исследуемая величина имеет закон распределения Пуассона.
3. Асимметрия и эксцесс для пуассоновский закон также уровни и вычисляются по формулам
Рассмотрим несколько задач.
—————————————-
Задача 1. Микропроцессор имеет 10000 ранзисторов, работающих независимо друг от друга. Вероятность того, что транзистор выйдет из строя во время работы прибора, является величиной маловероятной и составляет 0,0007. Определить математическое ожидание М (Х) и среднее квадратическое отклонение S (Х) случайной величины Х — исла транзисторов, выйдут из строя во время работы процессора.
Решение. Задача удовлетворяет всем законам пуассоновский распределения:
количество испытаний n=10000 велика;
вероятность р=0,0007 близка к нулю;
их произведение a=np=7<10.
На основе данных вычисляем заданные величины
————————————
Задача 2. В рыбацком городке 99,99% мужчин хотя бы раз в жизни были на рыбалке. Проводят социологические исследования среди 10000 наугад выбранных мужчин. Определить дисперсию D (X) и среднее квадратическое отклонени S (Х) случайной величины Х — числа мужчин, которые ни разу не были на рыбалке.
Определить дисперсию D (X) и среднее квадратическое отклонени S (Х) случайной величины Х — числа мужчин, которые ни разу не были на рыбалке.
Решение. егко убедиться, что величина Х имеет пуассоновский закон распределения. С условия задачи находим
По формулам находим дисперсию и среднее квадратическое отклонение
Можно найти в гугле еще много подобных задач, всех их объединяет изменение случайной величины по закону Пуассона. Схема нахождения числовых характеристик приведена выше и является общей для всех задач, кроме того формулы для вычислений достаточно простыми даже для школьников.
Распределение Пуассона
При рассмотрении маловероятных событий, имеющих место в большой серии независимых испытаний некоторое (конечное) число раз, вероятности появления этих событий подчиняются закону Пуассона или закону редких событий , где λ равна среднему числу появления событий в одинаковых независимых испытаниях, т.е. λ = n × p, где p – вероятность события при одном испытании, e = 2,71828, m -частота данного события, математическое ожидание M[X] равно λ.
Ряд распределения закона Пуассона имеет вид:
| X | 0 | 1 | 2 | … | m | … |
| P | e-λ | λe-λ | … | … |
M[X] = λ
Дисперсия распределения Пуассона
D[X] = λ
Закон Пуассона можно применять для совокупностей, достаточно больших по объему (n > 100) и имеющих достаточно малую долю единиц, обладающих данным признаком (p < 0,1).
При этом распределение Пуассона можно применить, когда на только не известно значение n – общего числа возможных результатов, но и когда не известно конечное число, которое n может представлять. Там, где есть среднее число случаев наступления события, вероятность наступления события описывается членами разложения:
Поэтому, если среднее число землетрясений равно одному в месяц, то m=1 и вероятность случаев в месяц будет следующей, рассчитанной по приблизительному значению e—m=0,3679:
| Число случаев | Вероятность | Приблизительный числовой эквивалент |
| 0 | e-m | 0,3679 |
| 1 | me-m | 0,3679 |
| 2 | e-m | 0,1839 |
| 3 | e-m | 0,0613 |
Пример. В результате проверки 1000 партий одинаковых изделий получено следующее распределение количества бракованных изделий в партии:
В результате проверки 1000 партий одинаковых изделий получено следующее распределение количества бракованных изделий в партии:
| Количество брака, m1 | 0 | 1 | 2 | 3 | 4 | Итого |
| Количество партий, содержащих данное число бракованных изделий, fi | 604 | 306 | 77 | 12 | 1 | 1000 |
Определим среднее число бракованных изделий в партии:
| 604 | 306 | 77 | 12 | 1 |
| 606 | 303 | 76 | 13 | 2 |
Сопоставление свидетельствует о соответствии эмпирического распределения распределению Пуассона.

Перейти к онлайн решению своей задачи
Пример №2. Отдел технического контроля проверил n партий однотипных изделий и установил, что число Х нестандартных изделий в одной партии имеет эмпирическое распределение, приведенное в таблице, в одной строке которой указано количество xi нестандартных изделий в одной партии, а в другой строке – количество n i партий, содержащих xi нестандартных изделий. Требуется при уровне значимости α=0.05 проверить гипотезу о том, что случайная величина Х (число нестандартных изделий в одной партии) распределена по закону Пуассона.
| xi | 0 | 1 | 2 | 3 | 4 | 5 |
| ni | 370 | 360 | 190 | 63 | 14 | 3 |
Проверим гипотезу о том, что Х распределено по закону Пуассона с помощью сервиса
проверка статистических гипотез.

где pi — вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону; λ = xср.
i = 1: p1 = 0.3679, np1 = 367.88
i = 2: p2 = 0.1839, np2 = 183.94
i = 3: p3 = 0.0613, np3 = 61.31
i = 4: p4 = 0.0153, np4 = 15.33
i = 5: p5 = 0.0031, np5 = 3.07
i = 6: 17=14 + 3
i = 6: 18.39=15.33 + 3.07
| i | Наблюдаемая частота ni | pi | Ожидаемая частота npi | Слагаемые статистики Пирсона Ki |
| 0 | 370 | 0.37 | 367.88 | 0.0122 |
| 1 | 360 | 0. 37 37
| 367.88 | 0.17 |
| 2 | 190 | 0.18 | 183.94 | 0.2 |
| 3 | 63 | 0.0613 | 61.31 | 0.0464 |
| 4 | 17 | 0.0153 | 18.39 | 0.11 |
| 1000 | 0.53 |
Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение Kнабл, тем сильнее довод против основной гипотезы.
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения «хи-квадрат» и заданным значениям s, k (число интервалов), r=1 (параметр λ).
Kkp = 11.

Наблюдаемое значение статистики Пирсона не попадает в критическую область: Кнабл < Kkp, поэтому нет оснований отвергать основную гипотезу. Справедливо предположение о том, что данные выборки имеют распределение Пуассона.
Перейти к онлайн решению своей задачи
Пример. В цехе с 10 станками ежедневно регистрировалось число вышедших из строя станков. Всего было проведено 200 наблюдений, результаты которых приведены ниже.
Необходимо:
- Определить исследуемый признак и его тип (дискретный или непрерывный).
- В зависимости от типа признака построить полигон или гистограмму относительных частот.
- На основе визуального анализа полигона (гистограммы) сформулировать гипотезу о законе распределения признака.
- Вычислить выборочные характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое (стандартное) отклонение.
- Для генеральной средней и дисперсии построить доверительные интервалы, соответствующие доверительной вероятности 0,99.

- При уровне значимости 0,05 проверить гипотезу о том, что число выбывших из строя станков имеет распределение Пуассона.
Решение. Задан дискретный признак. Строим таблицу для расчета показателей.
| xi | Кол-во, fi | xi·fi | Накопленная частота, S | (x-x)·f | (x-x)2·f | (x-x)3·f | Частота, fi/n |
| 0 | 41 | 0 | 41 | 73.8 | 132.84 | -239.11 | 0.21 |
| 1 | 62 | 62 | 103 | 49.6 | 39.68 | -31.74 | 0.31 |
| 2 | 45 | 90 | 148 | 9 | 1.8 | 0.36 | 0.23 |
| 3 | 22 | 66 | 170 | 26.4 | 31.68 | 38.02 | 0.11 |
| 4 | 16 | 64 | 186 | 35.2 | 77.44 | 170.37 | 0. 08 08 |
| 5 | 8 | 40 | 194 | 25.6 | 81.92 | 262.14 | 0.04 |
| 6 | 4 | 24 | 198 | 16.8 | 70.56 | 296.35 | 0.02 |
| 7 | 2 | 14 | 200 | 10.4 | 54.08 | 281.22 | 0.01 |
| 8 | 0 | 0 | 200 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 200 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 200 | 0 | 0 | 0 | 0 |
| 200 | 360 | 246.8 | 490 | 777.6 | 1 |
Находим показатели центра распределения.
Средняя взвешенная
Размах вариации — разность между максимальным и минимальным значениями признака первичного ряда.
R = Xmax — Xmin
R = 10 — 0 = 10
Дисперсия — характеризует меру разброса около ее среднего значения (мера рассеивания, т.
 е. отклонения от среднего).
е. отклонения от среднего).Несмещенная оценка дисперсии — состоятельная оценка дисперсии.
Среднее квадратическое отклонение.
Каждое значение ряда отличается от среднего значения 1.8 не более, чем на 1.57
Оценка среднеквадратического отклонения.
Доверительный интервал для генерального среднего.
Поскольку n>30, то определяем значение tkp
В этом случае 2Ф(tkp) = 1 — γ
Ф(tkp) = (1 — γ)/2 = 0.99/2 = 0.495
По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.495
tkp(γ) = (0.495) = 2.58
(1.8 — 0.29;1.8 + 0.29) = (1.51;2.09)
С вероятностью 0.99 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
Доверительный интервал для дисперсии.
Вероятность выхода за нижнюю границу равна P(χ2n-1H) = (1-γ)/2 = 0.
 005. Для количества степеней свободы k = 199, по таблице распределения хи-квадрат находим:
005. Для количества степеней свободы k = 199, по таблице распределения хи-квадрат находим:χ2(199;0.005) = 255.2642.
Случайная ошибка дисперсии:
Вероятность выхода за верхнюю границу равна P(χ2n-1 ≥ hB) = 1 — P(χ2n-1H) = 1 — 0.005 = 0.995. Для количества степеней свободы k = 199, по таблице распределения хи-квадрат находим:
χ2(199;0.995) = 152.241.
Случайная ошибка дисперсии:
(2.46 — 1.92; 2.46 + 3.22)
(0.54; 5.68)
Найдем верхнюю границу доверительного интервала для среднеквадратического отклонения с надежностью γ = 0.99.
P(χ2n-1 > hγ) = 0.99. Для количества степеней свободы k = 199, по таблице распределения хи-квадрат находим:
χ2(199;0.99) = 156.432.
Случайная ошибка дисперсии:
0 ≤ σ2 ≤ 3.13
Проверка гипотез о виде распределения.
2. Проверим гипотезу о том, что Х распределено по закону Пуассона.
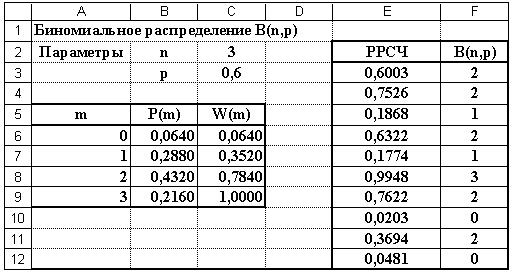
где pi — вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону.
Примем в качестве оценки параметра λ распределения Пуассона выборочную среднюю xср = 1.8. Следовательно, предполагаемый закон Пуассона имеет вид:
i = 0: p0 = 0.17, np0 = 33.06
i = 1: p1 = 0.3, np1 = 59.51
i = 2: p2 = 0.27, np2 = 53.56
i = 3: p3 = 0.16, np3 = 32.13
i = 4: p4 = 0.0723, np4 = 14.46
i = 5: p5 = 0.026, np5 = 5.21
i = 6: p6 = 0.00781, np6 = 1.56
i = 7: p7 = 0.00201, np7 = 0.4
i = 8: p8 = 0.000452, np8 = 0.0904
i = 9: p9 = 9.0E-5, np9 = 0.0181
i = 10: p10 = 1.6E-5, np10 = 0.00325
Объединим малочисленные частоты: (10,9,8,7,6) и соответствующие им теоретические частоты.

| i | Наблюдаемая частота ni | pi | Ожидаемая частота npi | Слагаемые статистики Пирсона Ki |
| 0 | 41 | 0.17 | 33.06 | 1.91 |
| 1 | 62 | 0.3 | 59.51 | 0.1 |
| 2 | 45 | 0.27 | 53.56 | 1.37 |
| 3 | 22 | 0.16 | 32.13 | 3.2 |
| 4 | 16 | 0.0723 | 14.46 | 0.16 |
| 5 | 8 | 0.026 | 5.21 | 1.5 |
| 6 | 6 | 0.0104 | 2.07 | 7.42 |
| 200 | 15.66 |
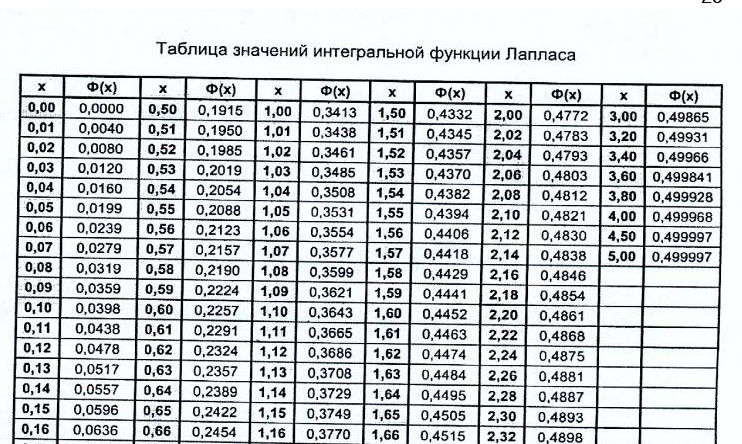
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения «хи-квадрат» и заданным значениям s, k (число интервалов), r=1 (параметр λ).
Kkp(0.05;5) = 11.07050; Kнабл = 15.66
Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл > Kkp, поэтому есть основания отвергать основную гипотезу. Данные выборки распределены не по закону Пуассона. Нанесем на один график и полигон частот, и вероятности появления событий по закону Пуассона.
Как вычислить вероятности Пуассона
Распределение Пуассона полезно для измерения того, сколько событий может произойти в течение заданного периода времени, например, количество покупателей, которые входят в магазин в течение следующего часа, количество посещений веб-сайта в течение следующей минуты и так далее. Процесс Пуассона происходит во времени, а не в серии испытаний; каждый интервал времени предполагается независимым от всех других интервалов.
Вы вычисляете вероятности Пуассона по следующей формуле:
Вот что представляет каждый элемент этой формулы:
e — константа, широко используемая в финансовых приложениях. Одним из наиболее важных применений является вычисление текущей стоимости денежных сумм, когда процентные ставки непрерывно начисляются — начисляются бесконечное число раз. В большинстве калькуляторов есть ключ с надписью e x , который можно использовать для вычисления значения e, возведенного в указанную степень. В Excel подходящей функцией для определения значения e является EXP.
Например, предположим, что количество сообщений, которые человек получает на свой мобильный телефон, составляет в среднем одно в час и что количество сообщений, получаемых каждый час, не зависит от всех других часов. Какова вероятность того, что он получит два сообщения в течение следующего часа?
В этом случае значение лямбда
равно 1, потому что среднее количество сообщений каждый час равно 1. Вероятность получения двух сообщений в течение следующего часа равна
Вероятность получения двух сообщений в течение следующего часа равна
Кроме того, вы можете получить результаты из таблицы Пуассона, настроенной как эта таблица.
В таблице показаны вероятности Пуассона для различных значений числа
.В примере с мобильным телефоном, потому что x = 2 и
соответствующая вероятность P ( X = 2) находится в строке « x = 2», а
Вероятность 0,1839.
Если вам не нужны формулы или таблицы, попробуйте специализированный калькулятор или Excel. Для Excel 2007 и более ранних версий используйте функцию ПУАССОН; для Excel 2010 используйте функцию ПУАССОН.РАСП.
Моменты распределения Пуассона используются для представления среднего значения распределения и дисперсии распределения. Как и в случае биномиального и геометрического распределения, эти моменты можно вычислить по упрощенным формулам.
Эта статья взята из книги:
- Бизнес-статистика для чайников,
Об авторе книги:
Алан Андерсон, доктор философии, преподаватель финансов, экономики, статистики и математики в университетах Фордем и Фэрфилд. как в колледжах Манхэттенвилл и Пёрч. Вне академической среды он имеет многолетний опыт работы экономистом, риск-менеджером и аналитиком по фиксированному доходу. Алан получил докторскую степень по экономике в Фордемском университете и степень магистра в области экономики. в финансовой инженерии из Политехнического университета.
как в колледжах Манхэттенвилл и Пёрч. Вне академической среды он имеет многолетний опыт работы экономистом, риск-менеджером и аналитиком по фиксированному доходу. Алан получил докторскую степень по экономике в Фордемском университете и степень магистра в области экономики. в финансовой инженерии из Политехнического университета.
Эту статью можно найти в категории:
- Расчет и анализ,
12.2 — Определение вероятности Пуассона
Пусть \(X\) равно количеству опечаток на печатной странице, в среднем 3 опечатки на странице. Какова вероятность того, что на случайно выбранной странице есть хотя бы одна опечатка ?
Мы можем найти требуемую вероятность непосредственно из p.m.f. Вероятность того, что \(X\) хотя бы один, равна: 9{-3}=4(0,0498)=0,1992\)
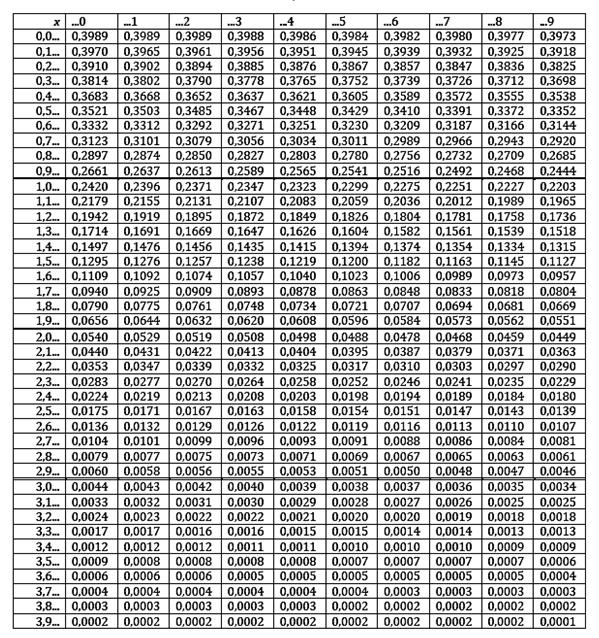
То есть вероятность найти не более одной опечатки на случайно выбранной странице составляет чуть менее 20%, когда среднее количество опечаток на странице равно 3.
Точно так же, как мы использовали кумулятивную таблицу вероятностей при поиске биномиальных вероятностей, мы могли бы в качестве альтернативы использовать кумулятивную таблицу вероятностей Пуассона, такую как таблица III в конце вашего учебника. Вы должны быть в состоянии использовать формулы, а также таблицы. Если вы посмотрите на таблицу, то увидите, что она состоит из трех страниц. Давайте просто взглянем на верхнюю часть первой страницы таблицы, чтобы понять, как она работает:
Таким образом, чтобы использовать таблицу в конце вашего учебника, а также таблицы в конце большинства учебников по вероятностям, чтобы найти кумулятивные вероятности Пуассона, сделайте следующее:
- Найдите столбец, возглавляемый соответствующий \(\лямбда\).
 Обратите внимание, что есть три строки, содержащие \(\lambda\) на первой странице таблицы, две строки, содержащие \(\lambda\), на второй странице таблицы и одна строка, содержащая \(\lambda\) на последняя страница таблицы.
Обратите внимание, что есть три строки, содержащие \(\lambda\) на первой странице таблицы, две строки, содержащие \(\lambda\), на второй странице таблицы и одна строка, содержащая \(\lambda\) на последняя страница таблицы. - Найдите \(x\) в первом столбце слева, для которого вы хотите найти \(F(x)=P(X\le x)\).
Попробуем на примере. Если \(X\) равно количеству опечаток на печатной странице со средним значением 3 опечатки на странице, какова вероятность того, что на случайно выбранной странице будет четыре опечатки ?
Решение
Вероятность того, что случайно выбранная страница содержит четыре опечатки, может быть записана как \(P(X=4)\). Мы можем вычислить \(P(X=4)\), вычитая \(P(X\le 3)\) из \(P(X\le 4)\). Чтобы найти \(P(X\le 3)\) и \(P(X\le 4)\) с помощью таблицы Пуассона, мы:
- Найдите столбец, возглавляемый \(\lambda=3\).
- Найдите 3 в первом столбце слева, так как мы хотим найти \(F(3)=P(X\le 3)\).
 И найдите 4 в первом столбце слева, так как мы хотим найти \(F(4)=P(X\le 4)\).
И найдите 4 в первом столбце слева, так как мы хотим найти \(F(4)=P(X\le 4)\).
Теперь все, что нам нужно сделать, это, во-первых, прочитать значение вероятности, где столбец \(\lambda=3\) и строка \(x=3\) пересекаются, и, во-вторых, прочитать значение вероятности, где Столбец \(\lambda=3\) и строка \(x=4\) пересекаются. Что вы получаете?
| \(\lambda = E(X)\) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| х | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
| 0 | 0,905 | 0,819 | 0,741 | 0,670 | 0,607 | 0,549 | 0,497 | 0,449 | 0,407 | 0,368 |
| 1 | 0,995 | 0,982 | 0,963 | 0,938 | 0,910 | 0,878 | 0,844 | 0,809 | 0,772 | 0,736 |
| 2 | 1. 000 000 | 0,999 | 0,996 | 0,992 | 0,986 | 0,970 | 0,966 | 0,953 | 0,937 | 0,920 |
| 3 | 1.000 | 1.000 | 1.000 | 0,999 | 0,998 | 0,997 | 0,994 | 0,991 | 0,987 | 0,981 |
| 4 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0,999 | 0,999 | 0,998 | 0,996 |
| 5 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0,999 |
| 6 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| х | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 |
| 0 | 0,333 | 0,301 | 0,273 | 0,247 | 0,223 | 0,202 | 0,183 | 0,165 | 0,150 | 0,135 |
| 1 | 0,699 | 0,663 | 0,627 | 0,592 | 0,558 | 0,525 | 0,493 | 0,463 | 0,434 | 0,403 |
| 2 | 0,900 | 0,879 | 0,857 | 0,833 | 0,809 | 0,830 | 0,757 | 0,731 | 0,704 | 0,677 |
| 3 | 0,974 | 0,966 | 0,957 | 0,946 | 0,934 | 0,921 | 0,907 | 0,981 | 0,875 | 0,857 |
| 4 | 0,995 | 0,992 | 0,989 | 0,986 | 0,981 | 0,976 | 0,970 | 0,964 | 0,956 | 0,947 |
| 5 | 0,999 | 0,998 | 0,998 | 0,997 | 0,996 | 0,994 | 0,992 | 0,990 | 0,987 | 0,983 |
| 6 | 1. 000 000 | 1.000 | 1.000 | 0,999 | 0,999 | 0,999 | 0,998 | 0,997 | 0,997 | 0,995 |
| 7 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0,999 | 0,999 | 0,999 |
| 8 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| х | 2,2 | 2,4 | 2,6 | 2,8 | 3,0 | 3,2 | 3,4 | 3,6 | 3,8 | 4,0 |
| 0 | 0,111 | 0,091 | 0,074 | 0,061 | 0,050 | 0,051 | 0,033 | 0,027 | 0,022 | 0,018 |
| 1 | 0,355 | 0,308 | 0,267 | 0,231 | 0,199 | 0,171 | 0,147 | 0,126 | 0,107 | 0,092 |
| 2 | 0,623 | 0,570 | 0,518 | 0,469 | 0,423 | 0,380 | 0,340 | 0,303 | 0,269 | 0,238 |
| 3 | 0,819 | 0,779 | 0,736 | 0,692 | 0,647 | 0,603 | 0,558 | 0,515 | 0,473 | 0,433 |
| 4 | 0,928 | 0,904 | 0,887 | 0,848 | 0,815 | 0,781 | 0,744 | 0,706 | 0,668 | 0,629 |
| 5 | 0,975 | 0,964 | 0,951 | 0,935 | 0,916 | 0,895 | 0,871 | 0,844 | 0,816 | 0,785 |
| 6 | 0,993 | 0,988 | 0,983 | 0,976 | 0,966 | 0,955 | 0,942 | 0,927 | 0,909 | 0,889 |
| 7 | 0,998 | 0,997 | 0,995 | 0,992 | 0,988 | 0,983 | 0,977 | 0,969 | 0,960 | 0,949 |
| 8 | 1. 000 000 | 0,990 | 0,999 | 0,998 | 0,993 | 0,994 | 0,992 | 0,988 | 0,984 | 0,979 |
| 9 | 1.000 | 1.000 | 1.000 | 0,999 | 0,999 | 0,998 | 0,997 | 0,996 | 0,994 | 0,992 |
| 10 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0,999 | 0,999 | 0,998 | 0,997 |
| 11 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0,999 | 0,999 |
| 12 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| \(\lambda = E(X)\) 901 45 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| х | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
| 0 | 0,905 | 0,819 | 0,741 | 0,670 | 0,607 | 0,549 | 0,497 | 0,449 | 0,407 | 0,368 |
| 1 | 0,995 | 0,982 | 0,963 | 0,938 | 0,910 | 0,878 | 0,844 | 0,809 | 0,772 | 0,736 |
| 2 | 1.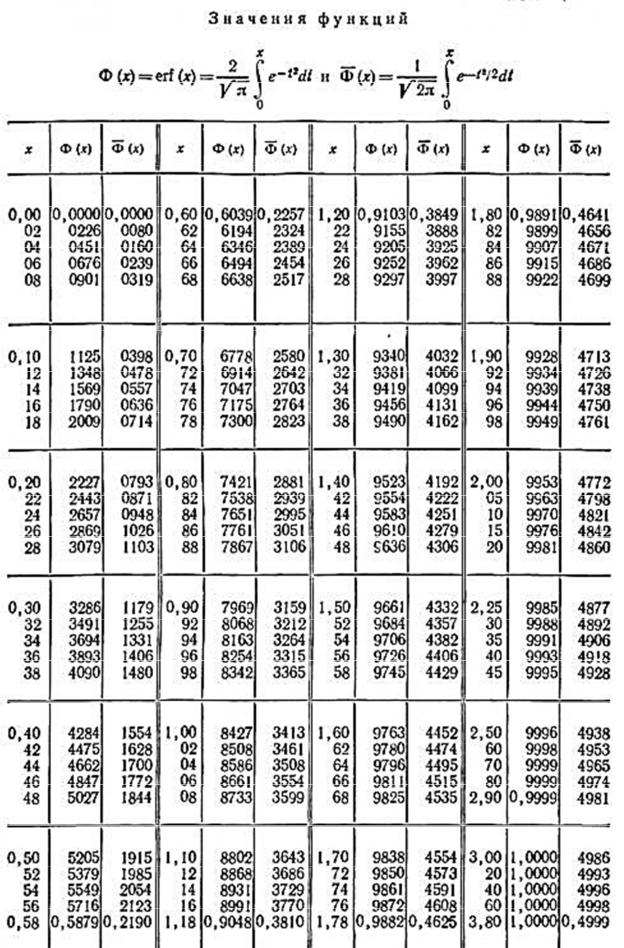 000 000 | 0,999 | 0,996 | 0,992 | 0,986 | 0,970 | 0,966 | 0,953 | 0,937 | 0,920 |
| 3 | 1.000 | 1.000 | 1.000 | 0,999 | 0,998 | 0,997 | 0,994 | 0,991 | 0,987 | 0,981 |
| 4 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0,999 | 0,999 | 0,998 | 0,996 |
| 5 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0,999 |
| 6 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| х | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 |
| 0 | 0,333 | 0,301 | 0,273 | 0,247 | 0,223 | 0,202 | 0,183 | 0,165 | 0,150 | 0,135 |
| 1 | 0,699 | 0,663 | 0,627 | 0,592 | 0,558 | 0,525 | 0,493 | 0,463 | 0,434 | 0,403 |
| 2 | 0,900 | 0,879 | 0,857 | 0,833 | 0,809 | 0,830 | 0,757 | 0,731 | 0,704 | 0,677 |
| 3 | 0,974 | 0,966 | 0,957 | 0,946 | 0,934 | 0,921 | 0,907 | 0,981 | 0,875 | 0,857 |
| 4 | 0,995 | 0,992 | 0,989 | 0,986 | 0,981 | 0,976 | 0,970 | 0,964 | 0,956 | 0,947 |
| 5 | 0,999 | 0,998 | 0,998 | 0,997 | 0,996 | 0,994 | 0,992 | 0,990 | 0,987 | 0,983 |
| 6 | 1.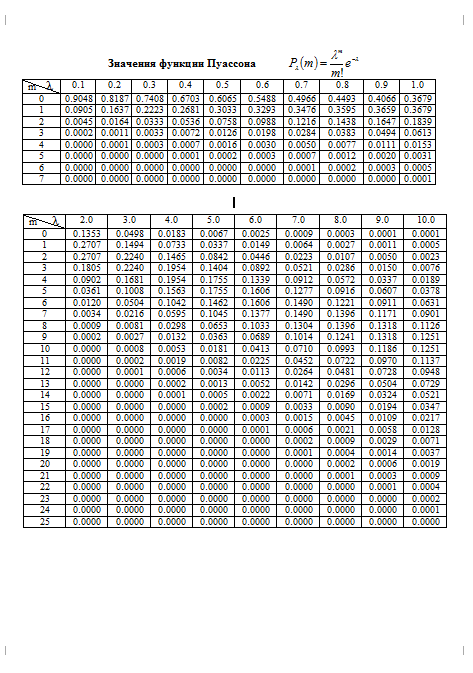 000 000 | 1.000 | 1.000 | 0,999 | 0,999 | 0,999 | 0,998 | 0,997 | 0,997 | 0,995 |
| 7 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0,999 | 0,999 | 0,999 |
| 8 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| х | 2,2 | 2,4 | 2,6 | 2,8 | 3,0 | 3,2 | 3,4 | 3,6 | 3,8 | 4,0 |
| 0 | 0,111 | 0,091 | 0,074 | 0,061 | 0,050 | 0,051 | 0,033 | 0,027 | 0,022 | 0,018 |
| 1 | 0,355 | 0,308 | 0,267 | 0,231 | 0,199 | 0,171 | 0,147 | 0,126 | 0,107 | 0,092 |
| 2 | 0,623 | 0,570 | 0,518 | 0,469 | 0,423 | 0,380 | 0,340 | 0,303 | 0,269 | 0,238 |
| 3 | 0,819 | 0,779 | 0,736 | 0,692 | 0,647 | 0,603 | 0,558 | 0,515 | 0,473 | 0,433 |
| 4 | 0,928 | 0,904 | 0,887 | 0,848 | 0,815 | 0,781 | 0,744 | 0,706 | 0,668 | 0,629 |
| 5 | 0,975 | 0,964 | 0,951 | 0,935 | 0,916 | 0,895 | 0,871 | 0,844 | 0,816 | 0,785 |
| 6 | 0,993 | 0,988 | 0,983 | 0,976 | 0,966 | 0,955 | 0,942 | 0,927 | 0,909 | 0,889 |
| 7 | 0,998 | 0,997 | 0,995 | 0,992 | 0,988 | 0,983 | 0,977 | 0,969 | 0,960 | 0,949 |
| 8 | 1.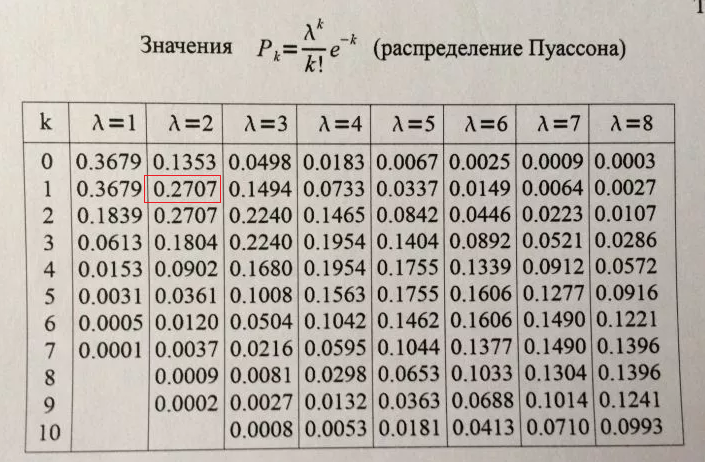 000 000 | 0,990 | 0,999 | 0,998 | 0,993 | 0,994 | 0,992 | 0,988 | 0,984 | 0,979 |
| 9 | 1.000 | 1.000 | 1.000 | 0,999 | 0,999 | 0,998 | 0,997 | 0,996 | 0,994 | 0,992 |
| 10 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0,999 | 0,999 | 0,998 | 0,997 |
| 11 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0,999 | 0,999 |
| 12 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
Совокупная таблица вероятностей Пуассона говорит нам, что нахождение \(P(X\le 4)=0,815\) и \(P(X\le 3)=0,647\).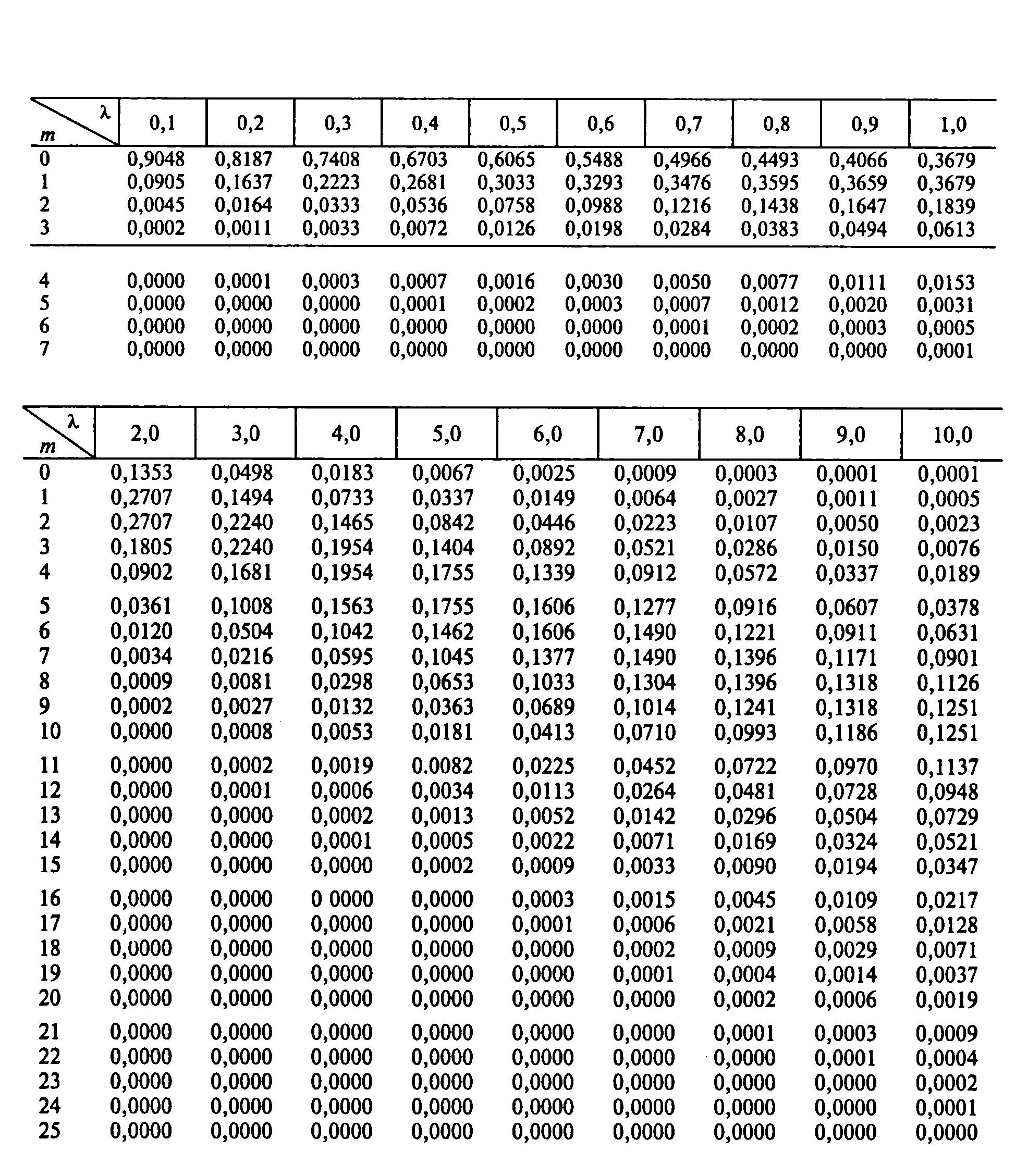 Следовательно:
Следовательно:
\(P(X=4)=P(X\le 4)-P(X\le 3)=0,815-0,647=0,168\)
То есть вероятность того, что на случайно выбранной странице будет четыре опечатки. Поскольку в этом случае это не потребует много работы, вы можете проверить, что вы получите тот же ответ, используя p.m.f. Пуассона.
Какова вероятность того, что три случайно выбранные страницы имеют более восьми опечаток на нем?
Решение
Для решения этой проблемы необходимо сделать еще один шаг. Напомним, что \(X\) обозначает количество опечаток на одной печатной странице. Затем определим новую случайную величину \(Y\), которая равна количеству опечаток на трех печатных страницах. Если среднее значение \(X\) равно 3 опечаткам на страницу, то среднее значение \(Y\) равно:
\(\lambda_Y=3 \text{ опечаток на одну страницу }\times 3\text{страниц} =9 \text{ опечаток на трех страницах}\)
Поиск желаемой вероятности включает в себя поиск:
\(P(Y>8)=1-P(Y\le 8)\)
где \(P(Y\le 8)\) находится путем в таблице Пуассона под столбцом, озаглавленным \(\lambda=9. 0\), и строкой, озаглавленной \(x=8\). Что вы получаете?
0\), и строкой, озаглавленной \(x=8\). Что вы получаете?
| x | 6,5 | 7,0 | 7,5 | 8,0 | 8,5 | 9,0 | 9,5 | 10,0 | 10,5 | 11,0 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0,002 | 0,001 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 1 | 0,011 | 0,007 | 0,005 | 0,003 | 0,002 | 0,001 | 0,001 | 0,000 | 0,000 | 0,000 |
| 2 | 0,043 | 0,030 | 0,020 | 0,014 | 0,009 | 0,006 | 0,004 | 0,003 | 0,002 | 0,001 |
| 3 | 0,112 | 0,082 | 0,059 | 0,042 | 0,030 | 0,021 | 0,015 | 0,010 | 0,007 | 0,005 |
| 4 | 0,224 | 0,173 | 0,132 | 0,100 | 0,074 | 0,055 | 0,040 | 0,029 | 0,021 | 0,015 |
| 5 | 0,369 | 0,301 | 0,241 | 0,191 | 0,150 | 0,116 | 0,089 | 0,067 | 0,050 | 0,015 |
| 6 | 0,527 | 0,450 | 0,378 | 0,313 | 0,256 | 0,207 | 0,165 | 0,130 | 0,102 | 0,079 |
| 7 | 0,673 | 0,599 | 0,525 | 0,453 | 0,386 | 0,324 | 0,269 | 0,220 | 0,179 | 0,143 |
| 8 | 0,792 | 0,729 | 0,662 | 0,593 | 0,523 | 0,456 | 0,392 | 0,333 | 0,279 | 0,232 |
| 9 | 0,877 | 0,830 | 0,776 | 0,717 | 0,653 | 0,587 | 0,522 | 0,458 | 0,397 | 0,341 |
| 10 | 0,933 | 0,901 | 0,862 | 0,816 | 0,763 | 0,706 | 0,645 | 0,583 | 0,521 | 0,460 |
| 11 | 0,966 | 0,947 | 0,921 | 0,888 | 0,849 | 0,803 | 0,752 | 0,697 | 0,639 | 0,579 |
| 12 | 0,984 | 0,973 | 0,957 | 0,936 | 0,909 | 0,876 | 0,836 | 0,792 | 0,742 | 0,689 |
| 13 | 0,993 | 0,987 | 0,978 | 0,966 | 0,949 | 0,926 | 0,898 | 0,864 | 0,825 | 0,781 |
| 14 | 0,997 | 0,994 | 0,990 | 0,983 | 0,973 | 0,959 | 0,940 | 0,917 | 0,888 | 0,854 |
| 15 | 0,999 | 0,998 | 0,995 | 0,992 | 0,986 | 0,978 | 0,967 | 0,951 | 0,932 | 0,907 |
| 16 | 1. 000 000 | 0,999 | 0,998 | 0,996 | 0,993 | 0,989 | 0,982 | 0,973 | 0,960 | 0,944 |
| 17 | 1.000 | 1.000 | 0,999 | 0,998 | 0,997 | 0,995 | 0,991 | 0,986 | 0,978 | 0,968 |
| 18 | 1.000 | 1.000 | 1.000 | 0,999 | 0,999 | 0,998 | 0,096 | 0,993 | 0,988 | 0,982 |
| 19 | 1.000 | 1.000 | 1.000 | 1.000 | 0,999 | 0,999 | 0,998 | 0,997 | 0,994 | 0,991 |
| 20 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0,999 | 0,998 | 0,997 | 0,995 |
| 21 | 1.000 | 1.000 | 1.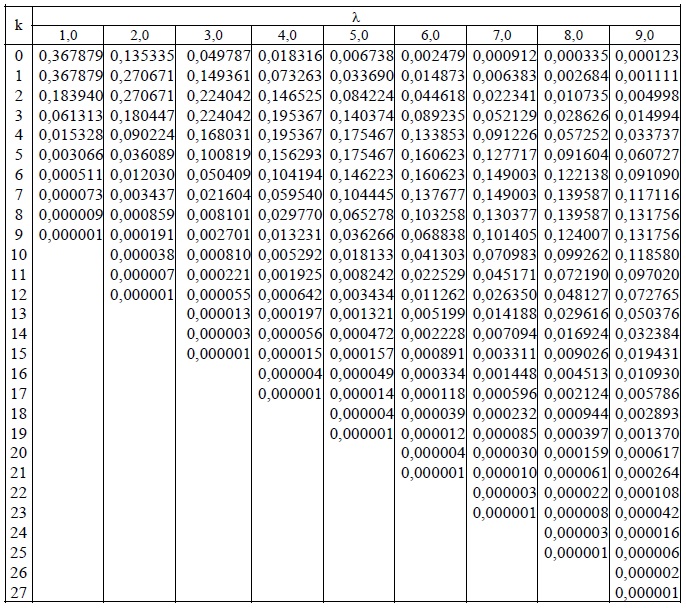 000 000 | 1.000 | 1.000 | 1.000 | 1.000 | 0,999 | 0,999 | 0,998 |
| 22 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0,999 | 0,999 |
| 23 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| х | 6,5 | 7,0 | 7,5 | 8,0 | 8,5 | 9,0 | 9,5 | 10,0 | 10,5 | 11,0 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0,002 | 0,001 | 0,001 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 1 | 0,011 | 0,007 | 0,005 | 0,003 | 0,002 | 0,001 | 0,001 | 0,000 | 0,000 | 0,000 |
| 2 | 0,043 | 0,030 | 0,020 | 0,014 | 0,009 | 0,006 | 0,004 | 0,003 | 0,002 | 0,001 |
| 3 | 0,112 | 0,082 | 0,059 | 0,042 | 0,030 | 0,021 | 0,015 | 0,010 | 0,007 | 0,005 |
| 4 | 0,224 | 0,173 | 0,132 | 0,100 | 0,074 | 0,055 | 0,040 | 0,029 | 0,021 | 0,015 |
| 5 | 0,369 | 0,301 | 0,241 | 0,191 | 0,150 | 0,116 | 0,089 | 0,067 | 0,050 | 0,015 |
| 6 | 0,527 | 0,450 | 0,378 | 0,313 | 0,256 | 0,207 | 0,165 | 0,130 | 0,102 | 0,079 |
| 7 | 0,673 | 0,599 | 0,525 | 0,453 | 0,386 | 0,324 | 0,269 | 0,220 | 0,179 | 0,143 |
| 8 | 0,792 | 0,729 | 0,662 | 0,593 | 0,523 | 0,456 | 0,392 | 0,333 | 0,279 | 0,232 |
| 9 | 0,877 | 0,830 | 0,776 | 0,717 | 0,653 | 0,587 | 0,522 | 0,458 | 0,397 | 0,341 |
| 10 | 0,933 | 0,901 | 0,862 | 0,816 | 0,763 | 0,706 | 0,645 | 0,583 | 0,521 | 0,460 |
| 11 | 0,966 | 0,947 | 0,921 | 0,888 | 0,849 | 0,803 | 0,752 | 0,697 | 0,639 | 0,579 |
| 12 | 0,984 | 0,973 | 0,957 | 0,936 | 0,909 | 0,876 | 0,836 | 0,792 | 0,742 | 0,689 |
| 13 | 0,993 | 0,987 | 0,978 | 0,966 | 0,949 | 0,926 | 0,898 | 0,864 | 0,825 | 0,781 |
| 14 | 0,997 | 0,994 | 0,990 | 0,983 | 0,973 | 0,959 | 0,940 | 0,917 | 0,888 | 0,854 |
| 15 | 0,999 | 0,998 | 0,995 | 0,992 | 0,986 | 0,978 | 0,967 | 0,951 | 0,932 | 0,907 |
| 16 | 1.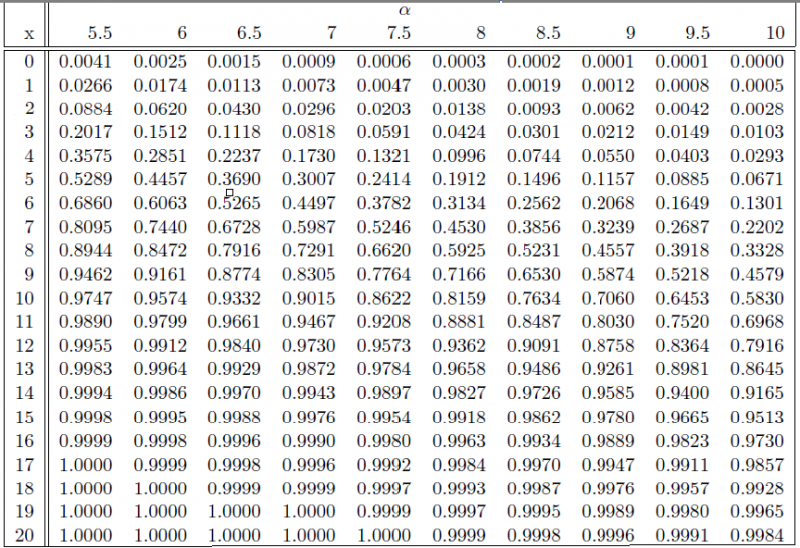 000 000 | 0,999 | 0,998 | 0,996 | 0,993 | 0,989 | 0,982 | 0,973 | 0,960 | 0,944 |
| 17 | 1.000 | 1.000 | 0,999 | 0,998 | 0,997 | 0,995 | 0,991 | 0,986 | 0,978 | 0,968 |
| 18 | 1.000 | 1.000 | 1.000 | 0,999 | 0,999 | 0,998 | 0,096 | 0,993 | 0,988 | 0,982 |
| 19 | 1.000 | 1.000 | 1.000 | 1.000 | 0,999 | 0,999 | 0,998 | 0,997 | 0,994 | 0,991 |
| 20 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0,999 | 0,998 | 0,997 | 0,995 |
| 21 | 1.000 | 1.000 | 1.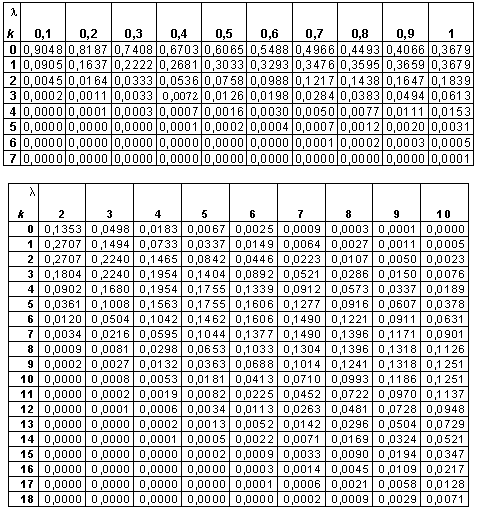 |

 Обратите внимание, что есть три строки, содержащие \(\lambda\) на первой странице таблицы, две строки, содержащие \(\lambda\), на второй странице таблицы и одна строка, содержащая \(\lambda\) на последняя страница таблицы.
Обратите внимание, что есть три строки, содержащие \(\lambda\) на первой странице таблицы, две строки, содержащие \(\lambda\), на второй странице таблицы и одна строка, содержащая \(\lambda\) на последняя страница таблицы. И найдите 4 в первом столбце слева, так как мы хотим найти \(F(4)=P(X\le 4)\).
И найдите 4 в первом столбце слева, так как мы хотим найти \(F(4)=P(X\le 4)\).