Что такое множество
Множество — это набор каких-либо объектов. Объекты, из которых состоит множество, называются элементами этого множества.
Например: множество школьников, множество машин, множество чисел.
В математике множество рассматривается намного шире. Мы не будем сильно углубляться в эту тему, поскольку она относится к высшей математике и на первых порах может создавать трудности для обучения. Мы рассмотрим только ту часть темы, с которой уже имели дело.
Обозначения
Множество чаще всего обозначают заглавными буквами латинского алфавита, а его элементы — строчными. При этом элементы заключаются в фигурные скобки.
Например, если наших друзей зовут Том, Джон и Лео, то мы можем задать множество друзей, элементами которого будут Том, Джон и Лео.
Обозначим множество наших друзей через заглавную латинскую букву F (friends), затем поставим знак равенства и в фигурных скобках перечислим наших друзей:
F = { Том, Джон, Лео }
Пример 2.
Запишем множество делителей числа 6.
Обозначим через любую заглавную латинскую букву данное множество, например, через букву D
D
затем поставим знак равенства и в фигурных скобках перечислим элементы данного множества, то есть перечислим делители числа 6
D = { 1, 2, 3, 6 }
Если какой-то элемент принадлежит заданному множеству, то эта принадлежность указывается с помощью знака принадлежности ∈. К примеру, делитель 2 принадлежит множеству делителей числа 6 (множеству D). Записывается это так:
2 ∈ D
Читается как «2 принадлежит множеству делителей числа 6»
Если какой-то элемент не принадлежит заданному множеству, то эта не принадлежность указывается с помощью зачёркнутого знака принадлежности ∉. К примеру, делитель 5 не принадлежит множеству D. Записывается это так:
5 ∉ D
Читается как «5 не принадлежит множеству делителей числа 6»
Кроме того, множество можно записывать прямым перечислением элементов, без заглавных букв.
Это может быть удобным, если множество состоит из небольшого количества элементов. Например, зададим множество из одного элемента. Пусть этим элементом будет наш друг Том:
{ Том }
Зададим множество, которое состоит из одного числа 2
{ 2 }
Зададим множество, которое состоит из двух чисел: 2 и 5
{ 2, 5 }
Множество натуральных чисел
Это первое множество с которым мы начали работать. Натуральными числами называют числа 1, 2, 3 и т.д.
Натуральные числа появились из-за потребности людей сосчитать те иные объекты. Например, посчитать количество кур, коров, лошадей. Натуральные числа возникают естественным образом при счёте.
В прошлых уроках, когда мы употребляли слово «число», чаще всего подразумевалось именно натуральное число.
В математике множество натуральных чисел обозначается заглавной латинской буквой N.
Например, укажем, что число 1 принадлежит множеству натуральных чисел.
Для этого записываем число 1, затем с помощью знака принадлежности ∈ указываем, что единица принадлежит множеству N
1 ∈ N
Читается как: «единица принадлежит множеству натуральных чисел»
Множество целых чисел
Множество целых чисел включает в себя все положительные и отрицательные числа, а также число 0.
Множество целых чисел обозначается заглавной латинской буквой Z.
Укажем, к примеру, что число −5 принадлежит множеству целых чисел:
−5 ∈ Z
Укажем, что 10 принадлежит множеству целых чисел:
10 ∈ Z
Укажем, что 0 принадлежит множеству целых чисел:
0 ∈ Z
В будущем все положительные и отрицательные числа мы будем называть одним словосочетанием — целые числа.
Множество рациональных чисел
Рациональные числа, это те самые обыкновенные дроби, которые мы изучаем по сей день.
Рациональное число — это число, которое может быть представлено в виде дроби , где a — числитель дроби, b — знаменатель.
В роли числителя и знаменателя могут быть любые числа, в том числе и целые (за исключением нуля, поскольку на нуль делить нельзя).
Например, представим, что вместо a стоит число 10, а вместо b — число 2
10 разделить на 2 равно 5. Видим, что число 5 может быть представлено в виде дроби , а значит число 5 входит во множество рациональных чисел.
Легко заметить, что число 5 также относится и ко множеству целых чисел. Стало быть множество целых чисел входит во множество рациональных чисел. А значит, во множество рациональных чисел входят не только обыкновенные дроби, но и целые числа вида −2, −1, 0, 1, 2.
Теперь представим, что вместо a стоит число 12, а вместо b — число 5.
12 разделить на 5 равно 2,4. Видим, что десятичная дробь 2,4 может быть представлена в виде дроби , а значит она входит во множество рациональных чисел. Отсюда делаем вывод, что во множество рациональных чисел входят не только обыкновенные дроби и целые числа, но и десятичные дроби.
Мы вычислили дробь и получили ответ 2,4. Но мы могли бы выделить в этой дроби целую часть:
При выделении целой части в дроби , получается смешанное число . Видим, что смешанное число тоже может быть представлено в виде дроби . Значит во множество рациональных чисел входят и смешанные числа.
В итоге мы приходим к выводу, что множество рациональных чисел содержат в себе:
- целые числа
- обыкновенные дроби
- десятичные дроби
- смешанные числа
Множество рациональных чисел обозначается заглавной латинской буквой Q.
Например укажем, что дробь принадлежит множеству рациональных чисел. Для этого записываем саму дробь , затем с помощью знака принадлежности ∈ указываем, что дробь принадлежит множеству рациональных чисел:
∈ Q
Укажем, что десятичная дробь 4,5 принадлежит множеству рациональных чисел:
4,5 ∈ Q
Укажем, что смешанное число принадлежит множеству рациональных чисел:
∈ Q
Вводный урок по множествам завершён.
В будущем мы рассмотрим множества намного лучше, а пока рассмотренного в данном уроке будет достаточно.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Используй кнопку ниже
1. Множество натуральных чисел
Определение: Множество называется числовым, если его элементами являются числа.
Известны следующие числовые системы:
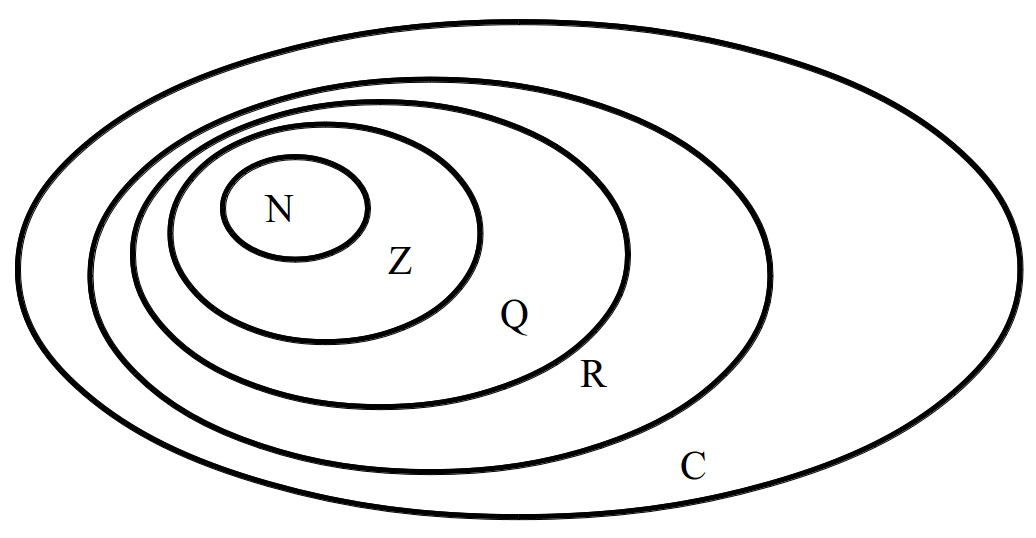
N — множество натуральных чисел;
Z — множество целых чисел;
Q — множество рациональных чисел;
R — множество действительных чисел;
С — множество комплексных чисел.
Между этими множествами установлены следующие отношения:
N Ì Z Ì Q Ì R Ì C.
В основе расширения числовых множеств лежат следующие принципы: если множество А расширяется до множества В, то:
1) А Ì B;
2) операции и отношения между элементами, выполнимые во множестве А, сохраняются и для элементов множества В;
3) во множестве В выполняются операции, не выполнимые или частично выполнимые во множестве А;
4) множество В является минимальным расширением множества А, обладающим свойствами 1) – 3).
Минимальность расширения множества А обладающее свойствами 1–3 понимается в том смысле, что: 1. выполняются свойства 1–3; 2. В – наименьшее множество для которого выполняются свойства 1–3 и для которого выполняется операция невыполнимая или частично выполнимая во множестве А. |
Множество натуральных
чисел N строго определяется с помощью аксиом
Пеано.
1. Существует натуральное число 1, не следующее ни за каким натуральным числом (натуральный ряд начинается с 1).
2. Каждое натуральное число следует только за одним и только одним натуральным числом (в натуральном ряду нет повторений).
3. За каждым натуральным числом следует одно и только одно натуральное число (натуральный ряд бесконечен).
4. Аксиома индукции. Пусть М Ì N. Если:
1) 1 Î М;
2) » а Î М множеству М принадлежит и следующий за а элемент а1 то множество М совпадает с множеством натуральных чисел.
Итак, множество N = { 1, 2, 3, 4,…}.
На аксиоме 4 основан метод математической индукции. Доказательство различных утверждений этим методом проводится от частного к общему, а затем делается вывод о справедливости данного утверждения.
П р и м е р. Доказать методом математической индукции следующее равенство:
Д о к а з а т е л ь с т в о.
1. Проверим справедливость данного утверждения для n = 1: , т.е. 1 = 1.
Проверка при n=1 ОБЪЯЗАТЕЛЬНА! |
2. Предположим, что данное равенство выполняется для k слагаемых, т.е. при n =k:
3. На основании предположения 2 докажем справедливость данного равенства для n = k+1:
Ho , а потому , а так как , следовательно
Теперь можно сделать
вывод о том, что данное равенство
справедливо
»
Во множестве натуральных чисел выполняются операции сложения и умножения, но не всегда выполняется операция вычитания. Расширяя множество N так, чтобы эта операция была выполнима, мы получаем множество целых чисел Z.
Расширяя – определяя
новую алгебраическую операцию. |
Поэтому Z=N È {0, -1, -2,…} или Z={…-3, -2, -1, 0, 1, 2, 3,…}, т.е. множество целых чисел Z содержит множество натуральных чисел, число нуль и числа, противоположные натуральным.
Основную роль во всей теории целых чисел играют следующие факты.
Т е о р е м а о д е л е н и и с о с т а т к о м. Для любого целого а и b
> 0 существуют и притом единственные целые q и r, такие, что а = bq + r, 0 £ r < | b |.О п р е д е л е н и е. Натуральное число р называется простым, если р > 1 и р не имеет положительных делителей, отличных от 1 и р.
О с н о в н а я т е о р е м
а а р и ф м е т и к и. Для
каждого натурального числа n > 1 существует единственное
разложение на
простые множители: ,
где p1, p2,
.
.., pk – простые числа,
а — натуральные числа. Разложение называется каноническим.
Единственность разложения понимается с точностью до порядка следования сомножителей. Например . Если сказано, что простые числа расположены в порядке возрастания, то данная оговорка не нужна. |
О п р е д е л е н и е. 1) Общим делителем целых чисел а1,
а2,
…, аn называется целое число d, такое, что a1 : d,
а2 : d,
…, аn : d.
2) Наибольшим
общим делителем целых чисел а1,
а2,
.
.., аn называется такой положительный общий
делитель чисел а
Наибольший общий делитель – это наибольший из их общих делителей. |
Обозначается: d = (а1, а2, …, аn).
Наибольший общий делитель целых чисел а и b может быть найден с помощью алгоритма Евклида, в основе которого лежит теорема о делении с остатком. Последний, отличный от нуля, остаток и будет наибольшим общим делителем чисел а и b.
П р и м е р. Найти НОД чисел 1173 и 323. Последовательным делением находим:
1173 = 323´3 + 204;
323=204´1+119;
204=119´1+85;
119=85´1+34;
85=34´2+17;
34=17´2;
так что
(1173, 323) = 17.
О п р е д е л е н и е. Наименьшим общим кратным целых чисел а1, а2, …, аn, отличных от нуля, называется наименьшее положительное число, кратное всем этим числам.
Наименьшее общее кратное – это наименьшее из их общих кратных. |
Обозначают: m=[ а1, а2, …, аn].
Пусть а и b целые числа, тогда
П р и м е р. Найти HOK чисел 1173 и 323.
Т.к. (1173, 323) = 17, то [1173, 323] =
Натуральные числа — определение, концепция, числовая линейка, примеры и часто задаваемые вопросы
Натуральные числа — это все положительные целые числа от 1 до бесконечности, являющиеся компонентом системы счисления. Натуральные числа — это только положительные целые числа, за исключением нуля, дробей, десятичных и отрицательных чисел, и они являются частью действительных чисел.
Натуральные числа также называют счетными числами. Давайте узнаем больше о натуральных числах, их свойствах и примерах.
Что такое натуральные числа?
Натуральные числа или счетные числа — это целые числа, которые образуются от 1 до бесконечности. Числа можно найти повсюду, их можно использовать для подсчета предметов, представления денег или обмена ими, расчета температуры, определения времени и так далее. Эти числа называются «натуральными числами», поскольку они используются для подсчета предметов. При подсчете предметов это может быть 5 стаканов, 6 книг, 1 бутылка и так далее. Поэтому другое название натуральных чисел — счетные числа. Совокупность всех целых чисел, кроме 0, называется натуральными числами. Эти фигуры играют важную роль в повседневных действиях и общении.
Натуральные числа Определение Натуральные числа — это числа, которые можно посчитать и которые являются составной частью действительных чисел. В набор натуральных чисел входят только положительные целые числа, такие как 1, 2, 3, 4, 5, 6 и т.
д. Натуральные числа начинаются с 1 и доходят до ∞.
Набор натуральных чисел
В математике набор натуральных чисел выражается как 1, 2, 3, … Набор натуральных чисел обозначается символом N. N = {1, 2, 3, 4, 5 , … ∞}. Один (1) — наименьшее натуральное число. Набор элементов называется набором (числа в данном контексте). Наименьший элемент в N равен 1, а следующий элемент с точки зрения 1 и N для любого элемента в N. 2 на 1 больше, чем 1, 3 на 1 больше, чем 2, и так далее. В приведенной ниже таблице объясняются различные формы множества натуральных чисел.
Установить форму | Пояснение |
| Форма выписки 9 0026 | N = Набор чисел, образующихся из 1. |
| Форма Roaster | N = {1, 2, 3, 4, 5, 6, …} |
| Форма построения набора | N = {x: x — натуральное число, начинающееся с 1} |
Натуральные числа — это подмножество целых чисел, и целые числа являются подмножеством целых чисел.
Точно так же целые числа являются подмножеством действительных чисел. Приведенная ниже диаграмма объясняет взаимосвязь w.r.t. наборы натуральных чисел, целых чисел, целых чисел и действительных чисел.
Примеры натуральных чисел
Неотрицательные целые числа также известны как натуральные числа (все положительные целые числа). 24, 57, 88, 979, 120502 и т. д. — лишь несколько примеров. Будет ли -4 натуральным числом? Нет. Поскольку это отрицательное целое число. Будет ли 3,6 натуральным числом? Нет. Поскольку это не целое число.
Натуральные четные числа
Четные натуральные числа — это четные числа, которые точно делятся на 2 и принадлежат множеству N. Таким образом, 2,4,6,8,… являются примерами четных натуральных чисел. Набор натуральных четных чисел представлен как {2, 4, 6, 8, 10, 12, …}.
Натуральные нечетные числа
Натуральные числа, являющиеся нечетными и принадлежащие множеству N, известны как нечетные натуральные числа, не делящиеся точно на 2.
Итак, 1, 3, 5, 7, … являются примерами нечетных натуральных чисел. Набор натуральных нечетных чисел представлен как {1, 3, 5, 7, 9, 11, 13, …}.
Наименьшее натуральное число
1 известно как наименьшее натуральное число. Натуральные числа генерируются из 1 и заканчиваются на ∞. Хотя целые числа генерируются из 0, поэтому наименьшее целое число равно 0.
Натуральные числа от 1 до 100
Натуральные числа являются частью целых чисел, натуральными или счетными числами от 1 до 100 являются 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100.
Принадлежит ли 0 натуральным числам?
Часто задают вопрос, является ли 0 натуральным числом.
Натуральные числа — это счетные числа. 0 не натуральное число. Так как подсчет начинается с 1 вместо 0 при подсчете любого количества предметов. Число 0 точно принадлежит целому числу. 0 также является частью целых чисел и представлен на числовой прямой. Однако даже на числовой прямой все, начиная с +1 и ее правой части, принадлежит к натуральным числам.
Набор целых чисел идентичен набору натуральных чисел, за исключением того, что он включает 0 в качестве дополнительного числа. В математике множество целых чисел выражается как 0, 1, 2, 3,… Буква W обозначает это. Из определений ясно, что любое натуральное число является целым числом. Кроме того, все целые числа, кроме 0, являются натуральными числами. Ниже приведены представления наборов натуральных чисел и целых чисел в форме ростера,
W = {0, 1, 2, 3, 4, 5, …}
N = {1, 2, 3, 4, 5, …}
Разница между натуральными и целыми числами
Натуральные числа, такие как 1, 2, 3, 4 и т.
д., являются положительными числами. Это числа, используемые для счета, и они продолжаются бесконечно. Целые числа, с другой стороны, являются натуральными числами, за исключением нуля, например, 1, 2, 3, 4 и так далее. Все целые числа и их отрицательные аналоги считаются целыми числами. -4, -3, -2, -1, 0,1, 2, 3, 4 и т. д. вот некоторые примеры. В таблице ниже объясняется разница между натуральными числами и целыми числами,
Натуральные числа | Целые числа |
| Наименьшие натуральное число — 1. | Наименьшее целое число — 0. |
| Все натуральные числа — целые числа. | Все целые числа не являются натуральными числами. |
| Представление множества натуральных чисел N = {1, 2, 3, 4, …} | Представление множества целых чисел W = {0, 1, 2, 3, …} |
В числовой строке набор натуральных и целых чисел показан ниже.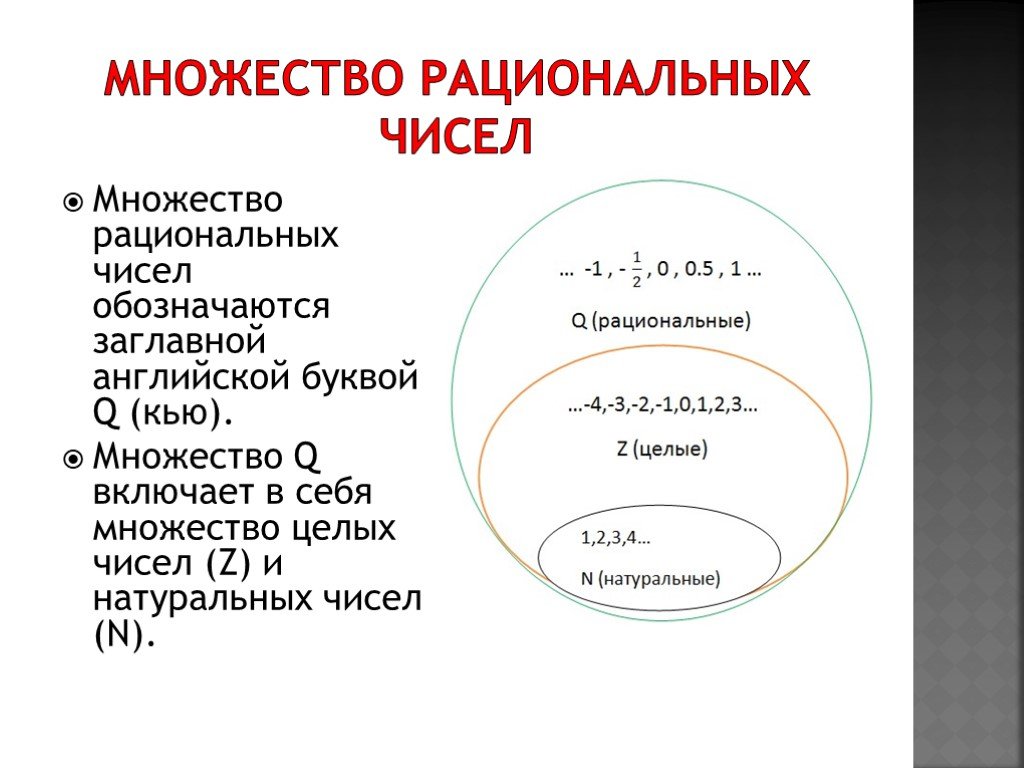
Натуральные числа представлены всеми положительными целыми числами или целыми числами справа от 0, тогда как целые числа представлены всеми положительными целыми числами плюс ноль. На приведенной ниже диаграмме показаны натуральные числа и целые числа на числовой прямой.
Первые 10 натуральных чисел
Первые 10 натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9, и 10. В форме набора обжарщиков первые 10 натуральных чисел представлены как
N = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
ЧислаСвойства натуральных чисел выведены из свойств чисел. Четыре операции с натуральными числами — сложение, вычитание, умножение и деление — приводят к четырем основным характеристикам натуральных чисел, которые показаны ниже:
- Свойство замыкания
- Переместительное свойство
- Ассоциативное свойство
- Распределительное свойство
Замыкающее свойство
При сложении и умножении двух или более натуральных чисел всегда получается натуральное число.
Свойство замыкания сложения равно a + b = c , т. е. 3 + 2 = 5, 9 + 8 = 17. Как видно из этого, сумма натуральных чисел всегда является натуральным числом. Свойство замыкания умножения: ab = c , т. е. 2 × 4 = 8, 7 × 8 = 56 и т. д. Это показывает, что натуральное число всегда является произведением двух натуральных чисел.
Примечание: Натуральные числа могут не подчиняться свойству замыкания, когда речь идет о вычитании и делении, что подразумевает, что вычитание или деление двух натуральных чисел может не дать натурального числа.
Ассоциативное свойство
При сложении и умножении натуральных целых чисел выполняется условие ассоциативности, т. е. a +(b + c) = (a + b) + c и a(b × c) = (a × b) c . Ассоциативное свойство сложения равно a + (b + c) = (a + b) + c , т.е. 1 + (3 + 5) = 1 + 8 = 9и тот же результат получается в (1 + 3) + 5 = 4 + 5 = 9. Ассоциативное свойство умножения равно a × (b × c) = (a × b) × c , т.
е. 2 × (2 × 1) = 2 × 2 = 4, и тот же результат получается в (a × b) × c = (2 × 2) × 1 = 4 × 1 = 4. Кратко опишем обе части ассоциативного свойства натуральных чисел,
- Ассоциативное свойство сложения: a + (b + c) = (a + b) + c
- Ассоциативное свойство умножения: a × (b × c) = (a × b) × c
Примечание: Свойство ассоциативности, с другой стороны, не выполняется для вычитания и деления натуральных чисел.
Коммутативное свойство
Даже если изменить последовательность чисел, сумма или произведение двух натуральных чисел останется прежним. Коммутативность N говорит, что a + b = b + a и ab = ba для любых a, b ∈ N. Давайте посмотрим на коммутативность сложения и коммутативность умножения натуральных чисел,
- Переместительное свойство сложения: a + b = b + a ⇒ Пример: 4 + 5 = 9 и b + a = 5 + 4 = 9.
- Переместительное свойство умножения: a × b = b × a ⇒ Пример: 3 × 2 = 6 и 2 × 3 = 6.
Распределительное свойство
Распределительное свойство натуральных чисел имеет два типа: распределительный закон умножения над сложением и распределительный закон умножения над вычитанием. Если нам дано a (b + c), то a может быть распределено между b и c и становится (ab + ac). Точно так же a(b – c) может стать (ab – ac).
- Распределительный закон умножения на сложение: a(b + c) = ab + ac.
- Распределительный закон умножения над умножением: a(b – c) = ab – ac.
Решенные примеры с натуральными числами
Пример 1. Определите натуральные числа среди данных чисел:
23, 98, 0, -98, 12.7, 11/7, 3. 9001 0
Ответ :
Поскольку отрицательные числа, 0, десятичные дроби и дроби не являются частью натуральных чисел. Следовательно, 0, -98, 12,7 и 11/7 не являются натуральными числами.
Таким образом, натуральные числа равны 23, 98 и 3.
Пример 2. Докажите распределительный закон умножения над сложением на примере.
Ответ:
Распределительный закон умножения над сложением гласит: a(b + c) = ab + ac.
Например, 4(10 + 20), здесь 4, 10 и 20 — все натуральные числа и, следовательно, должны подчиняться закону распределения. Следовательно,
4(10 + 20) = 4 × 10 + 4 × 20
4 × 30 = 40 + 80
120 = 120
Отсюда доказано.
Пример 3: Докажите распределительный закон умножения над вычитанием на примере.
Ответ:
Распределительный закон умножения над сложением гласит: a(b – c) = ab – ac.
Например, 7(3 – 6), здесь 7, 3 и 6 – все натуральные числа и, следовательно, должны подчиняться закону распределения. Следовательно,
7(3 – 6) = 7 × 3 – 7 × 6
7 × -3 = 21 + 42
-21 = -21
Следовательно, доказано.
Пример 4. Перечислите первые 10 натуральных чисел.
Ответ:
1, 2, 3, 4, 5, 6, 7, 8, 9 и 10 — первые десять натуральных чисел.
Пример 5: Определите ненатуральные числа среди данных чисел:
45, 9, 10, -8, 1,17, 98/3, 33/11.
Ответ:
Поскольку отрицательные числа, 0, десятичные дроби и дроби не являются частью натуральных чисел. Следовательно, -8, 1,17, 98/3 не натуральные числа. Обратите внимание, что 33/11 можно упростить до 3, а 3 — натуральное число.
Пример 6: Какова дисперсия первых 5 натуральных чисел?
Решение:
Формула для нахождения дисперсии первых n натуральных чисел: = (n 2 – 1)/12
. (5 2 -1 )/12
= 24/12
= 2
Часто задаваемые вопросы о натуральных числах
Вопрос 1: Каждое натуральное число является целым числом.
Правда или ложь?
Ответ:
Неверно. Каждое натуральное число не является целым числом, поскольку 0 присутствует в целых числах, но не в натуральных числах. Следовательно, утверждение неверно.
Вопрос 2: Запишите сумму первых 10 натуральных чисел.
Ответ:
1, 2, 3, 4, 5, 6, 7, 8, 9 и 10 — первые десять натуральных чисел. Следовательно, сумма первых 10 натуральных чисел будет равна 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9.+ 10 = 55.
Вопрос 3: Является ли 0 натуральным числом?
Ответ:
Нет, 0 не является частью натуральных чисел. 0 является частью целых чисел, и в этом основное различие между целыми числами и натуральными числами.
Вопрос 4: Чему равна сумма первых n натуральных чисел?
Ответ:
Формула суммы первых n натуральных чисел:
S = n (n + 1)/2
Здесь n — количество терминов.
Вопрос 5: Чему равна сумма квадратов n натуральных чисел?
Ответ:
Формула суммы квадратов n натуральных чисел:
S = n(n + 1)(2n + 1)/6
Вопрос 6: Что такое наименьшее натуральное число?
Ответ:
Наименьшее натуральное число равно 1. Натуральные числа начинаются с 1 и доходят до бесконечности. Следовательно, наименьшее натуральное число равно 1,9.0003
Вопрос 7: Найдите среднее первых n натуральных чисел.
Ответ:
Среднее значение первых n натуральных чисел равно
(n + 1)/2
Где n — количество членов.
Похожие статьи
- Целые числа
- Вещественные числа
- Рациональные числа
Комбинаторика — число сюръективных функций из множества из $m$ элементов в множество из $n$ элементов
Задавать вопрос
спросил
Изменено 4 года, 9 месяцев назад
Просмотрено 7к раз
$\begingroup$
Я пытался посчитать количество сюръективных (онто) функций от А до В.