Модель затраты-выпуск Леонтьева
Определение 1
Модель «затраты-выпуск» Леонтьева – это метод систематического количественного представления экономических связей между секторами системы хозяйствования.
Задачи межотраслевого баланса
Впервые идея изучения и анализа связей между отраслями экономики была предложена советскими статистиками-экономистами в процессе составления баланса народного хозяйства за 1923-24 год. Предложенный баланс содержал информацию о связях ключевых экономических отраслей и направления использования продукции в производстве.
Научная актуальность и перспективность анализа межотраслевых связей была осознана выпускником Санкт-Петербургского университета В. В. Леонтьевым.
Межотраслевой баланс выполняет следующие задачи:
- Характеризует воспроизводственные процессы в экономике по материально-вещественному составу для каждой отрасли;
- Отражает процессы производства и распределения продукции, которая создается в сфере материального производства;
- Детализирует счета товаров и услуг, производства, формирования доходов и действий с капиталом на уровне отраслей;
- Определяет роль факторов производства и их рациональное использование.

Сущность модели «затраты-выпуск» Леонтьева
Рассмотрим ключевые положения модели «затраты-выпуск» Леонтьева.
Как правило используются укрупненные показатели. Леонтьев составил для США межотраслевой баланс 1919 года и рассматривал 44 отрасли. В 1947 году был составлен баланс из 40 отраслей. В настоящее время большинстве случае используется баланс, состоящий из 600-700 отраслей.
На рисунке 1 представлена модель «затраты-выпуск».
Рисунок 1. Модель «затраты-выпуск». Автор24 — интернет-биржа студенческих работ
Строки и столбцы баланса содержат одинаковые отрасли. В строках отображаются выпуск продукции и ее конкретные потребители, а в столбцах – затраты на ее производство. данная система называется моделью Леонтьева «затраты-выпуск».
При пересечении отраслей-покупателей ($j$) и отраслей-продавцов($i$) образуются промежуточный спрос и затраты, т.е. производительное потребление произведенной продукции.
Пересечение $Xij$ является главной диагональю, внутриотраслевым потреблением произведенной продукции.
$W_{1i} = W_{1j}, W_{ni} = W_{nj}$
Другими словами, затраты и выпуск для каждой отрасли должны быть одинаковыми.
Каждая отрасль как по затратам, так и по выпуску содержит две принципиально разные части. Рассмотрим эти части по горизонтали. Строки отражают конкретные отрасли и лиц, которые потребляют данную продукцию. В данном примере все отрасли потребляют электроэнергию.
Первый сектор по горизонтали характеризует внутрипроизводительное потребление ($U$).
Ко второй части потребителей относятся населения, социальные учреждения и т.д. Их потребление – это конечное потребление, обозначаемое как $V$. Конечное потребление подразделяется на фонд потребления ($a_1$) и накопления ($b_1$).
Если рассматривать первую строку, то она будет включать $U_1, V_1. W_1 = U_1 + V_1$.
Как и строки, столбцы содержат две принципиально разные части. К первой части относятся промежуточные расходы, отражающие структуру использования ресурсов в экономике страны в целом, т.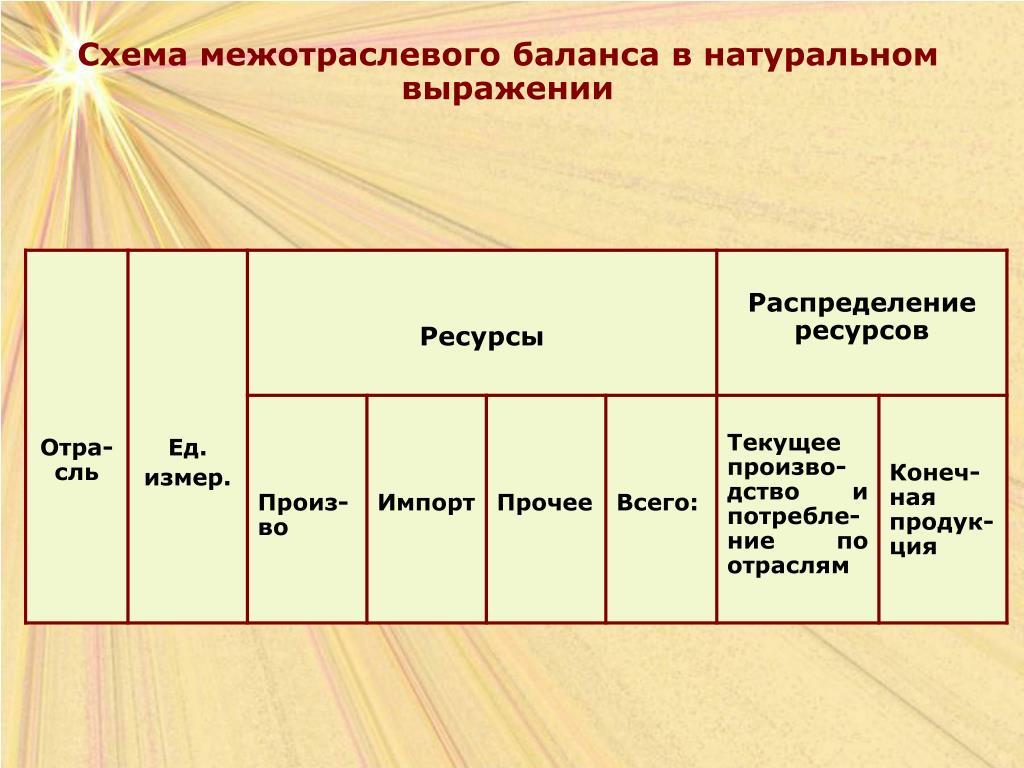 е. ресурсные потоки, их назначение и т.д.
е. ресурсные потоки, их назначение и т.д.
Ко второй части столбцов относятся собственные затраты всей отрасли на производство данных товаров. Эти затраты включают заработную плату, амортизацию, прибыль и налоги. Из собственных затрат образуется добавленная стоимость, сумма которой по всем отраслям экономики – это ВВП.
Рассмотрим более подробно затраты. При помощи межотраслевого баланса можно определить коэффициенты затрат трудовых, материальных и финансовых ресурсов.
Анализ данных коэффициентов дает возможность определить структурные сдвиги в экономике, а также показывает темпы развития конкретных отраслей. основываясь на анализе коэффициентов затрат выстраивается экономико-математическая модель.
Разные варианты решения проблем национальной экономики дают различные варианты экономического развития. На основе сравнения всех вариантов вырабатывается самая оптимальная модель роста экономики.
Модель «затраты-выпуск» выполняет статистическую и аналитическую функции.
Статистическая функция состоит в том, что система позволяет проверить согласованность экономической информации, характеризующей потоки производимой продукции.
Аналитическая функция выражается в возможности ее применения при анализе состояния, динамики процессов и моделировании вариантов экономического развития при изменении отдельных факторов. Именно с помощью симметричной модели «затраты-выпуск» Леонтьевым были разработаны методы анализа взаимосвязей выпуска продукции, первичных затрат и конечного спроса. Основу данного анализа составляет предположение о том, что затраты на изготовление продукции в течение конкретного временного периода являются величиной постоянной.
Значение модели Леонтьева для развития экономики
Замечание 1
Значение исследований Леонтьева в сфере построения межотраслевых балансов состоит в объединении абстрактных схем математиков-экономистов с практическим решением задач оптимизации деятельности народного хозяйства.
С помощью метода Леонтьева был усовершенствован математический аппарат, статистика, эконометрика, система национальных счетов.
Теория межотраслевого баланса Леонтьева позволила:
- Анализировать и прогнозировать развитие ключевых отраслей экономики на региональном, внутриотраслевом и межпродуктовом уровнях;
- Составлять объективный и актуальный прогноз относительно темпов и характера экономического развития;
- Определять основные макроэкономические показатели, при которых достигается равновесие национальной экономики;
- Рассчитывать полные и прямые затраты на изготовление единицы продукции;
- Определять ресурсоемкость как отдельных отраслей, так и национальной экономики в целом;
- Определять направления увеличения эффективности регионального и международного разделения труда.
Модель Леонтьева «затраты-выпуск»
Определим основные положения модели Леонтьева «затраты-выпуск».
Обычно используются укрупненные (агрегированные) показатели. Леонтьев составил межотраслевой баланс для США 1919 года и взял 44 отрасли. В 1947 году он составил баланс уже из 400 отраслей. Обычно используется баланс из 600-700 отраслей; особняком стоит Япония – 2 000 отраслей.
В строках и столбцах баланса указаны одни и те же отрасли. В строках учитывается выпуск продукции и ее конкретный потребитель, в столбцах – затраты по ее производству. Сама система называется
Пересечения отраслей-продавцов (i) и отраслей-покупателей (j) образуют промежуточный спрос и промежуточные затраты, т. е. это производительное потребление произведенных товаров.
Рис. 1. Модель Леонтьева «затраты–выпуск»
Пересечение Xij – главная диагональ, внутриотраслевое потребление произведенной продукции. Для таблицы в целом должно соблюдаться равенство: W1i = W1j, Wni = Wnj. Затраты и выпуск по каждой отрасли должны быть равны.
Для таблицы в целом должно соблюдаться равенство: W1i = W1j, Wni = Wnj. Затраты и выпуск по каждой отрасли должны быть равны.
Каждая отрасль и по затратам, и по выпуску состоит из двух принципиально разных частей. Рассмотрим эти части вначале по горизонтали. Строчки показывают, какие конкретные отрасли и лица являются потребителями данной продукции. В нашей простой схеме все четыре отрасли потребляют продукцию первой отрасли – электроэнергию.
Первая часть по горизонтали говорит о внутрипроизводительном потреблении (U).
Вторая часть потребителей – население, учреждения науки, культуры, здравоохранения и т. д. Их потребление называется конечным потреблением и обозначается буквой V. Конечное потребление делится на фонд потребления (a1) и фонд накопления (b1).
Таким образом, если мы возьмем первую строку, она будет состоять из U1 и V1: W1=U1+V1.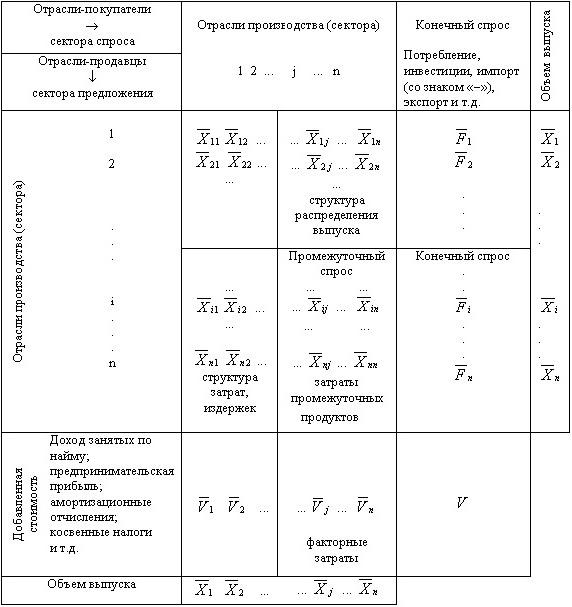
Столбцы также состоят из двух принципиально разных частей.
Первая часть –
Вторая часть столбцов – собственные затраты отрасли по производству данного вида товаров. Они состоят из заработной платы, амортизации, прибыли и налогов. Собственные затраты образуют добавленную стоимость. Сумма добавленной стоимости по всем отраслям образует валовой внутренний продукт (ВВП).
Остановимся более подробно на затратах. На основе межотраслевого баланса удается выяснить коэффициенты затрат финансовых, материальных и трудовых ресурсов, и эти коэффициенты выводятся в расчете на единицу выпускаемой продукции.
Анализ коэффициентов раскрывает структурные сдвиги в национальной экономике и показывает темпы развития отдельных отраслей.
При разных вариантах решения национальной экономической проблемы возможны и различные варианты развития экономики, может создаваться несколько моделей. Затем эти варианты сравнивают, и на основе сравнения вырабатывается наиболее оптимальная модель экономического роста.
Поскольку затраты включают прямые и косвенные затраты отраслей (косвенные затраты показывают потоки ресурсов), то разрабатываются три варианта коэффициентов: коэффициенты прямых затрат, коэффициенты косвенных затрат и коэффициенты полных затрат.
Если условно полные затраты принять за единицу, то возможно три варианта:
1. Отрасли для развития используют только свои внутренние ресурсы, прямые затраты. В этом случае прямые и полные затраты совпадают и равны единице.
2. Если отрасль для своего развития использует только поставки из других отраслей, то собственные затраты равны нулю, а косвенные единице.
3. Чаще всего и прямые, и косвенные затраты больше нуля, но меньше единицы.
Очень важен анализ направления потоков ресурсов в развивающуюся отрасль, и на основе этого анализа делается вывод, может ли национальная экономика выполнить поставленную задачу. Например, поставлена задача увеличить на 10 % выпуск автомобилей.
Необходимо проанализировать, какие отрасли будут поставщиками при увеличении объема производства (металлургия, машиностроение, химическая промышленность). Все эти отрасли должны направить в автомобилестроение на 10 % больше своих ресурсов.
Коэффициенты прямых и косвенных затрат в каждый момент показывают национальную статику, но мы знаем, что национальная экономика всегда находится в динамике, поэтому коэффициенты прямых, косвенных и полных затрат меняются со временем.
Возникает задача изучения динамики прямых и косвенных затрат. Автором теории этих процессов является американский ученый Стоун. Его теория называется PAS. Суть его метода состоит в том, что учитывается взаимозаменяемость поставок, косвенных затрат.
Его теория называется PAS. Суть его метода состоит в том, что учитывается взаимозаменяемость поставок, косвенных затрат.
Во-первых, под влиянием технического прогресса появляются товары-субституты, которые используются взамен традиционных товаров, сырья, материалов, комплектующих изделий и т. д. В результате этих процессов коэффициенты затрат по одним группам товаров уменьшаются, по другим – увеличиваются.
Во-вторых, в прямых затратах происходят изменения под влиянием технического прогресса, и в целом в полных затратах меняются пропорции между прямыми и косвенными затратами. Если происходит увеличение косвенных затрат, то тем самым в данной отрасли происходит увеличение затрат прошлого труда. Если растут прямые затраты, то увеличивается удельный вес затрат живого труда. При анализе этой таблицы обнаруживается, что когда происходит количественный экономический рост, то это приводит к увеличению удельного веса промежуточных затрат.
Когда же происходит качественный экономический рост, то, наоборот, сокращаются промежуточные затраты и промежуточный спрос, и в национальной экономике повышается удельный вес отраслей, производящих конечную продукцию.
Поэтому если мы начинаем анализировать национальную экономику страны, то мы видим по коэффициентам затрат, на каком этапе экономического роста она находится. Клетки промежуточных показателей наглядно показывают характер экономического роста.
В-третьих, в динамике учитываются изменения в ценах. Суть в том, что изменения цен изменяют потоки ресурсов. Те отрасли, которые снижают цену на свою продукцию, получают завышенные заказы, и эти отрасли более быстро развиваются, вытесняя продукцию тех отраслей, которые продолжают продавать свою продукцию по завышенным ценам.
При помощи модели Леонтьева «затраты-выпуск» можно сформулировать цели производства для национальной экономики. Цели производства, как это видно из таблицы, заключаются не в том, чтобы обеспечить определенный экономический рост, и не в том, чтобы этот рост был сбалансированным.
Цели производства, как это видно из таблицы, заключаются не в том, чтобы обеспечить определенный экономический рост, и не в том, чтобы этот рост был сбалансированным.
Цели производства оказываются следующими:
1. Удовлетворить потребности страны в продовольствии, не допустить зависимости национальной экономики от поставок продовольствия из-за рубежа.
2. Удовлетворить потребности в топливно-энергетических ресурсах.
3. Нарастить инвестиционный потенциал страны.
4. Технически перевооружить производство.
Значение работы Леонтьева в области построения межотраслевых балансов заключается также в соединении абстрактных схем экономистов-математиков с решением практических задач оптимизации работы народного хозяйства.
Метод Леонтьева позволил усовершенствовать математический аппарат путем определения тысяч новых коэффициентов, пригодных для создания экономико-математических моделей реальной экономики, способствовал совершенствованию статистики, эконометрики, созданию системы национальных счетов.
Модель затраты-выпуск Леонтьева — определение, цели, важность и сущность
Содержание:
В XX веке были созданы и развиты различные теории и методы регулирования мировой экономики. Потребность в таких исследованиях возросла, особенно после Великой депрессии (1929-1933 гг.) и Второй мировой войны. Возросла потребность в планировании (текущем, оперативном, стратегическом) и прогнозировании. Это объясняется главным образом тем, что современная экономика является открытой системой, построенной на прямых и обратных горизонтальных и вертикальных связях, и может успешно развиваться только в том случае, если этими связями эффективно управлять как на макро-, так и на микроуровне. В то же время проблема создания рациональной и высокоэффективной межотраслевой экономики имеет большое значение для всех стран.
Важным инструментом прогнозирования является разработанный В. Леонтьевым межотраслевой баланс равновесия, который может быть использован для анализа национальной экономики.
Реальное равновесие на рынке возможно только тогда, когда ожидания производителей и потребителей совпадают, поскольку на практике равновесие достигается достаточно редко, так как в условиях реальных экономических кризисов неизбежно неполное или неэффективное использование ресурсов. И все же можно утверждать, что необходимость метода баланса очевидна.
Таким образом, необходимо изучить модель Леонтьева «вход-выход», универсальность которой является редким явлением, а также рассмотреть специфику промежуточного баланса как метода равновесия, проследить историческое развитие модели Леонтьева и определить преимущества и недостатки этой модели.
Определение межсекторальной сбалансированности
Межотраслевой баланс — это соотношение между производством и распределением (распределением) социального продукта.
В современной экономической теории понятие межотраслевого баланса начинается с одной из моделей производственных отношений, основанных на экономико-математических отношениях.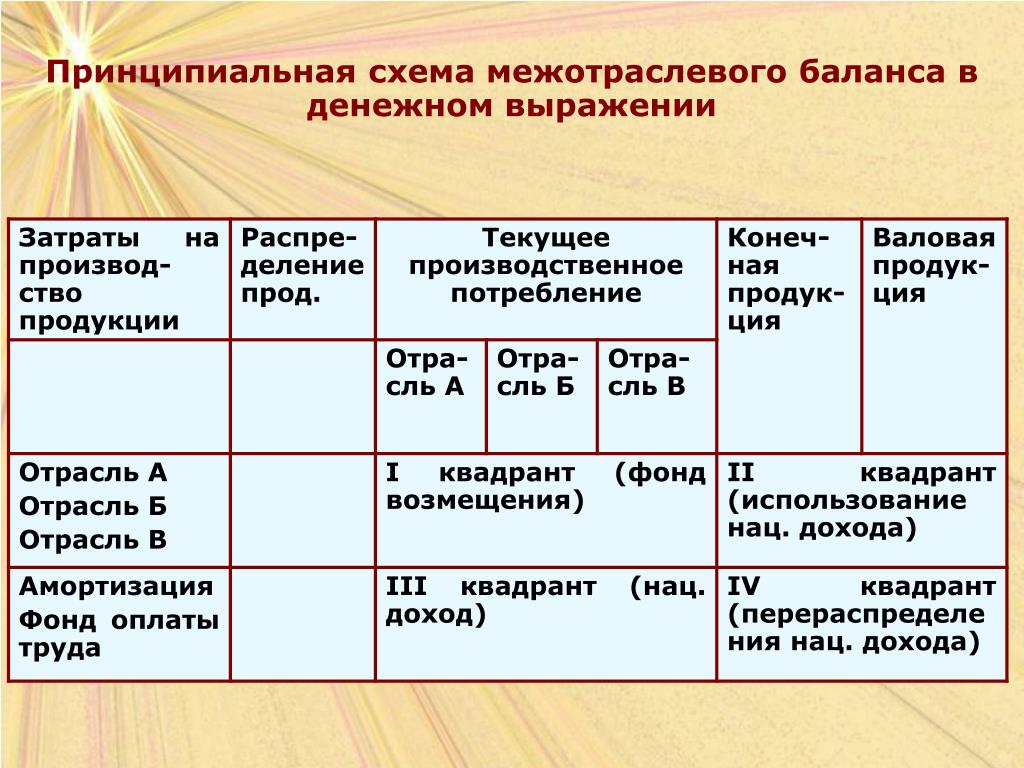
Использование такой модели отношений возможно в большинстве случаев при экономическом планировании и статистическом анализе трудовых отношений, поскольку она дает возможность детально рассмотреть пропорции национальной экономики как внутри сектора, так и в межотраслевом масштабе. Межотраслевой баланс (IAB) может быть рассчитан в натуральной и стоимостной форме.
MEB относится к балансовым моделям. Модель баланса понимается как система уравнений, каждое из которых выражает требование равновесия между производством отдельных экономических объектов, количеством продукции и совокупным спросом на эту продукцию. В этом случае мы рассматриваем систему экономических объектов, производящих определенный продукт, часть которого потребляется другими объектами системы, а другая часть выводится из системы как конечный продукт [3, с. 232].
Если вместо понятия конечного продукта ввести более общее понятие ресурса, то под балансовой моделью следует понимать систему уравнений, удовлетворяющую требованиям соответствия доступности ресурса и его использования.
Помимо требования соответствия каждого продукта и потребности в нем, можно привести такие примеры соответствия балансовой модели, как соответствие наличия рабочей силы и количества рабочих мест, платежеспособного спроса населения и предложения товаров и услуг и т.п. Под корреспонденцией понимается либо равенство, либо достаточность ресурсов для удовлетворения спроса и, следовательно, наличие определенного резерва.
Балансовый метод и основанные на нем модели баланса служат основным инструментом сохранения пропорций в экономике. Модели баланса, основанные на бухгалтерском балансе, характеризуют существующие пропорции, в которых ресурсная часть всегда равна расходной. Однако следует отметить, что равновесные модели не содержат механизма сравнения отдельных вариантов экономических решений и не обеспечивают взаимозаменяемости различных ресурсов, что не позволяет выбрать оптимальный вариант развития экономической системы. Это приводит к ограничениям балансовых моделей и метода баланса в целом.
Леонтьевская модель «вход-выход» — метод систематического количественного представления экономических отношений между секторами экономической системы.
Цели межотраслевого баланса
Идея изучения и анализа взаимосвязей между отраслями экономики была впервые предложена советскими статистиками при подготовке баланса национальной экономики на 1923-24 годы. В предлагаемом бухгалтерском балансе содержится информация о связях между основными отраслями экономики и направлением использования продукции в производстве.
Научную актуальность и перспективу анализа межотраслевых отношений представил выпускник Санкт-Петербургского университета В. В. Леонтьев.
Межотраслевой баланс выполняет следующие задачи:
- Характеризует процессы воспроизводства в экономике по материалу и составу материалов для каждой отрасли;
- Отражает процессы производства и распределения продукции, возникающие в материальном производстве;
- Детализирует счета по товарам и услугам, производству, получению доходов и операциям с капиталом на отраслевом уровне;
- Определяет роль факторов производства и их рациональное использование.

Важность леонтьевской модели для экономического развития
Важность леонтьевских исследований для развития межотраслевых равновесий заключается в сочетании абстрактных схем математических экономистов с практическими решениями по оптимизации экономики.
Математический аппарат, статистика, эконометрика и система национальных счетов были усовершенствованы с помощью метода Леонтьева.
Леонтьевская теория межотраслевого равновесия позволяет:
- Анализировать и прогнозировать результаты деятельности ключевых секторов экономики на региональном, внутриотраслевом и межотраслевом уровнях;
- Предоставить объективный и актуальный прогноз темпов и характера экономического развития;
- Определить ключевые макроэкономические показатели, при которых достигается равновесие экономики;
- Рассчитать общие и удельные затраты на производство единицы продукции;
- Определить ресурсоемкость как отдельных отраслей, так и экономики в целом;
- Определить направления повышения эффективности регионального и международного разделения труда.

Сущность леонтьевской модели ввода-вывода
Рассмотрим основные моменты леонтьевской модели ввода-вывода.
Как правило, используются агрегированные показатели. В 1919 году Леонтьев написал промышленный баланс США, в котором рассматривались 44 отрасли промышленности. В 1947 году был составлен баланс 40 отраслей промышленности. В настоящее время в большинстве случаев используется баланс, состоящий из 600-700 отраслей промышленности.
На рисунке 1 показана модель ввода-вывода.
Рисунок 1: Модель «затраты-выпуск».
Строки и столбцы баланса содержат одни и те же отрасли промышленности. Строки показывают выпуск продукции и ее конкретных потребителей, а колонки — стоимость ее производства. Эта система называется леонтьевской моделью себестоимости.
На пересечении отраслей промышленности — покупателя(j) и промышленности — продавца(i) формируется промежуточный спрос и себестоимость, т.е. продуктивное потребление произведенной продукции.
Пересечение Xij является главной диагональю — внутриотраслевым потреблением произведенной продукции. В целом, при составлении таблицы необходимо соблюдать следующее равенство:
В целом, при составлении таблицы необходимо соблюдать следующее равенство:
W1i=W1j, Wni=Wnj
Другими словами, стоимость и объем производства для каждой отрасли должны быть одинаковыми.
Каждая отрасль промышленности состоит из двух принципиально разных частей, как по себестоимости, так и по объему выпускаемой продукции. Рассмотрим эти части по горизонтали. Строки отражают конкретные отрасли промышленности и людей, которые потребляют определенную продукцию. В этом примере все секторы потребляют электроэнергию.
Первый горизонтальный сектор характеризует внутрипроизводственное потребление (U).
Вторая часть потребителей включает в себя домохозяйства, социальные учреждения и т.д. Их потребление — конечное потребление, обозначенное В. Окончательное потребление делится на потребительские фонды (a1) и сбережения (b1).
Если рассматривать первую строку, то она содержит U1,V1. W1=U1+V1.
W1=U1+V1.
Как и строки, колонны состоят из двух принципиально разных частей. Первая часть включает в себя промежуточные затраты, которые отражают структуру использования ресурсов в экономике в целом, т.е. потоки ресурсов, их назначение и т.д.
Вторая часть колонок содержит собственные затраты всей отрасли на производство этих товаров. Эти затраты включают заработную плату, амортизацию, прибыль и налоги. Из собственных затрат формируется добавленная стоимость, суммой которой для всех отраслей является ВВП.
Давайте рассмотрим расходы более подробно. С помощью промежуточного баланса можно определить коэффициенты трудовых, материальных и финансовых затрат.
Анализ этих коэффициентов позволяет определить структурные сдвиги в экономике, а также показывает темпы развития отдельных отраслей.
Различные варианты решения проблем национальной экономики приводят к различным вариантам экономического развития. На основе сравнения всех вариантов разработана наиболее оптимальная модель экономического роста.
Модель «вход-выход» выполняет статистические и аналитические функции.
Статистическая функция состоит в том, что система позволяет проверить непротиворечивость экономической информации, характеризующей производственные потоки.
Аналитическая функция выражается в возможности ее применения при анализе состояния дел, динамике процессов и моделировании вариантов экономического развития при изменении индивидуальных факторов. С помощью симметричной модели «вход-выход» Леонтьев разработал методы анализа соотношений между производством, первичными затратами и конечным спросом. В основе данного анализа лежит предположение, что производственные затраты являются постоянными в течение данного периода.
2.6: Приложения – Леонтьевские модели
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 37851
- Рупиндер Секон и Роберта Блум
- Колледж Де Анза
Цели обучения
В этом разделе мы рассмотрим применение матриц для моделирования экономических систем.
В 1930-х годах Василий Леонтьев использовал матрицы для моделирования экономических систем. Его модели, часто называемые моделями «затраты-выпуск», делят экономику на секторы, где каждый сектор производит товары и услуги не только для себя, но и для других секторов. Эти сектора зависят друг от друга, и общий ввод всегда равен общему выпуску. В 1973 года он получил Нобелевскую премию по экономике за свою работу в этой области. В этом разделе мы рассмотрим как закрытые, так и открытые модели, которые он разработал.
Закрытая модель
В качестве примера закрытой модели рассмотрим очень простую экономику, где есть только три сектора: еда, жилье и одежда.
Пример \(\PageIndex{1}\)
Предположим, что в деревне есть фермер, плотник и портной, которые производят три основных товара: еду, кров и одежду. Предположим, сам фермер потребляет 40% продуктов, которые он производит, и отдает 40% плотнику, а 20% портному. Тридцать процентов продукции плотника потребляет он сам, 40 процентов – фермер и 30 процентов – плотник. Пятьдесят процентов продукции портного используется им самим, 30 % — фермером и 20 % — портным. Напишите матрицу, описывающую эту замкнутую модель.
Пятьдесят процентов продукции портного используется им самим, 30 % — фермером и 20 % — портным. Напишите матрицу, описывающую эту замкнутую модель.
Решение
В приведенной ниже таблице описана приведенная выше информация.
| Доля, произведенная фермером | Доля, изготовленная плотником | Пропорция, изготовленная портным | |
| Доля, используемая фермером | .40 | .40 | .30 |
| Пропорция, используемая плотником | .40 | .30 | .20 |
| Пропорция, используемая портным | . 20 20 | .30 | .50 |
В матричной форме это можно записать следующим образом.
\[A=\left[\begin{array}{lll}
.40 & .40 & .30 \\
.40 & .30 & .20 \\
.20 & .30 & .50
\end{array}\right] \nonumber \]
Эта матрица называется матрицей ввода-вывода . Важно правильно прочитать матрицу. Например, запись \(A_{23}\), запись в строке 2 и столбце 3, представляет следующее.
\(A_{23}\) = 20% продукции портного используется плотником.
\(A_{33}\) = 50% продукции портного используется портным.
Пример \(\PageIndex{2}\)
В приведенном выше примере \(\PageIndex{1}\) сколько должен получить каждый человек за свои усилия?
Решение
Мы выбираем следующие переменные.
\(x\) = заработная плата фермера \(y\) = заработная плата плотника \(z\) = заработная плата портного
Как мы уже говорили ранее, в этой модели затраты должны равняться выпуску. То есть сумма, уплаченная каждым, равна сумме, полученной каждым.
То есть сумма, уплаченная каждым, равна сумме, полученной каждым.
Допустим, фермеру платят \(x\) долларов. Давайте теперь посмотрим на расходы фермера. Фермер использует 40% своего собственного производства, то есть из x долларов, которые ему платят, он платит себе 0,40x долларов, он платит 0,40y долларов плотнику и 0,30z портному. Поскольку расходы равны заработной плате, мы получаем следующее уравнение.
\[x=.40 x+.40 y+.30 z \nonumber \]
Таким же образом получаем
\begin{align}
y=&.40 x+.30 y+.20 z \\
z=&.20 x+.30 y+.50 z
\end{aligned}
Приведенная выше система может быть записана как
\[\left[\begin{array}{l}
x \\
y \ \
z
\end{массив}\right]=\left[\begin{array}{lll}
.40 & .40 & 30 \\
.40 & .30 & .20 \\
.20 & . 30 и .50
\end{массив}\right]\left[\begin{массив}{l}
x \\
y \\
z
\end{array}\right] \nonumber \]
Эту систему часто называют \(X = AX\)
Упрощение приводит к системе уравнений \( (I — A) X = 0\)
\begin{align}
. 60 x-.40 y-.30 z &=0 \\
60 x-.40 y-.30 z &=0 \\
-.40 x+.70 y-.20 z &=0 \ \
-.20 x-.30 y+.50 z &=0
\end{aligned}
Решение для \(x\), \(y\) и \(z\) с использованием метода Гаусса-Жордана , мы получаем
\[x =\frac{29}{26}t \quad y = \frac{12}{13}t \quad \text{ и } z = t \nonumber \]
Поскольку мы только пытаемся определить пропорции оплаты, мы можем выбрать любое значение t. Предположим, мы допустим \(t\(= $2600, тогда мы получаем
\[x =\$2900 \quad y = \$2400 \quad \text{ и } z = \$2600 \nonumber \]
Примечание. Использование Графический калькулятор или компьютерное приложение для решения систем линейных матричных уравнений в этих задачах настоятельно рекомендуется
Открытая модель
Открытая модель более реалистична, так как она имеет дело с экономикой, где секторы экономики не только удовлетворяют каждый потребности других, но они также удовлетворяют некоторые внешние потребности. В этом случае внешние потребности предъявляются потребителем. Но основная посылка остается той же: все, что производится, потребляется.0034
Но основная посылка остается той же: все, что производится, потребляется.0034
Давайте снова рассмотрим очень простой сценарий. Предположим, что хозяйство состоит из трех человек: фермера F, плотника C и портного T. Часть продукции фермера используется всеми тремя, а остальная часть используется потребителем. Точно так же часть продукции плотника и портного используется всеми тремя, а остальная часть используется потребителем.
Предположим, что все, что производит фермер, 20% потребляет он, 15% — плотник, 10% — портной, а остальные 40 миллиардов долларов потребляет потребитель. Он использует 10% продукции плотника, 25% — фермера, 5% — портного и 50 миллиардов долларов — потребителя. Пятнадцать процентов одежды используется портным, 10 процентов — фермером, 5 процентов — плотником, а оставшиеся 60 миллиардов долларов — потребителем. Запишем внутреннее потребление в следующую таблицу, а спрос выразим в виде матрицы D.
| F производит | C производит | Т производит | |
| F использует | . 20 20 | .25 | .10 |
| C использует | .15 | .10 | .05 |
| Т использует | .10 | .05 | .15 |
Потребительский спрос для каждой отрасли в миллиардах долларов приведен ниже.
\[\mathrm{D}=\left[\begin{array}{c}
40 \\
50 \\
60
\end{массив}\right] \nonumber \]
Пример \(\ PageIndex{3}\)
В приведенном выше примере каким должен быть в миллиардах долларов требуемый выпуск каждой отрасли для удовлетворения спроса, заданного матрицей \(D\)?
Решение
Мы выбираем следующие переменные.
x = выпуск фермера
y = выпуск плотника
z = выпуск портного
В закрытой модели наше уравнение было \(X = AX\), то есть общий ввод равен общему выпуску. На этот раз наше уравнение похоже, за исключением спроса со стороны потребителя.
На этот раз наше уравнение похоже, за исключением спроса со стороны потребителя.
Таким образом, наше уравнение для открытой модели должно быть \(X = AX + D\), где \(D\) представляет собой матрицу спроса.
Выразим это следующим образом:
\[X = AX + D \nonumber \]
\[\left[\begin{array}{l}
x \\
y \\
z
\end{ array}\right]=\left[\begin{array}{lll}
.20 & .25 & .10 \\
.15 & .10 & .05 \\
.10 & .05 & .15
\ end{массив}\right]\left[\begin{array}{l}
x \\
y \\
z
\end{массив}\right]+\left[\begin{array}{l}
40 \\
50 \\
60
\end{array}\right] \nonumber \]
Чтобы решить эту систему, запишем ее как 9{-1}=\left[\begin{array}{ccc}
1.3445 & .3835 & .1807 \\
.2336 & 1.1814 & .097 \\
.1719 & .1146 & 1.2034
\end{array} \right] \nonumber \]
\[{X}=\left[\begin{array}{ccc}
1.3445 & .3835 & .1807 \\
.2336 & 1.1814 & .097 \\
.1719 & . 1146 & 1.2034
1146 & 1.2034
\end{массив}\right]\left[\begin{array}{c}
40 \\
50 \\
60
\end{массив}\right] \nonumber \]
\ [X=\left[\begin{массив}{l}
83,7999 \\
74,2341 \\
84,8138
\end{array}\right] \nonumber \]
Три отрасли промышленности должны производить следующее количество товаров в миллиардах долларов.
Фермер = 83,7999 долл. Плотник = 74,2341 долл. Портной = 84,813 долл. отрасли. Другими словами, мы запрашиваем матрицу \(A\).
Пример \(\PageIndex{4}\)
Предположим, что экономика состоит из трех отраслей F, C и T. Каждая из отраслей производит для внутреннего потребления между собой, а также для внешнего спроса со стороны потребителя. В таблице показано использование продукции каждой отрасли в долларах.
| Ф | С | Т | Спрос | Всего | |
| Ф | 40 | 50 | 60 | 100 | 250 |
| С | 30 | 40 | 40 | 110 | 220 |
| Т | 20 | 30 | 30 | 120 | 200 |
В первой строке указано, что из 250 долларов, произведенных отраслью F, 40 долларов используются F, 50 долларов используются C, 60 долларов используются T, а оставшиеся 100 долларов используются потребителем. Аналогично описываются остальные строки.
Аналогично описываются остальные строки.
И снова общий ввод равен общему выпуску. Найдите долю количеств, потребляемых каждой из отраслей. Другими словами, найдите матрицу \(A\).
Решение
Нас просят определить следующее:
Сколько продукции каждой из трех отраслей F, C и T требуется для производства одной единицы F? Точно так же, какая часть продукции каждой из трех отраслей F, C и T требуется для производства одной единицы C? И, наконец, какая часть продукции каждой из трех отраслей F, C и T требуется для производства одной единицы T?
Поскольку мы ищем пропорции, нам нужно разделить производство каждой отрасли на общее производство каждой отрасли.
Анализируем следующим образом:
Чтобы произвести 250 единиц F, нам нужно использовать 40 единиц F, 30 единиц C и 20 единиц T.
Следовательно, чтобы произвести 1 единицу F, нам нужно использовать 40/250 единиц F, 30/250 единиц C и 20/250 единиц T.
Чтобы произвести 220 единиц C, нам нужно использовать 50 единиц F, 40 единиц C и 30 единиц T.
Следовательно, чтобы произвести 1 единицу C, нам нужно использовать 50/220 единиц F, 40/220 единиц C и 30/220 единиц T.
Чтобы произвести 200 единиц T, нам нужно использовать 60 единиц F, 40 единиц C и 30 единиц T.
Следовательно, для производства 1 единицы T нам нужно использовать 60/200 единиц F, 40/200 единиц C и 30/200 единиц T.
Получаем следующую матрицу.
\[\mathrm{A}=\left[\begin{array}{lll}
40 / 250 и 50 / 220 и 60 / 200 \\
30 / 250 и 40 / 220 и 40 / 200 \\
20 / 250 и 30 / 220 и 30 / 200
\end{array}\right]=\left[\begin{array}{ccc}
.1600 & .2273 & .3000 \\
.1200 & .1818 & .2000 \\
.0800 и .1364 и .1500
\end{массив}\right] \nonumber \]
Четко \(AX + D = X\)
\[\left[\begin{array}{lll}
40 / 250 и 50 / 220 и 60 / 200 \\
30 / 250 и 40 / 220 и 40 / 200 \\
20 / 250 и 30 / 220 и 30 / 200
\end{array}\right]\left[\begin{array}{l}
250 \\
220 \\
200
\end{массив}\right]+\left[\begin{array}{l}
100 \\
110 \\
120
\end{массив}\right] =\left[\begin{массив}{l}
250 \\
220 \\
200
\end{array}\right] \nonumber \]
Суммируем следующим образом:
ЗАКРЫТАЯ МОДЕЛЬ ЛЕОНТЬЕВА
- Все потребление находится внутри отраслей.
 Нет внешнего спроса.
Нет внешнего спроса. - Вход = Выход
- \(X = AX\) или \((I — A)X = 0\)
ОТКРЫТАЯ МОДЕЛЬ ЛЕОНТЬЕФА
- Помимо внутреннего потребления существует внешний спрос со стороны потребителя.
- Вход = Выход 9{-1} Д\)
Эта страница под названием 2.6: Applications — Leontief Models распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Рупиндером Секоном и Робертой Блум с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Рупиндер Сехон и Роберта Блум
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- закрытая модель (эконом)
- модели ввода-вывода
- Леонтьев модели
- открытая модель (эконом)
- источник@https://www.
 deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
Применение ценовой модели «затраты-выпуск» для выявления инфляционных процессов | Журнал экономических структур
- Исследования
- Открытый доступ
- Опубликовано:
- Михал Пшибылински ORCID: orcid.org/0000-0002-1909-3687 1 и
- Артур Горзалчинский ORCID: orcid.org/0000-0002-7435-3453 1
Журнал экономических структур том 11 , номер статьи: 5 (2022) Процитировать эту статью
1377 доступов
Сведения о показателях
Abstract
Мы пытаемся изучить потенциал ценовой модели «затраты-выпуск» для выявления механизмов ценообразования и передачи. В отличие от предыдущих исследований, в которых основное внимание уделялось преодолению конкретных ограничений модели, мы проверяем ее общую производительность. В представленном исследовании исторические значения широко используемого индекса потребительских цен были декомпозированы в соответствии с классической моделью цен «затраты-выпуск» для открытой экономики. Для определения источников инфляции использовалась последовательность моделирования ex post при различных допущениях. Это исследование требовало использования таблиц «затраты-выпуск» в ценах текущего и предыдущего года. Предлагаемый метод декомпозиции может стать отправной точкой для создания основы для изучения различных аспектов инфляционного процесса.
В отличие от предыдущих исследований, в которых основное внимание уделялось преодолению конкретных ограничений модели, мы проверяем ее общую производительность. В представленном исследовании исторические значения широко используемого индекса потребительских цен были декомпозированы в соответствии с классической моделью цен «затраты-выпуск» для открытой экономики. Для определения источников инфляции использовалась последовательность моделирования ex post при различных допущениях. Это исследование требовало использования таблиц «затраты-выпуск» в ценах текущего и предыдущего года. Предлагаемый метод декомпозиции может стать отправной точкой для создания основы для изучения различных аспектов инфляционного процесса.
Введение
Исследование чувствительности цен к внешним импульсам имеет большое значение для прогнозирования инфляции. Такой анализ часто проводится по заказу или при поддержке центральных банков, целью которых является достижение и поддержание стабильности цен.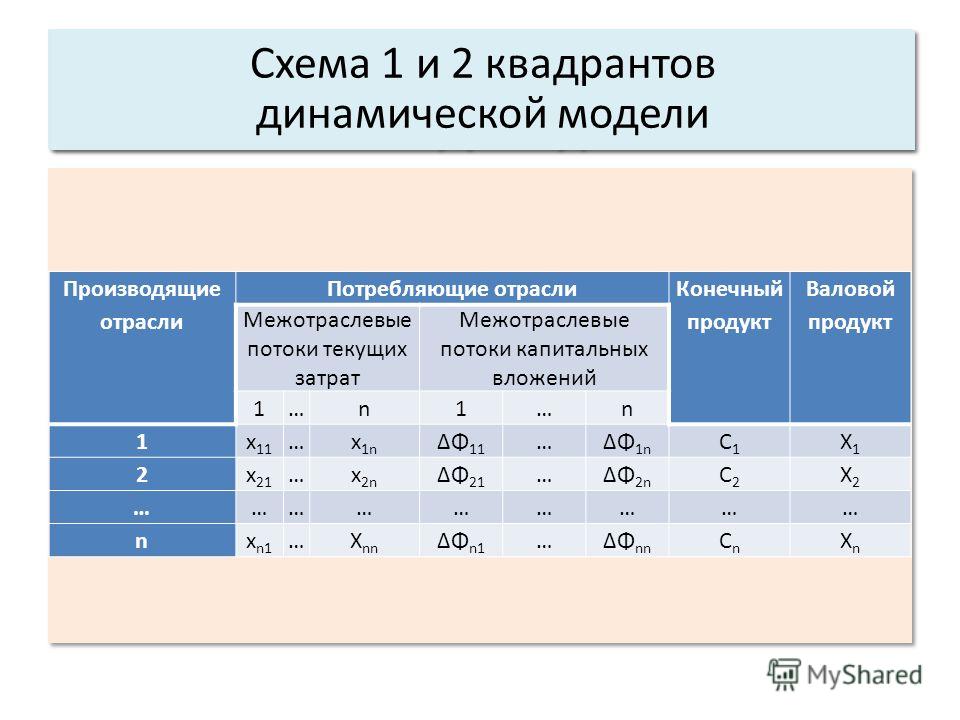 По практическим соображениям исследования переноса и ценообразования сосредоточены на двух основных первичных импульсах, основанных на теории затрат. Первый возникает из-за изменения цен на импорт (из-за изменения цен, выраженных в иностранной валюте, или изменения обменного курса). Второй — налоги, в основном НДС (например, Benedek et al., 2020; Ardalan and Kessing, 2019).). Другие исследования касаются переноса процентной ставки (Cook, 2008) и эффективности денежно-кредитной политики в целом (Leszczyńska-Paczesna, 2020).
По практическим соображениям исследования переноса и ценообразования сосредоточены на двух основных первичных импульсах, основанных на теории затрат. Первый возникает из-за изменения цен на импорт (из-за изменения цен, выраженных в иностранной валюте, или изменения обменного курса). Второй — налоги, в основном НДС (например, Benedek et al., 2020; Ardalan and Kessing, 2019).). Другие исследования касаются переноса процентной ставки (Cook, 2008) и эффективности денежно-кредитной политики в целом (Leszczyńska-Paczesna, 2020).
Среди вышеупомянутых направлений исследований наиболее интенсивная работа сосредоточена на переносе обменного курса (ERPT), что означает изучение того, как колебания обменного курса влияют на внутренние цены (например, Aron et al. 2014; Auer and Schoenle 2016; Пеннингс 2017). В целом, эти модели основаны на формуле затрат более или менее прямым образом. Некоторые из них сочетают в себе факторы стоимости и спроса (Shakeri and Gray, 2013; Beckman et al., 2019). ). Другие макроэкономические исследования исследуют роль процентных ставок и денежной массы. Большинство из них основаны на эконометрических моделях с несколькими уравнениями, таких как VAR, SVAR или VEC. Эти исследования не используют потенциал инструмента, известного на протяжении многих десятилетий, а именно ценовой модели «затраты-выпуск» (IO).
). Другие макроэкономические исследования исследуют роль процентных ставок и денежной массы. Большинство из них основаны на эконометрических моделях с несколькими уравнениями, таких как VAR, SVAR или VEC. Эти исследования не используют потенциал инструмента, известного на протяжении многих десятилетий, а именно ценовой модели «затраты-выпуск» (IO).
Модель возникла в основополагающей статье Леонтьева (1937), и он также был первым, кто применил ее (Леонтьев, 1946). Мы можем найти различные исследования, в которых начальным импульсом является изменение импортных цен (см., например, Wu et al. 2013) или добавленная стоимость единицы продукции и не включенные в них налоги (например, Lee et al. 2000; Boratyński 2006; Sharify and Sancho 2011). ERPT также можно исследовать, рассматривая цены на импортные товары как внешние цены, выраженные в иностранной валюте, умноженные на обменный курс (Aydoğuş et al. 2017). Проведенные до сих пор исследования сосредоточены на конкретных аспектах ценообразования, они не тестируют и не обсуждают общую эффективность модели. Представленное исследование призвано стать шагом к восполнению этого пробела.
Представленное исследование призвано стать шагом к восполнению этого пробела.
В этой статье мы представляем эмпирические расчеты, которые исследуют эффективность классической модели IO в воспроизведении механизмов ценообразования и ее потенциал для прогнозирования инфляции. В исследовании была предпринята попытка воспроизвести исторические значения индекса потребительских цен (ИПЦ) на основе классической ценовой модели IO. Мы начинаем с уровня цен в базисном году и, последовательно обновляя определенные элементы модели, получаем последовательность теоретических ИПЦ, в конечном итоге приходим к фактическому значению ИПЦ следующего года.
Различия в таких рассчитанных ИПЦ на каждом этапе этой процедуры можно интерпретировать как составляющие общей ошибки прогноза. Каждая такая составляющая отражает тот или иной экономический фактор, влияющий на инфляцию, или формальные (технические) неточности при обработке статистических данных. Из многочисленных вариантов декомпозиции мы пытаемся найти простой, убедительный, с ясным экономическим смыслом. Мы уделяем особое внимание широко обсуждаемому переносу цен импорта во внутренние цены, что приводит нас к определению «переноса затрат-выпуска».
Мы уделяем особое внимание широко обсуждаемому переносу цен импорта во внутренние цены, что приводит нас к определению «переноса затрат-выпуска».
Для использования предложенного ниже метода необходим доступ к таблицам затрат-выпуска, выраженным в текущих ценах, а также в ценах предыдущего года. Использование таблиц в постоянных и текущих ценах проанализировано в работе Дитценбахера и Темуршоева (2012). Это исследование было сосредоточено на выявлении различий в результатах, полученных для одних и тех же переменных для набора данных по Дании между 2000 и 2007 годами. Такие таблицы публикуются все чаще и чаще, но в настоящее время очень мало случаев, когда они представляют собой соответствующие временные ряды. Заметным исключением является Статистическое управление Дании, поэтому мы решили основывать наш эмпирический пример на данных, опубликованных этим учреждением.
Методы
Эмпирические исследования инфляции основаны на трех доминирующих теоретических положениях, а именно на денежной теории, теории спроса и стоимости. Ценовая модель IO делает возможным очень детальное исследование теории затрат. Вряд ли есть какие-либо размышления о монетарной теории или теории спроса, но это несовершенство можно превратить в силу, если рассмотреть, почему результаты моделирования отличаются от реальности.
Ценовая модель IO делает возможным очень детальное исследование теории затрат. Вряд ли есть какие-либо размышления о монетарной теории или теории спроса, но это несовершенство можно превратить в силу, если рассмотреть, почему результаты моделирования отличаются от реальности.
Модели IO очень подробно описывают экономику и создают больше возможностей для анализа изменений цен на отдельных рынках. Это преимущество иногда недооценивается макроэкономистами, потому что отдельная отрасль (или группа продуктов) имеет ограниченное влияние на совокупный уровень цен. 9{D}\) часто называют матрицей коэффициентов IO), поэтому издержки производства (т. е. стоимость затрат) получаются после умножения этих матриц на соответствующие цены. По практическим соображениям (отсутствие информации о количестве) договорные цены на продукцию приняты на уровне 1, что позволяет предположить, что количества потоков равны их значениям. При таком допущении матрицу коэффициентов IO в денежных единицах можно рассматривать как матрицу коэффициентов IO в физических единицах (то же самое относится к \({{\varvec{A}}}^{M}\)). {M}\) содержат индексы цен 9-го года.{М}+Т\).
{M}\) содержат индексы цен 9-го года.{М}+Т\).
Нижний индекс i означает группу продуктов; отсутствие индекса — макроэкономическая ценность; верхний индекс D — товары отечественного производства; верхний индекс M — импортная продукция; отсутствие такого надстрочного индекса — общее предложение (т.е. D + M ). T – стоимость налогов, взимаемых с потребления домохозяйств.
Последовательность расчетов
Эксперимент состоял из нескольких ex post симуляций, которые варьировались компонентами ценовой модели IO (Формула 2) и формулой взвешивания 3. Они отражали ряд прогнозов, в которых постепенно раскрывалось будущее. Результаты моделирования пронумерованы цифрами, указанными в верхних индексах. Отправной точкой является «наивный» прогноз, в котором не ожидается изменения цен: 9{*0}=1,\) это фактическая инфляция (ИПЦ-1).
Таким образом, описанная выше процедура разлагает инфляцию (или ошибку) на семь составляющих (видов ошибок), а именно:
E1: Изменения налогов, взимаемых с потребительских товаров, и баланс потребления нерезидентами и потребления отечественными жителей за границей. В последовательности Пааше он включает также изменения в структуре потребления.
В последовательности Пааше он включает также изменения в структуре потребления.
E2: Изменения (однородных) импортных цен.
E3: Изменения удельной добавленной стоимости (прочие налоги, заработная плата и валовая прибыль).
E4: Изменения параметров модели (матрицы A ).
E5: Допущение об однородности внутренних цен (цены на продукцию одинаковы для всех покупателей).
E6: Предположение об однородности цен (цены потребительских товаров такие же, как цены выпуска) Сноска 3 и, в последовательности Ласпейреса, также изменения в структуре потребления.
E7: Разница между ИПЦ и дефлятором потребления домашних хозяйств, полученным из таблицы «затраты-выпуск».
Последняя составляющая не имеет экономического смысла, но актуальна для практических задач экономического моделирования. При использовании моделей на основе IO, таких как INFORUM или CGE, этот компонент устраняет разрыв между ИПЦ, полученным из системы цен IO, и официальными данными ИПЦ, используемыми в других уравнениях.
Эта последовательность компонентов не единственная возможность разложения. Он был выбран из-за его экономического значения. В малой открытой экономике цены на импорт кажутся «наиболее экзогенным» фактором, поэтому эта составляющая предшествует добавленной стоимости и параметрам, которые (в некоторой степени) адаптируются к изменениям внешних цен.
Результаты и обсуждение
Для моделирования требовались таблицы потоков отечественной продукции и (отдельные) таблицы потоков импортной продукции, выраженные как в ценах текущего года, так и в ценах предыдущего года. Наиболее обширный доступный статистический материал, позволяющий провести такое исследование, можно найти в Статистическом управлении Дании, где измерения цен на основе затрат-выпуска имеют давнюю традицию (например, Hansen and Knudsen, 2005; Abildgren, 2006). Наборы таблиц «затраты-выпуск» охватывают период 1966–2019 гг. Сноска 4 Однако ИПЦ впервые был опубликован в 1980, поэтому наше исследование было ограничено периодом 1980–2019 гг. Таблицы, использованные в исследовании, представляют собой агрегацию на уровне 69 товарных групп. Категория «Туризм», представляющая собой баланс потребления нерезидентами в Дании и потребления резидентами Дании в остальном мире, была включена в налоги на потребление домохозяйств (переменные T и \({p}_{ Т}\)).
Таблицы, использованные в исследовании, представляют собой агрегацию на уровне 69 товарных групп. Категория «Туризм», представляющая собой баланс потребления нерезидентами в Дании и потребления резидентами Дании в остальном мире, была включена в налоги на потребление домохозяйств (переменные T и \({p}_{ Т}\)).
Результаты представлены на рис. 1. Фактические приращения ИПЦ сравниваются с вкладами каждого компонента. Компоненты Е5 и Е6 были сложены вместе и помещены на один график. Их значения были существенно ниже, чем у других компонентов, еще одной причиной их объединения была их интерпретация. Обе составляющие отражают изменения внутриотраслевой структуры цен.
Рис. 1 ИПЦ Дании и его компоненты. Сумма E 1… E 7 равна CPI-1. Источник: собственные расчеты, основанные на данных Статистического управления Дании. Это означает, что структура потребления домохозяйств из года в год меняется незначительно. В случае Е1 можно выделить три наблюдения, в которых заметны различия, а именно для лет 1986, 1995 и 2008 гг. Их источником являются исключительные колебания по статье «Туризм». Эти различия компенсируются в E6, где структура потребления переключается в последовательности Ласпейреса на t + 1.
Их источником являются исключительные колебания по статье «Туризм». Эти различия компенсируются в E6, где структура потребления переключается в последовательности Ласпейреса на t + 1.
Первые три компонента изменяются в соответствии с инфляцией, в то время как остальные четыре кажутся стабильными во времени, независимо от ИПЦ. Несомненно, основной движущей силой инфляции является удельная добавленная стоимость (Е3). Вторая важная составляющая — импортные цены (Е2), но ее вклад гораздо меньше. Эти результаты подтверждают процесс ценообразования, отраженный в модели IO. Налоги (Е1) коррелируют с инфляцией и роль этой составляющей неоднозначна; изменения налоговых ставок являются причиной инфляции, но сама инфляция увеличивает налоговые поступления. Пункт «Туризм» затемняет изображение.
Коэффициенты линейной корреляции между отдельными компонентами показаны в Таблице 1. Высокая корреляция между E2 и E3 предполагает, что изменения в ценах на импорт вызывают корректирующие механизмы, влияющие на добавленную стоимость. Корреляция положительная, что означает, что добавленная стоимость усиливает первичный импульс, поступающий из-за рубежа. Можно предположить, что другие корректировки связаны с изменением параметров модели, т.е.0046 A M матрицы (E4), в этом случае корреляция с E2 отрицательная. Отечественные фирмы сохраняют свои реальные доходы (и заработную плату) постоянными и пытаются уменьшить ценовой шок, изменяя технологию производства, что означает замещение промежуточных продуктов.
Корреляция положительная, что означает, что добавленная стоимость усиливает первичный импульс, поступающий из-за рубежа. Можно предположить, что другие корректировки связаны с изменением параметров модели, т.е.0046 A M матрицы (E4), в этом случае корреляция с E2 отрицательная. Отечественные фирмы сохраняют свои реальные доходы (и заработную плату) постоянными и пытаются уменьшить ценовой шок, изменяя технологию производства, что означает замещение промежуточных продуктов.
Небольшие значения E5 и E6 означают, что предположение об однородности цен не кажется значительным источником ошибок при прогнозировании ИПЦ. Это аргумент, который поощряет использование модели IO. Последний компонент (Е7) также носит «технический» характер. Сильная отрицательная корреляция между Е2 и Е6 может свидетельствовать о наличии эффекта замещения, т. е. зависимости структуры потребления от импортных цен.
Пытаясь связать наши результаты с общепринятыми, главным образом эконометрическими исследованиями переноса цен импорта на внутренний ИПЦ, мы должны подчеркнуть, что представленный выше метод показывает это явление с другой стороны.
Объяснение влияния импортных цен на ИПЦ следует начинать со сравнения фактического ИПЦ с ИПЦ* 2 , который показывает гипотетическую реакцию внутренних цен на внешние ценовые шоки согласно модели при прочих равных условиях. Различие между этими двумя временными рядами, показанными на рис. 2, особенно версией Ласпейреса, можно рассматривать как результат всех других явлений. К сожалению, мы не можем отличить те, которые вызваны изменениями импортных цен, от автономных изменений, вызванных монетарной или фискальной политикой, нестабильным рынком труда (заработная плата), изменениями потребительских предпочтений и т.д. Например, изменения в структуре потребления домохозяйств могут быть реакцией на изменение цен или результатом маркетинговых кампаний. Точно так же на политику, проводимую центральными банками, влияют различные экономические факторы, в том числе динамика импортных цен и обменных курсов.
Рис. 2 Затраты-выпуск импортных цен в ИПЦ (ИПЦ* 2 ) по сравнению с затратами-выпуском ИПЦ (ИПЦ* 6 ) и фактическим ИПЦ ( на основе Пааше [слева] и Ласпейреса [справа] формула ). Источник: собственные расчеты на основе данных Статистического управления Дании
Источник: собственные расчеты на основе данных Статистического управления Дании
Увеличенное изображение
Таким образом, применение представленного метода декомпозиции для исследования переноса цен импорта на ИПЦ может быть основано на выделении трех компонентов инфляции:
- 1.
Теоретическая передача затрат-выпуска импортных цен в ИПЦ, а именно ИПЦ *2 ,
- 2.
прочие эффекты, являющиеся реакцией на изменения импортных цен,
- 3.
другие экзогенные экономические факторы.
Кроме того, следует учитывать поправку, возникающую из-за разницы в определениях дефлятора-затраты (ИПЦ* 6 ) и фактического ИПЦ (таблица 1).
Полная таблица
Как видно из рис. 2, различия между ИПЦ и ИПЦ* 2 всегда положительны, а это означает, что рост затрат на импортную продукцию не единственное обоснование роста ИПЦ. Эти различия могут быть отправной точкой для выявления факторов 2 и 3 из приведенного выше списка. Сосредоточение внимания на различиях между ИПЦ* 2 и ИПЦ* 6 устраняет несоответствие в определениях между ИПЦ ввода-вывода и фактическим ИПЦ.
Выводы
В этой статье эмпирически исследуется потенциал стандартной модели затрат-выпуска для прогнозирования и моделирования инфляции с указанием конкретных источников ошибок. Каждая ошибка имеет экономический смысл и отражает некоторые факторы механизма ценообразования, хотя соответствие не всегда четкое, так как факторы взаимозависимы.
Авторы считают, что это исследование является вкладом в обсуждение инфляции, ее источников и путей передачи — обсуждение, которое должно привести к улучшению существующих методов прогнозирования. Частота используемых нами данных, по-видимому, является существенным ограничением для практического применения метода декомпозиции. Однако мы полагаем, что модель ценообразования можно модифицировать для получения прогнозов на более короткий период, например, включив в нее эффекты сезонности.
Частота используемых нами данных, по-видимому, является существенным ограничением для практического применения метода декомпозиции. Однако мы полагаем, что модель ценообразования можно модифицировать для получения прогнозов на более короткий период, например, включив в нее эффекты сезонности.
Механизм ценообразования представляет собой очень сложное явление, и большинство исследований сосредоточено на конкретных аспектах. Наше исследование предполагает, что ценовая модель IO может использоваться в качестве основы для интеграции исследований по этим аспектам. Хотя модель показывает только чистую стоимостную сторону инфляции, другие факторы могут быть проанализированы путем объяснения компонентов предлагаемой декомпозиции. Исследования, изучающие роль макроэкономических переменных, таких как процентная ставка, обменный курс или денежная масса, которые обычно основаны на эконометрических моделях, таких как VAR, SVAR или VEC, также могут быть включены в эту структуру.
Исследование было ограничено примером Дании из-за наличия статистического материала. Благодаря единой методике создания таблиц ввода-вывода описанную процедуру можно применять универсально. Необходимые временные ряды таблиц «затраты-выпуск», выраженные в ценах предыдущего года, наверняка станут широко доступными, а уровень детализации почти наверняка повысится.
Благодаря единой методике создания таблиц ввода-вывода описанную процедуру можно применять универсально. Необходимые временные ряды таблиц «затраты-выпуск», выраженные в ценах предыдущего года, наверняка станут широко доступными, а уровень детализации почти наверняка повысится.
Таким образом, представляется, что представленный анализ является хорошей отправной точкой для проведения дальнейших мероприятий в этой области. В свете полученных результатов наиболее интересными направлениями представляется рассмотрение большего количества компонентов, например элементов добавленной стоимости, разделяющих матриц параметров, валютного курса и исследования взаимозависимостей между ними. Получение большего количества эмпирического материала в виде временных рядов должно позволить использовать более сложные статистические и эконометрические методы вместо простых коэффициентов корреляции.
Доступность данных и материалов
Наборы данных, использованные и/или проанализированные в ходе текущего исследования, можно получить у соответствующего автора по обоснованному запросу.
Примечания
По практическим соображениям он также включает налоги на промежуточные продукты.
Под изменением налогов мы понимаем величину налогов в году t + 1, деленную на величину налогов в t + 1, выраженную в ценах прошлых лет.
Источником ошибки является внутриотраслевая специфика расходов домашних хозяйств. Например, в случае сельскохозяйственной продукции покупки домохозяйств включают яблоки и бананы, но не включают семена рапса или льна, которые в основном являются промежуточными продуктами. Если цены на яблоки и бананы будут двигаться в другом направлении, чем цены на рапс и лен, то индекс потребительских цен на сельскохозяйственную продукцию будет отличаться от индекса цен производителей. Дефлятор выпуска покажет только среднее изменение.
https://www.dst.dk/en/Statistik/emner/oekonomi/nationalregnskab/input–output [доступ 23 ноября 2021].

Сокращения
- CGE:
Вычислимое общее равновесие
- ИПЦ:
Индекс потребительских цен
- Ввод-вывод:
Вход-выход
- ERPT:
Перенос обменного курса
- СВАР:
Структурная векторная авторегрессия
- ВАР:
Векторная авторегрессия
- ВЭК:
Векторная коррекция ошибок
Ссылки
Абильдгрен К. (2006) Показатели базовой внутренней инфляции на основе затрат-выпуска: эмпирические данные из Дании, 1903–2002 гг.
 Econ Syst Res 19 (4): 409–423. https://doi.org/10.1080/09535310701698472
Econ Syst Res 19 (4): 409–423. https://doi.org/10.1080/09535310701698472Статья Google ученый
Ардалан А., Кессинг С.Г. (2019) Перенос налогов на европейский рынок пива. Империя Экон. https://doi.org/10.1007/s00181-019-01767-5
Артикул Google ученый
Арон Дж., Фаррелл Г., Мюлльбауэр Дж., Синклер П. (2014) Влияние обменного курса на импортные цены и денежно-кредитная политика в Южной Африке. J Dev Stud 50 (1): 144–164. https://doi.org/10.1080/00220388.2013.847179
Статья Google ученый
Auer R, Schoenle R (2016) Структура рынка и влияние обменного курса. J Инт Эконом 98(1):66–77. https://doi.org/10.1016/j.jinteco.2015.10.003
Статья Google ученый
Айдогуш О., Дегер С., Чалышкан Э.Т., Гюнал Г.Г. (2017) Модель переноса обменного курса «затраты-выпуск».
 Econ Syst Res 30 (3): 323–336. https://doi.org/10.1080/09535314.2017.1374243
Econ Syst Res 30 (3): 323–336. https://doi.org/10.1080/09535314.2017.1374243Статья Google ученый
Beckman J, Estrades C, Aguiar A (2019) Экспортные налоги, цены на продукты питания и бедность: глобальная оценка CGE. Продовольственная безопасность 11: 233–247. https://doi.org/10.1007/s12571-018-0876-2
Артикул Google ученый
Бенедек Д., Де Муий Р.А., Кин М., Вингендер П. (2020) Различные виды НДС. Int Tax Public Finan 27: 890–930. https://doi.org/10.1007/s10797-019-09566-5
Статья Google ученый
Боратыньски Ю. (2006) Косвенные налоги и ценообразование. Acta Univ Lodziensis Folia Oecon 198:111–134
Google ученый
Кук С. (2008) Эконометрический анализ переноса процентной ставки. Appl Finan Econ Lett 4(4):249–251. https://doi.
 org/10.1080/17446540701704372
org/10.1080/17446540701704372Статья Google ученый
Дитценбахер Э., Темуршоев Ю. (2012) Анализ влияния затрат-выпуска в текущих или постоянных ценах: имеет ли это значение? J Экономическая структура 1(1):1–18. https://doi.org/10.21642/JGEA.020101AF
Статья Google ученый
Хансен Б.В., Кнудсен Д. (2005) Инфляция, определяемая внутренним рынком. Danmarks Nationalbank Monetary Review, 4th Quarter, стр. 27–39
Lee C, Schulter G, O’Roark B (2000) Минимальная заработная плата и цены на продукты питания: анализ ценовых эффектов переноса. Int Food Agribus Manage Rev 3 (1): 111–128. https://doi.org/10.1016/S1096-7508(00)00032-X
Статья Google ученый
Леонтьев В. (1937) Взаимосвязь цен, выпуска, сбережений и инвестиций. Rev Econ Stat 19(3): 109–132. https://doi.org/10.2307/1927343
Статья Google ученый
Леонтьев В.
 (1946) Заработная плата, прибыль и цены. Q J Econ 61 (1): 26–39. https://doi.org/10.2307/1882402
(1946) Заработная плата, прибыль и цены. Q J Econ 61 (1): 26–39. https://doi.org/10.2307/1882402Статья Google ученый
Leszczyńska-Paczesna A (2020) Отраслевая жесткость цен и постоянство инфляции в Польше: двухсекторный DSGE-подход. Прага Econ Pap 29 (2): 152–186. https://doi.org/10.18267/j.pep.735
Артикул Google ученый
Pennings S (2017) Перенос обменных курсов конкурентов на импорт США и цены производителей. J Int Econ 105: 41–56. https://doi.org/10.1016/j.jinteco.2016.11.002
Статья Google ученый
Шакери М., Грей Р.С. (2013) Отраслевые детерминанты влияния обменного курса на цены канадских производителей. Автобус Int J Econ 20 (1): 15–38. https://doi.org/10.1080/13571516.2012.750044
Артикул Google ученый
Шарифи Н.
 , Санчо Ф. (2011) Новый подход к ценовой модели «затраты-выпуск». Эконом Модель 28 (1–2): 188–195. https://doi.org/10.1016/j.econmod.2010.09.012
, Санчо Ф. (2011) Новый подход к ценовой модели «затраты-выпуск». Эконом Модель 28 (1–2): 188–195. https://doi.org/10.1016/j.econmod.2010.09.012Статья Google ученый
Ву Л., Ли Дж., Чжан З. (2013) Инфляционный эффект шоков цен на нефть на несовершенном рынке: частичный анализ затрат-выпуска передачи. J Модель политики 35 (2): 354–369. https://doi.org/10.1016/j.jpolmod.2012.01.008
Статья Google ученый
Скачать ссылки
Благодарности
Мы хотели бы выразить нашу особую благодарность г-ну Питеру Рормосу Йенсену, с которым мы смогли прояснить сомнения относительно содержания отдельных ячеек, включенных в таблицы.
Финансирование
Неприменимо.
Информация об авторе
Авторы и организации
Факультет экономики и социологии Лодзинского университета, ул. Револуции, 39, 1905р. Street, 90-214, Łodź, Poland
Michał Przybyliński & Artur Gorzałczyński
Авторы
- Michał Przybyliński
Вы также можете искать публикации этого автора
PubMed Google Scholar
- Artur Gorzałczyński
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
Вклады
MP, AG участвовал в разработке и реализации исследования, в анализе результатов и в написании рукописи. Все авторы прочитали и одобрили окончательный вариант рукописи.
Все авторы прочитали и одобрили окончательный вариант рукописи.
Информация для авторов
М.П. является профессором и заведующим кафедрой теории и анализа экономических систем Лодзинского университета, Польша. А.Г. является ассистентом и доктором философии. студент экономического факультета Лодзинского университета.
Автор, ответственный за переписку
Связь с Михал Пжибылинский.
Заявление об этике
Конкурирующие интересы
Авторы заявляют, что у них нет конкурирующих интересов.
Дополнительная информация
Примечание издателя
Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
Права и разрешения
Открытый доступ Эта статья находится под лицензией Creative Commons Attribution 4.0 International License, которая разрешает использование, совместное использование, адаптацию, распространение и воспроизведение на любом носителе или в любом формате, при условии, что вы указываете соответствующие права на оригинальный автор(ы) и источник, предоставьте ссылку на лицензию Creative Commons и укажите, были ли внесены изменения. Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons на статью, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/.
Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons на статью, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/.
Перепечатки и разрешения
Об этой статье
Данные счетов ввода-вывода | Бюро экономического анализа США (BEA)
Файлы данных
Таблицы предложения
— Внутреннее предложение товаров по отраслям
- 1997-2021: 15 Industries iTable, 71 Industries iTable
- 2007, 2012: 405 Industries XLSX
Таблицы использования
— Использование товаров по отраслям
- 1997–2021: 15 Industries iTable, 71 Industries iTable
- 2007, 2012: 405 Industries XLSX
Матрицы импорта/до переопределения
— Использование импортных товаров по отраслям
- 1997–2021: 71 Отрасли XLSX
- 2007, 2012: 405 Industries XLSX
- Таблицы требований
- Производственные столы
- Исторические таблицы использования
- Всего требований
- Внутренние требования
- После переопределения таблиц
Товар по товарам/после переопределения/ценность производителя
—
Общие затраты по товарам, необходимые (прямо и косвенно) для доставки одного доллара товарной продукции конечным пользователям
- 1997–2021: 17 товаров iTable, 73 товаров iTable
- 2007, 2012: 405 товаров XLSX
Отрасль по товарам/после переопределения/ценность производителя
— Общие затраты по отраслям, необходимые (прямо и косвенно) для доставки одного доллара товарной продукции конечным пользователям
Отрасль по отраслям/После переопределения/Ценность производителя
– Суммарные затраты по отраслям, необходимые (прямо и косвенно) для доставки одного доллара продукции отрасли конечным пользователям
- 1997-2021: 15 отраслей iTable, 71 отрасль iTable
- 2007, 2012: 405 Industries XLSX
Дополнительная информация о выводе общих требований.
Таблицы внутренних потребностей были впервые опубликованы BEA 17 февраля 2017 г. Дополнительные сведения об этих статистических данных доступны в Обзоре текущей деятельности: представление таблиц внутренних потребностей за 1997–2015 гг.
Товар по товару/после переопределения/стоимость производителя
— Внутренние ресурсы по товарам, необходимые (прямо и косвенно) для доставки одного доллара товарной продукции конечным пользователям
- 1997–2021: 17 товаров XLSX, 73 товара XLSX
- 2007, 2012: 405 товаров XLSX
Отрасль по товарам/после переопределения/стоимость производителя
— Внутренние ресурсы по отраслям, необходимые (прямо или косвенно) для доставки одного доллара товарной продукции конечным пользователям
- 1997–2021: 15 отраслей XLSX, 71 отрасль XLSX
- 2007, 2012: 405 Industries XLSX
Отрасль по отраслям/После переопределения/Ценность производителя
– Внутренние ресурсы по отраслям, необходимые (прямо и косвенно) для доставки одного доллара отраслевой продукции конечным пользователям
- 1997–2021: 15 отраслей XLSX, 71 отрасль XLSX
- 2007, 2012: 405 Industries XLSX
Дополнительная информация о выводе внутренних требований.
Составление таблиц/после переопределения
— Производство товаров по отраслям после переопределения вторичного производства
- 1997-2021: 15 Industries iTable, 71 Industries iTable
- 2007, 2012: 405 Industries XLSX
Таблицы доли рынка/после переопределения
— Доля товарного производства по отраслям после переопределения
- 1997–2021: 15 отраслей XLSX, 71 отрасль XLSX
- 2007, 2012: 405 Industries XLSX
Использование таблиц/После переопределений/Производственная стоимость
— Использование товаров по отраслям после перераспределения ресурсов, связанных с переопределенным вторичным производством
Матрицы импорта/после переопределения
— Использование импортных товаров по отраслям
- 1997–2021: 71 отрасль XLSX
- 2007, 2012: 405 Industries XLSX
Прямые потребности/После переопределения/Ценность производителя
– Общие затраты по товарам, непосредственно необходимые для производства одного доллара отраслевой продукции
- 1997–2021: 15 Industries iTable, 71 Industries iTable
- 2007, 2012: 405 Industries XLSX
Прямые внутренние потребности/после переопределения/стоимость производителя
— Внутренние ресурсы по товарам, непосредственно необходимые для производства одного доллара отраслевой продукции
- 1997–2021: 15 отраслей XLSX, 71 отрасль XLSX
- 2007, 2012: 405 Industries XLSX
Таблицы использования/После переопределения/Покупательская стоимость
— Использование товаров по отраслям, оцененное в ценах покупателей
- 2007, 2012: 15 Industries iTable, 71 Industries iTable, 405 Industries XLSX
Таблицы после переопределения используются в качестве исходных данных для получения матриц общих потребностей и внутренних потребностей.



 Нет внешнего спроса.
Нет внешнего спроса. deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
 Econ Syst Res 19 (4): 409–423. https://doi.org/10.1080/09535310701698472
Econ Syst Res 19 (4): 409–423. https://doi.org/10.1080/09535310701698472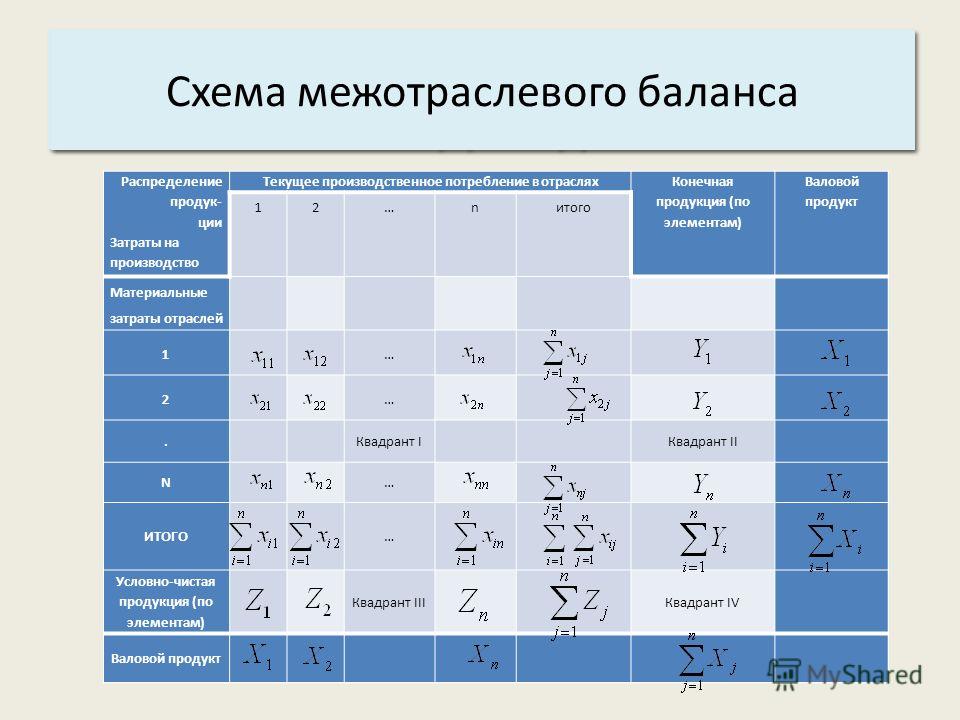 Econ Syst Res 30 (3): 323–336. https://doi.org/10.1080/09535314.2017.1374243
Econ Syst Res 30 (3): 323–336. https://doi.org/10.1080/09535314.2017.1374243 org/10.1080/17446540701704372
org/10.1080/17446540701704372 (1946) Заработная плата, прибыль и цены. Q J Econ 61 (1): 26–39. https://doi.org/10.2307/1882402
(1946) Заработная плата, прибыль и цены. Q J Econ 61 (1): 26–39. https://doi.org/10.2307/1882402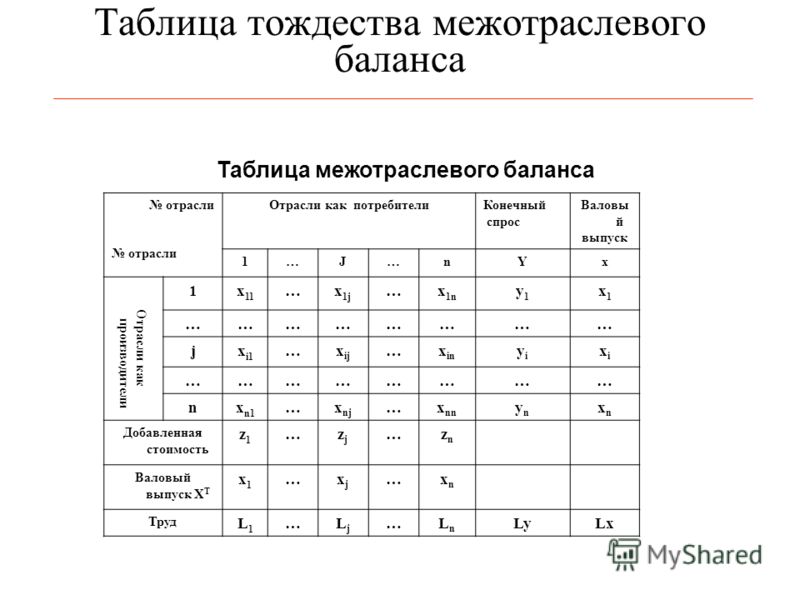 , Санчо Ф. (2011) Новый подход к ценовой модели «затраты-выпуск». Эконом Модель 28 (1–2): 188–195. https://doi.org/10.1016/j.econmod.2010.09.012
, Санчо Ф. (2011) Новый подход к ценовой модели «затраты-выпуск». Эконом Модель 28 (1–2): 188–195. https://doi.org/10.1016/j.econmod.2010.09.012