Раскрытие скобок с разными знаками. Минус меняет знаки в скобках
Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Этот прием носит название раскрытия скобок.
Раскрыть скобки означает избавить выражение от этих скобок.
Отдельного внимания заслуживает еще один момент, который касается особенностей записи решений при раскрытии скобок. Мы можем записать начальное выражение со скобками и полученный после раскрытия скобок результат как равенство. Например, после раскрытия скобок вместо выражения
3−(5−7) мы получаем выражение 3−5+7. Оба этих выражения мы можем записать в виде равенства 3−(5−7)=3−5+7.
И еще один важный момент. В математике для сокращения записей принято не писать знак плюс, если он стоит в выражении или в скобках первым. Например, если мы складываем два положительных числа, к примеру, семь и три, то пишем не +7+3, а просто 7+3, несмотря на то, что семерка тоже положительное число.
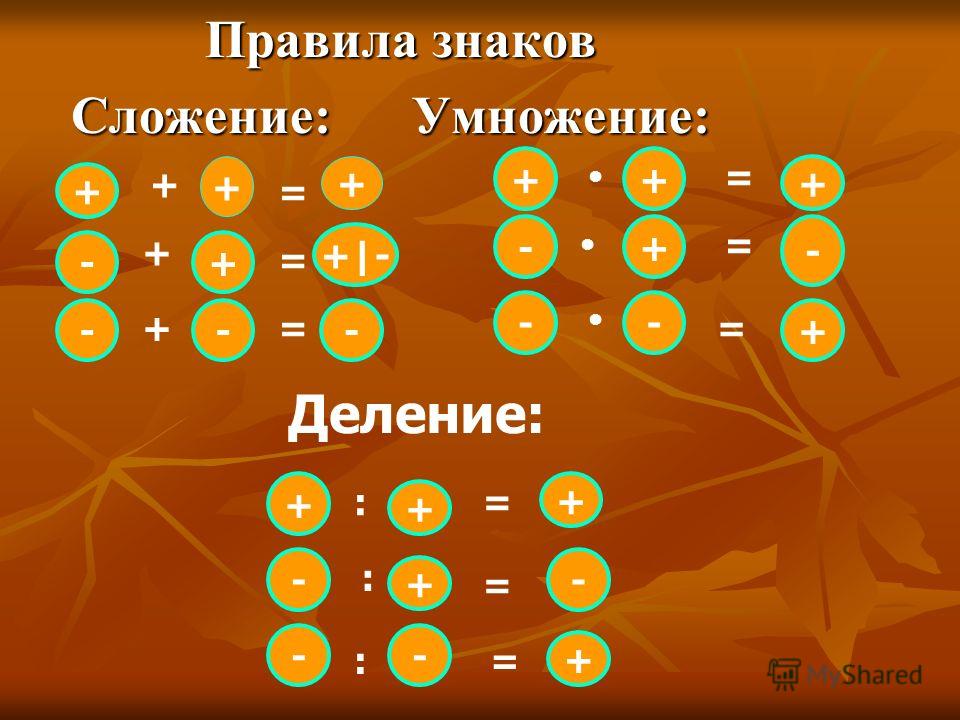
Правило раскрытия скобок при сложении
При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками.
Пример. Раскрыть скобки в выражении 2 + (7 + 3) Перед скобками плюс, значит знаки перед числами в скобках не меняем.
2 + (7 + 3) = 2 + 7 + 3
Правило раскрытия скобок при вычитании
Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но слагаемые, которые были в скобках, меняют свой знак на противоположный. Отсутствие знака перед первым слагаемым в скобках подразумевает знак +.
Пример. Раскрыть скобки в выражении 2 − (7 + 3)
Перед скобками стоит минус, значит нужно поменять знаки перед числами из скобок. В скобках перед цифрой 7 знака нет, это значит, что семерка положительная, считается, что перед ней знак +.
2 − (7 + 3) = 2 − (+ 7 + 3)
При раскрытии скобок убираем из примера минус, который был перед скобками, и сами скобки 2 − (+ 7 + 3) , а знаки, которые были в скобках, меняем на противоположные.
2 − (+ 7 + 3) = 2 − 7 − 3
Раскрытие скобок при умножении
Если перед скобками стоит знак умножения, то каждое число, стоящее внутри скобок, умножается на множитель, стоящий перед скобками. При этом умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус.
Таким образом, сскобки в произведениях раскрываются в соответствии с распределительным свойством умножения.
Пример. 2 · (9 — 7) = 2 · 9 — 2 · 7
При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй скобки.
(2 + 3) · (4 + 5) = 2 · 4 + 2 · 5 + 3 · 4 + 3 · 5
На самом деле, нет необходимости запоминать все правила, достаточно помнить только одно, вот это: c(a−b)=ca−cb. Почему? Потому что если в него вместо c подставить единицу, получится правило (a−b)=a−b. А если подставить минус единицу, получим правило −(a−b)=−a+b. Ну, а если вместо c подставить другую скобку – можно получить последнее правило.
Почему? Потому что если в него вместо c подставить единицу, получится правило (a−b)=a−b. А если подставить минус единицу, получим правило −(a−b)=−a+b. Ну, а если вместо c подставить другую скобку – можно получить последнее правило.
Раскрываем скобки при делении
Если после скобок стоит знак деления, то каждое число, стоящее внутри скобок, делится на делитель, стоящий после скобок, и наоборот.
Пример. (9 + 6) : 3=9: 3 + 6: 3
Как раскрыть вложенные скобки
Если в выражении присутствуют вложенные скобки, то их раскрывают по порядку, начиная с внешних или внутренних.
При этом важно при раскрытии одной из скобок не трогать остальные скобки, просто переписывая их как есть.
Пример. 12 — (a + (6 — b) — 3) = 12 — a — (6 — b) + 3 = 12 — a — 6 + b + 3 = 9 — a + b
Раскрытие скобок является одним из видов преобразования выражения. В этом разделе мы опишем правила раскрытия скобок, а также рассмотрим наиболее часто встречающиеся примеры задач.
Yandex.RTB R-A-339285-1
Что называется раскрытием скобок?
Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Например, заменить выражение 2 · (3 + 4) на выражение вида 2 · 3 + 2 · 4 без скобок. Этот прием носит название раскрытия скобок.
Определение 1
Под раскрытием скобок подразумевают приемы избавления от скобок и рассматривают его обычно в отношении выражений, которые могут содержать:
- знаки « + » или « — » перед скобками, в которые заключены суммы или разности;
- произведение числа, буквы или нескольких букв и суммы или разности, которая помещена в скобки.
Так мы привыкли рассматривать процесс раскрытия скобок в курсе школьной программы. Однако никто не мешает нам посмотреть на это действие шире. Мы можем назвать раскрытием скобок переход от выражения, которое содержит отрицательные числа в скобках, к выражению, не имеющему скобок. К примеру, мы можем перейти от 5 + (− 3) − (− 7) к 5 − 3 + 7 . Фактически, это тоже раскрытие скобок.
К примеру, мы можем перейти от 5 + (− 3) − (− 7) к 5 − 3 + 7 . Фактически, это тоже раскрытие скобок.
Точно также мы можем заменить произведение выражений в скобках вида (a + b) · (c + d) на сумму a · c + a · d + b · c + b · d . Такой прием также не противоречит смыслу раскрытия скобок.
Вот еще один пример. Мы можем допустить, что в выражениях вместо чисел и переменных могут быть использованы любые выражения. Например, выражению x 2 · 1 a — x + sin (b) будет соответствовать выражение без скобок вида x 2 · 1 a — x 2 · x + x 2 · sin (b) .
Отдельного внимания заслуживать еще один момент, который касается особенностей записи решений при раскрытии скобок. Мы можем записать начальное выражение со скобками и полученный после раскрытия скобок результат как равенство. Например, после раскрытия скобок вместо выражения 3 − (5 − 7) мы получаем выражение 3 − 5 + 7 . Оба этих выражения мы можем записать в виде равенства 3 − (5 − 7) = 3 − 5 + 7 .
Проведение действий с громоздкими выражениями может потребовать записи промежуточных результатов. Тогда решение будет иметь вид цепочки равенств. Например, 5 − (3 − (2 − 1)) = 5 − (3 − 2 + 1) = 5 − 3 + 2 − 1 или 5 − (3 − (2 − 1)) = 5 − 3 + (2 − 1) = 5 − 3 + 2 − 1 .
Тогда решение будет иметь вид цепочки равенств. Например, 5 − (3 − (2 − 1)) = 5 − (3 − 2 + 1) = 5 − 3 + 2 − 1 или 5 − (3 − (2 − 1)) = 5 − 3 + (2 − 1) = 5 − 3 + 2 − 1 .
Правила раскрытия скобок, примеры
Приступим к рассмотрению правил раскрытия скобок.
У одиночных чисел в скобках
Отрицательные числа в скобках часто встречаются в выражениях. Например, (− 4) и 3 + (− 4) . Положительные числа в скобках тоже имеют место быть.
Сформулируем правило раскрытия скобок, в которых заключены одиночные положительные числа. Предположим, что а – это любое положительное число. Тогда (а) мы можем заменить на а, + (а) на + а, — (а) на – а. Если вместо а взять конкретное число, то согласно правилу: число (5) запишется как 5 , выражение 3 + (5) без скобок примет вид 3 + 5 , так как + (5) заменяется на + 5 , а выражение 3 + (− 5) эквивалентно выражению 3 − 5 , так как + (− 5) заменяется на − 5 .
Положительные числа обычно записываются без использования скобок, так как скобки в этом случае излишни.
Теперь рассмотрим правило раскрытия скобок, внутри которых содержится одиночное отрицательное число. + (− a) мы заменяем на − a , − (− a) заменяется на + a . Если выражение начинается с отрицательного числа (− a) , которое записано в скобках, то скобки опускаются и вместо (− a) остается − a .
Приведем примеры: (− 5) можно записать как − 5 , (− 3) + 0 , 5 принимает вид − 3 + 0 , 5 , 4 + (− 3) превращается в 4 − 3 , а − (− 4) − (− 3) после раскрытия скобок принимает вид 4 + 3 , так как − (− 4) и − (− 3) заменяется на + 4 и + 3 .
Следует понимать, что записать выражение 3 · (− 5) как 3 · − 5 нельзя. Об этом речь пойдет в следующих пунктах.
Давайте посмотрим, на чем основываются правила раскрытия скобок.
Согласно правилу разность a − b равна a + (− b) . На основе свойств действий с числами мы можем составить цепочку равенств (a + (− b)) + b = a + ((− b) + b) = a + 0 = a , которая будет справедлива.
Основываясь на свойствах противоположных чисел и правил вычитания отрицательных чисел мы можем утверждать, что − (− a) = a , a − (− b) = a + b .
Встречаются выражения, которые составляются из числа, знаков минуса и нескольких пар скобок. Использование приведенных выше правил позволяет последовательно избавляться от скобок, продвигаясь от внутренних скобок к наружным или в обратном направлении. Примером такого выражения может быть − (− ((− (5)))) . Раскроем скобки, продвигаясь изнутри наружу: − (− ((− (5)))) = − (− ((− 5))) = − (− (− 5)) = − (5) = − 5 . Также этот пример можно разобрать и в обратном направлении: − (− ((− (5)))) = ((− (5))) = (− (5)) = − (5) = − 5 .
Под a и b можно понимать не только числа, но также произвольные числовые или буквенные выражения со знаком « + » впереди, которые не являются суммами или разностями. Во всех этих случаях можно применять правила точно также, как мы делали это в отношении одиночных чисел в скобках.
К примеру, после раскрытия скобок выражение − (− 2 · x) − (x 2) + (− 1 x) − (2 · x · y 2: z) примет вид 2 · x − x 2 − 1 x − 2 · x · y 2: z . Как мы это сделали? Мы знаем, что − (− 2 · x) есть + 2 · x , а так как это выражение стоит вначале, то + 2 · x можно записать как 2 · x , − (x 2) = − x 2 , + (− 1 x) = − 1 x и − (2 · x · y 2: z) = − 2 · x · y 2: z .
В произведениях двух чисел
Начнем с правила раскрытия скобок в произведении двух чисел.
Предположим, что a и b – это два положительных числа. В этом случае произведение двух отрицательных чисел − a и − b вида (− a) · (− b) мы можем заменить на (a · b) , а произведения двух чисел с противоположными знаками вида (− a) · b и a · (− b) заменить на
Верность первой части записанного правила подтверждается правилом умножения отрицательных чисел. Для подтверждения второй части правила мы можем использовать правила умножения чисел с разными знаками.
Для подтверждения второй части правила мы можем использовать правила умножения чисел с разными знаками.
Рассмотрим несколько примеров.
Пример 1
Рассмотрим алгоритм раскрытия скобок в произведении двух отрицательных чисел — 4 3 5 и — 2 , вида (- 2) · — 4 3 5 . Для этого заменим исходное выражение на 2 · 4 3 5 . Раскроем скобки и получим 2 · 4 3 5 .
А если мы возьмем частное отрицательных чисел (− 4) : (− 2) , то запись после раскрытия скобок будет иметь вид 4: 2
На месте отрицательных чисел − a и − b могут быть любые выражения со знаком минус впереди, которые не являются суммами или разностями. К примеру, это могут быть произведения, частные, дроби, степени, корни, логарифмы, тригонометрические функции и т.п.
Раскроем скобки в выражении — 3 · x x 2 + 1 · x · (- ln 5) . Согласно правилу, мы можем произвести следующие преобразования: — 3 · x x 2 + 1 · x · (- ln 5) = — 3 · x x 2 + 1 · x · ln 5 = 3 · x x 2 + 1 · x · ln 5 .
Выражение (− 3) · 2 можно преобразовать в выражение (− 3 · 2) . После этого можно раскрыть скобки: − 3 · 2 .
После этого можно раскрыть скобки: − 3 · 2 .
2 3 · — 4 5 = — 2 3 · 4 5 = — 2 3 · 4 5
Деление чисел с разными знаками также может потребовать предварительного раскрытия скобок: (− 5) : 2 = (− 5: 2) = − 5: 2 и 2 3 4: (- 3 , 5) = — 2 3 4: 3 , 5 = — 2 3 4: 3 , 5 .
Правило может быть использовано для выполнения умножения и деления выражений с разными знаками. Приведем два примера.
1 x + 1: x — 3 = — 1 x + 1: x — 3 = — 1 x + 1: x — 3
sin (x) · (- x 2) = (- sin (x) · x 2) = — sin (x) · x 2
В произведениях трех и большего количества чисел
Перейдем к произведенимя и частным, которые содержат большее количество чисел. Для раскрытия скобок здесь будет действовать следующее правило. При четном количестве отрицательных чисел можно опустить скобки, заменив числа противоположными. После этого необходимо заключить полученное выражение в новые скобки. При нечетном количестве отрицательных чисел, опустив скобки, заменить числа на противоположные. После этого полученное выражение необходимо взять в новые скобки и поставить перед ним знак минус.
После этого полученное выражение необходимо взять в новые скобки и поставить перед ним знак минус.
Пример 2
Для примера, возьмем выражение 5 · (− 3) · (− 2) , которое представляет собой произведение трех чисел. Отрицательных чисел два, следовательно, мы можем записать выражение как (5 · 3 · 2) и затем окончательно раскрыть скобки, получив выражение 5 · 3 · 2 .
В произведении (− 2 , 5) · (− 3) : (− 2) · 4: (− 1 , 25) : (− 1) пять чисел являются отрицательными. поэтому (− 2 , 5) · (− 3) : (− 2) · 4: (− 1 , 25) : (− 1) = (− 2 , 5 · 3: 2 · 4: 1 , 25: 1) . Окончательно раскрыв скобки, получаем −2,5·3:2·4:1,25:1 .
Обосновать приведенное выше правило можно следующим образом. Во-первых, такие выражения мы можем переписать как произведение, заменив умножением на обратное число деление. Представляем каждое отрицательное число как произведение множительного числа и — 1 или — 1 заменяем на (− 1) · a .
Используя переместительное свойство умножения меняем местами множители и переносим все множители, равные − 1 , в начало выражения. Произведение четного числа минус единиц равно 1 , а нечетного – равно − 1 , что позволяет нам использовать знак минус.
Произведение четного числа минус единиц равно 1 , а нечетного – равно − 1 , что позволяет нам использовать знак минус.
Если бы мы не использовали правило, то цепочка действий по раскрытию скобок в выражении — 2 3: (- 2) · 4: — 6 7 выглядела бы следующим образом:
2 3: (- 2) · 4: — 6 7 = — 2 3 · — 1 2 · 4 · — 7 6 = = (- 1) · 2 3 · (- 1) · 1 2 · 4 · (- 1) · 7 6 = = (- 1) · (- 1) · (- 1) · 2 3 · 1 2 · 4 · 7 6 = (- 1) · 2 3 · 1 2 · 4 · 7 6 = = — 2 3 · 1 2 · 4 · 7 6
Приведенное выше правило может быть использовано при раскрытии скобок в выражениях, которые представляют собой произведения и частные со знаком минус, не являющихся суммами или разностями. Возьмем для примера выражение
x 2 · (- x) : (- 1 x) · x — 3: 2 .
Его можно привести к выражению без скобок x 2 · x: 1 x · x — 3: 2 .
Раскрытие скобок, перед которыми стоит знак +
Рассмотрим правило, которое можно применить для раскрытия скобок, перед которыми стоит знак плюс, а «содержимое» этих скобок не умножается и не делится на какое-либо число или выражение.
Согласно правилу скобки вместе со стоящим перед ними знаком опускаются, при этом знаки всех слагаемых в скобках сохраняются. Если перед первым слагаемым в скобках не стоит никакого знака, то нужно поставить знак плюс.
Пример 3
Для примера приведем выражение (12 − 3 , 5) − 7 . Опустив скобки, мы сохраняем знаки слагаемых в скобках и ставим перед первым слагаемым знак плюс. Запись будет иметь вид (12 − 3 , 5) − 7 = + 12 − 3 , 5 − 7 . В приведенном примере знак перед первым слагаемым ставить не обязательно, так как + 12 − 3 , 5 − 7 = 12 − 3 , 5 − 7 .
Пример 4
Рассмотрим еще один пример. Возьмем выражение x + 2 a — 3 x 2 + 1 — x 2 — 4 + 1 x и проведем с ним действия x + 2 a — 3 x 2 + 1 — x 2 — 4 + 1 x = = x + 2 a — 3 x 2 + 1 — x 2 — 4 + 1 x
Вот еще один пример раскрытия скобок:
Пример 5
2 + x 2 + 1 x — x · y · z + 2 · x — 1 + (- 1 + x — x 2) = = 2 + x 2 + 1 x — x · y · z + 2 · x — 1 — 1 + x + x 2
Как раскрываются скобки, перед которыми стоит знак минус
Рассмотрим случаи, когда перед скобками стоит знак минус, и которые не не умножаются (или делятся) на какое-либо число или выражение. Согласно правилу раскрытия скобок, перед которыми стоит знак « — », скобки со знаком « — » опускаются, при этом знаки всех слагаемых внутри скобок меняются на противоположные.
Согласно правилу раскрытия скобок, перед которыми стоит знак « — », скобки со знаком « — » опускаются, при этом знаки всех слагаемых внутри скобок меняются на противоположные.
Пример 6
К примеру:
1 2 = 1 2 , — 1 x + 1 = — 1 x + 1 , — (- x 2) = x 2
Выражения с переменными могут быть преобразованы с использованием того же правила:
X + x 3 — 3 — — 2 · x 2 + 3 · x 3 · x + 1 x — 1 — x + 2 ,
получаем x — x 3 — 3 + 2 · x 2 — 3 · x 3 · x + 1 x — 1 — x + 2 .
Раскрытие скобок при умножении числа на скобку, выражения на скобку
Здесь мы рассмотрим случаи, когда нужно раскрыть скобки, которые умножаются или делятся на какое-либо число или выражение. Тут применимы формулы вида (a 1 ± a 2 ± … ± a n) · b = (a 1 · b ± a 2 · b ± … ± a n · b) или b · (a 1 ± a 2 ± … ± a n) = (b · a 1 ± b · a 2 ± … ± b · a n) , где a 1 , a 2 , … , a n и b – некоторые числа или выражения.
Пример 7
Например, проведем раскрытие скобок в выражении (3 − 7) · 2 . Согласно правилу, мы можем провести следующие преобразования: (3 − 7) · 2 = (3 · 2 − 7 · 2) . Получаем 3 · 2 − 7 · 2 .
Согласно правилу, мы можем провести следующие преобразования: (3 − 7) · 2 = (3 · 2 − 7 · 2) . Получаем 3 · 2 − 7 · 2 .
Раскрыв скобки в выражении 3 · x 2 · 1 — x + 1 x + 2 , получаем 3 x 2 · 1 — 3 · x 2 · x + 3 · x 2 · 1 x + 2 .
Умножение скобки на скобку
Рассмотрим произведение двух скобок вида (a 1 + a 2) · (b 1 + b 2) . Это поможет нам получить правило для раскрытия скобок при проведении умножения скобки на скобку.
Для того, чтобы решить приведенный пример, обозначим выражение (b 1 + b 2) как b . Это позволит нам использовать правило умножения скобки на выражение. Получим (a 1 + a 2) · (b 1 + b 2) = (a 1 + a 2) · b = (a 1 · b + a 2 · b) = a 1 · b + a 2 · b . Выполнив обратную замену b на (b 1 + b 2) , снова применим правило умножения выражения на скобку: a 1 · b + a 2 · b = = a 1 · (b 1 + b 2) + a 2 · (b 1 + b 2) = = (a 1 · b 1 + a 1 · b 2) + (a 2 · b 1 + a 2 · b 2) = = a 1 · b 1 + a 1 · b 2 + a 2 · b 1 + a 2 · b 2
Благодаря ряду несложных приемов мы можем прийти к сумме произведений каждого из слагаемых из первой скобки на каждое из слагаемых из второй скобки. Правило можно распространить на любое количество слагаемых внутри скобок.
Правило можно распространить на любое количество слагаемых внутри скобок.
Сформулируем правила умножения скобки на скобку: чтобы перемножить между собой две суммы, необходимо каждое из слагаемых первой суммы перемножить на каждое из слагаемых второй суммы и сложить полученные результаты.
Формула будет иметь вид:
(a 1 + a 2 + . . . + a m) · (b 1 + b 2 + . . . + b n) = = a 1 b 1 + a 1 b 2 + . . . + a 1 b n + + a 2 b 1 + a 2 b 2 + . . . + a 2 b n + + . . . + + a m b 1 + a m b 1 + . . . a m b n
Проведем раскрытие скобок в выражении (1 + x) · (x 2 + x + 6) Оно представляет собой произведение двух сумм. Запишем решение: (1 + x) · (x 2 + x + 6) = = (1 · x 2 + 1 · x + 1 · 6 + x · x 2 + x · x + x · 6) = = 1 · x 2 + 1 · x + 1 · 6 + x · x 2 + x · x + x · 6
Отдельно стоит остановиться на тех случаях, когда в скобках присутствует знак минус наряду со знаками плюс. Для примера возьмем выражение (1 − x) · (3 · x · y − 2 · x · y 3) .
Сначала представим выражения в скобках в виде сумм: (1 + (− x)) · (3 · x · y + (− 2 · x · y 3)) . Теперь мы можем применить правило: (1 + (− x)) · (3 · x · y + (− 2 · x · y 3)) = = (1 · 3 · x · y + 1 · (− 2 · x · y 3) + (− x) · 3 · x · y + (− x) · (− 2 · x · y 3))
Теперь мы можем применить правило: (1 + (− x)) · (3 · x · y + (− 2 · x · y 3)) = = (1 · 3 · x · y + 1 · (− 2 · x · y 3) + (− x) · 3 · x · y + (− x) · (− 2 · x · y 3))
Раскроем скобки: 1 · 3 · x · y − 1 · 2 · x · y 3 − x · 3 · x · y + x · 2 · x · y 3 .
Раскрытие скобок в произведениях нескольких скобок и выражений
При наличии в выражении трех и более выражений в скобках, раскрывать скобки необходимо последовательно. Начать преобразование необходимо с того, что два первых множителя берут в скобки. Внутри этих скобок мы можем проводить преобразования согласно правилам, рассмотренным выше. Например, скобки в выражении (2 + 4) · 3 · (5 + 7 · 8) .
В выражении содержится сразу три множителя (2 + 4) , 3 и (5 + 7 · 8) . Будем раскрывать скобки последовательно. Заключим первые два множителя еще в одни скобки, которые для наглядности сделаем красными: (2 + 4) · 3 · (5 + 7 · 8) = ((2 + 4) · 3) · (5 + 7 · 8) .
В соответствии с правилом умножения скобки на число мы можем провести следующие действия: ((2 + 4) · 3) · (5 + 7 · 8) = (2 · 3 + 4 · 3) · (5 + 7 · 8) .
Умножаем скобку на скобку: (2 · 3 + 4 · 3) · (5 + 7 · 8) = 2 · 3 · 5 + 2 · 3 · 7 · 8 + 4 · 3 · 5 + 4 · 3 · 7 · 8 .
Скобка в натуральной степени
Степени, основаниями которых являются некоторые выражения, записанные в скобках, с натуральными показателями можно рассматривать как произведение нескольких скобок. При этом по правилам из двух предыдущих пунктов их можно записать без этих скобок.
Рассмотрим процесс преобразования выражения (a + b + c) 2 . Его можно записать в виде произведения двух скобок (a + b + c) · (a + b + c) . Произведем умножение скобки на скобку и получим a · a + a · b + a · c + b · a + b · b + b · c + c · a + c · b + c · c .
Разберем еще один пример:
Пример 8
1 x + 2 3 = 1 x + 2 · 1 x + 2 · 1 x + 2 = = 1 x · 1 x + 1 x · 2 + 2 · 1 x + 2 · 2 · 1 x + 2 = = 1 x · 1 x · 1 x + 1 x · 2 · 1 x + 2 · 1 x · 1 x + 2 · 2 · 1 x + 1 x · 1 x · 2 + + 1 x 2 · 2 + 2 · 1 x · 2 + 2 · 2 · 2
Деление скобки на число и скобки на скобку
Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые. Например, (x 2 — x) : 4 = x 2: 4 — x: 4 .
Например, (x 2 — x) : 4 = x 2: 4 — x: 4 .
Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.
Например, нам необходимо раскрыть скобки в выражении (x + 2) : 2 3 . Для этого сначала заменим деление умножением на обратное число (x + 2) : 2 3 = (x + 2) · 2 3 . Умножим скобку на число (x + 2) · 2 3 = x · 2 3 + 2 · 2 3 .
Вот еще один пример деления на скобку:
Пример 9
1 x + x + 1: (x + 2) .
Заменим деление умножением: 1 x + x + 1 · 1 x + 2 .
Выполним умножение: 1 x + x + 1 · 1 x + 2 = 1 x · 1 x + 2 + x · 1 x + 2 + 1 · 1 x + 2 .
Порядок раскрытия скобок
Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида, т.е. в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.
Порядок выполнения действий:
- первым делом необходимо выполнить возведение скобок в натуральную степень;
- на втором этапе производится раскрытие скобок в произведениях и частных;
- заключительным шагом будет раскрытие скобок в суммах и разностях.

Рассмотрим порядок выполнения действий на примере выражения (− 5) + 3 · (− 2) : (− 4) − 6 · (− 7) . Намнем преобразование с выражений 3 · (− 2) : (− 4) и 6 · (− 7) , которые должны принять вид (3 · 2: 4) и (− 6 · 7) . При подстановке полученных результатов в исходное выражение получаем: (− 5) + 3 · (− 2) : (− 4) − 6 · (− 7) = (− 5) + (3 · 2: 4) − (− 6 · 7) . Раскрываем скобки: − 5 + 3 · 2: 4 + 6 · 7 .
Имея дело с выражениями, которые содержат скобки в скобках, удобно проводить преобразования, продвигаясь изнутри наружу.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
На этом уроке вы узнаете, как из выражения, содержащего скобки, путем преобразования получить выражение, в котором скобок нет. Вы научитесь раскрывать скобки, перед которыми стоит знак плюс и знак минус. Мы вспомним, как раскрывать скобки, используя распределительный закон умножения. Рассмотренные примеры позволят связать новый и ранее изученный материал в единое целое.
Тема: Решение уравнений
Урок: Раскрытие скобок
Как раскрыть скобки, перед которыми стоит знак «+». Использование сочетательного закона сложения.
Если к числу нужно прибавить сумму двух чисел, то можно к этому числу прибавить сначала первое слагаемое, а затем второе.
Слева от знака равно выражение со скобками, а справа — выражение без скобок. Значит, при переходе от левой части равенства к правой произошло раскрытие скобок.
Рассмотрим примеры.
Пример 1.
Раскрыв скобки, мы изменили порядок действий. Считать стало удобнее.
Пример 2.
Пример 3.
Заметим, что во всех трех примерах мы просто убирали скобки. Сформулируем правило:
Замечание.
Если первое слагаемое в скобках стоит без знака, то его надо записать со знаком «плюс».
Можно выполнить пример по действиям. Сначала к 889 прибавить 445. Это действие в уме выполнить можно, но это не очень просто. Раскроем скобки и увидим, что изменённый порядок действий значительно упростит вычисления.
Раскроем скобки и увидим, что изменённый порядок действий значительно упростит вычисления.
Если следовать указанному порядку действий, то нужно сначала из 512 вычесть 345, а затем к результату прибавить 1345. Раскрыв скобки, мы изменим порядок действий и значительно упростим вычисления.
Иллюстрирующий пример и правило.
Рассмотрим пример: . Найти значение выражения можно, сложив 2 и 5, а затем взять полученное число с противоположным знаком. Получим -7.
С другой стороны, тот же самый результат можно получить, сложив числа, противоположные исходным.
Сформулируем правило:
Пример 1.
Пример 2.
Правило не изменяется, если в скобках не два, а три или более слагаемых.
Пример 3.
Замечание. Знаки меняются на противоположные только перед слагаемыми.
Для того чтобы раскрыть скобки, в данном случае нужно вспомнить распределительное свойство.
Сначала умножим первую скобку на 2, а вторую — на 3.
Перед первой скобкой стоит знак «+», значит, знаки нужно оставить без изменения. Перед второй стоит знак «-», следовательно, все знаки нужно поменять на противоположные
Список литературы
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012.
- Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.
- Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс — ЗШ МИФИ, 2011.
- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
- Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. — Просвещение, 1989.
- Онлайн тесты по математике ().
- Можно скачать указанные в п.
 1.2. книги ().
1.2. книги ().
Домашнее задание
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012. (ссылка см. 1.2)
- Домашнее задание: № 1254, № 1255, № 1256 (б,г)
- Другие задания: № 1258(в), № 1248
сформировать способность к раскрытию скобок с
учетом знака, стоящего перед скобками;
Ход урока
I. Организационный момент.
Проверь-ка дружок
Ты готов на урок?
Всё ли на месте? Всё в порядке?
Ручка, книжка и тетрадка.
Все ли правильно сидят?
Все ль внимательно глядят?
Начать урок я хочу с вопроса к вам:
Как вы думаете, что самое ценное на Земле? (Ответы детей.)
Этот вопрос волновал человечество не одну тысячу лет. Вот какой ответ дал
известный ученый Аль-Бируни: “Знание – самое превосходное из владений. Все
стремятся к нему, само же оно не приходит”.
Вот какой ответ дал
известный ученый Аль-Бируни: “Знание – самое превосходное из владений. Все
стремятся к нему, само же оно не приходит”.
Пусть эти слова станут девизом нашего урока.
II. Актуализация прежних знаний, умений, навыков:
Устный счет:
1.1. Какое сегодня число?
2. Расскажите, что вы знаете о числе 20?
3. А где расположено это число на координатной прямой?
4. Назовите число ему обратное.
5. Назовите число ему противоположное.
6. Как называется число – 20?
7. Какие числа называются противоположными?
8. Какие числа называются отрицательными?
9. Чем равен модуль числа 20? – 20?
10. Чему равна сумма противоположных чисел?
2. Объясните следующие записи:
а) Гениальный математик древности Архимед родился в 0 287 г.
б) Гениальный русский математик Н.И.Лобаческий родился в 1792 г.
в) Первые олимпийские игры состоялись в Греции в – 776 г.
г) Первые Международные олимпийские игры состоялись в 1896 г.
д) XXII Олимпийские зимние игры состоялись в 2014 году.
3. Узнайте, какие числа крутятся на “математической карусели” (все действия выполняются устно).
II. Формирование новых знаний, умений, навыков.
Вы научились выполнять разные действия с целыми числами. Чем же будем заниматься дальше? Как будем решать примеры и уравнения?
Давайте найдем значение данных выражений
7 + (3 + 4) = -7 + 7 = 0
-7 + 3 + 4 = 0
Какой порядок действий в 1 примере? Сколько получилось в скобках? Порядок действий во втором примере? Результат первого действия? Что можно сказать об этих выражениях?
Конечно результаты первого и второго выражений одинаковы, значит между ними можно поставить знак равенства: -7 + (3 + 4) = -7 + 3 + 4
Что же мы сделали со скобками? (Опустили.)
Как вы думаете чем мы будем заниматься сегодня на уроке? (Дети формулируют тему урока.) В нашем примере, какой знак стоит перед скобками. (Плюс.)
И так мы подошли к следующему правилу:
Если перед скобками стоит знак +, то можно опустить скобки и этот знак +,
сохраняя знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках
записано без знака, то его надо записать со знаком +.
Если первое слагаемое в скобках
записано без знака, то его надо записать со знаком +.
А как быть, если перед скобками стоит знак минус?
В этом случае нужно рассуждать так же как при вычитании: необходимо прибавить число противоположное вычитаемому:
7 – (3 + 4) = -7 + (-7) = -7 + (-3) + (-4) = -7 – 3 – 4 = -14
– Итак, мы раскрыли скобки, когда перед ними стоял знак минус.
Правило раскрытия скобок, когда перед скобками стоит знак “-“.
Чтобы раскрыть скобки, перед которыми стоит знак -, надо заменить этот знак на +, поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.
Давайте послушаем правила раскрытия скобок в стихах:
Перед скобкой плюс стоит.
Он о том и говорит
Что ты скобки опускай
Да все знаки выпускай!
Перед скобкой минус строгий
Загородит нам дорогу
Чтобы скобки убирать
Надо знаки поменять!
Да ребята знак минус очень коварный, это “ сторож” у ворот(скобки), он
выпускает числа и переменные только тогда, когда они поменяют “ паспорта”, то
есть свои знаки.
Зачем вообще нужно раскрывать скобки? (Когда есть скобки, есть момент какой-то элемент незавершенности, какой-то тайны. Это – как закрытая дверь, за которой находится что-то интересное.) Вот сегодня мы изведали эту тайну.
Небольшой экскурс в историю:
Фигурные скобки появляются в сочинениях Виета (1593). Широкое применение скобки получили лишь в первой половине XVIII века, благодаря Лейбницу и ещё больше Эйлеру.
Физкультминутка.
III. Закрепление новых знаний, умений, навыков.
Работа по учебнику:
№ 1234 (раскройте скобки) – устно.
№ 1236(раскройте скобки) – устно.
№ 1235 (найдите значение выражения) – письменно.
№ 1238 (упростите выражения) – работа в парах.
IV. Подведение итогов урока.
1. Объявляются оценки.
2. Дом. задание. п.39 №1254 (а, б, в),1255 (а, б, в),1259.
3. Чему мы сегодня научились?
Что нового узнали?
И завершить урок я хочу пожеланиями каждому из вас:
“К математике способность проявляй,
Не ленись, а ежедневно развивай.
Умножай, дели, трудись, соображай,
С математикой дружить не забывай”.
На этом уроке вы узнаете, как из выражения, содержащего скобки, путем преобразования получить выражение, в котором скобок нет. Вы научитесь раскрывать скобки, перед которыми стоит знак плюс и знак минус. Мы вспомним, как раскрывать скобки, используя распределительный закон умножения. Рассмотренные примеры позволят связать новый и ранее изученный материал в единое целое.
Тема: Решение уравнений
Урок: Раскрытие скобок
Как раскрыть скобки, перед которыми стоит знак «+». Использование сочетательного закона сложения.
Если к числу нужно прибавить сумму двух чисел, то можно к этому числу прибавить сначала первое слагаемое, а затем второе.
Слева от знака равно выражение со скобками, а справа — выражение без скобок. Значит, при переходе от левой части равенства к правой произошло раскрытие скобок.
Рассмотрим примеры.
Пример 1.
Раскрыв скобки, мы изменили порядок действий. Считать стало удобнее.
Считать стало удобнее.
Пример 2.
Пример 3.
Заметим, что во всех трех примерах мы просто убирали скобки. Сформулируем правило:
Замечание.
Если первое слагаемое в скобках стоит без знака, то его надо записать со знаком «плюс».
Можно выполнить пример по действиям. Сначала к 889 прибавить 445. Это действие в уме выполнить можно, но это не очень просто. Раскроем скобки и увидим, что изменённый порядок действий значительно упростит вычисления.
Если следовать указанному порядку действий, то нужно сначала из 512 вычесть 345, а затем к результату прибавить 1345. Раскрыв скобки, мы изменим порядок действий и значительно упростим вычисления.
Иллюстрирующий пример и правило.
Рассмотрим пример: . Найти значение выражения можно, сложив 2 и 5, а затем взять полученное число с противоположным знаком. Получим -7.
С другой стороны, тот же самый результат можно получить, сложив числа, противоположные исходным.
Сформулируем правило:
Пример 1.
Пример 2.
Правило не изменяется, если в скобках не два, а три или более слагаемых.
Пример 3.
Замечание. Знаки меняются на противоположные только перед слагаемыми.
Для того чтобы раскрыть скобки, в данном случае нужно вспомнить распределительное свойство.
Сначала умножим первую скобку на 2, а вторую — на 3.
Перед первой скобкой стоит знак «+», значит, знаки нужно оставить без изменения. Перед второй стоит знак «-», следовательно, все знаки нужно поменять на противоположные
Список литературы
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012.
- Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.
- Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс — ЗШ МИФИ, 2011.

- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
- Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. — Просвещение, 1989.
- Онлайн тесты по математике ().
- Можно скачать указанные в п. 1.2. книги ().
Домашнее задание
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012. (ссылка см. 1.2)
- Домашнее задание: № 1254, № 1255, № 1256 (б,г)
- Другие задания: № 1258(в), № 1248
Репетитор по математике о методике вынужденных равенств — Колпаков Александр Николаевич
В школьной программе существует немало тем, к работе с которыми репетитор по математике прикладывает дополнительные усилия. В каждом классе таких тем найдется, как минимум, пара-тройка. Учитывая особенностей детского запоминания и скорости производимых ими умственных операций репетитору по математике приходится упрощать строгие обоснования, близкие к научным, ограничиваясь простыми примерами и задачами. Особенно часто и продуктивно методика примеров работает в 5 — 6 классе, в том возрасте, когда ребенок не ощущает потребность в полновесном и комплексном обосновании изучаемого. Более того, ребенок не в состоянии его воспринять полностью. Именно поэтому репетиторы по математике поголовно преподносят большинство элементарных основ и правил в 6 классе в декларативной форме: «Делай так, потому, что это правильно и не задавай лишних вопросов». Вот и все объяснение. Минус на минус дает плюс и будь любезен это запомнить. А почему именно плюс, 90% репетиторов по математике толком ответить не могут.
Особенно часто и продуктивно методика примеров работает в 5 — 6 классе, в том возрасте, когда ребенок не ощущает потребность в полновесном и комплексном обосновании изучаемого. Более того, ребенок не в состоянии его воспринять полностью. Именно поэтому репетиторы по математике поголовно преподносят большинство элементарных основ и правил в 6 классе в декларативной форме: «Делай так, потому, что это правильно и не задавай лишних вопросов». Вот и все объяснение. Минус на минус дает плюс и будь любезен это запомнить. А почему именно плюс, 90% репетиторов по математике толком ответить не могут.
Однако, если с Вами работает наблюдательный репетитор – толковый математик и педагог в одном лице, подготовленный к тому же еще и методически, то шансы получить приемлемые для 5 — 6 класса объяснения элементарных правил окажутся на порядок выше. В школах практически не рассказывают о причинах, побудивших создать «математическую азбуку» именно такой, какой ее знает любой мало-мальски грамотный выпускник. В этой статье я покажу простой метод, с помощью которого ребенку станет понятно, почему .
В этой статье я покажу простой метод, с помощью которого ребенку станет понятно, почему .
Подготовительная работа репетитора по математике
До обоснования правила умножения двух отрицательных чисел репетитору следует сначала обосновать тот факт, что при умножении положительного и отрицательного получается отрицательный результат, а модули чисел перемножаются. Это поясняется в учебниках, но далее возникает чувство, что тебя держат за дурака.
Умножение есть не что иное, как сокращенное обозначение результата сложения нескольких одинаковых слагаемых. В этом свете весьма логично будет сохранить это правило для отрицательных чисел и использовать запись для сокращенного обозначения суммы . Предположим, что репетитор по математике уже провел работу с темой «сложение отрицательных чисел» и его ученик с легкостью мышления Леонарда Эйлера 🙂 выдаст в примере ответ -15. Отлично. Тогда ему не составит большого труда смекнуть, что минус в ответ приходит потому, что складываются только отрицательные слагаемые (их 3 штуки), а модули умножаются по причине сложения равных модулей.
Разобравшись с умножением разнозначных чисел репетитору по математике впору перейти к главному аспекту. Учебники, на самом то деле, плохому учат, а именно искажают логические принципы получения выводов, основанных ни на чем. Говорится, что добавление «минуса» к одному из множителей примера меняет знак ответа на противоположный, поэтому, внимание « добавление второго знака поменяет его дважды, и мы получим положительное число 15». Приехали :). Разве это объяснение? Вот откуда берется непонимание, страх и даже ненависть к математике вместе с ее репетитором, с которым приходится заниматься в время, которое можно было бы потратить на более приятные занятия.
Правильным, на мой взгляд, будет воспользоваться главным принципом правил расширения числовых множеств, а именно: математические законы должны быть справедливыми и для новых чисел. То есть, если от перемены мест слагаемых сумма натуральных чисел не изменяется, то ровно так же должны себя вести и рациональные числа, иначе мы не сможем правильно преобразовывать буквенное выражение и, как следствие, решать уравнения, не зная наперед, какое число обозначено иксом: целое или дробное. Этот же принцип заложили наши предки –математики, которые еще в древности научились управлять отрицательными числами. Важнейший распределительный закон должен выполняться. Следствием его непоколебимого величия как раз и является тот факт, что «минус на минус будет плюс». Иначе он потеряет верность.
Этот же принцип заложили наши предки –математики, которые еще в древности научились управлять отрицательными числами. Важнейший распределительный закон должен выполняться. Следствием его непоколебимого величия как раз и является тот факт, что «минус на минус будет плюс». Иначе он потеряет верность.
Строгое доказательство этого факта в «основании математике» проводится, естественно, в произвольно-буквенном виде, что позволяет вести рассуждения без потери общности. Безусловно, репетитору по математике не стоит показывать такое доказательство ни в 6 классе, ни даже в 11 классе.
При работе в 5 — 6 классе необходимо учитывать важную особенность детского мышления, а именно принцип усвоения «от частного к общему», позволяющий экстраполировать подмеченные особенности тех или иных частных результатов на общие законы. Нужно подобрать удобное третье число к -5 и -3 и составить с тремя числами верное равенство с помощью распределительного свойства, из которого будет понятно, что . Репетитор по математике получит ответ 15 непосредственно в действиях и убедит ученика в логичности общего правила. Числам просто будет некуда завести репетитора, кроме получения правильного ответа. Таким образом злободневный вопрос о знаке и действиях с модулями обоснованно отпадет.
Репетитор по математике получит ответ 15 непосредственно в действиях и убедит ученика в логичности общего правила. Числам просто будет некуда завести репетитора, кроме получения правильного ответа. Таким образом злободневный вопрос о знаке и действиях с модулями обоснованно отпадет.
Мы подходим к главной части методики. Итак, репетитор по математике призывает на помощь какое-нибудь число, например , и записывает с его участием слудующее равенство . Его верность подкреплена распределительным законом.
Заметим, что к моменту объяснения нового правила все используемые арифметические действия оказываются в полной мере обоснованными (пара отрицательных множителей только одна) и не вызывают лишних вопросов у учеников. В левой части репетитор получает очевидный ответ -5, а в правой – сумму неизвестного результата (числа, обозначаемого как ) и числа -20. Очевидно, что единственным вариантом сохранить равенство остается вставка слагаемого +15 вместо неизвестного до данного момента обозначения .
Вот так, легко, внятно и быстро можно растопить огромный айсберг недопонимания, отвечая популярный ученический вопрос: «Почему минус на минус будет плюс?». Многие стесняются спрашивать репетитора по математике о том, что им непонятно и усложняют тем самым дальнейшее изучение предмета. Непонимание накапливается и вырождается в резкое неприятие математики как таковой. Это недопустимо.
Показанный пример является частью используемой методики вынужденных равенств, позволяющей репетитору по математике объяснять скользкие темы в доступной форме. Аналогичным образом объясняется правило введения отрицательных и дробных степеней, умножения обыкновенных дробей и др.
В заключение скажу, что хороший репетитор должен уметь предупреждать проблемы, связанные с расширением понятия «число» до того как программа подойдет к изучению конкретной темы. Важно постоянно напоминать ученику о единстве законов и тогда многие сложные вопросы найдут простые и понятные детям объяснения, близкие к их строгим / полным аналогам.
С уважением, Александр Николаевич, репетитор по математике для 5-11 класса. Москва. Строгино.
Что такое раскрыть скобки. Правило раскрытия скобок при произведении
В данной статье мы подробно рассмотрим основные правила такой важной темы курса математики, как раскрытие скобок. Знать правила раскрытия скобок нужно для того, чтобы верно решать уравнения, в которых они используются.
Как правильно раскрывать скобки при сложении
Раскрываем скобки, перед которыми стоит знак « + »
Эта самый простой случай, ибо если перед скобками стоит знак сложения, при раскрытии скобок знаки внутри них не меняются. Пример:
(9 + 3) + (1 — 6 + 9) = 9 + 3 + 1 — 6 + 9 = 16.
Как раскрыть скобки, перед которыми стоит знак « — »
В данном случае нужно переписать все слагаемые без скобок, но при этом сменить все знаки внутри них на противоположные. Знаки меняются только у слагаемых из тех скобок, перед которыми стоял знак « — ». Пример:
(9 + 3) — (1 — 6 + 9) = 9 + 3 — 1 + 6 — 9 = 8. 2) * 12 = 1728.
2) * 12 = 1728.
Как раскрыть 3 скобки
Бывают уравнения, в которых перемножаются сразу 3 скобки. В таком случае нужно сначала перемножить между собой слагаемые первых двух скобок, и затем сумму этого перемножения умножить на слагаемые третьей скобки. Пример:
(1 + 2) * (3 + 4) * (5 — 6) = (3 + 4 + 6 + 8) * (5 — 6) = — 21.
Данные правила раскрытия скобок одинаково распространяются для решения как линейных, так и тригонометрических уравнений.
П
родолжаю цикл методических статей на тему преподавания. Пришло время рассмотреть особенности индивидуальной работы репетитора по математике с учащимися 7-х классов . С великим удовольствием поделюсь своими соображениями о формах подачи одной из важнейших тем курса алгебры в 7 классе — «раскрытие скобок». Дабы не пытаться объять необъятное, остановимся на ее начальной ступени и разберем методику работы репетитора с умножением многочлена на многочлен. Как репетитор по математике действует в сложных ситуациях, когда слабый ученик не воспринимает классическую форму объяснения? Какие задания нужно готовить для сильного семиклассника? Рассмотрим эти и другие вопросы.
Казалось бы, ну что здесь сложного? «Скобки — это проще простого», — скажет любой отличник. «Есть распределительный закон и свойства степеней для работы с одночленами, общий алгоритм для любого количества слагаемых. Умножай каждое на каждое и приводи подобные». Однако, не все так просто в работе с отстающими. Вопреки стараниям репетитора по математике, учащиеся умудряются допускать ошибки самого разного калибра даже в простейших преобразованиях. Характер ошибок поражает своей разноплановостью: от мелких пропусков букв и знаков, до серьезных тупиковых «стоп-ошибок».
Что мешает школьнику правильно выполнить преобразования? Почему возможно непонимание?
Индивидуальных проблем существует огромное множество и одним из главных препятствий на пути усвоения и закрепления материала является затруднения в своевременном и быстром переключении внимания, сложность в обработке большого объема информации. Возможно, кому-то покажется странным, что я говорю о большом объеме, но слабому ученику 7 класса может не хватить ресурсов памяти и внимания даже для четырех слагаемых. Мешают коэффициенты, переменные, степени (показатели). Ученик путает очередность операций, забывает какие одночлены уже перемножены, а какие остались не тронутыми, не может вспомнить как их умножают и т. д.
Мешают коэффициенты, переменные, степени (показатели). Ученик путает очередность операций, забывает какие одночлены уже перемножены, а какие остались не тронутыми, не может вспомнить как их умножают и т. д.
Числовой подход репетитора по математике
Конечно же, нужно начинать с объяснений логики построения самого алгоритма. Как это сделать? Нужно поставить задачу: как изменить порядок действий в выражении , чтобы не поменялся результат? Я довольно часто привожу примеры, объясняющие работу тех или иных правил, на конкретных числах. А уже затем заменяю их буквами. Техника использования числового подхода будет описана ниже.
Проблемы мотивации .
В начале урока репетитору по математике трудно собрать ученика, если он не понимает актуальности изучаемого. В рамках программы за 6 — 7 класс сложно найти примеры использования правила умножения многочленов. Я бы сделал упор на необходимость учиться менять порядок действий в выражениях То, что это помогает решать задачи, ученик должен знать по опыту сложения подобных слагаемых. Ему же приходилось их складывать в при решении уравнений. Например, в 2х+5х+13=34 он использует, что 2х+5х=7х. Репетитор по математике просто должен акцентировать на этом внимание школьника.
Ему же приходилось их складывать в при решении уравнений. Например, в 2х+5х+13=34 он использует, что 2х+5х=7х. Репетитор по математике просто должен акцентировать на этом внимание школьника.
Учителя математики часто называют прием раскрытия скобок правилом «фонтанчика» .
Этот образ хорошо запоминается и его обязательно нужно использовать. Но как это правило доказывается? Напомним классическую форму, использующую очевидные тождественные преобразования:
(a+b)(c+d)=(a+b) c+(a+b) d=ac+bc+ad+bd
Репетитору по математике трудно что-либо здесь комментировать. Буквы говорят сами за себя. Да и не нужны сильному ученику 7 класса подробные объяснения. Однако, что делать со слабым, который в упор не видит в этой «буквенной мешанине» какого-либо содержания?
Основной проблемой, мешающей восприятию классического математического обоснования «фонтанчика», является непривычная форма записи первого множителя. Ни в 5 классе, ни 6 классе школьнику не приходилось перетаскивать первую скобку к каждому слагаемому второй. Дети имели дело только с числами (коэффициентами), расположенными, чаще всего, слева от скобок, например:
Дети имели дело только с числами (коэффициентами), расположенными, чаще всего, слева от скобок, например:
К окончанию 6 класса у школьника формируется визуальный образ объекта – определенное сочетание знаков (действий), связанных со скобками. И любое отклонение от привычного вида в сторону чего-то нового может дезориентировать семиклассника. Именно визуальный образ пары «число+скобка» репетитор по математике берет в оборот при объяснениях.
Можно предложить следующее объяснение. Репетитор рассуждает: «Если бы перед скобкой стояло какое-нибудь число, например 5, то смогли бы мы изменить порядок действий в этом выражении? Конечно. Тогда сделаем это . Подумай, изменится ли его результат, если вместо числа 5 мы вписать сумму 2+3, заключенную в скобки? Любой ученик скажет репетитору: «Какая разница, как писать: 5 или 2+3». Прекрасно. Получится запись . Репетитор по математике берет небольшую паузу, чтобы ученик зрительно запомнил картинку-образ объекта. Затем обращает его внимание на то, что скобка, как и число, «распределилась» или «прыгнула» к каждому слагаемому. Что это означает? Это означает, что данную операцию можно выполнять не только с числом, но и со скобкой. Получились две пары множителей и . С ними большая часть учеников легко справляется самостоятельно и выписывает репетитору результат . Важно сопоставить получившиеся пары с содержанием скобок 2+3 и 6+4 и станет понятно как они открываются.
Что это означает? Это означает, что данную операцию можно выполнять не только с числом, но и со скобкой. Получились две пары множителей и . С ними большая часть учеников легко справляется самостоятельно и выписывает репетитору результат . Важно сопоставить получившиеся пары с содержанием скобок 2+3 и 6+4 и станет понятно как они открываются.
Если необходимо, то после примера с числами репетитор по математике проводит буквенное доказательство. Оно оказывается легкой прогулкой по тем же самым частям предыдущего алгоритма.
Формирование навыка раскрытия скобок
Формирование навыка умножения скобок — один из важнейших этапов работы репетитора по математике с темой. И даже более важный чем этап объяснения логики правила «фонтанчика». Почему? Обоснования преобразований забудутся уже на следующий день, а навык, если он вовремя сформирован и закреплен, останется. Ученики выполняют операцию механически, как будто извлекают из памяти таблицу умножения. Этого и нужно добиваться. Почему? Если каждый раз при раскрытии скобок школьник будет вспоминать о том, почему раскрывается так, а не иначе, он забудет о задаче, которую решает. Именно поэтому оставшееся время урока репетитор по математике бросает на то, чтобы трансформировать понимание в механическое запоминание. Эта стратегия часто используется и в других темах.
Почему? Если каждый раз при раскрытии скобок школьник будет вспоминать о том, почему раскрывается так, а не иначе, он забудет о задаче, которую решает. Именно поэтому оставшееся время урока репетитор по математике бросает на то, чтобы трансформировать понимание в механическое запоминание. Эта стратегия часто используется и в других темах.
Как репетитору сформировать у школьника навык раскрытия скобок? Для этого ученик 7 класса должен выполнить ряд упражнений в достаточном для закрепления количестве. При этом возникает другая проблема. Слабый семиклассник не справляется с возросшим количеством преобразований. Пусть даже мелких. И ошибки сыплются одна за другой. Что должен предпринять репетитор по математике? Во-первых, нужно рекомендовать подрисовывать стрелки от каждого слагаемого к каждому. Если ученик очень слабый и не способен быстро переключаться с одного вида работы на другой, теряет концентрацию при выполнении несложных команд преподавателя, то репетитор по математике сам рисует эти стрелки. Причем не все сразу. Сначала репетитор соединяет первое слагаемое левой скобки с каждым слагаемым правой скобки и просит выполнить соответствующее умножение. Только после этого стрелки направляются от второго слагаемого в ту же правую скобку. Иными словами репетитор разделяет процесс на два этапа. Лучше выдерживать небольшую временную паузу (5-7 секунд) между первой и второй операцией.
Причем не все сразу. Сначала репетитор соединяет первое слагаемое левой скобки с каждым слагаемым правой скобки и просит выполнить соответствующее умножение. Только после этого стрелки направляются от второго слагаемого в ту же правую скобку. Иными словами репетитор разделяет процесс на два этапа. Лучше выдерживать небольшую временную паузу (5-7 секунд) между первой и второй операцией.
1) Один набор стрелок нужно рисовать над выражениями, а другой под ними.
2) Важно пропускать между строчками хотя бы пару клеток . Иначе запись будет очень плотной, а стрелки залезут не только на предыдущую строку, но и смешаются со стрелками от следующего упражнения.
3) В случае умножения скобок в формате 3 на 2 стрелки проводятся от короткой скобки к длинной. Иначе этих «фонтанчиков» будет не два, а три. Реализация третьего заметно усложняется в виду отсутствия для стрелок свободного пространства.
4) стрелки всегда направляются из одной точки. Один мой ученик все время порывался их поставить рядом и вот, что у него получалось:
Такое расположение не позволяет выделять и фиксировать текущее слагаемое, с которым ученик работает на каждом из этапов.
Работа пальцев репетитора
4) Для удержания внимания на отдельной паре умножаемых слагаемых, репетитор по математике прикладывает к ним два пальца. Это надо делать так, чтобы не закрывать ученику обзор. Для наиболее невнимательных школьников можно использовать метод «пульсации». Репетитор по математике подводит первый палец к началу стрелки (к одному из слагаемых) и фиксирует его, а вторым «стучит» по ее концу (по второму слагаемому). Пульсация помогает собрать внимание на том слагаемом, на которое ученик умножает. После того, как выполнено первое умножение на правую скобку, репетитор по математике говорит: «Теперь работаем с другим слагаемым». Репетитор передвигает к нему «неподвижный палец», а «пульсирующим» пробегает по слагаемым из другой скобки. Пульсация работает словно «поворотник» в автомобиле и позволяет собирать внимание рассеянного ученика на проводимой им операции. Если ребенок пишет мелко, то вместо пальцев используются два карандаша.
Оптимизация повторения
Как и при изучении любой другой темы курса алгебры умножение многочленов можно и нужно интегрировать с ранее пройденным материалом. Для этого репетитор по математике использует специальные задания-мостики, позволяющие найти применение изучаемого в различных математических объектах. Они не только соединяют темы в единое целое, но и весьма эффективно организуют повторение всего курса математики. И чем больше мостиков построит репетитор, тем лучше.
Для этого репетитор по математике использует специальные задания-мостики, позволяющие найти применение изучаемого в различных математических объектах. Они не только соединяют темы в единое целое, но и весьма эффективно организуют повторение всего курса математики. И чем больше мостиков построит репетитор, тем лучше.
Традиционно в учебниках алгебры для 7 класса расскрытие скобок интегрируется с решением линейных уравнений. В конце cписка номеров всегда имеются задания такого порядка: решить уравнение . При раскрытии скобок квадраты сокращаются и уравнение легко решается средствами 7 класса. Однако, почему-то про построение графика линейной функции авторы учебников благополучно забывают. Дабы исправить этот недостаток я бы посоветовал репетиторам по математике включать скобоки в аналитические выражения линейных функций, например . На таких упражнениях ученик не только тренирует навыки проведения тождественных преобразований, но еще и повторяет графики. Можно попросить найти точку пересечения двух «монстров», определить взаимное расположение прямых, найти точки их пересечения с осями и т. 3 \)
3 \)
Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.
Этот результат обычно формулируют в виде правила.
Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.
Мы уже неоднократно использовали это правило для умножения на сумму.
Произведение многочленов. Преобразование (упрощение) произведения двух многочленов
Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.
Обычно пользуются следующим правилом.
Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.
Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов
С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Пожалуй, наиболее часто
встречаются выражения \((a + b)^2, \; (a — b)^2 \) и \(a^2 — b^2 \), т. 2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.
2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.
Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми. Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.
На этом уроке вы узнаете, как из выражения, содержащего скобки, путем преобразования получить выражение, в котором скобок нет. Вы научитесь раскрывать скобки, перед которыми стоит знак плюс и знак минус. Мы вспомним, как раскрывать скобки, используя распределительный закон умножения. Рассмотренные примеры позволят связать новый и ранее изученный материал в единое целое.
Тема: Решение уравнений
Урок: Раскрытие скобок
Как раскрыть скобки, перед которыми стоит знак «+». Использование сочетательного закона сложения.
Если к числу нужно прибавить сумму двух чисел, то можно к этому числу прибавить сначала первое слагаемое, а затем второе.
Слева от знака равно выражение со скобками, а справа — выражение без скобок. Значит, при переходе от левой части равенства к правой произошло раскрытие скобок.
Рассмотрим примеры.
Пример 1.
Раскрыв скобки, мы изменили порядок действий. Считать стало удобнее.
Пример 2.
Пример 3.
Заметим, что во всех трех примерах мы просто убирали скобки. Сформулируем правило:
Замечание.
Если первое слагаемое в скобках стоит без знака, то его надо записать со знаком «плюс».
Можно выполнить пример по действиям. Сначала к 889 прибавить 445. Это действие в уме выполнить можно, но это не очень просто. Раскроем скобки и увидим, что изменённый порядок действий значительно упростит вычисления.
Если следовать указанному порядку действий, то нужно сначала из 512 вычесть 345, а затем к результату прибавить 1345. Раскрыв скобки, мы изменим порядок действий и значительно упростим вычисления.
Иллюстрирующий пример и правило.
Рассмотрим пример: . Найти значение выражения можно, сложив 2 и 5, а затем взять полученное число с противоположным знаком. Получим -7.
С другой стороны, тот же самый результат можно получить, сложив числа, противоположные исходным.
Сформулируем правило:
Пример 1.
Пример 2.
Правило не изменяется, если в скобках не два, а три или более слагаемых.
Пример 3.
Замечание. Знаки меняются на противоположные только перед слагаемыми.
Для того чтобы раскрыть скобки, в данном случае нужно вспомнить распределительное свойство.
Сначала умножим первую скобку на 2, а вторую — на 3.
Перед первой скобкой стоит знак «+», значит, знаки нужно оставить без изменения. Перед второй стоит знак «-», следовательно, все знаки нужно поменять на противоположные
Список литературы
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6.
 — М.: Мнемозина, 2012.
— М.: Мнемозина, 2012. - Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.
- Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс — ЗШ МИФИ, 2011.
- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
- Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. — Просвещение, 1989.
- Онлайн тесты по математике ().
- Можно скачать указанные в п. 1.2. книги ().
Домашнее задание
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012. (ссылка см. 1.2)
- Домашнее задание: № 1254, № 1255, № 1256 (б,г)
- Другие задания: № 1258(в), № 1248
Раскрытие скобок является одним из видов преобразования выражения. В этом разделе мы опишем правила раскрытия скобок, а также рассмотрим наиболее часто встречающиеся примеры задач.
В этом разделе мы опишем правила раскрытия скобок, а также рассмотрим наиболее часто встречающиеся примеры задач.
Yandex.RTB R-A-339285-1
Что называется раскрытием скобок?
Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Например, заменить выражение 2 · (3 + 4) на выражение вида 2 · 3 + 2 · 4 без скобок. Этот прием носит название раскрытия скобок.
Определение 1
Под раскрытием скобок подразумевают приемы избавления от скобок и рассматривают его обычно в отношении выражений, которые могут содержать:
- знаки « + » или « — » перед скобками, в которые заключены суммы или разности;
- произведение числа, буквы или нескольких букв и суммы или разности, которая помещена в скобки.
Так мы привыкли рассматривать процесс раскрытия скобок в курсе школьной программы. Однако никто не мешает нам посмотреть на это действие шире. Мы можем назвать раскрытием скобок переход от выражения, которое содержит отрицательные числа в скобках, к выражению, не имеющему скобок. К примеру, мы можем перейти от 5 + (− 3) − (− 7) к 5 − 3 + 7 . Фактически, это тоже раскрытие скобок.
Однако никто не мешает нам посмотреть на это действие шире. Мы можем назвать раскрытием скобок переход от выражения, которое содержит отрицательные числа в скобках, к выражению, не имеющему скобок. К примеру, мы можем перейти от 5 + (− 3) − (− 7) к 5 − 3 + 7 . Фактически, это тоже раскрытие скобок.
Точно также мы можем заменить произведение выражений в скобках вида (a + b) · (c + d) на сумму a · c + a · d + b · c + b · d . Такой прием также не противоречит смыслу раскрытия скобок.
Вот еще один пример. Мы можем допустить, что в выражениях вместо чисел и переменных могут быть использованы любые выражения. Например, выражению x 2 · 1 a — x + sin (b) будет соответствовать выражение без скобок вида x 2 · 1 a — x 2 · x + x 2 · sin (b) .
Отдельного внимания заслуживать еще один момент, который касается особенностей записи решений при раскрытии скобок. Мы можем записать начальное выражение со скобками и полученный после раскрытия скобок результат как равенство. Например, после раскрытия скобок вместо выражения 3 − (5 − 7) мы получаем выражение 3 − 5 + 7 . Оба этих выражения мы можем записать в виде равенства 3 − (5 − 7) = 3 − 5 + 7 .
Оба этих выражения мы можем записать в виде равенства 3 − (5 − 7) = 3 − 5 + 7 .
Проведение действий с громоздкими выражениями может потребовать записи промежуточных результатов. Тогда решение будет иметь вид цепочки равенств. Например, 5 − (3 − (2 − 1)) = 5 − (3 − 2 + 1) = 5 − 3 + 2 − 1 или 5 − (3 − (2 − 1)) = 5 − 3 + (2 − 1) = 5 − 3 + 2 − 1 .
Правила раскрытия скобок, примеры
Приступим к рассмотрению правил раскрытия скобок.
У одиночных чисел в скобках
Отрицательные числа в скобках часто встречаются в выражениях. Например, (− 4) и 3 + (− 4) . Положительные числа в скобках тоже имеют место быть.
Сформулируем правило раскрытия скобок, в которых заключены одиночные положительные числа. Предположим, что а – это любое положительное число. Тогда (а) мы можем заменить на а, + (а) на + а, — (а) на – а. Если вместо а взять конкретное число, то согласно правилу: число (5) запишется как 5 , выражение 3 + (5) без скобок примет вид 3 + 5 , так как + (5) заменяется на + 5 , а выражение 3 + (− 5) эквивалентно выражению 3 − 5 , так как + (− 5) заменяется на − 5 .
Положительные числа обычно записываются без использования скобок, так как скобки в этом случае излишни.
Теперь рассмотрим правило раскрытия скобок, внутри которых содержится одиночное отрицательное число. + (− a) мы заменяем на − a , − (− a) заменяется на + a . Если выражение начинается с отрицательного числа (− a) , которое записано в скобках, то скобки опускаются и вместо (− a) остается − a .
Приведем примеры: (− 5) можно записать как − 5 , (− 3) + 0 , 5 принимает вид − 3 + 0 , 5 , 4 + (− 3) превращается в 4 − 3 , а − (− 4) − (− 3) после раскрытия скобок принимает вид 4 + 3 , так как − (− 4) и − (− 3) заменяется на + 4 и + 3 .
Следует понимать, что записать выражение 3 · (− 5) как 3 · − 5 нельзя. Об этом речь пойдет в следующих пунктах.
Давайте посмотрим, на чем основываются правила раскрытия скобок.
Согласно правилу разность a − b равна a + (− b) . На основе свойств действий с числами мы можем составить цепочку равенств (a + (− b)) + b = a + ((− b) + b) = a + 0 = a , которая будет справедлива. Эта цепочка равенств в силу смысла вычитания доказывает, что выражение a + (− b) — это разность a − b .
Эта цепочка равенств в силу смысла вычитания доказывает, что выражение a + (− b) — это разность a − b .
Основываясь на свойствах противоположных чисел и правил вычитания отрицательных чисел мы можем утверждать, что − (− a) = a , a − (− b) = a + b .
Встречаются выражения, которые составляются из числа, знаков минуса и нескольких пар скобок. Использование приведенных выше правил позволяет последовательно избавляться от скобок, продвигаясь от внутренних скобок к наружным или в обратном направлении. Примером такого выражения может быть − (− ((− (5)))) . Раскроем скобки, продвигаясь изнутри наружу: − (− ((− (5)))) = − (− ((− 5))) = − (− (− 5)) = − (5) = − 5 . Также этот пример можно разобрать и в обратном направлении: − (− ((− (5)))) = ((− (5))) = (− (5)) = − (5) = − 5 .
Под a и b можно понимать не только числа, но также произвольные числовые или буквенные выражения со знаком « + » впереди, которые не являются суммами или разностями. Во всех этих случаях можно применять правила точно также, как мы делали это в отношении одиночных чисел в скобках.
К примеру, после раскрытия скобок выражение − (− 2 · x) − (x 2) + (− 1 x) − (2 · x · y 2: z) примет вид 2 · x − x 2 − 1 x − 2 · x · y 2: z . Как мы это сделали? Мы знаем, что − (− 2 · x) есть + 2 · x , а так как это выражение стоит вначале, то + 2 · x можно записать как 2 · x , − (x 2) = − x 2 , + (− 1 x) = − 1 x и − (2 · x · y 2: z) = − 2 · x · y 2: z .
В произведениях двух чисел
Начнем с правила раскрытия скобок в произведении двух чисел.
Предположим, что a и b – это два положительных числа. В этом случае произведение двух отрицательных чисел − a и − b вида (− a) · (− b) мы можем заменить на (a · b) , а произведения двух чисел с противоположными знаками вида (− a) · b и a · (− b) заменить на (− a · b) . Умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус.
Верность первой части записанного правила подтверждается правилом умножения отрицательных чисел.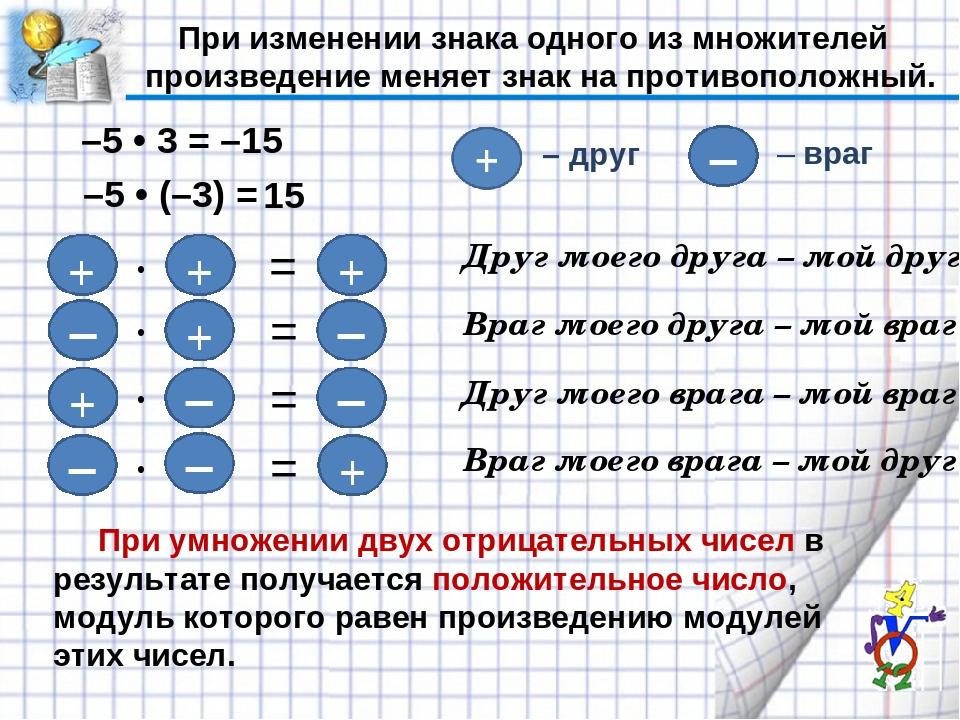 Для подтверждения второй части правила мы можем использовать правила умножения чисел с разными знаками.
Для подтверждения второй части правила мы можем использовать правила умножения чисел с разными знаками.
Рассмотрим несколько примеров.
Пример 1
Рассмотрим алгоритм раскрытия скобок в произведении двух отрицательных чисел — 4 3 5 и — 2 , вида (- 2) · — 4 3 5 . Для этого заменим исходное выражение на 2 · 4 3 5 . Раскроем скобки и получим 2 · 4 3 5 .
А если мы возьмем частное отрицательных чисел (− 4) : (− 2) , то запись после раскрытия скобок будет иметь вид 4: 2
На месте отрицательных чисел − a и − b могут быть любые выражения со знаком минус впереди, которые не являются суммами или разностями. К примеру, это могут быть произведения, частные, дроби, степени, корни, логарифмы, тригонометрические функции и т.п.
Раскроем скобки в выражении — 3 · x x 2 + 1 · x · (- ln 5) . Согласно правилу, мы можем произвести следующие преобразования: — 3 · x x 2 + 1 · x · (- ln 5) = — 3 · x x 2 + 1 · x · ln 5 = 3 · x x 2 + 1 · x · ln 5 .
Выражение (− 3) · 2 можно преобразовать в выражение (− 3 · 2) . После этого можно раскрыть скобки: − 3 · 2 .
После этого можно раскрыть скобки: − 3 · 2 .
2 3 · — 4 5 = — 2 3 · 4 5 = — 2 3 · 4 5
Деление чисел с разными знаками также может потребовать предварительного раскрытия скобок: (− 5) : 2 = (− 5: 2) = − 5: 2 и 2 3 4: (- 3 , 5) = — 2 3 4: 3 , 5 = — 2 3 4: 3 , 5 .
Правило может быть использовано для выполнения умножения и деления выражений с разными знаками. Приведем два примера.
1 x + 1: x — 3 = — 1 x + 1: x — 3 = — 1 x + 1: x — 3
sin (x) · (- x 2) = (- sin (x) · x 2) = — sin (x) · x 2
В произведениях трех и большего количества чисел
Перейдем к произведенимя и частным, которые содержат большее количество чисел. Для раскрытия скобок здесь будет действовать следующее правило. При четном количестве отрицательных чисел можно опустить скобки, заменив числа противоположными. После этого необходимо заключить полученное выражение в новые скобки. При нечетном количестве отрицательных чисел, опустив скобки, заменить числа на противоположные. После этого полученное выражение необходимо взять в новые скобки и поставить перед ним знак минус.
После этого полученное выражение необходимо взять в новые скобки и поставить перед ним знак минус.
Пример 2
Для примера, возьмем выражение 5 · (− 3) · (− 2) , которое представляет собой произведение трех чисел. Отрицательных чисел два, следовательно, мы можем записать выражение как (5 · 3 · 2) и затем окончательно раскрыть скобки, получив выражение 5 · 3 · 2 .
В произведении (− 2 , 5) · (− 3) : (− 2) · 4: (− 1 , 25) : (− 1) пять чисел являются отрицательными. поэтому (− 2 , 5) · (− 3) : (− 2) · 4: (− 1 , 25) : (− 1) = (− 2 , 5 · 3: 2 · 4: 1 , 25: 1) . Окончательно раскрыв скобки, получаем −2,5·3:2·4:1,25:1 .
Обосновать приведенное выше правило можно следующим образом. Во-первых, такие выражения мы можем переписать как произведение, заменив умножением на обратное число деление. Представляем каждое отрицательное число как произведение множительного числа и — 1 или — 1 заменяем на (− 1) · a .
Используя переместительное свойство умножения меняем местами множители и переносим все множители, равные − 1 , в начало выражения. Произведение четного числа минус единиц равно 1 , а нечетного – равно − 1 , что позволяет нам использовать знак минус.
Произведение четного числа минус единиц равно 1 , а нечетного – равно − 1 , что позволяет нам использовать знак минус.
Если бы мы не использовали правило, то цепочка действий по раскрытию скобок в выражении — 2 3: (- 2) · 4: — 6 7 выглядела бы следующим образом:
2 3: (- 2) · 4: — 6 7 = — 2 3 · — 1 2 · 4 · — 7 6 = = (- 1) · 2 3 · (- 1) · 1 2 · 4 · (- 1) · 7 6 = = (- 1) · (- 1) · (- 1) · 2 3 · 1 2 · 4 · 7 6 = (- 1) · 2 3 · 1 2 · 4 · 7 6 = = — 2 3 · 1 2 · 4 · 7 6
Приведенное выше правило может быть использовано при раскрытии скобок в выражениях, которые представляют собой произведения и частные со знаком минус, не являющихся суммами или разностями. Возьмем для примера выражение
x 2 · (- x) : (- 1 x) · x — 3: 2 .
Его можно привести к выражению без скобок x 2 · x: 1 x · x — 3: 2 .
Раскрытие скобок, перед которыми стоит знак +
Рассмотрим правило, которое можно применить для раскрытия скобок, перед которыми стоит знак плюс, а «содержимое» этих скобок не умножается и не делится на какое-либо число или выражение.
Согласно правилу скобки вместе со стоящим перед ними знаком опускаются, при этом знаки всех слагаемых в скобках сохраняются. Если перед первым слагаемым в скобках не стоит никакого знака, то нужно поставить знак плюс.
Пример 3
Для примера приведем выражение (12 − 3 , 5) − 7 . Опустив скобки, мы сохраняем знаки слагаемых в скобках и ставим перед первым слагаемым знак плюс. Запись будет иметь вид (12 − 3 , 5) − 7 = + 12 − 3 , 5 − 7 . В приведенном примере знак перед первым слагаемым ставить не обязательно, так как + 12 − 3 , 5 − 7 = 12 − 3 , 5 − 7 .
Пример 4
Рассмотрим еще один пример. Возьмем выражение x + 2 a — 3 x 2 + 1 — x 2 — 4 + 1 x и проведем с ним действия x + 2 a — 3 x 2 + 1 — x 2 — 4 + 1 x = = x + 2 a — 3 x 2 + 1 — x 2 — 4 + 1 x
Вот еще один пример раскрытия скобок:
Пример 5
2 + x 2 + 1 x — x · y · z + 2 · x — 1 + (- 1 + x — x 2) = = 2 + x 2 + 1 x — x · y · z + 2 · x — 1 — 1 + x + x 2
Как раскрываются скобки, перед которыми стоит знак минус
Рассмотрим случаи, когда перед скобками стоит знак минус, и которые не не умножаются (или делятся) на какое-либо число или выражение. Согласно правилу раскрытия скобок, перед которыми стоит знак « — », скобки со знаком « — » опускаются, при этом знаки всех слагаемых внутри скобок меняются на противоположные.
Согласно правилу раскрытия скобок, перед которыми стоит знак « — », скобки со знаком « — » опускаются, при этом знаки всех слагаемых внутри скобок меняются на противоположные.
Пример 6
К примеру:
1 2 = 1 2 , — 1 x + 1 = — 1 x + 1 , — (- x 2) = x 2
Выражения с переменными могут быть преобразованы с использованием того же правила:
X + x 3 — 3 — — 2 · x 2 + 3 · x 3 · x + 1 x — 1 — x + 2 ,
получаем x — x 3 — 3 + 2 · x 2 — 3 · x 3 · x + 1 x — 1 — x + 2 .
Раскрытие скобок при умножении числа на скобку, выражения на скобку
Здесь мы рассмотрим случаи, когда нужно раскрыть скобки, которые умножаются или делятся на какое-либо число или выражение. Тут применимы формулы вида (a 1 ± a 2 ± … ± a n) · b = (a 1 · b ± a 2 · b ± … ± a n · b) или b · (a 1 ± a 2 ± … ± a n) = (b · a 1 ± b · a 2 ± … ± b · a n) , где a 1 , a 2 , … , a n и b – некоторые числа или выражения.
Пример 7
Например, проведем раскрытие скобок в выражении (3 − 7) · 2 . Согласно правилу, мы можем провести следующие преобразования: (3 − 7) · 2 = (3 · 2 − 7 · 2) . Получаем 3 · 2 − 7 · 2 .
Согласно правилу, мы можем провести следующие преобразования: (3 − 7) · 2 = (3 · 2 − 7 · 2) . Получаем 3 · 2 − 7 · 2 .
Раскрыв скобки в выражении 3 · x 2 · 1 — x + 1 x + 2 , получаем 3 x 2 · 1 — 3 · x 2 · x + 3 · x 2 · 1 x + 2 .
Умножение скобки на скобку
Рассмотрим произведение двух скобок вида (a 1 + a 2) · (b 1 + b 2) . Это поможет нам получить правило для раскрытия скобок при проведении умножения скобки на скобку.
Для того, чтобы решить приведенный пример, обозначим выражение (b 1 + b 2) как b . Это позволит нам использовать правило умножения скобки на выражение. Получим (a 1 + a 2) · (b 1 + b 2) = (a 1 + a 2) · b = (a 1 · b + a 2 · b) = a 1 · b + a 2 · b . Выполнив обратную замену b на (b 1 + b 2) , снова применим правило умножения выражения на скобку: a 1 · b + a 2 · b = = a 1 · (b 1 + b 2) + a 2 · (b 1 + b 2) = = (a 1 · b 1 + a 1 · b 2) + (a 2 · b 1 + a 2 · b 2) = = a 1 · b 1 + a 1 · b 2 + a 2 · b 1 + a 2 · b 2
Благодаря ряду несложных приемов мы можем прийти к сумме произведений каждого из слагаемых из первой скобки на каждое из слагаемых из второй скобки. Правило можно распространить на любое количество слагаемых внутри скобок.
Правило можно распространить на любое количество слагаемых внутри скобок.
Сформулируем правила умножения скобки на скобку: чтобы перемножить между собой две суммы, необходимо каждое из слагаемых первой суммы перемножить на каждое из слагаемых второй суммы и сложить полученные результаты.
Формула будет иметь вид:
(a 1 + a 2 + . . . + a m) · (b 1 + b 2 + . . . + b n) = = a 1 b 1 + a 1 b 2 + . . . + a 1 b n + + a 2 b 1 + a 2 b 2 + . . . + a 2 b n + + . . . + + a m b 1 + a m b 1 + . . . a m b n
Проведем раскрытие скобок в выражении (1 + x) · (x 2 + x + 6) Оно представляет собой произведение двух сумм. Запишем решение: (1 + x) · (x 2 + x + 6) = = (1 · x 2 + 1 · x + 1 · 6 + x · x 2 + x · x + x · 6) = = 1 · x 2 + 1 · x + 1 · 6 + x · x 2 + x · x + x · 6
Отдельно стоит остановиться на тех случаях, когда в скобках присутствует знак минус наряду со знаками плюс. Для примера возьмем выражение (1 − x) · (3 · x · y − 2 · x · y 3) .
Сначала представим выражения в скобках в виде сумм: (1 + (− x)) · (3 · x · y + (− 2 · x · y 3)) . Теперь мы можем применить правило: (1 + (− x)) · (3 · x · y + (− 2 · x · y 3)) = = (1 · 3 · x · y + 1 · (− 2 · x · y 3) + (− x) · 3 · x · y + (− x) · (− 2 · x · y 3))
Теперь мы можем применить правило: (1 + (− x)) · (3 · x · y + (− 2 · x · y 3)) = = (1 · 3 · x · y + 1 · (− 2 · x · y 3) + (− x) · 3 · x · y + (− x) · (− 2 · x · y 3))
Раскроем скобки: 1 · 3 · x · y − 1 · 2 · x · y 3 − x · 3 · x · y + x · 2 · x · y 3 .
Раскрытие скобок в произведениях нескольких скобок и выражений
При наличии в выражении трех и более выражений в скобках, раскрывать скобки необходимо последовательно. Начать преобразование необходимо с того, что два первых множителя берут в скобки. Внутри этих скобок мы можем проводить преобразования согласно правилам, рассмотренным выше. Например, скобки в выражении (2 + 4) · 3 · (5 + 7 · 8) .
В выражении содержится сразу три множителя (2 + 4) , 3 и (5 + 7 · 8) . Будем раскрывать скобки последовательно. Заключим первые два множителя еще в одни скобки, которые для наглядности сделаем красными: (2 + 4) · 3 · (5 + 7 · 8) = ((2 + 4) · 3) · (5 + 7 · 8) .
В соответствии с правилом умножения скобки на число мы можем провести следующие действия: ((2 + 4) · 3) · (5 + 7 · 8) = (2 · 3 + 4 · 3) · (5 + 7 · 8) .
Умножаем скобку на скобку: (2 · 3 + 4 · 3) · (5 + 7 · 8) = 2 · 3 · 5 + 2 · 3 · 7 · 8 + 4 · 3 · 5 + 4 · 3 · 7 · 8 .
Скобка в натуральной степени
Степени, основаниями которых являются некоторые выражения, записанные в скобках, с натуральными показателями можно рассматривать как произведение нескольких скобок. При этом по правилам из двух предыдущих пунктов их можно записать без этих скобок.
Рассмотрим процесс преобразования выражения (a + b + c) 2 . Его можно записать в виде произведения двух скобок (a + b + c) · (a + b + c) . Произведем умножение скобки на скобку и получим a · a + a · b + a · c + b · a + b · b + b · c + c · a + c · b + c · c .
Разберем еще один пример:
Пример 8
1 x + 2 3 = 1 x + 2 · 1 x + 2 · 1 x + 2 = = 1 x · 1 x + 1 x · 2 + 2 · 1 x + 2 · 2 · 1 x + 2 = = 1 x · 1 x · 1 x + 1 x · 2 · 1 x + 2 · 1 x · 1 x + 2 · 2 · 1 x + 1 x · 1 x · 2 + + 1 x 2 · 2 + 2 · 1 x · 2 + 2 · 2 · 2
Деление скобки на число и скобки на скобку
Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые. Например, (x 2 — x) : 4 = x 2: 4 — x: 4 .
Например, (x 2 — x) : 4 = x 2: 4 — x: 4 .
Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.
Например, нам необходимо раскрыть скобки в выражении (x + 2) : 2 3 . Для этого сначала заменим деление умножением на обратное число (x + 2) : 2 3 = (x + 2) · 2 3 . Умножим скобку на число (x + 2) · 2 3 = x · 2 3 + 2 · 2 3 .
Вот еще один пример деления на скобку:
Пример 9
1 x + x + 1: (x + 2) .
Заменим деление умножением: 1 x + x + 1 · 1 x + 2 .
Выполним умножение: 1 x + x + 1 · 1 x + 2 = 1 x · 1 x + 2 + x · 1 x + 2 + 1 · 1 x + 2 .
Порядок раскрытия скобок
Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида, т.е. в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.
Порядок выполнения действий:
- первым делом необходимо выполнить возведение скобок в натуральную степень;
- на втором этапе производится раскрытие скобок в произведениях и частных;
- заключительным шагом будет раскрытие скобок в суммах и разностях.

Рассмотрим порядок выполнения действий на примере выражения (− 5) + 3 · (− 2) : (− 4) − 6 · (− 7) . Намнем преобразование с выражений 3 · (− 2) : (− 4) и 6 · (− 7) , которые должны принять вид (3 · 2: 4) и (− 6 · 7) . При подстановке полученных результатов в исходное выражение получаем: (− 5) + 3 · (− 2) : (− 4) − 6 · (− 7) = (− 5) + (3 · 2: 4) − (− 6 · 7) . Раскрываем скобки: − 5 + 3 · 2: 4 + 6 · 7 .
Имея дело с выражениями, которые содержат скобки в скобках, удобно проводить преобразования, продвигаясь изнутри наружу.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Negative Times A Negative – dy/dan
Зацени, Твиттер!
На этой неделе на моем семинаре в Монтерее, штат Калифорния, учитель математики по имени Пол подошел и сказал: «Я задаю всем один и тот же вопрос: что является числовой иллюстрацией того факта, что отрицательное число, умноженное на отрицательное число, является положительным количество?»
Я отправил его вопрос в Твиттер, и в течение следующих нескольких часов пришло более сотни ответов. Вы можете нажать на мой твит и увидеть многие из них. Я вытащил образец здесь:
Вы можете нажать на мой твит и увидеть многие из них. Я вытащил образец здесь:
@ddmeyer Я думаю об этом как о неоднократном вычитании долга или сокращении денежных потерь до тех пор, пока вы не получите прибыль.
— Крис Адамс (@MrAdamsProblems) 17 июня 2013 г.
@ddmeyer В сцене из фильма. Если машина в сцене движется назад, воспроизведение сцены в обратном направлении заставит машину двигаться вперед
— Крис Адамс (@MrAdamsProblems) 17 июня 2013 г.
@ddmeyer Подойдет ли этот пример (см. прилагаемое изображение примера)? Просто мысль. pic.twitter.com/xZSLKguaG
— Гэри А. Петко (@GaryPetko) 17 июня 2013 г.
@ddmeyer Если отрицательный заряд перемещается в направлении отрицательного электрического потенциала, электрическая потенциальная энергия увеличивается положительно на Vq
— Дуг Смит (@bcphysics) 17 июня 2013 г.
@dcox21 @ddmeyer Мой ученик: «Когда ты любишь любовь, это любовь, если ты ненавидишь любовь, это ненависть, но если ты ненавидишь, ненавидь любовь». #пример реального мира
— Эрик Бензель (@mrbenzel) 17 июня 2013 г.
@ddmeyer, забивая пенальти в футболе, продвигает команду вперед.
— Джеффри Баугус (@baugusj) 18 июня 2013 г.
Я оценил многие из этих иллюстраций (как и Пол, хотя он указал, что многие из них не числовые), но мое сердце принадлежит ответу Брайана Мейера:
@PaiMath @ddmeyer Немного. Насколько я знаю, отрицательные # были придуманы для долга. Раз они существуют, мы могли бы спросить, что происходит, когда мы размножаемся?
— Брайан Мейер (@doingmath) 17 июня 2013 г.
Видите ли, есть вещи, называемые отрицательными числами. Наши студенты понимают, что это полезные описания. Они понимают, как складывать и вычитать их. (Возможно, используя метафору, например, влезть в большую или меньшую задолженность.)
Наши студенты понимают, что это полезные описания. Они понимают, как складывать и вычитать их. (Возможно, используя метафору, например, влезть в большую или меньшую задолженность.)
Мы знаем, как складывать и вычитать положительных чисел, конечно, но мы также можем умножать и делить их. Верно ли то же самое для отрицательных чисел? Как будет выглядеть умножение и деление отрицательных чисел? Каковы ваши теории?
В этом посте у нас есть два очень разных принципа организации урока математики:
- Учащиеся будут выполнять сложную математическую работу, если мы сможем указать какую-то работу, в которой используется эта математика, или какой-то момент, когда это происходит в мире за пределами математического класса. .
- Учащиеся примутся за сложную математическую работу, если мы сможем предоставить нашим ученикам возможность узнать, что в ней любопытного и непонятного.
Кое-что совпадает, конечно, но не сильно.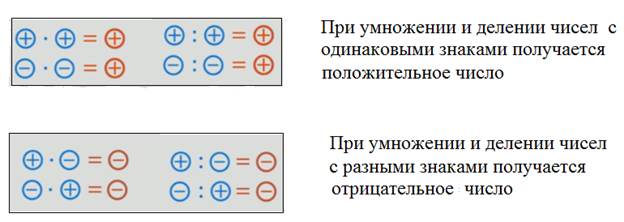 В течение года эти организационные принципы создают очень разные классы. В течение карьеры эти организационные принципы создают очень разных учителей. Давайте поговорим об этих различиях в комментариях.
В течение года эти организационные принципы создают очень разные классы. В течение карьеры эти организационные принципы создают очень разных учителей. Давайте поговорим об этих различиях в комментариях.
Всегда связанные :
- Сэмюэля Оттена, загнанного в угол реальным миром.
Избранный возврат
Брайан:
Я не уверен, почему они должны быть либо/или, или почему они поднимаются до организационных принципов.
Просто основано на истории математики, некоторые ее части очень практичны и основаны на реальном мире. Другие части более абстрактны и были обнаружены и разработаны задолго до того, как кто-либо нашел для них практическое применение или связь с остальной математикой.
Ребекка Филлипс:
«Потому что вам это нужно» и «Потому что это возможно» будут касаться разных детей, и разве я не должен пытаться вдохновить их всех?
Вот мой ответ.
Избранный комментарий
Scott Farrand:
Многие из приведенных вами примеров явно не относятся к умножению. Например, некоторые из них дали объяснение, почему отрицательное число отрицательного числа является положительным, что не совсем то же самое, что объяснить, почему отрицательное число, умноженное на отрицательное число, является положительным.
Также:
В данном вопросе о двух альтернативах Дэна для организации математического класса я предпочитаю второй. Создание недоумения и любопытства у учащихся требует, чтобы у них был некоторый комфорт и понимание, что приводит к небольшой интуиции или проекции, которая может показаться чем-то противоречащей, отсюда и удивление. Если учащийся просто привыкает применять формулу, которую он не понимает, то его трудно удивить результатом, связанным с этой формулой.
10 марта 2014 г. . Джеймс Ки вносит ценный вклад в наш проект.
2.4: Умножение и деление целых чисел
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 22469
- Дэвид Арнольд
- Колледж Редвудс
Прежде чем мы начнем, дайте знать, что целые числа удовлетворяют тем же свойствам умножения, что и целые числа.
Целочисленные свойства умножения
Коммутативное свойство. Если a и b — целые числа, то их произведение коммутирует. То есть
\[a \cdot b = b \cdot a.\nonumber \]
Ассоциативное свойство. Если a, b и c — целые числа, то их произведение ассоциативно. То есть
\[(a \cdot b) \cdot c = a \cdot (b \cdot c).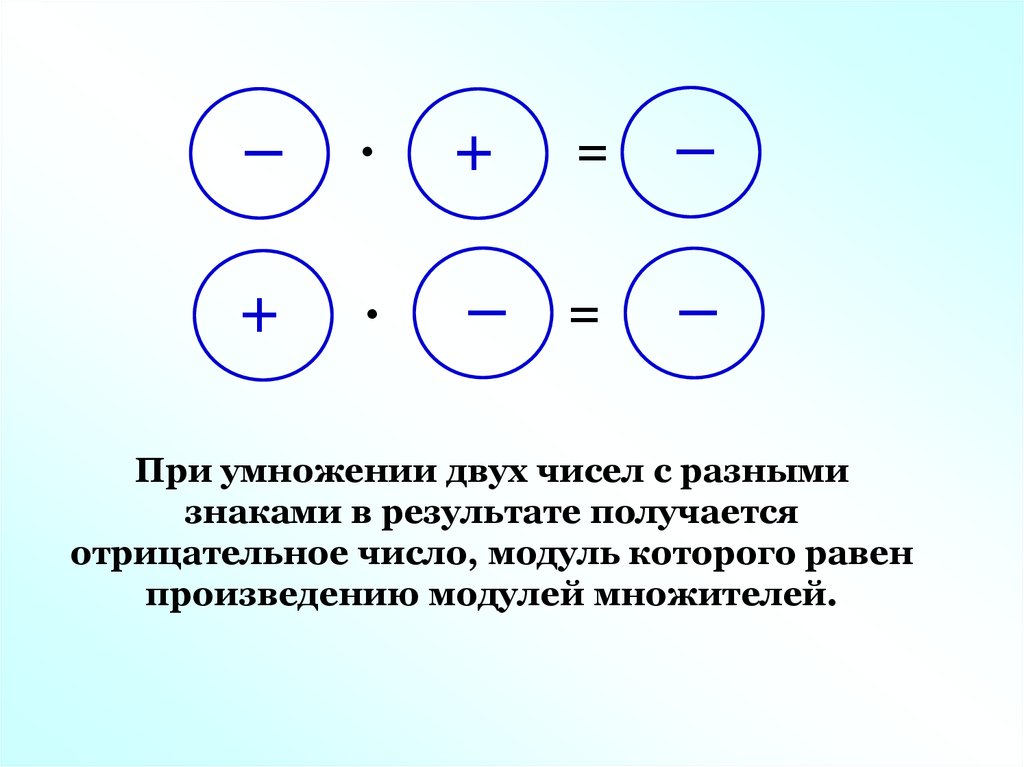 \nonumber \]
\nonumber \]
Свойство мультипликативной идентичности. Если a является любым целым числом, то
\[a \cdot 1 = a \text{ и } 1 \cdot a = a.\nonumber \]
Поскольку умножение любого целого числа на 1 возвращает идентичное целое число, целое число 1 называется мультипликативным тождеством .
В разделе 1.3 мы узнали, что умножение эквивалентно 9.0055 повторное добавление . Например,
\[ 3 \cdot 4 = \underbrace{4 + 4 + 4}_{\text{три четверки}} \nonumber \]
На числовой прямой три набора из четырех эквивалентны прохождению трех наборов из четырех единиц вправо, начиная с нуля, как показано на рисунке \(\PageIndex{1}\).
Рисунок \(\PageIndex{1}\): Обратите внимание, что 3 · 4 = 4 + 4 + 4. То есть 3 · 4 = 12.Этот пример и небольшое размышление должны убедить читателей, что произведение двух натуральных чисел будет всегда быть положительным целым числом.
Произведение двух положительных целых чисел
Если a и b — два положительных целых числа, то их произведение ab также является положительным целым числом.
Например, 2 · 3 = 6 и 13 · 117 = 1521. В каждом случае произведение двух натуральных чисел является положительным целым числом.
Произведение положительного целого числа на отрицательное целое число
Если мы продолжим мысль о том, что умножение эквивалентно многократному сложению, то должно быть, что
\[ 3 \cdot (-4) = \underbrace{-4+(-4)+(-4)}_{ \text{три отрицательных четверки}}. \nonumber\nonumber \]
Изображенное на числовой прямой число 3 · (−4) будет тогда эквивалентно прохождению трех наборов отрицательных четырех единиц (влево), начиная с нуля, как показано на рисунке \(\PageIndex {2}\).
Рисунок \(\PageIndex{2}\): обратите внимание, что 3 · (−4) = −4+(−4) + (−4). То есть 3 · (−4) = −12.Обратите внимание, по крайней мере в этом конкретном случае, что произведение положительного целого числа на отрицательное целое число является отрицательным целым числом.
Мы показали, что 3 · (−4) = −12. Однако целочисленное умножение коммутативно, поэтому также должно быть верно, что −4 · 3 = −12. То есть произведение отрицательного целого числа на положительное число также является отрицательным целым числом. Хотя это и не доказательство, этот аргумент мотивирует следующий факт о целочисленном умножении.
То есть произведение отрицательного целого числа на положительное число также является отрицательным целым числом. Хотя это и не доказательство, этот аргумент мотивирует следующий факт о целочисленном умножении.
Произведение положительного целого числа и отрицательного целого числа
Верны два факта:
- Если , то является положительным целым числом, а b — отрицательное целое число, тогда произведение на — отрицательное целое число.
- Если a — отрицательное целое число, а b — положительное целое число, то произведение ab является отрицательным целым числом.
Таким образом, например, 5 · (−12) = −60 и −13 · 2 = −26. В каждом случае ответ отрицательный, потому что мы берем продукт, в котором один из факторов положительный, а другой отрицательный.
Свойство распределения
Целые числа удовлетворяют свойству распределения.
Распределительное свойство
Пусть a , b и c будут целыми числами. Тогда
Тогда
\[a \cdot (b + c) = a \cdot b + a \cdot c.\nonumber \]
Мы говорим, что «умножение является дистрибутивным по отношению к сложению».
Обратите внимание, как «распределяется» a. и умножаются на каждый член в скобках.
Например, рассмотрим выражение 3 · (4 + 5). Мы можем вычислить это выражение в соответствии с порядком операций, упростив сначала выражение в скобках.
\[ \begin{align*} 3 \cdot (4 + 5) &= 3 \cdot 9 \\[4pt] &= 27 \end{align*}\nonumber \]
Но мы также можем использовать распределительное свойство, умножая каждый член в скобках на три, а затем упрощая результат.
\[ \begin{aligned} ~ & \textcolor{red}{ \text{ Распределите 3: }} 3 (4+5) \\
~ & \textcolor{red}{ \text{ Сначала выполните умножение: }}= 3 \cdot 4 + 3 \cdot 5 \\
~ & \textcolor{red}{ \text{ Добавить:}}=12+15 \\
~ & \textcolor{red}{ \text{ Sum:}}=27 \\
\end{aligned}\nonumber \]
Обратите внимание, что вычисление 3 · (4 + 5) с использованием свойства распределения дает тот же результат как оценка (2. 1) с использованием порядка операций.
1) с использованием порядка операций.
Мультипликативное свойство нуля
Распределительное свойство можно использовать для доказательства ряда важных свойств целых чисел. Одним из важных свойств является тот факт, что если вы умножаете целое число на ноль, произведение равно нулю. Вот доказательство этого факта, использующее дистрибутивное свойство.
Пусть a — любое целое число. Затем
\[ \begin{aligned} a \cdot 0 = a \cdot (0 + 0) ~ & \textcolor{red}{ \text{ Аддитивное свойство идентичности: = 0 + 0 = 0.}} \\ a \cdot 0 = a \cdot 0 + a \cdot 0 ~ & \textcolor{red}{ \text{ Распределить } a \text{ умножить каждый ноль в скобках.}} \end{aligned}\nonumber \]
Затем, чтобы «отменить» эффект сложения и · 0, вычтите и · 0 из обеих частей уравнения.
\[ \begin{align} a \cdot 0 — a \cdot 0 = a \cdot 0 + a \cdot 0 + a \cdot 0 — a \cdot 0 ~ & \textcolor{red}{ \text{ Вычесть } a \cdot 0 \text{ с обеих сторон.}} \\ 0 = a \cdot 0 ~ & \textcolor{red}{ a \cdot 0 — a \cdot 0 = 0 \text{ с каждой стороны. }} \end{выровнено}\nonumber \]
}} \end{выровнено}\nonumber \]
Мультипликативное свойство нуля
Пусть и представляют любое целое число. Тогда
a · 0 = 0 и 0 · a = 0.
Таким образом, например, −18 · 0 = 0 и 0 · 122 = 0.
Умножение на минус один
Вот еще полезное применение распределительного свойства.
\[ \begin{aligned} (-1) a + a = (-1)a + 1a ~ & \textcolor{red}{ \text{ Замените } a \text{ на } 1a.} \\
= (-1 + 1)a ~ & \textcolor{red}{ \text{ Используйте свойство дистрибутивности, чтобы выделить } a.} \\
=0a ~ & \textcolor{red}{ \text{ Заменить } -1+1 \text{ на } 0.} \\
=0~ & \textcolor{red}{ \text{ Заменить } 0a \text{ с 0.}} \end{aligned}\nonumber \]
Таким образом, (−1) a + a = 0. То есть, если вы добавите (−1) a к a , вы получить ноль. Однако аддитивное обратное свойство говорит, что — a — это уникальный номер , который вы добавляете к a , чтобы получить ноль. Вывод должен заключаться в том, что (−1) a = − и . Умножение на минус один −1(−4) = −(−4) = 4.
Вывод должен заключаться в том, что (−1) a = − и . Умножение на минус один −1(−4) = −(−4) = 4.
Это свойство весьма важно, как мы увидим в дальнейшей работе. Это не только говорит нам, что (-1) a = — a , но также говорит нам, что если мы видим — a , то это можно интерпретировать как означающее (-1) a .
Произведение двух отрицательных целых чисел
Мы можем использовать мультипликативное свойство -1, то есть (-1) a = — a , чтобы найти произведение двух отрицательных чисел.
\[ \begin{align} (-4)(-3) = [(-1)(4)](-3) ~ & \textcolor{red}{ \text{ Заменить } -4 \text{ на } (-1)(4).} \\ =(-1)[(4)(-3)] ~ & \textcolor{red}{ \text{ Используйте свойство ассоциативности для перегруппировки.}} \\ = ( -1)(-12) ~ & \textcolor{red}{ \text{ Мы знаем: } (4)(-3) = -12.} \\ = -(-12) ~ & \textcolor{red}{ (-1)а = -а. \text{ Здесь } (-1)(-12) = -(-12).} \\ =12 ~ & \textcolor{red}{ -(-a) = a. \text{ Здесь } -(-12) = 12.} \end{aligned}\nonumber \]
\text{ Здесь } -(-12) = 12.} \end{aligned}\nonumber \]
Таким образом, по крайней мере в случае (−4)(−3) произведение двух отрицательных целых чисел является положительным целым числом. Это верно в целом.
Произведение двух целых отрицательных чисел
Если оба числа a и b являются отрицательными целыми числами, то их произведение ab является положительным целым числом.
Таким образом, например, (−5)(−7) = 35 и (−112)(−6) = 672. В каждом случае ответ положительный, потому что произведение двух отрицательных целых чисел является положительным целым числом.
Запоминающее устройство
Вот простое запоминающее устройство, помогающее запомнить правила нахождения произведения двух целых чисел.
Похожие и непохожие знаки
Возможны два случая:
Непохожие знаки . Произведение двух целых чисел с разными знаками отрицательно. То есть:
(+)(-) = —
(-)(+) = —
Подобные знаки . Произведение двух целых чисел с одинаковыми знаками положительно. То есть:
Произведение двух целых чисел с одинаковыми знаками положительно. То есть:
(+)(+) = +
(-)(-)=+
Пример 1
Упростите: (a) (−3)(−2), (b) (4)(−10) и (c) (12)(−3).
Решение
В каждом примере мы используем подход знаков «нравится» и «не нравится».
а) Подобные знаки дают положительный результат. Следовательно, (−3)(−2) = 6,
б) В отличие от знаков дает отрицательный результат. Следовательно, (4)(−10) = −40.
в) В отличие от знаков дает отрицательный результат. Следовательно, (12)(−3) = −36.
Упражнение
Упростите: (a) (−12)(4) и (b) (−3)(−11).
- Ответить
(а) −48, (б) 33
Пример 2
Упростить (−3)(2)(−4)(−2).
Решение
Порядок действий требует, чтобы мы работали слева направо.
\[ \begin{align} (-3)(2)(-4)(-2) = (-6)(-4)(-2) ~ & \textcolor{red}{ \text{ Работа слева вправо: } (-3)(2) = -6. } \\ = (24)(-2) ~ & \textcolor{red}{ \text{ Работаем слева направо: } (-6)(-4 ) = 24.} \\ =-48 ~ & \textcolor{red}{ \text{ Умножить: } (24)(-2) = -48.} \end{aligned}\nonumber \] 94 = (-3)(-3)(-3)(-3) ~ & \textcolor{red}{ \text{ Напишите } -3 \text{ как множитель четыре раза.}} \\ =9(- 3)(-3) ~ & \textcolor{red}{ \text{ Работаем слева направо: } (-3)(-3) = 9.} \\ =-27(-3) ~ & \textcolor{red }{ \text{ Работа слева направо: } 9(-3) = -27.} \\ = 81 \end{aligned}\nonumber \]
} \\ = (24)(-2) ~ & \textcolor{red}{ \text{ Работаем слева направо: } (-6)(-4 ) = 24.} \\ =-48 ~ & \textcolor{red}{ \text{ Умножить: } (24)(-2) = -48.} \end{aligned}\nonumber \] 94 = (-3)(-3)(-3)(-3) ~ & \textcolor{red}{ \text{ Напишите } -3 \text{ как множитель четыре раза.}} \\ =9(- 3)(-3) ~ & \textcolor{red}{ \text{ Работаем слева направо: } (-3)(-3) = 9.} \\ =-27(-3) ~ & \textcolor{red }{ \text{ Работа слева направо: } 9(-3) = -27.} \\ = 81 \end{aligned}\nonumber \]
Упражнение
Упрощение: (a) (−2) 2 и (б) −2 2 .
- Ответить
(а) 4 и (б) −4
быстро оценивается как 64, поскольку имеет четное число отрицательных множителей.
Деление целых чисел
Предположим, что
\(\frac{12}{3} = 4\), поскольку \(3(4) = 12\) и \(\frac{-12}{-3} = 4\), потому что \(-3(4) = -12\).
Аналогично,
\(\frac{12}{-3} = -4\), потому что -3(-4) = 12 и \(\frac{-12}{3} = -4\) потому что \(3(-4) = -12\).
Таким образом, правила деления целых чисел совпадают с правилами умножения целых чисел.
Подобие и отличие знаков
Есть два случая:
Отличие знаков. Частное двух целых чисел с в отличие от знаков отрицательно. То есть
\[ \begin{array} \frac{(+)}{(-)} = — \\ \frac{(-)}{(+)} = — \end{array}\nonumber \ ]
Похожие знаки. Частное двух целых чисел с одинаковыми знаками положительно. То есть
\[ \begin{array} \frac{(+)}{(+)} = + \\ \frac{(-)}{(-)} = + \end{array}\nonumber \ ]
Так, например, 12/(−6) = −2 и −44/(−4) = 11. В первом случае разные знаки дают отрицательное частное. Во втором случае одинаковые знаки дают положительное частное.
Последнее напоминание.
Деление на ноль не определено
Если a является любым целым числом, то частное
\[ \frac{a}{0}\nonumber \]
не определено. Деление на ноль бессмысленно.
См. описание деления на ноль в Разделе 1. 3.
3.
Пример 4
Упростите: (a) −12/(−4), (b) 6/(−3) и (c) −15/0.
Решение
В каждом примере мы используем подход знаков «нравится» и «не нравится».
а) Подобные знаки дают положительный результат. Следовательно,
\[ \frac{-12}{-4} = 3.\nonumber \]
б) В отличие от знаков дает отрицательный результат. Следовательно,
\[ \frac{6}{-3} = -2.\nonumber \]
c) Деление на ноль не определено. Следовательно,
\[ \frac{-15}{0}\nonumber \]
не определено.
Упражнение
Упростите: (a) −24/4 и (b) −28/(−7).
- Ответить
(а) −6, (б) 4
Упражнения
В упражнениях 1-16 сформулируйте свойство умножения, описываемое данным тождеством.
1. (−2) (−16)(13) = (−2)(−16) (13)
2. (10) (−15)(−6) = (10)(−15) (−6)
3. (−17)(−10) = (−10)(−17)
4. (−5)(3) = (3)(−5)
5. (4 )(11) = (11)(4)
6. (−5)(−11) = (−11)(−5)
(−5)(−11) = (−11)(−5)
7. 16 · (8 + (−15) = 16 · 8 + 16 · (−15)
8. 1 · (−16 + (−6) = 1 · (−16) + 1 · (−6)
9. (17) (20)(11) = (17 )(20) (11)
10. (14) (-20)(-18) = (14)(-20) (-18)
11. -19 · 1 = -19
12. -17 · 1 = -17
13. 8 · 1=8
14. −20 · 1 = −20
15. 14 · (−12 + 7 = 14 · (−12) + 14 · 7
16. −14 · (− 3+6 = −14 · (−3) + (−14) · 6
В упражнениях 17–36 упростите каждое заданное выражение:
17, 4 · 7
18, 4 · 2
19. 3 · (−3)
20. 7 · (−9)
21. −1 · 10
22. −1 · 11
23. -1 · 0
24. -8 · 0
25. -1 · (-14)
26. -1 · (-13)
27. -1 · (-19)
28. −1 · (−17)
29. 2 · 0
30. −6 · 0
31. −3 · 8
32. 7 · (−3)
33. 7 · 9
34. 6 · 3
35. −1 · 5
36. −1 · 2
В упражнениях 37–48 упростите каждое заданное выражение.
37. (-7)(-1)(3)
38. (10)(6)(3)
(10)(6)(3)
39. (-7)(9)(10)(-10)
40. (-8)(-5)(7)(-9)
41. (6)(5)(8)
42. (7)(-1)(-9)
43 , (−10)(4)(−3)(8)
44. (8)(−2)(−5)(2)
45. (6)(−3)(−8)
46. (−5)(−4)(1)
47. (2)(1)(3)(4)
48. (7)(5)(1)(4)
В упражнениях 49-60, вычислите точное значение.
49. (−4) 4
50. (−3) 4
51. (-5) 4
52. (-2) 2
9000 53. (−2) 2 9000 53. 53. (−2) 2 9000 53. 5) 254. (−3) 3
55. (−6) 2
56. (−6) 4
57. (−4) 5
57 57. (-4) 5 57 57. (-4) 5 57 57. (-4) 5 57. 57. (-4) 5 57. (−4) 259. (−5) 3
60. (−3) 2
В упражнениях 61–84 упростите каждое заданное выражение.
61. −16 ÷ (−8)
62. −33 ÷ (−3)
63. \( \frac{-8}{1}\)
64. \(\frac{40} {-20}\)
65. \(\frac{-1}{0}\)
66. \(\frac{2}{0}\
67. −3 ÷ 3
68. −58 ÷ 29
69. \(\frac{56}{-28}\)
70. \(\frac{60}{-12}\)
71. 0 ÷ 15
72. 0 ÷ (−4)
73. \(\frac{63}{21}\)
74. \(\frac{-6}{-1}\)
75. \(\frac{78}{13}\)
76. \(\frac{-84}{-14}\)
77. 0 ÷ 5
78. 0 ÷ (−16)
79. \(\frac{17}{0}\)
80. \(\frac{-20}{0}\)
81. −45 ÷ 15
82. −28 ÷ 28
83. 12 ÷ 3
84. −22 ÷ (−22)
85. Акваланг . Дайвер опускается на 25 футов. Затем второй ныряльщик ныряет в 5 раз дальше, чем первый ныряльщик. Запишите конечную глубину второго ныряльщика в виде целого числа.
86. Инвестиционный убыток . Клуб инвесторов из пяти друзей потерял на сделке 4400 долларов. Если они делят убытки поровну, запишите потери каждого члена как целое число.
Ответы
1. Ассоциативность умножения 9
7. Распределительное свойство умножения
9. Ассоциативное свойство умножения
11. Мультипликативное свойство тождества
17. 28
19. −9
21. -10
23. 0
25. 14
27. 19
29. 0
31. −24
33. 63
35. −5
37. 21
39. 6300
41. 240
43. 960
45. 144
47. 24
49. 256
51. 625
53. 25
55. 36
57. −1024
59. −125
61. 2
63. −8.
67. −1
69. −2
71. 0
73. 3
75. 6
77. 0
79. Деление на ноль не определено.
81. −3 83. 4
85. −125 футов
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Дэвид Арнольд
- Лицензия
- CC BY-NC-SA
- Показать страницу TOC
- нет
- Метки
- Переместительное свойство умножения
- Деление целых чисел
- Умножение целых чисел
- Свойство мультипликативной идентичности
Преобразование отрицательного числа в положительное
1. Умножение на минус единицу для преобразования положительного числа
Умножение на минус единицу для преобразования положительного числа
2. Преобразование в абсолютное число с помощью функции ABS
3. Множественное использование специальной вставки
4. Удаление отрицательного знака с помощью быстрого заполнения
5. Применить пользовательское форматирование для отображения в виде положительных чисел
6. Запустить код VBA для преобразования в положительные числа
7. Использовать Power Query для преобразования Получить положительные числа
Заключение
Другие уроки
И вы будете удивлены, что у меня есть 7 различных способов, которые вы можете использовать для работы с отрицательными числами. На прошлой неделе я получил электронное письмо от одного из моих подписчиков с вопросом.
Эй, Пунит, сколько у нас есть способов преобразовать отрицательное число в положительное?
Вы знаете, то, о чем он просил, это обычное задание. Я уверен, это часто происходит с вами, когда вы получаете какие-то отрицательные числовые значения, а после этого конвертируете их в положительные.
В этом нет никакой #ракетной науки. Но вы когда-нибудь проверяли, как мои разные методы у вас есть для этого? Что ж, мне всегда интересно узнать о различных методах выполнения задачи в Excel.
Итак, на этот раз я взял лист бумаги и перечислил все методы, которые я могу использовать для преобразования отрицательного числа в положительное. Итак, сегодня в этом посте я хотел бы поделиться с вами всеми этими методами.
Начнем.
1. Умножьте на минус единицу, чтобы преобразовать положительное число
В отличие от меня, если вы хорошо разбираетесь в математике, я уверен, что вы знаете, что когда вы перемножаете два знака минус друг с другом, результат всегда положительный. Таким образом, вы можете использовать тот же метод в Excel, чтобы преобразовать отрицательное число в положительное.
Все, что вам нужно сделать, это просто умножить отрицательное значение на -1, и оно вернет положительное число вместо отрицательного.
=negative_value*-1
Ниже у вас есть диапазон ячеек с отрицательными числами. Поэтому, чтобы преобразовать их в положительные, вам просто нужно ввести формулу в ячейку B2 и перетащить ее до последней ячейки.
Поэтому, чтобы преобразовать их в положительные, вам просто нужно ввести формулу в ячейку B2 и перетащить ее до последней ячейки.
Примечание: Если у вас есть смешанные числа (как положительные, так и отрицательные), вы можете использовать вместо этого метод, описанный ниже.
=ЕСЛИ(A1<0,A1*-1,A1)
2. Преобразование в абсолютное число с помощью функции ABS
Превратить отрицательное число в положительное с помощью ABS довольно просто. Эта функция специально для этой задачи.
Краткое введение: Может преобразовать любое число в абсолютное число. Проще говоря, он вернет число после удаления его знака.
Синтаксис: =ABS(число)
Вам просто нужно передать отрицательное число в функцию, и она превратит его в положительное значение.
- В приведенном ниже примере у вас есть отрицательные значения из диапазона A2:A11.
- Введите =ABS(A2) в ячейку B2 и перетащите ее до последней ячейки.

Примечание : Эта функция работает, даже если у вас смешанные числа (как положительные, так и отрицательные).
Давайте подумаем о другой ситуации, когда вместо получения положительных чисел в другом столбце они нужны в том же столбце.
Для этого можно использовать специальную опцию вставки. Интересно, как? Позвольте мне сказать вам. В специальной опции вставки есть опции «операции», которые вы можете использовать для выполнения некоторых простых вычислений. Вы можете использовать эти же параметры, чтобы сделать отрицательные числа положительными без использования какой-либо формулы или добавления дополнительного столбца. Просто выполните следующие действия.
- Прежде всего, в любой ячейке рабочего листа введите -1.
- После этого скопируйте его.
- Теперь выберите диапазон ячеек, в которых у вас есть отрицательные числа.
- Щелкните правой кнопкой мыши ➜ Специальная вставка ➜ Операции ➜ Умножение.
- В конце нажмите OK.

Теперь все отрицательные числа преобразуются в положительные.
Единственное, о чем вам нужно позаботиться, это то, что это не динамический метод. Таким образом, вам нужно делать это снова и снова, если вы часто обновляете свои данные. Но этот метод быстрый и простой в использовании, и вам не нужна никакая формула.
4. Удаление отрицательного знака с помощью мгновенного заполнения
Я уверен, что вы использовали флэш-заполнение хотя бы раз в жизни, а если нет, то вы должны его использовать, это меняет правила игры. Это безумный способ превратить отрицательные числа в положительные, вот шаги.
- Прежде всего, в ячейке B2 введите положительное число для отрицательного числа, которое у вас есть в ячейке A2.
- После этого подойдите к ячейке B3 и нажмите сочетание клавиш Ctrl + E.
- В этот момент в столбце B у вас все числа в положительной форме.
- Теперь нажмите на маленький значок справа от столбца B и выберите «Принять предложения».

Поздравляем, вы преобразовали все отрицательные числа в положительные с помощью быстрой заливки.
Примечание : Этот метод также не является динамическим, но быстрым и простым в использовании.
5. Применить пользовательское форматирование для отображения в виде положительных чисел
Также возможно, что вместо преобразования отрицательного числа вы просто хотите отобразить его как положительное число. И в этой ситуации можно использовать пользовательское форматирование. Вот шаги к этому.
- Прежде всего, выделите диапазон ячеек, который необходимо преобразовать в положительные числа.
- После этого нажмите сочетание клавиш Ctrl + 1. Откроются пользовательские параметры форматирования.
- Теперь перейдите в «Пользовательский» и в строке ввода введите «#,###;#,###».
- В конце нажмите OK.
Это покажет все отрицательные числа как положительные. Но на самом деле все это по-прежнему отрицательное число, просто изменено форматирование.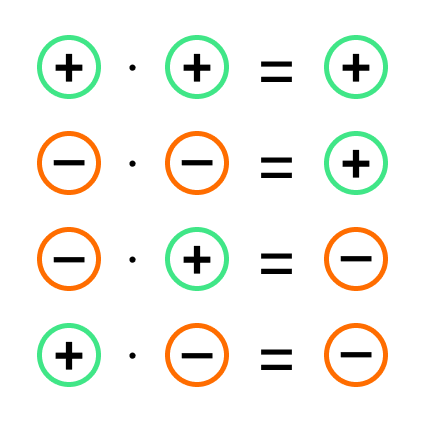
Если вы выберете ячейку и посмотрите на строку формул, вы можете убедиться, что это все еще отрицательное число. Таким образом, когда вы используете его в дальнейших вычислениях, оно будет действовать как отрицательное число.
6. Запустите код VBA для преобразования в положительные числа
Если вы любитель VBA, вы можете использовать простой код, чтобы мгновенно изменить знак отрицательных чисел.
Суб-номерP2N()
Dim myCell As Range
Для каждой выбранной ячейки myCell
Если myCell.Value <> "" Тогда
Если Числовой(myCell.Value) Тогда
myCell.Value = Abs(myCell.Value)
Конец, если
Конец, если
Следующая моя ячейка
End Sub Чтобы использовать этот код, вам просто нужно выбрать диапазон отрицательных чисел и запустить этот макрос. Во-первых, он проверит каждую выбранную ячейку, есть ли в ней числовое значение или нет, а затем преобразует его в положительное значение. Как только вы запустите этот код, вы не сможете отменить свое действие.
Связано: Учебное пособие по VBA
7. Используйте Power Query для преобразования. Получите положительные числа
Да, вы можете использовать запрос мощности для преобразования отрицательного числа в положительное число, и самое приятное то, что это одноразовая настройка. . Просто следуйте этим простым шагам.
- Прежде всего, выберите любую из ячеек из диапазона данных, где у вас есть отрицательные числа.
- После этого перейдите на вкладку Данные ➜ Из таблицы.
- Он преобразует диапазон в таблицу и загрузит ее в редакторе запросов.
- Теперь щелкните правой кнопкой мыши по столбцу и выберите Преобразование ➜ Абсолютное значение.
- В конце концов, в редакторе запросов питания перейдите на вкладку «Главная» ➜ «Закрыть» ➜ «Закрыть и загрузить».
Связано: Учебное пособие по Power Query
Заключение
Как я уже сказал, чтобы превратить отрицательное число в положительное, вам не нужно использовать ракетостроение.

 1.2. книги ().
1.2. книги ().

 — М.: Мнемозина, 2012.
— М.: Мнемозина, 2012.