Промежутки знакопостоянства функции. Нули функции
Числовые промежутки, на которых функция сохраняет свой знак (т.е. или ) называются промежутками знакопостоянства.
Значения аргумента при которых , называются нулями функции. Нули функции – это точки пересечения графика функции с осью Ох.
Пример 1.Найти область определения функции
Решение.
: (1)
Найдем соответствующее множество точек.
Неравенство равносильно неравенству
. Решая его, получаем (рис.1)
.
Условие
Рис.1
означает, что
, т.е. .
Приходим к заключению, что
. Получаем .
Таким образом система (1) равносильна системе
Значит .
Пример 2.Найти множество значений функции
Решение.
Найдем область определения функции.
: ;
;
.
Последнее условие выполняется только для . Вычисляем значение функции в этой точке: .
Значит .
Пример 3.Исследовать функцию на четность:
1) 2) 3)
Решение.
1. Замечаем, что для функция имеет . Значит, функция определена на симметричном множестве.
Рассмотрим ее значение для :
Поскольку выполняются оба условия четной функции, заключаем, что функция – четная.
2. Функция имеет .
Так как не является симметричным множеством, второе условие проверять нет необходимости. Эта функция не обладает свойством четности.
3. Очевидно, что функция имеет , т.е. определена на симметричном множестве и для нее
.
Оба условия нечетной функции выполняются, а потому данная функция является нечетной.
Пример 4.Пусть где . Причем, функция имеет период 2. Построить ее график.
Решение.
Построим график данной функции на (рис. 2).
Рис. 2
Исходя из определения периодической функции должно выполняться условие: , где .
Строим ее график, продолжая по периоду (рис. 3).
Рис. 3
Пример 5.Используя определение монотонной функции, найти значения а, при которых функция где монотонно возрастает.
Решение.Пусть . Функция монотонно возрастает, если выполняется или . Это означает, что
Поскольку , последнее неравенство выполняется, если , т.е .
Таким образом, функция возрастает для .
Пример 6.Дана функция
Определить промежутки знакопостоянства функции, нули функции. Построить график данной функции.
Решение. Так как на каждом из данных промежутков аналитические выражения, задающие функцию, определены в каждой точке, следовательно .
1. Исследуем функцию при . На данном промежутке функция принимает значение равное 1, т.е. она знакоположительна и нулей функции нет.
2. Пусть .
При таком условии функция задается формулой и . Функция знакоположительна. Здесь она имеет нуль .
3. Пусть .
Очевидно, что при этом условии , т.к. . Нулей функции на этом промежутке нет.
Построим график:
Если , строим часть прямой линии ;
Если – часть параболы ;
Если – часть прямой
Получили график заданной функции (рис.4).
Рис. 4
Таким образом, функция знакоположительна ; имеет нуль .
Задания
I уровень
1. 1. Найдите область определения функции:
1. Найдите область определения функции:
1) 2)
1.2. Исследуйте функцию на свойство четности:
1) 2)
1.3. Найдите множество значений функции
1.4. Для функции определите промежутки монотонности, нули, промежутки знакопостоянства. Постройте график функции.
II уровень
2.1. Найдите ОДЗ функции:
1) 2)
2.2. Найдите множество значений функции:
1) 2)
2.3. Задайте функцию аналитически:
1) линейную, если
2) квадратичную, если
2.4. Исследуйте функцию на четность:
1) 2)
2.5. Докажите, что функция:
1) убывает на
2) возрастает на
2.6. Исследуйте функцию на монотонность.
2.7. Пусть
Известно, что имеет период Т = 4. Постройте график функции.
III уровень
3. 1. Исследуйте функцию на четность. Найдите ее нули:
1. Исследуйте функцию на четность. Найдите ее нули:
1) 2)
3.2. Найдите нули функции, промежутки знакопостоянства, промежутки монотонности:
Постройте график.
3.3. Дана функция Найдите промежуток на котором она убывает.
3.4. Определите, при каком а функция является периодической.
3.5. Найдите если:
1) 2)
3.6. Определите, при каком значении аргумента значение функции равно –1.
3.7. Определите при каких значениях х график функции расположен выше графика функции
Дата добавления: 2016-07-27; просмотров: 11284; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Как определить знаки постоянства функции
Идёт приём заявок
Подать заявку
Для учеников 1-11 классов и дошкольников
Итак, мы познакомились с функцией, узнали, что такое область определения и область значений функции. Теперь рассмотрим свойства функций. Их существует много, однако, изучаются они постепенно. В 9 классе мы знакомимся с нулями функции, промежутками возрастания и убывания (монотонность) и промежутками знакопостоянства и чётностью (нечётностью) функции. Рассмотрим их подробно.
Теперь рассмотрим свойства функций. Их существует много, однако, изучаются они постепенно. В 9 классе мы знакомимся с нулями функции, промежутками возрастания и убывания (монотонность) и промежутками знакопостоянства и чётностью (нечётностью) функции. Рассмотрим их подробно.
Нулями функции называются значения независимой переменной (аргумента), при которых значение функции равно нулю. В графической интерпретации нулями функции являются абсциссы точек пересечения графика с осью абсцисс (осью х).
На графике нули функции: .
Для того, чтобы найти нули функции, заданной аналитически, необходимо решить уравнение: . Корни этого уравнения являются нулями функции.
Например, найти нули функции .
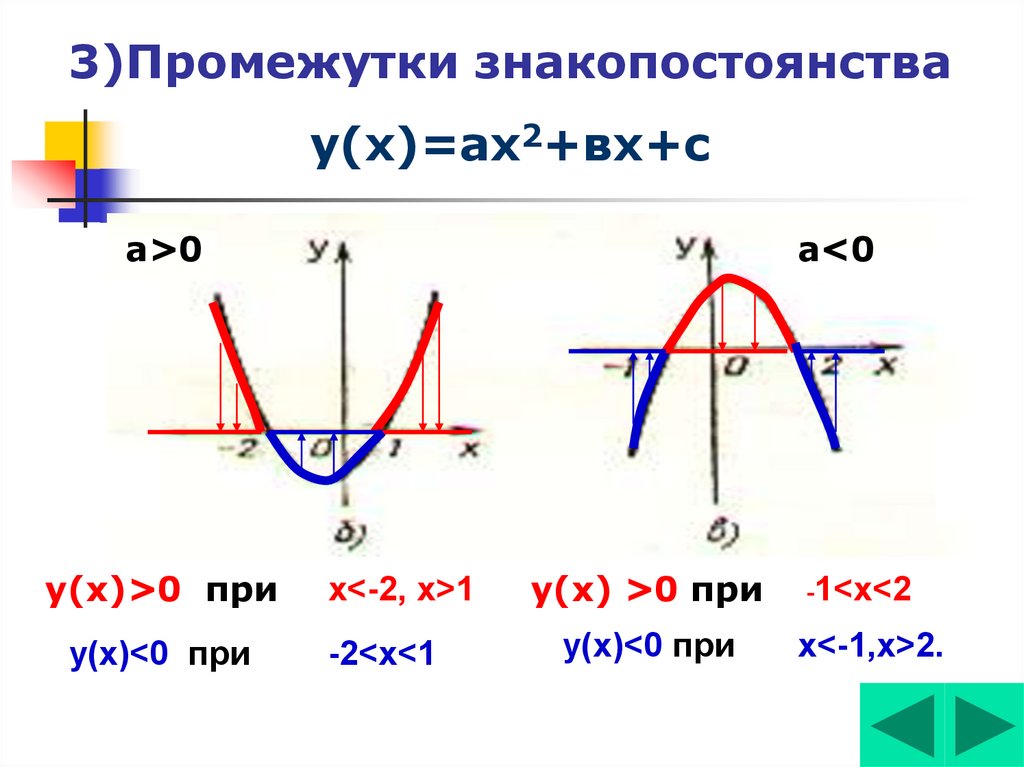
Промежутками знакопостоянства функции называются промежутки значений аргумента, на которых значения функции либо только положительны, либо только отрицательны. Другими словами, это те промежутки, на которых функция сохраняет свой знак.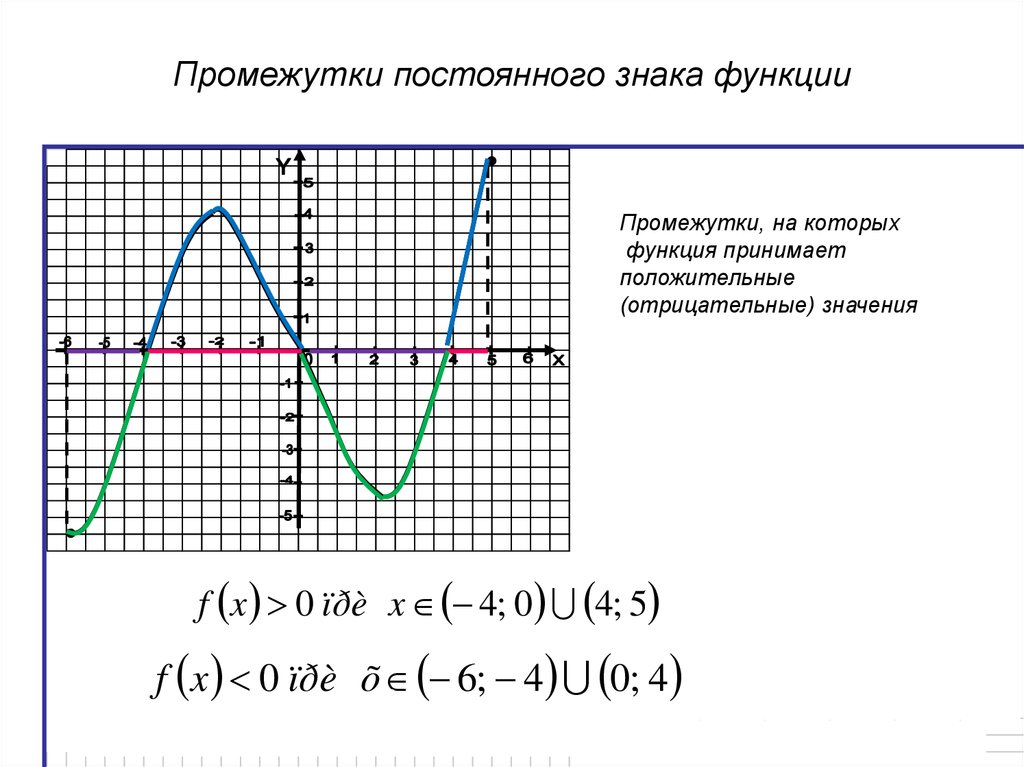
Рассматривая график сверху, найдём промежутки знакопостоянства.
функция принимает только положительные значения на тех участках графика, где он находится выше оси Ох, т.е. при ;
функция принимает только отрицательные значения на тех участках графика, где он находится ниже оси Ох, т.е. при .
Для того, чтобы найти промежутки знакопостоянства функции, заданной аналитически, необходимо решить неравенства: и . Решения этих неравенств и будут промежутками знакопостоянства функции.
Например, найти промежутки знакопостоянства функции .
Это неравенство можно решить двумя способами: с помощью систем неравенств и методом интервалов. Метод интервалов будет рассмотрен нами чуть позже, поэтому воспользуемся системами неравенств. Произведение двух множителей положительно, если эти множители имеют одинаковый знак. Значит, получается совокупность двух систем:
Теперь находим промежутки, на которых функция принимает отрицательные значения.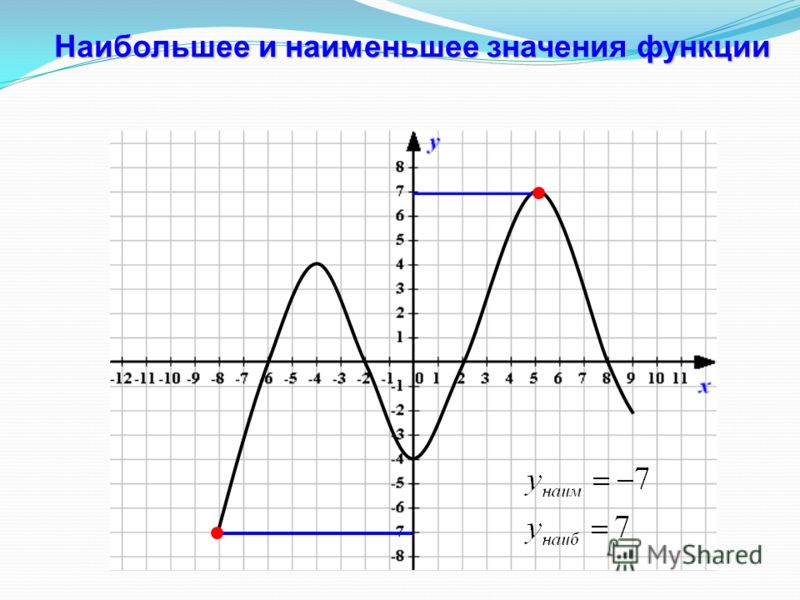
Произведение двух множителей отрицательно, если эти множители имеют разные знаки, т.е.
Чётной называется функция, если противоположным значениям аргумента соответствуют одинаковые значения функции, т.е. . График чётной функции симметричен относительно оси ординат (оси Оу).
Нечётной называется функция, если противоположным значениям аргумента соответствуют противоположные значения функции, т.е. . График нечётной функции симметричен относительно начала координат.
На рисунке слева график чётной функции, на рисунке справа – нечётной функции.
Для того, чтобы определить чётность функции, заданной аналитически, необходимо в заданную функцию вместо х подставить –х и произвести упрощение. Если в результате получится функция, равная заданной, то функция чётная; если получится функция, противоположная заданной, то она нечётная; если не получится ни один из предложенных вариантов, то функция не является ни чётной, ни нечётной.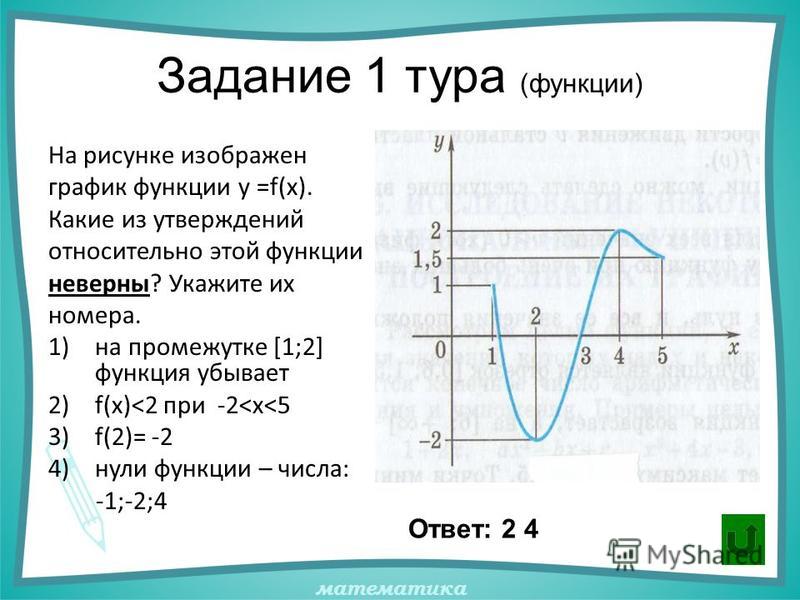
Например, исследовать на чётность функцию .
Находим значение этой функции при противоположном значении х, т.е.
Полученное выражение не совпадает с заданным и не противоположно ему, значит, функция не является ни чётной, ни нечётной. Её график не симметричен относительно оси Оу и не симметричен относительно начала координат.
Приведём ещё один пример: .
После упрощения получили выражение, полностью совпадающее с заданным. Значит, функция является чётной и её график симметричен относительно начала координат.
Функция называется возрастающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции (или меньшему значению аргумента соответствует меньшее значение функции), т.е. если при
Функция называется убывающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции (или меньшему значению аргумента соответствует большее значение функции), т.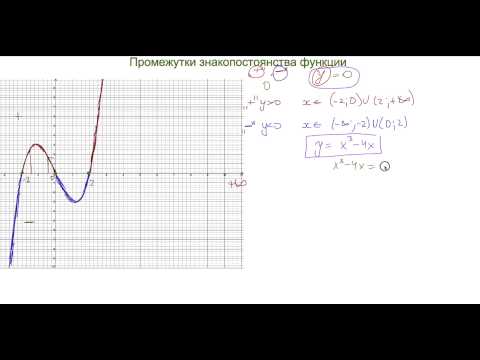 е. если при , то функция убывающая.
е. если при , то функция убывающая.
Для примера рассмотрим графики на рисунках выше.
Синий график: функция возрастает при
функция убывает при
Зелёный график: функция возрастает при
функция убывает при
Промежутки возрастания и убывания функции называются промежутками монотонности функции.
Если функция задана аналитически, то нахождение промежутков монотонности является более сложным процессом и он изучается в 11 классе. Мы ограничимся определением этих промежутков по графикам.
Наибольшим значением функции называется самое большое значение функции по сравнению со всеми остальными.
Наименьшим значением функции называется самое маленькое значение функции по сравнению со всеми остальными.
Строгое определение наибольшего и наименьшего значения функции будет дано в старших классах.
На синем графике наибольшего значения нет, т. к. график бесконечен в положительном направлении оси Оу. А наименьшее значение равно . Записывается это так: .
к. график бесконечен в положительном направлении оси Оу. А наименьшее значение равно . Записывается это так: .
На зелёном графике нет ни наибольшего, ни наименьшего значения функции.
На рисунках изображены части графиков нечётных функций. Достройте эти графики.
Аналитический способ.
Аналитический способ — это наиболее часто встречающийся способ задания функции.
Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у.
Графический способ.
При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом .
Словесный способ.
Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.
«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».
Табличный способ.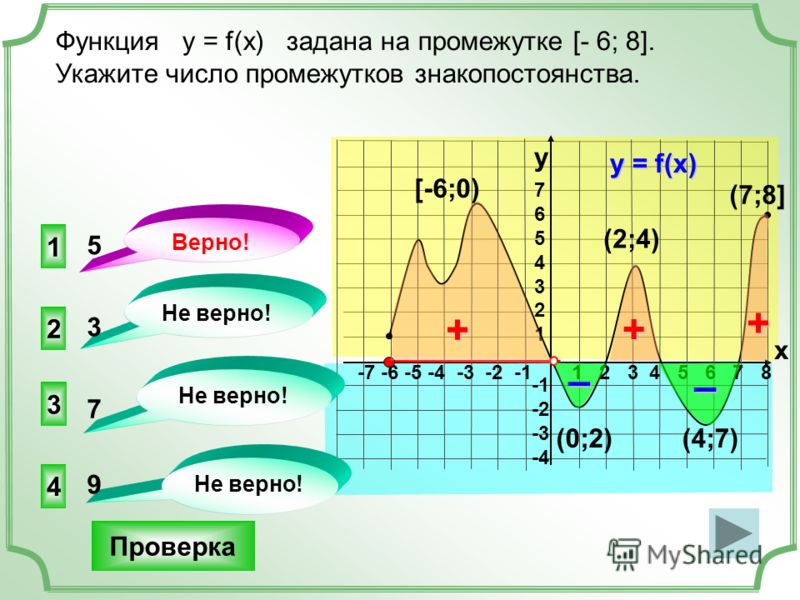
Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.
Типы ф-й
Сложная
Сложная функция — это функция от функции
Неявная
Неявные функции — это функции, заданные уравнением, не разрешенным относительно зависимой переменной.
Обратная
Если уравнение y=f(x) может быть однозначно разрешено относительного переменного x (т.е. сущ. Ф-я x=g(y) такая, что y=f[g(y)]), то ф-я x=g(y) – обратная по отношению к y=f(x).
Основные свойства функций.
1) Область определения функции и область значений функции.
Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
Область значений функции — это множество всех действительных значений y, которые принимает функция.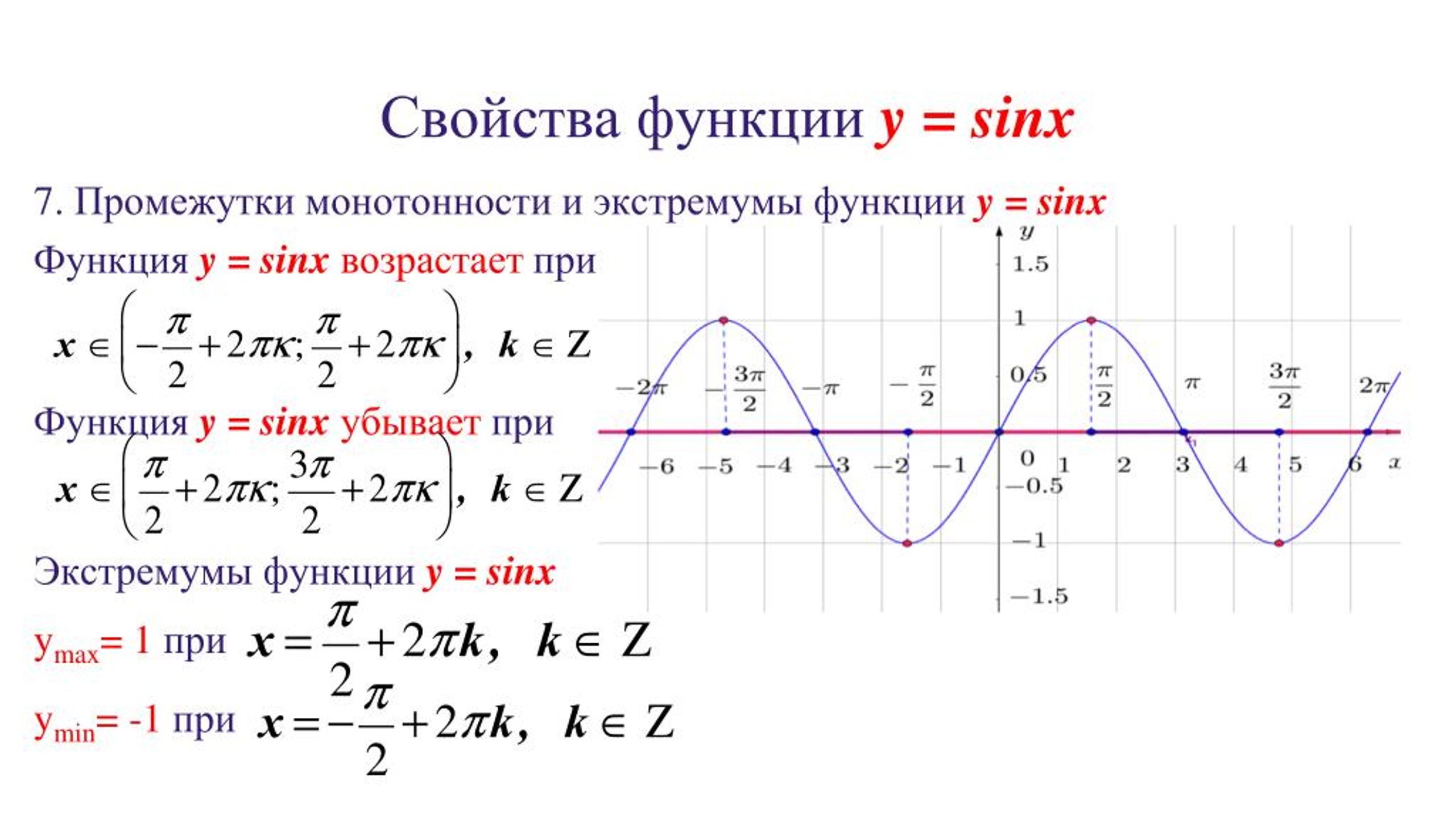
Нули функции.
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
Монотонность функции.
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Четность (нечетность) функции.
Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.
Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = — f(x).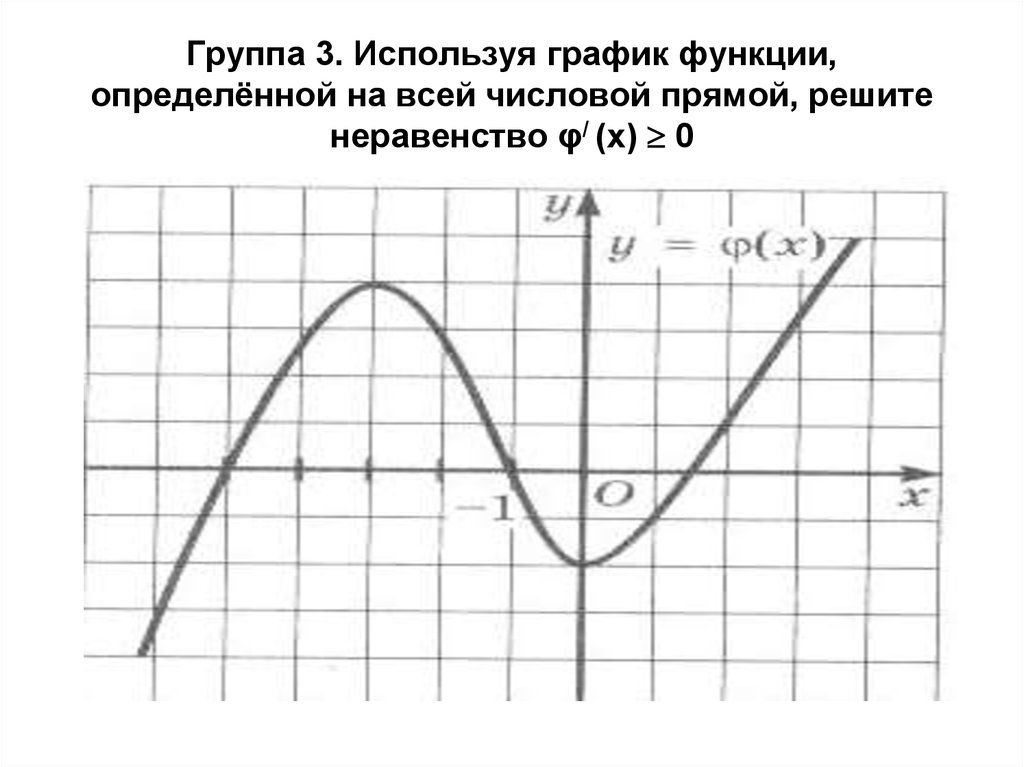 График нечетной функции симметричен относительно начала координат.
График нечетной функции симметричен относительно начала координат.
Ограниченная и неограниченная функции.
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция — неограниченная.
Периодическость функции.
Функция f(x) — периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
Предел ф-ии
Предел ф-ии (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.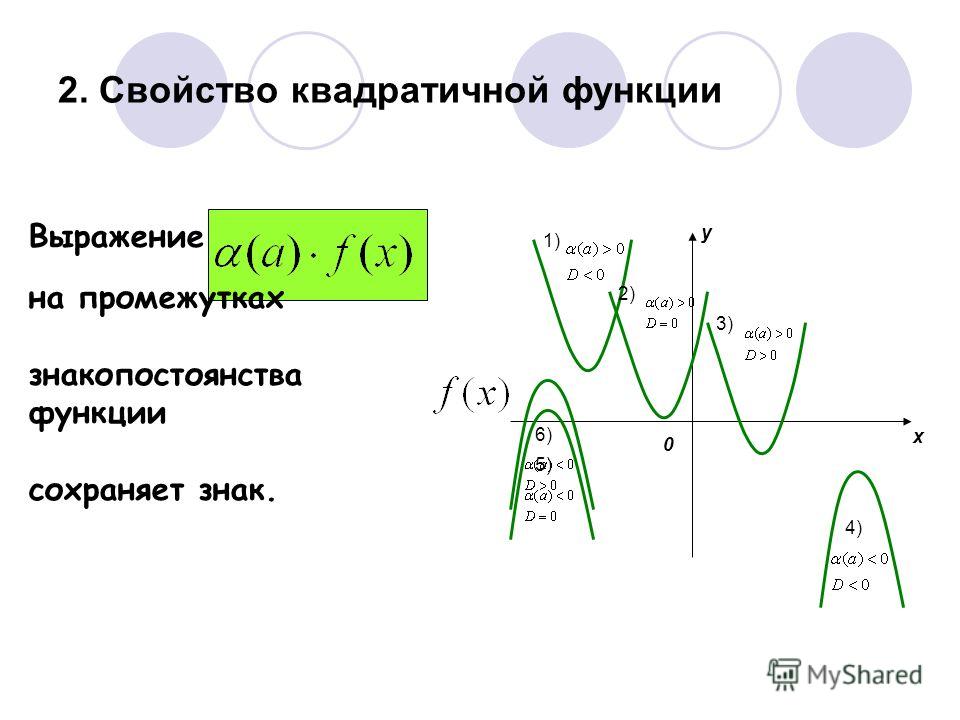
Последовательность an называется бесконечно малой, если
Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
Последовательность an называется бесконечно большой, если
Первый замечательный предел
Второй замечательный предел
Непрерывность ф-ии
Ф-яf(x) называется непрерывной при x = E, если
1) Эта ф-я определена в точке E, т.е. существует число f(E)
2) Существует конечный предел limf(x)
3) Этот предел равен значению ф-ии в точкеE, т.е. x -> E.
Точки разрыва
Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.
Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.
Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Производная сложной функции
Рассмотрим сложную функцию y = y(u(x))
Теорема 4. Если функции y = y(u), u = u(x) дифференцируемы (т.е. существуют производные y’u, u’x), тогда сложная функция y = y(u(x)) дифференцируема и y’x = y’u u’x.
Доказательство
Если аргумент x получит приращение Δx, то функция u получит приращение Δu = u(x + Δx) − u(x), а функция y получит приращение Δy = y(u + Δu) − y(u). Но тогда, воспользовавшись свойствами предела функции, получаем
Теорема доказана.
Доказательство
Если аргумент x получит приращение Δx, то функция f получит приращение Δy = f(x + Δx) − f(x).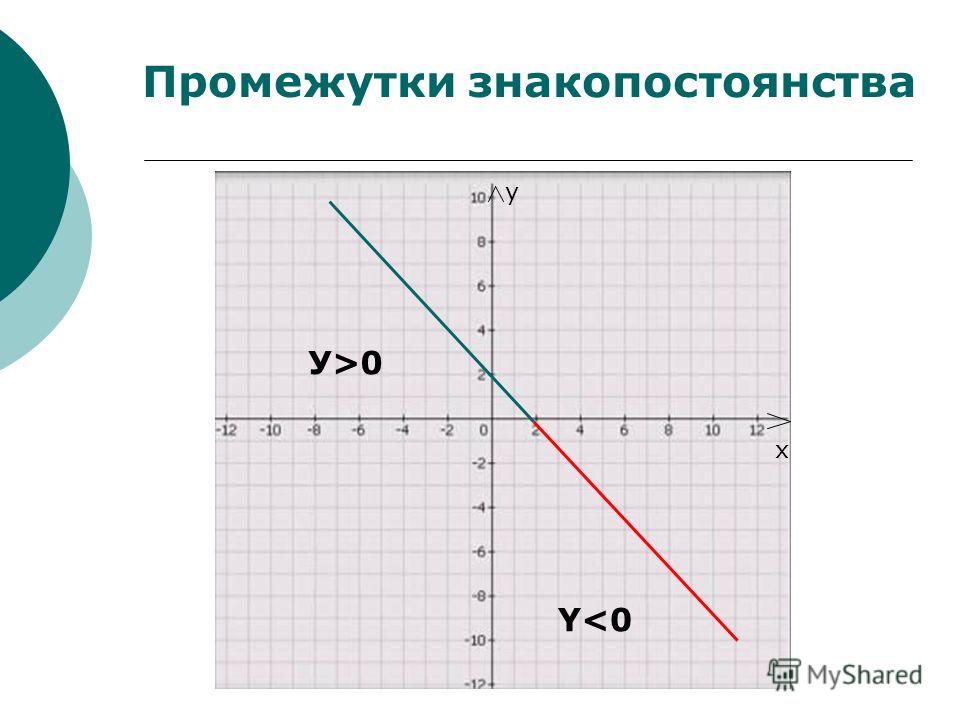 С другой стороны, для обратной функции g приращения Δx, Δy связаны следующим образом:Δx=g(y + Δy) − g(y).
С другой стороны, для обратной функции g приращения Δx, Δy связаны следующим образом:Δx=g(y + Δy) − g(y).
Теорема доказана.
Производные высших порядков
Дифференцируемость функции
Функция y=f(x)называется дифференцируемой в некоторой точке x0, если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.
Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что онадифференцируема на отрезке [а; b] или соответственно в интервале (а; b).
Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.
Правило Лопиталя
Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть или .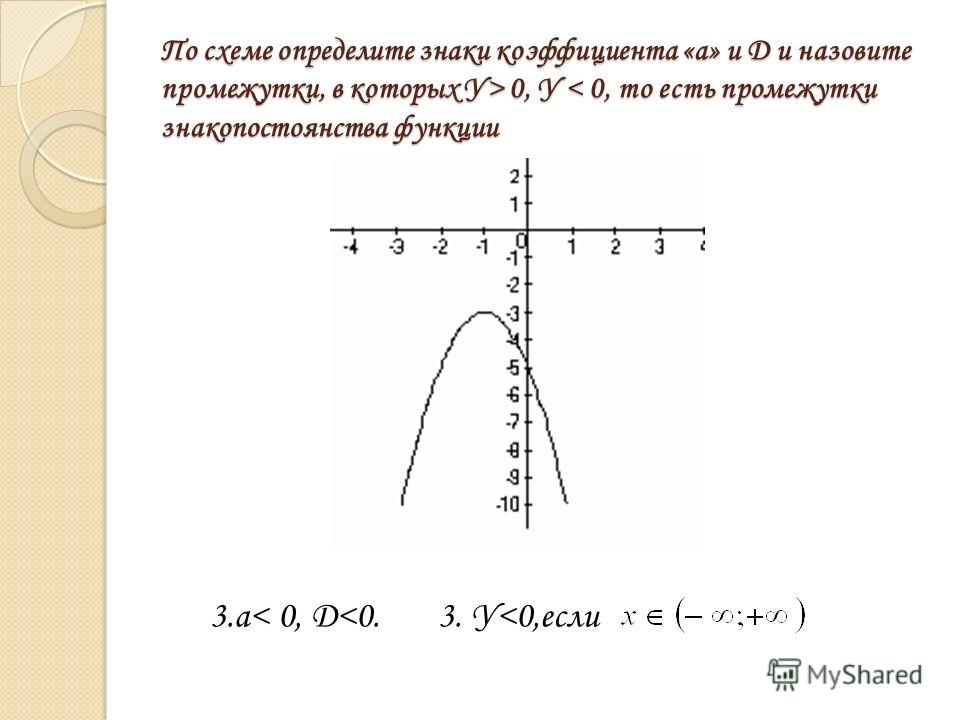 Тогда, если существует предел отношения производных этих функций , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
Тогда, если существует предел отношения производных этих функций , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
| (1) |
Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.
Например, найти . Этот предел существует . Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.
Заметим, что если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.
Вспомним, что к этим двум случаям сводятся случаи других неопределенностей: ∞·∞; 0·∞.
Для раскрытия неопределенностей 1∞, 10, ∞0 нужно прологарифмировать данную функцию и найти предел ее логарифма.
Монотонность ф-ии
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Экстремумы
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках — ее экстремумами.
Первое достаточное условие.
Пусть xо — критическая точка. Если f ‘ (x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае — минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.
Второе достаточное условие.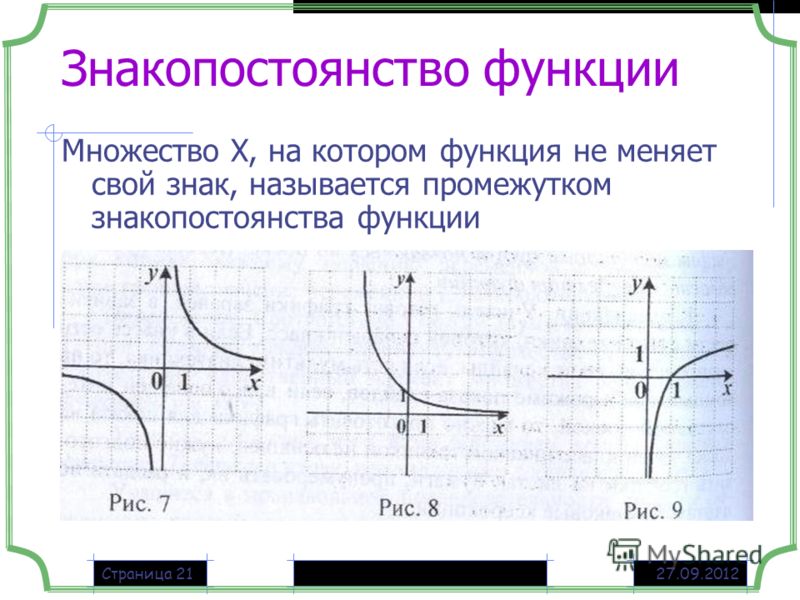 Пусть функция f(x) имеет производную
Пусть функция f(x) имеет производную
f ‘ (x) в окрестности точки xо и вторую производную f»(xo) в самой точке xо. Если f ‘(xо) = 0, f»(xo)>0 (f»(xo) 0 при x > x0. Тогда при x x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f »(x) > 0 при x x0.
Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.
Асимптоты графика функции
Прямая называется асимптотой графика функции y = f(x), если расстояние от переменной точки M графика до этой прямой при удалении точки M в бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении в бесконечность должна неограниченно приближаться к асимптоте.
Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее или с разных сторон, бесконечное множество раз пересекая асимптоту и переходя с одной ее стороны на другую.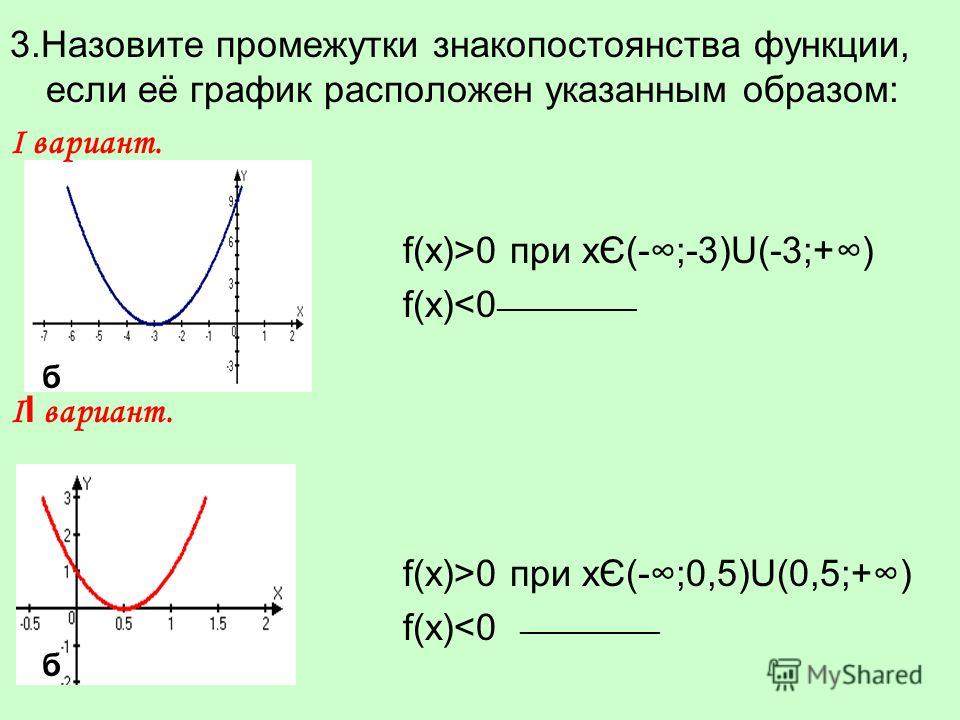
Формула Тейлора
Формула Тейлора показывает поведение функции в окрестности некоторой точки. Формула Тейлора функции часто используется при доказательстве теорем в дифференциальном исчислении.
ФОРМУЛА ТЕЙЛОРА
, где Rn(x) — остаточный член формулы Тейлора.
Аналитический способ.
Аналитический способ — это наиболее часто встречающийся способ задания функции.
Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у.
Графический способ.
При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом .
Словесный способ.
Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.
«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».
Табличный способ.
Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.
Типы ф-й
Сложная
Сложная функция — это функция от функции
Неявная
Неявные функции — это функции, заданные уравнением, не разрешенным относительно зависимой переменной.
Обратная
Если уравнение y=f(x) может быть однозначно разрешено относительного переменного x (т.е. сущ. Ф-я x=g(y) такая, что y=f[g(y)]), то ф-я x=g(y) – обратная по отношению к y=f(x).
Основные свойства функций.
1) Область определения функции и область значений функции.
Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
Область значений функции — это множество всех действительных значений y, которые принимает функция.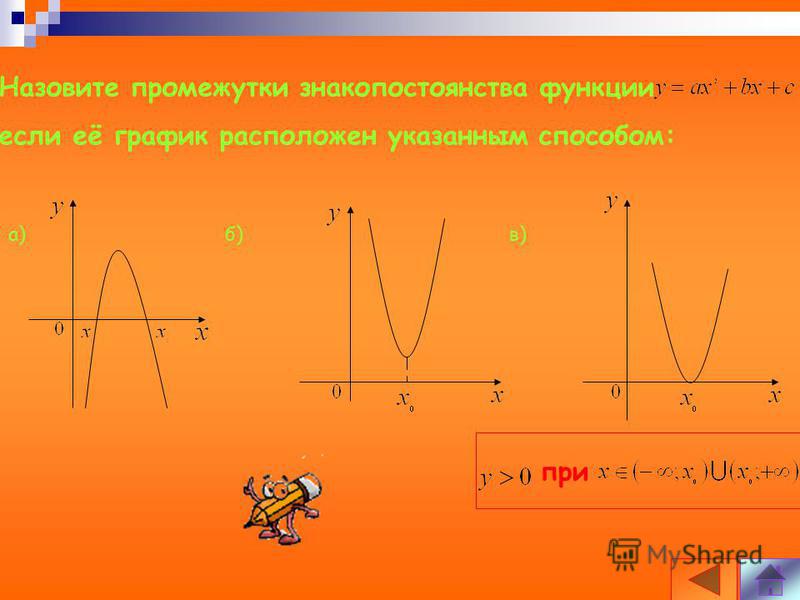
Нули функции.
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
Монотонность функции.
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Решение: Интервал знакопостоянства – это интервал, в каждой точке которого функция положительна либо отрицательна.
Существует следующий алгоритм метода интервалов :
- Находим область определения функции.
- Находим нули функции(точки пересечения графика с осью абсцисс).
- В большинстве заданий потребуется чертёж. Чертим ось и откладываем на ней точки разрыва (если они есть), а также нули функции (если они есть).
- Определяем знаки функции на интервалах, которые входят в область определения.
Теперь выполняем задание в указанном порядке:
1) x / (9 — x 2 ), видно, что (9 — x 2 ) ≠ 0, x 2 ≠ 9 , x1 ≠ — 3, x2 ≠ 3 ;
областью определения этой функции будут промежутки:
( -∞ ; — 3 ) ∪ (-3 ; 0) ∪ (0 ; 3) ∪ (3 ; ∞).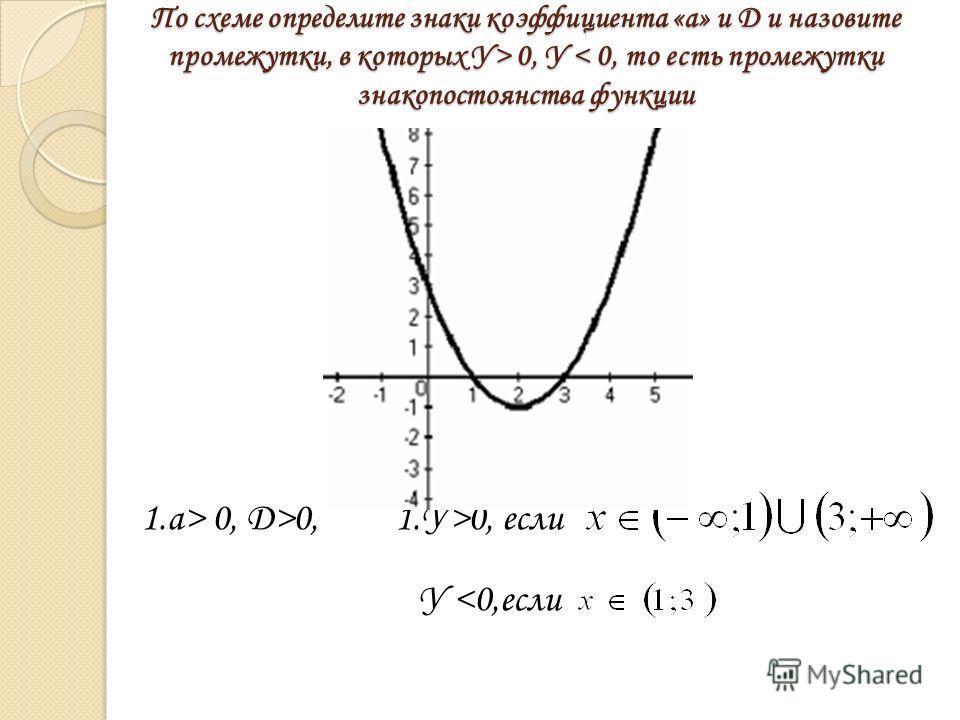
2) Находим нули функции. Для этого решаем уравнение .
В нашем случае: x / (9 — x 2 ) = 0; очевидно что x = 0
3) Откладываем все найденные точки на числовой оси OX точки:
Определяем знак функции на интервалах.
Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала.
Из ( -∞ ; — 3 ) берем число -4;
-4 / (9 – 16 ) = — 4 / — 7 > 0.; при x -> -∞ , f(x) -> ∞.
Из (-3 ; 0) выбери число -1;
Из (0 ; 3) выбери число 1;
1 / ( 9 – 1) > 0. при x -> 3 , f(x) -> ∞.
Из ( 3 ; ∞) выбери число 4;
Ответ: Промежутки знакопостоянства :
( -∞ ; — 3 ) ∪ (-3 ; 0) ∪ (0 ; 3) ∪ (3 ; ∞)
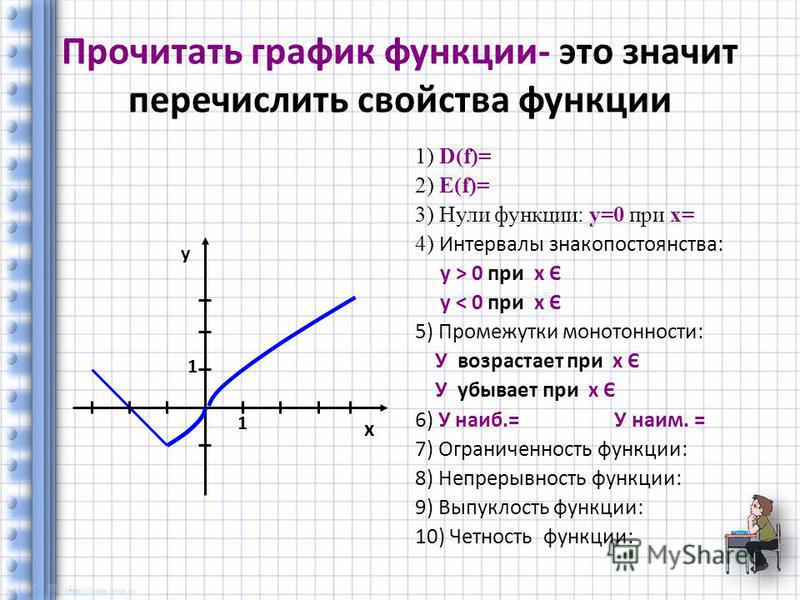
Свойства функции
В этой статье мы коротко суммируем сведения, которые касаются такого важного математического понятия, как функция. Мы поговорим о том, что такое числовая функция и какие свойства функции необходимо знать и уметь исследовать.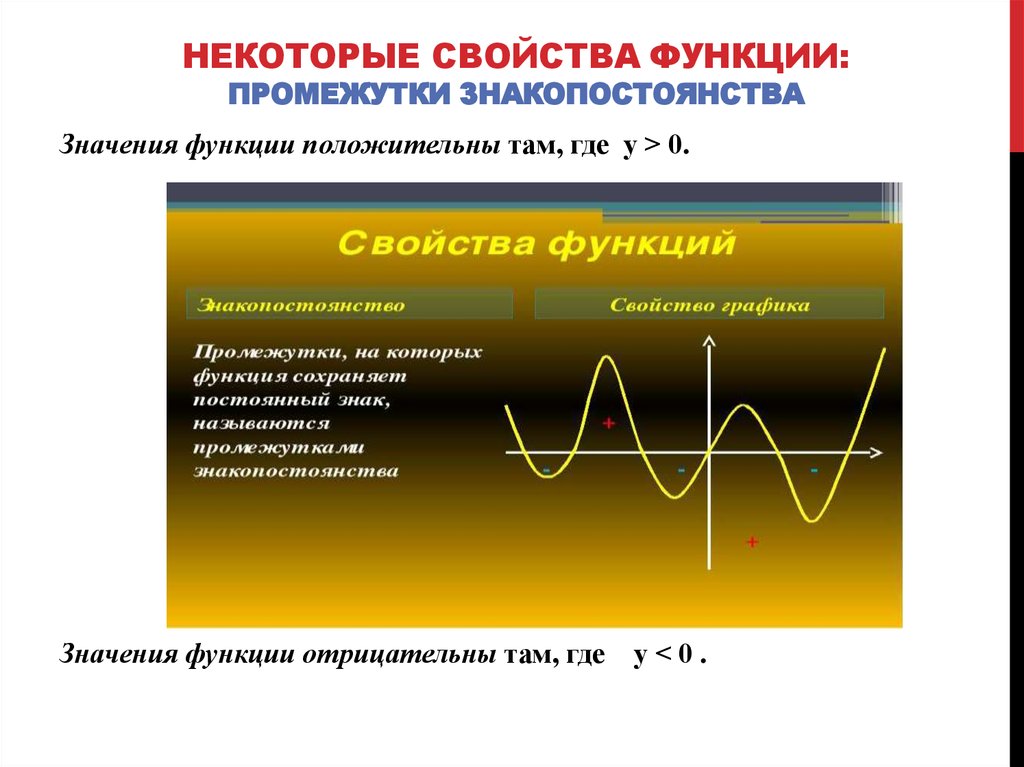
Что такое числовая функция? Пусть у нас есть два числовых множества: Х и Y, и между этими множествами есть определенная зависимость. То есть каждому элементу х из множества Х по определенному правилу ставится в соответствие единственный элемент y из множества Y.
Важно, что каждому элементу х из множества Х соответствует один и только один элемент y из множества Y.
Правило, с помощью которого каждому элементу из множества Х мы ставим в соответствие единственный элемент из множества Y, называется числовой функцией.
Множество Х называется областью определения функции.
Множество Y называется множеством значений значений функции.
Равенство называется уравнением функции. В этом уравнении — независимая переменная, или аргумент функции. — зависимая переменная.
Если мы возьмем все пары и поставим им в соответствие соответствующие точки координатной плоскости, то получим график функции. График функции — это графической изображение зависимости между множествами Х и Y.
График функции — это графической изображение зависимости между множествами Х и Y.
Свойства функции мы можем определить, глядя на график функции, и, наоборот, исследуя свойства функции мы можем построить ее график.
Основные свойства функций.
1. Область определения функции.
Область определения функции D(y)-это множество всех допустимых значений аргумента x ( независимой переменной x), при которых выражение, стоящее в правой части уравнения функции имеет смысл. Другими словами, это область допустимых значений выражения .
Чтобы по графику функции найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений х, на которых существует график функции.
2. Множество значений функции.
Множество значений функции Е(y)— это множество всех значений, которые может принимать зависимая переменная y.
Чтобы по графику функции найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений y, на которых существует график функции.
3. Нули функции.
Нули функции — это те значения аргумента х, при которых значение функции (y) равно нулю.
Чтобы найти нули функции , нужно решить уравнение . Корни этого уравнения и будут нулями функции .
Чтобы найти нули функции по ее графику, нужно найти точки пересечения графика с осью ОХ. Абсциссы точек пересечения и будут нулями функции .
4. Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции — это такие промежутки значений аргумента, на которых функция сохраняет свой знак, то есть или .
Чтобы найти промежутки знакопостоянства функции , нужно решить неравенства и .
Чтобы найти промежутки знакопостоянства функции по ее графику, нужно
- найти промежутки значений аргумента х, при которых график функции расположен выше оси ОХ — при этих значениях аргумента ,
- найти промежутки значений аргумента х, при которых график функции расположен ниже оси ОХ — при этих значениях аргумента .

5. Промежутки монотонности функции.
Промежутки монотонности функции — это такие промежутки значений аргумента х, при которых функция возрастает или убывает.
Говорят, что функция возрастает на промежутке I, если для любых двух значений аргумента , принадлежащих промежутку I таких, что выполняется соотношение:.
Другими словами, функция возрастает на промежутке I, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Чтобы по графику функции определить промежутки возрастания функции, нужно, двигаясь слева направо по линии графика функции, выделить промежутки значений аргумента х, на которых график идет вверх.
Говорят, что функция убывает на промежутке I, если для любых двух значений аргумента , принадлежащих промежутку I таких, что выполняется соотношение: .
Другими словами, функция убывает на промежутке I, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.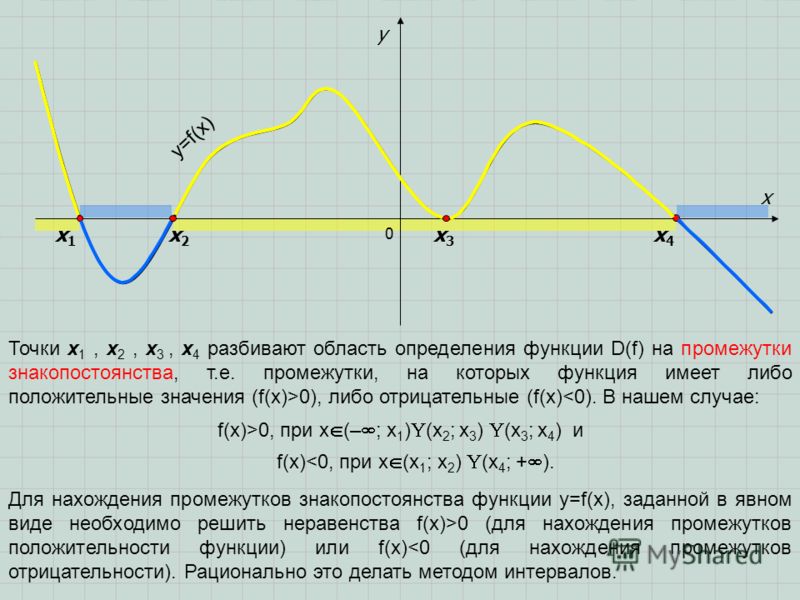
Чтобы по графику функции определить промежутки убывания функции, нужно, двигаясь слева направо вдоль линии графика функции, выделить промежутки значений аргумента х, на которых график идет вниз.
6. Точки максимума и минимума функции.
Точка называется точкой максимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:
.
Графически это означает что точка с абсциссой x_0 лежит выше других точек из окрестности I графика функции y=f(x).
Точка называется точкой минимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:
Графически это означает что точка с абсциссой лежит ниже других точек из окрестности I графика функции .
Обычно мы находим точки максимума и минимума функции, проводя исследование функции с помощью производной.
7. Четность (нечетность) функции.
Функция называется четной, если выполняются два условия:
а) Для любого значения аргумента , принадлежащего области определения функции, также принадлежит области определения функции.
Другими словами, область определения четной функции симметрична относительно начала координат.
б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение .
Функция называется нечетной, если выполняются два условия:
а) Для любого значения аргумента , принадлежащего области определения функции, также принадлежит области определения функции.
Другими словами, область определения нечетной функции симметрична относительно начала координат.
б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение .
Все функции делятся на четные, нечетные, и те, которые не являются четными и не являются нечетными. Они называются функциями общего вида.
Чтобы определить четность функции, нужно:
а). Найти область определения функции , и определить, является ли она симметричным множеством.
Если, например, число х=2 входит в область определения функции, а число х=-2 не входит, то D(y) не является симметричным множеством, и функция — функция общего вида.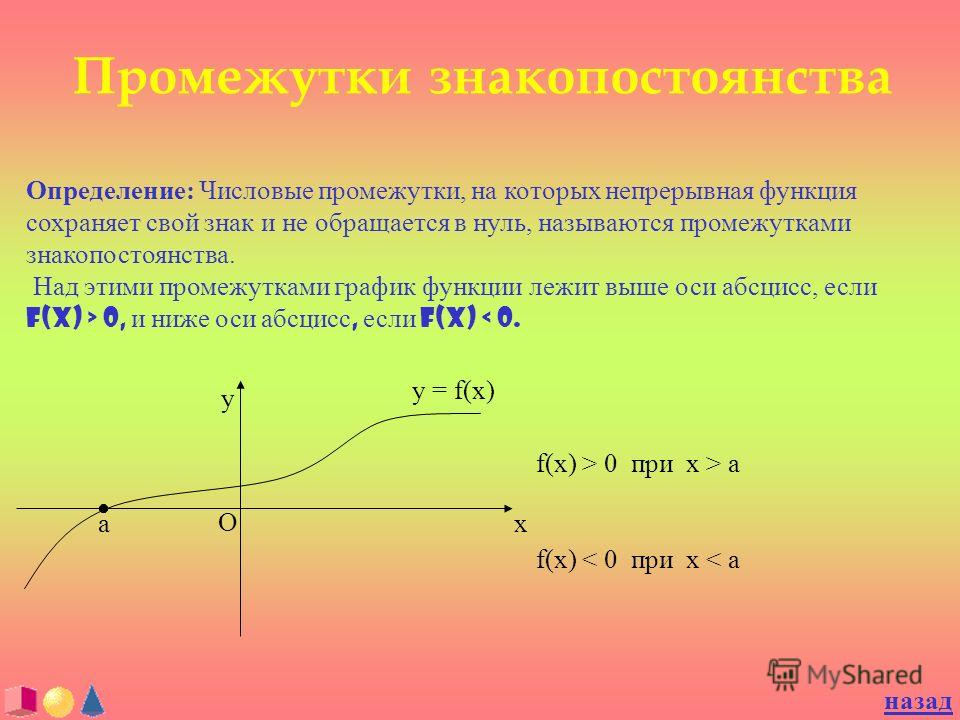
Если область определения функции — симметричное множество, то проверяем п. б)
б). В уравнение функции нужно вместо х подставить -х, упростить полученное выражение, и постараться привести его к виду или .
Если , то функция четная.
Если , то функция нечетная.
Если не удалось привести ни к тому ни к другому, то наша функция — общего вида.
График четной функции симметричен относительно оси ординат ( прямой OY ).
График нечетной функции симметричен относительно начала координат ( точки (0,0) ).
8. Периодичность функции.
Функция называется периодической, если существует такое положительное число Т, что
- для любого значения х из области определения функции, х+Т также принадлежит D(x)
В программе средней школы из числа периодических функций изучают только тригонометрические функции.
Предлагаю вам посмотреть ВИДЕОУРОК, в котором я рассказываю, как определить свойства функции по ее графику.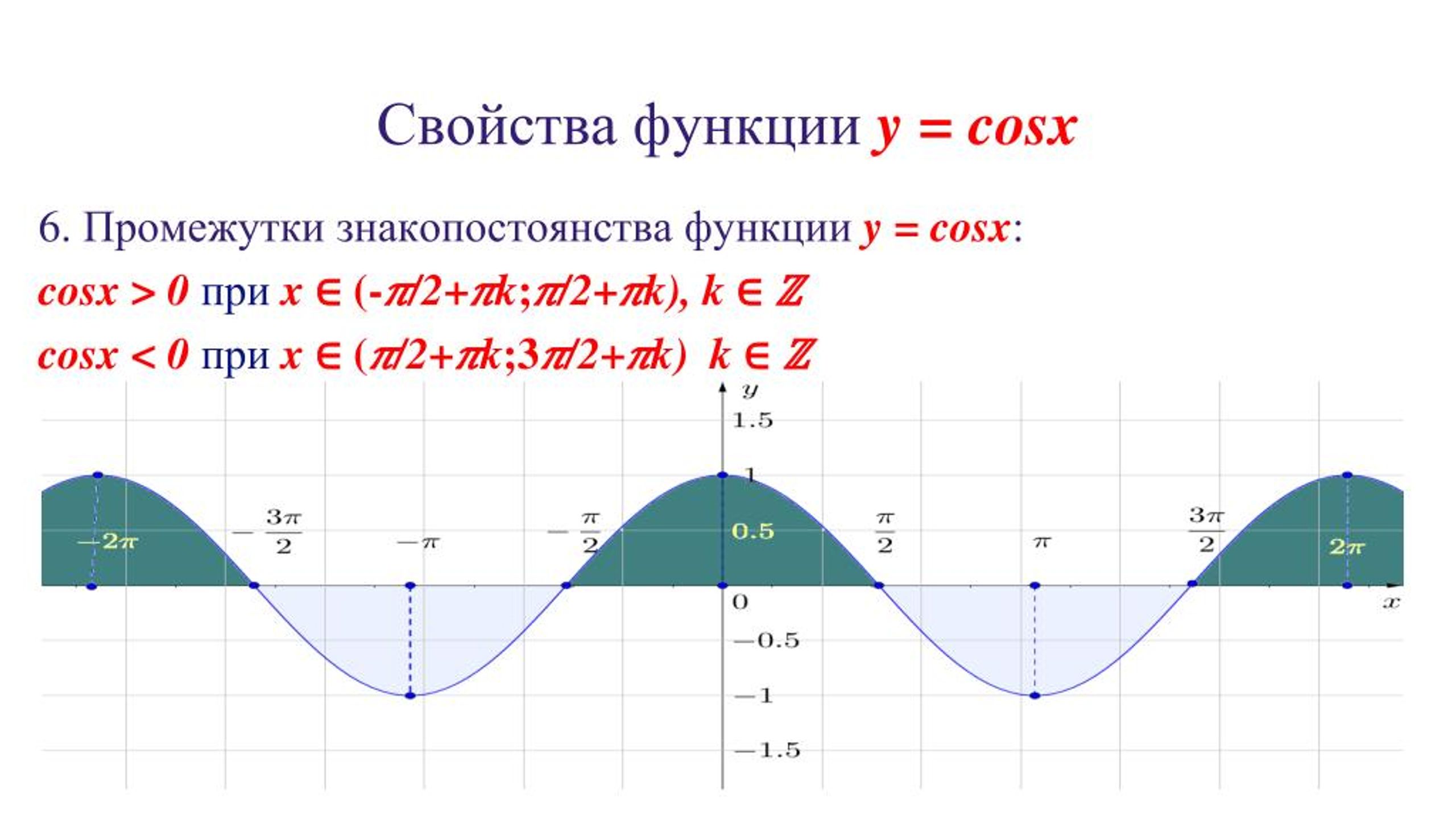
И.В. Фельдман, репетитор по математике.
Матмуни — Математика для успеха
Оценка
а)
б)
в)
г) 4f(2)
Позвольте быть дифференцируемой функцией, имеющей . Тогда равно
а) 18
б) 12
в) 36
г) 24
, тогда равно
а)
б) 1
в)
г) 0
Предположим, кубический х 3 – px + q имеет три различных действительных корня, когда p > 0 и q > 0, то какое из следующих утверждений верно?
a) Кубическое число имеет максимум при и
b) Кубическое имеет минимум при и максимум при
c) Кубическое имеет минимум при и максимум при
d) Кубическое имеет минимум при и при
Сколько действительных решений имеет уравнение
а) 5
б) 7
в) 1
г) 3
Значение c, при котором справедливо заключение теоремы о среднем значении для функции f(x) = ln e x на интервале [1, 3], равно
а)
б)
в)
г)
Функция f(x) = tan − 1 (sinx + cosx) является возрастающей функцией в
a)
b)
c)
d)
Пусть f : R → R — функция, определяемая формулой f(x) = min(x + 1, |x| + 1), тогда какое из следующих утверждений верно?
a) f(x) ≥ 1 для всех x R
b) f(x) не дифференцируема при x = 1
c) f(x) дифференцируема всюду
d) f(x) не дифференцируема дифференцируемый при x = 0
Функцию f : R – {0} → R можно сделать непрерывной, определив f(0) как
a) 2
b) -1
c) 0
d) 1
Функция имеет локальный минимум в точке
а) x = − 2
б) х = 0
в) х = 1
г) х = 2
Угол между касательными к кривой y = x 2 – 5x + 6 в точках (2, 0) и (3, 0) равен
а)
б)
в)
г)
Если x действительно, максимальное значение равно
а) 41
б) 1
в)
г)
Если x м y n = (x + y) m + n тогда
а)
б) ху
в)
г)
Ниже функция сопоставляется с интервалом, в котором она должна возрастать.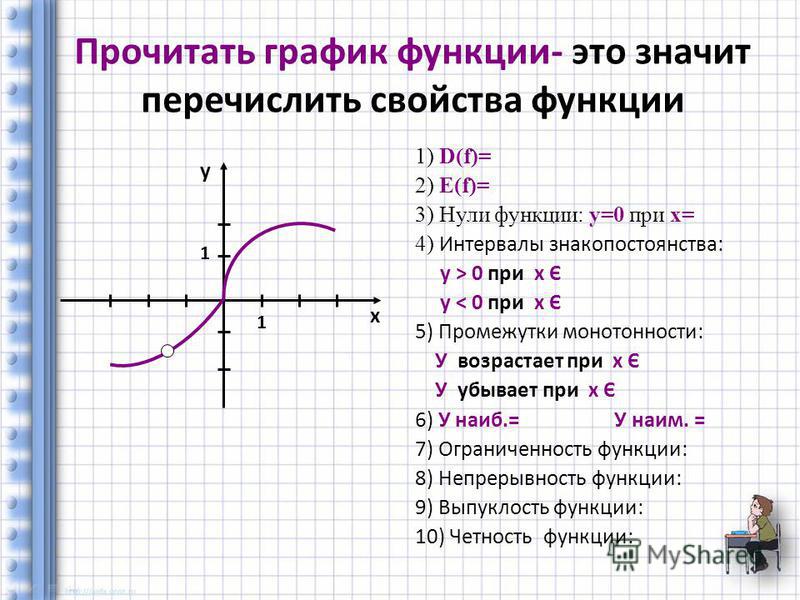 Какая из следующих пар составлена неверно?
Какая из следующих пар составлена неверно?
Интервал | Функция | ||
А. | 4 (0, ∞ | 4)0003 | x 3 + 6x 2 + 6 |
B. |
| 3x 2 – 2x + 1 | |
C. | [2, ∞) | 2x 3 – 3x 2 + 12x +60002 (−∞, ∞) | x 3 − 3x 2 + 3x + 3 |
Предположим, что f(x) дифференцируема при x = 1 и
a) 6
b) 5
c) 4
d) 3
Если f — вещественная дифференцируемая функция, удовлетворяющая условию |f(x) – f(y)| ≤ (x – y) 2 , x, y R и f(0) = 0, тогда f(1) равно
а) 1
б) 2
в) 0
г) – 1
Нормаль к кривой x = a(cosθ + θsinθ), y = a(sinθ – θcosθ) в любой точке θ такова, что
а) Это постоянное расстояние от начала координат
б) Она проходит через
c) составляет угол с осью x
d) проходит через начало координат
Пусть α, β — различные корни ax 2 + bx + c = 0, тогда равно
а)
б)
в)
г)
Сферический железный шар радиусом 10 см покрыт слоем льда одинаковой толщины, который тает со скоростью 50 см 3 /мин. При толщине льда 15 см скорость уменьшения толщины льда равна
При толщине льда 15 см скорость уменьшения толщины льда равна
а)
б)
в)
г)
Если разница между максимальным и минимальным значением u 2 равна
а)
б)
в)
г)
Если , то значения a, b равны
а) a R, b R
б) a = 1, b R
в) a R, b = 2
г) a = 1, b = 2
Пусть . Если f(x) непрерывно в , то равно
а) 1
б)
в)
г) 1
Если тогда
а)
б)
в)
г)
Нормаль к кривой x = a (1 + cosθ), y = asinθ при θ всегда проходит через неподвижную точку
а) (а, 0)
б) (0, а)
в) (0 , 0)
г) (а, а)
Измерение согласованности данных — DATAVERSITY
Измерение согласованности данных может сказать исследователю, насколько ценны и полезны его данные. Однако термин «согласованность данных» может сбивать с толку. Есть три его версии. Когда этот термин применяется к базам данных, он описывает согласованность данных в базе данных. При использовании с вычислительными стратегиями согласованность данных сосредоточена на использовании кэшей данных. Третья версия согласованности данных используется с аналитикой данных.
При использовании с вычислительными стратегиями согласованность данных сосредоточена на использовании кэшей данных. Третья версия согласованности данных используется с аналитикой данных.
Вообще говоря, непротиворечивость данных связана с преобразованиями формата, дублированием данных и отсутствующей информацией.
ПРИСОЕДИНЯЙТЕСЬ К НАМ НА КОНФЕРЕНЦИИ ПО УПРАВЛЕНИЮ ДАННЫМИ И КАЧЕСТВУ ИНФОРМАЦИИ
Узнайте из десятков практических примеров, руководств, семинаров и т. д. — 5–9 декабря 2022 г. в Вашингтоне, округ Колумбия (зарегистрируйтесь до 7 октября, чтобы сохранить до $400!)
Зарегистрируйтесь сейчас
«Несогласованность» данных вызывает проблемы, включая потерю информации и неверные результаты. Согласованность данных, с другой стороны, способствует точности и удобству использования доступных данных и может быть разницей между успехом бизнеса или его неудачей. Данные стали основой для принятия успешных бизнес-решений, а противоречивые данные могут привести к принятию ошибочных бизнес-решений.
Инструменты, упомянутые в этой статье, используются с системами SQL.
Непротиворечивость данных в базах данных
База данных представляет собой систематизированный, организованный набор данных. Он поддерживает электронные данные, хранящиеся в компьютерной системе, и позволяет изменять данные. База данных упрощает управление данными. Непротиворечивость базы данных основана на ряде правил, поддерживающих единообразие и точность, и использует «транзакции».
Транзакция базы данных — это процесс, который выполняется независимо в целях извлечения или обновления данных.
Транзакция базы данных по определению должна быть ACID-совместимой («ACID» означает атомарный, непротиворечивый, изолированный, устойчивый). Функция «непротиворечивость» помогает обеспечить согласованность данных в каждой транзакции. Функции ACID гарантируют достоверность данных, несмотря на сбои питания, ошибки и другие проблемы.
В идеале транзакция базы данных должна подчиняться закону «все или ничего». (Написание должно быть завершено, или оно не должно быть написано). Все правила проверки должны быть на месте для обеспечения согласованности. Если правила, поддерживающие единообразие и точность, не соблюдаются, вся транзакция будет аннулирована.
(Написание должно быть завершено, или оно не должно быть написано). Все правила проверки должны быть на месте для обеспечения согласованности. Если правила, поддерживающие единообразие и точность, не соблюдаются, вся транзакция будет аннулирована.
Правила непротиворечивости базы данных требуют, чтобы данные записывались и форматировались способами, которые поддерживают системное определение допустимых данных. Если происходит транзакция, которая пытается ввести противоречивые данные, вся транзакция откатывается и возвращается пользователю.
Согласованная современная база данных содержит данные, действительные в соответствии с четко определенными правилами, включая каскады, триггеры и ограничения. Транзакции базы данных должны изменять только затронутые данные.
Хранилище базы данных, которое по умолчанию обеспечивает согласованность всего набора данных, в целом вызывает меньше сбоев и проблем.
Отсутствие согласованности данных значительно повышает вероятность того, что данные в системе неоднородны, что может привести к отсутствию или частичности данных.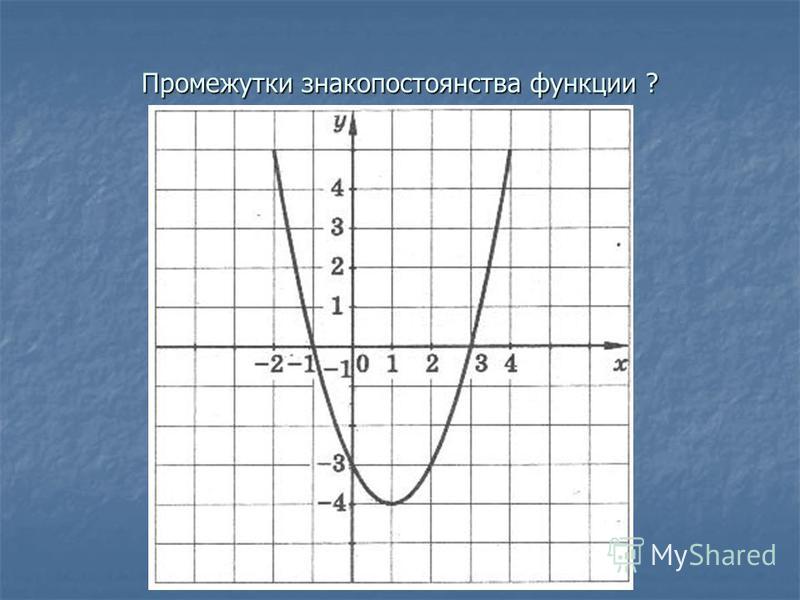 Обычно существует три вида непротиворечивости данных:
Обычно существует три вида непротиворечивости данных:
- Непротиворечивость на определенный момент времени направлена на обеспечение единообразия всех данных в системе в определенный момент времени. Этот процесс предотвращает потерю данных в случае сбоя системы или других проблем в сети. Он работает, ссылаясь на биты данных в системе с помощью временных меток и других маркеров согласованности. Это позволяет системе восстановить себя до определенного момента времени.
- Согласованность транзакций используется для обнаружения незавершенных транзакций и отката данных в случае обнаружения незавершенной транзакции.
- Согласованность приложений работает с согласованностью транзакций, которая существует между программами. Если банковская программа обменивается данными с налоговой программой, согласованность приложений способствует использованию единых форматов между ними.
Обеспечение соответствия компьютерной базы данных всем трем элементам непротиворечивости данных — лучший способ гарантировать, что данные не будут потеряны или повреждены при их перемещении по системе.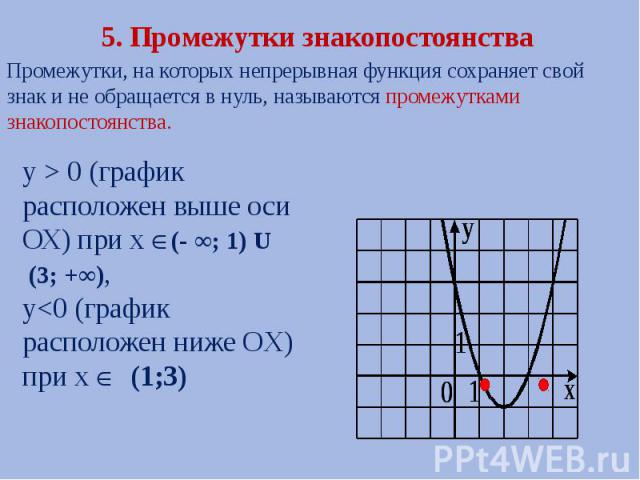
Измерение непротиворечивости данных в базах данных
Проверить непротиворечивость данных в базе данных относительно просто. «Проверка согласованности базы данных» (DBCC) может использоваться для измерения согласованности данных. Эти средства проверки помогают обеспечить как логическую, так и физическую согласованность базы данных. Следует отметить, что многие DBCC не вносят автоматических исправлений, и проблемы необходимо исправлять вручную. Рекомендуется проводить периодические проверки для обеспечения логической и физической непротиворечивости ваших данных. (Есть несколько более совершенных средств проверки согласованности базы данных, которые вносят некоторые исправления.)
По словам Microsoft, при использовании их облака лучший способ исправить ошибки базы данных — это сравнить текущую базу данных с последней хорошей резервной копией.
Непротиворечивость кэшей
«Кэширование» — это хранение данных, к которым часто обращаются, в удобном расположении поблизости (так называемом кэше).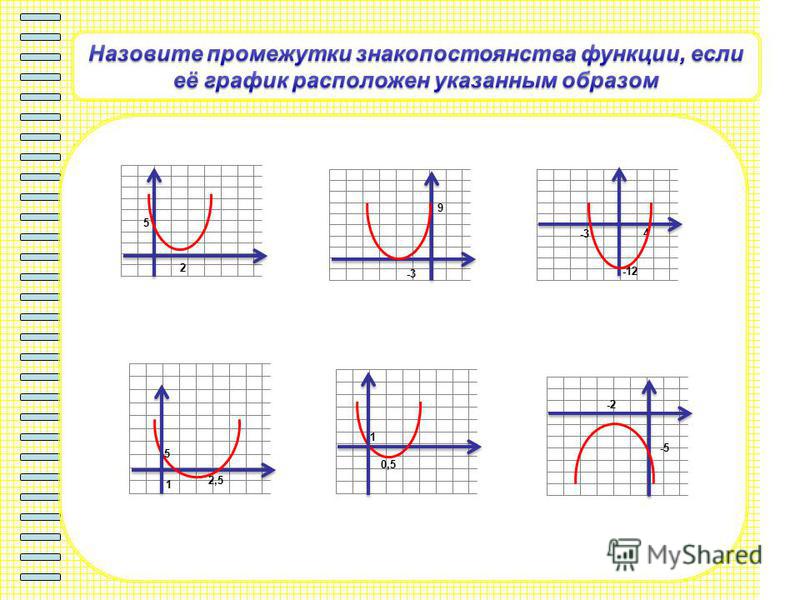 Распределенное кэширование — это расширение метода кэширования, при котором кэш распределяется между несколькими серверами или машинами и доступен для них.
Распределенное кэширование — это расширение метода кэширования, при котором кэш распределяется между несколькими серверами или машинами и доступен для них.
Распределенное кэширование — чрезвычайно полезная тактика, предназначенная для повышения производительности и скорости работы приложений. Распределенные кэши часто используются для обеспечения работы нескольких веб-сайтов и веб-приложений с высокой посещаемостью. Это позволяет быстрее и эффективнее извлекать данные.
Распределенные кэши обычно используют распределенное хеширование, которое использует алгоритм, называемый согласованным хешированием. Хеш-функция используется для сопоставления одной части данных и обычно идентифицирует объект для другой части данных, называемой хеш-кодом или хэшем.
Как правило, кэш сохраняет записи в течение коротких промежутков времени, после чего они стираются или обновляются. Если записи обновляются каждые пять минут, то запасы могут быть пятиминутными и устаревшими. Эта задержка создает «окно несоответствия», которое может вызвать проблемы с ожиданиями клиентов, если в базе данных есть другая, точная информация.
Улучшение согласованности кэшей
Компания Striim, поставщик облачных вычислений и платформ, разработала инструмент для устранения этого окна несогласованности. Он называется Hazelcast Striim Hot Cache и решает проблему, используя потоковые данные для синхронизации и обновления кеша в режиме реального времени. В результате и кэш, и связанное с ним приложение постоянно обновляются в режиме реального времени.
Их уровень высокоскоростного обмена сообщениями работает так, чтобы направить событие (обновления данных) на правильный узел — узел, на котором данные хранятся локально в этом кэше. Это делается с использованием согласованного алгоритма хеширования, применяемого к уровню обмена сообщениями и уровню кэширования.
Согласованность данных в аналитике
Данные, используемые для аналитики, обычно поступают из различных источников, использующих различные форматы. Количество вариантов зависит от количества или объема собираемых данных. При работе с аналитикой данных согласованность данных является частью процесса интеграции данных.
Поскольку данные для аналитики поступают из нескольких источников, данные могут быть представлены в нескольких форматах.
Платформы интеграции данных позволяют интегрировать данные, полученные из нескольких источников, и преобразовывать их в единый унифицированный формат. (Конфликты «значений» данных не могут быть исправлены методами интеграции данных.)
Согласованность данных отличается от целостности данных. Целостность данных фокусируется на качестве данных или их точности. Он стремится устранить ошибки и избыточную информацию, а также восполнить недостающую информацию. Согласованность данных выступает в качестве одной из мер поддержки целостности данных и фокусируется на форматировании и постоянном обновлении данных.
Согласованность данных как поддержка целостности данных гарантирует, что пользователи данных совместно используют одно и то же представление данных, включая изменения, внесенные пользователем, и изменения, внесенные другими. Несогласованность данных представляет собой вариации одних и тех же данных в разных местах.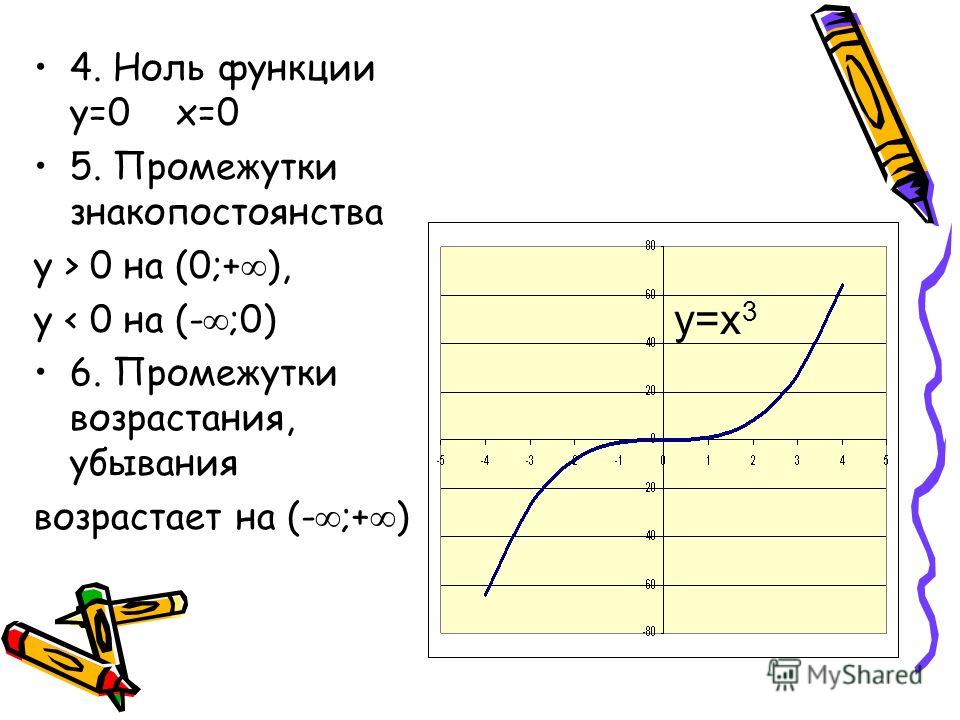
Измерение непротиворечивости данных в аналитике
Платформа Boomi предлагает инструменты для обнаружения проблем непротиворечивости, их измерения и исправления.
Термин «обработка данных» используется на веб-сайте Boomi для описания преобразования данных в другой формат, что делает их доступными для таких целей, как аналитика. Разработчики, осуществляющие преобразования, называются обработчиками данных.
Boomi Hub может предоставить чистые и точные данные, необходимые для сбора данных, важных для бизнеса. С помощью Boomi Hub правила интеграции данных и сервисы обогащения данных можно использовать для перехвата недостоверных данных до того, как они попадут в другие системы. Boomi может синхронизировать бизнес-данные, повышая точность, согласованность и полноту.
Изображение используется по лицензии Shutterstock.com
РЕГИСТРАЦИЯ НА КОНФЕРЕНЦИЮ ПО УПРАВЛЕНИЮ ДАННЫМИ И КАЧЕСТВУ ИНФОРМАЦИИ
Уровни согласованности в Azure Cosmos DB
- Статья
- 13 минут на чтение
ПРИМЕНЯЕТСЯ К: SQL API Кассандра API Гремлин API API таблиц API Azure Cosmos DB для MongoDB
Распределенные базы данных, которые полагаются на репликацию для обеспечения высокой доступности, низкой задержки или того и другого, должны найти фундаментальный компромисс между согласованностью чтения, доступностью, задержкой и пропускной способностью, как определено теоремой PACELC. Линеаризуемость модели строгой согласованности является золотым стандартом программируемости данных. Но это увеличивает цену из-за более высоких задержек записи из-за необходимости репликации и фиксации данных на больших расстояниях. Строгая согласованность также может пострадать от снижения доступности (во время сбоев), поскольку данные не могут реплицироваться и фиксироваться в каждом регионе. Согласованность в конечном счете обеспечивает более высокую доступность и лучшую производительность, но программировать приложения сложнее, поскольку данные могут быть не полностью согласованными во всех регионах.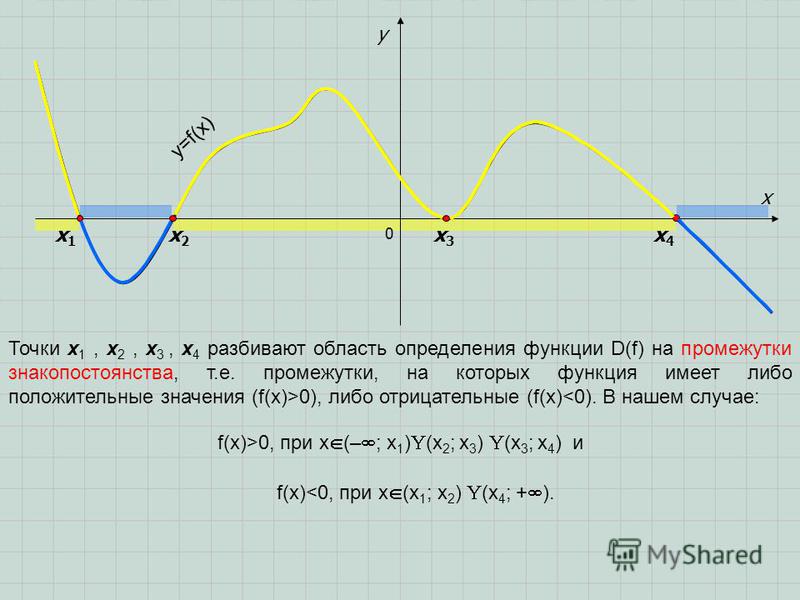
Большинство коммерчески доступных распределенных баз данных NoSQL, доступных сегодня на рынке, обеспечивают только строгую и окончательную согласованность. Azure Cosmos DB предлагает пять четко определенных уровней. Уровни от самого сильного к самому слабому:
- Сильный
- Ограниченное устаревание
- Сессия
- Согласованный префикс
- Возможный
Дополнительные сведения об уровне согласованности по умолчанию см. в разделе Настройка уровня согласованности по умолчанию или переопределение уровня согласованности по умолчанию.
Каждый уровень обеспечивает компромисс между доступностью и производительностью. На следующем изображении показаны различные уровни согласованности в виде спектра.
Уровни согласованности и API-интерфейсы Azure Cosmos DB
Azure Cosmos DB обеспечивает встроенную поддержку API-интерфейсов, совместимых с проводным протоколом, для популярных баз данных. К ним относятся MongoDB, Apache Cassandra, Gremlin и хранилище таблиц Azure. При использовании Gremlin API и Table API используется уровень согласованности по умолчанию, настроенный для учетной записи Azure Cosmos. Дополнительные сведения о сопоставлении уровней согласованности между API Cassandra или API для MongoDB и уровнями согласованности Azure Cosmos DB см. в разделе Сопоставление согласованности API Cassandra и Сопоставление согласованности API для MongoDB.
К ним относятся MongoDB, Apache Cassandra, Gremlin и хранилище таблиц Azure. При использовании Gremlin API и Table API используется уровень согласованности по умолчанию, настроенный для учетной записи Azure Cosmos. Дополнительные сведения о сопоставлении уровней согласованности между API Cassandra или API для MongoDB и уровнями согласованности Azure Cosmos DB см. в разделе Сопоставление согласованности API Cassandra и Сопоставление согласованности API для MongoDB.
Область согласованности чтения
Согласованность чтения применяется к одной операции чтения в пределах логического раздела. Операция чтения может выполняться удаленным клиентом или хранимой процедурой.
Настройка уровня согласованности по умолчанию
Вы можете настроить уровень согласованности по умолчанию в своей учетной записи Azure Cosmos в любое время. Уровень согласованности по умолчанию, настроенный для вашей учетной записи, применяется ко всем базам данных и контейнерам Azure Cosmos в этой учетной записи.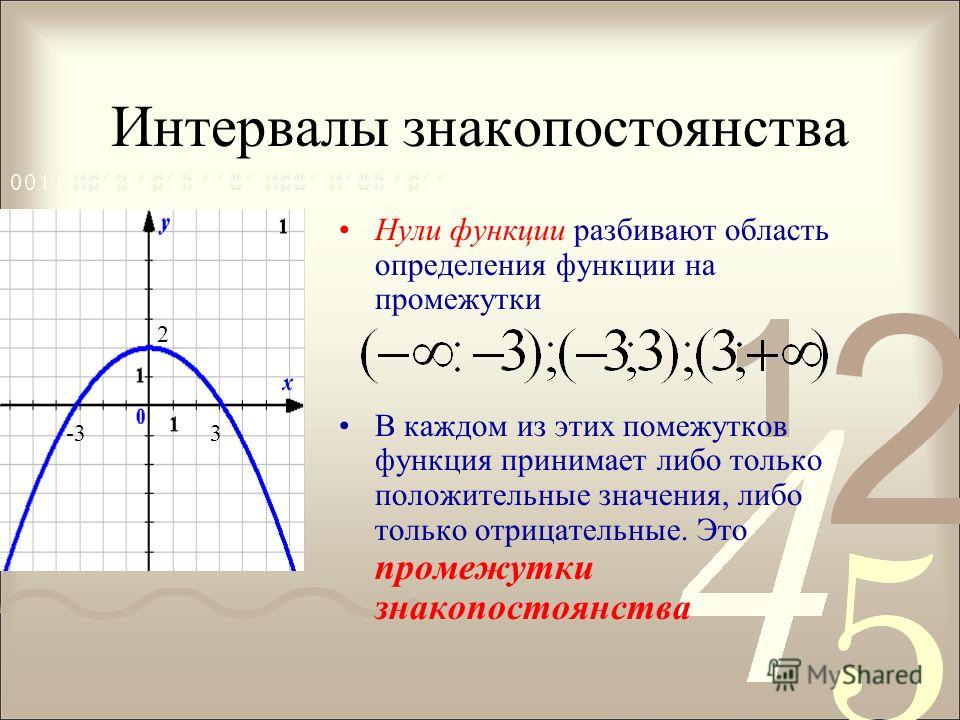 Все операции чтения и запросы к контейнеру или базе данных по умолчанию используют указанный уровень согласованности. Дополнительные сведения см. в разделе, как настроить уровень согласованности по умолчанию. Вы также можете переопределить уровень согласованности по умолчанию для конкретного запроса. Дополнительные сведения см. в статье о том, как переопределить уровень согласованности по умолчанию.
Все операции чтения и запросы к контейнеру или базе данных по умолчанию используют указанный уровень согласованности. Дополнительные сведения см. в разделе, как настроить уровень согласованности по умолчанию. Вы также можете переопределить уровень согласованности по умолчанию для конкретного запроса. Дополнительные сведения см. в статье о том, как переопределить уровень согласованности по умолчанию.
Совет
Переопределение уровня согласованности по умолчанию применяется только к операциям чтения в клиенте SDK. Учетная запись, настроенная на строгую согласованность по умолчанию, по-прежнему будет синхронно записывать и реплицировать данные в каждый регион в учетной записи. Когда экземпляр клиента SDK или запрос переопределяют это с помощью сеанса или более слабой согласованности, чтение будет выполняться с использованием одной реплики. Дополнительные сведения см. в разделе Уровни согласованности и пропускная способность.
Важно
Необходимо воссоздать любой экземпляр SDK после изменения уровня согласованности по умолчанию.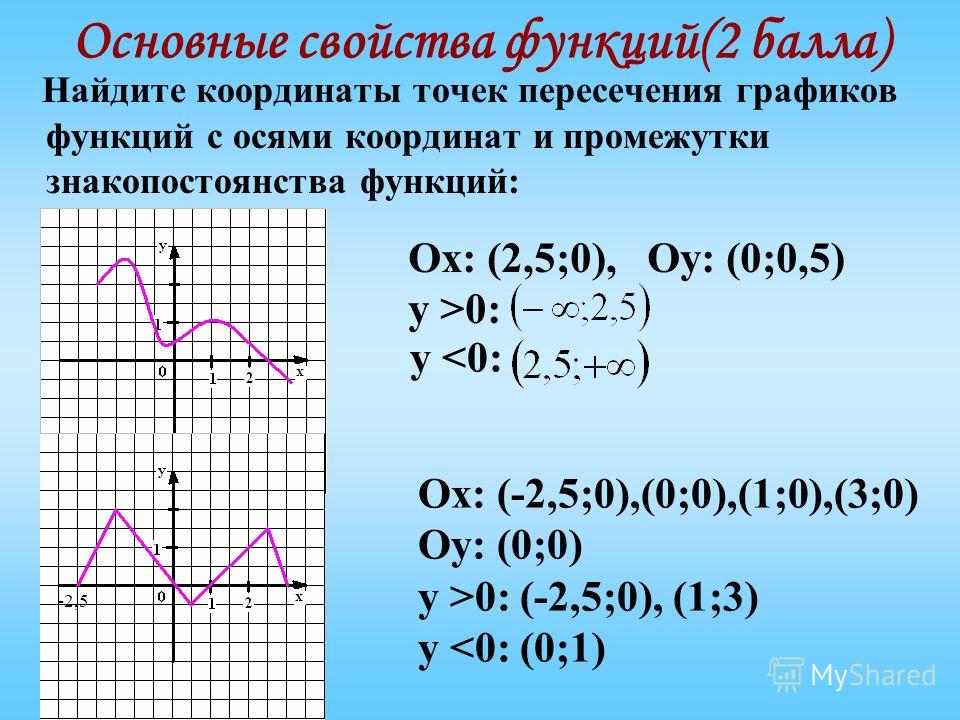 Это можно сделать, перезапустив приложение. Это гарантирует, что SDK использует новый уровень согласованности по умолчанию.
Это можно сделать, перезапустив приложение. Это гарантирует, что SDK использует новый уровень согласованности по умолчанию.
Гарантии, связанные с уровнями согласованности
Azure Cosmos DB гарантирует, что 100 процентов запросов на чтение соответствуют гарантии согласованности для выбранного уровня согласованности. Точные определения пяти уровней согласованности в Azure Cosmos DB с использованием языка спецификации TLA+ приведены в репозитории GitHub azure-cosmos-tla.
Семантика пяти уровней согласованности описана в следующих разделах.
Сильная согласованность
Сильная согласованность гарантирует линеаризуемость. Линеаризуемость относится к одновременному обслуживанию запросов. Чтения гарантированно возвращают самую последнюю зафиксированную версию элемента. Клиент никогда не увидит незафиксированную или частичную запись. Пользователям всегда гарантируется чтение последней зафиксированной записи.
Следующий рисунок иллюстрирует сильную согласованность с музыкальными нотами.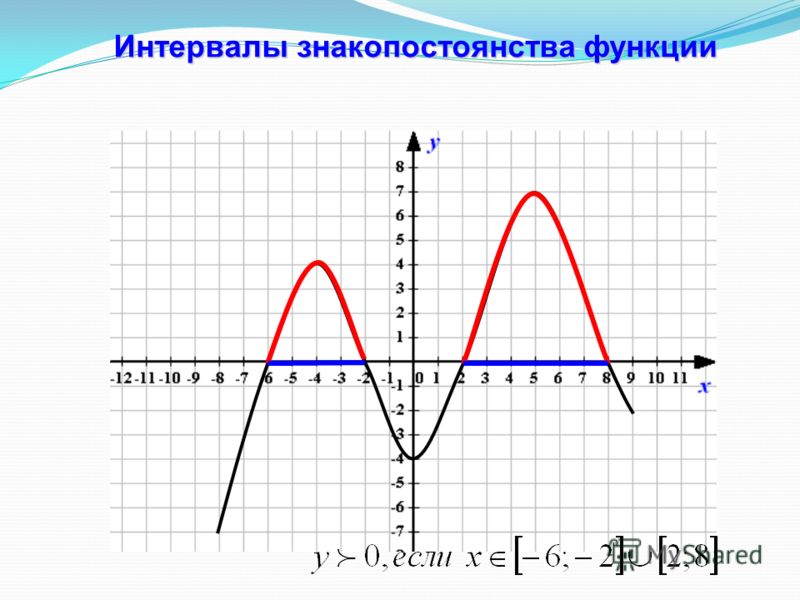 После записи данных в регион «Западная часть США 2» при чтении данных из других регионов вы получите самое последнее значение:
После записи данных в регион «Западная часть США 2» при чтении данных из других регионов вы получите самое последнее значение:
.
Согласованность с ограниченным устареванием
При согласованности с ограниченным устареванием операции чтения гарантированно соответствуют гарантии согласованного префикса. Чтение может отставать от записи не более чем на «K» версий (то есть «обновлений») элемента или на «T» временной интервал, в зависимости от того, какой из них наступит раньше. Другими словами, когда вы выбираете ограниченное устаревание, «устаревание» можно настроить двумя способами:
- Количество версий ( K ) элемента
- Чтение временного интервала ( T ) может отставать от записи
Для учетной записи с одним регионом минимальное значение K и T составляет 10 операций записи или 5 секунд. Для мультирегиональных аккаунтов минимальное значение K и T составляет 100 000 операций записи или 300 секунд.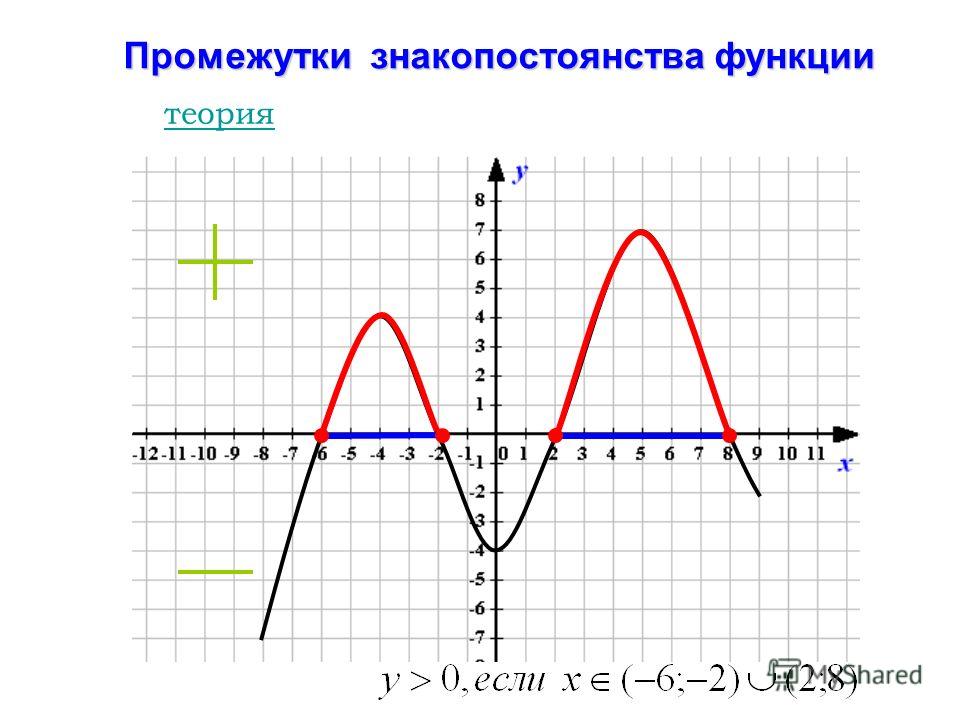
Ограниченное устаревание предлагает полный глобальный порядок за пределами «окна устаревания». Когда клиент выполняет операции чтения в области, допускающей запись, гарантии, обеспечиваемые согласованностью ограниченного устаревания, идентичны гарантиям строгой согласованности. По мере приближения окна устаревания либо по времени, либо по обновлениям, в зависимости от того, что ближе, служба будет ограничивать новые записи, чтобы позволить репликации наверстать упущенное и соблюдать гарантию согласованности.
Внутри окна устаревания Bounded Staleness обеспечивает следующие гарантии согласованности:
Согласованность для клиентов в одном регионе для учетной записи с одним регионом записи = Strong
Согласованность для клиентов в разных регионах для учетной записи с одним регионом записи = согласованный префикс
Согласованность для клиентов, записывающих в один регион для учетной записи с несколькими регионами записи = согласованный префикс
Согласованность для клиентов, записывающих в разные регионы для учетной записи с несколькими регионами записи = Eventual
Ограниченное устаревание часто выбирают глобально распределенные приложения, которые ожидают низкие задержки записи, но требуют полной гарантии глобального порядка.
 Ограниченное устаревание отлично подходит для приложений, поддерживающих совместную работу и совместное использование групп, бегущую строку, публикацию-подписку/постановку в очередь и т. д. На следующем рисунке показана согласованность ограниченного устаревания с музыкальными нотами. После записи данных в регион «Запад США 2» регионы «Восток США 2» и «Восток Австралии» считывают записанное значение на основе настроенного максимального времени задержки или максимального количества операций:
Ограниченное устаревание отлично подходит для приложений, поддерживающих совместную работу и совместное использование групп, бегущую строку, публикацию-подписку/постановку в очередь и т. д. На следующем рисунке показана согласованность ограниченного устаревания с музыкальными нотами. После записи данных в регион «Запад США 2» регионы «Восток США 2» и «Восток Австралии» считывают записанное значение на основе настроенного максимального времени задержки или максимального количества операций:
Согласованность сеанса
При согласованности сеанса в пределах одного клиентского сеанса операции чтения гарантированно соблюдают гарантии согласованного префикса, монотонного чтения, монотонной записи, чтения вашей записи и записи после чтения. Это предполагает наличие одного сеанса записи или совместное использование токена сеанса для нескольких авторов.
Клиенты вне сеанса, выполняющие запись, увидят следующие гарантии:
Согласованность для клиентов в одном регионе для учетной записи с одним регионом записи = согласованный префикс
Согласованность для клиентов в разных регионах для учетной записи с одним регионом записи = согласованный префикс
Согласованность для клиентов, записывающих в один регион для учетной записи с несколькими регионами записи = согласованный префикс
Согласованность для клиентов, записывающих в несколько регионов для учетной записи с несколькими регионами записи = Eventual
Согласованность для клиентов, использующих интегрированный кэш Azure Cosmos DB = Eventual
Согласованность сеанса— это наиболее широко используемый уровень согласованности как для одного региона, так и для глобально распределенных приложений.
 Он обеспечивает задержки записи, доступность и пропускную способность чтения, сравнимые с возможной согласованностью, но также предоставляет гарантии согласованности, которые соответствуют потребностям приложений, написанных для работы в контексте пользователя. Следующий рисунок иллюстрирует согласованность сеанса с музыкальными нотами. «Записывающее устройство West US 2» и «считывающее устройство West US 2» используют один и тот же сеанс (сеанс A), поэтому они оба считывают одни и те же данные одновременно. В то время как регион «Восток Австралии» использует «Сеанс B», он получает данные позже, но в том же порядке, что и запись.
Он обеспечивает задержки записи, доступность и пропускную способность чтения, сравнимые с возможной согласованностью, но также предоставляет гарантии согласованности, которые соответствуют потребностям приложений, написанных для работы в контексте пользователя. Следующий рисунок иллюстрирует согласованность сеанса с музыкальными нотами. «Записывающее устройство West US 2» и «считывающее устройство West US 2» используют один и тот же сеанс (сеанс A), поэтому они оба считывают одни и те же данные одновременно. В то время как регион «Восток Австралии» использует «Сеанс B», он получает данные позже, но в том же порядке, что и запись.
Непротиворечивая согласованность префикса
При согласованном префиксе обновления, сделанные при записи одного документа, видят конечную согласованность. Обновления, сделанные как пакет внутри транзакции, возвращаются в соответствии с транзакцией, в которой они были зафиксированы. Операции записи внутри транзакции нескольких документов всегда видны вместе.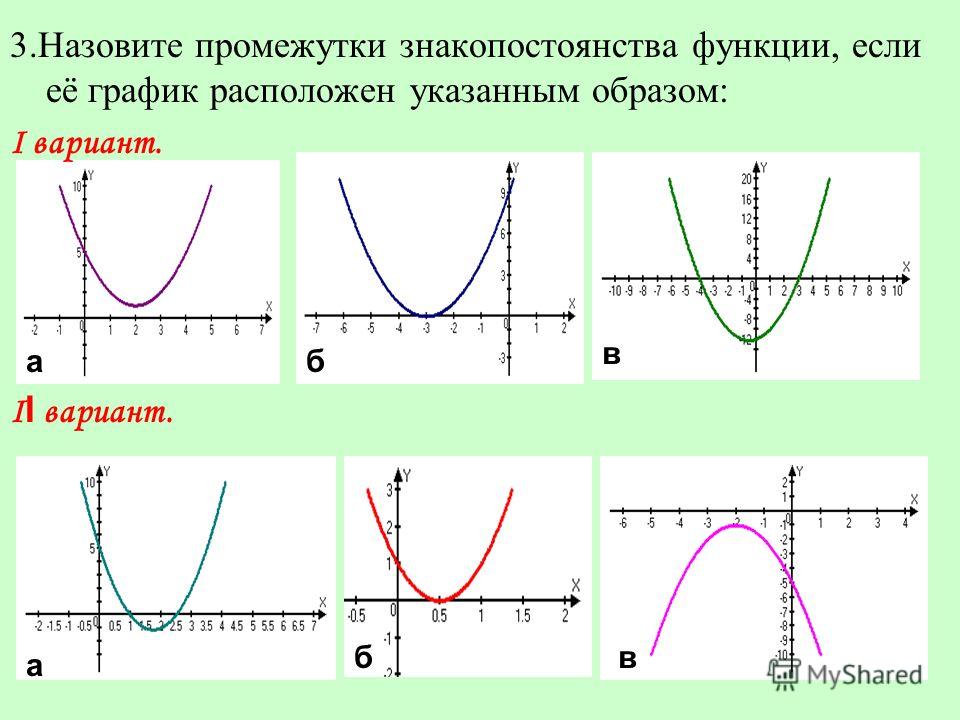
Предположим, что в документах Doc1 и Doc2 в рамках транзакций T1 и T2 выполняются две операции записи. Когда клиент выполняет чтение в любой реплике, пользователь увидит либо «Doc1 v1 и Doc2 v1», либо «Doc1 v2 и Doc2 v2», но никогда не «Doc1 v1 и Doc2 v2» или «Doc1 v2 и Doc2 v1» для одного и того же операция чтения или запроса.
Ниже приведены гарантии согласованности для согласованного префикса в контексте транзакции (запись одного документа см. конечную согласованность):
- Согласованность для клиентов в одном регионе для учетной записи с одним регионом записи = согласованный префикс
- Согласованность для клиентов в разных регионах для учетной записи с одним регионом записи = согласованный префикс
- Согласованность для клиентов, записывающих в один регион для учетной записи с несколькими регионами записи = согласованный префикс
- Согласованность для клиентов, выполняющих запись в несколько регионов для учетной записи с несколькими регионами записи = Eventual
На следующем рисунке показано соответствие префикса согласованности с музыкальными нотами.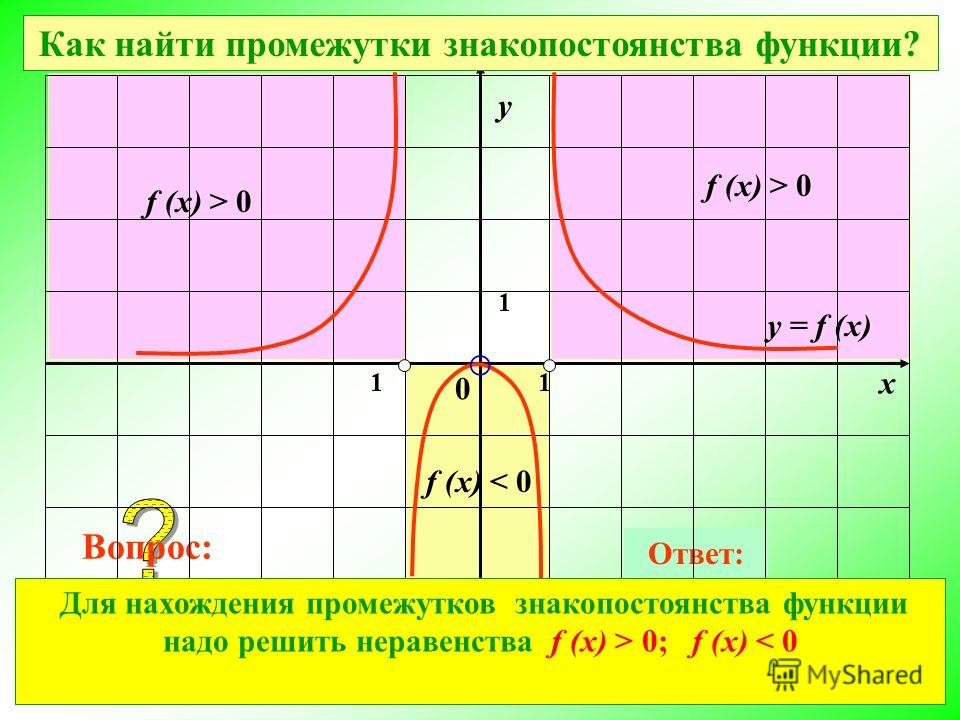 Во всех регионах читает никогда не видит, из строя пишет:
Во всех регионах читает никогда не видит, из строя пишет:
Согласованность в конечном счете
В согласованности в конечном счете не гарантируется порядок операций чтения. При отсутствии дальнейшей записи реплики в конечном итоге сходятся.
Непротиворечивость в конечном счете — это самая слабая форма согласованности, поскольку клиент может считывать значения, которые старше, чем те, которые он читал ранее. Согласованность в конечном счете идеальна, когда приложение не требует никаких гарантий упорядочения. Примеры включают количество ретвитов, лайков или комментариев без цепочек. Следующий рисунок иллюстрирует возможную согласованность с музыкальными нотами.
Гарантии согласованности на практике
На практике часто можно получить более сильные гарантии согласованности. Гарантии согласованности для операции чтения соответствуют актуальности и порядку состояния базы данных, которое вы запрашиваете. Согласованность чтения связана с порядком и распространением операций записи/обновления.
Если в базе данных нет операций записи, операция чтения с возможным , сеанс или согласованный префикс 9Уровни согласованности 0367, вероятно, дадут те же результаты, что и операция чтения с уровнем строгой согласованности.
Если ваша учетная запись Azure Cosmos настроена на уровень согласованности, отличный от строгой согласованности, вы можете узнать вероятность того, что ваши клиенты могут получать надежные и согласованные чтения для ваших рабочих нагрузок, просмотрев показатель Вероятностно ограниченное устаревание (PBS). . Эта метрика доступна на портале Azure. Дополнительные сведения см. в статье Отслеживание метрики вероятностно ограниченного устаревания (PBS).
Вероятностное ограниченное устаревание показывает, насколько возможной является ваша окончательная согласованность. Эта метрика дает представление о том, как часто вы можете получить более высокую согласованность, чем уровень согласованности, который вы в настоящее время настроили в своей учетной записи Azure Cosmos.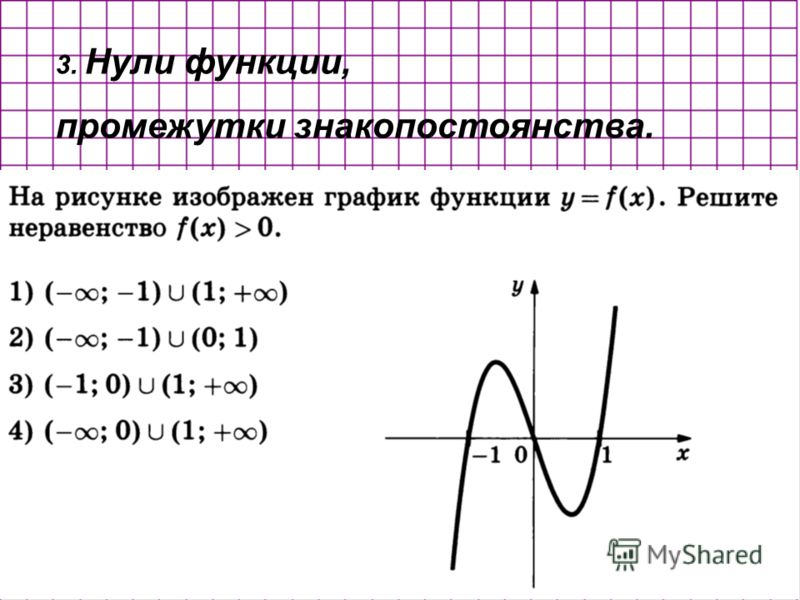 Другими словами, вы можете увидеть вероятность (измеряемую в миллисекундах) получения строго согласованных операций чтения для комбинации областей записи и чтения.
Другими словами, вы можете увидеть вероятность (измеряемую в миллисекундах) получения строго согласованных операций чтения для комбинации областей записи и чтения.
Уровни согласованности и задержка
Задержка чтения для всех уровней согласованности всегда гарантированно составляет менее 10 миллисекунд на 99-й процентиль. Средняя задержка чтения на 50-м процентиле обычно составляет 4 миллисекунды или меньше.
Задержка записи для всех уровней согласованности всегда гарантированно составляет менее 10 миллисекунд на 99-м процентиле. Средняя задержка записи на 50-м процентиле обычно составляет 5 миллисекунд или меньше. Учетные записи Azure Cosmos, которые охватывают несколько регионов и настроены с соблюдением строгой согласованности, являются исключением из этой гарантии.
Задержка записи и сильная согласованность
Для учетных записей Azure Cosmos, для которых настроена строгая согласованность с несколькими регионами, задержка записи равна удвоенному времени приема-передачи (RTT) между любым из двух самых удаленных регионов плюс 10 миллисекунд в 99-м процентиле. Высокий сетевой RTT между регионами приведет к более высокой задержке для запросов Cosmos DB, поскольку строгая согласованность завершает операцию только после того, как она была зафиксирована во всех регионах в учетной записи.
Высокий сетевой RTT между регионами приведет к более высокой задержке для запросов Cosmos DB, поскольку строгая согласованность завершает операцию только после того, как она была зафиксирована во всех регионах в учетной записи.
Точная задержка RTT зависит от расстояния со скоростью света и топологии сети Azure. Сеть Azure не предоставляет никаких соглашений об уровне обслуживания с задержкой для RTT между любыми двумя регионами Azure, однако она публикует статистику задержки в обоих направлениях сети Azure. Для вашей учетной записи Azure Cosmos задержки репликации отображаются на портале Azure. Вы можете использовать портал Azure (перейдите в колонку Метрики, выберите вкладку Согласованность) для отслеживания задержек репликации между различными регионами, связанными с вашей учетной записью Azure Cosmos.
Важно
Строгая согласованность для учетных записей с регионами, охватывающими более 5000 миль (8000 километров), по умолчанию заблокирована из-за высокой задержки записи.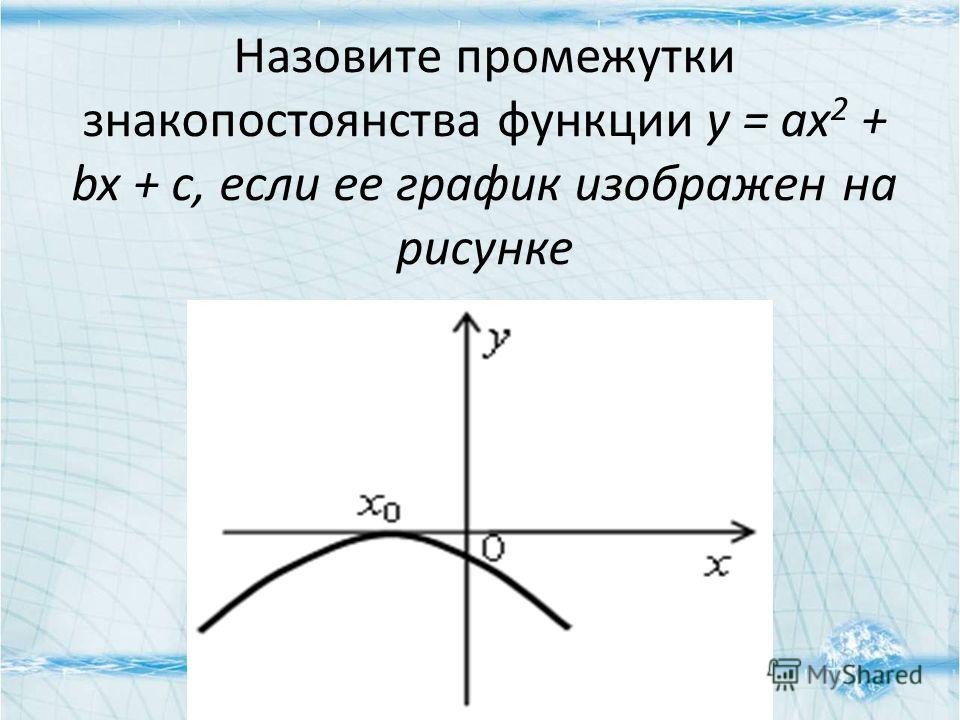 Чтобы включить эту возможность, обратитесь в службу поддержки.
Чтобы включить эту возможность, обратитесь в службу поддержки.
Уровни согласованности и пропускная способность
Для сильного и ограниченного устаревания чтение выполняется для двух реплик в наборе из четырех реплик (миноритарный кворум), чтобы обеспечить гарантии согласованности. Сеанс, согласованный префикс и возможное чтение одной реплики. В результате для того же количества единиц запросов пропускная способность чтения для сильного и ограниченного устаревания составляет половину от других уровней согласованности.
Для данного типа операций записи, таких как вставка, замена, вставка и удаление, пропускная способность записи для единиц запросов одинакова для всех уровней согласованности. Для строгой согласованности изменения должны быть зафиксированы в каждом регионе (глобальное большинство), в то время как для всех других уровней согласованности используется локальное большинство (три реплики в наборе из четырех реплик).
| Уровень консистенции | Кворум читает | Кворум записывает |
|---|---|---|
| Прочный | Местное меньшинство | Глобальное большинство |
| Ограниченное устаревание | Местное меньшинство | Местное большинство |
| Сеанс | Одиночная реплика (с использованием маркера сеанса) | Местное большинство |
| Согласованный префикс | Одиночная копия | Местное большинство |
| Возможный | Одиночная копия | Местное большинство |
Примечание
Стоимость операций чтения в секунду для локального меньшинства в два раза выше, чем для более слабых уровней согласованности, поскольку чтения выполняются из двух реплик, чтобы обеспечить гарантии согласованности для сильного и ограниченного устаревания.
Уровни согласованности и устойчивость данных
В среде глобально распределенной базы данных существует прямая связь между уровнем согласованности и устойчивостью данных в случае сбоя в масштабе региона. При разработке плана обеспечения непрерывности бизнеса необходимо понимать максимальный период последних обновлений данных, которые приложение может допустить при восстановлении после аварийного события. Период времени обновлений, который вы можете позволить себе потерять, известен как точка восстановления цель ( RPO ).
В таблице ниже определяется взаимосвязь между моделью согласованности и устойчивостью данных при сбое в регионе.
| Регион(ы) | Режим репликации | Уровень согласованности | РПО |
|---|---|---|---|
| 1 | Одна или несколько областей записи | Любая консистенция Уровень | < 240 минут |
| >1 | Одиночная область записи | Сеанс, согласованный префикс, конечный | < 15 минут |
| >1 | Одиночная область записи | Ограниченное устаревание | К и Т |
| >1 | Одиночная область записи | Сильный | 0 |
| >1 | Несколько областей записи | Сеанс, согласованный префикс, конечный | < 15 минут |
| >1 | Несколько областей записи | Ограниченное устаревание | К и Т |
K = Количество «K» версий (т.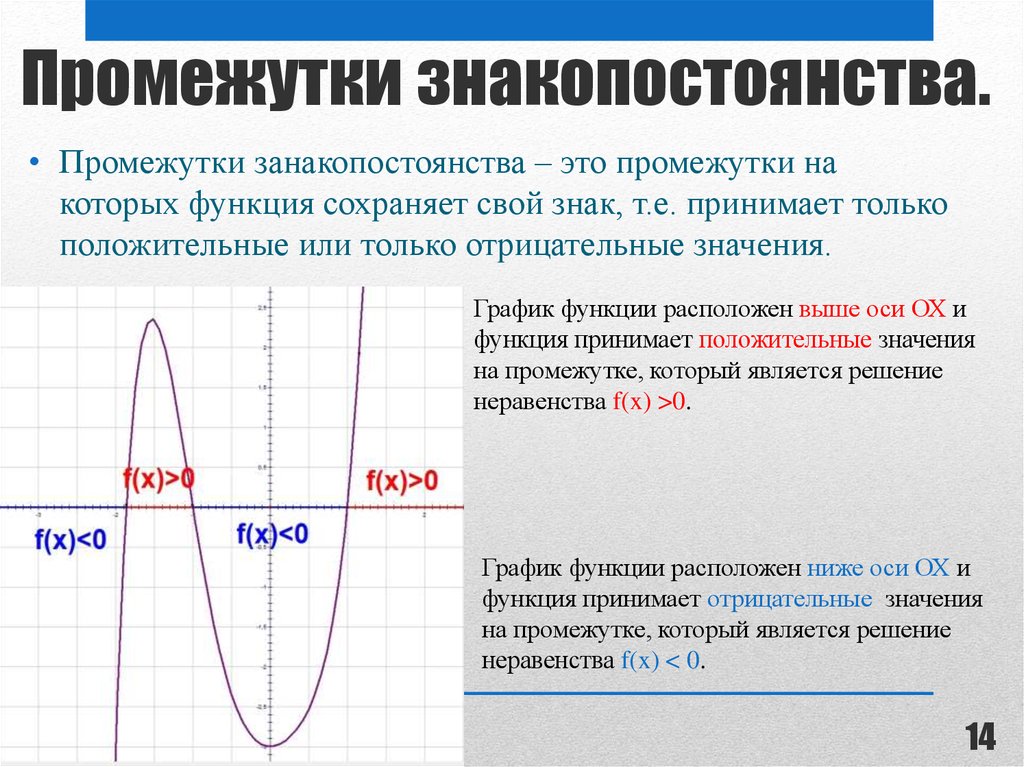 е. обновлений) элемента.
е. обновлений) элемента.
T = Интервал времени «T» с момента последнего обновления.
Для учетной записи одного региона минимальное значение K и T составляет 10 операций записи или 5 секунд. Для учетных записей с несколькими регионами минимальное значение K и T составляет 100 000 операций записи или 300 секунд. Это определяет минимальный RPO для данных при использовании Bounded Staleness.
Строгая согласованность и несколько областей записи
Учетные записи Cosmos, настроенные с несколькими областями записи, не могут быть настроены для строгой согласованности, поскольку распределенная система не может обеспечить нулевой RPO и нулевой RTO. Кроме того, при использовании строгой согласованности с несколькими регионами записи нет преимуществ в отношении задержки записи, поскольку запись в любой регион должна быть реплицирована и зафиксирована во всех настроенных регионах в учетной записи. Это приводит к той же задержке записи, что и учетная запись с одной областью записи.

 Ограниченное устаревание отлично подходит для приложений, поддерживающих совместную работу и совместное использование групп, бегущую строку, публикацию-подписку/постановку в очередь и т. д. На следующем рисунке показана согласованность ограниченного устаревания с музыкальными нотами. После записи данных в регион «Запад США 2» регионы «Восток США 2» и «Восток Австралии» считывают записанное значение на основе настроенного максимального времени задержки или максимального количества операций:
Ограниченное устаревание отлично подходит для приложений, поддерживающих совместную работу и совместное использование групп, бегущую строку, публикацию-подписку/постановку в очередь и т. д. На следующем рисунке показана согласованность ограниченного устаревания с музыкальными нотами. После записи данных в регион «Запад США 2» регионы «Восток США 2» и «Восток Австралии» считывают записанное значение на основе настроенного максимального времени задержки или максимального количества операций: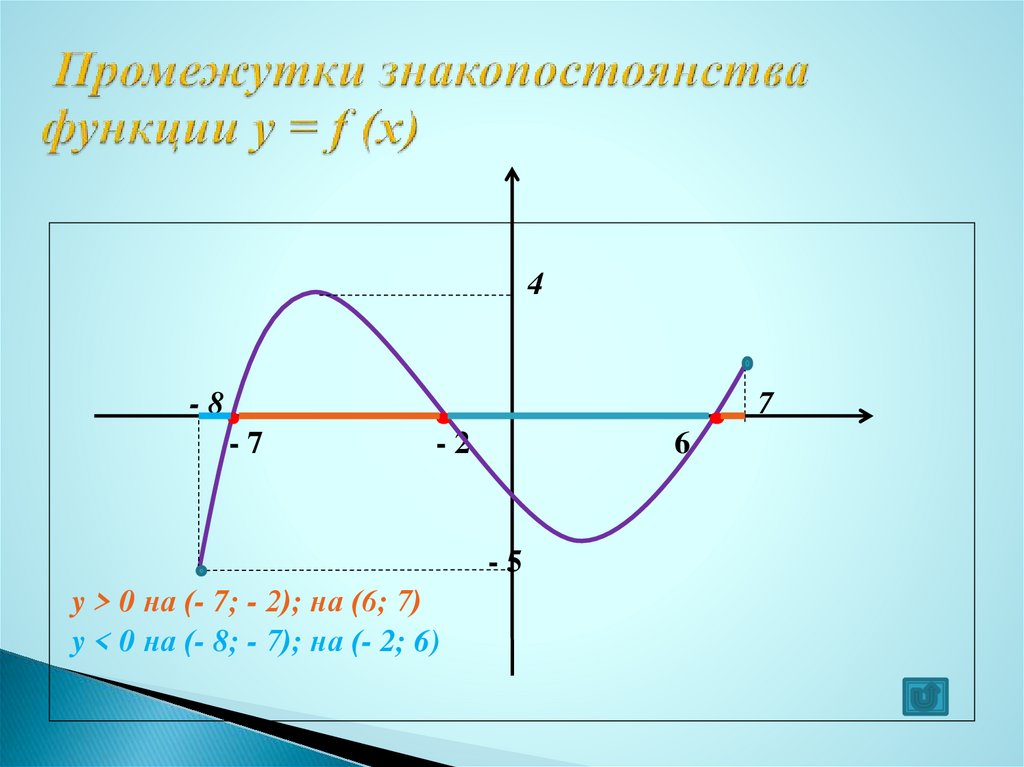 Он обеспечивает задержки записи, доступность и пропускную способность чтения, сравнимые с возможной согласованностью, но также предоставляет гарантии согласованности, которые соответствуют потребностям приложений, написанных для работы в контексте пользователя. Следующий рисунок иллюстрирует согласованность сеанса с музыкальными нотами. «Записывающее устройство West US 2» и «считывающее устройство West US 2» используют один и тот же сеанс (сеанс A), поэтому они оба считывают одни и те же данные одновременно. В то время как регион «Восток Австралии» использует «Сеанс B», он получает данные позже, но в том же порядке, что и запись.
Он обеспечивает задержки записи, доступность и пропускную способность чтения, сравнимые с возможной согласованностью, но также предоставляет гарантии согласованности, которые соответствуют потребностям приложений, написанных для работы в контексте пользователя. Следующий рисунок иллюстрирует согласованность сеанса с музыкальными нотами. «Записывающее устройство West US 2» и «считывающее устройство West US 2» используют один и тот же сеанс (сеанс A), поэтому они оба считывают одни и те же данные одновременно. В то время как регион «Восток Австралии» использует «Сеанс B», он получает данные позже, но в том же порядке, что и запись.