Уравнения и неравенства, содержащие переменную под знаком модуля
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
• СОДЕРЖАНИЕ
Понятие
модуля
Уравнения,
содержащие
переменную
под знаком модуля
Неравенства,
содержащие
переменную
под знаком модуля
3. Понятие модуля
Модулем числа а называется расстояние от началаотсчета до точки с координатой а
а|
|
Например:
|-7|=7
-7
Таким образом:
х
а
0
|
7 | =7
0
а, если а 0,
а
а, если а 0
х
7
оглавление
4.
Уравнения.содержащие переменную под знаком модуля| f(x) | = a
| f(x) | = |g(x) |
| f(x) | = g(x)
| f(x) | + | g(x) | = h(x)
5. Уравнение вида | f(x) | = a
Если а < 0, то уравнение решений не имеет
Если а = 0, то f(x) = 0
Если а > 0, то f(x) = а или f(x) = — а
Пример:
Решить уравнение: | 2х – 5 | = 13
Решение: 2х – 5 = 13 или 2х – 5 = — 13
2х = 13 + 5
2х = — 13 + 5
2х = 18
х =9
2х = — 8
х = -4
Ответ: х = 9 , х = — 4
Задачи для самостоятельного решения
оглавление
другой вид
6. Уравнение вида | f(x) | = a
Решите уравнение• 1) | 2х — 3| = 7
Ответ
• 2) .|х2 – х — 5| = 1 Ответ
• 3) | |х| — 2 |= 2
Ответ
оглавление
другой вид
• Ответ: х = 5, х = — 2
• Показать решение
назад
• Ответ: x = — 2, x = 3
• Показать решение
х
1
назад
17
2
• Ответ: x= 4, x= — 4 , x = 0
• Показать решение
назад
РЕШЕНИЕ:
| 2х – 3 | = 7
2х – 3 = 7 или
2х = 7 + 3 или
2х = 10 или
х = 5 или
2х – 3 = — 7
2х = — 7 + 3
2х = — 4
х =- 2
назад
РЕШЕНИЕ:
| х2 – х — 5 | = 1
х2 – х — 5 = 1 или
х2 – х — 6 = 0
D = 25
x1 = — 2, x2 = 3
х2 – х — 5 = -1
х2 – х — 4 = 0
D = 17
1 17
х1, 2
2
назад
РЕШЕНИЕ:
| |x| -2 | = 2
|x| -2 = 2
или |x| -2 = — 2
|x| = 2+ 2
|x| = — 2 +2
|x| = 4
|x| = 0
x = 4 или х = — 4
x = 0
назад
13.
Уравнение вида | f(x) | = g(x)• 1) определить условие, при котором уравнение имеет решение:g(x) ≥ 0
• 2) f(x) = g(x) или f(x) = — g(x)
• 3) Решить уравнения и выбрать корни, удовлетворяющие
условиюg(x) ≥ 0
• Пример: Решить уравнение:| х + 2| = 2( 3 – х)
• Определим при каких значениях х уравнение имеет решение
2( 3 – х) ≥ 0 => х ≤ 3
• Распишем данное уравнение на два:
х + 2 = 2( 3 – х) или х + 2 = — 2( 3 – х)
х = 4/3
х = 8 не удовлетворяет условию х ≤ 3
• Ответ: х = 4/3
Задачи для самостоятельного
решения
другой вид
Уравнение вида | f(x) | = g(x)
Решите уравнения
1) |5х + 2| = 3 – 3х
2) |х2 — 2х| = 3 — 2х
Ответ:
Ответ
другой вид
• Ответ: х = 1/8, х = — 2,5
• Показать решение
назад
• Ответ: х = 3 , х = 1
• Показать решение
назад
РЕШЕНИЕ:
• |5х + 2| = 3 – 3х
• Определим при каких значениях х уравнение
имеет решение: 3 – 3х ≥ 0 => х ≤ 1
• Распишем данное уравнение на два:
• 5х + 2 = 3 – 3х или 5х + 2 = — (3 – 3х)
• 5х + 3х = 3 – 2
5х — 3х = — 3 – 2
• 8х = 1
2х = — 5
• х = 1/8
х = — 2,5
• Оба корня удовлетворяют условию х ≤ 1
назад
РЕШЕНИЕ:
• |х2 -2 х| = 3 — 2х
• Определим при каких значениях х уравнение имеет
решение: 3 — 2х ≥ 0 => х ≤ 1,5
• Распишем данное уравнение на два:
• х2 –2 х =3 — 2х
или
х2 – 2х = — (3 — 2х )
• х2 = 3
х2 – 4х +3 = 0
• х= 3
х1 = 1 х2 = 3
Корни 3 и 3 не удовлетворяют условию х ≤ 1,5
Ответ: х = 3 х = 1
назад
19.
Уравнение вида | f(x) | = | g(x)|1способ: f(x) = g(x) или f(x) = — g(x)
2способ: возвести обе части уравнения в квадрат
Пример Решить уравнение: |х + 2| = |2х — 6|
1 способ: х + 2 = 2х – 6 или х + 2 = — (2х – 6)
х = 8
3х = 4
х = 4/3
2 способ: (|х + 2|)2 = (|2х — 6|)2 Воспользуемся свойством |а|2=а2
(х + 2)2 = (2х — 6)2
3х2 – 28х + 32 = 0 => х = 8, х = 4/3
Задачи для самостоятельного
решения
другой вид
Уравнение вида | f(x) | = |g(x)|
Решите уравнения
1) |х2 + х — 2| = |х +2|
2) |3 + х |= |х|
Ответ:
Ответ
другой вид
• Ответ: х = -2, х = 0, х = 2
• Показать решение
назад
• Ответ: х = -1,5
• Показать решение
назад
• РЕШЕНИЕ
|х2 + х — 2| = |х +2|
х2 + х — 2 = х +2 или х2 + х — 2 = — (х +2)
х2 = 4
х2 + 2х = 0
х = 2, х = — 2
х(х + 2) = 0
х = 0 х = -2
Ответ: х = -2, х = 0, х = 2
назад
• РЕШЕНИЕ
|3 + х| = |х|
3+х =х
или
3= 0
решений нет
Ответ: х = -1,5
назад
3+х =-х
2х = -3
х = -1,5
25.
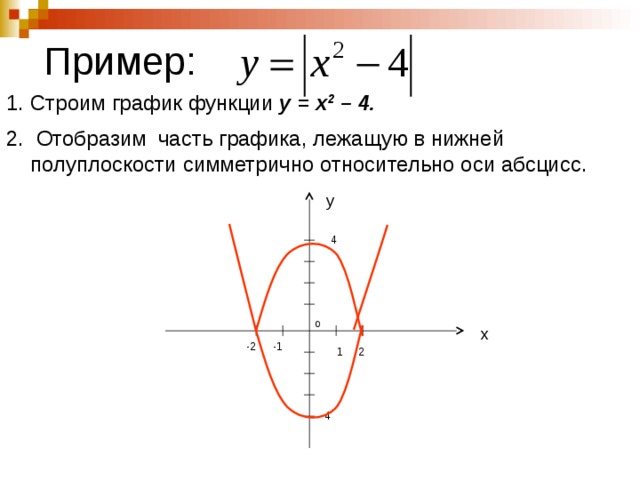Уравнение вида | f(x) | + | g(x)| = h(x)• При решении уравнений данного вида используетсяправило раскрытия модуля.
• Пример: Решить уравнение:|х-3| + |2х-1| =8
1
• Найдем нули функций, стоящих под знаком модуля: х= 3, х= 2
• Отметим эти точки на числовой прямой и определим знаки функций на
получившихся промежутках
1
2
х 3
2х 1
3
Рассмотрим решение уравнения на каждом промежутке
1
х
2
1
х 3
2
Задачи для самостоятельного
решения
х 3
Ответ:
оглавление
26. Уравнение вида | f(x) | + | g(x)| = h(x)
• Пример: Решить уравнение: |х-3| + |2х-1| =8х
1
1 2
3
х 3
2х 1
2
Раскроем модули с учетом знака функций на этом промежутке
— ( х-3 ) – ( 2х-1 ) = 8
— 3х +4 = 8
4
удовлетворяет условию
х
3
х
1
2
назад
27. Уравнение вида | f(x) | + | g(x)| = h(x)
Пример: Решить уравнение:|х-3| + |2х-1| =81
2
3
х 3
2х 1
1
х 3
2
Раскроим модули с учетом знака функций на этом промежутке
— ( х-3 ) + ( 2х-1 ) = 8
х+2=8
х=6 не удовлетворяет условию 1 х 3
2
назад
28.
Уравнение вида | f(x) | + | g(x)| = h(x)Пример: Решить уравнение:|х-3| + |2х-1| =81
2
3
х 3
х 3
2х 1
• Раскроем модули с учетом знака функций на этом
промежутке
( х-3 ) + ( 2х-1 ) = 8
3х — 4 = 8
х=4 удовлетворяет условию х 3
назад
29. Уравнение вида | f(x) | + | g(x)| = h(x)
Объединим все ответы1
2
1
х
2
х
4
3
3
1
х 3
2
решений нет
Ответ: х
4
3
Задачи для самостоятельного
решения
х 3
2х 1
х 3
х 4
х 4
назад
30. Раскрытие модуля
а, если а 0,а
а, если а 0
• Решить уравнение: | 2х — 4| = х +6
Раскроем модуль.
Если 2х – 4 ≥ 0 , т. е. х ≥ 2,
то 2х – 4 = х +6
х = 10 – удовлетворяет условию х ≥ 2
Если 2х – 4 < 0, т. е. х < 2,
то -(2х – 4) = х +6
х = — 2/3 – удовлетворяет условию х < 2
Ответ: х = -2/3, х = 10
Второй способ
оформления
31. Раскрытие модуля
а, если а 0,а
а, если а 0
• Решить уравнение: | 2х — 4| = х +6
Раскроем модуль.
Найдем нули функции, стоящей внутри знака модуля
2х – 4 = 0 => х = 2
Отметим точку с координатой 2 на прямой.
—
2
+
Определим знаки функции на получившихся промежутках
Рассмотрим неравенство отдельно на каждом промежутке:
Если х < 2, то 2х – 4 < 0 => -(2х – 4) = х +6
х = — 2/3 – удовлетворяет условию х < 2
Если х ≥ 2, то 2х – 4 ≥ 0 => 2х – 4 = х +6
х = 10 – удовлетворяет условию х ≥ 2
Ответ: х = -2/3, х = 10
назад
32. Уравнение вида | f(x) | + | g(x)| = h(x)
Решите уравнения2 х 3 х 1 2х 1
3 х 3 х 5 2х
х 2 х 2 2х
Ответ:
Ответ:
Ответ:
оглавление
• Ответ:
x 2
2
3
х 4
• Показать решение
назад
• Ответ:
x 2
• Показать решение
назад
• Ответ:
x ;0
• Показать решение
назад
36. Уравнение вида | f(x) | + | g(x) | = h(x)
• Задача 1. Решить уравнение 2 х 3 х 1 2х 1Найдем нули функций (х-3) и (х+1) , отметим эти точки на числовой
прямой и определим знаки этих функций на получившихся
промежутках
+
х-3
х+1
+
3 +
-1
х 1
2 х 3 ( х 1) 2х 1
2 х 6 х 1 2 х 1
5х 6
6
х
5
не
удовлетворяет условию
х 1
1 х 3
2 х 3 ( х 1) 2х 1
2 x 6 х 1 2 х 1
3x 8
2
x 2
3
удовлетворяет условию
х 3
2 х 3 ( х 1) 2х 1
2 x 6 х 1 2 х 1
х 4
удовлетворяет условию
х 3
1 х 3
Ответ:
x 2
2
х 4
3
назад
37.
Уравнение вида | f(x) | + | g(x) | = h(x)• Задача 1. Решить уравнение 3 х 3 х 5 2 хНайдем нули функций (3-х) и (х+5) , отметим эти точки на числовой
прямой и определим знаки этих функций на получившихся
промежутках
+
+
3-х
х+5
+
3 +
-5
х 5
5 х 3
3 х 3( х 5) 2х
3 х 3х 15 2х
18 0
3 х 3( х 5) 2х
3 x 3х 11 2х
6x 12
решений нет
x 2
удовлетворяет условию
х 3
3 х 3( х 5) 2х
3 x 3х 15 2х
х 9,5
не удовлетворяет условию
х 3
5 х 3
Ответ:
x 2
назад
38. Уравнение вида | f(x) | + | g(x) | = h(x)
• Задача 1. Решить уравнение х 2 х 2 2хНайдем нули функций (х-3) и (х+1) , отметим эти точки на числовой
прямой и определим знаки этих функций на получившихся
промежутках
+
х-2
х
+
2 +
0
х 0
х 2 х 2 2х
х 2 х 2 2х
2 2
верно при всех х
0 х 2
х 2 х 2 2х
x 2 х 2 2х
2x 0
с учетом условия
х 0
х ;0
x 0
удовлетворяет условию
0 х 2
Ответ:
х 2
х 2 х 2 2х
x 2 х 2 2х
х ;0
x 1
не удовлетворяет условию
х 2
назад
40.
Неравенствасодержащие переменную под знаком модуля|x| <a
| f(x) | < a
| f(x) | < |g(x) |
| f(x) | > |g(x) |
|x| >a
| f(x) | > a
| f(x) | + | g(x) | < h(x)
| f(x) | + | g(x) | > h(x)
41. Неравенства вида |x| < a
Неравенства вида |x| < a• Опираясь на понятие модуля:
|x| < a — это значит: расстояние от начала координат до точек,
удовлетворяющих данному условию должно быть меньше а.
На координатной прямой эти точки будут находиться правее нуля
до точки с координатой (а) и левее нуля до точки с координатой (а)
-а
х а; а
х
а
Пример: Решите неравенство |х| ≤ 6
Решение: Отметим на координатной прямой точки с координатами 6 и 6.
Решением будет множество точек, находящихся на отрезке 6;6
Ответ:
-6
6;6
6
Другой вид
х
42. Неравенства вида |x| > a
Неравенства вида |x| > aОпираясь на понятие модуля:
|x| > a — это значит: расстояние от начала координат до точек,
удовлетворяющих данному условию должно быть больше а.
На координатной прямой эти точки будут находиться правее с
координатой (а) и левее точки с координатой (-а)
-а
х
а
х ; а а;
Пример: Решите неравенство: | х| > 9
Решение: Отметим на координатной прямой точки с координатами
-9 и 9. Решением неравенства будет являться множество точек,
координаты которых меньше – 9 или больше 9
-9
Ответ : х ; 9 9;
9
х
Задачи для самостоятельного
решения
43. Решите неравенства
х 8Ответ : 8 х 8
х 3 8
Ответ : 11 х 11
х 2 16 Ответ : х 14 или х 14
13 2 х 5 Ответ : х 4 или х 4
x 2 16 0
Ответ : 4 х 4
Показать решение
75 3 x 2 0 Ответ : х 5 или х 5 Показать решение
ДРУГОЙ ВИД
44. Решение неравенства
x 2 16 0x 2 16
Извлекаем корень из обеих частей уравнения,
2
не забывая свойства : х х
х 4
-4
4
х
Ответ : 4 х 4
НАЗАД
45. Решение неравенства
75 3 x 2 03 x 2 75
x 2 25
Извлекаем корень из обеих частей уравнения,
не забывая свойства : х х
2
х 5
-5
5
х
Ответ : х 5 или х 5
Другой вид
46.
Неравенства вида |f(x)| < aНеравенства вида |f(x)| < a• Аналогично неравенству вида |x| < a , решением данного
неравенства будет являться множество точек, удовлетворяющих
условию — a < f(x) < a
Пример 1: Решите неравенство: | 2х — 3| ≤ 11
Решение: Это неравенство равносильно двойному неравенству
— 11 ≤ 2х — 3 ≤ 11
— 11 + 3 ≤ 2х ≤ 11 + 3
-8 ≤ 2х ≤14
-4 ≤ х ≤7
Ответ : х 4; 7
Другой вид
47. Неравенства вида |f(x)| > a
Неравенства вида |f(x)| > a• Аналогично неравенству вида |x| > a , решением данного
неравенства будет являться множество точек, удовлетворяющих
условиям f(x) < — a или f(x) > a
Пример 1: Решите неравенство: | х + 6| ≥ 4
Решение: Это неравенство равносильно неравенствам:
х + 6 ≤ — 4 или х + 6 ≥ 4
х ≤-4-6
х≥ 4-6
х≥ -2
х ≤ — 10
Ответ : х ; 10 2;
Задачи для
самостоятельного решения
48. Решите неравенства
2 х 3Ответ:
х 3 1 5
Ответ:
2 х 4 2 12
Ответ:
13 2 4 3х 5
Ответ:
ДРУГОЙ ВИД
2 х 3
Ответ : 1 х 5
Показать решение
назад
х 3 1 5
Ответ : 9 х 3
Показать решение
назад
2 х 4 2 12
Ответ : х 3 или х 7
Показать решение
назад
13 2 4 3х 5
8
Ответ : х 0 или х
3
Показать решение
назад
53.
Решение неравенства2 х 33 2 х 3
3 2 х 3 2
5 х 1
5 х 1
1 х 5
-1
5
Ответ : 1 х 5
х
НАЗАД
54. Решение неравенства
х 3 1 5х 3 6
6 х 3 6
6 3 х 6 3
9 х 3
-9
3
Ответ : 9 х 3
х
НАЗАД
55. Решение неравенства
2 х 4 2 122 х 4 10
2 х 4 10 или 2 х 4 10
2 х 6 или 2 х 14
х 3 или х 7
-3
7
Ответ : х 3 или х 7
х
НАЗАД
56. Решение неравенства
13 2 4 3х 52 4 3х 5 13
2 4 3х 8
4 3х 4
4 3 х 4 или 4 3 х 4
3 х 8 или 3 х 0
8
х
или х 0
3
0
8
3
8
Ответ : х 0 или х
3
х
НАЗАД
57. Неравенства вида
f ( x) g ( x)Неравенства вида f ( x) g ( x) или f ( x) g ( x)
можно решать двумя способами:
1. возведением обеих частей в квадрат
2. раскрывая модули по определению
Пример: Решить неравенство: 3х 2 х 1
1 способ: Т. к. обе части неравенства неотрицательны, то их можно
2
2
3
х
2
х
1
возвести в квадрат
Используя известное свойство, получим: (3х 2) 2 ( х 1) 2
Перенесем все слагаемы в левую часть и разложим на множители
по формуле разность квадратов:
(3х 2) ( х 1) (3х 2) ( х 1) 0
2 х 3 4 х 1 0
Решая методом интервалов, получим:
1 3
х
;
4 2
Второй
способ
58.
Неравенства видаf ( x) g ( x)Пример: Решить неравенство: 3х 2 х 1
2 способ: Найдем нули функции, стоящей внутри знака модуля, отметим эти
числа на числовой прямой и определим знаки этих функций на
получившихся промежутках:
—
—
+
-1
Решим неравенство на каждом промежутке:
х 1
3х-2
+
1 х
2
3
2
3
х+1
+
х
2
3
(3x 2) ( x 1)
(3 x 2) ( x 1)
(3x 2) ( x 1)
2x 3
4x 1
1
x
4
2x 3
x 1,5
x 1,5
с учетом данного условия:
-1
1
1,5
Решений нет
1
4
2
3
1 2
х
;
4 3
2
3
3
2
2 3
х
;
3 2
Объединяем второе и третье решение
1 3
х
;
4
2
59. Решите неравенство
2 х 2x 1Ответ:
ДРУГОЙ ВИД
2 х 2x 1
1
Ответ : x ; 3 ;
3
Показать решение
другой вид
61. Решение неравенства
2 х 2x 12 x
2
Возведем обе части в квадрат
2 x 1
2
Перенесем все в левую часть
и разложим по формуле разность квадратов
( 2 x 2 x 1)( 2 x 2 x 1) 0
( 3 x 1)( x 3) 0
—
+
Решаем неравенство методом интервалов
—
1
31
Ответ : x ; 3 ;
3
-3
х
НАЗАД
Неравенства вида
f ( x) g ( x) h( x)
• Неравенства данного вида решаются
методом раскрытия модулей, как и
уравнения такого типа .
• Рассмотрим решение данного вида
неравенств на примере:
63. Неравенства вида
f ( x) g ( x) h( x)3х 2 х 1 2 x
Пример: Решить неравенство:
2 способ: Найдем нули функции, стоящей внутри знака модуля, отметим эти
числа на числовой прямой и определим знаки этих функций на
—
—
+
-1
Решим неравенство на каждом промежутке:
х 1
1 х
2
3
2
3
(3x 2) ( x 1) 2 x (3x 2) ( x 1) 2 x
4x 3
3
x
4
с учетом данного условия:
1
3
4
Решений нет
6x 1
1
x
6
-1
3х-2
+
1
6
х+1
+
х
2
3
(3 x 2) ( x 1) 2 x
0x 3
Неравенство верно при всех х
2
3
1 2
х
;
6 3
2
3
2
х
;
3
Объединяем второе и третье решение
1
х
;
4
English Русский Правила
1.2 Решение линейных уравнений с модулем
Для
начала, стоит вспомнить, что такое модуль
числа.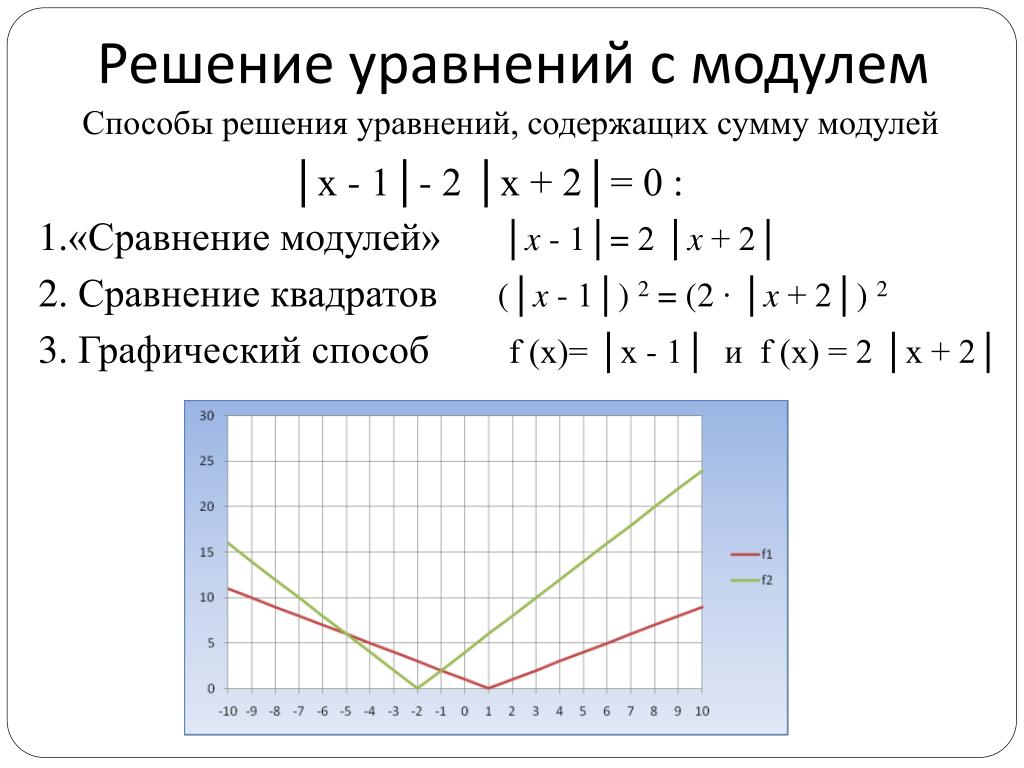
Итак, абсолютной величиной или
модулем числа называется само число х,
если х положителен, число (-х), если х
отрицателен, или нуль, если х=0. Значение
модуля может быть только положительным.
Чтобы понять решение параметрических уравнений, содержащих знак модуля, лучше всего продемонстрировать решение наглядно, т.е. привести примеры:
Пример 1. Решить уравнение |x-2|=b.
Так как, по определению модуля, |x-2| , то при b<0 данное уравнение решений не имеет. Если b=0, то уравнение имеет решение х=2.
Если b>0, то решениями уравнения являются числа x=2+b и x=2-b.
Ответ: при b<0 решений нет, при b=0 х=2, при b>0 х=2+b и x=2-b.
Пример 2. Решить уравнение |x-a|=|x-4|. Удобнее всего данное уравнение решить методом интервалов, для двух случаев:
a ;
4 .
1. Первый интервал:
;
Второй интервал:
, т.е. если а<4, то .
Третий интервал:
а=4, т.е. если а=4, то .
2. Первый интервал:
а=4,
.
В торой интервал:
a>4,т.е. если 4<а, то
Третий интервал:
Ответ: при а=4 х-любое;, при а<4 .
Пример 3. Для каждого значения параметра а найти все значения х, удовлетворяющие уравнению |x+3|– a| x – 1| =4.
Рассмотрим 3 промежутка: 1) , 2) , 3) и решим исходное уравнение на каждом промежутке.
1. , .
При а=1 уравнение не имеет решений, но при а 1 уравнение имеет корень . Теперь надо выяснить, при каких а х попадает на промежуток x< – 3, т.е. , , , . Следовательно, исходное уравнение на x< – 3 имеет один корень при , а на остальных а корней не имеет.
2. . .
При а= – 1 решением уравнения является любое х; но мы решаем на промежутке . Если а 1, то уравнение имеет один корень х=1.
3. . .
При а=1 решением является любое число, но мы решаем на . Если а 1, то х=1.
Ответ: при ; при а= – 1 и при а 1 х=1; при а=1 и при а 1 х=1.
1.3 Решение квадратных уравнений с параметром
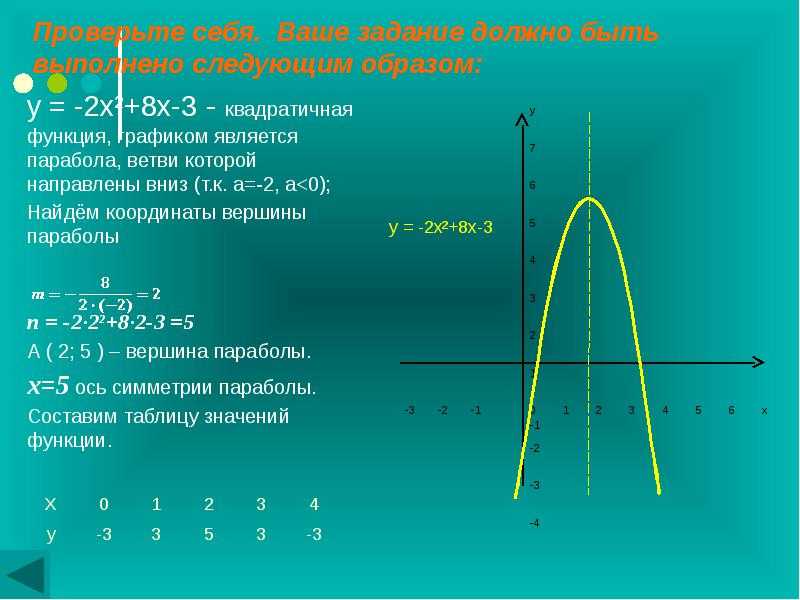
Для
начала напомню, что квадратное уравнение
– это уравнение вида
,
где а, b и с – числа, причем, а
0.
Условия параметрических квадратных уравнений могут быть различны, но для решений всех их нужно применять свойства обыкновенного квадратного уравнения :
а) Если D>0, а>0, то уравнение имеет два действительных различных корня, знаки которых при с>0 одинаковые и противоположны по знаку коэффициента b, а при с<0, причем по абсолютной величине больше тот, знак которого противоположен коэффициенту b.
б) Если D=0, а>0, то уравнение имеет два действительных и равных между собой корня, знак которых противоположен знаку коэффициента b.
в) Если D<0, а>0, то уравнение не имеет действительных корней.
Аналогично можно представить свойства корней при а<0. Кроме того, в квадратных уравнениях справедливы следующие утверждения:
Если поменять местами коэффициенты а и
с, то корни полученного квадратного уравнения будут обратны корням данного.
Если
поменять знак коэффициента b, корни
полученного квадратного уравнения
будут противоположны корням данного.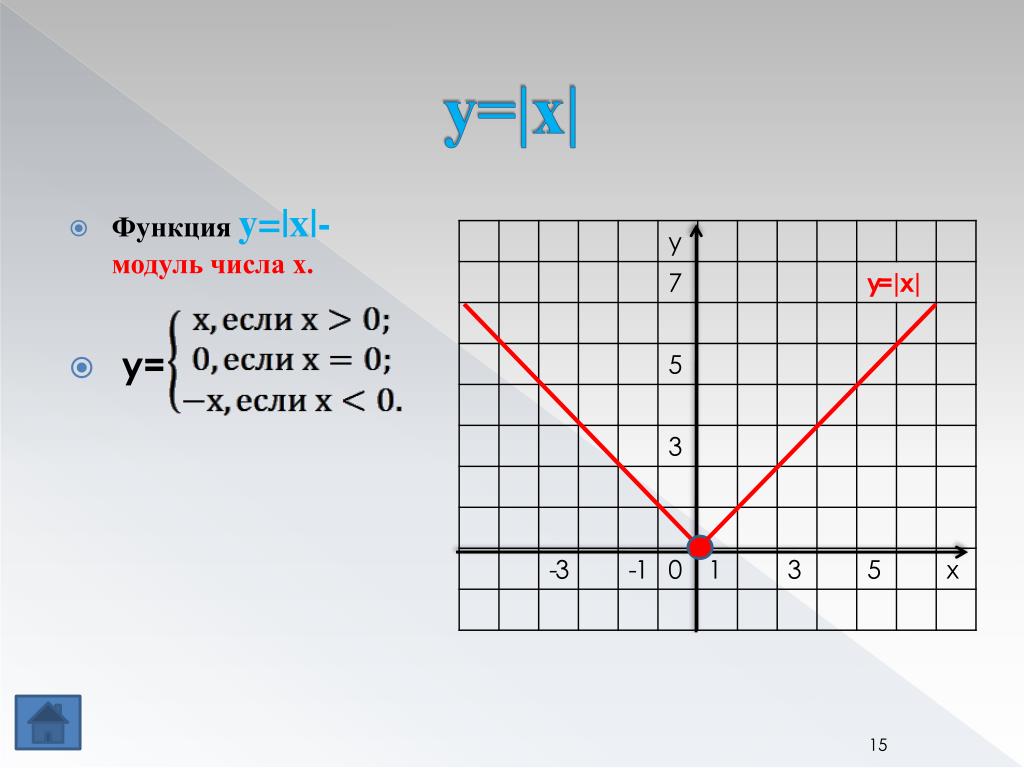
Если коэффициенты а и с разных знаков, то уравнение имеет действительные корни.
Пример1. Найти все значения параметра а, для которых квадратное уравнение : а) имеет два различных корня; б) не имеет корней; в) имеет два равных корня.
Данное уравнение по условию является квадратным, поэтому а -1. Рассмотрим дискриминант данного уравнения:
При а>-1 уравнение имеет два различных корня, т.к. D>0, при a<-1 уравнение корней не имеет, т.к. D<0, а двух одинаковых корней это уравнение иметь не может, т.к. D=0 при а=-1, а это противоречит условию задачи.
Пример2. Решить уравнение
При а=0 уравнение является линейным 2х+1=0, которое имеет единственное решение х=-0.5. А при а 0, уравнение является квадратным и его дискриминант D=4-4a.
При а>1 D<0 поэтому уравнение корней не имеет. При а=1 D=0, поэтому уравнение имеет два совпадающих корня =-1.
При a<1, но а 0, D>0 и данное уравнение имеет два различных корня
;
.
Ответ: и при a<1, но а 0; х=-0.5 при а=0; =-1 при а=1.
Пример3. Корни уравнения таковы, что . Найдите а.
По теореме Виета и . Возведём обе части первого равенства в квадрат: . Учитывая, что , а , получаем: или , . Проверка показывает, что все значения удовлетворяют условию.
Ответ:
Вторичная математика 3 Модуль 3 Ключ ответа
AllebildervideosshoppingMapsNewsbücher
Sucoptionen
[PDF] Вторичная математика III // Модуль 3
DeGeeter-Ryan.Weebly.com ›Uploads ›2HWSOLITION. / МОДУЛЬ 3. ПОЛИНОМИАЛЬНЫЕ ФУНКЦИИ — 3.5. НА СТАРТ, ВНИМАНИЕ, МАРШ! ГОТОВЫ. Тема: Решение линейных уравнений. Решите для х. 1. 5x + 13 = 48. Ответ: x …
[PDF] средняя математика iii // модуль 3
degeeter-ryan.weebly.com › загрузки › 2.4hwsolutions.pdf
Ответ: График касается оси X, не пересекая другую сторону. ИДТИ. Тема: Решение квадратных уравнений. Найдите нули в каждом уравнении, используя .
..
Учебный план для средней школы – проект Mathematics Vision | MVP
www.mathematicsvisionproject.org › second-mat…
Mathematics Three Notes Teacher · Введение в материалы · Модуль 1: Функции и их обратные · Модуль 2: Логарифмические функции · Модуль 3: Полиномиальные …
[PDF] Ключ ответов для RSG’s Secondary 3 Honors
www.mathematicsvisionproject.org › загрузки › 3 › answerkey3_h
Ответный ключ для RSG Secondary 3 Honors. 2.6H_RSG. ГОТОВЫ. 1 а. линейный б. / −3 = −23;. / = / — 1 + 6, 2 а. квадратичный б. / −3 = 4;.
[PDF] Вторичная математика 3 модуль 3 полиномиальные функции 3.2 ответы
rayvoltbike.tw › geektic › файлы › rumizoxazewelir
Вторичная математика 3 модуль 3 полиномиальные функции 3.2 ответы … Отсюда уравнение x2 Ã 6 5x = 0 имеет решения x = 2 и x = 3. таким же образом …
вторичная математика 2 модуль 3 ключ ответа 36 — Ristorante Liberty Sassari
ristoranteliberty.
it › вторичная-математика-2-модуль-3-ан…
Результаты 1 — 16 из 25 · Обзор теста модуля 3 ( Ответы) ВТОРИЧНАЯ МАТЕМАТИКА II // МОДУЛЬ 3 … 3 ключ ответа, ВТОРИЧНАЯ МАТЕМАТИКА 11 // МОДУЛЬ 1 КВАДРАТИЧНЫЕ ФУНКЦИИ — 1.
Вторичная математика 2 модуль 3 ключ ответа 36
visiteguidatepertutti.it › second-math- 2-module-3…
Secondary math 3 module 6 4 ключ ответа Math Case Study #2 5 Другой полезный… 3: учебный план и инструкции (математика) 64 рабочий лист 2 задание b ответы на …
Secondary math 3 module 8.5 ключ ответа
visiteguidatepertutti.it ›secondary-math-3-module-8…
Загрузите документ с ключом ответа Secondary math 1 module 3. 5 клавиша ответа Устройство работает БОЛЬШЕ. 5 ключ ответа Hier sollte eine Beschreibung angezeigt werden, …
География сообщества: ГИС в действии : Руководство для учителя
books.google.de › books
См. ключ ответа к модулю 3 для выбранных ответов оценивания .
Средняя школа: выделяет навыки, соответствующие 5–8 классам. Средняя школа …
Образовательные ресурсы
books.google.de › books
Дескрипторы — ключи ответов , учебные пособия , * Математика для начальной школы … Идентификаторы математики для средней школы — Оклахома Этот модуль был …
Ähnliche 0suchanfragen
ВТОРИЧНАЯ МАТЕМАТИКА 3, МОДУЛЬ 3.3, ключ ответа
ВТОРИЧНАЯ МАТЕМАТИКА 3, МОДУЛЬ 3.9, ключ ответа
Вспомогательная математика 3, МОДУЛЬ 3, полиномиальные функции 3.6, ключ ответа
ВТОРИЧНАЯ МАТЕМАТИКА 3, МОДУЛЬ 3.10, ключ ответа
Второй модуль математики 3, ключ ответа
Второй модуль математики 2, ключ ответа
Второй модуль математики 3, ключ ответа 3.4
Второй курс математики 2, модуль 3 3.11, ключ ответа
-5-answer-key — Googlesuche
AlleBilderVideosShoppingMapsNewsBücher
suchoptionen
[PDF] ОБЗОР РУКОВОДСТВА — формы линейных уравнений
ПРИМЕР КЛЮЧА.
(Урок 6,3). Напишите уравнение в стандартной форме для строки, содержащей (-3, 4) и (5, 0). м. Найдите наклон по заданным точкам. Яйи 0-4.
[PDF] alg Module 5 Quiz key.pdf
Teachers.dadeschools.net › khankollari › alg Module 5 Quiz key
Линейные функции. Модуль Quiz: B … Является ли каждая из функций линейной функцией? А у = 4х — 7 … МОДУЛЬ. 5 ключ. fCD f121 f131,714 щуповые подъемники 4 щуп fi3.
[PDF] Модуль 5 Количественное мышление Модуль 6 Формы линейных …
www.haslett.k12.mi.us › cms › lib › Centricity › Домен
Алгебра Раздел 3: Линейные функции, уравнения и неравенства. Модуль 5 … 6 Обзор учебного пособия/Готовы к работе?/Готовность к оценке… Викторина Модуль 5.
Модуль 5 Готовность к оценке — 5. Линейные функции — Mathleaks
mathleaks.com › … › Отношения и функции
Модуль 5 Оценка готовности — страницы 192 — 5. Линейные функции — Houghton Mifflin Harcourt Algebra 1, 2015 (9780544381896) — Алгебра 1 — Упражнения.
RWM102 Учебное пособие: Раздел 5: Графики линейных уравнений и…
Learn.saylor.org › mod › book › view
RWM102 Учебное пособие… Для ознакомления см. Решения уравнений в упорядоченных парах. … При построении графика линейного уравнения ключевым моментом, на который следует обратить внимание, является наклон.
МОДУЛЬ 5 Учебное пособие пересмотренное. )ФОРМА ПЕРЕХОДА НА СКЛОНЕ5)ФОРМА ТОЧНОГО НАКЛОН6)СТАНДАРТНАЯ ФОРМА7)Y ПЕРЕХВАТ 8)ЕДИНИЦА …
Модуль 5: Написание карточек с линейными функциями — Quizlet
quizlet.com › module-5-writing-linear-functions-flas…
Изучайте с помощью Quizlet и запоминайте карточки, содержащие такие термины, как таблица является линейной?, Уловка: как защититься от отрицательных значений, когда …
7 1 учебное пособие и графическое изображение экспоненциальных функций
verdellispilamberto.it › 7-1-изучение-руководство-и-вмешательство..
7-6 Практика экспоненциальных функций, ключ ответа.