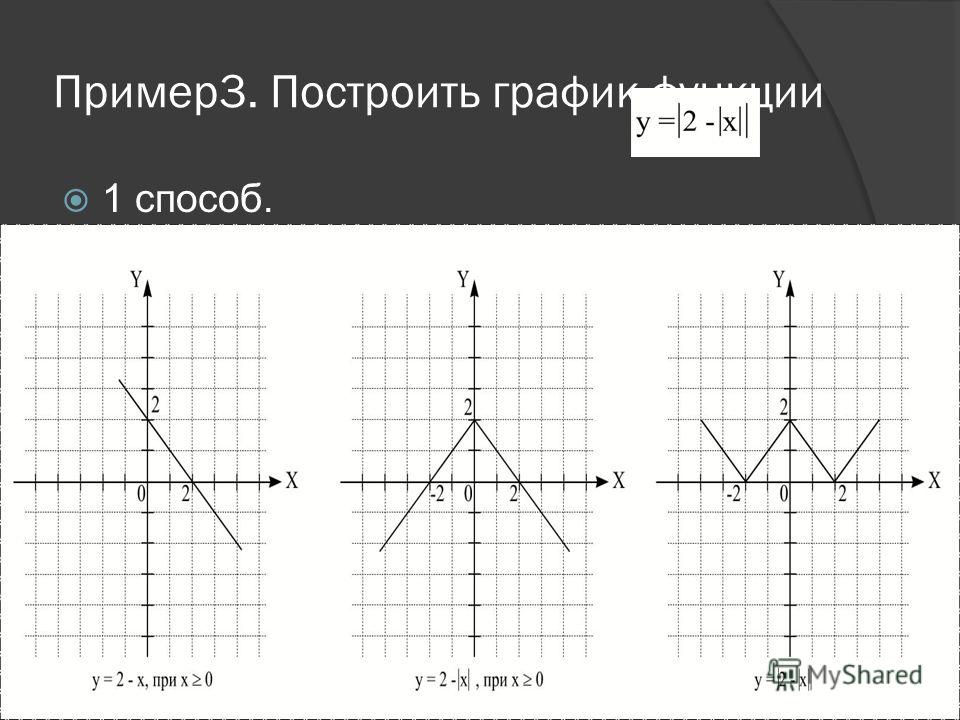
Преобразование графиков функций — подготовка к ЕГЭ по Математике
Анна Малкова
В этой статье мы расскажем об основных преобразованиях графиков функций. Что нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали. Как задать растяжение графика по горизонтали или вертикали. Как отразить график относительно оси Х или Y.
Очень жаль, что эта тема — полезная и очень интересная — выпадает из школьной программы. На нее постоянно не хватает времени. Из-за этого многим старшеклассникам не даются задачи с параметрами — которые на самом деле похожи на конструктор, где вы собираете решение из знакомых элементов. Хотя бы для того, чтобы решать задачи с параметрами, стоит научиться строить графики функций.
Но конечно, не только для того, чтобы сдать ЕГЭ. Первая лекция на первом курсе технического или экономического вуза посвящена функциям и графикам. Первые зачеты в курсе матанализа связаны с функциями и графиками.
Начнем со сдвигов графиков по Х и по Y.
1. Сдвиг по горизонтали.
Пусть функция задана формулой и Тогда график функции сдвинут относительно исходной на а вправо. График функции сдвинут относительно исходной на а влево.
2. Сдвиг по вертикали.
Пусть функция задана формулой и С — некоторое положительное число. Тогда график функции сдвинут относительно исходного на С вверх. График функции сдвинут относительно исходного на С вниз.
Теперь растяжение графика. Или сжатие.
3. Растяжение (сжатие) по горизонтали.
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в k раз по горизонтали, если , и сжат относительно исходного в k раз по горизонтали, если
4. Растяжение (сжатие) по вертикали.
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в М раз по вертикали, если , и сжат относительно исходного в М раз по вертикали, если
И отражение по горизонтали.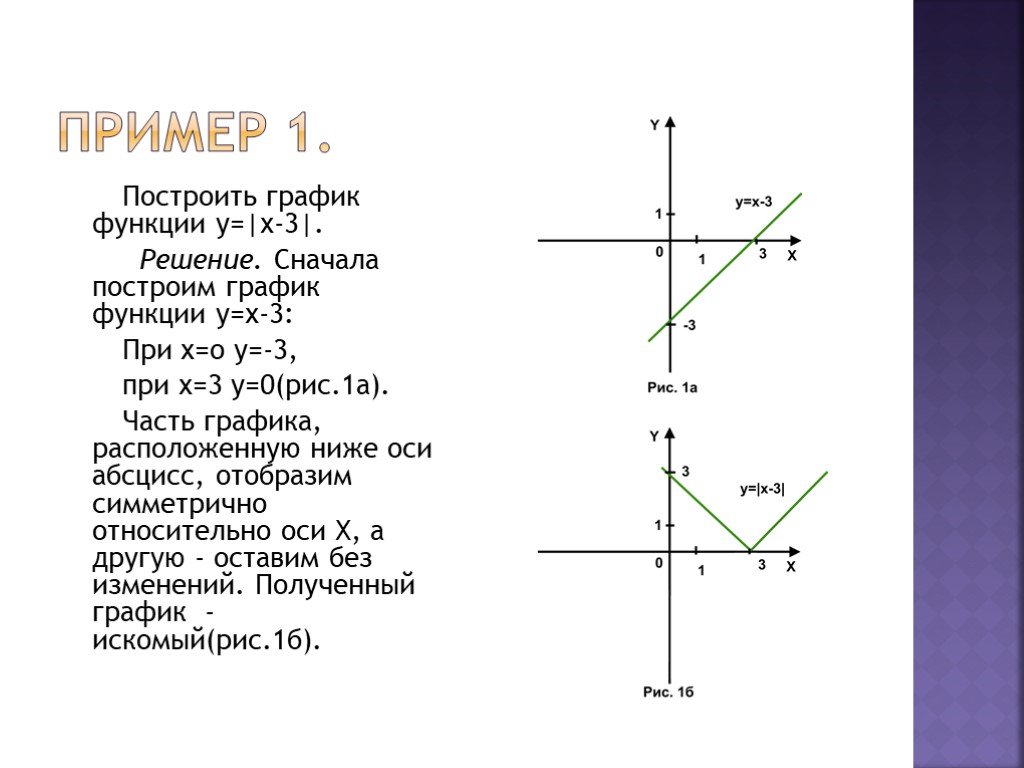
5. Отражение по горизонтали.
График функции симметричен графику функции относительно оси Y.
6. Отражение по вертикали.
График функции симметричен графику функции относительно оси Х.
Друзья, не возникло ли у вас ощущения, что вы все это где-то видели? Да, наверняка видели, если когда-либо редактировали изображения в графическом редакторе на компьютере. Изображение можно сдвинуть (по горизонтали или вертикали). Растянуть (по горизонтали или вертикали). Отразить. И все это мы делаем с графиками функций.
И еще два интересных преобразования. Здесь в формулах присутствует знак модуля. Если не помните, что такое модуль, — срочно повторите эту тему.
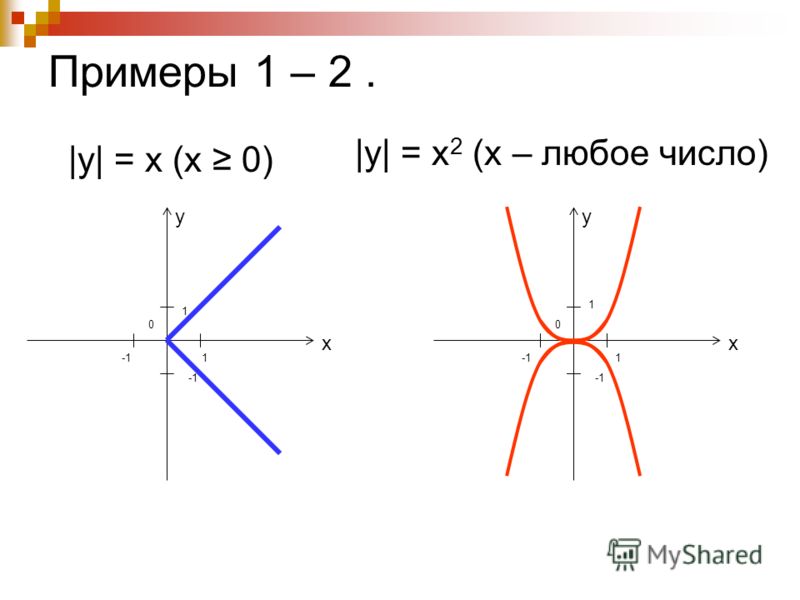
7. Графики функций и
На рисунке изображен график функции Она специально взята такая — несимметричная относительно нуля.
Построим график функции
Конечно же, мы пользуемся определением модуля.
Это мы и видим на графике.
Для неотрицательных значений х график остался таким же, как был. А вместо каждого отрицательного х мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси Х, заменилась на зеркально отраженную правую часть графика.
Теперь график функции Вы уже догадались, что будет. Вся часть графика, лежащая ниже оси Х, зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси Х, остается на месте.
Как определить по формуле функции, будет график преобразован по горизонтали (по Х) или по вертикали (по Y)? Разница очевидна. Если сначала мы что-либо делаем с аргументом х (прибавляем к нему какое-либо число, умножаем на какое-либо число или берем модуль) — преобразование по Х. Если сначала мы нашли функцию, а затем уже к значению функции что-то прибавили, или на какое-нибудь число умножили, или взяли модуль, — преобразование по Y.
Вот самые простые задачи на преобразование графиков.
1.
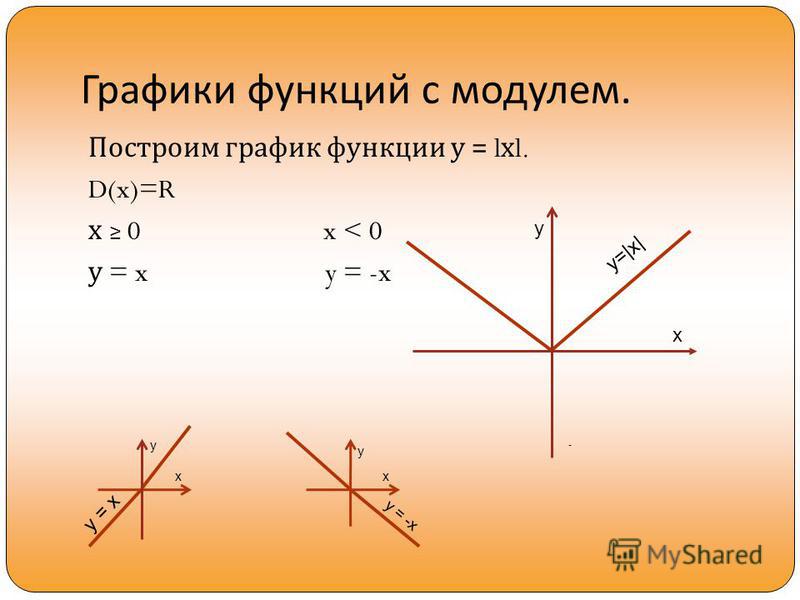Построим график функции
Это квадратичная парабола, сдвинутая на 3 влево по x и на 1 вниз по y.
Вершина в точке
2. Построим график функции
Выделим полный квадрат в формуле.
График — квадратичная парабола, сдвинутая на 2 вправо по x и на 5 вниз по y.
Обратите внимание: график функции пересекает ось y в точке На нашем графике это точка
Продолжение — в статье «Построение графиков функций».
Определение, графики, свойства, примеры решений
Функция модуля
Функция модуля определяется как вещественная функция $f : R \rightarrow R$ , y = |x| для каждого $x \in R$
Для каждого неотрицательного значения x, f(x) равно x. Но для отрицательных значений x значение f(x) равно отрицательному значению x
$f(x) = |x|= \begin{cases}
х & \текст{ если } х \geq 0 \\
-x & \text{ если } x < 0
\end{cases} $
Также называется функцией абсолютного значения
Пример
|-3| =3
|-2|=2
|2|=2
Мы знаем, что все действительные числа можно изобразить на прямой.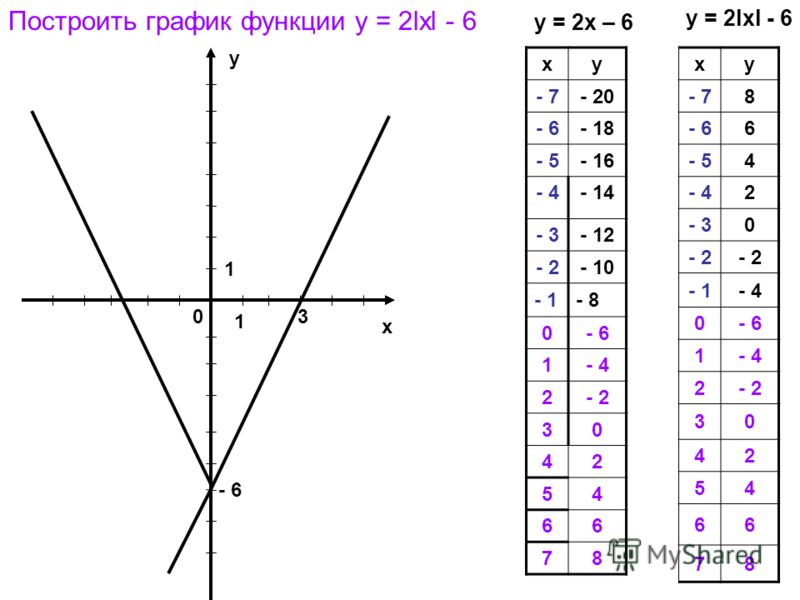
Функция абсолютного значения используется для измерения расстояния между двумя числами на числовой прямой. Таким образом, расстояние между x и 0 равно |x — 0| = |х|. Итак, |х| представляют расстояние числа от начала координат. Точно так же расстояние между x и y равно |x — y|. Таким образом, расстояние от -3 до -1 равно |-3 — (-1)| = |-3 + 1| = |2| = 2, а расстояние от -3 до 5 равно |-3 — 5| = |-8| = 8 9+ ={x \in R : x \geq 0}$
График функции модуля
График функции модуля показан ниже. Он совпадает с графиком функции тождества $y=x$ при $x \geq 0$ и при x< 0 является графиком линейной функции $y=-x$
Здесь при x=0 график имеет вид поворот вверх. Таким образом, x=0 является поворотной точкой на этом графике.
Свойства функции модуля
Функция модуля имеет следующие свойства:
1. Для любого действительного числа x мы имеем 92 \Leftrightarrow a < |x| < b \Leftrightarrow x \in (-b,-a) \cup (a,b)$
4.
если a отрицательно
a. |х| \geq a , x \in
реалов b. |х| \leq a , x =\phi$
3. Для действительных чисел x и y
a. |ху|=|х||у|
б. $ |\фракция {х}{у}| =\frac {|x|}{|y|} ,y \neq 0$
c. $|х +у | \leq |х| + |y|$
$|x -y| \leq |х| + |у| $
d. $|х + у | \geq |x| — |y|$
$|x -y| \geq |x| — |у| $
за $x,y \geq 0 \; а также \; |х| \geq |y| у или \; х, у < 0 \; а также \; |х| \geq |y| , |х-у| =|х| - |у|$
Решенные примеры модульных функций (функция абсолютного значения)
1. Найдите домен и диапазон функции ниже?
а. $y =|1-x|$
б. $y = 2 -|1-x|$
c. $y= \frac {2}{\sqrt {x -|x|}} $
Решение
а. $y =|1-x|$
Ясно, что это определено для $x \in R$. Итак, домен R
Теперь $|1 -x| \geq 0 $ для всех $x \in R$
Таким образом, диапазон равен $[0,\infty )$
b. $y = 2 -|1-x|$
Ясно, что это определено для $x \in R$.
Итак, домен R
Теперь $|1-x| \geq 0$ для всех $x \in R$
или
$-|1-x| \leq 0$
$2- |1-x| \leq 2$ для всех $x \in R$
Таким образом, диапазон равен $(-\infty,2]$
c.$y= \frac {2}{\sqrt {x -|x|}} $
Теперь
$x -|x|=\begin{case}
x-x=0 & \text{ если } x \geq 0 \\
x+x=2x & \text{ если } x \leq 0
\end{cases}$
Следовательно, $\frac {2}{\sqrt {x -|x|}}$ не определено для всех $x \in R$
Таким образом, область определения функции $\phi$
2. Нарисуйте график приведенной ниже функции?
а. у=х + |х|
б. у = х — | х |
в. у =|х-1|
Решение
Нам нужно преобразовать эту функцию в простую форму, прежде чем рисовать график
a. у=х + |х|
Это можно записать как
$y= x +|x| = \begin{случаи}
x+x=2x & \text{ если } x \geq 0 \\
x-x=0 & \text{ если } x < 0
\end{cases}$
Итак, это линейная функция y =2x для $x \geq 0$ и линейная функция y =0 для $x < 0$
Итак, график будет
b.
y = x -|x |
Это можно записать как
$y= x -|x| = \begin{случаи}
x-x=0 & \text{ если } x \geq 0 \\
х+х=2х & \текст{ если } х < 0
\end{case}$
Итак, график будет
c.y =|x-1|
Это можно записать как
$y= |x -1| = \begin{случаи} x-1 & \text{ если } x \geq 1 \\ 1 -x & \text{ если } x < 1 \end{cases}$
Итак, это линейная функция y =x-1 для $x \geq 1$ и линейная функция y =1-x для $x < 1$
Итак, график будет
Важно обратите внимание здесь. Поворотная точка графика x=1 здесь
Время опроса для функции абсолютного значения
Вопрос 1.Функция y =|x -5|. какое из следующих утверждений неверно
A.y(0)=5
B. y(-5)=0
C. y(-1)=6
D. y(10)=5
Вопрос 2.
Найдите диапазон функции $ y= \frac {|x -5|}{x-5} $
A. range={1}
B. range=R
C.range={-1,1}
D. range=$[0,\infty )$
Вопрос 3.
Найдите область определения функции, заданной в предыдущем вопросе 9-$
D. Ни один из этих
Вопрос 6.
Область определения и область значений функции f, определяемые формулой f (x) = 11 – |x −5| равно
A. Домен = R, Диапазон = R
B. Домен = R, Диапазон = $(-\infty, 11]$
C. Домен = R, Диапазон = R -{11}
D. Домен = R – {11}, диапазон =
р.
Читайте также
- Примечания
- Декартово произведение
- Что такое отношения
- Что такое функция
- Домен функции
- Диапазон функций
- Функция идентификации
- Постоянная функция
- Линейная функция
- Модули Функция
- Функция наибольшего целого числа
- Полиномиальная функция
- Алгебра действительных функций
- Задания
- Отношения и функции Класс 11 Рабочий лист
- NCERT Solutions Relationship and Functions class 11 Упражнение 2.
1 - NCERT Solutions Relationship and Functions class 11 Упражнение 2.2
- NCERT Solutions Relationship and Functions class 11 Упражнение 2.3
1Все математические функции, определенные в модуле Math в Python 3
Узнайте обо всех математических функциях, доступных в Python, и о том, как вы можете использовать их в своей программе.
Что такое математический модуль в Python?
Модуль math является стандартным модулем в Python и всегда доступен. Чтобы использовать математические функции в этом модуле, вы должны импортировать модуль, используя импорт математики .
Предоставляет доступ к базовым функциям библиотеки C. Например,
# Вычисление квадратного корня импортировать математику math.sqrt(4)
Этот модуль не поддерживает сложные типы данных . Модуль cmath является сложным аналогом.
Функции в математическом модуле Python
Вот список всех функций и атрибутов, определенных в математическом модуле , с кратким объяснением того, что они делают.
| Функция | Описание |
|---|---|
| потолок(х) | Возвращает наименьшее целое число, большее или равное x. |
| копия(х, у) | Возвращает x со знаком y |
| заводы(х) | Возвращает абсолютное значение x |
| факториал(х) | Возвращает факториал x |
| этаж(х) | Возвращает наибольшее целое число, меньшее или равное x |
| fмод(х, у) | Возвращает остаток от деления x на y |
| фрвып(х) | Возвращает мантиссу и показатель степени x в виде пары (m, e) |
| fsum(итерируемый) | Возвращает точную сумму значений с плавающей запятой в итерируемом |
| конечно(х) | Возвращает True, если x не является ни бесконечностью, ни NaN (не числом) |
| инф(х) | Возвращает True, если x является положительной или отрицательной бесконечностью |
| иснан(х) | Возвращает True, если x является NaN |
| лдэксп(х, я) | Возвращает x * (2**i) |
| модф(х) | Возвращает дробную и целую части x |
| ствол(х) | Возвращает усеченное целое значение x |
| ехр(х) | Возвращает e**x |
| expm1(x) | Возвращает е**х — 1 |
| лог(х[ б]) | Возвращает логарифм x по основанию b (по умолчанию e) |
| log1p(x) | Возвращает натуральный логарифм 1+x |
| log2(x) | Возвращает логарифм по основанию 2 x |
| log10(x) | Возвращает логарифм x 9 по основанию 10. |
| пау(х, у) | Возвращает x в степени y |
| кв.(х) | Возвращает квадратный корень из x | .
| акос(х) | Возвращает арккосинус x |
| асин(х) | Возвращает арксинус x |
| атан(х) | Возвращает арктангенс x |
| атан2(у, х) | Возвращает атан(у/х) |
| кос(х) | Возвращает косинус x |
| гипот(х, у) | Возвращает евклидову норму, sqrt(x*x + y*y) |
| грех(х) | Возвращает синус x |
| желто-коричневый(х) | Возвращает тангенс x |
| градусов(х) | Преобразует угол x из радианов в градусы |
| радиан(х) | Преобразует угол x из градусов в радианы |
| акош(х) | Возвращает аркгиперболический косинус x |
| асинх(х) | Возвращает аркгиперболический синус x |
| атан(х) | Возвращает аркгиперболический тангенс x |
| ш(х) | Возвращает гиперболический косинус x |
| ш(х) | Возвращает гиперболический косинус x |
| тан(х) | Возвращает гиперболический тангенс x |
| эфф(х) | Возвращает функцию ошибки на x |
| erfc(х) | Возвращает дополнительную функцию ошибки в x |
| гамма(х) | Возвращает функцию гаммы на x |
| лгамма(х) | Возвращает натуральный логарифм абсолютного значения гамма-функции при x | .
